What is the meaning of (statistical) life? Benefit–cost analysis in the time of COVID-19

Abstract

Efforts to support public policy decisions need to be conducted carefully and thoughtfully. Recent efforts to estimate the social benefits of reductions in mortality risks associated with COVID-19 interventions are likely understated. There are large uncertainties over how much larger the social benefits could be. This raises questions about how helpful conventional approaches to valuing mortality and morbidity risks for benefit–cost analyses can be in contexts such as the current crisis.

I. Introduction

Are the economic costs of policy interventions to limit the spread of COVID-19 worth the potential health benefits? How long should social distancing and shelter-in-place rules be in place for? These are the multi-trillion dollar questions that economists, public health experts, politicians, and your neighbour are currently debating.

But how do we answer these questions? When considering any policy intervention, it is important to get a sense of the costs and benefits of different courses of action. In many settings, including the COVID-19 pandemic, this is particularly challenging. While many of the costs, such as forgone income and production, are easily measured in your currency of choice, measuring the benefits is a lot harder.¹

In a recent interview the Governor for New York, Andrew Cuomo declared ‘you cannot put a value on a human life.’ (Cuomo, 2020). He is correct. Researchers instead estimate what is known as the value of a statistical life (VSL) (Drèze,1962; Schelling, 1968; Jones-Lee, 1974; Viscusi, 1992; Viscusi and Aldy, 2003; Banzhaf, 2014).

VSL estimates do not measure the value of life. The VSL represents aggregate demand for wide-spread, but individually very small, reductions in mortality risk, i.e. how much individuals are willing to pay for a very small reduction in the probability of death, paid for by forgoing the consumption of other goods and services. For example, if a policy reduced the risk of death by 0.00001 per person, 1 in 100,000, then it would take 100,000 people to accumulate a collective risk reduction of one ‘statistical life’. If, on average, each individual is willing to pay $100 per year to reduce the probability of dying by 0.00001, then collectively the group would be willing-to-pay $10m per year to prevent the loss of one ‘statistical life’. This is the value of a statistical life. If the policy applied to a large fraction of the country’s population, say 100m people (a thousand times as many), then the expected total number of lives saved would be 1,000 ‘statistical lives’, with a collective willingness to pay of $10 billion.

VSL estimates play a very large role in determining benefit–cost assessments for many government policies in the areas of health, transportation, and the environment. In a recent review of 115 major federal regulations in the United States, 70 per cent of the total benefits were directly attributable to the monetized value of reducing early mortality (OMB, 2014).

A considerable amount of work and effort goes into credibly estimating the value of a statistical life and there are a number of challenging issues that researchers need to account for when estimating and interpreting VSL estimates (see Viscusi and Aldy (2003) and Viscusi (2018) for an overview of estimates from the literature and Ashenfelter (2006), Cameron (2010), and Viscusi (2011) for a discussion of the empirical and conceptual issues). A broader issue is how any given VSL estimate is used in benefit–cost analysis. Almost all benefit–cost analyses apply VSL estimates to new populations. As such, it is important that VSL estimates are chosen carefully, and that the assumptions that give VSL estimates a meaningful interpretation are plausible, when applied to new contexts. These considerations are of particular importance in the context of COVID-19.

The COVID-19 crisis has prompted a slew of benefit–cost analyses using VSL estimates. This article calls for introspection. I argue that recent efforts have, in many cases, lacked clarity on some of these issues and may consequently have underestimated the social benefits of policy interventions to mitigate the spread of COVID-19. Ultimately, more questions are raised than answered. However, one conclusion is clear: when benefit–cost analysis is implemented, we need to ensure that it is implemented carefully and thoughtfully to most effectively serve and support public policy decisions.

II. Large vs small reductions in risk

VSL estimates are only valid when based on very small (marginal) changes in risk. When there are large changes in risk, VSL estimates may be too small. An important consideration in the face of large changes in risk is the distinction between willingness to pay (WTP) for a reduction in risk and willingness to accept (WTA) compensation to forgo reductions in mortality risk. When risks are small these distinctions don’t matter, as WTP ≈ WTA. However, when considering larger reductions in risk, an individual’s WTA compensation to forgo a reduction in mortality risk will be larger than their WTP for the same reduction in mortality risk, WTA > WTP.²

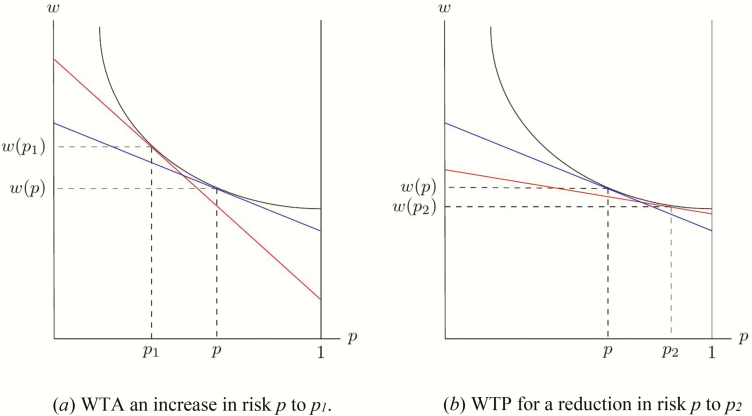
Consider the following example. Figure 1 shows an individual’s willingness to accept (a) and willingness to pay (b) for a large increase/decrease in risk. Moving from p to p₁, which reduces survival probabilities, we observe that the individual would need an increase in income, moving from w(p) to w(p₁). By contrast, reducing risk by the same amount, from p to p₂, we observe that the individual would be willing to reduce their income, moving from w(p) to w(p₂). The willingness to accept the large increase in risk, w(p₁)–w(p), is much larger than the willingness to pay for a reduction in risk of the same magnitude, w(p)–w(p₂). There are two additional insights that can be drawn from Figure 1. First, the VSL (represented by the red and blue lines, which captures the marginal rate of substitution between income and mortality risk, –dw(p)/dp) will be higher for people with higher baseline risk, represented by the steeper gradient. Second, in response to large changes in risk, the VSL based on willingness to accept/pay (represented by the red lines in Figure 1) will be larger/smaller than the VSL for small changes in risk (the blue line).

Figure 1:

WTA vs WTP for large changes in risk

Whether willingness to pay or willingness to accept is the more appropriate measure relates to property rights. WTP is appropriate when the individual does not have property rights—we want to know what the individual would pay for something to which they currently have no legal right. WTA is appropriate when the individual does have property rights—we are compensating the individual for the loss of something to which they do have a legal right. The right to life is conventionally regarded as the primary natural or human right (Garnsey, 2007). As such, when considering large reductions in mortality risk, WTA is arguably the more appropriate measure.

The COVID-19 pandemic reflects a context in which increases in mortality risk are large, at least for some groups of the population. VSL estimates are most often derived from hedonic wage models—a revealed preference approach. Researchers estimate the additional wages paid to workers in riskier jobs, capturing the compensating wage differentials associated with greater mortality risk. As such, VSL estimates are usually derived from contexts in which changes in risk and wages are relatively small. The wage–risk trade-offs upon which we base benefit–cost analyses for typically sized risk-reductions cannot confidently be extrapolated to the risks presented by COVID-19. In technical terms, the magnitude of the mortality risks avoided by social distancing and shelter-in-place policies is outside the domain of the risk reductions that have been used to estimate the VSL. Use of VSL estimates derived from very small changes in mortality risk could substantially underestimate the social benefits of policy interventions that seek to reduce risk of exposure. Any benefit–cost analysis of interventions that induce non-marginal reductions in mortality risk should be explicit about this issue.

III. Assumption: everyone is a middle-aged, male, blue-collar worker . . .

It is very easy, and tempting, to apply VSL estimates to new settings. Policy-makers crave a single number that they can employ in any context, and it would indeed be much easier if we could be confident that there was just one number that was always the right number to use when measuring the social benefits of risk reduction. However, the value of a statistical life is not a universal constant.

Willingness to pay for changes in mortality risk will be different for different people. Such differences may arise for a number of reasons, including: differences in how informed individuals are about risk reductions; differences in life expectancy; differences in risk aversion; differences in cultural or theological beliefs (e.g. some groups may believe in fatalism, the belief that fate governs major life outcomes, or theological determinism, the belief that all events are pre-ordained); differences in income. In practice, VSL estimates reflect the risk preferences of middle-aged, male, blue-collar workers. There is less credible evidence about the risk preferences of people that are not in this demographic, including the elderly, those with pre-existing health conditions that prevent them from working, carers, students, and children below working age. In the context of COVID-19, the people who face the greatest risks (the elderly, those with pre-existing conditions, and service workers) are not well represented in the populations that inform existing VSL estimates.

Willingness to pay for risk reductions depends on the nature of the risk in question. The context for many VSL estimates is sudden deaths due to industrial accidents. The type of risk presented by COVID-19 does not match the profile of risk used to support existing VSL estimates. COVID-19 presents unfamiliar and poorly understood risks that can involve weeks of severe illness, hospitalization, ventilators, and isolation from family and friends, before a lonely death among strangers. When a victim recovers, we do not yet know the extent of recovery, whether the disease will recur, or whether there are any long-term compromises to health. Cameron and DeShazo (2013) present suggestive evidence that willingness to pay is smaller when considering the risk of sudden death compared to the risk of death following illness.

IV. Should we use age-specific VSLs?

One of the most controversial issues associated with the use of VSL in benefit–cost analysis is whether VSL estimates should be differentiated by age. The controversy emerges because individuals think it unfair to value the lives of some people more than others. But this is not what the VSL represents. It represents individual willingness to pay for reductions in mortality risk. That said, the relationship between age and willingness to pay is theoretically ambiguous and the empirical evidence is mixed (Hammitt, 2007; Krupnick, 2007; Aldy and Viscusi, 2007). One might expect willingness to pay for an extension of life to fall as remaining life expectancy falls, but economic resources and exposure to risk also change over the life cycle and so willingness to pay could increase or remain constant as age increases. However, existing VSL estimates treat every risk reduction in the same way. There is no distinction between reducing the risk of someone who is likely to die in the next few years or reducing the risk of someone who is younger with dependants.

One strategy for constructing age-specific VSL estimates is to convert a given VSL estimate into the value of a statistical life year (VSLY). This is calculated using the following equation,

$${\displaystyle \begin{array}{l}{\displaystyle VSLY=\frac{rVSL}{1-{(1+r)}^{-L_{{\displaystyle \overline{a}}}}}}\end{array}}$$

where $L_{\overline{a}}$ represents the average number of remaining life years for the average person in the sample and r represents the real discount rate, commonly, but arbitrarily, assumed to be 3 per cent. If the average VSL estimate in a sample was $10.9m ($2020) and the average individual had 41 expected remaining life years, we would calculate the value of a statistical life year to be $465,565.25 ($2020). Age-specific VSL estimates can then be calculated for different ages, using the following equation,

$${\displaystyle \begin{array}{l}{\displaystyle VS{L}_a={\displaystyle \stackrel{L}{{\displaystyle {\displaystyle \sum ^{}}_{t=\mathrm{\ell }}}}}\frac{VSLY}{{(1+r)}^t}}\end{array}}$$

where t is the current expected life-years remaining in each age group and r is the real discount rate. For example, if 20-year-olds had 60 expected life-years remaining, $VS{L}_{20}$ would be $12.884m. If 80-year-olds had 8 expected life-years remaining, $VS{L}_{80}$ would be $3.268m.

There are a number of issues with this approach. First, this approach doesn’t reflect underlying heterogeneity in willingness to pay by age—it is based solely on differences in average life expectancy. It completely ignores the complexity of the underlying relationship between willingness to pay for a risk reduction and age. As discussed, one theoretical basis for using declining age-profile is that consumption and income decline with age, but one should model this explicitly for the population under study. Murphy and Topel (2006) provide a framework for this that can be used to construct population-specific age-adjusted VSL estimates. However, neither approach accounts for how willingness to pay varies with baseline risk. An individual facing a high probability of death has little incentive to limit their spending on risk reductions as the probability of survival is low. As such, age-specific VSL estimates may understate the willingness to pay for risk reductions. The net effect of these competing forces is unclear.

In the context of COVID-19 the benefits of social distancing are likely to accrue to older populations and so it is reasonable that VSL estimates reflect that. However, whether a declining age-profile is appropriate is unclear. Even if a declining age-profile is justified in normal circumstances, it is unclear whether it is appropriate if exposure to risk increases with age. The current situation is one in which increases in mortality risk are quite large for older populations. As discussed above, this would imply that willingness to pay based on marginal changes in risk is likely understated. If so, the true age-profile for the VSL in the context of COVID-19 could be flat, or even increasing with age if WTP/WTA was high enough. It seems likely that VSLY-derived estimates with a declining age-profile represent a lower bound on the social benefits associated with COVID-19 interventions.

V. Decision-making when lives are identifiable

As is hopefully clear, the use of VSL estimates is only applicable in settings where interventions consider a probabilistic loss of life—statistical lives. Using the value of a statistical life to aid decision-making is completely inappropriate when the lives at risk are identified. Identifiable lives reflect specific people who need help now, for example, individuals who are in need of rescuing.

When considering whether to save the life of a given individual, society’s choice cannot be based on the individual’s willingness to pay. Their willingness to pay doesn’t come into it. The tools of constrained optimization that economists use, and that provide the foundations of benefit–cost analysis, are not appropriate in these circumstances because the identified individual is unable to make a trade-off. Sadly, the COVID-19 pandemic is likely to put decision-makers in a position in which they have to make choices about identifiable lives. Society’s choice as to whether to give an ICU bed to one patient or another has nothing to do with the patients’ willingness to pay or the willingness to pay of their families. The choice has to be made on some other basis.

VI. The social value of life

The value of a statistical life is an analytical tool used in benefit–cost analysis, but its scope is limited. The VSL reflects private willingness to pay for a very small reduction in mortality risk. It does not capture the value of a person’s life to the rest of society. As such, the total benefits of interventions to reduce mortality risk will be understated as the social benefits are not accounted for. This is not a critique of VSL. VSL does not claim to measure such considerations. However, it is important to acknowledge that as an analytical tool the VSL does not provide a complete representation of the total benefits associated with reductions in mortality risk. This is true in any context, including the COVID-19 pandemic.

Henry Moseley was a physicist at Oxford in the early twentieth century, who died during the First World War in August 1915 at the age of 27. His contributions to physics prior to his death were monumental. The social cost of his death in terms of the further contributions he could have made is immeasurable. The social benefit to society associated with the fact that Isaac Newton did not die during the bubonic plague, or that C. S. Lewis and J. R. R. Tolkien did not lose their lives during the First World War, is equally immeasurable. Yet, we are cognizant of their existence. What of the scientists, artists, and innovators who lost their lives before new ideas were even conceived? We are not aware of these forgone benefits, but we are nevertheless worse off because they do not exist.

Society also bears the cost of grief and loss of companionship that is experienced by the family and friends of the deceased (Posner and Sunstein, 2015; Beckerman, 2019). As in the case of identifiable lives, it is not possible to credibly assign a monetary value to such considerations.

Measuring the value of a statistical life in a credible way is hard. Measuring the social costs of the loss of life in a credible way is arguably impossible. Inevitably, this means that such considerations are not included in benefit–cost analyses. However, not including something doesn’t mean that we shouldn’t acknowledge its existence. The social cost can be acknowledged, even if it is to state that the social benefits of intervention are understated due to our inability to measure the social costs associated with loss of life. Just because something can’t be measured, doesn’t mean that it has no value.

VII. Conclusion

The value of a statistical life (VSL) can be a very useful tool when used appropriately. However, it is often misunderstood and used inappropriately. In the context of COVID-19 there are three main issues. First, the mortality risks presented by COVID-19 are larger than the risks that typically underpin VSL estimates. When there are large changes in mortality risk, existing VSL estimates likely underestimate the social benefits of risk reductions. Second, the type of risk presented by COVID-19 does not match the profile of risks that underpin existing VSL estimates. Third, the populations at risk from COVID-19 do not match the populations used to support existing VSL estimates. Researchers should be clear to highlight differences and be explicit about the possible implications.

Ultimately, it is incredibly challenging to determine a credible and relevant measure of VSL that is appropriate for benefit–cost analysis in the time of COVID-19. This isn’t a problem with VSL per se. I argue that existing estimates likely represent a lower bound on the social benefits of reductions in mortality risk; however, there are large uncertainties over how much larger the social benefits could be. This raises questions about how helpful conventional benefit–cost analyses can be in the current crisis.

I thank David Bradford, Trudy Cameron, Andres Clarens, Scott Doney, Leora Friedberg, Cameron Hepburn, Michael Livermore, Jacquelyn Pless, Jay Shimshack, Bill Shobe, Alex Teytelboym, and Kip Viscusi for helpful comments and suggestions.