Modulation of finger muscle activation patterns across postures is coordinated across all muscle groups

Abstract

Successful grasp requires that grip forces be properly directed between the fingertips and the held object. Changes in digit posture significantly affect the mapping between muscle force and fingertip force. Joint torques must subsequently be altered to maintain the desired force direction at the fingertips. Our current understanding of the roles of hand muscles in force production remains incomplete, as past studies focused on a limited set of postures or force directions. To thoroughly examine how hand muscles adapt to changing external (force direction) and internal (posture) conditions, activation patterns of six index finger muscles were examined with intramuscular electrodes in 10 healthy subjects. Participants produced submaximal isometric forces in each of six orthogonal directions at nine different finger postures. Across force directions, participants significantly altered activation patterns to accommodate postural changes in the interphalangeal joint angles but not changes in the metacarpophalangeal joint angles. Modulation of activation levels of the extrinsic hand muscles, particularly the extensors, were as great as those of intrinsic muscles, suggesting that both extrinsic and intrinsic muscles were involved in creating the desired forces. Despite considerable between-subject variation in the absolute activation patterns, principal component analysis revealed that participants used similar strategies to accommodate the postural changes. The changes in muscle coordination also helped increase joint impedance in order to stabilize the end-point force direction. This effect counteracts the increased signal-dependent motor noise that arises with greater magnitude of muscle activation as interphalangeal joint flexion is increased. These results highlight the role of the extrinsic muscles in controlling fingertip force direction across finger postures.

NEW & NOTEWORTHY We examined how hand muscles adapt to changing external (force direction) and internal (posture) conditions. Muscle activations, particularly of the extrinsic extensors, were significantly affected by postural changes of the interphalangeal, but not metacarpophalangeal, joints. Joint impedance was modulated so that the effects of the signal-dependent motor noise on the force output were reduced. Comparisons with theoretical solutions showed that the chosen activation patterns occupied a small portion of the possible solution space, minimizing the maximum activation of any one muscle.

INTRODUCTION

The human species is characterized in large measure by the ability to create and manipulate tools. This capacity is made possible by the unparalleled dexterity of the human hand. The unique biomechanical structure of the hand contributes substantially to its fine motor control. For example, all muscles actuating the digits are located proximal to the metacarpophalangeal (MCP) joints. This arrangement reduces mass and inertia of the digits and allows increased range of motion, as the muscles do not restrict movement of adjacent bones as may occur at the elbow. Structures such as anatomical pulleys, guiding the extrinsic finger flexor tendons on the palmar side of the finger, and the extensor apparatus, controlling translation of tendon force to finger force on its dorsal side, help to maintain precise control while enabling the proximal muscle location.

Such a biomechanical arrangement, however, leads to complexity in motor control. All hand muscles actuate multiple degrees of freedom (DOF), and almost all directly affect more than one joint. The extensor apparatus has multiple insertions, while the anatomical pulleys interact with the tendons at multiple sites. The overall structure results in an intricate mapping between muscle activation and digit movement or force production. Extensive neural resources are devoted to controlling the large number of muscles and DOF in the hand, including a substantial portion of the monosynaptic corticomotoneuronal pathway, which is fundamental to fine manual dexterity (Lemon 2008).

To interact with tools and other objects, this neuromechanical system must adapt rapidly to changing conditions. To control an object, the direction and timing of digit tip forces must be precisely applied to the object (Cole et al. 2008; Darling et al. 1994; Flanagan et al. 2006; Johansson et al. 1999; Zhang et al. 2010). These forces must be maintained in the object coordinate frame across finger postures, despite any changes in object orientation with respect to the hand. Although this process is fundamental to human function, it remains incompletely understood.

Maier and Hepp-Reymond (1995) employed intramuscular electrodes to carefully describe muscle activation patterns during precision grip, but the study was limited to a single force direction (palmar) and posture. Valero-Cuevas et al. (1998) examined fingertip force production in multiple directions but at a single posture. Milner and Dhaliwal (2002) evaluated multiple postures but for a limited set of force directions and recorded from a limited set of muscles. Thus, although these studies have greatly contributed to the understanding of finger motor control, fundamental questions remain unanswered, in part because of the difficulty in studying the hand due to the redundancy in control of the system (Valero-Cuevas 2009) and the nonlinearities involved in translating muscle activations into net fingertip force.

In this study, we sought to address a number of these questions. First, we were interested in the extent to which finger posture dictates activation patterns. Joint rotation alters both the moment arm and the length of finger muscles (An et al. 1983; Qiu et al. 2017) as well as the excitability of the motoneurons (Kennedy and Cresswell 2001; Pietrosimone et al. 2008). These changes could help to compensate for the new posture, or they may increase the need to change activation patterns to accommodate a new finger posture in order to maintain the desired fingertip force. Second, different finger joints may have a varying impact on fingertip force production. The metacarpophalangeal (MCP) joints have the largest moment arms and thus the largest effects on musculotendon length (An et al. 1983). The proximal and distal interphalangeal (PIP and DIP, respectively) joints, however, impact the mapping of joint torque to fingertip force (Kamper et al. 2006; Qiu et al. 2017). Third, the different finger muscle groups (the extrinsic flexor muscles, extrinsic extensors, and intrinsics) may play different roles in accommodating postural and force direction changes. Prior studies have concluded, based on their experimental observations, that the intrinsic hand muscles mainly produce forces at the fingertip (Maier and Hepp-Reymond 1995) and/or control their directions across different postures (Milner and Dhaliwal 2002), whereas extrinsic hand muscles are primarily involved in multijoint movement production (Darling et al. 1994; Dennerlein et al. 1998; Schieber 1995) because of their biomechanical arrangement (Nimbarte et al. 2008). However, biomechanical studies also showed that the role of extrinsic finger extensor muscles could be critical in producing fingertip forces because of their unique biomechanics (particularly its contribution to the force production toward proximal direction; Valero-Cuevas et al. 2000). Knowledge in these areas would help efforts to restore fingertip force production after neuromuscular injury, through therapeutic interventions such as electrical stimulation (Kilgore et al. 2008; Zheng and Hu 2019) or the introduction of biomimetic devices (Lee et al. 2018).

To examine these questions, we focused on voluntary control of the index finger in response to alterations in task condition (force direction) or system state (postural changes). Muscle activation was recorded across index finger muscles during isometric force generation; visual feedback of three-dimensional force generation was provided to aid task performance. We hypothesized that changes in posture would result in significant changes in muscle activation patterns across force directions, thus demonstrating the need for active compensation. We further expected that PIP and DIP joint angles would have a greater impact than MCP angle on muscle activation patterns because of their role in the mapping from joint torque to fingertip force. Finally, we anticipated that whereas the intrinsic and extrinsic flexor muscles would primarily drive fingertip force production and thus have the greatest activation levels across directions, as indicated by prior studies (Maier and Hepp-Reymond 1995; Milner and Dhaliwal 2002), the contribution of the extrinsic extensor muscles to force production would be comparable to that of the other muscles, because of the unique biomechanical function of the extensors.

METHODS

Experimental Protocol

Ten subjects (mean age: 38.1 yr, range: 24–50 yr, 9 men, 1 woman) with no known hand impairment participated in this study. The dominant hand (the right hand in 9 cases and the left hand in 1 case) was tested in all subjects. All subjects gave written informed consent to participate in the study, which was conducted at the Rehabilitation Institute of Chicago with an approval by the Institutional Review Board of Northwestern University.

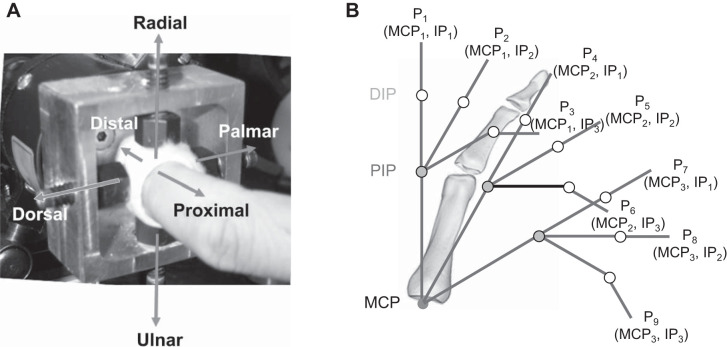
Subjects participated in two experimental sessions, held on two separate days. For both sessions, subjects were asked to produce forces in six specified directions with the index fingertip. The six orthogonal directions were defined with respect to the distal segment of the finger: dorsal/palmar, distal/proximal, radial/ulnar. To measure these forces, the tip of the index finger was affixed to a six-DOF load cell (model 20E12A-I25; JR3, Inc., Woodland, CA) through a set of four set screws embedded into casting material placed around the fingertip (Fig. 1A) (Cruz et al. 2005; Kamper et al. 2006). A post was positioned near the other three fingers to prevent contact with the load cell. The wrist was placed within a fiberglass cast that maintained neutral wrist flexion/extension and ulnar/radial deviation. This cast was subsequently secured to a tabletop with a magnetic clamp to prevent hand displacement (Kamper et al. 2003). Subjects created the six different forces at each of nine different finger postures (P₁–P₉). Namely, three metacarpophalangeal (MCP) angles (0°, 30°, and 60°) were explored at each of three combinations of proximal interphalangeal (PIP) and distal interphalangeal (DIP) joints: {(0°,0°), (30°,0°), (60°,30°)}. These postures spanned a considerable portion of the finger workspace (Fig. 1B).

Fig. 1.

Experimental setup. A: jig used to connect the tip of the index finger to the load cell for recording force data. B: 9 finger postures (P₁–P₉) tested in the experiment. The 6 different force directions are labeled, referenced to the distal finger segment. DIP, distal interphalangeal; IP, interphalangeal; MCP, metacarpophalangeal; PIP, proximal interphalangeal.

The purpose of the first session was to determine the maximum forces that could be generated in each direction at each posture, similar to a previous study (Milner and Dhaliwal 2002). Subjects maintained an isometric maximum force for an average of 3 s during each trial with a 1-min rest between trials. The force data, measured by the load cell, were filtered with a fourth-order low-pass Butterworth filter at 125 Hz and then sampled at 2 kHz.

In the second session, muscle activation patterns were measured with fine-wire electrodes, consisting of two 55-μm stainless steel intramuscular electrodes threaded through a single hypodermic needle (Burgar et al. 1997). Six of the seven muscles of the index finger were targeted for insertion: two extrinsic flexors (EF): first compartment of flexor digitorum profundus (FDP) and first compartment of flexor digitorum superficialis (FDS); two intrinsics (INT): first palmar interosseous (FPI) and first dorsal interosseous (FDI); and two extrinsic extensors (EE): first compartment of extensor digitorum communis (EDC) and extensor indicis (EI). The lumbrical was not included because of its relatively small size and concerns that the associated pain of the electrode would impede task performance for the number of trials required. Electrode insertion site was determined by muscle palpation, ultrasonography, and the literature (Burgar et al. 1997; Perotto 1994). Occasionally, muscles needed to first be located with tungsten needle microelectrodes (60 mm/5 KΩ; Frederick Haer & Co., Inc., Bowdoinham, ME), in accordance with published procedures (Burgar et al. 1997; Keen and Fuglevand 2004; Perotto 1994). During insertion of the bipolar fine-wire electrodes, the subject was asked to produce a light muscle contraction; auditory feedback from a speaker guided insertion into the muscle belly. Accurate placement of the electrodes after insertion was verified by appropriate finger movement evoked by electrical stimulation of the muscle (D330; Digitimer, Ltd., Welwyn Garden City, United Kingdom). Electromyographic (EMG) signals were sampled at 2 kHz.

In this second session, subjects were instructed to produce 25% of maximal force (maximal for the direction and posture) at the fingertip toward the target direction while keeping off-axis forces within a ±10% range of intended force (i.e., ±2.5% of the maximal force). The force production tasks were performed for the same six orthogonal directions as the first session. Both target and actual force levels were displayed in real time on a computer monitor, providing visual feedback to assist the subject in regulating force simultaneously along all three force axes. Subjects sometimes needed multiple trials to successfully perform the task. A trial was deemed successful when the specified force levels were achieved for roughly 3 s. One-minute rest breaks occurred between trials. To scale EMG amplitude with muscle activation, maximum voluntary contractions in each of the six directions were performed at both the beginning and the end of the experiment. The order was randomized across subjects.

Theoretical Activation Workspace

Using force fingertip data obtained from cadaver studies (Qiu et al. 2017) and a fingertip model (Barry et al. 2018), we found the theoretical solution space for muscle activation patterns that could produce the desired force profile for each force direction. Muscle activation levels were varied from 0% to 100% in increments of 10% for each of the seven muscles of the index finger. Solutions were found for six postures (P₂, P₃, P₅, P₆, P₈, P₉, excluding postures with DIP = PIP = 0°) and all six directional forces tested in the study. At each posture, the fingertip force vector of each of seven index finger muscles (f_i) was multiplied by its force capacity determined by the cross-sectional area of the muscle (Triandafilou and Kamper 2012). Then, given the target force vector (f_tar), the activation level of each muscle (0 < a_i < 1; i = 1, 2, …, 7; 1: FPI, 2: FDI, 3: LUM, 4: EI, 5: EDC, 6: FDP, 7: FDS) was determined by exploring sets of activation patterns spanning the activation space to find the solutions that reproduced the target force vector:

$$‖f_{\text{tar}}-f_{\text{rec}}‖<\epsilon ‖f_{\text{tar}}‖$$

where $f_{\text{rec}}={\displaystyle {\sum }_{i=1}^7{a}_i{f}_i}$. The error margin (ε) was set to 10% (of the target force magnitude), similar to the task criteria used in the experiment.

A total of 19,487,171 ( = 11⁷) possible coordination patterns were explored at each posture and each force direction with MATLAB (MathWorks, Inc., Natick, MA). For each force direction and posture, the size of the solution space (i.e., number of solutions) was determined. The range of activation levels of each muscle within each solution space was also computed.

The muscle activation levels of the theoretical solutions were categorized into the three muscle groups, i.e., EE, EF, and INT, and then averaged. Then the maximum and minimum activation levels of each muscle group, as well as the variability within each condition (force direction/posture), were examined.

Data Analysis

From the EMG data, the muscle activation patterns for each force direction at each posture were first computed. A principal component analysis (PCA) was then performed to identify common patterns of the posture-dependent modulation of the muscle activation pattern across subjects. From the fingertip force data, we estimated force conversion efficiency and joint impedance, based on the in vitro data set obtained from previous studies (Qiu et al. 2017).

Muscle activation pattern.

EMG data were filtered with an 80-Hz high-pass Butterworth filter to remove 60-Hz noise. Then, for a given target force, the time point was first determined as the time period over which the error between actual and desired force was minimal. For each trial, a sliding time window of 1 s was applied to the fingertip force data, and the time period with the minimum force error, i.e., root mean square (RMS) of the difference between the target and actual force vectors, was found. Once this time period was determined, the EMG magnitude of each muscle was quantified by the RMS value during this period. Finally, the activation level of each muscle was obtained by normalizing this estimated RMS value with its maximum RMS value obtained during the maximum voluntary contraction trials.

The muscle activation pattern (normalized activation level of 6 muscles) was analyzed with the statistical software SPSS (IBM Corp., Somers, NY). First, repeated-measures multivariate analysis of variance (MANOVA) was implemented for each of the six directions, with MCP joint angles (3 levels) and IP joint angles (3 levels) as the within-subject variables. Results showing factor significance (i.e., for the force direction with significant postural effects) led to further univariate analyses of variance (ANOVAs) for individual muscles. Mauchly’s sphericity test was run to check the equality of the variances of the differences between levels of the repeated-measures factor. In the case of violation of sphericity, the Greenhouse–Geisser method was employed to correct for variance inequality.

Posture-dependent modulation of activation patterns.

We further examined how muscle coordination patterns were modulated across postures. For each directional force, changes in the muscle coordination pattern between IP postures for a given MCP posture or between MCP postures for a given IP posture were estimated. Changes between IP postures were computed between IP₁ (0°,0°) and IP₂ (30°,0°) and between IP₂ (30°,0°) and IP₃ (60°,30°) (i.e., between postures 1–2, 2–3, 4–5, 5–6, 7–8, and 8–9 in Fig. 1). Similarly, changes between MCP postures were estimated between MCP₁ (0°) and MCP₂ (30°) and between MCP₂ (30°) and MCP₃ (60°) (i.e., between postures 1–4, 4–7, 2–5, 5–8, 3–6, and 6–9).

Then, for the joint posture that was found to have significant effects on muscle coordination (either IP or MCP), a PCA was implemented on the changes in the muscle activation pattern between the postures with a significant effect (either IP or MCP) for that joint (MCP) or joints (IP). The principal component (PC) explaining the largest amount of variance in the posture-dependent modulation of the muscle activation pattern was computed. The resulting PCs for each subject indicate the elemental patterns of the subject-specific modulation of muscle coordination across the postures of the joint with significant impacts. We then compared the PCs from all subjects to assess whether a similar strategy was apparent across all subjects. The average of the PCs that explained the largest variance (i.e., first PC) across subjects would represent the elemental pattern of posture-dependent modulation of muscle coordination. If a muscle is modulated consistently across subjects (i.e., its activation level is either increased or decreased) along with the postural change, we expect to find this muscle activation to be significantly different from zero in the average of the first PCs.

Task domain: end-point force efficiency and joint-level impedance.

We computed the effects of the posture on the conversion of muscle force to end-point (fingertip) force and on the impedance of the individual finger joints. For the conversion efficiency, the magnitude of the resultant fingertip force was divided by the total magnitude of the fingertip forces created by individual muscles; these forces were estimated by multiplying physiological cross-sectional areas (PCSAs) (An et al. 1985) by the maximal muscle stress value (35 N/cm²; Zajac 1989). Additionally, the areas of the envelope created by the fingertip force vectors produced by the three muscle groups (EE, EF, INT) were displayed in the sagittal plane for the four directional forces within that plane (palmar/dorsal/distal/proximal).

Postural changes may also require greater muscle activation to produce the same desired fingertip force. This greater muscle activation could increase signal-dependent noise (SDN), as the noise in the neural signal increases with muscle activation (Harris and Wolpert 1998). Previous studies suggested that the central nervous system (CNS) controls joint/end-point impedance to reduce the end-point variability/error (Jones et al. 2002; Osu et al. 2004) or instability (Selen et al. 2009) that arises from the SDN. We computed the joint impedance to examine the effects of the postural changes on the motor control associated with SDN. The theoretical joint impedance was computed from the activation pattern chosen by the participant, similar to previous studies that quantified the joint impedance produced by muscle contraction (Osu and Gomi 1999; Pfeifer et al. 2012). Briefly, activation level of each muscle was converted to muscle stiffness, which is proportional to muscle force and inversely proportional to optimal fiber length. The muscle stiffness was then converted to the joint stiffness K using the moment arm values (An et al. 1983); here, the joint stiffness is represented as a differential operator that relates the small variation in joint torque to small angular displacement (Osu and Gomi 1999; Pfeifer et al. 2012).

$$\text{K}=\frac{\partial \tau }{\partial \theta }=\text{A}\cdot \text{S}\cdot {\text{A}}^T$$

$${\rm K}=\left[\begin{array}{ccc}{K}_{11}& K_{12}& K_{13}\\ K_{21}& K_{22}& K_{23}\\ K_{31}& K_{32}& K_{33}\end{array}\right]\text{,}\text{\hspace{0.17em}\hspace{0.17em}A}=\left[\begin{array}{cccccc}-d_{11}& -d_{12}& -d_{13}& -d_{14}& d_{15}& d_{16}\\ -d_{21}& -d_{22}& -d_{23}& -d_{24}& d_{25}& d_{26}\\ d_{31}& d_{32}& -d_{33}& -d_{34}& d_{35}& d_{36}\end{array}\right]\text{,}\text{\hspace{0.17em}\hspace{0.17em}S}=\text{diag}\left[s_1,s_2,\mathrm{...},s_6\right],s_j=\gamma f_j/l_j^0$$

Here, d_ij denotes the moment arm of muscle j (1: FPI; 2: FDI; 3: EI; 4: EDC; 5: FDP; 6: FDS) about joint i (1: DIP; 2: PIP; 3: MCP) (An et al. 1983) and s_j denotes the muscle stiffness that is proportional to the ratio of muscle force f_j divided by optimal fiber length $l_j^0$ (Infantolino and Challis 2010). As the joint stiffness needs to be increased in proportion to the target force magnitude, the estimated joint stiffness was then normalized by the target fingertip force magnitude for each subject. Note that, in our model, the intrinsic muscle stiffness and/or tendon stiffness were not considered, as we aim to quantify only the contribution of active muscle contraction to joint impedance.

RESULTS

Data from one male subject were excluded because of loss of signal in the FDI electrode during the experiment. The data from the other nine subjects were included in all analyses.

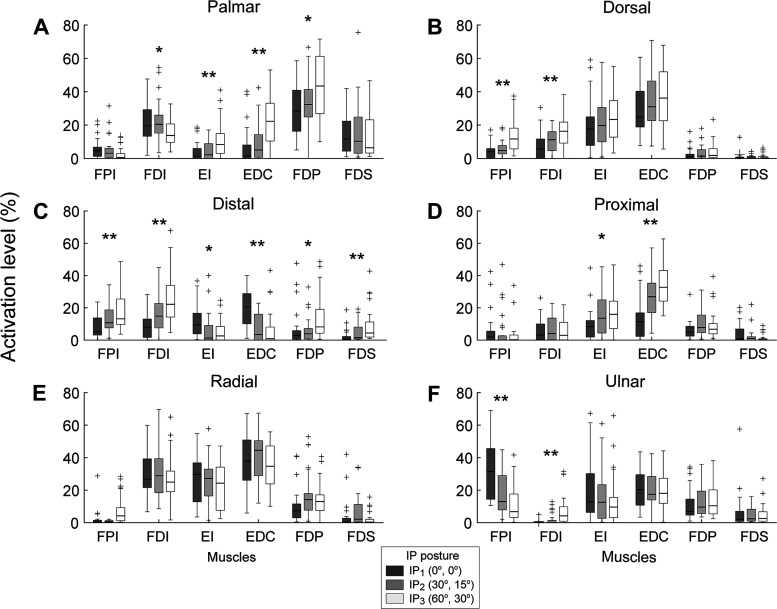
Subjects exhibited distinct muscle coordination patterns across directions and postures (Fig. 2). The initial analysis (repeated-measures MANOVA) showed that the activation level was significantly different across IP postures (all P values < 0.001) but not across MCP postures (all P values > 0.150) for all directions. No significant IP × MCP interaction was found (all P values > 0.650).

Fig. 2.

Muscle activation for each of the 6 muscles at the 3 interphalangeal (IP) postures: (0°,0°), (30°,0°), (60°,30°). Values averaged across all subjects at all 3 metacarpophalangeal (MCP) angles (0°,30°,60°). Error bars indicate 1 SD. A: palmar. B: dorsal. C: distal. D: proximal. E: radial. F: ulnar. EDC, 1st compartment of extensor digitorum communis; EI, extensor indicis; FDI, 1st dorsal interosseous; FDP, 1st compartment of flexor digitorum profundus; FDS, 1st compartment of flexor digitorum superficialis; FPI, 1st palmar interosseous. Statistically significant difference between IP postures: *P < 0.05, **P < 0.01.

Activation Level of Three Muscle Groups

One especially striking feature in the observed muscle activations was the prevalence of the EE (EDC and EI) muscle activation across directions. The EE muscles exhibited relatively high activation levels across postures and the highest mean activation levels for three of the six directions (dorsal, proximal, and radial). For the dorsal and radial directions, for example, the mean EDC activation was 32.9% and 38.1%, respectively, to create 25% of maximum voluntary force. Even for the palmar and distal directions, for which EDC activation was lowest, EDC was still one of the muscles with the highest activation level for certain IP postures, such as for the most flexed IP posture. Among all six muscles, EDC was the only one with a mean activation of >10% for every force direction.

Effects of Postural Changes on Coordination of Three Muscle Groups

The muscle activation patterns were found to be significantly affected by the IP posture in all six directions (all P values < 0.001). Follow-up univariate analyses for individual muscles showed that the IP posture had significant effects on the INT muscles (observed in all 6 directions; 8 of 12 cases) and EE muscles (in 4 directions; 6 of 12 cases) to a similar degree but not as much on the EF muscles (only in 2 directions; 3 of 12 cases) (see Fig. 2).

The patterns of the posture-dependent modulation were also different across muscles, which resulted in a change in the muscle coordination patterns as the IP joints flexed. For instance, the IP posture affected the activation of all six muscles during the distal fingertip force production (Fig. 2C), but different patterns of change were observed across the muscle groups. Namely, INT and EF activation increased but EE activation decreased as IP joints were flexed. This produced changes in the muscle coordination pattern. Conversely, for the palmar fingertip force (Fig. 2A), INT activation decreased as the IP joints were flexed, but EE and EF activation increased.

Patterns Underlying Adaptation to Postural Changes: Principal Component Analysis

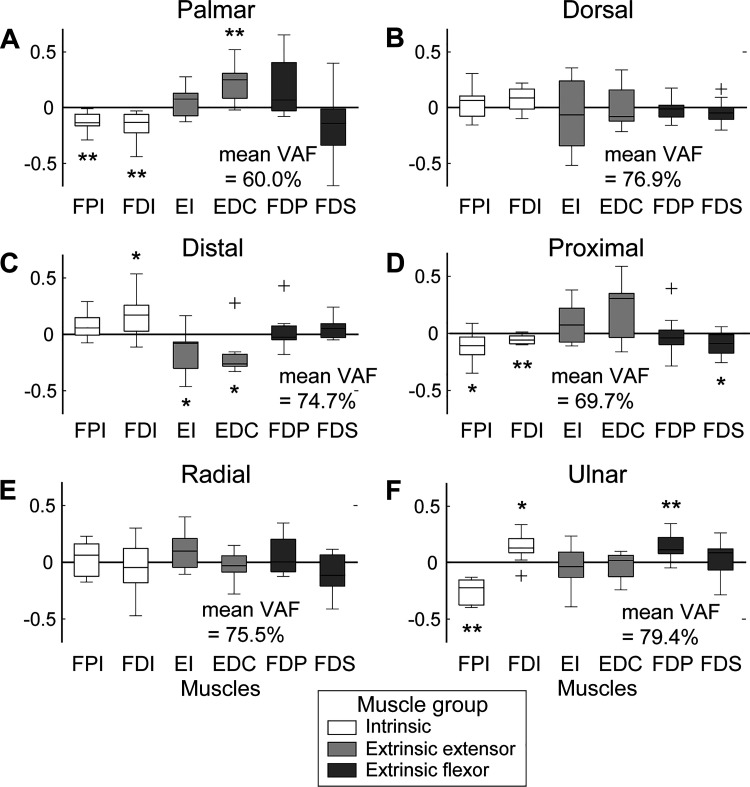
Principal component analyses of the modulation patterns further supported the idea that, across subjects, muscles in all three groups (INT, EE, EF) were modulated to adapt to the IP posture change (i.e., nonzero components indicated by * and ** in Fig. 3). The activation of the INT and EE muscles was modulated the most, whereas their actual changes (i.e., increase vs. decrease) generally exhibited opposite patterns (Fig. 3, A and C).

Fig. 3.

First principal component averaged across subjects: palmar (A), dorsal (B), distal (C), proximal (D), radial (E), and ulnar (F). EDC, 1st compartment of extensor digitorum communis; EI, extensor indicis; FDI, 1st dorsal interosseous; FDP, 1st compartment of flexor digitorum profundus; FDS, 1st compartment of flexor digitorum superficialis; FPI, first palmar interosseous. * and ** indicate muscle activations that were significantly different from 0 (*P < 0.05, **P < 0.01). Variability accounted for (VAF) by these components is also displayed for each direction.

Effects of Postural Changes on Task Mechanics: Force Conversion Efficiency and Joint Impedance

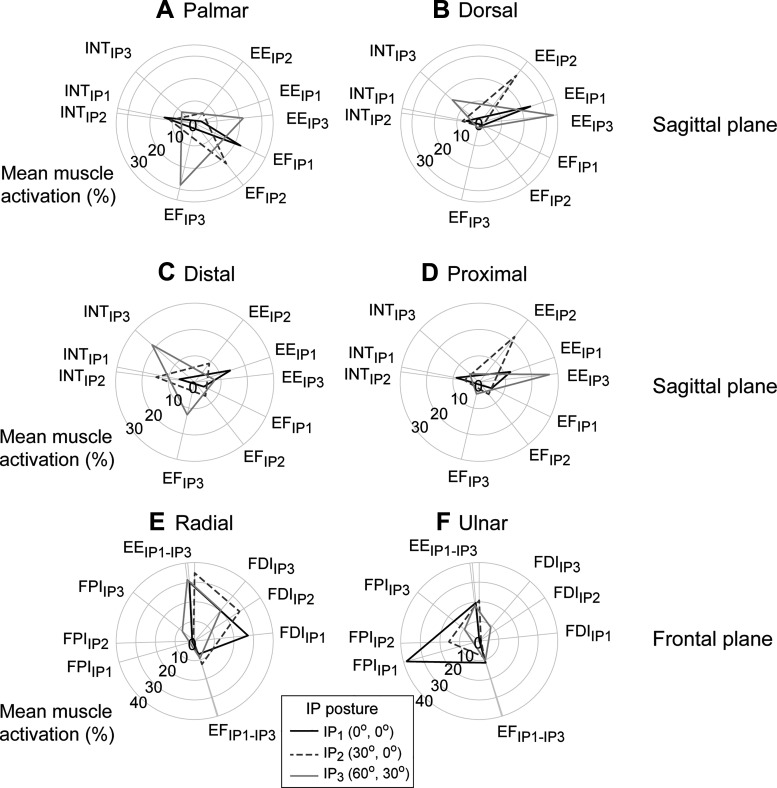
For the fingertip forces in the sagittal plane (palmar/dorsal and distal/proximal), IP flexion led to an increase in the size of the activation envelope at the fingertip, indicating that greater levels of muscle activation were adopted across the three muscle groups (Fig. 4). In most cases, magnitudes of the force components produced especially by the INT and EE muscles were significantly affected by the postural change. Force conversion efficiency was the lowest for the dorsal direction (mean 18.8%) and the highest for the distal direction (mean 64.3%) (Table 1). The conversion efficiency in the distal and proximal directions was significantly affected by the IP posture, as the efficiency significantly decreased as the IP joint flexed.

Fig. 4.

Activation of 3 muscle groups represented in the direction of their fingertip force vectors: palmar (A), dorsal (B), distal (C), proximal (D), ulnar (E), and radial (F). Activation level is indicated by radius of the plot for the muscle/muscle groups. In the radial plots, the activation level of each muscle group was plotted at the angle of the fingertip force vector that it produces at a given interphalangeal (IP) posture. The force vectors were plotted in the sagittal plane (A–D) or the frontal plane (E and F). EE, extrinsic extensor; EF, extrinsic flexor; FDI, 1st dorsal interosseous; FPI, 1st palmar interosseous; INT, intrinsic muscle.

Table 1.

Force efficiency across three IP postures for six force directions

IP Posture	Palmar	Dorsal	Distal	Proximal	Radial	Ulnar
1	28.9	17.3	89.3	61.3	31.0	28.0
2	31.5	20.0	62.9	38.8	25.3	44.4
3	25.2	19.1	40.8	22.7	34.1	41.8
Mean (SD)	28.5 (3.2)	18.8 (1.3)	64.3 (24.3)	40.9 (19.4)	30.1 (4.5)	38.1 (8.8)

IP, interphalangeal.

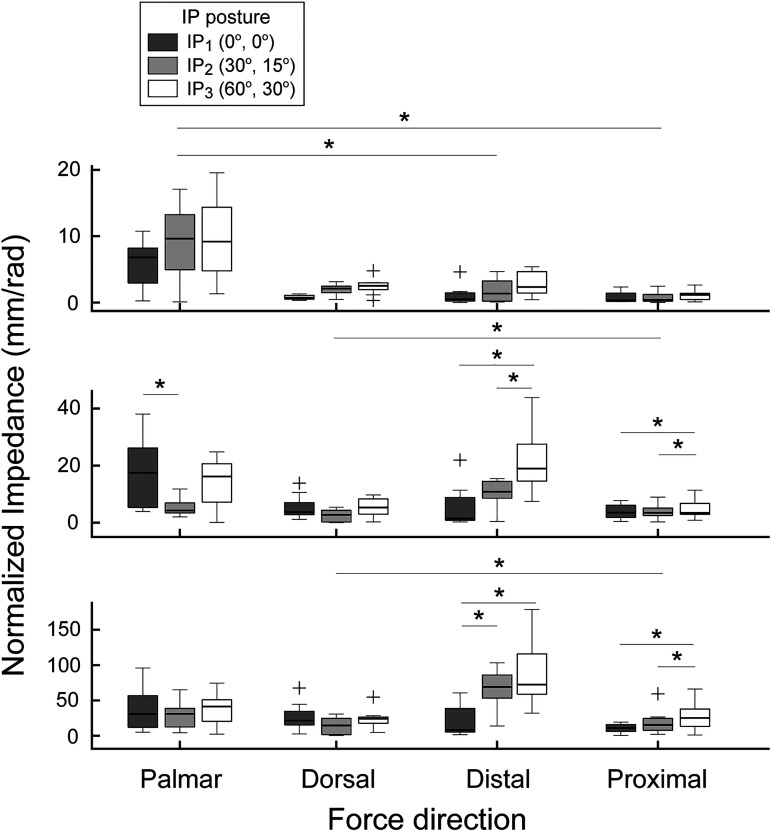
Postural effects on the joint impedance were also found to be significantly different across force directions. Among the four directional forces in the sagittal plane (palmar, dorsal, distal, and proximal forces), IP flexion led to a significant decrease in the joint impedance during the palmar/dorsal force production. Thus, IP flexion led to decreased tendon force (or joint moment) to fingertip force conversion, specifically between IP₁ and IP₂. In contrast, the joint impedance increased as the IP joints were flexed for the distal/proximal forces, for which IP flexion increased the tendon force to fingertip force conversion (Fig. 5). The observed patterns of between-posture differences in the joint impedance were opposite to that in the force efficiency (Table 1). On the other hand, no significant posture-dependent changes were observed for the joint impedances for the forces in the frontal plane (i.e., radial/ulnar).

Fig. 5.

Normalized joint impedance across four force directions in sagittal plane. As the interphalangeal (IP) joint flexion increased, the joint impedance significantly increased during distal and proximal fingertip force production but largely decreased during palmar and dorsal force production. Here, + denotes outliers outside 1.5 interquartile range (*P < 0.05).

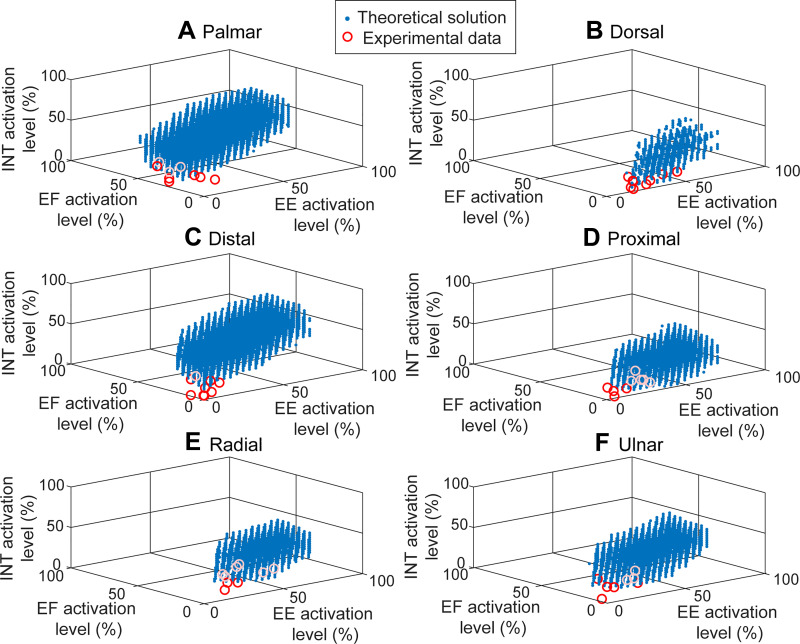
Muscle Activation Workspace: Theoretical Solutions vs. Experimental Data

Computer simulations with the cadaveric force data showed that, for all six directional forces, a wide range of muscle coordination patterns could theoretically produce the given target force (Table 2). The average activation level of these theoretical solutions varied significantly (Table 2). A large majority of solutions for all force directions involved activation of at least one muscle group of >50% (1,913,800 of 2,073,456; 92.3%). The largest number of solutions was found for the palmar force (mean number of solutions = 226,418 per posture) and the smallest for the dorsal force (mean number = 3,161 per posture) (see Fig. 6). The largest variability in the theoretical solution space was observed in the activation of the EE muscle group. The muscle activation patterns recorded during the experiment, however, were found to be confined within a very limited subspace of these possible solutions. Compared with the theoretical solutions, the muscle activation levels of the experimental data were generally low across subjects, with activation levels below 50% for every muscle. The mean activation levels of the muscles were the highest for the radial direction (mean ± SD = 19.2 ± 1.4%) and the lowest for the proximal direction (mean ± SD = 10.3 ± 2.4%). Overall, across six directions, the mean activation level of the experimental data was similar to the minimum values of the theoretical solutions, as indicated by the location of these data in the feasible workspace (circles in Fig. 6).

Table 2.

Theoretical solutions of muscle activation patterns: number of solutions and average activation levels across six muscles: maximum, minimum, and average values

	Palmar	Dorsal	Distal	Proximal	Radial	Ulnar
	Number of solutions
Posture
2	241,878	1,596	76,687	13,729	3,196	5,222
3	566,305	3,993	819	2,979	15,506	1,249
5	286,907	1,223	110,440	5,678	1,503	13,703
6	65,727	2,897	121,856	1,926	1,197	9,637
8	185,778	3,672	285,156	1,292	83	5,066
9	8,912	5,583	16,576	2,367	18	94
Mean	226,418	3,161	101,922	4,662	3,584	5,829
	Average activation levels across muscles, %
Maximum	86.7 (28.0)	60.0 (46.9)	78.3 (34.9)	56.7 (42.7)	66.7 (42.7)	65.0 (42.8)
Minimum	6.7 (12.1)	11.7 (20.4)	5.0 (8.4)	11.7 (20.4)	16.7 (32.0)	5.0 (8.4)
Mean	47.2 (12.3)	30.6 (9.5)	46.3 (11.2)	32.5 (7.1)	42.7 (7.0)	42.7 (7.6)

Fig. 6.

Activation patterns of the 3 muscle groups [extrinsic extensor (EE), extrinsic flexor (EF), intrinsic (INT)] in posture 2 [metacarpophalangeal (MCP) = 0°, proximal interphalangeal (PIP) = 30°, distal interphalangeal (DIP) = 0°] required to produce fingertip forces toward 6 orthogonal directions: palmar (A), dorsal (B), distal (C), proximal (D), radial (E), and ulnar (F). Blue dots indicate all possible (theoretical) coordination patterns producing target force (computed from cadaveric data), and red/white circles denote actual (experimental) coordination patterns obtained from the 9 subjects. The experimental data were generally confined to the lower boundary of the solution space, indicating that the activation patterns that minimize the overall activation level of all muscle groups were typically selected by subjects.

DISCUSSION

The proximal location of the muscles controlling the fingers and thumb provides many advantages but complicates the translation of muscle force into joint torque and, ultimately, force production at the digit tips. Proper magnitude and direction of fingertip forces are crucial to the dexterous manipulation of objects, a defining capability of humans. This study explored key issues related to sensorimotor control of the fingers when subjected to changes in task (desired fingertip force direction) and system state (finger posture). The main findings of this study are that 1) IP but not MCP posture significantly affected muscle coordination patterns; 2) extrinsic extensor muscles play a large role in force production across directions; and 3) IP flexion affects joint impedance across force directions. These findings highlight important neurophysiological principles underlying multimuscle coordination of fingertip force production, each of which is delineated below.

Effects of Postural Changes: IP vs. MCP

Change in finger posture did necessitate a significant change in activation pattern, but only for changes in IP rotation. MCP did not significantly affect the coordination patterns. Of all the finger joints, MCP rotation has the greatest impact on muscle length and moment arm (An et al. 1983). Its impact on the motor control of fingertip force production, however, is somewhat muted by the fact that the ratio of joint torques, not the absolute magnitudes of the torques, has a greater impact on the direction of the fingertip force. Furthermore, the changes in muscle length and moment arm may have differing effects on net joint torque. For instance, MCP flexion will shorten the long flexor muscles and thus reduce muscle force (decreasing the joint moment) but will increase their moment arms (increasing the joint moment).

In contrast, IP flexion significantly affects the biomechanical mapping of joint moments to fingertip force, as described by the Jacobian matrix (Valero-Cuevas et al. 1998). The change in mapping led to a significant change in activation patterns. Our results, significant impact of IP but not MCP postures on muscle coordination, suggest that the CNS distinguishes between postural changes of the MCP and IP joints and responds accordingly. Studies have shown that finger proprioception at the joint level is quite accurate (Proske and Gandevia 2012).

Roles of Different Muscle Groups

To accommodate the IP postural changes, participants altered activation levels across all three muscle groups, but overall the changes in the extrinsic extensors and the intrinsic muscles were found to be the greatest. Although overall a substantial degree of between-subject variability was present in the absolute muscle coordination patterns (see large standard deviation values in Fig. 2), in accordance with prior studies examining submaximal hand forces (Close and Kidd 1969; Long et al. 1970; Long and Brown 1964; Maier and Hepp-Reymond 1995; Vigouroux et al. 2007), patterns were apparent in the relative changes in activation patterns with changing IP posture. The PCA identified consistent change patterns in the activation of the EE and INT muscles across subjects.

Although the importance of the intrinsic hand muscles in adjusting fingertip force directions (and magnitudes) was previously recognized (Maier and Hepp-Reymond 1995; Milner and Dhaliwal 2002), this study highlighted the significant involvement of the finger extensor muscles in adjusting the force direction. Significant alterations in EE activation accompanied IP postural changes for a range of directions. This does not necessarily reject our hypothesis, as the INT muscles showed the largest degree of posture-dependent modulation (8 of 12 cases), but the degree of posture-dependent changes of the EE muscles (6 of 12 cases) was much greater than that of the EF muscles (3 of 12 cases). Additionally, the magnitude of EE activation was surprisingly large. When the activations of the three muscle groups were compared, the activation levels of the extrinsic extensors (EDC and EI) were relatively large with respect to the extrinsic flexor and intrinsic muscles. Across all directions, EDC had the greatest activation, indicating its importance in force production.

The contribution of the extrinsic extensor muscles to fingertip force production has also been suggested by previous studies. In a simulation study (Valero-Cuevas et al. 2000), a simulated paralysis of the EDC muscle (low radial palsy) led to a significant reduction in the palmar force at the fingertip. Several observational studies also found that the activation of the EDC muscle was relatively high during isometric force production, particularly toward dorsal and palmar directions (Keenan and Massey 2012; Valero-Cuevas et al. 2000). It appears that, because of their unique biomechanical function (dorsal-proximal force), the EE muscles play a pivotal role in generating fingertip force across a variety of force directions. The EE muscles need to be activated not only during the fingertip force production toward dorsal or proximal directions but also when the distal or palmar directional forces are produced, in order to create a net force in the desired direction.

It is also important to note that our findings contradict the conclusions from several previous studies that demonstrated that the extrinsic finger extensor muscles are not as involved in the force production or its postural modulation as the intrinsic hand muscles or the extrinsic finger flexors (Maier and Hepp-Reymond 1995; Milner and Dhaliwal 2002). We postulate that such discrepancy may be explained by the difference in the experimental design and/or adopted analysis methods. For instance, when the direction of the fingertip force does not need to be precisely controlled (e.g., Maier and Hepp-Reymond 1995), the extrinsic extensors may not need to be significantly involved, as the distal (shear) force produced by the intrinsic hand muscles does not need to be precisely compensated (Valero-Cuevas et al. 2000). Differences in the analytical methods could have also contributed to this discrepancy; the sensitivity of each muscle control to the postural change was assessed in Milner and Dhaliwal (2002) by comparing the force directions where its maximum activation was required across postures (i.e., orientation angle). Although the directionality of the extrinsic finger extensor (force direction for which its maximal activation is required) was not found to be affected by the postural change, the shape of the activation diagram (activation level across different force directions) appears to significantly change (e.g., see Fig. 2 of Milner and Dhaliwal 2002), indicating that its contribution toward forces in different directions substantially varied. We believe that the direction quantification of the muscle coordination patterns across postures in this study allowed us to highlight the role of the extrinsic extensor muscles in the adaptation to the postural changes. Additionally, the difference in the experimental conditions may have contributed to the discrepancy in the role of extrinsic extensor muscles (i.e., the effects of posture on their activation); note, in our study, the posture-dependent modulation of the extrinsic extensor muscles at the extended posture (DIP, PIP = 0°, 0°), which was not examined in previous studies.

Thus, nerve injuries that affect the extrinsic extensors, such as those arising from stroke, can profoundly impact hand function (Cruz et al. 2005; Lang et al. 2009). Impairment of the extensors may contribute to the impaired pinch force direction observed in stroke survivors (Seo et al. 2010). Indeed, improved palmar force production following training was associated with increased EDC activity (Seo et al. 2011). Additionally, compensating for compromised control of the extrinsic extensors to produce finger extension may be very challenging. Our simulation results revealed that a relatively small number of activation patterns could be used to create the desired dorsal force; in contrast, the solution space for the palmar force was 70 times larger. The extrinsic extensors should be a primary target for therapeutic rehabilitation.

Joint Impedance: Reducing Effects of Noise on Motor Output

The joint impedance also appears to be an important factor that affects the muscle coordination patterns. As the IP joints flex, the mechanical efficiency of the muscle force-fingertip force conversion either increases (dorsal/palmar forces) or decreases (distal/proximal forces). Such changes in the efficiency also indicate that the effects of motor noise will also be either increased (dorsal/palmar) or decreased (distal/proximal). The joint impedance values computed from the muscle activation patterns were found to covary with the observed posture-dependent changes in the effects of motor noise (Fig. 5), thereby suggesting that the CNS may attempt to reduce the effects of signal-dependent noise on motor output (Jones et al. 2002).

Selection of Muscle Activation Patterns: Implications for Optimality in Muscle Coordination

The simulations suggested a significant number of solutions, muscle activations that would achieve the desired force criteria. Compared with these possible workspaces of muscle coordination patterns obtained from the simulation, however, the muscle activation patterns actually employed by the subjects were found to be confined to a relatively small portion of the entire workspace, as the absolute activation level of all muscles was kept relatively low (Fig. 3). Although the large majority of solutions (92.3%) within the theoretical solution space involved activation of at least one muscle group of greater than 50%, the experimental data showed that the mean activation levels of all muscles across postures were smaller than 50% for all subjects tested.

Different optimality criteria (e.g., minimizing effort or motor variability) have been postulated to explain muscle coordination patterns controlling other body segments during human behaviors (Diedrichsen et al. 2010; Harris and Wolpert 1998; Scott 2004; Todorov and Jordan 2002). As of yet, however, investigations on how the hand muscles are coordinated remain largely observational (Darling et al. 1994; Darling and Cole 1990; Kamper et al. 2006; Long and Brown 1964; Maier and Hepp-Reymond 1995; Milner and Dhaliwal 2002; Valero-Cuevas et al. 1998), since activation patterns of the hand muscles were typically examined/described without employing specific performance criteria, possibly because of the complexity of the hand musculoskeletal structure that hampers the theoretical model development (difficulty in constructing cost function) and/or the experimental procedure (difficulty in measuring many muscles). Comparison of the experimental and theoretical solutions in the present study showed that, despite considerable between-subject variability, people generally chose the muscle coordination patterns with the lowest activation level from a much larger number of coordination patterns that can meet the task goal. As the observed between-subject variability appears to be much smaller than the variability in the possible activation patterns (Fig. 6), our results support the notion that, for the hand muscle coordination, the central nervous system attempts to minimize the level of effort to be exerted (Diedrichsen et al. 2010).

Potential Limitations

In our experimental protocol, subjects were asked to control for the three fingertip forces but not the fingertip moments, possibly leading to greater variation in activation patterns across subjects. However, meeting the stringent force requirements alone was often quite challenging for subjects; thus, additional moment requirements would have been very difficult to attain simultaneously.

The joint impedance was not directly measured with perturbation methods (e.g., Selen et al. 2009) but indirectly estimated with a musculoskeletal model combined with the recorded muscle activation patterns. As acknowledged by other studies that used similar approaches to estimate the joint impedance (Pfeifer et al. 2012), the model-based estimation of joint impedance is subject to model errors, which are, in our case, the possible errors (and between-subject variabilities) in the fingertip force vectors produced by the finger muscles.

Small changes in the finger postures were often observed during the task. Since the human finger is not comprised of rigid segments connected by ideal revolute joints, a small degree of finger joint rotation was possible even though all six DOFs of the end point (fingertip) were fixed; for instance, when the PIP and DIP joints were fully extended, i.e., IP = (0°, 0°), subjects often hyperextended their PIP joints and flexed MCP joints to create distal forces. Such aberrations in posture could have affected the muscle coordination patterns.

The number of female subjects was relatively low (1 of 10 subjects) among our participants. Sex could affect finger joint stiffness (Dionysian et al. 2005), which could lead to different patterns of muscle coordination (e.g., increased coactivation level, as shown in Milner and Franklin 1998). Further study with more female subjects is needed to determine the generalizability of the findings.

We did not record from the lumbrical muscle because of time constraints and concerns about subject discomfort/pain, which could have impacted their performance. We do not anticipate, however, that motor control of the lumbrical muscle would have been so different from that of the six other muscles as to substantially alter our results. Our computational simulation also showed that overall muscle coordination patterns remain largely unchanged with the addition of the lumbrical muscle, possibly because of its small cross-sectional area (An et al. 1985).

GRANTS

This work was in part supported by the National Institutes of Health (1R01 NS-052369-01A1) and by the National Science Foundation (CBET-1452763).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

D.G.K. conceived and designed research; D.Q., H.C.F., and D.G.K. performed experiments; S.W.L., D.Q., M.O.C., and D.G.K. analyzed data; S.W.L., D.Q., H.C.F., M.O.C., and D.G.K. interpreted results of experiments; S.W.L. prepared figures; S.W.L., D.Q., and D.G.K. drafted manuscript; S.W.L., D.Q., H.C.F., M.O.C., and D.G.K. edited and revised manuscript; S.W.L., D.Q., H.C.F., M.O.C., and D.G.K. approved final version of manuscript.