Abstract
Ocean-driven basal melting of Antarctica’s floating ice shelves accounts for about half of their mass loss in steady-state, where gains in ice shelf mass are balanced by losses. Ice shelf thickness changes driven by varying basal melt rates modulate mass loss from the grounded ice sheet and its contribution to sea level, and the changing meltwater fluxes influence climate processes in the Southern Ocean. Existing continent-wide melt rate datasets have no temporal variability, introducing uncertainties in sea level and climate projections. Here, we combine surface height data from satellite radar altimeters with satellite-derived ice velocities and a new model of firn-layer evolution to generate a high-resolution map of time-averaged (2010–2018) basal melt rates, and time series (1994–2018) of meltwater fluxes for most ice shelves. Total basal meltwater flux in 1994 (1090±150 Gt/yr) was not significantly different from the steady-state value (1100±60 Gt/yr), but increased to 1570±140 Gt/yr in 2009, followed by a decline to 1160±150 Gt/yr in 2018. For the four largest “cold-water” ice shelves we partition meltwater fluxes into deep and shallow sources to reveal distinct signatures of temporal variability, providing insights into climate forcing of basal melting and the impact of this melting on the Southern Ocean.
The mass budget of the Antarctic Ice Sheet is primarily controlled by mass gain from net snow accumulation and mass loss from basal melting and iceberg calving of its floating ice shelves. These ice shelf mass loss processes act to maintain the ice shelf in steady state; however, many ice shelves are experiencing net mass loss1 and thinning2 due to ocean-driven basal melting in excess of the steady-state values. Confined ice shelves reduce the speed of grounded ice flowing into them by exerting back-stress from sidewall friction and basal pinning points, a process called “buttressing”3. Excess basal melting in recent decades has reduced buttressing and increased dynamic mass loss of grounded ice, which has increased Antarctica’s contribution to sea level rise4,5.
Ice shelf melting has been categorized into three modes corresponding to distinct oceanographic processes6. Mode 1 melting occurs at the deep grounding lines of “cold-water” ice shelves, and is driven by inflows of cold, dense High Salinity Shelf Water (HSSW) that is produced through sea ice formation on the continental shelf7. Rising plumes of buoyant and potentially supercooled meltwater (referred to as Ice Shelf Water; ISW) formed from Mode 1 melting can lead to refreezing downstream, creating a layer of “marine ice” on the ice shelf base8. Mode 2 melting occurs at “warm-water” ice shelves where a subsurface layer of warm Circumpolar Deep Water (CDW) or modified CDW (mCDW) is transported into the ice-shelf cavity. Mode 3 melting occurs near the ice front where seasonally warmed Antarctic Surface Water (AASW) can be transported under shallow ice by tides and other modes of ocean variability. The relative contributions of these modes to total melting are highly variable around Antarctica, both in space and time, since each mode is influenced by several external processes including regional atmospheric and oceanic conditions and the production and transport of sea ice9,10.
The changing net fluxes and distribution of freshwater from ice shelf basal melting influence other components of the climate system through processes such as: the production and extent of sea ice, which modifies the exchange of heat, freshwater, and gases (e.g., CO2) between the atmosphere and Southern Ocean11,12; formation of Antarctic Bottom Water that is a major driver of the global ocean overturning circulation13; and generation of nearshore coastal currents that advect freshwater and other tracers to connect different regions around Antarctica14,15. Despite the projected impacts of changes in ice shelf melting on Southern Ocean dynamics and global climate variability16, the current generation of global climate models such as those used in the Coupled Model Intercomparison Project17 do not include realistic representations of meltwater fluxes18.
Satellite-derived estimates of basal melt rates
Currently, the best available circum-Antarctic datasets for ice shelf basal melt rate are derived from Ice, Cloud and land Elevation Satellite (ICESat) laser altimetry acquired during 2003–200819,20. These estimates are six-year averages for the satellite’s operational period, with no information about temporal variability. Although ICESat’s orbit to 86°S sampled all Antarctic ice shelves, it had relatively wide cross-track spacing, particularly for the northerly ice shelves (Figure S1). Existing data therefore cannot capture critical properties of meltwater fluxes from ice shelves, such as small spatial scales of melting in channels21,22 or the large decadal variability inferred from oceanographic observations in West Antarctica4.
A sequence of four European Space Agency satellite missions carrying radar altimeters have continuously acquired ranging data that allow us to estimate surface height change over Antarctica’s ice shelves from 1994 to 2018: ERS-1, ERS-2, and Envisat (1992–2010) to 81.5°S and CryoSat-2 (2010–) to 88°S. CryoSat-2 samples all ice shelf areas, with higher track density than prior altimeters (Figure S1). Together with its innovative Synthetic Aperture Radar-Interferometric (SARIn) mode of operation23, the orbit for CryoSat-2 allows for estimating height change with higher spatial resolution and accuracy than the previous radar altimeters22. Here, we estimate time-averaged (over eight years; 2010–2018) basal melt rates at high spatial resolution (500-m grid cells) for all ice shelves where sufficient data are available by combining height changes from CryoSat-2 radar altimetry with satellite-derived ice velocities and a new model of surface mass balance and firn state variability (Methods). We then use the continuous height record from the four altimetry missions to estimate basal melt rates in 10-km grid cells for every year from 1994 to 2018 for all Antarctic ice shelf regions where sufficient data are available.
Spatial distribution of basal melt rates
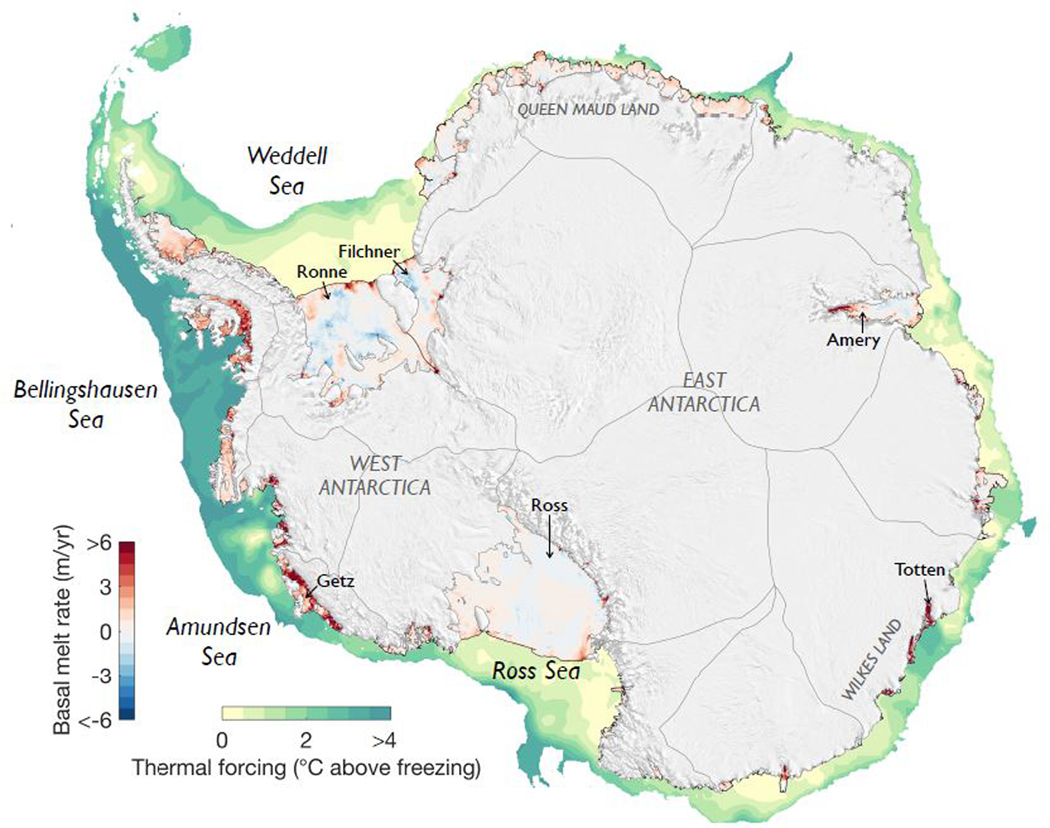
The spatial distribution of time-averaged ice shelf melt rates around Antarctica during 2010–2018 (Figure 1) shows large differences between warm- and cold-water ice shelves. Cold-water ice shelves (such as Ross, Ronne, Filchner, and Amery) show high melt rates under thick ice near grounding lines and thin ice near ice fronts (Figure 1, ice draft shown in Figure S2) separated by zones of refreezing. Warm-water ice shelves such as those in the Amundsen and Bellingshausen seas typically have high melt rates, consistent with the higher values of thermal forcing (temperature above the pressure-dependent, in situ freezing point of seawater) found near their ice fronts.
Figure 1: Basal melt rates of Antarctic ice shelves using CryoSat-2 altimetry.
Rates are averaged over 2010–2018 and shown at 500 m posting. The units are m of ice equivalent, assuming an ice density of 917 kg/m3. The thermal forcing, defined as the temperature above the in situ freezing point of seawater, is mapped for water depths <1500 m. For water depths less than 200 m the seafloor thermal forcing is shown, and for water depths >200 m, the maximum thermal forcing between 200 m and 800 m is shown (Methods Section S2).
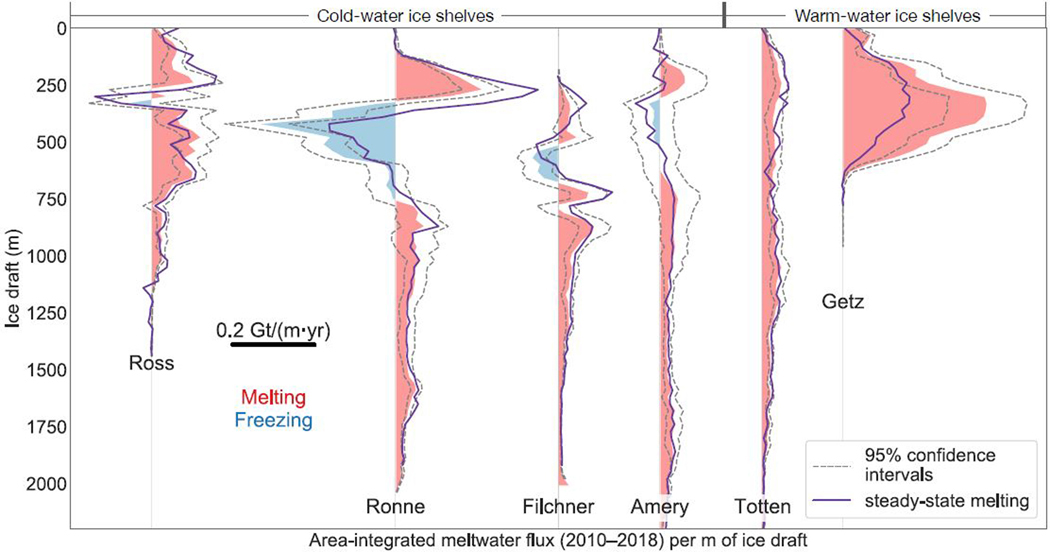
Area-integrated meltwater fluxes binned by ice draft for four cold-water and two warm-water ice shelves (Figure 2) provide further insight into the different modes of melting occurring at different locations. Melting for regions of deep ice draft under the large cold-water ice shelves is dominated by Mode 1 processes. In steady state, refreezing rates can be high, and about half of all Mode 1 meltwater produced under Ronne Ice Shelf and about a fifth of all meltwater produced under Amery Ice Shelf is subsequently refrozen as marine ice. The predicted thickness of marine ice estimated from our refreezing rates for Ronne and Amery ice shelves agrees well with independent estimates from airborne radar sounding and satellite radar altimetry (Figure S3). Refreezing typically starts at ice drafts that are around 50% of the grounding line depth, consistent with predictions from idealized models that use buoyant plume theory24,25. The ranges of ice draft for regions with refreezing (Figure 2) also correspond with the approximate depths for the subsurface plumes of cold ISW found along ice fronts26–28, which subsequently contribute to the formation of AABW29.
Figure 2: Vertical structure of melting and refreezing rates for selected ice shelves.
Depth-dependence of area-integrated meltwater flux (2010–2018) per m of ice shelf draft (depth of the ice shelf base below sea level) for six major ice shelves (locations shown in Figure 1). The scale for the horizontal axis is shown by the solid black line within the figure. The shaded regions in red and blue represent the mean values, and the dashed lines represent 95% confidence intervals. The purple lines are hypothetical steady-state meltwater fluxes (i.e., the meltwater fluxes required to maintain constant ice shelf mass). Warm-water ice shelves are distinguished from cold-water ice shelves by their higher average rates of meltwater production driven by intrusions of warm Circumpolar Deep Water (CDW) or modified CDW into the ice shelf cavity.
Cold-water ice shelves also have regions of relatively high basal melt rates under shallower ice along the ice fronts (Figure 1, 2), primarily due to Mode 3 melting. Unlike regions undergoing Mode 1 melting that are close to the deep grounding lines where ice shelf thinning could substantially reduce buttressing30,31, regions of Mode 3 melting are typically within the “passive ice zones”32 that provide little buttressing to grounded ice. However, the elevated melt rates contribute to increased ocean stratification along the ice front that influences cross-front exchanges of ocean heat33 and the seasonal cycle of sea ice formation close to the ice front34, both of which feed back into the seasonal cycle of ice shelf melt rates35,36.
Under warm-water ice shelves, high melt rates are associated with subsurface flows of CDW and mCDW (Mode 2 melting). Melting in excess of steady state caused rapid thinning of several warm-water ice shelves in the Amundsen and Bellingshausen Sea sectors during 2010–2018 (Figure S4). For some ice shelves in these sectors (e.g., George VI, Wilkins, and Dotson) the highest rates of thinning occurred in narrow basal channels with high melt rates. Getz Ice Shelf, the largest single source of meltwater from the Antarctic ice shelves (Table S1), shows excess melting at depths between 250 m and 700 m (Figure 2). Warm-water ice shelves outside the Amundsen and Bellingshausen seas sector, such as Totten Ice Shelf in East Antarctica, show insignificant rates of excess melting.
Variations in ice shelf melt rates between 1994 and 2018
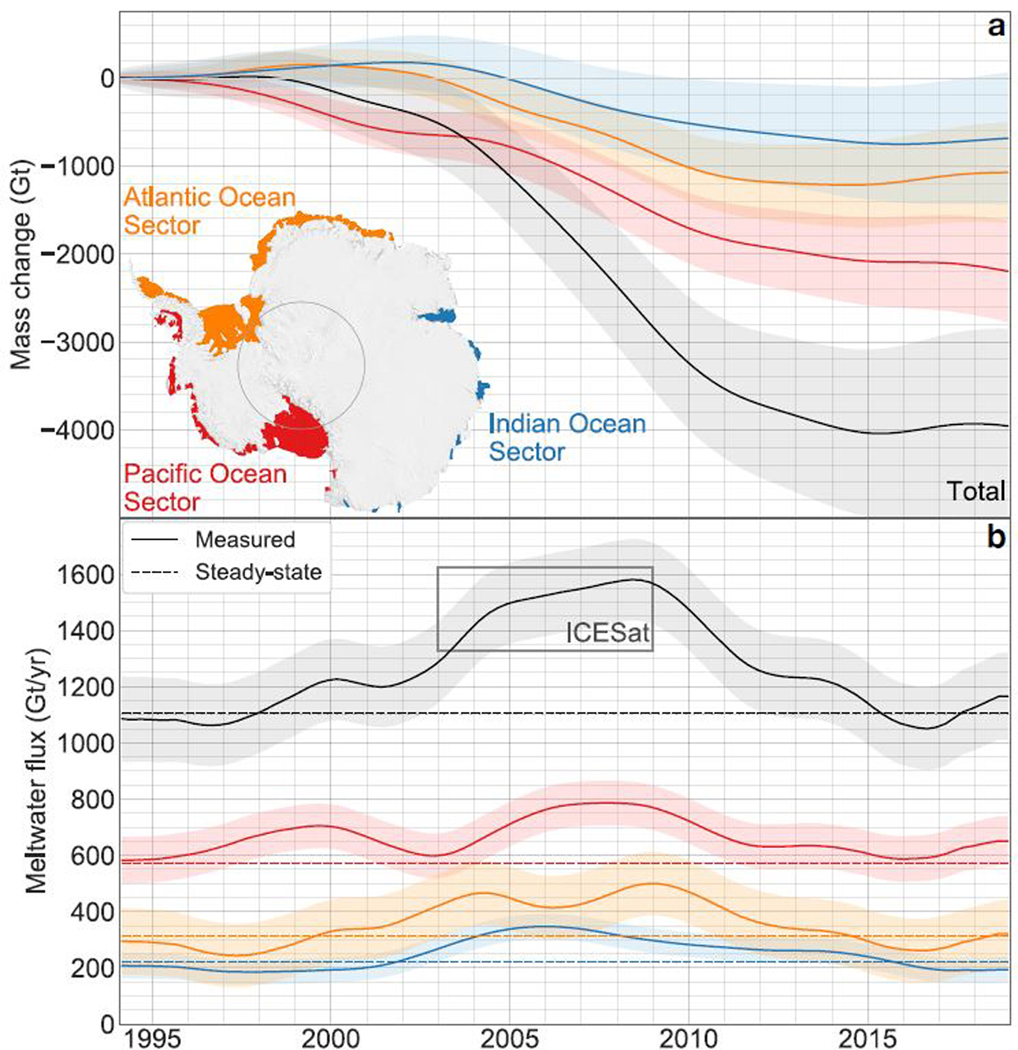
Our estimate for net mass loss from all of Antarctica’s ice shelves from 1994 to 2018 is 3960±1100 Gt (Figure 3a; error range is the 95% confidence interval, Section S5). Most of this mass loss was from the Pacific Ocean Sector ice shelves. For reference, the net loss of grounded ice from the Antarctic Ice Sheet during 1992–2017 was 2660±560 Gt37. The total meltwater flux, based on the area-integrated basal melt rate over all Antarctic ice shelves averaged over 1994–2018, was 1260±150 Gt/yr, which was 160±150 Gt/yr higher than the steady-state rate of 1100±60 Gt/yr (Figure 3b). Meltwater fluxes varied substantially with time: an increase of 480±210 Gt/yr, from 1090±150 Gt/yr at the start of the record in 1994 to 1570±140 Gt/yr in 2009 was offset by a subsequent decrease of 410±210 Gt/yr to 1160±150 Gt/yr in 2018. Our estimate of time-averaged meltwater flux for the ICESat-era (2003–2008) is 1500±140 Gt/yr, which is consistent with two previous ICESat-based estimates of 1500±240 Gt/yr19 and 1450±170 Gt/yr20. The ICESat-era estimate of meltwater flux exceeds our 25-year average by 240±210 Gt/yr, and exceeds our steady-state estimate by 400±160 Gt/yr, highlighting the importance of long, continuous records to provide context to results from individual missions1 or between two non-overlapping missions38.
Figure 3: Variations in Antarctic ice shelf mass between 1994 and 2018.
(a) Cumulative ice shelf mass change between 1994 and 2018 for the Pacific (red), Atlantic (blue), and Indian (orange) ocean sectors of Antarctica, with shading showing 95% confidence intervals. The region definitions are shown on the map, and the combined total for all ice shelves is shown in black. (b) Meltwater fluxes for 1994–2018 from ocean-driven ice shelf basal melting for the same regions. Dashed lines represent meltwater fluxes in steady-state, where the mass of the ice shelves is constant through time. Total meltwater flux estimates for the ICESat era are averaged between two studies19,20.
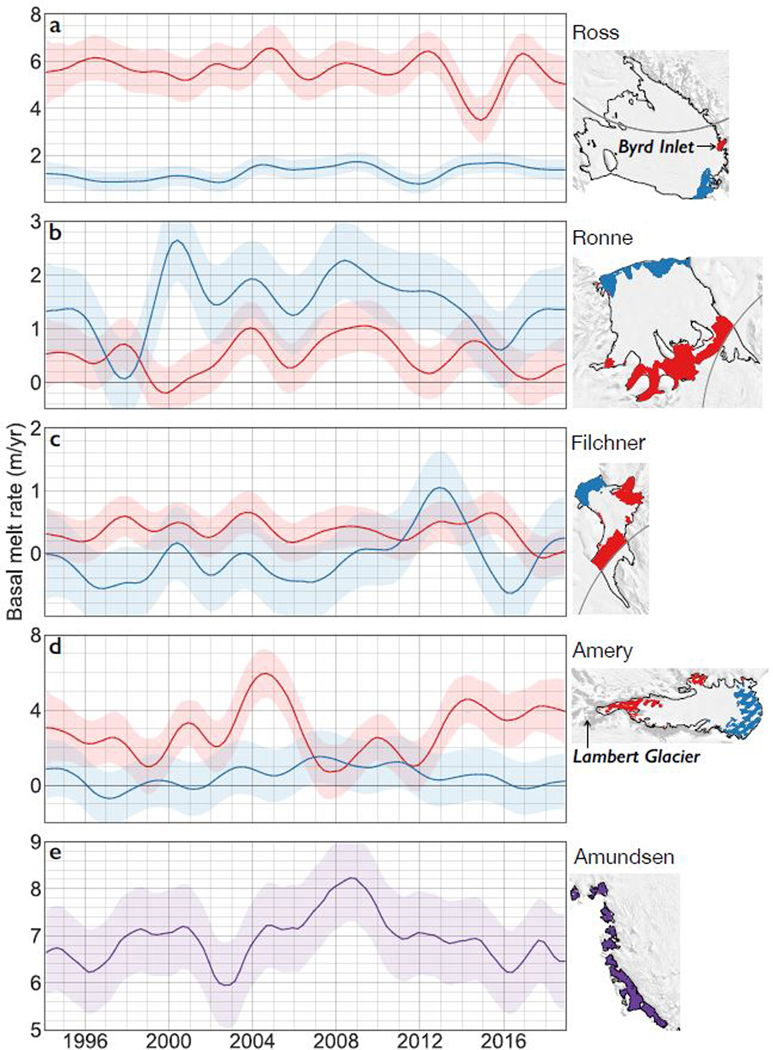
We examined the temporal variability in melt rates from different modes for the four largest cold-water ice shelves by calculating spatial averages over select regions (Figure 4a-d) of deep ice draft (Mode 1) and shallow draft (mostly Mode 3). For Ross Ice Shelf, the timing of the minimum in Mode 1 melt rates in Byrd Inlet near 2015 is consistent with the 2013–2014 minimum in HSSW salinity on the Ross Sea continental shelf39 and the time scale for advection of HSSW to Byrd Glacier36. Lower salinity for HSSW reduces the negative buoyancy driving HSSW under the ice front and downslope to the deep grounding line of Byrd Glacier, weakening the circulation of HSSW into Byrd Inlet and the resulting melting. Mode 1 melting of Filchner and Ronne ice shelves has been hypothesized to have increased following the formation of an exceptionally large polynya during the 1997–1998 austral summer40. This hypothesis was based on a sharp decline in ocean temperatures at an instrumented site (Site 5; Figure S5) on Ronne Ice Shelf near the southwestern Berkner Island coast between 2000 and 2003, attributed40 to increased ISW formation following a period of high Mode 1 melting. Our data also support this hypothesis, with increased melt rates at deep ice drafts under Filchner Ice Shelf during 1999–2000 and decreased melt rates (including a short-lived transition to refreezing) at Site 5 between 2000 and 2004 (Figure S5). Melt rates of Amery Ice Shelf, spatially averaged for deep ice drafts, varied from near 0 to 6.5 m yr−1 with particularly high values between 2003 and 2007. We speculate that this maximum could be associated with a continuous drainage of a ~0.8 km3 subglacial lake under Lambert Glacier between 2003 and 200641; subglacial discharge is known to drive energetic plumes42,43 that increase basal melt rates near grounding lines.
Figure 4: Time-dependent basal melt rates for different modes of melting.
(a-d) Area-averaged basal melt rates for selected regions within the four largest Antarctic ice shelves. Regions shown in red experience melting predominantly from cold, High Salinity Shelf Water inflows at deep ice drafts (Mode 1), while regions shown in blue typically experience melting from intrusions of Antarctic Surface Water at shallow ice drafts (Mode 3). (e) Basal melt rates for Amundsen Sea ice shelves, which experience melting from inflows of warm Circumpolar Deep Water (Mode 2). Gaps in the spatial coverage reflect the sampling of the altimeters prior to CryoSat-2.
For Amundsen Sea ice shelves, melt rates showed substantial variability, with the highest sustained rates occurring in the late 2000s (Figure 4e). Variability in Mode 2 melting of Amundsen Sea ice shelves has been previously identified in ocean observations and linked to variability in the tropical Pacific at both interannual44,45 and decadal4 time scales. The magnitude of our estimates of variability in melt rates of Dotson Ice Shelf (around 60 Gt/yr peak to trough) agrees with the variability in independent estimates of meltwater flux from repeated oceanographic sections along the ice-shelf front4 (Figure S6) but is larger than the variability expected from an ocean model that used atmospheric forcing from the same period46. Excess basal melting and changes in ice shelf extent (Figure S8, Table S1) in the Amundsen Sea sector between 1994 and 2018 could be due to a longer-term increase in the thickness of CDW incursions under ice shelf cavities associated with atmospheric and oceanic responses to anthropogenic forcing47.
Our new estimates of time-varying melt rates permit assessment of whether ocean circulation models can represent the complex feedbacks between water mass production and conversion processes acting under the ice shelves and over the continental shelves north of the ice fronts. The large temporal variability of melting in all three modes (Figure 4) will contribute to changes in the distribution of different water masses over the Antarctic continental shelf seas and into the global ocean. The ISW produced through Mode 1 melting contributes to the formation of particularly cold, dense forms of AABW26,48,49. Changes in Mode 2 and Mode 3 melting modify the fluxes of meltwater into the upper ocean in adjacent coastal regions15,34. Increased ocean stratification from shallow sources of cold, buoyant water alters the seasonal cycle of sea ice50 and decreases the potential for deep convection that drives production of Dense Shelf Water types including HSSW. Changes in relative strengths of these melt modes modify the geostrophic ocean circulation over the Antarctic continental shelf seas, feeding back into the transport of ocean heat between coastal sectors and into the sub-ice-shelf cavities7.
We have produced two new datasets of basal melt rates for nearly all of Antarctica’s ice shelves. One dataset provides melt rates at high spatial resolution (500 m grid) for most ice shelf areas, averaged over the period 2010–2018. The second dataset allows for the evaluation of annual estimates of basal melt rates at lower spatial resolution (>10 km) for the period 1994–2018. Together, these datasets reveal large variability in total meltwater fluxes from individual Antarctic ice shelves, with distinct, regionally variable, signatures of temporal variability for different modes of ocean-driven melting. Our data can be used to better isolate the glaciological and climate drivers of processes that modulate current ice sheet mass loss and provide improved metrics for calibration and validation of melt rates used in both ice-ocean and Earth-system models.
Methods
S1. Melt rates from Lagrangian CryoSat-2 analysis, 2010–2018
In a Lagrangian reference frame (following a parcel of ice), and assuming that the ice shelf is floating in hydrostatic balance, the net ice shelf height change observed using satellite altimetry , where h is the ice shelf surface height relative to the height of the ocean surface , is related to the surface mass balance (; kg/(m2 yr)), basal melt rate () in m of ice equivalent per year, ice shelf divergence (; in m of ice equivalent per year) and changes in firn air content (; m) through51
| (S1) |
where v is the two-dimensional grid of ice surface velocity vectors (m/yr), is ice shelf thickness in units of m of ice equivalent, is the density of ocean water (assumed to be 1028 kg/m3), and is the density of ice (assumed to be 917 kg/m3). Here, is given by , where H is the total ice shelf thickness (surface to base). In the following subsections we describe the various datasets used in our estimation of through Equation S1.
S1.1. Height of the ocean surface
We estimated the height of ocean surface as
| (S2) |
where is the height of the EIGEN-6C4 geoid52, is mean dynamic topography from DTU13MDT53, is the ocean tide from the CATS2008 tide model54 (an update to the model described by ref. 55), is a correction for the inverse barometer effect due to atmospheric pressure variability and is obtained from the MOG2D Dynamic Atmosphere Correction56, is the ocean load tide estimated using the TPXO7.2 model57, and is the increase in mean sea-level around the Antarctic coast reported by ref. 58. Of the terms on the right-hand side of Equation S2, we only considered temporal variability of and and
S1.2. Lagrangian height changes
We derived , following ref. 51, by first advecting the locations of CryoSat-2 footprints, initially at , to their 2015 locations using
| (S3) |
where is 0.01 years. For , we used ice velocities from a 2015 mosaic derived from Landsat-8 feature tracking at 300 m posting59. For the ice shelves where the southern limit of these velocity data (82.4°S) did not include the entire area (Filchner, Ronne and Ross), we filled in data gaps in the 2015 mosaic using 1996–2016 mean values from ref. 60. The velocity data were adjusted to reflect velocities in the Antarctic Polar Stereographic projection with a standard parallel of 71° and a standard longitude of 0°. We converted latitudes and longitudes of CryoSat-2 data into using the same projection. Using the advected CryoSat-2 data, we estimated and associated uncertainties in grid cells at 500 m spacing and 1 km resolution using the ‘plane fit’ technique described by ref. 61 (their Section S1). We discarded data in a grid cell when the uncertainty in estimated from the plane fit was greater than 0.5 m yr−1.
S1.3. Thickness change due to ice shelf divergence
We estimated the term in Equation S1 using ice thickness estimated from CryoSat-2 data following ref. 61 but using the advected footprint locations as described in Section S1.1. For, we used strain rate estimates and associated uncertainties from ref. 62, based on velocity data collected between 2013 and 2016 north of 82.4°S. Over Filchner, Ronne and Ross ice shelves these data did not extend to their southern limits. Therefore, we used values of provided by ref. 51 for Filchner, Ronne, and Ross ice shelves.
S1.4. Surface mass balance () and height changes from firn processes
For the term, we used NASA’s global Modern-Era Retrospective analysis for Research and Applications, Version 2 (MERRA-2)63, which we combined with an offline high-resolution MERRA-2 ‘replay,’ denoted M2R12K64, to derive a hybrid product referred to as ‘MERRA-2 Hybrid.’ M2R12K is a high-resolution MERRA-2 run (12.5 km) specifically targeted over the Antarctic and spanning 2000–2014. To maintain the fine spatial resolution of the M2R12K, it’s mean seasonal cycle is combined with the seasonal residuals from the full MERRA-2 period (1980–2019). Thus, MERRA-2 Hybrid combines the fine spatial resolution from M2R12K with the longer time record from MERRA-2. We used MERRA-2 Hybrid forcings (precipitation minus evaporation, skin temperature, and meltwater flux from a degree-day model) for simulations of the firn column using the densification equations described in ref. 65 implemented in the Community Firn Model (CFM)66 to estimate 64. We refer to this firn densification model as GSFC-FDMv0, which is calibrated with ~200 firn depth-density profiles from both the Greenland and Antarctic Ice Sheets and includes both dry and wet firn processes. We assume that because of the low spatial resolution of the firn model output compared to the distances over which the CryoSat-2 footprints were advected in the Lagrangian framework. GSFC-FDMv0 provides values at 12.5 km spatial posting and 5-day temporal sampling64. We interpolated these data in space to the grid cells at 500 m spacing used to derive (Section S1.2). Details regarding GSFC-FDMv0 are within the Supplementary Materials of ref. 64.
S1.5. Steady-state basal melt rates
We estimated the “steady-state” basal melt rate, , required to keep ice shelves in steady-state mass balance (equivalent to assuming that there is no net change in ) using
| (S4) |
where represents the time-average value. There is no temporal variability in our estimates of : we used the 1994–2018 mean values from the MERRA-2 Hybrid (precipitation minus evaporation: P-E) for and assumed that outside the Amundsen Sea sector there was no change in in time during our observation period.
S1.6. Depth-dependence of area-integrated meltwater fluxes
We estimated the ice shelf draft, , the depth of the ice shelf base below mean sea level, using . For grid cells in which we were not able to estimate using the methodology described in Section S1, we used values estimated using BedMachine67 data (Figure S2e). We then calculated area-integrated meltwater fluxes as a function of ice shelf draft (Figure 2) by integrating in discrete bins of at 30 m spacing.
S2. Ocean thermal forcing
We define thermal forcing, (Figure 1), as the temperature above the in situ freezing point of seawater, . We obtained profiles of ocean temperature () and salinity () from the World Ocean Database 201868, then obtained the values of where is pressure, from the function described by ref. 69 and implemented in the Gibbs SeaWater (GSW) Oceanographic Toolbox of TEOS-1070. We only used profiles that satisfied one of the following criteria: (i) profile extends to at least 800 m in water depth zb deeper than 800 m; or (ii) profile extends to within 150 m of the seabed (evaluated from Rtopo271) for zb < 800 m. We then determined maximum thermal forcing as the maximum value of in the depth range 200-min(zb, 800) m. The limit of 200 m is designed to exclude summer-warmed Antarctic Surface Water and focus on deeper water masses on the continental shelf that have access to the cavities under ice shelves; i.e., primarily Mode 1 and Mode 2 melting. For zb < 200 m, we take the value of at the deepest point in the profile. The values of were then interpolated to a 25-km uniform polar stereographic grid, with standard latitude and longitude of 71°S, 0°E, using a bi-cubic distance weighting scheme, modified to increase weightings along isobath and lower weightings across isobaths, consistent with known strong barotropic control of circulation over Antarctica’s continental shelves and along the shelf break72,73.
S3. Time series of height change from Eulerian ERS-1, ERS-2, Envisat, and CryoSat-2 analysis
In addition to 2010–2018 mean values of from Lagrangian analysis of CryoSat-2 data, we also estimated time-varying melt rates derived using Eulerian analysis of height change derived from ERS-1, ERS-2, Envisat, and CryoSat-2 altimetry. We used consistent 10 km grid cells at 1 km posting for all missions, and data were averaged in time to three-month intervals. To merge height change data from all four missions to produce a continuous time series spanning 1992–2018, we only considered grid cells where there were sufficient data from all four missions, as described below.
S3.1. Estimating altimeter-derived height changes
We obtained ERS-1, ERS-2, and Envisat height data () from refs. 74,75. We corrected for change in the ocean surface using Equation S2.
We first derived height changes for each mission separately. For each grid cell, we estimated height changes for each mission if there were at least 15 data points spanning at least 3 years using:
| (S5) |
where represents surface topography, is time in decimal years, s is a satellite ascending/descending binary flag (0 or 1), is backscatter, and is a binary mode flag that is only applied to data from ERS-1 or ERS-2, based on whether the heights were from ocean-mode or ice-mode data. The parameters in Equation S4 () were estimated using a robust linear regression where outliers outside the min(3, 10 m) range were discarded in 10 iterations. We estimated standard errors of the regression for each of the parameters in Equation S5, and discarded grid cells with an error greater than 0.3 m/yr in , The residuals in the linear regression were binned in three-month intervals and contain any temporal signal that is not included in a linear trend as well as noise.
The height-change rate () estimate for an ice shelf for each individual mission was then
| (S6) |
We processed CryoSat-2 data using the Eulerian ‘plane-fit’ technique described in ref. 61 (their Section S1) after applying the same geophysical corrections used for ERS-1, ERS-2, and Envisat data.
S3.2. Merging of altimeter time series
To avoid biases from different spatial sampling, we discarded data from all grid cells which did not contain height change measurements from all four missions. For grid cells where sufficient data were available, we then merged the height change time series from the four radar altimeters by ensuring that height-change rate during the time periods with overlapping data was equal to the average of the height-change rates estimated from each altimeter. Therefore, we imposed during 1995–1996, during 2002–2003, and during 2010–2011. In addition to a merged multi-mission time series, we also obtained a merged height-change time series referenced to the height at by integrating in time.
S3.3. Influence of surface melting on radar-derived height changes
We found large decreases in RA-derived height changes between 1992 and 1994 across Antarctica. In some previous studies2,76, data from this period were excluded due to this anomalous signal. Using surface melt data from RACMO and a positive degree day model based on MERRA-264, we found that this change in RA-derived height change was primarily due to a large circum-Antarctic surface melt event in December 1991. This melt event likely created a bright radar reflector, and its burial following subsequent snowfall was tracked by the radar altimeter, which caused a downward trend in estimated height. Due to the large effect of this event across several ice shelves around Antarctica, we excluded this period in our analysis.
For Ross Ice Shelf, we found large changes in height following anomalous surface melt events during the austral summers of 1991/1992, 2002–2003, and 2015/2016. Two of these (1991/1992 and 2015/2016) were the largest surface melt events over the ice shelf during the 1980–2016 period77. We accounted for the radar response following such events by estimating a time series of using height changes measured over grounded ice adjacent to the floating ice shelf, following the methodology of ref. 51. We derived height changes over grounded ice up to 100 km from the ice shelf boundary in grid cells at 5 km spacing using the plane-fit technique described by ref. 78. Each grid cell had at least 15 data points spanning a time interval of at least 3 years. We discarded grid cells with an uncertainty in estimated greater than 0.3 m/yr. Since there were too few data to apply a spatially variable correction over the ice shelf, we followed ref. 51 to use a single time series for the entire ice shelf.
S4. Time series of melt rates
From the merged multi-mission Eulerian height-change rate time series spanning 1994 to 2018, we derived time series of basal melt rate anomalies (, relative to the 2010–2018 mean) using
| (S7) |
where , and are anomalies (relative to the 2010–2018 mean) in rates of altimeter-derived height change, firn-air content from GSFC-FDMv0, and MERRA-2 P-E data, respectively, smoothed to three-month time scales using a moving average filter. We only considered anomalies in for the Amundsen Sea sector, for which we used time-variable estimates of from ref. 79 for the 1994–2013 period and from ref. 80 for the 2014–2017 period. Gaps in the time series of were filled using linear interpolation. We produced time series of basal melt rates, , by adding high resolution melt rates from CryoSat-2 analysis (Section S1) to the time series of melt rate anomalies . We assume that there was no change in in regions south of 81.5°S, the orbit limit of the ERS-1, ERS-2 and Envisat satellites.
S5. Uncertainty estimation
We compared GSFC-FDMv0 estimates of to previously published estimates from an atmospheric model (RACMO2.3p281) and the associated firn densification model (IMAU-FDM82) between 1979 and 2016 (the time period available for RACMO and IMAU-FDM). Using this comparison, we derived an uncertainty estimate using the combination of: (a) sensitivity tests to quantify uncertainties from the assumption of steady state climate that is used to spin up a firn densification model1 (Figure S7a); and (b) standard deviations of differences between GSFC-FDMv0 and IMAU-FDM estimates of values during 1980–2016 at GSFC-FDMv0 grid cell locations (these values are shown in Figure S7b for annual time scales, but they are smaller for the longer time scales typically considered in this study). We assumed that these uncertainties were Gaussian and uncorrelated, and added them in quadrature.
We estimated uncertainties for all terms in Equation S5 as the uncertainties from the linear regression, and propagated these to in Equation S6. Uncertainties in were estimated as the standard deviation of heights from the residuals of Equation S5 within each quarterly bin. Uncertainties in were provided by ref. 62, uncertainties in were estimated using a moving standard deviation at annual time scales, and the uncertainties in the advection of heights from Lagrangian processing were not considered; compared to previously described uncertainty sources, the three sources here represent a substantially smaller component of total uncertainty. We propagated these uncertainties to the filtered time series of basal melt rate using a bootstrap approach. For each ice shelf (or in the case of the top four panels of Figure 4, for regions within large ice shelves), we applied a filter to the average time series that included both a gradient and a smoothing operator to estimate . The residuals from the filtered time series were resampled 100 times, and each sample was combined with Gaussian random noise from the error sources described previously. These samples were added back to and integrated to produce 100 resampled time series , which were used to produce 100 time series of . The standard deviation of provided the final uncertainty in . We estimated uncertainties in melt rates in the eight sectors around Antarctica by summing the uncertainties from all ice shelves in each sector in quadrature (Table S1).
S6. Estimates of marine ice thickness
We estimated thickness of marine ice () under Ronne and Amery ice shelves from our steady-state basal melt rate estimates, , using83
| (S8) |
where and represents the distance along a flowline. Here, we use instead of the time-stamped estimate () because the value of is a function of the accumulation and strain rates of an ice shelf at decadal to centennial time scales. We generated flowlines for Ronne and Amery ice shelves, and solved Equation S8 using with year, assuming at the beginning of the flowline. Our estimated values of for both ice shelves show good agreement with independent estimates derived by differencing thicknesses derived from satellite altimetry and from radar sounding84,85 (Figure S3).
S7. Changes in iceberg calving rates
We have so far only considered temporal variability in ice shelf mass and meltwater flux due to changes in ice shelf basal melt rates relative to steady-state values. However, ice shelf hydrofracture in the Antarctic Peninsula86 and excess iceberg calving rates due to long-term dynamic thinning of Amundsen Sea87 have also contributed to net ice shelf mass loss and increases in meltwater export to the upper ocean in recent decades. We estimated net mass loss due to changes in ice shelf extent from ice shelf thickness estimates generated using elevations from the ERS-1 geodetic phase (1994–1995) for regions where ice shelf areas decreased; these were excluded from previous thickness estimates88. We estimated a net mass loss of 1650±200 Gt from Antarctic Peninsula ice shelves during our record (Figure S7) due to the hydrofracture-induced collapse of Larsen A, Larsen B, and sections of Wilkins ice shelves89,90. Additionally, net retreat of Thwaites, Pine Island, and Getz ice shelves in the Amundsen Sea contributed to a combined net mass loss of 1230±70 Gt. The combined mass loss from excess calving of Antarctic Peninsula and Amundsen Sea sector ice shelves was 2880±210 Gt, which is comparable to our circum-Antarctic mass loss estimate of 3960±1100 Gt from thinning ice shelves (Figure 3a).
Supplementary Material
Acknowledgements:
This study was funded by NASA grants NNX17AI03G and NNX17AG63G. SA was also supported by the NASA Earth and Space Science Fellowship. We thank the two anonymous reviewers, members of the Scripps Polar Center, Susan Howard, and Keith Nicholls for their important contributions to this manuscript.
Footnotes
The authors declare no competing interests.
Data Availability: ERS-1, ERS-2, Envisat, and CryoSat-2 radar altimetry data are available from the European Space Agency (ERS-1 and ERS-2 data from ftp://ra-ftp-ds.eo.esa.int/, Envisat data from ftp://ra2-ftp-ds.eo.esa.int/, and CryoSat-2 level-2 SARIn-mode data from ftp://science-pds.cryosat.esa.int/SIR_SIN_L2). We provide two datasets at doi.org/10.6075/J04Q7SHT: (i) basal melt rates at high spatial resolution (500 m grid cells, average for the period 2010 to 2018) and (ii) changes in height from satellite altimetry, firn air content from GSFC-FDMv0, and precipitation minus evaporation from MERRA-2 at 10 km grid cells and three-month intervals for 1994 to 2018. (ii) can be used to estimate time-varying basal melt rates using Equation S7.
Code Availability: The Matlab, Python, and shell scripts used for the analyses described in this study can be obtained from the corresponding author upon reasonable request. Code to read and visualize the derived data products described in this manuscript, and to reproduce the major elements of Figures 1 to 4 is available at https://github.com/sioglaciology/ice_shelf_change.
References
- 1.Pritchard HD et al. Antarctic ice-sheet loss driven by basal melting of ice shelves. Nature 484, 502–505 (2012). [DOI] [PubMed] [Google Scholar]
- 2.Paolo FS, Fricker HA & Padman L Volume loss from Antarctic ice shelves is accelerating. Science 348, 327–331 (2015). [DOI] [PubMed] [Google Scholar]
- 3.Thomas RH, Sanderson TJO & Rose KE Effect of climatic warming on the West Antarctic ice sheet. Nature 277, 355–358 (1979). [Google Scholar]
- 4.Jenkins A et al. West Antarctic Ice Sheet retreat in the Amundsen Sea driven by decadal oceanic variability. Nature Geosci 11, 733–738 (2018). [Google Scholar]
- 5.Nerem RS et al. Climate-change–driven accelerated sea-level rise detected in the altimeter era. PNAS 115, 2022–2025 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Jacobs SS, Helmer HH, Doake CSM, Jenkins A & Frolich RM Melting of ice shelves and the mass balance of Antarctica. Journal of Glaciology 38, 375–387 (1992). [Google Scholar]
- 7.Nicholls KW Predicted reduction in basal melt rates of an Antarctic ice shelf in a warmer climate. Nature 388, 460–462 (1997). [Google Scholar]
- 8.Lewis EL & Perkin RG Ice pumps and their rates. Journal of Geophysical Research: Oceans 91, 11756–11762 (1986). [Google Scholar]
- 9.Turner J et al. Atmosphere-ocean-ice interactions in the Amundsen Sea Embayment, West Antarctica. Reviews of Geophysics 55, 235–276 (2017). [Google Scholar]
- 10.Rintoul SR The global influence of localized dynamics in the Southern Ocean. Nature 558, 209–218 (2018). [DOI] [PubMed] [Google Scholar]
- 11.Pauling AG, Smith IJ, Langhorne PJ & Bitz CM Time-Dependent Freshwater Input From Ice Shelves: Impacts on Antarctic Sea Ice and the Southern Ocean in an Earth System Model. Geophysical Research Letters 44, 10,454–10,461 (2017). [Google Scholar]
- 12.Merino N et al. Impact of increasing antarctic glacial freshwater release on regional sea-ice cover in the Southern Ocean. Ocean Modelling 121, 76–89 (2018). [Google Scholar]
- 13.Fogwill CJ, Phipps SJ, Turney CSM & Golledge NR Sensitivity of the Southern Ocean to enhanced regional Antarctic ice sheet meltwater input. Earth’s Future 3, 317–329 (2015). [Google Scholar]
- 14.Moffat C, Beardsley RC, Owens B & van Lipzig N A first description of the Antarctic Peninsula Coastal Current. Deep Sea Research Part II: Topical Studies in Oceanography 55, 277–293 (2008). [Google Scholar]
- 15.Nakayama Y, Timmermann R, Rodehacke CB, Schröder M & Hellmer HH Modeling the spreading of glacial meltwater from the Amundsen and Bellingshausen Seas. Geophysical Research Letters 41, 7942–7949 (2014). [Google Scholar]
- 16.Golledge NR et al. Global environmental consequences of twenty-first-century ice-sheet melt. Nature 566, 65–72 (2019). [DOI] [PubMed] [Google Scholar]
- 17.Eyring V et al. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geoscientific Model Development 9, 1937–1958 (2016). [Google Scholar]
- 18.Jourdain NC et al. A protocol for calculating basal melt rates in the ISMIP6 Antarctic ice sheet projections. The Cryosphere Discuss. 2019, 1–33 (2019). [Google Scholar]
- 19.Rignot E, Jacobs S, Mouginot J & Scheuchl B Ice-Shelf Melting Around Antarctica. Science 341, 266–270 (2013). [DOI] [PubMed] [Google Scholar]
- 20.Depoorter MA et al. Calving fluxes and basal melt rates of Antarctic ice shelves. Nature 502, 89–92 (2013). [DOI] [PubMed] [Google Scholar]
- 21.Dutrieux P et al. Pine Island glacier ice shelf melt distributed at kilometre scales. The Cryosphere 7, 1543–1555 (2013). [Google Scholar]
- 22.Gourmelen N et al. Channelized Melting Drives Thinning Under a Rapidly Melting Antarctic Ice Shelf. Geophysical Research Letters 44, 9796–9804 (2017). [Google Scholar]
- 23.Wingham DJ CryoSat: a mission to determine fluctuations in the Earth’s ice fields. in IEEE International Geoscience and Remote Sensing Symposium vol. 3 1750–1752 vol.3 (2002). [Google Scholar]
- 24.Lane-Serff GF On meltwater under ice shelves. Journal of Geophysical Research: Oceans 100, 6961–6965 (1995). [Google Scholar]
- 25.Holland PR, Feltham DL & Jenkins A Ice Shelf Water plume flow beneath Filchner-Ronne Ice Shelf, Antarctica. Journal of Geophysical Research: Oceans 112, (2007). [Google Scholar]
- 26.Foldvik A Ice shelf water overflow and bottom water formation in the southern Weddell Sea. Journal of Geophysical Research 109, (2004). [Google Scholar]
- 27.Smethie WM & Jacobs SS Circulation and melting under the Ross Ice Shelf: estimates from evolving CFC, salinity and temperature fields in the Ross Sea. Deep Sea Research Part I: Oceanographic Research Papers 52, 959–978 (2005). [Google Scholar]
- 28.Herraiz-Borreguero L, Lannuzel D, Merwe P van der, Treverrow, A. & Pedro, J. B. Large flux of iron from the Amery Ice Shelf marine ice to Prydz Bay, East Antarctica. Journal of Geophysical Research: Oceans 121, 6009–6020 (2016). [Google Scholar]
- 29.Schlosser P et al. Oxygen 18 and helium as tracers of ice shelf water and water/ice interaction in the Weddell Sea. Journal of Geophysical Research 95, 3253 (1990). [Google Scholar]
- 30.Reese R, Gudmundsson GH, Levermann A & Winkelmann R The far reach of ice-shelf thinning in Antarctica. Nature Clim Change 8, 53–57 (2018). [Google Scholar]
- 31.Goldberg DN, Gourmelen N, Kimura S, Millan R & Snow K How Accurately Should We Model Ice Shelf Melt Rates? Geophysical Research Letters 46, 189–199 (2019). [Google Scholar]
- 32.Fürst JJ et al. The safety band of Antarctic ice shelves. Nature Climate Change 6, 479–482 (2016). [Google Scholar]
- 33.Malyarenko A, Robinson NJ, Williams MJM & Langhorne PJ A Wedge Mechanism for Summer Surface Water Inflow Into the Ross Ice Shelf Cavity. Journal of Geophysical Research: Oceans 124, 1196–1214 (2019). [Google Scholar]
- 34.Porter DF et al. Evolution of the Seasonal Surface Mixed Layer of the Ross Sea, Antarctica, Observed With Autonomous Profiling Floats. Journal of Geophysical Research: Oceans 124, 4934–4953 (2019). [Google Scholar]
- 35.Stewart CL, Christoffersen P, Nicholls KW, Williams MJM & Dowdeswell JA Basal melting of Ross Ice Shelf from solar heat absorption in an ice-front polynya. Nat. Geosci. 12, 435–440 (2019). [Google Scholar]
- 36.Tinto KJ et al. Ross Ice Shelf response to climate driven by the tectonic imprint on seafloor bathymetry. Nat. Geosci. 12, 441–449 (2019). [Google Scholar]
- 37.The IMBIE team. Mass balance of the Antarctic Ice Sheet from 1992 to 2017. Nature 558, 219–222 (2018). [DOI] [PubMed] [Google Scholar]
- 38.Smith B et al. Pervasive ice sheet mass loss reflects competing ocean and atmosphere processes. Science (2020) doi: 10.1126/science.aaz5845. [DOI] [PubMed] [Google Scholar]
- 39.Castagno P et al. Rebound of shelf water salinity in the Ross Sea. Nature Communications 10, 5441 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Nicholls KW & Østerhus S Interannual variability and ventilation timescales in the ocean cavity beneath Filchner-Ronne Ice Shelf, Antarctica. Journal of Geophysical Research: Oceans 109, (2004). [Google Scholar]
- 41.Smith BE, Fricker HA, Joughin IR & Tulaczyk S An inventory of active subglacial lakes in Antarctica detected by ICESat (2003–2008). Journal of Glaciology 55, 573–595 (2009). [Google Scholar]
- 42.Motyka RJ, Dryer WP, Amundson J, Truffer M & Fahnestock M Rapid submarine melting driven by subglacial discharge, LeConte Glacier, Alaska. Geophysical Research Letters 40, 5153–5158 (2013). [Google Scholar]
- 43.Washam P, Nicholls KW, Münchow A & Padman L Summer surface melt thins Petermann Gletscher Ice Shelf by enhancing channelized basal melt. Journal of Glaciology 65, 662–674 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Dutrieux P et al. Strong Sensitivity of Pine Island Ice-Shelf Melting to Climatic Variability. Science 343, 174–178 (2014). [DOI] [PubMed] [Google Scholar]
- 45.Paolo FS et al. Response of Pacific-sector Antarctic ice shelves to the El Niño/Southern Oscillation. Nature Geosci 11, 121–126 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Kimura S et al. Oceanographic Controls on the Variability of Ice-Shelf Basal Melting and Circulation of Glacial Meltwater in the Amundsen Sea Embayment, Antarctica. Journal of Geophysical Research: Oceans 122, 10131–10155 (2017). [Google Scholar]
- 47.Holland PR, Bracegirdle TJ, Dutrieux P, Jenkins A & Steig EJ West Antarctic ice loss influenced by internal climate variability and anthropogenic forcing. Nat. Geosci. 12, 718–724 (2019). [Google Scholar]
- 48.Budillon G, Castagno P, Aliani S, Spezie G & Padman L Thermohaline variability and Antarctic bottom water formation at the Ross Sea shelf break. Deep Sea Research Part I: Oceanographic Research Papers 58, 1002–1018 (2011). [Google Scholar]
- 49.Williams GD et al. The suppression of Antarctic bottom water formation by melting ice shelves in Prydz Bay. Nat Commun 7, 1–9 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Petty AA, Holland PR & Feltham DL Sea ice and the ocean mixed layer over the Antarctic shelf seas. The Cryosphere 8, 761–783 (2014). [Google Scholar]
References only in Methods
- 51.Moholdt G, Padman L & Fricker HA Basal mass budget of Ross and Filchner-Ronne ice shelves, Antarctica, derived from Lagrangian analysis of ICESat altimetry. Journal of Geophysical Research: Earth Surface 119, 2361–2380 (2014). [Google Scholar]
- 52.Förste C et al. EIGEN-6C4-The latest combined global gravity field model including GOCE data up to degree and order 1949 of GFZ Potsdam and GRGS Toulouse. in EGU general assembly conference abstracts vol. 16 (2014). [Google Scholar]
- 53.Andersen O, Knudsen P & Stenseng L The DTU13 MSS (Mean Sea Surface) and MDT (Mean Dynamic Topography) from 20 Years of Satellite Altimetry in IGFS 2014 (eds. Jin S & Barzaghi R) 111–121 (Springer International Publishing, 2016). [Google Scholar]
- 54.Howard SL, Padman L & Erofeeva SY CATS2008: Circum-Antarctic Tidal Simulation version 2008. (2019) doi: 10.15784/601235. [DOI] [Google Scholar]
- 55.Padman L, Fricker HA, Coleman R, Howard S & Erofeeva L A new tide model for the Antarctic ice shelves and seas. Annals of Glaciology 34, 247–254 (2002). [Google Scholar]
- 56.Carrère L & Lyard F Modeling the barotropic response of the global ocean to atmospheric wind and pressure forcing - comparisons with observations. Geophysical Research Letters 30, (2003). [Google Scholar]
- 57.Egbert GD & Erofeeva SY Efficient Inverse Modeling of Barotropic Ocean Tides. J. Atmos. Oceanic Technol. 19, 183–204 (2002). [Google Scholar]
- 58.Rye CD et al. Rapid sea-level rise along the Antarctic margins in response to increased glacial discharge. Nature Geoscience 7, 732–735 (2014). [Google Scholar]
- 59.Gardner AS et al. Increased West Antarctic and unchanged East Antarctic ice discharge over the last 7 years. The Cryosphere 12, 521–547 (2018). [Google Scholar]
- 60.Rignot E, Mouginot J & Scheuchl B MEaSUREs InSAR-Based Antarctica Ice Velocity Map, Version 2 (2017). [Google Scholar]
- 61.Adusumilli S et al. Variable Basal Melt Rates of Antarctic Peninsula Ice Shelves, 1994–2016. Geophysical Research Letters 45, 4086–4095 (2018). [Google Scholar]
- 62.Alley KE et al. Continent-wide estimates of Antarctic strain rates from Landsat 8-derived velocity grids. Journal of Glaciology 64, 321–332 (2018). [Google Scholar]
- 63.Gelaro R et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). Journal of Climate 30, 5419–5454 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Smith BE et al. Pervasive ice sheet mass loss reflects competing ocean and atmosphere processes (Accepted for publication). Science (2020). [DOI] [PubMed] [Google Scholar]
- 65.Arthern RJ, Vaughan DG, Rankin AM, Mulvaney R & Thomas ER In situ measurements of Antarctic snow compaction compared with predictions of models. Journal of Geophysical Research: Earth Surface 115, (2010). [Google Scholar]
- 66.Stevens CM et al. The Community Firn Model (CFM) v1.0. Geoscientific Model Development Discussions 1–37 (2020) doi: 10.5194/gmd-2019-361. [DOI] [Google Scholar]
- 67.Morlighem M et al. Deep glacial troughs and stabilizing ridges unveiled beneath the margins of the Antarctic ice sheet. Nature Geoscience 13, 132–137 (2020). [Google Scholar]
- 68.Boyer Tim P.; Antonov John I.; Baranova Olga K.; Coleman Carla; Garcia Hernan E.; Grodsky Alexandra; Johnson Daphne R.; Locarnini Ricardo A.; Mishonov Alexey V.; O’Brien Todd D.; Paver Christopher R.; Reagan James R.; Seidov Dan; Smolyar Igor V.; Zweng Melissa M. NCEI Standard Product: World Ocean Database (WOD). (2018). [Google Scholar]
- 69.McDougall TJ, Barker PM, Feistel R & Galton-Fenzi BK Melting of Ice and Sea Ice into Seawater and Frazil Ice Formation. J. Phys. Oceanogr. 44, 1751–1775 (2014). [Google Scholar]
- 70.McDougall Trevor J. & Barker Paul M. Getting started with TEOS-10 and the Gibbs Seawater (GSW) oceanographic toolbox. SCOR/IAPSO WG 127, 1–28 (2011). [Google Scholar]
- 71.Schaffer J et al. A global, high-resolution data set of ice sheet topography, cavity geometry, and ocean bathymetry. Earth System Science Data 8, 543–557 (2016). [Google Scholar]
- 72.Dunn JR & Ridgway KR Mapping ocean properties in regions of complex topography. Deep Sea Research Part I: Oceanographic Research Papers 49, 591–604 (2002). [Google Scholar]
- 73.Dinniman MS, Klinck JM & Smith WO A model study of Circumpolar Deep Water on the West Antarctic Peninsula and Ross Sea continental shelves. Deep Sea Research Part II: Topical Studies in Oceanography 58, 1508–1523 (2011). [Google Scholar]
- 74.Brockley DJ et al. REAPER: Reprocessing 12 Years of ERS-1 and ERS-2 Altimeters and Microwave Radiometer Data. IEEE Transactions on Geoscience and Remote Sensing 55, 5506–5514 (2017). [Google Scholar]
- 75.Soussi B et al. ENVISAT Altimetry Level 2 Product Handbook. (2018). [Google Scholar]
- 76.Paolo FS, Fricker HA & Padman L Constructing improved decadal records of Antarctic ice shelf height change from multiple satellite radar altimeters. Remote Sensing of Environment 177, 192–205 (2016). [Google Scholar]
- 77.Nicolas JP et al. January 2016 extensive summer melt in West Antarctica favoured by strong El Niño. Nat Commun 8, 1–10 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.McMillan M et al. Increased ice losses from Antarctica detected by CryoSat-2. Geophysical Research Letters 41, 3899–3905 (2014). [Google Scholar]
- 79.Mouginot J, Rignot E & Scheuchl B Sustained increase in ice discharge from the Amundsen Sea Embayment, West Antarctica, from 1973 to 2013. Geophysical Research Letters 41, 1576–1584 (2014). [Google Scholar]
- 80.Mouginot J, Rignot E, Scheuchl B & Millan R Comprehensive Annual Ice Sheet Velocity Mapping Using Landsat-8, Sentinel-1, and RADARSAT-2 Data. Remote Sensing 9, 364 (2017). [Google Scholar]
- 81.Wessem JM van et al. Modelling the climate and surface mass balance of polar ice sheets using RACMO2 – Part 2: Antarctica (1979–2016). The Cryosphere 12, 1479–1498 (2018). [Google Scholar]
- 82.Ligtenberg SRM, Helsen MM & Broeke MR van den. An improved semi-empirical model for the densification of Antarctic firn. The Cryosphere 5, 809–819 (2011). [Google Scholar]
- 83.Joughin I & Vaughan DG Marine ice beneath the Filchner–Ronne Ice Shelf, Antarctica: a comparison of estimated thickness distributions. Annals of Glaciology 39, 511–517 (2004). [Google Scholar]
- 84.Fricker HA, Popov S, Allison I & Young N Distribution of marine ice beneath the Amery Ice Shelf. Geophysical Research Letters 28, 2241–2244 (2001). [Google Scholar]
- 85.Lambrecht A, Sandhäger H, Vaughan DG & Mayer C New ice thickness maps of Filchner–Ronne Ice Shelf, Antarctica, with specific focus on grounding lines and marine ice. Antarctic Science 19, 521–532 (2007). [Google Scholar]
- 86.Cook AJ & Vaughan DG Overview of areal changes of the ice shelves on the Antarctic Peninsula over the past 50 years. The Cryosphere 22 (2010). [Google Scholar]
- 87.MacGregor JA, Catania GA, Markowski MS & Andrews AG Widespread rifting and retreat of ice-shelf margins in the eastern Amundsen Sea Embayment between 1972 and 2011. Journal of Glaciology 58, 458–466 (2012). [Google Scholar]
- 88.Griggs JA & Bamber JL Antarctic ice-shelf thickness from satellite radar altimetry. Journal of Glaciology 57, 485–498 (2011). [Google Scholar]
- 89.Scambos TA, Bohlander JA, Shuman CA & Skvarca P Glacier acceleration and thinning after ice shelf collapse in the Larsen B embayment, Antarctica. Geophysical Research Letters 31, (2004). [Google Scholar]
- 90.Scambos T et al. Ice shelf disintegration by plate bending and hydro-fracture: Satellite observations and model results of the 2008 Wilkins ice shelf break-ups. Earth and Planetary Science Letters 280, 51–60 (2009). [Google Scholar]
- 91.Mouginot J, Scheuchl B & Rignot E MEaSUREs Antarctic Boundaries for IPY 2007–2009 from Satellite Radar, Version 2. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.