Simulation of coronavirus disease 2019 (COVID-19) scenarios with possibility of reinfection

Abstract

Epidemiological models of COVID-19 transmission assume that recovered individuals have a fully protected immunity. To date, there is no definite answer about whether people who recover from COVID-19 can be reinfected with the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). In the absence of a clear answer about the risk of reinfection, it is instructive to consider the possible scenarios. To study the epidemiological dynamics with the possibility of reinfection, I use a Susceptible-Exposed-Infectious-Resistant-Susceptible model with the time-varying transmission rate. I consider three different ways of modeling reinfection. The crucial feature of this study is that I explore both the difference between the reinfection and no-reinfection scenarios and how the mitigation measures affect this difference. The principal results are the following. First, the dynamics of the reinfection and no-reinfection scenarios are indistinguishable before the infection peak. Second, the mitigation measures delay not only the infection peak, but also the moment when the difference between the reinfection and no-reinfection scenarios becomes prominent. These results are robust to various modeling assumptions.

1. Introduction

The rapid spread of coronavirus disease 2019 (COVID-19) creates significant challenges for economies and healthcare systems of many countries around the world. The situation evolves extremely quickly and, to date, there is a high degree of uncertainty about the future outcomes of the pandemic. As of September 1, 2020, there have been 25.9 million confirmed cases globally, including about 860 thousand deaths, see [28].

One of the crucial questions that still has no definite answer is whether people who recover from COVID-19 can be reinfected with the severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2). The case reports are scarce — there are a few of them about positive testing after recovering from COVID-19 in China, Japan, and South Korea — and it is not clear whether these patients are truly reinfected or not. Shi et al. [24] discuss the immune responses induced by COVID-19. Another study, Bao et al. [4], using the sample of four rhesus macaques, conclude that the primary SARS-CoV-2 infection could protect from subsequent reinfections. In turn, An et al. [1], show that 38 out of 262 patients, i.e. 14.5 percent, recovered from COVID-19, tested positive for SARS-CoV-2, using polymerase chain reaction (PCR) tests, after being discharged from the hospital in Shenzhen. Those patients did not show obviously clinical symptoms and disease progression upon readmission. A recent study by To et al. [25] shows the results of the whole genome sequencing that was performed directly on respiratory specimens collected during two episodes of COVID-19 in a patient. Epidemiological, clinical, serological, and genomic analyses confirmed that the patient had reinfection instead of persistent viral shedding from the first infection. Their paper suggests that SARS-CoV-2 may continue to circulate among the human populations despite herd immunity due to natural infection or vaccination.

In the absence of a clear answer about the risk of reinfection with the new coronavirus, it is instructive to be aware of the possible scenarios. This study aims at providing the attempt in this direction. I use a Susceptible-Exposed-Infectious-Resistant-Susceptible (SEIRS) model that differs from a standard SEIR model, considered in Hethcote [11] and Chowell et al. [8], and, in application to COVID-19, Kucharski et al. [14], Lin et al. [18], Prem et al. [20], and Wang et al. [27], among others, with an additional assumption that recovered individuals can become susceptible to infection again. In methodologically related papers, Reynolds et al. [22] and Etbaigha et al. [9] study the reinfection of swines with influenza A virus (IAV). The simulations considered in this paper are by no means the definitive quantitative forecasts. Instead, the purpose is to show the patterns of the disease dynamics if people can be reinfected with the new coronavirus. In fact, the risk of reinfection would definitely affect the scope and duration of policies that are currently in place.

I consider three different ways of modeling reinfection. I begin with the model where individuals have constant immunity waning rate and study the effects of the mitigation policies captured by the changes in the transmission rate and hence the reproduction number. The basic reproduction number, R ₀, is a crucial parameter for evaluation the spread of the infection and the effects of mitigation measures. Existing estimates for COVID-19 suggest that R ₀ is between 2 and 6. Using the data from Wuhan, China, Wu et al. [29] estimate R ₀ to be 2.68 (95% confidence interval (CI): 2.47–2.86). Using the data from mainland China, Zhao et al. [30] conclude that the mean estimate of R ₀ ranges from 2.24 (95% CI: 1.96–2.55) to 3.58 (95% CI: 2.89–4.39). Using the data for Italy, Remuzzi and Remuzzi [21] propose R ₀ to be in the range 2.76–3.25. Using the data for Japan, Kuniya [15] estimates R ₀ to be 2.6 (95% CI: 2.4–2.8). Fauci et al. [10] propose R ₀ to be 2.2. Sanche et al. [23] obtain a higher median estimate, $R_0=5.7$(95% CI: 3.8–8.9). Beyond that, Korolev [13] shows that estimates of R ₀ are highly sensitive to the values of epidemiologic parameters. In the simulations, I consider the range of values of the basic reproduction number.

Crucially, in each model experiment I consider not only how different are the reinfection and no-reinfection scenarios, but also how the mitigation measures affect this difference. To check the robustness of my findings about the role of the mitigation measures with and without reinfection, I turn to the alternative modeling assumptions about reinfection. First, I assume that individuals, once being reinfected, have a milder form of the disease. Second, instead of a constant immunity waning rate, I assume that the individuals that are resistant at some date (those who were infected in the past) become susceptible again. The conceptual framework that I use can be easily incorporated into more complex models in future studies.

2. Model

Consider a SEIRS model with constant population N normalized to one. Each period of time, the population consists of four classes: susceptible (S), exposed (E), infected (I), and resistant (recovered) (R):

$$S\left(t\right)+E\left(t\right)+I\left(t\right)+R\left(t\right)=N,\forall t\ge 0$$ (1)

Since $N=1,$variables S, E, I, and R correspond to the fractions of the population. I assume that recovered individuals can become susceptible to infection again at rate ω. The compartmental model is formulated by the following set of ordinary differential equations:

$$\frac{dS\left(t\right)}{dt}=-\beta \left(t\right)\frac{S\left(t\right)}{N}I\left(t\right)+\omega R\left(t\right)$$ (2)

$$\frac{dE\left(t\right)}{dt}=\beta \left(t\right)\frac{S\left(t\right)}{N}I\left(t\right)-\sigma E\left(t\right)$$ (3)

$$\frac{dI\left(t\right)}{dt}=\sigma E\left(t\right)-\gamma I\left(t\right)$$ (4)

$$\frac{dR\left(t\right)}{dt}=\gamma I\left(t\right)-\omega R\left(t\right)$$ (5)

The transmission rate, β(t), accounts for the rate at which infected individuals interact with others and transmit the disease and is given by

$$\beta \left(t\right)=\gamma \tilde{R}\left(t\right)$$ (6)

where $\tilde{R}\left(t\right)$is the time-varying reproduction number. Absent mitigation measures, $\tilde{R}$corresponds to the basic reproduction number, R ₀. To simplify notation, here and thereafter I omit explicit dependence of $\tilde{R}$on time whenever it does not cause confusion. The transmission rate, β(t), captures the impact of all mitigation measures such as quarantine, travel restrictions, or social distancing. To study scenarios under different mitigation policies, I adapt a flexible functional form for the time-varying reproduction number. Following [3], I parameterize $\tilde{R}\left(t\right)$as follows:

$${\tilde{R}}_1\left(t\right)=\exp (-{\eta }_{1}t){\tilde{R}}_1\left(0\right)+(1-\exp (-{\eta }_{1}t))R_1^{*}$$ (7)

$${\tilde{R}}_2\left(t\right)=\exp (-{\eta }_{2}t){\tilde{R}}_2\left(0\right)+(1-\exp (-{\eta }_{2}t))R_2^{*}$$ (8)

$$\tilde{R}\left(t\right)=\frac{1}{2}({\tilde{R}}_1\left(t\right)+{\tilde{R}}_2\left(t\right))$$ (9)

where ${\tilde{R}}_1\left(0\right)$and ${\tilde{R}}_2\left(0\right)$($R_1^{*}$and $R_2^{*}$) are the initial (long-run) values for ${\tilde{R}}_1$and ${\tilde{R}}_2$. Parameter η ₁determines the rate at which ${\tilde{R}}_1$converges to $R_1^{*}$. In turn, parameter η ₂governs the rate at which ${\tilde{R}}_2$converges to $R_2^{*}$. By appropriately choosing the parameter values, I can capture different scenarios of the mitigation policies. In particular, in the simulations in Section 3, I vary the speed of imposing the mitigation measures and also consider the scenario when extremely severe mitigation measures at the beginning of the pandemic are followed by their gradual relaxation. From (7)–(9), the dynamics of ${\tilde{R}}_1,$ ${\tilde{R}}_2,$and $\tilde{R}$is described by the following equations:

$$\frac{d{\tilde{R}}_1\left(t\right)}{dt}=-{\eta }_1({\tilde{R}}_1\left(t\right)-R_1^{*})$$ (10)

$$\frac{d{\tilde{R}}_2\left(t\right)}{dt}=-{\eta }_2({\tilde{R}}_2\left(t\right)-R_2^{*})$$ (11)

$$\frac{d\tilde{R}\left(t\right)}{dt}=-\frac{1}{2}{\eta }_1({\tilde{R}}_1\left(t\right)-R_1^{*})-\frac{1}{2}{\eta }_2({\tilde{R}}_2\left(t\right)-R_2^{*})$$ (12)

Parameters (σ, γ, ω) represent the characteristics of COVID-19 and assumed to be constant. For parameters σ and γ, I take the estimates from the literature. The parameter σ stands for the mean incubation period of the disease, and its estimates vary from 1/5.2 to 1/3, see [18] and [27]. Following [16] and [27], I adopt a mean latent period of 5.2 days (infection rate, $\sigma =1/5.2$). Next, I adopt a mean infectious period of 18 days (recovery rate, $\gamma =1/18$) in line with [7]and [27]. Parameter ω, the immunity waning rate, is of the main interest for this paper, and since, to date, there are no credible estimates of it, I consider the range of different values, ω ∈ {0, 1/365, 1/183, 1/120, 1/60}. To et al. [25] show that the second episode of asymptomatic infection occurred 142 days after the first symptomatic episode in an apparently immunocompetent patient. This period is consistent with considered range of ω. The case $\omega =0$corresponds to no reinfection. The value of ω is driven by immunity waning after the infection or the rate of virus mutation. Next, the initial values for actively infected and exposed population are taken for the United States and set to $I\left(0\right)=1/1000,$i.e. 0.1 percent of the population, and $E\left(0\right)=43.75\times I\left(0\right)$respectively. I use March 16–17, 2020 as the initial date (March 17, 2020 was a day at which the last U.S. state reported its first case, see [19]). I take $I\left(0\right)=1/1000$from [5]. Official data reports around 4500 cases in the United States on March 16, and they assume that this represents 1.5 percent of all cases. This rate of underreporting is derived by Hortaçsu et al. [12] for March 9, 2020. $E\left(0\right)=43.75\times I\left(0\right)$corresponds to the estimates for the United States by Peirlinck et al. [19].

Throughout the simulations, I fully acknowledge that only a fraction of the model-generated cases are reported in reality. Li et al. [17] study the critical importance of undocumented COVID-19 cases for understanding the overall prevalence and pandemic potential of this disease. Lin et al. [18] emphasize that the reporting rate is time-varying.

3. Model simulations

In this section, I use the assumptions about the time paths for $\tilde{R}$from [3]. This allows me to clearly compare the outcomes under reinfection with his conclusions from the simulations without reinfection. In the first model experiment, I assume that $\tilde{R}$is fixed over time. This reflects the scenarios when mitigation efforts do not change over time.

In the first model experiment, I consider a range of values of the basic reproduction number $\tilde{R}=R_0\in \{1.6,1.8,2.0,2.2,2.5,2.8,3.0\}$. The upper bound of this range captures the estimates from the literature discussed in Section 1. Lower values of R ₀correspond to lower levels of the disease transmission. The mitigation measures — quarantine, travel restrictions, or social distancing — can reduce the basic reproduction number. Anderson et al. [2] provide a thorough discussion of this question. Critically, in my simulations, I vary both ω and R ₀. By comparing the simulated series under different values of ω and R ₀, I follow two goals. First, given R ₀, I compare the outcomes of the reinfection and no-reinfection scenarios. Second, given ω, I demonstrate the effects of the mitigation measures (expressed through the lower values of R ₀) under the reinfection and no-reinfection scenarios.

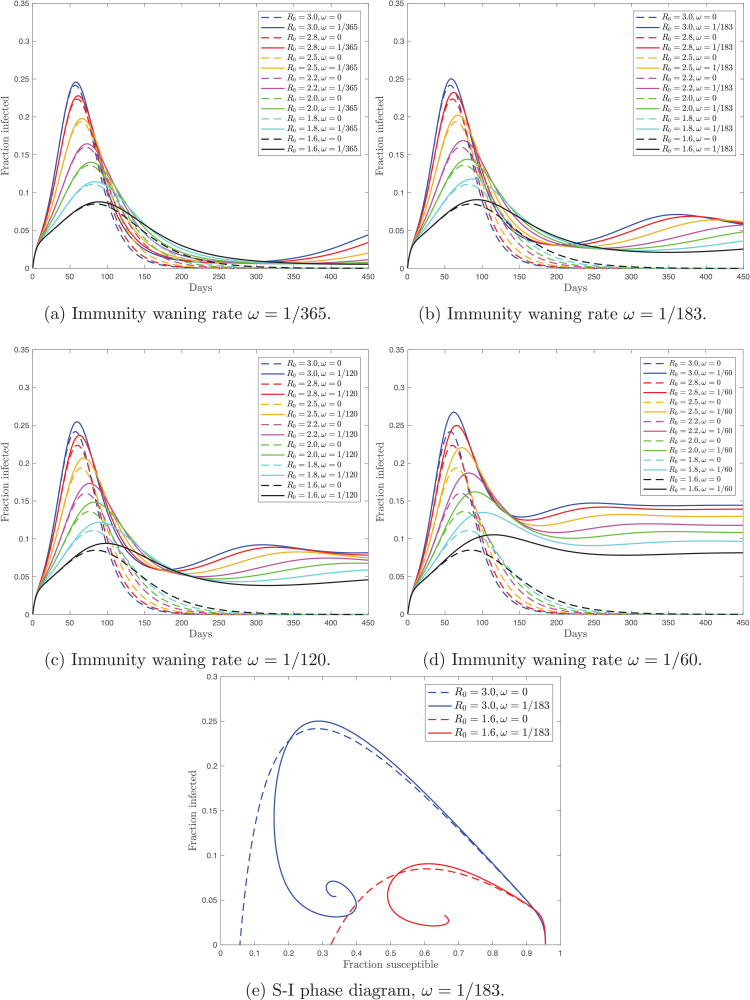
Fig. 1 shows the time paths for the simulated fraction of the actively infected population with (solid lines) and without (dashed lines) reinfection under different values of R ₀. This model experiment implies that lower R ₀ leads to delaying the infection peak both with and without reinfection. Second, under the reinfection scenario, the size of the peak is greater than without reinfection. The difference in the peak values is decreasing in R ₀. Third, with reinfection, the fraction of the actively infected population exhibits asymmetric dynamics around the peak. Crucially, before the peak, the time paths with and without reinfection are indistinguishable. However, after the peak, the reinfection series is unambiguously above the no-reinfection series. Therefore, by reducing the transmission rate with the mitigation measures, we delay the infection peak, and hence delay the moment when the difference between the reinfection and no-reinfection scenarios becomes sizeable. Finally, notice that, with reinfection, there can be multiple-wave disease outbreaks. In a related study, [6] discuss the role of homologous reinfection in driving multiple-wave influenza outbreaks. Next, Fig. 1e contains the phase diagram where I plot the fraction of the susceptible population against the fraction of the actively infected population. The solution of the model under both reinfection and no-reinfection scenarios starts in the bottom right corner where I(0) is close to zero and S(0) is close to one. This phase diagram also illustrates that before the peak two scenarios — with and without reinfection — are almost indistinguishable.

Fig. 1.

Panels (a)–(d) show the fraction of the actively infected population over time under the reinfection (solid) and no-reinfection (dashed) scenarios and with different values of the basic reproduction number, R₀. Panels (a)–(d) differ in the size of the immunity waning ratio, ω. Panel (e) contains the phase diagram that shows the evolution of the fraction of the actively infected population against the fraction of the susceptible population with and without reinfection.

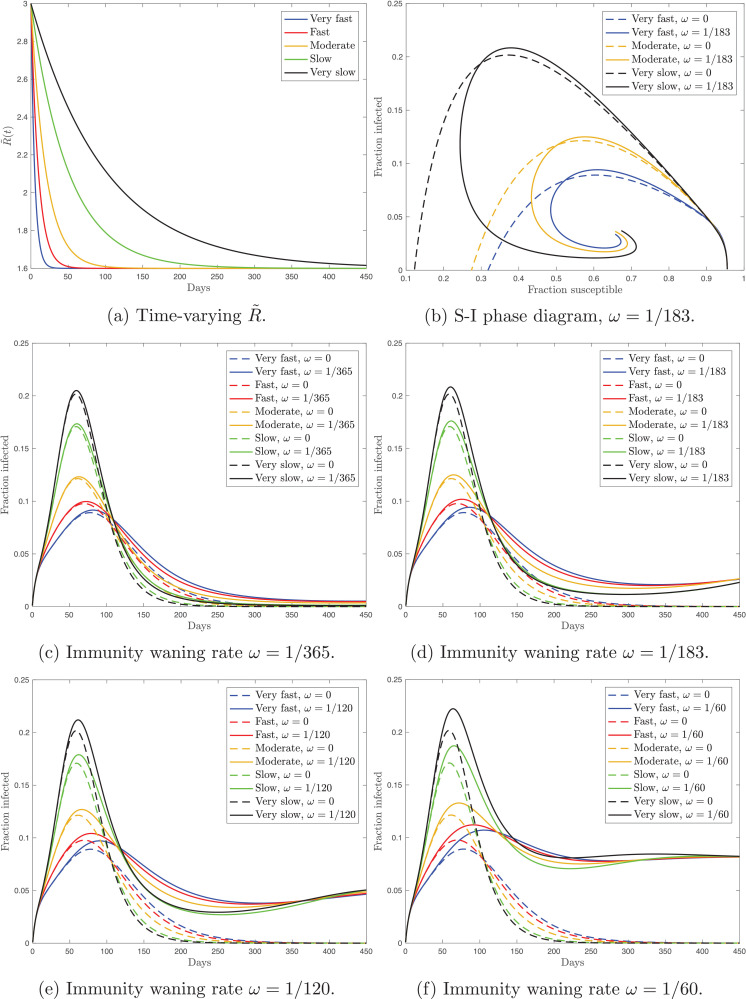
In the second model experiment, I assume that $\tilde{R}$gradually decreases at different speed. To capture the scenarious under different speed of implementation, following [3], I set ${\tilde{R}}_1\left(0\right)={\tilde{R}}_2\left(0\right)=3,$ $R_1^{*}=R_2^{*}=1.6,$and vary parameters η ₁ and η ₂ with ${\eta }_1={\eta }_2\equiv \eta$. There are five scenarios: very fast ($\eta =1/5$), fast ($\eta =1/10$), moderate ($\eta =1/20$), slow ($\eta =1/50$), and very slow ($\eta =1/100$). Higher values of ηgovern higher rate of convergence of $\tilde{R}$to the long-run value of 1.6. Fig. 2 shows the time paths for $\tilde{R}$and the simulated fraction of the actively infected population with (solid lines) and without (dashed lines) reinfection. This model experiment implies that the speed of implementation affects the timing of the peak and its size. Faster implementation of mitigation measures leads to delaying the infection peak both with and without reinfection. Next, similarly to the simulation from Fig. 1, under the reinfection scenario, the fraction of the actively infected population exhibits asymmetric dynamics around the peak. Relative to the no-reinfection scenario, reinfection affects the epidemic duration, the size of the infection peak, and the timing of the infection peak. Furthermore, to provide additional evidence to the dynamics of the solution, in Fig. 2b I show the phase diagram where plot the fraction of the susceptible population against the fraction of the actively infected population.

Fig. 2.

Panel (a) shows the time paths for the time-varying reproduction number, $\tilde{R}$. Panel (b) contains the phase diagram that shows the evolution of the fraction of the actively infected population against the fraction of the susceptible population with and without reinfection. Panels (c)–(e) show the fraction of the actively infected population over time under the reinfection (solid) and no-reinfection (dashed) scenarios and with different speed of the change in $\tilde{R}$. Panels (c)–(e) differ in the size of the immunity waning ratio, ω.

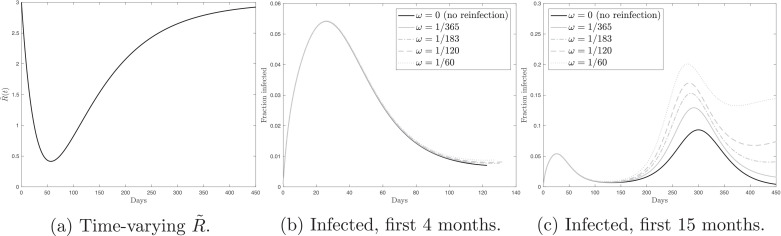
In the third model experiment, I assume that $\tilde{R}$significantly drops at the beginning, as a result of extremely severe mitigation measures, and then gradually goes up, as the mitigation measures are relaxed. Following [3], I set ${\tilde{R}}_1\left(0\right)=10,$ ${\tilde{R}}_2\left(0\right)=-4,$ $R_1^{*}=-10,$ $R_2^{*}=4,$ ${\eta }_1=1/35,$and ${\eta }_2=1/100$. Given the initial and long-run values of the reproduction number and η ₁ > η ₂, ${\tilde{R}}_1\left(t\right)$is rapidly decreasing function while ${\tilde{R}}_2\left(t\right)$is slowly increasing function. As a result, the time path for $\tilde{R}\left(t\right)$has a U-shaped form, see Fig. 3 a. The other two panels of Fig. 3 show the simulated fraction of the actively infected population with and without reinfection. Under the temporary and extremely severe mitigation measures, in the first four months, as shown in Fig. 3b, the fraction of the actively infected population substantially goes down. Moreover, the dynamics is identical for the scenarios with and without the possibility of reinfection. Turning to the first 15 months of the pandemic, shown in Fig. 3c, we see that gradual relaxation that follows the initial extremely severe mitigation measures, leads to a subsequent peak. Therefore, relaxation of the mitigation measures, driven by the optimistic dynamics in the first months, eventually leads to the epidemic. Motivated by the observation that early mitigation measures delay the peak but not its size, because the population does not acquire herd immunity, Toda [26] studies the optimal mitigation policy. He shows that it is optimal to initiate the mitigation measures once the number of cases reaches some threshold fraction of the population.

Fig. 3.

Panel (a) shows the time path for the time-varying reproduction number, $\tilde{R}$. Panel (b) shows the fraction of the actively infected population over time under the temporary and extremely severe mitigation measures in the first 4 months. Panel (c) shows the fraction of the actively infected population over time under the temporary and extremely severe mitigation measures in the first 15 months. In panels (b) and (c), black solid line ($\omega =0$) corresponds to the no-reinfection scenario. The grey lines (ω > 0) correspond to the reinfection scenarios. The lines coincide in panel (b).

4. Alternative reinfection assumptions

4.1. Milder disease after reinfection

I consider two alternative ways of modeling reinfection. First, I assume that individuals, once being reinfected, have a milder form of the disease. This is in line with [1] who discuss the clinical characteristics of the recovered COVID-19 patients with redetectable positive RNA test. When readmitted to the hospital, these patients showed no obvious clinical symptoms or disease progression. In the model, I assume that the individuals who become susceptible after being recovered, have lower transmission rate and higher recovery rate. At each point in time, the population, normalized to one, consists of seven classes: primary-susceptible (S_p), secondary-susceptible (S_s), primary-exposed (E_p), secondary-exposed (E_s), primary-infected (I_p), secondary-infected (I_s), and resistant (recovered) (R):

$$S_p\left(t\right)+S_s\left(t\right)+E_p\left(t\right)+E_s\left(t\right)+I_p\left(t\right)+I_s\left(t\right)+R\left(t\right)=N,\forall t\ge 0$$ (13)

Individuals belong to S_p, E_p, or I_p if they were not infected before. Individuals belong to S_s, E_s, or I_s after being recovered. The compartmental model is formulated as follows:

$$\frac{d{S}_p\left(t\right)}{dt}=-({\beta }_p{I}_p\left(t\right)+{\beta }_s{I}_s\left(t\right))\frac{S_p\left(t\right)}{N}$$ (14)

$$\frac{d{S}_s\left(t\right)}{dt}=-({\beta }_p{I}_p\left(t\right)+{\beta }_s{I}_s\left(t\right))\frac{S_s\left(t\right)}{N}+\omega R\left(t\right)$$ (15)

$$\frac{d{E}_p\left(t\right)}{dt}=({\beta }_p{I}_p\left(t\right)+{\beta }_s{I}_s\left(t\right))\frac{S_p\left(t\right)}{N}-{\sigma }_p{E}_p\left(t\right)$$ (16)

$$\frac{d{E}_s\left(t\right)}{dt}=({\beta }_p{I}_p\left(t\right)+{\beta }_s{I}_s\left(t\right))\frac{S_s\left(t\right)}{N}-{\sigma }_s{E}_s\left(t\right)$$ (17)

$$\frac{d{I}_p\left(t\right)}{dt}={\sigma }_p{E}_p\left(t\right)-{\gamma }_p{I}_p\left(t\right)$$ (18)

$$\frac{d{I}_s\left(t\right)}{dt}={\sigma }_s{E}_s\left(t\right)-{\gamma }_s{I}_s\left(t\right)$$ (19)

$$\frac{dR\left(t\right)}{dt}={\gamma }_p{I}_p\left(t\right)+{\gamma }_s{I}_s\left(t\right)-\omega R\left(t\right)$$ (20)

Note that susceptible individuals, both those who have never been infected and those who have recovered and are currently susceptible again, become exposed after contacting with both primary- and secondary-infected individuals. In the absence of the parameter estimates for COVID-19, I assume that ${\beta }_s={\beta }_p/2,$ ${\gamma }_s=2{\gamma }_p,$and ${\sigma }_s={\sigma }_p$. Following the previous simulations, I set ${\sigma }_p=1/5.2$and ${\gamma }_p=1/18$. The initial values are $I_p\left(0\right)=1/1000,$ $E_p\left(0\right)=43.75\times I_p\left(0\right),$as in Section 2, and $S_s\left(0\right)=E_s\left(0\right)=I_s\left(0\right)=R\left(0\right)=0$.

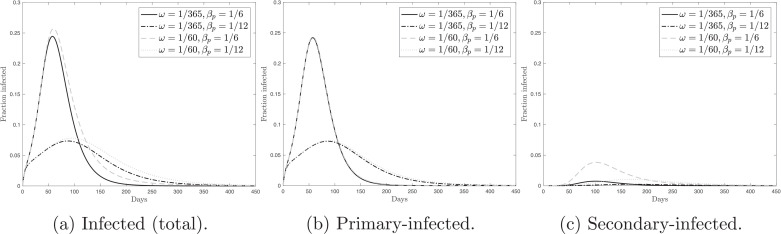
Fig. 4 shows the simulated time paths for the fraction of the actively infected population — total (primary and secondary), primary, and secondary. In these simulations, I consider several scenarios. They are characterized by four combinations of the immunity waning rate and primary-transmission rate, β_p. The immunity waning rate takes two values, $\omega =1/365$and $\omega =1/60$. Thus, I use the lower and upper bounds of the range considered in the previous simulations. The primary-transmission rate also takes two values, ${\beta }_p=1/6$and ${\beta }_p=1/12$. The case ${\beta }_p=1/6$corresponds to $R_0=3.0$in the baseline SEIRS model from Section 2, while the case ${\beta }_p=1/12$corresponds to $R_0=1.5$. We can see from Fig. 4that the dynamics of the total fraction of the actively infected population is almost entirely driven by the primary-infected people. There is a limited role of reinfection in the general epidemic dynamics.

Fig. 4.

Panel (a) shows the fraction of the total (primary and secondary) actively infected population over time. Panel (b) shows the fraction of the actively primary-infected population over time. Panel (c) shows the fraction of the actively secondary-infected population over time. Panels (a)–(c) consider various combinations of the immunity waning rate, ω, and the primary-transmission rate, β_p.

4.2. One-time reinfection

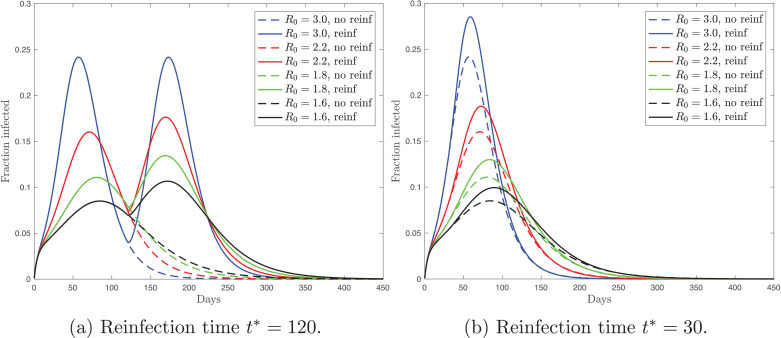
Second, instead of a constant immunity waning rate, I assume that the individuals, that are resistant at date t* (those who were infected in the past), become susceptible again. In particular, I consider a standard SEIR model, i.e. one described by Eqs. (1)–(5) with $\omega =0$. Before date t*, the dynamics of the model coincides with the no-reinfection case. At date t*, resistant individuals join the pool of susceptible population. Formally this is described by $S\left(t^{*}\right)=S(t^{*}-dt)+R(t^{*}-dt)$as dt → 0. Therefore, at date t* the fraction of resistant population goes down to zero, while the fraction of susceptible population discretely goes up. To illustrate the patterns that arise under this modeling approach of reinfection, I choose two time thresholds, $t^{*}=120$and $t^{*}=30$.

Fig. 5 shows the time paths for the fraction of the actively infected population. For each scenario, I consider a range of the basic reproduction number values. First, my model simulations imply that if the infection peak occurs before t*, as in Fig. 5a, then reinfection leads to a double peak. Second, if the infection peak occurs shortly after t*, as in Fig. 5b, then reinfection results in a higher single peak. Notice that the simulated series are consistent with the conclusion from Section 3 that the mitigation measures (lower R ₀) delay not only the infection peak, but also the moment when the difference between the reinfection and no-reinfection scenarios becomes prominent.

Fig. 5.

Fraction of the actively infected population over time under the reinfection (solid) and no-reinfection (dashed) scenarios and with different values of the basic reproduction number, R₀. Panels (a) and (b) differ in the time of reinfection.

5. Conclusion

To date, the immune response, including duration of immunity, to SARS-CoV-2 infection is not yet understood. Unless it is clearly known that patients with COVID-19 are unlikely to be reinfected, it is instructive to consider the possible scenarios. In this paper, I study how the possibility of reinfection shapes the epidemiological dynamics at the population level. To explore the difference in the dynamics of the disease under the reinfection and no-reinfection scenarios and, furthermore, the effects of the mitigation measures, I use a SEIRS model and consider three different ways of modeling reinfection. A key finding is that the mitigation measures delay not only the infection peak, but also the moment when the difference between the reinfection and no-reinfection scenarios becomes prominent. This result is robust to various modeling assumptions. The framework is simple and therefore can serve as a baseline for more complex models.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.