Radiomics Analysis Using Stability Selection Supervised Component Analysis for Right-censored Survival Data

Abstract

Radiomics is a newly emerging field that involves the extraction of massive quantitative features from biomedical images by using data-characterization algorithms. Distinctive imaging features identified from biomedical images can be used for prognosis and therapeutic response prediction, and they can provide a noninvasive approach for personalized therapy. So far, many of the published radiomics studies utilize existing out of the box algorithms to identify the prognostic markers from biomedical images that are not specific to radiomics data. To better utilize biomedical images, we propose a novel machine learning approach, stability selection supervised principal component analysis (SSSuperPCA) that identifies stable features from radiomics big data coupled with dimension reduction for right-censored survival outcomes.

The proposed approach allows us to identify a set of stable features that are highly associated with the survival outcomes in a simple yet meaningful manner, while controlling the per-family error rate. We evaluate the performance of SSSuperPCA using simulations and real data sets for non-small cell lung cancer and head and neck cancer, and compare it with other machine learning algorithms.

The results demonstrate that our method has a competitive edge over other existing methods in identifying the prognostic markers from biomedical imaging data for the prediction of right-censored survival outcomes.

1. Introduction

Bioimaging has emerged as an important diagnostic and prognostic tool in cancer. Imaging, as a non-invasive technique, has an advantage over other invasive clinical options and can generate a large amount of radiomics texture features that might be useful for predicting prognosis and therapeutic response for various conditions. In addition, it can provide valuable information for individualized treatments. Previous studies for analyzing bioimaging data have mostly focused on categorical outcomes. Success stories include the decipherment of not-otherwise-specified tumor for non-small-cell lung cancer by utilizing the features extracted from computed tomography (CT) imaging [1], the segmenting of brain tumor with data extracted from contrast-enhanced T1 and FLAIR magnetic resonance imaging (MRI) [2], and the segmentation and characterization of uterine for patients with major uterine disorders by using variables extracted from magnetic resonance imaging [3].

As radiomics texture features are of high dimension in nature, traditional statistical and computational models are not suitable. Recently, Cheng et al. have introduced machine learning classification methods for radiomics biomarkers to predict survival by dichotomizing the censored continuous survival data at a specific time cutoff [4]. The objective is to stratify patients into two survival classes by relevant survival time. However, due to the right-censored nature of the data, dichotomizing the survival time into binary outcome will lead to loss of information and biased estimation. A recent effort has been conducted to evaluate existing prognostic modeling methods for radiomics data with 1,610 features [5]. The researchers have found that the combinations of machine learning algorithms and feature selection methods may have an impact on the prediction of overall survival. Nevertheless, none of the combinations investigated in their studies stand out as their performances are quite similar when applied to one real data set.

For radiomics study, it is important to assess the clinical relevance of radiomics features and examine its performance and stability for predicting prognosis. Methods applied to radiomics data should be reliable and accurate for clinical use [6]. Biomarker predictors obtained from the one-time experiment may not be easily generalizable. Also, texture features with higher stability tend to be more informative and have higher prognostic performance as well as reproducibility. This has been demonstrated by Aerts et al. [7]. To the best of our knowledge, many of the radiomics studies have been conducted by using some existing out of the box algorithms that are not specific to high-dimensional radiomics data and do not focus on identifying stable features that can be more applicable to clinical settings [8]. Unlike genomics [9], there is currently a lack of prognostic algorithms that are designed explicitly for high-dimensional radiomics data. In this research, we focus on modeling texture features for cancer prognosis prediction with over 10,000 features extracted from biomedical images in a stable manner.

In this paper, we present a novel algorithm SSSuperPCA, a stability selection supervised principal component analysis tool for radiomics data, and apply it to two real radiomics data sets. Our objective is to address the issue of the lack of novel prognostic tools that can directly predict right-censored data for radiomics texture big data. We also benchmark our proposed SSSuperPCA against other regression and machine learning methods.

2. Materials and Methods

Our proposed algorithm, stability selection supervised principal component analysis (SSSuperPCA) integrates stability selection with supervised principal component analysis for the prediction of right-censored survival data.

Stability selection was first introduced by Meinshausen and Buhlmann [10]. It is a generic approach that can be applied to a wide range of statistical techniques for feature selection in high-dimensional data. In contrast to other feature selection algorithms that aim to find the best predictors, stability selection identifies a set of stable features that are chosen with high probability with the rationale for consistent predictions. The idea of stability selection is to perform feature selection on many smaller samples called subsamples that are resampled without replacement from the original data. Selected features will then be based on the aggregated results from the subsamples. Average selection probabilities will be computed for each feature, from which we can expect strong relevant features with higher selection probabilities close to 1 while irrelevant features with probabilities close to 0 [10]. Shah and Samworth [11] proposed a refined version of stability selection called complementary pairs stability selection that uses the subsamples as well as its complementary pairs. A narrower error bound could be derived with the modified Markov’s inequality that assumed unimodality or r-concavity for the distribution of the selected frequencies. In order to tackle high-dimensional feature selection for -omics data with right-censored survival outcomes, Mayr et al. put forward a boosted C-index stability selection that combined complementary pairs stability selection and C-index boosting to filter out informative features and to acquire the risk prediction that maximized its discriminatory power [12]. Bair et al. first introduced the supervised principal components analysis that integrated principal component analysis (PCA), an orthogonal linear transformation technique for dimensionality reduction, with generalized regression to address the issue of high-dimensional data [13]. When dealing with the number of features far exceeding the number of observations, the conventional method may yield unsatisfactory results because of sparsity. Supervised PCA can generate favorable results through the use of the subsets of the selected features that account for their correlation with the outcome. This approach can reduce the potential problems caused by the noisy features of the prediction model and keep the model’s simplicity at the same time. Supervised PCA has been applied to the area of bioinformatics studies for most scenarios, such as genome-wide association analysis [14] and microarray gene expression analysis [15]. Radiomics, the recently emerging research field which extracts high dimensional quantitative features from medical images by using advanced data-characterization extraction algorithms, can also take advantage of the unique characteristics of supervised PCA. For example, Kickingereder et al. incorporated supervised PCA with radiomics to provide a noninvasive approach as a novel decision tool for improving decision-support in the treatment of glioblastoma patients [16].

The analysis was performed using our R package, SSSuperPCA that was built on mboost, stabs and superpc under R version 3.4.3. The R package SSSuperPCA is available on the website: http://web.hku.hk/~herbpang/SSSuperPCA.html.

2.1. Stability Selection Supervised Principal Component Analysis (SSSuperPCA)

SSSuperPCA identifies the informative features from a large set of quantitative features extracted from biomedical images and predicts right-censored survival outcomes with supervised PCA to obtain the prediction model. Here, the continuous additive predictor η derived from the prediction model is defined as follows:

$$\eta ={\beta }_0+\sum _{i=1}^n{\beta }_i\times x_i=X^T\beta$$ (1)

where X = (1, x₁, x₂, ⋯ , x_n)^T is the feature vector and β = (β₀, β₁, β₂, ⋯ , β_n)^T is the corresponding regression coefficients vector of additive predictors.

The aim of the proposed algorithm is to identify a prediction model that aims to optimize the truncated concordance index (C-index) proposed by Uno et al [17], which will be further explained in section 2.2. The algorithm has seven basic steps:

1. Categorize the features into M subgroups based on the decreasing order of the average Uno’s truncated C-index that was derived from the k-fold cross-validation of a univariate Cox proportional hazards regression model trained on the training partition;

2. Apply the complementary pairs stability selection with boosted C-index for each subgroup. Set the number of subsampling replicates to B which will lead to 2 × B subsamples under the scheme of complementary pairs.

   1. Initialize the estimation of the continuous additive predictor ${\widehat{\eta }}^0$ for each subsample and the corresponding features in each subgroup. For example, set ${\widehat{\beta }}^0=0$ which will make ${\widehat{\eta }}^0=0$. Set m = 1 and a large maximum number of iterations m_stop.

   2. Compute the negative gradient vector of the loss function and figure out its value at ${\widehat{\eta }}^{m-1}$ that was derived from the previous iteration.

   3. Fit the negative gradient vector of the loss function to x_l, the features in the subgroup, through the base learners Cox proportional hazard regression model b_l(·).

   4. Select the feature that minimizes the value of the loss function under the least-squares criterion.

   5. Update the continuous additive predictor with the feature selected in d).

   6. Stop if m meets the stop value m_stop. Otherwise, update m = m + 1 and return to step a).

   7. Average the selection probabilities that are derived from the 2 × B subsamples and return features that exceed the preset selection probability threshold π_thr.

3. Aggregate the selected features obtained from each subgroup.

4. Estimate the standardized correlation coefficients, like proportional hazards for survival data, for each feature selected form stability selection through the univariate Cox proportional hazards regression.

5. Construct the reduced features matrix by using features whose absolute correlation coefficients exceeds the correlation threshold θ_thr that estimated via cross-validation.

6. Compute the principal components of the reduced features matrix.

7. Predict the right-censored survival outcome in the Cox proportional hazards regression model by using the first few principal components and return the stable features selected in step 3).

Unlike the conventional principal component analysis, SSSuperPCA performs singular value decomposition on the reduced data matrix to incorporate features that are highly correlated with the outcome. The input feature matrix for SSSuperPCA in step 4, whose components are features resulted from the stability selection with boosted C-index, should be standardized before performing prediction.

2.2. Stability Selection with Boosted C-Index

The concordance index (C-index) is a routine criterion in biomedical studies that measures the rank-based agreement probability between the continuous additive predictor and right-censored survival outcome. C-index may take values from 0.5(random predictor) to 1 (perfect prediction accuracy).

In general, C-index provides a global assessment of the discriminative ability of the fitted survival models. However, C-index may result in biased estimation because of the unknown true censoring pattern for all patients in practice. Observation pairs that cannot be ordered due to censoring will be omitted in the evaluation. To overcome this shortcoming, Uno proposed the truncated C-index that is independent with the censoring distribution and could consistently produce an asymptotically unbiased estimation of the conventional C-index [17]. The truncated C-index estimator is formulated as below:

$${\widehat{C}}_{Uno}(T,\eta ,\tau )=\sum _{i=1}^n\sum _{j=1}^n{w}_{ij}I({\eta }_i>{\eta }_j)$$ (2)

where $w_{ij}=\frac{{\Delta }_i{\{\widehat{G}(T_i)\}}^{-2}I(T_j<T_j,T_i<\tau )}{{\sum }_{i=1}^n{\sum }_{j=1}^n{\Delta }_i{\{\widehat{G}(T_i)\}}^{-2}I(T_j<T_j,T_i<\tau )},$ with T denotes the observed survival time subject to censoring, G(·) is the Kaplan-Meier estimator of the survival function that accounts for the censoring time, Δ is the censoring indicator and I(·) is the indicator function. τ is a pre-specified time point, T_i,T_j are survival times, and η_i, η_j are the predictors of two observations from an independent and identically distribution.

To obtain the optimal regression coefficient β that maximizes the truncated C-index, the component-wise gradient boosting algorithm [18] which is computationally efficient for high-dimensional data has been adopted. The idea is to update the base-learner in each boosting iteration through adding features that best fit the least square criterion of the negative gradient vector that derived from the loss function. However, Uno’s truncated C-index estimator it is non-differentiable with respect to η, directly using it as the loss function for gradient boosting is out of the question. Therefore, an approximate approach that uses the sigmoid function has been applied to smooth the Uno’s truncated C-index [19].

The smoothed estimator is given below.

$${\widehat{C}}_{smooth}(T,\eta )=\sum _{i,j}{w}_{ij}\times \frac{1}{1+\exp \left(\frac{{\eta }_i-{\eta }_j}{\sigma }\right)}$$ (3)

σ is a positive parameter which controls the accuracy of the sigmoid approximation. Previous studies demonstrated that the sigmoid approximation and its corresponding outcomes were not sensitive to σ when σ is small enough [19].

To avoid the problems of overfitting while ensuring the selection of informative features, boosted C-index was incorporated with complementary pairs stability selection proposed by Shah and Samworth. The general concept is to use 2 × B complementary pairs of size n/2 (the subsamples and its complement as well) and fit the boosted C-index model to select a pre-specified number of features on each of the subsample. Average selection probabilities will be calculated for each feature after aggregating the selection results of all the 2 × B subsamples and only features that beyond a threshold will remain in the final selection list. By cooperating with stability selection under exchangeable assumptions for the set of selected variables in each subsample, we may control the upper bound of the per-family error rate (PFER) with the inequality showed below.

$$E(V)\le \frac{q^2}{(2{\pi }_{thr}-1)\times p}$$ (4)

where E(V) is the expected number of false positive selected features, π_thr is the probability threshold for stability selection, q is the number of features that need to be selected on each subsample, and p is the number of total features.

PFER metric, as the main characteristic of stability selection, can strictly control the noisy features that are falsely included. Meanwhile, the features matrix extracted from the biomedical images could be sparse (the number of features is much greater than the number of observations) or the features are not highly correlated with the outcomes. Thus, less features would be selected when applying the stability selection with boosted C-index algorithm to radiomics data. To tackle this problem and to include more informative features as the input for Supervised PCA, we first grade all the features based on the Uno’s truncated C-index that derived from a univariate Cox proportional hazards model and categorize the features into subgroups based on the ranking, then we perform stability selection with boosted C-index on the subgroups and aggregate the features selected from each subgroup as the final conclusion. In our experiments, the number of complementary pairs (B) was set to 50 which led to 100 subsamples, and the number of uniquely selected variables (q) in each subsample was set to a lower bound as a function of PFER, stability selection π_thr and the number of total features (p). The probability threshold for stability selection π_thr was chosen to be slightly higher than 0.5 to include more features selected from the biomedical images and to reduce possible information loss.

2.3. Supervised PCA

The features that are selected through the stability selection with boosted C-index will serve as the entry matrix for Supervised PCA. Denote X_n×p as the standardized feature matrix, where n is the number of observations and p is the number of features.

First, the standardized regression coefficients C = (β₁, β₂, ⋯, β_p) that measure the effect on the survival outcome will be estimated through the univariate Cox proportional hazards regression model. Let $X_{n\times p_1}^{\theta }$ be the new feature matrix that consists of the columns of X_n×p whose absolute value of the standardized regression coefficients exceed the threshold θ. Here the optimal value of θ is determined by cross-validation of the log partial-likelihood ratio statistics. The singular value decomposition of $X_{n\times p_1}^{\theta }$ is $X_{n\times p_1}^{\theta }=U_{\theta }{D}_{\theta }{V}_{\theta }^T$, where the dimension of U_θ , D_θ , and V_θ are n × m, m × m, p₁ × m, and m = min(n, p₁) . $U_{\theta }=(u_{\theta }^1,u_{\theta }^2,\cdots ,u_{\theta }^m)$ is the supervised principal component of $X_{n\times p_1}^{\theta }$. The last step is to use the first k supervised principal components to fit the Cox proportional hazards regression model and the number of supervised principal components k, used in final prediction is usually no more than three in practice. The threshold of regression coefficient Θ and the number of supervised principal components used in our experiments were determined through 5-fold cross-validation on training data.

2.4. Comparison with Other Machine Learning Algorithms

We compared the stability selection supervised principal component analysis and different machine learning algorithms for radiomics survival data. The algorithms compared include C-Index stability selection with supervised principal component analysis, supervised principal component analysis without stability selection, Cox proportional hazards regression model [20], lasso and elastic-net based Cox proportional hazards regression model [21], survival random forests [22], and three recently proposed deep neural network-based survival models, DNNSurv [23], Deephit [24], and DeepSurv [25]. The basic cox proportional hazards regression is implemented with R package survival, and the univariate Cox regression was employed to filter out the top K statistically significant features, then the forward and backward stepwise Cox regression were applied to the K features to build the prediction model. Based on Altman’s [26] guideline on the maximum number of variables to be examined in a regression model and made a tradeoff between the model complexity and the prediction bias, we set K = 10 in our study. The lasso and elastic-net based Cox regression approaches are available as Coxnet in R. 5-fold cross-validation was used to determine the optimal shrinkage parameter λ for lasso and elastic-net based Cox regression in the training data set. The weight for L1 penalty and L2 penalty terms in elastic-net Cox regression is fixed to 0.5. The survival random forests is carried through R package randomForestSRC, with the number of trees equals to 1000 and the split rule is set to ‘log-rank’. The three deep neural network-based survival models are implemented with python, and the corresponding hyper-parameters tuning is determined through a random hyper-parameter optimization search scheme [27].

2.5. Data Sets and Generation of Texture Features

We considered the two data sets, head and neck cancer [28] and non-small cell lung cancer [29], which are available on The Cancer Imaging Archive (TCIA) [30]. For both data sets, only subjects with Computed Tomography (CT) and its corresponding radiotherapy structure set (RTSTRUCT) files are included. For non-small cell lung cancer data set, 106 subjects were excluded. There are multiple contour types in the RTSTRUCT files for the head and neck data set. To stay consistent with the contouring information, 79 cases with gross tumor volume (GTV) which has the highest frequency were included. The feature extraction part was conducted with Matlab by using the algorithm proposed by Vallieres et al. [31]. There are total of 23 non-texture features and 43 texture features extracted from the tumor regions. The non-texture features are volume, size, solidity, and eccentricity, and 19 histogram-based features that include energy, total energy, entropy, minimum, 10th percentile, 90th percentile, maximum, mean, median, interquartile range, range, mean absolute deviation, robust mean absolute deviation, root mean squared, standard deviation, skewness, kurtosis, variance and uniformity. The texture features include gray-level co-occurrence matrix (GLCM), gray-level run-length matrix (GLRLM), gray-level size zone matrix (GLSZM) and neighbourhood gray-tone difference matrix (NGTDM). We have excluded first-order (histogram) features, as these require predefined bins and do not consider the spatial and topological information which has been pointed out by Li et al. as a disadvantage [32]. Details of these features could be found in the work of Vallieres et al. [31] . Different extraction parameters setting were evaluated to investigate the influence of the extraction parameters on the predictive texture features. In our experiment, we investigated four extraction parameters, wavelet band-pass filleting (ratio of 1/2, 2/3, 3/4, 4/3, 3/2, 2 were investigated), isotropic voxel size (value of 1mm, 2mm, 3mm, 4mm and 5mm were tested), gray-level quantization algorithms (Equal-probability and Lloyd-Max quantization algorithms) and number of gray-levels in quantized volume (8, 16, 32 and 64 were tested). General information regarding sample size and the number of features of the two data sets are listed in Table 1.

Table 1.

Radiomics data sets used

Data Set	Sample Size	Number of Non-Texture Features	Number of Texture Features
Non-Small Cell Lung Cancer	316	23	43×240 = 10320+
Head and Neck Cancer	79	23	43×240 = 10320+

⁺Considering the full set of texture extraction parameters combinations (total 240 combinations) and 43 texture features, there are 10320 texture features in total.

The 10,343 features extracted from the CT/RTSTRUCT image files are used to predict the overall survival of the patients, and a risk score will be applied to categorize the patients into high-risk and low-risk groups. The measurement matrices used in our experiment are Uno’s C-index that assesses the discriminative ability of the model, Brier score that indicates the overall model performance, and the log-rank statistics that evaluate whether the survival time of the two groups is statistically significantly different or not. As one of the data set has data from two hospital centers, we generated histogram plots and compared the distribution of the top stable features from the two hospital centers using Kolmogorov-Smirnov test. To enhance the computation efficiency of SSSuperPCA, we set the number of features subgroups (M) for non-small cell lung cancer and head and neck cancer data sets to 1 and 5, respectively. This decision is made based on the empirical evidence in our study.

In order to understand how well our approach performs both under the null of no informative stable features and under the alternative with different situations, we simulated data with a different number of stable features and different sample size based on the mean and covariance structure obtained from the non-small cell lung cancer data. Our simulation setup is quite similar to Pang et al. [9, 33]. For each simulated data, the total number of radiomics features is 3,000, the regression coefficients for stable features are sampled from a normal distribution with zero mean and a standard deviation 3, and the regression coefficients of the remaining features are all set to zero. With simulated radiomics features and the corresponding effect sizes, we can simulate the survival time and censoring status accordingly. In our simulation, the sample size is set to 150, 200 and 250 while the number of stable features is assigned to 0, 5, 15 and 25, respectively. In total, we simulated twelve different scenarios and 100 independent data for each scenario.

3. Results

In this section, we applied our algorithm to assess its abilities in predicting survival using biomedical images from two cancer data sets and compared its performance with the five machine learning algorithms. For the two data sets, we randomly selected 65 percent of the observations as a training set to build the model, and the remaining 35 percent was used as a testing set to evaluate the performance of the models. This procedure was repeated 100 times to calculate the average values for the three measurements mentioned above.

3.1. Simulation Studies

We simulated 100 data sets for each scenario with different sample size and the number of stable features as described before. For each data set, we split it into training and testing set and estimated the corresponding measures of Uno’s C-index, Brier score, and log-rank statistics.

The detailed results of Uno’s C-index for alternative scenarios are shown in Table 2, and the remaining two measures of alternative cases, as well as the results for null scenarios, are provided in the Supplementary Tables 1–3. For the results of null scenarios, the Uno’s C-index for different sample size were 0.492, 0.491, and 0.511, respectively. Considering the results of the alternative scenarios, as the number of stable features increased from 5 to 25 along with the number of sample size increased from 150 to 250, the Uno’s C-index increased from 0.550 to 0.624, the Brier score dropped from 0.152 to 0.148 and the log-rank statistics increased from 2.914 to 6.104. A clear pattern was observed, as the number of top stable features increases, the performance of SSSuperPCA improves. The same trend could also be identified for the sample size, while the impact was not as significant as the number of top stable features. However, as the sample size and the number of stable features increased, the improvement of its performance became less impressive.

Table 2.

Average Uno’s c-index of the simulated data sets under different scenarios

Number of informative features over 3000 features	Size 150	Size 200	Size 250
5	0.550	0.552	0.561
15	0.586	0.586	0.589
25	0.613	0.621	0.624

3.2. Application to non-small cell lung cancer data set

The non-small cell lung cancer (NSCLC) data contained 208 events out of 316 observations and the median survival time was 543 days. The results of non-small cell lung cancer data showed that our proposed algorithms SSSuperPCA, which integrates stability selection with boosted C-index and supervised PCA, performed better than supervised PCA without stability selection. SSSuperPCA increased the Uno’s C-index from 0.600 to 0.632, and the log-rank statistics from 7.071 to 8.844 when compared with supervised PCA without stability selection. The Brier score of SSSuperPCA was lower than that of supervised PCA, which suggested that the prediction model of SSSuperPCA was also better. We also aggregated the stable features that selected through our algorithm SSSuperPCA in the 100 times’ running to further understanding the stable features that contribute most to predict the survival of non-small cell lung cancer patients. In summary, the top three features were selected as stable features for more than 90 times. The highly selected features including two non-texture features, volume, size and one texture features of small zone emphasis. Volume and size are two features that describe the size and shape of the tumor region and small zone emphasis is used to assess the homogeneity of the texture. It is acceptable that the tumor region characteristic would have higher prognostic power for survival prediction of non-small cell lung cancer patients. A detailed definition of these features could be found in Vallieres’s paper.

Table 3 presents the average measurements for the six algorithms with non-small cell lung cancer data. In general, the performance of SSSuperPCA was higher than other algorithms compared using this data set based on the Uno’s C-index, Brier score, and log-rank statistics. For this data set, we observed that the survival random forests generated the worst prediction for survival, only slighter better than a random guess. For the Cox proportional hazards regression model, lasso and elastic-net based Cox proportional hazards regression model, these algorithms produced quite similar results with Uno’s C-index around 0.600, Brier Score equal to 0.152, and log-rank statistics close to 5. The survival random forests and the three deep neural network-based models, DNNSurv, Deephit, and DeepSurv were the four algorithms that produced poor prediction for survival, with the values of the concordance statistics proposed by Uno only marginally higher than a random prediction. Figure 1 shows the scatter plots of the SSSuperPCA against the other four algorithms when considering Uno’s C-index. Points above/on the reference line means that Uno’s C-index of SSSuperPCA is no less than the value of algorithms compared. The scatter plots for Brier score and log-rank statistics are provided in Supplementary Figures 1 and 2.

Table 3.

The comparison of stability selection supervised principal component analysis with five machine learning algorithms with data non-small cell lung cancer

Non-Small Cell Lung Cancer	C-Index+	Brier Score	Log-Rank Statistic
SSSuperPCA*	0.632 (0.626,0.638)	0.148 (0.147,0.149)	8.844 (7.954,9.765)
C-Index Stability Selection SuperPCA	0.609 (0.597,0.620)	0.149 (0.147,0.150)	8.173 (7.168,9.192)
Supervised PCA	0.600 (0.587,0.612)	0.149 (0.148,0.151)	7.071 (6.169,8.024)
Cox Regression	0.599 (0.590,0.607)	0.152 (0.150,0.153)	5.463 (4.619,6.355)
Survival Random Forests	0.545 (0.538,0.551)	0.156 (0.155,0.157)	1.535 (1.239,1.848)
LASSO Cox	0.600 (0.593,0.607)	0.152 (0.151,0.153)	4.906 (4.226,5.612)
ENET Cox	0.596 (0.588,0.604)	0.152 (0.151,0.153)	4.561 (3.929,5.239)
DNNSurv	0.512 (0.509,0.515)	0.157 (0.156,0.158)	1.155 (0.874,1.471)
Deephit	0.534 (0.527,0.541)	0.157 (0.156,0.158)	1.163 (0.888,1.471)
DeepSurv	0.518 (0.505,0.530)	0.154 (0.153,0.155)	4.199 (3.452,4.978)

The results are the average values that based on 100 times random training/testing splits.

^*SSSuperPCA: Stability selection supervised principal component analysis.

⁺Concordance statistics proposed by Uno et al. that do not depend on the censoring distribution.

Confidence interval at 95% confidence level is calculated from bootstrap percentile method.

Figure 1.

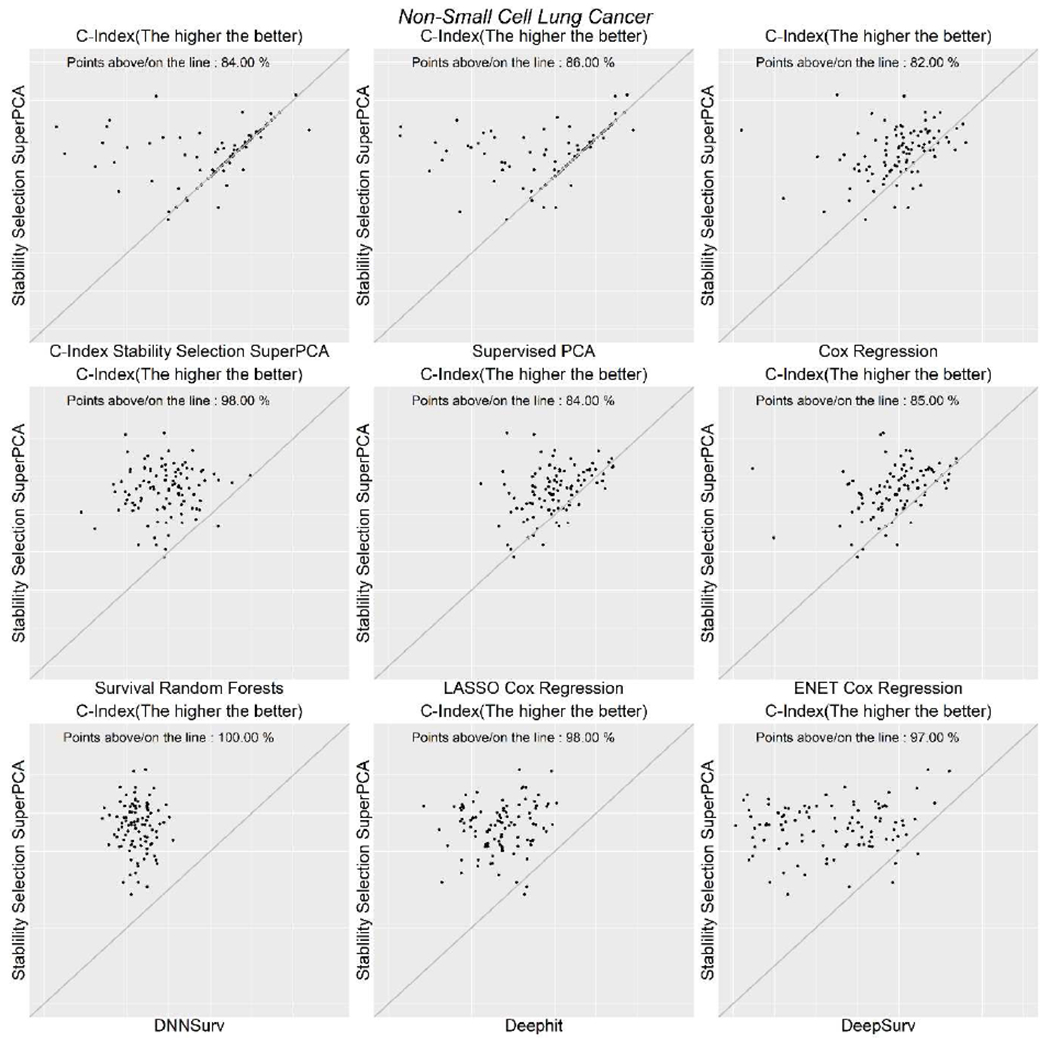
Scatterplots of Uno’s C-index for non-small cell lung cancer data.

In addition, we tested the top machine learning algorithms combined with feature selection methods that were mentioned in Leger’s study [5]. For non-small cell lung cancer data, the boosted gradient linear model combined with univariate selection could achieve the best performance, with the Uno’s C-index, Brier score, and log-rank statistics equal to 0.589, 0.153, and 4.074, respectively.

3.3. Application to head and neck cancer data set

The patients of head and neck cancer data set we used were collected from the two cohorts, 30 observations from Centre hospitalier universitaire de Sherbrooke and 49 observations from Hôpital général juif de Montréal, QC, Canada. Before performing survival analysis, a log-rank test was used to evaluate the difference between the two studies and the corresponding p-value is 0.812, which indicates we could not reject the null hypothesis of no difference between the two studies. In total, we have 15 death events within the two studies. SSSuperPCA outperformed supervised PCA without stability selection again with head and neck cancer data. It increased the Uno’s C-index, log-rank statistics of Supervised PCA from 0.661 to 0.701 and 2.316 to 2.379, respectively. The top three selected stable features for head-and-neck cancer data were zone-size non-uniformity, large zone high gray-level emphasis, and small zone emphasis. The three texture features that quantify the intratumor heterogeneity and homogeneous are components of the gray-level size zone matrix. We generated histogram plots for the three top selected stable features from the two centers. Their corresponding p-values are greater than 0.90, which indicates that there are no significant differences in the distribution of the identified stable radiomics features from the two centers. Table 4 shows the average measurements for the six algorithms with head and neck cancer data. Same as the non-small cell lung cancer data set, the Cox proportional hazards regression model, lasso, and elastic-net based Cox proportional hazards regression model generated almost identical results with Uno’s C-index of around 0.630, Brier Score equal to 0.060, and log-rank statistics close to 1.

Table 4.

The comparison of stability selection supervised principal component analysis with five machine learning algorithms with data head and neck cancer

Head and Neck Cancer	C-Index+	Brier Score	Log-Rank Statistic
SSSuperPCA*	0.701 (0.669,0.731)	0.057 (0.053,0.061)	2.379 (2.040,2.742)
C-Index Stability Selection SuperPCA	0.671 (0.638,0.702)	0.057 (0.053,0.060)	2.177 (1.844,2.535)
Supervised PCA	0.661 (0.630,0.692)	0.057 (0.053,0.060)	2.316 (1.945,2.715)
Cox Regression	0.644 (0.611,0.675)	0.060 (0.056,0.064)	1.207 (0.935,1.502)
Survival Random Forests	0.679 (0.649,0.709)	0.059 (0.056,0.063)	1.025 (0.783,1.297)
LASSO Cox	0.627 (0.594,0.659)	0.060 (0.056,0.064)	1.087 (0.837,1.364)
ENET Cox	0.628 (0.596,0.661)	0.060 (0.056,0.064)	0.936 (0.720,1.188)
DNNSurv	0.578 (0.557,0.600)	0.059 (0.055,0.063)	1.300 (0.966,1.676)
Deephit	0.616 (0.590,0.643)	0.060 (0.056,0.064)	1.169 (0.878,1.475)
DeepSurv	0.627 (0.595,0.659)	0.061 (0.057,0.065)	0.779 (0.593,0.986)

The results are the average values that based on 100 times random training/testing splits.

^*SSSuperPCA: Stability selection supervised principal component analysis.

⁺Concordance statistics proposed by Uno et al. that do not depend on the censoring distribution.

Confidence interval at 95% confidence level is calculated from bootstrap percentile method.

Unlike its performance in non-small cell lung cancer data set, survival random forests had higher c-index for head-and-neck cancer when compared to other algorithms except for SSSuperPCA. DeepSurv was the best performer among the three deep neural network-based models. However, its performance was only comparable to that of the Cox regression-based algorithms. Figure 2 shows the scatter plots of the SSSuperPCA against the other five algorithms when considering the Uno’s C-Index and scatter plots for Brier score, and log-rank statistics are provided in Supplementary Figures 3 and 4.

Figure 2.

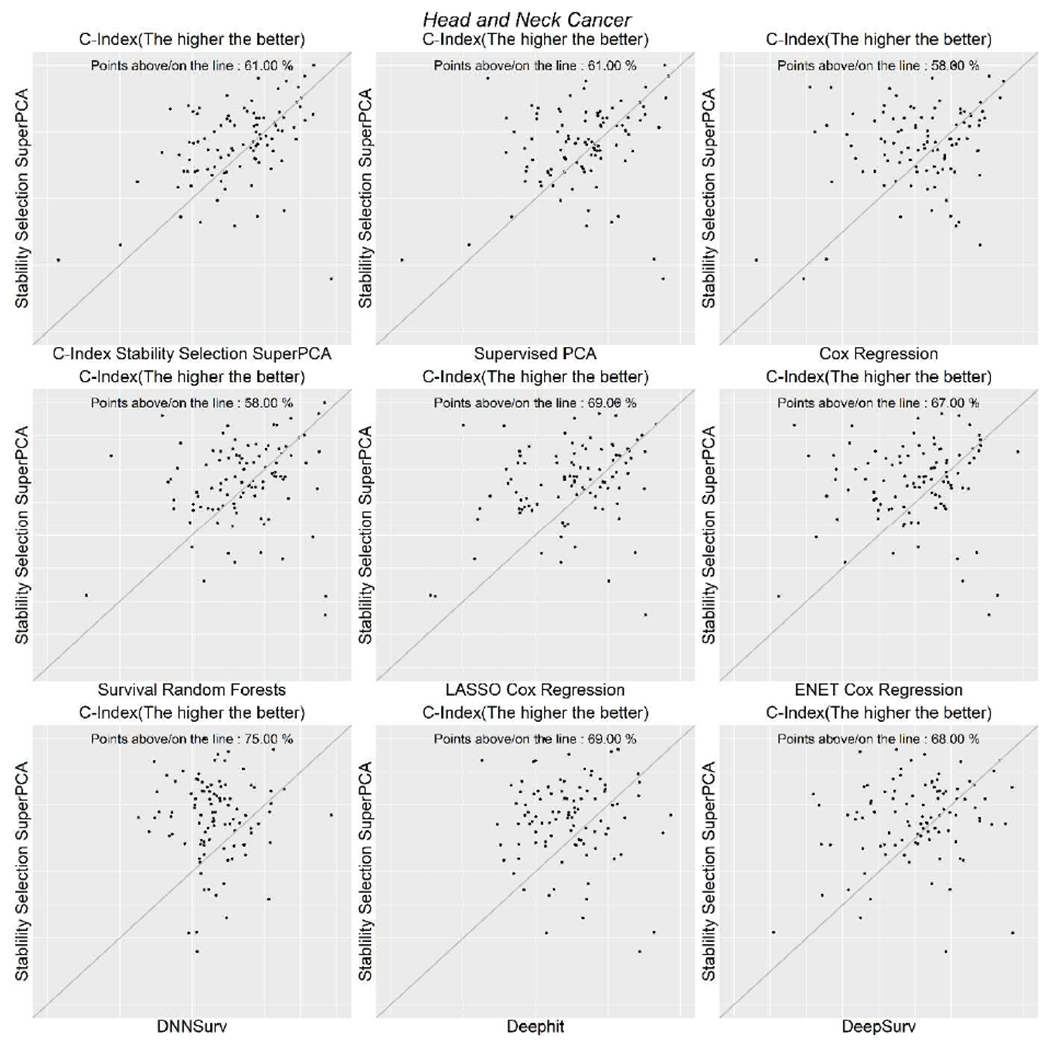
Scatterplots of Uno’s C-index for head and neck cancer data.

Figure 3 shows the density plots of the two data sets regarding the three measurements, which can provide an overall view of the performance of the six algorithms. Considering the top algorithms compared in Leger’s study, survival regression combined with minimum redundancy maximum relevance would give the best survival prediction for head and neck cancer data with Uno’s C-index, Brier score, log-rank statistics equal to 0.684, 0.061, and 1.413, respectively.

Figure 3.

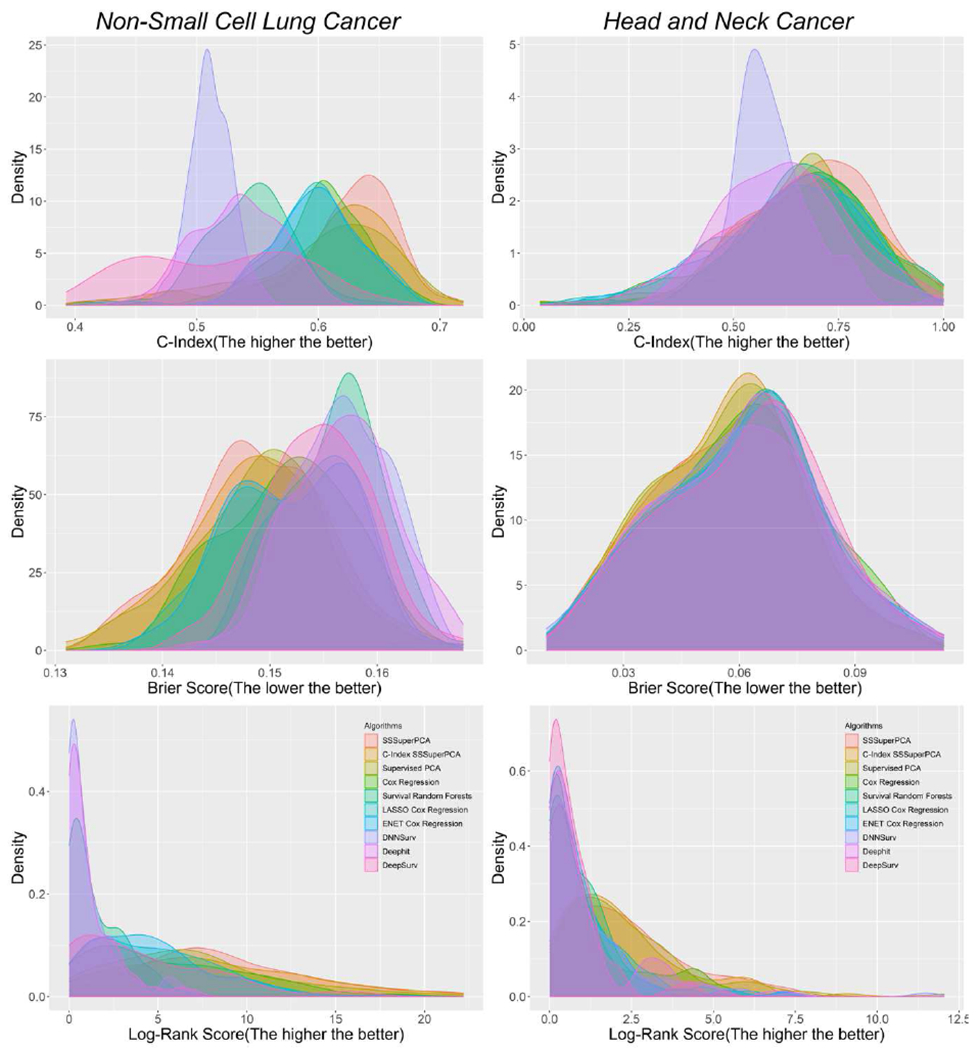
Density plots of three measures of six algorithms for the two data sets.

4. Discussion

In this paper, we have proposed a new algorithm for radiomics analysis with right-censored survival data by coupling boosted stability selection with supervised principal component analysis. This approach allows us to identify a set of stable features that are highly associated with the survival outcomes and predict the survival in a simple and meaningful manner. Using two different biomedical images cancer data sets, we have successfully demonstrated that our algorithm is able to identify a set of biologically relevant stable features that can help researchers better predict the survival of cancer patients and assist doctors in their treatment decisions.

In our experiments, non-small cell lung cancer and head and neck cancer data sets were used to evaluate the performance of SSSuperPCA. Results from both sets of data showed consistent patterns that SSSuperPCA could improve the performance of supervised PCA and also outperformed other regression and machine learning algorithms. In this study, we aggregated the stable features that were selected by our algorithm SSSuperPCA in the 100 runs for the two data set and calculated the frequency of these stable features. Two non-texture features that quantified the compactness of tumor shape and one texture feature that assessed the homogeneity of tumor characteristics were identified as the top three highly selected stable features from the non-small cell lung cancer data. Three texture features, as parts of the gray-level size zone matrix, describing the intratumor heterogeneity and heterogeneity, were discovered from the head and neck cancer data. These types of radiomics features were also suggested as the potential biomarkers for lung cancer and head and neck cancer in other studies [7, 34]. The gray-level non-uniformity and wavelet gray-level non-uniformity highpass-lowpass-highpass that measure the intratumor heterogeneity were two of the four consistency radiomics signatures for the prediction of survival in Aerts’ study.

The above results have demonstrated that our algorithm is able to identify stable features that have the higher prognostic ability. The stable features identified from the head and neck cancer data are not as stable as the non-small cell lung cancer data set. This could be due to the smaller sample size or a different disease type with more complex bioimages than those in the other data set. In addition, a simulation study based on non-small cell lung cancer data has also been conducted to assess the performance of SSSuperPCA under different scenarios. In general, when the number of stable features increased or the sample size increased, the performance of our algorithm improved.

There are two features selection parts involved in SSSuperPCA. In the first stage, stability selection with boosted C-index is employed to identify a set of stable features that are correlated with the right-censored survival outcome while controlling for the per-family error rate. Unlike some conventional feature selection methods that utilize conventional C-index for high-dimensional data may lead to biased results due to censoring distribution. On the other hand, stability selection with boosted C-index is less sensitive to the underlying censoring distribution and can yield good variable selection results. This has been demonstrated in the comparison of SSSuperPCA and C-Index Stability Selection SuperPCA on two real data sets. It is then followed by a semi-supervised strategy through supervised principal component analysis that enables SSSuperPCA to identify the gross correlation structure along with the corresponding survival outcomes and to pare down the influence of these less informative features. With the combined two-staged feature selection, SSSuperPCA can significantly reduce the data dimensionality and identify informative stable features as well. One drawback is that the high-dimensional radiomics features generated with different extraction parameters could be correlated to some extent. But our study has highlighted that SSSuperPCA is capable of identifying highly stable features like zone-size non-uniformity, large zone high gray-level emphasis and small zone emphasis in our experiments. Another drawback of our approach is that the selection model used in stability selection and the prediction model used in supervised PCA are based on Cox proportional hazards model. Once the assumption is violated, the prediction results could be misleading, and we may consider replacing the Cox proportional hazards model to the accelerated failure time model with a certain distribution, such as log-normal distribution or Weibull distribution. However, this may not be a major problem under some circumstances as the hazard ratio could be interpreted as the geometric mean of hazard ratio over time points when the assumption is violated [35]. Although our application data sets are based on CT scans, our method can be applied to MRI bioimage data as input as well. In conclusion, our approach is able to pick up a set of stable features via boosted survival model from radiomics data, control the per-family error rate and perform well in survival prediction. While the field is still in its infancy, the proposed algorithm would motivate and draw the interest of other researchers to develop novel algorithms for bioimage informatics analysis.

Highlights:

• Bioimaging can provide valuable information for individualized treatments.

• Stability selection supervised principal component analysis can better utilize bioimages.

• Our algorithm outperformed the other algorithms on two real data sets.

• It can identify most stable biological meaningful features for clinical settings.