Functional biodynamics of human-body system: A mathematical axiomatics with functional learning and aging in life cycle

Abstract

“Systems neuroergonomics” (Mau, J. In: R. Wang and X. Pan, editors, Advances in Cognitive Neurodynamics (V), chapter 59, pages 431–437, Springer Science+Business Media, Singapore, 2016) showed a separation of human-body system’s functional organization from its cellular material in order to open a holistic perspective that can comprise all body functions. This was achieved with a strictly hierarchical structure in drill-down from system’s functional whole to base functional elements. Implied multi-scale functional dynamics with coherent up-scaling were mathematically described in an axiomatic way, but the daily wake/sleep dynamics cover mainly anticipated functional challenges. Here, the theory is expanded to permit “functional learning” in the sense of adjustment of functional capacities to meet higher demand. “Functional aging” as a whole-body frailty is derived from biodynamic entropy that eventually drives the living to meet its inevitable destiny, death. The ages at which frailty begins to dominate can currently be obtained only from official life tables as population averages and are different for men and women, accordingly. The objective is to develop a mathematical theory in medicine from an axiomatic approach to phenomenological biodynamics, in which cognition is viewed as an embodied activity.

Introduction

The ultimate objective would be a coherent mathematical description of a person’s behavioral and his or her body’s physiological dynamics from a systems automation viewpoint. Despite an immense body of evidence about anatomical structures and physiological functions consolidated by many generations of doctors, an integrating understanding of human-body’s functional parts, their dynamic cooperation with respective controls that extend across several scales, is lacking. This is in the spirit of Varela et al. (1991) who introduced the “view of cognition as embodied action” into cognitive science.

Regarding cognitive neurodynamics as part of whole human-body system dynamics, controls of the former must be assumed to be interwoven with physiological controls of the latter, in particular with those in charge of body-system’s vital functions of energy supply. In fact, Binkofski et al. (2011) investigated the selfish brain hypothesis by Peters et al. (2004) which holds that the hypothalamus prioritizes higher energy demand by the brain, and they found indeed higher blood–glucose levels under transcranial direct–current electric stimulation of brain activity. This can be explained by the hypothalamus’ role as a superordinate control center that orchestrates hormone releases from pancreas, adrenal, and thyroid glands via the hypothalamic-pituitary (HP) axis to control systemic blood glucose levels. That transcranial direct–current electric stimulation can indeed influence cognitive task-solving abilities, was shown by Dockery et al. (2009) for planning ability and by Hecht et al. (2010) for decision-making.

This motivated the present author to discuss systems neuroergonomics (Mau 2016c) for which the human-operated machine at work in Fig. 1 served as an intuitive example. The motivation for the current abstraction is a holistic functional understanding of a person’s biological body as a system made to serve a purpose, and therefore expected to be similar in functional structures to engineered systems that are designed to produce or achieve specific things. Figure 1 guides further elaboration of the concept: The first to notice are a bulky energy unit behind the operator’s cabin, then the big arm with the grabber’s claw and the undercarriage for locomotion in physical tasks. Invisible is that part of the human-operator’s brain that takes a commander’s role in cognitive task-solving and enacts such commander’s operational decisions via human-body’s motor function nervous system as volitive musculo-skeletal locomotion of hands, arms, legs, and feet which engage the excavator’s engineered steering equipment for final transmission of commands to grab arm and wheels; all physiological functions of the human-operator’s biological body are deliberately disregarded for the purpose of illustration of the abstract concept that will be detailed mathematically in Sect. 2.

Fig. 1.

An excavator with human operator as a cognitive human-machine system designed for physical task-solving in civil engineering. Photo copyright The author; permission granted by courtesy of Irmgard Wassenberg Ltd

A purely functional view of whole human-body system is adopted that separates system’s functional organization from its material realization in the spirit of Sachsse (1974)’s paradigmatic interpretation of Wiener (1961)-sense cybernetics: the structure of couplings—“schaltgefüge”—(between system’s elements) is independent of its physical realization. The approach is to develop first a holistic structure within which functional dynamics of any effectuation system (“wirk-gefüge”) would evolve, and then to define phenomenological dynamics within such structure axiomatically—in the spirit of phenomenological thermodynamics. Specifically, a hierarchical functional structure is chosen that permits an “onion peeling”-kind of drill-down approach instead of conventional bottom-up—keeping in mind Francis J. Doyle III’s acid remarks on “the idea that underlied early publicity of the Human Genome Project (genetic code influences protein levels and protein functions, hence sheds light on causes of disease)” which he denounced as logically flawed: “as if the raw materials list for an aircraft (sheet metal, nuts, bolts, rivets, etc.)” would allow one to predict its behavior in flight—for an engineer, it clearly is their functional interaction, regulation and control, that determine actual outcome given material parts (Seborg et al. 2011, p.467).

It will be seen that the hierarchical functional structure by-passes complexity and still lends itself to holistic and up-scalable dynamics from “ground-level” to functional whole. For self-containedness, underlying concepts that were published in several conference proceedings articles in recent years will be summarized selectively, with some new approaches and extensions, in Sect. 2. Latest extensions, functional learning and functional aging, will be addressed in Sects. 3 and 4, respectively.

Basic concepts

Life sphere setting, system functional architecture, emergence

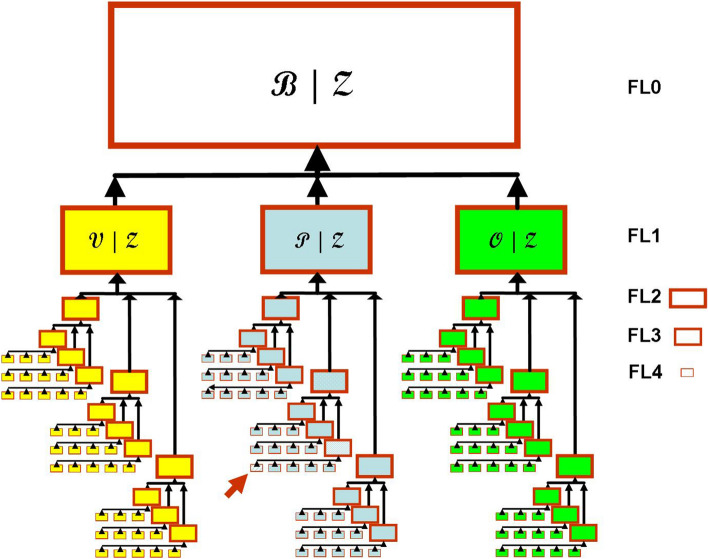
Consider human body-system $\mathcal{B}$’s functional whole $\mathcal{B}$$\mid$$\mathcal{Z}$, with $\mid$$\mathcal{Z}$ expressing functional disregard of material realization in $\mathcal{B}$’s cellular system $\mathcal{Z}$. As a non-autarkic bio-automaton, $\mathcal{B}$ needs an eco-sphere habitat to keep its ${10}^{14}$ body cells alive and to maintain all physiological functions, as well as a socio-sphere setting, the least for reproductive mating: Fig. 2(left) lists main driving forces in body system’s internal and person’s behavioral dynamics. As both cognitive and physical task-solving are involved in $\mathcal{B}$’s “hunting for food and mating partners”, their functional dynamics must be studied in context of whole $\mathcal{B}$$\mid$$\mathcal{Z}$. In further break-down, one understands every functional unit FU as a functional aggregate FA of next-lower level (“smaller”) FUs cooperating in joint commitment to their FA’s task, cf. Fig. 3 for illustration. In notation, for some fixed level $\mathrm{FL}k$, $k>1$, say, consider m functional units ${\mathrm{FU}}_i$, $i=1,\cdots ,m$, to form a functional aggregate $\mathrm{FA}$,

$$\begin{array}{c}\hfill \mathrm{FA}=\{{\mathrm{FU}}_1,\cdots ,{\mathrm{FU}}_m\},\end{array}$$ 1

then. Counting functional levels from top to bottom, with $\mathrm{FL}0$ for the whole, $\mathrm{FA}$ of $\mathrm{FL}k$ emerges as some functional unit $\mathrm{FU}$ of $\mathrm{FL}(k-1)$, in an intuitive notation,

$$\begin{array}{c}\hfill {\mathrm{FA}}^{\mathrm{FL}k}={\mathrm{FU}}^{\mathrm{FL}(k-1)},\end{array}$$ 2

for all levels $k>1$.

Fig. 2.

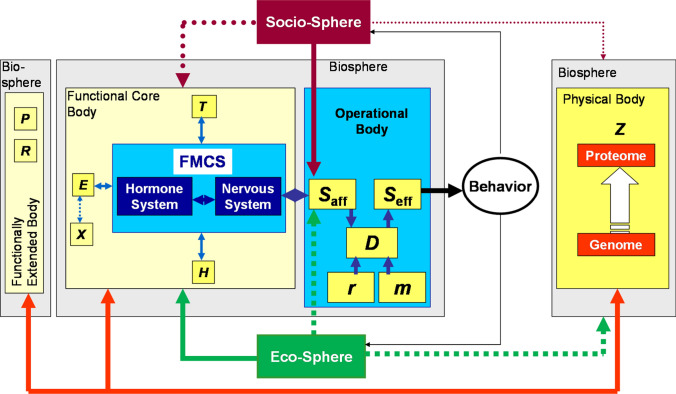
Left: Person’s life-sphere setting in his or her bio-sphere $\mathcal{B}$ body’s surroundings in habitual eco-sphere $\mathcal{E}(\mathcal{B})$ and socio-sphere $\mathcal{S}(\mathcal{B})$ embedding, from Mau (2016a). Right: Socio-sphere engages primarily operational functions in cognitive task-solving, from Mau (2016c)

Fig. 3.

Pathways of functional dynamics in System Functional Architecture (SFA): From top, functional whole $\mathcal{B}$$\mid$$\mathcal{Z}$, and the canonical components of vital, physical production, and operational functions, from Mau (2019)

Whenever material realization can be disregarded in a holistic structural analysis, this kind of hierarchical built-up is called System Functional Architecture SFA. The decomposition into three components, $\mathcal{V}$$\mid$$\mathcal{Z}$ (vital functions for energizing all other functions, including system-wide functional management and control), $\mathcal{P}$$\mid$$\mathcal{Z}$ (physical production functions for auto-movement or moving things), and $\mathcal{O}$$\mid$$\mathcal{Z}$ (cognitive functions of operational decision-making based on outside-world information, own operational goals, memory of past experience, and on current motivation to enact decisions) are canonical “wirk”-components of any effectuation system (wirk-gefüge); a thought-model system is a construction-building excavator at work in Fig. 1, with human driver’s cognitive-operational functions for $\mathcal{O}$$\mid$$\mathcal{Z}$, wheels and grabbing shovel as $\mathcal{P}$$\mid$$\mathcal{Z}$, and power unit as $\mathcal{V}$$\mid$$\mathcal{Z}$. In further drill-down, Fig. 4 develops the components seen in Fig. 2(right) where FL1 components in human-body system are interpreted as aggregates and decomposed into their respective functional units of FL2. The concept of aggregate’s action emerging from its units’ interaction—depicted for function levels FL1 to FL0 in Fig. 5—can be generalized to a common rationale for dynamics within SFA.

Fig. 4.

Functional components at FL2 in break-down from FL1 in Fig. 2(right), from (Mau 2016b, 2017): Physical ($\mathsf{P}$) and reproductive ($\mathsf{R}$) subsystems of $\mathcal{P}$$\mid$$\mathcal{Z}$, energy ($\mathsf{E}$), in-body transportation ($\mathsf{T}$), “home-land security” ($\mathsf{H}$), xeno-biotic residence ($\mathsf{X}$), and functional management and control ($\mathsf{FMCS}$) of $\mathcal{V}$$\mid$$\mathcal{Z}$, received sensory signals (${\mathsf{S}}_{\mathsf{aff}}$), decision-making ($\mathsf{D}$) with reasoning ($\mathsf{r}$) and motivation ($\mathsf{m}$), en-acting command signals (${\mathsf{S}}_{\mathsf{eff}}$) of $\mathcal{O}$$\mid$$\mathcal{Z}$

Fig. 5.

Person’s operational activity, perceived as his or her behavior by body’s outside world, emerges from functional interaction of body-system’s canonical components of effectuation, from Mau (2018a)

Paradigm 1

(Functional Biodynamics Paradigm) Upper level action emerges from lower level interaction, and interaction of a functional aggregate’s constituent functional units express in aggregate’s actions.

With notation as in Eq. 1 for any functional aggregate, it will then suffice to combine the dynamic models of its m $\mathrm{FL}k$ units ${\mathrm{FU}}_i$, $i=1,\cdots ,m$, into a dynamic model of their aggregate ${\mathrm{FA}}^{\mathrm{FL}k}$, for any function level $k>0$. As by Eq. 2 any $\mathrm{FL}k$ functional aggregate shows as $\mathrm{FL}(k-1)$ functional unit, per-functional-unit dynamic models and per-functional-aggregate dynamic models must be of same type to achieve coherent multi-scale mathematical dynamics within SFA.

Daily functional dynamics

Two requirements have to be met: (1) the dynamic model must be simple enough to permit cross-level translation, and (2) the 24-hours wake-sleep cycle of moderately exhaustive labor and subsequent restorative rest must be represented. Hence, a simple supply-chain model with first-order kinetics of in-flow of energy, an intermediate storage, and another first-order kinetics of out-flow of energy by demand, is chosen for day-to-day dynamics within every functional unit as explained in 2.2.1, next. Then, its suitability for up-scaling will be shown in 2.2.2.

Charge-transfer dynamics in a single functional unit

Though originally published in the terminology of direct-current electric circuits by Mau (2018b), the dynamic model will now be described in terms of intensity functions, cf. Mau (2018a) and (Mau 2020, App. B) for introduction in general terms. The most intuitively understood explanation of this dynamic concept is the decelaration of a car when approaching a red traffic light: the closer to the stopping line, the less the car’s velocity, in a gentle approach. More technically speaking, one adjusts speed at time t to t-current residual path-to-destination; for any t, the ratio generates an intensity function in time t which, in the simplest case, is a constant.

Consider a kind of supply-chain logistics as depicted in Fig. 6: from an inexhaustible “source”, “charges” are supplied to an end-consumer via an intermediate “capacitor” (synonymously a hub, or a storage, depending on context). Though some terminology is borrowed from direct-current electric circuits, no specific real-world physical interpretation is assumed: the setting is strictly axiomatic as in Mau (2018b). With its legend, Fig. 6 has the briefest account of constructs and ingredients.

Fig. 6.

Generic effectuation dynamics in a single functional unit: A ubiquitous energizing source of potential difference $U_0$, a supply-part capacitor (center left) of capacity C that permits maximal charge $Q_{\max }=C{U}_0$ and a demand-part capacitor (center right) for discharge service to an end-consumer of t-current power demand $P_e(t)$; $Q_s(t)$ charge accumulated by time t matches $Q_c(t)$ charge available for discharge at time t; ${\lambda }_s(t)$ and ${\lambda }_c(t)$ denote intensities of charging and of discharging respective capacitors; from Mau (2019)

Then, denote t-current residual charge necessary to reach full charge $Q_{s,\max }=U_{0}C$ on the supply-part capacitor by

$$\begin{array}{c}\hfill Q_{s,\mathrm{res}}(t)=Q_{s,\max }-Q_s(t),t\ge 0,\end{array}$$ 3

and the t-current residual charge on the demand-part capacitor by $Q_{d,\mathrm{res}}(t)$ as $Q_{d,\mathrm{res}}(t)=Q_c(t)$. Supply-part charge increments $\mathrm{d}{Q}_s(t)$ and demand-part charge decrements—or synonymously discharge increments—$\mathrm{d}{Q}_c(t)$ are each proportional to the pertinent t-current residual charges “due for transfer”, $Q_{s,\mathrm{res}}(t)$ and $Q_{d,\mathrm{res}}(t)=Q_c(t)$, respectively.

Proposition 1

Functions $Q_s$and $Q_c$can then be assumed to permit factorizations of their increments on any arbitrarily chosen interval $]t,t+\mathrm{d}t]$with some non-decreasing positive real-valued differentiable functions, ${\Lambda }_s={({\Lambda }_s(t))}_{t>0}$and ${\Lambda }_d={({\Lambda }_d(t))}_{t>0}$, respectively,

$$\begin{array}{c}\hfill \mathrm{d}{Q}_s(t)=\mathrm{d}{\Lambda }_s(t)Q_{s,\mathrm{res}}(t),\mathrm{d}{Q}_c(t)=-\mathrm{d}{\Lambda }_c(t)Q_c(t)\end{array}$$ 4

Proof

In fact, let $q_{s,\mathrm{res}}(t)$ and $q_c(t)$ denote the relative charges to supply- and from demand-part capacitors, respectively, $q_{s,\mathrm{res}}(t)=1-Q_s(t)/Q_{s,\max }$ and $q_c(t)=Q_c(t)/Q_{c,\max }$. Then, $0\le q_{s,\mathrm{res}}(t)\le 1$ and $0\le q_c(t)\le 1$ are both monotonically decreasing functions and differentiable in t, with ${\dot{q}}_{s,\mathrm{res}}(t)=-{\dot{Q}}_s(t)/Q_{s,\max }$ and ${\dot{q}}_c(t)={\dot{Q}}_c(t)/Q_{c,\max }$. The proposition then follows from choosing

$$\begin{array}{c}\hfill {\Lambda }_s(t)\stackrel{\mathrm{def}}{=}-log{q}_{s,\mathrm{res}}(t),{\Lambda }_c(t)\stackrel{\mathrm{def}}{=}-log{q}_c(t)\end{array}$$ 5

$\square$

Corresponding equations were presented by Mau (2018b) for the approach via pseudo-electric twin-circuits. However, the intensity-function approach lends itself more easily to expansion of the theory, and also to identification and estimation of parameters from experimental observations. Note that cumulative intensity functions ${\Lambda }_s$ and ${\Lambda }_c$ are dimensionless, irrespective of metric dimensions of charges Q. These functions permit uniquely defined—up to a constant—representations of their differentials, $\mathrm{d}{\Lambda }_s(t)={\lambda }_s(t)\mathrm{d}t$ and $\mathrm{d}{\Lambda }_c(t)={\lambda }_c(t)\mathrm{d}t$, with ${\lambda }_s$, ${\lambda }_c$ positive real functions, called (charge-transfer) intensities of charging and discharging capacitors, respectively. In reliability analysis, intensities are used to include additional factors that are involved in transfer dynamics. Let $\mathbf{z}$ be a vector of such covariates, then

$$\begin{array}{c}\hfill \mathrm{d}{\Lambda }_s(t;\mathbf{z})={\lambda }_s(t;\mathbf{z})\mathrm{d}t,\mathrm{d}{\Lambda }_c(t;\mathbf{z})={\lambda }_c(t;\mathbf{z})\mathrm{d}t\end{array}$$ 6

introduce $\mathbf{z}$ into Eq. (4), cf. Andersen et al. (1993) for statistical inference.

Up-scaling to functional aggregate dynamics

Definition 1

[Axiomatic Wirkgefüge Mau (2018b)] If generic first-order kinetics of $\mathrm{FA}=\{{\mathrm{FU}}_1,\cdots ,{\mathrm{FU}}_m\}$ arise from those of individual ${\mathrm{FU}}_i$, $i=1,\cdots ,m$, by summing respective capacities and charges in supply-parts and demand-parts,

$$\begin{array}{cc}\hfill C_s^{\mathrm{FA}}=& \sum _{\mathrm{FU}\in \mathrm{FA}}{C}_s^{\mathrm{FU}},C_d^{\mathrm{FA}}=\sum _{\mathrm{FU}\in \mathrm{FA}}{C}_d^{\mathrm{FU}},\hfill \\ \hfill Q_s^{\mathrm{FA}}(t)=& \sum _{\mathrm{FU}\in \mathrm{FA}}{Q}_s^{\mathrm{FU}}(t),Q_d^{\mathrm{FA}}(t)=\sum _{\mathrm{FU}\in \mathrm{FA}}{Q}_d^{\mathrm{FU}}(t),\hfill \end{array}$$

for all functional levels $\mathrm{FL}k$, $k>1$, in a given System Functional Architecture, then this set of equations constitutes an axiomatic wirkgefüge.

One next has to show that dynamics of Eq. (4) in Proposition 1, active within each element of a $\mathrm{FL}k$ functional aggregate, actually translate to those of a functional unit at $\mathrm{FL}(k-1)$, in the sense of (2). Because the original proof in Mau (2018b) used the pseudo-electric twin-circuit representation, another proof is given here in terms of (cumulative) intensity functions.

Theorem 1

Consider ${\Lambda }_s(t)$and ${\Lambda }_c(t)$as in Proposition1for some $\mathrm{FA}$as in (1), then

$$\begin{array}{c}\hfill \mathrm{d}{\Lambda }_s^{\mathrm{FA}}(t)=\sum _{\mathrm{FU}\in \mathrm{FA}}\mathrm{d}{\Lambda }_s^{\mathrm{FU}}(t)\frac{C_s^{\mathrm{FU}}}{C_s^{\mathrm{FA}}},\mathrm{d}{\Lambda }_c^{\mathrm{FA}}(t)=\sum _{\mathrm{FU}\in \mathrm{FA}}\mathrm{d}{\Lambda }_c^{\mathrm{FU}}(t)\frac{C_d^{\mathrm{FU}}}{C_d^{\mathrm{FA}}}\end{array}$$ 7

Proof

For the supply-part,

$$\begin{array}{c}\hfill \sum _{\mathrm{FU}\in \mathrm{FA}}\left[U_0,C_s^{\mathrm{FU}},-,Q_s^{\mathrm{FU}},(t)\right]\mathrm{d}{\Lambda }_s^{\mathrm{FU}}(t)=\sum _{\mathrm{FU}\in \mathrm{FA}}\mathrm{d}{Q}_s^{\mathrm{FU}}(t)\end{array}$$ 8

and by equations in Def. 1, the right-hand side equals $\mathrm{d}{Q}_s^{\mathrm{FA}}(t)$ with its analogous representation

$$\begin{array}{c}\hfill \mathrm{d}{Q}_s^{\mathrm{FA}}(t)=\left[U_0,C_s^{\mathrm{FA}},-,Q_s^{\mathrm{FA}},(t)\right]\mathrm{d}{\Lambda }_s^{\mathrm{FA}}(t);\end{array}$$ 9

the terms in square brackets represent the residual charges for transfer to respective supply-part capacitors. As all supply-part capacitors are assumed to be in a parallel connection, equal potential differences cancel out,

$$\begin{array}{c}\hfill \frac{Q_{s,\mathrm{res}}^{\mathrm{FU}}(t)}{Q_{s,\mathrm{res}}^{\mathrm{FA}}(t)}=\frac{C_s^{\mathrm{FU}}}{C_s^{\mathrm{FA}}}\end{array}$$ 10

For the demand-part, replace $C_s$ with $C_d$ above and assume that all demand-part capacitors are in a parallel connection and then use

$$\begin{array}{c}\hfill \frac{Q_c^{\mathrm{FU}}(t)}{Q_c^{\mathrm{FA}}(t)}=\frac{C_d^{\mathrm{FU}}}{C_d^{\mathrm{FA}}},\end{array}$$ 11

the proof is along the same lines as for the supply-part above. $\square$

Up-scaled intensities of charge transfers at functional level $\mathrm{FL}(k-1)$ are then capacity-weighted sums of intensities of next-lower functional level $\mathrm{FL}k$.

Daily rhythms

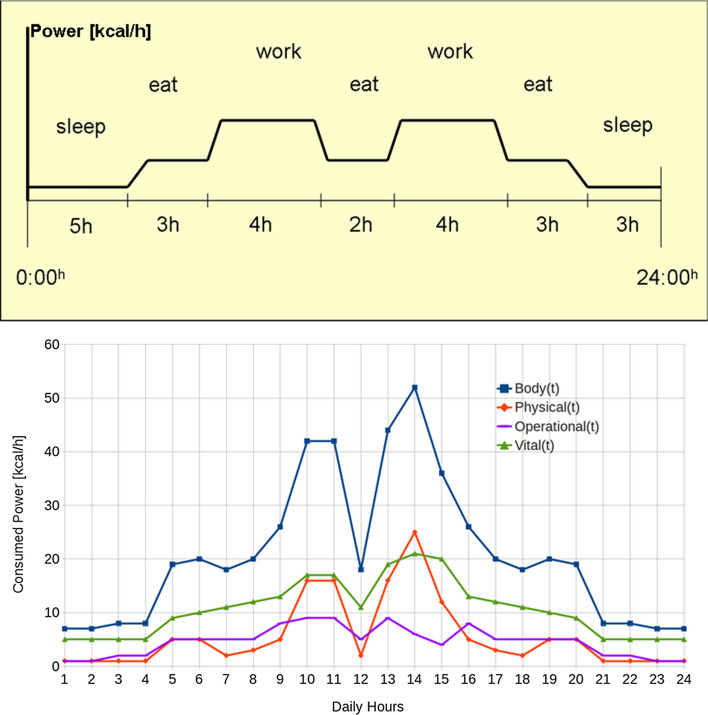
Rhythms arise with faster-than-average release and slower-than-average refill of buffers sized for average consumption under common scenarios. For engineered systems, energy buffers are sized to balance average energy demand and average energy supply for the expected duration of a mission, and oscillations of shortage and surplus would decrease system efficiency. In the living, rhythms mark a design motif: though energy buffers will also adjust to average demand, living systems are able to release currently available energy very fast and almost completely in order to escape from a sudden vital threat. Data from a standard physiology textbook (Hall 2011) can be used to construct some quantitative examples: As one of slow refill of energy buffers, i.e. capacitors as in Fig. 6, at level of whole human-body system, consider a 70kg man who consumes 65kcal/h during 8h at sleep-phase minimum to sustain vital physiological functions (low breathing, lying flat with little movement, calm brain activity); as an example of fast-release and subsequent slow restoration of average consumption levels, consider an athlete who runs 100m in 10s and then sits with close to minimal wake-phase resting power of 100kcal/h for a while until the energy for moderately normal wake-labor, e.g. 200kcal/h “walking slowly (2.6 miles per hour)”, returns. Therefore, one has to understand wake-sleep cycles as an advantageous design feature in the living as it permits more flexibility in variant scenarios of exposure and task-solving than engineered systems can achieve. To illustrate how rhythms can be accommodated within SFA, energy consumption rates of a human-body system during a full 24-h period are chosen. To fix ideas, consider first the over-simplified scenario of a schematic 24-h power profile in Fig. 7(top) with only three kinds of activity, sleeping, eating/clearing, and working, with transitions from one phase to the next. For a break-down from whole functional body $\mathcal{B}$$\mid$$\mathcal{Z}$ into its components of vital $\mathcal{V}$$\mid$$\mathcal{Z}$, physical $\mathcal{P}$$\mid$$\mathcal{Z}$ and operational $\mathcal{O}$$\mid$$\mathcal{Z}$ functions, a refined set of activities is needed to generate a changing mix as seen in Fig. 7(bottom): deep sleep (2h), awakening (2h), getting up (1h), dressing (1h), eating (1h), clearing (1h), going to work (1h), workplace mid-effort labor (2h), lunch break (1h), mid-effort labor (1h), heavy-effort labor (1h), low-effort labor (1h), going home (1h), clearing (1h), eating (1h), undressing (1h), going to bed (1h), sleeping off (2h), deep sleep (2h). With approximate data for whole body energy consumption, one can attribute respective percentages to vital, physical and cognitive operational functions within each activity, for example a higher cognitive demand when going to work or to home and in mid-effort labor, but a very high physical demand in high-effort labor—depending on prevalent dominance of physical or cognitive tasks in an activity. While the data in Fig. 7(bottom) is now still an artefact for illustration of the principle, experimental data will become available with the advent of pertinent biometrical technologies.

Fig. 7.

Top: Schematic 24h power profile with a sleep-phase offset (65kcal/h for a 70kg man) for minimal demand, unscaled, “eat” for meals including light activity of daily living, and finite slopes in preparations for transition from one kind of activity to the next (from Mau (2018a)). Bottom: Daily consumed power profiles in vital (green), physical (red), and operational (purple) functions in a changing mix (based on artificial data as explained in the text) add to a total-body profile similar to the one above

Functional learning

Functional learning in a single functional unit

With a functional unit’s capacity as its ability to perform according to a specific demand, understand functional learning as an expansion of this capacity in order to perform according to a higher demand; this can be represented by an enlarged capacity C of the capacitors in Fig. 6. Physical exercise in muscle training shall show the path, cf. Kenney et al. (2020). Learning is then seen as training for higher performance in some functional feature, and shall emerge from kind of high-intensity progressive resistance strength functional challenging found to be effective in muscle training by Raymond et al. (2013). This fits into the present mathematical setting, since levels of available charge $Q_c(t)$ on the demand-part capacitor generate the driving force for charge transfers to the end-consumer by $U_c(t)=Q_c(t)/C$, and then translate into end-consumer’s performance in terms of power; hence, enlarged capacity C in all desirable functionalities is necessary. Note, that larger levels of capacity C imply larger levels of $Q_{s,\max }=U_{0}C$ and be reminded that $Q_{c,\max }=Q_{s,\max }$ because of “mirroring”.

One first has to digress from the time scale of 24-hours in wake-sleep cycles to the coarser scale of whole days, which may again be taken as practically continuous when observing that one year of life has 365.25 days on average. Denote time in days by $\tau$, then, and consider days at which exhaustive discharges from $ϵ$-almost maximum levels of charge available for transfer occur; assume that permissible discharge would come to a halt before reaching destructive levels of $Q_c(t)<Q_{c,\min }$ on the demand-part capacitor. Define size of an $ϵ$-exhaustive discharge $Q_{c,\max ,ϵ}$ then by

$$\begin{array}{c}\hfill Q_{c,\max ,ϵ}+ϵ=Q_{c,\max }-Q_{c,\min },\end{array}$$ 12

for some small value of $ϵ>0$. Any occurrence of an $ϵ$-exhaustive discharge is considered as a functional challenge, cf. Fig. 8.

Fig. 8.

Left: Illustration of notation in Eq. 12: $Q_{c,\min }$ the critical level. For small values of $ϵ>0$, fast discharge of the yellow-colored volume to the critical level can occur in strong exercise. Right: Occurrences of functionally challenging demands are shown as a point-process realization in the lower part, the “book-keeping” kind of function above has a step of size one, whenever an occurrence is recorded in elapsing time from left to right

Definition 2

[Functional Challenge] A capacity-enhancing functional challenge (CEFC) on the demand-part capacitor occurs with an $ϵ$-exhaustive discharge in a very small time interval, in other words, there is some $t_c$, $0<t_c<t_{\max }$, such that $Q_{c,\max }-ϵ\le Q_c(t_c)\le Q_{c,\max }$ and $Q_c(t_c+\mathrm{d}t)=Q_{c,\min }$, equivalently,

$$\begin{array}{c}\hfill \mathrm{d}{Q}_c(t_c)=Q_{c,\max ,ϵ}.\end{array}$$ 13

Note that an $ϵ$-exhaustive discharge shall occur at most once a day, when $ϵ$ is sufficiently small and restoration to full charge levels needs a phase of “restorative sleep”.

Let $D(\tau )$ denote the indicator of occurrence of a CEFC event during day $\tau$,

$$D(\tau )=\begin{array}{c}1:\exists t\in \tau :\text{d}{Q}_c(t_c)=\text{d}{Q}_{c,max}\\ 0:\forall t\in \tau :\text{d}{Q}_c(t_c)\ne \text{d}{Q}_{c,max}\end{array}$$ 14

Denote the point-function of occurrences of CEFC events in $\tau$-time by function $D={(D(\tau ))}_{0<\tau <{\tau }_{\max }}$: for any $0<\tau <{\tau }_{\max }$, $\tau$ is an occurrence time of CEFC, if and only if $D(\tau )=1$. Denote the ordered sequence of occurrence times by

$$\begin{array}{c}\hfill 0={\tau }_0<{\tau }_1<{\tau }_2<\dots <{\tau }_k<{\tau }_{k+1}<\dots \end{array}$$ 15

The associated counting function of occurrences of CEFC events in $\tau$-time,

$$\begin{array}{c}\hfill N_D(\tau )=\sum _{{\tau }_i\le \tau }D({\tau }_i),\end{array}$$ 16

is a positive and increasing step function with jumps of size 1 at exactly the times in (15), right-continuous with left-hand limits (“cadlag”), and bounded on any finite $\tau$-interval. If occurrence times in (15) were random, ${(N_D(\tau ))}_{0<\tau <{\tau }_{\max }}$ would be studied further as a counting (random) process, which offers an entry point for statistical data analysis, cf. Andersen et al. (1993). Within the present scope, stochastification is not needed beyond motivation of the particular deterministic function to be chosen for expansion of a functional unit’s capacity, as explained at the beginning of this subsection: When “hits” emanate from a “source” by a Poisson law, as for example in radioactive decay, with constant rate ${\beta }^{-1}$, $\beta >0$, and when at least $\alpha$ “hits” are required to elicit an oncogenic response in living tissue, integer $\alpha >0$, the probability $F(\tau ;\alpha ,\beta )$ of occurrence of at least one such response within a fixed time span of duration $\tau$ is

$$\begin{array}{c}\hfill F(\tau ;\alpha ,\beta )=\sum _{l>\alpha }\frac{{\left(\frac{\tau }{\beta }\right)}^l}{l!}{e}^{-\frac{\tau }{\beta }}.\end{array}$$ 17

This is the multi-hit model of carcinogenesis, cf. Belikov (2017) for recent evidence in a variety of tumors. Rewriting the right-hand side as

$$\begin{array}{c}\hfill F(\tau ;\alpha ,\beta )=\frac{1}{\alpha !\beta }{\int }_0^{\tau }{\left(\frac{u}{\beta }\right)}^{\alpha }{e}^{-\frac{u}{\beta }}\mathrm{d}u,\end{array}$$ 18

$\alpha !\beta F(·;\alpha ,\beta )$ is generally known as an incomplete Gamma function, and $F(·;\alpha ,\beta )$ represents the (cumulative) distribution function of a Gamma (random) distribution with integer $\alpha >0$ and real $\beta >0$ as parameters, in probability theory; in particular, ${lim}_{\tau \to \infty }F(\tau ;\alpha ,\beta )=1$ and the shape of $F(·;\alpha ,\beta )$ as a function in $\tau$ will approximate the S-shaped one of the standard normal distribution, with increasing values of $\alpha$; cf. Mood and Graybill (1963) for this and some more detail.

Definition 3

[Multi-hit Enhancement] A stress-induced enhancement of functional capacity from baseline $C(0)=C$ to $C(\tau )$ in $\tau$ units of $\tau$-time is then obtained from

$$\begin{array}{c}\hfill C(\tau )=C(0)\left[1,+,F,(,\tau ,;,\alpha ,,,\beta ,)\right],\end{array}$$ 19

for choices of parameters according to a preferred rate of enhancement.

Of note, with a dose-dependent extension of the multi-hit model due to Rai and Van Ryzin (1981), one can include the size of $ϵ$-exhaustive discharges $\mathrm{d}{Q}_c(t_c)$.

Functional learning in Systems Functional Architecture

Generic functional learning was based on repeated occurrences of demand-part capacitor’s rapid discharge down to critical levels, called functional challenges. In a System Functional Architecture with its sequence of functional levels, $\mathrm{FL}k$, $k=0,1,\cdots$, expanded capacities of lower-level functional units can only affect capacities of upper-level functional units when embedded via functional aggregation, cf. Theorem 1.

Then, expanded functional capacities from lower functional levels translate into functional capacities at upper functional levels, but effects get ’diluted’ from other functional units’ unchanged capacities, the higher one follows the expanded capacity up:

$$\begin{array}{cc}& \frac{C_s^{\mathrm{FU}}(\tau )}{C_s^{\mathrm{FA}}(\tau )}=\hfill \\ \hfill & \frac{C_s^{{\mathrm{FU}}_i}(\tau )}{C_s^{{\mathrm{FU}}_1}(0)+\cdots +C_s^{{\mathrm{FU}}_{i-1}}(0)+C_s^{{\mathrm{FU}}_i}(\tau )+C_s^{{\mathrm{FU}}_{i+1}}(0)+\cdots +C_s^{{\mathrm{FU}}_m}(0)}\hfill \end{array}$$ 20

For illustration, training of a single muscle will not make a champion. This inconspicuous remark points top-down: define the capacity goal—as well as limits—of functional whole, the single FU at FL0, understand it as a functional aggregate in the sense of (2) with $k=1$, and find its level FL1 functional units as in (1); for example, an athlete may focus on physical functions, a chess-champion on cognitive functions.

Functional aging

Here, functional aging will only be considered for $\mathcal{B}$$\mid$$\mathcal{Z}$, the functional whole, cf. Fig. 3. The time scale is then lifetime in years of age, denoted by $\theta$.

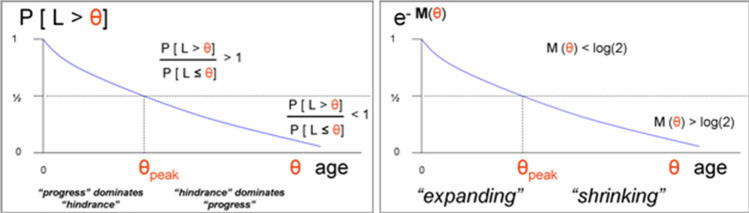
In the first place, aging is elapsing time in life, and the time span from birth to death is lifetime, the time spent alive. In disregard of all other aspects that surround the evolvement of a life, the deterministic intensity function (force of mortality), $\mu$ of age $\theta$, cf. Fig. 9(right), catches this aspect completely, as $\mu (\theta )$ represents a person’s $\theta$-current instantaneous conditional risk-of-death, “conditional” because to be meaningful the person must still be alive to have the risk, which is tantamount to the chance not to die. Then, $\mu (\theta )$ can be seen as the speed in elapsing age $\theta$ by which the probability to survive any longer approaches zero. As long as specific biomarkers are not available to determine a person’s $\mu (\theta )$, it must be estimated from official life tables as a demographic force of mortality, an average across the person’s pertinent population, cf. Chiang (1980) for the methodology.

Fig. 9.

Left: Schematic life-time representation of increasing functional capacity from birth to some maximum around or in mid-life years followed by decreasing functional capacity (from Mau (2019)). Right: State diagram of a simple death process with one transient “life” state 0, one absorbing “death” state 1, and transition intensity function $\mu$ of age $\theta$ as the demographic force of mortality, or demographic Linhart-sense entropic force, in a population

Functional aging, by contrast, means physiological frailty, a functional degrading as a shrinking ability of $\mathcal{B}$$\mid$$\mathcal{Z}$ to perform common tasks; it may be ascribed to an insufficient supply of charge that cannot meet daily functional needs anymore, and an according downsizing of capacities in “buffers”, see Fig. 6. Causes will be variant, but main categories are suggested from System Functional Architecture, and a steam-powered railway locomotive is an intuitive analogue of whole human-body system for illustration:

• Dysfunctional components within a functional aggregate FA, the effects of which may resist autonomous balancing-out and then compromise upper-level functions, cf. Fig. 3 with a functional unit marked with an arrow at FL3 in $\mathcal{P}$$\mid$$\mathcal{Z}$;

• Failures in coordination of interaction between a functional aggregate’s components, cf. Fig.5 for FL1;

• Functionally compromised cellular material, due to, e.g., space-occupying lesions or tissue weakened by wear-out, or loss of genomic integrity induced by lysosphingolipid imbalance recently described by Ahuja et al. (2019);

However durable the material and however resourceful the source energy reservoir, consumed total charge within the system will be bounded, such that relative-to-maximum consumable total, F, say, will be of sigmoid shape between zero and one in elapsing service time $\theta$ with some density function as schematically depicted in Fig. 9(left). This suggests a further analogy with axiomatic phenomenological thermodynamics, when heat is replaced by time as in G.A. Linhart’s chronodynamics in natural growth processes of a mass, cf. (Starikov 2012, 2019) for a recent elaborate account of Linhart’s work. Since the relative-to-maximum cumulative function F will own all properties of a (deterministic) distribution function of a probability distribution, there exists then a synthetic probability measure P with a real-valued random variable L, cf. Loève (1963), representing lifetime, such that

$$\begin{array}{c}\hfill P\{L\le \theta \}=F(\theta ),P\{L>\theta \}=1-F(\theta )\end{array}$$ 21

In application of the intensity concept in 2.2.1(first paragraph), consider $\theta$-current density $\dot{F}(\theta )$ relative to residual “path” $1-F(\theta )$ as accumulating in progressing time $\theta$ to a cumulative intensity function

$$\begin{array}{c}\hfill M(\theta )={\int }_0^{\theta }\frac{\dot{F}(s)}{1-F(s-)}ds\end{array}$$ 22

which solves the differential equation $dF(\theta )=dM(\theta )[1-F(\theta -)]$ with $M(0)=0$. Rewriting as

$$\begin{array}{c}\hfill 1-F(\theta )=e^{-M(\theta )},\end{array}$$ 23

shows M as Linhart’s chronodynamic entropy, and accordingly,

$$\begin{array}{c}\hfill M(\theta )=-log[P\{L>\theta \}]\end{array}$$ 24

which is tantamount to Boltzmann’s definition of thermodynamic entropy.

As stronger vitality at age $\theta$ expresses in larger survival probability beyond $\theta$, $P\{L>\theta \}$, Eq. (24) implies a concurrently smaller value of entropy $M(\theta )$ that reflects lower frailty: though the relationship is not one-to-one, the two are tied together. Of interest is then age ${\theta }_{\mathrm{peak}}$, at which $P\{L>\theta \}$ and $P\{L\le \theta \}$ come apar, cf. Fig. 10(left), and alternatively, $M(\theta )=log(2)$, cf. Fig. 10(right). For demographic entropy, one gets, for example, ${\theta }_{\mathrm{peak}}=37$ years of age for men and ${\theta }_{\mathrm{peak}}=40$ years of age for women as population averages in the German Federal State North-Rhine Westphalia 1986/88 (Mau 2019). Determination of personalized entropy at peak, $M(\theta )=log(2)$, may become possible with further research by Leo Kurian and co-workers on biomarkers for loss of genomic integrity induced by lysosphingolipid imbalance, as the conclusion “cardiac-specific accumulation of dihydrosphingosine levels drive the decline in cardiac health” from their recent results (Ahuja, Bartsch, Yao et al. 2019) was “a somewhat unexpected finding that our body obviously destroys itself during aging” (Jürgen Hescheler, private communication, December 2019).

Fig. 10.

The two displays show the same survival function, though in different notations - left: commonly known survival probability, right: written in terms of cumulative intensity and hence entropy. The turning point is ${\theta }_{\mathrm{peak}}$ when the probability of longer survival gives way to the probability of not-to-live-longer, and it corresponds to entropy of $log2$, cf. Fig. 9

Discussion

The merits of an axiomatic approach are known from thermodynamics and probability theory, cf. Starikov (2019) for a recent review and Kolmogoroff (1933), respectively: abstract properties of phenomena, e.g. temperature and probability, can be postulated in a mathematical form and implications be obtained for comparison with experimental outcomes, or for prediction, all despite uncertain, incomplete, or inaccessible knowledge about underlying basic mechanisms from which said phenomena would emerge. This legitimizes an axiomatic biodynamics.

System Functional Architecture as introduced by (Mau 2016a, b, 2019) implies a hierarchical structure of functional scale levels as well as a delegation of all material properties to a base level, as done in “layer” concepts of computer System Network Architecture and comparable design standards (Kuo 1981). It is then a necessary environment for a holistic and multi-scale coherent axiomatic theory.

Design motifs of living nature and engineered systems can be quite similar, as suggested in the subtitle of Norbert Wiener’s seminal work on cybernetics (Wiener 1961), control and communication in the animal and the machine, and a little earlier by Fritz Kahn, who illustrated human-body physiology as a factory in art-work for lay press (von Debschitz and von Debschitz 2013): man and machine share in being made for purpose—production of some kind—but differ in purpose.

Technically, human-body system is an autonomously acting bio-reactor, though non-autarkic as it is vitally dependent on uninterrupted oxygen-logistics for permanent combustion of ingested nutrients to keep its ${10}^{14}$ body cells alive. This cellular system is living-nature’s sole material option—and in this role comparable to metal, plastics, stone or wood that engineers use in fabrication of their machines and buildings. Accordingly, design principles of living nature will be fundamentally different. For example, the living’s rhythm of labor and restoration is a distinct design principle for a widely unspecified range of operational options and limited resources.

Learning is a core requirement to remain “fitted and witted” for self-sustained life, as living nature does not provide the learned competence to meet life’s challenges, only a genetic recipe. Learning for wits starts from functional activity and is triggered by volition to overcome a met functional deficit, in order to fulfill a task, to pursue in a mission, or to satisfy an ambition: learning just for no purpose is not an option in living nature, and not in engineered systems made for a purpose, either. And, learning needs a functional option, as horses will never swim like fish, much less fly like bird; it then becomes an issue of expanding an available capacity currently too low for one’s intention.

Functional learning in the present theoretical set-up is about functional task-solving capacity-enhancement. Functional learning is not watching how to do things, nor is it taking up abstract knowledge, or theory in education, as this can provide only recipes that have to be translated for implementation into an intended action. It is then kind of “learning by doing”.

Though systems differ substantially in mission, design, and material realization for a designated environment, effectuation dynamics characterized by intensity functions with their translations apply throughout and across all levels in functional up-scaling or down-scaling within a system. However, effects of an expanded—or a shrinking, for that purpose—capacity can be followed only upwards from the functional level at which they occur.

Three technical points have to be made,

• The immediate release (13) adopted for “upgrading mechanics” can be spread out to a short interval during the day;

• In human-body system during child development to adulthood, also capacities of vital functions (lung, cardio-vascular logistics, digestive systems, nervous system) are expanded, parallel to growth of osseous structures, by genetic programs;

• The generality of “charges” mandates a remark on identification and estimation of charge-transfer dynamics: one suggestion is to consider implied charge-transfer work (Mau 2018a) as this was seen not to change the intensity functions that characterize dynamics.

To conclude, this work may be seen as an interpretation of embodied action—if not precisely in the spirit of, so still motivated by Varela et al (1991) who introduced the “view of cognition as embodied action” into cognitive science. Building on the present axiomatics, Clark and Chalmers’ (1998) understanding that the two-way interaction between a person’s body-system and his or her life-sphere surroundings creates a “cognitive system in its own right”, has been taken up by the present author (Mau 2020), recently.

Funding

My visit to Faculty of Physical Chemistry, University of Belgrade, May 2019, was funded by Ministry of Education, Science and Technological Development of Republic of Serbia; additionally, some expenses were covered by Society of Physical Chemists of Serbia. My participation at the 7th International Conference of the Serbian Society of Mechanics in Sremski Karlovci, June 2019, was also funded by this Ministry, though through Mathematical Institute SASA, Belgrade, Grant ON174001 “Dynamics of Hybrid Systems with Complex Structures, Mechanics of Materials”, and some additional expenses were covered by the Serbian Society of Mechanics.

Compliance with ethical standards

Conflicts of interest

The authors declare that they have no conflict of interest.

Consent for publication

Written consent to publish the photo in Fig. 1 was received 26 June 2020.