Thermodynamic equilibrium dose-response models for MERS-CoV infection reveal a potential protective role of human lung mucus but not for SARS-CoV-2

Highlights

• •Prototype dose-response model for initial infection by respiratory coronaviruses developed based on molecular parameters;
• •Number of free virus particles not bound to mucus in the lung modelled as a function of virus dose in mucus and thermodynamic association constant;
• •Binding of MERS-CoV to human mucin may contribute to lower human-to-human transmission compared to SARS-CoV-2;
• •Binding of MERS-CoV and SARS-CoV-2 to cellular receptors is not a limiting factor in infection;
• •This model may help evaluate the impact of distance in the transmission of SARS-CoV-2.

Abstract

Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) and Middle East respiratory syndrome coronavirus (MERS-CoV) infect the human respiratory tract. A prototype thermodynamic equilibrium model is presented here for the probability of the virions getting through the mucus barrier and infecting epithelial cells based on the binding affinity (K_mucin) of the virions to mucin molecules in the mucus and parameters for binding and infection of the epithelial cell. Both MERS-CoV and SARS-CoV-2 bind strongly to their cellular receptors, DDP4 and ACE2, respectively, and infect very efficiently both bronchus and lung ex vivo cell cultures which are not protected by a mucus barrier. According to the model, mucin binding could reduce the infectivity for MERS-CoV compared to SARS-CoV-2 by at least 100-fold depending on the magnitude of K_mucin. Specifically K_mucin values up to 10⁶ M⁻¹ have little protective effect and thus the mucus barrier would not remove SARS-CoV-2 which does not bind to sialic acids (SA) and hence would have a very low K_mucin. Depending on the viability of individual virions, the ID₅₀ for SARS-CoV-2 is estimated to be ~500 virions (viral RNA genomic copies) representing 1 to 2 pfu. In contrast MERS-CoV binds both SA and human mucin and a K_mucin of 5 × 10⁹ M⁻¹ as reported for lectins would mop up 99.83% of the virus according to the model with the ID₅₀ for MERS-CoV estimated to be ~295,000 virions (viral RNA genomic copies) representing 819 pfu. This could in part explain why MERS-CoV is poorly transmitted from human to human compared to SARS-CoV-2. Some coronaviruses use an esterase to escape the mucin, although MERS-CoV does not. Instead, it is shown here that “clustering” of virions into single aerosol particles as recently reported for rotavirus in extracellular vesicles could provide a co-operative mechanism whereby MERS-CoV could theoretically overcome the mucin barrier locally and a small proportion of 10 μm diameter aerosol particles could contain ~70 virions based on reported maximum levels in saliva. Although recent evidence suggests SARS-CoV-2 initiates infection in the nasal epithelium, the thermodynamic equilibrium models presented here could complement published approaches for modelling the physical entry of pathogens to the lung based on the fate and transport of the pathogen particles (as for anthrax spores) to develop a dose-response model for aerosol exposure to respiratory viruses. This would enable the infectivity through aerosols to be defined based on molecular parameters as well as physical parameters. The role of the spike proteins of MERS-CoV and SARS-CoV-2 binding to SA and heparan sulphate, respectively, may be to aid non-specific attachment to the host cell. It is proposed that a high K_mucin is the cost for subsequent binding of MERS-CoV to SAs on the cell surface to partially overcome the unfavourable entropy of immobilisation as the virus adopts the correct orientation for spike protein interactions with its protein cellular receptor DPP4.

1. Introduction

Severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) emerged in December 2019, causing a respiratory disease (coronavirus disease 2019, COVID-19) of varying severity in Wuhan, China, subsequently leading to a pandemic (Hui et al 2020). By 8 Aug 2020 there had been some 19.4 million cases of SARS-CoV-2 worldwide with 721,906 deaths globally (Anon 2020). Like SARS-CoV-2 other beta coronaviruses (CoVs) such as severe acute respiratory syndrome virus (SARS-CoV) and Middle East respiratory syndrome coronavirus (MERS-CoV) also infect the human respiratory tract and causes severe zoonotic respiratory disease. MERS-CoV is transmitted sporadically to humans from its dromedary camel (Camelus dromedarius) reservoir, causing severe respiratory disease with ~35% fatality rate (Li et al. 2017). A major difference is that both SARS-CoV and SARS-CoV-2 are readily transmitted between humans by close contact, while MERS-CoV is not (Rabaan et al. 2020). Person-to-person community transmission of SARS-CoV-2 is highly efficient while MERS-CoV is transmitted occasionally by human-to-human contact (Killerby et al.2020) through infectious aerosolized particles often in hospital settings (Adhikawi et al. 2019). Thus, humans are considered transient or terminal hosts for MERS-CoV, with no evidence for sustained human-to-human community transmission. In naturally infected camels, MERS-CoV RNA has been recovered most commonly from nasal swabs but also from faecal swabs, rectal swabs, and lung tissue (Killerby et al. 2020). Levels of MERS-CoV RNA and SARS-CoV-2 RNA copies per cm³ of sputum or tracheal aspirate in infected humans are similar with median MERS-CoV levels of 10^5.5 copies (mild group) to 10^7.2 copies (severe group) (Oh et al. 2016) and median SARS-CoV-2 levels of 10^5.9 to 10^6.7 copies (Pan et al. 2020;To et al. 2020). This suggests these two viruses differ fundamentally in their infectiousness to humans. All three viruses infect bronchus and lung cells with high efficiency and indeed MERS-CoV seems to be the most efficient. Specifically in bronchus cell cultures, MERS-CoV replication competence is similar to that for SARS-CoV-2 and higher than SARS-CoV while in lung cell cultures, MERS-CoV-2 replication is higher than SARS-CoV and SARS-CoV-2 (Hui et al. 2020). While SARS-CoV-2 spike protein may not bind to sialic acid (SA) glycans (Hao et al. 2020) and hence to human mucins, that MERS-CoV spike protein does bind human mucin is well-documented (Li et al. 2017). Since both SARS-CoV-2 and MERS-CoV spike proteins bind strongly to their respective cellular receptors, it may be other factors such as differences in mucin binding affinity that affect infectivity. This is addressed here.

Previously a thermodynamic mechanistic approach was developed to use molecular biology data measured using biochemical methods to calibrate a dose-response model for a virus infecting the human intestine (Gale 2018). Here that model is developed for respiratory viruses such as MERS-CoV and SARS-CoV-2 by focusing on the removal of virus by mucus in the lung through entrapment (Zanin et al. 2016). The objective of this paper is to demonstrate a method to calibrate part of a dose-response model for respiratory viruses such as MERS-CoV and SARS-CoV-2 using available thermodynamic data for the key molecular interactions between the human host and viral factors during each stage of the infection process. The physical barriers and transport of the virions in the airways also have to be included in the model as for inhaled anthrax (Weir and Haas 2011) depending on where in the respiratory system the virus initiates infection, which may be in the nasal epithelium in the case of SARS-CoV-2 (Hou et al. 2020). A key physical barrier is the mucus gel layer which consists of 97% water and 3% solids, representing polymeric mucins. In its protective role, mucus entraps microbes and particles removing them from the lungs via the co-ordinated beating of motile cilia (Ridley and Thornton 2018). The major mucins produced in the airways of the human lung are the secreted polymeric mucins MUC5AC and MUC5B (Ridley and Thornton 2018) and present a barrier to respiratory viruses including influenza A virus (IAV) and adenovirus (De Graaf and Fouchier, 2014; Zanin et al. 2016; McAuley et al. 2017; Stonebraker et al. 2004). Mucins contain SA glycans to which proteins called lectins bind with high affinity, and in this respect viral surface proteins such as IAV haemagglutinin (HA) and MERS-CoV spike protein can be considered as lectins. Lectins show great specificity in the SAs to which they bind (De Graaf and Fouchier, 2014). The spike S1^A protein of MERS-CoV is particularly suited to bind human respiratory mucin but not to bovine submaxillary mucin (BSM) reflecting differences in the molecular structure of the SAs (Li et al. 2017). Similarly the mouse hepatitis coronavirus (MHV) and SARS-CoV do not bind BSM (Peng et al. 2012) and to the author's knowledge it is not known if they bind human mucin. In contrast to MERS-CoV, the spike protein of SARS-CoV-2 does not bind to SA (Hao et al. 2020) suggesting it does not bind to mucins. This may represent a fundamental difference between SARS-CoV-2 and MERS-CoV and it is suggested here that this may enhance the ability of SARS-CoV-2 to diffuse through the mucus barrier to reach the lung epithelial cells compared to MERS-CoV which, it is proposed here, becomes trapped in the mucus and removed. Indeed SARS-CoV, SARS-CoV-2 and MERS-CoV are all able to replicate well in ex-vivo cultures of both human bronchus cells and lung cells (Hui et al. 2020). Unlike in the lung in vivo, cell cultures do not have a protective mucous barrier, suggesting that once through the mucus barrier, the three viruses readily infect bronchus and lung cells. Of course, there are other differences too, and the presence of a furin-like cleavage site on the spike protein in SARS-CoV-2 facilitates the spike protein priming and might also increase the efficiency of the spread of SARS-CoV-2 compared to SARS-CoV and MERS-CoV (Rabaan et al. 2020). The fact that SARS-CoV-2 may initiate infection in the nasal epithelium would also increase its human-to-human transmission efficiency.

A dose-response model has been fitted to death data for MHV in mice and also for SARS-CoV in transgenic mice expressing human angiotensin-converting enzyme 2 (hACE2) which is the receptor for SARS-CoV (Watanabe et al. 2010). The ID₅₀ (death in mice through intranasal challenge) was estimated to be 280 plaque-forming units (pfu) (95% CI = 130 to 530 pfu) with p₁, the probability of death from a single virion, being 0.00246 (Huang 2013). Dose-response models such as that for MHV and SARS-CoV in mice (Watanabe et al. 2010) assume that the individual virions in a dose act independently and therefore that the risk of infection increases linearly (at low doses at least) with exposure dose, V_exposure. This may not necessarily be the case if virions in a high dose “cooperate” through overwhelming a host defence mechanism, in this case the mucins in the mucus in the lung. It is shown here for a virus that binds mucins that dispersion of the virus in the lung mucus could greatly decrease the fraction of free virus remaining to go on to infect the cells of the lung epithelium compared to the same dose concentrated (or clustered) in a single particle. Thus it is suggested here that rare, high-virion load aerosol particles may be important for MERS-CoV to get through the mucus barrier such that the virions comprising a dispersed dose may be overwhelmed by the mucin defences while the same number of virions if “acting together” may locally overwhelm the mucin defence such that more manage to get through the mucus to the lung epithelial cells. Conceptually this “co-operative action” is analogous to a team of 10 persons forming a human triangle such that one person successfully scales a high wall while acting individually none of the 10 persons can clear the wall. In contrast to MERS-CoV, aerosol particles containing a single virion of SARS-CoV-2 would be more infectious. The actual ID₅₀ in terms of number of virions and the value of p₁ depend on the virion (genomic RNA copy number) to pfu ratio. It is not suggested that all those virions comprising a pfu have to co-operate to initiate infection. Instead only a small proportion of virions are viable in terms of being able to initiate infection. It is assumed that all virions whether viable or not are able to bind SA and hence bind mucin through the spike protein in the case of MERS-CoV.

The co-operative effect is only relevant if single aerosol particles small enough to get into the bronchus i.e. <10 μm in diameter (Van Leuken et al. 2016) contain multiple virions. Otherwise the virions must be considered to be fully dispersed and acting independently. A small proportion of 10 μm diameter aerosol particles as produced in coughs from IAV-infected persons (Lindsley et al. 2012) could contain multiple SARS-CoV-2 or MERS-CoV virions. Viral RNA loads for MERS-CoV and SARS-CoV-2 in infected persons of 10⁹ copies per cm³ of sputum have been reported (Oh et al. 2016; To et al. 2020) and even up to 10¹¹ copies per cm³ saliva (Adhikari et al. 2019; Pan et al. 2020). Thus Pan et al. (2020) reported a maximum viral load of SARS-CoV-2 from 80 COVID-19 patients of 1.34 × 10¹¹ copies per cm³ of sputum such that a 10 μm diameter particle of volume of 5.24 × 10⁻⁷ mm³ would contain some 70 virions. It should be emphasized these high load particles would represent only a very small proportion and most inhaled aerosol particles would contain either zero or just one virion because the median was 7.5 × 10⁵ to 10^6.7 copies of SARS-CoV-2 RNA per cm³ of sputum (Pan et al. 2020;To et al. 2020). The mean for MERS-CoV was 6.3 × 10⁸ copies per cm³ saliva (Adhikari et al 2019). However, the thermodynamic dose-response model developed here does need to be able to accommodate inhalation of both particles with a single virion and particles with a cluster of virions in the case of those respiratory viruses such as MERS-CoV that bind to human mucin. Clustering mechanisms such as the secretion in stools of ~0.5 μm diameter extracellular vesicles reported by Santiana et al. (2018) as containing ~15 rotavirus virions could result in some <1 μm diameter particles which are produced in coughs in abundance (Lindsley et al. 2012) containing high virion doses although this has not been demonstrated for coronaviruses (CoVs). Lim et al. (2016) merely say that the assembly of CoV particles is completed through budding of the CoV nucleocapsid through membranes early in the secretory pathway from the endoplasmic reticulum to the Golgi. Bhar and Jones (2019) propose an alternate role (in addition to the role of virion cell binding) for the histo-blood group antigens in norovirus infection as a means of viral aggregation. Another mechanism of aggregation is through multiple viruses binding to a bacterium as in the case of human norovirus and poliovirus attaching to commensal Enterobacter bacteria (Bhar and Jones 2019).

2. Methods

The abbreviations are listed in Table 1 .

Table 1.

List of abbreviations

(h)ACE2	(Human) Angiotensin-converting enzyme 2
BSM	Bovine submaxillary mucin,
CBD	Carbohydrate binding domain on a lectin or virus spike protein
CoV	Coronavirus
Cr	Host cell receptor
Ctotal	Total number of cells in human lung that have ACE2 receptors and can bind SARS-CoV-2
C.VT	Number of host cells with bound virus at temperature T
dpi	Days post infection
DPP4	dipeptidyl peptidase 4 (also called CD26), protein receptor for MERS-CoV
Fc	Fraction of virus dose bound to lung cells
Fv	Fraction of virus in lung mucus not bound to mucin, i.e. free
Ftrans	Fraction of the challenge dose, Vexposure, that is transported through the nasal airways to reach the mucus in the lung-lining fluid
GP	Viral (glyco)protein on virus surface that binds to Cr
HA	Haemagglutinin
HE	Haemagglutinin-esterase
HIV	Human immunodeficiency virus
IAV	Influenza A virus
L	Avogadro number = 6.022 × 1023 molecules per mol
Kmucin	Association constant for binding of virus to mucin at temperature T
Ka_virus_T	Association constant for binding of virus to host cells at temperature T
Kd_mucin	Dissociation constant for each CBD/SA interaction
Kd_receptor_T	Dissociation constant for GP from Cr at temperature T
LLF	Lung lining fluid
M	Molar (moles dm−3)
Nv	Number of GP/Cr contacts made on virus binding to cell
Nm	Number of GP/SA contacts made on virus binding to mucin molecule
MERS-CoV	Middle East respiratory syndrome coronavirus
MHV	Mouse hepatitis coronavirus
Mucfree	Number of free mucin molecules, i.e., not bound to virus
Muctotal	Total number of mucin molecules in given volume of mucus
NA	Neuraminidase
p1	Probability of infection of host by exposure to a single virion
pbudding	Probability progeny virions exit the infected cell
pentry	Probability that a virion bound to cell surface enters that cell
pcell	Probability, given a virion has bound to the surface of a lung epithelial cell, that that cell becomes infected and releases its progeny viruses
phost	Probability of successful infection of the host;
ppfu	Probability that a given virion (represented in the exposure as a viral RNA copy) is itself capable of initiating infection in a cell
pvirogenesis	Probability virus replicates within cell after entry and progeny virions are assembled.
pfu	Plaque-forming unit
R	Ideal gas constant = 8.31 J/mol/K
S1A	Head of CoV spike protein that binds SA
S1B	Head of CoV spike protein that binds protein Cr
S2	Stalk of CoV spike protein involved in membrane fusion and virus entry
SARS-CoV	Severe acute respiratory syndrome coronavirus
ΔSa_immob	Change in entropy on immobilization of whole virus on binding to cell surface
ΔSa_mucin	Change in entropy on immobilization of whole virus on binding to mucin
SA	Sialic acid
TMPRSS	Transmembrane protease/serine protease that cleaves spike protein into S1 and S2
Vexpsoure	Airborne exposure to a given dose of virions
Vfree	Virus not bound to mucin molecules
Vmucus	Virus dose entering mucus in lung lining fluid
V.Muc	Number of viruses with bound mucin

2.1. Basic lung model

The human lung surface area was determined as 24–69 m² with some studies indicating the internal lung surface area to be about 130 m² (Fröhlich et al. 2016). Determination of the volume of the lining fluid in the lung (LLF), also called epithelial lining fluid or airway surface liquid, is more complicated than for the gastrointestinal fluids because lung volumes are much smaller. In the literature different volumes of 12 cm³, 20–40 cm³, 25 cm³, 10–30 cm³ and 17–20 cm³ have been indicated in different studies reviewed by Fröhlich et al. (2016). Based on the body weight-dependent data obtained in sheep (0.37 ± 0.15 cm³/kg), a 70 kg human would possess 26 cm³ of LLF. The total number of cells in the human lung is 230 × 10⁹ of which 30% are endothelial and 24% are alveolar cells (Crapo et al 1982). Lukassen et al. (2020) investigated ACE2, transmembrane protease/serine protease (TMPRSS2) and furin expression levels in the transcriptome across cell types in lung tissue. Of 39,778 lung cells studied, only 104 expressed ACE2 and TMPRSS2 and/or furin, suggesting that only 0.26% of lung cells are susceptible to infection by SARS-CoV-2. The number of cells expressing ACE2 was 206 accounting for 0.52% of the lung cells (Lukassen et al. 2020). Therefore the total number of lung cells that can bind SARS-CoV-2, C_total, is estimated to be 0.52% of 230 × 10⁹ = 1.2 × 10⁹ cells.

2.2. Thermodynamic approach for calibrating a dose-response model for infection of the human lung by a virus

Infection of the host is defined here as the infection of one or more cells in the host such that virogenesis and viral egress successfully take place in at least one cell of the host. The progeny viruses may then go on to infect other host cells leading to disease progression, which is not considered here. The response considered here, namely initial infection, happens before the innate immune response and the acquired immune response both of which are important for stopping progression of infection in the host (Lim et al. 2016). The probability, p_host, of being infected by airborne exposure to a given dose of virions, V_expsoure, may be described mathematically as

$${\mathit{p}}_{\mathit{host}}=1-{\left(1-{\mathit{p}}_1\right)}^{V_{exposure}}$$ (1)

where p₁ is the probability of infection of the susceptible person by a single virion in an aerosol particle. Although Eq. 1 represents a dose-response for a set of equally susceptible individuals it is important to note that p₁ itself may vary between individuals within a population depending for example on genetic factors (Plante et al. 2020) and overall health of the individuals. This is addressed here for individuals with differing concentrations of mucin in the LLF.

At a cellular level, the probability of infection of the host, p_host, equals the probability of successful infection of at least one bronchus or lung cell and is related to the number of bronchus/lung cells (C.V_T) with bound virus by:-

$${\mathit{p}}_{\mathit{host}}=1-{\left(1-{\mathit{p}}_{\mathit{cell}}\right)}^{C.V_T}$$ (2)

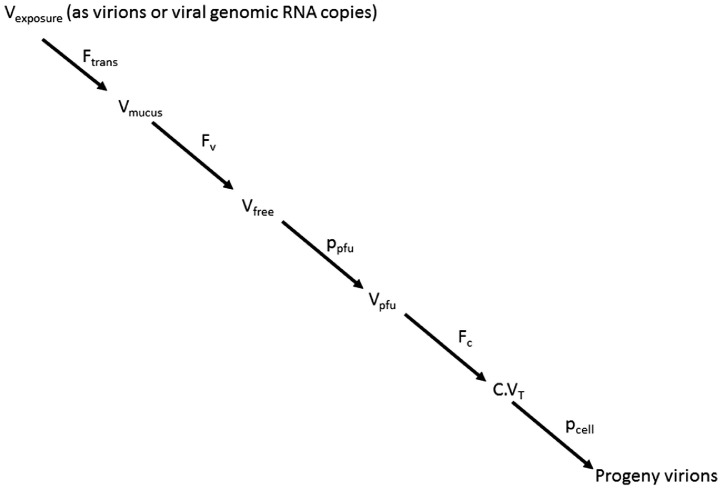
where p_cell is the probability of successful infection of a host bronchus/lung cell given a virus has bound to its surface. Thus the more bronchus/lung cells with bound virus then the greater the chance that infection will be successful in at least one of them. Based on the thermodynamic approach described previously (Gale 2018) and accommodating the fate and transport of the virions through the airways (Weir and Haas 2011) the development of the dose-response is broken down into five steps as shown in Fig. 1: -

• 1Estimation of the fraction, F_trans, of the exposure dose, V_exposure, that is transported through the nasal airways to reach the mucus in the lung-lining fluid of the nasal epithelium/bronchus/lung;
• 2Calculation of the number, V_free, of viruses getting through the host defences e.g. mucins and pathogen pattern recognition receptors to the lung epithelium. This is dependent on the fraction, F_v, of the total virions (V_mucus) in the mucus which are not bound to mucin;
• 3Estimation of the probability, p_pfu that a given virion (represented in the exposure as a viral RNA genomic copy) is fit and actually capable at the molecular level of binding to and initiating infection in a susceptible host cell such that it could be detected as a pfu;
• 4Calculation of C.V_T as the fraction, F_c, of viruses bound to cells based on the thermodynamics of virus/host cell binding and in particular the number and strength of the virus glycoprotein (GP)/cell receptor (Cr) interactions together with the parameter ΔS_{a_immob}, which is the change in entropy on immobilization of whole virus on binding to the cell surface (Gale 2019; Gale, 2020); and
• 5Estimation of the probability p_cell which depends on the ability of the bound virus to enter the cell, replicate and bud releasing progeny virions (Gale, 2017).

Fig. 1.

Pathway from virus exposure to infection of cell.

The total number, V_free, of viruses surviving the mucin barrier, and getting through to the lung epithelium from Fig. 1 is given by

$${\mathit{V}}_{\mathit{free}}={\mathit{F}}_{\mathit{trans}}\times {\mathit{F}}_{\mathit{v}}\times {\mathit{V}}_{\mathit{exposure}}$$ (3)

However, the C.V_T term in Eq. 2 cannot be replaced by V_free calculated as Eq. 3 because C.V_T should be an integer to represent a whole number of cells. As an alternative approach from Fig. 1, the probability, p₁, of infection of the host by exposure to a single virion in Eq. 1 may be expressed as

$$p_1=F_{trans}\times F_v\times p_{pfu}\times F_c\times p_{cell}$$ (4)

since the F_trans, F_v and F_c terms may be interpreted as probabilities. Thus a prototype thermodynamic dose-response for a respiratory virus in humans is given by:-

$$p_{host}=1-{\left(1-\left(F_{trans}\times F_v\times p_{pfu}\times F_c\times p_{cell}\right)\right)}^{V_{exposure}}$$ (5)

It should be noted that the p_pfu term represents the fitness of the virion itself, while the p_cell term represents the ability of a host cell with bound (viable) virus to undertake and complete virogenesis. The two terms are completely unrelated.

2.3. Estimation of F_trans, the fraction of inhaled virions which are transported through the airways to reach the mucus in the lung lining fluid

Weir and Haas (2011) model anthrax spore transport through three regions of the respiratory system namely i) the nasal cavity and larynx, ii) the trachea and first branches of the bronchioles and iii) the respiratory bronchioles and alveoli. The model here for SARS-CoV-2 is based on cells within the lung and bronchioles expressing hACE2 being able to bind SARS-CoV-2 and on the basis of data from Hui et al. (2020) and Lukassen et al. (2020), SARS-CoV-2 only needs to get to the bronchus and does not need to reach the alveoli, unlike spores of B. anthracis, to initiate infection in a host. In the case of MERS-CoV which uses a different cell surface receptor from SARS-CoV-2, namely dipeptidyl peptidase 4 (DPP4 or CD26) and possibly certain glycans, cells of the bronchial submucosal glands and bronchus are targeted (Hui et al. 2020; Li et al. 2017). The prototype model presented here does not formally assess the fate and transport of the virus through the respiratory system as described by Weir and Haas (2011) for anthrax spores, and F_trans is set to 1 such that all the SARS-CoV-2 and MERS-CoV virions in the exposure are assumed to get to the mucus in the bronchus. This is justified for SARS-CoV-2 because recent evidence suggests that the nasal surfaces might be the dominant initial site for respiratory tract infection with likely subsequent aspiration-mediated virus seeding to the lung in SARS-CoV-2 pathogenesis (Hou et al. 2020). It is suggested here that determining F_trans is much more important for anthrax because once inhaled anthrax spores are infectious only after being transported to the alveoli (Weir and Haas 2011). According to Hou et al. (2020) the nose contains the highest percentage of ACE2-expressing ciliated cells in the proximal airways with high SARS-CoV-2 infectivity of nasal epithelium and a gradient in infectivity characterized by a marked reduction in the distal lung (bronchioles and alveoli). As Hou et al. (2020) point out, aerosol deposition and fomite mechanical delivery deposition modelling suggest that aerosols containing virus inhaled by subjects achieve the highest density of deposition, i.e., highest viral loading per unit surface area, in the nose. This is completely different to the anthrax model and on the basis of the data of Hou et al. (2020) the prototype SARS-CoV-2 model here only needs to focus on the nasal epithelium.

2.4. Prediction of F_v, the fraction of viruses in the mucus layer which are free to bind to receptors on the lung epithelium

It is assumed that one virus binds to one mucin molecule to give a virus/mucin complex (V.Muc) in a dynamic equilibrium (Gale 2018).

$$V_{free}+Mu{c}_{free}\leftrightarrow V.Muc$$

The strength of the binding is reflected by the association constant, K_mucin, between virus and mucin and is expressed as:-

$$K_{mucin}=\frac{\left[V·Muc\right]}{\left[V_{free}\right]\left[Mu{c}_{free}\right]}$$ (6)

The fraction of free virus (F_v) is given by:-

$${\mathit{F}}_{\mathit{V}}=\frac{\left[{\mathit{V}}_{\mathit{free}}\right]}{\left[V_{free}\right]+\left[\mathit{V}·\mathit{Mu}c\right]}$$ (7)

Replacing [V.Muc] with Eq. 6 and rearranging gives F_v in terms of the free mucin concentration [Muc_free] and K_mucin in Eq. 8.

$${\mathit{F}}_{\mathit{V}}=\frac{1}{1+{\mathit{K}}_{\mathit{mucin}}\left[\mathit{Mu}{\mathit{c}}_{\mathit{free}}\right]}$$ (8)

2.4.1. Estimation of [Muc_free] in non-smokers

Kesimer et al. (2017) reported mean (±SE) concentrations of 108±20 pmol per cm³ for MUC5B and 10±4 pmol per cm³ for MUC5AC in lung mucus from persons who had never smoked. The mean concentration for MUC5AC plus MUC5B in non-smokers is therefore 118 pmol per cm³, which is 1.18 × 10⁻⁷ M. Using the Avogadro number, L = 6.022 × 10²³ molecules per mol, 118 pmol equates to 7.1 × 10¹⁰ molecules of MUC5AC and MUC5B in total per mm³ volume of lung mucus.

2.4.2. Variation in lung mucin concentrations between individual non-smokers

It is important for a dose-response model to accommodate variation between indivduals in their susceptibility to infection. Kesimer et al. (2017) measured absolute concentrations of MUC5B and MUC5AC in 19 non-smoker participants and reported large variation between individuals. Thus although the mean [MUC5B] absolute concentration was 108 pmol/cm³ the minimum was 20 pmol/cm³ and the maximum was 300 pmol/cm³.

2.4.3. Calculation of F_v for dispersed virus using Equation 8

The degree of localised dispersion of the virus in the mucus is an important consideration in the methodology in relation to calculation of [Muc_free] in Eq. 8. Where the virus is well dispersed in the lung mucus such that everywhere [V_mucus] << [Muc_total], then F_v can be calculated from Eq. 8 using [Muc_total] to approximate [Muc_free]. The fact that with Muc_total >> V_mucus everywhere in the lung means that even with all the viruses in the initial challenge dose bound to mucin, Muc_free ~ Muc_total and therefore [Muc_total] can be used to approximate [Muc_free] in Eq. 8. Thus [Muc_free] is set to 1.18 × 10⁻⁷ M in Eq. 8 for non-smokers.

2.4.4. Calculation of F_v for locally aggregated virus using the difference equation approach

When K_mucin is large and where [V_mucus] approaches or exceeds [Muc_total] locally, [Muc_free] becomes much smaller than [Muc_total] as the virus overwhelms and mops up all the free mucin molecules. In the extreme all the local mucins molecules are bound to virus and [Muc_free] tends to 0 locally. Therefore the difference equation approach has to be used as described previously (Gale 2018). Briefly K_mucin values are calculated using Eq. 6 for the range of V_free, Muc_free and V.Muc combinations from V.Muc = 1 to V.Muc = V_mucus (or to V.Muc = Muc_total depending on which is the lesser) assuming Muc_total = 7.1 × 10¹⁰ molecules of MUC5AC and MUC5B in total per mm³ and converted to their respective concentrations [V_free], [Muc_free] and [V.Muc] by dividing by 10⁻⁶ dm³/mm³ and by L. The fraction of free virus, F_v, is then calculated as V_free/V_mucus.

2.4.5. Values of K_mucin

For the purpose of demonstration of the model, K_mucin values from 1 M⁻¹ to 10²² M⁻¹ are used. K_mucin is related to the number N_m of interactions between carbohydrate binding domains (CBDs) on the lectin (virus) and the SA glycans on the mucin according to:-

$${\mathrm{K}}_{\text{mucin}}=\frac{1}{{\left({\mathrm{K}}_{\mathrm{d}\_\text{mucin}}\right)}^{N_m}}\times {\mathrm{e}}^{\frac{\Delta {\mathrm{S}}_{\mathrm{a}\_\text{muci}\mathrm{n}}}{\mathrm{R}}}$$ (9)

where K_{d_mucin} is the dissociation constant for each CBD/SA interaction, ΔS_{a_mucin} is the change in entropy on immobilization of whole virus on binding to mucin and R is the ideal gas constant (Gale 2018).

2.5. Modelling the effect of the virus:mucin ratio on the fraction, F_v, of free virus

Two scenarios are modelled for each virion:mucin ratio.

2.5.1. Scenario 1: Inhaled aerosol particles with different viral loads are each engulfed in 1 mm³ of mucus

For the purpose of undertaking the difference equation approach a 1 mm³ volume (10⁻⁶ dm³) is chosen to represent the volume of mucus into which the virus dose (V_mucus) is dispersed as the airborne particle(s) enter(s) the LLF of the lung. This volume of mucus contains 7.1 × 10¹⁰ mucin molecules. It is assumed that virus doses of 2x, 1x, 0.5x and 0.1 × 7.1 × 10¹⁰ virions respectively (Table 2 ) are effectively exposed to the 7.1 × 10¹⁰ mucins in 1 mm³ of mucus as they pass through the mucus to the lung epithelium. In effect the 1 mm³ volume of mucus represents the limit of the aerosol dispersion in the mucus, such that within that 1 mm³ volume as many virions as possible (given the dose) are exposed to mucins. It can be envisaged as providing the thinnest layer of mucus film that maximises the number of viruses in the dose that are in direct contact with mucus and hence exposed to a mucin. Eq. 6 is based on concentrations and K_mucin will be same whether it's calculated using 7.1 × 10⁴ viruses and 7.1 × 10⁴ mucins in a volume of 10⁻⁶ mm³ for example or using 7.1 × 10¹⁰ virus and 7.1 × 10¹⁰ mucins in 1 mm³ as performed here in the model. However, although a dose of 7.1 × 10⁴ SARS-CoV-2 virions is perhaps more realistic as an inhaled dose based on 10^8.94 virions per cm³ of saliva (To et al. 2020), it is preferable to use values of 7.1 × 10¹⁰ virus and 7.1 × 10¹⁰ mucins in the difference equation approach to achieve the greater range of simulated K_mucin values and greater incremental sensitivity. So with 7.1 × 10⁴ viruses and 7.1 × 10⁴ mucins the highest K_mucin that can be achieved with the difference equation approach is 10^16.6 M⁻¹. This compares to 10^28.6 M⁻¹ which can be achieved with 7.1 × 10¹⁰ viruses and 7.1 × 10¹⁰ mucins in 1 mm³.

Table 2.

Fraction, F_v, of free virus in lung mucus calculated by difference equation approach for range of virion to mucin molecule ratios representing exposure of virion to mucins at the aerosol particle/mucus interface.

Scenario 1: Number of virions to number of mucin molecules in 1 mm3 volume of mucus	Scenario 2: Number of virions to number of mucin molecules (volume of mucus)	Local ratio virion:mucin at aerosol particle/mucus interface	Fv at K mucin = 1010 M−1 (Reduction in risk by mucus)	Fv at K mucin = 1022 M−1.
1.42 × 1011 virions to 7.1 × 1010 mucins	7.1 × 1010 virions to 3.55 × 1010 mucins in 0.5 mm3.	2:1	0.5004 (2-fold)	*0.5000
1.07 × 1011 virions to 7.1 × 1010 mucins	7.1 × 1010 virions to 4.73 × 1010 mucins in 0.666 mm3.	1.5:1	0.334 (3-fold)	*0.333
7.1 × 1010 virions to 7.1 × 1010 mucins	7.1 × 1010 virions to 7.1 × 1010 mucins in 1 mm3.	1:1	0.0286 (35-fold)	0.3 × 10−7
3.55 × 1010 virions to 7.1 × 1010 mucins	7.1 × 1010 virions to 1.42 × 1011 mucins in 2 mm3.	1:2	0.00169 (588-fold)	1.4 × 10−11
<0.71 × 1010 virions to 7.1 × 1010 mucins	7.1 × 1010 virions to >7.1 × 1011 mucins in >10 mm3.	<0.1:1 (Eq. 8)	0.00085 (1,176-fold)	<10−15

*limit of what is achievable given ratio

2.5.2. Scenario 2: Aerosol particles with the same viral load are each engulfed in different volumes of mucus

A dose of 7.1 × 10¹⁰ virions is locally dispersed into 0.5 mm³ (representing 2 virions per mucin), 1 mm³ (representing 1 virion per mucin), 2 mm³ (representing 1 virion per 2 mucins) and 10 mm³ (representing 1 virion per 10 mucins) of lung mucus with [Muc_total] = 1.18 × 10⁻⁷ M.

2.6. Estimation of p_pfu, the probability that a virion (as represented by a viral RNA genomic copy) is capable of initiating infection in a cell

Not all virions produced during infection are capable of initiating infection in a subsequent host. Thus Bull et al. (2012) showed only 0.01% of norovirus particles could initiate infection in humans because each of the virions is different due to the mutant spectrum. According to Vicenzi et al. (2004) approximately 360 viral genomes of SARS-CoV are required to generate a pfu. This can be interpreted as 359 of every 360 virions being unable to initiate infection (non-infectious). Thus p_pfu is calculated as 1/360 = 0.0028.

2.7. Calculation of the fraction, F_c, of virus bound to cells from the association constant, K_{a_virus_T} representing the strength of virus binding to host cells

Central to calculation of the number of lung epithelial cells with bound virus is the association constant, K_{a_virus_T} which represents the strength of binding of whole virus to a lung cell at temperature T (Gale 2019, Gale, 2020). This is calculated as

$${\mathrm{K}}_{\mathrm{a}\_\text{virus}\_\mathrm{T}}=\frac{1}{{\left({\mathrm{K}}_{\mathrm{d}\_\text{receptor}\_\mathrm{T}}\right)}^{N_v}}\times {\mathrm{e}}^{\frac{\Delta {\mathrm{S}}_{\mathrm{a}\_\text{immo}\mathrm{b}}}{\mathrm{R}}}$$ (10)

where K_{d_receptor_T} is the dissociation constant for the CoV spike trimer protein from its proteinaceous cellular receptor, Cr, at temperature T, N_v is the number of spike protein trimer/Cr interactions on virus/host cell binding and ΔS_{a_immob} is the change in entropy on immobilization of whole virus on binding to the cell surface (Gale 2019, Gale, 2020).

2.7.1. Values of K_{d_receptor_T} for SARS-CoV, SARS-CoV-2 and MERS-CoV

The dissociation constant, K_{d_receptor_T} represents the strength of the interaction between the CoV spike protein and Cr with smaller values representing stronger binding. Wrapp et al. (2020) demonstrate that each SARS-CoV-2 trimer binds just one ACE2 with a K _{d_receptor_T} of 1.47 × 10⁻⁸ M. This is much higher affinity binding than the K _{d_receptor_T} of 1.85 × 10⁻⁷ M for the SARS-CoV spike trimer binding to a single ACE2 reported by Kirchdoerfer et al. (2018). The value of K_{d_receptor_T} for each MERS spike protein binding to its CD26 (DPP4) cellular receptor is 1.67 × 10⁻⁸ M (Lu et al., 2013).

2.7.2. Values of N_v

There are on average 74 spike trimers per SARS-CoV virion (Neumann et al. 2011) each of which could in theory make at least one interaction with ACE2. According to Guo et al. (2018) 10% of the IAV virus surface could be in contact with a surface, such that approximately 7 IAV HA trimers can interact with receptor-loaded SA molecules. Thus N_v could be as high as 7 spike trimer protein/receptor contacts in the case of MERS-CoV, SARS-CoV and SARS-CoV-2 which are of similar size to IAV. Yuan et al. (2017) hypothesize that for MERS-CoV bound on the cell surface, one DPP4 receptor may crosslink two S trimers by binding to receptor-binding domains, one from each trimer thus giving large values for N_v involving multiple spike proteins linked together with DPP4 receptors.

2.7.3. Values of ΔS_{a_immob}

The parameter ΔS_{a_immob} was first identified in a thermodynamic analysis of the effect of temperature on virus binding to host cells (Gale 2019) and not surprisingly there are no data for its magnitude as yet although it is likely to be large and negative depending on the degree of immobilisation of the whole virus on binding to the host cell. The translational entropy of a particle of molecular weight 2.5 × 10⁸ Da as for Rous sarcoma virus (Vogt and Simon 1999) is estimated to be +350 J/mol/K using the Sackur-Tetrode equation (P. Gale unpublished results). Assuming half of this entropy is lost on cell binding and that the rotational entropy lost is similar (Finkelstein and Janin 1989) then ΔS_{a_immob} would approximate -350 J/mol/K although estimates based on Eq. 10 suggest values as low as -1,091 J/mol/K (Gale 2020). This large negative entropy change may be offset to some degree by non-specific attachment of the virus to the cell surface through SA and heparan sulphate binding as proposed for HIV such that much of the entropy loss of ΔS_{a_immob} on virus binding is taken prior to specific GP/Cr binding (Gale 2020). For the purpose of the prototype model developed here a value of -350 J/mol/K is used for ΔS_{a_immob}.

2.7.4. Demonstration that F_c ~ 1 in the lung model for K_{a_virus_T} >~10¹⁴ M⁻¹

The previous thermodynamic dose response models for virus binding in the human intestine (Gale 2018) and in the arthropod midgut (Gale 2019) have both shown that when K_{a_virus_T} is >~10¹⁵ M⁻¹ then its actual value is not important because at high virus doses all the host cells have bound virus while at low virus doses all the viruses are bound to host cells. This is therefore investigated for the lung model. Using the difference equation approach (Gale 2018) for binding of 1,000 virions in 25 cm³ of LLF, the fraction, F_c, of virus dose bound to lung cells as a function of K_{a_virus_T} was calculated for C_total = 1.2 × 10⁹ cells and for C.V_T = 1 to 1,000 (representing all viruses bound).

2.8. Estimation of p_cell

The parameter p_cell is the probability of viral entry (through fusion of the virus envelope with the host cell membrane) combined with the probabilities of each of the subsequent steps of virogenesis within the cell being completed, including viral polyprotein synthesis and cleavage by the virus-coded main protease (Zhang et al. 2020), viral RNA replication and capsid assembly followed by budding (viral egress) of progeny virions from the infected cell. Thus p_cell can be broken down into three conditional probabilities:-

$$p_{cell}=p_{entry}\times p_{virogenesis}\times p_{budding}$$ (11)

where p_entry, p_virogenesis and p_budding are the probabilities of entry of a bound virus into the cell interior, synthesis of the viral protein and RNAs within the cell and egress of the virus from the cell, respectively. Entry of the bound SARS-CoV-2 virion to the cell through fusion of the viral envelope with the host cell membrane is mediated by the spike protein S2 subunit which is conserved among coronaviruses (Walls et al. 2017). Cleavage at S1/S2 occurs upon biogenesis and viral egress for some coronaviruses, such as MHV and MERS-CoV (Walls et al. 2017). TMPRSS processing of SARS-CoV and MERS-CoV spike protein occurs at the cell membrane (Walls et al. 2017). Hoffmann et al. (2020) demonstrated efficient proteolytic processing of SARS-CoV-2 spike protein by TMPRSS2 in human kidney cell lines suggesting that fusion and entry should occur with high efficiency in human kidney cells at least, such that p_entry is high. The values for the probabilities p_virogenesis and p_budding for SARS-CoV-2 are also assumed to be high on the basis of ex vivo studies of SARS-CoV-2 infection in bronchus and lung cell cultures (Hui et al. 2020). It is assumed here that overall p_cell is highly efficient with a probability of 0.5 for the purpose of this prototype model.

3. Results

3.1. Increasing K_mucin decreases the fraction of free virus particularly at lower virus to mucin ratios

The predicted fractions of free virus and the efficacy of virus removal by the mucus barrier are presented for a range of virus:mucin ratios in Table 2 and plotted in Fig. 2 as a function of K_mucin. The results for Scenario 2 are identical to those for Scenario 1 in Table 2 which is not surprising since the values of [V_free] and [Muc_free] in the denominator of Eq. 6 are simply interchanged with the same [V.Muc] in the numerator. It is concluded that the results in Table 2 may be interpreted either in terms of challenge of a varying virus dose in a given fixed volume of mucus, or in terms of dispersion of a given fixed dose, V_mucus, of virions carried on an inhaled aerosol within differing “local microenvironment” volumes of the mucus in the LLF in the lung.

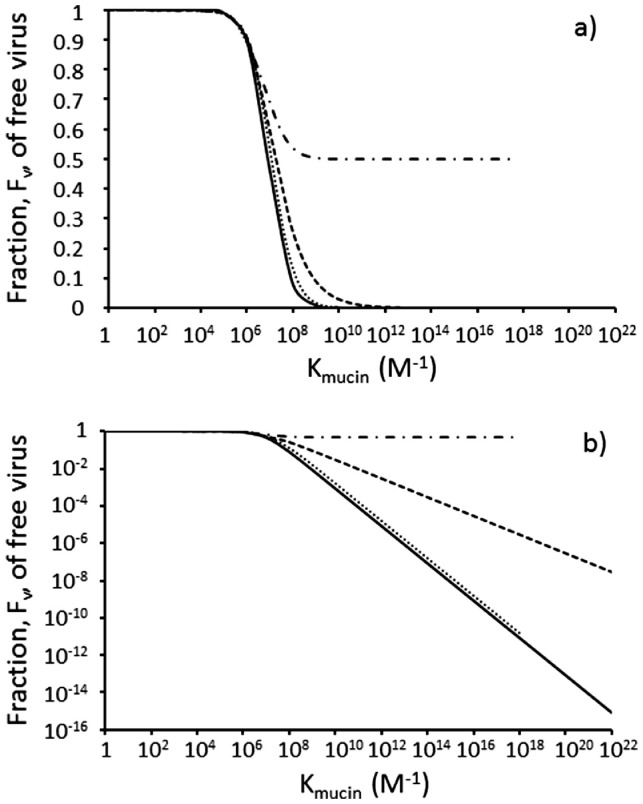
Fig. 2.

The fraction, F_v, of free virus in mucus calculated by the difference equation approach decreases with increasing magnitude of the association constant, K_mucin, for binding of virus to mucin and is strongly affected by the local virus to mucin molecule ratio which is set to 2:1 (dash-dotted line), 1:1 (dashed line), 1:2 (dotted line) and <0.1:1 (solid line). The solid line is also represented by Eq. 8 for fully dispersed virus with [Muc_free] = 1.18 × 10⁻⁷ M. In a) the y-axis is linear to visualise the effect for the 2:1 virus:mucin ratio. In b) the y-axis is logarithm transformed to visualise small fractions of F_v as the virus becomes more dispersed in the mucus.

Low values of K_mucin have relatively little impact with F_v greater than 0.9 up to values of K_mucin ~10⁶ M⁻¹ (Fig. 2a) as expected for weak binding. At values of K_mucin >10⁶ M⁻¹ values of F_v decrease significantly with increasing K_mucin (Fig. 2b). The decrease in F_v is enhanced with decreasing local virus:mucin ratio. For the highest virus:mucin ratio of 2:1, the value of F_v can never fall below 0.5 (Fig. 2a) irrespective of K_mucin because there is only sufficient mucin to mop up half of the virus dose, the other half of the virus dose remaining free to go on and infect lung epithelial cells. For virus:mucin ratios of 1:1 or less, Fig. 2b shows that above K_mucin of ~10⁶ M⁻¹ the fraction, F_v, of free virus decreases linearly with increasing K_mucin. The minimum value of F_v which is achievable at the 1:1 ratio is 1.4 × 10⁻¹¹ reflecting just 1 in the 7.1 × 10¹⁰ viruses being free. This is not achieved for the 1:1 ratio even with a K_mucin as high as 10²² M⁻¹ (dashed line in Fig. 2b). The minimum value of F_v which is achievable at the 1 virus:2 mucin ratio is 2.8 × 10⁻¹¹ reflecting just 1 in the 3.55 × 10¹⁰ viruses being free. This is achieved at a K_mucin of 10¹⁸ M⁻¹ and therefore the dotted line terminates at K_mucin ~10¹⁸ M⁻¹ (Fig. 2b). With the difference method approach it was not possible to achieve a K_mucin of >10¹⁸ M⁻¹ for the 2 virus:1 mucin ratio simulation which is why the dash-dotted line in Fig. 2 also terminates at K_mucin ~10¹⁸ M⁻¹. Using Eq. 8, values of F_v can be calculated for all values of K_mucin (solid line in Fig. 2b) and superimpose those for the 0.1 virion:1 mucin ratio.

3.2. Reducing the local virus:mucin ratio increases the efficiency of the mucus barrier

A K_mucin of 10¹⁰ M⁻¹ is typical for lectins binding to mucins (see below). Table 2 presents the values of F_v over the range of local virion:mucin ratios for K_mucin = 10¹⁰ M⁻¹. At a local concentration of 2 virus to 1 mucin molecule, 50% of the virus is free such that the mucus barrier only reduces the risk by 2-fold. At a local ratio of 1:1, 2.9% of the virus is free representing a 35-fold reduction in risk by the mucus barrier, while decreasing the local ratio to 1 virus to 2 mucins reduced the free virus fraction to 0.17% representing a 588-fold reduction in risk by the mucus barrier. Fully dispersing the virus dose in the lung mucin such that the number of mucin molecules greatly exceeds the number of viruses reduces the fraction of free virus to 0.085% such that the risk is reduced almost 1,200-fold by the mucus barrier. These effects are even more marked for K_mucin of 10²² M⁻¹ such that all the virus is bound at a ratio of 1 virus to 2 mucins (Table 2).

3.3. Modelling the number, C.V_T, of lung epithelial cells with bound virion

3.3.1. Most of the virus in the lung is predicted to be bound to cells at K_{a_virus_T} >10¹⁴ M⁻¹

The fraction, F_c, of virus bound to cells in the lung as a function of K_{a_virus_T} is plotted in Fig. 3 and compared with the fractions of bound virus in the human intestine model (Gale 2018) and the mosquito midgut model (Gale 2019). Due to the higher concentration of target cells in the lung, lower values of K_{a_virus_T} achieve greater virus binding than for the intestine and midgut models. Indeed 90% of the virus is bound to lung cells when K_{a_virus_T} >10¹⁴ M⁻¹. Thus F_c may be assumed to approximate 1 in Equation 5 if K_{a_virus_T} >10¹⁴ M⁻¹.

Fig. 3.

The major proportion of virions is predicted to be bound to host cells in the human lung when K_{a_virus_T} > ~10¹⁴ M⁻¹. Fraction, F_c, of virus dose of 1,000 virions predicted to be bound to host cells as a function of K_{a_virus_T} for the human lung (solid line, C_total = 1.2 × 10⁹ cells in 0.025 dm³ of lung lining fluid, [C_total] = 8.0 × 10⁻¹⁴ M); human intestine (dashed line, C_total = 4.15 × 10⁸ cells in 0.314 dm³ of gut contents, [C_total] = 2.2 × 10⁻¹⁵ M) and mosquito midgut (dotted line, C_total = 1 × 10³ cells in 10⁻⁶ dm³ of midgut contents, [C_total] = 1.7 × 10⁻¹⁵ M) as calculated by the difference equation approach (Gale 2018).

3.3.2. K_{a_virus_T} is >10¹⁴ M⁻¹ for the three CoVs if the number of trimer/receptor contacts is at least five

Values of K_{a_virus_T} are calculated for SARS-CoV, SARS-CoV-2 and MERS-CoV using the reported K_{d_receptor_T} values for the spike trimer binding and assuming ΔS_{a_immob} = -350 J/mol/K in Eq. 10 for four and five spike trimer/receptor interactions (Table 3 ). With N_v = 4 spike trimer/receptor contacts, values of K_{a_virus_T} are well below 10¹⁴ M⁻¹ while with N_v = 5 spike trimer/receptor contacts values of K_{a_virus_T} are >10¹⁴ M⁻¹ for all three viruses.

Table 3.

Values of K_{a_virus_T} calculated for SARS-CoV, SARS-CoV-2 and MERS-CoV using the reported K_{d_receptor_T} values (see text) for the spike trimer binding and assuming ΔS_{a_immob} = -350 J/mol/K (see text) in Eq. 10 for four and five spike trimer/receptor interactions.

	SARS-CoV	SARS-CoV-2	MERS-CoV
Kd_receptor_T (M)	1.85 × 10−7	1.50 × 10−8	1.67 × 10−8
Ka_virus_T (M−1) Nv = 4	4.36 × 108	1.01 × 1013	6.57 × 1012
Ka_virus_T (M−1) Nv = 5	2.36 × 1015	6.73 × 1020	3.93 × 1020

3.4. Prototype dose-response model for initial infection in the lung by dispersed coronavirus

F_v values were calculated as 0.999, 0.894, 8.4 × 10⁻³, and 8.47 × 10⁻⁶ for virus fully dispersed in lung mucus according to Equation 8 using [Muc_total] = 1.18 × 10⁻⁷ M and K_mucin values of 10³ M⁻¹, 10⁶ M⁻¹, 10⁹ M⁻¹ and 10¹² M⁻¹ to represent N_m = 1, 2, 3, and 4 contacts of K_{d_mucin} = 10⁻³ M, respectively (Eq. 9). These represent virus removals of 0.012%, 10.5%, 99.1% and 99.999% respectively. The probabilities, p_host, of infection over a range of virion exposures according to Equation 5 are compared for the four F_v values in Fig. 4 . As expected from Fig. 2, increasing K_mucin from 10³ M⁻¹ to 10⁶ M⁻¹ representing a second additional spike protein/SA contact has little effect on reducing the infectivity. For these low values of K_mucin, the infectivity reflects the proportion of virions in the dose that are actually capable of initiating infection as represented by the value of p_pfu with predicted ID₅₀s of 498 virions (1.4 pfu) and 558 virions (1.6 pfu) for K_mucin values of 10³ M⁻¹ and 10⁶ M⁻¹  respectively (based on the assumed value of 0.5 for p_cell). However increasing K_mucin to 10⁹ M⁻¹ representing a third additional spike protein/SA contact increases the ID₅₀ by ~100-fold to 59,243 virions (165 pfu) (Fig. 4). Increasing K_mucin by a further 1,000-fold to 10¹² M⁻¹ representing a forth additional spike protein/SA contact on binding with mucin increases the ID₅₀ by 1,000-fold to ~5.87 × 10⁷ virions (163,000 pfu) (Fig. 4). With a K_mucin value of 5 × 10⁹ M⁻¹ as for a lectin, F_v = 1.7 × 10⁻³ representing a 99.8% removal of the virus by the mucus giving an ID₅₀ of 2.95 × 10⁵ virions (819 pfu). Validation of the model in Fig. 4 for SARS-CoV-2 and MERS-CoV is not possible currently because there are no data for infectivity in humans. However, data for the proportion of dead mice after challenge by intranasal inoculation with increasing doses of SARS-CoV and MHV from Watanabe et al. (2010) are plotted as filled squares and open squares, respectively, in Fig. 4. The doses in units of pfu from Watanabe et al. (2010) have been converted to virions (or RNA genomic copies) by multiplying by 1/p_pfu for comparison with the model output here.

Fig. 4.

Prototype dose-response models according to Equation 5 for respiratory coronavirus virion exposure with F_trans = 1, p_pfu = 0.0028, F_c = 1 and p_cell = 0.5. F_v values calculated with Equation 8 using [Muc_free] ~ [Muc_total] = 1.18 × 10⁻⁷ M assuming K_mucin values of 10³ M⁻¹ (dashed line), 10⁶ M⁻¹ (solid line), 10⁹ M⁻¹ (dash-dot line), and 10¹² M⁻¹ (dotted line) to represent N_m = 1, 2, 3, and 4 spike protein/mucin SA contacts, respectively, of K_{d_mucin} = 10⁻³ M (Eq. 9). Also K_mucin = 5 × 10⁹ M⁻¹ (dash-dot-dot line) as for the lectin soy bean agglutinin binding to porcine submaxillary mucin (Dam and Brewer 2010). Squares represent proportion of mice which died after intranasal challenge of mouse hepatitis coronavirus (open) or SARS-CoV (filled) from Watanabe et al. (2010) assuming 1 pfu = 360 virions or genomic copies. In b) the y-axis is logarithm transformed to visualise risks from low doses of dispersed virus.

3.5. Estimation of values for p₁

From Equation 4, values for p₁, the risk of initial infection from exposure to a single virion, are 1.39 × 10⁻³, 1.24 × 10⁻³, 1.17 × 10⁻⁵, 2.35 × 10⁻⁶ and 1.18 × 10⁻⁸ for K_mucin values of 10³ M⁻¹, 10⁶ M⁻¹, 10⁹ M⁻¹, 5 × 10⁹ M⁻¹ and 10¹² M⁻¹ respectively with [Muc_total] = 1.18 × 10⁻⁷ M, thus completing the dose-response in Equation 1.

3.6. Predicted effect on efficiency of mucus barrier of variation between individuals in the concentrations of mucins in lung mucus

Assuming full dispersion in the mucus, the virus removals by the mucus barrier with a K_mucin value of 10¹⁰ M⁻¹ ranged from 200-fold to 3,000-fold as calculated by Equation 8 using minimum and maximum [MUC5B] reported by Keismer et al. (2017) for 19 non-smokers (Table 4 ). The variation between individuals in concentrations of MUC5B in lung mucus for non-smokers (Table 4) affects the dose-response with predicted ID₅₀s varying from 1.0 × 10⁵ virions (278 pfu) up to 1.5 × 10⁶ virions (4,160 pfu) with K_mucin at 10¹⁰ M⁻¹ (Fig. 5 ).

Table 4.

Variation in absolute concentration of MUC5B in lung mucus from 19 non-smokers affects predicted efficiency of mucus barrier at removing respiratory viruses. MUC5B concentrations from Kesimer et al. (2017).

Participant	[MUC5B] (M)	Fv from Equation 8 (Kmucin = 1010 M−1)	Overall removal of virus by mucus
Minimum	2.0 × 10−8	0.005	201-fold
Mean	1.08 × 10−7	0.000925	1,081-fold
Maximum	3.0 × 10−7	0.000333	3,001-fold

Fig. 5.

Dose-response for respiratory coronavirus virion exposure varies between individuals depending on MUC5B concentration in the mucus (Table 4) according to Equation 5 (with F_trans = 1, p_pfu = 0.0028, F_c = 1 and p_cell = 0.5) for SARS-CoV-2 fully dispersed in lung mucus with K_mucin = 10¹⁰ M⁻¹ and F_v values calculated with Equation 8 using [Muc_free] ~ [Muc_total] = 0.2 × 10⁻⁷ M (dotted line), 1.08 × 10⁻⁷ M (solid line) and 3.0 × 10⁻⁷ M (dash-dot line).

4. Discussion

The work here builds on the thermodynamic approach developed previously for faecal/oral viruses in the human intestine (Gale 2018) and focuses on the fraction, F_v, of exposure dose, V_exposure, which is not bound to mucins in the lung mucus in the LLF and is therefore free to bind to and infect lung epithelial cells. Prototype dose-response models are plotted in Fig. 4 for a range of K_mucin values and in Fig. 5 to demonstrate the effect of varying [Muc_total] in different individual non-smokers.

The models in Fig. 4 and Fig. 5 represent the risk according to Equation 5 from virions which are fully dispersed in the mucus using F_v calculated with Equation 8. Equation 5 cannot be used with F_v values from Table 2 for aggregated virus doses (i.e. where local V_mucus ≥ Muc_total) because F_v calculated by the difference equation approach is dependent on both the aggregation state of the virions and the number of virions in the inhaled aerosol particle, both of which affect the local virus:mucin ratio and hence [Muc_free] (in Equation 8) where the aerosol interfaces with the mucus barrier.

The key conclusion of the prototype dose-response models is that dispersed SARS-CoV-2 virions are highly infectious to human without an effective mucus barrier in the lung with a predicted ID₅₀ ~500 virions which equates to 1 to 2 pfu. This ID₅₀ is dependent on the value of p_pfu which is given a point value of 0.0028 here based on 360 genomic copies per pfu. Adhikari et al. (2019) use a point value of 1,239 genomic copies per pfu for MERS-CoV based on SARS-CoV data and note the reported values ranged from 1:1 to 300:1 to 1,200-1,600:1. Using different point values would proportionately affect the number of virions comprising an ID₅₀ and is a source of uncertainty addressed by Adhikari et al. (2019). The low ID₅₀ values of 1 to 2 pfu for SARS-CoV-2 in the absence of effective mucin binding reflect both the tight binding of the virion to the host cell through the high affinity spike protein/hACE2 interactions such that K_{a_virus_T} is high (Table 3) and the efficient priming of the spike protein by proteolytic cleavage for fusion, such that p_entry is high. Increasing the magnitude of K_mucin as suggested here for MERS-CoV directly reduces the infectivity, such that with K_mucin =10¹² M⁻¹, the predicted ID₅₀ ~ 5.87 × 10⁷ virions or 163,000 pfu. In terms of other applications, this prototype dose-response model may be used to test the effect of antiviral drugs on the infectivity. For example from drug inhibition data on the viral main protease (Zhang et al. 2020) it may be possible to model the effect of the drug on p_virogenesis in Eq. 11 and hence assess the shift in dose response (Fig. 4) in the presence of the drug.

4.1. Fate and transport of the virions to the lung mucus

The dose response developed here is based on a virion dose being deposited in the mucus in the LLF in the bronchus and with F_trans = 1 in effect assumes 100% of the inhaled dose is deposited there. Deposition is a critical step in the initiation of infection by anthrax and varies between 9% and 30% of the inhaled dose depending on the host species (Gutting et al 2015). Specifically SARS-CoV-2 infects the nasal epithelium (Hou et al. 2020), the ciliated, mucus-secreting, and club cells of bronchial epithelium and the type 1 pneumocytes in the lung (Hui et al 2020). On the basis of the recent data of Hou et al. (2020) the model for SARS-CoV-2 only needs to focus on the nasal epithelium such that assuming F_trans = 1 may be justified. The prototype model here does not include lung air flow and pathogen transport principles as used in the anthrax model of Weir and Haas (2011). Instead, it is assumed that the fate of the virions deposited in the mucus in the LLF depends on whether each virion becomes bound subsequently to the mucins in the mucus and hence removed from the lung or remains free to bind to a host epithelial cell and initiate infection. This is accommodated in the F_v term, which is determined by both K_mucin and the mucin concentration according to Equation 8. To develop the model it may be possible to apply the fate and transport approaches developed by Weir and Haas (2011) to viruses using the K_mucin and mucin concentrations and also other diffusion approaches such as that developed for viruses moving through mucus (Erickson et al. 2015). A further difference between anthrax spores and SARS-CoV-2 is that cell tropism for the latter is dependent on the presence of the hACE2 receptor and the TMPRSS that cleaves spike protein into S1 and S2 (Lukassen et al. 2020; Hou et al. 2020). Although hACE2 and TMPRSS are expressed in cells from the lung and epithelial cells from the subsegmental bronchial branches, only a small proportion of cells express both (Lukassen et al. 2020) and are hence susceptible to SARS-CoV-2 infection. This is accommodated in the C_total term in this model which affects how F_c varies with K_{a_virus_T} as shown for the human lung, human intestine and arthropod midgut models in Fig. 3.

4.2. The mucus barrier in the human lung may be more effective against MERS-CoV which binds human mucin than against SARS-CoV-2 which does not bind SA

It might be thought that the similarity of the dose-response data for MHV and SARS-CoV in the mouse data of Watanabe et al. (2010) presented as symbols in Fig. 4 argues against the importance of the mucus barrier in the thermodynamic dose-response model because the spike protein of MHV binds SA (Li et al 2017) while the spike protein of SARS-CoV-2 does not (Hao et al 2010). However, MHV differs from other CoVs in coding for an additional spike protein, the haemagglutinin-esterase (HE), which allows virions to elute from SA surfaces and hence provides the virions with a means of escape from irreversible attachment to non-cell-associated sialoglycoconjugates such as mucins (Langereis et al., 2011). Thus although MHV spike protein itself binds to SAs (Li et al. 2017) while SARS-CoV does not, the ability of the MHV to escape the mucin barrier would explain its similar dose-response in mice to SARS-CoV in the data of Watanabe et al. (2010) plotted in Fig. 4.

Adhikari et al. (2019) adopt the SARS-CoV dose-response model of Watanabe et al. (2010) as a surrogate for MERS-CoV in humans. However MERS-CoV may be different from SARS-CoV and SARS-CoV-2 in that it binds to human mucin through SAs (Li et al. 2017). More significantly it does not encode an HE protein (Du et al. 2017) with which to release itself from the SAs on the mucins (Langereis et al., 2011). Some beta-coronaviruses (as discussed for MHV above) do produce the HE protein which helps in the viral spread through the mucosa (Rabaan et al. 2020).Thus MERS-CoV may be effectively trapped by mucus in the human lung and according to the model here, this would increase the ID₅₀ for MERS-CoV relative to that for SARS-CoV-2 and may contribute to explaining why MERS-CoV is less efficiently transmitted from person to person in the community.

4.3. Obtaining data on K_mucin for MERS-CoV and SARS-CoV-2 binding to mucins in human lung mucus

The results in Fig. 4 emphasise the potential of the mucus as a major barrier depending on the magnitude of the parameter K_mucin. Although SARS-CoV-2 does not bind to SAs (Hao et al. 2020), spike protein interactions with SA have been reported for several CoVs including MERS-CoV (Li et al. 2017). These interactions are mediated by the N-terminal domain (S1^A) of the spike protein while proteinaceous receptors (e.g. hACE2) are generally bound via S1^B (Li et al. 2017). From Fig. 2a it can be seen that for the mucus to have any effect the magnitude of K_mucin must exceed 10⁶ M⁻¹ and that K_mucin values of 10¹⁰ M⁻¹ are required to achieve >1,000-fold removal of dispersed virus (Fig. 2b). Dam and Brewer (2010) report a K_mucin value of 5.0 × 10⁹ M⁻¹ for the lectin soy bean agglutinin binding to porcine submaxillary mucin which has multiple GalNAc sugars to bind. Similarly Vataira macrocarpa lectin has a K_mucin of 1.0 × 10¹⁰ M⁻¹ with porcine submaxillary mucin. Thus K_mucin values of 10¹⁰ M⁻¹ used in the prototype dose response model (Fig. 4) may be realistic for MERS-CoV. Interactions between carbohydrate binding domains (CBDs) on proteins and monomeric SAs are generally weak with K_{d_mucin} values ~ 10⁻³ M (Taylor and Drickamer, 2006; Fei et al. 2015) and indeed Li et al. (2017) describe the S1^A/SA interaction as weak for MERS-CoV. However, by making multiple contacts with the virus the affinity can be hugely increased according to Eq. 9 and Li et al. (2017) only detected MERS-CoV S1^A binding to mucin when presented on nanoparticles such that multivalent (i.e. N_m > 1) CBD/SA interactions could be made thus enhancing binding affinity as expected from Eq. 9. For MERS-CoV the three S1^A subunits of the spike trimer could each bind SA (i.e. one SA bound per S monomer). There are also 74 trimer spikes on each MERS-CoV virion (Neuman et al. 2011) so in theory there is potential for the virion to make multiple interactions with the multiple SAs on a mucin molecule such that K_mucin could become very large. Thus N_m = 4 CBD/SA interactions each of K_{d_mucin} = 10⁻³ M would give a K_mucin of ~10¹² M⁻¹ according to Eq. 9. The magnitude of ΔS_{a_mucin} for immobilisation of the virus on the mucin surface in Eq. 9 is likely to be small because, unlike ΔS_{a_immob} for virus binding to a cell surface, binding to mucus is random.

Most mucins have a high SA content which, along with the high sulphate content, results in a strongly negative surface charge (Zanin et al. 2016). Hao et al. (2020) have shown that SARS-CoV-2 spike protein binds to heparan sulphate which also contains multiple sulphate groups. Moreover, basic amino acid residues (i.e. positively charged), known to constitute heparin binding domains are solvent accessible on the SARS-CoV-2 spike protein surface and form a continuous patch that is suitable for heparin binding (Mycroft-West et al. 2020). Human CoV NL63 also binds heparan sulphate which is used by this coronavirus for its attachment to target cells (Milewska et al 2014). This suggests SARS-CoV-2 and other human CoVs could bind to negatively charged groups on mucins despite not binding to SAs (Hao et al. 2020). Thus binding of SARS-CoV and SARS-CoV-2 to human mucins will only be determined by experiment with human mucin itself and cannot be ruled out at this stage even though Hao et al. (2020) report it does not bind SA.

4.4. The degree of local dispersion/clustering of the virions in the lung mucus greatly affects the removal efficacy of the mucus

According to Scenario 2 in Table 2 inhalation of a fixed dose of SARS-CoV-2 virions dispersed across many aerosol particles may pose a greatly diminished risk compared to the same dose inhaled as a “cluster” in a single aerosol particle (providing K_mucin ≥10¹⁰ M⁻¹). The virus:mucin ratio in Table 2 represents the local virion:mucin contact ratio and not the virus to mucin ratio across the whole 25 cm³ of LLF which will be very low and representing an average. As the virus dose in the aerosol becomes more dispersed in the mucus then the local Muc_total begins to exceed V_mucus such that each virus is in effect surrounded by mucin molecules and has no contact or protective shielding effect from other viruses in the challenge dose from the aerosol particle. The model here suggests that the “local dilution” of a clustered virus dose from an aerosol only has to be ~>2-fold (Fig. 2) to almost maximise the effect of the protective mucus barrier. Thus according to the model each virus only needs to be surrounded by 2 mucin molecules of K_mucin ≥ 10¹⁰ M⁻¹ in order to achieve a 588-fold reduction in risk of the virus getting to the epithelium and initiating infection. Infinite dilution as represented by the output of Equation 8 halves the risk again giving at the limit a 1,176-fold reduction in risk with <0.1% of the initial virus dose now free to bind to lung cells and initiate infection (Table 2).

4.5. The greatest change in risk occurs at the local virion/mucin ratio of 1:1 akin to a threshold

A four-fold increase in the local virus concentration in the mucus from 1 virion per 2 mucins to 2 virions per mucin gives ~300-fold increase in F_v (Table 2) and hence the risk of infection. This represents a co-operative effect within a virus “cluster” and breaks away from the traditional concept of independent action of pathogen infection although there is no absolute threshold effect in the model here. Bhar and Jones (2019) also challenge the “free independent virus particle” idea of viral transmission with the discovery of mechanisms by which multiple viral particles can infect the same cell simultaneously.

4.6. Impact of cell-tethered mucins is not considered here

The model here only considered the secreted mucins, MUC5B and MUC5AC, in the mucus and does not consider the cell-tethered mucins which may present an additional barrier to respiratory viruses. The cell-tethered mucins such as MUC1 and MUC4 form the basis of a gel-like layer surrounding the cilia (periciliary layer) that is essential for normal ciliary action to move mucus out of the airways (Ridley and Thornton 2018). The cell-tethered mucins provide a barrier function to mucosal pathogens by displaying sites for pathogen binding, acting as a releasable decoy, and sterically blocking binding of pathogens to underlying cellular receptors (McAuley et al. 2017). The cell-tethered mucin MUC1 gives protection against IAV H1N1 (McAuley et al. 2017). There is some evidence in mice that MUC4 gives protection to mice against SARS-CoV with Muc4^−/− mice showing a modest 62% higher titre at 2 days post infection (dpi) and a 51% higher titre at 4 dpi as compared to wild type mice, although the increases were not statically significant (Plante et al. 2020). In contrast, Muc1^−/− mice displayed a more rapid statistically significant rise in pulmonary IAV H1N1 loads compared to wild type mice at 1 to 3 dpi, although levels were comparable at 5 to 7 dpi (McAuley et al. 2017). Overall MUC4 offered protection to female mice against SARS-CoV and chikungunya virus pathogenesis although it was concluded this may not reflect a direct role such as the physical barrier function of mucin (Plante et al. 2020).

4.7. Uncertainty in the assumption that F_c = 1 i.e. all virus not bound to mucin is bound to lung epithelial cells

It is shown in Fig. 3 that >90% of the virus is bound to lung cells in the human lung model when K_{a_virus_T} exceeds 10¹⁴ M⁻¹, thus greatly simplifying the model because F_c in Equation 5 does not have to be calculated for each dose using the difference equation approach (Gale 2018) but can be assumed to approximate 1. While there is a published value of K_{d_receptor_T} for SARS-CoV-2 spike trimer protein binding to a single hACE2 (Wrapp et al. 2020), there is no information on the number of contacts, N_v which must be at least five (Table 3) depending on ΔS_{a_immob} to ensure K_{a_virus_T} >10¹⁴ M⁻¹ according to Eq. 10. According to Yang et al. (2005) HIV virions bearing IAV HA required 8 or 9 HA trimers for virus entry and Guo et al. (2018) suggest that approximately 7 IAV HA trimers can interact with receptor-loaded SA molecules. It is concluded that although there is considerable uncertainty in the exact value of N_v for SARS-CoV-2 and MERS-CoV it is likely to be greater than 4 for both and on the basis that N_v could be as high as 7 spike trimer protein/receptor interactions it is concluded that K_{a_virus_T} is >10¹⁴ M⁻¹ according to Eq. 10 such that F_c can be assumed to approximate 1. This is in agreement with Walls et al. (2020) who suggest the observed tight binding of SARS-CoV-2 S1^B to hACE2 could partially explain the efficient transmission of SARS-CoV-2 in humans.

It should also be noted that ΔS_{a_immob} in Eq. 10 is an unknown parameter for any virus and depends on the size of the virus (Gale 2019; Gale, 2020) together with how restricted virion mobility is on attachment to a host cell. The ΔS_{a_immob} of –350 J/mol/K used in Table 3 is estimated using the Sackur-Tetrode equation. A less negative ΔS_{a_immob} at –170 J/mol/K for example would require just three GP/Cr contacts to achieve K_{a_virus_T} of >10¹⁴ M⁻¹ for SARS-CoV-2 according to Eq. 10 and ultimately it would be better to measure K_{a_virus_T} experimentally if possible.

4.8. The host cell infection component of the prototype dose-response for SARS-CoV-2 is defined solely by cell binding and entry

As a probability, p_cell, can take a value between 0 (cell is refractory) and 1 (cell is fully permissive) and a value of 0.5 is assigned here on the basis of the efficiency of cleavage of SARS-CoV-2 spike protein by human cells (Hoffmann et al. 2020). The values of p_virogenesis and p_budding are assumed to ~1 in the calculation of p_cell in Eq. 11. In effect therefore the component of the dose-response for SARS-CoV-2 infection of human lungs is based solely on K_{d_receptor_T}, N_v and p_entry. This appears to be acceptable for assessing the zoonotic potential of bat CoVs. Thus Menachery et al. (2020) argue that the combination of receptor binding and proteolytic activation by endogenous proteases permits zoonotic CoV infection as with MERS-CoV and SARS-CoV, and can be used to evaluate zoonotic virus populations in bats for emergence threats. There are several human host cell proteases that can cleave the spike protein. Thus SARS-CoV can use the endosomal cysteine proteases cathepsin B and L and the serine protease TMPRSS2 for S protein priming in cell lines, and inhibition of both proteases is required for robust blockade of viral entry (Hoffmann et al. 2020). However, only TMPRSS2 activity is essential for SARS-CoV viral spread and pathogenesis in the infected host whereas CatB/L activity is dispensable (Hoffmann et al. 2020). Therefore p_entry should be based on the probability of cleavage by TMPRSS2 in order to model for spread of the virus in the body.

4.9. Comparing the prototype thermodynamic dose-response model for initial infection with published dose-response data for coronavirus death in mice

Although the K_mucin value from Dam and Brewer (2010) of 5 × 10⁹ M⁻¹ for lectin binding to porcine submaxillary mucin gives a good approximations to the MHV and SARS-CoV mouse death data (symbols in Fig. 4), this is not evidence of validation of the model here because MHV escapes mucin and SARS-CoV does not bind mucin and thus K_mucin values would be expected to be very small (certainly <10⁶ M⁻¹) such that the predicted dose-response curve for initial infection by MHV and SARS-CoV in mice (solid line in Fig. 4) would have ID₅₀s of ~500 virions (1 to 2 pfu) according to the model here. It should be stressed that the data of Watanabe et al. (2010) as represented by the symbols in Fig. 4 are not comparable with the model outputs here, the former representing death while the latter represents initial infection of one or more epithelial cells in the nose or bronchus, with no inclusion of the effect of the innate immune response which is important in disease progression and illness in CoV infection (Lim et al. 2016). It is therefore not surprising that the ID₅₀ for death (symbols) is higher than the ID₅₀ for infection with low K_mucin (solid line) in Fig. 4.

4.10. Is the dose-response for SARS-CoV a good surrogate for SARS-CoV-2?

Although similar, there are some notable differences between the SARS-CoV-2 and SARS-CoV spike proteins (Rabaan et al. 2020; Wrapp et al. 2020). The key amino acid residues involved in ACE2 binding are largely different and the SARS-CoV-2 trimer binds to ACE2 with a ~12-fold lower K_{d_receptor_T} than that of the SARS-CoV trimer (Table 3). The binding of SARS-CoV-2 is predicted to be much stronger than for SARS-CoV according to K_{a_virus_T} values as the number of spike trimer/ACE2 contacts increase (Table 3). According to the model here in Fig. 3 this difference could be overcome by a sufficient number, N_v, of spike trimer/hACE2 contacts such that K_{a_virus_T} exceeds 10¹⁴ M⁻¹ (Table 3). However, the TMPRSS cleavage site in the spike protein sequence of SARS-CoV-2 may also account for the increased infectivity of SARS-CoV-2 relative to SARS-CoV (Hao et al 2020; Rabaan et al. 2020) such that p_cell may be lower for SARS-CoV than for SARS-CoV-2. Thus the dose-response of Watanabe et al. (2010) based on SARS-CoV and MHV in mice may not be appropriate for SARS-CoV-2 although in the absence of data it is used as a surrogate dose-response in airborne risk assessment (Buonanno et al. 2020).

4.11. Both SARS-CoV and MHV bind to host cells with high affinity consistent with similar dose-response models in mice

Although each SARS-CoV spike trimer could bind three ACE2 receptors, the stoichiometry of spike trimers binding ACE2 is complicated for SARS-CoV (Kirchdoerfer et al. 2018) with most trimers just binding one ACE2. This is because the three copies of SARS-CoV S1^A protein which bind ACE2 are all located on the top of the spike trimer and are near each other, leading to steric clashes between bound ACE2 molecules (Shang et al. 2020). This contrasts with mouse hepatitis coronavirus (MHV) for which three receptor molecules bind to the sides of the spike trimer, where there is no steric clash (Shang et al. 2020). Thus each MHV trimer binds three receptors (Kirchdoerfer et al. 2018) and depending on the number of receptor molecules on host cell membranes, Shang et al. (2020) conclude that the high stoichiometry of receptor binding by MHV spike potentially allows efficient viral attachment to target cells. Thus in addition to not being bound by mucins, both MHV and SARS-CoV could attach to host cells with high affinity consistent with their similar dose-response curves for death in mice (symbols in Fig. 4).

4.12. Limitations of the model developed here

In addition to lack of data on the magnitude of K_mucin for viruses associating with mucins, current understanding of mucin functions is limited. This is partly due to the complexity of mucus and its interactions (Zanin et al. 2016). The interaction between mucins and respiratory pathogens is also more complicated than mere entrapment (Zanin et al. 2016). The model here only considers entrapment of the virus, and does not consider mechanisms for the virus to evade the mucus which do not appear to be known for CoVs. Although mucus is an important host barrier to IAV, the neuraminidase (NA) protein of IAV is important in evading this barrier, such that viruses with low NA activity, or viruses treated with NA inhibitors, are severely impeded by mucus in vitro (Zanin et al. 2016). Another limitation of the model is that it is possible that more than one virus can bind a mucin molecule since each mucin molecule has multiple SAs (Zanin et al. 2016).

According to Guo et al. (2018) equilibrium binding models (such as those developed here) are poorly applicable to the IAV-receptor interaction because the virus rolls over a surface (such as a host cell) coated with receptors enabled by NA activity. Migration of attached IAV particles over a receptor coated-surface depends on the very high K_{d_receptor_T} (0.0003 to 0.003 M) values (i.e. low affinity binding) of monovalent HA/SA interactions resulting in their rapid formation and dissociation. Guo et al. (2018) hypothesize that NA, in combination with the highly dynamic formation and release of individual HA-SA interactions, drives virus rolling by the generation of a receptor gradient due to the receptor destroying activity of NA. This is a different strategy from SARS-CoV-2 cell binding for which K_{d_receptor_T} for the trimer is very low at 1.5 × 10⁻⁸ M (Wrapp et al. 2020) and SARS-CoV-2 and MERS-CoV do not appear to utilize enzymes for viral release with only group 2a coronaviruses (human CoV-HKU1, MHV) having haemagglutinin esterases (de Groot 2006). It is concluded that the equilibrium binding models (such as those used here and previously (Gale 2018)) are applicable to coronaviruses, although not for IAV virions which have both HA and NA present in their viral envelopes. It may also not be applicable to MHV which also has HE.

4.13. The role of sialic acids: ΔS_{a_immob} vs K_mucin

Unlike IAV which only binds SA receptors, the spike protein trimers of CoV bind to protein Cr receptors with very high affinity. This raises the question of why some CoV spike proteins e.g. MERS-CoV, also bind to SAs, which according to the model here would hinder their movement through the mucus barrier. Other viruses also use non-specific attachment factors that bind the virus on the cell surface without initiating endocytosis and viral entry, for which specific receptors are required. In the case of tick-borne encephalitis virus, HIV, pseudorabies virus, sindbis virus, Semliki Forest virus, hepatitis E virus and Rift Valley fever virus the attachment factor is heparan sulphate, a negatively-charged glycosaminoglycan (Pulkkinen et al. 2018). SARS-CoV-2 spike protein also binds heparan sulphate (Hao et al., 2020). It was previously proposed that the attachment factors including cell surface SAs and heparan sulphate serve to take some of the entropy loss of ΔS_{a_immob} on virus binding (Gale 2020). Specifically for MERS-CoV, Li et al. (2017) provide evidence that SAs may serve as low-affinity attachment receptors and thereby aid viral entry through increasing the likelihood of MERS-CoV spike engagement with the DPP4 entry receptor. Thus the potential loss of the virus through binding to SAs on mucins in the mucus as suggested by the model here may be a trade-off for non-specific binding of viral spike proteins to SAs on the cell surface in overcoming the unfavourable ΔS_{a_immob}. In this respect, the magnitude of K_mucin in the F_v term plays off against that of ΔS_{a_immob} in the F_c term in Fig. 1.

5. Conclusions

The conclusions are:-

• 1The outline of a thermodynamic equilibrium model for a dose-response for SARS-CoV-2 and MERS-CoV is set out here based on molecular parameters. The available parameters for the spike trimer/cell receptor interactions suggest the association constant for virus binding to a human bronchus/lung cell will be so high that any virion getting through the mucus barrier will bind to these cells resulting in entry through spike protein fusion which is also known to be efficient for both viruses.
• 2It is known that mucin proteins in lung mucus present a barrier to respiratory viruses. According to the model outlined here, the mucus in the 25 cm³ volume of lung lining fluid could present a significant barrier to infection of lung cells in humans by coronaviruses if the magnitude of the association constant (K_mucin) defining the strength of binding of the virion to human mucin is at least 10⁹ M⁻¹ (as has been reported for lectins' binding to mucins).
• 3The magnitude of K_mucin is currently unknown for any virus to the author's knowledge. While SARS-CoV-2 spike protein does not bind sialic acid, the spike protein of MERS-CoV does and indeed MERS-CoV has been shown to bind human mucin. A K_mucin of at least 10¹⁰ M⁻¹ could theoretically be achieved for MERS-CoV with four low affinity contacts between virus spike protein and monomeric sialic acids on the mucin each with dissociation constants of ~10⁻³ M (which is typical for carbohydrate binding domains on proteins binding to monomeric sialic acids). This could contribute to more efficient removal of MERS-CoV by the mucus barrier in the lung and hence its reduced human-to-human transmission compared to SARS-CoV-2. However SARS-CoV-2 spike protein has positively charged groups which could interact with negatively charged acidic groups on the mucins and its binding to human mucin cannot be ruled out without definitive data.
• 4The mucus barrier may be more effective against fully dispersed virions in the case of MERS-CoV that binds human mucin. Some coronaviruses use an esterase to escape the mucin, although MERS-CoV does not. Instead, it is shown here that “clustering” of virions into single aerosol particles as recently reported for rotavirus in extracellular vesicles could provide a co-operative mechanism whereby MERS-CoV could theoretically overcomes the mucin barrier locally. In this respect the rare, high virion-load aerosol particles may be more important for transmission of MERS-CoV.
• 5Assuming efficient transport to the mucus in the lung bronchus (or nasal epithelium in the case of SARS-CoV-2) and depending on the viability of individual virions, the ID₅₀ for SARS-CoV-2 initial infection is estimated to be ~500 virions (viral RNA genomic copies) representing 1 to 2 pfu. Assuming a K_mucin of 5 × 10⁹ M⁻¹ as for lectin/mucin binding, the ID₅₀ for MERS-CoV initial infection is estimated to be ~295,000 virions (viral RNA genomic copies) representing 819 pfu.
• 6The thermodynamic equilibrium approach developed here based on virus binding to mucins according to K_mucin and the mucin concentration in mucus could complement inhalation models based on fate and transport as for anthrax spores in the lungs.
• 7It is proposed that K_mucin is the cost for binding of viruses to sialic acids on the cell surface to partially overcome the unfavourable entropy of immobilisation of a virus.

Author Statement

I wrote this paper based on my previous thermodynamic dose-response models with no funding. It is my contribution to the global response against COVID-19.

Disclaimer

The views expressed in this paper are those of the author and not necessarily those of any organisations.

Declaration of Competing Interest

None declared.