Efficient formulation of polarizable Gaussian multipole electrostatics for biomolecular simulations

Abstract

Molecular dynamics simulations of biomolecules have been widely adopted in biomedical studies. As classical point-charge models continue to be used in routine biomolecular applications, there have been growing demands on developing polarizable force fields for handling more complicated biomolecular processes. Here, we focus on a recently proposed polarizable Gaussian Multipole (pGM) model for biomolecular simulations. A key benefit of pGM is its screening of all short-range electrostatic interactions in a physically consistent manner, which is critical for stable charge-fitting and is needed to reproduce molecular anisotropy. Another advantage of pGM is that each atom’s multipoles are represented by a single Gaussian function or its derivatives, allowing for more efficient electrostatics than other Gaussian-based models. In this study, we present an efficient formulation for the pGM model defined with respect to a local frame formed with a set of covalent basis vectors. The covalent basis vectors are chosen to be along each atom’s covalent bonding directions. The new local frame can better accommodate the fact that permanent dipoles are primarily aligned along covalent bonds due to the differences in electronegativity of bonded atoms. It also allows molecular flexibility during molecular simulations and facilitates an efficient formulation of analytical electrostatic forces without explicit torque computation. Subsequent numerical tests show that analytical atomic forces agree excellently with numerical finite-difference forces for the tested system. Finally, the new pGM electrostatics algorithm is interfaced with the particle mesh Ewald (PME) implementation in Amber for molecular simulations under the periodic boundary conditions. To validate the overall pGM/PME electrostatics, we conducted an NVE simulation for a small water box of 512 water molecules. Our results show that to achieve energy conservation in the polarizable model, it is important to ensure enough accuracy on both PME and induction iteration. It is hoped that the reformulated pGM model will facilitate the development of future force fields based on the pGM electrostatics for applications in biomolecular systems and processes where polarization plays crucial roles.

I. INTRODUCTION

Atomistic simulations of biomolecules have been applied in a wide range of biological systems.¹ While additive nonpolarizable models will continue to play important roles,^2–4 nonadditive polarizable models are expected to extend our ability to study more complex biomolecular systems and processes. Nonpolarizable models typically use fixed atom-centered partial charges to model electrostatics and include the polarization response to the environment (mostly in water) only in an averaged, mean-field manner. Subsequently, nonpolarizable models that provide excellent descriptions of the homogeneous bulk phase are poor models for gas-phase clusters or in nonpolar solvents. The importance of modeling nonadditive effects is well known.⁵ For example, the gas-phase water dimer interaction energy is overestimated by more than 30% in the TIP5P model.⁶ Similarly, for large biomolecular systems, there are concerns that such models cannot correctly account for situations where the same nonpolarizable moiety is exposed to different electrostatic environments/solvents, either within a single large structure or during a simulation process. In addition, there is an inherent inconsistency in most nonpolarizable models related to their static inclusion of average bulk polarization within the potential. This results in internal energies and other properties that are derived against a gas-phase reference state, which is already “pre-polarized” for the liquid phase. These limitations lead to issues in modeling multiple important problems such as pH-dependent processes, ion-dependent interactions, order–disorder transition, and enzymatic reactions.

In response to the above concerns, much effort has been invested on the inclusion of explicit polarization within the molecular mechanics (MM) potentials.^7–9 Several methods are available to explicitly model polarization in molecular simulations, such as the Drude oscillator,^10,11 fluctuating charges,¹² and induced dipoles.^6,13,14 The use of polarizable point dipoles is a classical approach with a long history in molecular simulation.¹⁵ The original induced dipole model of Applequist places the induced point dipoles on atom centers.¹⁶ However, this model suffers from the so-called “polarization catastrophe”: when the interaction between two mutually interacting induced dipoles with atomic polarizabilities diverges at a finite distance. Thole proposed a solution by applying a damping function to the induced dipole–induced dipole interactions.¹⁷ However, a drawback to this model is that it does not prescribe how the induced dipoles and permanent charges interact. A great deal of effort has been devoted to developing modern polarizable models, including the fluctuating charge models^18,19 in the context of Optimized Potentials for Liquid Simulations-All Atoms (OPLS-AA), the fluctuating charge model and the Drude oscillator model^20–23 in the context of Chemistry at Harvard Molecular Mechanics (CHARMM), and detailed multipole expansions and more complicated MM potentials in the context of Amoeba.²⁴ In Amber, polarization was implemented with the induced dipoles.²⁵ In Amber ff12pol, the induced dipoles are calculated using Thole models to avoid “polarization catastrophe.”^26–29

Another limitation of widely adopted nonpolarizable models is their use of partial atomic charges in the electrostatic models, which often lack sufficient mathematical flexibility to describe the electrostatic potential (ESP) around molecules. Williams showed that optimal least-squares fitting of atom-centered partial charges resulted in relative root-mean-square errors of 3%–10% over a set of grid points in a shell outside the surface of a series of small polar molecules.³⁰ These errors were reduced by 2–3 orders of magnitude via the use of higher atomic multipoles.⁶ In Amoeba force fields, multipoles are placed on each atom, allowing better capture of electrostatic potential distribution around molecules.^31,32 The Gaussian electrostatic model (GEM) is a force field based on density fitting, which can extend to arbitrary angular momenta (multipoles).^33–35 Of course, there are many other proposals to model electronic polarization in the literature.^12,36–38

Recently, Elking et al. proposed a polarizable multipole model with Gaussian charge densities.³⁹ A key benefit of the polarizable Gaussian Multipole (pGM) model is its screening of all short-range electrostatic interactions in a physically consistent manner. This is critical for stable charge-fitting in polarizable force fields when the polarizations of 1–2 and 1–3 charges are included and are needed to reproduce molecular anisotropy, as discussed in Ref. 40. Of course, this strategy would also require us to redesign the valence terms to retain close to harmonic behaviors. An advantage of pGM is that each atom’s multipoles are represented by a single Gaussian function and its derivatives with different amplitudes. Therefore, pGM is a minimalist Gaussian polarizable model. In comparison, the GEM model^33–35 treats nuclear charges explicitly and uses Hermite Gaussian auxiliary basis sets to reproduce atomic electron density, so it has the potential to represent the short-range interactions more faithfully than the pGM model. However, because the computational cost of the nonbonded electrostatic calculation scales as the squared number of functions on each atom, the multiple functions used to represent each atom in the GEM can notably increase the simulation cost. The increased number of parameters associated with the functions may also pose additional challenges in parameterization. Another major difference is that the GEM,^33–35 like several other efforts, such as X-Pol⁴¹ and Amoeba,^31,32 uses electronic densities to model molecular polarization and other effects. In comparison, our pGM model follows the Amber tradition and uses the ab initio electrostatic potential to fit the parameters of atomic partial charges and dipoles.

Most macromolecular simulations with long-range electrostatic interactions are performed using periodic boundary conditions. A rigorous treatment of electrostatic interactions in periodic boundary conditions requires a careful treatment of the associated lattice sums. Thus, the widely used lattice sum methods, such as particle mesh Ewald (PME), need to be extended to handle multipolar related summations. Fortunately, efficient implementations of PME of dipoles and higher multipoles are already available in widely used software packages, such as Amber.^42,43 This greatly simplifies the integration of pGM with PME for molecular simulations.

In Secs. II and III, we first describe the detailed pGM electrostatics scheme with a focus on how to define the atomic Gaussian multipoles and associated analytical algorithms for force computation. This is followed by algorithmic details of interfacing pGM and PME. We then present the validation of the analytical force formulation and accuracy discussion of pGM in PME simulations. Finally, we conclude the manuscript with a brief discussion of the next steps in our development.

II. THEORY

A. Gaussian density representation of charge distribution

The Gaussian multipole model represents the charge distribution on each atom as a Gaussian-shaped multipole expansion. Hence, an nth order Gaussian multipole with the radius of 1/β, located at position $\stackrel{\rightharpoonup }{R}$, is³⁹

$${\rho }^{\left(n\right)}\left(\stackrel{\rightharpoonup }{r};\stackrel{\rightharpoonup }{R}\right)={\mathrm{\Theta }}^{\left(n\right)}\cdot {\nabla }_R^{\left(n\right)}{\left(\frac{\beta }{\sqrt{\pi }}\right)}^3\exp \left(-{\beta }^2|\stackrel{\rightharpoonup }{r}-\stackrel{\rightharpoonup }{R}{|}^2\right).$$ (1)

Here, Θ⁽ⁿ⁾ is the nth rank momentum tensor and ∇⁽ⁿ⁾ is the nth rank gradient operator (Subsection 1 of the Appendix).

In our current pGM model, only monopoles and dipoles are retained, so only the first two terms are needed at each atom as shown below,

$$\begin{array}{cc}\hfill {\rho }^{\left(0\right)}\left(\stackrel{\rightharpoonup }{r};\stackrel{\rightharpoonup }{R}\right)& =q{\left(\frac{\beta }{\sqrt{\pi }}\right)}^3\text{exp}\left(-{\beta }^2|\stackrel{\rightharpoonup }{r}-\stackrel{\rightharpoonup }{R}{|}^2\right),\hfill \\ \hfill {\rho }^{\left(1\right)}\left(\stackrel{\rightharpoonup }{r};\stackrel{\rightharpoonup }{R}\right)& =\stackrel{\rightharpoonup }{\mu }\cdot {\nabla }_R{\left(\frac{\beta }{\sqrt{\pi }}\right)}^3\text{exp}\left(-{\beta }^2|\stackrel{\rightharpoonup }{r}-\stackrel{\rightharpoonup }{R}{|}^2\right),\hfill \end{array}$$ (2)

where the zeroth-order term represents a monopole and the first-order term represents a dipole.

Once the charge densities are defined, as in Eq. (2), the pairwise Coulombic interaction energy expressions needed for the current pGM model are as follows:

• (1)Monopole–monopole:

$$q_1{q}_2\frac{erf\left({\beta }_{12}{R}_{12}\right)}{R_{12}}.$$ (3)

• (2)Monopole–dipole:

$$q_1{\stackrel{\rightharpoonup }{\mu }}_2\cdot {\nabla }_2\frac{erf\left({\beta }_{12}{R}_{12}\right)}{R_{12}}.$$ (4)

• (3)Dipole–dipole:

$$\left({\stackrel{\rightharpoonup }{\mu }}_1\cdot {\nabla }_1\right)\left({\stackrel{\rightharpoonup }{\mu }}_2\cdot {\nabla }_2\right)\frac{erf\left({\beta }_{12}{R}_{12}\right)}{R_{12}},$$ (5)

where erf() is the error function, and

$${\beta }_{12}=\frac{{\beta }_1{\beta }_2}{\sqrt{{{\beta }_1}^2+{{\beta }_2}^2}}\text{\hspace{1em}and\hspace{1em}}{R}_{12}=\left|{\stackrel{\rightharpoonup }{R}}_1-{\stackrel{\rightharpoonup }{R}}_2\right|.$$ (6)

Finally, it is often convenient to introduce the dipole–dipole interaction tensor ${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{T}}}_{12}={\nabla }_1{\nabla }_2\frac{erf\left({\beta }_{12}{R}_{12}\right)}{R_{12}}$ so that Eq. (5) can be simplified as ${\stackrel{\rightharpoonup }{\mu }}_1\cdot {\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{T}}}_{12}\cdot {\stackrel{\rightharpoonup }{\mu }}_2$. Here, it is worth pointing out an important convention used throughout this manuscript. All gradient operators paired with a dipole only operate on coordinates. For example, the gradient operator in ${\stackrel{\rightharpoonup }{\mu }}_1\cdot {\nabla }_1$ only operates on the atomic coordinates that follow. On the other hand, all other gradient operators that are not paired with a dipole are used in the normal sense. This convention is adopted throughout this manuscript.

It can be shown that an effective potential and corresponding effective field at atomic center ${\stackrel{\rightharpoonup }{R}}_1$ can be defined as

$$\begin{array}{cc}\hfill {\varphi }^{effective}& =\left(q_2+{\stackrel{\rightharpoonup }{\mu }}_2\cdot {\nabla }_2\right)\frac{erf\left({\beta }_{12}{R}_{12}\right)}{R_{12}},\hfill \\ \hfill E^{effective}& =-\left(q_2+{\stackrel{\rightharpoonup }{\mu }}_2\cdot {\nabla }_2\right){\nabla }_1\frac{\text{erf}\left({\beta }_{12}{R}_{12}\right)}{R_{12}}\hfill \end{array}$$ (7)

due to a charge distribution at atomic center ${\stackrel{\rightharpoonup }{R}}_2$ so that the pairwise Coulomb energies in Eq. (3)–(5) can be reproduced when an effective point charge of q₁ and an effective point dipole ${\stackrel{\rightharpoonup }{\mu }}_1$ are placed at atomic center ${\stackrel{\rightharpoonup }{R}}_1$. The use of the effective potential and field simplifies the derivation of pairwise Coulombic force calculations, as shown below. Note that these are different from the real Coulombic potential and field due to Gaussian charges and dipoles. For example, the real potential at any location ${\stackrel{\rightharpoonup }{R}}_1$ due to atom 2 at ${\stackrel{\rightharpoonup }{R}}_2$ is

$${\varphi }^{real}=\left(q_2+{\stackrel{\rightharpoonup }{\mu }}_2\cdot {\nabla }_2\right)\frac{erf\left({\beta }_2{R}_{12}\right)}{R_{12}}.$$ (8)

B. Gaussian multipoles in pGM

In our current pGM model, interactions are modeled with both permanent and induced atomic multipoles at atomic centers, both of which are truncated at the dipole level. The framework can be easily extended to higher-order multipoles, if needed in future developments.

1. Permanent multipoles

Permanent multipoles are the first part of the pGM model and are defined with respect to a local frame overlapped with atom’s covalent bonds. This choice is based on the fact that atomic moments result from atomic covalent bonding interactions. This is also because covalent bonding interactions are along the stiffest degrees of freedom of a molecule. Thus, our design follows the logic that the induced moments are meant to be responsible for changes in molecular moments due to the changes in soft degrees of freedom in molecular simulations. Of course, the partition between permanent and induced moments is somewhat artificial in a moment fitting procedure. Therefore, we refer to permanent multipoles in our pGM model as covalent multipoles in the following discussion.

The zeroth-order covalent multipoles, i.e., covalent monopoles, are simply the atomic partial charges as in other polarizable or nonpolarizable force fields. The first-order multipoles, i.e., covalent dipoles, are expressed in linear combinations of certain basis vectors. We define the basis vectors to be along the bonding directions or, more precisely, covalent interaction directions. Thus, there may be more covalent interactions than the number of bonds needed to fully define all covalent dipoles on an atom. For example, hydrogen atoms in water are with covalent dipole moments not 100% along the H–O bonds, so virtual H–H bonds may be needed to define covalent dipoles more accurately. On the other hand, sp3 carbon atoms may have up to four covalent dipoles due to the presence of four bonds, though the presence of symmetry often reduces the number of unique covalent dipoles. The new local frame originates from a physical consideration that permanent dipole moments are primarily aligned along the covalent bonds due to the differences in electronegativity of bonded atoms.

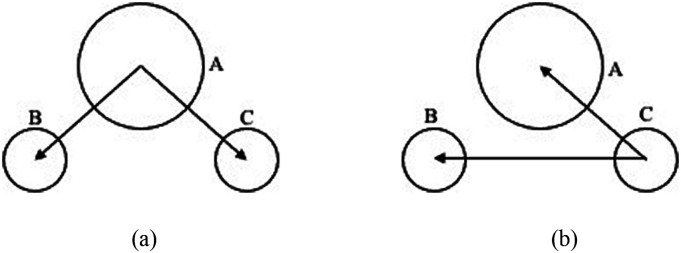
An illustration of basis vectors is shown in Fig. 1 for O and H atoms of water, and we refer to these as the covalent basis vectors (CBVs). The local frame formed by CBVs on an atom is termed its CBV frame. Another representative case is the alpha carbon atom in proteins, which has four bonds, so there can be four basis vectors in its CBV frame to define the covalent dipoles.

FIG. 1.

Definition of covalent basis vectors for atoms in the water molecule. (a) For covalent dipoles centered at A (oxygen), the two basis vectors are ${\stackrel{\rightharpoonup }{e}}^{BA}$ and ${\stackrel{\rightharpoonup }{e}}^{CA}$, which are defined as unit vectors along its two O–H bonds whose two covalent dipoles are the same due to symmetry. (b) For covalent dipoles centered at C (hydrogen), the two basis vectors are ${\stackrel{\rightharpoonup }{e}}^{AC}$, the unit vector along the H–O bond, and ${\stackrel{\rightharpoonup }{e}}^{BC}$, the unit vector along the H–H virtual bond. The covalent dipoles centered at the other hydrogen atom B can be defined similarly.

The CBV frame is also chosen for the sake of simplifying force calculations because the basis vectors are directly dependent on the positions of atoms. For example, the gradient of a covalent dipole vector used extensively in force calculations can be obtained easily within the CBV frame as

$$\nabla \left(\stackrel{\rightharpoonup }{u}\right)=\nabla \left({\sum }_i{u}_i\frac{{\stackrel{\rightharpoonup }{R}}_i}{\left|{\stackrel{\rightharpoonup }{R}}_i\right|}\right)={\sum }_i{u}_i\left(\frac{\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{I}}}{\left|{\stackrel{\rightharpoonup }{R}}_i\right|}-\frac{{\stackrel{\rightharpoonup }{R}}_i{\stackrel{\rightharpoonup }{R}}_i}{{\left|{\stackrel{\rightharpoonup }{R}}_i\right|}^3}\right),$$ (9)

where $\stackrel{\rightharpoonup }{u}$ is the permanent dipole of an atom, ${\stackrel{\rightharpoonup }{R}}_i$ is the vector pointing from the atom to its ith bonded atom (including virtually), $\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{I}}$ is the identity tensor, and the summation is over all covalent interactions of the atom.

Even if quadrupoles are not used in the current pGM model, it is instructive to outline how they are defined in the CBV frame. Given the covalent basis vectors defined above, covalent basis tensors are constructed as dyadic tensors, with each of which formed as a dyadic product of two covalent basis vectors. For example, in the case of oxygen atom with two covalent basis vectors (${\stackrel{\rightharpoonup }{e}}^{BA},{\stackrel{\rightharpoonup }{e}}^{CA}$) in Fig. 1(a), there are up to four dyadic tensors (${\stackrel{\rightharpoonup }{e}}^{BA}{\stackrel{\rightharpoonup }{e}}^{BA},{\stackrel{\rightharpoonup }{e}}^{CA}{\stackrel{\rightharpoonup }{e}}^{CA},{\stackrel{\rightharpoonup }{e}}^{BA}{\stackrel{\rightharpoonup }{e}}^{CA},\text{\hspace{0.17em}and\hspace{0.17em}}{\stackrel{\rightharpoonup }{e}}^{CA}{\stackrel{\rightharpoonup }{e}}^{BA}$) available to define its quadrupole.

2. Induced multipoles

Induced multipoles are the second part of the pGM model. Only first-order terms, i.e., the induced dipoles, are used. The pGM polarization scheme can naturally avoid the well-known polarization catastrophe in point polarizable models without employing any artificial screening factors¹⁷ because distributed dipole densities instead of point dipoles are induced at atomic centers.⁴⁴

In the current pGM model, the linear polarization relation is retained as follows:

$$\begin{array}{cc}\hfill {\stackrel{\rightharpoonup }{p}}_i& ={\alpha }_i{\stackrel{\rightharpoonup }{E}}_i^{effective}\hfill \\ \hfill & ={\alpha }_i\left({\stackrel{\rightharpoonup }{E}}_i^{covalent,effective}-{\sum }_{j\ne i}{\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{T}}}_{ij}\cdot {\stackrel{\rightharpoonup }{p}}_j\right),\hfill \\ \hfill {\stackrel{\rightharpoonup }{E}}_i^{covalent,effective}& =-{\sum }_{j\ne i}\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right){\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}},\hfill \\ \hfill {\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{T}}}_{ij}& ={\nabla }_i{\nabla }_j\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}},\hfill \end{array}$$ (10)

where ${\stackrel{\rightharpoonup }{p}}_i$ is the induced dipole and α_i is the polarizability coefficient of atom i; ${\stackrel{\rightharpoonup }{E}}_i^{effective}$ is the total effective electric field at atom i, which contains two parts: (1) the effective field of covalent dipoles, ${\stackrel{\rightharpoonup }{E}}_i^{covalent,effective}$ [Eq. (7)], and (2) that of the induced dipoles, $-{\sum }_{j\ne i}{\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{T}}}_{ij}\cdot {\stackrel{\rightharpoonup }{p}}_j$. Note that we have used the effective electric field instead of the real electric field to define the induced dipoles in the pGM model. One reason is to ensure the symmetry of ${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{T}}}_{ij}$, which greatly reduces the complexity of force calculation later.⁴⁴ To simplify the following discussion, we drop the effective superscript as we plan to use effective electric fields in all subsequent discussions of energy and force calculations in the pGM model.

Another issue worth pointing out about induced dipoles is their self-energies. The linear polarization itself implies a self-energy term of the form

$$U=\frac{1}{2}\frac{{\stackrel{\rightharpoonup }{p}}^2}{\alpha }.$$ (11)

The derivation can be found in many publications.⁴⁵ However, the pGM model, due to its use of Gaussian distributions of multipoles, posts extra difficulty. For example, a Gaussian charge distribution itself has self-energy, or assembly energy, of the form

$$U=\frac{q^2\beta }{\sqrt{2\pi }}+\frac{{\beta }^3{\left(\stackrel{\rightharpoonup }{\mu }+\stackrel{\rightharpoonup }{p}\right)}^2}{3\sqrt{2\pi }}.$$ (12)

Clearly, the self-energy is different from Eq. (11), and it does not lead to a linear polarization behavior. In fact, it is difficult to assess the physical meaning for the nonlinear assembly energy, just like it is hard to discuss the physical meaning of the infinitely large assembly/self-energy for a point charge. Thus, for the current model development, we do not consider self-energies beyond Eq. (11).

C. Total electrostatic energy and forces in pGM model

From the introduction of the pGM model in Secs. II A and II B, it is clear that the electrostatic potential energy of the system can be divided into two parts:

• (1)Covalent dipole–covalent dipole interaction energy:

$$\begin{array}{ll}\hfill U_{covalent--covalent}=& \frac{1}{2}{\sum }_i^N{\sum }_{j\ne i}^N\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right)\hfill \\ \hfill & \times \left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}.\hfill \end{array}$$ (13)

• (2)Induced energy:

$$\begin{array}{ccc}\hfill U_{induced}& =\hfill & U_{induced--covalent}+U_{induced--induced}+U_{self}\hfill \\ \hfill & =\hfill & -{\sum }_i^N{\stackrel{\rightharpoonup }{p}}_i\cdot {\stackrel{\rightharpoonup }{E}}_i^{covalent}+\frac{1}{2}{\sum }_i^N{\sum }_{j\ne i}^N\left({\stackrel{\rightharpoonup }{p}}_i\cdot {\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{T}}}_{ij}\cdot {\stackrel{\rightharpoonup }{p}}_j\right)\hfill \\ \hfill & \hfill & +\frac{1}{2}{\sum }_i^N{\stackrel{\rightharpoonup }{p}}_i\cdot \left({\stackrel{\rightharpoonup }{E}}_i^{covalent}-{\sum }_{j\ne i}^N\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{T}}{i}_j\cdot {\stackrel{\rightharpoonup }{p}}_j\right)\hfill \\ \hfill & =\hfill & -\frac{1}{2}{\sum }_i^N{\stackrel{\rightharpoonup }{p}}_i\cdot {\stackrel{\rightharpoonup }{E}}_i^{covalent}\hfill \end{array}$$ (14)

where N denotes the number of atoms in the system. Thus, atomic electrostatic forces can be derived as negative gradients of the above two potential energy terms.

When computing gradients for the covalent–dipole interaction energy, it is very important to know which quantities are the variables of the virtual displacement of atom i. There are two types of variables: (1) pairwise distances between atom i and all other atoms and (2) covalent dipoles on atom i and covalent dipoles on atoms covalently interacting with atom i. Given this classification of variables, we can group the terms in Eq. (13) into four different parts and discuss their gradients with respect to ${\stackrel{\rightharpoonup }{R}}_i$, separately.

The detailed derivations are presented in Subsection 2 of the Appendix, and the final force expression for the covalent–dipole interaction energy is

$$\begin{array}{ccc}\hfill {\stackrel{\rightharpoonup }{F}}_i^{covalent--covalent}& =\hfill & -{\sum }_j^N{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_j\right)\cdot {\sum }_{k\ne j}^N{\nabla }_j\left(q_k+{\stackrel{\rightharpoonup }{u}}_k\cdot {\nabla }_k\right)\frac{\text{erf}\left({\beta }_{jk}{R}_{jk}\right)}{R_{jk}}\hfill \\ \hfill & \hfill & -\left(q_i+{\stackrel{\rightharpoonup }{u}}_i\cdot {\nabla }_i\right){\sum }_{j\ne i}^N\left(q_j+{\stackrel{\rightharpoonup }{u}}_j\cdot {\nabla }_j\right){\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}},\hfill \\ \hfill & \hfill & \hfill \end{array}$$ (15)

where N denotes the number of atoms in the system. Briefly, the first term is from the derivatives over the covalent dipoles, and the second term is from derivatives over the pairwise distances.

The derivation of forces for the induced energy in Eq. (14) is not that straightforward. We first need to express the induced dipole, ${\stackrel{\rightharpoonup }{p}}_i$, in terms of fields from covalent dipoles only, not as their definition in Eq. (10). This is because ${\stackrel{\rightharpoonup }{p}}_i$ appears on both sides of Eq. (10), i.e., the induced dipoles mutually influence each other, so it is difficult to take their derivatives. Instead, we proceed by expressing ${\stackrel{\rightharpoonup }{p}}_i$, as shown in Subsection 2 of the Appendix, as

$$p_i^s={A^{-1}}_{ij}^{st}{E}_j^{covalent,t},$$ (16)

where ${A^{-1}}_{ij}^{st}$ is an 3N × 3N matrix, which we do not know the expression of, and s, t and i, j are coordinate component indices and atom indices, respectively. Next, Eq. (14) can be rewritten as

$$U=-\frac{1}{2}{A^{-1}}_{jk}^{st}{E}_j^{covalent,s}{E}_k^{covalent,t},$$ (17)

where Einstein’s index notation is employed for j, k, s, and t so that a repeated index implies a summation over all possible values of the index, i.e., Eq. (17) is a quadruple summation. Even if we do not know the expression of matrix $A^{-1}$, we can still obtain its gradient with respect to ${\stackrel{\rightharpoonup }{R}}_k$, or the virtual displacement of atom k,

$$\frac{\partial {A^{-1}}_{ij}^{st}}{\partial x_k^w}=-{A^{-1}}_{i{i}^{\prime }}^{s{s}^{\prime }}\frac{\partial T_{i^{\prime }{j}^{\prime }}^{s^{\prime }{t}^{\prime }}}{\partial x_k^w}{A^{-1}}_{j^{\prime }j}^{t^{\prime }t},$$ (18)

where w refers to coordinate indices (x¹, x², x³), all primed indices follow Einstein’s index notation, and T is the dipole–dipole interaction tensor.

Given the above preparations, the induced part of the force can be obtained as

$$\begin{array}{ll}\hfill {\stackrel{\rightharpoonup }{F}}_i^{induced}& =-{\stackrel{\rightharpoonup }{p}}_i\cdot {\nabla }_i{\sum }_{j\ne i}^N\left({\stackrel{\rightharpoonup }{p}}_j\cdot {\nabla }_j\right){\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}\hfill \\ \hfill & +{\sum }_j^N{\nabla }_i\left({\stackrel{\rightharpoonup }{E}}_j^{covalent}\right)\cdot {\stackrel{\rightharpoonup }{p}}_j,\hfill \end{array}$$ (19)

where N denotes the number of atoms in the system. Details are presented in Subsection 2 of the Appendix. Briefly, the first term is obtained from the derivative of matrix A⁻¹, and the second term is calculated as the derivative of the covalent field ${\stackrel{\rightharpoonup }{E}}_j^{covalent}$ as follows:

$${\nabla }_i\left({\stackrel{\rightharpoonup }{E}}_j^{covalent}\right)=\left\{\begin{array}{cc}-{\sum }_{k\ne j}^n{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_k\right)\cdot {\nabla }_k{\nabla }_j\frac{\text{erf}\left({\beta }_{jk}{R}_{jk}\right)}{{\beta }_{jk}{R}_{jk}}-\left(q_i+{\stackrel{\rightharpoonup }{u}}_i\cdot {\nabla }_i\right){\nabla }_i{\nabla }_j\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{{\beta }_{ij}{R}_{ij}}\hfill & ifj\ne i\hfill \\ -{\sum }_{k\ne i}^n{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_k\right)\cdot {\nabla }_k{\nabla }_i\frac{\text{erf}\left({\beta }_{ik}{R}_{ik}\right)}{{\beta }_{ik}{R}_{ik}}-{\sum }_{k\ne i}^N\left(q_k+{\stackrel{\rightharpoonup }{u}}_k\cdot {\nabla }_k\right){\nabla }_i{\nabla }_i\frac{\text{erf}\left({\beta }_{ik}{R}_{ik}\right)}{{\beta }_{ik}{R}_{ik}}\hfill & ifj=i,\hfill \end{array}\right.$$ (20)

where n denotes all atoms that are covalently (including virtually) bonded with atom i and atom i itself.

In practice, force calculations must be combined with an Ewald summation or particle mesh Ewald (PME) technique to handle long-range under periodic boundary conditions. This is to be discussed in detail in Sec. II E.

D. Ewald summation and PME in pGM

The Ewald summation was introduced to compute the electrostatic energy of an infinite lattice under periodic boundary conditions.⁴⁶ The basic idea is to put a mask Gaussian charge distribution on the real charge on each atom. Then, a direct-space pairwise summation is conducted to compute the electric field due to real charges masked by the Gaussian charges. This step can be executed with a reasonably short cutoff distance due to the very fast decay after applying the mask Gaussian charges. Next, the field generated by the mask Gaussians can be computed efficiently by a reciprocal-space summation to bring back the original electric field due to the real charges. Finally, a correction step is used to remove interactions not needed in the original electrostatic model. Similar to its use in point charge/dipole models, a mask Gaussian distribution is also used on each moment of each atom in the pGM model,

$$\begin{array}{ccc}\hfill {\rho }_i^{mask}\left(\stackrel{\rightharpoonup }{r};{\stackrel{\rightharpoonup }{R}}_i\right)& =\hfill & q_i{\left(\frac{{{\beta }_0}^2}{\pi }\right)}^{\frac{3}{2}}\exp \left(-{{\beta }_0}^2{\left|\stackrel{\rightharpoonup }{r}-{\stackrel{\rightharpoonup }{R}}_i\right|}^2\right)\hfill \\ \hfill & \hfill & +\left({\stackrel{\rightharpoonup }{\mu }}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\nabla }_{R_i}{\left(\frac{{{\beta }_0}^2}{\pi }\right)}^{\frac{3}{2}}\exp \left(-{{\beta }_0}^2{\left|\stackrel{\rightharpoonup }{r}-{\stackrel{\rightharpoonup }{R}}_i\right|}^2\right),\hfill \end{array}$$ (21)

where β₀ is an adjustable parameter usually in the range of about $\frac{1}{5}\sim \frac{1}{2}$ Å⁻¹, universal for all atoms.

1. Direct summation

Given that the mask distribution is also a Gaussian function, it is straightforward to compute the electrostatic potential, field, and the gradient of the field of a masked pGM charge distribution as follows:

$${\varphi }_i={\sum }_{j\ne i}^N\left[q_j+\left({\stackrel{\rightharpoonup }{\mu }}_j+{\stackrel{\rightharpoonup }{p}}_j\right)\cdot {\nabla }_j\right]\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}},$$ (22)

$${\stackrel{\rightharpoonup }{E}}_i=-{\sum }_{j\ne i}^N\left[q_j+\left({\stackrel{\rightharpoonup }{\mu }}_j+{\stackrel{\rightharpoonup }{p}}_j\right)\cdot {\nabla }_j\right]{\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}},$$ (23)

$${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{E}}}_i=-{\sum }_{j\ne i}^N\left[q_j+\left({\stackrel{\rightharpoonup }{\mu }}_j+{\stackrel{\rightharpoonup }{p}}_j\right)\cdot {\nabla }_j\right]{\nabla }_i{\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)-\text{erf}\left({\beta }_0{R}_{ij}\right)}{R_{ij}}.$$ (24)

For the current pGM model, no higher-order field is needed. Here, N represents all the atoms including those in the periodic boxes, but their influence would decay to zero very quickly due to the masking effect.

Another point worth pointing out is that the real field of the mask Gaussian multipoles is used, i.e., β₀ is used instead of ${\beta }_{i0}=\frac{{\beta }_i{\beta }_0}{\sqrt{{{\beta }_i}^2+{{\beta }_0}^2}}$ in the above expressions. The mixed use is not an issue because mask multipoles do not really exist; their role is just a mathematical treatment in the Ewald summation as long as the effect is exactly canceled out in the later step.

2. Reciprocal summation

The reciprocal summation of the pGM model follows the same procedure as a traditional point polarizable model.⁴³ Thus, the electrostatic potential, field, and gradient of the field can be shown as

$${\varphi }_i=\frac{1}{\pi V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{{\beta }_0}^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)S\left(\stackrel{\rightharpoonup }{m}\right),$$ (25)

$${\stackrel{\rightharpoonup }{E}}_i=\frac{2i}{V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\stackrel{\rightharpoonup }{m}\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{{\beta }_0}^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)S\left(\stackrel{\rightharpoonup }{m}\right),$$ (26)

$${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{E}}}_i=-\frac{4\pi }{V}{\sum }_{\stackrel{\rightharpoonup }{m}\ne 0}\stackrel{\rightharpoonup }{m}\stackrel{\rightharpoonup }{m}\frac{\exp \left(-\frac{{\pi }^2{\stackrel{\rightharpoonup }{m}}^2}{{{\beta }_0}^2}\right)}{{\stackrel{\rightharpoonup }{m}}^2}\exp \left(-2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_i\right)S\left(\stackrel{\rightharpoonup }{m}\right),$$ (27)

where the i’s that are not subscripts but the imaginary units, V is the volume of the unit cell, and $\stackrel{\rightharpoonup }{m}$ is the reciprocal space vector. $S\left(\stackrel{\rightharpoonup }{m}\right)$ is the structure factor,

$$\begin{array}{cc}\hfill S\left(\stackrel{\rightharpoonup }{m}\right)& ={\sum }_{j=1}^N{\tilde{L}}_j\left(\stackrel{\rightharpoonup }{m}\right)\exp \left(2\pi i\stackrel{\rightharpoonup }{m}\cdot {\stackrel{\rightharpoonup }{R}}_j\right),\hfill \\ \hfill {\tilde{L}}_j\left(\stackrel{\rightharpoonup }{m}\right)& =q_j+2\pi i\left({\stackrel{\rightharpoonup }{\mu }}_j+{\stackrel{\rightharpoonup }{p}}_j\right)\cdot \stackrel{\rightharpoonup }{m}.\hfill \end{array}$$ (28)

Here, N is the number of atoms in the primary simulation box only.

3. Correction

The PME correction term is used to handle various specific situations in a force field. For example, most force fields have masked bonded (1–2 and 1–3) atom pairs, which result in no electrostatic interactions between these pairwise atoms. Thus, the interactions among these masked pairs must be removed. However, in the current pGM model, we do not have any masked pairs, so there is no need for such correction.

Another correction that needs paying attention to is the self-interaction correction. This is the only correction in the pGM model. The self-potential, self-field, and gradient of the self-field can be shown as^42,43

$${\varphi }_i=\frac{2q_i{\beta }_0}{\sqrt{\pi }},$$ (29)

$${\stackrel{\rightharpoonup }{E}}_i=-\frac{4\left({\stackrel{\rightharpoonup }{\mu }}_i+{\stackrel{\rightharpoonup }{p}}_i\right){{\beta }_0}^3}{3\sqrt{\pi }},$$ (30)

$${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{E}}}_i=\frac{4q_i{{\beta }_0}^3}{3\sqrt{\pi }}\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{I}}.$$ (31)

These terms need to be properly subtracted to obtain the correct potential, field, and field gradient, respectively

In summary, the similarity between the Ewald summation in the pGM model and that in the polarizable point charge/dipole model shows that the PME molecular dynamics (MD) engine for the point charge/dipole model can be easily transplanted over for pGM applications with little revision. There are excellent literature studies discussing the details of PME for polarizable point dipole models and can be safely omitted in this work.^42,43

E. Computing forces with the Ewald summation and PME

As pointed out at the end of Sec. II C, analytical force expressions [Eqs. (15) and (19)] cannot be used directly in typical MD simulations since all summations are over infinite numbers of atoms with periodic boundary conditions. They must be combined with an Ewald summation or a PME technique to facilitate solvated-phase simulations. To bypass the infinite summations, the force expressions are reformulated in terms of fields and its derivatives, which are also the quantities that an Ewald or PME procedure would return. The key to express Eqs. (15) and (19) with fields and gradients of fields is to consider the following quantities together:

$$\begin{array}{cc}\hfill {\stackrel{\rightharpoonup }{E}}_i^{covalent}=& -{\sum }_{j\ne i}^N\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right){\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}},\hfill \\ \hfill {\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{E}}}_i^{covalent}=& -{\sum }_{j\ne i}^N\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right){\nabla }_i{\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}},\hfill \\ \hfill {\stackrel{\rightharpoonup }{E}}_i^{induced}=& -{\sum }_{j\ne i}^N{\stackrel{\rightharpoonup }{p}}_j\cdot {\nabla }_j{\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}},\hfill \\ \hfill {\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{E}}}_i^{induced}=& -{\sum }_{j\ne i}^N{\stackrel{\rightharpoonup }{p}}_j\cdot {\nabla }_j{\nabla }_i{\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}},\hfill \end{array}$$ (32)

where N denotes all atoms in the system, including those of the periodic boxes. Thus, these are all infinite summations.

A key step is in the computation of ${\stackrel{\rightharpoonup }{F}}_{induced}^i$, where term ${\sum }_j^N{\nabla }_i\left({\stackrel{\rightharpoonup }{E}}_j^{covalent}\right)\cdot {\stackrel{\rightharpoonup }{p}}_j$ also has to be reformulated accordingly. Given that Eq. (20) for ${\nabla }_i\left({\stackrel{\rightharpoonup }{E}}_j^{covalent}\right)$ lists two separate terms for j = i and j ≠ i, we can rewrite ${\sum }_j^N{\nabla }_i\left({\stackrel{\rightharpoonup }{E}}_j^{covalent}\right)\cdot {\stackrel{\rightharpoonup }{p}}_j$ as follows:

$$\begin{array}{ccc}\hfill & \hfill & {\sum }_j^N{\nabla }_i\left({\stackrel{\rightharpoonup }{E}}_j^{covalent}\right)\cdot {\stackrel{\rightharpoonup }{p}}_j\hfill \\ \hfill & \hfill & ={\sum }_{j\ne i}^N{\sum }_{k\ne j}^n\left(-{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_k\right)\right)\cdot {\nabla }_k\left({\stackrel{\rightharpoonup }{p}}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{jk}{R}_{jk}\right)}{{\beta }_{jk}{R}_{jk}}\hfill \\ \hfill & \hfill & -{\sum }_{j\ne i}^N\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right){\nabla }_i\left({\stackrel{\rightharpoonup }{p}}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{{\beta }_{ij}{R}_{ij}}\hfill \\ \hfill & \hfill & -{\sum }_{k\ne i}^n{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_k\right)\cdot {\nabla }_k\left({\stackrel{\rightharpoonup }{p}}_i\cdot {\nabla }_i\right)\frac{\text{erf}\left({\beta }_{ik}{R}_{ik}\right)}{{\beta }_{ik}{R}_{ik}}\hfill \\ \hfill & \hfill & -{\sum }_{k\ne i}^N\left(q_k+{\stackrel{\rightharpoonup }{\mu }}_k\cdot {\nabla }_k\right){\nabla }_i\left({\stackrel{\rightharpoonup }{p}}_i\cdot {\nabla }_i\right)\frac{\text{erf}\left({\beta }_{ik}{R}_{ik}\right)}{{\beta }_{ik}{R}_{ik}},\hfill \end{array}$$ (33)

where both j = i and j ≠ i terms in Eq. (20) are needed due to the outermost summation over j. Combining the first and third terms of Eq. (33) gives

$$\begin{array}{ccc}\hfill & \hfill & {\sum }_j^N{\sum }_{k\ne j}^n\left(-{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_k\right)\right)\cdot {\nabla }_k\left({\stackrel{\rightharpoonup }{p}}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{jk}{R}_{jk}\right)}{{\beta }_{jk}{R}_{jk}}\hfill \\ \hfill & \hfill & -{\sum }_{j\ne i}^N\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right){\nabla }_i\left({\stackrel{\rightharpoonup }{p}}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{{\beta }_{ij}{R}_{ij}}\hfill \\ \hfill & \hfill & -{\sum }_{k\ne i}^N\left(q_k+{\stackrel{\rightharpoonup }{\mu }}_k\cdot {\nabla }_k\right){\nabla }_i\left({\stackrel{\rightharpoonup }{p}}_i\cdot {\nabla }_i\right)\frac{\text{erf}\left({\beta }_{ik}{R}_{ik}\right)}{{\beta }_{ik}{R}_{ik}}.\hfill \end{array}$$ (34)

Exchanging the summation order for the first term leads to

$$\begin{array}{ccc}\hfill & \hfill & {\sum }_k^n{\sum }_{j\ne k}^N\left(-{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_k\right)\right)\cdot {\nabla }_k\left({\stackrel{\rightharpoonup }{p}}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{jk}{R}_{jk}\right)}{{\beta }_{jk}{R}_{jk}}\hfill \\ \hfill & \hfill & -{\sum }_{j\ne i}^N\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right){\nabla }_i\left({\stackrel{\rightharpoonup }{p}}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{{\beta }_{ij}{R}_{ij}}\hfill \\ \hfill & \hfill & -{\sum }_{k\ne i}^N\left(q_k+{\stackrel{\rightharpoonup }{\mu }}_k\cdot {\nabla }_k\right){\nabla }_i\left({\stackrel{\rightharpoonup }{p}}_i\cdot {\nabla }_i\right)\frac{\text{erf}\left({\beta }_{ik}{R}_{ik}\right)}{{\beta }_{ik}{R}_{ik}}.\hfill \end{array}$$ (35)

Substitution of the expressions of electric fields and derivatives in Eq. (32) gives

$$\begin{array}{ll}\hfill \sum _j^N{\nabla }_i\left({\stackrel{\rightharpoonup }{E}}_j^{covalent}\right)\cdot {\stackrel{\rightharpoonup }{p}}_j& ={\sum }_k^n{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_k\right)\cdot {\stackrel{\rightharpoonup }{E}}_k^{induced}+q_i{\stackrel{\rightharpoonup }{E}}_i^{induced}\hfill \\ \hfill & +{\stackrel{\rightharpoonup }{u}}_i\cdot {\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{E}}}_i^{induced}+{\stackrel{\rightharpoonup }{p}}_i\cdot {\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{E}}}_i^{covalent}.\hfill \end{array}$$ (36)

Here, n are those atoms that covalently interact with atom i.

Given the above preparations, Eqs. (15) and (19) can finally be expressed as follows after the substitution of Eqs. (32) and (36):

$$\begin{array}{ccc}\hfill {\stackrel{\rightharpoonup }{F}}_i^{covalent--covalent}& =\hfill & {\sum }_j^n{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_j\right)\cdot {\stackrel{\rightharpoonup }{E}}_j^{covalent}+q_i{\stackrel{\rightharpoonup }{E}}_i^{covalent}+{\stackrel{\rightharpoonup }{u}}_i\cdot {\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{E}}}_i^{covalent},\hfill \\ \hfill & \hfill & \hfill \end{array}$$ (37)

$$\begin{array}{ccc}\hfill {\stackrel{\rightharpoonup }{F}}_i^{induced}& =\hfill & {\sum }_j^n{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_j\right)\cdot {\stackrel{\rightharpoonup }{E}}_j^{induced}+q_i{\stackrel{\rightharpoonup }{E}}_i^{induced}+{\stackrel{\rightharpoonup }{p}}_i\cdot {\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{E}}}_i^{induced}\hfill \\ \hfill & \hfill & +{\stackrel{\rightharpoonup }{u}}_i\cdot {\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{E}}}_i^{induced}+{\stackrel{\rightharpoonup }{p}}_i\cdot {\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{E}}}_i^{covalent}.\hfill \end{array}$$ (38)

Adding these two terms together, the final force expression is obtained as

$${\stackrel{\rightharpoonup }{F}}_i={\sum }_j^n{\nabla }_i\left({\stackrel{\rightharpoonup }{u}}_j\right)\cdot {\stackrel{\rightharpoonup }{E}}_j+q_i{\stackrel{\rightharpoonup }{E}}_i+\left({\stackrel{\rightharpoonup }{u}}_i+{\stackrel{\rightharpoonup }{p}}_i\right)\cdot {\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{E}}}_i.$$ (39)

Equation (39) shows that a key step in this algorithm is to accumulate the atomic electric potential and its first and second derivatives from various components, including both reciprocal and direct summations.

III. RESULTS AND DISCUSSION

A. Validation of analytical electrostatic force expression

To validate the pGM force expressions, e.g., Eq. (15) or (19), we constructed a small toy system of two water molecules in free space. The detailed water pGM parameters are listed in Table I. These parameters were derived with an iterative Restrained ESP (RESP) procedure for the pGM model with quantum mechanical ESP data from a B3LYP/aug-cc-pVTZ calculation of the water dimer.

TABLE I.

Two water molecules in free space. The permanent dipole moments are expressed in the CBV frame according to Fig. 1. The moments in the CBV frame can be obtained via a least square fitting procedure from either the ESP data or the permanent dipole moments in the lab frame.

Tested atoms	Water-1 O	Water-1 H1	Water-1 H2	Water-2 O	Water-2 H1	Water-2 H2
Charge (e)	−1.797 045 4	0.898 522 70	0.898 522 70	−1.797 045 4	0.898 522 70	0.898 522 70
Covalent dipole moment (e Å)	−0.371 441 54	0.151 706 58	0.151 706 58	−0.371 441 54	0.151 706 58	0.151 706 58
	−0.371 441 54	−0.022 490 434	−0.022 490 434	−0.371 441 54	−0.022 490 434	−0.022 490 434
Polarizability (Å3)	1.448 980 10	0.427 350 00	0.427 350 00	1.448 980 10	0.427 350 00	0.427 350 00
Gaussian radius (Å)	0.806 624 90	0.714 759 70	0.714 759 70	0.806 624 90	0.714 759 70	0.714 759 70
Coordinates (Å)	−1.387 669	−1.734 110	−1.756 164	1.514 536	1.919 419	0.555 921
	−0.006 775	0.790 147	−0.740 122	0.007 522	−0.047 517	−0.008 485
	0.110 728	−0.310 036	−0.397 708	−0.121 554	0.751 251	0.043 101

Two methods were used to calculate the atomic forces. The first method is to use the force expressions to calculate forces analytically. The second method is to calculate forces numerically via the finite-difference method based on the fact that each force is the negative gradient of potential energy. Here, the potential energy was computed with Eqs. (13) and (14). The finite-difference coordinate displacement was set to be 1 × 10⁻⁶ Å, and the induced dipole accuracy was set to 1 × 10⁻⁹. The two sets of atomic forces are listed in Table II. It is clear that the differences between the two sets of atomic forces appear only on the ninth digit after the decimal point.

TABLE II.

Atomic forces (e²/Ų) computed via the analytical expression and the finite difference procedure and their differences.

Tested atoms	Water-1 O	Water-1 H1	Water-1 H2	Water-2 O	Water-2 H1	Water-2 H2
Analytical forces	(0.096 951 679,	(−0.049 846 750,	(−0.042 834 464,	(0.055 862 413,	(−0.248 587 088,	(0.188 454 211,
	−0.008 409 817,	−0.237 351 651,	0.245 826 708,	0.009 291 242,	0.001 371 87,	−0.010 728 352,
	0.124 608 301)	−0.076 271 576)	−0.048 683 253)	−0.136 952 953)	−0.041 030 761)	0.178 330 242)
Finite-difference forces	(0.096 951 679,	(−0.049 846 749,	(−0.042 834 464,	(0.055 862 412,	(−0.248 587 086,	(0.188 454 212,
	−0.008 409 817,	−0.237 351 652,	0.245 826 707,	0.009 291 241,	0.001 371 87,	−0.010 728 352,
	0.124 608 301)	−0.076 271 576)	−0.048 683 253)	−0.136 952 954)	−0.041 030 761)	0.178 330 242)
Deviations	(−0.3 × 10−9,	(0.6 × 10−9,	(0.02 × 10−9,	(−1.4 × 10−9,	(2.0 × 10−9,	(0.8 × 10−9,
	−0.3 × 10−9,	−1.1 × 10−9,	−1.0 × 10−9,	−0.9 × 10−9,	1.1 × 10−9,	0.2 × 10−10,
	0.5 × 10−9)	0.2 × 10−9)	−0.4 × 10−9)	−0.9 × 10−9)	−0.1 × 10−10)	−0.3 × 10−9)

There is also an indirect way to confirm the correctness of the force expression, which is to utilize the fact that the total force of the system should always be zero in any direction. If we add up all atomic forces, the system net force (in e²/Ų) is 1 × 10⁻⁹, 2 × 10⁻¹⁷, and 3 × 10⁻¹⁷, for x, y, and z directions, respectively. The overall error here is consistent with the induction tolerance used in the testing, 1 × 10⁻⁹.

B. Accuracy of pGM electrostatic energy and forces in PME

To achieve aqueous-phase simulations, an Ewald summation or PME technique is essential for any electrostatic model. Although there are various publications discussing the accuracy of PME,^42,43,47,48 we have to acknowledge the fact that the pGM model has a higher accuracy requirement than classical point-charge force fields due to the presence of dipoles. In general, higher moments would require higher PME accuracy. This can be appreciated from the perspective of two considerations. First, the interaction energy between two dipoles decays faster with distance (1/r³) than that between two charges (1/r). Second, the second derivatives of the potential are needed to compute forces on dipoles [Eq. (39)], whereas only first derivatives, e.g., electric fields, are needed to compute forces on charges. Due to these differences, we have to carefully examine the accuracy requirement of PME methods used in our model.

To test the accuracy, we only look at the most difficult pairwise interactions so that the errors reported below are the maximum errors in the tested water system. For the reciprocal part, we focus on the electrostatic field between the bonded O atom and H atoms whose interactions are the strongest and thus the most difficult in PME. For the direct summation part, we focus on the electrostatic field between two H atoms. Because they have the smallest Gaussian radii, their interactions converge slowly in the direct summation. Thus, to guarantee a given accuracy level for forces in the pGM model, we need to consider both PME components.

In the following analysis, we set the grid spacing to 1 Å for PME as in most biomolecular simulations and varied other parameters to see how accuracy changes in both the reciprocal and the direct summation components. Because our model contains both charges and dipoles, we analyzed their field separately to assess the impact of different setups on their accuracy of the electric field. The test results are shown in Tables III–V.

TABLE III.

Errors of reciprocal potentials and derivatives generated by the dipole of the water-1 H¹ atom on the water-1 O atom at different PME setups. The analytical values [Eqs. (25)–(28)] were calculated using MATLAB. The interpolation order refers to the rank of the B-spline interpolation method used in PME (see Ref. 48 for details).

Interpolation order		5	6	7	8	9
Ewald coefficient β0 = 0.3 Å−1	Potential	8.2 × 10−5	2.8 × 10−5	1.5 × 10−7	3.4 × 10−6	2.7 × 10−6
	First derivative	3.0 × 10−4	6.4 × 10−5	9.2 × 10−6	7.6 × 10−6	3.9 × 10−6
	Second derivative	1.3 × 10−3	3.9 × 10−4	4.6 × 10−5	1.6 × 10−5	5.7 × 10−6
Ewald coefficient β0 = 0.4 Å−1	Potential	1.2 × 10−4	4.0 × 10−5	4.3 × 10−6	3.5 × 10−8	5.4 × 10−6
	First derivative	1.3 × 10−3	4.6 × 10−4	1.5 × 10−4	6.5 × 10−5	2.5 × 10−5
	Second derivative	2.6 × 10−3	1.6 × 10−3	4.0 × 10−4	1.9 × 10−4	8.1 × 10−5
Ewald coefficient β0 = 0.5 Å−1	Potential	2.6 × 10−4	1.1 × 10−4	1.7 × 10−4	6.1 × 10−5	9.1 × 10−5
	First derivative	5.1 × 10−3	2.5 × 10−3	1.2 × 10−3	7.2 × 10−4	4.0 × 10−4
	Second derivative	8.8 × 10−3	5.5 × 10−3	2.4 × 10−3	1.3 × 10−3	8.8 × 10−4

TABLE IV.

Errors of reciprocal potentials and derivatives generated by the charge of the water-1 H¹ atom on the water-1 O atom at different PME setups. The analytical values [Eqs. (25)–(28)] were calculated using MATLAB. The interpolation order refers to the rank of the B-spline interpolation method used in PME (see Ref. 48 for details).

Interpolation order		5	6	7	8	9
Ewald coefficient β0 = 0.3 Å−1	Potential	1.4 × 10−6	3.7 × 10−8	6.5 × 10−8	1.4 × 10−8	5.3 × 10−9
	First derivative	1.8 × 10−4	3.8 × 10−5	5.5 × 10−6	1.1 × 10−6	3.4 × 10−7
	Second derivative	7.7 × 10−4	2.1 × 10−4	3.0 × 10−5	7.8 × 10−6	1.8 × 10−6
Ewald coefficient β0 = 0.4 Å−1	Potential	1.4 × 10−5	3.7 × 10−6	1.6 × 10−6	6.8 × 10−7	3.2 × 10−7
	First derivative	7.4 × 10−4	1.1 × 10−4	6.1 × 10−5	2.1 × 10−5	1.0 × 10−5
	Second derivative	2.5 × 10−3	7.7 × 10−4	2.1 × 10−4	7.5 × 10−5	3.0 × 10−5
Ewald coefficient β0 = 0.5 Å−1	Potential	8.1 × 10−5	3.9 × 10−5	1.9 × 10−5	1.2 × 10−5	7.0 × 10−6
	First derivative	2.5 × 10−3	7.8 × 10−4	4.5 × 10−4	2.6 × 10−4	1.5 × 10−4
	Second derivative	6.7 × 10−3	2.6 × 10−3	1.1 × 10−3	6.3 × 10−4	3.4 × 10−4

TABLE V.

Errors of direct summation potentials for Gaussian potentials between two H atoms at different PME setups. These values are the difference between two error functions, erf(βR_c) − erf(β₀R_c). Here, R_c is the direct summation cutoff distance, and $\beta =1/\left(0.7147597\cdot \sqrt{2}\right){\text{Å}}^{-1}$ for the H atom pairs.

Cutoff distance (Å)	7	8	9	10	11
β0 = 0.3 Å−1	3.0 × 10−3	6.9 × 10−4	1.3 × 10−4	2.2 × 10−5	3.1 × 10−6
β0 = 0.4 Å−1	7.5 × 10−5	6.0 × 10−6	3.6 × 10−7	1.5 × 10−8	4.9 × 10−10
β0 = 0.5 Å−1	7.4 × 10−7	1.5 × 10−8	2.0 × 10−10	1.5 × 10−12	7.3 × 10−15

It is clear from the above analyses that the pGM model demands a higher accuracy level than classical point-charge models. This is as expected for any electrostatic model with dipoles or higher moments. For the reciprocal part, the field generated by dipoles is more difficult to handle than that of charges in PME. Comparing Tables III and IV, we can see that the errors of dipole fields are about twice larger than those of charge fields. Furthermore, Tables III and IV show that the second derivatives are the most difficult in PME. Thus, to ensure the accuracy of the reciprocal summation of PME, we need to make sure that the second derivatives reach a specified accuracy level. For example, if we use 5 × 10⁻⁵ as the accuracy threshold, which is a common choice, we have to set Ewald β₀ = 0.3 Å⁻¹ and the interpolation order 7 or higher in the PME setup (Table III). Of course, the use of smaller grid spacing would increase the accuracy but with a higher overhead in reciprocal summation. We will explore the best tradeoff in accuracy and efficiency for realistic biomolecular systems in a later publication.

Situations are similar for the direct summation part. To reach a common accuracy threshold of 5 × 10⁻⁵, if we set β₀ = 0.3 Å⁻¹ as in the reciprocal part, the direct space cutoff should be set to a relatively longer cutoff distance of 10 Å, as shown in Table V. Of course, a choice of larger β₀ (i.e., 0.35 Å⁻¹) would allow a commonly used cutoff distance of 9 Å. However, this would require a higher interpolation order to achieve the similar level of accuracy.

C. NVE simulations of the water box

Given all the accuracy considerations in Sec. III B, we performed a pure water simulation to test the energy conservation behavior in an NVE run with the PME treatment. The electrostatic parameters were derived from those in Table I and transplanted onto the TIP3P water model. We used 512 water molecules in a truncatedoctahedron box of 27.5 Å. The dimension of the particle mesh grid is 30³, so the grid spacing is a bit less than 1 Å. The PME β₀ = 0.35 Å⁻¹, the real space cutoff was set as 9 Å, and the interpolation order was 8 so that the overall PME error was less than 5 × 10⁻⁵.

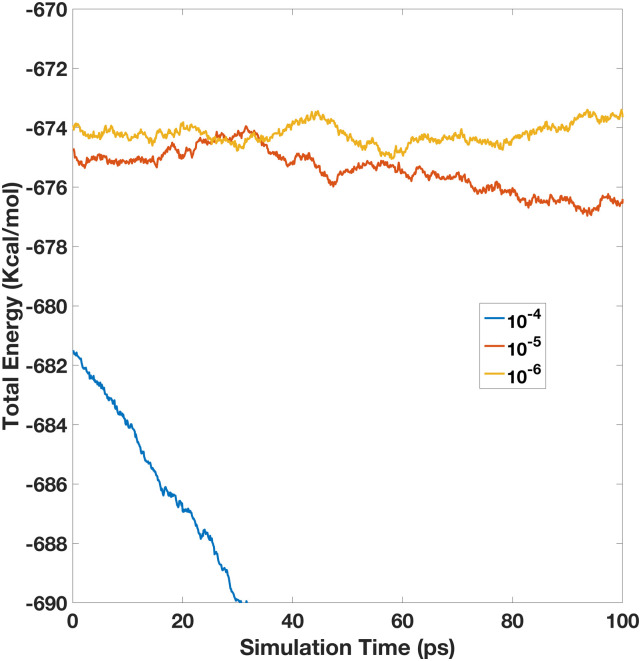
We first tested a range of induction tolerance criteria, ranging from 10⁻³ to 10⁻⁶. Our experiments show that 10⁻³ and 10⁻⁴ are clearly not sufficient for the induction iteration, leading to decreasing energy throughout the MD simulations. This is consistent with previous findings in the developments of polarizable point dipole models.⁴² Specifically, the energy in the NVE run of 10⁻³ drifts too fast so that it is already out of the plotting range at the 100th step, the very first data point. The rest of the energy plots over the simulation time are shown below in Fig. 2. The initial testing shows that the energy convergence became much better after we tighten the iteration tolerance to 10⁻⁵. Although the total energy still drifts down a little, but much slower. Finally, after we tighten it to 10⁻⁶, the total energy is basically conserved. Of course, the total energy fluctuation does exist.

FIG. 2.

Total energy vs the simulation time for the 512-water box simulation. Here, all the simulations are performed with a 5 × 10⁻⁵ PME accuracy, but with different induction iteration tolerances (1 × 10⁻⁴–1 × 10⁻⁶).

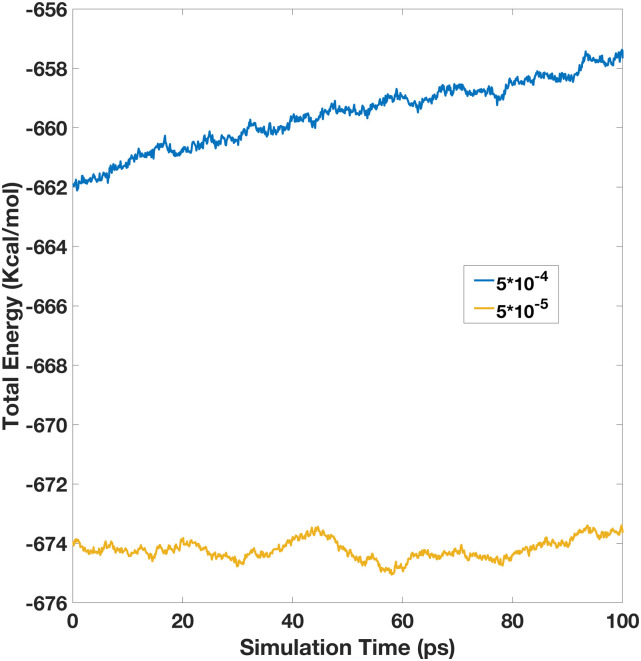
Next, we also studied the influences of the PME setup on the energy conservation. To compare with the NVE run with the high PME accuracy above, we collected a comparable NVE run with the same induction tolerance of 10⁻⁶, but with a somewhat lower PME setting. The real space cutoff was set as 8 Å, and the interpolation order was set as 6, but others remained to be the same, which leads to a lower PME accuracy of ∼5 × 10⁻⁴. The total energy is more positive because there are fewer van der Waals pairs. As shown in Fig. 3, the total energy also drifts noticeably, though it becomes more positive over time. In summary, our experiment shows that high enough accuracy in both the PME calculation and the induction iteration is necessary for a polarizable dipole model with permanent dipoles to achieve energy conservation. Furthermore, we expect that even higher accuracy is necessary if higher moments, i.e., quadrupoles, are used in future pGM developments as higher derivatives are needed from the PME calculation.

FIG. 3.

Total energy vs the simulation time for the 512-water box simulation. Here, both simulations were performed with a 1 × 10⁻⁶ induction iteration tolerance, but with different PME accuracies, low for 5 × 10⁻⁴ and high for 5 × 10⁻⁵.

IV. CONCLUSION

In this work, we proposed an efficient formulation for the polarizable Gaussian Multipole (pGM) model for biomolecular simulations. First, a local frame based on the covalent basis vectors (CBV)/tensors was used to set up the permanent (covalent) multipoles on all atoms. The CBV frame nicely allows the intrinsic molecular flexibility during simulations and facilitates an efficient expression of the electrostatic forces in the closed form. Based on the new CBV local frame, we then derived the analytical force expressions for the pGM model. Finally, we outlined how to interface the pGM electrostatics seamlessly with the PME implementation for molecular simulations under the periodic boundary conditions.

To validate the analytical force expression for the pGM model defined on the CBV frame, we studied the accuracy of the analytical atomic forces with a finite-different force analysis for a water dimer. The analysis shows a very good consistency between the analytical and numerical forces, with an error comparable to the finite difference uncertainty. In addition, total analytical and numerical forces of the water dimer are very close to zero with an error consistent with the induction iteration tolerance.

Next, we analyzed the PME setups necessary for accurate pGM energy and force calculations. It was found that the pGM model requires higher accuracy than the classical point-charge models due to the presence of dipoles. This is because the electrostatic field generated by dipoles is much more difficult to interpolate than that of charges in PME, and the error of the dipole field is about twice that of the charge field. In addition, the second derivative of the potential is needed, which is the more difficult to compute accurately in PME to ensure accurate pGM forces.

To validate the overall electrostatic framework for the reformulated pGM model, we conducted an NVE simulation for a small water box of 512 water molecules. Our results show that to achieve energy conservation, it is important to ensure enough accuracy on both PME and induced dipoles. With a 5 × 10⁻⁵ accuracy on PME and a 1 × 10⁻⁶ tolerance for the induced dipoles, the tested NVE water simulation in the pGM model was shown to conserve energy reasonably well. Future development will be necessary to improve the efficiency of the pGM model in both the PME setup and induction iteration to bring out the potential of the pGM model.

DATA AVAILABILITY

The algorithms developed in this study and the validation data are deposited in the Amber repository and will be made publicly available in the next Amber/AmberTools release at http://ambermd.org/.

APPENDIX: BOYS SERIAL AND DERIVATION OF ANALYTICAL PGM FORCES

1. Tensor format of Boys serial

In this study, Boys functions up to rank 3 were used and are listed below as reference. Higher ranked tensors and Boys functions can be found in the literature.^44,49

Boys functions up to rank 3 are

$$B_0\left(x\right)=\frac{\text{erf}\left(x\right)}{x},$$

$$B_1\left(x\right)=\frac{\text{erf}\left(x\right)}{x^3}-\frac{2}{\sqrt{\pi }}{e}^{-x^2}\frac{1}{x^2},$$

$$B_2\left(x\right)=\frac{3\text{erf}\left(x\right)}{x^5}-\frac{2}{\sqrt{\pi }}{e}^{-x^2}\frac{1}{x^4}\left(3+2x^2\right),$$

$$B_3\left(x\right)=\frac{15\text{erf}\left(x\right)}{x^7}-\frac{2}{\sqrt{\pi }}{e}^{-x^2}\frac{1}{x^6}\left(15+10x^2+4x^4\right).$$

The associated tensors are

$$\nabla \frac{\text{erf}\left(\beta R\right)}{R}=-\stackrel{\rightharpoonup }{R}{\beta }^3{B}_1\left(\beta R\right),$$

$$\nabla \nabla \frac{\text{erf}\left(\beta R\right)}{R}={\widehat{x}}_p{\widehat{x}}_q\left(R_p{R}_q{\beta }^5{B}_2\left(\beta R\right)-{\delta }_{pq}{\beta }^3{B}_1\left(\beta R\right)\right),$$

$$\begin{array}{ll}\hfill \nabla \nabla \nabla \frac{\text{erf}\left(\beta R\right)}{R}& ={\widehat{x}}_p{\widehat{x}}_q{\widehat{x}}_r\left(\left({\delta }_{pq}{R}_r+{\delta }_{pr}{R}_q+{\delta }_{rq}{R}_p\right){\beta }^5{B}_2\left(\beta R\right)\right.\hfill \\ \hfill & \left.-R_p{R}_q{R}_r{\beta }^7{B}_3\left(\beta R\right)\right).\hfill \end{array}$$

2. Force derivation

We proceed in two steps: covalent–covalent interactions and induced interactions, as shown in Sec. II C. First, we consider interaction energies due to covalent multipoles interacting with covalent multipoles.

The system can be split into two groups of atoms, bonded atoms and nonbonded atoms. The bonded group has those atoms bonded to the atom to be considered (including itself), and the nonbonded group has the rest. In the bonded group, the atoms can be further split into two subgroups: the atom that is currently under consideration, termed as the bonded-moving atom below, and the other atoms in the bonded group are termed bonded-non-moving atoms. A total of three groups of atoms can be classified.

Thus, we can rewrite the covalent–covalent interaction energy as the following four parts.

• (1)Nonbonded atoms interacting with bonded-non-moving atoms:

$$U=\sum _i^{bonded-non-moving}\sum _j^{nonbonded}\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right)\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}.$$

• (2)Nonbonded atoms interacting with bonded-moving atom i:

$$U=\sum _j^{nonbonded}\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right)\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}.$$

• (3)Bonded-non-moving atoms interacting with bonded-non-moving atoms:

$$\begin{array}{ll}\hfill U& =\frac{1}{2}\sum _i^{bonded-non-moving}\sum _{j\ne i}^{bonded-non-moving}\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right)\hfill \\ \hfill & \times \left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}.\hfill \end{array}$$

• (4)Bonded-non-moving atoms interacting with bonded-moving atom i:

$$U=\sum _j^{bonded-non-moving}\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right)\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}.$$

Apparently, there should be a fifth part of interaction energy, nonbonded atoms interacting with nonbonded atoms. However, this part of energy does not change in the force calculation, so we omit its expression here. Of course, atom i’s self-interaction is also ignored, as discussed in the text.

Next, force on bonded-moving atom (i) can be derived as the negative gradient of the above energy terms. When computing the gradient, it is worth pointing out that nothing varies on the nonbonded atoms, only the dipole directions vary on the bonded-non-moving atoms, and both dipole directions and positions of the bonded-moving atoms vary. The above four energy parts thus lead to the following four force components, respectively:

$${\left({\stackrel{\rightharpoonup }{F}}_i\right)}_1=-\sum _k^{bonded-non-moving}\sum _j^{nonbonded}{\nabla }_i\left({\stackrel{\rightharpoonup }{\mu }}_k\right)\cdot {\nabla }_k\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{kj}{R}_{kj}\right)}{R_{kj}},$$

$$\begin{array}{ll}\hfill {\left({\stackrel{\rightharpoonup }{F}}_i\right)}_2& =-\sum _j^{nonbonded}{\nabla }_i\left({\stackrel{\rightharpoonup }{\mu }}_i\right)\cdot {\nabla }_i\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}\hfill \\ \hfill & -\sum _j^{nonbonded}\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right)\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right){\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}},\hfill \end{array}$$

$$\begin{array}{ll}\hfill {\left({\stackrel{\rightharpoonup }{F}}_i\right)}_3& =-\sum _k^{bonded-non-moving}\sum _{j\ne k}^{bonded-non-moving}{\nabla }_i\left({\stackrel{\rightharpoonup }{\mu }}_k\right)\hfill \\ \hfill & \cdot {\nabla }_k\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{kj}{R}_{kj}\right)}{R_{kj}},\hfill \end{array}$$

$$\begin{array}{ll}\hfill {\left({\stackrel{\rightharpoonup }{F}}_i\right)}_4& =-\sum _j^{bonded-non-moving}{\nabla }_i\left({\stackrel{\rightharpoonup }{\mu }}_i\right)\cdot {\nabla }_i\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}\hfill \\ \hfill & -\sum _j^{bonded-non-moving}\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right){\nabla }_i\left({\stackrel{\rightharpoonup }{\mu }}_j\right)\cdot {\nabla }_j\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}\hfill \\ \hfill & -\sum _j^{bonded-non-moving}\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right)\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right){\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}.\hfill \end{array}$$

Summing up all four components, the final force expression is

$$\begin{array}{ll}\hfill {\stackrel{\rightharpoonup }{F}}_i& =-\sum _k^n\sum _{j\ne k}^N{\nabla }_i\left({\stackrel{\rightharpoonup }{\mu }}_k\right)\cdot {\nabla }_k\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{kj}{R}_{kj}\right)}{R_{kj}}\hfill \\ \hfill & -\sum _{j\ne i}^N\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right)\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right){\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}.\hfill \end{array}$$

Here, n and N follow the same notation as Sec. II C, the number of atoms in the bonded group and the system, respectively.

Second, we consider energies caused by the induced dipoles. As stated before, the induced energy contains three parts, induced dipoles interacting with covalent multipoles, induced dipoles interacting with induced dipoles, and induced dipole self-energy $\frac{1}{2}\stackrel{\rightharpoonup }{p}\cdot \stackrel{\rightharpoonup }{E}$. From Sec. II C, we know that the total induced energy is

$$\frac{1}{2}\sum _i^N-{\stackrel{\rightharpoonup }{p}}_i\cdot {\stackrel{\rightharpoonup }{E}}_i^0,$$

where ${\stackrel{\rightharpoonup }{E}}_i^0$ is the electric field on atom i only by covalent multipoles.

The induced dipoles are determined by the total electric field,

$${\stackrel{\rightharpoonup }{p}}_i={\alpha }_i{\stackrel{\rightharpoonup }{E}}_i={\alpha }_i\left({\stackrel{\rightharpoonup }{E}}_i^0-\sum _{j\ne i}^N{\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{T}}}_{ij}\cdot {\stackrel{\rightharpoonup }{p}}_j\right),$$

$${\stackrel{\rightharpoonup }{\stackrel{\rightharpoonup }{T}}}_{ij}={\nabla }_i{\nabla }_j\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}.$$

Changing the above expressions into the component format and applying Einstein’s index notation, we obtain

$$p_i^s={\alpha }_i\left(E_i^{0,s}-T_{ij}^{st}{p}_j^t\right),$$

where s and t are component indices. Rearrangement leads to

$$\left(\frac{1}{{\alpha }_j}{\delta }_{ij}^{st}+T_{ij}^{st}\right)p_j^t=A_{ij}^{st}{p}_j^t=E_i^{0,s}.$$

If we assume that $A_{ij}^{st}$ is inversible and its inverse matrix is ${A^{-1}}_{ij}^{st}$, we have

$$p_i^s={A^{-1}}_{ij}^{st}{E}_j^{0,t},$$

where ${A^{-1}}_{ij}^{st}$ is a 3N × 3N matrix, symmetrical for both atom index and component index,

$${A^{-1}}_{ij}^{st}={A^{-1}}_{ij}^{ts}={A^{-1}}_{ji}^{st}.$$

The gradient of A⁻¹ is

$$\frac{\partial {A^{-1}}_{ij}^{st}}{\partial x_k^w}=-{A^{-1}}_{i{i}^{\prime }}^{s{s}^{\prime }}\frac{\partial A_{i^{\prime }{j}^{\prime }}^{s^{\prime }{t}^{\prime }}}{\partial x_k^w}{A^{-1}}_{i^{\prime }j}^{s^{\prime }t}=-{A^{-1}}_{i{i}^{\prime }}^{s{s}^{\prime }}\frac{\partial T_{i^{\prime }{j}^{\prime }}^{s^{\prime }{t}^{\prime }}}{\partial x_k^w}{A^{-1}}_{j^{\prime }j}^{t^{\prime }t},$$

where w refers to coordinate indices (x¹, x², x³). It is obvious that i′ or j′ has to be equal to k for T to have a nonzero value. We have

$$\frac{\partial T_{i^{\prime }{j}^{\prime }}^{s^{\prime }{t}^{\prime }}}{\partial x_k^w}=\frac{\partial T_{k{j}^{\prime }}^{s^{\prime }{t}^{\prime }}}{\partial x_k^w}+\frac{\partial T_{i^{\prime }k}^{s^{\prime }{t}^{\prime }}}{\partial x_k^w}.$$

Based on the above relations, the force expressed as the negative gradient of the induced energy is

$$\begin{array}{ccc}\hfill F_i^w& =\hfill & \frac{\partial }{\partial x_i^w}\left(\frac{1}{2}{\stackrel{\rightharpoonup }{p}}_j\cdot {\stackrel{\rightharpoonup }{E}}_j^0\right)=\frac{\partial }{\partial x_i^w}\left(\frac{1}{2}{A^{-1}}_{jk}^{st}{E}_j^{0,s}{E}_k^{0,t}\right)=\frac{1}{2}\frac{\partial {A^{-1}}_{jk}^{st}}{\partial x_i^w}{E}_j^{0,s}{E}_k^{0,t}+{A^{-1}}_{jk}^{st}{E}_j^{0,s}\frac{\partial E_k^{0,t}}{\partial x_i^w}\hfill \\ \hfill & =\hfill & -\frac{1}{2}{A^{-1}}_{j{j}^{\prime }}^{s{s}^{\prime }}\frac{\partial T_{j^{\prime }{k}^{\prime }}^{s^{\prime }{t}^{\prime }}}{\partial x_i^w}{A^{-1}}_{k^{\prime }k}^{t^{\prime }t}{E}_j^{0,s}{E}_k^{0,t}+p_k^t\frac{\partial E_k^{0,t}}{\partial x_i^w}=-\frac{1}{2}{p}_{j^{\prime }}^{s^{\prime }}\frac{\partial T_{j^{\prime }{k}^{\prime }}^{s^{\prime }{t}^{\prime }}}{\partial x_i^w}{p}_{k^{\prime }}^{t^{\prime }}+p_k^t\frac{\partial E_k^{0,t}}{\partial x_i^w}=-p_i^{s^{\prime }}\frac{\partial T_{i{k}^{\prime }}^{s^{\prime }{t}^{\prime }}}{\partial x_i^w}{p}_{k^{\prime }}^{t^{\prime }}+p_k^t\frac{\partial E_k^{0,t}}{\partial x_i^w}.\hfill \end{array}$$

Rewriting the above component format into the vector/tensor format, we have

$${\stackrel{\rightharpoonup }{F}}_i=-\sum _{j\ne i}^N{\stackrel{\rightharpoonup }{p}}_i\cdot {\nabla }_i\left({\stackrel{\rightharpoonup }{p}}_j\cdot {\nabla }_j\right){\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}+\sum _j^N{\nabla }_i\left({\stackrel{\rightharpoonup }{E}}_j^0\right)\cdot {\stackrel{\rightharpoonup }{p}}_j.$$

The next step is to evaluate ${\nabla }_i\left({\stackrel{\rightharpoonup }{E}}_j^0\right)$. Following the similar strategy used in covalent–covalent interactions, we split the system into two groups: non-moving atoms and moving atom (i.e., atom i).

When computing the derivative of the field on a non-moving atom j, it is worth pointing out that the other nonbonded non-moving atoms are not influenced by the virtual displacement of atom i, so only bonded non-moving atoms are considered below,

$$\begin{array}{ccc}\hfill {\nabla }_i\left({\stackrel{\rightharpoonup }{E}}_j^0\right)& =\hfill & {\nabla }_i\left(\sum _{k\ne j}^{bonded--non--moving}-{\nabla }_j\left(q_k+{\stackrel{\rightharpoonup }{\mu }}_k\cdot {\nabla }_k\right)\frac{\text{erf}\left({\beta }_{kj}{R}_{kj}\right)}{R_{kj}}-{\nabla }_j\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}\right)\hfill \\ \hfill & =\hfill & \sum _{k\ne j}^{bonded--non--moving}-{\nabla }_i\left({\stackrel{\rightharpoonup }{\mu }}_k\right)\cdot {\nabla }_k{\nabla }_j\frac{\text{erf}\left({\beta }_{kj}{R}_{kj}\right)}{R_{kj}}-{\nabla }_i\left({\stackrel{\rightharpoonup }{\mu }}_i\right)\cdot {\nabla }_i{\nabla }_j\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}-\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right){\nabla }_i{\nabla }_j\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}\hfill \\ \hfill & =\hfill & \sum _{k\ne j}^n-{\nabla }_i\left({\stackrel{\rightharpoonup }{\mu }}_k\right)\cdot {\nabla }_k{\nabla }_j\frac{\text{erf}\left({\beta }_{kj}{R}_{kj}\right)}{R_{kj}}-\left(q_i+{\stackrel{\rightharpoonup }{\mu }}_i\cdot {\nabla }_i\right){\nabla }_i{\nabla }_j\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}.\hfill \end{array}$$

Here, n represents the number of atoms in the bonded group, including atom i.

Next, we compute the derivative of the field on the moving atom, i.e., atom i, as follows:

$$\begin{array}{ccc}\hfill {\nabla }_i\left({\stackrel{\rightharpoonup }{E}}_i^0\right)& =\hfill & {\nabla }_i\left(\sum _{j\ne i}^n-{\nabla }_i\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}-\sum _j^{nonbonded}{\nabla }_i\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right)\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}\right)\hfill \\ \hfill & =\hfill & \sum _{j\ne i}^n-{\nabla }_i\left({\stackrel{\rightharpoonup }{\mu }}_j\right)\cdot {\nabla }_j{\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}-\sum _{j\ne i}^n\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right){\nabla }_i{\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}-\sum _{j\ne i}^{nonbonded}\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right){\nabla }_i{\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}\hfill \\ \hfill & =\hfill & -\sum _{j\ne i}^n{\nabla }_i\left({\stackrel{\rightharpoonup }{\mu }}_j\right)\cdot {\nabla }_j{\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}-\sum _{j\ne i}^N\left(q_j+{\stackrel{\rightharpoonup }{\mu }}_j\cdot {\nabla }_j\right){\nabla }_i{\nabla }_i\frac{\text{erf}\left({\beta }_{ij}{R}_{ij}\right)}{R_{ij}}.\hfill \end{array}$$

Here, N represents the number of all atoms in the system.