Abstract
In biological systems, polymeric materials block the movement of some macromolecules while allowing the selective passage of others. In some cases, binding enables selective transport, while in others the most inert particles appear to transit most rapidly. To study the general principles of filtering, we develop a model motivated by features of the nuclear pore complex (NPC) which are highly conserved and could potentially be applied to other biological systems. The NPC allows selective transport of proteins called transport factors which transiently bind to disordered, flexible proteins called FG Nups. While the NPC is tuned for transport factors and their cargo, we show that a single feature is sufficient for selective transport: the bound-state motion resulting from transient binding to flexible filaments. Inter-chain transfer without unbinding can further improve selectivity, especially for crosslinked chains. We generalize this observation to model nanoparticle transport through mucus and show that bound-state motion accelerates transport of transient nanoparticle application, even with clearance by mucus flow. Our model provides a framework to control binding-induced selective transport in biopolymeric materials.
INTRODUCTION
Living systems control the localization and movement of molecules, nanoparticles, viruses, and other organisms using selective filters made of biopolymers [1]. These filters regulate access to genetic material (the nuclear pore complex, or NPC), cells (the pericellular matrix), tissues (the extracellular matrix), and organs (mucus). In addition to their protective role, polymeric biomaterials can inhibit delivery of therapeutic agents. How particle binding affects motion and filtering is unclear: binding to the pericellular matrix facilitates uptake of nanoparticles by single cells, and transport factors that bind to proteins in the NPC move rapidly through it [2, 3]. In contrast, binding inhibits the uptake of nanoparticles that bind to airway mucus, and many viruses minimize binding interactions [4–8]. Mucus presents a particularly formidable challenge to nanoparticle drug delivery, where vectors tend to be of a similar size to pathogens, the exclusion of which is the primary role of mucus. While particle size, charge, and binding interactions are known to affect filtering, the physical principles that underlie mobility and transport in polymeric biomaterials are not fully understood [1].
The nuclear pore complex (NPC) relies on binding for selective transport and is important for diverse cellular processes including gene regulation and translation [3]. The NPC selectively filters molecular traffic between the nucleus and cytoplasm of eukaryotic cells, preventing the passage of most macromolecules while allowing the rapid passage of others of similar size and charge. A defining feature of molecules allowed passage is that they bind, either directly or indirectly, to the selective barrier of the NPC. Transport occurs through the central channel, ~50 nm in diameter and ~100 nm long. The selective barrier filling the central channel is made from disordered proteins, the FG nucleoporins (FG Nups), which contain repeated phenylalanine-glycine (FG) motifs (Fig. 1). Transport factors that directly bind to the FG repeats can cross the NPC and carry cargo with them [3]. Transport through the NPC is remarkably fast, with pore residence times ~10 ms [9, 10]. Consistent with this, the binding kinetics of FG Nup-transport factor interactions are rapid, often approaching diffusion-limited [11, 12].
Figure 1.
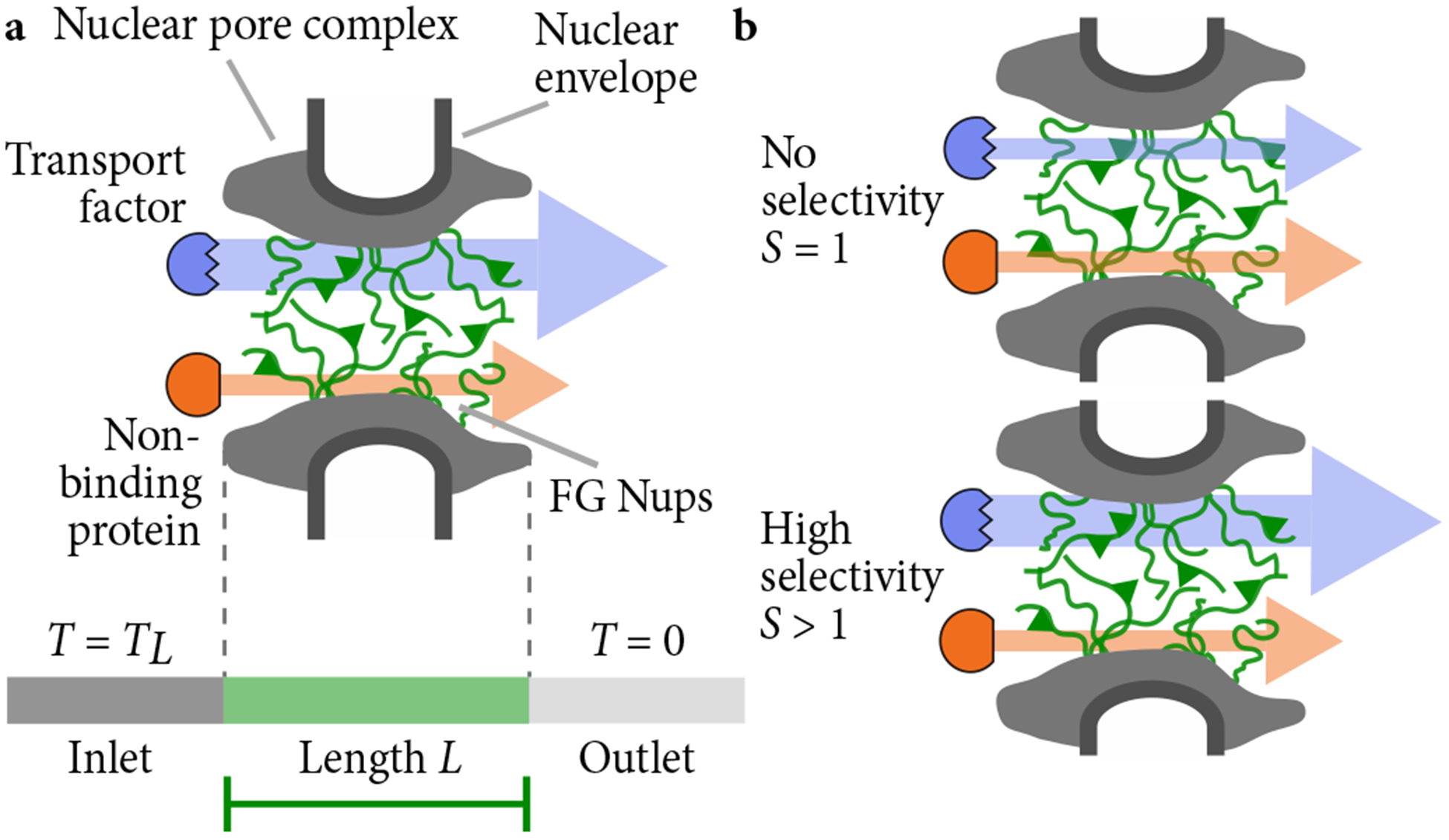
Schematics of the nuclear pore complex and model. (a) The nuclear pore complex (grey) is filled with FG Nups (green polymers) that selectively passage transport factors that bind to FG Nups (blue) while blocking non-binding proteins (red). The central channel of the pore has length L. Protein concentration is high on the left (inlet) and low on the right (outlet). (b) Selectivity quantifies the degree of selective transport through the pore. A non-selective pore with S = 1 has the same flux for a transport factor as for a non-binding protein (top). A selective pore with S > 1 has a larger flux for a transport factor than a non-binding protein (lower).
Current optimally-designed nanoparticles for drug delivery through mucus minimize binding interactions, a striking difference from nuclear transport. These mucus-penetrating particles with minimal interactions with mucus have enhanced delivery properties over those that bind to lung, eye, and vaginal mucosa [4, 6, 13, 14]. In contrast, the flagella or pili of a number of bacteria bind to mucus, suggesting a possible role for binding interactions in helping pathogens pass through mucus barriers [15–18]. This raises the question of which features of binding contribute to the passage of bacteria through mucus barriers and whether those mechanisms could be applied to nanoparticles as well.
Binding does not always enhance flux across a barrier. Mechanisms of selective transport based on binding include transport by mobile carriers and particle motion directly from one binding site to the next [19–26]. In general, selectivity requires that particles move while bound. Systems without binding, such as oil barriers separating aqueous reservoirs, have higher flux as a consequence of higher concentration within the barrier. In this case, the flux across the barrier is J = γDΔ c/L, if is the partition coefficient, D is the diffusion coefficient, Δc is the concentration difference across the barrier, and L is the barrier length. Binding-based concentration is the basis of several models of selective transport in the NPC which represent binding and diffusion using an effective free-energy landscape of the barrier to passage. In this picture, binding of transport factors to FG Nups provides a free-energy gain which offsets the energy barrier and is presumed to allow for more effective transport [27]. Details of the free energy landscape have seen extensive exploration both in vivo and in vitro [28–33], but that work has not typically investigated the underlying molecular mechanisms.
In this paper we study molecular mechanisms arising from simple, conserved features of the NPC that could potentially be applied to other biological and synthetic systems. Biomimetic filters or drug-delivery vehicles lack the full complexity of the FG barrier or FG Nup-transport factor interactions. Therefore, we focus on two features of binding between some transport factors and FG repeats: First, binding is diffusion-limited and transient between individual FG repeats and transport factors [11, 12]. While some transport factors bind more tightly, such transport factor-FG interactions typically require active release [34]. Second, FG Nups remain fully disordered and highly dynamic upon binding [11, 12, 35–37]. We developed a model to determine whether these two features are sufficient to produce binding-induced selective transport.
To compare the contributions of different molecular mechanisms of selective transport, we develop a hierarchy of models, beginning with a continuum model of bound-state diffusion. This model confirms that bound mobility is sufficient for selective transport. Then we consider two molecular mechanisms of bound diffusion: first a model of diffusion with transient binding to flexible polymers, and second a model of multivalent binding interactions that allow inter-chain transfers while bound. Finally, we extend the continuum model to include features specific to mucus barriers, including fluid clearance and mucus sloughing to study how these effects modify selectivity arising from bound-state diffusion.
BOUND MOBILITY CONTROLS SELECTIVITY IN A MINIMAL MODEL OF TRANSPORT THROUGH A POLYMER BARRIER
To understand how binding can cause selective transport, we formulated a minimal model. Because we are using the NPC as our model system, we use NPC-related terminology. However, to keep our model relevant to a wider range of biopolymer filters, we neglect NPC-specific features and consider only the effect of multivalent binding to flexible tethers. The NPC-specific features we neglect include a wide capture area [38], varying landscape along the axis of the NPC [28–31, 39], varying pore composition [40–43], active release from the pore [30, 44, 45], and modulation of FG Nup dynamics by transport factors [46, 47].
To compare model predictions to experiment, we consider the smallest transport factor nuclear transport factor 2 (NTF2), a homodimer that selectively passes through the nuclear pore without active release. While similarly-sized non-specific proteins can passage the NPC, the inert transport rate is significantly reduced: NTF2 is estimated to have 30–120 times higher flux through the NPC than GFP [48–50]. NTF2 may be less affected by transient crosslinking in the NPC because of its small size.
Although it is typically assumed that transport factors within the NPC are always bound to FG Nups, binding is sufficiently rapid that there can be many unbinding events during transport. The dissociation constant of NTF2 for FG Nups has been measured at values between nanomolar and millimolar [12, 51–55]. Assuming that binding is diffusion limited, the slower end of this range corresponds to an unbinding rate of 1 s−1, incommensurate with transport in the absence of active release. However, the fastest unbinding rate is 10−6 s−1, allowing for up to 104 unbinding events during a 10-ms transport event. If the measured KD recently obtained for the interaction of NTF2 with a specific portion of the FG Nup Nsp1 (4.3 mM) [55], is representative of all NTF2-FG interactions, then NTF2 is expected to spend approximately 50% of its time unbound while in the NPC.
We model transport factor diffusion within the NPC including binding kinetics and diffusion of the transport factor in both free and bound states. We define the transport selectivity S as the ratio of the steady-state flux of a binding versus an otherwise identical non-binding species [Fig. 1(b)]
| (1) |
We focus on transport within the pore, since in single-molecule measurements most of the transport time is spent in a random walk within the central channel [9, 31]. Here we consider the limit in which binding kinetics provide the only barriers to entry and exit from the pore. If we assume instead that entry and exit are rate-limiting, the selectivity is given by S = (1+eν)/(1+e|ν−ϵ|), where is the effective free-energy cost of placing an otherwise identical but non-binding particle into the pore, and ϵ is the free-energy gain due to binding to the pore. We impose a fixed transport factor concentration difference across the barrier, consistent with passive transport. In mucosal and biomimetic systems, the exterior concentration would be imposed by the delivery mechanism, which is well described by this model.
In order to determine the degree of selective transport resulting from bound diffusion, we consider a barrier of length L (~ 100 nm) that separates two reservoirs [Fig. 1(a)]. Within the barrier are free transport factor (concentration T), free FG Nups (N), and bound transport factor-FG Nup complex (C), with total FG Nup concentration Nt = N + C. Transport factor diffusion within the barrier (0 < x < L) is described by the reaction-diffusion equations [19]
| (2) |
| (3) |
Transport factor-FG Nup binding has on-rate constant kon, off-rate koff, and dissociation constant KD = koff/kon. We include competition between transport factors for FG binding sites and assume that the barrier properties are independent of transport-factor concentration [46, 56, 57]. Total FG Nup concentration Nt = 4.7 mM was determined from an estimate of the number of TF binding sites (800), and the volume of a cylinder of diameter 60 nm and length L. The diffusion constants of free (DF) and bound (DB) transport factors are spatially constant. The free diffusion coefficient of a TF within the pore was determined from the flux of a non-binding species [48] to be DF = 0.12 μm2/s. The fixed reservoir transport factor concentrations are TL (inlet, left) and 0 (outlet, right). The barrier imposed by the FG Nups to a TF and its non-binding counterpart is incorporated into the effective TF concentration at the edge of the gel. We estimate this barrier ≈ 1.5 kBT for an NTF2 sized molecule [28]. We estimate the cytoplasmic concentration of NTF2 is 5 μM. Then TL = 5 × e−1.5μM = 1 μM.
We numerically integrated the full nonlinear equations to find the flux of transport factor across the barrier, J = −DF ∂T/∂x|x=L. We integrated the equations in MATLAB using Crank-Nicolson stepping for the linear portion and forward Euler for the non-linear portion. Because flux measured in experiments is typically linearly proportional to transport factor concentration, transport factors likely remain below binding saturation in the NPC [58, 59]. Therefore, we also solved Eqs. (2, 3) analytically in the low-binding limit by making the change of variables C = NtT/KD + Cx, which separates C into a term that is in local equilibrium and a spatially-dependent term. This change of variables leads to a fourth-order ODE which can be solved analytically (see Appendix).
Two key differences distinguish our model from that of Yang et al., who also explicitly considered bound diffusion [22]. First, we solve the full nonlinear equations. Second, we enforce the requirement that transport factors unbind before leaving the pore, which has significant effects. Omitting this restriction overestimates selectivity for rapid bound diffusion and underestimates it for slow bound diffusion (Figs. 8, 10).
Our model shows that selective transport is not possible either at steady-state or during initial transient dynamics if bound transport factors do not move (DB = 0), and in general reducing the bound mobility reduces the selectivity [60, 61]. If DB = 0, the steady-state flux J = DF TL/L for both binding and non-binding proteins, so S = 1 (Figs. 2, 8). While the binding transport factor accumulates within the pore, its immobility means transport is not increased compared to the non-binding case. In other words, the concentration within the barrier is increased by binding, but the mobility and therefore flux of particles is proportionately reduced [62].. Notably, this effect is independent of binding kinetics. Prior to steady state, binding slows transport [Fig. 2(a)]. In systems such as airway mucus, immobilization by binding may increase the time available for degradation or active clearance, consistent with the observation that binding tends to inhibit selective transport in those systems [4–6]. This effect is related to the binding-site barrier seen in antibody delivery to tumors [63], and observations that non-binding nanoparticles are often more effective in drug delivery to tumors than binding particles [1].
Figure 2.
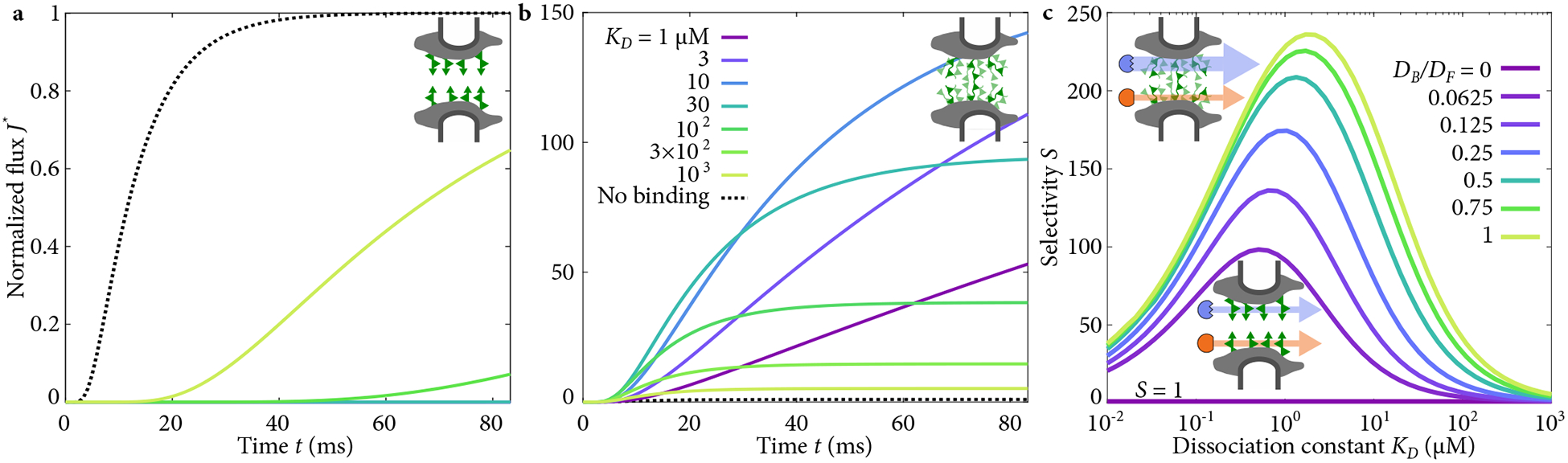
Flux through the pore and selectivity for transport factors with varying bound mobility. (a) Flux as a function of time when transport factors are immobile while bound, with varying binding affinity as in (b). (b) Flux as a function of time when transport factors are mobile while bound with DB = DF , with varying binding affinity. Note change in y-axis scale. (c) Selectivity as a function of dissociation constant with varying bound diffusion coefficient.
When bound transport factors are mobile (DB > 0), transport is enhanced for the binding particle: it is selective by a factor of up to 240 for experimentally relevant parameters [Figs. 2(b,c), 8]. We examined how binding kinetics influence transport and found an optimal dissociation constant of KD ~ 1 μM for high selectivity [Fig. 2(c)]. We allow KD to vary, given that the affinity of NTF2 for relatively few FG Nups has been reproducibly measured [12, 52, 53, 55]. Selectivity decreases for high KD because binding is too weak to significantly increase transport factor concentration in the pore. For low KD, tight binding causes the concentration of bound complexes to become approximately constant across the pore. Because diffusive flux is driven by a concentration gradient, washing out the gradient by tight binding decreases flux and selectivity.
BOUND DIFFUSION DUE TO TRANSIENT BINDING TO DYNAMIC POLYMERS
We next examined molecular mechanisms in bound diffusion, beginning with a model incorporating rapid binding to flexible polymers. Previous measurements have found that FG Nups are flexible and dynamic [11, 36, 64], which would allow a transport factor bound far from the anchored end of an FG Nup to move while bound. The bound motion depends on the polymer properties and binding kinetics, with more flexible polymers and more transient binding resulting in higher bound diffusion.
To quantify mobility while bound to flexible polymers, we developed a minimal model. Flexible polymers can be approximated as entropic springs if they are not highly stretched [65]. Therefore, a bound transport factor that diffuses while attached to a spring-like tether can be represented as diffusion in a harmonic potential well (Fig. 3). The width of the harmonic well is related to the effective length of the flexible domain: if FG Nups are not crosslinked, the effective length is the full FG Nup length, while if they are crosslinked or entangled, the length is reduced [48]. The probability density of the position of a transport factor that binds to a well with center x = 0 is , where , k is the spring constant of FG Nup tethering and β = 1/kBT is the inverse thermal energy [66]. The transport factor mean-squared displacement (MSD) is then . The typical MSD during a binding event depends on the probability density of binding lifetime ρ(t) = exp(−t/τ)/τ, where τ = 1/koff is the mean bound lifetime:
| (4) |
Here we assume that the spring constant is that of a worm-like chain polymer , where Lc is the contour length and the persistence length [65].
Figure 3.
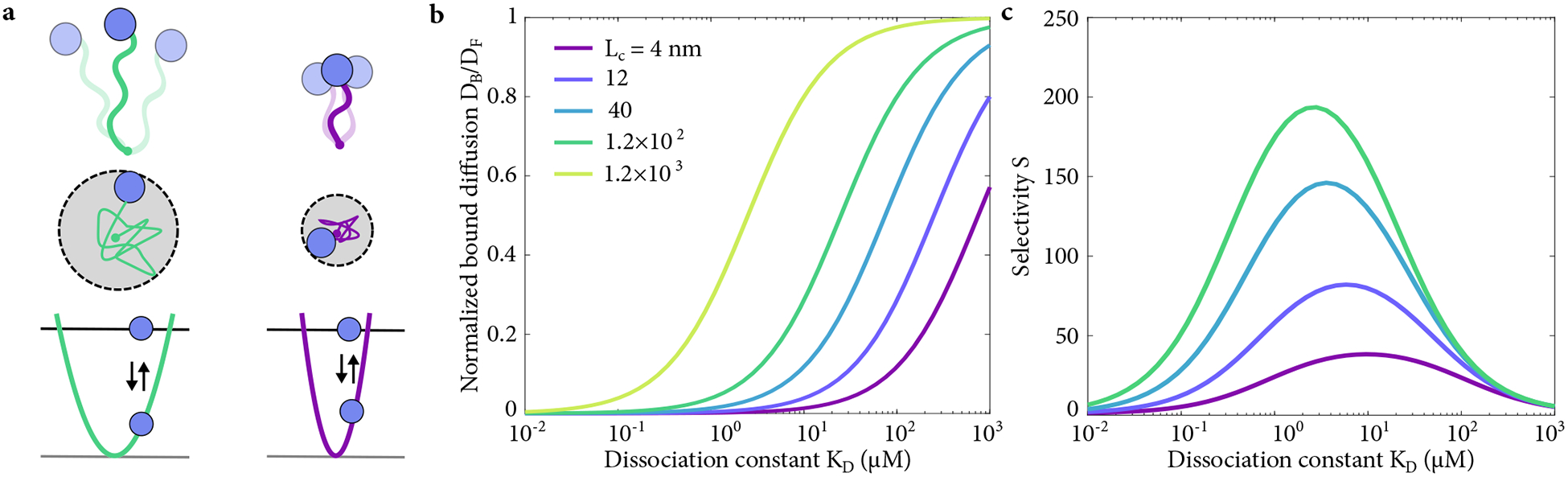
(a) Schematic of the flexible tether model of bound-state diffusion. FG Nups are treated as entropic springs that constrain the motion of TFs more (top and center left, longer FG Nup) or less (top and center right, shorter Nup), which corresponds to changing width of the harmonic potential well (lower). (b) Ratio of bound to free diffusion coefficient as a function of dissociation constant, with varying polymer length in the tethered-diffusion model. (c) Selectivity as a function of KD, with varying polymer length in the tethered-diffusion model.
Because transport factor-FG Nup interactions have fast binding kinetics [11, 12], we estimate the bound diffusion coefficient by averaging over many binding events, while considering only bound motion. We make the approximation that the diffusion is Fickian, with 〈x(t)2〉 ∝ t, despite the slightly subdiffusive effects of binding to an energy well, since transient binding renders this effect minimal. The bound diffusion constant is then given by
| (5) |
Here quantifies how polymer properties tune the bound-state diffusion coefficient: bound mobility increases with increasing chain length or persistence length, or decreasing binding lifetime (Fig. 3). When DP is large (DF /DP ≪ 1), DB approaches DF , since the long chains barely affect transport factor motion during the short binding event. For small DP (DF/DP ≫ 1), transport factor motion is inhibited by a short tether, giving DB ≈ DP /3 ≪ DF. This shows that the kinetics of transport factor-FG Nup interaction are a primary determinant of the bound mobility: the faster the binding kinetics, the higher the bound diffusion constant. These relationships between microscopic binding properties and selectivity are possible because we explicitly consider the process of binding, in contrast to others that assume local chemical equilibrium, giving significantly different results (Fig. 9) [19, 30].
A strength of this simple model is that we can quantitatively predict the bound diffusion constant based on polymer properties and binding kinetics. Flexible disordered proteins typically have low persistence length, [67]. If the on-rate constant is diffusion-limited, kon = 10−3 μM−1 μs−1 [11, 12], then the binding affinity determines the off rate. Disordered FG Nups have Lc ≈ 100–280 nm, (250–700 amino acids in length [68] with a contour length of approximately 0.4 nm per amino acid). FG nups are thought to be somewhat entangled or transiently croolinked, and so we considered Lc as small as 4 nm, the inter-FG spacing on a single FG Nup chain. Even in this case, we find significant selectivity (Fig. 3).
Our model provides a quantitative tool to evaluate selective transport within NPC mimics made directly from FG Nups. Because binding does not always lead to selective transport, we analyze whether these synthetic materials would act as selective filters. Materials formed in vitro by spontaneous self-assembly of FG Nups [69] or transient crosslinking by alpha-helical peptides [70] show strong selective entry. Using published data, we used our theory to predict whether these gels would show selective transport through a 100-nm barrier (Table II, Appendix). Predicted selectivity is ~ 10, with the predicted selectivity of one hydrogel S ≈ 200, apparently the most selective synthetic gel to date [69].
Using a conservative set of parameters, our tethered diffusion model predicts values of selectivity which agree with experimental measurements in the NPC (Table I). Our results explain how key features of some transport factor-FG interactions result in selective flux through the NPC. Bound transport factors are mobile due to rapid binding kinetics and thermally-driven diffusion while bound to flexible polymers. These results suggest that features such as active release, dissolution of crosslinks within a gel phase, and a wide capture area are not necessary for selective transport of NTF2 [38, 44, 69].
Table I.
Comparison between experimental results for NTF2 and GFP and model predictions. Flux measured in molecules per pore per second.
BOUND DIFFUSION DUE TO INTER-CHAIN TRANSFER
In addition to tethered diffusion, bound motion can arise from multivalent FG Nup-transport factor interactions that allow transfer between polymer chains while remaining bound [46, 71]. The multivalent nature of transport factor-FG interactions has been assumed to be a key contributor to selectivity because a transport factor can bind simultaneously to more than one FG Nup, moving hand-over-hand while remaining bound [23, 31, 47, 53]. Consistent with this, transport factors may slide between nearby FG sites rather than fully unbinding and re-binding [23]. If the newly-bound FG repeat is on a neighboring chain, the FG tether site that constrains transport-factor motion moves while the transport factor remains bound.
To determine the relative contributions to selectivity of inter-chain transfer and tethered diffusion, we modeled both mechanisms. We simulated a transport factor that undergoes tethered diffusion when bound to an FG Nup and can directly transition between neighboring, randomly distributed tethers without unbinding (Fig. 4, Appendix). Intra-chain transfers do not change the flux; therefore we neglect them.
Figure 4.
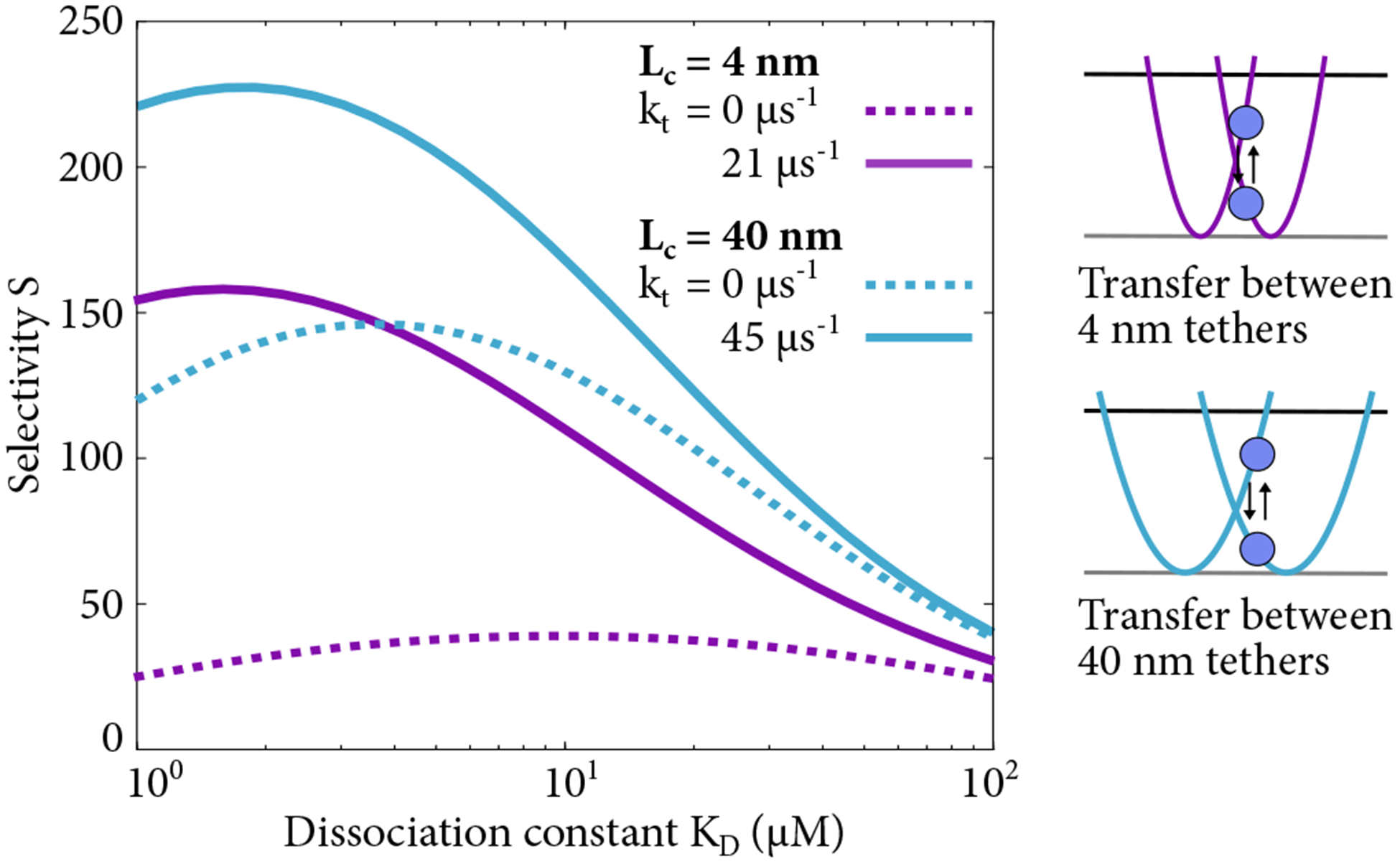
Selectivity as a function of KD with and without inter-chain transfer for FG Nup contour lengths Lc = 4 nm and Lc = 40 nm. FG Nups are entropic springs that constrain the motion of transport factors, and inter-chain transfer allows a transport factors to move from one FG Nup to another without unbinding at rate kt, which corresponds to switching from one harmonic well to another.
Inter-chain transfer increases selectivity by up to a factor of 6 for tight binding and short chains, which is the regime where tethered diffusion provides only limited selectivity (Figs. 4, 12). For weaker binding and longer chains, inter-chain transfer leads to a modest increase in selectivity of up to 30%.
EFFECTS OF BARRIER AND RESERVOIR DYNAMICS ON TRANSPORT IN MUCOSAL SYSTEMS
Bound diffusion might be relevant to other biopolymer filters such as mucus barriers. In contrast to the NPC, current optimally-designed nanoparticles for delivery through mucus lack binding interactions [4, 8, 14, 72]. Those particles that do bind are less effective at delivery to the underlying tissue. However, these particles were not designed with the explicit aim of bound diffusion: previously-designed particles either contained charged surfaces to interact non-specifically with highly charged mucus or contained monovalent binding motifs which would likely become immobilized while bound. As a result of these binding interactions, such particles are typically observed at the mucosal surface and are unable to penetrate. For antibody-based delivery of pharmacological agents this restriction has been termed the binding-site barrier and may explain the efficacy of antiviral antibodies whose weak mucus binding is increased upon multivalent antigen interactions [63, 73].
Our model suggests that nanoparticles could be designed to take advantage of bound diffusion in order to more effectively penetrate mucus barriers. For example, large numbers of very weakly binding motifs could coat nanoparticle-based delivery vehicles, or those motifs could be attached to nanoparticles via flexible polymers.
Mucus dynamics differ from the NPC because mucus and the surrounding fluid are cleared, potentially affecting the efficacy of selective transport arising from bound diffusion. Therefore we consider two additional features in our model. First, liquid on the surface of the mucus is often only present transiently. For example, our tears and blinking clear the liquid from the surface of the tear film in the eye [75]. Second, even for mucosal surfaces which enable more long-term exposure to external agents, the mucus grows and is shed [76].
Transient drug application
To model the effect of clearance of the surrounding fluid on transport kinetics, we extend our model to study the transient application of a concentration gradient. A substance (T) is introduced to the mucosal surface (N) for a short time td, then is removed. For td = 2 s, a constant nonzero concentration of drug is applied to the exterior of the mucosal layer (the fluid in Fig. 5). For t > td, that liquid is cleared, and the concentration of drug is returned to zero, mimicking the clearance of the surrounding fluid, e.g., due to blinking. To focus on clearance, we retain the approximation that the mucus is both homogeneous and stationary, and the cells are assumed to be perfectly absorbing. We selected parameters consistent with those in the literature for the eye tear film. We calculated flux and accumulation for a mucus barrier with thickness L = 5 μm [77]. The free diffusion constant was DF = 0.5 μm2/s, corresponding roughly to a 300 nm particle diffusing in water. We assumed a 10 mM concentration of binding sites.
Figure 5.
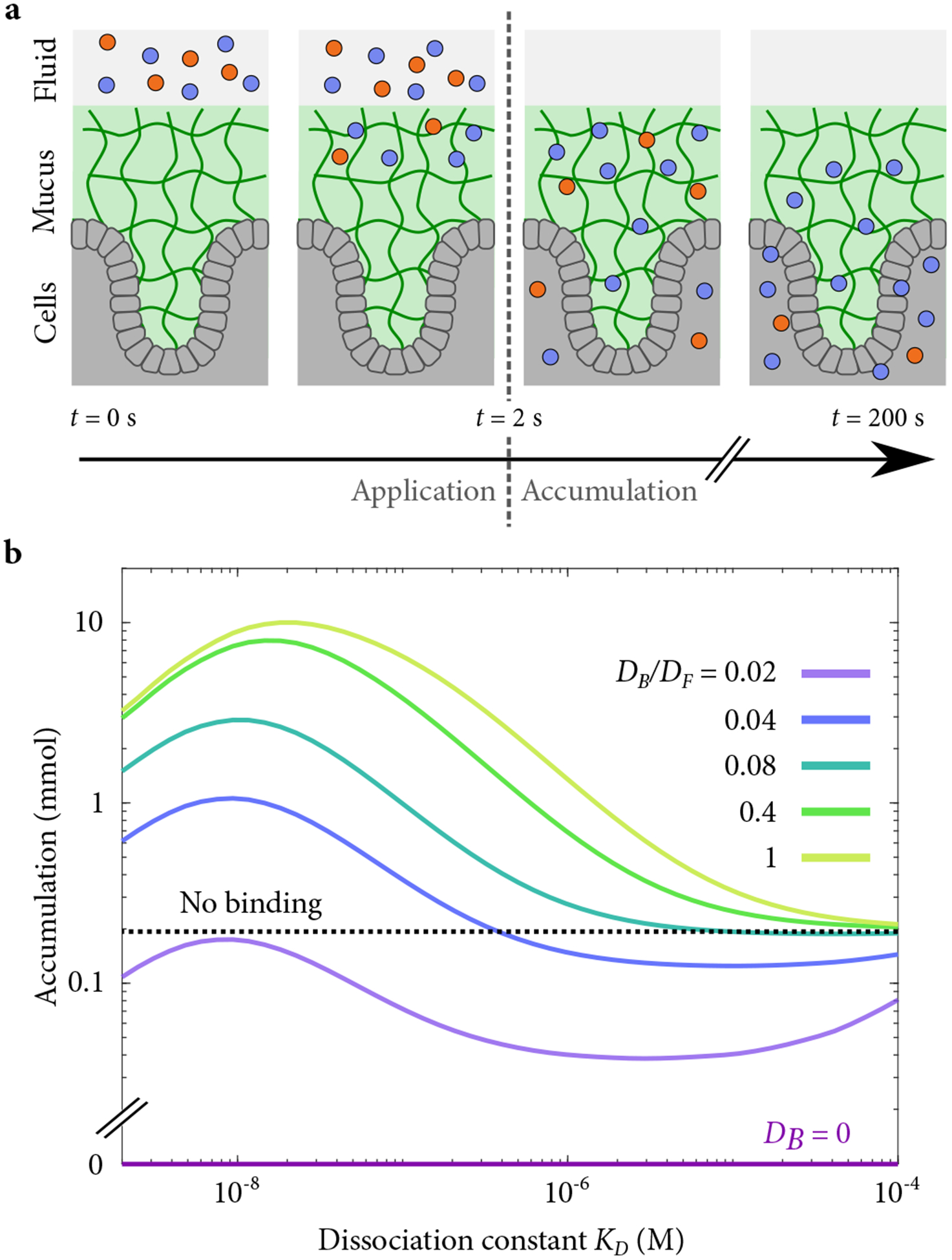
(a) Schematic of simulated transient drug application showing binding (blue) and inert (red) particles introduced to the fluid above a mucus layer (green) and subsequently washed away. Some particles are retained in the mucus layer for a time, and some of those enter the cells below (grey). Figure adapted from [74]. (b) Accumulation for a 2-s application followed by a 200-s accumulation period.
When the external reservoir is only transiently high in concentration, binding which immobilizes particles is particularly ineffective at transporting the drug to the cells. All particles that bind will have initial transient behavior with binding occurring quickly. The particles are thus delayed in reaching the tissue surface. Once the surrounding liquid is replaced, the steady loss of drug to the surrounding media is faster than diffusion to the tissue surface. For binding without diffusion, the transport to the tissue was typically orders of magnitude slower than that of an inert particle for reasonable parameter values (Fig. 5).
Remarkably, bound-state diffusion can deliver more molecules to the tissue surface than can the absence of binding (Fig. 5). The mucus binds particles and their passage to the tissue continues when the inert particles have diffused away. As with nuclear pore transport, there is an optimal binding affinity for transport. For our parameters, the optimal dissociation constant is KD ≈ 100 nM, giving a selectivity S ≈ 50. If possible experimentally, this increase would be similar to or greater than improvements from making particles more inert [74]. Bound diffusion would be particularly valuable in cases where the kinetics of absorption to the surface can be limiting, for example, if the concentration of cell surface receptors or internalization of bound species is low relative to the applied concentration. We do not explicitly model the rate of absorption at the tissue surface in our model. However, for the perfectly absorbing boundary conditions we consider, the instantaneous concentration at the tissue surface is steadier with binding than without (Fig. 6). Thus, the mucus itself can act as a sustained drug release platform.
Figure 6.
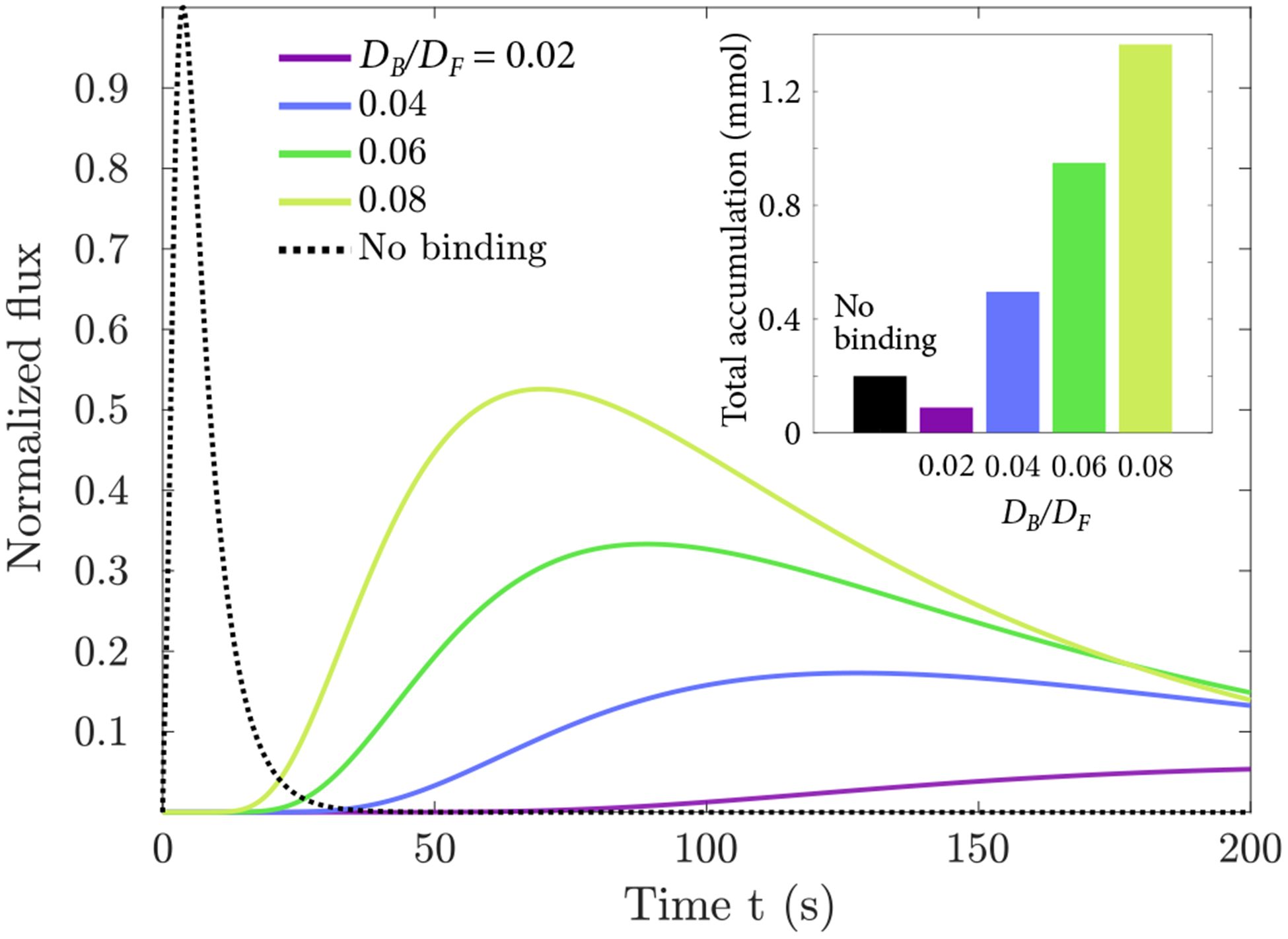
Normalized flux for a 2-s application followed by a 200-s accumulation period, shown for several values of bound diffusion constant ratio DB/DF . Inset: Total accumulated flux after 200 s as a function of DB/DF .
Mucosal dynamics
A significant problem in drug delivery to many mucosal systems is the continuous production and sloughing of mucus. We consider an approximate model including outward flux to represent mucus sloughing: mucus and surrounding fluid are produced on one surface and disappear on the other, ignoring spatial and temporal inhomogeneities such as those occurring during coughing [76]. We considered the same transient drug application as above. No increase in transport of mucus occurs with outward flow relative to the case of stationary mucus, but we analyze whether bound diffusion still increases flux across the barrier even in the presence of an outward flow (Fig. 7).
Figure 7.
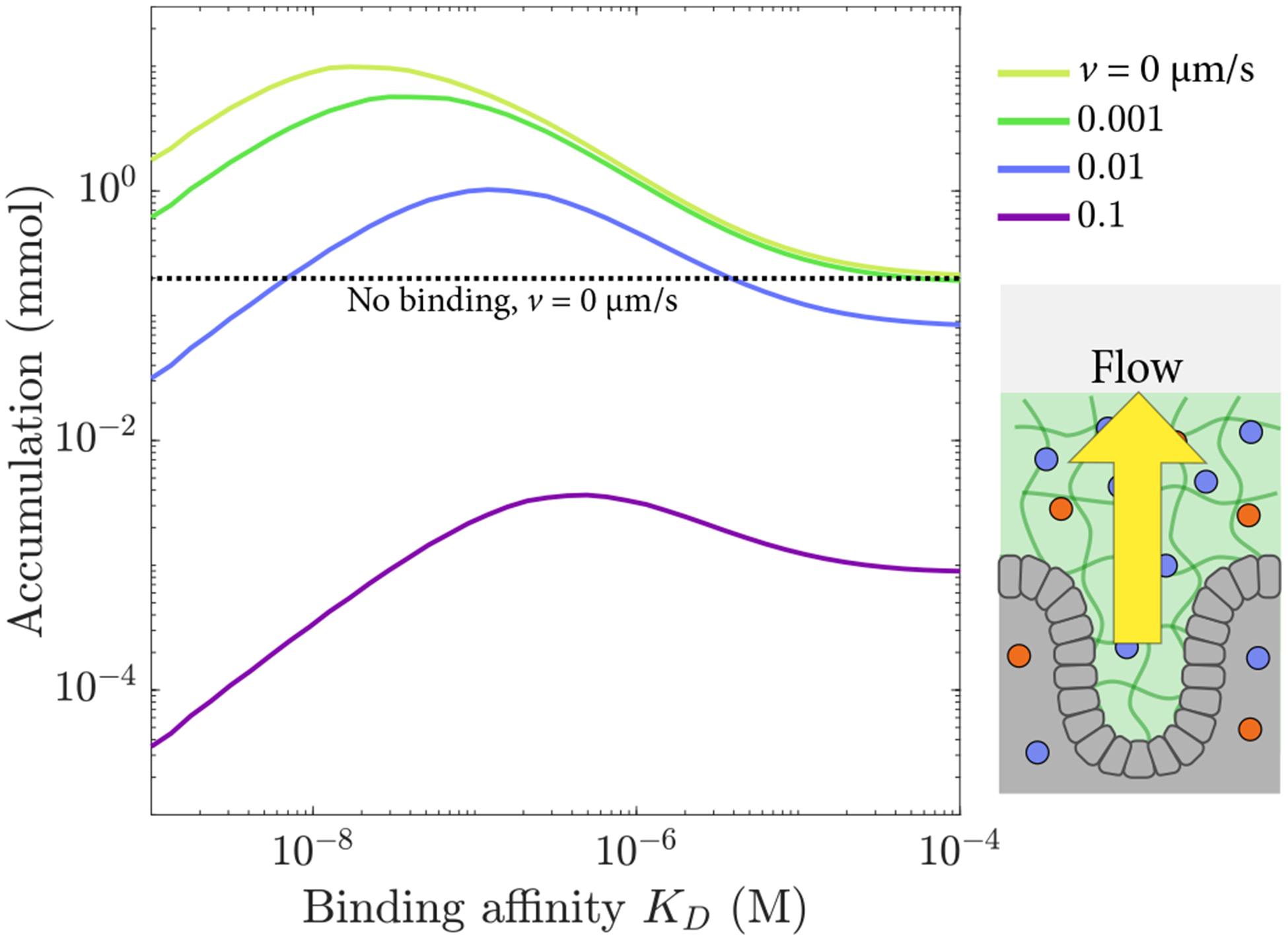
Total accumulation for a 2-s application followed by a 200-s accumulation period as a function of dissociation constant KD, shown for several values of the flow velocity v away from the barrier.
Bound diffusion can improve delivery efficacy to the underlying tissues even with outward flow. The relevant timescale for particles to diffuse across a mucus barrier of length lm is , whereas the mucus is completely replaced on a timescale of τr = lm/v. If τd ≪ τr, then bound diffusion is effective for increasing delivery through the barrier, whereas in the opposite limit it is not, as particles are removed from the barrier more rapidly than they can diffuse through it (Fig. 7). Using the parameters described above, bound diffusion should be effective for v ≪ 0.2 μm/s, in agreement with the accumulation curves in Fig. 7. The expected value of mucus velocity away from the eye was calculated using a tear secretion rate of 4 μL/min [78] and assuming an eye surface area of 1 cm2, resulting in a velocity of 0.1 μm/s. As tears contain 0.01% mucins [79] and mucus layers typically contain 2–5% mucins [80], we scaled the velocity proportionately for a final expected velocity of v = 2 × 10−3 μm/s, well within the regime in which bound diffusion can improve accumulation.
CONCLUSIONS
In this paper we developed a hierarchical model of bound state diffusion and used physically realistic parameters and boundary conditions to predict selective transport in the NPC and mucus. Our results show that both tethered diffusion and inter-chain transfer can lead to significant selectivity in the NPC. As tethered diffusion could be engineered into nanoparticle-based drug delivery vessels, we additionally tested whether bound-diffusion based selectivity was robust to mucus-specific features such as transient application and active shedding.
We focus on dynamic multivalent binding to flexible tethers, two conserved features of the NPC that may be present in a wide variety of biological systems (DNA binding proteins, mucus, extracellular matrix, membrane-less organelles) and could be engineered into drug delivery systems [81–84]. Membrane-less organelles contain multivalent binding and flexible polymers [85], making selective transport a likely, though potentially under-appreciated, phenomenon in those systems. Our work is consistent with previous work showing that bound-state diffusion is necessary for selective transport (Fig. 2) and complements other proposals for mechanisms of bound-diffusion that include solute binding to mobile carriers [19, 21], and a hand-off between multivalent binding sites [20, 22]. Our work also complements work which considers transient crosslinks that inhibit motion and forces generated by binding to dynamic polymers [24, 25, 86].
We quantitatively compared the relative contributions of two mechanisms of bound diffusion: (1) tethered diffusion during transient binding events to flexible polymers and (2) inter-chain transfer of multivalent transport factors between flexible polymers. We built on significant previous interest in inter-chain transfer [22, 23] by determining its quantitative contribution to selective transport. Our model predicts that the dominant molecular mechanism of bound diffusion in the nuclear pore depends on the extent to which the FG Nups are crosslinked (Fig. 4). If the FG Nups form polymer brushes with long effective contour length (~40 nm), tethered diffusion is the primary mechanism, and is sufficient to provide high selectivity (Fig. 3). FG Nups are most likely somewhat entangled or crosslinked [48, 54, 69], which increases the importance of inter-chain transfer. However, even for tether length as short as the typical inter-FG spacing along each FG Nup (~4 nm), tethered diffusion still has the potential to contribute significantly (Fig. 3), because the fast kinetics of FG Nup-transport factor interactions mean that even motion while bound to short polymer segments can contribute to selectivity. This effect persists even if the transport factor is nearly always bound, as long as it unbinds and binds frequently; a transport factor that is bound >99% of the time to 4-nm tethers can still have selectivity from only tethered diffusion of S ~ 40 (Fig. 3).
Experimental measurements of NPC selectivity are quantitatively reproduced by our model of tethered diffusion, which relies on the flexibility of FG Nups and the rapid kinetics of FG Nup-transport factor binding. For conservative parameter choices, tethered diffusion produces values of the bound diffusion constant which result in selectivity of up to 200. A range of selectivity has been measured experimentally for NTF2 which agrees well with the model’s predictions (Table I), despite the minimal nature of the model.
Our model suggests that the principle of bound diffusion could be used design nanoparticles which pass more effectively through mucus barriers and provide a more uniform flux to the cells’ surface than those that are inert, potentially improving drug delivery. In our model of transient drug application, particles with bound-state mobility pass through the barrier up to 50-fold more effectively than those that do not bind, and orders of magnitude more effectively than particles that are immobilized by binding (Fig. 5). Even when the bound diffusion constant is small relative to the free diffusion constant (DB ~ DF /20), bound diffusion can increase total accumulation in the underlying tissue while also providing a more uniform flux over time, acting as a sustained-release mechanism (Fig. 6). In contrast, current nanoparticle design focuses on inert mucus-penetrating particles for drug delivery [4–6]. The addition of an outward flux of mucus to model clearance decreases but does not re move the benefits of bound diffusion for moderate values of outward velocity (Fig. 7). Nanoparticles designed for bound-state mobility within mucus barriers may therefore be able to improve drug delivery.
ACKNOWLEDGMENTS
We thank Noel Clark, Matthew Glaser, and Franck Vernerey for useful discussions, computational resources of the BioFrontiers Institute, and funding from NIH R35 GM119755 and K25GM110486, NSF DMR1725065 and DMR1420736, the Boettcher Foundation, and a CU innovative seed grant.
Flux in the linear binding approximation
The analytical solution for flux can be directly derived in the linear case. For ease of calculation, we reverse the concentration gradient found in the main text, so that T(0) = 0 and T(L) = TL, allowing us to calculate flux at x = 0. The reaction-diffusion equations (2, 3) at steady state in the linear limit N ≈ Nt are
| (6) |
| (7) |
The change of variables C = Cx + NtKAT (KA = kon/koff = 1/KD ) yields
| (8) |
| (9) |
Substituting makes equation (9) a fourth-order ODE
| (10) |
where λ2 = koff (DF + NtKADB)/(DF DB). Solutions to this equation have the form T(x) = b+mx+feλx+ge−λx, where b, m, f and g are constants fixed by four boundary conditions: free TF concentration is fixed at the edges of the pore, with T(0) = 0, T(L) = TL. No flux of bound TF into or out of the pore occurs, giving ∂C/∂x|x=0 = 0, ∂C/∂x|x=L = 0. The constants of integration are
| (11) |
| (12) |
| (13) |
| (14) |
where ζ = 2NtKA − 2NtKAeLλ + LNtKAλ − (DF/koff)Lλ3 − (DF/koff)Lλ3eLλ + LNtKAλeLλ. This leads to a concentration profile of bound TFs
| (15) |
To determine the selectivity, we calculate the steady-state flux out of the pore J = −DF∂T/∂x|x=0, giving
| (16) |
| (17) |
For a non-binding particle, C(x) = 0, T = TLx/L, and
| (18) |
We note that the selectivity J/Jn is then independent of TL in the linear approximation.
Figure 8.
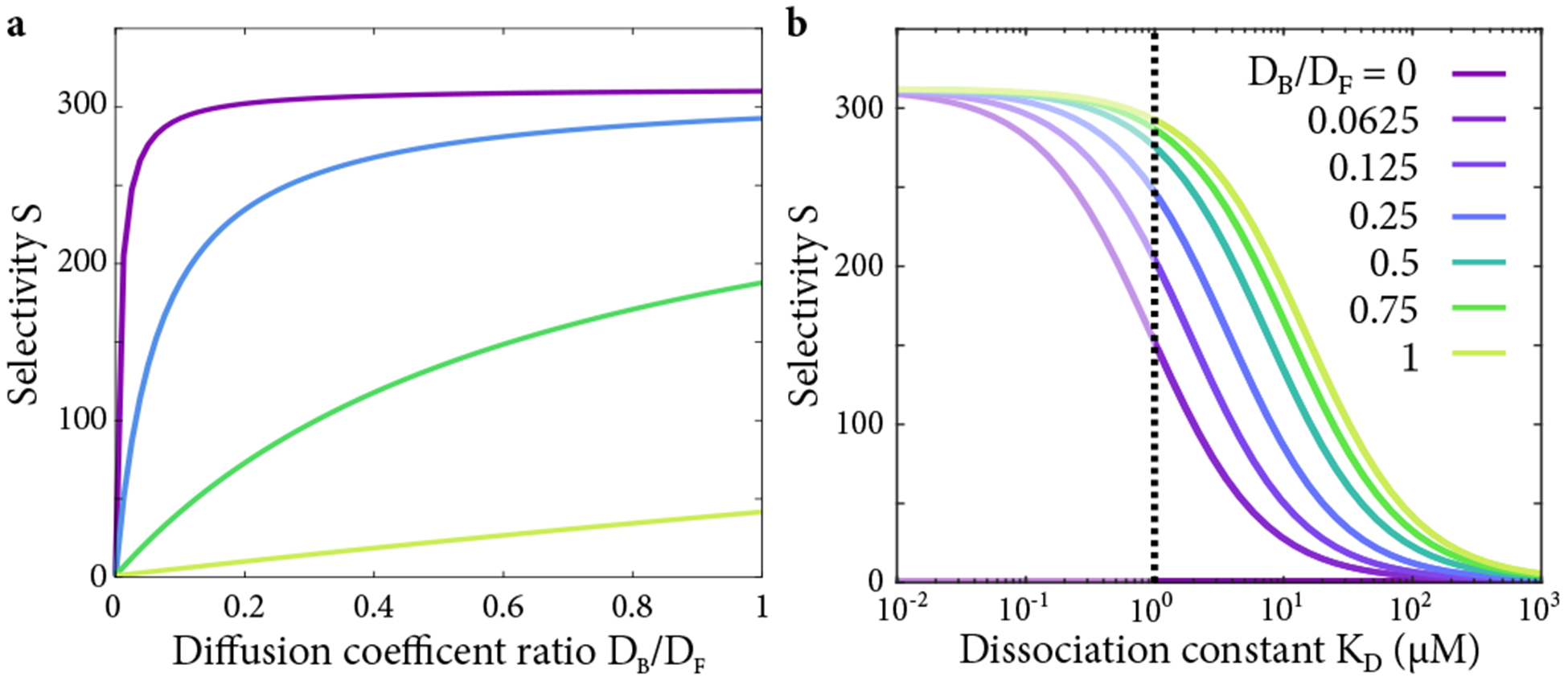
(a) Selectivity as a function of diffusion coefficient ratio, with varying dissociation constant in the linear approximation. (b) Selectivity as a function of dissociation constant, with varying diffusion coefficient ratio, in the linear approximation. The full nonlinear solution should be used to the left of the dotted line.
Figure 9.
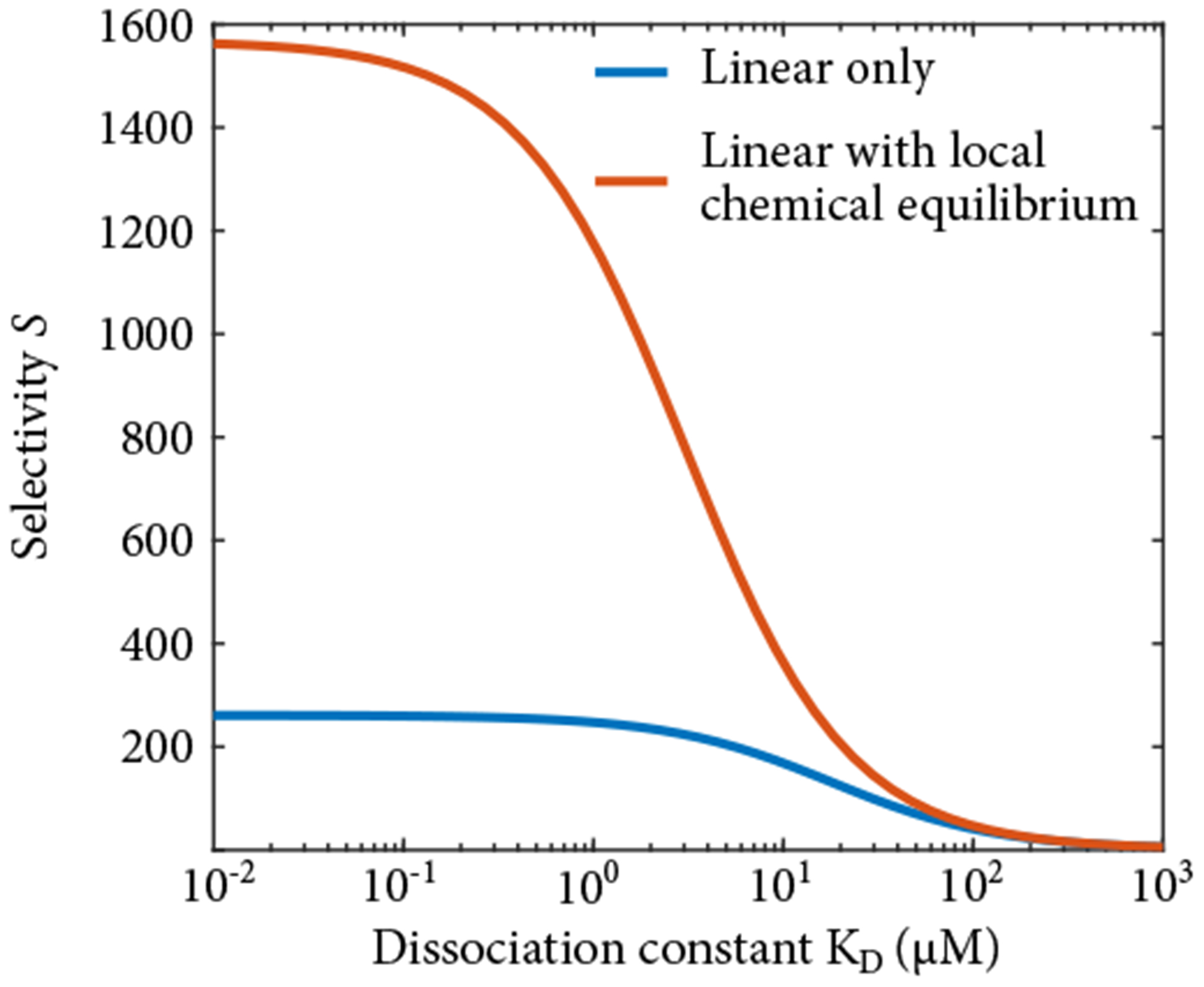
The blue curve shows the selectivity in the linear regime where we have explicitly considered tethered diffusion (Lc = 120 nm). In contrast, in the red curve we have assumed local chemical equilibrium to test whether simply including tethered diffusion into that model can be a good approximation for the solutions to the full binding model. This leads to quantitatively different predicted fluxes. With local chemical equilibrium, the boundary conditions must be incorrect - bound complex leaves the gel and the flux of transport factor on either end of the gel is not equal.
Inter-chain transfer simulation
In our simulation of TF motion with transfer between FG Nups while bound, we represented each FG Nup as an entropic spring (represented by a harmonic potential well). Well positions were randomly chosen from a uniform distribution, with the exception that we always placed one well at the starting position of the TF. The particle (the TF) started the simulation bound to this FG Nup, and remained bound to a Nup throughout the simulation. While bound to one FG Nup, the TF diffused within the harmonic well representing that FG Nup. We recorded the position and mean-squared displacement of the TF from its starting location, which we then used to determine a bound diffusion coefficient, as described in more detail below. The TF could move between tethers by changing the well in which it moved.
The TF moved in the harmonic potential of the FG Nup according to Brownian dynamics. TF position updated using a force-dependent diffusive step [87, 88]
| (19) |
where F is the force acting on the particle, Γ is the drag coefficient, δt is the timestep, and δx is a random Brownian step drawn from a Gaussian distribution with variance σ2 = 2Dδt. The drag coefficient of a spherical particle at low Reynolds number is given by Stokes’ Law as Γ = 6πηr, where η is the fluid’s viscosity and r is the sphere’s radius. This result can be combined with the Einstein relation D = kBT/(6πηr) to give
| (20) |
Figure 10.
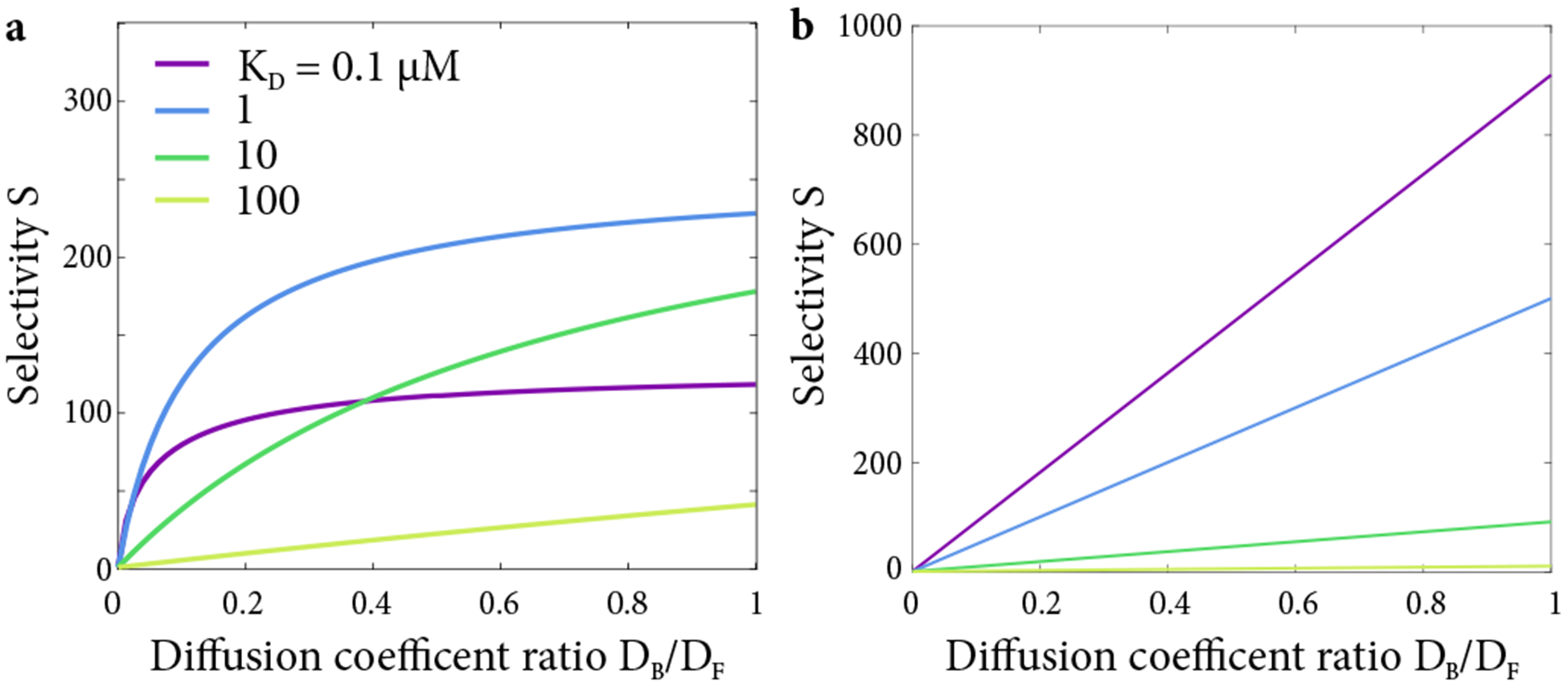
(a) Selectivity as a function of diffusion coefficient ratio, with varying dissociation constant in the full nonlinear model (b) Selectivity S as a function of diffusion coefficient ratio using the model described in Yang et al. [22]. The transport factor concentration in the reservoir is TL = 1 μM and the total Nup concentration is Nt = 1 mM.
The force F = −kΔx, where k is the spring constant of the FG Nup and Δx is the displacement of the particle from the Nup attachment point. We model the FG Nup as a worm-like-chain at small extension, so that , where is the tether persistence length and Lc is the contour length. Then
| (21) |
where K is the normalized spring constant .
We constructed the transfer probability Pt to satisfy the principle of detailed balance. During every iteration of the simulation, we picked an FG Nup at random from a list of the M Nups near enough to have a reasonable probability of transfer. TF transfer to the new FG Nup was attempted with success probability
| (22) |
Here the base transfer rate rt is a dimensionless input parameter, and the change in free energy (in units of kBT ) between the current Nup and the proposed new Nup is
| (23) |
where K is the normalized spring constant, x is the particle’s current position, xcur is the anchor location of the Nup to which the particle is currently bound, and xnew is the anchor location of the proposed new Nup. Note that when a transfer succeeded, the energy landscape changed to that of the new Nup, but the TF’s position did not change during the transfer. There is no upper bound on Pt, but we adjusted the timestep to ensure that Pt was greater than unity no more than 0.5% of the time that a transfer was attempted.
Figure 11.
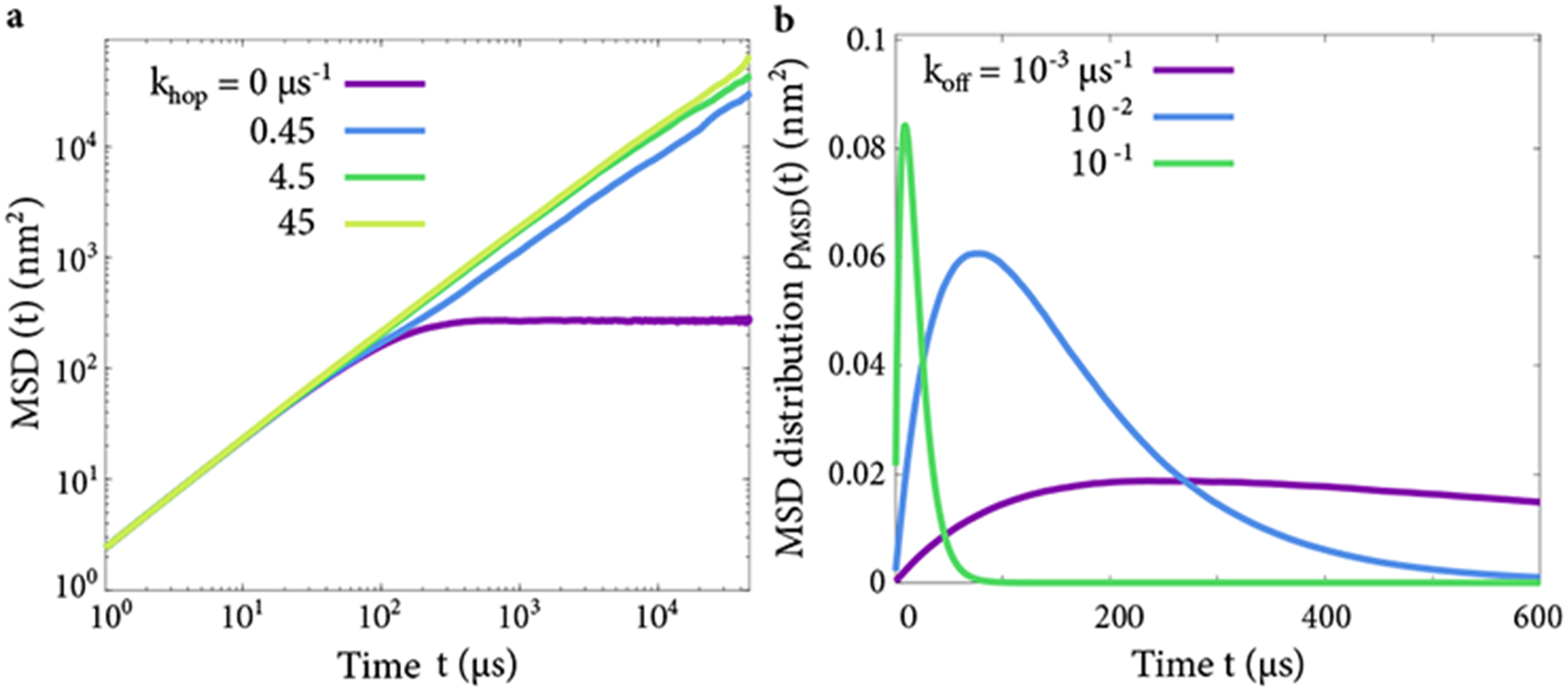
(a) Examples of mean-squared displacement (MSD) of a simulated TF in the inter-chain transfer model, with varying transfer rate. (b) Examples of MSD distributions ρMSD(t) used in estimating the diffusion coefficient, with varying unbinding rate. Tethers have 40 nm contour length; other parameters are as discussed in the main text.
We ran each simulation for 107 time steps with δt = 0.01 μs and recorded the particle’s position every 100 time steps. We calculated the mean-squared displacement (MSD) 〈x2〉 of the TF and averaged it over 100 runs [Fig. 11(a)]. We then computed
| (24) |
as shown in Fig. 11(b), and numerically integrated the distribution in time. We determined the bound diffusion coefficient from the typical MSD-per-binding-event using
| (25) |
Here, the factor of 1/2 is appropriate because we consider a one-dimensional random walk.
Figure 12.
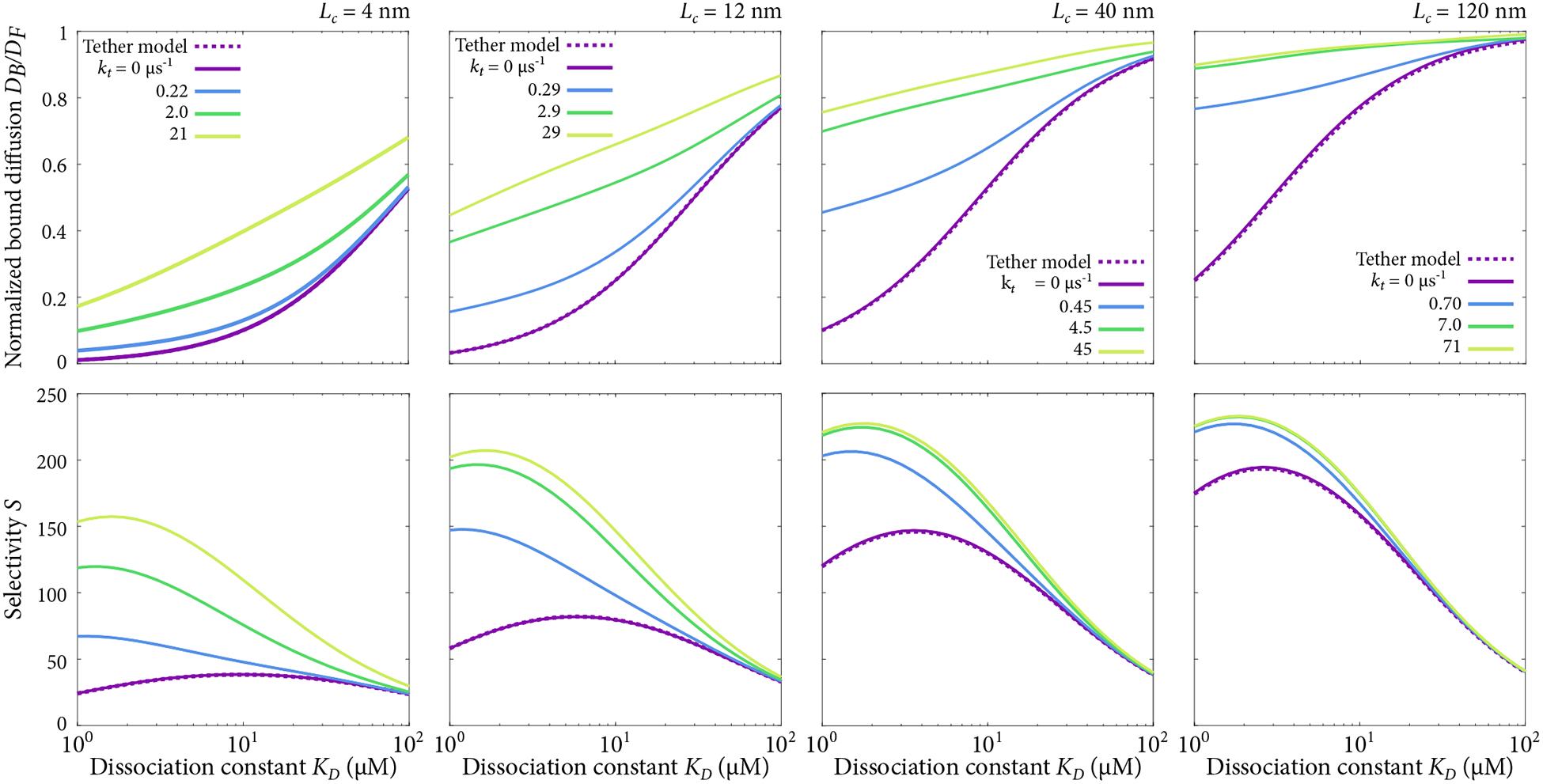
Diffusion constant ratio DB/DF (top) and selectivity S (bottom) for model incorporating tethered diffusion and inter-chain transfer. Polymer contour lengths of Lc = 4, 12, 40, and 120 nm are shown with a number of transfer rates kt.
Table II.
Predicted selectivity S (for a 100-nm barrier) of FG Nup hydrogels in previous work. We took partition and diffusion coefficients from tables in references or calculated them using concentration plots. We determined the dissociation constant KD from the partition coefficient of the binding species (PB) and non-binding species (PN) and the Nup concentration Nt using KD ≈ (PI/PB)Nt. Note that the measured PB is an underestimate of the true partition coefficient. We estimated the bound diffusion coefficient from the in-gel (effective) diffusion coefficient (Deff) and the probability of the binding species being bound (pb ≈ 1 − KD/Nt) using DB = pbDeff. We used the reaction-diffusion equations discussed in the main text to estimate the selectivity. Because partition coefficient estimates were lower bounds, we also calculated selectivity assuming that the reported partition coefficients were 10% of their actual value. P - Nsp1 (274–601) - P * refers to a fusion between Nsp1 (274–601) and a pentameric coiled-coil P which facilitates the aggregation of the Nsp1 domain into hydrogels. See [70].
| Nup fragment | Nup concentration | Molecule | MW | Partition coeff. | Diffusion coeff. in gel | Diffusion coeff. free | KD | DB | DB/DF | S | S with 10x partition coeff. | Notes |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nsp1 (2–601) | 3 mM | IBB-MBP-mEGFP-ImpB MBP-mCherry |
510 kD 70 kD |
100 0.16 |
0.17 μm2 /s | 4.03 μm2 /s | 4.8 μM | 0.17 μm2 /s | 0.04 | 42 | 50 | [89] |
| Nup57 (1–223)-Nup49 (1–246) | 3.7 mM | IBB-MBP-mEGFP-ImpB MBP-mCherry |
510 kD 70 kD |
400 0.15 |
0.1 μm2 /s | 2.7 μm2 /s | 1.4 μM | 0.1 μm2 /s | 0.04 | 69 | 45 | [89] |
| Nup57 (1–223)-Nsp1 (2–601)-Nup49 (1–246) | 1.7 mM | IBB-MBP-mEGFP-ImpB MBP-mCherry |
510 kD 70 kD |
350 0.1 |
0.24 μm2 /s | 4.03 μm2 /s | 0.48 μM | 0.24 μm2 /s | 0.06 | 38 | 16 | [89] |
| Nsp1 (2–175) | 3.0 mM | IBB-MBP-mEGFP-ImpB MBP-mCherry |
510 kD 70 kD |
100 3 |
0.04 μm2 /s | 12.1 μm2 /s | 90 μM | 0.04 μm2 /s | 0.003 | 1.4 | 4.3 | [90] |
| Nsp1 (2–601) | 3.0 mM | IBB-MBP-mEGFP-ImpB MBP-mCherry |
510 kD 70 kD |
60 0.4 |
0.22 μm2 /s | 6.94 μm2 /s | 20 μM | 0.22 μm2 /s | 0.03 | 15 | 40 | [90] |
| Nsp1 (1–601) | 2.2 mM | IBB-Redstar-ImpB IBB-Redstar |
530 kD 150 kD |
1000 0.3 |
0.1 μm2 /s | 0.2 μm2 /s | 0.66 μM | 0.1 μm2 /s | 0.5 | 230 | 100 | [69] |
| Nsp1 (1–601) | 2.2 mM | GFP-ImpB IBB-Redstar |
124 kD 150 kD |
100 0.3 |
0.1–0.2 μm2 /s | 0.2 μm2 /s | 6.6 μM | 0.1–0.2 μm2 /s | 0.5–1 | 210–250 | 230–240 | [69] |
| Nsp1 (1–601) | 2.2 mM | GFP-ImpB acRedStar |
124 kD 117 kD |
100 0.05 |
0.1–0.2 μm2 /s | 0.2–1 μm2 /s | 1.1 μM | 0.1–0.2 μm2 /s | 0.1–1 | 94–260 | 53–130 | [69] |
| P - Nsp1 (274–601) - P * | 4.4 mM | IBB-MBP-mEGFP-ImpB IBB-MBP-mEGFP |
510 kD 100 kD |
7 0.9 |
2.78 μm2 /s | 16.0 μm2 /s | 560 μM | 2.42 μm2 /s | 0.15 | 5.3 | 25 | [70] |
References
- [1].Witten J and Ribbeck K, Nanoscale 9, 8080 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Zhou R, Zhou H, Xiong B, He Y, and Yeung ES, Journal of the American Chemical Society 134, 13404 (2012). [DOI] [PubMed] [Google Scholar]
- [3].Strambio-De-Castillia C, Niepel M, and Rout MP, Nature Reviews Molecular Cell Biology 11, 490 (2010). [DOI] [PubMed] [Google Scholar]
- [4].Schneider AFL and Hackenberger CPR, Current Opinion in Biotechnology 48, 61 (2017). [DOI] [PubMed] [Google Scholar]
- [5].Huang X, Chisholm J, Zhuang J, Xiao Y, Duncan G, Chen X, Suk JS, and Hanes J, Proceedings of the National Academy of Sciences 114, E6595 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Mastorakos P, da Silva AL, Chisholm J, Song E, Choi WK, Boyle MP, Morales MM, Hanes J, and Suk JS, Proceedings of the National Academy of Sciences 112, 8720 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Olmsted SS, Padgett JL, Yudin AI, Whaley KJ, Moench TR, and Cone RA, Biophysical Journal 81, 1930 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Lai SK, Hida K, Shukair S, Wang Y-Y, Figueiredo A, Cone R, Hope TJ, and Hanes J, Journal of Virology 83, 11196 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Yang W, Gelles J, and Musser SM, Proceedings of the National Academy of Sciences of the United States of America 101, 12887 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Moussavi-Baygi R, Jamali Y, Karimi R, and Mofrad MRK, PLoS computational biology 7, e1002049 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Hough LE, Dutta K, Sparks S, Temel DB, Kamal A, Tetenbaum-Novatt J, Rout MP, and Cowburn D, eLife , e10027 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Milles S, Mercadante D, Aramburu IV, Jensen MR, Banterle N, Koehler C, Tyagi S, Clarke J, Shammas SL, Blackledge M, Gräter F, and Lemke EA, Cell 163, 734 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [13].Lai SK, Suk JS, Pace A, Wang Y-Y, Yang M, Mert O, Chen J, Kim J, and Hanes J, Biomaterials 32, 6285 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Tang C-JC, Fu R-H, Wu K-S, Hsu W-B, and Tang TK, Nature Cell Biology 11, 825 (2009). [DOI] [PubMed] [Google Scholar]
- [15].Juge N, Trends in Microbiology 20, 30 (2012). [DOI] [PubMed] [Google Scholar]
- [16].Plotkowski MC and Puchelle E, Eur Respir J. , 14 (1993). [PubMed] [Google Scholar]
- [17].Arora SK, Ritchings BW, Almira EC, Lory S, and Ramphal R, Infection and Immunity 66, 1000 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Martins M, Aymeric L, du Merle L, Danne C, Robbe-Masselot C, Trieu-Cuot P, Sansonetti P, and Dramsi S, The Journal of Infectious Diseases 212, 1646 (2015). [DOI] [PubMed] [Google Scholar]
- [19].Wyman J, Journal of Biological Chemistry 241, 115 (1966). [PubMed] [Google Scholar]
- [20].Cussler EL, Aris R, and Bhown A, Journal of Membrane Science 43, 149 (1989). [Google Scholar]
- [21].Berezhkovskii AM and Bezrukov SM, Biophysical Journal 88, L17 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Yang YJ, Mai DJ, Dursch TJ, and Olsen BD, Biomacromolecules (2018), 10.1021/acs.biomac.8b00556. [DOI] [PubMed] [Google Scholar]
- [23].Raveh B, Karp JM, Sparks S, Dutta K, Rout MP, Sali A, and Cowburn D, Proceedings of the National Academy of Sciences 113, E2489 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [24].Fogelson B and Keener JP, Biophysical Journal 115, 108 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Goodrich CP, Brenner MP, and Ribbeck K, Nature Communications 9, 4348 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Cai L-H, Panyukov S, and Rubinstein M, Macromolecules 48, 847 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Rout MP, Aitchison JD, Magnasco MO, and Chait BT, Trends in cell biology 13, 622 (2003). [DOI] [PubMed] [Google Scholar]
- [28].Timney BL, Raveh B, Mironska R, Trivedi JM, Kim SJ, Russel D, Wente SR, Sali A, and Rout MP, J Cell Biol , jcb.201601004 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Tagliazucchi M, Peleg O, Kroeger M, Rabin Y, and Szleifer I, Proceedings of the National Academy of Sciences of the United States of America 110, 3363 (2013), wOS:000315841900039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30].Zilman A, Talia SD, Chait BT, Rout MP, and Magnasco MO, PLOS Computational Biology 3, e125 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Tu L-C, Fu G, Zilman A, and Musser SM, The EMBO journal 32, 3220 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Ro S, Gopinathan A, and Kim YW, Physical Review E 98, 012403 (2018). [DOI] [PubMed] [Google Scholar]
- [33].Ghavami A, van der Giessen E, and Onck PR, PLOS ONE 11, e0148876 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Tan PS, Aramburu IV, Mercadante D, Tyagi S, Chowdhury A, Spitz D, Shammas SL, Gräter F, and Lemke EA, Cell Reports 22, 3660 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Mercadante D, Milles S, Lemke EA, and Gräter F, Biophysical Journal 108, 193a (2015). [Google Scholar]
- [36].Milles S and Lemke EA, Angewandte Chemie International Edition 53, 7364 (2014). [DOI] [PubMed] [Google Scholar]
- [37].Moussavi-Baygi R and Mofrad MRK, Scientific Reports 6 (2016), 10.1038/srep29991. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Pagliara S, Dettmer SL, and Keyser UF, Physical Review Letters 113 (2014), 10.1103/Phys-RevLett.113.048102. [DOI] [PubMed] [Google Scholar]
- [39].Ghavami A, Veenho LM , van der Giessen E, and Onck PR, Biophysical Journal 107, 1393 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Strawn LA, Shen T, Shulga N, Goldfarb DS, and Wente SR, Nature cell biology 6, 197 (2004), pMID: 15039779. [DOI] [PubMed] [Google Scholar]
- [41].Zeitler B and Weis K, J Cell Biol 167, 583 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Kowalczyk SW, Kapinos L, Blosser TR, Magalhães T, van Nies P, Lim RYH, and Dekker C, Nature Nanotechnology 6, 433 (2011). [DOI] [PubMed] [Google Scholar]
- [43].Jovanovic-Talisman T, Tetenbaum-Novatt J, McKenney AS, Zilman A, Peters R, Rout MP, and Chait BT, Nature 457, 1023 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Lowe AR, Siegel JJ, Kalab P, Siu M, Weis K, and Liphardt JT, Nature , 1 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Mincer JS and Simon SM, Proceedings Of The National Academy Of Sciences Of The United States Of America 108, E351 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [46].Lowe AR, Tang JH, Yassif J, Graf M, Huang WYC, Groves JT, Weis K, and Liphardt JT, eLife , e04052 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Kapinos LE, Schoch RL, Wagner RS, Schleicher KD, and Lim RYH, Biophysical Journal 106, 1751 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Ribbeck K and Görlich D, The EMBO Journal 20, 1320 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49].Siebrasse JP and Peters R, EMBO reports 3, 887 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Kiskin NI, Siebrasse JP, and Peters R, Biophysical Journal 85, 2311 (2003). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Pyhtila B and Rexach M, Journal of Biological Chemistry 278, 42699 (2003). [DOI] [PubMed] [Google Scholar]
- [52].Gilchrist D, Mykytka B, and Rexach M, Journal of Biological Chemistry 277, 18161 (2002). [DOI] [PubMed] [Google Scholar]
- [53].Tetenbaum-Novatt J, Hough LE, Mironska R, McKenney AS, and Rout MP, Molecular & Cellular Proteomics : MCP 11, 31 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54].Vovk A, Gu C, Opferman MG, Kapinos LE, Lim RY, Coalson RD, Jasnow D, and Zilman A, eLife 5, e10785 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Hayama R, Sparks S, Hecht LM, Dutta K, Karp JM, Cabana CM, Rout MP, and Cowburn D, Journal of Biological Chemistry 293, 4555 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56].Zilman A, Talia SD, Jovanovic-Talisman T, Chait BT, Rout MP, and Magnasco MO, PLOS Computational Biology 6, e1000804 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Kapinos LE, Huang B, Rencurel C, and Lim RYH, J Cell Biol , jcb.201702092 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [58].Timney BL, Tetenbaum-Novatt J, Agate DS, Williams R, Zhang W, Chait BT, and Rout MP, J Cell Biol 175, 579 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Schmidt HB and Görlich D, eLife 4, e04251 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Berezhkovskii AM, Pustovoit MA, and Bezrukov SM, The Journal of Chemical Physics 116, 9952 (2002). [Google Scholar]
- [61].Kutchai H, Jacquez JA, and Mather FJ, Biophysical Journal 10, 38 (1970). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Bickel T and Bruinsma R, Biophysical Journal 83, 3079 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [63].Juweid M, Neumann R, Paik C, Perez-Bacete MJ, Sato J, van Osdol W, and Weinstein JN, Cancer Research 52, 5144 (1992). [PubMed] [Google Scholar]
- [64].Lim RYH, Fahrenkrog B, Köser J, Schwarz-Herion K, Deng J, and Aebi U, Science 318, 640 (2007). [DOI] [PubMed] [Google Scholar]
- [65].Howard J, Mechanics of Motor Proteins and Cytoskeleton, 1st ed. (Sinauer Associates, 2001). [Google Scholar]
- [66].Doi M and Edwards SF, The Theory of Polymer Dynamics (Clarendon Press, 1988). [Google Scholar]
- [67].Receveur-Bréchot V and Durand D, Current Protein & Peptide Science 13, 55 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Patel SS, Belmont BJ, Sante JM, and Rexach MF, Cell 129, 83 (2007). [DOI] [PubMed] [Google Scholar]
- [69].Frey S and Görlich D, Cell 130, 512 (2007). [DOI] [PubMed] [Google Scholar]
- [70].Kim J, Li WA, Choi Y, Lewin SA, Verbeke CS, Drano G , and Mooney DJ, Nature biotechnology 33, 64 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [71].Schoch RL, Kapinos LE, and Lim RYH, Proceedings of the National Academy of Sciences 109, 16911 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72].Schopf LR, Popov AM, Enlow EM, Bourassa JL, Ong WZ, Nowak P, and Chen H, Translational Vision Science & Technology 4, 11 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [73].Chen A, McKinley SA, Wang S, Shi F, Mucha PJ, Forest MG, and Lai SK, Biophysical Journal 106, 2028 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74].Ensign LM, Tang BC, Wang Y-Y, Tse TA, Hoen T, Cone R, and Hanes J, Science Translational Medicine 4, 138ra79 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Kompella UB, Kadam RS, and Lee VH, Therapeutic Delivery 1, 435 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [76].Cone RA, Advanced Drug Delivery Reviews 61, 75 (2009). [DOI] [PubMed] [Google Scholar]
- [77].Aranha dos Santos V, Schmetterer L, Gröschl M, Garhofer G, Schmidl D, Kucera M, Unterhuber A, Hermand J-P, and Werkmeister RM, Optics Express 23, 21043 (2015). [DOI] [PubMed] [Google Scholar]
- [78].Rentka A, Hársfalvi J, Berta A, Köröskényi K, Szekanecz Z, Szücs G, Szodoray P, and Kemény-Beke Á, Mediators of Inflammation 2015 (2015), 10.1155/2015/573681. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [79].Sosnik A, das Neves J, and Sarmento B, Progress in Polymer Science Topical Issue on Biomaterials, 39, 2030 (2014). [Google Scholar]
- [80].Lock JY, Carlson TL, and Carrier RL, Advanced Drug Delivery Reviews 124, 34 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81].Stefferson MW, Norris SL, Vernerey FJ, Betterton MD, and Hough LE, Physical Biology 14, 045008 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [82].Braga J, McNally JG, and Carmo-Fonseca M, Biophysical Journal 92, 2694 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [83].Feric M, Vaidya N, Harmon TS, Mitrea DM, Zhu L, Richardson TM, Kriwacki RW, Pappu RV, and Brangwynne CP, Cell 165, 1686 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [84].Brangwynne CP, Tompa P, and Pappu RV, Nature Physics 11, 899 (2015). [Google Scholar]
- [85].Boeynaems S, Holehouse AS, Weinhardt V, Kovacs D, Lindt JV, Larabell C, Bosch LVD, Das R, Tompa P, Pappu RV, and Gitler A, bioRxiv , 492793 (2018). [Google Scholar]
- [86].Fogelson B and Keener J, SIAM Journal on Applied Mathematics , 1405 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [87].Grassia PS, Hinch EJ, and Nitsche LC, Journal of Fluid Mechanics 282, 373 (1995). [Google Scholar]
- [88].Blackwell R, Edelmaier C, Sweezy-Schindler O, Lamson A, Gergely ZR, O’Toole E, Crapo A, Hough LE, McIntosh JR, Glaser MA, and Betterton MD, Science Advances 3, e1601603 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [89].Frey S and Görlich D, The EMBO Journal 28, 2554 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- [90].Ader C, Frey S, Maas W, Schmidt HB, Gorlich D, and Baldus M, Proceedings of the National Academy of Sciences 107, 6281 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]


