Abstract
There are many local varieties of sweet potatoes which are cultivated and consumed in Indonesia. The food industry which uses sweet potato as the main raw material has been developed in West Java. Demand for orange-fleshed sweet potato is high, but the supply of demand has not been fulfilled. This is because the varieties that are widely cultivated do not meet consumer standards and preferences, so new superior genotypes are needed following demand. Currently, selection of stable and high-yielding genotypes and accordance with consumer and industry preferences is one of the focuses of sweet potato research. Orange-fleshed sweet potato multi locations testing in accordance with consumer and industry preferences, can be used as a basis for consideration in the development program. The purpose of this study were to identify genotype by environment interactions (GEIs) and t select superior genotypes and to estimate yield stability across three locations in West Java, Indonesia. Combined analysis of variance (ANOVA) was used to determine significant differences between each genotype tested in term of yield and to estimated genotype by environment interactions (GEIs). Additive Main Effects and Multiplicative Interaction (AMMI), Genotype Plus Genotype by Environment Interactions (GGE) biplots, and Parametric and non-parametric stability measurements were used to determine yield stability from genotypes tested in all locations (Sumedang Regency, Bandung Regency, Karawang Regency). Data in this article showed that the genotypes, environments, and GEIs had an effect on sweet potato yields, with influences of 35.03%, 18.87%, and 46.01%, respectively. The results in this data also indicate that some new sweet potato genotypes have stable and high yields in three environments in West Java, Indonesia. So they were can be used for development in sweet potato breeding programs.
Keywords: AMMI, GGE biplot, Stability, Orange-fleshed sweet potato
Specifications Table
| Subject | Data Article (Agricultural and Biological Science) |
| Specific subject area | Agricultural and Biological Science (general), Agronomy and Crop Science |
| Type of data | Table Figure |
| How data were acquired | Data was obtained by conducted field observations in three different locations. Data tables and figures were obtained by analyzing raw data using Genstat 12th software, Microsoft Excel 2010, and STABILITYSOFT. |
| Data format | Analyzed |
| Parameters for data collection | The conditions were considered for data collection was environmental conditions of the experiment. |
| Description of data collection | This data was collected by measured the yield of new sweet potatoes planted at three different locations. Harvest was done when the plants are 18 weeks after planting. The yields of each genotype are weighed whole by used a digital scale. The observed trait was tuber yield per plot. Yields were converted in tons / ha |
| Data source location | City/Town/Region: Sumedang, Bandung, Karawang Country: Indonesia Latitude and longitude for collected samples/data: latitude 6 ° 55′00.6 "S, longitude 107 ° 46′18.3" E (Sumedang); latitude 7° 03′35.3 "S, longitude 107 ° 38′46.5" E (Bandung); latitude 6 ° 20′15.1 "S, longitude 107 ° 18′20.2" E (Karawang) Altitude: 753 m.a.s.l. (Sumedang); 996 m.a.s.l. (Bandung); 24 m.a.s.l. (Karawang) |
| Data accessibility | With the article |
Value of the Data
-
•
This data set provides additional information about the effect of different environmental conditions on the yield of new orange-fleshed sweet potatoes.
-
•
The dataset in this article provides information to researchers, farmers, and industry users, about the stability of new orange-fleshed sweet potato yields planted in West Java, Indonesia.
-
•
The data provided can be useful in genetic studies and plant breeding programs, especially the stability of sweet potato yields, as well as for industrial users for the development of planting areas.
1. Data Description
Sweet potatoes usually have different yield potential if planted in diverse environments. Potential yield is one of the important characters in crops [1]. The yield can be also provided economic value to farmers, the community, and also industry users. In the food industry, information about suitable planting locations is one of the important things in the development of planting raw materials. Yields also play an important role in the development of sweet potatoes. This can also be a benchmark for farmers and industry in using certain varieties. Information about GEIs is very important in sweet potato breeding programs [2]. The existence of GEIs makes it difficult in the process of plants selection [2,3]. Stable and high yield are ideal genotypes expected by plant breeders and farmers [4,5]. This data set consists of information about the yields of 23 genotypes of new orange-fleshed sweet potatoes crossing which were planted in three different locations in West Java, Indonesia. The data presented in this article consists of three (3) figures and four (4) tables.
Table 1 shows the results of a combined variance analysis of genotypes tested in three environments. Table 2 presents the variation of yield from 23 sweet potato genotypes in three locations, while Table 3 shows the yield stability values in three environments with ASV and GSI models. Table 4 presented the parametric and non-parametric stability measurements for sweet potato genotypes. Based on the parametric stability in Table 4, ten genotypes in the current study showed higher bi values, indicating better adaptability of these genotypes to high-yielding environments. It is shown that MZ276, with b = 1.04, and MZ121 with b = 0.78, have slopes nearest to 1.00 among the 23 genotypes in the data set. On this criteria, MZ276 and MZ121 would be selected as the most stable of the 23 genotypes over the three environments in this multilocations test. Furthermore, these genotypes have the smallest deviation from regression on site index. This is measured by the deviation mean square of S2di of all genotypes and yield. In contrast, MZ202, MZ214, and MZ237 performs to be adapted to better environments. This is confirmed by the slope for this genotypes, bi = 2.12; bi = 3.48; and bi = 4.01, respectively, which is greater than 1 and also showed the highest yield out of 23 genotypes over three environments. Measurements S(1), S(2), S(3), and S(6) estimate MZ119, MZ127, and MZ270 as the most stable. NP(1) estimated MZ270, MZ276, and Beta-2 as the most stable genotypes, while NP(2), NP(3), and NP(4) selected mz119 as the most stable genotypes. Based on the combination of parametric and non-parametric stability measurements, genotypes that have a low average rank (AR) are stable genotypes [4].
Table 1.
Combined variance analysis of 23 sweet potato genotypes.
| Source | Df | SS | MS | F | F_prob | |
|---|---|---|---|---|---|---|
| Block(Environments) | 6 | 0.36 | 0.06 | 0.30 | 0.97324 | |
| Genotypes (G) | 22 | 134.65 | 6.12 | 32.27 | 0.00000 | ** |
| Locations (E) | 2 | 72.52 | 36.26 | 641.61 | 0.00000 | ** |
| Interactions (GEIs) | 44 | 176.88 | 4.02 | 21.17 | 0.00000 | ** |
| Min. (ton/ha) | 0.05 | |||||
| Max. (ton/ha) | 39.72 | |||||
| Average (ton/ha) | 11.93 | |||||
| CV (%) | 13.82 |
Df= Degree freedom; SS= Sum of Square; MS= Mean of Square; Min. = Minimum Value; Max.= Maximum Value; ** p<0.01.
Table 2.
Yield potential different on orange-fleshed sweet potato in each location.
| Genotypes | Sumedang | Bandung | Karawang | |||
|---|---|---|---|---|---|---|
| MZ119 | 17.40 | cd | 17.10 | a | 15.30 | abc |
| MZ121 | 17.70 | cd | 18.70 | a | 7.65 | def |
| MZ127 | 12.70 | de | 15.80 | a | 9.20 | def |
| MZ128 | 11.20 | de | 17.10 | a | 6.40 | def |
| MZ154 | 27.90 | ab | 2.90 | de | 5.75 | efg |
| MZ202 | 33.50 | ab | 12.90 | a | 16.80 | ab |
| MZ214 | 34.10 | ab | 15.00 | a | 0.10 | i |
| MZ235 | 11.50 | de | 1.00 | e | 0.75 | hi |
| MZ236 | 2.70 | g | 3.60 | cd | 2.65 | gh |
| MZ237 | 37.23 | a | 4.50 | bcd | 2.85 | gh |
| MZ247 | 23.50 | bc | 7.10 | b | 11.35 | bcd |
| MZ270 | 6.10 | f | 1.10 | e | 0.10 | i |
| MZ276 | 12.60 | de | 6.70 | bc | 2.55 | gh |
| MZ290 | 13.70 | de | 2.00 | de | 0.10 | i |
| MZ332 | 24.93 | bc | 2.70 | de | 19.20 | a |
| MZ462 | 4.10 | fg | 4.00 | bcd | 17.80 | a |
| MZ496 | 37.20 | a | 1.90 | de | 5.35 | fg |
| Kidal | 10.96 | de | 16.97 | a | 10.62 | bcd |
| Rancing | 13.70 | de | 17.71 | a | 16.34 | ab |
| Beniazuma | 10.35 | e | 19.00 | a | 9.83 | cdef |
| Beta-2 | 11.36 | de | 13.52 | a | 9.20 | cdef |
| Keriting Maja | 12.22 | de | 18.18 | a | 8.68 | def |
| AC-Putih | 10.89 | e | 15.62 | a | 10.44 | bcde |
| Kidal | 17.40 | cd | 17.10 | a | 15.30 | abc |
| Mean | 17.28 | 10.22 | 8.22 | |||
| CV (%) | 9.29 | 13.65 | 18.28 | |||
Means followed by the same letter are not significantly difference, while those followed by different letters had significant difference at the 5% level by Duncan test; CV = coefficient of variation.
Table 3.
Mean performance of sweet potato genotypes based on AMMI Stability Value (ASV) and Genotype Stability Index (GSI).
| No. | Genotype | MY | RMY | IPCA[1] | IPCA[2] | ASV | RASV | GSI | RGSI |
|---|---|---|---|---|---|---|---|---|---|
| 1 | MZ119 | 16.60 | 2 | 0.81 | −0.17 | 1.58 | 5 | 7 | 1 |
| 2 | MZ121 | 14.68 | 8 | 0.54 | 1.22 | 1.60 | 6 | 14 | 2 |
| 3 | MZ127 | 12.57 | 13 | 0.99 | 0.49 | 1.98 | 10 | 23 | 7 |
| 4 | MZ128 | 11.57 | 16 | 1.13 | 1.06 | 2.44 | 12 | 28 | 18 |
| 5 | MZ154 | 12.18 | 15 | −1.90 | −0.37 | 3.70 | 19 | 34 | 22 |
| 6 | MZ202 | 21.07 | 1 | −1.33 | −0.62 | 2.65 | 16 | 17 | 4 |
| 7 | MZ214 | 16.40 | 3 | −2.02 | 2.22 | 4.50 | 21 | 24 | 9 |
| 8 | MZ235 | 4.42 | 21 | −0.33 | −0.20 | 0.66 | 3 | 24 | 10 |
| 9 | MZ236 | 2.98 | 22 | 0.99 | −0.33 | 1.95 | 9 | 31 | 21 |
| 10 | MZ237 | 14.86 | 6 | −3.02 | 0.48 | 5.88 | 22 | 28 | 19 |
| 11 | MZ247 | 13.98 | 9 | −0.82 | −0.76 | 1.76 | 7 | 16 | 3 |
| 12 | MZ270 | 2.43 | 23 | 0.29 | −0.20 | 0.60 | 2 | 25 | 13 |
| 13 | MZ276 | 7.28 | 19 | 0.04 | 0.30 | 0.31 | 1 | 20 | 6 |
| 14 | MZ290 | 5.27 | 20 | −0.54 | 0.08 | 1.06 | 4 | 24 | 11 |
| 15 | MZ332 | 15.61 | 5 | −0.94 | −2.52 | 3.11 | 18 | 23 | 8 |
| 16 | MZ462 | 8.63 | 18 | 1.56 | −2.56 | 3.96 | 20 | 38 | 23 |
| 17 | MZ496 | 14.82 | 7 | −3.09 | −0.25 | 5.99 | 23 | 30 | 20 |
| 18 | Kidal | 12.85 | 12 | 1.35 | 0.39 | 2.64 | 15 | 27 | 16 |
| 19 | Rancing | 15.92 | 4 | 1.34 | −0.33 | 2.62 | 14 | 18 | 5 |
| 20 | Beniazuma | 13.06 | 10 | 1.53 | 0.77 | 3.06 | 17 | 27 | 17 |
| 21 | Beta-2 | 11.36 | 17 | 0.99 | 0.16 | 1.91 | 8 | 25 | 14 |
| 22 | Keriting Maja | 13.03 | 11 | 1.20 | 0.88 | 2.48 | 13 | 24 | 12 |
| 23 | AC-Putih | 12.32 | 14 | 1.25 | 0.24 | 2.43 | 11 | 25 | 15 |
MY= Mean yield; RMY=Rank of Mean Yield; IPCA = Interaction Principal Component AxisASV= AMMI Stability Value; RASV= Rank of ASV; GSI= Genotype Stability Index; RGSI= Rank of GSI.
Table 4.
Yield stability based on parametic and non-parametric measures.
| Genotype | Y | S⁽¹⁾ | S⁽²⁾ | S⁽³⁾ | S⁽⁶⁾ | NP⁽¹⁾ | NP⁽²⁾ | NP⁽³⁾ | NP⁽⁴⁾ | Wᵢ² | σ²ᵢ | s²dᵢ | bᵢ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SP1 | 16.60 | 2.67 | 4.33 | 0.50 | 0.27 | 4.67 | 0.09 | 0.20 | 0.15 | 31.44 | 14.22 | 0.15 | 0.18 | |
| SP2 | 14.68 | 7.33 | 30.33 | 3.71 | 0.69 | 7.33 | 0.21 | 0.38 | 0.45 | 49.27 | 23.98 | 6.73 | 0.78 | |
| SP3 | 12.57 | 2.67 | 4.33 | 0.63 | 0.34 | 4.00 | 0.21 | 0.22 | 0.20 | 51.80 | 25.37 | 2.93 | 0.17 | |
| SP4 | 11.57 | 7.33 | 32.33 | 5.54 | 1.09 | 10.33 | 0.57 | 0.63 | 0.63 | 87.28 | 44.80 | 8.02 | 0.17 | |
| SP5 | 12.18 | 8.67 | 46.33 | 8.18 | 1.35 | 10.33 | 0.46 | 0.65 | 0.76 | 172.16 | 91.28 | 5.18 | 2.73 | |
| SP6 | 21.07 | 6.00 | 24.33 | 2.75 | 0.64 | 7.67 | 0.16 | 0.33 | 0.34 | 92.13 | 47.45 | 4.97 | 2.12 | |
| SP7 | 16.40 | 13.33 | 103.00 | 17.17 | 1.83 | 10.33 | 0.43 | 0.68 | 1.11 | 310.96 | 167.29 | 4.71 | 3.48 | |
| SP8 | 4.42 | 5.33 | 16.33 | 7.00 | 1.86 | 3.67 | 1.15 | 0.61 | 1.14 | 5.91 | 0.24 | 0.39 | 1.26 | |
| SP9 | 2.98 | 4.00 | 10.33 | 4.43 | 1.57 | 6.00 | 2.19 | 1.05 | 0.86 | 48.60 | 23.62 | 0.08 | -0.03 | |
| SP10 | 14.86 | 10.67 | 76.00 | 11.69 | 1.54 | 13.00 | 0.42 | 0.71 | 0.82 | 433.24 | 234.25 | 3.05 | 4.01 | |
| SP11 | 13.98 | 4.67 | 14.33 | 1.87 | 0.57 | 5.33 | 0.15 | 0.33 | 0.30 | 45.27 | 21.79 | 4.15 | 1.60 | |
| SP12 | 2.43 | 1.33 | 1.00 | 1.00 | 1.00 | 2.00 | 4.33 | 0.82 | 0.67 | 4.89 | -0.32 | 0.01 | 0.67 | |
| SP13 | 7.28 | 4.00 | 10.33 | 2.38 | 0.85 | 2.67 | 0.48 | 0.29 | 0.46 | 2.31 | -1.73 | 0.32 | 1.04 | |
| SP14 | 5.27 | 8.00 | 39.00 | 13.00 | 2.33 | 5.33 | 0.77 | 0.64 | 1.33 | 14.02 | 4.68 | 0.11 | 1.54 | |
| SP15 | 15.61 | 12.00 | 86.33 | 11.26 | 1.35 | 8.33 | 0.32 | 0.55 | 0.78 | 194.53 | 103.53 | 27.24 | 1.29 | |
| SP16 | 8.63 | 13.33 | 105.33 | 19.75 | 2.13 | 12.67 | 0.56 | 0.87 | 1.25 | 272.19 | 146.06 | 10.01 | -1.11 | |
| SP17 | 14.82 | 12.67 | 97.00 | 17.64 | 2.00 | 14.00 | 0.55 | 0.90 | 1.15 | 448.73 | 242.73 | 9.49 | 3.90 | |
| C1 | 12.85 | 7.33 | 40.33 | 6.05 | 1.10 | 6.67 | 0.39 | 0.51 | 0.55 | 88.64 | 45.55 | 3.40 | -0.20 | |
| C2 | 15.92 | 4.67 | 16.33 | 1.85 | 0.53 | 8.00 | 0.17 | 0.42 | 0.26 | 86.68 | 44.47 | 0.33 | -0.36 | |
| C3 | 13.06 | 12.67 | 91.00 | 13.00 | 1.43 | 10.33 | 0.39 | 0.61 | 0.90 | 123.76 | 64.78 | 7.07 | -0.28 | |
| C4 | 11.36 | 3.33 | 8.33 | 1.47 | 0.59 | 3.00 | 0.44 | 0.31 | 0.29 | 46.04 | 22.21 | 1.27 | 0.10 | |
| C5 | 13.03 | 7.33 | 34.33 | 4.79 | 0.93 | 9.00 | 0.32 | 0.45 | 0.51 | 85.44 | 43.79 | 6.56 | 0.07 | |
| C6 | 12.32 | 7.33 | 37.00 | 6.17 | 1.17 | 4.33 | 0.38 | 0.51 | 0.61 | 74.47 | 37.78 | 2.23 | -0.14 | |
| Genotype | Y | S⁽¹⁾ | S⁽²⁾ | S⁽³⁾ | S⁽⁶⁾ | NP⁽¹⁾ | NP⁽²⁾ | NP⁽³⁾ | NP⁽⁴⁾ | Wᵢ² | σ²ᵢ | s²dᵢ | bi | AR |
| SP1 | 2 | 2 | 3 | 1 | 1 | 7 | 1 | 1 | 1 | 5 | 5 | 4 | 11 | 3.38 |
| SP2 | 8 | 11 | 11 | 9 | 7 | 12 | 6 | 7 | 7 | 9 | 9 | 18 | 2 | 8.92 |
| SP3 | 13 | 2 | 2 | 2 | 2 | 5 | 5 | 2 | 2 | 10 | 10 | 10 | 13 | 6.00 |
| SP4 | 16 | 11 | 12 | 12 | 11 | 17 | 19 | 15 | 12 | 14 | 14 | 20 | 12 | 14.23 |
| SP5 | 15 | 17 | 17 | 16 | 15 | 17 | 15 | 17 | 14 | 18 | 18 | 16 | 19 | 16.46 |
| SP6 | 1 | 10 | 10 | 8 | 6 | 13 | 3 | 6 | 6 | 16 | 16 | 15 | 18 | 9.85 |
| SP7 | 3 | 22 | 22 | 21 | 19 | 17 | 13 | 18 | 19 | 21 | 21 | 14 | 21 | 17.77 |
| SP8 | 21 | 9 | 8 | 15 | 20 | 4 | 21 | 14 | 20 | 3 | 3 | 7 | 3 | 11.38 |
| SP9 | 22 | 5 | 6 | 10 | 18 | 10 | 22 | 23 | 17 | 8 | 8 | 2 | 17 | 12.92 |
| SP10 | 6 | 18 | 18 | 18 | 17 | 22 | 12 | 19 | 16 | 22 | 22 | 11 | 23 | 17.23 |
| SP11 | 9 | 7 | 7 | 6 | 4 | 8 | 2 | 5 | 5 | 6 | 6 | 13 | 7 | 6.54 |
| SP12 | 23 | 1 | 1 | 3 | 10 | 1 | 23 | 20 | 13 | 2 | 2 | 1 | 5 | 8.08 |
| SP13 | 19 | 5 | 5 | 7 | 8 | 2 | 16 | 3 | 8 | 1 | 1 | 5 | 1 | 6.23 |
| SP14 | 20 | 16 | 15 | 19 | 23 | 8 | 20 | 16 | 23 | 4 | 4 | 3 | 6 | 13.62 |
| SP15 | 5 | 19 | 19 | 17 | 14 | 15 | 8 | 12 | 15 | 19 | 19 | 23 | 4 | 14.54 |
| SP16 | 18 | 22 | 23 | 23 | 22 | 21 | 18 | 21 | 22 | 20 | 20 | 22 | 20 | 20.92 |
| SP17 | 7 | 20 | 21 | 22 | 21 | 23 | 17 | 22 | 21 | 23 | 23 | 21 | 22 | 20.23 |
| C1 | 12 | 11 | 16 | 13 | 12 | 11 | 11 | 10 | 10 | 15 | 15 | 12 | 10 | 12.15 |
| C2 | 4 | 7 | 9 | 5 | 3 | 14 | 4 | 8 | 3 | 13 | 13 | 6 | 8 | 7.46 |
| C3 | 10 | 20 | 20 | 19 | 16 | 17 | 10 | 13 | 18 | 17 | 17 | 19 | 9 | 15.77 |
| C4 | 17 | 4 | 4 | 4 | 5 | 3 | 14 | 4 | 4 | 7 | 7 | 8 | 15 | 7.38 |
| C5 | 11 | 11 | 13 | 11 | 9 | 16 | 7 | 9 | 9 | 12 | 12 | 17 | 16 | 11.77 |
| C6 | 14 | 11 | 14 | 14 | 13 | 6 | 9 | 11 | 11 | 11 | 11 | 9 | 14 | 11.38 |
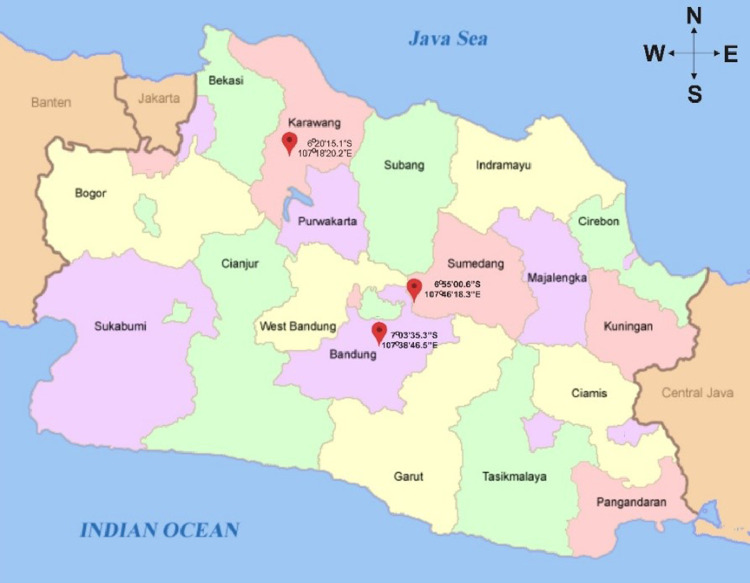
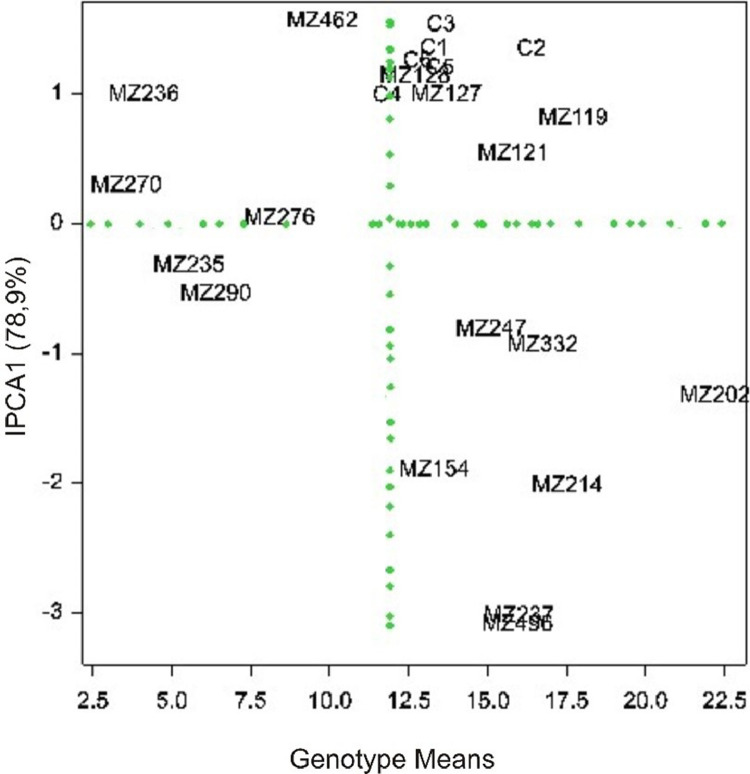
Fig. 1 shows the different planting locations in West Java, Indonesia. Fig. 2 shows the results of stability analysis used AMMI. In the Fig. 2, the horizontal line shows zero interaction with environment (PCA1). Sweet potato genotypes close to the line have a small GEIs effect or stable. The vertical center line represents the average value of sweet potato yield. Genotypes on the right-hand side have higher yields (above the overall average) compared to those on the left-hand side. Genotypes that approach the zero IPCA1 line are stated to be the most stable and high yield, they were MZ119, MZ121, MZ247, and MZ332.
Fig. 1.
Field Trial Location in West Java, Indonesia.
Fig. 2.
Biplot analysis of genotype by environment interaction based on AMMI1 model for the IPCA1 scores and sweet potato genotype in three location (1 = Sumedang regency, 2 = Bandung regency, and 3 = Kawarang regency) for yield character.
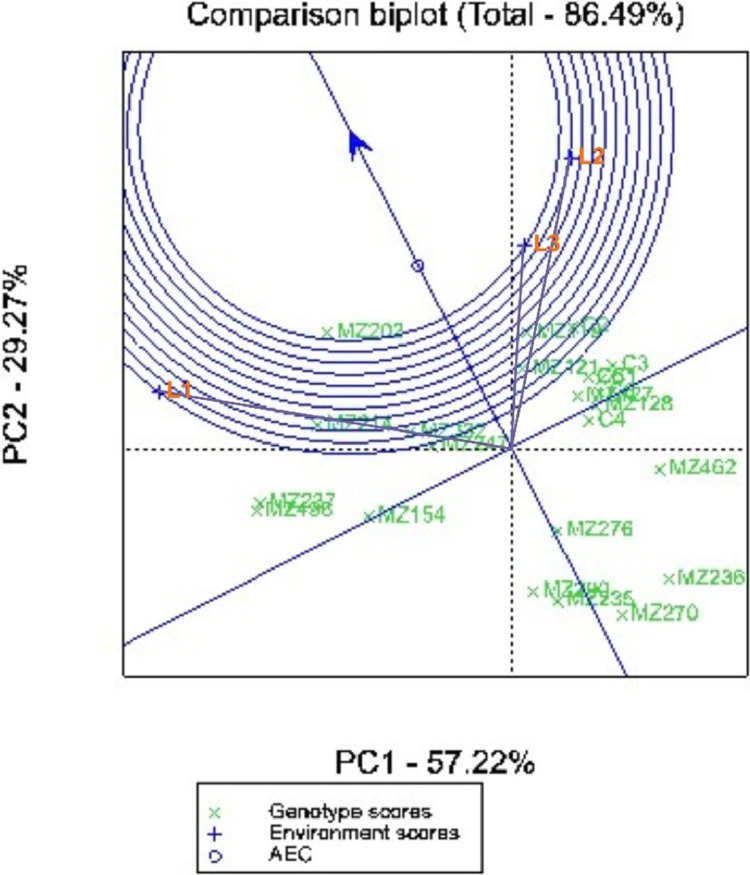
Fig. 3, showed the experimental location differ in discriminating ability and representativeness on the performance of sweet potato genotypes. The length of the experimental location vector from the biplot origin shows the discriminating ability of the location on superior genotypes for yield. The representativeness of the experimental location was indicated by the small angle between the experimental location and the average environmental axis. L3 (Karawang), has small angle to the average environmental compared (AEC), which means it was more representative than other locations. L1 (Sumedang), has the longest vector from the biplot origin, so it has good discriminating ability compared to other locations. L2 (bandung) has the second longest vector after L1 and has the second smaller angle to the AEC after L3. L2 and L3 both fall into the firts concentric circle of the ideal environment and closer to average environment compared L1. Thus, L2 had better discriminating ability and representativeness, and is an ideal location for evaluating the yield of sweet potato genotypes.
Fig. 3.
Rank's of the experimental location (L1 = Sumedang regency, L2 = Bandung regency, and L3 = Kawarang regency) based on discriminative and representativeness for sweet potato genotypes yield.
2. Experimental Design, Materials and Methods
2.1. Plant materials
The genetic materials used include seventeen new breeding genotypes, namely, MZ119, MZ121, MZ127, MZ128, MZ154, MZ202, MZ214, MZ235, MZ236, MZ237, MZ247, MZ270, MZ276, MZ290, MZ332, MZ462, MZ496, and six commercial varieties as checks, namely, Kidal (C1), Rancing (C2), Beniazuma (C3), Beta-2 (C4), Keriting Maja (C5), and AC Putih (C6). These tubers were previously selected based on consumer preferences.
2.2. Description of experimental locations
Field experiments of this study were conducted in Sumedang regency, Bandung regency, and Karawang regency (Fig. 1). Sumedang regency was located at latitude 6 ° 55′00.6 "S, longitude 107 ° 46′18.3" E and altitude 753 m.a.s.l. Bandung regency was located at latitude 7 ° 03′35.3 "S, longitude 107 ° 38′46.5" E and altitude 996 m.a.s.l. Karawang regency was located at latitude 6 ° 20′15.1 "S, longitude 107 ° 18′20.2" E and altitude 24 m.a.s.l.
2.3. Experimental design and planting
Field experiments were carried out in three locations, Sumedang regency, Bandung regency, and Karawang regency (Fig. 1). Seventeen (17) new sweet potato genotypes and six (6) check varieties at each trial location were planted using a Randomized Block Design that was repeated 3 times. Each genotype was planted in blocks measured 25 × 100 centimeters in a row along 5 m. The first planting was carried out in Sumedang regency on January–May 2017. This was followed by planting in Bandung regency on January–May 2018. In Karawang regency was carried out on February–July 2018.
2.4. Data collection
This data was collected by measured the yield of new sweet potatoes planted at three different locations. Harvest was done when the plants are 18 weeks after planting. The yields of each genotype are weighed whole by used a digital scale.The observed trait was tuber yield per plot. The data were collected at the time of harvest. The weight (kg) of sample obtained from a 5 m2 plot of each genotype. Yields were converted in tons/ha.
2.5. Data analysis
An estimation of the GEIs was carried out for all genotypes. The statistical model for combined ANOVA of the environments was as follows:
| (1) |
where Yijkl is the value in plot l of genotype i, and the value in location j of each replication k; μ is the grand mean; Gi is the influence of genotype i; Ej is the influence of the location; GEij is the influence of interaction between genotype i and location j; Rk(j) is the influence of replicate k on location j; Bl(k) is the influence of repeat k on plot l; and εijkl is the influence error of genotype i in plot l and repeat k of location j, respectively.
Genotype by environment interactions (GEIs) were estimated with combined analysis of variance (ANOVA) using the GenStat 12th statistical software, so as to determine significant differences between each genotype tested in the three environments. The yield difference of each genotype by Duncan test method at a probability level of 5%.
AMMI model were analyzed with GenStat 12th statistical software. This analysis used to determine the GEIs, assess the adaptability and stability of genotypes planted in three locations. Identification of stable genotypes using AMMI following the study of [6]:
| (2) |
where: Yijk is the yield in location j from genotype i of replication k, μ is the average of grand yield, Gi is the influence of genotype i, Ej is the influence of the location j, λk is the value of primer component k, αik and γjk were the vector score for the genotype i and location j to component k, ρijr is a mistake from genotype i and location j
While ASV was estimated following the study of [7]:
| (3) |
Were: ss IPCA1, ss IPCA2 were the sum of square in IPCA 1 and 2, which shows the score of the main component because of the high contribution in genotype by location interactions. IPCA1 and IPCA2 were the first and second from IPCA scores for each genotype from the AMMI analysis.
The value of the Genotype Stability Index (GSIg) of each sweet potato genotype was calculated based on the gth genotype rank in three environments based on ASV Rank (RASVg) and gth genotype rank based on the average yield in three environments (RMYg) with the following equation:
| (4) |
GSIg was analyzed using Microsoft excel 2010.
The model for a GGE biplot following [8] with the formula:
| (5) |
where Ῡij is the yield performance in location j from genotype i, μi is the overall average yield, βj is the influence of location j, k is the number of primer components; λk is the singular value from the primer component k; and αik and γjk is the value of genotype i and location j for primer component k; εij is the error of genotype i in location j. GGE Biplot was analyzed using the GenStat 12th statistical software. This analysis was used to determine the ability of discriminating and representativeness of the field trials on sweet potato genotypes.
Identification of stable genotypes among stable was conducted using parametric and non-parametric stability models. The Eberhart and Russell method [9]uses to identify stability genotype based on linear regressions. If the variance deviation (S2di) = 0, and the regression slope (bi) = 1 indicated the genotype was stable. Wricke's Ecovalence (Wi2) following [10] with the formula:
| (6) |
Shukla's stability variance (σ2i) following [11]with the formula:
| (7) |
Where xij: the total yield of genotype i in location j; : the average yield of genotype i; : Average yield of the location j; : the grand mean; p and q: the numbers of genotypes and location.
Stability non-parameters (S(i)) models following [12,13] with the formula:
| (8) |
| (9) |
| (10) |
| (11) |
where rij: rank of stability from genotype i in the location j; : mean rank across all location for each genotype; and N: number of location. Stability parameters (NP(i)) following [14] with the formula:
| (12) |
| (13) |
| (14) |
| (15) |
where : stability rank in location j from genotype i based on adjusted data; : median rank for adjusted data; Mdi: Original data from the same parameters. N: number of location. To calculate stability genotypes based on parametric and non-parametric statistic models, we used online software STABILITYSOFT [15].
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships which have, or could be perceived to have, influenced the work reported in this article.
Acknowledgments
This research was funded by RISPRO LPDP, Ministry of Finance of the Republic of Indonesia to Dr. Sc.Agr. Agung Karuniawan, Ir., M.Sc.Agr. from Faculty of Agriculture, Universitas Padjadjaran (UNPAD). Highly apreciation to mr. Koko Tjintokohadi M.Sc. and Dr.Sc.Agr. Wolfgang J. Gruneberg for Providing the seed materials from CIP.
Footnotes
Supplementary material associated with this article can be found, in the online version, at doi:10.1016/j.dib.2020.106297.
Contributor Information
Haris Maulana, Email: harisunpad89@gmail.com.
Agung Karuniawan, Email: agung.karuniawan@unpad.ac.id.
Appendix. Supplementary materials
References
- 1.Mustamu Y A, Tjintokohadi K, Gruneberg W J, Karuniawan A, Ruswandi D. Selection of superior genotype of sweet-potato in Indonesia based on stability and adaptability. Chil. J. Agric. Res. 2018;78(4):461–469. [Google Scholar]
- 2.Andrade M I. Genotype x environment interaction and selection for drought adaptation in sweetpotato (Ipomoea batatas [L .] Lam .) in mozambique. Euphytica. 2016;209:261–280. [Google Scholar]
- 3.Temesgen T, Keneni G, Sefera T, Jarso M. Yield stability and relationships among stability parameters in faba bean (Vicia faba L .) genotypes. Crop J. 2015;3(3):258–268. [Google Scholar]
- 4.Vaezi B. Integrating different stability models to investigate genotype × environment interactions and identify stable and high-yielding barley genotypes. Euphytica. 2019;5:63. [Google Scholar]
- 5.Mafouasson H N A, Gracen V, Yeboah M A, Ntsefong G N, Tandzi L N, Mutengwa C S. Genotype-by-environment interaction and yield stability of maize single cross hybrids developed from tropical inbred lines. Agronomy. 2018;8(62):1–17. [Google Scholar]
- 6.Gauch H G. A simple protocol for AMMI analysis of yield trials. Crop Sci. 2013;53:1860–1869. [Google Scholar]
- 7.Purchase J L, Hatting H, van Deventer C S. Genotype × environment interaction of winter wheat (Triticum aestivum L .) in South Africa: II. Stability analysis of yield performance. South Afr. J. Plant Soil. 2000;17:101–107. [Google Scholar]
- 8.Yan W, Kang M S, Ma B, Woods S, Cornelius P L. GGE Biplot vs . AMMI analysis of genotype-by-environment data. Crop Sci. 2007;47(2):641–653. [Google Scholar]
- 9.Eberhart S A, Russell W A. Stability parameters for comparing varieties1. Crop Sci. 1966;6(1):36–40. [Google Scholar]
- 10.Wricke G. Übereine methode zur erfassung der ökologischen streubreite in feldversuchen. Z. Pflanzenzüch. 1962;47:92–96. [Google Scholar]
- 11.Shukla G K. Some statistical aspects of partitioning geno- type-environmental components of variability. Heredity (Edinb) 1972;29:237–245. doi: 10.1038/hdy.1972.87. [DOI] [PubMed] [Google Scholar]
- 12.Nassar R, Huhn M. Studies on estimation of phenotypic stability: tests of significance for nonparametric measures of phenotypic stability. Biometrics. 1987;43(1):45–53. [Google Scholar]
- 13.Huehn M. Nonparametric measures of phenotypic stability. Part 1: theory. Euphytica. 1990;47:189–194. [Google Scholar]
- 14.Thennarasu K. PJ School, IARI; New Delhi, India: 1995. On Certain Non-parametric Procedures for Studying Genotype-Environment Interactions and Yield Stability, PhD thesis. [Google Scholar]
- 15.Pour-aboughadareh A, Yousefian M, Moradkhani H, Poczai P, Siddique K H M. STABILITYSOFT: a new online program to calculate parametric and non- parametric stability statistics for crop traits. Appl. Plant Sci. 2019;7(1):1–6. doi: 10.1002/aps3.1211. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.