Multiscale computation delivers organophosphorus reactivity and stereoselectivity to immunoglobulin scavengers

Significance

Developed quantum mechanics/molecular mechanics (QM/MM) supercomputation is used to identify maturation of immunoglobulin (Ig) reactivity through optimization of amino acids in the catalytic core, focused on enhanced nucleophilic attack on phosphorus. A computationally optimized variant, l-Leu47Lys, delivers 340-fold reactivity enhancement for paraoxon relative to wild-type Ig-paraoxonase resulting from substrate-induced ionization of the Tyr37 nucleophile. Variant antibody stereoselectivity toward a P-chiral phenylphosphonate toxin results from starkly contrasting solvent-assisted or general base catalytic mechanisms relative to the parent Ig-paraoxonase. These mechanisms are defined by crystallographic and QM/MM analyses as resulting from changed substrate orientation and participating amino acid conformations within the catalytic site.

Abstract

Quantum mechanics/molecular mechanics (QM/MM) maturation of an immunoglobulin (Ig) powered by supercomputation delivers novel functionality to this catalytic template and facilitates artificial evolution of biocatalysts. We here employ density functional theory-based (DFT-b) tight binding and funnel metadynamics to advance our earlier QM/MM maturation of A17 Ig-paraoxonase (WTIgP) as a reactibody for organophosphorus toxins. It enables regulation of biocatalytic activity for tyrosine nucleophilic attack on phosphorus. The single amino acid substitution l-Leu47Lys results in 340-fold enhanced reactivity for paraoxon. The computed ground-state complex shows substrate-induced ionization of the nucleophilic l-Tyr37, now H-bonded to l-Lys47, resulting from repositioning of l-Lys47. Multiple antibody structural homologs, selected by phenylphosphonate covalent capture, show contrasting enantioselectivities for a P-chiral phenylphosphonate toxin. That is defined by crystallographic analysis of phenylphosphonylated reaction products for antibodies A5 and WTIgP. DFT-b analysis using QM regions based on these structures identifies transition states for the favored and disfavored reactions with surprising results. This stereoselection analysis is extended by funnel metadynamics to a range of WTIgP variants whose predicted stereoselectivity is endorsed by experimental analysis. The algorithms used here offer prospects for tailored design of highly evolved, genetically encoded organophosphorus scavengers and for broader functionalities of members of the Ig superfamily, including cell surface-exposed receptors.

The immunoglobulin (Ig) superfamily has delivered catalysts for a very wide range of nonclassical enzymatic transformations during last three decades (1–4). In contrast to naturally evolved active sites of enzymes, catalytic antibodies present a “pluripotent” center capable of being differentiated into designed functionality (5). A set of effective bioscavengers against organophosphorus (OP) nerve agents is high on the demand list for pharmacological products (6, 7), while structural hypervisibility of Igs makes them favorable templates to provide an appropriate trap for inactivating this family of OP toxins (8). Our success using combinatorial approaches, designed to screen antibody and Ig-related receptor variants for modulating a predisposed parental activity, has significantly expanded our understanding of this problem (8–11). Recently, an Ig variable fragment that emulates cooperative functionality for catalysis, termed a “reactibody,” was obtained by mechanism-based, irreversible, covalent reaction (8, 10). It is thus evident that modern quantum mechanics/molecular mechanics (QM/MM) simulation methods can dramatically enhance the process of artificial evolution of biocatalysts (12). Previously, we have developed the concept of QM/MM Ig maturation and achieved substantially improved catalytic efficiency for A17 Ig-paraoxonase (WTIgP) (13). We here present algorithms, based on the combination of density functional theory-based (DFT-b) (14) and funnel metadynamics (15, 16), designed to balance proximity of the substrate to a target tyrosine with the mechanistically essential “in-line” orientation of the WTIgP tyrosyl oxygen to optimize its reactivity toward the OP substrate. Additionally, this has made possible the rationalization of the stereoselectivity observed for contrasting Ig-variant–selective capture of discrete enantiomers of a chiral OP agent. We believe that these approaches can be applied broadly across modern enzymology, enabling in silico differentiation of enzyme active sites

Results and Discussion

Crystal Structure of WTIgP, Modified by Paraoxon, Is the Platform for Covalent Catalysis Selection.

In order to optimize the reactivity of Ig-paraoxonase for OP substrates, accurate orientation in a pre-transition state (pre-TS) complex must be selected. Calculations of antibody–ligand interactions have been based hitherto using a variety of methodologies (17–20). Previously, we docked paraoxon (POX) into the active center of WTIgP (13). We now describe a crystal structure of POX-modified WTIgP (Protein Data Bank [PDB]: 6Y49, 1.65-Å resolution; see SI Appendix, Fig. S1 and Table S1), analysis of which shows the light chain Ser35 of WTIgP coordinates an isolated water positioned to make H-bonds to both l-Ser35 (1.9 Å) and the phosphoryl oxygen (1.3 Å). Importantly, we found no H-bonds to the diethyl phosphoryl residue from polar neighboring amino acid residues. It is evidently located in the active site solely by van der Waals forces (SI Appendix, Fig. S1). Clearly, the dominant feature in the formation of the reaction complex is the correct orientation of the 4-nitrophenolate oxygen for “in-line” displacement by the attacking l-Tyr37 oxygen (21). These data are consistent with the low efficiency of WTIgP modification by POX (Table 1) and at the same time explain the very slow dephosphorylation of the covalent diethyl phosphate (DEP) derivative of WTIgP (8). This crystal structure has enabled us accurately to position POX in a group of substrate complexes by restrained docking of the 4-nitrophenol (4-NP) leaving group using the three phosphoryl oxygens of the DEP moiety as fixed loci and exchanging the fourth, axial coordination at phosphorus from Tyr37 to 4-NP with inversion of stereochemistry. The substrate complexes thus obtained were used as starting points for further QM/MM maturation (SI Appendix, Fig. S2) with the most appropriate selected for detailed development.

Table 1.

Kinetic parameters and Gibbs energy of activation for the interaction of POX with WTIgP and its variants

	k2 × 103, s−1	KD, μM	k2/KD, M−1 × s−1	ΔG‡,* kcal/mol	ΔG‡QMMM,† kcal/mol
l-Ser35Arg	2.0 ± 0.2	630 ± 25	3.1 ± 0.5	21.2 ± 0.3	20.1
l-Ser35Lys	2.3 ± 0.3	2,270 ± 120	1.0 ± 0.2	21.1 ± 0.4	21.6
l-Leu47Arg	3.1 ± 0.7	1,350 ± 200	2.3 ± 0.9	20.9 ± 0.8	23.1
l-Leu47Lys	1.3 ± 0.07	170 ± 8	7.7 ± 0.8	21.4 ± 0.7	17.8
WTIgP	ND§	ND	0.0225	ND	23.5

All measurements performed in triplicates in 50 mM sodium phosphate, pH 7.4, at 35 °C. Data represent mean ± SD.

^*ΔG^‡, Gibbs energy of activation calculated using Eyring–Polanyi equation.

^†ΔG^‡_QMMM, Gibbs free energy for TS formation calculated by QM/MM metadynamics.

^§ND, not determined because of the low rate of reaction.

In Silico Library Screening of WTIgP Variants Complexed with Paraoxon to Target Enhanced Deprotonation of Nucleophilic Tyrosine l-Tyr37.

We have previously selected three amino acid residues in the WTIgP light chain capable of improving both substrate stabilization and nucleophilicity of l-Tyr37, namely l-Ser35, l-Trp36, and l-Leu47 (13). Of these, l-Trp36 is seen to be orientated away from the reaction center and thus appears to have a stabilizing role as a structure maker in the wild-type (WT) antibody. In contrast, l-Ser35 and l-Leu47 side chains are directed into the active site, and their variants should create only minor perturbation of the antibody structure. We therefore generated a virtual library of WTIgP variants in which the l-Ser35 and the l-Leu47 positions were simultaneously replaced by polar amino acids selected from Gln, Asn, Lys, Arg, His, Ser, Thr, and Tyr. We used the WTIgP–POX complex described above and froze the loci of its four phosphate oxygens while freeing all remaining atoms to enable optimization of their best docking positions. We employed PyRosetta to take into account the proximity of variant amino acid residues to the hydroxyl group of l-Tyr37 (22).

The library of WTIgP–POX binary complexes thus obtained was used to estimate the reaction barrier of l-Tyr37 deprotonation using DFT-b metadynamics simulations rather than the PM6-D3H4 theory level used earlier (13). This has the advantage of more accurate reaction barriers compared to PM6-D3H4, although optimized parameters set for 3OB have to be applied (14). As before, deprotonation of l-Tyr37 leads to nucleophilic attack at phosphorus as the key step in POX modification of WTIgP (13). We note that Hamiltonians of the PM6 family tend to favor the pentacoordinate state for phosphorus as a transition state for reaction (23), thus affecting the efficiency of in silico maturation. We earlier showed that use of the Hamiltonian DFT-b leads to quantitative agreement between the computed value of the reaction barrier with experimental data for reactivation of butyrylcholinesterase bound to DEP (24), which led us to observe the progress of the full reaction in a single trajectory, and thence to a simplified selection process.

Using this DFT-b approach, we identified eight variants of WTIgP having the lowest Gibbs free energies for l-Tyr37 activation (SI Appendix, Table S2). The two best scores have glutamine in position l-35, where it donates an (N)-H-bond to l-Tyr37 and this stabilizes the anionic form of tyrosine. However, QM-simulation using these variants delivered an unequilibrated conformation characterized by a high local concentration of negative charge caused by closure of the side-chain carbonyl oxygen of l-Gln35 toward the POX phosphoryl oxygen atom. This conformation resulted in high-amplitude oscillation for the l-Tyr37 O–H bond leading to rapid tyrosine deprotonation and subsequent proton transfer to the phosphoryl oxygen. This event is clearly an artifact of the defined QM system, and we therefore removed these variants from further analysis, focusing our attention exclusively on l-Leu47Lys and l-Leu47Arg.

A Virtually Selected l-Leu47Lys Variant of WTIgP Displays the Highest Catalytic Efficiency Delivered Using Specific Base Activation of the Nucleophilic Tyrosine.

Two newly selected variants of WTIgP, hereafter identified as l-Leu47Arg and l-Leu47Lys, were compared in terms of their catalytic parameters with our earlier l-Ser35Arg and l-Ser35Lys variants for which the catalytic efficiency results from an increased ability to orientate bound POX for enhanced covalent reaction (13). Steady-state kinetic data on the reactivity of yeast-expressed and purified Fab fragments now demonstrated that the new l-Leu47Lys variant exhibits a 340-fold increase in bimolecular rate constant compared to WT antibody (7.7 and 0.0225 M⁻¹⋅s⁻¹, respectively; Table 1), and better than twofold higher than that of the new l-Leu47Arg and previously studied l-Ser35Arg variants.

To describe the reaction pathway of the newly selected variants, we first obtained high-resolution Fab crystal structures for the apoproteins l-Leu47Lys and l-Leu47Arg (PDB: 5TJD, 2.1-Å resolution, and PDB: 6Y1K (SI Appendix, Fig. S3A), 1.65-Å resolution, respectively; SI Appendix, Table S1) and for POX bound to l-Leu47Lys and to l-Leu47Arg (PDB: 6Y1M, 2.0-Å resolution, and PDB: 6Y1L (SI Appendix, Fig. S3B), 1.4-Å resolution, respectively; SI Appendix, Table S1). In the apo-l-Leu47Lys variant, Lys47 cannot directly activate Tyr37 as it is not positioned for effective H-bonding (r_DA 3.6 Å, ∠_DHA 123°) but only coordinates the tyrosine indirectly via a bridging water (Fig. 1A). Next, we introduced the POX molecule, as described above, and used QM/MM equilibrating simulation to generate a ground-state (GS) complex. This shows the formation of a bridged ion-pair in the TS complex with the anionic Tyr37 oxygen accepting H-bond from the l-Lys47 ammonium group (r_NH—O 1.5 Å; ∠_N-H—O 176°) and positioned directly in-line (178°) with the 4-NP leaving group at 2.4 Å from phosphorus (Fig. 1B). We then applied QM/MM two-dimensional (2D) metadynamics computation to deliver the lowest energy TS from this GS complex. It identified a compact trigonal bipyramid (tbp) (r_DA 3.6 Å, in-line angle 176°) with the Lys47 ammonium group H-bonded to the Tyr37 oxygen (2.0 Å, 168°) (Fig. 1C). Notably, the Tyr37 oxygen has closed 0.6 Å on phosphorus, while the phosphorus–4-NP bond has lengthened by 0.2 Å (SI Appendix, Table S3). The tbp geometry of this computed TS fits well into the cavity visible above the diethyl tyrosyl phosphate in the product crystal structure (SI Appendix, Fig. S4). Finally, the reaction leads to a product complex by loss of the 4-NP anion with the Tyr37 oxygen phosphorylated by DEP. Its crystal structure shows Lys47 shifted 1.2 Å away from its position in the unmodified Tyr37, placing it too remote (4.4 Å) for H-bonding to the DEP moiety (Fig. 1D).

Fig. 1.

Structure (Left) and cartoon representations of the four stages in the catalytic mechanism of reaction of POX with the l-Leu47Lys variant. (A) Crystal structure and H-bonding of the apo-antibody l-Leu47Lys variant (PDB: 5TJD). (B) Ionization of the l-Tyr37 residue in a GS substrate complex with POX computed by QM/MM simulation. (C) QM/MM computed TS in the active site with trigonal bipyramidyl phosphorus. (D) Crystal structure and H-bonding of the l-Leu47Lys variant covalently linked to DEP (PDB: 6Y1M) (H-bond network, black dashes; light-chain carbons, light blue; heavy carbons, light green; nitrogen, blue; oxygen, red; phosphorus, orange; and POX carbons, yellow).

Three features of the computed TS are significant. First, the phosphorus is midway between the donor and acceptor oxygens (r_OP values, 1.8 Å; SI Appendix, Table S3), which suggests parity between the effective pK_a values of the two phenolic oxygens as a result of the H-bonding from Lys47 to Tyr37 (Fig. 1C). Second, the donor–acceptor distance (3.6 Å) for phosphoryl transfer in this triester reaction is much shorter than for a typical monoester transfer (∼4.2 to 4.3 Å) (21). Third, the direction of approach of the phosphoryl group to the phenolic oxygen is almost perpendicular to the aromatic ring of Tyr37. This is evidently driven by overlap of the phosphorus LUMO with the Tyr37 ψ₄ HOMO and minimization of steric interactions with the tyrosine ring atoms while it is comparable to geometry of phosphorylation of trigonal nitrogen in creatine and arginine kinases (25, 26). We note that all four structures (Fig. 1 A–D) show multiple waters within the reaction core, some participating in location of catalytic residues, and this is contrary to the observed exclusion of water from enzyme-catalyzed TSs for phosphoryl transfer (21). This failure to exclude water is likely a problem to be resolved to achieve improvement of antibody catalysis of phosphoryl transfer reactions.

Catalytic Efficacy of WTIgP Variants Is Determined by a Delicate Balance between Nucleophilicity and Substrate Orientation.

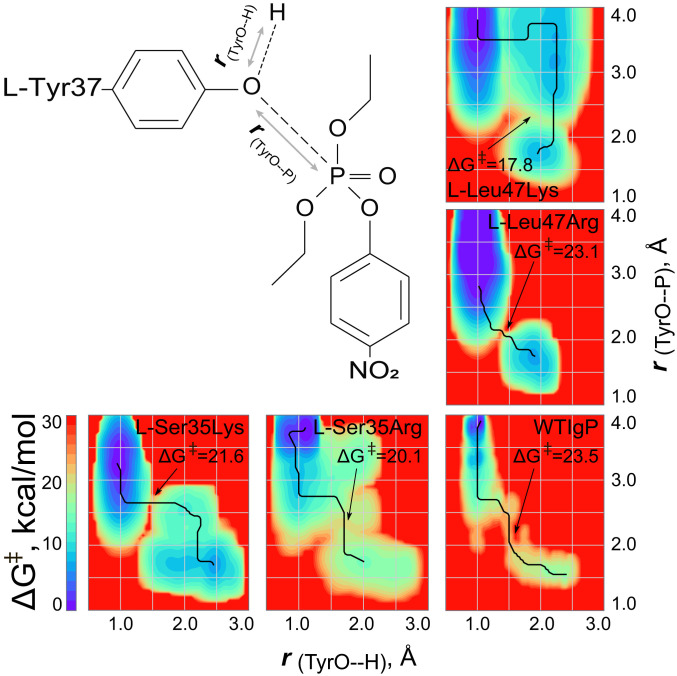
The reactivity shown by Ig-based paraoxonases can be evaluated as the combination of two processes, activation of the nucleophile and orientation of the POX substrate. We therefore applied 2D scanning of Gibbs free energy values for tbp formation from the substrate complex using QM/MM metadynamics with coordinates representing two collective variables: i) the distance between the oxygen atom of the reactive Tyr37 with close polar proton in the QM system, and ii) the distance of the Tyr37 oxygen from the phosphorus atom (Fig. 2).

Fig. 2.

Two-dimensional free energy surface from QM/MM metadynamics simulations of GS formation from the substrate complex for the WTIgP and its variants. Abscissa represents the minimal distance from the oxygen atom of Tyr37 to close polar hydrogen in the QM subsystem within a radius of 3 Å. The ordinate is the distance from the l-Tyr37 oxygen to the phosphorus. Reaction paths are indicated (black lines) with relevant energy maxima marked (arrows).

The energy plot for l-Leu47Lys differs markedly from all other Ig paraoxonase variants, indicating that the reactive tyrosine is deprotonated before TS formation (Figs. 1B and 2). Moreover the energy barrier on the reaction pathway is 17.8 kcal⋅mol⁻¹, which is 2 kcal⋅mol⁻¹ lower than the barrier for l-Ser35Arg, the next-best variant, and primarily involves phosphorus migration between donor and acceptor oxygens. The other Ig paraoxonase variants show a very different energy profile: Shortening of the Tyr37–O to phosphorus distance by ∼1 Å precedes deprotonation of Tyr37 and thereafter leads to TS formation (Fig. 2).

The Gibbs free energy for TS formation as calculated by QM/MM metadynamics (Fig. 2) does not match the observed values for k₂ (Table 1). We therefore evaluated ΔΔG⁰ for POX noncovalent binding utilizing forcefield funnel metadynamics (15) with coordinates representing two collective variables: i) the angle between l-Tyr37C_β atom, phosphorus, and the 4-NP anionic oxygen, and ii) the distance from the Tyr37C_β to the POX phosphorus (Fig. 3 and SI Appendix, Fig. S5). The window of reaction (denoted by a black rectangle) restricts the Tyr37C_β–P–O_POX angle to 120 to 180° and the Tyr37C_β–P distance to 6 to 9 Å selected to deliver productive nucleophilic attack of the Tyr37 oxygen atom at phosphorus. Our previous best variant l-Ser35Arg has an energy minimum in this reaction window, showing the validity of funnel metadynamics analysis for the capability of this variant Ig-paraoxonase (SI Appendix, Fig. S5). The 2D plots for the new variants show that nonproductive positions are predominant. For the best variant, l-Leu47Lys, the most stable binding position has too small an angle to meet the above criteria but can be transposed into the “reaction window” over a 3.2 kcal⋅mol⁻¹ barrier. For the next best variant, l-Lue47Arg, the most stable binding locus has a good angle but is too distant from phosphorus to meet these criteria and can readily be transposed into the reaction window over a 2.2 kcal⋅mol⁻¹ barrier. The WTIgP has a single deep binding pocket, remote from the reaction window in both angle and O–P distance and can only be transposed into the reaction window over a 5.8 kcal⋅mol⁻¹ barrier.

Fig. 3.

Funnel metadynamics analysis for binding POX in the active site of l-Leu47Lys. The free energy landscape is computed using a reweighted Gibbs free energy as a function of two CVs: i) distance between l-Tyr37-С_β to phosphorus and ii) angle O_Tyr–P–O_4-NP, $\angle$O–P–O_4-NP. Insets 1 and 2 show conformations for energy minima with reaction boundaries outside of window of reaction. The deprotonation of Tyr37–OH (depicted in Fig. 1B) is initiated at r(TyrC_β–P) 7.8 Å (that is equivalent r_OP 4.1 Å; Inset 3). Energies normalized based on minimal value; difference energies depicted are limited to 20 kcal/mol because all critical values are ≤19 kcal/mol.

We next computed the Gibbs energy of activation for the reaction of WTIgP and its variants with POX. Simulated ΔG^‡ values were very similar to experimental ones, showing that our combination of QM/MM and funnel metadynamics correctly predicts the Gibbs energy of activation (Table 2 and SI Appendix, Table S4). The negative values of enthalpy and entropy of formation for noncovalent complex in cases of l-Ser35Arg, l-Leu47Arg, and l-Ser35Lys contrast with the positive entropy value for the case of l-Leu47Lys, suggesting that binding of POX by l-Leu47Lys is entropically driven and commensurate with proton release triggered by POX substrate binding (SI Appendix, Fig. S6). We found that best convergence of calculated and experimental values was delivered by the choice of Tyr37C_β, rather than the more proximate Tyr37C_ζ, for the funnel metadynamics fulcrum. This is likely because the funnel metadynamics simulation of ligand binding requires collective variables that employ fixed components of the protein. In the metadynamics simulation, we used the center of mass of fixed residues H-Pro42 and l-Pro41 as the collective variable for the position of the ligand along the x axis. This choice of amino acids remote from the active center is dictated by the desire to minimize the effect of restraints on the mobility of residues of the active center. Its limitation is a low resolution of simulation with respect to local orientation of POX (Table 2).

Table 2.

Simulation and experimental analysis of Gibbs energy activation of TS formation of WTIgP and its variants in reaction with POX from substrate complex to TS

	ΔG‡,* kcal/mol	ΔG‡Cζ,† kcal/mol	ΔG‡Cβ,§ kcal/mol
l-Ser35Arg	21.2 ± 0.3	21.5	21.3
l-Ser35Lys	21.1 ± 0.4	25.7	23.8
l-Leu47Arg	20.9 ± 0.8	30.0	25.3
l-Leu47Lys	21.4 ± 0.7	24.6	21.3
WTIgP	ND¶	28.5	29.3

^*ΔG^‡, Gibbs energy of activation calculated using Eyring–Polanyi equation.

^†ΔG^‡_Cζ, Gibbs free energy for TS formation calculated by combined QM/MM and funnel metadynamics using the following constraints: dTyrO–P = 1.5 to 4 Å; angle Tyr_Cζ–P–O_4-NP = 145 to 180°.

^§ΔG^‡_Cβ, Gibbs free energy for TS formation calculated by combined QM/MM and funnel metadynamics using the following constrains: dTyrC_β–P = 6 to 9 Å; angle Tyr_Cβ–P–O_4-NP = 120 to 180°.

^¶ND, not determined because of low rate of reaction.

Experimental Determination of the Stereoselectivity of Reaction of Antibodies with a Chiral Arylphosphonate and Their In Silico Analysis.

The majority of organophosphorus enzyme inhibitors and toxins are chiral at phosphorus (7). We therefore addressed one of the main problems of biocatalysis: the stereoselectivity of the reaction of WTIgP with a racemic P-chiral phenylphosphonate agent linked to the ability to rationalize it by computational analysis. While Bigley and Raushel (27) have carried out a broad range studies on OP agents, they have focused on chiral selectivity based on discrimination between the three phosphorus ligands as characterized by large, small, and leaving group. Their work described selectivities for 4-acetylphenyl isopropyl methylphosphonate of R_P/S_P as 20:1 and for 4-acetylphenyl methylphenylphosphonate as of 1:3,000 for the WT bacterial phosphotriesterase under examination. However, for three G-agents and one V-agent, the corresponding stereoselectivity was less than 26-fold. We launched our investigation using the crystal structures of product complexes for the reactions of WTIgP [PDB: 2ZXC (8)] and its A5 homolog (PDB: 6Y1N; 2.2-Å resolution; SI Appendix, Table S1) with a racemic phenylphosphonate substrate rac-XOP (p-nitrophenyl 8-methyl-8-azabicyclo[3.2.1]octyl phenylphosphonate). Our initial experimental results with WTIgP gave a crystal structure for the product complex of the phenylphosphonate showing stereoselective binding of the product to l-Tyr37 with exclusive (S_P)-chirality (Fig. 4 A and B). This establishes (R_P)-substrate selectivity for WTIgP since this reaction must involve inversion of configuration at phosphorus. The active site shows a cavity adjacent to the product occupied by six waters indicating a probable binding site for 4-NP leaving group of XOP (PDB: 2ZXC) (8).

Fig. 4.

Analysis of the enantioselectivity of WTIgP and its homolog A5 for racemic phenylphosphonate. (A) Structure of (R_P)-enantiomer of XOP. (B) Crystal structure of product complex of this reaction showing the (S_P)-stereochemistry of the inverted phenylphosphonate product. (C) DFT-b best fit for in-line TS for reaction of (R_P)-XOP with WTIgP. (D) QM mechanism and orientation of the favored isomer and (E) disfavored isomer in the reaction of WTIgP with XOP. (F) Structure of (S_P)-enantiomer of XOP. (G) Crystal structure of the product complex of this reaction showing the (R_P)-stereochemistry of the inverted phenylphosphonate product. (H) DFT-b computed TS for reaction of (S_P)-XOP with A5 antibody. (I) QM mechanism and orientation of the favored isomer and (J) the disfavored isomer in reaction of A5 with XOP.

For the A5 homolog, the result of the corresponding structural analysis identifies precisely the opposite stereoselectivity. The product of reaction with rac-XOP has exclusively (R_P)-stereochemistry. Unexpectedly, this crystal structure for antibody A5 shows that OP capture uses l-Tyr33 as nucleophile for the (S_P)-phenylphosphonate (Fig. 4 F and G), which contrasts strongly with the homologous WTIgP antibody use of l-Tyr37 for the (R_P)-phenylphosphonate (Fig. 4 A and B).

We computed the TSs for these two stereoselective reactions by positioning each substrate isomer into the crystal structures of modified antibody WTIgP (PDB: 2XZC) and A5 (PDB: 6Y1N) and locating the 4-NP leaving group in line and opposed to the reactive l-Tyr37 or l-Tyr33, respectively. After superposing the three phosphorus-ligand atoms of the tropinyloxy, phosphoryloxy, and phenyl-carbon for the XOP substrate with the corresponding atoms in the XOP-product crystal structures, we docked the XOP substrate, keeping r_OP in the range of 2.4 to 2.7 Å while allowing free movement and rotation of the resulting pre-TS structures. These reactant complexes were submitted to DFT-b development to identify the minimum energy TS for each XOP enantiomer. The correspondence of these TS structures to the product structures for the reaction of WTIgP and A5 with the preferred XOP enantiomer validates this procedure (Fig. 4 B, C, G, and H). For the (R_P)-enantiomer, the active l-Tyr37 lies at the base of a deep cleft between the WTIgP light and heavy chains with its oxygen 2.2 Å from the XOP phosphorus and in-line with the 4-NP oxygen (172°) and 3.9 Å from it. The 4-NP residue is well accommodated in a cavity on the face of the heavy chain and the phenyl group is lodged in a cavity on the face of the light chain. That places the tropinyl moiety orientated toward solvent water near the mouth of the cavity with its ammonium proton directed at bulk solvent. The key to catalysis in this TS is the presence of an additional water to relay proton transfer from the nucleophilic tyrosine hydroxyl to the phosphoryl oxygen, as envisaged by Warshel for the computed TS for the neutral hydrolysis of methyl pyrophosphate with an additional water (28) (Fig. 4D and SI Appendix, Fig. S7A). Indeed, in the computed TS, the high energy point on the reaction coordinate is concerted transfer of the two protons, followed by P–O bond formation that develops rapidly and is concerted with P–O bond breaking, showing a minimum r_DA of 3.8 Å (Fig. 4 C and D).

The corresponding TS identified for the disfavored (S_P)-XOP enantiomer locates the three phosphorus ligands with the minimum reorganization in the same cavity. The phenyl and 4-NP groups occupy the same locations while the tropinyl and phosphoryl oxygens interchange places with a rotation of the tropinyl O–P bond by 40° to enable the tropinyl moiety to fit the same location but with its N–H group now donating a good H-bond to the backbone carbonyl of H-Asn105 (SI Appendix, Fig. S7B). In this TS, the nearest water to the phosphoryl oxygen is >6 Å from the tyrosyl hydroxyl group, making participation of a catalytic “additional” water unrealizable. By default, this TS requires a four-center transfer of proton to the P=O oxygen (Fig. 4E), which is some 8 kcal⋅mol⁻¹ higher energy than that for the six-center TS of the (R_P)-enantiomer (SI Appendix, Fig. S7A). That figure is close to the value of 6 to 9 kcal/mol determined for the neutral hydrolysis of methyl pyrophosphate (28) and more than large enough to explain the stereoselection of WTIgP for the (R_P)-enantiomer of the chiral OP agent.

We next computed the TSs for the A5 antibody based on the structure of its product from reaction with the (S_P)-XOP enantiomer (PDB: 6Y1N). We readily identified the structure of the TS for the A5(S_P)-XOP enantiomer with its three phosphorus ligands close to their positions in the product structure (Fig. 4 G and H). This puts the 4-NP group in face-to-face contact with Trp91 and close to the antibody surface (SI Appendix, Fig. S7D). The TS now has the hydroxyl oxygen of Tyr33 in-line (165°) with the leaving group with an r_DA 4.1 Å. The important catalytic feature is a pair of water molecules coordinated to the carboxylate anion of l-Asp35, one of which accepts a H-bond from the tyrosyl-OH group. The energy curve for the reaction coordinate shows the TS involves proton transfer from Tyr33 to Asp35 via that captive water. It precedes P–O bond formation and breaking, which is concerted and symmetrical with a minimum r_DA 3.82 Å and involves both the tyrosyl oxygen and phosphorus moving toward each other in a classical general base catalyzed reaction mechanism (Fig. 4I).

Moving to the reaction of Tyr33 with the (R_P)-XOP isomer, we inverted the stereochemistry for the (S_P)-XOP isomer by interchanging the 4-NP and tropinyl moiety ligand positions while maintaining the Tyr33 and phenyl ligand locations unchanged. We then computed the TS as before (SI Appendix, Fig. S7С). This TS shows the phosphorus has moved 2 Å and the Tyr33 ring rotating 80° around the C2–O2 axis relative to the (S_P)-enantiomer in order to maintain the in-line relationship of Tyr33–OH with the 4-NP oxygen. These changes also enable l-Arg51 to adopt a conformation close to that in the product structure, enabling it to donate two H-bonds to the phosphoryl oxygen (1.8 and 2.1 Å) (Fig. 4J and SI Appendix, Fig. S7C). This results in an early TS involving proton transfer from Tyr33 to Asp35, with an r_DA 4.23 Å, and with only small lengthening for the leaving group P–O bond. This is also a classical general base catalysis mechanism (Fig. 4J), as for the (S_P)-enantiomer substrate, although it does not explain the large observed difference in reactivity of A5 for the two XOP enantiomers. We conclude that the best explanation for that stereoselectivity is that the TS for the (R_P)-enantiomer clearly shows the XOP moiety is located on the surface of the Fv region of A5 (SI Appendix, Fig. S7C), with the likely outcome that its binding to the protein is weak and results in a large K_M value.

We therefore explored the potential of funnel metadynamics for prediction of the enantioselectivity for an Ig-mediated covalent reaction through analysis of the frequency of the phenylphosphonate occupation of the window of reaction for WTIgP homologs, namely A21 and A46 (Fig. 5A). Our computations predict that the A46 variant should show (S_P)-reactant selectivity with the A21 variant showing (R_P)-reactant selectivity. Finally, we matched these data with the results of Western blot analysis for (R_P)- and (S_P)-phenylphosphonate modification of WTIgP and its homologs expressed either as Fab fragments or as scFv-Fc. There results clearly show that WTIgP and A21 variants show reactivity for the XOP (R_P)-isomer, while all other IgGs manifest a strong preference for the (S_P)-isomer (Fig. 5B).

Fig. 5.

Funnel metadynamics prediction of enantioselectivity of WTIgP and its homologs for XOP substrate capture. (A) Free energy landscape of noncovalent binding of A21 and A46 antibodies with (R_P)- and (S_P)-enantiomers of phenylphosphonate. The window of reaction is denoted by a black rectangle that restricts the TyrC_β–O–P angle to 120 to 180° and the TyrC_β–P distance r(TyrC_β–P) in the range of 6 to 9 Å selected to deliver productive nucleophilic attack of the tyrosine oxygen atom on phosphorus. (B) Western blot analysis of covalent modification of antibodies Fab and scFv-Fc fragments by biotinylated phenylphosphonate X (R_P)- and (S_P)-isomers.

Conclusion

In the present study of the development of an organophosphate-metabolizing antibody, we have demonstrated the merits of an improved computational approach that has identified variants with increased reactivity. This has resulted from a combination of optimized orientation of the OP substrate for “in-line” phosphoryl transfer (21) combined with enhancement of nucleophilicity of the reactive tyrosyl oxygen. We show that the nature and position of supporting amino acid residues in the active center determine the reaction mechanism dramatically. In the l-Leu47Lys variant, a unique nucleophilic mechanism has been accomplished by specific base activation that creates an ion-pair between l-Lys47 and l-Tyr37 following substrate binding. The experimental failure to realize the activity predicted in silico for the corresponding l-Leu47Arg variant is attributable to unexpected ion-pair conformation with a second shell residue, H-Asp106, that effectively denies direct interaction of the guanidinium moiety with the tyrosyl oxygen. We identified two antibodies, A5 and WTIgP, that show opposite stereoselectivity for the enantiomers of a chiral phosphonate agent, confirmed by the X-ray structures of the products of their reaction with racemic phosphonate. Unexpectedly, the two antibodies employ different tyrosines as nucleophile for the same enantiomeric phosphonate esters. DFT analysis of these reactions show that WTIgP achieves stereoselectivity by a solvent-assisted mechanism while A5 employs general base activation of the key tyrosine mediated by a specific water. Funnel metadynamics are applied to predict the enantiomer selectivity for A21 and A46 variants with results fully compatible with Western blot analysis of the stereoselectivities of a set of the antibodies. Thus, the use of modern simulation methods now makes viable the prediction and generation of artificial biocatalysts with unique features to target biomolecular processes.

Materials and Methods

Computational Mutant Generation.

Python module itertools was used to create the list of mutants from polar nonacidic amino acids. All 56 mutants were subjected to model building. Mutant residues conformations were generated with the PyRosetta framework (22). Rosetta energy function (15, 29) was used for packing mutant and neighboring residues in proximity less than 10 Å.

Two-Dimensional QM/MM and Funnel Metadynamics.

A well-tempered metadynamics approach was used to overcome the activation barrier (30). In the simulation run, we used two collective variables (CVs): the TyrO–H and TyrO–P distances. Hills with a width of 0.01 and 0.02 nm and a height of 0.5 kJ/mol was chosen, and the Hill addition frequency was selected as one Hill every 100th step. Funnel metadynamics was done as described in the original publication of Limongelli et al. (15).

Evaluation of Reaction Kinetic Parameters for the A5, A21, and WTIgP and Its Variants.

Kinetic measurements were made as previously described (10, 13). Briefly, reactions of WTIgP and A5 (10 μM) with XOP or WTIgP variants (10 μM) with POX over a concentration range of 70 to 1,500 μM were carried out in 50 mM sodium phosphate buffer, pH 7.4, at various temperatures. Reaction rates were determined from the changes in absorbance at 400 nm resulting from to 4-NP formation, and rate constants were calculated using a 4-NP extinction coefficient ε of 12,300 M⁻¹⋅cm⁻¹. Modifications of rate constants k₂ and equilibrium constants K_D were estimated by Kitz–Wilson analysis using DynaFit software (31).

Identification of Stereoselectivity.

rac-XOP was synthesized and biotinylated as described (32). Pure S_P- and R_P-isomers of biotinylated XOP (BtX) were isolated from the cross-reaction with equivalent WTIgP or A5 reactibody-phosphonate molar concentration (24 μM Fabs and 24 μM rac-XOP) using high-performance liquid chromatography with a C18 column. A21 Fab-fragment and scFv-Fc variants of antibodies were incubated with biotinylated S_P- and R_P-isomers for 1 h at 37 °C in PBS buffer and analyzed by Western blot with streptavidin-HRP staining. Concentrations of antibodies are normalized as confirmed by comparable staining of light chains or Fc-fragment on the same blots.

More detailed methods are described in SI Appendix, Supplementary Methods.

Data Availability.

All study data are included in the article and SI Appendix.