Low-dimensional dynamics for working memory and time encoding

Significance

A fundamental challenge in studying neural activity that evolves over time is understanding what computational capabilities can be supported by the activity and when these dynamics change to support different computational demands. We develop analyses to parcellate neural activity into computationally distinct dynamical regimes. The regimes we consider each have different computational capabilities, including the ability to keep track of time or preserve information robustly against the flow of time in working memory. We apply our analyses to neural activity and find that low-dimensional trajectories provide a mechanism for the brain to solve the problem of storing information across time while simultaneously retaining the timing information necessary for anticipating events and coordinating behavior.

Abstract

Our decisions often depend on multiple sensory experiences separated by time delays. The brain can remember these experiences and, simultaneously, estimate the timing between events. To understand the mechanisms underlying working memory and time encoding, we analyze neural activity recorded during delays in four experiments on nonhuman primates. To disambiguate potential mechanisms, we propose two analyses, namely, decoding the passage of time from neural data and computing the cumulative dimensionality of the neural trajectory over time. Time can be decoded with high precision in tasks where timing information is relevant and with lower precision when irrelevant for performing the task. Neural trajectories are always observed to be low-dimensional. In addition, our results further constrain the mechanisms underlying time encoding as we find that the linear “ramping” component of each neuron’s firing rate strongly contributes to the slow timescale variations that make decoding time possible. These constraints rule out working memory models that rely on constant, sustained activity and neural networks with high-dimensional trajectories, like reservoir networks. Instead, recurrent networks trained with backpropagation capture the time-encoding properties and the dimensionality observed in the data.

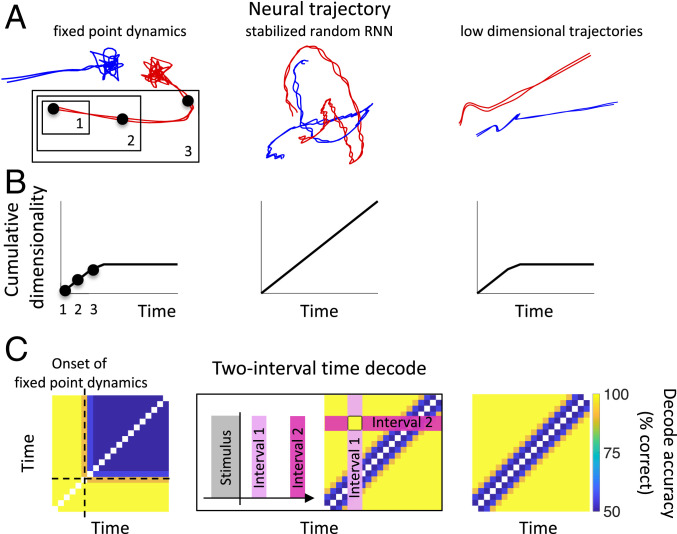
When events like sensory inputs and motor responses are separated by time delays, our decisions often depend on 1) remembering information across these delays and 2) tracking the passage of time during the delay period to anticipate stimuli and plan future actions. Here, we analyzed the delay activity recorded in monkeys during four different experiments to understand the neural representations that enable monkeys to preserve over time the information about a particular event in working memory (1, 2) and, at the same time, to measure the interval that passed since that event (3, 4). In order to explain the recorded representations, we considered three classes of neural network mechanisms that have been suggested by previous work (Fig. 1).

Fig. 1.

Three hypotheses for neural dynamics, which can be disambiguated by decoding time and dimensionality. (A) Trajectories in the firing-rate space: the firing rates of a population of simulated neurons are shown after they have been projected onto a two-dimensional space. (Left) A transient response is followed by fixed-point dynamics. Information about two behavioral states is stored in separate fixed points colored in red and blue. The two lines for each behavioral state correspond to two different trials. These fixed points are attractors of the dynamics, and the fluctuations around them are due to noise. (Center) A randomly connected “reservoir” of neurons generates chaotic trajectories. The trajectories have been stabilized as in Laje and Buonomano (17). The neural activity at each time point is unique, and these changing firing rates can be used as a clock to perform different computations at different times. Importantly, the red and blue trajectories are distinct and linearly separable for all times, so the behavioral state is also encoded throughout the interval. (Right) Low-dimensional trajectories: a transient is followed by linearly ramping neural responses. (B) To compute the cumulative dimensionality, the neural trajectory is first subdivided into nonoverlapping intervals (three example intervals are highlighted with black dots in A). The cumulative dimensionality at time $t$ is the dimensionality of the neural trajectory spanning intervals 1 through $t$ (see SI Appendix, Fig. S1 for details). The cumulative dimensionality of the neural activity over time increases linearly in the standard stabilized random RNN (Center). This is in contrast to fixed-point and ramping dynamics, where the cumulative dimensionality increases during an initial transient and then plateaus during the fixed-point and ramping intervals. These two dynamical regimes yield the same cumulative dimensionality; however, they are disambiguated by computing the two-interval time decode. (C) Two-interval time-decode matrix for the simulated data shown in A. Subdivide the time after stimulus offset into nonoverlapping intervals. Take the vector of firing rates recorded from all neurons during a single interval (interval 1 after stimulus offset, for example), and train a binary classifier to discriminate between this and another interval (interval 2). Test the classifier on held-out trials and record the performance. This number, between 50 and 100%, from the classifier trained to discriminate intervals i and j is recorded in pixel (i,j) of the “two-interval time-decode matrix.” If the decode accuracy is 100%, the pixel is colored yellow (as shown in the example in Center), and if the decode accuracy is 50%, the pixel is colored blue. (Left) The block of time where the decode is near chance level (50%) is a signature of fixed-point dynamics; once the fixed point is reached, a classifier cannot discriminate different time points. In contrast, for the stabilized random RNN and low-dimensional trajectories, it is possible to decode time (down to some limiting precision due to noise in the firing rates).

The first mechanism is often used to model working memory (see e.g., refs. 5 and 6). It is based on the hypothesis that there are neural circuits that behave like an attractor neural network (5, 7, 8) (Fig. 1, A–C, Left), in which different events (e.g., different sensory stimuli) lead to different stable fixed points of the neural dynamics. Persistent activity, widely observed in many cortical areas, has been interpreted as an expression of attractor dynamics (see, e.g., ref. 9). For these dynamical systems, the information about the event preceding the delay is preserved as long as the neural activity remains in the vicinity of the fixed point representing the event. However, once the fixed point is reached, the variations of the neural activity are only due to noise; all timing information is lost, and time is not encoded.

Time and memory encoding can be obtained simultaneously in a category of models known as reservoir networks, liquid-state machines, or echo-state networks (10–16). These are recurrent neural networks (RNNs) with random connectivity that can generate high-dimensional chaotic trajectories (Fig. 1A, Center). If these trajectories are reproducible, then they can be used as clocks as the network state will always be at the same location in the firing-rate space after a certain time interval. Thanks to the high dimensionality, one can implement the clock using a simple linear readout. Moreover, a linear readout is also sufficient to decode any other variable that is encoded in the initial state. To identify this computational regime, we note that a prediction of the reservoir-computing framework is that the pattern of neural activity at each time point is linearly separable from the patterns of neural activity at other time points. If this is true, then it will be possible to decode the “passage of time” from the neural population (Fig. 1C, Center), regardless of whether or not timing information is relevant for the task. However, there are a few problems with these models. In principle, they are very powerful, as they can generate any input–output function. However, this would require an exponential number of neurons, or equivalently, the memory span would grow only logarithmically with the number of neurons. Moreover, the trajectories are chaotic, and so inherently unstable and not robust to noise. To overcome this limitation, recent theoretical work (17, 18) has demonstrated ways of making them robust by stabilizing an initial chaotic trajectory, produced by a randomly connected RNN, so it is reproducible from trial to trial. This “stabilized random RNN” is the reservoir network we will study.

The third category of models is one in which the activity varies in time but across trajectories that are low-dimensional (19–22). For these models, it is still possible to encode time and also to encode different values of other variables along separate trajectories (Fig. 1, A–C, Right; see also Discussion). Working memory, in these models, does not rely on constant rates around a fixed activity pattern as in standard attractor models; however, the low-dimensional evolving trajectories can still provide a substrate for stable memories, similar to attractor models of memory storage via constant activity. One advantage of a low-dimensional evolving trajectory is that time can also be encoded, something not possible with constant neural activity.

To disambiguate between these potential mechanisms, we propose two analyses, namely, decoding the passage of time from neural data and computing the cumulative dimensionality of the neural trajectory over time (Fig. 1B). Using these analyses, we show that the last scenario is compatible with four datasets from monkeys performing a diverse set of working memory tasks (Fig. 2). Time can be decoded with high precision when timing information is explicitly required for performing the task, consistent with the idea that stable neural trajectories act as a clock to perform the task, and with low precision when it is not. Neural trajectories for all tasks are low-dimensional; they evolve such that the cumulative dimensionality of the neural activity over time quickly saturates.

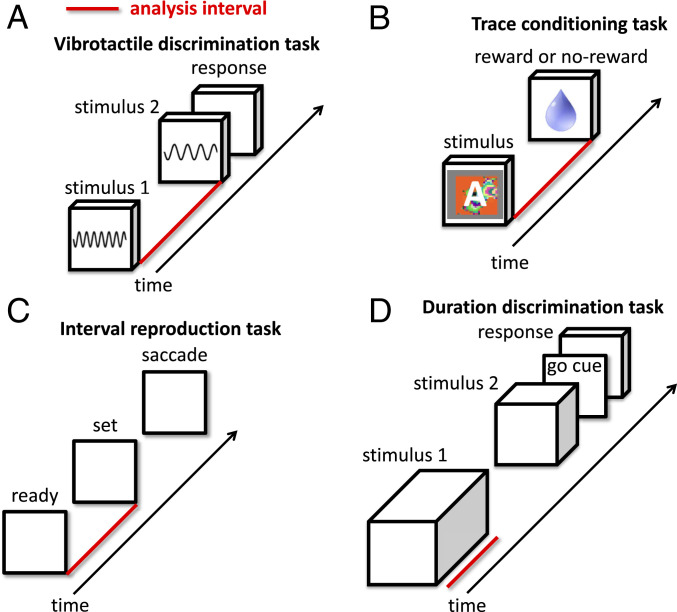
Fig. 2.

Four tasks analyzed in this paper. Red bars indicate time intervals that were analyzed. To better understand neural dynamics in the absence of external events, we only analyzed intervals with over 1,000 ms between changes in sensory stimuli. (A) In the vibrotactile-discrimination task of Romo et al. (38), a mechanical probe vibrates the monkey’s finger at one of seven frequencies. Then, there is either a 3- or 6-s delay interval before the monkey’s finger is vibrated again at a different frequency. The monkey’s task is to report whether the frequency of the second stimulus is higher or lower than that of the first. (B) In the context-dependent trace-conditioning task of Saez et al. (39), monkeys were presented with one of two visual stimuli, A or B. After a 1.5-s delay period, the monkey was either rewarded or not. This is a context-dependent task: in context 1, stimulus A is rewarded and stimulus B is not, whereas, in context 2, the associations are reversed (stimulus A is not rewarded and stimulus B is rewarded). Monkeys learned the current context and displayed anticipatory licking after the appropriate stimuli. (C) In the ready-set-go interval-reproduction task of Jazayeri and Shadlen (41), the monkey tracks the duration between ready and set cues in order to reproduce the same interval with a self-initiated saccade at the appropriate time after the set cue. The interval between ready and set cues was at least 1 s for all analyses. (D) In the duration-discrimination task of Genovesio et al. (42), the monkey compares the duration of two stimuli and then reports which stimulus was on longer. The duration of stimulus 1 was at least 1 s for all analyses.

To determine if the observed low-dimensional trajectories are sufficient to perform the tasks, we trained artificial RNNs to mimic the behavior of monkeys performing the four tasks analyzed in this paper. The inputs to the RNN are time-varying signals representing sensory stimuli, and we adjusted the parameters of the RNN so its time-varying outputs are the desired behavioral responses (8, 23–37). In these artificial RNNs, we have complete information about the network connectivity and moment-by-moment firing patterns and know, by design, that these are the only computational mechanisms being used to solve the tasks. The RNNs allow us to study the complete set of task dynamics, something we would not be able to do with only the data. The RNNs are important because they allow us to conclude that low-dimensional trajectories are sufficient for solving the tasks we have considered. Our analyses of the data and RNN models agree, and so we can be more confident that we are characterizing the sufficient set of task-relevant dynamics for the tasks. In addition, the RNN dynamics, obtained as the result of optimizing for a clear behavioral goal, suggests a functional role for the different dynamics observed in the data.

In the following sections, we present the results of the two analyses introduced in Fig. 1. First, we present the two-interval time decode for all datasets. Then we probe, in more detail, the differences in neural dynamics between tasks that explicitly require tracking time and those that do not. Second, we show the cumulative dimensionality for all datasets. We then explore the implications of low-dimensional trajectories and their benefits in allowing computations learned at one point in time to generalize to other times.

Task Summaries

We analyzed electrode recordings from monkeys performing four tasks (SI Appendix, Neural Data). Two tasks explicitly required the monkey to keep track of timing information, and two tasks did not. To better understand neural dynamics in the absence of sensory stimuli, we only analyzed tasks with long delay periods over 1,000 ms.

Vibrotactile-Discrimination Task (38).

In this task, a mechanical probe vibrates the monkey’s finger at one of seven frequencies. Then, there is either a 3- or 6-s delay interval before the monkey’s finger is vibrated again at a different frequency. The monkey’s task is to report whether the frequency of the second stimulus is higher or lower than that of the first (Fig. 2A).

Trace-Conditioning Task (39).

In this task, monkeys were presented with one of two visual stimuli, A or B. After a 1.5-s delay period, the monkey was either rewarded or not (Fig. 2B). This is a context-dependent task: in context 1, stimulus A is rewarded and stimulus B is not, whereas, in context 2, the associations are reversed (stimulus A is not rewarded and stimulus B is rewarded). The trials are presented in contextual blocks; all trials within a block have the same context. The monkey displays anticipatory behavior, and in context 1, starts licking the water spout after stimulus A and not after stimulus B. In context 2, the monkey also performs as expected, licking after stimulus B and not after stimulus A. In the study by Saez et al. (39), it was shown that the monkey is not just relearning the changing associations between stimuli and reward but has actually created an abstract representation of context (see also ref. 40).

Interval-Reproduction Task (41).

This task required the monkey to keep track of the interval duration between the ready and set cues (demarcated by two peripheral flashes) in order to reproduce the same interval with a self-initiated saccadic eye movement at the appropriate time after the set cue (Fig. 2C).

Duration-Discrimination Task (42).

This task required the monkey to compare the duration of two visual stimuli (S1 and S2) sequentially presented and then report which stimuli lasted longer on that trial (Fig. 2D). Each of the two stimuli could be either a red square or a blue circle. The “go-cue”’ to initiate the monkey’s response was the presentation of the two stimuli (S1 and S2) simultaneously on the right and left side of the screen, whereupon the monkey would press a switch below the image of the stimulus that had lasted longer on that trial. On each trial, the left and right assignment of S1 and S2 was random so the motor response could not be prepared in advance of this go-cue.

Decoding Time

Decoding time from the recorded patterns of activity is a powerful way of gaining insight into the dynamics of the neural circuits. Indeed, temporal information can be extracted only if some components of the neural dynamics are reproducible across trials, as our method trains and tests on different trials in the typical cross-validated manner. To assess whether there is any information about the time that passed since the last sensory event, we train a decoder to discriminate between two different time intervals (Fig. 1). We call this analysis the two-interval time decode. This type of discriminability is a necessary condition for time to be encoded in the neural activity (if all time intervals are indistinguishable, then, of course, time is not encoded). The two-interval time-decode analysis helps us to identify the time variations that are consistent across trials and to ignore the often large dynamical components that are just noise.

To disambiguate fixed-point dynamics from the other dynamics shown in Fig. 1A, we could, in a noiseless, idealized setting, simply compute the speed of the neural trajectory instead of the two-interval time decode. The speed would go to zero at a fixed point and be nonzero everywhere else. However, in real data, even at a fixed point, the trajectory may have nonzero speed as it jitters around this fixed point. So, in practice, the speed is nonzero for all three sets of dynamics. Furthermore, behaviorally a “slow” or “fast” neural trajectory may only be meaningful when compared with the noise of the trajectory. A slow neural trajectory may encode timing information if the trial-to-trial fluctuations are small enough such that a downstream neuron is able to accurately and consistently disambiguate neighboring time points. However, if this same neural trajectory has larger trial-to-trial noise, then a downstream neuron may not be able to consistently disambiguate neighboring time points, and this trajectory would not reliably encode timing information. For these reasons, we extract timing information in a way that takes into account both the speed of the trajectory and the trial-to-trial noise, by using linear classifiers to extract information from the neural population. We think of a linear classifier as a minimal model for what a downstream neuron can extract, and by training and testing the classifier on nonoverlapping sets of trials, we are able to quantify the information that is able to be consistently extracted through the trial-to-trial fluctuations in the neural population.

Decoding Time in Tasks That Do Not Explicitly Require Tracking Time.

We first discuss the two-interval time decode for the vibrotactile-discrimination task (Fig. 2A). Data from this task have been extensively analyzed (see, e.g., refs. 20, 26, and 43–48) and modeled (see, e.g., refs. 20, 26, and 49), and it is known that several neurons exhibit a time-dependent ramping-average activity (20, 43, 44). However, in previous work, time has never been explicitly decoded.

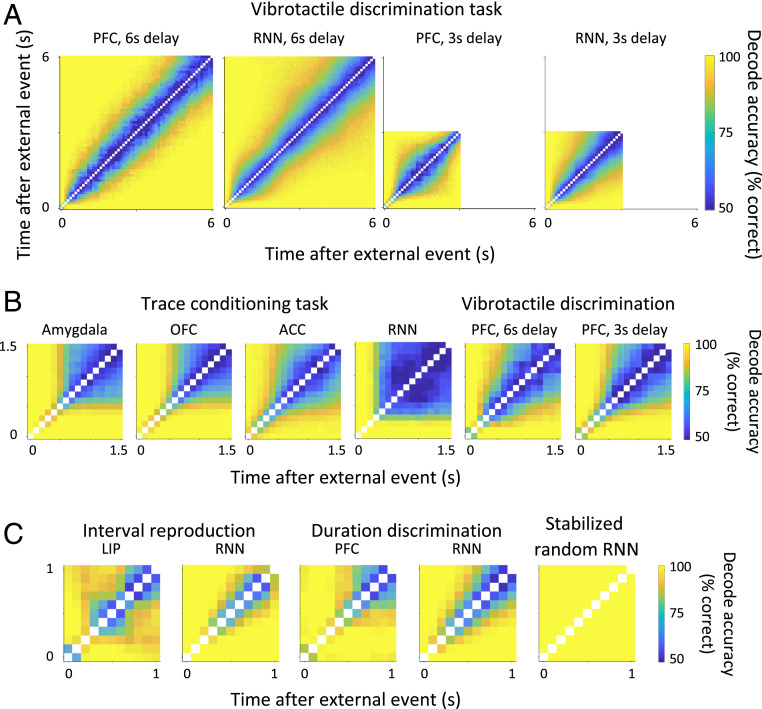
Fig. 3A shows the two-interval time-decode analysis for the vibrotactile-discrimination task for delay intervals of 3 and 6 s (data are aligned to the offset of the first vibrotactile stimulation). The long delay-period intervals used in this task reveal that it is possible to discriminate between neural activity at different time points but only if these time points are sufficiently separated in time, which means that time is encoded with a limited precision. This precision is similar in the 3- and 6-s cases. The two-interval time-decode plots are similar to those of the trace-conditioning task (see Fig. 2B for an overview of the task), as shown in Fig. 3B. The intervals where time cannot be decoded in the trace-conditioning task are signatures of fixed-point dynamics; however, the trace-conditioning task has a delay between external events of only 1.5 s, so there is the possibility that the dynamics have variations on a longer timescale, similar to the vibrotactile-discrimination task, that we cannot observe with this dataset. We discuss this point in more detail in Timing Uncertainty. Note that the inability to decode time in the trace-conditioning task, after the initial transient following stimulus offset, is not simply due to noisy neural responses that have lost all informational content as other task-relevant variables, like context and whether the monkey receives a water reward or not, can be decoded as shown in SI Appendix, Fig. S10 and by Saez et al. (39).

Fig. 3.

Two-interval time decode. (A) The two-interval time-decode analysis for the vibrotactile-discrimination task for delay intervals of 3 and 6 s is shown for both the data and RNN model. The longer delay-period intervals used in this task reveal neural dynamics that evolve slowly, on a timescale of approximately half a second (see also Fig. 5B). Time can be decoded but with limited precision. (B) Two-interval time-decode matrices for the vibrotactile-discrimination task and trace-conditioning task are similar during the delay interval after stimulus offset, when truncating the vibrotactile dataset to match the 1,500-ms delay interval used in the trace-conditioning task. The similarities in these two datasets suggest the observations in the trace-conditioning task are compatible with a slowly varying dynamics, which have been truncated due to the shorter 1,500-ms delay interval used in this experiment (see also SI Appendix, Fig. S12). (C) Two-interval time-decode matrices for the interval-reproduction task (41), duration-discrimination task (42), and stabilized random RNN (17) reveal that time is encoded with higher precision in tasks that explicitly require tracking time. Times are aligned to the ready cue for the interval-reproduction task, S1 onset for the duration-discrimination task, and stimulus offset for the stabilized random RNN. There are no external events during the 1,000-ms interval over which the two-interval time decode is shown, i.e., no external inputs or visual stimuli were changed during this 1,000-ms interval.

Decoding Time in a RNN Model.

The dynamics observed in the vibrotactile-discrimination task are also generated by a RNN model trained to reproduce the experimentally observed behavior of discriminating frequency pairs. Importantly, the RNN must also contain an extra anticipatory output that predicts the time of the next event after the delay period, namely, the delivery of the second vibrotactile frequency (SI Appendix, Fig. S5). The anticipatory output is essential; without it, the RNN model uses only fixed-point dynamics to store the frequency of the first stimulus and does not generate evolving dynamics. With the anticipatory output, the network reproduces the two-interval time-decode plots of Fig. 3A; without it, the two-interval time decode is a solid block of blue after the initial transient following stimulus offset. This is significant because neural connectivity in the artificial RNN was initialized randomly before training, and unit activity was not constrained to replicate neural data during training; the artificial RNN was only told “what” to do but not “how” it should be done (8, 27, 29). We trained the network using backpropagation through time (50) as it has been used successfully to create artificial neural networks that explain neural activity at the level of firing rates for a diverse range of tasks, supporting its utility for hypothesis generation (51–53). The anticipatory output of the RNN suggests the monkey may also be anticipating the next event in the trial, and this is the reason for the evolving dynamics observed in the neural data.

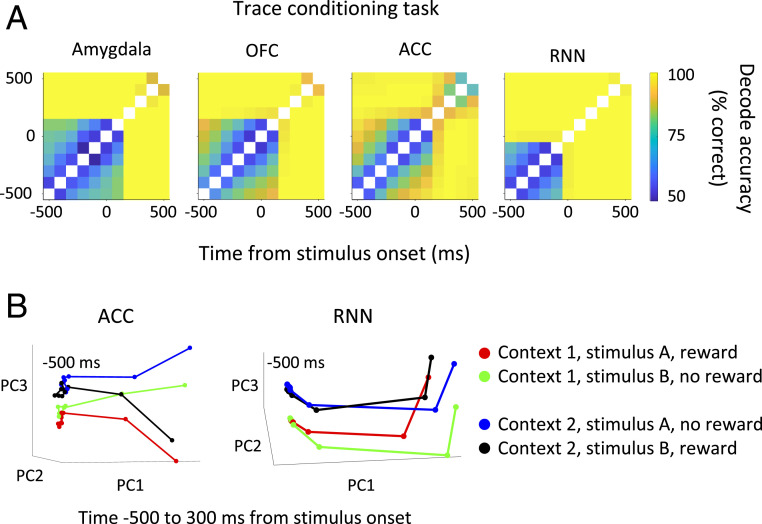
We also created a RNN to mimic monkey behavior during the trace-conditioning task. The model not only reproduces the two-interval time decode of the data, as shown in Fig. 3B, but predicted fixed-point activity outside the delay period that we then verified in the data. We trained the RNN to mimic the monkey’s anticipatory licking and predict the upcoming reward (SI Appendix, Fig. S6). After training is complete, the weights of the RNN are fixed and the model produces the appropriate context-dependent responses for any sequence of stimuli and changing contexts. The RNN is not explicitly given contextual information and must infer it from the pairing of stimulus and reward. Importantly, during the delay, there is no input and the dynamics are entirely driven by the recurrent dynamics. Before stimulus onset, the RNN transitions to one of two fixed points during the intertrial interval to store contextual information between trials (Fig. 4). The signatures of fixed points in the RNN model are also present in the electrode data (Fig. 4), suggesting the monkey may also be using these fixed-point dynamics to store contextual information. The emergence of contextual fixed points in the RNN is surprising because we started with a randomly connected network that knew nothing about context or anything else; context, which is a latent variable, was not present at the beginning of training, and this information is never explicitly given to the network. The RNN formed an abstract understanding of the environment just by learning to generate the right behavior. This contextually dependent behavior is enabled by our use of a RNN (see also SI Appendix, Fig. S7 for an extended explanation). Our understanding of the RNN model for the trace-conditioning task has allowed us to strengthen our interpretation of the neural dynamics observed in the data.

Fig. 4.

Decoding time from neural activity reveals signatures of fixed-point dynamics. (A) Pixel (i,j) is the decode accuracy of a binary classifier trained to discriminate time points i and j using 100-ms bins of neural activity. The blocks of time where the decode is near chance level (50%) are signatures of fixed-point dynamics. The pattern of fixed points seen in the data agrees with the RNN model. In the model, the fixed points before stimulus onset store contextual information. Importantly, a linear classifier can easily discriminate other task-relevant quantities during these time intervals so the poor time decode is not simply due to noisy neural responses that have lost all informational content (SI Appendix, Fig. S10). (B) The average neural trajectories for all four trial types are plotted on the three principal components capturing most of the variance. Time is discretized in 100-ms nonoverlapping bins (denoted by dots) and shown from −500 to 300 ms relative to stimulus onset. During the fixed-point interval before stimulus onset, the trajectories cluster according to context.

Decoding Time in Tasks Where Timing Is Important.

The reservoir-computing paradigm, in which a randomly connected recurrent network with stabilized trajectories is used to perform computations, uses the same “reservoir” for all computations and so timing information should be encoded the same regardless of the task being performed. However, it is also possible that the task actually shapes the neural dynamics and time encoding varies depending on the demands of the task. To test this, we now analyze two datasets in which timing information is necessary to solve the task, namely, the ready-set-go interval-reproduction task (Fig. 2C) and the duration-discrimination task (Fig. 2D). Note that in both previous tasks we have considered the monkey was not explicitly required to keep track of timing information. We decoded the passage of time in these datasets during intervals in which the monkey had to keep track of timing information, i.e., the interval between ready and set cues for the ready-set-go interval-reproduction task and the S1 interval for the duration-discrimination task. To better study the neural dynamics in the absence of external events, we only analyzed trials in which no visual stimuli were changed for 1,000 ms. We found that we could decode time with higher precision than in the datasets where timing information was not explicitly required (see Fig. 3C for the two-interval time decode for the interval-reproduction task, duration-discrimination task, and stabilized random RNN).

Timing Uncertainty.

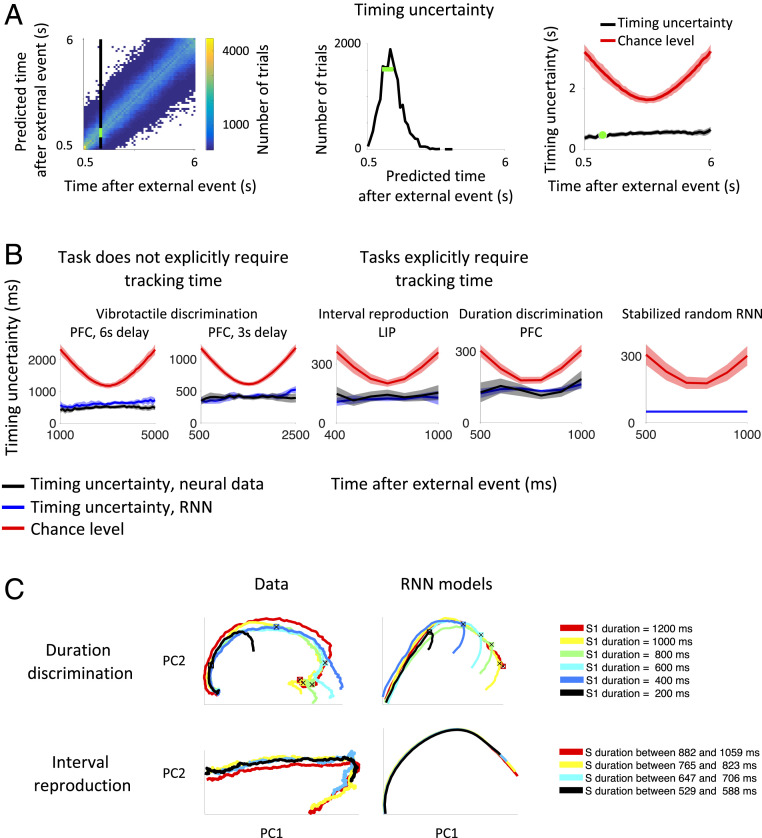
To quantify the timing uncertainty of the neural data at a given point in time, we train a classifier to predict the time this recording was made and then use the spread of predictions when classifying firing rates from different trials as our measure of timing uncertainty (Fig. 5A). This classifier takes the firing rates from all neurons at a given time point (time is discretized in 100-ms bins) and predicts the time this recording was made. This is in contrast to the two-interval time-decode analysis where the binary classifier only discriminates between two time points; the classifier attempts to predict the actual time point within the trial, e.g., 1,000 ms after stimulus offset, or, in other words, it decides what is the most likely class among all of the classes that correspond to different time bins. For this reason, it is a multiclass classifier.

Fig. 5.

(A) To quantify the precision with which time is encoded, we estimated the temporal uncertainty at each point in time by training a classifier to report the time point a neural recording was made and then compare this prediction with the actual time (SI Appendix, Fig. S3); we repeat this classification for many trials, obtaining a distribution about the true time. Left shows the distribution of predicted versus actual times for the vibrotactile-discrimination task, excluding the initial transient after stimulus offset. The distribution of predictions at a single time point, marked by the vertical black line, is replotted in Center. The green bar shows the SD of this distribution. The “timing uncertainty” is the SD of this distribution and contributes a single data point to the “timing uncertainty” graph (Right) (green dot). The timing uncertainty for all time points is shown in black. The chance level is shown in red. (B) The timing uncertainty for the neural data (black curves) and RNN models (blue curves) is less than chance level (red curves) and has better resolution for tasks in which timing information is explicitly required, as in the duration-discrimination task and the ready-set-go interval-reproduction task (note the scales on the y axes are different). This is consistent with the idea that stable neural trajectories act as a clock to perform the task. Error bars show two SDs. (C) Visualization of these putative neural clocks after projecting the neural activity onto the first two principal components capturing the most variance. The left column shows the data for the two tasks that require keeping track of time, and the right column shows the RNN models. Trajectories show the intervals when time is being tracked. For the duration-discrimination task, this is the interval when stimulus one (S1) is on the screen. For the interval-reproduction task, this is the “sample” interval between ready and set cues, denoted by S in the figure legend. Colors indicate the duration of the interval. To better visualize these neural clocks, we include data from all durations, not just durations over 1,000 ms as in B. Principal axes were computed using only data from the longest duration (red curves; first principal component explains over 50% of the variance for all datasets and models), and then data from the shorter durations were projected onto these axes. The black crosses plotted on the trajectories of the duration-discrimination task indicate when the visual stimulus changed to indicate when the monkey should stop counting the duration of the interval, i.e., S1 offset. After this cue, the neural activity gets off the “clock.” All neurons were included that were recorded for 10 or more trials for each duration.

The prediction of the multiclass classifier is compared with the actual time to obtain the timing uncertainty. After performing this classification on many trials, we obtain a distribution of predictions around the true value (Fig. 5A and SI Appendix, Fig. S3). The timing uncertainty shown in Fig. 5B (black curves) is the SD of this distribution of predicted values minus the true value. The chance level for the timing uncertainty (red curves in Fig. 5B) is computed by training and testing the classifier on neural data with random time labels. The chance level is U-shaped as a classifier with uniform, random predictions can make larger errors when the true value is at the edge of the interval.

The tasks that explicitly require tracking time have a smaller timing uncertainty as shown in Fig. 5B. The smaller timing uncertainty is not due to a larger number of neurons or more trials. For example, the timing uncertainty for the interval-reproduction task is computed using the fewest neurons and trials out of any of the datasets: 48 neurons and a mean/median number of trials of 60/49 per neuron. This is in contrast to, for example, the vibrotactile-discrimination dataset where tracking time is not explicitly required, which has 160 neurons (mean/median: 159/176 trials per neuron) and 139 neurons (mean/median: 91/91 trials per neuron) for the 3- and 6-s delay intervals (see SI Appendix, Neural Data for the numbers of neurons and trials for each task). Furthermore, over the interval analyzed in Fig. 5B, the duration-discrimination dataset has smaller mean (6 Hz) and median (3 Hz) firing rates than the vibrotactile-discrimination dataset (mean/median: 11/10 Hz for the 6-s delay; mean/median: 9/7 for the 3-s delay). The smaller timing uncertainty for the tasks that explicitly require tracking time is also not due to a few high firing neurons (SI Appendix, Fig. S11).

These results provide support for the scenario in which the task can shape the neural dynamics depending on whether or not timing information is important in the task. In the case of the vibrotactile-discrimination task analyzed in Decoding Time in Tasks That Do Not Explicitly Require Tracking Time, time could be decoded with lower precision. One could argue that in that case, timing information is not strictly necessary to perform the task, but it could help to prepare the monkey for the arrival of the stimulus, an interpretation that is supported by our RNN model that replicates the experimental findings only when it is trained to predict the time of the upcoming arrival of the second stimulus. So, the difference between the three tasks in which we could decode time is in the relative importance of the timing information, which seems to shape the neural dynamics.

The timing uncertainty in the trace-conditioning task, where we could not decode time (at least after an initial transient following stimulus offset) is compatible with two interpretations: 1) fixed-point dynamics or 2) the same slowly varying dynamics observed in the vibrotactile-discrimination task, which have been truncated at 1,500 ms due to the shorter delay interval used in the trace-conditioning task. In SI Appendix, Fig. S12, the timing uncertainty is shown during the 500-ms interval with putative fixed-point dynamics in the trace-conditioning task and for an arbitrary 500-ms interval after the transient following stimulus offset in the vibrotactile-discrimination task. In all brain regions, the timing uncertainty is near chance level when this short interval is considered, and plots are similar even if the tasks and the brain areas are different. After the transient following stimulus offset, the timing uncertainty of the neural data is near chance level over an interval of half a second for both the vibrotactile-discrimination task (38) and the trace-conditioning task (39). This 500-ms timing uncertainty is consistent with the idea that time is encoded in an imprecise way when timing information is not explicitly required by the task.

The Importance of Ramping Activity for Time Encoding.

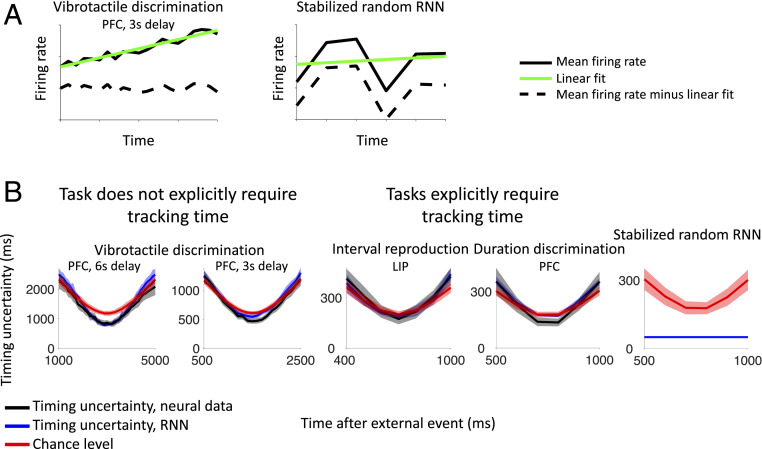
Next, we tried to identify the component of the dynamics that is most important for encoding time in all of the cases in which we could decode it. As we will show, the linear “ramping” component of each neuron’s firing rate appears to contain most of the information about time (54–56). Although for one of the datasets (38), it is known that the ramping component dominates the average dynamics of single neurons (44), it was not clear whether the noise would allow for time decoding on a trial-by-trial basis. Moreover, it is still possible that on top of the ramps, there are other consistent dynamical components that the time decoder might use. These components could be compatible with those generated by a stabilized random RNN, and they might explain, at least partially, our ability to decode time. It turns out that when the linear component is removed, the performance of the time decoder is close to chance, indicating that the other dynamical components do not contribute much to time encoding.

Fig. 6 shows the timing uncertainty in our ability to classify trials after the linear component is removed for all of the experiments in which time could be decoded (compare with Fig. 5). For each neuron, we calculated the linear fit to the average firing rate across trials, during the intervals shown in Fig. 6. We then subtracted this linear fit from the neuron’s firing rate on every single trial. The mean firing rate across trials from two example neurons is shown in Fig. 6A, before and after the linear fit is subtracted. After the linear ramping component is removed, we compute the timing uncertainty, by classifying single trials as we do to compute the timing uncertainty in all figures, and see that the timing uncertainty is near chance level for both tasks in which timing information is, and is not, explicitly relevant (Fig. 6B, black curves). This is also observed in the RNN models we trained to solve the experimental tasks (Fig. 6B, blue curves). In contrast, for the stabilized random RNN (17), it is still possible to decode time with high accuracy even after the linear component has been removed (Fig. 6B, rightmost graph). Our analyses suggest timing information in the neural data is encoded in low-dimensional, predominantly ramping, activity. It is important to stress that the neurons that exhibit ramping activity also typically encode other variables. We do not observe segregated populations of highly specialized neurons (SI Appendix, Fig. S13), in agreement with other studies (40, 57).

Fig. 6.

The linear ramping component of each neuron’s firing rate drives the decoder’s ability to estimate the passage of time (compare with Fig. 5). (A) For each neuron, we calculate the linear fit to the average firing rate across trials during the same time interval as in Fig. 5. We then subtract this linear fit from the firing rate on every single trial and calculate the timing uncertainty. (B) After the linear ramping component is removed, the timing uncertainty in both the neural data (black curves) and trained RNN models (blue curves) is near chance level (red curves). In contrast, for the untrained RNN with stabilized chaotic dynamics (17), it is still possible to decode time with high accuracy, down to the limiting resolution set by the 100-ms time bin of the analysis, even after the linear component has been removed. Error bars show two SDs.

Low-Dimensional Trajectories for Better Generalization

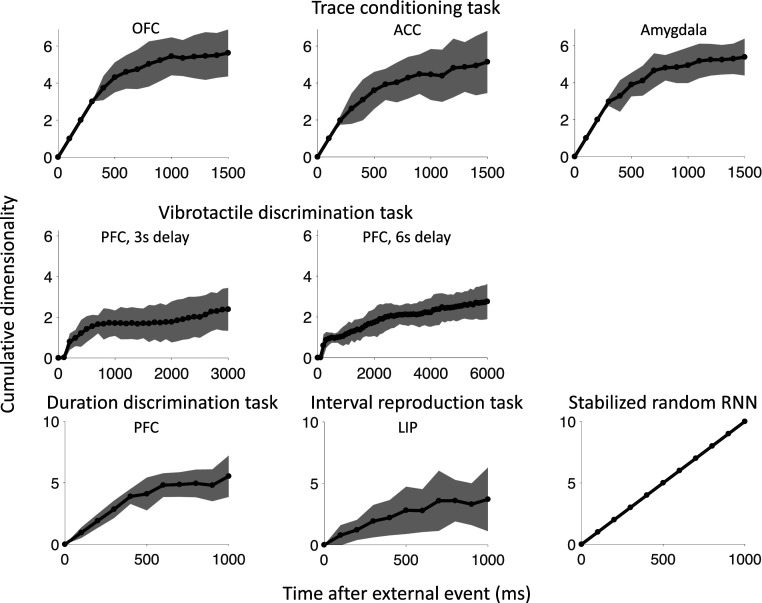
In this section, we compute the cumulative dimensionality of the neural trajectory as it evolves over time. Our method for computing dimensionality (SI Appendix, Fig. S1) helps to identify the variations that are consistent across trials and to ignore the often large dynamical components that are just noise (for example, see SI Appendix, Fig. S2). The cumulative dimensionality of the neural trajectory is an informative quantity because it not only helps identify the neural regime (Fig. 1) but has implications for the generalization capabilities of a network, in particular, how well computations learned at one point in time generalize to other times.

Monkeys performing working memory tasks are able to store task-relevant variables across the delay period in a way that generalizes to new delay intervals. For example, if the duration of the delay interval is increased, the monkey will generalize to the new task without needing to retrain. This generalization ability places constraints on the types of neural dynamics that support working memory. As we show in Generalization across Time, neural trajectories with high cumulative dimensionality do not allow for good generalization, suggesting a monkey relying on these dynamics would need to retrain to adjust to a longer delay interval. In contrast, data with low cumulative dimensionality enables computations learned at one point in time to generalize to other points in time.

The cumulative dimensionality over time is shown in Fig. 7, during the interval between external events, e.g., after stimulus offset and before the reward for the trace-conditioning task (see SI Appendix, Fig. S14 for the RNN models). For all datasets, the dimensionality increases much slower than in the case of the stabilized random RNN (17), which explores new dimensions of state space at each point in time. After an initial rapid increase, which terminates around 500 ms in all datasets, the cumulative dimensionality increases very slowly or saturates. The initial rapid increase reflects the ability to decode time with high precision, which is probably due to a relatively fast transient that follows the offset of the stimulus. The slow increase observed in the remaining part of the delay is consistent with the strong linear ramping component observed in Fig. 6 as ramping activity would cause the neural trajectory to lie along a single line in state space, and so the cumulative dimensionality would be one (SI Appendix, Fig. S15). The cumulative dimensionality is stable as the number of time points along the neural trajectory is varied (firing rates are computed in time bins that vary between 25 and 100 ms) and when the numbers of neurons are equalized between datasets, as shown in SI Appendix, Figs. S16–S19.

Fig. 7.

The cumulative dimensionality of the neural activity increases slowly over time after a transient of ∼500 ms. In contrast, the cumulative dimensionality increases linearly in the stabilized random network (17). The top and middle rows show dimensionality for tasks in which timing is not explicitly important. The bottom row shows dimensionality for tasks in which timing is required. The cumulative dimensionality for the RNN models is similar and is shown in SI Appendix, Fig. S14. Error bars show two SDs.

Generalization across Time.

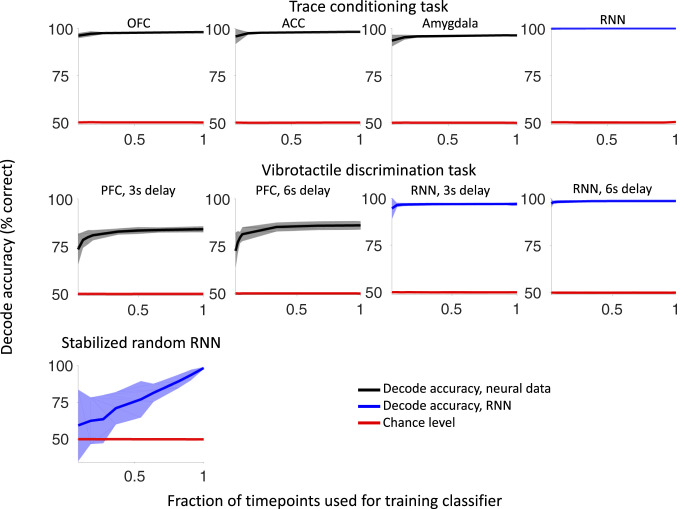
The low-dimensional ramping trajectories seen in the neural data may offer computational benefits, allowing computations to generalize across time (58). For example, consider the trace-conditioning task (39), where the offset of a visual stimulus is followed by a delay period and then either a water reward or no reward. Imagine a readout neuron learns to linearly combine neural activity from the prefrontal cortex after the offset of the visual stimulus in order to predict whether a reward will be delivered. After some time has elapsed, e.g., a second, will this same neuron still be able to correctly predict the upcoming reward? Will this same linear combination of information from the prefrontal cortex still be useful at a different time? The answer depends on how the neural dynamics evolve. The low-dimensional ramping trajectories of the neural data allow a linear classifier trained at a few points in time to have predictive power at other points in time (Fig. 8 and SI Appendix, Fig. S4 and Decode Generalization). Note that when only a single time point is used for training the classifier, we cycle through each and every time point in the interval. When multiple time points are used for training the classifier, we randomly select time points on each iteration of cross-validation. In the trace-conditioning task (Fig. 8, top row), a linear classifier trained to decode the value of the stimulus on a fraction of time points can decode the value with an accuracy close to 100% also at the other time points. In the vibrotactile-discrimination task, a classifier trained to decode high versus low vibrotactile stimuli can also generalize across time, although the decoding performance is lower than in the case of reward decoding. This is compatible with the stability of the geometry of neural representations observed by Spaak et al. (58) and with the ability of a linear readout to generalize across the experimental conditions observed by Bernardi et al. (40). This ability to generalize to other time points is also observed in the RNN model trained with backpropagation (Fig. 8; see all of the plots with the label “RNN”). In contrast, for the high-dimensional neural dynamics of the simulated stabilized random RNN, a linear classifier trained at a few points in time performs at near chance level at other points in time (Fig. 8, bottom row).

Fig. 8.

Decode generalization when classifying neural activity with low and high cumulative dimensionality. The decode accuracy of a binary classifier (colored in black for data and blue for RNN models) is shown as the number of time points used during training is varied. The chance level is shown in red. The neural activity with low cumulative dimensionality allows a classifier trained at a single time point to perform with high accuracy when tested at other times. This is in contrast to neural activity with high cumulative dimensionality (bottom row) where a decoder trained at a single time point performs at chance level when tested at other time points. To assess generalization performance, the classifier is always tested on trials that were not used during training and tested on time points from the entire delay interval with the exception of the first 500 ms after stimulus offset for the neural datasets. In the top row, the decoder classifies rewarded versus nonrewarded trials. In the middle row, the decoder classifies high versus low frequencies. In the bottom row, the decoder classifies trials from the two patterns the network is trained to produce in the study by Laje and Buonomano (17). The plotted decode accuracy is the mean of the classifier performance across this interval, when tested on trials that were not used during training. Error bars show two SDs.

Discussion

Delay activity is widely observed in cortical recordings and is believed to be important for two functions that could be difficult to combine in the same neural circuit: the first is to preserve information robustly against the flow of time (working memory); the second is to actually track the passage of time to anticipate stimuli and plan future actions. To understand the mechanisms underlying working memory and time encoding, we analyzed neural activity recorded during delays in four experiments on nonhuman primates. To disambiguate potential mechanisms, we proposed two analyses, namely, decoding the passage of time from neural data and computing the cumulative dimensionality of the neural trajectory as it evolves over time.

When we started to study the dynamics of these datasets, we had a very specific hypothesis to test: that the neural trajectories in the firing-rate space would be high-dimensional, as predicted by powerful randomly connected neural network models known as reservoir networks (or echo-state networks or liquid-state machines). We intended to test the idea that time can be decoded from the neural activity thanks to these high-dimensional trajectories. In these networks, time decoding should be possible in every brain area regardless of whether or not timing information is relevant for the task (12).

Our first analysis, of the trace-conditioning task of Saez et al. (39), revealed that time decoding is near chance level when the dynamics are likely to be internally generated and not driven by sensory stimuli. The result was so surprising that we decided to analyze another three datasets with longer delay intervals and also datasets where timing information was explicitly required to solve the task. When we analyzed data from the vibrotactile-discrimination task with longer delay intervals of 3 and 6 s, we found a similar inability to decode time when truncating the dataset at 1.5 s after stimulus offset to match the 1.5-s delay interval of the trace-conditioning task. However, decoding time across the whole delay interval revealed it is possible to discriminate between neural activity at different time points but only if these time points are sufficiently separated in time, which means that time is encoded with a limited precision.

The following observations are consistent across all four datasets: 1) the trajectories are always low-dimensional; 2) time can be decoded with low precision in tasks in which the timing information is not relevant for the task and with higher precision in tasks in which the animal is explicitly asked to keep track of the passage of time. Furthermore, the ability to decode time relies mainly on the ramping component of the activity. This is true when a transient of ∼500 ms following the offset of the stimulus is excluded from the analysis. During these 500 ms, it is likely that the activity is still driven by the sensory input and does not reflect the internal dynamics of the neural circuits. This is consistent with recent experiments on rodents (21, 22) that show that neural trajectories are low-dimensional, with a time-varying component that is dominated by ramping activity (46, 48). Our analyses extend previous studies and show that these low-dimensional, ramping, trajectories (59) encode the passage of time (60, 61). Interestingly, when the timing information was explicitly required to perform the task, time could be decoded with a higher accuracy, but the trajectories were still low-dimensional, suggesting that the mechanisms underlying time encoding are similar.

Our experimental observations are incompatible with the predictions of a standard reservoir network. This pushed us to try different models to reproduce the data. The RNN models that we trained using backpropagation through time (BPTT) reproduce the dimensionality and time decoding results of the four datasets that we analyzed. The RNN models allow us to conclude that low-dimensional trajectories are sufficient for solving the tasks we have considered, an insight that would be difficult to obtain without these models.

The RNNs also provide a functional interpretation for some of the specific features in the data. The RNN dynamics are optimized, by design, for a particular task, and so agreement between the neural data and RNNs suggests the features our analyses uncovered in the neural data are important for the tasks and not merely an interesting byproduct of some unrelated dynamical processes in the brain. In the vibrotactile-discrimination task, the RNN allowed us to take a hypothesis, namely that the monkey was attempting to anticipate the next stimulus and turn this into a prediction about neural dynamics that we could then compare with neural data. The agreement between the data and RNN, after including this goal, then suggests that the monkey in this task is trying to anticipate when future events in the trial are going to happen even when that is not required by the experimenter. In the trace-conditioning task, the RNN settled into one of two fixed points to store information about which of the two contexts it was in. These contextual fixed points were outside of the delay interval we were initially analyzing, but when we looked in the electrode recordings, we found a similar pattern of fixed points before stimulus onset. The RNN suggests these fixed points in the neural data may also be encoding contextual information for the monkey.

The success of these simulated RNN models is surprising given that both the model units and training algorithm differ from the brain. BPTT is an artificial algorithm, for which there is no comparable biologically plausible implementation at the moment. Methods have been proposed for biologically plausible learning in recurrent networks (62, 63), but it should not be assumed that these methods scale to harder problems, as this scaling has proven difficult for biological approximations to backpropagation for feedforward networks (64). However, the brain and the simulated RNNs that we built share similar constraints as they are both trained to perform the same tasks efficiently in the presence of noise. This is probably why some of the features of the neural representations are similar. It remains possible that some of the important mechanisms are actually implemented in a very different way. For example, the ramping activity might be a consequence of some biochemical processes that are present at the level of individual neurons or synapses in the biological brain (65, 66). These processes might happen within the network that generates the ramping activity, or they might be generated in other brain areas. These processes are not explicitly modeled in our RNN, in which all of the elements are simple rate neurons, but they can be imitated in the recurrent network by tuning the weights between neurons or potentially by combining canonical circuits, each devoted to implementing a specific biochemical process. A more complex analysis will be developed to reveal these canonical circuits. In the meantime, it is important to keep in mind that we do not necessarily expect a one-to-one correspondence between the neurons in the RNN and the neurons in the brain.

The time-decoding results for all datasets are consistent with a common interpretation, namely, time can be decoded with high precision in tasks where timing information is relevant and with lower precision when irrelevant for performing the task. However, it is also possible that the interval where the time decode was near chance level in the trace-conditioning task indicates fixed-point dynamics. This interpretation would be strengthened if the delay interval used in this task had been longer than 1,500 ms and we had continued to observe the persistence of these putative fixed-point dynamics. The 1,500-ms delay interval used in this task may not allow us to see longer timescale variations that would be present if a longer delay interval had been used, and this dataset is, in fact, consistent with the other three. This interpretation is suggested by similarities between the neural dynamics of the trace-conditioning and vibrotactile-discrimination datasets, the two datasets where timing information is not explicitly required to perform the task. The first 1,500 ms of the delay period for the vibrotactile-discrimination dataset looks similar to the 1,500-ms delay period for the trace-conditioning task (Fig. 3B). Furthermore, after an initial transient, any 500-ms interval of the vibrotactile-discrimination task has a timing uncertainty near chance level, similar to the 500-ms interval near chance level in the trace-conditioning task (SI Appendix, Fig. S12). However, because the delay periods used in the vibrotactile-discrimination task are longer (3 and 6 s), we can see the network dynamics evolve on timescales longer than 500 ms.

One of the robust results of our analysis is that the observed trajectories in the firing-rate space are low-dimensional. This contrasts with other studies in which the dimensionality of the neural representations was reported to be high (see, e.g., refs. 67–69) or as high-dimensional as it could be (70). However, it is important to stress that the dimensionality measured in these other studies is the dimensionality at a single time point over multiple conditions of the experiment (a single condition in the vibrotactile-discrimination task, for example, is all trials with the same initial vibrotactile frequency), whereas we are measuring the dimensionality of a single condition over multiple time points. So, it seems that the trajectories corresponding to each condition have low dimensionality, whereas the dimensionality across different conditions is high for tasks like the one studied by Rigotti et al. (67). To maximize the ability to generalize, the dimensionality should be the minimal required by the task, and indeed, we observed that the RNN models we trained with backpropagation generate low-dimensional trajectories, in agreement with recent work (71, 72). This is an indication that high dimensionality is not needed in the tasks we considered.

Low dimensionality allows for better generalization, but this comes at a cost. The points of a high-dimensional trajectory can be separated arbitrarily by a simple linear readout. This is often not the case for the low-dimensional trajectories that we observed (indeed, our time decoder illustrated in SI Appendix, Fig. S3A is nonlinear). However, there are situations in which a nonlinear decoder is not required to be able to generate a specific response at a particular time. For example, even in the low-dimensional case in which a trajectory is perfectly linear, it is often possible to linearly separate the last point from the others. So, a linear readout would be able to report that a certain time bin is at the end of a given interval and “anticipate” the arrival of a stimulus. For more complex computations on the low-dimensional trajectories, the brain might employ a nonlinear decoder, which could easily be implemented by a downstream neural circuit that involves at least one hidden layer.

Reservoir networks may be able to reproduce the dimensionality profiles we see in the data, but this seems unlikely. It is possible that the dynamics are chaotic but with an autocorrelation time that is relatively long, comparable with the entire delay interval that we considered. In this case, the activity would change slowly, preventing the neural circuit from exploring a large portion of the firing-rate space in the limited time of the experiment. The cumulative dimensionality would still grow linearly but on a much longer timescale, and on the timescale of the experiment, it would be approximately constant. Although possible, this scenario would have to assume that the autocorrelation time can vary on multiple timescales in order to explain the rapid variations observed during the initial transients and, at the same time, the very slow variations observed later, when the cumulative dimensionality stops growing. To match the saturating cumulative dimensionality observed in the data it may be possible to extend the reservoir-computing framework; instead of stabilizing a randomly connected network (leading to high cumulative dimensionality), a network that has some structured and some random elements may be used as a reservoir (73–75). This is left as an interesting future direction. However, even if the saturating cumulative dimensionality could be replicated, there are aspects of these datasets which do not seem compatible with completely random dynamics of the neural trajectories (for example, Figs. 4B and 5C).

Several studies on rodents demonstrate sequential activation of neurons over multisecond timescales. Individual neurons fire at specific moments in spatial and nonspatial tasks in the hippocampus (see, e.g., refs. 76 and 77) and in the striatum (78–80). The cells in the hippocampus have been called “time cells” for their response properties. By reading out these representations, it is possible to decode time both in the hippocampus (81), with an average decode error of 2 s, and in the striatum (78), where the error was typically less than 10% of the total interval (12 to 60 s). These representations are inherently high-dimensional because at every time step, a new cell is activated and hence a new dimension is explored. The cumulative dimensionality would then grow linearly with time. Hence, these neural representations are rather different from the ones that we observed. One possible reason is that in these brain areas, time has been combined nonlinearly with other variables like the position of the animal or relevant memories in the hippocampus or motor responses in the striatum. It is also possible that these representations are only observed when the animal is engaged in a task that requires some movement. In our case, during the delay, no salient event occurs in the environment, and most likely the animals do not generate reproducible motor outputs. Finally, it could be that rodents and nonhuman primates adopt very different strategies for encoding time (82).

A fundamental challenge in studying neural activity that evolves over time is understanding what computational capabilities can be supported by the activity and when these dynamics change to support different computational demands. Our time-decode and cumulative-dimensionality analyses offer a tool for parcellating neural activity into computationally distinct regimes across time by objective classification of electrophysiological activity. In this work, we apply these analyses to delay-period activity and find that low-dimensional trajectories provide a mechanism for the brain to solve the problem of time-invariant generalization while retaining the timing information necessary for anticipating events and coordinating behavior in a dynamic environment.

Methods Summary

The procedure for calculating the two-interval time-decode matrix and the timing uncertainty are in SI Appendix, Decoding Time. Our measure for the cumulative neural dimensionality over time, from Fig. 7, is in SI Appendix, Neural Dimensionality. The decode generalization analysis of Fig. 8 is in SI Appendix, Decode Generalization. The RNN models for each of the four tasks are detailed in SI Appendix, Model Description. The electrode recordings are described in SI Appendix, Neural Data.

Data Availability.

Data available upon reasonable request.