Mesoscale diffusion magnetic resonance imaging of the ex vivo human hippocampus

Abstract

Mesoscale diffusion magnetic resonance imaging (MRI) endeavors to bridge the gap between macroscopic white matter tractography and microscopic studies investigating the cytoarchitecture of human brain tissue. To ensure a robust measurement of diffusion at the mesoscale, acquisition parameters were arrayed to investigate their effects on scalar indices (mean, radial, axial diffusivity, and fractional anisotropy) and streamlines (i.e., graphical representation of axonal tracts) in hippocampal layers. A mesoscale resolution afforded segementation of the pyramidal cell layer (CA1‐4), the dentate gyrus, as well as stratum moleculare, radiatum, and oriens. Using ex vivo samples, surgically excised from patients with intractable epilepsy (n = 3), we found that shorter diffusion times (23.7 ms) with a b‐value of 4,000 s/mm² were advantageous at the mesoscale, providing a compromise between mean diffusivity and fractional anisotropy measurements. Spatial resolution and sample orientation exerted a major effect on tractography, whereas the number of diffusion gradient encoding directions minimally affected scalar indices and streamline density. A sample temperature of 15°C provided a compromise between increasing signal‐to‐noise ratio and increasing the diffusion properties of the tissue. Optimization of the acquisition afforded a system's view of intra‐ and extra‐hippocampal connections. Tractography reflected histological boundaries of hippocampal layers. Individual layer connectivity was visualized, as well as streamlines emanating from individual sub‐fields. The perforant path, subiculum and angular bundle demonstrated extra‐hippocampal connections. Histology of the samples confirmed individual cell layers corresponding to ROIs defined on MR images. We anticipate that this ex vivo mesoscale imaging will yield novel insights into human hippocampal connectivity.

Mesoscale diffusion magnetic resonance imaging (MRI) endeavors to bridge the gap between macroscopic white matter tractography and microscopic studies investigating the cytoarchitecture of human brain tissue. We here optimized the mesoscale acquisition of diffusion MRI on the human hippocampus to resolve intra‐hippocampal connections which are relevant to neurological conditions, such as epilepsy and Alzheimer's disease.

1. INTRODUCTION

The human hippocampus is a complex neuroanatomical structure composed of different cell layers that interconnect in a tri‐synaptic pathway that is involved in memory and spatial navigation (Strange, Witter, Lein, & Moser, 2014). Visualizing hippocampal sub‐fields, such as the cornu ammonis 1 (CA1) and dentate gyrus (DG), as well as their geometric arrangement from the head to the tail of the hippocampus, with its integration in the mesial temporal lobe, is crucial to improve our understanding of its function in aging and disease (Augustinack et al., 2010; Colon‐Perez et al., 2015; Coras et al., 2014; Shah et al., 2018; Shepherd, Ozarslan, Yachnis, King, & Blackband, 2007). A high spatial resolution (<1 mm) is required to visualize sub‐fields in vivo (Thomas et al., 2008), as well as ex vivo (Adler et al., 2014). We have previously demonstrated that mesoscale diffusion MRI at a 0.001 μl voxel volume is required to reliably distinguish cell layers within sub‐fields (Modo, Hitchens, Liu, & Richardson, 2016), producing a resolution ×8,000 higher than in standard clinical DTI (Figure 1a). Definition of cell layers is essential to probe intra‐regional connectivity, which was adept at visualizing aberrant connections in a hippocampus excised from a mesial temporal lobe epilepsy (MTLE) patient (Modo et al., 2016). However, the acquisition parameters of mesoscale diffusion MR images for tractography remain poorly defined.

FIGURE 1.

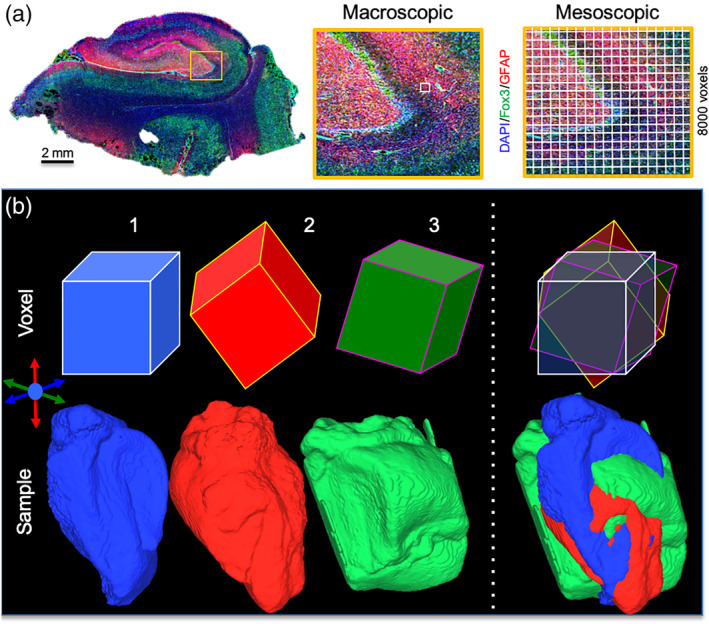
Diffusion MRI at the mesoscale. Histological section of a human hippocampus excised from a patient with mesial temporal lobe epilepsy (DAPI = cell nuclei, Fox3 = neurons; glial fibrillary acid protein, GFAP = astrocytes). On clinical scanners diffusion tensor imaging typically uses an 8 μl spatial resolution, which is a large voxel covering several hippocampal layers and make it difficult to define sub‐fields and individual lamina. In contrast, at a mesoscale resolution (0.001 μl) aimed at probing connectivity between different cell layers, a sufficient delineation of each layer is achieved. This resolution produces 8,000 voxels for each voxel used in a typical clinical DTI scan (a). in vivo scans typically produce diffusion images that are aligned along the gradient axis and the main magnetic field. However, the orientation of ex vivo samples in relation to the diffusion encoding direction can differ and affect the detection of axonal tracts, as well as the definition of cell layers. This can affect inter‐sample variability in measurements, but also impact consistency and reliability of measuring multiple times the same sample (b)

Interrogating gray matter connectivity requires an acquisition paradigm tailored to detect water diffusion at the mesoscale (0.1–1 cm), rather than the macroscale (>1 cm) typically used to image anisotropic callosal connectivity (Burcaw, Fieremans, & Novikov, 2015; Roebroeck, Miller, & Aggarwal, 2018; Rulseh, Keller, Tintera, Kozisek, & Vymazal, 2013; Savadjiev et al., 2014). Macroscopic white matter in the brain is mostly composed of long axonal tracts that are highly anisotropic within a given voxel, whereas mesoscale gray matter contains a much smaller volume fraction (i.e., packing density) of axons and considerably higher numbers of neurons. Long diffusion times are favorable for macroscopic white matter tractography (Rane, Nair, & Duong, 2010), but short diffusion times might be required to probe the mesoscale at higher fields (Kunz, Sizonenko, Huppi, Gruetter, & van de Looij, 2013). The extracellular space is also less compact in gray matter, producing a less anisotropic space. Measuring the diffusion signal in tissues is dependent on a variety of acquisition parameters, including diffusion time (Cleary et al., 2011; De Santis, Jones, & Roebroeck, 2016; Latour, Svoboda, Mitra, & Sotak, 1994; Ozarslan, Shepherd, Koay, Blackband, & Basser, 2012), gradient strength (Han et al., 2006; Jones et al., 2018), b‐value (Kaden, Kelm, Carson, Does, & Alexander, 2016; Tournier, Calamante, & Connelly, 2013; Xie et al., 2015), as well as the number of diffusion gradient directions (NDGD) (Lebel, Benner, & Beaulieu, 2012; Ni, Kavcic, Zhu, Ekholm, & Zhong, 2006; Zhang, Deng, Wang, & Wang, 2009).

To define appropriate acquisition parameters at the mesoscale, prolonged scanning times are required. The use of ex vivo fixed tissue samples is advantageous for this purpose, as it affords acquisition of different parameters affecting the diffusion signal on the same sample without tissue perfusion or subject movement. The orientation of the sample along the diffusion encoding direction and main magnetic field can potentially affect the diffusion tensor and impact the mapping of fiber tracts (Glenn et al., 2016). A further potential confounding issue could be tissue decay due to the time interval to fixation, which is especially a concern with postmortem tissue, where the fractional anisotropy (FA) and mean diffusivity (MD) have been shown to decrease with longer fixation delays (D'Arceuil & de Crespigny, 2007; Scheurer et al., 2011; Shepherd et al., 2009). The use of hippocampi surgically excised for the treatment of MTLE minimizes this fixation delay. Still, fixation using different chemicals is known to affect diffusion properties of tissue (Bourne, Bongers, Chatterjee, Sved, & Watson, 2016; Oguz et al., 2013; Thelwall, Shepherd, Stanisz, & Blackband, 2006) with axial diffusivity (AD) being commonly reduced, whereas radial diffusivity (RD) is increased (Richardson et al., 2014). Tissue fixation therefore can affect the diffusion signal and bias absolute measurements of scalar indices. Morphological changes, including volumetric changes, can also occur due to the fixation process (Schulz et al., 2011; Wehrl et al., 2015), as well as prolonged storage in the fixative solution (van Duijn et al., 2011). A recent comparison of the human hippocampi imaged both in vivo and ex vivo in the same subjects showed the general effect of regions appearing smaller in vivo, but there were some disproportionate effects in certain areas (Wisse et al., 2017). The average time of fixation was 38 days, with an average time between in vivo and ex vivo scans being 2.3 years. However, their finding of satisfactory in vivo/ex vivo registration suggests that the surgically excised hippocampi in our study can provide a high‐quality sample reflecting in vivo anatomy and tissue properties. Sample temperature can affect diffusion properties (Thelwall et al., 2006), with physiological temperature (37°C) producing a higher diffusivity than ex vivo samples at room temperature (21°C). However, lower temperatures for ex vivo scanning can be advantageous, as they produce higher SNR and also ensure long‐term tissue integrity.

The purpose of this study was to investigate the diffusion signal at the mesoscale and its use for tractography (i.e., tracing of micrometer‐dimension axonal connections). The influence of acquisition parameters on the measurement of scalar indices (i.e., mean diffusivity, axial diffusivity, radial diffusivity, and fractional anisotropy) is explored by varying diffusion time (13.6, 23.7, 98.7 ms), b‐value (1,000, 4,000, 10,000 s/mm²), voxel size (100, 250, 450 μm), as well as the number of diffusion directions (12, 48, 256). We further evaluated the contribution of sample temperature (8, 15, 22, 30°C) to tissue water diffusion, as well as how orientation of samples affected the tracing of streamlines. Definition of hippocampal structures on MD maps were further compared with histological images to ensure a faithful representation and delineation of anatomy.

2. MATERIAL AND METHODS

2.1. Specimen collection

In all cases, anterior temporal lobectomy was recommended by a multidisciplinary epilepsy board to treat intractable mesial temporal lobe epilepsy (MTLE). Preoperative MRIs revealed T2 hyperintensities with minimal hippocampal volume loss indicative of mesial temporal sclerosis. Specimen excision was achieved via en bloc hippocampectomy. Research procedures were approved by the Institutional Review Board of the University of Pittsburgh. Acquisition parameter experiments were conducted on a left hippocampus specimen, donated by a 45‐year‐old Caucasian male with an 8‐year history of MTLE (sample volume 1,689.64 mm³). In addition to this sample, orientation scans were performed on a right hippocampus donated by a 68‐year‐old female patient with a history of 17 years of MTLE (sample volume 1,281.63 mm³), as well as another right hippocampus from a 63‐year‐old female patient with 59 years of MTLE (sample volume 1,497.31 mm³).

2.2. Specimen fixation

Hippocampi were coronally cut postexcision, with the anterior (head) portion designated for clinical histopathological analyses and the posterior portion (body) for this study. The posterior portion was fixed immediately following surgery in formaldehyde (4%) for 48 hr before transfer and storage in phosphate buffered saline (PBS) at 4°C. Specimens (~20 × 12 × 12 mm) were prepared for MR imaging by immersion in proton‐free Fluorinert (Sigma‐Aldrich, St. Louis, MO) inside a syringe with a Luer cap for long duration immobilization, while avoiding the generation of air bubbles and dehydration.

2.3. MR data acquisition

All imaging experiments were initiated within 14 days after surgical excision using an 11.7 T/89 mm Bruker Avance AV3 HD microimaging scanner with a 16‐channel shim insert, a Micro 2.5 gradient insert, capable of up to 150 G/cm, a 20‐mm diameter quadrature birdcage RF coil and Paravision 6.0.1 (Bruker Biospin, Billerica, MA). Variable temperature control was achieved with a Bruker SmartCooler BCU‐1 40/50 air chiller and a probe heater with a thermocouple feed‐back loop to maintain the sample temperature to within ±0.1° C. Prior to imaging, specimens were warmed gradually and maintained at 8, 15, 22, or 30°C. In order to minimize sample degradation, lower sample temperature scans were performed first. DTI images were acquired with a 3D Pulsed Gradient Spin Echo (PGSE) sequence (NEX = 1; FOV = 25.6 × 12.8 × 12.8 mm; 256 × 128 × 128 Matrix; BW = 65 kHz) using the settings outlined in Table 1. Variation of diffusion time (t_D) and gradient strength was achieved by adjusting diffusion duration, but maintaining a constant b‐value. Total scanning time per condition ranged from 3.5 to 74 hr with a total scanning time of 723 hr for the acquisition experiments. MRI datasets are available from the corresponding author upon request.

TABLE 1.

Arrayed diffusion MRI acquisition parameters using a 3D pulsed gradient spin echo (PGSE) sequence (TR = 1,100 ms, TE = 25 ms; NEX = 1; FOV = 25.6 × 12.8 × 12.8 mm)

Parameter	Duration δ (ms)	Spacing Δ (ms)	Diffusion time tD Δ‐δ /3 (ms)	Diffusion weighting b‐value (s/mm2)	Gradient strength G (mT/m)	Diffusion directions	Spatial resolution (μm)	Temp. (°C)	Time (hr)
Diffusion time	4	15	13.6	4,000	544	12	100	15	63
		25*	23.7		410
		100**	98.7		200
b‐value	4	15	13.6	1,000	270	12	100	15	63
				4,000	544
				10,000	855
Resolution	4	15	13.6	4,000	544	12	100	15	63
							200		16.5
							450		3.5
Directions	4	15	13.6	4,000	544	12	450	8	3.5
						48			14
						256			74
Temp.	4	15	13.6	4,000	544	12	100	8	63
								15
								22
								30

Note: Bold and italics lettering indicate the standard acquisition parameter. *TE = 34.9 ms; **TE = 109.9 ms.

To probe the influence of different sample orientations in the magnetic field on diffusion measurement and tractography (Figure 1b), a mesoscale resolution 3D T₂‐weighted Spin Echo scan (as above) was acquired for three samples using three orientations (~0, 90 and 180°) along the dorsal‐ventral axis of the sample inside the syringe (i.e., parallel to the magnetic field). Diffusion tensor images were acquired using a standardized 3D Pulsed Gradient Spin Echo sequence (TR = 1,100 ms, TE = 25 ms, diffusion duration δ = 4 ms, diffusion spacing Δ = 15 ms, t_D = 13.6 ms, 12 non‐colinear diffusion directions, b‐value = 4,000 s/mm², 100 μm isotropic resolution) at 8°C to minimize sample degradation. Scanning time per sample/orientation was 63 hr. Samples were completely removed between scans with field map shimming up to third order shims, radiofrequency pulse power and water frequency being readjusted.

2.4. Diffusion image preprocessing

Diffusion MR images were processed using DSI Studio (http://www.dsistudio.labsolver.org; Yeh, Verstynen, Wang, Fernandez‐Miranda, & Tseng, 2013) to check the gradient table and correct for eddy current distortions, and the sample was masked using a signal threshold to remove the background prior to processing. No up‐sampling or motion correction was used. Reconstruction of the scalar maps was achieved by performing an Eigenvector analysis on the calculated tensor (Jiang, van Zijl, Kim, Pearlson, & Mori, 2006). Scalar indices of diffusion, notably fractional anisotropy (FA), mean diffusivity (MD), radial diffusivity (RD), and axial diffusivity (AD) were calculated to probe and compare the diffusion signal between different acquisition protocols (Basser, Mattiello, & LeBihan, 1994).

2.5. Signal‐to‐noise comparison

SNR is known to have a major impact on computed scalar indices and tractography (Farrell et al., 2007; Polders et al., 2011; Wang, Chia, Ahmed, & Rollins, 2014). An SNR >10 has been suggested to be adequate for diffusion MRI‐based tractography with some diffusion encoding directions (Descoteaux, Deriche, Knosche, & Anwander, 2009), although others indicate that an SNR >3 is sufficient (Jones, Knosche, & Turner, 2013). Signal‐to‐noise ratio (SNR) was computed as a measure of image quality for the different acquisition parameter conditions. SNR was calculated by dividing the mean signal intensity of the tissue signal in the center slice by the SD of nontissue background noise (SNR = S/σN) (Henkelman, 1985; Kaufman, Kramer, Crooks, & Ortendahl, 1989). We report the SNR of two images for each condition, the SNR for a b₀ image and the SNR for the diffusion‐encoding image with the lowest signal intensity (Farrell et al., 2007). As scalar indices are based on tensor calculations, noise in these maps does not behave in a random fashion, as is the case in the frequency domain or k‐space. SNR for scalar indices was therefore not calculated.

2.6. Segmentation of hippocampal lamina

Mean diffusivity images yielded the most robust contrast between hippocampal cell layers (i.e., lamina) and were thus utilized in manual segmentation of intrahippocampal structures. Based on the anatomical literature (Duvernoy, Cattin, & Risold, 2013; Mai, Majtanik, & Paxinos, 2016; Yushkevich et al., 2015), the granule cell layer (GCL) of the dentate gyrus (DG), the pyramidal cell layer (PCL) in cornu ammonis 1 (CA1), CA2, CA3, CA4, stratum radiatum (S.R.), stratum moleculare (S.M.), and stratum oriens (S.O.) were identified and traced manually for each slice. Intra‐ (M.L.) and inter‐rater (M.L. and A.M.) reliability were evaluated using a Pearson correlation (criterion r > 0.9) and a comparison of voxel counts for all ROIs (<10% deviation tolerance). For orientation scans, manual ROIs were drawn for each scan. In order to determine the level of contrast between intrahippocampal lamina, contrast ratios were calculated between layers (DG/CA1; DG/S.M.; CA1/S.R.; S.M./S.R.; CA4/S.R.; CA3/CA2; CA2/CA1; CA1/S.O.) (Modo et al., 2016). Extra‐hippocampal structures were considered to be the fimbria, subiculum, angular bundle and enthorhinal cortex, which variably were included in surgical samples.

2.7. Tractography

Fiber tract reconstructions of the whole specimen were performed using the diffusion tensor imaging (DTI) model in DSI Studio with a local multi‐direction deterministic Euler fiber‐tracking algorithm (Yeh et al., 2013). This approach will resolve only one local fiber direction per voxel, but can visualize multiple streamlines passing through a single voxel. To evaluate the effects of acquisition parameters and sample orientation on the generation of streamlines, fiber tracts were reconstructed using the following parameters: 1 seed/voxel with random sub‐voxel positioning and trilinear interpolation in all orientations, fractional anisotropy thresholded to 0.02, angular threshold of 60°, a 0.05 mm step size (half the voxel length), minimum length 0.2 mm (twice the voxel length), maximum length 50 mm (diagonal length of whole hippocampus × 1.5), smoothing 0.2 (propagation vector accounts for 20% of incoming streamline direction), Otsu 0.6, and thread count of 12. The total number of streamlines were recorded for a comparison between acquisition parameters. The number of streamlines/voxel provided a normalization to the total number of voxels in the sample that evaluated the efficiency of streamline generation and allowed a comparison across different voxel sizes. To account for samples of different sizes and comparison with other studies, streamline density (streamlines/mm³) was calculated. Anatomical knowledge of established connections in the hippocampus (e.g., CA1 to CA3) were used to determine the appropriate tracing of streamlines across multiple anatomical structures. Spurious streamlines were defined as individual streamlines that erred outside of the main “fiber tract”. Only a few instances of these occurred. These spurious fibers were removed and not counted in the streamline results. In order to determine reproducibility of tract reconstruction, the entire tractography pipeline (pre‐processing, defining ROIs, tractography) was reprocessed three times. To evaluate variability due to sample orientation, coefficient of variations (CoV) were calculated by dividing the SD by the mean value for a scalar index and streamlines (Besseling et al., 2012; Smith, Tournier, Calamante, & Connelly, 2015).

2.8. Immunohistochemistry

Hippocampal sections were cut at 50 μm thickness on a cryostat (Leica) after the sample was cryoprotected in 30% sucrose + 0.5% Sodium Azide. Sections were washed 3 × 5 min in PBS prior to the overnight application of the pan‐neuronal rabbit anti‐Fox3 antibody (1:1000, Abcam, ab104225) and the astrocytic marker mouse anti‐glial fibrillary acid protein (GFAP, 1:3000 Sigma, G3893). Sections were washed 3 × 5 min with PBS prior to incubation with an appropriate AlexaFluor secondary antibodies (1:500, Molecular Probes) for 1 hr. After removal of the secondaries, the nuclear counterstain DAPI (1:10,000, 5 min) was applied before a final set of three washes (5 min each) with PBS. Sections were coverslipped with Vectashield for fluorescence (Vector Labs). Using an AxioImager M2 microscope (Zeiss) interfaced with a motorized stage controlled by Stereo Investigator software (MBF), individual multi‐color microscopic images (×20 objective) were acquired prior to automatic tiling of these to reconstruct the entire section. A background removal function was run in FIJI to account for autofluorescence and inhomogeneities evident due to image tiling.

3. RESULTS

3.1. Segmentation of cell layers on mesoscale MR images of the human hippocampus

Ex vivo MR imaging provided a detailed anatomical view of the human hippocampus that afforded measurements of sample dimensions (Figure 2a), as well as delineation of hippocampal subfields and lamina (Figure 2b). Sufficient SNR (>10) was achieved to compute tractography and to visualize intra‐hippocampal connectivity (Figure 2c). Subtle differences in morphology in the body of the hippocampus were also apparent along the anterior–posterior coronal axis of the scan (Figure 2d). Based on these images, a complete segmentation of the hippocampus into its constitutive lamina was achieved (Figure 2e) and allowed assessment of overlap between segmented ROIs (Figure 2f). To evaluate the reliability of manually‐defined ROIs, both intra‐ (M.L.) and inter‐rater (M.L. and A.M.) reliability were evaluated visually (Figure 2g), as well as quantitatively. A high reliability of ROIs was evident on the intra‐ and inter‐rater reliability, as determined by a Pearson correlation (r > 0.95, p < .01, Figure 2h). Some minor differences in volume measurements were, however, also apparent between experimenters on CA3, DG, and S.R. (Figure 2i).

FIGURE 2.

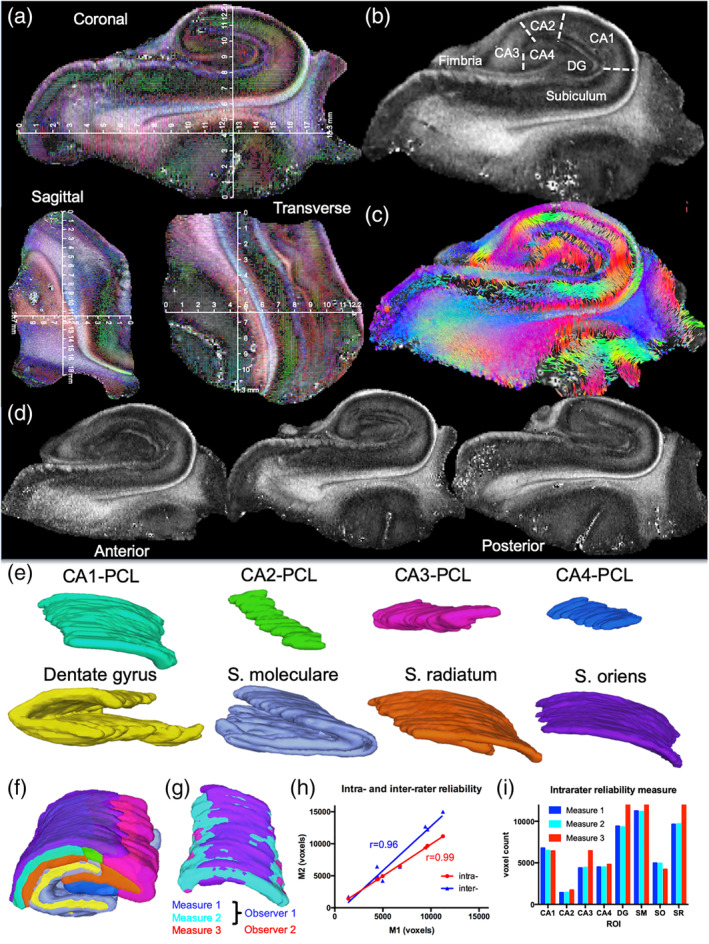
Mesoscale diffusion MRI of the hippocampus and its sub‐fields. Coronal, sagittal, and transverse view of a hippocampal sample with physical dimensions overlaid on the diffusion encoded color (DEC) fractional anisotropy (FA) image (a). A middle coronal FA slice of the hippocampus highlights the contrast definition between different cell layers (b). A streamline image of the same slice further highlights intra‐hippocampal connectivity (c). Anterior–posterior morphological differences were apparent, but a robust definition of different cell layers was evident across the sample (d). Different cell layers, such as the pyramidal cell layer (PCL) of CA1‐CA4 sub‐field were delineated. The granule cell layer (GCL) of the dentate gyrus (DG), as well as intermediate layers, such as stratum moleculare (S.M.), radiatum (S.R.), and oriens (S.O.), were also readily identified based on signal contrast (e). These region‐of‐interest (ROI) delineations afforded a system's view of the hippocampus (f). To probe the reliability of these delineations, the ROIs of two experimenters were compared for intra‐ and inter‐rater reliability (g). A very high (r > 0.95) inter‐ and intra‐rater reliability was evident (h). This was also evident on a direct comparison between absolute measures for each region, although an inter‐rater discrepancy in volume was measured for CA3 (31%), DG (26%), and stratum radiatum (21%) (i)

3.2. Shorter diffusion times are advantageous at the mesoscale

Diffusion time is the pivotal acquisition parameter for DTI, as it defines the time over which the movement and interaction of water molecules is measured. In the hippocampus, a shorter diffusion time (13.6 ms) had an SNR 5x larger compared with the longest diffusion time of 98.7 ms (Table 2). The diffusion‐sensing images for the long echo time experiment had a minimum SNR = 7.9, below the recommended SNR > 10 threshold for tractography. With an average tissue T₂ of ~56 ms, increased spin–spin relaxation makes a considerable contribution to the loss in SNR at the longest diffusion time. The lower quality data was evident in MD (Figure 3a) and FA maps (Figure 3b). Absolute measurement of MD was reduced by 36% with the long diffusion time (Table 2). The measured FA was increased dramatically in the long diffusion time by more than twice the value of the short diffusion time and reduced streamline density by 22% (Table 2). Although MD contrast between regions, such as CA1/DG and S.M./S.R. was high for the long diffusion times, other regions were poorly discriminated, such as S.M./S.R. and CA3/S.R. (Figure 3c). More equivalent contrast between all regions was evident with the shortest diffusion time of 13.6 ms. The shorter diffusion times also produced the highest streamline densities across all regions compared to the longer diffusion time (Figure 3d). Although overall the shortest diffusion time produced the highest density of streamlines, the 23.7 ms diffusion time produced a higher density of streamlines across more ROIs. This demonstrates that the shorter diffusion times may be more favorable for generating streamlines at the mesoscale.

TABLE 2.

Diffusion MR acquisition parameters: Scalar indices and tractography measurements

Parameter		b0 SNR	Min. SNR	MD (μm2/ms)	AD (μm2/ms)	RD (μm2/ms)	FA	Streamlines	Streamline/voxel	Streamline/mm3
Diffusion time (ms)	13.6	61.5	24.4	0.243	0.291	0.219	0.188	952,786	0.5039	504.11
	23.7	58.9	24.8	0.241	0.292	0.215	0.201	906,855	0.4796	479.81
	98.7	12.6	7.9	0.156	0.237	0.116	0.520	743,304	0.3931	393.28
b‐value (s/mm2)	1,000	65.3	49.5	0.348	0.446	0.299	0.268	925,692	0.4896	489.78
	4,000	61.5	24.4	0.243	0.291	0.219	0.188	952,786	0.5039	504.11
	10,000	64.5	17.7	0.144	0.164	0.131	0.146	892,850	0.4722	472.40
Voxel size (μm)	100	61.5	24.4	0.243	0.291	0.219	0.188	952,786	0.5039	504.11
	200	119.8	86.22	0.244	0.291	0.220	0.178	107,689	0.4997	59.66
	450	139.3	121.5	0.252	0.302	0.227	0.184	8,937	0.4877	5.11
Temp. (°C)	8	66.6	27.1	0.247	0.299	0.221	0.192	919,968	0.4865	486.75
	15	61.5	24.4	0.243	0.291	0.219	0.188	952,786	0.5039	504.11
	22	60.3	22.6	0.276	0.331	0.248	0.186	869,107	0.4596	459.81
	30	55.2	17.7	0.322	0.385	0.290	0.184	881,113	0.4660	466.19

Note: Standard ex vivo mesoscale acquisition parameters for spin echo diffusion tensor imaging are presented in bold, whereas lines in italics reflect the standard measurement for each array. Streamlines were computed using 1 seed/voxel.

FIGURE 3.

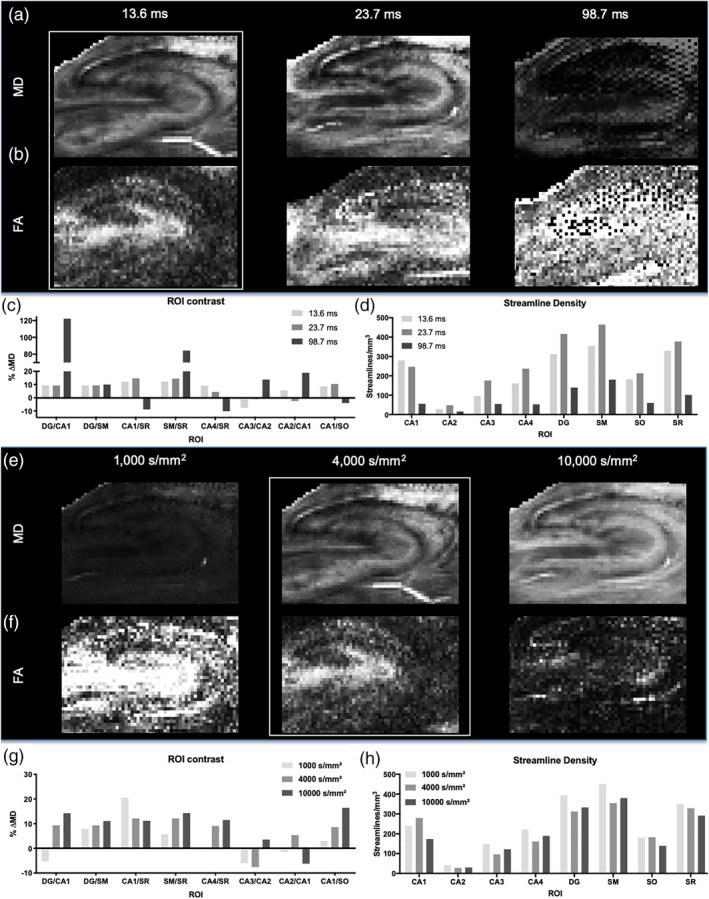
Defining diffusion time and b‐value for mesoscale DTI. Diffusion time was varied to define appropriate parameters to measure scalar indices, as well as to compute streamlines to probe intra‐hippocampal connections. Mean diffusivity (MD) images revealed good signal‐to‐noise and contrast at shorter diffusion times (a). Fractional anisotropy (FA) also demonstrated that shorter diffusion times were favorable to probe the mesoscale, with higher diffusion times suffering from a poor signal‐to‐noise (b). The contrast difference in MD (% ΔMD) was consistent for the 13.6 and 23.7 ms diffusion times, but the longer 98.7 ms diffusion time led to an increase in signal noise that affected regional contrast (c). This was further reflected in streamline density being the highest for the 23.7 ms diffusion time and being dramatically reduced for the longer 98.7 ms diffusion time (d). MD was increased as b‐value was increased (e), whereas FA showed the opposite trend (f). Contrast on MD images showed greater differences between ROIs with higher b‐value (g), but conversely fewer streamlines were detected with the highest b‐value. A medium b‐value of 4,000 s/mm² therefore provided a compromise between a robust regional contrast and streamline density

3.3. b‐value of 4,000 s/mm² provided a compromise between mean diffusivity and fractional anisotropy

The b‐value characterizes the degree of diffusion weighting produced by the strength and timing of the gradients. The lowest b‐value tested, 1,000 s/mm², yielded poor tissue contrast on MD maps, with the high b‐value of 10,000 s/mm² providing a more distinct laminar contrast (Figure 3e). All scalar indices were higher for a b‐value of 1,000 s/mm² and decreased with higher b‐values (Table 2). However, for FA maps, the high b‐value did not produce a robust definition of layers compared to the low b‐value FA map (Figure 3f), illustrating that the computed FA decreased with increasing b‐value. The intermediary b‐value of 4,000 s/mm² provided a compromise to yield a robust discrimination between layers on MD and FA maps. Contrast between ROIs was heterogenous with different b‐values providing better contrast between lamina. A high b‐value in general provided a more robust distinction of layers (Figure 3g). A b‐value of 1,000 s/mm² only produced about a 2.9% lower streamline density, whereas a b‐value of 10,000 s/mm² resulted in a 6.7% decrease of streamline density compared to a b‐value of 4,000 s/mm² (Table 2). Apart from CA1, the lower b‐value of 1,000 s/mm² provided the highest density of streamlines in different ROIs (Figure 3h).

3.4. Spatial resolution exerts a major effect on streamline detection

The key factor to define mesoscale imaging is the spatial resolution. The highest resolution achieved in this study, 100 μm isotropic, produced the most robust contrast on the MD maps (Figure 4a), as well as the FA maps (Figure 4b). The number of voxels acquired at each resolution highlights the volumetric difference in anatomical definition that is achieved using these scans: 100 μm (1,890,630 voxels), 200 μm (215,496 voxels), and 450 μm resolution (18,325 voxels), but the time penalty for higher resolution is substantive with 100 μm resolution being 3.8 times longer than the 200 μm acquisition and 18 times longer than the 450 μm scan. Although resolution itself afforded a greater definition of hippocampal lamina, SNR was also a factor with the 100 μm resolution scans achieving an SNR of 61.5, whereas 450 μm resolution scans yielded an SNR of 139.3 (Table 2). Whole sample scalar indices were comparable between different resolutions, indicating that the diffusion measurement of the tissue microstructure is reliably documented across these different spatial resolutions (Table 2). A comparison between ROIs, however, was not feasible due to an inability to define different hippocampal lamina on the 450 μm resolution scans. Although the number of streamlines generated for each voxel was similar for each resolution, the absolute streamline density (as defined by mm³) was highly dependent on the number of voxels acquired. A high 100 μm spatial resolution produced a 100‐fold greater streamline density than the 450 μm resolution (Table 2). Streamline density therefore proportionally scales with the number of voxels acquired on the sample.

FIGURE 4.

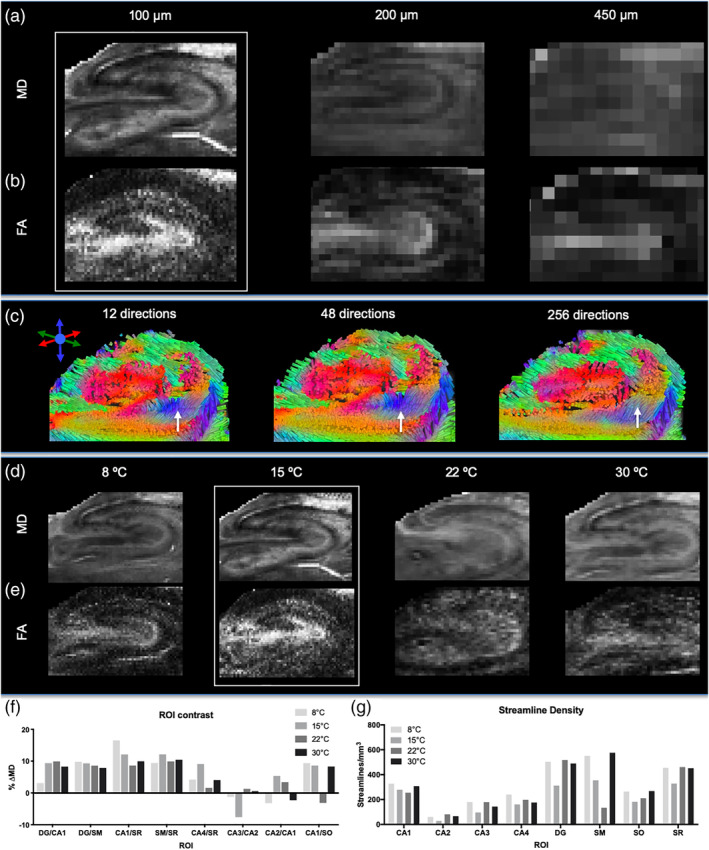
Spatial resolution, diffusion directions and sample temperature. Increasing resolution improves the definition of anatomical layers and reduces partial volume effects that decrease signal across the sample (a). This difference in spatial resolution is also reflected on FA (b). With a large voxel size (450 μm resolution), different number of gradient encoding directions revealed some subtle difference in, for instance, the subiculum (arrow in c). A large number of directions is favorable to ensure a more complete coverage of diffusion space. A sample temperature of 15°C was favorable for MD (d) and FA contrast (e). A comparison of MD contrast for different ROIs revealed a fairly consistent contrast between cell layers at different temperatures (f), but streamline density was higher at 22 and 30°C (g)

3.5. Number of diffusion gradient directions has minimal impact on scalar indices and tractography

The number of diffusion gradient directions (NDGD) probes the three‐dimensional diffusion space and determines the accuracy of the diffusion tensor. However, an increase in NDGD also increases scanning time. Acquiring 256 directions at 100 μm isotropic resolution using a spin echo scan would have taken over 56 days of continuous scanning. A lower isotropic resolution of 450 μm was therefore used for this experiment (Table 1). SNR for the b0 was 61.5 and the lowest directional SNR was 24.4. MD was the only scalar index, where 12 directions estimated a 26% higher value compared to 48 and 256 directions. AD (0.255 μm²/ms), RD (0.200 μm²/ms), FA (0.162) were equivalent between different NDGD. The absolute number (9,266 to 9,276 streamlines) and density of streamlines (5.30 streamlines/mm³) were also not affected by NDGD. Visually, only small differences in streamline angularity were observed (Figure 4c). Using the acquisition method described here, 12 diffusion encoding directions were therefore sufficient to estimate scalar indices, as well as streamlines.

3.6. Sample temperature affects SNR, MD, and detection of streamlines

The movement of water is dependent on temperature. The 11.7 Tesla vertical‐bore microimaging system used for these studies had variable temperature control, similar to that found on NMR spectrometers. Therefore, we could accurately control and maintain the sample temperature for the duration of the experiment. MD maps at four temperatures are shown in Figure 4d. Mean diffusivity at the highest temperature (30°C) was 32.5% higher compared to the lowest temperature (8°C) (Table 2). An increase in diffusion with higher temperature was evident for all scalar indices. Conversely, SNR at the lowest temperature was 10% higher than at the highest temperature (Table 2). Mean FA marginally decreased (4.2%) with temperature (Figure 4e). Streamline density was highest at 15°C with 504.11 streamlines/mm³ (Table 2). Regional contrast on MD images was fairly consistent between regions, with lower temperatures (8 and 15°C) showing some better contrast between CA1/S.R. (Figure 4f). Streamline density indicated subtle differences in the CA1 region, but revealed major differences in streamline density in the stratum moleculare (Figure 4g). It is interesting to note that streamline density in regions with a high cellular density, such as the CA regions, are not affected much by temperature, whereas regions with a high number of passing fibers, such as stratum moleculare and dentate gyrus, exhibit noticeable differences due to temperature.

3.7. Sample orientation affected streamline tracing

The alignment of the sample in the magnetic field and along diffusion encoding directions revealed substantial differences in visible streamlines (Figure 5a). Orientation 3 (coronal slices of sample oriented 180° in relation to magnetic field) provided the most robust and consistent connections between the DG and CA1 with parallel fibers continuing to the subiculum. Fibers fanning in and out of the perforant path were also readily visible using this orientation, whereas the other two orientations did not clearly visualize these features. A quantitative evaluation of different orientations on three different samples indicated a high consistency in volume measurements based on ROIs (Figure 5b). Little variability in measurements of MD (Figure 5c), AD (Figure 5d), RD (Figure 5e), and FA (Figure 5f) were observed. However, streamline density was more variable, especially for stratum radiatum and moleculare (Figure 5g). Coefficient of variation (CoV) calculations for the three repeats for each sample further showed a very consistent pattern between subjects' volume measurements, but not for streamlines (Figure 5h). This pattern was further illustrated by scalar measurements being fairly consistent across ROIs, whereas streamlines revealed a high variability (CoV >0.2) (Figure 5i). Especially, the dentate gyrus, as well as the stratum radiatum and moleculare, measurements were variable. These results indicate that volume measurements and scalar indices are robustly measured irrespective of sample orientation, but orientation can impact the tracing of connectivity in small irregular tissue samples.

FIGURE 5.

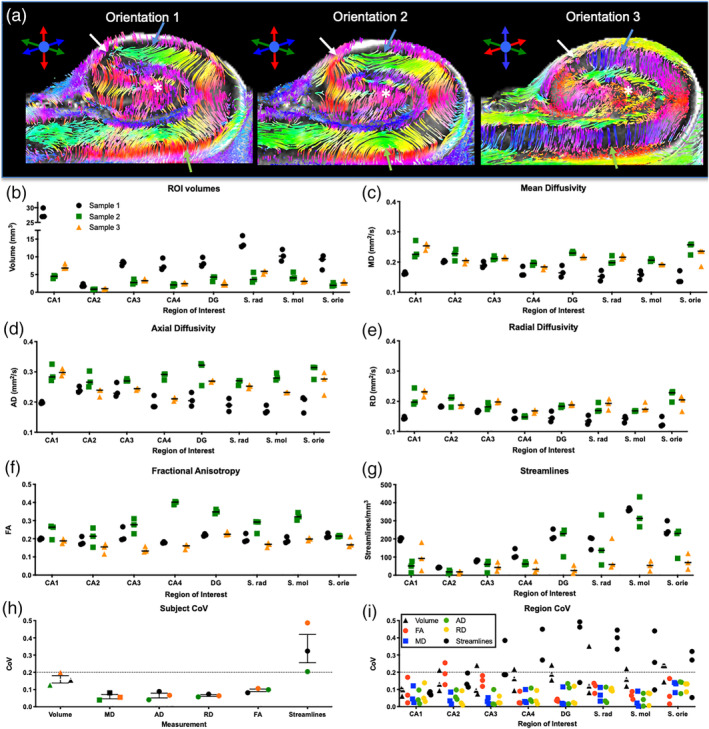
Sample orientation. Orientation of the sample in relation to the diffusion encoding directions revealed marked differences in the presence and appearance of streamlines within the hippocampus (a). A quantitative evaluation of the effects of three sample orientations for three different samples revealed a measurement consistency for volume (b), mean diffusivity (c), axial diffusivity (d), radial diffusivity (e), and fractional anisotropy (f). In some cases, streamline density between orientations were fairly consistent, but in others there were marked differences (arrows), especially for stratum radiatum, moleculare and oriens (g). To establish consistency between acquisitions, for each measure, a coefficient of variation (CoV) was calculated. CoV values <0.2 are considered consistent, whereas higher values are thought to be inconsistent. Volume and scalar indices here were found to be consistent between subjects, but streamline measures for each subject were above the 0.2 threshold (h). A comparison of ROIs for streamlines further highlighted this inconsistency, but also revealed that certain regions are less consistent than others (i). For instance, CA1 provided fairly consistent estimates of streamline density irrespective of orientation, whereas stratum radiatum was inconsistent for all three samples

3.8. Examining intra‐hippocampal connectivity

To improve the visualization of hippocampal connectivity, we here defined acquisition parameters that produce high quality diffusion images for tractography. A central coronal cut through the sample revealed the classical view of the hippocampal subfields (Figure 6a), as revealed by the laminar connections which are color‐coded for local directionality (Figure 6b). A transverse view of the hippocampus afforded a better delineation of individual lamina (e.g., GCL, S.M./S.R., PCL) and their connectivity (Figure 6c). In a central cut along the sagittal direction, however, cell layers were more difficult to distinguish based on the pattern of streamlines (Figure 6d). A higher magnification view of the central coronal view of the hippocampus emphasized the directionality of fibers in the hippocampus, but also showed a clear definition of point‐to‐point connections between layers, such as the GCL and PCL (Figure 6e). The perforant path, gathering fibers from different cell layers, demonstrated how a whole systems analysis of the hippocampus can be achieved using tractography (Figure 6f). Connectivity between different cell layers and sub‐fields can be interrogated to dissect intra‐hippocampal connectivity (Figure 6g). This can, for instance, be used to view sub‐field connectivity with streamlines defined in different colors (Figure 6h).

FIGURE 6.

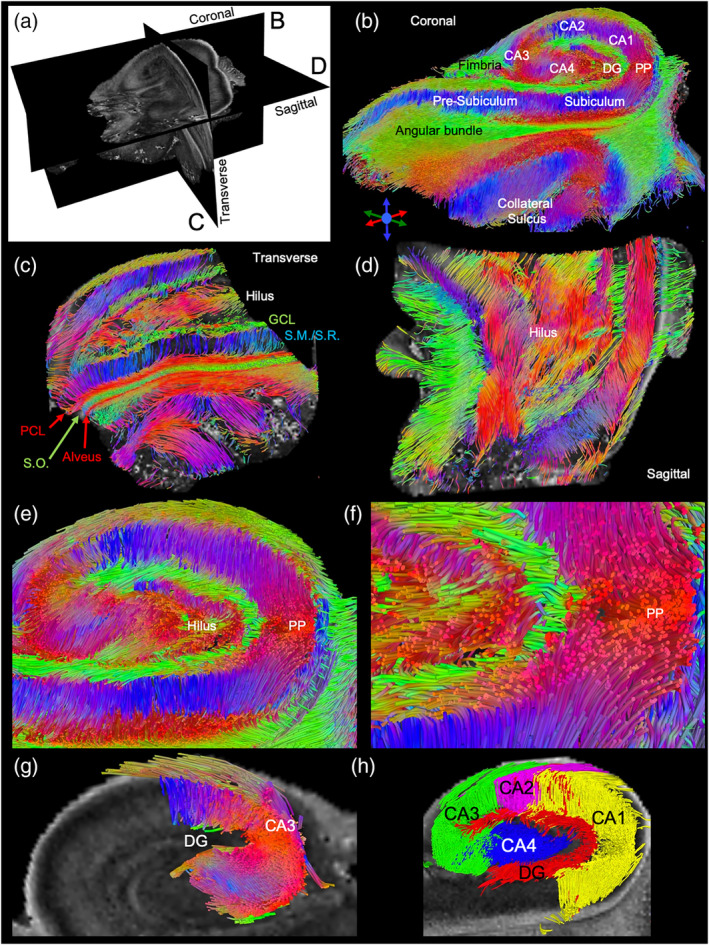
Tractography of the human hippocampus. A three‐dimensional view of the hippocampus using fractional anisotropy images (a). The coronal central slice cut of the streamlines affords an identification of both sub‐fields, such as CA1 and dentate gyrus, but also reveals individual layers. Efferent and afferent hippocampal connections are also evident (b). The transverse view reveals that layers at the tail end of the hippocampus merge with streamlines being highly organized in between layers (c). A sagittal view further illustrates the organizational complexity of intrahippocampal connections in three‐dimensions (d). Within the hippocampus, a robust detection of streamlines connecting neighboring cell layers affords interrogation of layer‐to‐layer connectivity, as well as the intertwined efferent and afferent connections from the different layers (e). The perforant path (PP) can be readily visualized with bundled streamlines fanning out into different cell layers (f). Short distance connections, such as mossy fiber connections between CA3 and dentate gyrus, can also be selectively defined (g). Defining streamlines from each sub‐field hence affords a system view of hippocampal connectivity in three‐dimensions that currently cannot be provided by any other method (h)

3.9. Tractography reflects histological boundaries of hippocampal layers

A comparison between tractography images of the hippocampus and the corresponding histological slice revealed a faithful representation of anatomical features (Figure 7a). The complementarity between the two imaging modalities demonstrated that MRI can provide measures of local and long‐distance connectivity, whereas histology provided measures of cellular composition. For instance, DAPI reveals general cellularity and cell density of different cell layers, whereas FOX3 specifies which cells are of a neuronal phenotype (Figure 7b). The presence of astrocytes, as well as gliosis, is indicated by glial fibrillary acid protein (GFAP). Gliosis was evident here in the stratum radiatum, along the cornu ammonis fields, but also the external limb of the granule cell layer. This gliosis potentially affected the variability of connections using tractography. A focus on the hilus further revealed a loss of neurons in the internal limb of the granule cell layers and reactive astrocytes throughout this region (Figure 7c). These cellular changes potentially can affect diffusivity measurements in these regions, as well as influence the propagation of tracings from these seeds and passing fibers. There was also evidence of neuronal loss in the pyramidal cell layer of the CA1 region, as typically a high density of neurons is observed in this cell layer (Figure 7d). Tractography therefore potentially provides a noninvasive means to study disease burden based on changes in streamline density in conjunction with measurements in scalar indices.

FIGURE 7.

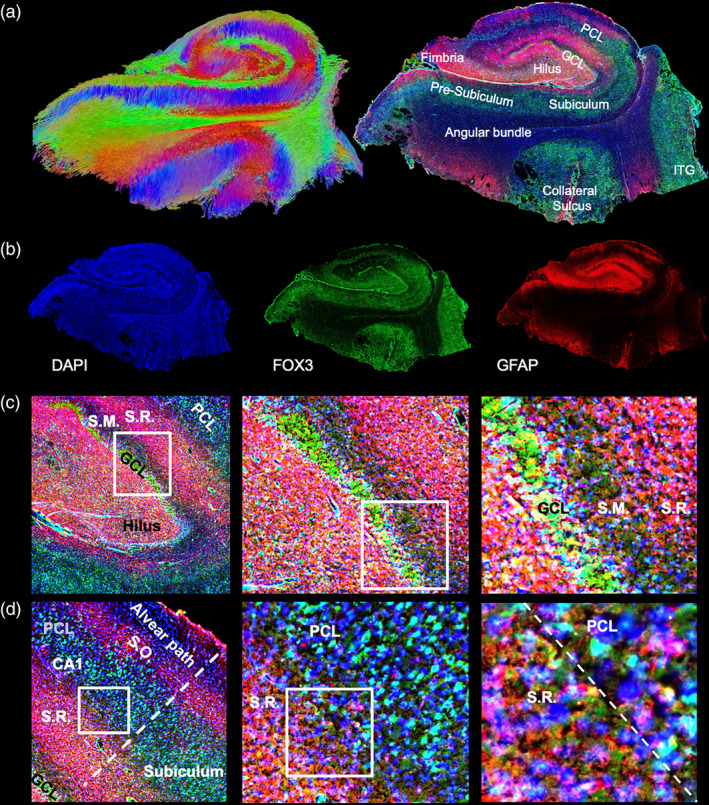
Histological comparison. A coronal view of a central tractography slice with its corresponding histological slice reveals the complementarity of information provided by both techniques (a; ITG = inferior temporal gyrus). Tractography indicates systems wide connectivity, whereas immunohistochemistry provides information regarding cellular composition (b). The dentate gyrus is most commonly affected by MTLE, including neuronal loss of cells in the granule cell layer (GCL). There is also evidence of gliosis as indicated by the abundant presence of reactive astrocytes. These are mostly confined to the stratum radiatum (S.M.) along the cornu ammonis (CA) layer, but also the hilar region. The stratum moleculare (S.M.) and pyramidal cell layer (PCL) do not show signs of gliosis (c). However, the PCL in the CA1 region revealed a scatter staining of neurons, indicative of neuronal loss in this region. A fairly sharp boundary between the PCL and S.R. was defined by gliosis, although no scarring (i.e., a sharp compact border) was evident between the layers (d)

4. DISCUSSION

The hippocampus is a key neuroanatomical structure involved in memory and aging, but also often the focal point of epileptic seizures and neurodegenerative disorders, such as Alzheimer's disease (Coras et al., 2014; Duvernoy et al., 2013). To gain a better understanding of its role in normal mnemonic functions, as well as how these are affected by disease, it is paramount to develop sophisticated tools that can accurately measure its structural volume, as well axonal connections that are defining hippocampal functions (Colon‐Perez et al., 2015; Yushkevich et al., 2009). Mesoscale diffusion MRI is potentially a tool that can be used for these investigations, but a more detailed understanding of the impact of acquisition parameters on diffusion measurements are required (Khambhati, Sizemore, Betzel, & Bassett, 2018; Novikov, Fieremans, Jespersen, & Kiselev, 2018). We here demonstrated that shorter diffusion times are advantageous to acquire diffusion scalar indices, as well as to define streamlines at the mesoscale. Higher resolution provides greater anatomical detail that is required to map connections between closely associated structures. Ideally an isotropic resolution <0.2 mm is achieved to investigate separate hippocampal lamina. The use of these acquisition parameters provided an exquisite visualization of intra‐hippocampal connections at the mesoscale, which corresponded to the histological ground truth.

4.1. Measuring diffusion at the mesoscale

The key difference between macroscopic and mesoscopic diffusion MRI is the spatial resolution. A spatial resolution of <0.2 mm isotropic is required to probe the mesoscale in human hippocampi, which is consistent with our previous observations (Modo et al., 2016). The diffusion time probed by macroscopic DTI is therefore much longer than what is required to uncover mesoscopic diffusion (Burcaw et al., 2015; Veraart, Fieremans, & Novikov, 2019). We here demonstrated that a longer diffusion time (98.7 ms) reduces the streamline density in the hippocampus, with a 23.7 ms diffusion time being favorable for a 100 μm isotropic resolution. Shorter diffusion times (<10 ms) are weighted more toward a hindered (i.e., cellular) diffusion compartment, whereas longer diffusion times (>50 ms) are thought to represent the restricted (i.e., axonal) compartment (Kunz et al., 2013; Li et al., 2016). Imaging of white matter tracts predominantly requires the detection of the restricted compartment and longer diffusion times are therefore preferable. Imaging of gray and white matter diffusion at the mesoscale requires diffusion times that are sensitive to both restricted and hindered diffusion. At the mesoscale, a mixture of bundled, crossing and kissing axonal fiber tracts, as well as their sparse fanning out into tissue are visualized and therefore a diffusion time measuring multiple types of compartments is desirable (Ozarslan et al., 2012; Ozarslan et al., 2013). A further consideration with gray matter diffusion is the presence of neurites, which also produce a restricted diffusion, albeit less anisotropic than axonal connections (De Santis et al., 2016; Kaden et al., 2016). In the context of hippocampal imaging, ideally cellularity of lamina, neurite density and axonal connectivity are visualized to capture the complex cytoarchitectural organization of intra‐ and extra‐hippocampal connectivity.

As resolution decreases, shorter diffusion times are required to visualize more accurately the prevailing cytoarchitecture by capturing cellular size and fraction, as well as neurite density and axonal connectivity (Burcaw et al., 2015). To capture these different compartments, more complex acquisition paradigms using multiple diffusion times and b‐values will be required (Novikov et al., 2018). A single set of acquisition parameters is therefore unlikely to sufficiently sample the diffusion properties of tissues. For instance, poor tissue contrast was evident here with a low (1,000 s/mm²) and high b‐value (10,000 s/mm²). A b‐value of 1,000 s/mm² achieved poor tissue contrast on MD maps, but achieved the highest FA contrast, whereas a b‐value of 10,000 s/mm² exhibited the opposite pattern. Consistent with other ex vivo diffusion MR experiments (Dyrby et al., 2011), a b‐value of 4,000 s/mm² provided a compromise between both. Ideally multiple shells of b‐values (low, medium, high) will be used to more fully sample the diffusion spectrum (Wu & Alexander, 2007). However, spin echo sequences for diffusion MRI require long acquisition times that are not suitable for mesoscale hybrid DTI. Gradient echo and echo planar imaging (EPI) sequences are more efficient in acquiring the diffusion signal and large numbers of diffusion directions can be packaged into multiple shells (e.g., Hybrid DTI) (Aganj et al., 2010; Daianu, Jacobs, Weitz, Town, & Thompson, 2015; Portnoy, Flint, Blackband, & Stanisz, 2013; Wu & Alexander, 2007), but these images typically lack anatomical detail required to define different cell layers. Both approaches require a trade‐off, with spin echo images revealing a detailed anatomy, whereas EPI‐based hybrid DTI being more suitable for complex diffusion models aimed at reconstructing tissue connectivity. Implementation of a compressed sensing approach can be used to dramatically reduce acquisition times by up to a factor of 8 (Wang et al., 2018; Zhang et al., 2020), making mesoscale imaging more practical with reasonable scanning times (~8 hr/sample rather than 64 hr/sample).

4.2. Ex vivo MR imaging of hippocampal samples

For in vivo imaging, compartmentalization is the main consideration, as all samples are acquired at physiological temperature and therefore have equal thermodynamics. However, with samples imaged ex vivo, temperature can be controlled and hence the dynamics of water movement in and between diffusion compartments (Hasegawa, Latour, Sotak, Dardzinski, & Fisher, 1994; Thelwall et al., 2006). For instance, contrast between the pyramidal cell layer in CA1 versus the stratum radiatum was higher at 8°C, as lower temperatures improve SNR. As expected from fundamental thermodynamics, higher temperature should increase the diffusion coefficient. Here, MD increased 32% between 15 and 30°C. Interestingly, we did not observe a significant change in mean MD between the 8 and 15°C measurements. Higher temperatures can be advantageous to measure diffusion properties of tissues, but this needs to be balanced against lower SNR. Prolonged higher temperatures may also promote a deterioration in sample quality. Diffusion in high cell density layers was less affected by temperature than less dense tissues due to the mobility of water in extracellular space. This is further reflected in the streamline density being increased with higher temperature in the stratum moleculare, radiatum and oriens, but overall lower temperatures produced a higher streamline density due to better SNR. A compromise between SNR, diffusion, and preservation of sample quality here indicated that a temperature of 15°C is the most suitable for long ex vivo diffusion MRI studies. Since MD is dependent on sample temperature and the relationship is not uniform between tissue of different properties, one should consider sample temperature equilibration and regulation during DTI measurements. ex vivo studies aimed at characterizing microstructural anatomy and connectivity could also benefit from imaging the same sample at different temperatures.

An issue that can be of concern to ex vivo imaging of tissue samples is the orientation of tissues relative to the static magnetic field and magnetic field gradients. In clinical MR, patient orientation is standardized and involves a larger spherical sample. Therefore, no significant variations are to be expected compared to smaller oddly‐shaped samples in an experimental setting. The surgical samples used in this study were of nonuniform dimensions and irregular shapes, which creates a challenge for uniform magnetic field shimming. In solving for a global minimum of field deviation from the resonance frequency, local static magnetic field gradients can be generated in the tissue where a perpendicular surface component interacts with B₀. Since the ends of the tissue samples can be small relative to the sample size, large local field gradients may not be evident in the overall water line shape. A static field gradient can interact with diffusion gradients, potentially distorting the principle axis of the diffusion tensor relative to anatomy. This effect can be more evident at high field, high resolution, and in tissues with low intrinsic FA.

In our study, it was evident that there were differences in streamline tracing based on the samples' orientation in the scanner. Using a 180° orientation of the coronal sample produced perpendicular streamlines in the stratum radiatum, as expected based on anatomical studies, whereas in the other two orientations this was not the case. Quantitatively this was further evidenced by a high CoV, which was over the acceptable threshold of 0.2 for many hippocampal regions. An interesting point, is that this variability with sample position was not evident for scalar measures. For high‐resolution scanning, it is imperative that the sample is immobilized, and firmly secured in the magnet, as high amplitude gradient switching can cause vibrational motion. Here we used a perfluorocarbon (PFC) oil for sample emersion to avoid tissue dehydration and help with magnetic susceptibility matching at tissue interfaces. Our samples were secured in a disposable syringe with a plunger, since tissue floats in the high‐density PFC oil. Sample contact with the plastic syringe further creates areas of differing magnetic susceptibility that can be hard to compensate for, even with high‐order shims.

Although six diffusion directions have been deemed sufficient to generate valid tractograms (Lebel et al., 2012), and a higher NDGD here did not increase streamline density, a higher number of diffusion encoding directions (e.g., HARDI) is desirable to more completely probe connectivity, irrespective of the sample's orientation. Although a high spatial resolution is used here, voxel geometry and potential partial volume effects of smaller connections can still influence tractography and contribute to the variability of streamlines across different orientations (Bach, Fritzsche, Stieltjes, & Laun, 2014). Positioning of the sample, but also the isotropic geometry of the voxel needs consideration (and standardization) for multiple sample scanning paradigms to ensure reproducibility (Tudela, Munoz‐Moreno, Lopez‐Gil, & Soria, 2017).

4.3. Mapping intra‐hippocampal networks

There remains a poor understanding of the complexity of connectivity in the human hippocampus (Augustinack et al., 2010; Colon‐Perez et al., 2015; Coras et al., 2014; Strange et al., 2014; Vos de Wael et al., 2018). Macroscopic in vivo studies of the human hippocampus in aging, as well as disease, provide useful insights into how the overall structure is affected, but generally lack the resolution at which individual cell layers and connections between these can be interrogated. ex vivo studies on fixed human hippocampi aim to bridge this gap between macroscopic in vivo studies and microscopic histological studies (Augustinack et al., 2010; Colon‐Perez et al., 2015; Coras et al., 2014; Modo et al., 2016; Shepherd et al., 2007). However, only a few studies have acquired datasets at a resolution that probes the mesoscale to reveal connectivity (Augustinack et al., 2010; Beaujoin et al., 2018; Colon‐Perez et al., 2015; Coras et al., 2014; Modo et al., 2016; Yushkevich et al., 2009). A pipeline for ex vivo imaging has been established that provides robust high quality diffusion measurements for more than 3 years after tissue fixation, including the hippocampus (Dyrby et al., 2011). We here provide a more detailed analysis of how acquisition parameters affect diffusion measurements at the mesoscale to investigate hippocampal connectivity. Using optimized acquisition parameters, it was possible here to visualize the laminar structure of the hippocampus and to reliably define these, even if the sample orientation was different. Tractography further aided in defining the laminar layers with streamlines often showing a preferential direction in a single layer compared to the adjacent structure.

Ex vivo imaging avoids motion artifacts that are common in vivo, but small movement of the sample over the long scanning durations could still compromise the data integrity. As there is no pulsatile blood flow that could affect diffusion measurement, erroneous tracing of signal due to large or small blood vessels within ex vivo samples can be excluded (Dyrby et al., 2011). Still, diffusion barriers along cell layers can occur and potentially produce spurious streamlines that separate one cell layer from another. Fixation of samples for ex vivo imaging is required to prevent degradation of the tissue over long scanning durations (Richardson et al., 2014). Although absolute measurements of scalar indices in vivo and ex vivo might differ to some degree, the relative changes between hippocampal lamina is likely to be preserved (Richardson et al., 2014). It remains less clear if fixation affects the detection of connectivity (Roebroeck et al., 2018), but it is evident here that a robust tractography was achieved on these tissues.

Ex vivo MRI on hippocampal samples can therefore provide novel insights into the three‐dimensional nature of laminar connectivity to improve our understanding of networks that drive cognition, but also aberrant connectivity that underpins epileptic seizures (Adler et al., 2018; Vos de Wael et al., 2018; Yushkevich et al., 2009). The small bore ultra‐high MR field (11.7 T) used here and long acquisition time do not readily translate into widely available high field clinical MRI (7 and 9.4 T) settings, but achieving a 0.2 mm isotropic resolution is increasingly within the reach of clinical studies (Jones et al., 2018; Kemper, De Martino, Emmerling, Yacoub, & Goebel, 2018; Roebroeck et al., 2018; Thomas et al., 2008).

5. CONCLUSIONS

Intrahippocampal connectivity requires mesoscale imaging to unravel the three‐dimensional structure of axons projecting from one layer to another. We here demonstrated how acquisition parameters affect diffusion measurements at the mesoscale. We also noted several new developments that are required to improve image acquisition (i.e., hybrid DTI) at the mesoscale. Using optimized parameters, the intricate mesh of connections inside the hippocampus and those connecting it with surrounding cortical structures were revealed. This approach can improve our understanding of normal hippocampal connectivity and how this is impacted by aging, genetic abnormalities, as well as disease.

DISCLOSURE OF INTERESTS

The authors have no personal financial or institutional interest in the results described in this article.

AUTHOR CONTRIBUTIONS

Maria Ly processed the data and defined ROIs on the acquisition parameter scans; Lesley Foley acquired the MRI data sets; Ashwinee Manivannan defined ROIs on the orientation scans and helped with the tractography analysis: T. Kevin Hitchens contributed to the study design; R. Mark Richardson provided the samples and provided funding; Michel Modo conceived of the study, provided funding, oversaw the experiments, processed orientation scans and tractography data, compiled figures and wrote the manuscript.

Ly M, Foley L, Manivannan A, Hitchens TK, Richardson RM, Modo M. Mesoscale diffusion magnetic resonance imaging of the ex vivo human hippocampus. Hum Brain Mapp. 2020;41:4200–4218. 10.1002/hbm.25119

DATA AVAILABILITY STATEMENT

MRI data sets are available from the corresponding author upon request.