Finding specificity in structural brain alterations through Bayesian reverse inference

Abstract

In the field of neuroimaging reverse inferences can lead us to suppose the involvement of cognitive processes from certain patterns of brain activity. However, the same reasoning holds if we substitute “brain activity” with “brain alteration” and “cognitive process” with “brain disorder.” The fact that different brain disorders exhibit a high degree of overlap in their patterns of structural alterations makes forward inference‐based analyses less suitable for identifying brain areas whose alteration is specific to a certain pathology. In the forward inference‐based analyses, in fact, it is impossible to distinguish between areas that are altered by the majority of brain disorders and areas that are specifically affected by certain diseases. To address this issue and allow the identification of highly pathology‐specific altered areas we used the Bayes' factor technique, which was employed, as a proof of concept, on voxel‐based morphometry data of schizophrenia and Alzheimer's disease. This technique allows to calculate the ratio between the likelihoods of two alternative hypotheses (in our case, that the alteration of the voxel is specific for the brain disorder under scrutiny or that the alteration is not specific). We then performed temporal simulations of the alterations' spread associated with different pathologies. The Bayes' factor values calculated on these simulated data were able to reveal that the areas, which are more specific to a certain disease, are also the ones to be early altered. This study puts forward a new analytical instrument capable of innovating the methodological approach to the investigation of brain pathology.

We created Bayesian reverse inference maps of the two most represented pathologies in BrainMap (schizophrenia and Alzheimer's disease). We provided evidence that Bayesian reverse inference is capable of identifying the cerebral areas exhibiting a higher alteration specificity to a certain pathology. We performed temporal simulations of the alteration spreads associated with different pathologies, revealing that the areas, which are more specific to a certain disease, are also the ones to be early altered.

1. INTRODUCTION

Studying the distribution of co‐altered areas in the pathological brain is fundamental to better understand how neuropathologies spread and develop, as well as to improve categorizations and diagnoses (Hyman, 2010). The psychopathological models in the Diagnostic and Statistical Manual of Mental Disorders (DSM, American Psychiatric Association, 2013) and the International Statistical Classification of Diseases (ICD, World Health Organization, 2007) consider both psychiatric and neurological conditions as distinct clinical constructs with different etiologies. However, growing evidence is challenging this view (Buckholtz & Meyer‐Lindenberg, 2012; Nolen‐Hoeksema & Watkins, 2011). For example, large‐scale phenotypic studies and etiological investigations suggest that brain disorders are frequently characterized by polygenic inheritance with multiple small‐effect risk alleles causing a constant diffusion of genetic liability, thus ruling out any rigid classification of mental illnesses (Buckholtz & Meyer‐Lindenberg, 2012; Gejman, Sanders, & Kendler, 2011; Krueger, 1999). Comorbidity, too, defies rigid categorization. Co‐occurrences of psychiatric diseases are rather frequent than exceptional (Cauda et al., 2017; Cauda et al., 2018; Goodkind et al., 2015; van den Heuvel & Sporns, 2019); this large diversity in symptomatology, dimensionality and comorbidity (Kessler et al., 2005; Krueger & Markon, 2011; Markon, 2010) points to a profound revision of models of classification (Krueger & Markon, 2006).

A transdiagnostic approach can meet this new need, as it is able to highlight important differences and similarities in brain disorders. Several studies already show that a variety of psychiatric and neurological conditions preferentially target certain brain regions (Buckholtz & Meyer‐Lindenberg, 2012; Cauda et al., 2017; Cauda et al., 2019; Cauda, Nani, Costa, et al., 2018; Cole, Repovs, & Anticevic, 2014; Goodkind et al., 2015; Liloia et al., 2018; McTeague, Goodkind, & Etkin, 2016). More specifically, Cauda et al. (2019) showed that most of brain disorders are likely to produce anatomical alterations that largely overlap with each other, thus demonstrating that there is a common set of regions (such as the insula, the anterior cingulate cortex (ACC), some of the prefrontal and anterior temporal areas) which is altered by the majority of brain disorders (in these areas more than 90% of pathologies have at least one focus of alteration). In contrast, there are very few brain areas specifically altered by one or a limited number of diseases (Liloia et al., 2018). This large overlap of altered regions makes them scarcely informative about the development of neuropathological processes, because in these regions the alteration pattern is rather nonspecific. Furthermore, analyses based on forward inferences (Poldrack, 2006) cannot help us, as they tend to treat in the same way both the areas having high or low specificity. Instead, an approach based on Bayesian reverse inferences can extract relevant information from patterns of altered regions. There are, however, important issues that need to be addressed, which this study aims to tackle. Let us see three points in more details.

First, using the anatomical likelihood estimation (ALE) values as source data, it is possible to create, through a Bayesian reverse inference approach, a map of alterations caused by brain disorders, and identify the areas, if any, that are more specific for these diseases.

Researchers generally apply forward inferences by asking what are the areas affected by certain pathology; in our case, we are interested in reverse inferences by asking what are the pathological conditions that might have produced a specific alteration pattern. The probability that a specific pattern of gray matter (GM) alterations may be related to a specific brain disorder is not equivalent to the probability that a specific brain disorder may be related to a specific pattern of GM alterations: P(GM alteration|brain disease) ≠ P(brain disease|GM alteration). The reason of the not equality of the relation between the two probabilities could be due to various factors, such as noise, incomplete knowledge of the anatomical and/or functional relationship. To our best knowledge, this kind of calculus has never been tried before on meta‐analytical data of morphological alterations but only on healthy subjects' task‐based fMRI data (Poldrack, 2006, 2011; Yarkoni, Poldrack, Nichols, Van Essen, & Wager, 2011). A study (Sprooten et al., 2017), which tried a type of reverse inference over functional data of psychiatric patients, was not based on a Bayesian reverse inference, as authors applied a Chi squared test with the Yates' correction on a cross tables diagnosis‐by‐region and tested whether studies about different psychiatric conditions report similar results. The authors, in sum, calculated a form of correlation between the number of studies of the pathology‐by‐region and those of another pathology.

Second assuming the equiprobability of the priors, the calculus of the Bayes' factor (BF) index can measure the involvement of an altered area in a brain disorder as well as avoid the potential bias of the inhomogeneous representativeness of diseases within a database.

The possibility of the reverse inference from neuroimaging data has been extensively explored (Hutzler, 2014; Machery, 2014; Montagna, Wager, Barrett, Johnson, & Nichols, 2018; Poldrack, 2006, 2011, 2012; Poldrack & Yarkoni, 2016; Wager et al., 2015; Woolrich et al., 2009). On the legitimacy of the method per se see Lieberman and Eisenberger (2015), Poldrack (2013), Lieberman (2015), Yarkoni (2015a), Yarkoni (2015b), ShackmanLab (2015), Wager et al. (2016), Gelman (2017), Machery (2014) and Hutzler (2014). With a pioneering study, Poldrack (2006) highlighted the difficulties in the field of functional neuroimaging because the usual kind of inference that can be applied to neuroimaging data is of the form: if a process X is involved then the Y brain is activated, and also because it has been highlighted that very specific patterns of activations associated with pathological conditions are extremely infrequent (Fox & Friston, 2012; Poldrack, 2011). Difficulties in making a reverse inference correctly have been discussed in the debate raised after the publication of Lieberman and Eisenberger (2015) (Gelman, 2017; Lieberman, 2015; Poldrack, 2013; ShackmanLab, 2015; Wager et al., 2016; Yarkoni, 2015a, 2015b), who claimed that activity of the anterior dorsal cingulate is selective for pain. These findings, however, have been criticized (Gelman, 2017; Lieberman, 2015; Poldrack, 2013; ShackmanLab, 2015; Wager et al., 2016; Yarkoni, 2015a, 2015b).

To better assess the involvement of a certain brain activation in a cognitive process we propose to use the BF index (Jeffreys, 1961), which is the ratio between the likelihoods of two alternative hypotheses. The choice of prior probabilities is the most complex issue in the Bayesian approach to meta‐analytical data. Priors are generally set to 0.5, so that neither hypothesis P(H₁) nor hypothesis P(H₂) is privileged, where H₁is the hypothesis of specificity and H₂ the hypothesis of nonspecificity, respectively. It should be noted that with a sufficient amount of data, as it is our case, the BF should converge to the value “true,” even though the priors are supposed to be equiprobable. It is plausible that, even though you and I can have different prior beliefs, more often we will agree over the form of the likelihood, so that, if we gather enough data, the posterior will become very close (Lee, 2012). In any case, to avoid the introduction of prior densities regarding the parameters, and to assess whether or not the use of inhomogeneous data may produce incorrect BF values, we propose to apply the Schwarz criterion (Kass & Raftery, 1995; Schwarz, 1978), which, for large samples, can be considered as an approximation of the logarithm of BF. As postulated by the Schwarz criterion, our hypothesis is that the BF values, calculated with equiprobable priors, converge to the Bayesian information criterion (BIC) if they do not suffer from the bias due to the inhomogeneity of the sample.

Third, considering neuropathology in its temporal progression, the BF index can detect which cerebral areas are likely to be altered early.

As alterations develop from few to many (Cauda et al., 2018), reverse inferences may identify as more specific to a certain brain disorder the areas that are affected early. Theoretically, the maximum level of overlap between altered regions reaches its limit when all the brain is affected. In this hypothetical case, each brain pathology would alter most of the cerebral areas. So, when abnormalities gradually spread (Fornito, Zalesky, & Breakspear, 2015; Goedert, Masuda‐Suzukake, & Falcon, 2017; Iturria‐Medina & Evans, 2015; Yates, 2012; Zhou, Gennatas, Kramer, Miller, & Seeley, 2012), the overlap of alterations caused by different pathologies will be greater and greater, thus reducing the degree of specificity of the areas that are progressively more altered (for an infographic see Figure S4). The capacity of the BF index to highlight more informative altered regions was tested by applying the calculus on simulations of diseases with different stages of alteration spread.

2. MATERIALS AND METHODS

As a proof of concept, we put forward a map based on Bayesian reverse inference of the two most represented brain diseases in the BrainMap database (http://brainmap.org/), namely schizophrenia (SCZ) and Alzheimer's disease (AD).

BrainMap is an online open access database of published functional and voxel‐based morphometry (VBM) experiments that reports both the coordinate‐based results (x,y,z) in standard brain space (Talairach or MNI) and a hierarchical coding scheme of meta‐data concerning the experimental methods and conditions (Fox et al., 2005; Fox & Lancaster, 2002; Laird, Lancaster, & Fox, 2005; Vanasse et al., 2018). At the time of the selection phase (April 2018), BrainMap included meta‐data associated with more than 4,000 publications, containing over 19,000 experiments, 148,000 subjects and 149,000 coordinate‐based results.

2.1. Selection of studies

First, we queried the VBM BrainMap database sector (Vanasse et al., 2018). By means of the software application Sleuth (v.2.4), we employed a double systematic search to retrieve the eligible voxel‐based results for each of the two brain disorders of interest. The search algorithms were constructed as follows:

For the meta‐analysis of SCZ:

• SCZ QUERY A) [Experiments Context IS Disease] AND [Experiment Contrast IS Gray Matter] AND [Experiments Observed Changes IS Controls>Patients] AND [Experiments Observed Changes IS Controls<Patients] AND [Subjects Diagnosis IS Schizophrenia];

• SCZ QUERY B) [Experiments Context IS Disease] AND [Experiment Contrast IS Gray Matter] AND [Experiments Observed Changes IS Controls>Patients] AND [Experiments Observed Changes IS Controls<Patients] AND [Subjects Diagnosis IS NOT Schizophrenia].

For the meta‐analysis of AD:

• AD QUERY A) [Experiments Context IS Disease] AND [Experiment Contrast IS Gray Matter] AND [Experiments Observed Changes IS Controls>Patients] AND [Experiments Observed Changes IS Controls<Patients] AND [Subjects Diagnosis IS Alzheimer's Disease];

• AD QUERY B) [Experiments Context IS Disease] AND [Experiment Contrast IS Gray Matter] AND [Experiments Observed Changes IS Controls>Patients] AND [Experiments Observed Changes IS Controls<Patients] AND [Subjects Diagnosis IS NOT Alzheimer's Disease].

Therefore, two researchers screened all the identified articles in order to ascertain that: (a) a specific whole‐brain VBM analysis was performed, (b) a comparison between pathological sample and healthy control participants was included, (c) GM decrease/increase changes in pathological sample were included, (d) locations of GM changes were reported in a definite stereotactic brain space (i.e., Talairach or MNI).

On the basis of the aforementioned criteria, we included in our analyses: 114 articles, for a total of 147 experiments, 1754 GM changes and 4,944 subjects (SCZ QUERY A); 693 articles, for a total of 1,211 experiments, 9,353 GM changes and 41,746 subjects (SCZ QUERY B); 55 articles, for a total of 83 experiments, 961 GM changes and 1,297 subjects (AD QUERY A); 760 articles, for a total of 1,277 experiments, 10,151 GM changes, and 49,194 subjects (AD QUERY B). Descriptive information of interest and meta‐data of GM changes were extracted from each selected article (see Table S1 for detailed information about the description and distribution of the VBM data set included in the meta‐analysis). In order to facilitate subsequent analyses, coordinate‐based results from MNI stereotactic space were converted into Talairach space by using Lancaster's icbm2tal transformation (Laird et al., 2010; Lancaster et al., 2007).

The selection of studies was performed according to the preferred reporting items for systematic reviews and meta‐analyses (PRISMA) Statement international guidelines (Liberati et al., 2009; Moher, Liberati, Tetzlaff, & Altman, 2009). The overview of the selection strategy is illustrated in Figure S1 (PRISMA flow chart).

2.2. ALE and creation of the modeled activation maps

We performed an ALE using the random effects algorithm of GingerAle (v.2.3.6, http://brainmap.org/ale) (Eickhoff et al., 2009; Eickhoff, Bzdok, Laird, Kurth, & Fox, 2012; Turkeltaub et al., 2012). The ALE is a quantitative voxel‐based meta‐analysis technique capable of providing information about the anatomical reliability of results through a statistical comparison on the basis of a sample of reference studies from the existing literature (Laird et al., 2005).

To describe the theory behind the ALE method we follow the description and nomenclature used in Samartsidis, Montagna, Nichols, and Johnson (2017). The idea of ALE is to model, for each voxel, the probability that it is a true location of a focus reported as Gaussian distribution centered on it. Given a study i, the map based on a single location x_ik is given by:

$$L_{\mathit{ik}}\left(v\right)=c{\varphi }_3\left(v|{\mathit{x}}_{\mathit{ik}},{\sigma }^2\mathit{I}\right)$$

with ϕ₃(x; μ, ∑) is a three‐dimensional Gaussian distribution with mean and covariance μ, ∑ evaluated at $\mathit{x}\in {\mathbb{R}}^3$, I is the identity matrix and c is a normalization constant ensuring that the sum of ϕ₃ over voxels equals to one. In this way L_ik(v) is the probability that the voxel v is the true location of x_ik.

The only free parameter is σ_i, which is determined in an empirical study by Eickhoff et al. (2009) associating the number of subjects n_i in each study with the SD σ_i.

The next step of the ALE procedure is to merge the maps L_ik in a single study map L_i. This map quantifies the probability of how the focus near v is really located in v. The final ALE statistic is computed as follows:

$$l\left(v\right)=1-\prod _i\left(1-L_i\left(v\right)\right)$$ (1)

This formula represents the probability that one of the closest activations is located in voxel v.

The significance test of ALE is obtained using a Monte Carlo procedure. For each location, multiple statistics are created by sampling activation maps from random location. The null ALE statistic is obtained as follows:

$$l^{*}\left(v\right)=1-\prod _i\left(1-L_i\left(v^{*}\right)\right)$$

in which v* is drawn uniformly from all possible brain locations. The null distribution can be used to calculate p‐values uncorrected or not, see Eickhoff et al. (2012) for a more detailed description.

2.3. Reverse inference and Bayes' factor

The framework of the reverse inference is the Bayes' theorem. In general, reverse inference in neuroimaging provides information about the involvement of brain areas in cognitive processes. Through a reverse inference we can infer the posterior probability of a certain cognitive process M starting from a pattern of brain activation A. This inference is based on the conditional probability or likelihood P(A|M) and a prior probability P(M), that is, the probability we have before acquiring any clues on brain activations. Neuroimaging data can provide information on the likelihood of M given A.

The same reasoning still holds if we substitute “brain activity A" with “brain alteration A” and “cognitive process M" with “brain disorder M". In this case, the reverse inference leads us to infer the posterior probability of a pathology P(M|A) from a certain pattern of brain alterations P(A|M) using the Bayes' theorem:

$$P\left(M|A\right)=\frac{P\left(A|M\right)P\left(M\right)}{P\left(A|M\right)P\left(M\right)+P\left(A|\neg M\right)P\left(\neg M\right)},$$

where the ¬ symbol is the logical NOT.

Therefore, given the brain alteration A and the prior probability that the disease M occurs, it is possible to assess the posterior probability that M occurs on the basis of A. This choice depends on the information that we know before calculating the likelihood. In the literature, there is no general consensus as to how this choice should be made—for a review of the several proposals put forward to address this point see Carlin and Louis (2008).

The Bayesian approach to testing hypotheses has been developed by Jeffreys (1961) as part of his scientific program to study inference. Within this approach, given two competing hypotheses, the statistical models represent the probability that data are in accord with one or the other hypothesis and the Bayes' theorem is used to determine the posterior probability of the two hypotheses. By calculating the ratio between the two hypotheses we obtain a relation that can be expressed in words as “Posterior odds = Bayes' Factor × prior odds”.

The BF is the ratio between the posterior and prior odds and represents a summary of evidence in favor of one of the two hypotheses. The BF is similar to a likelihood ratio. However, differently from the likelihood ratio, in the Bayesian framework there is no necessity of sampling the distribution to assess the sample, because all the inferences are conditional on the sample at hand. The BF therefore is a summary measure of the information contained in the data about the plausibility of the model.

We will adopt an objective Bayesian reasoning in which we try to introduce little prior knowledge into the problem. This perspective leads to consider the priors ratio P(H₁)/P(H₂) to be 1, meaning that the prior probability is equal. This position is reasonable because the resulting BF can be corrected with other ratios if the priors change. With this choice, we have that the likelihood ratio is equal to the posterior ratio, which is an important step because in the case of specificity the two hypotheses are each the complementary of the other, so that we obtain:

$$\mathrm{BF}=\frac{P\left(H_1|D\right)}{1-\mathrm{P}\left(H_1|D\right)}$$ (2)

according to which the BF is equal to the odd ratio of the posterior.

The framework within which the BF can be calculated on the basis of meta‐analytic data are the following. The likelihood of the data are calculated as usual: the parameters of the Gaussian distribution are obtained as a function of the number of subjects used in the experiments under examination. That means that we do not use Bayes to determine the posterior of the parameters: rather, in this context the parameters are given and processed as usual in the ALE meta‐analysis. The Bayesian hypothesis test is applied to the successive steps of the analysis. Therefore, the data used for the calculation of the BF are the final ALE map obtained as usual with GingerALE software (Eickhoff et al., 2009; Eickhoff et al., 2012; Turkeltaub et al., 2012).

For the analysis of VBM data the competing hypotheses were: (a) the alteration of the voxel was specific for the brain disorder under scrutiny; (b) or the alteration was not (¬) specific. We needed therefore to calculate the ALE maps derived from all the experiments in which the detected alterations were associated with a specific brain disorder and the ALE maps derived from all the experiments in which the detected alterations were not associated with that specific brain disorder. The final result of this process was the BF, a number between [0, ∞] representing how much the data could support the model Disease or ¬Disease.

Following Kass and Raftery (1995), the BF value can be interpreted as follows (Table 1).

TABLE 1.

Bayes' factor points associated with different forces of evidence

Bayes' factor (BF)	Force of evidence
1 to 3	Not worth more than a mere mention
>3 to 20	Positive
>20 to 150	Strong
>150	Very strong

2.4. The Bayes' factor and temporal evolution of brain diseases

Because the BF does not guarantee to highlight the earliest areas, but it does so in virtue of statistical considerations, we run a simulation to understand this aspect. As already showed (Cauda, Nani, Costa, et al., 2018; Cauda, Nani, Manuello, et al., 2018; Crossley et al., 2014; Iturria‐Medina & Evans, 2015; Raj, Kuceyeski, & Weiner, 2012; Tatu et al., 2018; Yates, 2012), neuropathological alterations are supposed to be distributed across the brain following structural and functional connectivity pathways. In order to simulate the alteration spread related to a certain pathology we used the anatomical connectivity matrix derived from Hagmann et al. (2008). Specifically, we used the average fiber tract density between two brain areas, obtained from healthy individuals with a parcellation of gray matter in 998 areas (nodes). First, we simulated a target pathology, that is, AD; AD is the ideal candidate because its areas of inception are well known. To do so, we selected three nodes for each cerebral hemisphere on the basis of the anatomopathological knowledge about AD (Braak & Del Tredici, 2011). These six nodes were selected because of their proximity to the transentorhinal cortex, which is known to be one of the earliest sites of neurofibrillary deposition in AD (Braak, Alafuzoff, Arzberger, Kretzschmar, & Del Tredici, 2006), and were used as starting points for a simulated pathological spread. The model of simulation was based on the diffusion equation already applied in Cauda, Nani, Manuello, et al. (2018), which is the following:

$$\frac{d\mathrm{x}\left(t\right)}{\mathit{dt}}=-\beta \mathcal{L}\mathrm{x}\left(\mathrm{t}\right)$$

where x is the concentration of the disease factor, β is the diffusivity constant controlling propagation speed and the matrix $\mathcal{L}$ is the Laplacian graph defined as:

$$\mathcal{L}=I-{\mathrm{\Delta }}^{-1/2}E{\mathrm{\Delta }}^{1/2}$$

in which E is the matrix of the edges representing the connection strength between nodes and Δ is the diagonal matrix with δ_i = ∑_je_ij as the ith diagonal element. The solution of this equation is:

$$\mathrm{x}\left(t\right)=\exp \left(-\beta \mathcal{L}t\right){\mathrm{x}}_0$$

This formula describes the evolution of an initial configuration x₀. The initial condition determines where the pathology begins to spread, that is, which nodes are the earliest to be altered. Thus, by considering different initial conditions, it is possible to simulate different temporal evolutions of brain diseases. The entire temporal span of the alterations' spread was subdivided in 1000 time points (arbitrary units), from the initial condition (in which few nodes are altered) to the state of equilibrium (in which all the nodes are altered). After obtaining the diffusion data, we randomly selected for each simulation 100 time points so as to have a simulated picture of the uneven distribution of pathological alterations. In each of these time points we analyzed for every node the degree of its alteration; the nodes that showed a degree of alteration over a predetermined threshold were considered as being actually altered. Subsequently, every selected time point with its surviving altered nodes was treated as an experiment, thus generating different MA maps obtained from simulated patients (from 6 to 20); all these MA maps were eventually united in an ALE map.

To simulate other possible pathologies (up to 30), we selected for each disease six bilateral nodes (three for each side) that were used to study the temporal evolution of the alterations' spread. Overall, we generated 1,000 time points for every simulated disease. As we did for the target pathology, we randomly selected 100 time points, to analyze the uneven distribution of alterations in different temporal series. Simulating different number of patients (from 6 to 20), each time point generated an MA map, which was united with the other MA maps of the other time points in an ALE map. Finally, the MA maps obtained from the target pathology (i.e., AD) and those obtained from the other simulated diseases were used for the BF calculus.

2.5. Validation

To assess the efficacy of our algorithm we have performed an analysis of reverse inference on fMRI data about pain tasks obtained from the BrainMap database; this analysis has been already carried out by Yarkoni et al. (2011), and its results are also available on the Neurosynth platform (core tools) as well as in Yarkoni (2015b). We made the following two queries in the functional BrainMap database sector (April 2018):

• A ‐ PAIN) [Experiments Context IS Normal Mapping] AND [Experiments Activation IS Activation Only] AND [Subjects Diagnosis IS Normals] AND [Experiments Imaging Modality IS fMRI] AND [Experiments Paradigm Class IS Pain Monitor/Discrimination];

• B ‐ NO PAIN) [Experiments Context IS Normal Mapping] AND [Experiments Activation IS Activation Only] AND [Subjects Diagnosis IS Normals] AND [Experiments Imaging Modality IS fMRI] AND [Experiments Paradigm Class IS NOT Pain Monitor/Discrimination].

We retrieved 81 articles, for a total of 261 experiments, 2,604 foci and 1,157 subjects (QUERY A); and 3,141 articles, for a total of 10,209 experiments, 87,409 foci, and 58,367 subjects (QUERY B) (see Figure S2 PRISMA flow chart for the overview of the selection strategy, Table S2 for the sample characteristics and Table S3 for more information about the selected fMRI data set, respectively).

From the data retrieved with Sleuth 2.4, we calculated the ALE for the condition “pain” and for the condition “no‐pain.” On the basis of the priors p(H_i) = 0.5, i = 1, 2, we determined the posterior probability and then the BF was determined as in (2), where in our case D means the voxel v, so that the posterior, was defined as:

$$P\left(H_1|v\right)=\frac{P\left(v|H_1\right)}{\left(P\left(v|H_1\right)+P\left(v|H_2\right)\right)}$$

where P(v|H₁) is the likelihood obtained by Equation (1) under the “pain” condition and P(v|H₂) is the likelihood obtained in the “no pain” condition. The results of our analysis were compared visually with those of Poldrack (2006) as they are illustrated in Figure 2 of his study (Poldrack, 2006) as well as with the results of an association map produced by Neurosynth (Yarkoni et al., 2011). Indeed, the standard output of Neurosynth is not actually a BF map, so comparisons are necessarily to be made by analogy.

FIGURE 2.

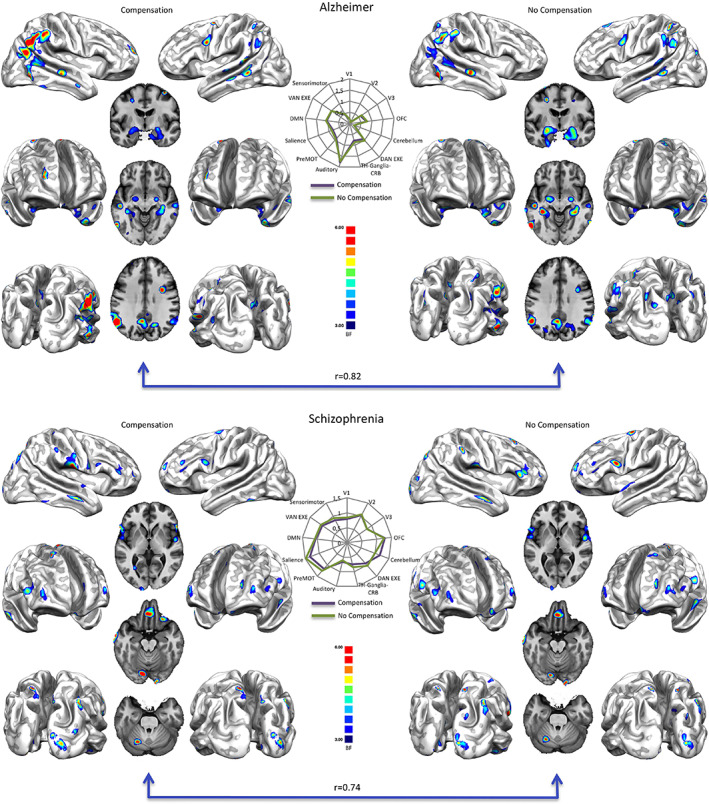
Top right: Bayes' factor (BF) map of Alzheimer's disease calculated with equiprobable priors over BrainMap data. Top left: Bayes' factor map of Alzheimer's disease calculated with equiprobable priors over BrainMap data, compensated for the different representativeness of pathologies in the database. Bottom right: Bayes' factor (BF) map of schizophrenia calculated with equiprobable priors over BrainMap data. Bottom left: Bayes' factor map of schizophrenia calculated with equiprobable priors over BrainMap data, compensated for the different representativeness of pathologies in the database. Middle: Radar maps illustrating the comparison between the network‐based decomposition of previous results expressed in mean Bayes' factor values. Bayes' factor maps are expressed in normalized BF values. See Table S4 and S5 for the specific numeric visualization

2.6. Validation of the priors: Schwarz criterion and Bayes' information criterion

To test and consolidate the results obtained for the specificity with meta‐analytic data we used a different method that do not use the prior as in the BF obtained in the previous section. It is possible to avoid the introduction in the model of the prior density with the help of the following formula:

$$S=\log P\left(D|H_1\right)-\log P\left(D|H_2\right)-\frac{1}{2}\left(d_1-d_2\right)\log \left(n\right)$$ (3)

where θ_k are the estimations with regard to the different hypotheses H_k, d_k is the dimension of θ_k, and n is the numerosity of the sample. If n → ∞, it is possible to show the validity of the following relation, called Schwarz criterion (Schwarz, 1978):

$$\frac{S-\log \mathit{BF}}{\log \mathit{BF}}\to 0$$

The Schwarz criterion, therefore, tends to the BF. If we consider the BIC, which is defined as:

$$\mathit{BIC}=d\mathit{log}\left(n\right)-2\log \left(P\left(D|{\theta }_k\right)\right)$$

we can see that, from (3), minus twice the Schwarz criterion is the difference between the BIC of the two hypotheses—for an in‐depth description of this theme see Kass and Raftery (1995). Finally, if we multiply the BIC for minus 0.5, we obtain the S value, which can be compared with the BF. As pointed out in the introduction, we can observe that the BIC depends on the number of samples (log(n)); it is therefore a way of verifying whether or not the choice of 0.5 as prior is correct for the BF calculus. If we obtain convergent results, we would be relatively confident that the rationale for choosing equiprobable priors is, at least with large samples, sound.

2.7. Stability against sample unbalances: Sample unbalance compensation

To minimize the potential bias of the inhomogeneous representativeness of brain disorders in the database, we generated a single sample for every brain disease by determining an ALE map of all the experiments about that specific disease. BF maps constructed with this compensatory procedure were correlated to the original BF maps obtained without compensation.

2.8. The file drawer problem or robustness against noise: Fail‐safe

The “fail‐safe” technique is frequently used in classical meta‐analyses of both medical and psychological studies. It was first introduced by Rosenthal (1979) and a specific approach for assessing the robustness of results against potential publication bias in ALE meta‐analyses was recently developed by Acar, Seurinck, Eickhoff, and Moerkerke (2018). This method presumes that there are unpublished studies with contra‐evidence results, and consequently estimates the number of these studies that can be added to the meta‐analysis before results get invalidated. In other words, the procedure requires to introduce into the sample increasing amount of noise (i.e., unreported experiments) in order to assess how statistically robust is the meta‐analytic result. Here the “fail‐safe” technique has been used to address the possibility that in BrainMap an amount of contra‐evidence experiments has not been stored.

We used the code developed by Acar et al. (2018), which is available on Github (https://github.com/NeuroStat/GenerateNull). The procedure can be divided into two steps: noise generation and robustness estimation. In the first step, the required amount of noise experiments is obtained. It must be noted that in doing this, the algorithm is constrained by the distributions of the number of foci and the number of subjects of the real meta‐analytic sample (i.e., experiments retrieved from BrainMap). In other words, if the experiments in the original meta‐analysis had a sample‐size between 10 and 20, and reported between 10 and 20 foci (i.e., peak values) each, the simulated experiments will also have a number of foci and subjects comprised between 10 and 20. This lends the noise realistic features. The spatial localization of peaks is then randomly sampled from the same gray matter mask used in the ALE computation. In order to correctly estimate the noise, the first step was repeated for each disorder separately (i.e., AD, SCZ, and pain).

In the second step, the noise experiments and the original meta‐analytic sample are combined and fed into the ALE algorithm. Results were tested for statistical significance with 1,000 permutations, as implemented in GingerALE. In other words, the second step allows to re‐run the meta‐analysis taking into account potential experiments “remained in the drawer.” This procedure was iterated several times (and for each of the three disorders considered) adding an increasing amount of noise experiments (between $\frac{k}{2}$ and 3k, where k is the number of the original studies). The ALE maps obtained at each level where then combined to show the robustness of the effect (i.e., the amount of noise that can be added before the true effect detected by ALE loses statistical significance). There are currently no normative values to interpret the fail‐safe results in the context of ALE meta‐analysis applied to VBM experiments. As pointed out by Acar et al. (2018), the minimum amount of injected noise of 5k + 10 proposed by Rosenthal (1979) for behavioral studies seems to be excessively high to be extended to fMRI field. For the scope of the present work, we considered 3k a reasonable upper bound. Taking SCZ as an example, this means that for each of the 114 experiments included in the original meta‐analysis, three more experiments remained unreported (for a total of 342).

Finally, A BF map was computed for each level of noise, and correlated with the BF map originally obtained for the set of real experiments (a threshold level of three BF points was used for each map). This allowed us to test the degree to which BF is affected by potential not included experiments.

3. RESULTS

3.1. Bayes' factor

3.1.1. Comparison with previous results

To test our algorithm, we replicated the analysis performed in Yarkoni et al. (2011). Figure 1 (middle and bottom rows, and Table S6) shows the results of the reverse inference on pain tasks data queried from BrainMap as well as the association map provided for “pain” by Neurosynth. Our results are very similar, albeit more conservative, to those of Neurosynth as well as to those shown by Yarkoni (Yarkoni, 2015b; Yarkoni et al., 2011). However, differences are to be expected, given the variability of input data and the methods used for constructing the maps (ALE vs. MKDA; see Wager, Lindquist, & Kaplan, 2007). Moreover, Neurosynth does not provide a BF map but an association map expressed in z scores (for a detailed discussion see Yarkoni, 2015b; Yarkoni et al., 2011).

FIGURE 1.

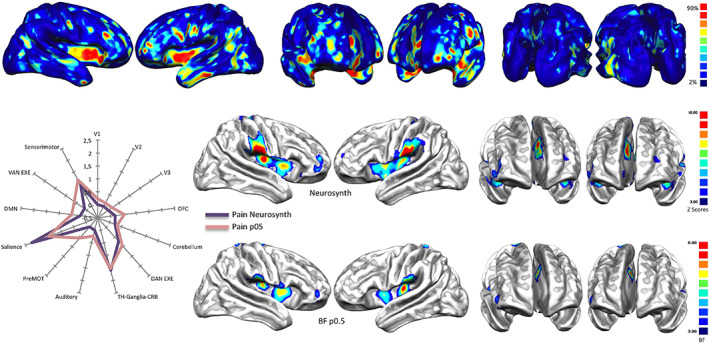
Top: Base rates reports of how many pathologies of the VBM BrainMap database cause alterations in every area of the brain. Areas highlighted in red are those in which more than the 90% of pathologies cause at least an alteration. Middle and bottom: Association test (expressed in z points) over the term ‘Pain’ performed with Neurosynth and compared with a Bayes' factor (expressed in normalized BF values) map calculated with equiprobable priors over BrainMap data (see Table S6 for the specific numeric visualization). Left panel: Radar map illustrating the comparison between the network‐based decomposition of previous results expressed in z mean points (Neurosynth) and Bayes' factor values

3.1.2. Alzheimer's disease and schizophrenia

Overall, the maps of specificity reveal that the two most represented pathologies in BrainMap are characterized by certain areas with positive BF values (see Table 1 and Supplementary Results in the Supplementary Material). It should be noted that the right parahippocampus is the only region in AD reporting a strong BF value (i.e., BF 21), whereas middle positive BF values (i.e., BF between 10 and 20) are exhibited by the left inferior parietal lobule and the right caudate tail. Others positive values (i.e., BF between 4 and 9) in AD were found in the bilateral hippocampus‐amygdala complex, in the right posterior cingulate cortex and supramarginal gyrus, as well as in the left superior temporal gyrus and superior parietal lobe (see Table S5 for a numeric visualization and Figure 2 top right). The resulting specificity map for the SCZ condition shows middle positive BF values in the right postcentral and inferior frontal areas, in the left orbital gyrus, superior frontal and temporal areas. Other positive BF values in SCZ were found in the bilateral precunei, in the right uncus, inferior/middle temporal gyri and in the left medial frontal areas (see also Table S4 and Figure 2 bottom right).

3.1.3. The Bayes' factor and temporal evolution of brain diseases

Figure 3 shows the temporal evolution of the simulated target pathology (i.e., AD), the foci from which the pathology begins to spread (top left panel), and the temporal evolution of all the other simulated pathologies used for statistical comparison (middle panel). The figure also illustrates the BF map calculated on the synthetic data (bottom panel), as well as the comparison between the areas showing a BF > 10 and the starting points (nodes) of the simulated target pathology (right panel).

FIGURE 3.

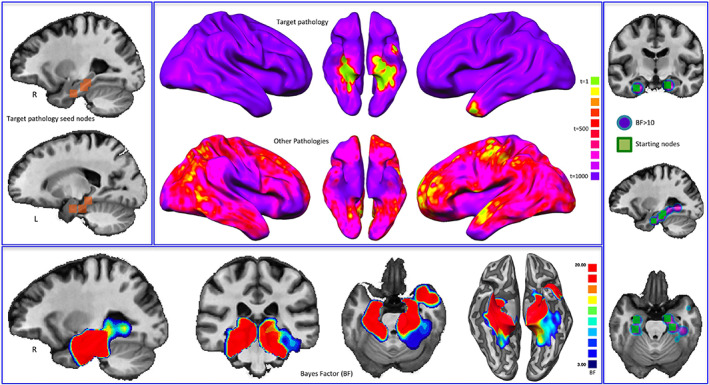
Bayes' factor (BF) and the temporal evolution of pathologies. Top left: Starting nodes of the target pathology (Alzheimer's disease, AD). Middle: Temporal evolution (expressed in arbitrary time points) both of the target pathology and of all the other simulated pathologies. Colors from green to violet show the areas that are altered from early to late phases of the simulated pathological spread. Bottom: BF values calculated on synthetic data. Right panel: Comparison between the areas showing a BF > 10 and the starting points of the simulated target pathology

3.2. Validation

3.2.1. Sample unbalance compensation

Original BF maps obtained without compensation (Figure 2 top right and bottom right) and those obtained with the compensatory procedure (Figure 2, top left and bottom left) show high correlation values: 0.82 for AD and 0.74 for SCZ, respectively (see Figure 2, middle panel).

3.2.2. Bayes' information criterion

To test how much the choice of equiprobable priors can influence the BF values, we compared the BIC with the BF map related to pain and generated with equiprobable priors (Figure 4). Results show that both the techniques produce maps that are extremely similar to each other (r = 0.88). This high correlation leads us to think that the choice of equiprobable priors does not bias the BF calculus.

FIGURE 4.

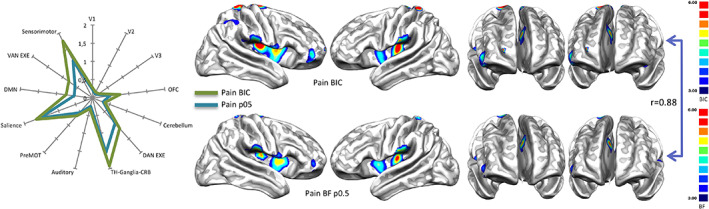
Right panel: Comparison between the results of the Bayes' information criterion (BIC), expressed in S value (see Methods section), performed over the term 'Pain' and the Bayes' factor (BF) map calculated with equiprobable priors over BrainMap data. Left panel: Radar map illustrating the comparison between the network‐based decomposition of previous results expressed in mean BIC and BF values. Bayes' factor maps are expressed in normalized BF values. See Table S6 for the specific numeric visualization

3.2.3. Fail‐safe

Compared to the results related to AD and SCZ, the ones related to the pain condition are more vulnerable to the noise injections. In fact, for the pain condition most of brain areas with significant BF values do not survive after an amount of noise over 100% (Figure 5, left panel). In this case, the most surviving areas are the sensorimotor and, to a lesser extent, the posterior insular. In contrast, AD and SCZ have higher correlations even with great quantities of noise injection. In particular, with regard to SCZ, the correlation is still at r = 0.67 after an amount of noise of 300%, while with regard to AD, the correlation is at r = 0.55 after an amount of noise over 150% (Figure 5, middle and right panels). In the case of AD, the most surviving areas are those associated with the posterior component of the default mode network (DMN). In the case of SCZ, most of the areas with significant BF values survive after huge noise injections, save for the most anterior prefrontal areas. Figure 6 shows how the correlation between BF maps, derived from AD, SCZ, and the pain condition and obtained with and without noise, drops at r = 0.3 after an amount of noise over 150%.

FIGURE 5.

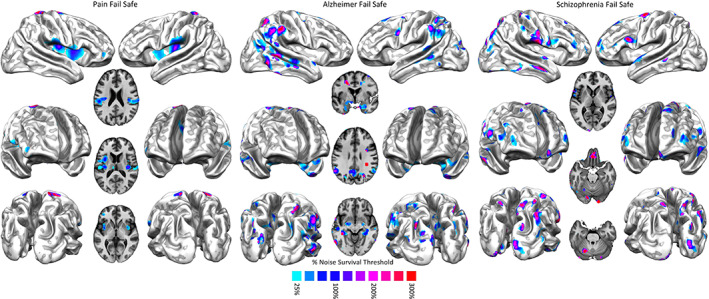
Left panel: Fail‐safe results of the Bayes' factor calculated over pain data. Areas colored from blue to red show increasing resistances to progressively greater injections of noise in the data set. Middle panel: Fail‐safe results of the Bayes' factor calculated over Alzheimer's disease data. Areas colored from blue to red show increasing resistances to progressively greater injections of noise in the data set. Right panel: Fail‐safe results of the Bayes' factor calculated over schizophrenia data. Areas colored from blue to red show increasing resistances to progressively greater injections of noise in the data set

FIGURE 6.

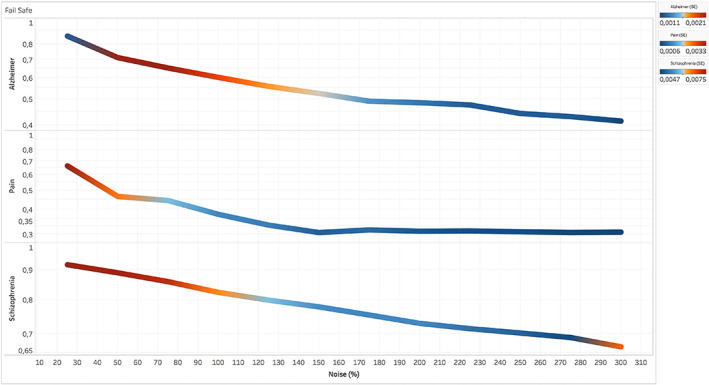
Fail‐safe results of the Bayes' factor (BF) of three data sets (i.e., pain, Alzheimer's disease, and schizophrenia) obtained from the correlational values between the BF map calculated without injections of noise and BF maps calculated with progressively increasing injections of noise. Colors from blue to red indicate increasing values of standard deviation between the r values calculated in the different runs of the fail‐safe procedure

4. DISCUSSION

In this study, we have applied a Bayesian reverse inference method to map the pathological brain and identify its altered regions that are specific to the two most represented disorders in BrainMap database (i.e., AD and SCZ). This specificity is expressed in terms of BF, positive values of which (>3, but rarely superior to 20) characterize the structural alteration profiles both of AD and of SCZ. In particular, the posterior components of the DMN, the amygdalae, the hippocampus and parahippocampus exhibit positive specificity in the BF map of AD. Although the BF values of these areas are positive, they are not strong and just the parahippocampus shows a BF that is slightly superior to 20 (see Figure S3 and Tables S4, S5, and S6).

With regard to AD, our findings are in accordance with well‐established research and have been also further supported recently by our group (Manuello et al., 2018). Volumetric changes involving the hippocampus/parahippocampus, and especially the entorhinal cortex, have been repeatedly considered as relevant features in the development of AD (Jack Jr. et al., 1997; Rabinovici et al., 2007; Whitwell et al., 2007). In fact, the atrophy of the medial temporal lobe, generally involving the amygdala (Poulin, Dautoff, Morris, Barrett, & Dickerson, 2011), is a significant biomarker that helps predict the evolution from mild cognitive impairment to AD (Devanand et al., 2007). Furthermore, resting‐state fMRI investigations provide evidence that AD is associated with a decreased functional connectivity within the DMN (Zhu, Majumdar, Korolev, Berger, & Bozoki, 2013). If we consider the progressive tauopathy that characterizes AD, the typical involvement of both entorhinal and parahippocampal districts may indicate that these are key regions for the deposition of pathologic tau in this condition (Braak & Braak, 1991; Braak & Del Tredici, 2011; Jack Jr. et al., 2018; Lowe et al., 2018; Ossenkoppele et al., 2016; Price & Morris, 1999). The deterioration of the mesial temporal (hippocampal/parahippocampal/entorhinal) cortex, in association with the posterior portions of the DMN, can be successfully identified by structural neuroimaging techniques (both VBM and cortical thickness) with different outcomes for sensibility/specificity in comparison to normal isocortical atrophy (Diaz‐de‐Grenu et al., 2014). The highest BF values in the parahippocampus and the transentorhinal regions (Taylor & Probst, 2008) demonstrate that high BF values are telltale signs of the cerebral areas that are the earliest to be altered.

With regard to SCZ, we observe that the insula, the ACC, the ventromedial prefrontal cortex, the dorsolateral prefrontal cortex, and the medial thalamus show an increased specificity compared to other altered areas. The BF values of these areas are positive but not strong (ranging between 3 and 20 points). In morphometric studies of SCZ, the involvement of the insular cortex is frequently reported (Bora et al., 2011; Brandl et al., 2019; Wylie & Tregellas, 2010). Also, decreases in gray or white matter volumes have been observed in both ACC and various sites of the prefrontal cortex (Baiano et al., 2007; Ellison‐Wright, Glahn, Laird, Thelen, & Bullmore, 2008; Glahn et al., 2008; Honea, Crow, Passingham, & Mackay, 2005; Kim, Kim, & Jeong, 2017; Koo et al., 2008; Narr et al., 2005; Nesvag et al., 2008). The thalamus, too, is supposed to play a role in SCZ, on the basis of its many connections with several brain structures, especially with the prefrontal cortex (Alelu‐Paz & Gimenez‐Amaya, 2008; Pergola, Selvaggi, Trizio, Bertolino, & Blasi, 2015; van Erp et al., 2016). The complex GM alterations reported by scientific literature in patients with SCZ (in particular in insular and prefrontal regions) (Kelly et al., 2018; van Erp et al., 2018) principally impact on areas whose disruption is directly associated with episodes of psychosis and their long‐term outcome (Palaniyappan et al., 2016; Zuliani et al., 2018), as well as with cognitive ability and the development of cognitive disturbances (Sasabayashi et al., 2017). The specific structural pattern, characterized by altered cortical thickness/volume associated with a perturbed cortical gyrification (both hyper‐ and hypogyria), reflects the involvement of a strong genetic or very early developmental background (Docherty et al., 2015; Spalthoff, Gaser, & Nenadic, 2018). For all these reasons, SCZ can be considered as a model of neurodevelopmental disorder with high heritability (Andreasen, 2010; Hilker et al., 2018).

The analysis of the alteration specificity put forward in this study is complementary to the transdiagnostic alteration patterns observed in previous investigations (Buckholtz & Meyer‐Lindenberg, 2012; Cauda et al., 2017; Cauda, Nani, Costa, et al., 2018; Cole et al., 2014; Goodkind et al., 2015; McTeague et al., 2016; Poldrack, 2006, 2011; Yarkoni et al., 2011). These two approaches provide an overarching picture of the pathological brain, which is of great interest for a better understanding of how neuropathological processes affect this organ. Interestingly, although many cerebral areas are altered by the majority of brain diseases, patterns of alterations that seem specific to certain conditions can emerge. The study of these typical profiles of alterations promises to give valuable insights for the improvement of our clinical tools.

4.1. The temporal evolution of brain diseases

It should be noted that when a specific brain disease (especially the neurodegenerative ones) is in its terminal stages, many areas of the brain would be affected. Therefore, if neuropathologies were studied during their advanced developments, they would show a great overlap of alterations. Differently from the discipline of pathological anatomy, which carries out postmortem studies of the human brain, neuroimaging techniques usually examine mixed pathological populations exhibiting different phases of brain degeneration. Moreover, many studies are conducted on patients after their first diagnosis. These samples of individuals, therefore, are not expected to have areas showing great overlap of alterations (Cauda et al., 2019).

Clearly, the simulation shows that the BF calculus can capture, albeit with some approximation, the earliest points of the simulated spread. In other words, the BF calculus is able to identify the areas that are more precociously altered and, therefore, to distinguish between them and those regions that are affected later. This result emphasizes the importance to use reverse inference techniques for studying the anatomical alterations caused by brain diseases, as these techniques can provide a window into the initial stages of neuropathological development, thus making possible the identification of patterns of alteration spread as specific biomarkers of the early phases of brain disease in view of patients' selection for disease‐modifying clinical trials (Pratt & Hall, 2018; Rohrer et al., 2015; Weiner et al., 2017) as well as for assessing the efficacy of therapies (Cummings, Ritter, & Zhong, 2018; Lawrie, O'Donovan, Saks, Burns, & Lieberman, 2016; Marizzoni et al., 2018).

Indeed, with regard to AD and SCZ, it has been possible to identify with our Bayesian reverse inference method not only the areas that appear to be early affected (Braak & Del Tredici, 2011; Nenadic et al., 2015) but also the sites of the main pathological alterations of these two conditions, which are characterized by tauopathy and complex structural alterations related to a genetic/neurodevelopmental background (Jack Jr. et al., 2018; Spalthoff et al., 2018). For instance, analyses of real data about AD have revealed that the parahippocampus is the area with the strongest BF values (superior to 20; see Table S5), a result that is in line with well‐established scientific evidence (Taylor & Probst, 2008).

This result supports well the hypothesis that high values of BF might be proportional to the degree of alteration earliness exhibited by those areas. Furthermore, the conceptual implication suggested by high BF values deserves attention: in fact, the more specific is a brain area for a disease, the greater the likelihood for that area to be precociously involved in the progression of the disease. Therefore, although the BF calculus cannot exactly pinpoint the very first starting site of a neuropathological process, it can identify the areas that are probably affected early and differentiate them from those that appear to be affected later.

4.2. Validation

The analyses carried out in this study to understand how a sample that is not uniformly balanced could bias the BF results, along with the choice for setting the priors, have led us to think that the entity of the potential biases is not as serious as to invalidate the BF calculus. In fact, the strategies used to overcome those difficulties, both in the case of the compensation of the inhomogeneity of the sample and in the case of the choice of the priors, have produced results very similar to those obtained without these procedures. Still, further research is needed to finally solve these problems. Especially with regard to the choice of the priors, we need further investigations with the help of empirical as well as Bayesian empirical techniques for their calculus.

The fail‐safe analysis has showed that the BF results obtained from the anatomical alteration data of AD and SCZ are rather solid, as they survive after relevant injections of noise and they are not, therefore, strongly affected by publication bias (Acar et al., 2018). In particular, the results about SCZ are the best surviving, followed by the results about AD and, at a certain distance, by the results about the pain condition. Therefore, BF values obtained from VBM data were more resistant to publication bias than those obtained from functional data.

4.3. Limitations

The analysis on meta‐analytical data, which are characterized by a certain degree of deterioration as well as of spatial uncertainty, might have increased the overlap between regions affected by different pathologies and, as a consequence, reduced the capacity of revealing small areas with high specificity. This aspect notwithstanding, the necessity of using a huge repository, in which data of a large number of brain disorders are stored, compels to adopt a meta‐analytical approach. Poldrack (2011) claimed that the BrainMap database might be biased by the fact that the studies are introduced manually, as this could lead to a partial sample of the literature. In contrast, the database of Neurosynth, which uses an automated process for selecting articles, should have a more comprehensive sample. We agree only in part with this criticism. In fact, even if we could create an all‐inclusive database of task‐based fMRI studies, the bias because the various cognitive domains are not uniformly represented would not be definitely ruled out. This is because all the topics of research do not have the same interest for the scientific community: for instance, (i) some tasks or pathologies are more or less studied than others, independently of their relative frequency; (ii) some other task or pathologies are more difficult to study and, therefore, less investigated; (iii) the automated selection process for introducing experiments in a database can make classification mistakes, which are sometimes more frequent than those occurring with a nonautomated selection; (iv) Neurosynth does not differentiate between activation and deactivation. In any case, the aim of the present study is not to explore all the strengths and weaknesses of databases, such as BrainMap or Neurosynth, but rather to propose solutions and try to overcome the problems raised in the debate about the reverse inference.

Although we have devised strategies to avoid the problem of the inhomogeneity of the BrainMap samples, and though the inhomogeneous distribution of data concerns the priors regarding the parameters of the likelihood model rather than the priors regarding the hypotheses, the uneven representation of pathologies may nonetheless have biased some results of the reverse inference. However, so far the use of BrainMap is the only way to create maps of GM alterations capable of giving an overarching picture of the pathological brain. As matter of fact, the frequency of distribution of pathologies in a database cannot represent accurately the frequency of distribution of pathologies in the real world. This is so because certain conditions are more investigated than others, independently of their incidence in the population, so that they are sampled with varying frequencies in the literature. Moreover, BrainMap contains only a fraction of all the neuroimaging literature about brain disorders and the addition of new studies is not principally directed to reduce this inhomogeneity. So, the amount of results that researchers report is inevitably related to their expectations as well as to the fact that some research topics are more prevalent than others; and the BrainMap database inevitably reflects that bias. Furthermore, even though our model can exclude possible two identical studies, it cannot control if more than one study has been carried out on the big same data set, such as COBRE (Calhoun et al., 2011) or ADNI (Wyman et al., 2013). As a consequence, our estimates may be biased upwards. Nonetheless, the validation analysis through the BIC, the compensation of the base rates of different pathologies, and the fail‐safe technique have showed that the potential biases of the sample are unlikely to invalidate our results.

Since a choice about the prior must be made, on the basis of our validation analyses and in absence of better strategies, we propose to choose equal priors (i.e., 50%). Needless to say, even though our validation analyses are encouraging, equal priors have both strengths and weaknesses; hopefully future procedures will provide better solutions. In the meantime, however, we think that the choice of equal priors is a valuable strategy and should be adopted. This would encourage the use of reverse inference techniques for the study of alterations caused by brain diseases, a study that, in our opinion, is essential to better understand the pathological brain, especially in light of the fact that many brain areas are nonspecific to pathologies but, rather, exhibit a great overlap of alterations. Indeed, in spite of the problems already discussed, a study based on the reverse inference obtained from brain alterations data are extremely interesting, as it allows the identification of the areas that are more specific and/or precociously altered in a certain pathology. This obviously does not allow sustaining that the alteration of a certain area is strictly specific to just one pathology, but certainly it allows to identify which areas, whose alteration is frequently associated with more or less brain disorders, are more or less specific and informative. In addition, we can compare results obtained from different pathological processes with each other, as well as compare different patterns of GM alteration associated with the same pathology, so as to reach a pathological imprint that is more specific to that pathology.

Finally, our simulations of alteration spreads related to different pathologies are based on the premise that alterations move diffusively along brain connectivity pathways. Although this underlying mechanism has been confirmed by recent research (Cauda, Nani, Costa, et al., 2018; Cauda, Nani, Manuello, et al., 2018; Crossley et al., 2014; Fornito et al., 2015; Iturria‐Medina & Evans, 2015; Manuello et al., 2018; Raj et al., 2012; Tatu et al., 2018; Zhou et al., 2012), it is not the only one that might play a role in the alteration spread. Moreover, the contributions of different mechanisms can vary with regard to the type of pathology affecting the brain, so that our simulations, even though they offer in our view the best approximation to real pathological spreads with the available data, do not pretend to grasp all the complexities of the actual phenomenon.

Another criticism concerns the fact that over time patients develop more diffuse structural abnormalities, so that the reliability of an abnormality may become lower due to the nature of how the disease evolves. However, it seems plausible that a likelihood model underlying the BF could explicitly represent the progression of the disease by using the diffusion patterns employed here to simulate data. Nonetheless, since this BF approach is able to make inferences about the areas that are early altered, it should also be possible that this phenomenon may be a feature of the data and not of this particular approach.

A further limitation is that the BF is calculated in a univariate manner: each voxel or area is considered in isolation without taking into account a possible influence of other areas or voxels. Currently we are trying to develop an approach capable of considering a joint probability in which more variables (voxels or areas) are taken into consideration; this view, however, poses several methodological problems, which are mostly related to the expansion of the parameters' space and, consequently, to the difficulty in performing the calculation.

5. CONCLUSION

Although transdiagnostic research provides evidence that many sites of the brain are altered by several pathological processes, this study shows that a Bayesian reverse inference is capable of identifying the cerebral areas exhibiting a high alteration specificity to certain pathologies. This approach allows to distinguish between areas that are altered by most of brain diseases and areas that are altered by a limited number of pathologies and, therefore, can be considered more specific to a certain pathology. It is also capable of identifying the areas that are likely to be affected early, thus opening a new window into the in vivo study of the pathological brain. These findings offer interesting prospects for better characterizing brain disorders, as well as a new way to perform VBM meta‐analyses, thus hopefully contributing to the intriguing quest for deciphering the complex landscape of alteration patterns of the pathological brain.

CONFLICT OF INTERESTS

The authors report no competing interests.

Supporting information

Appendix S1: Supporting Information

Cauda F, Nani A, Liloia D, et al. Finding specificity in structural brain alterations through Bayesian reverse inference. Hum Brain Mapp. 2020;41:4155–4172. 10.1002/hbm.25105

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are openly available in the BrainMap database at http://brainmap.org/sleuth/.