Forecasting of COVID-19 pandemic: From integer derivatives to fractional derivatives

Highlights

• •A new compartmental mathematical model has been proposed incorporating imperfect quarantine and ineffective lockdown policies.
• •With an aim to gain a deeper understanding about probable peak dates and sizes, a fractional model has been developed by using the concept of Caputo derivative.
• •Adams-Bashforth-Moulton numerical scheme has been applied for numerical simulations of the fractional model.
• •Efficacy of confinement measures is found to be the most significant parameter in controlling the transmission dynamics of COVID-19.

Abstract

In this work, a new compartmental mathematical model of COVID-19 pandemic has been proposed incorporating imperfect quarantine and disrespectful behavior of citizens towards lockdown policies, which are evident in most of the developing countries. An integer derivative model has been proposed initially and then the formula for calculating basic reproductive number, ${\mathcal{R}}_0$ of the model has been presented. Cameroon has been considered as a representative for the developing countries and the epidemic threshold, ${\mathcal{R}}_0$ has been estimated to be  ~ 3.41 $(95\%\text{CI}:2.2-4.4)$ as of July 9, 2020. Using real data compiled by the Cameroonian government, model calibration has been performed through an optimization algorithm based on renowned trust-region-reflective (TRR) algorithm. Based on our projection results, the probable peak date is estimated to be on August 1, 2020 with approximately 1073 $(95\%\text{CI}:714-1654)$ daily confirmed cases. The tally of cumulative infected cases could reach  ~ 20, 100 $(95\%\text{CI}:17,343-24,584)$ cases by the end of August 2020. Later, global sensitivity analysis has been applied to quantify the most dominating model mechanisms that significantly affect the progression dynamics of COVID-19. Importantly, Caputo derivative concept has been performed to formulate a fractional model to gain a deeper insight into the probable peak dates and sizes in Cameroon. By showing the existence and uniqueness of solutions, a numerical scheme has been constructed using the Adams-Bashforth-Moulton method. Numerical simulations have enlightened the fact that if the fractional order α is close to unity, then the solutions will converge to the integer model solutions, and the decrease of the fractional-order parameter (0  <  α  <  1) leads to the delaying of the epidemic peaks.

1. Introduction

In the late December 2019, the World Health Organization (WHO) was enlightened about sudden new cases of a unique pneumonia and the specific cause of this infection was an enigma for the health authorities of the city of Wuhan in China. A few days later, it has been unearthed that this pneumonia is caused by a virulent virus and it has been named officially as the novel coronavirus (2019-nCoV). The modes of transmission are similar to the viruses responsible for the previous epidemics of SARS and MERS [31]. However, this virus was found to be more contagious and has been the cause of millions of deaths worldwide since January 2020. To date, there is no clinically established treatment or specific vaccine for COVID-19. Nevertheless, according to the suggestions of different prudent infectious disease specialists, several countries have started using chloroquine combined with azithromycin as alternative drugs [15]. Several non-pharmaceutical interventions such as physical distancing, wearing face masks in public places, home quarantine, isolation and countrywide lockdown policies have been promoted to curb the spread of the virus [27].

Cameroon, a country in sub-Saharan Africa, had its first confirmed case on March 05, 2020. It was a 58-year-old French citizen, arrived at Yaoundé airport on February 24, 2020 [22]. With an aim to quell the spread of the virus, the government undertook several policies such as closing the borders, introducing confinement measures, prohibiting large gatherings of people, closures of all kinds of educational institutions (from kindergarten to university), wearing face masks in public places and so on. In addition, Cameroonian government implemented contact-tracing strategy together with mass-media sanitisation campaigns. Contact-tracing consists of search, or identify all individuals who have had a contact with a confirmed case and force them to be quarantined if they are COVID-19 positive [24]. The scarcity of medical resources in maximum sub-Saharan African countries compelled authorities to request asymptomatic cases of COVID-19 to be self-quarantined in their home while taking medication (conventional or not) following proper health guidelines [16]. The main problem encountered by health workers is the stigmatization of COVID-19 patients. Indeed, like the cases of HIV/AIDS in Africa, stigma pushes confirmed cases or those who have had direct contact with a confirmed case of COVID-19 to run away from hospitals, and in this way they are contributing to the rapid spread of the virus in the community [23], [37].

Different types of mathematical models have been playing notable roles in predicting the transmission dynamics of infectious diseases and different effective control measures can be designed to limit the community transmission in the community. Several models have already been proposed to predict the transmission dynamics of COVID-19 and to study the impact of different control measures imposed by different governments [1], [26]. Although these models have similarities, each of them presents specifications related to the evolution of COVID-19 and various control measures deployed by several respective governments. A model considered in [1], describes the interactions among the bats and unknown hosts, human population and population of virus in reservoir (seafood market). In this paper, Atangana-Baleanu derivative concept has been implemented successfully. However, confined or quarantined class and isolated class have not been considered in this study. In a recent study, Nabi [26] has proposed a new Susceptible-Exposed-Symptomatic Infectious-Asymptomatic Infectious-Quarantined-Hospitalized-Recovered-Dead (SEI_DI_UQHRD) compartmental mathematical model and calibrated model parameters to project the future dynamics of COVID-19 for various COVID-19 hotspots. Although he considered a quarantine compartment, he did not consider the possibility of those quarantined people to contract the virus. Although this consideration goes well with certain developed countries (France, Italy, Russia and Spain), certain realities [27] of COVID-19 pandemic in several developing countries and maximum African countries have not been taken into account in any model. In case of Cameroon, several crucial factors such as violation of containment measures and negligence towards confinement measures must be taken into account to understand the actual transmission dynamics of COVID-19. Importantly, numerous daily wage-earners are compelled to go out to fetch food for their family members contravening all confinement orders. In this way, they are getting infected and spreading the viruses to their family members as well as neighbors [27]. Therefore, it would be prudent to envisage the future outbreak dynamics of COVID-19 in developing countries with imperfect confinement. Moreover, some people are fleeing from quarantine centres and returning back to their families due to the stigmatization of COVID-19 patients. Henceforth, considering perfect quarantine could be highly debatable if we want to model and forecast the transmission dynamics of COVID-19 in developing countries.

Fractional calculus or non-integer order calculus, a branch of mathematical analysis, contains the theory of fractional-order derivatives operators. The history of non-integer order calculus is more than 300 years old and modern fractional calculus is a rapidly evolving field in theory, analysis and applications with a view to handling complicated real-world problems. A plethora of concepts regarding fractional derivatives have already been introduced and applied by researchers in various branches of Science and Engineering [13], [17], [32]. Atangana-Baleanu (AB), Caputo-Fabrizio (CF), and Caputo derivatives are the most commonly used derivatives in solving real-world problems. Grunwald-Letnikov fractional operators have been applied comprehensively in the field of image processing. AB, CF, and Caputo fractional derivatives have different kernel properties. Caputo derivative is defined with power-law type kernel (non-local but singular), Caputo-Fabrizio with exponentially decaying type kernel (non-singular) and AB derivative in the Caputo sense has Mittag–Leffler type kernel [36]. A new generalised Caputo type fractional derivative has been introduced in [30]. Asymptotic stability of generalised Caputo FDEs has been introduced by Baleanu in [5]. Integer-order derivative operators have lucid geometric and physical interpretations, which clearly simplify their applications in tackling real-world challenges. Recently, various techniques have been proposed by researchers to describe the solution of non-linear fractional differential equations. A new technique for solving non-linear Volterra integro-differential equations in Atangana-Baleanu derivative sense has been introduced in [12]. Another technique with the uses of Genocchi polynomials has been proposed in [35]. A new technique to solve multi-variable order differential equations in AB sense has been introduced by Ganji et al. [11].

In this paper, a new compartmental COVID-19 model has been studied rigorously with the help of Caputo fractional derivatives. The advantage of applying Caputo fractional derivatives to analyse the proposed COVID-19 model is the dynamics of the model can be observed more deeply using the real-time data. In this framework, real-time data can be compared with the model outputs in a precise manner. Fractional derivatives can be a suitable alternative to integer derivatives in studying complex dynamics as there are always some limitations of integer derivatives described in [2]. Podlubny has given the geometric and physical significance of Riemann-Liouville fractional integral in [33]. As compared to the Riemann-Liouville fractional derivative, Caputo fractional derivative has the identical physical interpretation [33]. In a physical model, fractional derivatives manage systems with memory that ensure the evolving system state is reliant on its past states as well.

The aim of this work is to forecast the probable time and size of the epidemic peaks of the novel coronavirus outbreak in Cameroon by studying a realistic compartmental model using the robust concept of Caputo fractional derivative. A compartmental mathematical model of COVID-19 progression dynamics has been proposed incorporating the efficacy of confinement measures and imperfect quarantine. Estimation of parameters is performed by using real-time data, followed by a projection of the evolution of the disease. Global sensitivity analysis is applied to determine the influential mechanisms in the model that drive the transmission dynamics of the disease. Afterwards, the integer model is transformed into a fractional model in Caputo sense and the existence and uniqueness of solutions have been presented. Using the Adams-Bashforth-Moulton scheme, a numerical scheme for the fractional model has been constructed. Several numerical simulations have been performed to compare the result obtained by the integer-order model with the fractional model outputs.

The entire paper is organized as follows. Model formulation and basic properties are presented in Section 2. Section 3 is devoted to model calibration using real-time data of reported cases of COVID-19 in Cameroon, global sensitivity analysis of the proposed model, and forecasting of the disease future dynamics. In Section 4, the compartmental model is transformed into a fractional model in the Caputo sense, following by the existence and uniqueness of solutions, construction of a numerical scheme and numerical simulations in which the coefficient of fractional order has been varied. The paper ends with some insightful observations and fundamental findings.

2. Model formulation

A compartmental differential equation has been proposed to describe the transmission dynamics of the COVID-19. The spread starts with an introduction of at least one infected human into a completely susceptible population. The human population has been categorized into seven compartments according to their epidemiological status, i.e {S(t), C(t), E(t), A(t), Q(t), H(t), R(t)} which represent the number of susceptible individuals, confined individuals, infected individuals in incubation period, asymptomatic infectious individuals (undetected but infectious) including those who fled quarantine, quarantined individuals or confirmed infected individuals, hospitalised and recovered individuals respectively. So, the total number of human population, denoted by N, at any time can be represented by $N\left(t\right)=S\left(t\right)+C\left(t\right)+E\left(t\right)+A\left(t\right)+Q\left(t\right)+H\left(t\right)+R\left(t\right)$. The formulation of the model are subject to some assumptions listed below..

• •Migration is not considered in this model formulation. Most of the countries banned all international flights after identifying new COVID-19 cases. Hence, it is judicious to consider a closed population [26].
• •Vital dynamics (birth and natural deaths) are ignored. The idea is to observe what may happen in the short-term. For example, to have a birth we need around 9 months on an average, and to have a natural death rate which is the inverse of the average life expectancy i.e. 1/55 per year in any developing country like Cameroon and no one would expect the disease to stay so long.
• •Confinement is not perfect. Indeed, in some developing countries, due to insufficient financial income in households, people are not showing proper respect to the confinement measures imposed by the government, and are forced to go out to ensure daily meal for their families.
• •The immunity is considered to be perfect. Without any confirmed proof of lost of immunity, it is assumed that recovered individuals develop certain immunity against the disease [9], [29].
• •Hospitalized patients (in respiratory support) can not spread the disease as they remain under closed supervision.

The flow diagram of the proposed model is depicted in Fig. 1 , where susceptible individuals decrease either via confinement at a rate c, or via infection by a direct contact with an infectious individual (A or Q).

$$\lambda =\beta \frac{A\left(t\right)+\eta Q\left(t\right)}{N\left(t\right)}$$ (1)

In (1), β is the effective contact rate (that is, contact capable of leading to COVID-19 infection). The modification and dimensionless parameter 0 ≤ η < 1 accounts for the assumed reduction in transmissibility of quarantined symptomatic carriers relative to unquarantined asymptomatic carriers. Since the confinement is not perfect, confined individuals move to the latent class at a rate $(1-ϵ)\lambda ,$ where 0 ≤ ϵ ≤ 1 is the efficacy of confinement. This is in contrast a variation of SEIR-style models recently employed in [9], [29], where the authors consider that confined individuals are not exposed to COVID-19 infection. Indeed, in developing country such as Cameroon, since the confinement is not perfect, it is practical that an infected individual can infect a confined person by returning back home. This phenomenon was also observed at the beginning of the epidemic in a developed country such as Italy, where old confined individuals had been infected by their grandchildren who are asymptomatic carriers [16]. After the incubation period of 1/γ, a proportion q of infected individuals move to the asymptomatic class A, and the other $(1-q)$ proportion of infected individuals move to the quarantine class. It is important to note that asymptomatic class A include all infectious individual who are not maintaining quarantine and those who have fled the quarantine. The rate of transition from unquarantined asymptomatic infectious to quarantine infectious class, unquarantined asymptomatic infectious to hospitalised class, unquarantined asymptomatic infectious to recovered class and hospitalised to recovered class are r ₁ σ ₁, r ₂ σ ₁, $(1-r_1-r_2){\sigma }_1$ and σ ₃ respectively. Moreover, r ₃ σ ₂, r ₄ σ ₂ and $(1-r_3-r_4){\sigma }_2$ are the transition rates of quarantined infectious to unquarantined infectious, quarantined infectious to hospitalised class, and quarantined infectious to recovered class respectively. Importantly, δ_a, δ_q and δ_h are the disease-induced death rate of unquarantined infectious, quarantined infectious and hospitalised patients respectively. The above assumptions led to the following nonlinear system of ordinary differential equations,

$$\{\begin{array}{cc}\frac{dS}{dt}\left(t\right)\hfill & =pC\left(t\right)-cS\left(t\right)-\left[\frac{\beta \left(A\right(t)+\eta Q(t\left)\right)}{N\left(t\right)}\right]S\left(t\right),\hfill \\ \frac{dC}{dt}\left(t\right)\hfill & =cS\left(t\right)-pC\left(t\right)-(1-ϵ)\left[\frac{\beta \left(A\right(t)+\eta Q(t\left)\right)}{N\left(t\right)}\right]C\left(t\right),\hfill \\ \frac{dE}{dt}\left(t\right)\hfill & =\left[\frac{\beta \left(A\right(t)+\eta Q(t\left)\right)}{N\left(t\right)}\right]\left[S\right(t)+(1-ϵ\left)C\right(t\left)\right]-\gamma E\left(t\right),\hfill \\ \frac{dA}{dt}\left(t\right)\hfill & =q\gamma E\left(t\right)+r_3{\sigma }_{2}Q\left(t\right)-({\sigma }_1+{\delta }_a)A\left(t\right),\hfill \\ \frac{dQ}{dt}\left(t\right)\hfill & =(1-q)\gamma E\left(t\right)+r_1{\sigma }_{1}A\left(t\right)-({\sigma }_2+{\delta }_q)Q\left(t\right)\hfill \\ \frac{dH}{dt}\left(t\right)\hfill & =r_2{\sigma }_{1}A\left(t\right)+r_4{\sigma }_{2}Q\left(t\right)-({\sigma }_3+{\delta }_h)H\left(t\right)\hfill \\ \frac{dR}{dt}\left(t\right)\hfill & =(1-r_1-r_2){\sigma }_{1}A\left(t\right)+(1-r_3-r_4){\sigma }_{2}Q\left(t\right)+{\sigma }_{3}H\left(t\right)\hfill \end{array}$$ (2)

The parameters are described in Table 1 .

Fig. 1.

Schematic diagram of the proposed model (2).

Table 1.

Model parameters and their description.

Parameter	Description
β	Infectious effective contact rate
η	Infectiousness factor for quarantined infectious individual
p	Transition rate from confined class to unconfined class
c	Transition rate from unconfined class to confined class
ϵ	Efficacy of confinement
γ	Transition rate from exposed class to infectious class
q	Fraction of exposed that become quarantined infectious
σ1	Transition rate from unquaratined class to quarantined class
	and recovered class
σ2	Transition rate from quaratined class to unquarantined,
	hospitalised and recovered class
σ3	Transition rate from hospitalised class to recovered class
r1	Fraction of unquaratined infectious that become quarantined infectious
r2	Fraction of unquaratined infectious that become hospitalised
r3	Fraction of quarantined infectious that become unquarantined infectious
r4	Fraction of quarantined infectious that become hospitalised
δa	Disease-induced death rate, unquarantined infectious
δq	Disease-induced death rate, quarantined infectious
δh	Disease-induced death rate, hospitalised

We set $x={(S,C,E,A,Q,H,R)}^{\prime }$ the vector of state variable, Let $f:{\mathbb{R}}^7\to {\mathbb{R}}^7$ the right hand side of system (2), which is a continuously differentiable function on ${\mathbb{R}}^7$. According to Walter [39, Theorem III.10.VI], for any initial condition in Ω, a unique solution of (2) exists, at least locally, and remains in Ω for its maximal interval of existence [39, Theorem III.10.XVI]. Hence, model (2) is biologically well-defined.

2.1. Positivity and boundedness of solutions

Here, we will prove that all state variables of model (2) are non-negative for all time, i.e, solutions of the model (2) with positive initial data remain positive for all time t > 0. The following result can be obtained.

Lemma 1

Solutions of COVID-19 model (2) with positive initial conditions are positive for all t ≥ 0.

Proof

Assume that $\varphi \left(t\right)=\left(S\right(t),C(t),E(t),A(t),Q(t),H(t),R(t\left)\right)$ is a solution of (2) with positive initial conditions. Let us consider E(t) for t ≥ 0. It follows from the third equation of system (2) that

$$\begin{array}{ccc}& & E\left(t\right)=\hfill \\ & & E\left(0\right)\exp \left[\underset{0}{\overset{t}{\int }}(\beta \frac{A\left(\tau \right)+\eta Q\left(\tau \right)}{N\left(\tau \right)}(S\left(\tau \right)+(1-ϵ)C\left(\tau \right))-\gamma )d\tau \right].\hfill \end{array}$$

Since E(0) ≥ 0, it follows that E(t) ≥ 0 for t ≥ 0. We proceed with the same for A(t), Q(t), H(t) and R(t). Now, it remains to prove that S(t) and C(t) are also positive. Assume the contrary, and let $\overline{t}$ such that $S\left(\overline{t}\right)=0$ and $C\left(\overline{t}\right)\ge 0$. From the first equation of (2), it follows that $\frac{dS\left(t\right)}{dt}{|}_{t=\overline{t}}=pC\left(\overline{t}\right),$ which means that S(t) < 0 for $t\in (\overline{t}-\zeta ,\overline{t})$ with ζ a small positive constant. This leads to a contradiction. Thus S(t) ≥ 0 for t ≥ 0. We proceed with the same to prove that C(t) ≥ 0. □

Lemma 2

Solutions of COVID-19 model (2) with positive initial conditions are bounded by the total population N ₀ .

Proof

Let $N\left(t\right)=S\left(t\right)+C\left(t\right)+E\left(t\right)+A\left(t\right)+Q\left(t\right)+H\left(t\right)+R\left(t\right)$. Thus, in absence of disease, we have

$$\frac{dN\left(t\right)}{dt}=0\iff N\left(t\right)=cte:=N_0$$

where N ₀ is equal to the total population. It follows that for all t ≥ 0, we have S(t) ≤ N ₀, C(t) ≤ N ₀, E(t) ≤ N ₀, A(t) ≤ N ₀, Q(t) ≤ N ₀, H(t) ≤ N ₀ and R(t) ≤ N ₀, with $N\left(t\right)=S\left(t\right)+C\left(t\right)+E\left(t\right)+A\left(t\right)+Q\left(t\right)+H\left(t\right)+R\left(t\right)\le N_0$. □

In what follows, we study the model (2) in the following set

$$\mathcal{D}=\{{(S,C,E,A,Q,H,R)}^{\prime }\in {\mathbb{R}}_{+}^7:S+C+E+A+Q+H+R\le N_0\}$$

which is positively-invariant and attracting region for the model (2).

2.2. The control reproduction number

Now, we define the following manifold, in which any point is a disease-free equilibrium (DFE) of the model (2)

$$\mathcal{W}=\{{(S,C,0,0,0,0,0)}^{\prime }\in \mathbb{R},cS=pC,0<S,C,S+C\le N_0\}.$$ (3)

Note that $\mathcal{W}\subset \mathcal{D}$. In the following, we will work with the largest disease-free equilibrium point denoted by x ₀ (see [14]). Assuming $S+C=N_0,$ it follows that

$$x_0={(S_0,C_0,0,0,0,0,0)}^{\prime }={(\frac{p{N}_0}{p+c},\frac{c{N}_0}{p+c},0,0,0,0,0)}^{\prime }$$

Using notations in [38], matrices $F$ and $V$ for the new infection terms and the remaining transfer terms are, respectively, given by

$$\begin{array}{ccc}\mathrm{F}& =& \left(\begin{array}{ccc}0& \beta \frac{{\mathrm{S}}_0+(1-ϵ){\mathrm{C}}_0}{{\mathrm{N}}_0}& \eta \beta \frac{{\mathrm{S}}_0+(1-ϵ){\mathrm{C}}_0}{{\mathrm{N}}_0}\\ 0& 0& 0\\ 0& 0& 0\end{array}\right),\\ \mathrm{V}& =& \left(\begin{array}{ccc}\gamma & 0& 0\\ -\mathrm{q}\gamma & ({\sigma }_1+{\delta }_{\mathrm{a}})& -{\mathrm{r}}_3{\sigma }_2\\ -(1-\mathrm{q})\gamma & -{\mathrm{r}}_1{\sigma }_1& ({\sigma }_2+{\delta }_{\mathrm{q}})\end{array}\right).\end{array}$$ (4)

Then, the control reproduction ratio is defined, following [38], as the spectral radius of the next generation matrix, $F{V}^{-1}$:

$$\begin{array}{ccc}\hfill {\mathcal{R}}_c& & =\rho \left(F{V}^{-1}\right)=\beta \frac{S_0+(1-ϵ)C_0}{N_0}\hfill \\ & & \times \frac{(r_1{\sigma }_1\eta +({\sigma }_2+{\delta }_q))q+(({\sigma }_1+{\delta }_a)\eta +{\sigma }_2{r}_3)(1-q)}{({\sigma }_1+{\delta }_a)({\sigma }_2+{\delta }_q)-r_1{r}_3{\sigma }_1{\sigma }_2}\hfill \end{array}$$ (5)

where ρ( · ) represents the spectral radius operator.

The formula for control reproduction number has been formulated. Indeed, the insightful epidemic threshold, ${\mathcal{R}}_c$ calculates the average number of new secondary COVID-19 cases generated by a COVID-19 positive individual in a population, where a certain fraction of susceptible people are confined. The control of COVID-19 pandemic is governed by the application of some control measures, which contribute to bring down ${\mathcal{R}}_c$ under unity [38]. Hence, we claim the following result which is a direct consequence of the next generation operator method [38, Theorem 2].

Lemma 3

If ${\mathcal{R}}_c<1,$ the disease-free equilibrium x ₀ is locally asymptotically stable and unstable if ${\mathcal{R}}_c>1$.

Proof

Note the two last equations of the system (2) are uncoupled to the remaining equations of the system. Since the total population, N ₀, is constant, we have $S+C=N_0-(E+A+Q+H+R)$. So, the local stability of the COVID-19 model (2) can be studied through the remaining system of state variables (E, A, Q). Thus, we obtain that the Jacobian matrix associated to these variables is given by

$$\mathcal{J}=\left(\begin{array}{ccc}-\gamma & \beta \frac{(S_0+(1-ϵ)C_0)}{N_0}& \beta \eta \frac{(S_0+(1-ϵ)C_0)}{N_0}\\ q\gamma & -({\sigma }_1+{\delta }_a)& r_3{\sigma }_2\\ (1-q)\gamma & r_1{\sigma }_1& -({\sigma }_2+{\delta }_q)\end{array}\right)$$

The eigenvalues of $\mathcal{J}$ are the roots of the following characteristic polynomial:

$$P_{\mathcal{J}}\left(x\right)=x^3+a_2{x}^2+a_{1}x+a_0,$$

where, $a_2=\gamma +k_2+k_1,$ $a_1=(k_1{k}_2-{\sigma }_1{\sigma }_2{r}_1{r}_3)[\frac{N_0{k}_2+N_0{k}_1}{N_0(k_1{k}_2-{\sigma }_1{\sigma }_2{r}_1{r}_3)}\gamma +1-\gamma \frac{\left(\eta \right(1-q)+q)}{q(k_2+r_1{\sigma }_1\eta )+(1-q)(\eta k_1+r_3{\sigma }_2)}{\mathcal{R}}_c]$ and $a_0=\gamma (k_1{k}_2-r_1{r}_3{\sigma }_1{\sigma }_2)(1-{\mathcal{R}}_{\mathbf{c}})$. Note that a ₂ is always positive. a ₀ and a ₁ are positive provide that ${\mathcal{R}}_c<1$. Thus, it follows that $\mathcal{J}$ has all its eigenvalues with negative real parts. Hence, the disease-free equilibrium, x ₀, is locally asymptotically stable whenever ${\mathcal{R}}_c<1$. □

Remark 1

Lemma 3 implies that if ${\mathcal{R}}_c<1,$ then a sufficiently small flow of infected individuals will not generate an outbreak of COVID-19, whereas for ${\mathcal{R}}_c>1,$ epidemic curve reaches a peak by growing exponentially and then decreases to zero as t → ∞.

The better control of the COVID-19 can be established by the fact that the DFE x ₀ is globally asymptotically stable (GAS). In this context, we claim the following result.

Theorem 1

If ${\mathcal{R}}_c<1,$ then the manifold, $\mathcal{W},$ of disease-free equilibrium points of the model (2) is GAS in $\mathcal{D}$ .

Proof

Assume that ${\mathcal{R}}_c<1$. Let $X={(S,C,R)}^{\prime }$ and $Y={(E,A,Q)}^{\prime }$. Since

$$\frac{S}{N}<1\text{and}\frac{C}{N}<1,$$

we deduce that

$$\begin{array}{cc}f(X,Y)\hfill & =(F-V)Y-\mathcal{F}(X,Y)+\mathcal{V}(X,Y)\hfill \\ & =\left(\begin{array}{c}\beta (A+\eta Q)(1-\frac{S}{N})+(1-ϵ)\beta (A+\eta Q)(1-\frac{C}{N})\\ 0\\ 0\end{array}\right)\hfill \\ & \ge 0_{{\mathbb{R}}^3}\hfill \end{array}$$

where $\mathcal{F}={(\beta (A+\eta Q)\frac{(S+(1-ϵ\left)C\right)}{N},0,0)}^{\prime }$ and $\mathcal{V}=\left(\begin{array}{c}\gamma E\\ -q\gamma E+({\sigma }_1+{\delta }_a)A-r_3{\sigma }_{2}Q\\ -(1-q)\gamma E-r_1{\sigma }_{1}A+({\sigma }_2+{\delta }_q)Q\end{array}\right)$.

Since $\frac{dY}{dt}=(F-V)Y-f(X,Y),$ it follows that

$$\frac{dY}{dt}\le (F-V)Y.$$ (6)

Thus from Van den Driessche and Watmough [38, Theorem 2], it follows that $s(F-V)<0$ if and only if ${\mathcal{R}}_c<1$ where s(M) is the stability modulus of the matrix M. Therefore, the trajectories of the auxiliary system whose right-hand side (6) converges to zero whenever ${\mathcal{R}}_c<1$. Since all the state variables are non-negative and $F-V$ is a Metzler matrix, by the comparison theorem [18], it follows that $\underset{t⟶+\infty }{lim}Y\left(t\right)={(0,0,0)}^{\prime }$. Thus, $\underset{t⟶+\infty }{lim}Y\left(t\right)={(S_{★},C_{★})}^{\prime },$ where $S_{★},C_{★}\in \mathcal{W}$. This shows that $\mathcal{W}$ is an attractive manifold. Moreover, $\mathcal{W}$ is locally asymptotically stable when ${\mathcal{R}}_0<1$. We conclude that in system (2), the manifold $\mathcal{W}$ is globally asymptotically stable when ${\mathcal{R}}_c<1$. □

In the absence of confinement measures, i.e. $ϵ=0,$ ${\mathcal{R}}_c$ converges to the basic reproduction number, ${\mathcal{R}}_0,$ given by

$${\mathcal{R}}_0=\beta \frac{(r_1{\sigma }_1\eta +({\sigma }_2+{\delta }_q))q+(({\sigma }_1+{\delta }_a)\eta +{\sigma }_2{r}_3)(1-q)}{({\sigma }_1+{\delta }_a)({\sigma }_2+{\delta }_q)-r_1{r}_3{\sigma }_1{\sigma }_2}.$$ (7)

Using (5), it follows that

$${\mathcal{R}}_c={\mathcal{R}}_0\left(\frac{S_0+(1-ϵ)C_0}{N_0}\right)={\mathcal{R}}_0\left(\frac{p+(1-ϵ)c}{p+c}\right).$$ (8)

In the next section, numerical simulations have been performed rigorously. Parameters considered in our simulations are either estimated from real data or related to the COVID-19 outbreak data in Cameroon.

3. Model calibration and forecasting

Like in many countries in sub-Saharan Africa, the actual situation of COVID-19 in Cameroon is getting worsened as time progresses. The entire country is struggling with economic recession as the number of COVID-19 cases is surging day by day. With an aim to quell the spread of COVID-19 pandemic, the government of Cameroon has deployed certain control measures such as closures of educational institutions, drinking places and different hangout places. Cameroonian health authorities tried to monitor the pandemic situation in the country closely. Since no non-governmental organization is empowered to carry out tests, the only statistics we have used here to calibrate our model are those communicated by the Cameroonian ministry of public health through daily press briefings [25]. Also, these control measures decreed by the government have really impacted certain economical activity sectors. A lot of people found themselves in technical unemployment due to closures of different hangout places, restaurants and business places. As a consequence, many workers were forced to go out of home in search of some work opportunities, which may allow them to support themselves and their families.

The number of COVID-19 positive cases (NPC) per day, the number of recovered cases (NRC) per day and the number of death cases (NDC) per day in Cameroon, have been taken from the summarized table online on the evolution site of COVID-19 [34], from early March to early July 2020. Time = 0 corresponds to March 7, 2020 and time =124 stands for the day July 08, 2020. As of July 10, 2020, the total death toll is 359, the total number of recovered cases is 11,525 and the total number of positive cases is 14,916 in Cameroon [34].

The model (2) calibration has been performed using a newly developed optimization algorithm based on trust-region-reflective (TRR) algorithm, which can be regarded as an evolution of Levenberg-Marquardt algorithm [26]. This robust optimization procedure can be used effectively for solving nonlinear least-squares problems. This algorithm has been implemented using the lsqcurvefit function, which is available in the Optimization Toolbox in MATLAB. Necessary model parameters have been estimated using this optimization technique. Daily infected cases data have been collected from a trusted data repository, which is available online [34]. A 7-day moving average of the daily reported cases has been used for our model calibration due to highly volatile nature of real data Fig. 2 . It has been observed that the number of daily testing in Cameroon has been really inconsistent. With an aim to capture the real outbreak scenario, the 7-day moving average has been used in this regard. According to recent statistics, the total population of Cameroon is found to be 26,548,238 [34]. For initial conditions, we take $S\left(0\right)=$26,548,237, $C\left(0\right)=E\left(0\right)=A\left(0\right)=H\left(0\right)=R\left(0\right)=0$ and $Q\left(0\right)=1$. The solutions have been obtained after resolving the following optimization problem numerically.

$$\underset{\psi }{min}\parallel (NP{C}_{predict}\left(t\right),NR{C}_{predict}\left(t\right))-(NP{C}_{data},NR{C}_{data})\parallel$$ (9)

where $\psi =\{\beta ,{\sigma }_1,{\sigma }_2,{\sigma }_3,r_1,r_2,r_3,r_4,{\delta }_a,{\delta }_q,{\delta }_h,\eta ,p,c,ϵ,\gamma ,q\},$ is displayed in Table 2

Fig. 2.

Fitting performance of the model for daily infected cases in Cameroon from March 07 to June 26, 2020.

Table 2.

Calibration of the model parameters using a newly developed optimization algorithm based on well-known Trust-region-reflective algorithm.

Parameter	Probable range	base value	TRR output	References
β	0.5–1.5	0.5	0.8646	[9], [21]
σ1	0.001–0.1	0.03	0.0099	[26]
σ2	0.1–0.9	0.3	0.3387	[26]
σ3	0.1–0.9	0.3	0.7	[26]
r1	0.1–0.9	0.5	0.304	Estimated
r2	0.1–0.9	0.5	0.3	Estimated
r3	0.1–0.9	0.5	0.25	Estimated
r4	0.1–0.9	0.5	0.324	Estimated
δa	0.001–0.1	0.01	0.1	[10]
δq	0.001–0.1	0.01	0.08	[10]
δh	0.001–0.1	0.01	0.0999	[10]
η	0.4–0.6	0.5	0.6	[9], [21]
p	0.0005–0.1	0.05	0.001	Estimated
c	0.001–0.1	0.005	0.02	Estimated
ϵ	0.1–0.99	0.7	0.596	Estimated
γ	1/14-1/3	1/5.1	0.2	[9], [21]
q	0.001–0.5	0.2	0.1124	Estimated

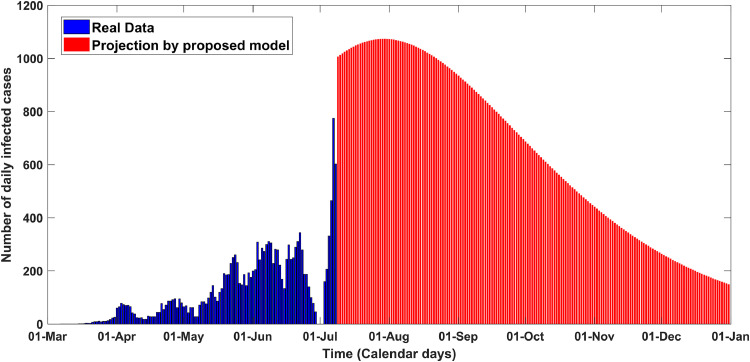
It is evident in Figs. 2 and 3 that the model responses fit really well with the real-time data. According to model projection results, the number of daily confirmed infected cases in Cameroon seems reaching the peak around August 1, with about  ~ 1073 $(95\%CI:714-1654)$ cases Fig. 4 . The epidemic threshold, ${\mathcal{R}}_0$ is estimated about  ~ 3.41 $(95\%CI:2.2-4.4)$ as of July 08, which is consistent $(\sim 2-7)$ with the prior studies of COVID-19 [26]. This crucial epidemiological parameter could surge in coming days due to scant diagnostics and ineffective non-pharmaceutical interventions . The tally of cumulative infected cases has been projected to reach 20,100 $(95\%CI:17,343-24,584)$ Fig. 5 around late August if current trend is maintained, and the estimated death toll could reach 2150 in the end. The epidemic could fade out in the middle of March 2021. The required features used to generate this scenario have been presented in Table 2.

Fig. 3.

Fitting performance of the model for cumulative infected cases in Cameroon from March 07 to July 08, 2020.

Fig. 4.

Daily new reported cases calibrated and projected for Cameroon from early March to late december 2020.

Fig. 5.

Cumulative infected cases fitted and projected for Cameroon early March to late december 2020.

Partial Rank Correlation Coefficient (PRCC) method has been carried out to quantify the most dominant mechanisms, which are significantly responsible for the transmission dynamics of COVID-19. PRCC is a global sensitivity analysis method, which is used to quantify the relationship between model response function (outputs) and model parameters (sampled by Latin Hypercube Sampling method) in an outbreak setting [28]. PRCC values are ranged between −1 and 1. A negative PRCC value indicates a negative correlation between the model output and respective input parameter, whereas a positive PRCC value depicts a positive correlation between response function and corresponding model parameter. As we can see from Fig. 6 , direct infectious contact rate (β) and the efficacy of confinement measures (ϵ) are the most dominant mechanisms that drive the transmission dynamics of COVID-19 disease, while using the unquarantined asymptomatic carriers (A) has been used as the model response function. The PRCC indexes are 0.85 and $-0.695$ respectively. Again, similar result has been found, when the confined infectious individual class (Q) has been used as the model response function Fig. 7 . In this case, the PRCC indexes are estimated to be 0.885 and $-0.69$ accordingly. Importantly, the public health implication of this scenario is that, the transmission dynamics of COVID-19 can be controlled effectively in the community by reducing the direct infectious contact rate and strengthening the confinement measures. Direct transmission rate can be limited by promoting several non-pharmaceutical measures such as maintaining physical distance carefully, wearing face-masks in public places and following health guidelines properly. However, it is often really challenging for the government of a developing country to implement strict confinement policies [27].

Fig. 6.

PRCC analysis of the proposed SCEAQHR model, while using the unquarantined asymptomatic cases as model response function.

Fig. 7.

PRCC analysis of the proposed SCEAQHR model, while using the confirmed infected quarantined individuals as model response function.

4. Fractional-order COVID-19 model

Thanks to the memory effect which represents an advantage of the fractional derivative compared to the ordinary derivative, the theory and the application of fractional calculus have been widely used to model dynamic processes in the fields of science, engineering and many others [3], [4]. Before presenting the fractional model with Caputo derivative, we give the definition of fractional derivative in Caputo sense, and some useful results (see [20]).

4.1. Preliminaries and fractional model

Here, we present definition and some results about Caputo (C) derivative.

Definition 1

The Caputo non- integer order derivative of $g\in C_{-1}^k$ is presented as

$$\begin{array}{ccc}& & D_t^{\alpha }g\left(t\right)=\hfill \\ & & \{\begin{array}{cc}\frac{d^{k}g\left(t\right)}{d{t}^k},& \alpha =k\in \mathbb{N}\\ \frac{1}{\Gamma (k-\alpha )}{\int }_0^t{(t-\vartheta )}^{k-\alpha -1}{g}^{\left(k\right)}\left(\vartheta \right)d\vartheta ,& k-1<\alpha <k,k\in \mathbb{N}.\end{array}\hfill \end{array}$$ (10)

Lemma 4

If 0 < β < 1 and m is an integer (non-negative), then ∃ the $+ve$ constants C _β,1 and C _β,2 only dependent on β, s.t

$${(m+1)}^{\beta }-m^{\beta }\le C_{\beta ,1}{(m+1)}^{\beta -1},$$

and

$${(m+2)}^{\beta +1}-2{(m+1)}^{\beta +1}+m^{\beta +1}\le C_{\beta ,2}{(m+1)}^{\beta -1}.$$

Lemma 5

Let us assume $d_{p,n}={(n-p)}^{\beta -1}(p=1,2,\dots ,n-1)$ $\&$ $d_{p,n}=0$ for p ≥ n, β, M, h, T > 0, mh ≤ T $\&$ m is a $+ve$ integer. Let ${\sum }_{p=m}^{p=n}{d}_{p,n}\left|e_p\right|=0$ for k > n ≥ 1. If

$$|e_n|\le M{h}^{\beta }\sum _{p=1}^{n-1}{d}_{p,n}|e_p|+|{\eta }_0|,n=1,2,\dots ,m,$$

then

$$|e_m|\le C|{\eta }_0|,m=1,2,\dots$$

where C is a $+ve$ constant independent of m $\&$ h.

By Replacing the integer derivative order of the ODE COVID-19 model (2) by the fractional-order model in Caputo sense, we obtain the following fractional model

$$\{\begin{array}{cc}{}_{t_0}^C{D}_t^{\alpha }S\left(t\right)\hfill & =pC\left(t\right)-cS\left(t\right)-\left[\frac{\beta \left(A\right(t)+\eta Q(t\left)\right)}{N\left(t\right)}\right]S\left(t\right),\hfill \\ {}_{t_0}^C{D}_t^{\alpha }C\left(t\right)\hfill & =cS\left(t\right)-pC\left(t\right)-(1-ϵ)\left[\frac{\beta \left(A\right(t)+\eta Q(t\left)\right)}{N\left(t\right)}\right]C\left(t\right),\hfill \\ {}_{t_0}^C{D}_t^{\alpha }E\left(t\right)\hfill & =\left[\frac{\beta \left(A\right(t)+\eta Q(t\left)\right)}{N\left(t\right)}\right]\left[S\right(t)+(1-ϵ\left)C\right(t\left)\right]-\gamma E\left(t\right),\hfill \\ {}_{t_0}^C{D}_t^{\alpha }A\left(t\right)\hfill & =q\gamma E\left(t\right)+r_3{\sigma }_{2}Q\left(t\right)-({\sigma }_1+{\delta }_a)A\left(t\right),\hfill \\ {}_{t_0}^C{D}_t^{\alpha }Q\left(t\right)\hfill & =(1-q)\gamma E\left(t\right)+r_1{\sigma }_{1}A\left(t\right)+({\sigma }_2+{\delta }_q)Q\left(t\right)\hfill \\ {}_{t_0}^C{D}_t^{\alpha }H\left(t\right)\hfill & =r_2{\sigma }_{1}A\left(t\right)+r_4{\sigma }_{2}Q\left(t\right)-({\sigma }_3+{\delta }_h)H\left(t\right)\hfill \\ {}_{t_0}^C{D}_t^{\alpha }R\left(t\right)\hfill & =(1-r_1-r_2){\sigma }_{1}A\left(t\right)+(1-r_3-r_4){\sigma }_{2}Q\left(t\right)+{\sigma }_{3}H\left(t\right)\hfill \end{array}$$ (11)

4.2. Existence and uniqueness analysis

In this portion of the study, we will provide the existence of the unique solution for the proposed fractional-order model under the Caputo fractional operator by applying fixed-point results. In this setting, $\mathcal{B}$ is the Banach space of real-valued continuous functions defined on an interval $\mathcal{I}$ with the associated norm

$$\begin{array}{ccc}\hfill \parallel (S,C,E,A,Q,H,R)\parallel & & =\parallel S\parallel +\parallel C\parallel +\parallel E\parallel +\parallel A\parallel \hfill \\ & & +\parallel Q\parallel +\parallel H\parallel +\parallel R\parallel ,\hfill \end{array}$$

where $\parallel S\parallel =sup\left\{\right|S\left(t\right)|:t\in \mathcal{I}\},\parallel C\parallel =sup\left\{\right|C\left(t\right)|:t\in \mathcal{I}\},\parallel E\parallel =sup\left\{\right|E\left(t\right)|:t\in \mathcal{I}\},\parallel A\parallel =sup\left\{\right|A\left(t\right)|:t\in \mathcal{I}\},\parallel Q\parallel =sup\left\{\right|Q\left(t\right)|:t\in \mathcal{I}\},$ $\parallel H\parallel =\sup \left\{\right|H\left(t\right)|:t\in \mathcal{I}\},$ $\parallel R\parallel =\sup \left\{\right|R\left(t\right)|:t\in \mathcal{I}\},$ and $\mathcal{B}=\mathcal{E}\left(\mathcal{I}\right)\times \mathcal{E}\left(\mathcal{I}\right)\times \mathcal{E}\left(\mathcal{I}\right)\times \mathcal{E}\left(\mathcal{I}\right)\times \mathcal{E}\left(\mathcal{I}\right)\times \mathcal{E}\left(\mathcal{I}\right)\times \mathcal{E}\left(\mathcal{I}\right),$ with $\mathcal{E}\left(\mathcal{I}\right)$ denotes the Banach space of real-valued continuous functions on $\mathcal{I}$ and the associated sup norm. For convenience the proposed system (11) can be rewritten in the equivalent form given below.

$$\begin{array}{cc}& {}^C{D}_t^{\alpha }S\left(t\right)=G_1(t,S),\hfill \\ & {}^C{D}_t^{\alpha }C\left(t\right)=G_2(t,C),\hfill \\ & {}^C{D}_t^{\alpha }E\left(t\right)=G_3(t,E),\hfill \\ & {}^C{D}_t^{\alpha }A\left(t\right)=G_4(t,A)\hfill \\ & {}^C{D}_t^{\alpha }Q\left(t\right)=G_5(t,Q)\hfill \\ & {}^C{D}_t^{\alpha }H\left(t\right)=G_6(t,H)\hfill \\ & {}^C{D}_t^{\alpha }R\left(t\right)=G_7(t,R)\hfill \end{array}$$ (12)

By applying the Caputo fractional integral operator, the above system (12), reduces to the following integral equation of Volterra type with the Caputo fractional integral of order 0 < α < 1.

$$\begin{array}{cc}& S\left(t\right)-S\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}{G}_1(\chi ,S)d\chi ,\hfill \\ & C\left(t\right)-C\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}{G}_2(\chi ,C)d\chi ,\hfill \\ & E\left(t\right)-E\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}{G}_3(\chi ,E)d\chi ,\hfill \\ & A\left(t\right)-A\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}{G}_4(\chi ,A)d\chi ,\hfill \\ & Q\left(t\right)-Q\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}{G}_5(\chi ,Q)d\chi ,\hfill \\ & H\left(t\right)-H\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}{G}_6(\chi ,H)d\chi ,\hfill \\ & R\left(t\right)-R\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}{G}_7(\chi ,R)d\chi ,\hfill \end{array}$$ (13)

Now we prove that the kernels G ₁; G ₂; G ₃; G ₄; G ₅; G ₆  and  G ₇ fulfil the Lipschitz condition and contraction under some assumptions. In the following theorem, we have proved for G ₁ and can proceeds for the rest in a similar patron.

Theorem 2

Let us consider the following inequality

$$0\le \beta (k_1+\eta k_2)+c<1.$$

The kernel G ₁ satisfies the Lipschitz condition as well as contraction if the above inequality is satisfied.

Proof

For S and S ₁ we proceed as below:

$$\begin{array}{cc}\parallel G_1(t,S)-G_1(t,S_1)\parallel \hfill & =\parallel -c(S-S_1)-\left[\frac{\beta \left(A\right(t)+\eta Q(t\left)\right)}{N\left(t\right)}\right](S-S_1)\parallel \hfill \\ & \le c\parallel S-S_1\parallel +\parallel \left[\frac{\beta \left(A\right(t)+\eta Q(t\left)\right)}{N\left(t\right)}\right](S-S_1)\parallel \hfill \\ & \le c\parallel S-S_1\parallel +\parallel \beta (\parallel A\left(t\right)\parallel \hfill \\ & +\eta \parallel Q\left(t\right)\parallel )\parallel (S-S_1)\parallel \hfill \end{array}$$

Since A(t) and Q(t) are bounded functions, i.e, ∥A(t)∥ ≤ k ₁ and ∥Q(t)∥ ≤ k ₂, by the property of norm function, above inequality can be written as

$$\begin{array}{cc}\parallel G_1(t,S)-G_1(t,S_1)\parallel \hfill & \le c\parallel S-S_1\parallel +\parallel \beta (\parallel A\left(t\right)\parallel \hfill \\ & +\eta \parallel Q\left(t\right)\parallel )\parallel (S-S_1)\parallel \hfill \\ & \le \{\beta (k_1+\eta k_2)+c\}\parallel S\left(t\right)-S\left(t_1\right)\parallel \hfill \\ & \le V_1\parallel S\left(t\right)-S\left(t_1\right)\parallel .\hfill \end{array}$$

Here $V_1=\{\beta (k_1+\eta k_2)+c\}$ which implies that

$$\parallel G_1(t,S)-G_1(t,S_1)\parallel \le V_1\parallel S\left(t\right)-S\left(t_1\right)\parallel .$$ (14)

Hence, for G ₁ the Lipschitz condition is obtained and if an additionally $0\le \beta (k_1+\eta k_2)+c<1,$ we obtain a contraction. The Lipschitz condition can be easily verified for the rest of the cases and given as follows:

$$\begin{array}{cc}& \parallel G_2(t,C)-G_2(t,C_1)\parallel \le V_2\parallel C\left(t\right)-C\left(t_1\right)\parallel ,\hfill \\ & \parallel G_3(t,E)-G_3(t,E_1)\parallel \le V_3\parallel E\left(t\right)-E\left(t_1\right)\parallel ,\hfill \\ & \parallel G_4(t,A)-G_4(t,A_1)\parallel \le V_4\parallel A\left(t\right)-A\left(t_1\right)\parallel ,\hfill \\ & \parallel G_5(t,Q)-G_5(t,Q_1)\parallel \le V_5\parallel Q\left(t\right)-Q\left(t_1\right)\parallel ,\hfill \\ & \parallel G_6(t,H)-G_6(t,H_1)\parallel \le V_6\parallel H\left(t\right)-H\left(t_1\right)\parallel ,\hfill \\ & \parallel G_7(t,R)-G_7(t,R_1)\parallel \le V_7\parallel R\left(t\right)-R\left(t_1\right)\parallel ,\hfill \end{array}$$ (15)

 □

Recursively, the expressions in (13) can be written as

$$\begin{array}{cc}& S_n\left(t\right)-S\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}{G}_1(\chi ,S_{n-1})d\chi ,\hfill \\ & C_n\left(t\right)-C\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}{G}_2(\chi ,C_{n-1})d\chi ,\hfill \\ & E_n\left(t\right)-E\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}{G}_3(\chi ,E_{n-1})d\chi ,\hfill \\ & A_n\left(t\right)-A\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}{G}_4(\chi ,A_{n-1})d\chi ,\hfill \\ & Q_n\left(t\right)-Q\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}{G}_5(\chi ,Q_{n-1})d\chi ,\hfill \\ & H_n\left(t\right)-H\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}{G}_6(\chi ,H_{n-1})d\chi ,\hfill \\ & R_n\left(t\right)-R\left(0\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}{G}_7(\chi ,R_{n-1})d\chi ,\hfill \end{array}$$ (16)

The difference between successive terms of system (12) in recursive form is given below:

$$\begin{array}{cc}{\varphi }_{1n}\left(t\right)\hfill & =S_n\left(t\right)-S_{n-1}\left(t\right)\hfill \\ & =\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}(G_1(\chi ,S_{n-1})-G_1(\chi ,S_{n-2}))d\chi ,\hfill \\ {\varphi }_{2n}\left(t\right)\hfill & =C_n\left(t\right)-C_{n-1}\left(t\right)\hfill \\ & =\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}(G_2(\chi ,C_{n-1})-G_2(\chi ,C_{n-2}))d\chi ,\hfill \\ {\varphi }_{3n}\left(t\right)\hfill & =E_n\left(t\right)-E_{n-1}\left(t\right)\hfill \\ & =\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}(G_3(\chi ,E_{n-1})-G_3(\chi ,E_{n-2}))d\chi ,\hfill \\ {\varphi }_{4n}\left(t\right)\hfill & =A_n\left(t\right)-A_{n-1}\left(t\right)\hfill \\ & =\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}(G_4(\chi ,A_{n-1})-G_4(\chi ,A_{n-2}))d\chi ,\hfill \\ {\varphi }_{5n}\left(t\right)\hfill & =Q_n\left(t\right)-Q_{n-1}\left(t\right)\hfill \\ & =\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}(G_5(\chi ,Q_{n-1})-G_5(\chi ,Q_{n-2}))d\chi ,\hfill \\ {\varphi }_{6n}\left(t\right)\hfill & =H_n\left(t\right)-H_{n-1}\left(t\right)\hfill \\ & =\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}(G_6(\chi ,H_{n-1})-G_6(\chi ,H_{n-2}))d\chi ,\hfill \\ {\varphi }_{7n}\left(t\right)\hfill & =R_n\left(t\right)-R_{n-1}\left(t\right)\hfill \\ & =\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}(G_7(\chi ,R_{n-1})-G_7(\chi ,R_{n-2}))d\chi ,\hfill \end{array}$$ (17)

With below initial conditions $S_0\left(t\right)=S\left(0\right),$ $C_0\left(t\right)=C\left(0\right),$ $E_0\left(t\right)=E\left(0\right),$ $A_0\left(t\right)=A\left(0\right),$ $Q_0\left(t\right)=Q\left(0\right),$ $H_0\left(t\right)=H\left(0\right),$ and $R_0\left(t\right)=R\left(0\right)$.

Taking norm of the first equation of (17), we obtain

$$\begin{array}{cc}\parallel {\varphi }_{1n}\left(t\right)\parallel =\parallel S_n\left(t\right)-S_{n-1}\left(t\right)\parallel \hfill & =\parallel \frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-\chi )}^{\alpha -1}(G_1(\chi ,S_{n-1})\hfill \\ & -G_1(\chi ,S_{n-2}))d\chi \parallel .\hfill \\ & \le \frac{1}{\Gamma \left(\alpha \right)}\parallel {\int }_0^t{(t-\chi )}^{\alpha -1}(G_1(\chi ,S_{n-1})\hfill \\ & -G_1(\chi ,S_{n-2}))d\chi \parallel \hfill \end{array}$$ (18)

Using Lipschitz condition (14) we obtained

$$\parallel S_n\left(t\right)-S_{n-1}\left(t\right)\parallel \le \frac{1}{\Gamma \left(\alpha \right)}{V}_1{\int }_0^t{(t-\chi )}^{\alpha -1}\parallel S_{n-1}-S_{n-2}\parallel d\chi .$$ (19)

Thus, we have

$$\parallel {\varphi }_{1n}\left(t\right)\parallel \le \frac{1}{\Gamma \left(\alpha \right)}{V}_1{\int }_0^t{(t-\chi )}^{\alpha -1}\parallel {\varphi }_{1(n-1)}\left(\chi \right)\parallel d\chi .$$ (20)

Similarly, for the rest of equations in system (12) we obtained

$$\begin{array}{c}\parallel {\varphi }_{2n}\left(t\right)\parallel \le \frac{1}{\Gamma \left(\alpha \right)}{V}_2{\int }_0^t{(t-\chi )}^{\alpha -1}\parallel {\varphi }_{2(n-1)}\left(\chi \right)\parallel d\chi ,\hfill \\ \parallel {\varphi }_{3n}\left(t\right)\parallel \le \frac{1}{\Gamma \left(\alpha \right)}{V}_3{\int }_0^t{(t-\chi )}^{\alpha -1}\parallel {\varphi }_{3(n-1)}\left(\chi \right)\parallel d\chi ,\hfill \\ \parallel {\varphi }_{4n}\left(t\right)\parallel \le \frac{1}{\Gamma \left(\alpha \right)}{V}_4{\int }_0^t{(t-\chi )}^{\alpha -1}\parallel {\varphi }_{4(n-1)}\left(\chi \right)\parallel d\chi ,\hfill \\ \parallel {\varphi }_{5n}\left(t\right)\parallel \le \frac{1}{\Gamma \left(\alpha \right)}{V}_5{\int }_0^t{(t-\chi )}^{\alpha -1}\parallel {\varphi }_{5(n-1)}\left(\chi \right)\parallel d\chi ,\hfill \\ \parallel {\varphi }_{6n}\left(t\right)\parallel \le \frac{1}{\Gamma \left(\alpha \right)}{V}_6{\int }_0^t{(t-\chi )}^{\alpha -1}\parallel {\varphi }_{6(n-1)}\left(\chi \right)\parallel d\chi ,\hfill \\ \parallel {\varphi }_{7n}\left(t\right)\parallel \le \frac{1}{\Gamma \left(\alpha \right)}{V}_7{\int }_0^t{(t-\chi )}^{\alpha -1}\parallel {\varphi }_{7(n-1)}\left(\chi \right)\parallel d\chi .\hfill \end{array}$$ (21)

From above we can write that

$$\{\begin{array}{c}{S}_n\left(t\right)=\sum _{i=1}^n{\varphi }_{1i}\left(t\right),\hfill \\ C_n\left(t\right)=\sum _{i=1}^n{\varphi }_{2i}\left(t\right),\hfill \\ E_n\left(t\right)=\sum _{i=1}^n{\varphi }_{3i}\left(t\right),\hfill \\ A_n\left(t\right)=\sum _{i=1}^n{\varphi }_{4i}\left(t\right),\hfill \\ Q_n\left(t\right)=\sum _{i=1}^n{\varphi }_{5i}\left(t\right),\hfill \\ H_n\left(t\right)=\sum _{i=1}^n{\varphi }_{6i}\left(t\right),\hfill \\ R_n\left(t\right)=\sum _{i=1}^n{\varphi }_{7i}\left(t\right).\hfill \end{array}$$ (22)

Now, we claim the following result which guaranteed the uniqueness of solution of model (12).

Theorem 3

The proposed fractional epidemic model (12) has a unique solution for t ∈ [0, T] if the following inequality holds

$$\frac{1}{\Gamma \left(\alpha \right)}{b}^{\alpha }{V}_i<1,\text{for}i=1,2,\dots ,7.$$ (23)

Proof

As we have shown that the kernels condition given in (14) holds. So, by considering the Eqs. (20) and (29), and by applying the recursive technique we obtained the succeeding results as below:

$$\begin{array}{cc}\parallel {\varphi }_{1n}\left(t\right)\parallel \le \parallel S_0\left(t\right)\parallel {\left[\frac{1}{\Gamma \left(\alpha \right)}{V}_1{b}^{\alpha }\right]}^n,\hfill & \parallel {\varphi }_{2n}\left(t\right)\parallel \le \parallel C_0\left(t\right)\parallel {\left[\frac{1}{\Gamma \left(\alpha \right)}{V}_2{b}^{\alpha }\right]}^n,\hfill \\ \parallel {\varphi }_{3n}\left(t\right)\parallel \le \parallel E_0\left(t\right)\parallel {\left[\frac{1}{\Gamma \left(\alpha \right)}{V}_3{b}^{\alpha }\right]}^n,\hfill & \parallel {\varphi }_{4n}\left(t\right)\parallel \le \parallel A_0\left(t\right)\parallel {\left[\frac{1}{\Gamma \left(\alpha \right)}{V}_4{b}^{\alpha }\right]}^n,\hfill \\ \parallel {\varphi }_{5n}\left(t\right)\parallel \le \parallel Q_0\left(t\right)\parallel {\left[\frac{1}{\Gamma \left(\alpha \right)}{V}_5{b}^{\alpha }\right]}^n,\hfill & \parallel {\varphi }_{6n}\left(t\right)\parallel \le \parallel H_0\left(t\right)\parallel {\left[\frac{1}{\Gamma \left(\alpha \right)}{V}_6{b}^{\alpha }\right]}^n,\hfill \\ \parallel {\varphi }_{7n}\left(t\right)\parallel \le \parallel R_0\left(t\right)\parallel {\left[\frac{1}{\Gamma \left(\alpha \right)}{V}_7{b}^{\alpha }\right]}^n\hfill & .\hfill \end{array}$$ (24)

Therefore, the above mentioned sequences exist and satisfy ∥ϕ _1n(t)∥ → 0, ∥ϕ _2n(t)∥ → 0, ∥ϕ _3n(t)∥ → 0, ∥ϕ _4n(t)∥ → 0, ∥ϕ _5n(t)∥ → 0, ∥ϕ _6n(t)∥ → 0, ∥ϕ _7n(t)∥ → 0 as  n → ∞. Furthermore, from Eq. (24) and employing the triangle inequality for any k, we obtain

$$\begin{array}{cc}& \parallel S_{n+k}\left(t\right)-S_n\left(t\right)\parallel \le \sum _{j=n+1}^{n+k}{T}_1^j=\frac{T_1^{n+1}-T_1^{n+k+1}}{1-T_1},\hfill \\ & \parallel C_{n+k}\left(t\right)-C_n\left(t\right)\parallel \le \sum _{j=n+1}^{n+k}{T}_2^j=\frac{T_2^{n+1}-T_2^{n+k+1}}{1-T_2},\hfill \\ & \parallel E_{n+k}\left(t\right)-E_n\left(t\right)\parallel \le \sum _{j=n+1}^{n+k}{T}_3^j=\frac{T_3^{n+1}-T_3^{n+k+1}}{1-T_3},\hfill \\ & \parallel A_{n+k}\left(t\right)-A_n\left(t\right)\parallel \le \sum _{j=n+1}^{n+k}{T}_4^j=\frac{T_4^{n+1}-T_4^{n+k+1}}{1-T_4},\hfill \\ & \parallel Q_{n+k}\left(t\right)-Q_n\left(t\right)\parallel \le \sum _{j=n+1}^{n+k}{T}_5^j=\frac{T_5^{n+1}-T_5^{n+k+1}}{1-T_5},\hfill \\ & \parallel H_{n+k}\left(t\right)-H_n\left(t\right)\parallel \le \sum _{j=n+1}^{n+k}{T}_6^j=\frac{T_6^{n+1}-T_6^{n+k+1}}{1-T_6},\hfill \\ & \parallel R_{n+k}\left(t\right)-R_n\left(t\right)\parallel \le \sum _{j=n+1}^{n+k}{T}_7^j=\frac{T_7^{n+1}-T_7^{n+k+1}}{1-T_7},\hfill \end{array}$$ (25)

where $\frac{1}{\Gamma \left(\alpha \right)}{b}^{\alpha }{V}_i<1$ by assertion and $T_i=\left[\frac{1}{\Gamma \left(\alpha \right)}{V}_i{b}^{\alpha }\right]{}^n,$ $i=1,2,\dots ,7$.

Therefore, S_n, C_n, E_n, A_n, Q_n, H_n, R_n are regarded as the Cauchy sequence in G(J). Hence, they are uniformly convergent as described in [20]. Applying the limit theory on Eq. (16) when n → ∞ indicates that the limit of these sequences is the unique solution of the model (12). Ultimately, the existence of a unique solution for (12) has been achieved. □

4.3. Numerical analysis for Caputo fractional derivative

4.3.1. Solution of the projected model

In view of the fact that most of the fractional differential equations (FDEs) do not have exact analytic solutions, so approximation and numerical techniques must be employed. Numerous analytical and numerical methods have been put up to solve the FDEs. For numerical solutions of the system (11), one can apply the generalized Adams-Bashforth-Moulton method. To provide the exact solution by means of this algorithm, we take into account the following nonlinear fractional differential equation [19]:

$$\{\begin{array}{ccc}{D}_t^{\alpha }h\left(t\right)\hfill & =g(t,h(t\left)\right),\hfill & 0\le t\le T,\hfill \\ h^{\left(k\right)}\left(0\right)\hfill & =h_0^k,\hfill & k=0,1,2,\dots ,m-1,wherem=\left[\alpha \right].\hfill \end{array}$$ (26)

This equation is equivalent to Volterra integral equation:

$$h\left(t\right)=\sum _{k=0}^{m-1}{h}_0^k\frac{t^k}{k!}+\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^t{(t-s)}^{\alpha -1}g(s,h\left(s\right))ds$$ (27)

Diethelm and Neville [7] employed the predictor-correctors scheme based on the Adams-Bashforth-Moulton algorithm [6]. So we use again this same technique to find the solution of the projected model (11).

For α ∈ [0, 1], 0 ≤ t ≤ T and setting $h=T/N$ and $t_n=nh,$ for $n=0,1,2,\dots ,N\in Z^{+},$ the solution of the projected model is

$$\begin{array}{cc}{S}_{n+1}\hfill & =S_0+\frac{h^{\alpha }}{\Gamma (\alpha +2)}(p{C}_{n+1}^P-c{S}_{n+1}^P-\left[\frac{\beta (A_{n+1}^P+\eta Q_{n+1}^P)}{N}\right]S_{n+1}^P)\hfill \\ & +\frac{h^{\alpha }}{\Gamma (\alpha +2)}\sum _{j=0}^n{a}_{j,n+1}(p{C}_j-c{S}_j-\left[\frac{\beta (A_j+\eta Q_j)}{N}\right]S_j),\hfill \\ C_{n+1}\hfill & =C_0+\frac{h^{\alpha }}{\Gamma (\alpha +2)}(-p{C}_{n+1}^P+c{S}_{n+1}^P-(1-ϵ)\left[\frac{\beta (A_{n+1}^P+\eta Q_{n+1}^P)}{N}\right]C_{n+1}^P)\hfill \\ & +\frac{h^{\alpha }}{\Gamma (\alpha +2)}\sum _{j=0}^n{a}_{j,n+1}(-p{C}_j+c{S}_j-(1-ϵ)\left[\frac{\beta (A_j+\eta Q_j)}{N}\right]C_j),\hfill \\ E_{n+1}\hfill & =E_0+\frac{h^{\alpha }}{\Gamma (\alpha +2)}(\left[\frac{\beta (A_{n+1}^P+\eta Q_{n+1}^P)}{N}\right][S_{n+1}^P+(1-ϵ)C_{n+1}^P]-\gamma E_{n+1}^P)\hfill \\ & +\frac{h^{\alpha }}{\Gamma (\alpha +2)}\sum _{j=0}^n{a}_{j,n+1}(\left[\frac{\beta (A_j+\eta Q_j)}{N}\right][S_j+(1-ϵ)C_j]-\gamma E_j),\hfill \\ A_{n+1}\hfill & =A_0+\frac{h^{\alpha }}{\Gamma (\alpha +2)}(q\gamma E_{n+1}^P+r_3{\sigma }_2{Q}_{n+1}^P-({\sigma }_1+{\delta }_a)A_{n+1}^P)\hfill \\ & +\frac{h^{\alpha }}{\Gamma (\alpha +2)}\sum _{j=0}^n{a}_{j,n+1}(q\gamma E_j+r_3{\sigma }_2{Q}_j-({\sigma }_1+{\delta }_a)A_j),\hfill \\ Q_{n+1}\hfill & =Q_0+\frac{h^{\alpha }}{\Gamma (\alpha +2)}((1-q)\gamma E_{n+1}^P+r_1{\sigma }_1{A}_{n+1}^P+({\sigma }_2+{\delta }_q)Q_{n+1}^P)\hfill \\ & +\frac{h^{\alpha }}{\Gamma (\alpha +2)}\sum _{j=0}^n{a}_{j,n+1}((1-q)\gamma E_j+r_1{\sigma }_1{A}_j+({\sigma }_2+{\delta }_q)Q_j),\hfill \\ H_{n+1}\hfill & =H_0+\frac{h^{\alpha }}{\Gamma (\alpha +2)}(r_2{\sigma }_1{A}_{n+1}^P+r_4{\sigma }_2{Q}_{n+1}^P-({\sigma }_3+{\delta }_h)H_{n+1}^P)\hfill \\ & +\frac{h^{\alpha }}{\Gamma (\alpha +2)}\sum _{j=0}^n{a}_{j,n+1}(r_2{\sigma }_1{A}_j+r_4{\sigma }_2{Q}_j-({\sigma }_3+{\delta }_h)H_j),\hfill \\ R_{n+1}\hfill & =R_0+\frac{h^{\alpha }}{\Gamma (\alpha +2)}\hfill \\ & \times ((1-r_1-r_2){\sigma }_1{A}_{n+1}^P+(1-r_3-r_4){\sigma }_2{Q}_{n+1}^P+{\sigma }_3{H}_{n+1}^P)\hfill \\ & +\frac{h^{\alpha }}{\Gamma (\alpha +2)}\sum _{j=0}^n{a}_{j,n+1}\hfill \\ & \times ((1-r_1-r_2){\sigma }_1{A}_j+(1-r_3-r_4){\sigma }_2{Q}_j+{\sigma }_3{H}_j),\hfill \end{array}$$ (28)

where

$$\begin{array}{cc}{S}_{n+1}^P\hfill & =S_0+\frac{1}{\Gamma \left(\alpha \right)}\sum _{j=0}^n{b}_{j,n+1}(p{C}_j-c{S}_j-\left[\frac{\beta (A_j+\eta Q_j)}{N}\right]S_j),\hfill \\ C_{n+1}^P\hfill & =C_0+\frac{1}{\Gamma \left(\alpha \right)}\sum _{j=0}^n{b}_{j,n+1}(-p{C}_j+c{S}_j-(1-ϵ)\left[\frac{\beta (A_j+\eta Q_j)}{N}\right]C_j),\hfill \\ E_{n+1}^P\hfill & =E_0+\frac{1}{\Gamma \left(\alpha \right)}\sum _{j=0}^n{b}_{j,n+1}(\left[\frac{\beta (A_j+\eta Q_j)}{N}\right][S_j+(1-ϵ)C_j]-\gamma E_j),\hfill \\ A_{n+1}^P\hfill & =A_0+\frac{1}{\Gamma \left(\alpha \right)}\sum _{j=0}^n{b}_{j,n+1}(q\gamma E_j+r_3{\sigma }_2{Q}_j-({\sigma }_1+{\delta }_a)A_j),\hfill \\ Q_{n+1}^P\hfill & =Q_0+\frac{1}{\Gamma \left(\alpha \right)}\sum _{j=0}^n{b}_{j,n+1}((1-q)\gamma E_j+r_1{\sigma }_1{A}_j+({\sigma }_2+{\delta }_q)Q_j),\hfill \\ H_{n+1}^P\hfill & =H_0+\frac{1}{\Gamma \left(\alpha \right)}\sum _{j=0}^n{b}_{j,n+1}(r_2{\sigma }_1{A}_j+r_4{\sigma }_2{Q}_j-({\sigma }_3+{\delta }_h)H_j),\hfill \\ R_{n+1}^P\hfill & =R_0+\frac{1}{\Gamma \left(\alpha \right)}\sum _{j=0}^n{b}_{j,n+1}\hfill \\ & \times ((1-r_1-r_2){\sigma }_1{A}_j+(1-r_3-r_4){\sigma }_2{Q}_j+{\sigma }_3{H}_j),\hfill \end{array}$$ (29)

and

$$\begin{array}{c}\hfill a_{j,n+1}=\{\begin{array}{c}{n}^{\alpha +1}-(n-\alpha )(n+1),j=0,\hfill \\ {(n-j+2)}^{\alpha +1}-2{(n-j+1)}^{\alpha +1}+{(n-j)}^{\alpha +1}1\le j\le n,\hfill \\ 1,j=n+1,\hfill \end{array}\end{array}$$

$$b_{j,n+1}=\frac{h^{\alpha }}{\alpha }({(n-j+1)}^{\alpha }-{(n-j)}^{\alpha }),0\le j\le n.$$

4.3.2. Stability analysis

Theorem 4

The numerical method (28) - (29) is conditionally stable.

Proof

Let $\widetilde{S_0},\widetilde{S_j}(j=0,\dots ,n+1)$ and ${\tilde{S}}_{n+1}^P(n=0,\dots ,N-1)$ be perturbations of $S_0,S_{j}and{S}_{n+1}^P,$ respectively. Then, the following perturbation equations are obtained by using Eqs. (20) and (29)

$${\tilde{S}}_{n+1}^P=\widetilde{S_0}+\frac{1}{\Gamma \left(\alpha \right)}\sum _{j=0}^n{b}_{j,n+1}(G_1(t_j,S_j+\widetilde{S_j})-G_1(t_j,S_j)),$$ (30)

$$\begin{array}{c}{\tilde{S}}_{n+1}=\widetilde{S_0}+\frac{h^{\alpha }}{\Gamma (\alpha +2)}(G_1(t_{n+1},S_{n+1}^P+{\tilde{S}}_{n+1}^P)-G_1(t_{n+1},S_{n+1}^P))\hfill \\ +\frac{h^{\alpha }}{\Gamma (\alpha +2)}\sum _{j=0}^n{a}_{j,n+1}(G_1(t_j,S_j+{\tilde{S}}_j)-G_1(t_j,S_j)),\hfill \end{array}$$ (31)

Using the Lipschitz condition, we obtain

$$|{\tilde{S}}_{n+1}|\le {\zeta }_0+\frac{h^{\alpha }M}{\Gamma (\alpha +2)}\left(\right|{\tilde{S}}_{n+1}^P|+\sum _{j=1}^n{a}_{j,n+1}\left|{\tilde{S}}_j\right|),$$ (32)

where ${\zeta }_0={\max }_{0\le n\le N}\left\{\right|\widetilde{S_0}|+\frac{h^{\alpha }M{a}_{n,0}}{\Gamma (\alpha +2)}|\widetilde{S_0}\left|\right\}.$ Also, from Eq. (3.18) in [20] we derive

$$|{\tilde{S}}_{n+1}^P|\le {\eta }_0+\frac{M}{\Gamma \left(\alpha \right)}\sum _{j=1}^n{b}_{j,n+1}\left|{\tilde{S}}_j\right|,$$ (33)

where ${\eta }_0={\max }_{0\le n\le N}\left\{\right|{\tilde{S}}_0|+\frac{M{b}_{n,0}}{\Gamma \left(\alpha \right)}|{\tilde{S}}_0\left|\right\}.$ Substituting $|{\tilde{S}}_{n+1}^P|$ from Eq. (33) into Eq. (32) results

$$\begin{array}{cc}|{\tilde{S}}_{n+1}|\hfill & \le {\gamma }_0+\frac{h^{\alpha }M}{\Gamma (\alpha +2)}\left(\frac{M}{\Gamma \left(\alpha \right)}\sum _{j=1}^n{b}_{j,n+1}|{\tilde{S}}_j|+\sum _{j=1}^n{a}_{j,n+1}\left|{\tilde{S}}_j\right|\right)\hfill \\ & \le {\gamma }_0+\frac{h^{\alpha }M}{\Gamma (\alpha +2)}\sum _{j=1}^n(\frac{M}{\Gamma \left(\alpha \right)}{b}_{j,n+1}+a_{j,n+1})\left|\widetilde{S_j}\right|\hfill \\ & \le {\gamma }_0+\frac{h^{\alpha }M{C}_{\alpha ,2}}{\Gamma (\alpha +2)}\sum _{j=1}^n{(n+1-j)}^{\alpha -1}\left|\widetilde{S_j}\right|,\hfill \end{array}$$ (34)

where ${\gamma }_0=\max \{{\zeta }_0+\frac{h^{\alpha }M{a}_{n+1,n+1}}{\Gamma (\alpha +2)}{\eta }_0\}.$ C _α,2 is a positive constant only depends on α (Lemma 4) and h is assumed to be small enough. Applying Lemma 2 concludes $|{\tilde{S}}_{n+1}|\le C{\gamma }_0.$ which completes the proof. □

4.3.3. Simulation results

By replacing the integer order model with the fractional order model, we have studied the real-time Cameroonian data. The advantage of using Caputo fractional derivative to study the current real-time data is to predict the epidemic peaks more clearly at different fractional order values α. Parameter values use here are found in Table 2, and for which the basic reproduction number, ${\mathcal{R}}_0$ is equal to 3.41. For initials conditions, we take $S\left(0\right)=26548238,$ $C\left(0\right)=E\left(0\right)=A\left(0\right)=H\left(0\right)=R\left(0\right)=0,$ $Q\left(0\right)=1,$ and a fixed time step size of $h=2^{-8}$. The value of the fractional-order derivatives are $\alpha =1,0.9,0.8,0.7,0.6,0.5$.

Firstly, figures have been analysed at integer order (denoted by red line) for the given model and then we analyse the nature of the compartmental model at different fractional values to give more peak predictions for the real-time data. It has been observed that onset of the epidemic peaks is delayed, when the value of order α decreases. In Figs. 8 and 9 , one can see that when $\alpha ⟶1$ the solutions of our fractional model (11) converge to the solutions of the integer model (2). From above simulations, it can be conveyed that there are so much uncertainties of epidemic peaks for the given real-time data range. Caputo derivative works well to study these biological phenomenons. Robust forecasting results of COVID-19 outbreak can be achieved by applying our model structure as imperfect quarantine and unsound confinement which are the harsh realities in developing countries have been taken into account meticulously.

Fig. 8.

Numerical simulation of the Caputo COVID-19 model (11) with values as in Table 2.

Fig. 9.

Numerical simulation of the Caputo COVID-19 model (11) with values as in Table 2.

5. Conclusion

A compartmental mathematical model has been formulated and studied to predict the evolution of the novel coronavirus disease (COVID-19) in Cameroon. After presenting the model with integer derivatives, the basic reproductive number, ${\mathcal{R}}_0$ of the model has been computed, which represents the number of secondary COVID-19 positive cases caused by a single infectious person in a completely susceptible Cameroonian population. The dynamics of the disease is highly influenced by the value of this epidemic threshold. Indeed, if ${\mathcal{R}}_0<1,$ then a sufficiently small influx of infected individuals will not generate an outbreak of the COVID-19, and if ${\mathcal{R}}_0>1,$ then a sufficiently small influx of infected individuals will generate an outbreak of the COVID-19. Using real data communicated by the Cameroonian government, our model has been calibrated using a newly developed optimization algorithm based on well-known trust-region-reflective (TRR) algorithm. With the result of this model calibration, the probable peak date is estimated to be on August 01, 2020 with approximately 1073 $(95\%CI:714-1654)$ daily new confirmed cases, and which corresponds to approximately  ~ 20, 100 $(95\%CI:17,343-24,584)$ cumulative infected cases. As of July 11, according to the recent statistics communicated by the health authorities of Cameroon, nearly 14,916 confirmed cases have already been identified. This difference between the real-time data communicated by the government and the predictions of our model can be explained by the fact that the fear of COVID-19 within inhabitants pushes the wealthy individuals towards private hospitals, which are not only giving false test results but also overbidding the treatment of this disease [8].

Global sensitivity analysis has been performed implementing partial rank correlation coefficient (PRCC) analysis to quantify the most crucial parameters, which can significantly affect the progression dynamics of COVID-19. It has been unearthed in our analysis that the direct infectious contact rate (β) and the efficacy of confinement measures (ϵ) are the most influential parameters in controlling the outbreak of COVID-19. This ignites some insightful public health implications. Reducing physical contact between people through social distancing, wearing face-masks as a daily practice and tightening up confinement measures could bring the spread of coronavirus to a halt.

Eventually, the concept of Caputo derivatives has been deployed to formulate the fractional model and the existence and uniqueness of the solutions have also been presented. Using generalized Adams-Bashforth-Moulton method, a numerical scheme has been constructed for the fractional model. Numerical simulations enlighten that for $\alpha =1$, the solutions of our fractional model converge to the solutions of the integer model, and the decrease of the fractional-order parameter (0 < α < 1) leads to delay of the onset of the epidemic peaks.

Declaration of Competing Interest

This work does not have any conflict of interest. No funding is received for this study.