Abstract
The discrimination of non-focal class (NFC) and focal class (FC), is vital in localizing the epileptogenic zone (EZ) during neurosurgery. In the conventional diagnosis method, the neurologist has to visually examine the long hour electroencephalogram (EEG) signals, which consumes time and is prone to error. Hence, in this present work, automated diagnosis of FC EEG signals from NFC EEG signals is developed using the Fast Walsh–Hadamard Transform (FWHT) method, entropies, and artificial neural network (ANN). The FWHT analyzes the EEG signals in the frequency domain and decomposes it into the Hadamard coefficients. Five different nonlinear features, namely approximate entropy (ApEn), log-energy entropy (LogEn), fuzzy entropy (FuzzyEn), sample entropy (SampEn), and permutation entropy (PermEn) are extracted from the decomposed Hadamard coefficients. The extracted features detail the nonlinearity in the NFC and the FC EEG signals. The judicious entropy features are supplied to the ANN classifier, with a 10-fold cross-validation method to classify the NFC and FC classes. Two publicly available datasets such as the University of Bonn and Bern-Barcelona dataset are used to evaluate the proposed approach. A maximum sensitivity of 99.70%, the accuracy of 99.50%, and specificity of 99.30% with the 3750 pairs of NFC and FC signal are achieved using the Bern-Barcelona dataset, while the accuracy of 92.80%, the sensitivity of 91%, and specificity of 94.60% is achieved using University of Bonn dataset. Compared to the existing technique, the proposed approach attained a maximum classification performance in both the dataset.
Keywords: fast Walsh–Hadamard transform, feature extraction, entropy, classification, artificial neural network
1. Introduction
Epilepsy is a nervous system syndrome originated by the frequent occurrence of the seizures [1] owing to the sudden abnormal flow of electrical activity in the central nervous system which results in unconsciousness, disability in body movement [2], and also sudden unexpected death in epilepsy (SUDEP) that occurs one in 1000 adults and one in 4500 children each year. According to the International League Against Epilepsy (ILAE), drug-resistant epilepsy is referred to as the epileptic seizures which are unresponsive to the antiepileptic drugs and which results in the treatment through surgery. About more than 60% of the drug-resistant patients are affected with focal epilepsy, which affects the particular section of the neural system, whereas 20% of drug-resistant patients have generalized epilepsy; all parts of the brain are influenced [3]. The estimation of the epileptogenic zone (EZ) before the surgical procedure is a primary requirement for the neurosurgeons.
The electroencephalogram (EEG) is non-invasive clinical equipment to screen the characteristics of the encephalon activity [4] by attaching the electrodes on the scalp over a certain duration known as scalp EEG whereas implanting electrodes in the cerebrum before the surgical treatment is known as intracranial EEG. The conventional EEG-based approach for epileptic diagnosis and estimation of EZ needs tiresome manual inspection of EEG signals done by eminently qualified neurologists [5], hence an increasing demand to automate it is on the rise. In recent years, to assist the neurologists in identifying the EZ, many computer-aided automated diagnosis tools have been developed using signal processing techniques and machine learning algorithms.
In literature, various machine learning [6] methodologies have been proposed [7] for health care problems [8,9] to provide a solution. Various entropy measures with the combination of classifiers were introduced to provide the classification of non-focal class (NFC) and focal class (FC) EEG signals in the Bern-Barcelona (BB) dataset [10]. In [11], 15 levels of flexible analytic wavelet transform (FAWT) were used for the EEG signal decomposition into different sub-bands, and the entropy measures were computed from every sub-band to classify the signals, which attained 94.41% classification accuracy with least-square support vector machine (LS-SVM) classifier. In [12], authors computed the sample entropy (SampEn), Reyni’s entropy (RE), and approximate entropy (ApEn) from EEG signals, and fed it into Non-Nested Generalized Exemplars classifier (NNge) for discriminating the NFC and FC, which achieved an accuracy of 98%. In [13], authors achieved an accuracy of 94.5% using LS-SVM classifier, with the extracted entropy features from the decomposed sub-bands using the orthogonal wavelet filter banks, which are based on the time-frequency domain. In [14], the neighborhood component analysis (NCA) with support vector machine (SVM) attained the sensitivity of 97.6%, the accuracy of 96.1%, and specificity of 94.4% in distinguishing the NFC and FC EEG signals.
In [15], empirical mode decomposition (EMD) was employed for the decomposition of the signals into various intrinsic mode functions (IMF), and log energy (LogEn) entropy feature was extracted from each IMF. An accuracy of 89.4% was achieved using the k-nearest neighbor (k-NN) classifier with the computed features. In [16], tunable-Q wavelet transform (TQWT) was used to classify the NFC and FC with the LS-SVM classifier. In [17], four different classifiers were used with the differential entropy feature vector for classification of NFC and FC. Among these, the random forest (RF) classifier attained specificity of 95%, accuracy of 78.5%, and sensitivity of 95%. In [18], discrete wavelet transform (DWT) with level six and feature ranking methods was used for discriminating the NFC and FC. In [19], the TQWT was employed to decompose the EEG signals, and the LS-SVM classifier with the entropy features provided better discrimination of NFC and FC EEG signals. In [20], the 50 pairs of NFC and 50 pairs of FC EEG signals were used to evaluate the performance of entropy measures in discrimination of NFC and FC. In [21], the empirical wavelet transform (EWT) was employed to analyze the NFC and FC EEG signals. In [22], EMD with entropy features and LS-SVM was employed to discriminate 3750 pairs of NFC and FC EEG signals. In [23], the author used DWT to analyze the EEG signals and various coefficients decomposed, and from each coefficient, the statistical data as features were extracted. The University of Bonn dataset and the BB dataset were used to evaluate the DWT with the statistical feature approach in the classification of NFC and FC EEG signals, with SVM classifier. For the University of Bonn database, an accuracy of 88%, and for the BB dataset, an accuracy of 83.74% was achieved. In [24], multiple features and SVM classifiers were employed for the classification of NFC and FC. This method achieved an accuracy of 92.15%, sensitivity of 94.56%, and specificity of 89.74%. In [25], delay PermEn method and SVM classification were performed to localize the EZ. The adaptive neuro-fuzzy inference system (ANFIS) classifier was used to discriminate the NFC and FC cases using the extracted features, which achieved 100% specificity, 99% accuracy, and 98% sensitivity [26]. In [27], Filter banks were applied to obtain different frequency bands from the signals, and they attained an accuracy of 89.7% for 50 pairs and 89.52% for 750 pairs of NFC and FC EEG signals with LS-SVM classifier, respectively. In [28], the extracted entropy features were fed into the LS-SVM classifier to characterize the FC signal and achieved an accuracy of 82%. In [29], FAWT was developed to decompose the EEG signal into several sub-bands, and fractal dimension features were extracted. The obtained features were classified by a classifier. In [30], a complex wavelet transform (CWT) was applied, and statistical features were supplied into the ANFIS classifier to classify NFC and FC. In [31], DWT was used for the extraction of the features where the optimum features were selected from the extracted statistical features by engaging the genetic algorithm (GA). The comparative study of three different classifiers in distinguishing the NFC and FC was studied.
In [32], an unsupervised methodology of NFC and FC classification performed by autoregressive (AR) modeling, the non-parametric statistical test was performed to provide efficient classification. In [33], energy measures and entropies were analyzed from the differential operation of the EEG signal, those features were fed into SVM for classification, and they got an accuracy of 88.14%. In [34], they used a bivariate EMD to classify NFC and FC signals. Entropy features were extracted, and those were given to the SVM and achieved 86.89% of accuracy. In [35], they used three distinct deep neural networks such as LeNet, AlexNet, and GooLeNet to discriminate NFC and FC EEG signals, and their method achieves a classification accuracy of 100%. In [36], long short-term memory (LSTM) algorithm was applied for the classification, with different k-folds. Based on several experiments, the 10-fold validation was chosen to be the best. In [37], synchro squeezing transform and deep convolutional neural network were utilized, and it provides better classification performance. In [38], a convolutional neural network was applied on the scalp EEG signals to outperform the classification. In [39], the authors have proposed the supervised epileptic seizure detection algorithm to analyze long term EEG signals for reducing the computational complexity. In [40], EEG rhythm-based Taylor Fourier filter bank was designed, and two classifiers, namely, K-NN and SVM classifiers were used engaged, which achieved an accuracy of 94.88%. In [41], FAWT decomposition method with entropy features was classified by the SVM classifier, which achieved better accuracy. In [42], variational mode decomposition (VMD) was performed on the EEG signals in the DWT domain, and the computed entropy features classified by ensemble stacking provided 95.2% accuracy. In [43], EMD method was employed to investigate signals justified as IMFS. The features were extracted from the IMFs via phase space reconstruction and classified by the neural networks. In [44], the third-order cumulant function was proposed for the discrimination of EEG signals with the help of the SVM classifier.
Although the various methods in the literature have provided an efficient classification performance, still their respective performance has to be improved. Hence, in this work, the FWHT technique is used to analyze the NFC and FC signals, and five individual entropy measures are extracted from the decomposed EEG signals. ANN classifier is utilized to classify the extracted features for evaluating the performance of the proposed approach in discrimination of NFC and FC EEG signals. For this work, the two datasets, namely the University of Bonn and BB dataset, are used. The performance is evaluated, and the results with the state-of-art techniques are compared. The proposed method attained the highest classification performance in both datasets.
2. Materials and Methods
2.1. Dataset Used
In this paper, the two publicly available EEG databases for the automatic classification of NFC and FC EEG signals are used.
2.1.1. University of Bonn Dataset
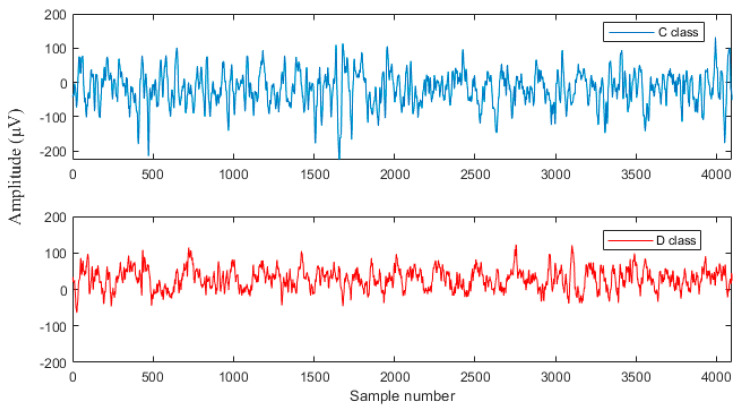
The University of Bonn EEG dataset was used to analyze the proposed work. The dataset consists of 500 EEG recorded files with five classes (A, B, C, D, and E), every single containing single-channel EEG sectors with 100 signals [45]. A and B classes are recordings of the healthy person during eyes open and close. C and D classes are recordings of the epileptic subjects during the interictal stage during the non-existence of seizures. E class is recordings of the epileptic subject during seizure activity. The removal of artifacts is done by visual examination. This work mainly focuses on the classification of NFC and FC EEG signals. Hence, the classes C and D were alone used in this work. The C and D groups consist of EEG signals of duration 23.6 s, which was measured from the focal epileptic subjects. The EEG signals measured at EZ using the depth electrodes are in class D, and class C consists of EEG signals measured from the hippocampal formation of the opposite hemisphere of the brain. Each EEG record consists of 4096 samples, and the sampling frequency is 173.61 Hz. The total time lengths of the signals in the dataset are 23.6 s [45]. The samples of C and D EEG signals are shown in Figure 1.
Figure 1.
Sample of University of Bonn dataset.
2.1.2. Bern-Barcelona Dataset
An open-access dataset BB was engaged in conducting all the experimentations in this present work. The dataset consists of intracranial EEG recordings of two classes, namely NFC and FC. Each class contains 3750 pairs of EEG recordings represented by x and y from five epileptic subjects [46] who have experienced the temporal lobe epilepsy, where all the subjects had a surgical treatment result. In FC recordings, x is recorded to discern the 1st ictal signal from the channels, and y is denoted as neighboring channels. In NFC, x and y are the records of the remaining neighboring channels. Three subjects were cured completely from seizures, whereas two subjects had the sensation of the seizures. FC signals were obtained from the epileptic region, whereas NFC signals were collected from the other region of the brain.
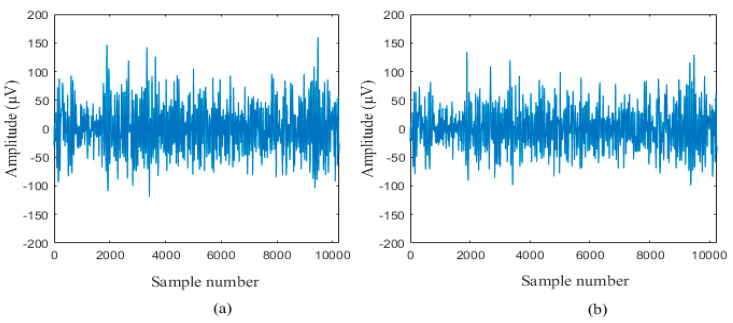
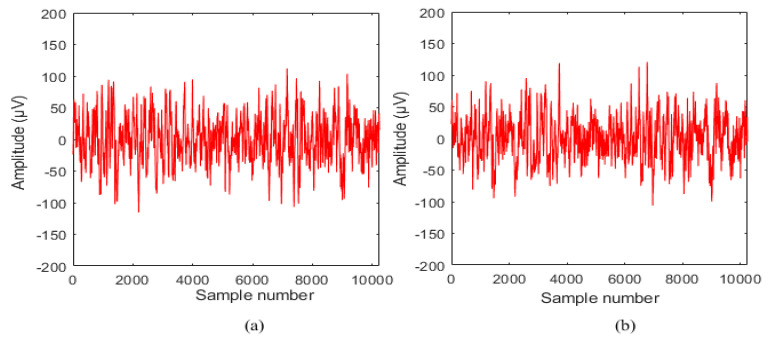
Each EEG recordings consist of 10,240 samples with a sampling rate of 512 Hz [22]. These EEG records were preprocessed using the bandpass filter to remove artifacts. The time duration of each EEG recording is 20 s. The entire 3750 pairs of NFC and FC recordings in the BB dataset were utilized in this study. The sample of NFC and FC signals are shown in Figure 2 and Figure 3.
Figure 2.
A sample of non-focal class (NFC) electroencephalogram (EEG) signal (a) x channel and (b) y channel.
Figure 3.
A sample of focal class (FC) EEG signal (a) x channel and (b) y channel.
2.2. Fast Walsh Hadamard Transform
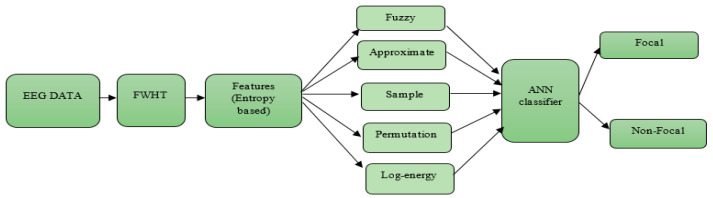
In this paper, a technique based on the frequency domain utilized for the classification of NFC and FC EEG signals is proposed. The block diagram of the proposed method is given in Figure 4. FWHT was used to extract the discriminating features from the EEG signal [47]. FWHT is an efficient technique to estimate the Walsh–Hadamard Transform (WHT), which involves the conversion of time-domain signals into frequency domain [48].
Figure 4.
Block diagram of the proposed work.
FWHT decays the signal into a set of orthogonal, rectangular waveforms called Walsh functions with the values of +1 or −1 [49]. The unique sequence value will be assigned with each Walsh function. The execution of the FWHT algorithm is comprehended by the addition and subtraction function. FWHT has the competency to identify the signals more precisely, that consist of a sharp disruption in the signal. FWHT decomposes the signal samples with a length of into coefficients. FWHT returns the coefficient of the Discrete Walsh–Hadamard Transform (DWHT) of the signal. The FWHT of the data samples of x(n) and is given as follows [50]
| (1) |
where N indicates the total samples number and is the Walsh function (Walsh matrix) which is given by the following equation [51]
| (2) |
In the 1 × 1 matrix the value of is equal to 1. Therefore, and can be written as
| (3) |
| (4) |
The Walsh function can also be written as
| (5) |
The FWHT is a product of a data sequence whose length is 1 × N and the Walsh matrix with a length of N × N [50].
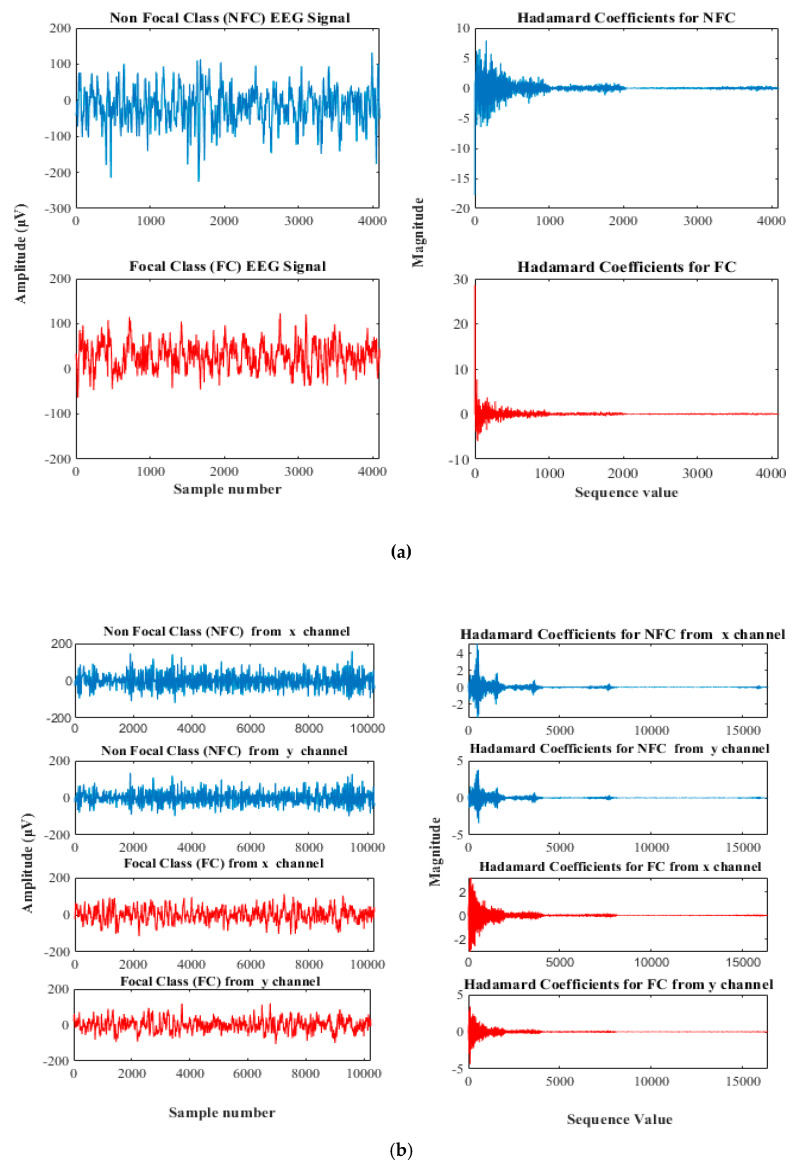
The main advantage of this transform is it requires less storage space to store decomposed coefficients, and signal reconstruction is faster. FWHT works on the signals with length equal to a power of 2. If the length is less than the power of 2, its length is padded with zeros to the next greater power of 2 before processing [52]. In this work, the FWHT was applied to analyze the EEG signal from the University of Bonn database, of sample size 4096, which is two to the power of 12 (). Hence, it is decomposed to 4096 Hadamard coefficients. Whereas, in the BB data set, 10,240 samples are available. Since it has value less than the power of two (10,240 > ) it is padded with zeroes till the next greater power of two so that 16,384 () Hadamard coefficients are decomposed and shown in Figure 5.
Figure 5.
The plot of EEG signal and its Hadamard coefficient for (a) University of Bonn and (b) Bern-Barcelona Dataset.
2.3. Feature Extraction
Feature extraction is an essential process for event classification of signals and images in the medical field for clinical diagnosis [53]. In this study, five nonlinear entropy-based discriminating features from the decomposed Hadamard coefficient of EEG signal were extracted. The entropy features compute the randomness of the time sequence of the EEG signals algebraically. These measures reflect the information of inspected anarchy within the intracortical area [54]. The extracted features are given as follows:
2.3.1. Approximate Entropy (ApEn)
ApEn computes the stochasticity and consistency in the manifold dimension. It is a scale-invariant which relates the resemblance of the samples in the EEG [54]. The logarithmic probability that the signal with N sample points reiterates itself within the lenience of p for k points and for next m + 1 points is expressed in ApEn. For a given time sequence y(i) of length N, length N – k + 1 vectors Y(1), Y(2),…,Y(N – k + 1) are constructed. The ApEn is
| (6) |
where
| (7) |
where, is denoted as correlation integral signifying the probability of a vector Y(i) remaining alike to Y(j) in lenience limit p. It is widely engaged in the miscellaneous zone of biomedical signal processing.
2.3.2. Sample Entropy (SampEn)
SampEn is used to compute the consistency in the signal efficiently than ApEn [55], and it is a revised form of ApEn, beneficial for complexity reduction in the EEG signal. It is not reliant on the length of the time cycles [12]. The greater SampEn value suggests that the signal is predicted less effectively, and a lower SampEn predicts the signal more effectively [54]. In SampEn, the bias instigated by the self matches is prevented from extemporizing the function. For a given signal y(i), the sample entropy is given as follows
| (8) |
where the parameters are defined as
| (9) |
| (10) |
where, is the sum, L[Y(i),Y(j)] ≤ r, without the self matches. The parameter L[Y(i),Y(j)] is the interval between Y(i) and Y(j) and can be written as
| (11) |
2.3.3. Permutation Entropy (PermEn)
PermEn is employed to estimate the difficulty in the time sequence by comparing the neighbor time-series signals [56]. It is a non-stationary time series approach that provides efficient and robust and quick results [54]. The relationship between the distinct number of equidistant values for past and present esteem are labeled by mapping onto a symbolic sequence from the continuous-time sequence record. y(t) for t = 1, 2, … is embedded into a k dimensional space to accomplish the mapping. The time-series data can be as follows [57]
| (12) |
where, k corresponds to the embedding measurement, and τ is the time gap. For the k embedding dimension, the conceivable permutations will be k!. The embedded time vectors X(t) will be given by a j symbol sequence, and pj represents a probability distribution for each symbol. HPermEn, of a specified time sequence, x(t), is defined as follows [57]
| (13) |
where the number of dissimilar symbols is J for a specified embedding dimension that is (J ≤ k!). The normalization factor is written as therefore 0 ≤≤1.
2.3.4. Fuzzy Entropy (FuzzyEn)
FuzzyEn signifies the information of consistency, and it is implemented from the fuzzy sets [58]. FuzzyEn measure on the EEG signal has a specific function, which is known as the membership function, with a value that remains from 0 to 1 [59]. FuzzyEn is a continuous function which is used to estimate resemblance in the time sequence of the signal [60]. The time sequence signal of y(i) with N signifies the sample number and k represents the length, the vector sequences are considered as
| (14) |
where, denotes successive values, instigated with the kth point and comprehensive by baseline removal.
| (15) |
The fuzzy function written in exponential form is given as,
| (16) |
where is the absolute distance of the points.
The function for and for is given as
| (17) |
| (18) |
For the finite dataset, the factor of FuzzyEn (k,n,p) of the negative natural logarithm order of the deviancy of and [58]
| (19) |
2.3.5. Log-Energy Entropy (LogEn)
LogEn is employed to compute the amount of contribution of signals. Mathematically, LogEn is formulated as
| (20) |
where, N corresponds to the total interval of the signal, and yi is the ith signal samples. In [15,61], the authors attained high classification accuracy by LogEn feature.
2.4. Artificial Neural Network (ANN) Classifier
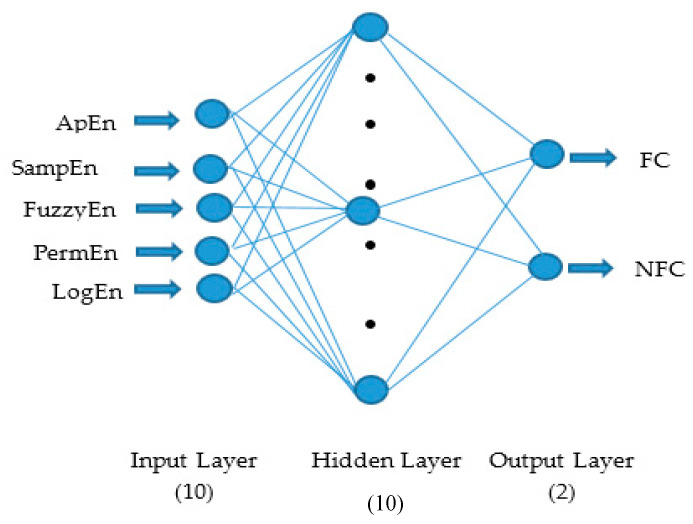
ANN comprises the output layer, input layer, and one or more hidden layer (middle layer) with a more number of processing nodes or artificial neurons connected with each other shown in Figure 6. The connection between two neurons controlled by weights, which can be adjustable so as to increase the accuracy of the system [62]. ANN is a biologically inspired model that classifies a single layer and multiple layer architecture where the feed-forward multilayered neural network is communally used for physical modeling [63]. ANN follows the supervised learning methodology, and also it overwhelmed the hitch due to the nonlinearly separable problem in the single-layer perceptron.
Figure 6.
Artificial neural network.
ANN learning is realized by various training algorithms based on training rules or functions. The training algorithm involves training the neural network to perform its function. In this work, five entropy features per channel, hence a total of 10 nonlinear features, are given as an input to the input layer to perform the discrimination between the NFC and FC signals. A feed-forward multilayered neural network is communally used for physical modeling [63]. The few hidden neurons are not efficient for classification [64]. Hence, the total hidden neurons considered in this study is 10. Levenberg–Marquardt backpropagation (LMBP) training algorithm, which is a class of quasi-newton algorithms, is used to train the neural network. LMBP algorithm is an iterative approach that discovers the minimum function that is an amount of quadrangle of nonlinear function [65].
The classification performance is calculated for individual NFC and FC subjects based on the classification sensitivity, accuracy, positive predictive value, specificity, and negative predictive value which are given below
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
In the above equation corresponds to true positive, is defined as true negative, referred to as false positive, and represents false negative.
3. Results and Discussion
The NFC and FC EEG signals acquired from BB and University of Bonn dataset datasets were employed to investigate the proposed methodology. In this work, the Hadamard coefficients in the individual pairs of the NFC and FC EEG signals were calculated by the effective decomposition method. FWHT transforms the time series signals to the frequency-dependent signals so as to analyze the nonlinear characteristics. In the BB dataset, 3750 pairs of signals and C and D classes of the University of Bonn dataset were taken for the experiment. Judicious features were extracted from the decomposed Hadamard coefficient of EEG signals that were used for the identification of NFC and FC EEG signals. The entropy features provide the characteristics of the nonlinearity existing in the signals to distinguish the variation present in the two classes for the classification. The entropy measures, namely SampEn, FuzzEn, LogEn, PermEn, and ApEn per channel, were extracted. Hence, a total of 10 features from the BB dataset and five features from the University of Bonn dataset were extracted. Student’s t-test was conducted on the extracted features of both databases to identify the statistically significant features (p < 0.01). The obtained p-values for different extracted features were found to be lesser than 0.01. Hence, all the features were fed into the ANN classifier with different combinations listed in Table 1 and Table 2. Ten-fold cross-validation was performed to validate the classification performance. Figure 7 and Figure 8 show the variation of the NFC and FC EEG signals in the University of Bonn and BB data, respectively.
Table 1.
The classification results using the combination of entropy features for the Bern-Barcelona (BB) dataset.
| Feature | Accuracy (%) | Sensitivity (%) | Specificity (%) |
|---|---|---|---|
| Single feature | |||
| ApEn | 62.89 | 67.22 | 58.56 |
| SampEn | 96.84 | 100 | 93.69 |
| PermEn | 57.05 | 40.90 | 73.20 |
| FuzzyEn | 67.82 | 73.03 | 62.62 |
| LogEn | 59.89 | 61.80 | 57.98 |
| Two features | |||
| SampEn, ApEn | 97.41 | 99.14 | 95.68 |
| SampEn, LogEn | 98.80 | 97.98 | 99.74 |
| SampEn, PermEn | 96.75 | 99.98 | 93.53 |
| SampEn, FuzzyEn | 96.53 | 94.33 | 99 |
| ApEn, LogEn | 66.89 | 68.01 | 65.77 |
| ApEn, PermEn | 63.79 | 63.57 | 64 |
| ApEn, FuzzyEn | 70.89 | 74.27 | 67.46 |
| LogEn, PermEn | 61.21 | 58.82 | 63.60 |
| LogEn, FuzzyEn | 70.83 | 74.05 | 67.61 |
| PermEn, FuzzyEn | 69.44 | 75.00 | 63.88 |
| Three features | |||
| SampEn, ApEn, LogEn | 98.78 | 99.29 | 98.17 |
| SampEn, ApEn, PermEn | 98.30 | 99.47 | 97.13 |
| SampEn, ApEn, FuzzyEn | 98.47 | 99.15 | 97.80 |
| SampEn, PermEn, LogEn | 98.28 | 99.86 | 96.69 |
| SampEn, LogEn, FuzzyEn | 98.89 | 99.76 | 98.02 |
| SampEn, FuzzyEn, PermEn | 98.98 | 99.78 | 98.17 |
| ApEn, LogEn, PermEn | 67.47 | 67.34 | 67.59 |
| ApEn, LogEn, FuzzyEn | 74.25 | 78.10 | 70.41 |
| LogEn, PermEn, FuzzyEn | 71.80 | 74.56 | 69.05 |
| PermEn, FuzzyEn, ApEn | 71.50 | 74.84 | 68.16 |
| Four features | |||
| SampEn, ApEn, FuzzyEn, PermEn | 98.54 | 99.27 | 97.81 |
| SampEn, ApEn, FuzzyEn, LogEn | 98.40 | 99.11 | 97.70 |
| SampEn, FuzzyEn, PermEn, LogEn | 99.43 | 99.89 | 98.96 |
| SampEn, LogEn, ApEn, PermEn | 98.33 | 99.12 | 97.55 |
| ApEn, FuzzyEn, PermEn, LogEn | 74.95 | 78.35 | 71.54 |
| Five features | |||
| SampEn, ApEn, FuzzyEn, LogEn, Perm | 99.50 | 99.70 | 99.30 |
Table 2.
The classification results using the combination of entropy features for the University of Bonn dataset.
| Feature | Accuracy (%) | Sensitivity (%) | Specificity (%) |
|---|---|---|---|
| Single feature | |||
| ApEn | 62.60 | 42 | 83.20 |
| SampEn | 64.15 | 56.30 | 72 |
| PermEn | 59.80 | 62.20 | 57.40 |
| FuzzyEn | 64.85 | 48.90 | 80.80 |
| LogEn | 66.90 | 64.70 | 69.10 |
| Two features | |||
| SampEn, ApEn | 72.60 | 64.80 | 80.40 |
| SampEn, LogEn | 79.40 | 72.60 | 86.2 |
| SampEn, PermEn | 67.35 | 62.80 | 71.90 |
| SampEn, FuzzyEn | 75.80 | 66.80 | 84.80 |
| ApEn, LogEn | 79.75 | 72 | 87.5 |
| ApEn, PermEn | 68.70 | 56.90 | 80.50 |
| ApEn, FuzzyEn | 78.05 | 70.60 | 85.50 |
| LogEn, PermEn | 76.45 | 77.40 | 75.50 |
| LogEn, FuzzyEn | 79.60 | 71.20 | 88 |
| PermEn, FuzzyEn | 72.85 | 70.40 | 75.30 |
| Three features | |||
| SampEn, ApEn, LogEn | 84.35 | 79.20 | 89.50 |
| SampEn, ApEn, PermEn | 73.50 | 70.40 | 76.60 |
| SampEn, ApEn, FuzzyEn | 82.35 | 77.40 | 87.30 |
| SampEn, PermEn, LogEn | 82.75 | 77.70 | 87.80 |
| SampEn, LogEn, FuzzyEn | 87.35 | 86.10 | 88.60 |
| SampEn, FuzzyEn, PermEn | 84.15 | 78.50 | 89.80 |
| ApEn, LogEn, PermEn | 86.70 | 81.70 | 91.70 |
| ApEn, LogEn, FuzzyEn | 84.30 | 80 | 88.60 |
| LogEn, PermEn, FuzzyEn | 84 | 78.40 | 89.60 |
| PermEn, FuzzyEn, ApEn | 84.25 | 80.40 | 88.10 |
| Four features | |||
| SampEn, ApEn, FuzzyEn, PermEn | 90.25 | 88 | 92.50 |
| SampEn, ApEn, FuzzyEn, LogEn | 89.55 | 87.70 | 91.40 |
| SampEn, FuzzyEn, PermEn, LogEn | 88 | 86.50 | 89.50 |
| SampEn, LogEn, ApEn, PermEn | 89.85 | 88.70 | 91 |
| ApEn, FuzzyEn, PermEn, LogEn | 90.75 | 87.70 | 93.80 |
| Five features | |||
| SampEn, ApEn, FuzzyEn, LogEn, Perm | 92.80 | 91 | 94.60 |
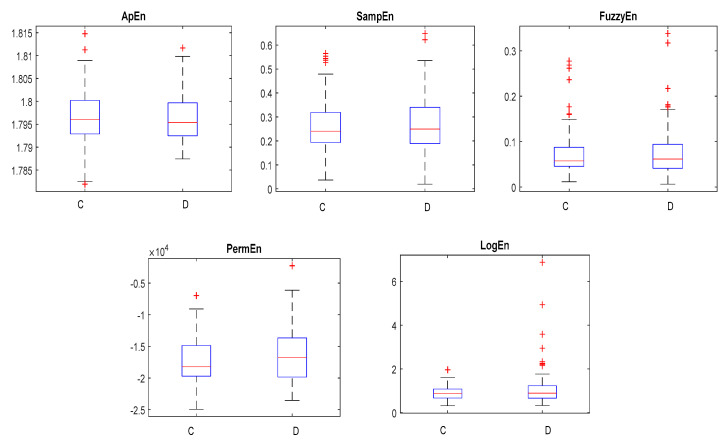
Figure 7.
The box plots of the C and D classes in the University of Bonn dataset.
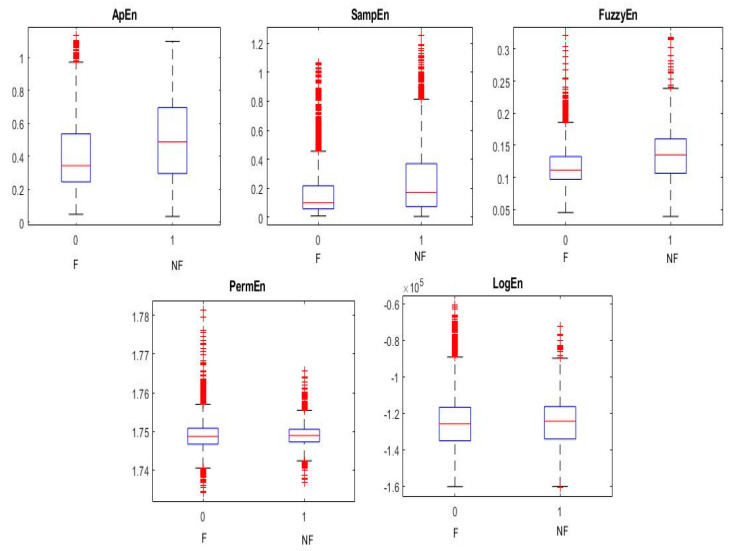
Figure 8.
The box plots of the NFC and FC classes in the Bern-Barcelona dataset.
The entropy measures with single features and multiple combinations were given as an input to the ANN classifier to identify the feature set with better classification performance. With LogEn feature the classification of NFC and FC using the University of Bonn database attained an accuracy of 66.90%. While in the BB dataset, when the SampEn feature was given as input to the ANN classifier accuracy of 96.84%, the sensitivity of 100% and specificity of 93.69% were attained. In order to improve the precision of the overall performance, the combination of features such as two features, three features, four features, and five features were done for both the datasets and listed in Table 1 and Table 2. Compared to different combinations with SampEn, an accuracy greater than 98% is seen in the BB dataset, while a maximum accuracy of 99.50% was attained for five feature combinations. It can also be noted that the combination of four features (SampEn, FuzzyEn, PermEn, LogEn), attained an accuracy of 94.43%, which is more or less equal to the accuracy attained by the five feature combination. On the other hand, for the University of Bonn database, the combination of five features attained a maximum accuracy of 92.80%. Hence, based on the results, the five feature combination was chosen as the best feature set for the classification of NFC and FC EEG signals.
The classification performance in terms of accuracy, sensitivity, and specificity for the University of Bonn database is 92.80%, 91%, and 94.60%. Similarly, for the BB dataset, the proposed method provides specificity of 99.36%, accuracy of 99.50%, and the sensitivity of 99.70%.
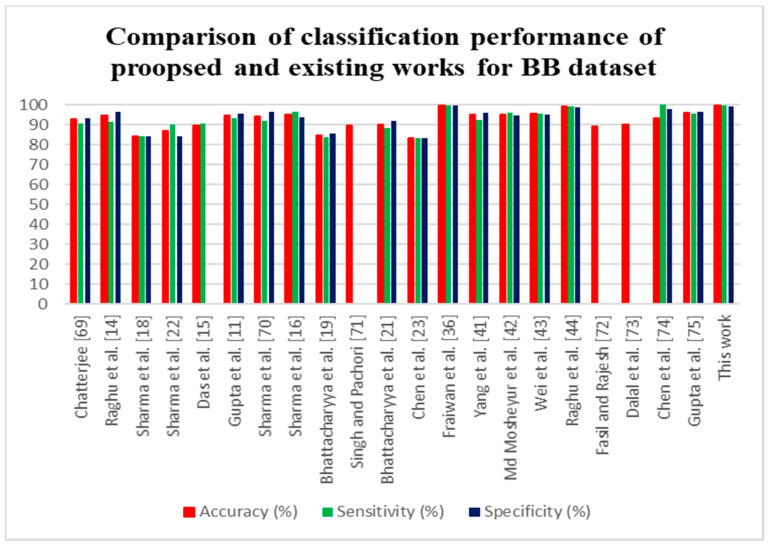
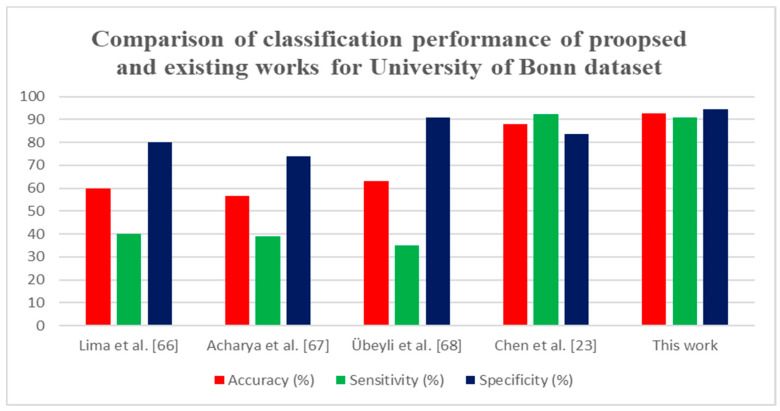
The classification performance of the proposed method was compared with the existing methods, which are tabulated in Table 3.
Table 3.
Comparison of the performance of the proposed and existing method.
| Author Name | Number of Signal Pairs | Methodology | Classifiers | Accuracy | Sensitivity | Specificity |
|---|---|---|---|---|---|---|
| BB dataset | ||||||
| Chatterjee [69] | 3750 pairs | Higher order moments in EMD-TKEO domain | SVM | 92.65 | 90.70 | 93.15 |
| Raghu et al. [14] | 3750 pairs | NCA and entropies | LS-SVM | 94.5 | 91.5 | 96.56 |
| Sharma et al. [18] | 50 pairs | DWT and seven different entropies | LS-SVM | 84 | 84 | 84 |
| Sharma et al. [22] | 50 pairs | EM, and six different entropies | LS-SVM | 87 | 90 | 84 |
| Das et al. [15] | 50 pairs | EMD, DWT, and three nonlinear features | k-NN | 89.4 | 90.7 | - |
| Gupta et al. [11] | 3750 pairs | FAWT and three different entropies | LS-SVM | 94.41 | 93.25 | 95.57 |
| Sharma et al. [13] | 3750 pairs | Orthogonal wavelet filter banks, entropy measures | LS-SVM | 94.25 | 91.95 | 96.56 |
| Sharma et al. [16] | 3750 pairs | TQWT and three different entropies | LS-SVM | 95 | 96.37 | 93.47 |
| Bhattacharyya et al. [19] | 3750 pairs | TQWT based multivariate sub-band fuzzy entropy | LS-SVM | 84.67 | 83.86 | 85.46 |
| Singh and Pachori [29] | 50 pairs | Fourier rhythms, bandwidth features | LS-SVM | 89.7 | - | - |
| Bhattacharyya et al. [21] | 50 pairs | EWT, area computed from RPS rhythms | LS-SVM | 90 | 88 | 92 |
| Chen et al. [23] | 3750 pairs | DWT and statistical features | SVM | 83.07 | 83.05 | 83.09 |
| Fraiwan et al. [36] | 3750 pairs | - | LSTM | 99.60 | 99.65 | 99.55 |
| Yang et al. [41] | 3750 pairs | FAWT and entropies | LS-SVM | 94.80 | 92.27 | 96.10 |
| Md Mosheyur et al. [42] | 3750 pairs | VMD-DWT and entropies | Ensemble stacking | 95.2 | 96.1 | 94.4 |
| Wei et al. [43] | 3750 pairs | EMD, IMF based | Neural network | 95.37 | 95.52 | 95.23 |
| Raghu et al. [44] | 3750 pairs | Third order cumulant function | SVM | 99 | 99.33 | 98.66 |
| Fasil and Rajesh [70] | 3750 pairs | Time domain exponential energy | SVM | 89 | - | - |
| Dalal et al. [29] | 50 pairs | Flexible time-frequency coverage analytic wavelet transform and Fractal dimension | Robust energy-based least square twin support vector machine |
90.2 | - | - |
| Chen et al. [71] | 50 Pairs | ARMA, EMD, singular values | SVM | 93 | 100 | 97.9 |
| Gupta et al. [72] | 3750 pairs | Fourier–Bessel series expansion based flexible time-frequency coverage wavelet transform, mixture correntropy, exponential energy | LS-SVM | 95.85 | 95.47 | 96.24 |
| This work | 3750 pairs | FWHT + Entropies | ANN | 99.50 | 99.70 | 99.30 |
| University of Bonn dataset | ||||||
| Lima et al. [66] | 200 signals | DWT and statistical features | RVM | 60 | 40 | 80 |
| Acharya et al. [67] | 200 signals | WPD and PCA | GMM | 56.50 | 39 | 74 |
| Übeyli et al. [68] | 200 signals | DWT and statistical features | ANN | 63 | 35 | 91 |
| Chen et al. [23] | 200 signals | DWT and statistical features | SVM | 88 | 92.24 | 83.76 |
| This work | 200 signals | FWHT + Entropies | ANN | 92.80 | 91 | 94.60 |
Various techniques have been proposed for EEG signal classification for epileptic seizure detection. The FAWT decomposition method [11,41] was employed, with LS-SVM classifier, which attained an accuracy of 94.41% and 94.80%, respectively, for the 3750 pairs of signals. Table 3 shows that many authors examined the entropy as features for classification of FC and NFC; it proves that compared to other features, different entropy features are more discriminate in classifying the FC and NFC classes. In [15,16,18,21], they have only examined the 50 pairs of EEG signals. In [15,22,43], EMD method was proposed for the feature extraction. In [42], VMD-DWT decomposition was performed to detect the epileptic seizures and achieved 95.2% of accuracy. In [36], the deep learning LSTM based features were evaluated for the classification of NFC and FC EEG signals. The proposed approach with the BB dataset attained an accuracy of 99.50%. It can also be noted that compared to the existing techniques with DWT, and WPD [66,67,68] the proposed approach attained an accuracy of 92.80% with University of Bonn dataset. Thus, it can be concluded that the proposed method provides a higher classification performance than all other methods.
The comparison of the proposed method with prevailing techniques is presented in Figure 9 and Figure 10 for the BB dataset and University of Bonn dataset. It is also proved that the proposed technique reached maximum accuracy than the already existing techniques. The key benefit of the proposed method is its computational efficiency and constancy. In the future deep learning, approaches will be used to analyze the automatic recognition of epileptic seizures.
Figure 9.
Comparison of classification performance proposed method with existing methods for the BB dataset.
Figure 10.
Comparison of classification performance proposed method with existing methods for the University of Bonn dataset.
4. Conclusions
The main aspiration of this present study was to afford an automated diagnosis tool for NFC and FC signals, to assist the neurologist in localization of the EZ for the clinical decision making. Therefore, the feature extraction approach called the FWHT method was used to decompose the EEG signals into different coefficients. Five significant entropy features were extracted from the decomposed coefficients and fed into the ANN classifier, for discrimination of NFC and FC signals. The classification performance of single entropy features and multiple combinations of features were employed to obtain a better classification performance. Simulation performance reveals that the combination of five entropies achieved highest classification accuracy. Maximum accuracy of 92.80% was achieved for the University of Bonn dataset and 99.50% for the BB dataset. Compared to the state-of-art techniques, the proposed approach attained maximum accuracy with reduced computational performance. The performance proposed method exceeds other methods, and it can be used for clinical practice at medical centers. Future research direction comprises the advancement of the proposed method using deep learning approaches and to diagnose other diseases, namely neurodegenerative disorders and mental disorders.
Acknowledgments
The authors would like to acknowledge the Karunya Institute of Technology and Sciences for providing the facilities. In addition, the authors would also like to extend their gratitude to the University of Deusto for providing the technical support.
Author Contributions
Conceptualization, P.J., M.S.P.S., N.J.S., and S.T.G.; Data curation, P.J.; Formal analysis, P.J., and M.S.P.S.; Funding acquisition, S.T.G., M.A.M., M.S.M., and B.G.-Z.; Methodology, P.J.; Resources, M.S.P.S., and S.T.G.; Supervision, M.S.P.S., and S.T.G.; Validation, N.J.S.; Visualization, P.J., and N.J.S.; Writing—original draft, P.J.; Writing—review and editing, M.S.P.S., M.A.M., M.S.M., B.G.-Z. and S.T.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding from Basque Country Government.
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Chiang C., Chang N., Chen T., Chen H., Chen L. Seizure Prediction Based on Classiffication of EEG Synchronization Patterns with On-line Retraining and Post-Processing Scheme; Proceedings of the 33rd Annual International Conference of the IEEE EMBS; Boston, MA, USA. 30 August–3 September 2011; pp. 7564–7569. [DOI] [PubMed] [Google Scholar]
- 2.Chu H., Chung C.K., Jeong W., Cho K.H. Predicting epileptic seizures from scalp EEG based on attractor state analysis. Comput. Methods Programs Biomed. 2017;143:75–87. doi: 10.1016/j.cmpb.2017.03.002. [DOI] [PubMed] [Google Scholar]
- 3.Park C., Choi G., Kim J., Kim S., Kim T., Min K., Jung K., Chong J. Epileptic Seizure Detection for Multi-channel EEG with Deep Convolutional Neural Network; Proceedings of the 2018 International Conference on Electronics, Information, and Communication (ICEIC); Honolulu, HI, USA. 24–27 January 2018; pp. 1–5. [Google Scholar]
- 4.Shahid A., Kamel N., Malik A.S., Jatoi M.A. Epileptic seizure detection using the singular values of EEG signals; Proceedings of the 2013 International Conference on Complex Medical Engineering (ICME); Beijing, China. 25–28 May 2013; pp. 652–655. [Google Scholar]
- 5.Chen L.L., Zhang J., Zou J.Z., Zhao C.J., Wang G.S. A framework on wavelet-based non-linear features and extreme learning machine for epileptic seizure detection. Biomed. Signal Process. Control. 2014;10:1–10. doi: 10.1016/j.bspc.2013.11.010. [DOI] [Google Scholar]
- 6.Abd Ghani M.K., Mohammed M.A., Arunkumar N., Mostafa S.A., Ibrahim D.A., Abdullah M.K., Jaber M.M., Abdulhay E., Ramirez-Gonzalez G., Burhanuddin M.A. Decision-level fusion scheme for nasopharyngeal carcinoma identification using machine learning techniques. Neural Comput. Appl. 2020;32:625–638. doi: 10.1007/s00521-018-3882-6. [DOI] [Google Scholar]
- 7.Obaid O.I., Mohammed M.A., Ghani M.K.A., Mostafa A., Taha F. Evaluating the performance of machine learning techniques in the classification of Wisconsin Breast Cancer. Int. J. Eng. Technol. 2018;7:160–166. [Google Scholar]
- 8.Mutlag A.A., Khanapi Abd Ghani M., Mohammed M.A., Maashi M.S., Mohd O., Mostafa S.A., Abdulkareem K.H., Marques G., de la Torre Díez I. MAFC: Multi-Agent Fog Computing Model for Healthcare Critical Tasks Management. Sensors. 2020;20:1853. doi: 10.3390/s20071853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Mohammed M.A., Ghani M.K.A., Arunkumar N.A., Mostafa S.A., Abdullah M.K., Burhanuddin M.A. Trainable model for segmenting and identifying Nasopharyngeal carcinoma. Comput. Electr. Eng. 2018;71:372–387. doi: 10.1016/j.compeleceng.2018.07.044. [DOI] [Google Scholar]
- 10.Mohammed M.A. Benchmarking Methodology for Selection of Optimal COVID-19 Diagnostic Model Based on Entropy and TOPSIS Methods. IEEE Access. 2020;8:99115–99131. doi: 10.1109/ACCESS.2020.2995597. [DOI] [Google Scholar]
- 11.Gupta V., Priya T., Kumar A., Bilas R., Rajendra U. Automated detection of focal EEG signals using features extracted from flexible analytic wavelet transform. Pattern Recognit. Lett. 2017;94:180–188. doi: 10.1016/j.patrec.2017.03.017. [DOI] [Google Scholar]
- 12.Arunkumar N., Ramkumar K., Venkatraman V., Abdulhay E., Lawrence S., Kadry S., Segal S. Classification of focal and non focal EEG using entropies. Pattern Recognit. Lett. 2017;94:112–117. [Google Scholar]
- 13.Sharma M., Dhere A., Bilas R., Acharya U.R. Systems An automatic detection of focal EEG signals using new class of time-frequency localized orthogonal wavelet filter bank. Knowl. Based Syst. 2017;118:217–227. doi: 10.1016/j.knosys.2016.11.024. [DOI] [Google Scholar]
- 14.Raghu S., Sriraam N. Classification of focal and Non-focal EEG signals using neighborhood component analysis and machine learning algorithms. Expert Syst. Appl. 2018;113:18–32. doi: 10.1016/j.eswa.2018.06.031. [DOI] [Google Scholar]
- 15.Das A.B., Imamul M., Bhuiyan H. Discrimination and classification of NFC and FC EEG signals using entropy-based features in the EMD-DWT domain. Biomed. Signal Process. Control. 2016;29:11–21. doi: 10.1016/j.bspc.2016.05.004. [DOI] [Google Scholar]
- 16.Sharma R., Kumar M., Bilas R., Acharya U.R. Decision support system for focal EEG signals using tunable-Q wavelet transform. J. Comput. Sci. 2017;20:52–60. doi: 10.1016/j.jocs.2017.03.022. [DOI] [Google Scholar]
- 17.Kumar M.R., Rao Y.S. Epileptic seizures classification in EEG signal based on semantic features and variational mode decomposition. Clust. Comput. 2019;22:13521–13531. doi: 10.1007/s10586-018-1995-4. [DOI] [Google Scholar]
- 18.Sharma R., Pachori R.B., Acharya U.R. An Integrated Index for the Identification of Focal Electroencephalogram Signals Using Discrete Wavelet Transform and Entropy Measures. Entropy. 2015;17:5218–5240. doi: 10.3390/e17085218. [DOI] [Google Scholar]
- 19.Bhattacharyya A., Pachori R.B., Acharya U.R. Tunable-Q Wavelet Transform Based Multivariate Sub-Band Fuzzy Entropy with Application to Focal EEG Signal Analysis. Entropy. 2017;19:99. doi: 10.3390/e19030099. [DOI] [Google Scholar]
- 20.Arunkumar N., Kumar K.R., Venkataraman V. Entropy features for focal EEG and non focal EEG. J. Comput. Sci. 2018;27:440–444. doi: 10.1016/j.jocs.2018.02.002. [DOI] [Google Scholar]
- 21.Bhattacharyya A., Sharma M., Bilas R. A novel approach for automated detection of focal EEG signals using empirical wavelet transform. Neural Comput. Appl. 2018;29:47–57. doi: 10.1007/s00521-016-2646-4. [DOI] [Google Scholar]
- 22.Sharma R., Pachori R.B., Acharya U.R. Application of Entropy Measures on Intrinsic Mode Functions for the Automated Identification of Focal Electroencephalogram Signals. Entropy. 2015;17:669–691. doi: 10.3390/e17020669. [DOI] [Google Scholar]
- 23.Chen D., Wan S., Bao F.S. Epileptic Focus Localization Using Discrete Wavelet Transform Based on Interictal Intracranial EEG. Trans. Neural Syst. Rehabil. Eng. 2016;25:413–425. doi: 10.1109/TNSRE.2016.2604393. [DOI] [PubMed] [Google Scholar]
- 24.Sriraam N., Raghu S. Classification of Focal and Non Focal Epileptic Seizures Using Multi-Features and SVM Classifier. Image Signal Process. 2017;41:160. doi: 10.1007/s10916-017-0800-x. [DOI] [PubMed] [Google Scholar]
- 25.Zhu G., Li Y., Paul P., Wang S. Epileptogenic Focus Detection in Intracranial EEG based on Delay Permutation Entropy. Int. Symp. Comput. Models Life Sci. 2013;1559:31–36. [Google Scholar]
- 26.Deivasigamani S., Senthilpari C., Yong W.H. Classification of Focal and Nonfocal EEG Signals Using ANFIS Classifier for Epilepsy Detection. Int. J. Imaging Syst. Technol. 2016;26:277–283. doi: 10.1002/ima.22199. [DOI] [Google Scholar]
- 27.Singh P., Pachori R.B. Classification of focal and non-focal EEG signals using features derived from fourier based rhythms. J. Mech. Med. Biol. 2017;17:1740002. doi: 10.1142/S0219519417400024. [DOI] [Google Scholar]
- 28.Abhinaya B., Charanya D., Thanaraj K.P. Feature Extraction and Selection of a Combination of Entropy Features for Real-time Epilepsy Detection. Int. J. Eng. Comput. Sci. 2016;5:16073–16078. doi: 10.18535/ijecs/v5i4.03. [DOI] [Google Scholar]
- 29.Dalal M., Tanveer M., Pachori R.B. Machine Intelligence and Signal Analysis. Volume 748. Springer; Singapore: 2019. Automated Identification system for Focal EEG Signals Using Fractal Dimension of FAWT-Based Sub-bands Signals; pp. 583–596. [Google Scholar]
- 30.Deivasigamani S., Senthilpari C., Wong H.Y. Computer Aided Automatic Detection and Classification of EEG Signals for Screening Epilepsy Disorder. J. Inf. Sci. Eng. 2018;34:687–700. [Google Scholar]
- 31.Sathish E., Sivakumaran N., Simon S.P., Raghavan S. Genetic Algorithm based Feature Selection for Classification of NFC and FC Intracranial Electroencephalographic Signals. J. Sci. Ind. Res. 2017;76:614–619. [Google Scholar]
- 32.Gao Z., Lu G., Yan P., Lyu C., Li X., Shang W. Automatic Change Detection for Real-Time Monitoring of EEG Signals. Front. Physiol. 2018;9:325. doi: 10.3389/fphys.2018.00325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Fasil O.K., Rajesh R., Thasleema T.M. Influence of differential features in non-focal and focal EEG signal classification; Proceedings of the 2017 IEEE Region 10 Humanitarian Technology Conference (R10-HTC); Dhaka, Bangladesh. 21–23 December 2017; pp. 646–649. [Google Scholar]
- 34.Itakura T., Tanaka T. Epileptic Focus Localization Based on Bivariate Empirical Mode Decomposition and Entropy; Proceedings of the 2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC); Kuala Lumpur, Malaysia. 12–15 December 2017; pp. 1426–1429. [Google Scholar]
- 35.Bashar M.K., Reza F., Idris Z., Yoshida H. Epileptic seizure classification from intracranical EEG signals: A comparative study EEG-based seizure classification; Proceedings of the 2016 IEEE EMBS Conference on Biomedical Engineering and Sciences (IECBES); Kuala Lumpur, Malaysia. 4–8 December 2016; pp. 96–101. [Google Scholar]
- 36.Fraiwan L., Alkhodari M. Classification of non-focal and focal Epileptic patients using single channel EEG and Long short-term memory learning system. IEEE Access. 2020;8:77255–77262. doi: 10.1109/ACCESS.2020.2989442. [DOI] [Google Scholar]
- 37.Srirangan M., Tripathy R.K., Pachori R.B. Time-frequency domain deep convolutional neural network and non-focal EEG signals. IEEE Sensors. 2020;20:3078–3086. [Google Scholar]
- 38.Poomipat B., Apiwat L., Jitkomut S. Automatic epileptic seizure onset-offset detection based on CNN in scalp EEG; Proceedings of the 2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP); Barcelona, Spain. 4–8 May 2020; pp. 1225–1229. [Google Scholar]
- 39.Raheel A., Sajid S., Syed A.H., Soltan A., Awais M.K. Epileptic seizure detection with a reduced montage: A way forward for Ambulatory EEG devices. IEEE Access. 2020;8:65880–65890. [Google Scholar]
- 40.Jose A., Mario R.A., Alejandro Z., Tripathy R.K., Pachori R.B. EEG-Rhythm specific Taylor-Fourier bank implemented with O-splines for the detection of epilepsy using EEG signals. IEEE Sensors. 2020;20:6542–6551. [Google Scholar]
- 41.Yang Y., Wanzhong C., Mingyang L., Tao J., Yun J., Xiao Z. Automatic focal and non-focal EEG detection using entropy based features from flexible analytic wavelet transform. Biomed. Signal Process. Control. 2020;57:101761. [Google Scholar]
- 42.Md Mosheyur R., Mohammed I.H.B., Anindya B.D. Classification of focal and non-focal EEG signals in VMD-DWT domain using ensemble stacking. Biomed. Signal Process. Control. 2019;50:72–82. [Google Scholar]
- 43.Wei Z., Mengqing L., Chenzhi Y., Qinghui W., Fenglin L., Ying W. Classification of focal and non-focal EEG signals using empirical mode decomposition (EMD), phase space reconstruction and neural networks. Artif. Intell. Rev. 2019;52:625–647. [Google Scholar]
- 44.Raghu S., Pradip S., Pachori R.B. Automated focal EEG signal detection based on third order cumulant function. Biomed. Signal Process. Control. 2020;58:101856. [Google Scholar]
- 45.Andrzejak R.G., Schindler K., Rummel C. Nonrandomness, nonlinear dependence, and nonstationarity of electroencephalographic recordings from epilepsy patients. Phys. Rev. E. 2012;86 doi: 10.1103/PhysRevE.86.046206. [DOI] [PubMed] [Google Scholar]
- 46.Andrzejak R.G., Lehnertz K., Mormann F., Rieke C., David P., Elger C.E. Indications of nonlinear deterministic and finite-dimensional structures in time series of brain electrical activity: Dependence on recording region and brain state. Phys. Rev. E. 2001;64 doi: 10.1103/PhysRevE.64.061907. [DOI] [PubMed] [Google Scholar]
- 47.Saka K., Aydemir Ö., Öztürk M. Classification of EEG Signals Recorded During Right/Left Hand Movement Imagery Using Fast Walsh Hadamard Transform Based Features; Proceedings of the 2016 39th International Conference on Telecommunications and Signal Processing (TSP); Vienna, Austria. 27–29 June 2016; pp. 413–416. [Google Scholar]
- 48.Sareen S., Sood S.K., Kumar S. An Automatic Prediction of Epileptic Seizures Using Cloud Computing and Wireless Sensor Networks. J. Med. Syst. 2016;40:226. doi: 10.1007/s10916-016-0579-1. [DOI] [PubMed] [Google Scholar]
- 49.Sareen S., Sood S.K., Kumar S. A Cloud-Based Seizure Alert System for Epileptic Patients That Uses Higher-Order Statistics. Cloud Comput. 2016;18:56–67. doi: 10.1109/MCSE.2016.82. [DOI] [Google Scholar]
- 50.Camara C., Peris-lopez P., Tapiador J.E. Human Identification Using Compressed ECG Signals. J. Med. Syst. 2015;39:148. doi: 10.1007/s10916-015-0323-2. [DOI] [PubMed] [Google Scholar]
- 51.Amira A., Bouridance A., Milligan P., Roula M. Novel FPGA implementations of Walsh-Hadamard transforms for signal processing. IEEE Proc. Image Signal Process. 2001;148:377–383. doi: 10.1049/ip-vis:20010674. [DOI] [Google Scholar]
- 52.Deveci T.C., Cakir S., Cetin A.E. Energy Efficient Hadamard Neural Networks. arXiv. 2018:1–15.1805.05421 [Google Scholar]
- 53.Jothiraj S.N., Selvaraj T.G., Ramasamy B., Deivendran N.P., Subathra M.S.P. Classification of EEG signals for detection of epileptic seizure activities based on feature extraction from brain maps using image processing algorithms. IET Image Process. 2018;12:2153–2162. doi: 10.1049/iet-ipr.2018.5418. [DOI] [Google Scholar]
- 54.Acharya U.R., Fujita H., Sudarshan V.K., Bhat S., Koh J.E.W. Application of entropies for automated diagnosis of epilepsy using EEG signals: A review. Knowl. Based Syst. 2015;88:85–96. doi: 10.1016/j.knosys.2015.08.004. [DOI] [Google Scholar]
- 55.Jord J., Oltra S. Noisy EEG signals classification based on entropy metrics. Performance assessment using first and second generation statistics. Comput. Biol. Med. 2017;87:141–151. doi: 10.1016/j.compbiomed.2017.05.028. [DOI] [PubMed] [Google Scholar]
- 56.Cao Y., Tung W., Gao J.B., Protopopescu V.A., Hively L.M., Way R., Jose S. Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. E. 2004;70:046217. doi: 10.1103/PhysRevE.70.046217. [DOI] [PubMed] [Google Scholar]
- 57.Nicolaou N., Georgiou J. Detection of epileptic electroencephalogram based on Permutation Entropy and Support Vector Machines. Expert Syst. Appl. 2012;39:202–209. doi: 10.1016/j.eswa.2011.07.008. [DOI] [Google Scholar]
- 58.Chen W., Wang Z., Xie H., Yu W. Characterization of Surface EMG Signal Based on Fuzzy Entropy. IEEE Trans. Neural Syst. Rehabil. Eng. 2007;15:266–272. doi: 10.1109/TNSRE.2007.897025. [DOI] [PubMed] [Google Scholar]
- 59.Xie H., Chen W., Liu H. Complexity analysis of the biomedical signal using fuzzy entropy measurement. Appl. Soft Comput. 2011;11:2871–2879. doi: 10.1016/j.asoc.2010.11.020. [DOI] [Google Scholar]
- 60.Xiang J., Li C., Li H., Cao R., Wang B., Han X., Chen J. The detection of epileptic seizure signals based on fuzzy entropy. J. Neurosci. Methods. 2015;243:18–25. doi: 10.1016/j.jneumeth.2015.01.015. [DOI] [PubMed] [Google Scholar]
- 61.Serap A., Hamdi M.S., Sadik K. Log Energy Entropy-Based EEG Classification with Multilayer Neural Networks in Seizure. Ann. Biomed. Eng. 2009;37:2626–2630. doi: 10.1007/s10439-009-9795-x. [DOI] [PubMed] [Google Scholar]
- 62.Bala R., Kumar D. Classification Using ANN: A Review. Int. J. Comput. Intell. Res. 2017;13:1811–1820. [Google Scholar]
- 63.Subasi A., Kiymk M.K., Alkan A., Koklukaya E. Neural network classification of EEG signals by using AR with MLE processing for epleptic seizure detection. Math. Comput. Appl. 2005;10:57–70. [Google Scholar]
- 64.Kumar N., Malik H. Automatic Classification for Neural Signals in Epilepsy Using Artificial Neural Network. EasyChair Prepr. 2018 doi: 10.29007/lfrr. [DOI] [Google Scholar]
- 65.Sharma B., Venugopalan P.K. Comparison of Neural Network Training Functions for Hematoma Classification in Brain CT Images. IOSR J. Comput. Eng. 2014;16:31–35. doi: 10.9790/0661-16123135. [DOI] [Google Scholar]
- 66.Lima C.A., Coelho A.L., Chagas S. Automatic EEG signal classification for epilepsy diagnosis with Relevance Vector Machines. Expert Syst. Appl. 2009;36:10054–10059. doi: 10.1016/j.eswa.2009.01.022. [DOI] [Google Scholar]
- 67.Acharya U.R., Sree S.V., Alvin A.P.C., Suri J.S. Use of principal component analysis for automatic classification of epileptic EEG activities in wavelet framework. Expert Syst. Appl. 2012;39:9072–9078. doi: 10.1016/j.eswa.2012.02.040. [DOI] [Google Scholar]
- 68.Übeyli E.D. Combined neural network model employing wavelet coefficients for EEG signals classification. Digit. Signal Process. 2009;19:297–308. doi: 10.1016/j.dsp.2008.07.004. [DOI] [Google Scholar]
- 69.Chatterjee S. Detection of focal electroencephalogram signals using higher-order moments in EMD-TKEO domain. Healthc. Technol. Lett. 2019;6:64–69. doi: 10.1049/htl.2018.5036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Fasil O.K., Rajesh R. Time-domain exponential energy for epileptic EEG signal classification. Neurosci. Lett. 2019;694:1–8. doi: 10.1016/j.neulet.2018.10.062. [DOI] [PubMed] [Google Scholar]
- 71.Chen Z., Lu G., Xie Z., Shang W. A Unified Framework and Method for EEG-Based Early Epileptic Seizure Detection and Epilepsy Diagnosis. IEEE Access. 2020;8:20080–20092. doi: 10.1109/ACCESS.2020.2969055. [DOI] [Google Scholar]
- 72.Gupta V., Pachori R.B. Classification of focal EEG signals using FBSE based flexible time-frequency coverage wavelet transform. Biomed. Signal Process. Control. 2020 doi: 10.1016/j.bspc.2020.102124. in press. [DOI] [Google Scholar]