Reconstruction of Bennu Particle Events From Sparse Data

Abstract

OSIRIS‐REx began observing particle ejection events shortly after entering orbit around near‐Earth asteroid (101955) Bennu in January 2019. For some of these events, the only observations of the ejected particles come from the first two images taken immediately after the event by OSIRIS‐REx's NavCam 1 imager. Without three or more observations of each particle, traditional orbit determination is not possible. However, by assuming that the particles all ejected at the same time and location for a given event, and approximating that their velocities remained constant after ejection (a reasonable approximation for fast‐moving particles, i.e., with velocities on the order of 10 cm/s or greater, given Bennu's weak gravity), we show that it is possible to estimate the particles' states from only two observations each. We applied this newly developed technique to reconstruct the particle ejection events observed by the OSIRIS‐REx spacecraft during orbit about Bennu. Particles were estimated to have ejected with inertial velocities ranging from 7 cm/s to 3.3 m/s, leading to a variety of trajectory types. Most (>80%) of the analyzed events were estimated to have originated from midlatitude regions and to have occurred after noon (local solar time), between 12:44 and 18:52. Comparison with higher‐fidelity orbit determination solutions for the events with sufficient observations demonstrates the validity of our approach and also sheds light on its biases. Our technique offers the capacity to meaningfully constrain the properties of particle ejection events from limited data.

Key Points

• We show how Bennu's particle ejection events can be reconstructed using only two observations

• For each event, we estimate the particle velocities and ejection location

• Velocities ranged from 7 cm/s to 3.3 m/s, and most observed events took place after noon

1. Introduction

NASA's Origins, Spectral Interpretation, Resource Identification, and Security Regolith Explorer (OSIRIS‐REx) spacecraft, launched in September 2016, entered orbit around near‐Earth asteroid (101955) Bennu for the first time on 31 December 2018 (Lauretta et al., 2017). One week later, on 6 January 2019, the TAGCAMS camera system onboard the OSIRIS‐REx spacecraft observed particles being ejected from the surface of Bennu (Hergenrother et al., 2019; Lauretta et al., 2019) in optical navigation (OpNav) images taken by its NavCam 1 imager (Bos et al., 2018). This ejection event was captured by chance during an OpNav imaging campaign that included two long‐exposure (5 s) images of Bennu taken roughly 7 min apart every 2 hr (Lauretta, Hergenrother, et al., 2019). As a result of this relatively low imaging cadence, the only images that contained observations of particles ejected during this event were the two long‐exposure images taken immediately following it. Traditional orbit determination (OD) requires at least three observations for reliable trajectory estimation. Therefore, in the absence of a third observation of the particles ejected during this event, we developed a new technique to estimate the particles' trajectories given only two observations. This technique relies on the assumption that all the particles were ejected from the exact same location and the approximation that the particle velocities remained constant after ejection. This constant velocity approximation is reasonable for fast‐moving particles observed soon after ejection given the weak gravity of Bennu, which has an average surface acceleration of 0.00006 m/s² (Barnouin et al., 2019; Scheeres et al., 2019). Traditional OD techniques using high‐fidelity force models allow for more accurate and precise particle trajectory and ejection location estimation, but our technique makes it possible to characterize all of the observed particle events, including those with too few observations for OD.

Since the initial discovery of the particle ejection phenomenon, the OSIRIS‐REx team has observed several more ejection events with NavCam. During orbital operations in January 2019, the cadence of long‐exposure NavCam images was increased from every 2 hr to every 30 min, and then later to every 20 min, to better capture particle ejection events (Lauretta, Hergenrother, et al., 2019). As a result of the increased imaging cadences, some of the particles from subsequent ejection events were observed in three or more images. This allows for higher‐fidelity particle trajectory estimation by traditional OD, which provides an independent solution for the ejection time and location of the associated events (Leonard et al., 2020). Independent solutions generated through traditional OD enable us to verify the results of our newly developed two‐image technique and offer insight into the error introduced by its assumptions and approximations.

Here we outline the methodology for this new approach, including relevant derivations. We then apply it to estimate the ejection locations and particle velocities for 11 ejection events observed by NavCam 1 during the Orbital A, Detailed Survey, and Orbital B mission phases (Lauretta et al., 2017). Finally, we compare our results to independent OD results for two of these events for which we have observations of the same particles in three or more images: the 19 January and 11 February events.

2. Method

2.1. Detections and Track Identification

For a given ejection event, the two NavCam images taken immediately after the event were corrected for distortion, registered on the center of Bennu, and differenced to highlight any objects moving with respect to Bennu. Stars were distinguished from particles by making use of the fact that, unlike particles, all stars in an image pair have the same apparent motion with respect to Bennu.

For each event, a pattern of nonstellar point sources near the limb of Bennu was observed in the first image that repeated itself in the second image, but farther from the limb and more spread out. Associated pairs of detections (tracks) were made from this pattern and used for the radiant estimation and particle state determination. Point source centroiding for most of the particles was provided by the automated object detection capabilities of the Goddard Image Analysis and Navigation Tool (GIANT), described in detail by Liounis et al. (2020). Particles that were not automatically detected by GIANT were manually added to the data set using the KinetX Image Processing (KXIMP) optical navigation software suite (Jackman & Dumont, 2013; Jackman et al., 2017). There were very few point source detections added this way (<1%) as the vast majority were automatically detected by GIANT.

Some detected particles presented as streaks or trails in one or more images and therefore provided position information for the object at both the start and end of the image exposure. If a streak was present in both images for an event, it could be treated as a four‐epoch track. All of these streaked particles were manually added to the data set as the GIANT automatic object detection is not sensitive to streaked objects. A least squares streak fitting algorithm was used to determine the end points of each streak while taking the imager's point spread function into account.

2.2. Radiant Point Estimation

Using the two observations for each particle, the common radiant point of all the particles within the image could be estimated by assuming that all particles ejected from the same location and that the particles' velocities remained constant in magnitude and direction after ejection and thus traveled in straight lines within the differenced image. The radiant point was found by performing a least squares estimation of the intersection point of all the lines connecting the two sets of observations, as shown in Figure 1. The root‐mean‐square distance from the point of closest approach of each line to the estimated radiant point was used for the 1‐sigma uncertainty. The assumption that the particles traveled in straight lines introduced a bias into our radiant point solution based on the particle velocities and the time between ejection and the first image, as discussed further in section 4.

Figure 1.

Track identification and radiant point estimation for the 6 January event. Bennu is saturated in the long‐exposure NavCam images used to create this figure, so no surface detail is visible (see the image processing description in Lauretta, Hergenrother, et al., 2019). (a) The NavCam images of the event are registered and differenced. Objects from the first image appear white, and objects from the second image appear black. (b) Particles detected in both images allow us to find a repeated pattern, (c) which is used to make associations that show the particles' apparent motion. (d) When the apparent motion is traced backward, the lines intersect at a common radiant point (red cross) on Bennu.

2.3. Ejection Epoch Estimation

The epoch (moment in time) that each particle ejected from the radiant point was estimated by comparing the angular displacements of each observation from the radiant point. To infer the 3‐D states of the particles, our assumptions of a common ejection location and constant particle velocities lead to a requirement within the model that all particles ejected at the same time, but when only two observations are available, the ejection epoch is nondeterministic and coupled with ambiguity in the orientation of the ejecta cone. To obtain an estimate of the ejection epoch for these events, the trajectories were initially constrained to the image plane, and therefore, the observation angle rate was constrained to be constant. This causes particles traveling toward or away from the spacecraft to predict later or earlier event times, respectively. The time of the event was taken as the median of the times estimated using each individual particle, and the standard deviation of the times was used for the 1‐sigma uncertainty. By taking the median time, we are assuming that the median particle is traveling within the image plane, effectively centering the ejecta cone around the image plane. The image plane has no physical connection to the ejection event, but it is a reasonable approximation to assume that the ejecta cone is centered around the image plane because these events occurred close to the limb from the perspective of the spacecraft—the geometry that provides the best viewing conditions for observing ejection events. A possible future improvement to this technique would be to use the surface normal vector at the ejection location to constrain the orientation of the ejecta cone instead of the image plane.

When there were streaked objects captured in both of the images, a more robust method was used to determine the time that each object left the radiant point, given by equation (20). Three observations allow for a deterministic solution of the event epoch that removes the ejecta cone orientation ambiguity. This method essentially uses the successive streak lengths to infer whether each particle is moving toward or away from the camera. If the streak is longer in the second image, this is interpreted as the particle traveling toward the camera at constant velocity, and if the streak is shorter in the second image, this is interpreted as the particle traveling away from the camera at constant velocity. The full derivation for this solution is provided in section 6. Streaked objects captured in both images provided four observations (at the beginning and end of each image's exposure), so event epoch estimates were found by taking the average of the epochs estimated using different combinations of three observations for each streaked particle.

2.4. Ejection Location Estimation and Uncertainty

The radiant point within the image corresponds to two unique solutions for the 3‐D ejection location on the surface of Bennu: a point closer to the spacecraft on the near side of Bennu and a point on the far side of Bennu, out of view of the camera. The ray‐tracing routines in the NAIF SPICE toolkit (Acton, 1996; Acton et al., 2017) were used to determine these two surface locations. Rays were traced from the spacecraft's location at the time of the first image toward the estimated radiant point to find where they intersect the Bennu shape model using the asteroid rotation state at the estimated event time. This provided the solution for the point on the near side of Bennu. To obtain the solution on the far side of Bennu, the vertex was placed along the spacecraft‐to‐radiant vector but on the opposite side of Bennu, and the ray was traced back toward the spacecraft.

The uncertainty in the surface location of the estimated origin point was found by sampling both the pixel‐space radiant point uncertainty and the event time uncertainty at their 3‐sigma values and then performing the same ray‐tracing method as described. The Mersenne Twister Monte Carlo method (Matsumoto & Nishimura, 1998) was used to verify the statistical validity of the resulting 3‐sigma contours by sampling a simple Gaussian distribution of the event time and radiant point uncertainties and then again performing the ray tracing.

If the images were taken long enough after the event that the estimated radiant point did not fall on the disk of Bennu (a variable amount of time depending on the event), as was the case for the 11 February event (discussed further in section 4), the uncertainties were inflated by increasing integer factors until the Monte Carlo method resulted in ray tracing that intersected the body. For the 11 February event, this meant increasing our radiant point uncertainty by a factor of 5. The mean of the Monte Carlo results that intersected the body was then used for the ejection location solution.

2.5. Three‐Dimensional Object States

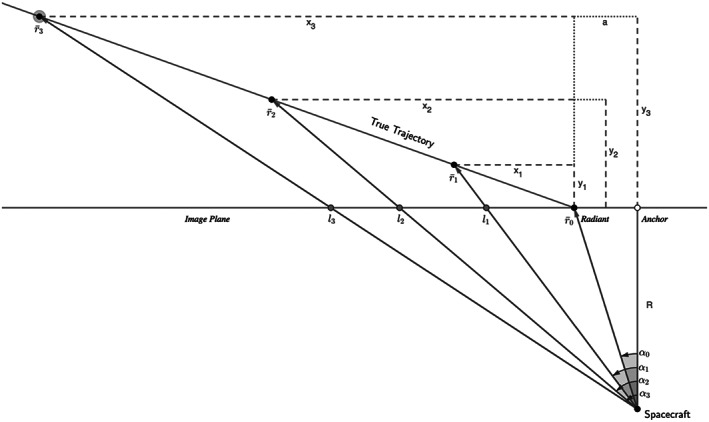
Three‐dimensional object states were inferred by comparing the observed observation angle rate to the observation angle rate expected for an object at the same angular displacement from the radiant that left the origin point at the estimated event time and traveled perfectly within the plane of the image (perpendicular to the camera's boresight). Particles appearing faster than the expected in‐plane rate were inferred to be moving toward the camera, and objects appearing slower than the in‐plane rate were inferred to be moving away from the camera. This again assumed that the objects experienced no accelerations (they were traveling in straight lines) and that every particle was ejected at the same time. The linear geometry that results from these assumptions is shown in Figure 2.

Figure 2.

The linear geometry that results from assuming that the particles' velocities remain constant. A particle following a linear trajectory connecting the 3‐D positions ${\overline{r}}_{1,2,3}$ appears within the image at the locations l _1,2,3 when observed at the times t _1,2,3. The x and y components of each 3‐D position with respect to the radiant point are also shown where the x direction is parallel to the line connecting the observations within the image plane, and the y direction is parallel to the camera boresight. The z direction completes the right‐hand rule, such that the z component of each position is zero.

By combining this 3‐D information with the two solutions for the ejection location on the surface of Bennu, we found the 3‐D positions of each object. The 3‐D velocities were then calculated using the position of each object at the two image times. There are two unique solutions for each object's position and velocity that correspond to the two unique solutions for the ejection location. The full derivation for this 3‐D projection is provided in section 6.

3. Results

Our technique was first used to reconstruct the 6 January event, producing the 3‐D visualization of the event shown in Figure 3 that includes 117 analyzed particles. We then applied the technique to 10 other ejection events observed by OSIRIS‐REx, ranging from 2 to 30 analyzed particles. The results of the reconstruction of the three events with the most observed particles (6 January, 19 January, and 11 February 2019) are summarized in Table 1, and the results for the eight smaller events are summarized in Table 2. Our solutions for the event surface locations, shown in Figure 4, were mostly at midlatitudes between 14°N and 47°N. The exception was the 6 January event, which was estimated to have occurred between about 57°S and 75°S. In addition, most of the events had similar local solar times (LSTs), occurring in the late afternoon as seen in Figure 5. All but two of the smaller events had LSTs between 12:44 and 18:52 with a median LST of 17:22.

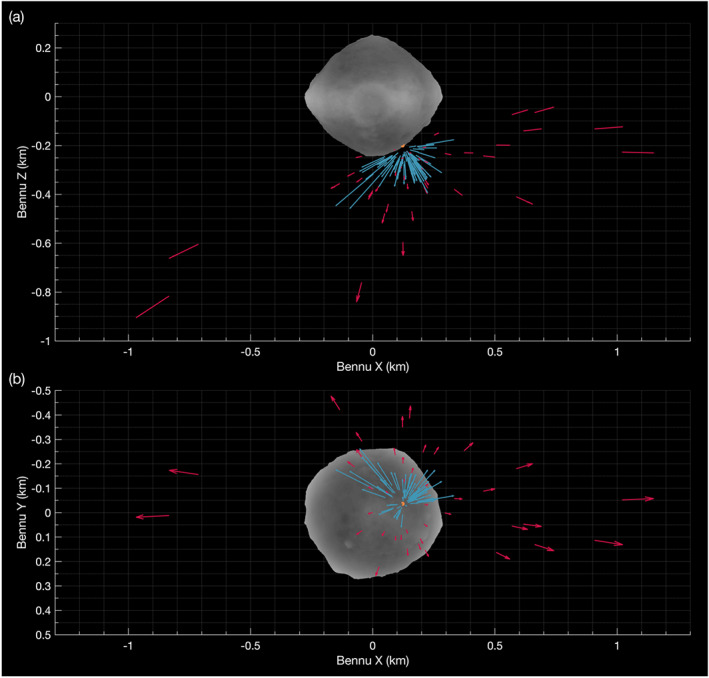
Figure 3.

The 6 January ejection event reconstruction shown from (a) Bennu's −Y side and (b) Bennu's south (−Z) pole on a shape model of the asteroid. Vectors originate from the particles' estimated positions at the time of the first image of the event (20:56:13 UTC) and point in the velocity vector direction. Vector lengths show distance traveled over roughly 7 min for particles detected in two images (blue) or 1 min for the higher‐velocity particles that appeared as streaks in a single image (red). Also shown is the estimated ejection location (orange dot).

Table 1.

Reconstruction of the Largest Observed Particle Ejection Events

Event date and		6 January 2019		19 January 2019		11 February 2019
time (UTC, ±1σ)		20:50:28 ± 47 s		00:53:55 ± 40 s		23:28:35 ± 38 s
Ejection location		Near	Far	Neara	Far	Nearb	Far
Latitude (°, ±3σ)		$-75.0_{-2.8}^{+12.7}$	$-57.3_{-17.5}^{+1.5}$	$46.6_{-6.0}^{+2.9}$	$23.2_{-3.8}^{+5.7}$	$11.0_{-6.6}^{+7.9}$	$25.2_{-9.8}^{+11.3}$
Longitude (°, ±3σ)		$325.3_{-10.3}^{+18.9}$	$343.7_{-14.7}^{+3.8}$	$327.7_{-3.5}^{+4.6}$	$334.2_{-3.9}^{+3.7}$	$59.7_{-7.5}^{+8.1}$	$60.1_{-8.0}^{+8.2}$
Local solar time (±3σ)		$15:22_{-00:36}^{+01:06}$	$16:35_{-01:05}^{+00:06}$	$16:10_{-00:06}^{+00:09}$	$16:36_{-00:06}^{+00:04}$	$18:12_{-00:22}^{+00:24}$	$18:13_{-00:23}^{+00:24}$
Particles analyzedb		117		13		30
Inertial	Minc	0.069	0.072	0.482	0.511	0.086	0.090
particle	Median	0.210	0.220	0.851	0.902	0.131	0.136
velocities	Mean	0.464	0.486	0.866	0.918	0.151	0.158
(m/s)	Maxb	3.111	3.261	1.221	1.294	0.511	0.533

^a The near solutions for the 19 January and 11 February events were ruled out as possibilities by Leonard et al. (2020) based on higher‐fidelity OD analysis enabled by three or more observations (see section 4).

^b Slower particles were observed in later images that are not included in this analysis.

^c Particles were observed up to the edge of the image fields of view, meaning that if there were any faster particles, they would not have been observed.

Table 2.

Reconstruction of the Smaller Observed Particle Ejection Events

Event date and	Ejection Location (±3σ)				Inertial particle velocities (m/s)
time (UTC, ±1σ)	Latitude (°)	Longitude (°)	Local solar time	Particles analyzed	Min	Mean	Median	Max
29 January 2019	Near $17.19_{-3.79}^{+1.28}$	$102.11_{-1.11}^{+1.25}$	18:52±00:03	4	0.114	0.142	0.135	0.184
00:12:14 ± 7 s
4 February 2019	Far   $32.72_{-12.42}^{+11.05}$	$109.74_{-15.44}^{+17.60}$	$18:25_{-00:47}^{+00:53}$	4	0.133	0.179	0.171	0.242
06:18:04 ± 67 s
5 February 2019	Near $46.68_{-48.06}^{+19.63}$	$60.89_{-111.84}^{+98.91}$	$17:22_{-07:27}^{+05:53}$	3	0.178	0.229	0.195	0.314
04:04:28 ± 415 s
8 February 2019	Near $40.35_{-0.65}^{+0.71}$	$238.66_{-1.36}^{+1.47}$	12:44±00:04	3	0.359	0.404	0.420	0.435
06:29:52 ± 17 s
8 February 2019	Far $33.89_{-13.27}^{+8.76}$	$309.66_{-12.35}^{+16.34}$	$01:34_{-00:46}^{+01:00}$	2	0.200	0.203	0.203	0.206
20:49:32 ± 22 s
12 February 2019	Near 39.13 ${}_{-44.45}^{+45.68}$	32.08 ${}_{-66.89}^{+59.64}$	21:11 ${}_{-03:34}^{+03:50}$	3	0.196	0.317	0.335	0.420
08:55:45 ± 239 s	Far 23.97 ${}_{-61.29}^{+60.83}$	125.70 ${}_{-67.33}^{+67.44}$	03:26 ${}_{-03:47}^{+03:24}$		0.230	0.372	0.393	0.493
19 April 2019	Near $14.53_{-18.88}^{+20.90}$	$265.34_{-77.81}^{+50.53}$	$18:14_{-02:54}^{+01:39}$	18	0.099	0.237	0.221	0.506
01:46:52 ± 639 s
18 June 2019	Near $16.26_{-5.83}^{+5.61}$	$291.24_{-6.06}^{+7.24}$	17:32±00:07	7	0.411	0.702	0.564	1.585
12:54:01 ± 79 s

Note. Only near or far solution shown when one solution could be ruled out either through independent solutions from Leonard et al. (2020) or through observations of particles in front of Bennu indicating that the far solution was not plausible.

Figure 4.

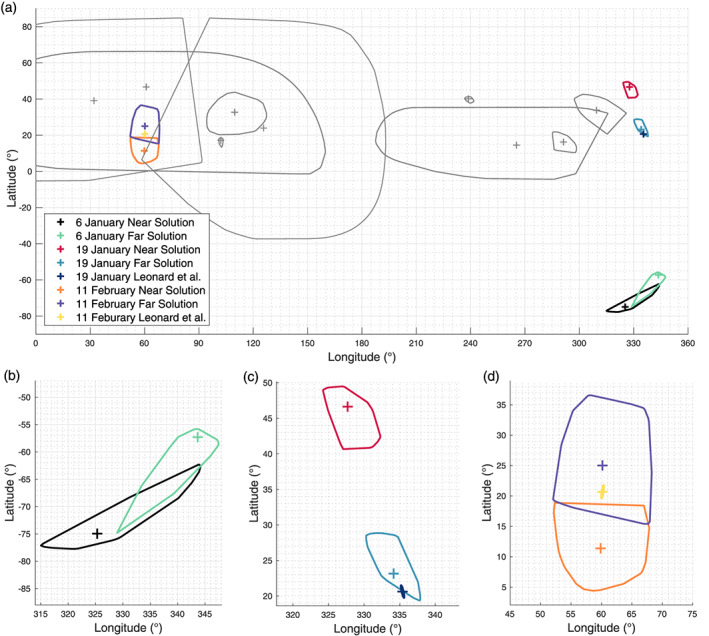
(a) Ejection location solutions for all events shown with 3‐sigma uncertainties on a global grid. The three largest observed events (Table 1) are shown in color as specified in the legend. Eight smaller events (Table 2) are shown in gray. (b–d) Locations of the three events with the most observed particles: (b) 6 January, (c) 19 January, and (d) 11 February. Also shown are the independent solutions for the 19 January and 11 February events from Leonard et al. (2020).

Figure 5.

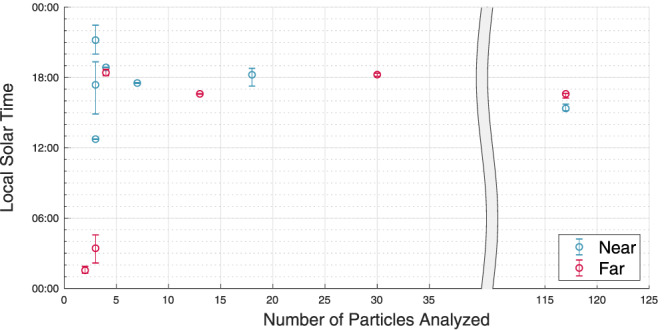
Estimated local solar times for all analyzed ejection events with error bars indicating 1‐sigma uncertainties. Both near and far solutions are shown for all events except those for which one solution could be ruled out either through independent solutions from Leonard et al. (2020) or through observations of particles in front of Bennu indicating that the far solution was not plausible.

We estimated inertial particle ejection velocities from 7 cm/s to 3.3 m/s in a wide cone of directions (as seen in Figures 3 and 6). The ejection velocities were similar across most of the observed events, but no velocities above 50 cm/s were estimated in the smaller events (those with fewer than five analyzed particles) as seen in Table 2. The greatest range of velocities was seen in the larger events, especially the 6 January event, but there exists an observational bias in this analysis. We can only use this technique to estimate velocities for those particles that were either observed in both of the first two images of the event or that appeared as streaks (allowing us to treat the endpoints of the streak as two separate observations in time). In some of the events, there were particles without two observations in the first two images whose velocities therefore could not be estimated. This is especially true for the 19 January event where at least 30 slower‐moving particles were observed in later images that did not appear in the first images of the event and thus were not included in this analysis. We only included particles observed in the first two images due to the error associated with using slower‐moving particles with this technique, as discussed in section 4. In addition, in many events we observed particles up to the edge of the image fields of view, meaning that if there were any faster‐moving particles, they would not have been observed. Therefore, there are likely particles ejecting with velocities outside the range presented here.

Figure 6.

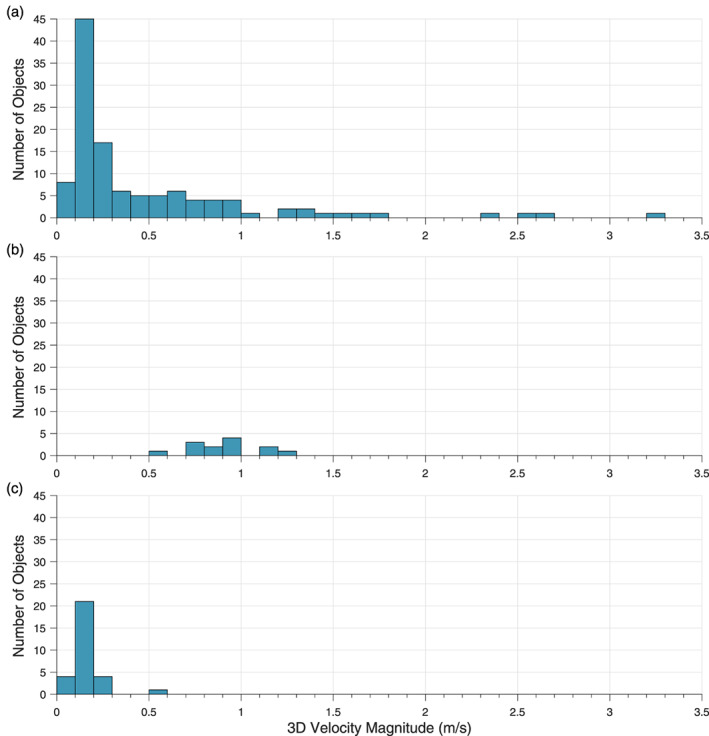
Ejection velocity magnitudes of the particles analyzed for the three largest ejection events on (a) 6 January, (b) 19 January, and (c) 11 February. Far solution velocities are shown for all three events.

The ejection velocities range from well below to well above Bennu's approximate escape velocity of 20 cm/s (Lauretta et al., 2019; Scheeres et al., 2019), which indicates that the particles are being ejected into a variety of trajectory types. The fastest‐moving particles are ejected into hyperbolic escape trajectories that take them out of Bennu's gravitational sphere of influence within several minutes, while particles ejected at velocities close to the escape velocity can enter orbital trajectories. Lauretta, Hergenrother, et al. (2019) find that particles ejected with velocities in the range of 15 to 20 cm/s have longer‐lived orbital trajectories. Of the 194 particles included in our analysis across all 11 events, we estimated 48 (25%) to have ejection velocities in this range. Particles ejected with slower velocities likely enter suborbital trajectories that reimpact the surface soon after the event (Lauretta et al., 2019; Leonard et al., 2020).

Two of the events, 19 January and 18 June, featured streaked objects in both of the two images, which allowed us to employ the more robust “3‐epoch” method of estimating the ejection time (described in the section 2.3) that provides additional information about the 3‐D orientation of the ejecta cone. For the 19 January event, this method estimated an event time roughly 40 s later than the simpler “2‐epoch” method, indicating that most of the particles were traveling away from the spacecraft. This suggests that the far ejection location solution is more likely, which is consistent with the independent solution from Leonard et al. (2020). For the 18 June event, the 3‐epoch method estimated an event time almost two minutes earlier than the 2‐epoch method. This indicates that all of the particles were traveling toward the spacecraft, suggesting that the near ejection location is much more likely. This is consistent with the fact that particles were observed in front of the disk of Bennu in the images of this event, effectively ruling out the far ejection location solution as a possibility. For both events, the more robust ejection time solution was used for all the results presented here.

4. Verification and Error Analysis

Due to the increased image cadence after the discovery of the 6 January event, many of the subsequent events had greater imaging coverage, which allowed for an independent solution for the ejection location of these events using traditional OD (Leonard et al., 2020). These results validate our newly developed technique and shed light on potential biases in our solution due to the approximations that we made. Here we will compare our results to the OD solutions for the events on 19 January and 11 February, the next two largest observed events after the 6 January event. The OD solutions for the ejection locations are much closer to the far solutions for both of these events, as seen in Figure 4, effectively ruling out the near solution as a possibility for each. Similarly, we were able to rule out either the near or far solution for most of the smaller events as indicated by the results presented in Table 2.

The approximation that the particle velocities remain constant after ejection introduces a bias and increases the uncertainty in our solutions dependent on the elapsed time between the event and the imaging, as well as the speed of the particles. Our technique works best for fast‐moving particles ejected into hyperbolic escape trajectories where a linear trajectory remains a reasonable approximation for several minutes after ejection. These are particles ejected at velocities higher than Bennu's escape velocity of ∼20 cm/s (Lauretta et al., 2019; Scheeres et al., 2019) with the fastest particles having the least amount of error. Slower‐moving particles will deviate from the linear trajectory as they curve back toward Bennu under the influence of its gravity. The more time that passes between ejection and imaging, the less accurately the linear approximation will be able to reconstruct these particles' ejection states, and eventually, the solution becomes too uncertain to be meaningful or useful. In general, we consider a solution meaningful if the ejection location can be constrained to within roughly a quarter hemisphere of Bennu (3σ) and the LST can be constrained to either an a.m. or p.m. time (3σ). If an event had uncertainties larger than this, then we would no longer consider the solution meaningful or useful. In addition to increasing the uncertainty in the solution, this effect will bias our radiant point solution toward the limb, eventually moving the solution off‐body. This is clearly seen in the results for the 11 February event, where almost all of the particles' estimated velocities were less than 20 cm/s, and the first image was not taken until approximately 12 min after ejection. Assuming that these particles traveled in straight lines leads to a radiant point solution that is not on the surface of Bennu, as seen in Figure 7. This same effect will bias our estimate of the event time to later than when it actually occurred because the particles will seem closer to the radiant point, thus shortening the apparent travel time since ejection.

Figure 7.

The 11 February event radiant point estimation using the registered and differenced NavCam images. The slower‐moving particles have begun to curve back toward Bennu under the influence of its gravity. If we assume that they travelled in straight lines and trace their paths backward (yellow vectors), the estimated radiant point (red cross) is off‐body, showing the biasing effect of the approximations that we made with respect to the independent OD solution of Leonard et al. (2020) (blue cross, on body).

This bias is seen for both the 19 January and 11 February events when we compare our estimated radiant points and event times to the OD solutions of Leonard et al. (2020). For 19 January, our far ejection location solution is roughly 3‐sigma away from the OD solution, biased toward the limb from the perspective of the spacecraft. The OD solution for the ejection time (00:53:41 UTC ± 4 s) is well within our 1‐sigma uncertainty, but our solution is 14 s later. The 11 February event was much more biased, with the estimated radiant point off‐body and our estimated ejection time over 1 min later than the OD solution (23:27:28 UTC ± 6 s). To get an on‐body ejection location for this event, we inflated our radiant point uncertainty five times and used the mean value of the Monte Carlo ray traces that intersected the body, as discussed in section 2.

Future analysis may allow us to estimate and add a correction factor to our technique, based on particle velocities and the time between ejection and the first image, that we can use to refine our radiant point solution for those events for which the higher‐fidelity OD is not feasible or reliable due to a scarcity of data.

5. Conclusion

Particles are being ejected periodically from the surface of near‐Earth asteroid Bennu. We developed a new technique to analyze particle ejection events for which there is a scarcity of imaging data and applied it to 11 ejection events observed by OSIRIS‐REx during proximity operations. This analysis indicates that most events occurred at similar times of day (LST). We estimated ejection velocities in the range of 7 cm/s to 3.3 m/s, with particles dispersing in a wide cone of directions on a variety of trajectory types. A comparison with the independent ejection location solutions produced through OD verified our technique. It also revealed the biasing effect of our assumptions and approximations, which could allow us to add corrections to our technique in the future. Our technique will be applied to any future events that are observed as OSIRIS‐REx continues to explore Bennu, further shedding light on the characteristics and nature of this phenomenon.

6. Derivations

6.1. Nomenclature

Radiant

= The ejection location. There are two possible locations for each event (near and far).

ImagePlane

= The plane perpendicular to the camera's boresight and containing the ejection location. There is one image plane for each ejection location solution (near and far).

Anchor

= The closest point to the spacecraft in the image plane along the line defined by particle observations. Each particle has a unique anchor point.

t_i

= ith observation epoch.

l_i

= ith observation location within the image with respect to the radiant.

α_i

= ith observation's angular displacement from the anchor.

a

= Distance between anchor point and radiant.

R

= Distance between spacecraft and anchor.

${\overline{r}}_i$

= 3‐D vector from spacecraft to location of particle at timet _i.

${\overline{r}}_{sc-l_i}$

= 3‐D vector from spacecraft to the in‐image‐plane observation locationl _i.

x_i

= In‐plane component of particle position at timet _i with respect to the ejection location.

y_i

= Out‐of‐plane component of particle position at timet _i with respect to the ejection location.

ω_ij

= Observation angle rate ( $\dot{\alpha }$) computed using thei _th andj _th observations (or the estimated radiant point for index 0).

t₀

= Ejection epoch.

Subscripts

 

i

= ith detection epoch index

0

= radiant epoch index

6.2. Equations

By using similar triangles defined by the detection angles α,

$$\frac{x_i+a}{y_i+R}=\frac{l_i+a}{R}.$$ (1)

And by assuming constant 3‐D (true) velocity,

$$\frac{y_j}{t_j-t_0}=\frac{y_i}{t_i-t_0},$$ (2)

$$\frac{x_j}{t_j-t_0}=\frac{x_i}{t_i-t_0}.$$ (3)

Given these three sets of equations and n observations,

$$\begin{array}{ccc}\hfill & \text{\# unknowns}=\hfill & \hfill 2n+1,\\ \hfill & \text{\# knowns}=\hfill & \hfill n+2(n-1)=3n-2.\end{array}$$

Therefore, three observations constrain the ejection epoch and 3‐D velocities. More than three gives multiple solutions that can be averaged. If only two observations are available, an ambiguity exists between the coupled ejection epoch and the direction of the particle's 3‐D velocity.

$$\begin{array}{ccc}\hfill n& =2\hfill & \hfill \text{underconstrained},\\ \hfill n& =3\hfill & \hfill \text{deterministic},& \hfill \\ \hfill n& >3\hfill & \hfill \text{overconstrained}.\end{array}$$

6.3. Ejection Epoch Given Two Observations

When only two observations were available, the observation angle rate was initially assumed to have remained constant since ejection.

$$\frac{l_j-l_i}{t_j-t_i}=\frac{l_i}{t_i-t_0},$$ (4)

$$t_0=t_i-\frac{l_i}{l_j-l_i}(t_j-t_i).$$ (5)

6.4. Ejection Epoch Given Three or More Observations

From equation (1),

$$\begin{array}{ccc}\hfill R(x_i+a)& =(l_i+a)(y_i+R),\hfill & \hfill \\ \hfill R{x}_i+Ra& =l_i{y}_i+a{y}_i+l_{i}R+aR,\hfill \\ \hfill x_i& =\frac{l_i+a}{R}{y}_i+l_i.\hfill \end{array}$$ (6)

Now, letting τ _i = t _i − t ₀, equations (2) and (3) become

$$\frac{y_i}{y_j}=\frac{{\tau }_i}{{\tau }_j},$$ (7)

$$\frac{x_i}{x_j}=\frac{{\tau }_i}{{\tau }_j}.$$ (8)

Substituting equation (6) into equation (8),

$$\begin{array}{ccc}\hfill \frac{\frac{(l_i+a)}{R}{y}_i+l_i}{\frac{(l_j+a)}{R}{y}_j+l_j}& =\frac{{\tau }_i}{{\tau }_j},\hfill & \hfill \\ \hfill \frac{(l_i+a)y_i+l_{i}R}{(l_j+a)y_j+l_{j}R}& =\frac{{\tau }_i}{{\tau }_j},\hfill \\ \hfill \frac{m_i{y}_i+n_i}{m_j{y}_j+n_j}& =\frac{{\tau }_i}{{\tau }_j}.\hfill \end{array}$$ (9)

Setting j = 1 and letting m _i = l _i + 1, n _i = l _i R, and ${\delta }_i=\frac{{\tau }_i}{{\tau }_1}$,

$$\frac{m_i{y}_i+n_i}{m_1{y}_1+n_1}={\delta }_i,$$ (10)

and from equation (6),

$$y_i={\delta }_i{y}_1.$$ (11)

Combining (10) and (11) gives

$$\begin{array}{ccc}\hfill \frac{m_i{\delta }_i{y}_1+n_i}{m_1{y}_1+n_1}& ={\delta }_i\hfill & \hfill \\ \hfill m_i{\delta }_i{y}_1+n_i& =m_1{\delta }_i{y}_1+n_1{\delta }_i\hfill \\ \hfill (m_i-m_1){\delta }_i{y}_1& =n_1{\delta }_i-n_i\hfill \\ \hfill y_1& =\frac{n_1{\delta }_i-n_i}{(m_i-m_1){\delta }_i}.\hfill \end{array}$$ (12)

Let i = 2, 3, and equate

$$\begin{array}{ccc}\hfill \frac{n_1{\delta }_2-n_2}{(m_2-m_1){\delta }_2}& =\frac{n_1{\delta }_3-n_2}{(m_3-m_1){\delta }_3}\hfill & \hfill \\ \hfill (n_1{\delta }_2-n_2)(m_3-m_1){\delta }_3& =(n_1{\delta }_3-n_3)(m_2-m_1){\delta }_2\hfill \\ \hfill n_1(m_3-m_1){\delta }_2{\delta }_3-n_2(m_3-m_1){\delta }_3& =n_1(m_2-m_1){\delta }_2{\delta }_3-n_3(m_2-m_1){\delta }_2\hfill \\ \hfill n_1(m_3-m_2){\delta }_2{\delta }_3+n_3(m_2-m_1){\delta }_2-n_2(m_3-m_1){\delta }_3& =0\hfill \\ \hfill n_1(m_3-m_2)\frac{{\tau }_2{\tau }_3}{{\tau }_1^2}+n_3(m_2-m_1)\frac{{\tau }_2}{{\tau }_1}-n_2(m_3-m_1)\frac{{\tau }_3}{{\tau }_1}& =0\hfill \\ \hfill n_1(m_3-m_2){\tau }_2{\tau }_3+n_3(m_2-m_1){\tau }_2{\tau }_1-n_2(m_3-m_1){\tau }_3{\tau }_1& =0.\hfill \end{array}$$ (13)

Expanding the terms,

$$\begin{array}{ccc}\hfill {\tau }_i{\tau }_j& =(t_i-t_0)(t_j-t_0)\hfill & \hfill \\ \hfill & =t_i{t}_j-(t_i+t_j)t_0+t_0^2.\hfill \end{array}$$ (14)

Substituting (14) into (13) and letting k _ij = m _i − m _j, T _ij = t _i t _j, and q _ij = t _i + t _j,

$$\begin{array}{ccc}\hfill n_1{k}_{32}(T_{32}-q_{32}{t}_0+t_0^2)& \hfill & \hfill \\ \hfill +n_3{k}_{21}(T_{21}-q_{21}{t}_0+t_0^2)& \hfill \\ \hfill +n_2{k}_{31}(T_{31}-q_{31}{t}_0+t_0^2)& =0\hfill \\ \hfill [n_1{k}_{32}+n_3{k}_{21}-n_2{k}_{31}]t_0^2+[n_2{k}_{31}{q}_{31}-n_1{k}_{32}{q}_{32}-n_3{k}_{21}{q}_{21}]t_0+& [n_1{k}_{32}{T}_{32}+n_3{k}_{21}{T}_{21}-n_2{k}_{31}{T}_{31}]=0\hfill \\ \hfill a{t}_0^2+b{t}_0+c& =0.\hfill \end{array}$$ (15)

Expanding the coefficients,

$$\begin{array}{ccc}\hfill a& =n_1{k}_{32}+n_3{k}_{21}-n_2{k}_{31}\hfill & \hfill \\ \hfill & =n_1(m_3-m_2)+n_3(m_2-m_1)-n_2(m_3-m_1)\hfill \\ \hfill & =l_{1}R(l_3-l_2)+l_{3}R(l_2-l_1)-l_{2}R(l_3-l_1)\hfill \\ \hfill & =R[l_1{l}_3-l_1{l}_2+l_3{l}_2-l_3{l}_1-l_2{l}_3+l_2{l}_1]\hfill \\ \hfill a& =0,\hfill \end{array}$$ (16)

$$\begin{array}{ccc}\hfill b& =n_2{k}_{31}{q}_{31}-n_1{k}_{32}{q}_{32}-n_3{k}_{21}{q}_{21}\hfill & \hfill \\ \hfill & =l_{2}R(l_3-l_1)(t_3+t_1)-l_{1}R(l_3-l_2)(t_3+t_2)-l_{3}R(l_2-l_1)(t_2+t_1)\hfill \\ \hfill & =R[(l_2(l_3-l_1)-l_3(l_2-l_1))t_1+(-l_1(l_3-l_2)-l_3(l_2-l_1))t_2\hfill \\ \hfill & +(l_2(l_3-l_1)-l_1(l_3-l_2))t_3]\hfill \\ \hfill b& =R[l_1(l_3-l_2)t_1+l_2(l_1-l_3)t_2+l_3(l_2-l_1)t_3],\hfill \end{array}$$ (17)

$$\begin{array}{ccc}\hfill c& =l_{1}R(l_3-l_2)t_3{t}_2+l_{3}R(l_2-l_1)t_2{t}_1-l_{2}R(l_3-l_1)t_3{t}_1\hfill & \hfill \\ \hfill c& =R[l_1(l_3-l_2)t_3{t}_2+l_2(l_1-l_3)t_3{t}_1+l_3(l_2-l_1)t_2{t}_1].\hfill \end{array}$$ (18)

Substituting these values in and solving for the ejection epoch t ₀,

$$\begin{array}{ccc}\hfill a{t}_0^2+b{t}_0+c& =0\hfill & \hfill \\ \hfill 0+b{t}_0+c& =0\hfill \\ \hfill t_0& =-\frac{c}{b}\hfill \\ \hfill & =-\frac{R[l_1(l_3-l_2)t_3{t}_2+l_2(l_1-l_3)t_3{t}_1+l_3(l_2-l_1)t_2{t}_1]}{R[l_1(l_3-l_2)t_1+l_2(l_1-l_3)t_2+l_3(l_2-l_1)t_3]}\hfill \\ \hfill t_0& =-\frac{[l_1(l_3-l_2)t_3{t}_2+l_2(l_1-l_3)t_3{t}_1+l_3(l_2-l_1)t_2{t}_1]}{[l_1(l_3-l_2)t_1-l_2(l_1-l_3)t_2+l_3(l_2-l_1)t_3]}.\hfill \end{array}$$ (19)

This can be put into a convenient matrix form:

$$\begin{array}{cccccc}\hfill A& =\left[\begin{array}{ccc}{t}_3{t}_2& t_3{t}_1& t_2{t}_1\end{array}\right]\hfill & \hfill B& =\left[\begin{array}{ccc}{t}_1& t_2& t_3\end{array}\right]\hfill & \hfill C& =\left[\begin{array}{c}{l}_1(l_3-l_2)\\ l_2(l_1-l_3)\\ l_3(l_2-l_1)\end{array}\right],\hfill \end{array}$$

$$t_0=\frac{-AC}{BC}.$$ (20)

6.5. Three‐Dimensional Positions Given Ejection Epoch and Three Observations

Taking equation (4) for epochs i and j and dividing and substituting equation (6),

$$\begin{array}{ccc}\hfill \frac{x_j}{x_i}& =\frac{(l_j+a)y_j+l_{j}R}{(l_i+a)y_i+l_{i}R}\hfill & \hfill \\ \hfill \frac{{\tau }_j}{{\tau }_i}& =\frac{(l_j+a)y_j+l_{j}R}{(l_i+a)y_i+l_{i}R}\hfill \\ \hfill (l_i+a){\tau }_j{y}_i+l_i{\tau }_{j}R& =(l_j+a){\tau }_i{y}_j+l_j{\tau }_{i}R\hfill \\ \hfill (l_i+a){\tau }_j{y}_i+(l_j+a){\tau }_i{y}_j& =(l_j{\tau }_i-l_i{\tau }_j)R\hfill \\ \hfill (l_i+a){\tau }_j{y}_i+(l_j+a){\tau }_i\frac{{\tau }_j}{{\tau }_i}{y}_j& =(l_j{\tau }_i-l_i{\tau }_j)R\hfill \\ \hfill (l_i-l_j){\tau }_j{y}_i& =(l_j{\tau }_i-l_i{\tau }_j)R\hfill \\ \hfill y_i& =-\left[\frac{(\frac{{\tau }_i}{{\tau }_j})l_j-l_i}{l_j-l_i}\right]R.\hfill \end{array}$$ (21)

Constructing the spacecraft to particle position vector,

$$\begin{array}{ccc}\hfill {\overline{r}}_i& =(R+y_i)\frac{1}{cos{\alpha }_i}{\widehat{r}}_i\hfill & \hfill \\ \hfill & =\frac{l_j(1-\frac{{\tau }_i}{{\tau }_j})}{l_j-l_i}\frac{R}{cos{\alpha }_i}{\widehat{r}}_i\hfill \\ \hfill & =\frac{l_j(1-\frac{{\tau }_i}{{\tau }_j})}{l_j-l_i}\frac{cos{\alpha }_0}{cos{\alpha }_i}|{\overline{r}}_0|{\widehat{r}}_i\hfill \\ \hfill & =\frac{l_j}{{\tau }_j}\left(\frac{{\tau }_j-{\tau }_i}{l_j-l_i}\right)\frac{cos{\alpha }_0}{cos{\alpha }_i}|{\overline{r}}_0|{\widehat{r}}_i\hfill \\ \hfill & =\frac{{\omega }_{i0}}{{\omega }_{j0}}\frac{cos{\alpha }_0}{cos{\alpha }_i}|{\overline{r}}_0|{\widehat{r}}_i\hfill \\ \hfill {\overline{r}}_i& =\frac{{\omega }_{i0}}{{\omega }_{j0}}\frac{cos{\alpha }_0}{cos{\alpha }_i}|{\overline{r}}_0|{\widehat{r}}_{sc-l_i}\hfill \end{array}$$ (22)

recall that ${\overline{r}}_0$ is the vector from the spacecraft to the ejection location, ${\overline{r}}_{sc-l_i}$ is the vector from the spacecraft to the observation l _i, and ω _ij is the observation angle rate computed using the ith and jth observations (or the radiant for index 0).

Pelgrift, J. Y. , Lessac‐Chenen, E. J. , Adam, C. D. , Leonard, J. M. , Nelson, D. S. , McCarthy, L. , et al. (2020). Reconstruction of Bennu particle events from sparse data. Earth and Space Science. 7, e2019EA000938 10.1029/2019EA000938