Estimating serotype-specific efficacy of pneumococcal conjugate vaccines using hierarchical models

Abstract

Pneumococcal conjugate vaccines (PCVs) target 10 or 13 specific serotypes. To evaluate the overall efficacy of these products, the vaccine-targeted serotypes are typically aggregated into a single group. However, it is often desirable to evaluate variations in effects for different serotypes. These serotype-specific estimates are often based on small counts, resulting in a high degree of uncertainty (i.e., large standard errors and wide confidence intervals). An alternative is to use a hierarchical Bayesian statistical model, which estimates overall effectiveness while simultaneously providing estimates of serotype-specific vaccine effects. These shrunken serotype-specific estimators often have smaller mean squared errors (MSEs) than unbiased versions due to a large decrease in posterior uncertainty. We re-analyzed published data from a randomized controlled trial on the efficacy of PCV13 against community-acquired pneumonia caused by vaccine-targeted serotype using a hierarchical model. This model provides a potential framework for obtaining estimates of serotype-specific vaccine effects with reduced MSEs.

Introduction

Pneumococcus is a diverse bacterial pathogen with more than 90 identified serotypes. Pneumococcal conjugate vaccines (PCVs) protect against a subset of these serotypes, with currently-available vaccines targeting 10 or 13 serotypes, and next-generation vaccines targeting 15 or 20 serotypes. To evaluate vaccine efficacy for these products, the vaccine-targeted serotypes are typically aggregated into a single group to estimate an overall effect [1, 2]. It is often desirable to also evaluate variations in effects for different serotypes for cost effectiveness purposes or to understand the influence of individual serotypes on overall estimates [3, 4]. However, these serotype-specific estimates are often based on small counts, resulting in a high degree of uncertainty.

Analyses of vaccine effects typically either pool all vaccine serotypes together, assuming that the vaccine serotypes are interchangeable; or they estimate effectiveness for each serotype separately. A compromise approach is to use a hierarchical Bayesian statistical model that can estimate overall effectiveness across all vaccine-targeted serotypes while simultaneously providing serotype-specific estimates. With this approach, the estimate of effectiveness obtained for each serotype is somewhere between the overall average effect and the effect that would be estimated by analyzing each serotype individually. For serotypes with larger counts, the estimate will align more closely to the estimate that would be obtained by analyzing each serotype individually, while for serotypes with smaller counts, the estimate will be pulled closer to the overall estimate. These shrunken estimators often have smaller mean squared errors (MSEs) than unbiased versions.

In this study, we re-analyzed serotype-specific vaccine efficacy data from CAPITA, which was a randomized controlled trial that evaluated the effects of PCV against pneumococcal pneumonia [5]. This hierarchical Bayesian model provides a potential framework for obtaining estimates of serotype-specific vaccine efficacy and effectiveness with reduced MSEs.

Methods

Data

The CAPITA data were from Bonten, et al. [5]. Adults were randomized to receive either the 13-valent PCV (PCV13) or a placebo. Our analyses focus on the data presented in Table S11: number of cases of first episode non-bacteremic community-acquired pneumonia (CAP) caused by a serotype targeted by PCV13, according to the per protocol analysis. For our analyses, we consider the responses from the vaccinees and controls as multinomial distributed vectors where each participant could end up in one of 14 different categories: with CAP caused by one of the 13 vaccine-targeted serotypes or as someone who did not develop CAP caused by a vaccine-targeted serotype.

Overall estimate of efficacy

The first analysis is a multinomial logistic regression where the outcome is the number of cases of each of the 13 vaccine-targeted serotypes and the number of people who did not develop CAP caused by a vaccine-targeted serotype (‘non-cases’) in the vacinees and in the placebos. We first assumed that the vaccine efficacy was the same for all targeted serotypes such that

$${\mathit{Y}}_i|n_i,{\mathit{p}}_i\sim \mathrm{Multinomial}(n_i,{\mathit{p}}_i),i=\mathrm{1,2}$$

$$p_{ij}=\frac{\exp \{{\beta }_{0j}+{\beta }_1{\mathrm{x}}_i\}}{1+{\sum }_{k=1}^{13}\exp \{{\beta }_{0k}+{\beta }_1{\mathrm{x}}_i\}},j=1,\dots ,13$$

where Y_i is a vector that contains the number of cases due to each serotype (Y_i1,…,Y_i13) and the number of non-cases (Y_i14) for treatment group i (i=1: placebo, i=2: PCV13), n_i is the number of study participants in treatment group i where the sum of the counts across all categories of Y_i is equal to n_i, and x_i is an indicator for vaccine status (x₁=0: placebo, x₂=1: PCV13). The probabilities that control how many people in treatment group i end up in each category are defined by the p_i vector, which has a unique entry for each vaccine-targeted serotype and non-case category, p_ij, j=1,…,14. The probability of being a non-case is given as $p_{i14}=1-{\sum }_{k=1}^{13}{p}_{ik}$. Vaccine efficacy for serotype j (j=1,…,13) is defined as 100(1 − p_2j/p_1j) and the overall efficacy is defined as $100(1-{\sum }_{k=1}^{13}{p}_{2k}/{\sum }_{k=1}^{13}{p}_{1k})$. In this model, all estimated effects are the same since the vaccine efficacy parameter (β₁) is shared across all serotypes. We fit the model in the Bayesian setting while specifying weakly informative, independent normally distributed prior distributions for the regression parameters (mean 0, standard deviation (SD) 100).

Serotype-specific estimates of efficacy

Building on the model above, we next allow the vaccine effect to vary by serotype such that

$$p_{ij}=\frac{\exp \{{\beta }_{0j}+{\beta }_{1j}{\mathrm{x}}_i\}}{1+{\sum }_{k=1}^{13}\exp \{{\beta }_{0k}+{\beta }_{1k}{\mathrm{x}}_i\}},j=1,\dots ,13.$$

We evaluated two versions of this model: one where the serotype-specific intercepts (β_0j) and slopes (β_1j) were estimated independently for each serotype and one where they were estimated hierarchically. For the non-hierarchical version, each β_0j and β_1j were assigned independent, weakly informative normal priors (mean 0, SD 100). For the hierarchical model, these regression parameters were once again assigned independent, normally distributed prior distributions. However, the means and variances of these prior distributions were treated as unknown parameters; ${\beta }_{0j}\sim \mathrm{Normal}({\mu }_0,{\sigma }_0^2)$ and ${\beta }_{1j}\sim \mathrm{Normal}({\mu }_1,{\sigma }_1^2)$, j=1,…,13. These hyper-parameters were then assigned weakly informative priors to allow the data to determine the appropriate amount of shrinkage between the two extreme scenarios considered previously (shared vaccine effect, varying vaccine effect) such that μ₀,μ₁∼Normal(0,100²) and σ₀,σ₁∼Uniform(0,100). Vaccine efficacy was estimated as previously detailed.

All model fitting was performed using rjags [6] with three separate Markov chains and a burn-in period of 10,000 iterations (i.e., before convergence of the models) in each chain. Posterior inference was based on 300,000 samples (100,000 from each chain), and vaccine efficacy was summarized using posterior medians and 95% highest posterior density intervals. Forest plots were generated with rmeta [7]. Analyses were performed with R statistical software [8]. All code and data are available on a public github repository: https://github.com/weinbergerlab/capita-hierarchical. In addition, we assessed the sensitivity of the non-hierarchical and hierarchical results to our prior distribution choices and found that they were relatively robust overall, with no substantive differences in conclusions.

Results

Overall estimate of efficacy

There were 61 cases of vaccine-type pneumococcal pneumonia among the placebo recipients and 33 cases among the vaccinees. Without accounting for serotype, the estimated efficacy was 44.9% (95% credible interval (CrI): 20.6–66.8%). This is close to the efficacy estimate reported in the original study (45.0%, 95% confidence interval: 14.2–65.3%).

Serotype-specific efficacy, estimated separately

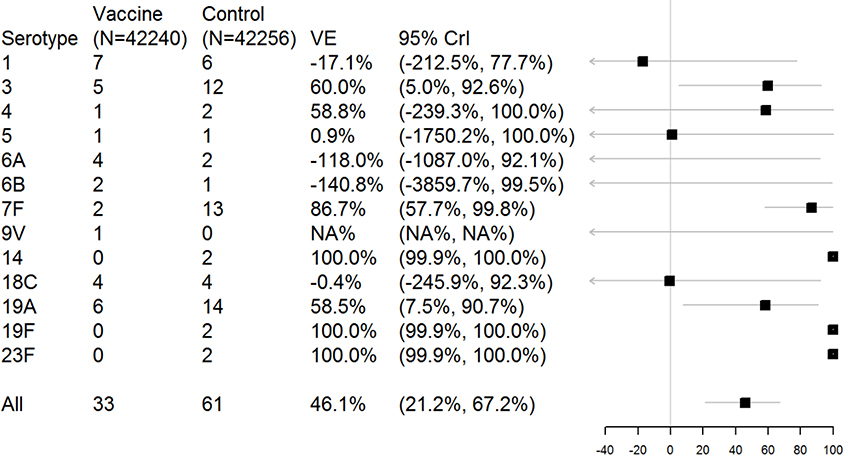
Aside from serotypes 3, 7F, and 19A, the majority of serotypes lacked sufficient case counts to yield informative estimates when analyzed separately (Figure 1). Many serotypes had 0 or 1 cases in one of the study arms, which led to estimation instability. For instance, the estimates for serotypes 14, 19F, and 23F were 100% because there were 0 cases in the vaccinated group. Serotype 18C, with 4 cases each in the case and placebo group, had an estimated efficacy of essentially 0% with a wide CrI (−246–92%). Additionally, some serotypes had point estimates of vaccine efficacy that were strongly negative. For instance, serotype 6A had 4 cases in the vaccine group and 2 in the placebo group, for a vaccine efficacy of −118% (95% CrI: −1087–92%). No reasonable estimate could be obtained for serotype 9V (1 case in vaccine group, 0 in placebo group). The overall estimate of vaccine efficacy from this model was 46.1% (95% CrI: 21.2–67.2%).

Figure 1.

Estimates of serotype-specific vaccine efficacy (VE) from a non-hierarchical model. The plot shows the posterior median and 95% highest posterior density credible intervals (CrIs).

Serotype-specific efficacy, estimated hierarchically

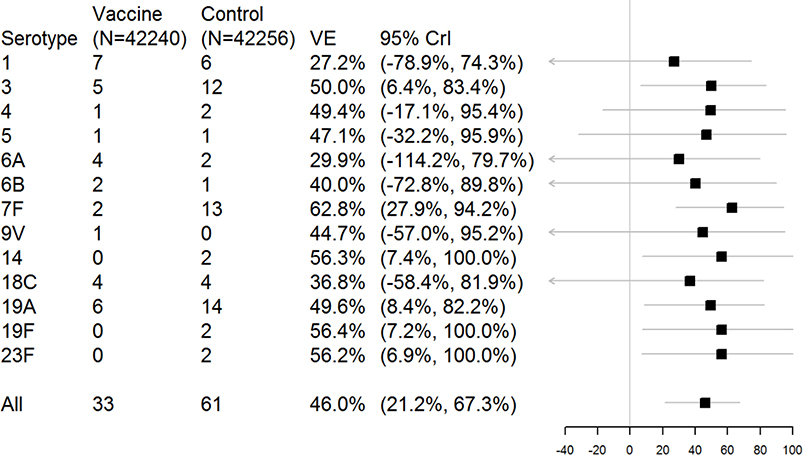
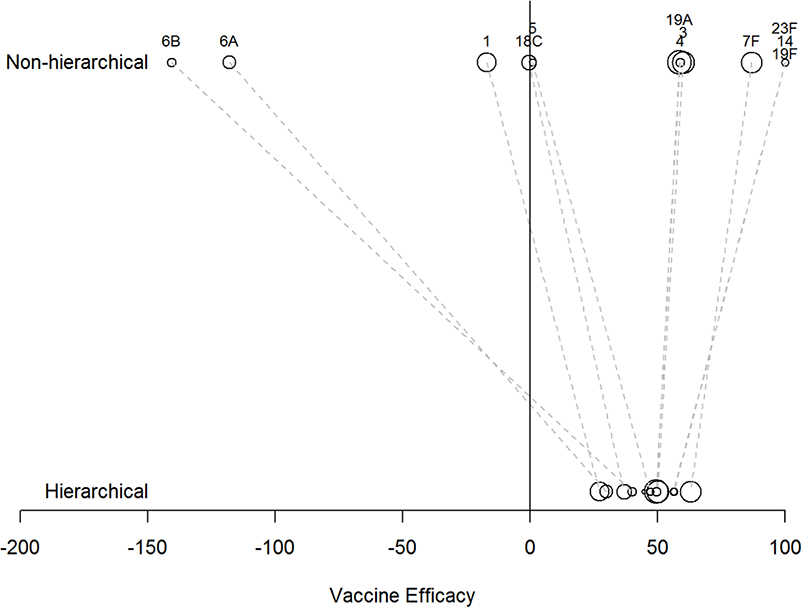
Compared to the estimates shown in Figure 1, the serotype-specific effects were pulled towards the overall vaccine effect estimate (Figures 2 and 3), with serotypes with fewer observed cases pulled more strongly towards the overall estimate (Figure 3). For serotypes where the observed data were consistent with the overall average, even if there were few counts, the CrIs were narrow and excluded zero (Serotypes 3, 7F, 14, 19A, 19F, 23F; Figure 2). In contrast, for serotypes 1, 6A, 6B, and 9V, where more cases occurred among the vaccine recipients than the placebos, the point estimates of vaccine efficacy were generally pulled towards zero with wide CrIs. The overall estimate of vaccine efficacy from this model was 46.0% (21.2–67.3%).

Figure 2.

Estimates of serotype-specific vaccine efficacy (VE) from a hierarchical model. The plot shows the posterior median and 95% highest posterior density credible intervals (CrIs).

Figure 3.

Comparison of the point estimates (posterior medians) of vaccine efficacy for each serotype from the non-hierarchical model and the hierarchical model. The area of the bubble is proportional to the number of cases of pneumonia due to that serotype in both study arms.

Discussion

We estimate serotype-specific vaccine effects using hierarchical Bayesian modeling. A hierarchical approach may allow for increased stability when estimating efficacy for serotypes with small case counts and reductions in uncertainty for these estimates. However, it is important to consider the assumptions of the model before interpreting the results. In this work, we assumed that the serotype-specific vaccine effects can vary but that they all arise from a common Gaussian distribution with shared mean and variance. If this assumption is violated, then it could result in inappropriate shrinkage estimates, and updates to the hierarchical structure should be considered (e.g., a mixture model).

In the analysis presented here, we used a multinomial likelihood given the structure of the data. However, this general approach could be applied to other study designs and likelihoods. For instance, the same general structure of priors for the parameters could be used to estimate serotype-specific effectiveness using data from other study designs (e.g., a case-control study or ‘indirect cohort’ analysis of vaccine effects on invasive pneumococcal disease). Future applications should carefully consider the data generating mechanism when selecting a likelihood for the observed data and how this choice impacts the definition of vaccine efficacy.

In conclusion, hierarchical modeling may represent a useful approach for obtaining estimates of serotype-specific vaccine efficacy that are more stable for serotypes with small case counts and have reduced uncertainty than traditional unbiased estimators. This approach balances the need for serotype-specific estimates with the challenges of using sparse data and can be easily extended to alternative study designs.