A Comparison of Random Forest Variable Selection Methods for Classification Prediction Modeling

Abstract

Random forest classification is a popular machine learning method for developing prediction models in many research settings. Often in prediction modeling, a goal is to reduce the number of variables needed to obtain a prediction in order to reduce the burden of data collection and improve efficiency. Several variable selection methods exist for the setting of random forest classification; however, there is a paucity of literature to guide users as to which method may be preferable for different types of datasets. Using 311 classification datasets freely available online, we evaluate the prediction error rates, number of variables, computation times and area under the receiver operating curve for many random forest variable selection methods. We compare random forest variable selection methods for different types of datasets (datasets with binary outcomes, datasets with many predictors, and datasets with imbalanced outcomes) and for different types of methods (standard random forest versus conditional random forest methods and test based versus performance based methods). Based on our study, the best variable selection methods for most datasets are Jiang’s method and the method implemented in the VSURF R package. For datasets with many predictors, the methods implemented in the R packages varSelRF and Boruta are preferable due to computational efficiency. A significant contribution of this study is the ability to assess different variable selection techniques in the setting of random forest classification in order to identify preferable methods based on applications in expert and intelligent systems.

1. Introduction

Random forest is a popular machine learning procedure which can be used to develop prediction models. First introduced by Breiman in 2001 (Breiman, 2001), random forests are a collection of classification and regression trees (Breiman, Friedman, Olshen, & Stone, 1984), which are simple models using binary splits on predictor variables to determine outcome predictions. Decision trees are easy to use in practice, offering an intuitive method for predicting outcome which splits “high” versus “low” values of a predictor related to outcome. Though it offers many benefits, decision tree methodology often provides poor accuracy for complex datasets (e.g. large datasets and datasets with complex variable interactions). In the random forest setting, many classification and regression trees are constructed using randomly selected training datasets and random subsets of predictor variables for modeling outcomes. Results from each tree are aggregated to give a prediction for each observation. Therefore, random forest often provides higher accuracy compared to a single decision tree model while maintaining some of the beneficial qualities of tree models (e.g. ability to interpret relationships between predictors and outcome) (Speiser, Durkalski, & Lee, 2015). Random forests consistently offer among the highest prediction accuracy compared to other models in the setting of classification (Fernández-Delgado, Cernadas, Barro, & Amorim, 2014).

A major benefit of using random forest for prediction modeling is the ability to handle datasets with a large number of predictor variables; however, often in practice, the number of predictors required for obtaining outcome predictions should be minimized to improve efficiency. For example, rather than using all variables available in the electronic medical record, one may prefer to use only a subset of the most important variables when developing a medical prediction model. In prediction modeling, an interest is often to determine the most important predictors that should be included in a reduced, parsimonious model. This can be achieved by performing variable selection, in which optimal predictors are identified based on statistical characteristics such as importance or accuracy. Developing prediction models using variable selection may reduce the burden of data collection and may improve efficiency of prediction in practice. Since many modern datasets have hundreds or thousands of possible predictors, variable selection is often a necessary part of prediction model development.

Variable selection in the random forest framework is a relevant consideration for many applications in expert systems and applications. In general, the overall goal of many expert systems is to aid in decision making for a complex problem. This fits the goal of prediction modeling, in which we use a dataset to develop a model (random forest in this study) which will provide predictions of an outcome of interest. To increase efficiency of obtaining model predictions, variable selection may be used in order to identify a subset of predictor variables to be included in a final, simpler model. There are many applications for which this occurs in expert system development, for instance, developing a medical decision support tool, a projection model for stock market prices and a business analytics model to maximize profits. There are several methods available for performing variable selection in the setting of random forest classification. Many R packages provide random forest variable selection procedures, including boruta (Kursa & Rudnicki, 2010), varSelRF (Díaz-Uriarte & De Andres, 2006), VSURF (Genuer, Poggi, & Tuleau-Malot, 2015), caret (Kuhn, 2008), party (Hothorn, Hornik, Strobl, & Zeileis, 2010), randomForestSRC (Ishwaran & Kogalur, 2014), RRF (Deng & Runger, 2013), vita (Janitza, Celik, & Boulesteix, 2015), AUCRF (V. Urrea & M. L. Calle, 2012) and fuzzyForest (Conn, Ngun, Li, & Ramirez, 2015). Several other methods have been proposed in the literature (e.g. Hapfelmeier (2013), Svetnik (2004), Jiang (2004) and Altmann (2010)). While there are many methods for random forest variable selection for classification problems available, there is a paucity of guidance in the literature about which methods are preferable in terms of prediction error rate (out-of-bag), parsimony (number of variables), computation time and area under the receiver operating curve (AUC) for different types of datasets. Sanchez-Pinto (2018), Degenhardt (2017), Cadenas (2013) and Hapfelmeier (2013) assess variable selection methods for random forest classification, but most of these papers compare only a handful of methods. Additionally, these papers are limited in scope due to the use of synthetic simulated data which are not always representative of real-world datasets or a small number of application datasets. A final limitation of the current random forest variable selection literature is that computation times for different procedures are rarely reported. Given these limitations, there is a need to compare variable selection procedures for a large number of random forest classification problems in order to provide recommendations about which procedures are appropriate for different types of datasets.

The remainder of this paper is structured in the following manner. Section 2 summarizes methods and implementation for random forest variable selection for classification in the current literature. The design of the current study is presented in Section 3, including the datasets used and evaluation metrics for the variable selection procedures. Section 4 provides a summary of results comparing error rates, parsimony and computation time for the variable selection procedures. Discussion and conclusions are presented in Section 5.

2. Methods for Random Forest Variable Selection for Classification

Variable selection methods for random forest classification are thoroughly described in the literature (e.g. (Cadenas, et al., 2013; Cano, et al., 2017; Degenhardt, et al., 2017; Hapfelmeier & Ulm, 2013; Sanchez-Pinto, et al., 2018)); thus, in the interest of brevity, we summarize only the main idea of each method and provide parameter settings used in the present study. In chronological order by year of publication, the methods we compared are presented in Table 1. Methods which use a backward elimination approach with conditional inference forest include Svetnik’s method (2004), Jiang’s method (2004), and Hapfelmeier’s method (2013). Some methods use a backward elimination procedure with standard implementation of random forest, including varSelRF (Díaz-Uriarte & De Andres, 2006), caret (Kuhn, 2008) and randomForestSRC (Ishwaran & Kogalur, 2014). A stepwise selection procedure is implemented in VSURF (Genuer, et al., 2015), whereas RRF (Deng & Runger, 2013) uses a regularized random forest procedure and a forward selection approach. Altmann’s method (2010), Boruta (Kursa & Rudnicki, 2010) and Janitza’s method (2015) use random forest importance measures to perform variable selection. Similar to Hapfelmeier’s categorization (2013), we define variable selection methods as being test based or performance based. Performance based approaches select variables based on changes in the prediction accuracy when variables are added or deleted from models, and include methods by Svetnik and Jiang, varSelRF, caret, RRF, SRC and VSURF. Test based approaches select variables based on statistical or permutation tests, and include methods by Altmann, Hapfelmeier and Janitza, as well as Boruta.

Table 1:

Summary of variable selection methods for random forest classification

Abbreviation in Paper	Publication	R package/Implementation	Approach	Type of forest method	Summary	Parameter Settings
RF	Breiman 2001 [1]	randomForest	N/A	Random forest	No variable selection	Default
RFtuned	Breiman 2001 [1]	randomForest	N/A	Random forest	No variable selection, tuned with tuneRF() function	Default
Svetnik	Svetnik 2004 [16]	Uses party, code from Hapfelmeier [15]	Performance Based	Conditional Inference Forest	Uses backward elimination based on importance measures and k-fold validation	# trees=100, # folds=5, # repetitions=20
Jiang	Jiang 2004 [17]	Uses party, code from Hapfelmeier [15]	Performance Based	Conditional Inference Forest	Similar to Svetnik but provides mechanism to prevent overfitting	# trees=1000
varSelRF	Diaz Uriarte 2007 [6]	varSelRF	Performance Based	Random forest	Uses backward elimination, criteria to remove variables based on maintaining similar error rate to full model	Default
Caret	Kuhn 2008 [8]	caret	Performance Based	Random forest	Uses recursive feature elimination, criteria to remove variables based on maintaining similar error rate to full model	Default
Altmann	Altmann 2010 [18]	vita	Test Based	Random forest	Based on a parametric test of repeated permutations of importance measures	Default
Boruta	Kursa 2010 [5]	Boruta	Test Based	Random forest	Based on a permutation test using a hold out approach for importance measures	Default
Hapfelmeier	Hapfelmeier 2013 [15]	Uses party, code from Hapfelmeier [15]	Test Based	Conditional Inference Forest	Similar to Altmann, but uses unbiased importance measures	# permutations=100, # trees=100, alpha=0.05
RRF	Deng 2013 [11]	RRF	Performance Based	Random Forest	Based on a regularized random forest, which uses forward selection to sequentially add variables until there is no further information gain	Default
SRC	Ishwaran 2014 [10]	randomForestSRC	Performance Based	Random Forest	Uses backward elimination based on minimal depth of predictors	Default
VSURF	Genuer 2015 [7]	VSURF	Performance Based	Random Forest	Stepwise selection procedure which implements backward elimination then forward selection based on importance measures and error rate	Default
Janitza	Janitza 2015 [12]	Vita	Test Based	Random forest	Similar to Altmann, but also uses cross validation	Default

In addition to these methods, we considered using two others but ultimately decided not to use them in our study. These included the backward elimination method based on area under the receiver operating curve implemented in the AUCRF R package by Urrea (V. Urrea & M. Calle, 2012), which was not included because it is limited to binary outcomes, and the method for variable selection in the presence of correlated variables implemented in the fuzzyForest R package by Conn (Conn, et al., 2015), which was not included because it required specification of a correlation structure by a user. Our goal was to be as inclusive as possible in terms of using all available variable selection methods for random forest classification to thoroughly evaluate and compare methods.

3. Design of Study

We analyzed datasets freely available on R software using the OpenML R package (website: https://www.openml.org/home) (Casalicchio, et al., 2017). We used the following constraints to select the datasets for this study: the research question for the dataset was designated as supervised classification (i.e. the task was supervised classification) and there were no missing predictor or outcome values in the dataset. Due to computational constraints associated with some methods, we limited the datasets to those with outcomes having 8 or less levels (categories in the outcome variable), 1000 or less predictors and 1000 or less observations. We limited the dataset size because a previous study by Degenhardt (2017) investigated random forest variable selection for big datasets in the field of omics, so we decided to exclude this from our study. We also omitted datasets in which the standard random forest produced an error message using the R package randomForest, though this was quite rare (2 datasets).

Overall with these specifications, we analyzed 311 total datasets, which had a mean (standard deviation (SD)) number of outcome classes of 2.4 (1.0). There were an average (SD) of 22 (33) predictors in the datasets, with an average (SD) of 322 (285) observations. Figure 1 displays the distribution of the number of outcome classes, predictors and observations for the datasets, as well as the proportion of observations in the majority outcome class. Details about the characteristics of datasets used in this study are included within the Supplementary Dataset Listing File. Datasets are from a variety of expert systems application areas, including medicine, business, environmental science, basic science, agriculture, psychology, education, computer science, and nutrition.

Figure 1:

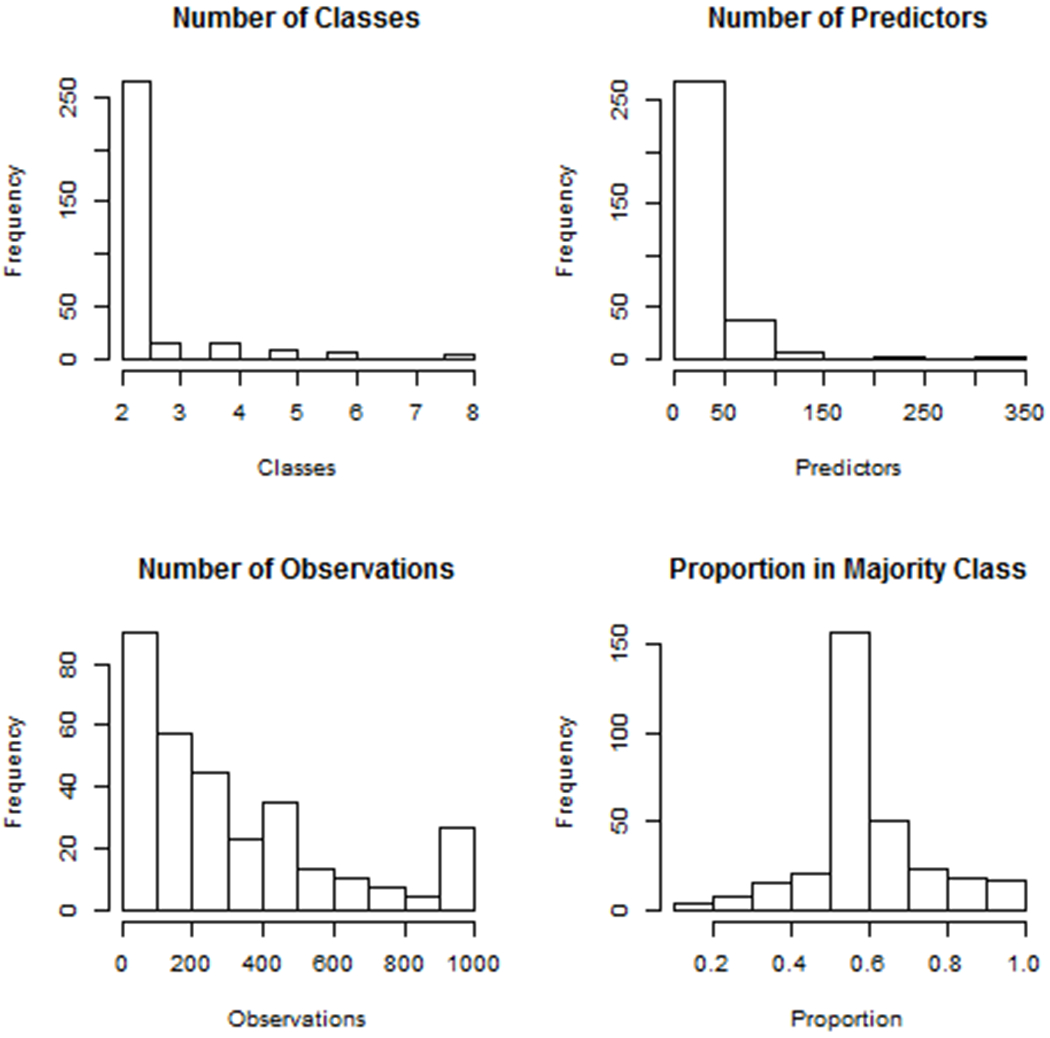
This figure displays characteristics of datasets used for the study, including the number of outcome classes, number of predictor variables, number of observations, and the proportion of the majority outcome class.

For each of the datasets described above, we performed variable selection using the methods listed in Table 1 and developed a standard random forest model using the R package randomForest (Liaw & Weiner, 2002) and random forest with the parameter mtry tuned for comparison. The methods in Table 1 which had an R package available were used with default values. The remaining methods which used the R package party were implemented based on code provided by Hapfelmeier (Hapfelmeier & Ulm, 2013). For each variable selection method and dataset, we recorded the prediction error rate (defined as the proportion of incorrect predictions for the out-of-bag data), number of variables used, computation time and AUC. To obtain AUC estimates, we employed the R package multiROC (Wei, Wang, & Jia, 2019). We used R version 3.4.1 on a computer with an Intel® Core™ i1-7700 CPU 3.60 GHz, 3600 Mhz, 4 Cores, 8 Logical Processors and 16.0 GB of RAM. Code used to implement and evaluate the variable selection methods is provided in the Supplementary Code File.

4. Results

4.1. Results for all datasets

We compared the distributions of the out-of-bag error rate, number of variables included within the reduced models, the computation times and AUC of the variable selection procedures in Figure 2 and Table 2. The mean out-of-bag error rates ranged from 16% to 23% across the variable selection methods and all had right skewed distributions. The top three methods with the lowest mean out-of-bag error rates were the VSURF method, the Boruta method and the method by Altmann. Some of the models had quite large out-of-bag error rates (greater than 0.5) for some datasets, which indicated that these models did not predict outcomes well.

Figure 2:

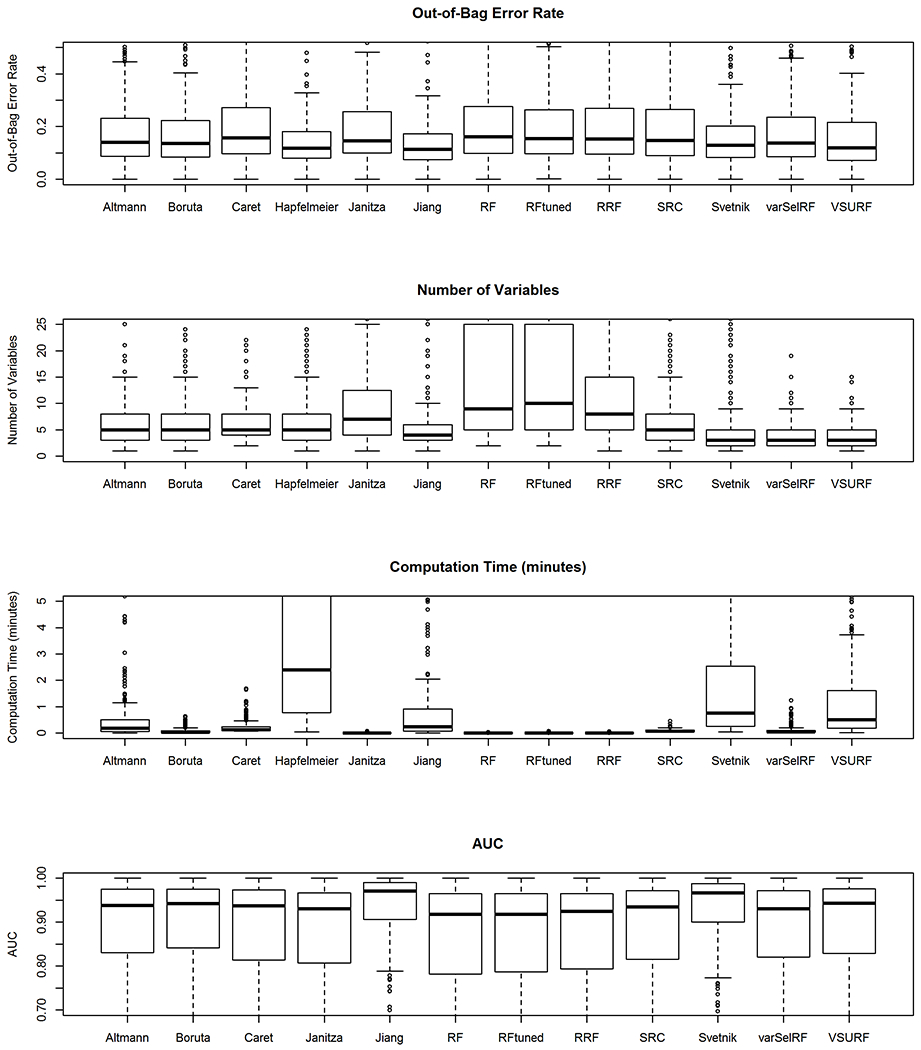
This figure displays boxplots of out-of-bag error rate, number of variables, computation time (minutes) and AUC for the variable selection methods for random forest classification.

Table 2:

Distribution of error rates, computation time and number of variables used for variable selection procedures

OOB Error Rate		Number of Variables		Computation Time (minutes)		AUC
Model (N)	Mean (SD)	Model (N)	Mean (SD)	Model (N)	Mean (SD)	Model (N)	Mean (SD)
VSURF (251)	0.156 (0.136)	VSURF (251)	3.442 (2.312)	RF (308)	0.003 (0.005)	Jiang (291)	0.929 (0.106)
Boruta (292)	0.17 (0.142)	VarSelRF (308)	3.877 (3.703)	RRF (297)	0.004 (0.008)	Svetnik (292)	0.924 (0.103)
Altmann (297)	0.179 (0.148)	Jiang (291)	5.131 (5.405)	RF Tuned (301)	0.004 (0.009)	Boruta (292)	0.89 (0.133)
VarSelRF (308)	0.18 (0.148)	Svetnik (292)	6.182 (8.479)	Janitza (183)	0.007 (0.01)	Caret (298)	0.888 (0.133)
SRC (311)	0.188 (0.154)	SRC (311)	7.19 (8.089)	Boruta (292)	0.061 (0.098)	Janitza (183)	0.888 (0.13)
Janitza (183)	0.196 (0.147)	Boruta (292)	7.86 (9.777)	SRC (311)	0.089 (0.054)	VarSelRF (308)	0.887 (0.13)
RF Tuned (301)	0.196 (0.151)	Hapfelmeier (290)	8.021 (10.05)	VarSelRF (308)	0.106 (0.165)	SRC (311)	0.885 (0.137)
RRF (297)	0.196 (0.154)	Altmann (297)	9.421 (18.898)	Caret (298)	0.225 (0.264)	Altmann (297)	0.883 (0.147)
Caret (298)	0.2 (0.157)	RRF (297)	10.603 (7.95)	Altmann (297)	0.554 (0.971)	VSURF (251)	0.881 (0.138)
RF (308)	0.203 (0.158)	Caret (298)	11.718 (25.606)	Jiang (291)	1.314 (3.396)	RRF (297)	0.873 (0.13)
Jiang (291)	0.22 (0.488)	Janitza (183)	14.914 (27.864)	VSURF (251)	1.754 (2.937)	RF Tuned (301)	0.87 (0.131)
Hapfelmeier (290)	0.23 (0.503)	RF (308)	21.418 (32.653)	Svetnik (292)	3.2 (7.794)	RF (308)	0.865 (0.133)
Svetnik (292)	0.232 (0.41)	RF Tuned (301)	21.77 (32.942)	Hapfelmeier (290)	16.16 (42.77)	Hapfelmeier	NA

N: Number of datasets that compiled for the models.

SD: Standard deviation.

OOB: Out-of-bag

The distributions of the number of variables included within the models were also right skewed. Most methods had a median number of variables around three to eleven. The VSURF method offered the lowest mean number of variables (3.4), followed by the varSelRF method (3.9) and Jiang’s method (5.1). The standard random forest had a mean of 21.4 variables and the tuned random forest had a mean of 21.8, which were the largest because no variable selection was performed.

Standard random forest had the lowest computation time, which was similar to that of RRF and the tuned random forest. Methods with the greatest computation time (greater than a minute on average) were Jiang’s method (1.3 minutes), VSURF (2.9 minutes), Svetnik’s method (3.2 minutes) and Hapfelmeier’s method (16.2 minutes). These methods additionally had the largest variability in computation time, ranging from several seconds up to several minutes. The method by Hapfelmeier had the highest computation time by a large margin.

Values of AUC for the models ranged from 0.865 up to 0.929, which indicated that most of the models offered good fit. Jiang’s method and Svetnik’s method had slightly higher mean AUC compared to the other models. We omitted Hapfelmeier’s method from the AUC results due to its large computation time.

It should be noted that some of the methods for certain datasets either produced error messages or did not provide a final model. Table 2 contains the number of datasets (N) used for each of the methods. The SRC method was the only one to provide predictions for every dataset. Most methods had less than twenty missing prediction models. The Janitza method had the most predictions omitted for our study because it provided no selected predictors for 128 datasets, thereby producing missing values for out-of-bag error, number of variables, computation time and AUC.

The median out-of-bag error rate was plotted by median computation time, median number of variables and median AUC within Figure 3. Jiang’s method, Hapfelmeier’s method and the VSURF method had low out-of-bag error rates and number of variables; however, Hapfelmeier’s method had much higher computation times compared to other methods. The VSURF method had slightly higher computation time compared to Jiang’s method. Jiang’s method produced the highest AUC, whereas the VSURF method also offered good AUC relative to most other methods. The Boruta method, the varSelRF method, and Altmann’s method for variable selection had fairly low out-of-bag error rates, low computation times and moderate number of variables. Standard random forest (no variable selection performed) had the lowest computation times and highest number of variables, whereas the tuned random forest with no variable selection also had the highest number of variables with a slightly lower error rate. The median computation times, out-of-bag error rates, number of variables and AUC were similar for the standard random forest, the tuned random forest and the RRF. There were no obvious clusters of methods in terms of comparing error rate and computation time, error rate and number of variables or error rate and AUC.

Figure 3:

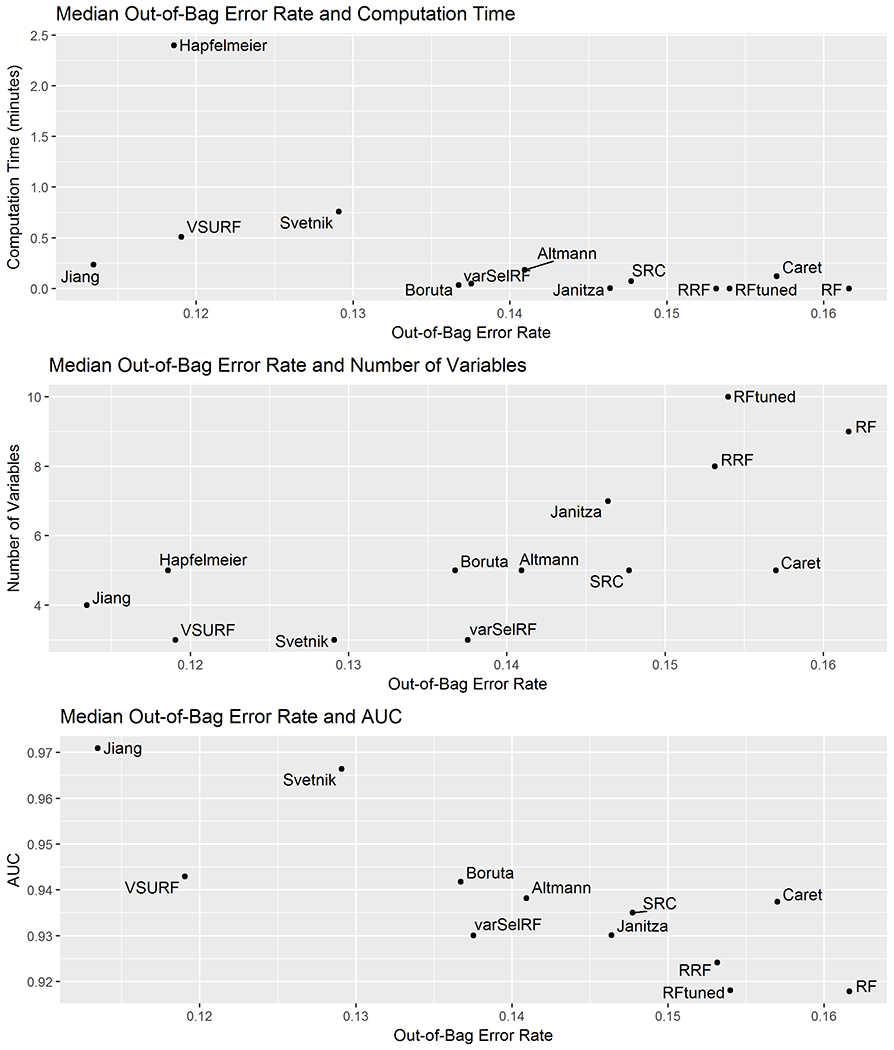
This figure displays plots of the median out-of-bag error rate by median computation time, median number of variables and median AUC.

Because some of the methods would not compile for some datasets, we also investigated performance of the methods based on datasets for which all methods compiled. Table 3 displays the distribution of the out-of-bag error rate, number of variables included within the reduced models, the computation times and AUC of the variable selection procedures excluding all datasets for which at least one of the methods did not give a final model. There were 141 datasets used in this analysis. Though there were 170 datasets which had a least one variable selection procedure not produce a final model, the results for out-of-bag error, number of variables, computation times and AUC were fairly similar to that of Table 2 (i.e. the analysis including all non-missing results for the variable selection procedures). The main difference was that methods with the smallest error rates were VSURF, varSelRF, Boruta then Altmann in the analysis with no missing data (Table 3), but the order was VSURF, Boruta, Altmann, then varSelRF in the analysis including missing data (Table 2). However, the error rates across these methods were quite similar.

Table 3:

Distribution of error rates, computation time and number of variables used for variable selection procedures excluding all datasets for which at least one of the methods did not give a final model (141 datasets used in this analysis)

OOB Error Rate		Number of Variables		Computation Time (minutes)		AUC
Model	Mean (SD)	Model	Mean (SD)	Model	Mean (SD)	Model	Mean (SD)
VSURF	0.155 (0.113)	VSURF	3.489 (1.999)	RF	0.003 (0.005)	Jiang	0.929 (0.106)
VarSelRF	0.163 (0.111)	VarSelRF	3.972 (2.775)	RRF	0.004 (0.005)	Svetnik	0.924 (0.103)
Boruta	0.166 (0.115)	Jiang	5.014 (4.559)	RF Tuned	0.005 (0.007)	Boruta	0.89 (0.133)
Altmann	0.172 (0.12)	Svetnik	6.823 (9.546)	Janitza	0.008 (0.01)	Caret	0.888 (0.133)
Janitza	0.174 (0.115)	SRC	8.532 (9.917)	Boruta	0.082 (0.1)	Janitza	0.888 (0.13)
SRC	0.181 (0.114)	Boruta	8.823 (10.603)	SRC	0.089 (0.051)	varSelRF	0.887 (0.13)
RRF	0.185 (0.116)	Hapfelmeier	9.206 (10.608)	VarSelRF	0.139 (0.185)	SRC	0.885 (0.137)
RF Tuned	0.187 (0.117)	Altmann	12.894 (24.502)	Caret	0.264 (0.276)	Altmann	0.883 (0.147)
Caret	0.191 (0.121)	RRF	14.248 (6.905)	Altmann	0.67 (1.063)	VSURF	0.881 (0.138)
Jiang	0.193 (0.316)	Caret	16.099 (35.16)	VSURF	1.76 (2.401)	RRF	0.873 (0.13)
RF	0.196 (0.115)	Janitza	17.319 (30.93)	Jiang	1.944 (4.325)	RFtuned	0.87 (0.131)
Hapfelmeier	0.204 (0.322)	RF Tuned	34.22 (41.728)	Svetnik	5.008 (10.413)	RF	0.865 (0.133)
Svetnik	0.23 (0.366)	RF	34.22 (41.728)	Hapfelmeier	25.179 (55.017)	Hapfelmeier	NA

N: Number of datasets that compiled for the models.

SD: Standard deviation.

OOB: Out-of-bag

4.2. Comparing methods grouped by characteristics of datasets

4.2.1. Results for datasets with binary outcome

We also analyzed the results for the subset of datasets which contained a binary, or two class, outcome (Supplementary Table 1 and Supplementary Figure 1). There were 264 datasets with binary outcomes. Results were similar to those presented in Section 4.1 for all datasets. Hepfelmeier’s method, Jiang’s method, the VSURF method, and Svetnik’s method had high computation times and low out-of-bag error rates. The Boruta method, Altmann’s method, and the varSelRF method had fairly low out-of-bag error rates and computation times, and varSelRF offered the lowest number of variables among these methods.

4.2.2. Results for datasets with many predictor variables

An analysis was performed for the subset of datasets with many predictors, which we defined as more than 50 predictor variables (Supplementary Table 2 and Supplementary Figure 2). There were 44 datasets with more than 50 predictors. Similar to previous results, Hapfelmeier’s method had by far the highest computation times compared to all other methods. Boruta and varSelRF had fairly low out-of-bag error rates, low computation times, and low number of variables included. VSURF had the lowest error rate and number of variables, but this was coupled with a relatively high mean computation time of approximately four minutes.

4.2.3. Results for datasets with imbalanced outcomes

A final analysis was performed for the subset of datasets with imbalanced outcomes, which we defined as the majority outcome class containing greater than 60% of the observations (Supplementary Table 3 and Supplementary Figure 3). There were 107 datasets which had imbalanced outcomes. Again, Hapfelmeier’s method had the highest mean computation time. The out-of-bag error rates for the methods were in a tighter range compared to other analyses, which ranged from 12% to 16% on average. While Jiang’s method had slightly higher computation times compared to other methods, this method offered the lowest number of variables.

4.3. Comparing methods grouped by characteristics of the methods

4.3.1. Results for comparing standard random forest and conditional random forest methods

The type of random forest implemented differs among the variable selection methods (Table 1). The majority of methods use standard random forest; these include varSelRF, Caret, Altmann’s method, Boruta, RRF, SRC, VSURF and Janitza’s method. The other variable selection procedures use conditional random forest, including the methods by Svetnik, Jiang, and Hapfelmeier. In general, methods which use conditional random forest have higher computation times and lower error rates compared to methods which use standard random forest (Figure 3). An exception to this was VSURF, which has slightly higher computation times and lower error rates compared to other methods which also use standard random forest.

4.3.2. Results for comparing test based and performance based methods

The random forest variable selection procedures also differed in terms of their approach being based on either a permutation test or performance (accuracy). Methods which select variables based on a permutation test include Altmann’s method, Boruta, Hapfelmeier’s method and Janitza’s method, whereas methods which select variables based on performance in terms of accuracy include Svetnik’s method, Jiang’s method, varSelRF, Caret, RRF, SRC and VSURF. When grouping by test or performance based methods, there is no discernable pattern in regards to error rates, computation times, number of variables selected or AUC.

5. Discussion

In this paper, we provided a comparison of methods available for random forest variable selection in the setting of classification using 311 datasets freely available online. The methods with the lowest out-of-bag error rate, as well as the lowest computation time and number of variables were preferable. Of secondary interest was high values of AUC. Overall, methods by Jiang and VSURF had the lowest amount of error and best parsimony (fewest number of variables), but this was also coupled with higher computation times. A reason that the Jiang method had high computation time is because it used k-fold validation to select variables, which can be computationally expensive. The VSURF method likely had high computation times because it uses a stepwise procedure for selecting variables, in which variables are eliminated and then possibly added back, which may be associated with higher computation time. In every analysis, Hapfelmeier’s method had the highest computation time, which likely happened because it has to compile permutations for every variable which is at a high computational expense. Althann’s method, varSelRF, and Boruta generally performed similarly for different types of datasets, with low computation time, fairly low error rates, and moderate to good parsimony. This was generally similar when analyzing the subset of datasets which had binary outcomes. Computation times were reasonable for models with binary outcomes, with medians a minute or less for most models, except for Hapfelmeier’s method and Svetnik’s method. For datasets with a larger number of predictor variables, VSURF had median computation times around five minutes, whereas varSelRF and Boruta had much lower computation times with slightly higher error rates. The lower computation time of varSelRF and Boruta was likely because these are backward elimination procedures, which performed faster than stepwise selection or k-fold validation selection approach used by VSURF. Though VSURF offered the lowest median error rate for the datasets, it also did not provide a model (i.e. it selected no variables) for 60 datasets. Janitza’s method, however, did not provide a model for 128 datasets, which was by far the worst in terms of being able to be applied to a variety of datasets. A summary of advantages and disadvantages of the methods employed in our study is presented in Supplementary Table 4.

It was interesting that the error rates of many methods were similar (means ranging from 16-23% overall), while parsimony, computation times and AUC were quite different comparing different methods. The small differences in error rates may be because many of the methods are similar, or even nested within each other by including tweaks to the algorithms for selecting variables. Though we were expecting similar methods to cluster together in groups (e.g., in the Figure 3 plots), this did not happen for the overall analysis when comparing test based and performance based methods. This suggests that the type of method (test or performance) does not differentially impact the overall performance of the variable selection method in terms of error rate, computation time, parsimony, and AUC. However, methods which use conditional random forest typically do behave similarly: these methods tended to have lower error rates compared to standard random forest methods, albeit accompanied by much higher computation times as well. Methods for variable selection which use conditional random forest may be preferable for datasets with known underlying associations between predictors and outcome because conditional random forest is typically better at correctly identifying significant associations between predictors and outcome compared to standard random forest. For datasets where there is not as much prior information about known predictors of outcome, standard random forest variable selection methods may be preferable because it focuses on optimizing accuracy more than identifying correct predictor-outcome relationships.

Our results should be considered in the greater context of previous literature comparing variable selection methods for random forest classification. Consistent with findings from Sanchez-Pinto (2018), our study found that VSURF had slightly better prediction error compared to Boruta and RRF. Degenhardt (2017) focused on omics datasets which were quite large, but concluded that Boruta and Altmann were suitable for low dimensional data; however, this study did not include RRF, Hapfelmeier, Jiang, Svetnik, SRC, or Caret methodology for variable selection. The study by Cadenas (2013) used twenty-four datasets to compare random forest variable selection methods, with a focus on microarray data. Similar to our study, they found that VSURF had the among the lowest error rates. Though it focused on proposing a new variable selection procedure, Hapfelmeier (2013) also compared methods within a simulation study, which produced lower error compared to Altmann, Jiang, varSelRF, Svetnik, and VSURF. In our study, Hapfelmeier’s method had high computation times, moderate parsimony and higher mean error rate compared to other methods.

There are some limitations of our study which should be discussed. Firstly, we only included datasets with 1000 or less observations, so our results may not generalize to the setting of high dimensional data. We included this constraint due to computational expense—some of the larger datasets available were taking several hours to complete, and because a previous study had already investigated the problem of variable selection in the setting of high dimensional data (Degenhardt, et al., 2017). A future study could repeat our analysis in the setting of high dimensional data, perhaps using parallel computing to speed up run time. Secondly, we only included data with no missing values. It would be interesting to reproduce this analysis with imputed data to determine the effect of missing data on variable selection in the setting of random forest classification. Although we constrained our datasets in this manner, we were able to analyze 311 datasets with varying number of predictors and observations. Therefore, these results can be used as a guide to choosing which type of variable selection procedure may be preferable depending on the type of outcome (binary or multi-class; balanced or imbalanced) and dataset (large or small number of predictors).

There are several avenues of future work stemming from this study. Aside from conducting this study in large datasets as suggested above, one might also consider inclusion of missing data within the context of variable selection. In the present study, we only included datasets with no missing values, so it would be interesting to assess the amount of missing data and how imputation impacts variable selection in the random forest framework. Additionally, one might conduct a similar study using continuous outcomes within the random forest framework (our study focused on categorical outcomes only). Finally, variable selection techniques outside the random forest framework could be added for comparison to determine if random forest variable selection methods are preferable to other methods.

A primary contribution of our study was the ability to assess different variable selection techniques in the setting of random forest classification. Specifically, our study provided computation times for models, which addressed an important gap in the current variable selection literature. Based on our results to optimize error rate, parsimony, computation time and AUC, we recommend use of VSURF or Jiang for datasets which contain a binary outcome, datasets with imbalanced outcome, and datasets which have less than fifty predictors. A downside of VSURF is that it may not select any variables for a final model, so this method may not be ideal for noisy datasets (i.e. datasets with messy data) or datasets with weak predictors of the outcome. For datasets with many predictors, we recommend use of varSelRF or Boruta because these are more computationally efficient compared to other methods.