Exploring potentially alternative non-canonical DNA duplex structures through simulation.

Abstract

Hopkins proposed an alternative and chirally distinct family of double stranded DNA models that have antiparallel chains with 5’ → 3’ senses opposite to those of the right-handed Watson-Crick (WC) family. Termed configuration II, this family of double stranded DNA models contains both right-handed, II-R, and left-handed, II-L, forms, with Z-DNA as an example of the latter. Relative interstrand binding energies for six DNA duplex models, two each of configuration I-R (standard Watson-Crick canonical B-DNA), II-R and II-L for the duplex d(CGCGAATTCGCG), have been estimated under identical conditions using MM-PBSA analysis from molecular dynamics (MD) trajectories using three different AMBER force fields. These simulations support the stereo chemical soundness of configuration II dsDNA forms. Recent force fields (bsc1 and OL15) successfully render stable II-L structures, whereas the previous force field, bsc0, generated stable II-R structures although with an energy difference between II-R and II-L of ~30 kcal/mol.

INTRODUCTION

For over 60 years, the right-handed Watson-Crick (WC) canonical B-DNA structural model(Crick & Watson, 1954; Watson & Crick, 1953) for complementary double-stranded DNA (dsDNA) has been a familiar and textbook representation of DNA in its native form. Nonetheless, another family of very similar dsDNA structures was proposed by Hopkins(Hopkins, 1981) that differs from the canonical WC family (e. g. A, B, C-DNA) of models in having the two antiparallel single-strand chains (ssDNA) arranged with opposite relative 5’ → 3’ senses. This model family, termed configuration II, contains both right-handed, II-R, and left-handed, II-L, forms and is chirally distinct from the WC family, configuration I-R(Hopkins, 1983). It has remained relatively unfamiliar since the only known example of configuration II dsDNA observed to date experimentally is the left-handed Z-form. Z-DNA is commonly limited to alternating pyrimidine-purine sequences as an irregular II-L form that was first found in an X-ray crystal study of the duplex d(CGCGCG)(Wang et al., 1979). Here, ‘regular’ refers to the fact that all bases in both strands have the same conformation: either anti or syn. In regular I-R or II-L configurations, all bases are in the anti-conformation; in regular II-R configurations, all bases are in the syn conformation. In this sense, Z-DNA is ‘irregular’ in having syn purines and anti pyrimidines.

Most importantly, there is some evidence that Z-DNA exist in living systems(Pohl & Jovin, 1972; A Rich, Nordheim, & Wang, 1984; Alexander Rich & Zhang, 2003). Thus, it is possible that other configuration II forms (closely-related topologically to Z-DNA) are stable and potentially used biologically. In fact, Hopkins hypothesized that a much broader range of configuration II DNAs play important intracellular roles(Hopkins, 1984a, 1984b, 1986). In this work, we investigate and compare the structure and stabilities of configuration II vs. I dsDNA structures under typical conditions and define situations that might potentially favor chain configuration II. To this end, molecular dynamics (MD) simulations of six models (two each of the three regular dsDNA forms: I-R, II-R and II-L) have been conducted under identical conditions in explicit ionic solution. Simulations were performed using the most recent versions of the AMBER force fields for DNA, specifically bsc1(Ivani et al., 2015) and OL15(Zgarbová et al., 2011, 2013, 2015); these two force fields were developed independently by two different research groups and provide simulations of DNA duplexes that are in better agreement with experimental DNA structures than any other force field to date(Rodrigo Galindo-Murillo et al., 2016). The previous force field version, bsc0(Pérez et al., 2007), was also used as a control. Free energies were estimated using the Poisson-Boltzmann Surface Area (MM-PBSA(Srinivasan, Cheatham 3rd, Cieplak, Kollman, & Case, 1998)) methodology from the resulting MD. As part of this process, interstrand binding energies have been estimated.

METHODS

Initial DNA Models.

Six B-DNA like models (rise ~3.4 Å, twist ~36°), two each of configuration I-R, II-R and II-L, respectively, using the same sequence of d(CGCGAATTCGCG) were studied in simulations under identical conditions. Five of the six initial duplex models were generated from theoretical coordinates; the sixth is from single-crystal X-ray diffraction analysis. Hydrogen atoms were added when missing using the LEaP module of the AmberTools 14 suite of programs. Each model coordinate set served as a starting structure for five independent simulations, each with at least 20 μs of sampling time. A total of 90 independent simulations were performed (6 systems with 5 independent copies each, each with 3 different force fields). Images of the initial models are shown in Figure 1 and the details of each model is shown in Table 1. Initial coordinate files (PDB format) for each model are available in the supporting information and for download at http://amber.utah.edu/configurationII/. The configuration I models are right-handed Watson-Crick models. Configuration II-R are right-handed forms with chain senses opposites to WC models. The first 3 of the following configuration II models (II-Ra, II-Rb and II-L) were built using repeated cycles of energy minimization and averaging of measured atomic coordinates. Configuration II-L correspond to left-handed forms with chain senses opposite to Watson-Crick models.

Figure 1.

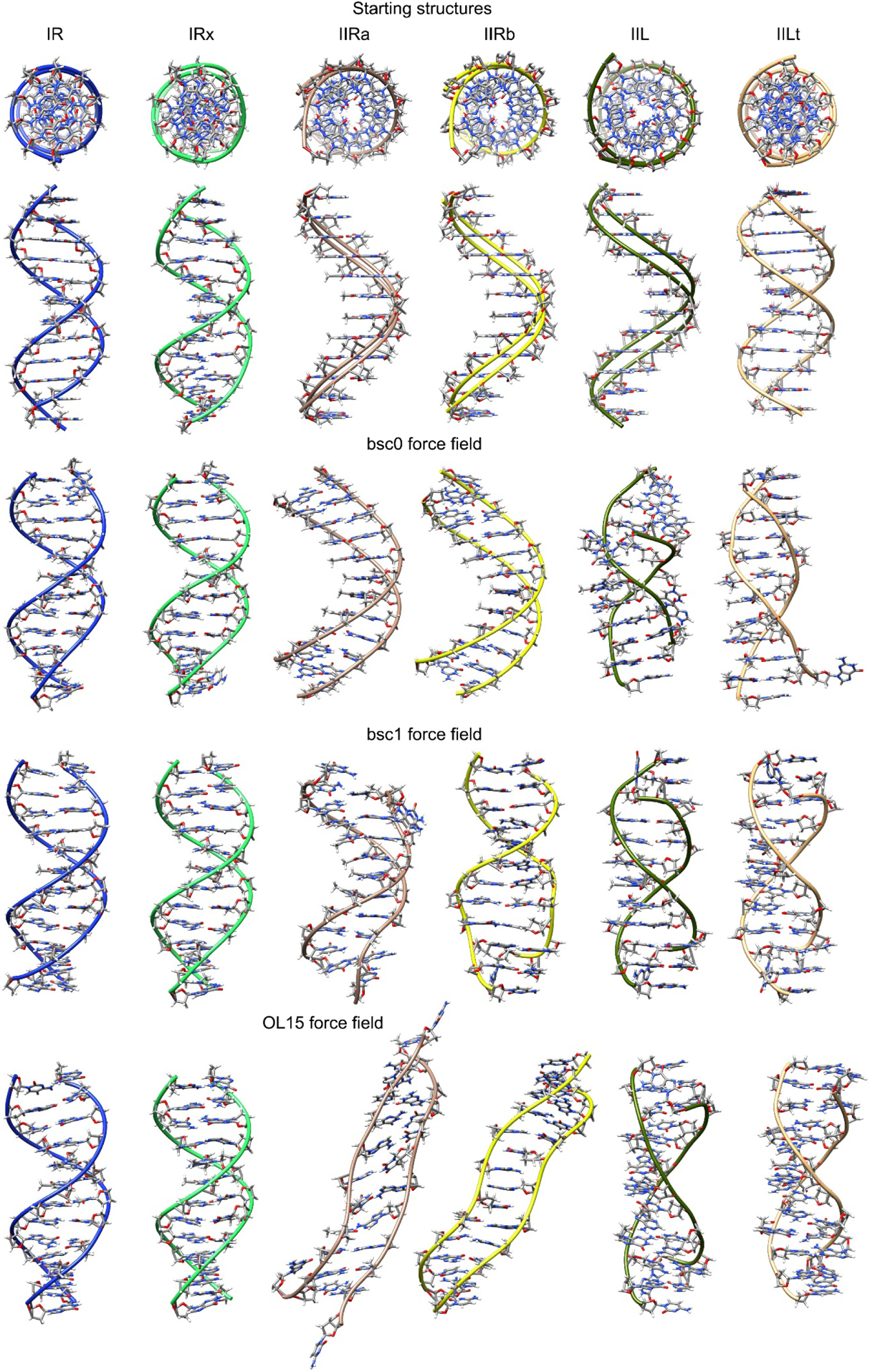
Top: initial constructed structures used in this study shown in two perspectives. Under these are structures for each force field showing the representative structure from the most populated cluster over all the frames from the five independent sampled trajectories. Refer to the on-line article for the color version of the image.

Table 1:

Name and description of the systems used in this work.

Name of the system	Description	Starting structure example (only central base pairs shown, hydrogen atoms hidden for clarity, red is oxygen, blue is nitrogen, orange is phosphorous and grey is carbon atoms).
I-R	This model was constructed from idealized cylindrical coordinates based on X-ray fiber diffraction data(Arnott, Campbell, & Chandrasekaran, 1976). (rise = 3.38 Å, twist = 36.0°).
I-Rx	These coordinates are directly from the analysis of the 1.4 Å resolution single crystal X-ray diffraction data of the PDB entry code 355D(Shui, McFail-Isom, Hu, & Williams, 1998) (mean rise 3.29 Å, mean twist = 35.4°).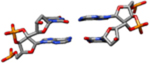
II-Ra	Theoretical cylindrical coordinate data of a DNA form having bases perpendicular to the helix axis was used to build this model (rise = 3.4 Å, twist = 34.6°).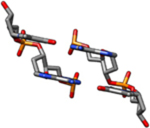
II-Rb	The coordinates for this model are similar to the II-Ra coordinates above but with C2’-endo sugars, rather than C4’-exo (rise = 3.4 Å, twist = 34.6°).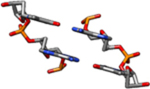
II-L	This model was constructed from theoretical cylindrical coordinates of a DNA form having bases perpendicular to the helix axis(Alexander Rich & Zhang, 2003).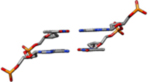
II-Lt	Coordinates for this model were built from theoretical cylindrical coordinates of a left-handed form of DNA designed to satisfy B-DNA fiber diffraction constraints(Gupta, Bansal, & Sasisekharan, 1980). Bases are tilted relative to the helix axis. (rise = 3.4 Å, twist = −36.0°).

Molecular Dynamics protocol.

MD simulations were performed using the parm99 force field(Cheatham 3rd, Cieplak, & Kollman, 1999) with the bsc0 modifications(Pérez et al., 2007), the bsc1 modifications, and the OL15 modifications as mentioned earlier. Using the models described above as starting structures, the topology and coordinate files were created using the LEaP module present in AmberTools 14. Explicit water was added using the TIP3P(Jorgensen, Chandrasekhar, Madura, Impey, & Klein, 1983) water model with a truncated octahedral box using a minimum distance of 10 Å around the solute and the edge of the box. Na⁺ counter ions were added to reach a net charge of 0 using the Joung-Cheatham ion parameters(Joung & Cheatham 3rd, 2008). Periodic boundary conditions were applied. A non-bonded cutoff of 8 Å was employed and the SHAKE algorithm(Ryckaert, Ciccotti, & Berendsen, 1977) to contain hydrogen bonds. Long range electrostatics were calculated using the particle mesh Ewald method with default parameters(Cheatham 3rd, Miller, Spector, Cieplak, & Kollman, 1998; Essmann et al., 1995). Each model was initially minimized using 500 steps of steepest descent and 500 steps of conjugated gradient using a harmonic restriction on the solute with a value of 20 kcal/mol·Å. A heating process was done using the same restriction on the solute and slowly heating for 50 ps to a final temperature of 300K. Temperature was maintained with Langevin dynamics (collision frequency = 2 ps⁻¹). After heating, the restraints on the DNA atoms were slowly reduced from 20 kcal/mol-Å to 0.5 kcal/mol-Å in 5 steps, each step lasting 50 ps. Five independent copies were minimized for each system and unrestrained MD was then conducted at NTP conditions for 20 μs using the pmemd.cuda module(Götz et al., 2012; Le Grand, Götz, & Walker, 2013; Salomon-Ferrer et al., 2013). The resulting trajectories where concatenated and all analysis and further post-processing was performed in this aggregated trajectory data. All simulations were run using AMBER14(Case et al., 2014) and analysis was done using CPPTRAJ(Roe & Cheatham 3rd, 2013) and Curves+(Lavery, Moakher, Maddocks, Petkeviciute, & Zakrzewska, 2009). The free energies of the six dsDNA models were estimated from the MD data using the mmpbsa.py tool available in AMBER14(Miller et al., 2012). Relative binding energies of the two strands could also be estimated since trajectories of each duplex were treated with one DNA chain being defined as the ‘receptor’, the other as the ‘ligand’ and combined as the ‘complex’.

RESULTS

The representative structures of the most populated cluster using all the frames from the five independent trajectories for each system are presented in Figure 1. The structures for both the I-R systems, regardless of the force field show a consistent Watson-Crick DNA duplex structure which is not the case for the rest of the studied variations where we observe highly distorted geometries. In Table 2 we present the fraction from the total frames that the representative structure shown in Figure 1 is populated. For the I-R system which represent the configuration I models (right-handed Watson-Crick models) we observe a 55% of population from the total frames for bsc0. More recent and robust force fields show 81% and 61% for bsc1 and OL15 respectively. This is in accordance with the root mean square deviation values (Table 2) which show that both bsc1 and OL15 are in better agreement with the reference structure than bsc0. The same trend is observed for I-Rx, which is also a right-handed WC model: good agreement with the reference structure with bsc0 and better agreement with bsc1 and OL15 (higher overall population and lower RMSD values). To further test the validity of the simulations starting from the I-R and I-Rx systems, we measured the RMS deviation from the familiar Drew-Dickerson dodecamer (DDD) average NMR structure (PDB code 1NAJ(Wu, Delaglio, Tjandra, Zhurkin, & Bax, 2003)). The average RMSD value between the I-R system considering only the ten inner residues is 1.7 Å, 1.4 Å and 1.6 Å for the bsc0, bsc1 and OL15 force fields respectively, whereas for the I-Rx system, the RMSD values for bsc0, bsc1 and OL15 are 1.5 Å, 1.2 Å and 1.1 Å. For the DDD, and WC dsDNA models in general, the use of the AMBER force fields bsc1 and OL15 render structures that have increased similarities with experimental observations than the previous bsc0 version(Dans et al., 2017; R. Galindo-Murillo, Roe, & Cheatham 3rd, 2014; Rodrigo Galindo-Murillo et al., 2016; Rodrigo Galindo-Murillo, Roe, & Cheatham 3rd, 2014). Configuration II-R are right-handed forms with chain senses opposite to WC models. The previous version of the AMBER force field, bsc0, showed representative cluster populations of ~80% and ~94% for the II-Ra and II-Rb systems with an average RMSD deviation from the initial structure of ~5 Å. On the contrary, both of the refined force fields, bsc1 and OL15 do not reach a representative structure with more than ~2% population. In these cases, the cluster analysis generated hundreds of clusters that were populated with single structures that could not be included in any other cluster due to elevated structural difference. The average RMSD difference is ~9 Å and ~7 Å for bsc1 and OL15 respectively. Visual inspection of the trajectories for both II-R systems showed extreme fraying events and complete melt of the DNA duplex for bsc1 and OL15 force fields as can be partially observed from Figure 1.

Table 2:

Fraction of the total frames (in %) that the structure is present in the five aggregated trajectories and root mean square deviation values using the starting structures as a reference (Figure 1). All residues includes bases 1 through 24, inner residues are bases 3–10 and 15–22. Analysis performed using the full trajectories from the five independent copies.

	Population (%)				RMSD (Å) All residues			RMSD (Å) Inner residues
	bsc0	bsc1	OL15		bsc0	bsc1	OL15	bsc0	bsc1	OL15
I-R	55.2	81.1	61.7		2.8	2.2	2.2	2.2	1.8	1.9
I-Rx	56.8	76.4	65.6		2.6	2.2	2.2	2.0	1.7	1.6
II-Ra	79.9	9.3	1.7		4.1	9.8	7.1	3.4	8.8	6.0
II-Rb	94.2	1.3	1.6		3.4	9.0	7.0	2.8	7.9	6.3
II-L	19.7	54.7	56.2		8.6	7.6	8.1	7.8	7.1	7.5
II-Lt	35.5	63.6	62.7		6.3	6.7	4.9	5.9	6.4	4.5

To further study the reason behind these behaviors for the II-R structures, Figure 2 shows a histogram of the population for the χ dihedrals in each case. The bsc0 force field is highly populated in the syn conformation for both II-Ra and II-Rb in accordance with the previous results. A slight population of anti is observed for the II-Ra system whereas for the II-Rb is the anti population is negligible with bsc0. In the case of bsc1, it seems that the population is divided between the anti and syn in an approximately equivalent manner which is not the case for OL15 where an elevated population in the syn is evident, although, OL15 also shows population of anti. The average value for each χ dihedral is shown in Table 3. As discussed, values for II-Ra and II-Rb sampled with bsc0 are all between the expected values for the syn configuration (+60° to +80°).

Figure 2:

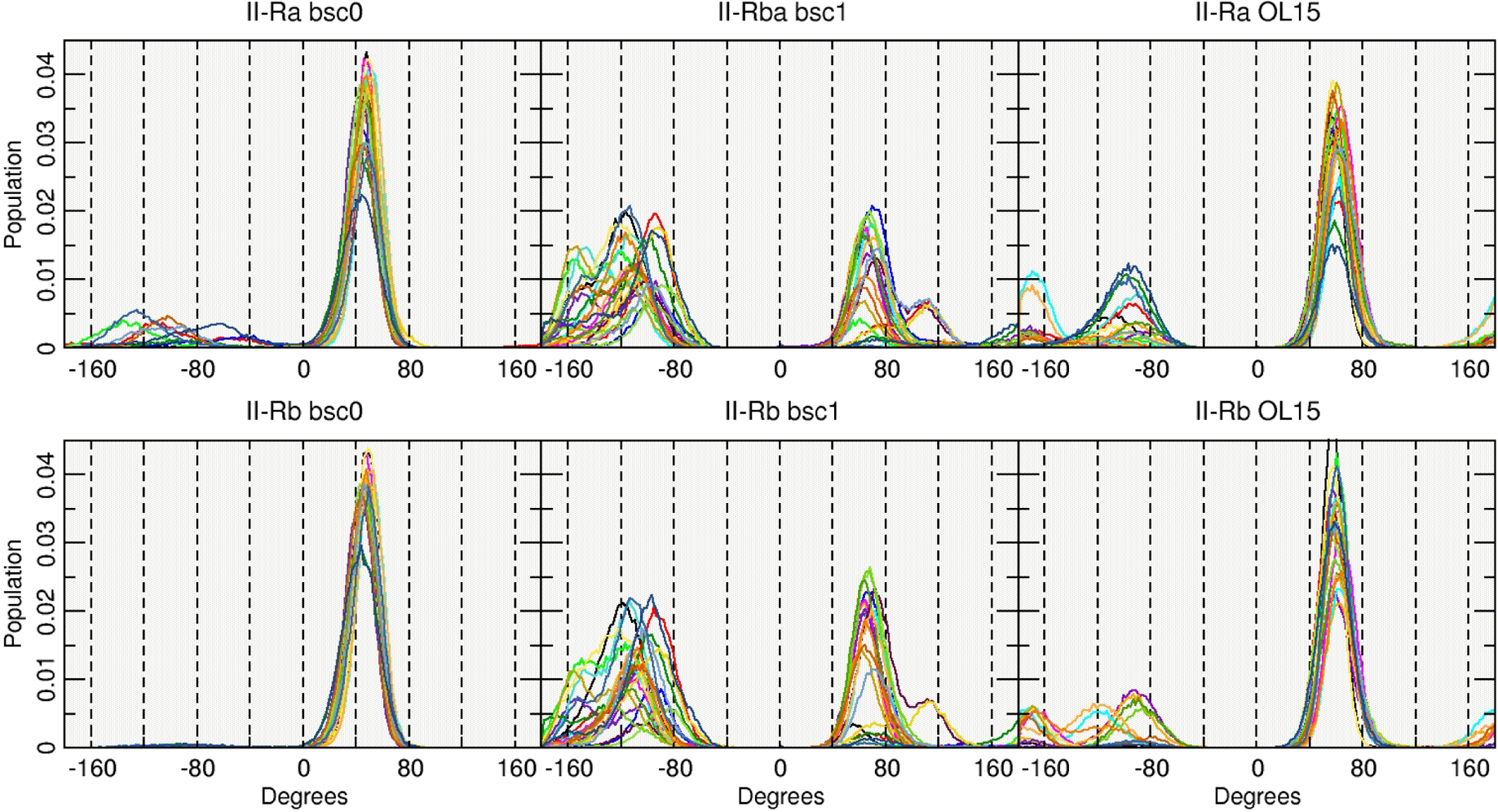
Population histograms of the values for the χ angle using the entire aggregated trajectory. Each line represents one base out of the 24 present on the DDD.

Table 3:

Average values for the χ angle for all the bases (pyr: O4’-C1’-N1-C2; pur: O4’-C1’-N9-C4. Syn: χ = 60 > χ > 80°; anti: = −115 > χ > 180°; high anti: = −60 > χ > −90°). Analysis performed using every 10^th frame of the five independent trajectories run (~53000 frames). Bold-underlined text is syn position.

	I-R			I-Rx			II-Ra			II-Rb			II-L			II-Lt
Base:	bsc0	bsc1	OL15	bsc0	bsc1	OL15	bsc0	bsc1	OL15	bsc0	bsc1	OL15	bsc0	bsc1	OL15	bsc0	bsc1	OL15
Chain 1
C 1	29.1	−81.4	4.3	30.5	−73.8	13.0	42.3	−123.7	11.8	46.5	−107.7	52.3	−54.8	−124.2	−88.2	−127.6	−143.4	−130.7
G 2	−95.0	−100.8	−96.5	−94.9	−96.7	−97.0	15.2	−37.0	4.1	45.9	−86.9	56.7	71.8	68.5	70.7	59.4	107.1	67.7
C 3	−123.0	−120.5	−112.3	−122.9	−120.9	−110.4	12.6	−110.8	37.9	44.1	−122.0	60.4	−150.5	−147.1	−132.9	−150.9	−154.3	−144.5
G 4	−105.0	−98.3	−98.4	−104.4	−97.4	−100.7	31.6	25.0	58.6	44.6	19.7	58.8	55.7	67.7	68.1	64.8	100.1	68.0
A 5	−119.2	−113.7	−105.3	−119.1	−113.5	−105.1	45.0	−29.9	43.0	44.1	−11.8	6.3	−52.9	−126.0	−39.5	−90.4	−98.9	−113.8
A 6	−121.6	−116.8	−112.4	−121.8	−116.8	−111.6	45.2	−12.5	40.1	44.8	−18.6	18.4	−29.3	46.6	70.0	70.1	37.3	70.2
T 7	−126.7	−120.2	−119.3	−126.8	−120.0	−117.6	50.1	−33.7	−1.0	49.8	−18.7	14.2	−79.2	−142.9	−104.1	−94.0	−138.6	−148.9
T 8	−123.8	−115.7	−115.1	−123.8	−114.3	−113.9	46.4	−32.3	53.5	46.6	−17.6	34.4	−52.0	45.3	29.9	32.9	31.9	67.0
C 9	−124.0	−110.8	−104.9	−123.9	−113.3	−105.0	40.9	−35.0	48.2	41.1	−21.2	54.2	−108.1	−140.1	−122.7	−102.1	−140.1	−139.8
G 10	−111.1	−106.7	−103.5	−111.2	−105.8	−106.9	45.6	6.3	59.0	45.2	57.8	58.1	40.5	105.3	67.6	25.0	84.8	68.1
C 11	−110.8	−113.0	−103.7	−110.9	−116.7	−103.7	47.2	−125.2	5.5	47.1	−119.7	36.2	−144.7	−142.7	−137.6	−139.2	−142.4	−145.2
G 12	−92.7	−102.2	−106.5	−95.0	−106.9	−92.5	32.7	−91.4	−13.2	38.3	−82.3	55.9	−26.8	−55.3	0.2	20.7	−57.7	38.5
Chain 2
C 13	29.4	−66.3	−12.2	28.6	−65.3	18.4	44.1	−123.5	26.9	46.6	−123.8	31.2	−40.8	−136.3	−68.4	−104.4	−139.1	−105.2
G 14	−95.0	−100.5	−97.3	−95.0	−99.6	−96.5	48.3	−42.3	38.4	47.1	−33.4	57.7	68.5	70.9	71.7	35.7	71.5	70.3
C 15	−123.4	−119.9	−111.7	−123.0	−118.9	−111.3	44.1	−98.9	51.2	43.9	−58.2	36.7	−150.8	−153.8	−137.5	−136.5	−146.0	−148.0
G 16	−104.4	−98.1	−98.7	−104.7	−99.8	−100.9	42.5	12.2	58.3	42.5	33.7	58.9	39.5	100.2	67.9	53.7	66.3	68.2
A 17	−119.1	−113.8	−105.5	−118.9	−113.2	−105.2	44.1	−0.7	41.3	45.1	23.6	27.0	−46.8	−94.9	−45.4	−37.3	−103.5	−111.7
A 18	−121.6	−116.9	−112.4	−121.7	−117.1	−111.5	45.5	−23.6	39.4	44.8	−2.1	21.6	−29.0	45.3	70.5	32.6	34.7	75.2
T 19	−126.8	−120.1	−119.3	−126.8	−120.2	−117.8	49.8	−31.1	19.4	49.6	−21.0	3.6	−105.5	−140.9	−100.4	−126.6	−137.0	−142.9
T 20	−123.6	−115.5	−115.1	−123.7	−115.5	−113.8	45.5	−60.7	42.6	45.2	−28.6	6.7	−63.3	44.9	31.0	15.8	28.5	31.1
C 21	−124.1	−111.5	−104.7	−124.0	−110.7	−104.8	15.9	−74.1	47.9	41.8	−26.6	38.0	−100.3	−139.9	−118.9	−147.4	−147.2	−138.4
G 22	−111.2	−105.8	−103.3	−111.2	−106.3	−107.1	16.9	17.7	47.7	45.4	−39.2	59.0	69.2	71.9	68.0	63.3	112.5	67.8
C 23	−110.5	−114.2	−103.2	−110.7	−113.4	−103.5	4.6	−122.8	−14.0	43.9	−114.5	54.0	−145.7	−142.0	−136.9	−148.8	−149.2	−144.4
G 24	−97.7	−103.1	−105.2	−89.6	−100.7	−97.0	13.0	−78.4	−28.4	37.7	−92.5	55.1	−20.6	−64.1	4.1	38.5	−56.7	28.7

The bsc1 shows average χ values in the inner base-pairs that are in the range of −10° to −70° that corresponds closer to a high-anti value, which explains the shape of the representative cluster shown in Figure 1, resembling the I-R structures. Contrary to bsc1, OL15 has average values in the inner-base pairs between +10° to +60°, closer to the canonical syn values. This suggests that while the bsc1 is closer to a normal sense DNA on which the χ angle is in its anti configuration, the OL15 is preferring to remain in the syn conformation, resembling the starting model. Monitoring the angles as a function of time show that χ is flipping back and forth between syn and anti, and therefore the structure is not effectively “trapped” in syn in simulations on the 20 μs timescale, however the structures are very dynamic as evidenced by the presence of a large number of low population clusters.

Simulations regarding the Z-like forms resulted in less distorted structures (Figure 1). Both II-L and II-Lt are represented in a higher population for bsc1 and OL15 (Table 2). It is remarkable that even though the starting structures for both II-L and II-Lt forms have all syn configurations for all the bases, both of the models undergo conformational changes that lead to anti/syn transitions in each strand (Table 3). This alternation is in phase with the two d(CGCG) end segments as though each was in a Z-form of the d(CGCG) tetramer. The use of bsc1 and OL15 overall produced a more persistent anti/syn alternation whereas for bsc0, the II-L presented high-anti population in the inner AATT residues. However, this regular anti/syn alternation persist right through the intervening, non-alternating d(AATT) segment of the II-Lt structure Despite the fact that the starting II-L topology is the same for both models II-L and II-Lt, their initial structures differ significantly in appearance (Figure 1). Thus, based on only one example, differences in their behaviors during MD simulation apparently reflect differences in these initial structures. In order to get a sense of the timescale that the anti/syn distribution requires, in Figure 3 we present the values of the glycosidic bond of four of the inner residues, CGAA, for II-L and II-Lt. The figure displays only the starting 1200 ns of simulation. For II-L, both bsc0 and bsc1 appear to be populating the anti/syn configuration at the beginning of the sampling time which means that the glycosidic bonds shifted in the early equilibration steps. It seems that OL15 requires at least 400 ns of sampling time to achieve the final anti/syn distribution for the presented CGAA tetramer. For the II-L system, a ‘nearly regular’ alternation of anti/syn configuration is achieved at the beginning of the simulation with few deviations for the remaining sampled time.

Figure 3:

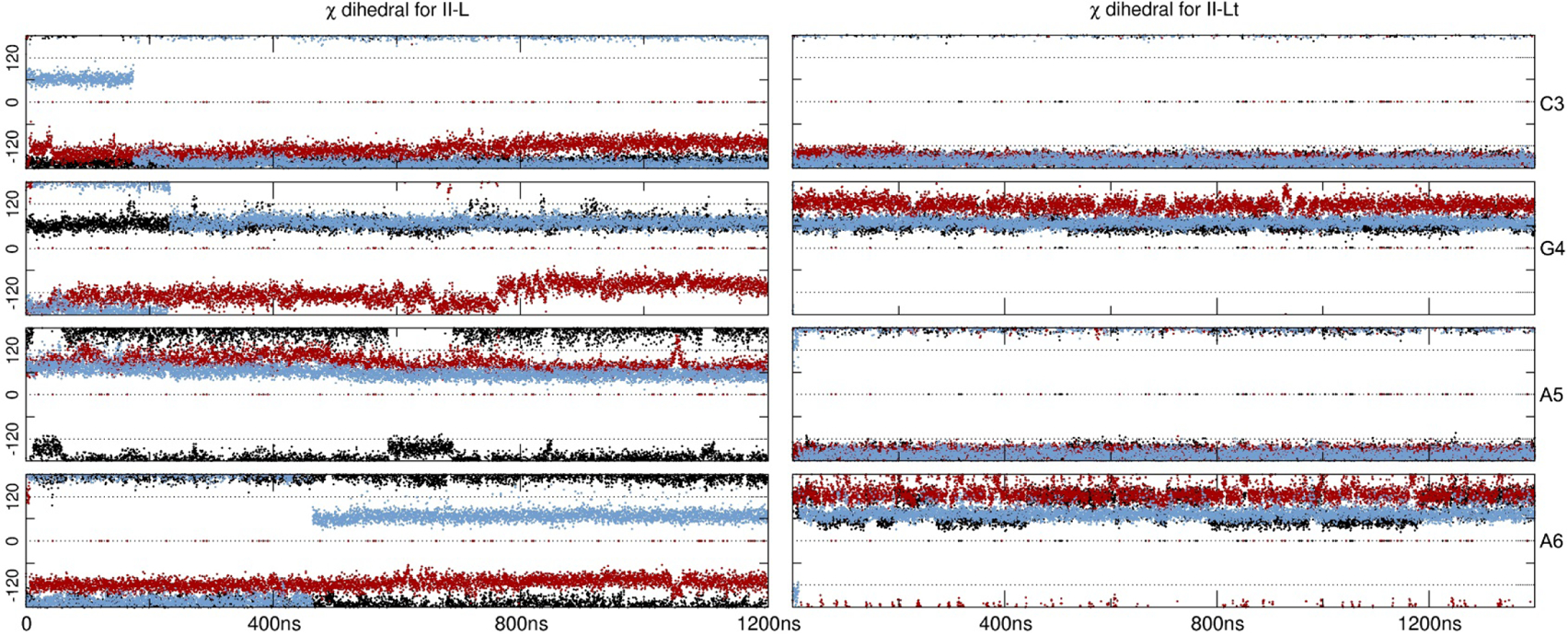
Glycosidic angles (in degrees) for the inner residues CGAA. Black represents bsc0, red is bsc1 and blue is OL15. Only the very first 1200 ns are shown of the first copy.

Estimated Interstrand Binding Energies.

The MM-PBSA protocol was used to extract binding energies for each double stranded DNA configuration, setting up one of the strand as “receptor” and the complementary strand as the “ligand”. Extracting and calculating energy values in order to study the overall stability of the systems, exposed a few challenges. First, a simple average of the energy values, calculated from the aggregated trajectories generated nonsensical results (i. e. extremely high standard deviations). This was caused by including all the frames from the sampled trajectories, which in turn included highly distorted structures, i. e. fraying of 2^nd and 3^rd terminal base pairs, interstrand base-pair flipping and miss pairing of DNA bases. Second, an average result of the energy calculations was sensitive upon what frames from the trajectory were selected. Since we are using a composite of five independent runs, we chose to present the interstrand binding profile by calculating the ΔG values every 10 frames and considering only the central base pairs (GAATTC). This allows to see the energy landscape across the entire aggregated trajectory and the distribution of such values (Figure 4). As previously discussed, both I-R and I-Rx simulations that represent WC type DNA are stable, showing interstrand binding energy values of ~−45 kcal/mol and ~−42 kcal/mol respectively (averaging the three tested force fields). Similar results are obtained for the II-L and II-Lt structures with average ΔG values of ~−50 kcal/mol and ~−40 kcal/mol although with a more dispersed distribution across a range of ~15 kcal/mol. The most populated structures for the II-R models generated by the bsc0 force field produced an average binding energy of ~−14 kcal/mol, whereas both bsc1 and OL15 do not show any representative structure and the energy values are dispersed within a ~100 kcals/mol range.

Figure 4:

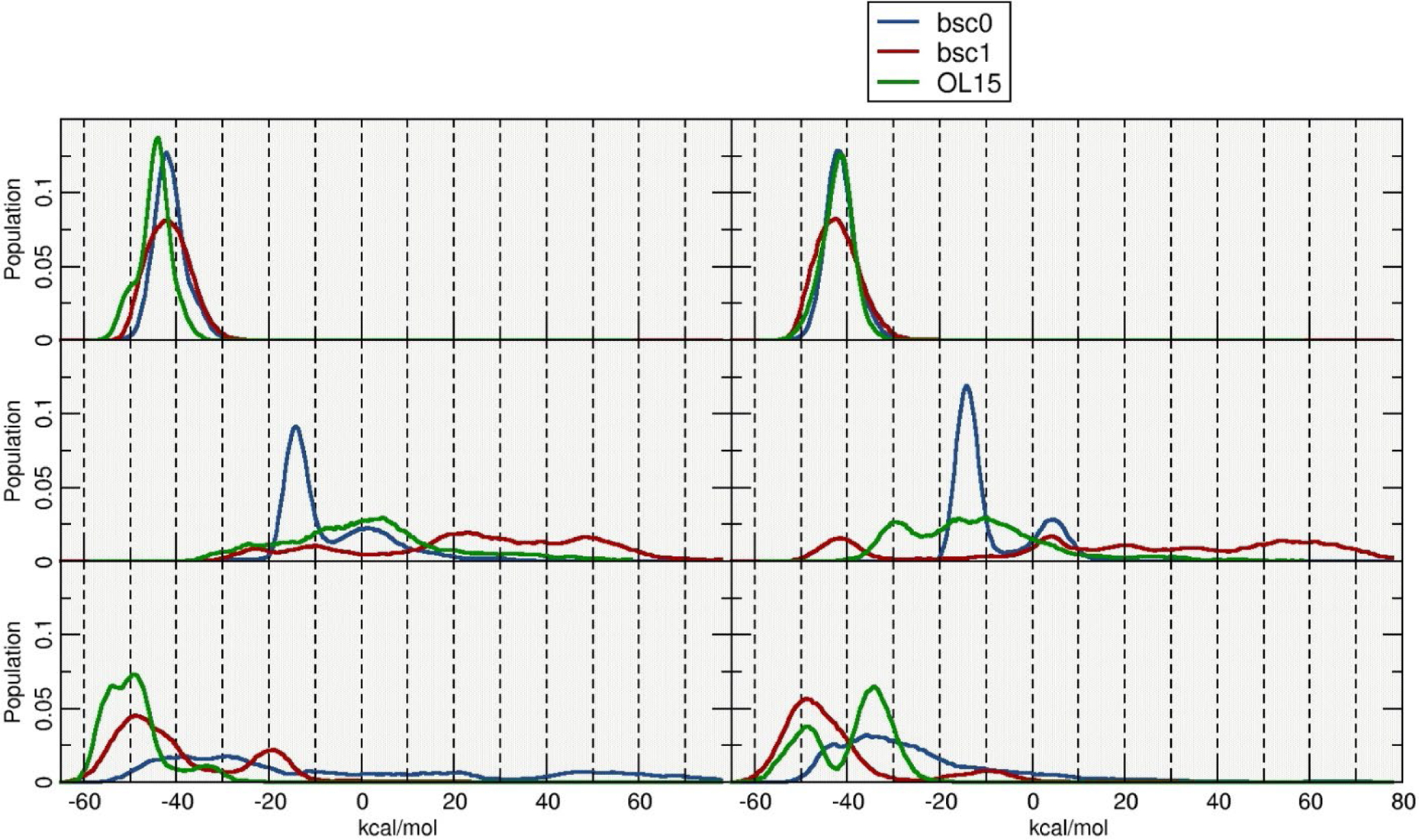
Histogram plots of the estimated interstrand ΔG values. Calculations were performed using blocks of 10 frames for a total of ~4600 independent calculations.

It is important to notice that the inherent limitations of the MM-PBSA methodology could result in high uncertainty margins(Islam, Stadlbauer, Neidle, Haider, & Sponer, 2016). We observed these inaccuracies early on the analysis stage and inspected carefully each trajectory to identify as much as possible the source errors in the energy measurement. As mentioned, fraying events on both sides of the double stranded DNA chain where found to be the highest source of variability. Different approaches where tested and considered in an effort to reduce the error, which was achieved focusing on the central base-pairs, where the base-pairing was found to be more constant throughout the sampled space.

Relative Model Stability in Simulation.

Since the model sequences and conditions for the simulations were identical, any differences in behavior between models can be attributed to how the structural topology of each model is treated by the different tested force fields. During the aggregated simulation time of each of the six models, the I-R and I-Rx WC models and the Z-type II-L and II-Lt models remained base paired throughout, although, multiple fraying events are observed within the first and second base pairs. This observation has been reported previously and is expected(R. Galindo-Murillo et al., 2014; Rodrigo Galindo-Murillo et al., 2014). Thus, these results do not indicate any inherent stereo chemical instability in these models. Results regarding II-Ra and II-Rb generates only stable structures via the use of the bsc0 force field, with a small population of structures nearly isoenergetic to the I-R structures. Visual inspection of the trajectory data revealed that these stable structures are present throughout the five independent copies. Both bsc1 and OL15 produce largely distorted, frayed, melted, and higher energy structures as more sampling time is accumulated.

Molecular Compactness: configuration II vs. I.

The II-R and II-L structures are perceptibly more compact than the two I-R models, as noted in the original study³. More concretely, however, Table 4 lists for each final model both the Solvent Accessible Surface Area (SASA) and data on inter chain P-P distances.

Table 4:

Average solvent accessible surface area and average P-P distance as calculated from the aggregated trajectory (every 10^th frame) and using all the residues.

	SASA				Average P-P distance
	bsc0	bsc1	OL15		bsc0	bsc1	OL15
I-R	4379	4355	4362		20.3	19.9	19.8
I-Rx	4381	4341	4355		20.3	19.9	19.7
II-Ra	4190	4239	4255		8.2	13.8	9.9
II-Rb	4214	4266	4268		8.4	15.5	11.0
II-L	3851	4043	4122		15.4	17.5	15.0
II-Lt	4103	4053	4120		14.3	19.1	15.4

The mean SASAs for the Configuration II models (including the two Z-DNA 12-mers) are lower than those for the WC structures, as is consistent with having more compact forms. Likewise, the lower interchain P-P distances for the Configuration II structures are consistent with this same conclusion. Being more compact, configuration II structures including Z-DNA, generally have much closer interstrand P-P distances, than WC DNA (Table 4). Earlier experimental data on this system show unambiguously that this left-handed form is of configuration II-L. The transitions in the II-L models from the regular II-L or II-Lt forms to the irregular, Z-like forms, II-Lz or II-Ltz involve reorientation of the atoms of the backbone chains and the attached sugar moieties, but do not require disrupting base-pairs or H-bonds. Here, the base and angles vary in the range between 247 – 27 (i. e. anti, high-syn, syn). As noted in early modeling studies(Hopkins, 1981, 1983), the barrier to this transition is apparently small and should provide a facile pathway if ΔG < 0. However, a more significant energetic barrier lies in the inter conversion between II-R forms and II-L forms (including Z-DNA). Finally, the significantly more complex inter conversion between I-R and II-L forms involving chirally distinct dsDNA families and is not well understood(Hopkins, 1983). In antiparallel strands of G-quadruplex structures, it has been shown that the anti/syn alternation is energetically preferred over a syn/anti alternation(Šponer et al., 2013). Thus, by analogy, sequences of alternating d(pyr-pur) should favor the anti/syn alternation whereas alternating d(pur-pyr) might assume a syn/anti alternation.

On average, hydrogen bond interaction energies in aqueous solution typically lie in the range of −3 to −6 kcal/mol(Jeffrey & Saenger, 1991). Quantum mechanical calculations of base-pair interaction energies in the gas phase for CG pairs are reported to be −27.5 (−9.2 per H-bond) kcal/mol and for AT base pairs, −15.0 (−7.5 per H-bond) kcal/mol(Sponer, Jurecka, & Hobza, 2004). However, because of water competition for DNA donor and acceptor sites, interaction energies in aqueous solution are expected to be much smaller and more consistent with the results here (−4.2 kcal/mol per H-bond).

Hopkins hypothesized a number of reasons why the configuration II forms of DNA have not been more commonly observed:

1. Native vs. synthetic DNA –

One tenet of molecular biology is that dsDNAs having the same strand sequences are identical. Thus, native (i. e. extracted from the environment of a living cell) and synthetic (i. e. formed and annealed in-vitro) dsDNAs of the same sequence are assumed to be indistinguishable. Yet, despite the progress made based on this belief, there is no direct experimental evidence for its correctness. It is certainly true for ssDNA where the structural topology, whether native or synthetic, is fundamentally fixed by the covalent bonds and the chiral stereochemistry of β–D-2’-deoxyribose, so there is no doubt that two ssDNA strands of the same sequence are congruent. However, this is not necessarily true for two helical dsDNAs having the same chain sequences, formed under different conditions. Assuming that the bases of their two complementary, antiparallel single strands are held together by canonical Watson-Crick hydrogen-bonding, two additional chiral features of the secondary structure need to be specified(Alexander Rich & Zhang, 2003) to insure topological equivalence: first, the direction of the helical twist about the long axis, either right- or left-handed, but, in addition, the more subtle and generally unknown relative senses of the two antiparallel chains when viewed about a pseudo-dyad axis in the minor groove. If the 5’→3’ senses of the two antiparallel chains appear to form a clockwise couple, the DNA is of configuration I (WC DNA); if the senses form a counterclockwise couple, it is of configuration II. Thus, only by knowing both of these extra parameters can the structural equivalence of two dsDNAs of the same sequence be established.

2. Cellular vs. in vitro environments –

Ion concentrations used for in vitro studies (e. g. 1–100 mM) are often significantly lower than those found in vivo. For example, in mammalian cells, a typical Na⁺ concentration in blood is about 145 mM or about 139 mM for K⁺ in the cytosol. In more specialized cells such as squid axons, these values are about 440 mM and 400 mM respectively(Lodish et al., 2000). It is well known(Jeffrey & Saenger, 1991) that higher ion concentrations promote formation of compact and condensed forms of DNA. Additionally, with a total macromolecular concentration inside a cell of up to 400 g/l, more than 5% to 40% of the total cellular volume is excluded to other molecules of a comparable size. This striking phenomenon, known as ‘macromolecular crowding’ or ‘the excluded volume effect’, also favors compact macromolecular forms that minimize the volume they exclude. Yet, this variable is generally neglected for in vitro experiments. Since both of the complementary effects are present in vivo, one might expect that the more compact configuration II structures would be favored there.

3. X-ray fiber diffraction –

Although X-ray fiber diffraction has been used to study both dsDNAs taken from living cells as well as created synthetically, data resolution from this technique is highly limited because of sample inhomogeneity. Thus, only broad, general structural details of DNA can be discerned and subtle differences, as between dsDNAs from different environments, would not be apparent in the data.

4. X-ray single crystal diffraction –

Primarily because of the difficulty of handling, purifying and crystallizing DNA from living cells while maintaining physiological conditions, no single crystal X-ray studies of unique sequence native DNA are known to have been conducted to date.

5. NMR –

As one of the most powerful multi-dimensional methods for determining molecular structure in solution, nuclear magnetic resonance (NMR) can, in principle, be used to determine the structures of both synthetic and native dsDNA under identical solution conditions. Unfortunately, the data provided by NMR for dsDNA is insufficient (i.e., underdetermined), so that additional information lie covalent bonding, relative strand arrangement, handedness and chiral details, is also required for a complete structural solution. For example, in practice, canonical Watson-Crick B- or A- forms of DNA (configuration II-L) might be used. Thus, the potential for the actual structure being of configuration II-R or of a different form that Z-DNA is not investigated, in general. Nonetheless, the result of using the wrong template can be far-reaching. One limitation of NMR solution studies (and of normal X-ray crystal or fiber diffraction studies) is that the data results in only magnitudes or intensities without phase or direction information. Thus, a chiral molecular structure and that of its mirror image (enantiomer) cannot be distinguished without additional data or procedure. For example, the mirror image of the canonical WC (configuration I-R) B-form of DNA has all the characteristics of configuration II-L B-form DNA, except that the sugar moieties in the enantiomer are in the unnatural L-form. Thus, if one used a WC B-form DNA template in an NMR experiment (or in an X-ray crystal experiment employing the molecular replacement method) and the molecule in solution (the crystal) was actually of configuration II-L, a properly refined structure based on this template would appear to contain unacceptable L-deoxyriboses.

CONCLUSION

We have explored the stability of the antiparallel chains in the configuration II family of dsDNA using extensive sampling time, multiple independent copies and the most up to date force fields available for nucleic acids. The relative interstrand binding energies of the II-R models estimated here under identical conditions are shown to be significantly higher than those for the I-R structures at atmospheric pressure, room temperature and two ionic strengths. Both II-Ra and II-Rb configurations rendered multiple highly distorted and melted structures with two of the force fields that are routinely used, with tested success, to model dsDNA. Our simulations suggest it is highly unlikely that configuration II dsDNA forms would be observed in vitro at conditions similar to those of the simulations. Both of the II-L models undergo a transition to the alternating anti/syn Z-like forms early in the MD simulations with both bsc1 and OL15. As expected and previously reported, bsc0 is not able to properly represent either of the II-L structures. By no means is this work intended to benchmark or expose that a force field is better than the other; the use of three different force fields allowed us to do proper comparisons and somehow confirm the presented simulations. It is clear that the use of the force field greatly altered the results, hence, the present work opens more questions until more experimental evidence is available or analyzed.

ABBREVIATIONS

WC

Watson-Crick

MD

Molecular Dynamics

BSC

Barcelona Supercomputing Center

OL15

Olomouc 2015