Measuring transverse relaxation in highly paramagnetic systems

Abstract

The enhancement of nuclear relaxation rates due to the interaction with a paramagnetic center (known as Paramagnetic Relaxation Enhancement) is a powerful source of structural and dynamics information, widely used in structural biology. However, many signals affected by the hyperfine interaction relax faster than the evolution periods of common NMR experiments and therefore they are broadened beyond detection. This gives rise to a so-called blind sphere around the paramagnetic center, which is a major limitation in the use of PREs. Reducing the blind sphere is extremely important in paramagnetic metalloproteins. The identification, characterization, and proper structural restraining of the first coordination sphere of the metal ion(s) and its immediate neighboring regions is key to understand their biological function. The novel HSQC scheme we propose here, that we termed R₂-weighted, HSQC-AP, achieves this aim by detecting signals that escaped detection in a conventional HSQC experiment and provides fully reliable R₂ values in the range of ¹H R₂ rates ca. 50–400 s⁻¹. Independently on the type of paramagnetic center and on the size of the molecule, this experiment decreases the radius of the blind sphere and increases the number of detectable PREs. Here, we report the validation of this approach for the case of PioC, a small protein containing a high potential 4Fe-4S cluster in the reduced [Fe₄S₄]²⁺ form. The blind sphere was contracted to a minimal extent, enabling the measurement of R₂ rates for the cluster coordinating residues.

Introduction

The hyperfine interaction between electron and nuclear spins gives rise to additional contributions to chemical shifts and nuclear relaxation, both of which can be used as a source of structural restraints (Piccioli and Turano 2015; Turner et al. 1998). Nowadays, NMR solution structures of paramagnetic macromolecules are obtained by a combination of conventional restraints (Ab et al. 2006; Mori et al. 2008), such as NOE and residual dipolar couplings, and of paramagnetic-based restraints (Arnesano et al. 2006; Clore 2015; Kudhair, et al. 2280; Parigi et al. 2019; Pintacuda et al. 2007). Depending on which paramagnet is present in the system, different combinations of contact shifts, pseudocontact shifts, paramagnetic relaxation enhancements and cross correlation rates can be used (Koehler and Meiler 2011; Clore and Iwahara 2009; Kateb and Piccioli 2003; Pintacuda 2004). However, since about two decades, many groups have promoted the use of paramagnetism-based NMR restraints to study also diamagnetic proteins: metal binding tags have been used as spin-labels and provide various restraints capable to complement the NMR information available on a native, diamagnetic, derivative (Iwahara et al. 2004; Miao 2019; Matei and Gronenborn 2016; Liu et al. 2014; Nitsche and Otting 2017; Joss and Haussinger 2019). NMR of paramagnetic systems is not anymore a playground reserved to scientists working with inorganic or bio-inorganic systems, but a tool for a larger community of structural biologists with many potential applications (Tang et al. 2006; Softley et al. 2020).

Very recently, we have shown that structural restraints derived from Paramagnetic Relaxation Enhancements (PRE) can be used as the unique source of restraints for the structure calculation of small metalloproteins (Trindade et al. 2020b). A key point for a successful PRE-only approach is the availability of many accurate relaxation rate values measured throughout the entire protein, including the close proximity of the paramagnetic center, where nuclear spins are strongly affected by paramagnetism. When hyperfine shifted signals are well isolated outside the bulk diamagnetic envelope, they can be characterized using 1D experiments and relaxation based filters (Inubushi and Becker 1983), although usually only a few signals, arising from the side chains of metal-bound residues, can be identified via this approach (Hansen and Led 2006; Sato et al. 2003; Brancaccio 2017). Paramagnetic relaxation depends on γ² of the observed nucleus, therefore ¹³C or ¹⁵N direct detection (Arnesano 2003; Kolczak et al. 1999; Lin et al. 2003) have been successful as an efficient alternative to ¹H detected experiments, not only for assignment purposes (Bermel 2005; Machonkin et al. 2002; Bertini et al. 2005b) but also for the obtainment of PREs. However, the ¹⁵ N HSQC experiment still remains the “easiest” molecular fingerprint, therefore methods to exploit the use of ¹H_N T₁ and T₂ rates are welcome.

To date, relaxation-based restraints are indeed obtained via ¹H T₁ and T₂ measurements from ¹⁵N HSQC-type experiments (Donaldson 2001; Iwahara et al. 2007). However, many signals affected by the hyperfine interaction relax faster than the evolution periods used in these experiments; therefore, they will be broadened beyond detection or, when they are detected, their intensity decay cannot be properly sampled. Thus, we need to design novel pulse sequences to measure R₂ and R₁ rates of resonances that escape detection in conventional HSQC experiments. For longitudinal ¹H relaxation rates, we have shown that an inversion recovery filtered ¹⁵N HSQC experiment acquired in antiphase (¹⁵N IR-HSQC-AP) (Ciofi-Baffoni et al. 2014) is very effective for the identification of signals severely affected by paramagnetism, and also for obtaining R₁ rates faster than those measurable in established experiments. However, it has been reported that ¹H R₂ values are less susceptible to internal motions and cross relaxation than ¹H R₁ values (Iwahara et al. 2004; Iwahara and Clore 2010). Therefore, we are interested to develop an experiment to obtain accurate measurements of ¹H transverse relaxation also in the close proximity of a paramagnetic center.

The experiment we present here has been customized for the case of the HiPIP (High Potential Iron-sulfur Protein) PioC from Rhodopseudomonas palustris TIE-1 (Bird, et al. 2014). PioC has 54 amino acids, contains the typical HiPIP binding motif CXXCX_nCX_mC and it is the smallest HiPIP isolated so far. Due to the high reduction potential (E⁰ =  + 450 mV vs SHE) of the [Fe₄S₄]³⁺/[Fe₄S₄]²⁺ redox pair (both oxidation states are paramagnetic), the protein is stable in the reduced [Fe₄S₄]²⁺ state. The paramagnetic ¹H NMR spectrum of PioC is very similar to the NMR spectra of other HiPIPs in the reduced state (Bertini 1992), thus indicating that the electronic relaxation time (τ_e) in PioC must be similar to previously studied HiPIPs (Banci et al. 2018). However, PioC is the smallest HiPIP isolated so far and about 60% of the protein is affected by paramagnetic relaxation. Counter-intuitively, the small size of the protein makes it more difficult to study, because paramagnetic effects are active in the majority of the protein, scalar and dipolar couplings are quenched and a number of HN signals are not observable in a conventional HSQC experiment (Cheng and Markley 1995; Machonkin et al. 2005; Lin 2009). Throughout this article we will first review why experimental approaches that are effective to study proteins containing metal bindings tags are not equally efficient for native metalloproteins; then we will discuss how implementation of this novel HSQC scheme allows the measurement of relaxation rate values in a range 50–400 s⁻¹. Rates in this range were once very difficult to measure reliably, however they are necessary to reduce the blind sphere enabling the characterization, and proper structural restraining of the first coordination sphere of the metal ion(s) and its immediate surrounding residues.

Materials and methods

Protein expression and purification

PioC was expressed and purified as previously reported (Bird et al. 2014). Uniformly ¹⁵N labeled samples of PioC were produced and the expression and purification protocol was identical throughout except in the addition of ammonium sulfate (¹⁵N₂, 99%) in the M9 minimal media. BL21 DE3 cells were double transformed with pET32h, a plasmid containing the construct thioredoxin–6xHis–thrombin cleavage site–PioC, and with pDB1281, a plasmid that carries the machinery for the assembly of iron-sulfur clusters. Cells were grown in Luria–Bertani (LB) medium supplemented with 100 mg*dm⁻³ ampicillin and 35 mg*dm⁻³ chloramphenicol until the OD_600nm of 0.6 where they were induced with 1.0 mM arabinose and 20 μM FeCl₃ and 200 μM cysteine were added. Cells were again incubated until the OD_600nm of 1 and then harvested and washed in M9 minimal media salts before resuspension in M9 minimal media. Once re-suspended, cells were incubated for one hour before induction with 0.5 mM IPTG. After 4 h cells were harvested by centrifugation and disrupted using a French Press at 1000 psi. The lysate was ultra-centrifuged at 204,709×g for 90 min at 4 °C to remove cell membranes and debris and the supernatant was dialyzed overnight against 50 mM potassium phosphate buffer pH 5.8 with 300 mM NaCl before injection in a His-trap affinity column (GE Healthcare). The fraction containing Histag-PioC eluted with 250 mM imidazole and was incubated overnight with Thrombin (GE Healthcare) for digestion. The final purified PioC (His-tag free) was then concentrated from the flow through of a 2nd passage through the His-trap column using an Amicon Ultra Centrifugal Filter (Millipore) with a 3 kDa cutoff. The purity of PioC was confirmed by SDS-PAGE with Blue Safe staining (NzyTech) and by UV–Visible spectroscopy.

NMR spectroscopy

Measurements of ¹H R₂ transverse relaxation rates were carried out using 11.7 T Bruker AVANCE 500 equipped with a triple resonance, inverse detection, cryoprobe (TXI). ¹H_N R₂ measurements were obtained from a series of R₂-weighted ¹⁵ N-HSQC-AP experiments, developed throughout this article. For each experiment, 256 scans were collected over 256 increments. Acquisition time and recycle delay were 47.1 ms and 150 ms. A series of sixteen R₂-weighted ¹⁵N-HSQC-AP experiments was recorded, using INEPT transfer periods of 0.2 ms, 0.4 ms, 0.6 ms, 0.8 ms, 1.2 ms, 1.6 ms, 2.0 ms, 2.4 ms, 2.8 ms, 3.2 ms, 4.0 ms, 4.8 ms, 5.6 ms, 6.4 ms, 8.0 ms, 10.0 ms. Total experimental time was about 58 h. ¹H_N R₂ measurements have been obtained also with the established approach (Donaldson 2001), in which a relaxation delay T is inserted into the INEPT building block of an in-phase ¹⁵ N HSQC experiment. For each experiment, 32 scans were collected over 156 increments, using acquisition time and recycle delay of 47.1 ms and 4 s, respectively. A series of fourteen¹⁵N-HSQC-IP experiments was recorded using relaxation delays T of 13.3 ms, 17.3 ms, 21.3 ms, 33.3 ms, 45.3 ms, 57.3 ms, 69.3 ms, 81.3 ms, 93.3 ms, 117.3 ms, 141.3 ms, 165.3 ms, 205.3 ms and 245.3 ms. A 1400 μs selective ¹H_N inversion pulse was used for ³JH_NH_α decoupling. Total experimental time was about 80 h. Both series have been performed using 256 × 1024 data point matrices, over spectral windows of 80.0 ppm × 21.7 ppm. Squared cosine weighting functions and apodization were used in both dimensions prior to FT, spectra dimensions was 512 × 2048 data points. Peak intensities were used to calculate R₂ values, using the equations described in the results section. All relaxation data were analyzed using the Bruker Topspin Dynamics Center.

NMR assignment of PioC

The backbone NMR assignment of PioC (Trindade et al. 2020a) has been published on Biomolecular NMR Assignment and deposited in the BMRB data bank (ID 34487).

Results

State of the art: an overview

The state-of-the-art approach for ¹H R₂ relaxation is to use a ¹⁵N HSQC experiment and insert a relaxation period within the INEPT block to measure H_N rates (Donaldson 2001). Relaxation rates R₂ can then be obtained either by collecting, for each H_N signal, a complete decay curve or by measuring R₂ rates from a two time-point measurement, thereby enabling the direct determination of R₂ values and their associated errors without any fitting procedure (Iwahara et al. 2007). For non-deuterated proteins, band selective ¹H 180° pulses should be used to avoid the evolution of ³JH_NHα coupling during the relaxation period. The paramagnetic contribution to the overall nuclear relaxation is given (Bertini et al. 2016) by Eq. (1)

$$R_{2\text{obs}}=R_{2\text{para}}+R_{2\text{dia}}$$ 1

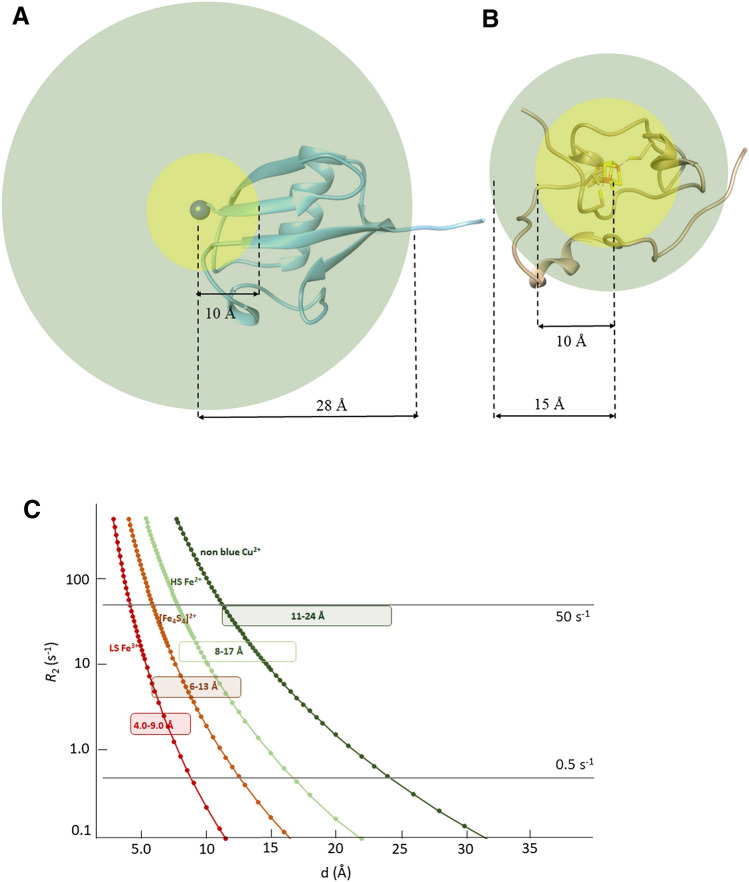
when R_2dia and R_2obs values can be measured with high precision and accuracy (Iwahara et al. 2007), then very small values of paramagnetic relaxation enhancement R_2para can be obtained by the difference of the two measured values. This has been exploited by attaching a metal binding peptide, such as ATCUN or HHP at the N-terminus site of a diamagnetic protein, as shown in Fig. 1a (Donaldson 2001). Metal binding peptides containing ions with long electronic correlation times, such as, for instance, Cu²⁺ or Mn²⁺, provide paramagnetic relaxation enhancements that can be measured, in the case of Cu²⁺ ion, for all protons located approximately 10–30 Å apart from the metal center (Donaldson 2001; Harford and Sarkar 1997; Jensen et al. 2004; Keizers and Ubbink 2011). The strength of this approach is that, within the above range, both R_2obs and R_2dia can be experimentally measured with high accuracy and R_2para as small as 0.5 s⁻¹ can be obtained, thus allowing the use of Paramagnetic Relaxation Enhancement (PRE, hereafter) for long metal-to-proton distance restraints. Protein–protein interaction surfaces and catalytic centers typically fall within this range, therefore one could obtain additional structural information for protein–protein/protein–ligand interactions, structure refinement, etc. (Battiste and Wagner 2000; Hass and Ubbink 2014; Cetiner 2019; Anthis and Clore 2015; Spronk 2018). On the other hand, signals at less than 12 Å from the copper(II) ion will experience R_2para larger than 50 s⁻¹, that will give rise to signals that, in the R₂ experiment, will be very weak and eventually broadened beyond detection. The loss of information typically occurs in a protein region where no catalytic reactions or biochemical events occur, since the metal binding peptide is attached far from the protein core, usually at the N-term site. In metalloproteins, however, the topology of the system is completely different: the metal center(s) and its first coordination sphere always constitute the core region for the protein function. Structural biologists are therefore interested to obtain detailed information in the close proximity of the metal center(s), where the biochemically relevant events occur. Assuming the same paramagnetic relaxation enhancement of the previously described situation, we face a loss of information in the most interesting part of the protein. Such blind region (Balayssac et al. 2006) is, indeed, always the core region of a metalloprotein (Fig. 1B). In this frame, reducing the blind sphere around the paramagnetic center(s) by measuring relaxation rates of nuclear spins that are most affected by paramagnetism becomes extremely important.

Fig. 1.

Measurable paramagnetic relaxation enhancements vs metal-to-proton distances. a Assuming a 10 Å blind sphere and a 10–30 Å sphere where PREs can be measured, the use of a metal binding tag at the N-term site of Ubiquitin (Donaldson 2001) gives measurable PRE for about 90% of the protein. b When the same relaxation enhancement parameters is considered for a small metalloprotein such as HiPIP (Trindade et al. 2020b), more than 70% of the protein would fall in the blind sphere. c Different electronic correlation times (τ_e) provide different dimensions for the regions affected by PREs. Assuming 50 s¹ and 0.5 s⁻¹ as upper and lower limits for the detection of PREs, the simulated behavior of paramagnetic centers with different τ_e is shown

The replacement of Cu(II), i.e. the metal ion used in the case of Ubiquitin shown in Fig. 1a, with another metal ion will change the radius of the sphere where paramagnetic relaxation enhancement is effective and measurable, but the above consideration will remain: the metal center is always surrounded by a blind sphere, where signals are broadened beyond detection, and by an outer sphere, in which PREs can be measured and factorized. The situation is described in Fig. 1c, where we considered 50 s⁻¹ as upper limit value to obtain reliable R₂ measurements and 0.5 s⁻¹ as lower limit for the precision of the measurement. At 500 MHz, considering a protein of small size and neglecting contact relaxation, R₂ is dominated by the Solomon equation (Solomon 1955) which, in turn, depends on the electronic relaxation time. For τ_e = 5*10^–9 s, which is an estimate for the electronic relaxation time of non-blue Cu²⁺ chromophores, ¹H signals at less than 11 Å are predicted to be unobservable while those at more than 24 Å are almost unaffected by paramagnetism. Different cases may occur for iron ions: for a high spin (S = 2) Fe²⁺, with typical τ_e = 5*10^–12 s, the above limits would be, respectively, 8 Å and 17 Å, while for a low spin (S = 1/2) Fe³⁺, with τ_e = 1*10^–12 s, they would be 4 Å and 9 Å, respectively. Different electronic relaxation times, together with other experimental parameters, such as magnetic field strength and protein size will give rise to different radii for the blind sphere and for the sphere where PREs are measurable. Also the replacement of ¹H with ¹³C or ¹⁵ N nuclei reduces both spheres and provides an alternate route to obtain PREs (Mateos et al. 2019). To extend the range of application of PREs in ¹H detected experiments it is necessary, on the one hand, to increase the accuracy of experimental methods and observe smaller PRE values and, on the other hand, to measure with reliability R₂ values larger than those achievable with the existing experimental approaches.

As extensively studied in the past, [Fe₄S₄]²⁺ clusters in proteins have an electronic ground state S = 0 due to the antiferromagnetic coupling (Phillips et al. 1970; Mouesca and Lamotte 1998; Bertini et al. 1992). However, each iron ion is formally in the oxidation state Fe^2.5+ and the system is paramagnetic at room temperature due to the population of the excited energy levels of the electron spin ladder (Banci et al. 1990). The distribution of population among the spin levels depends on the extent of the antiferromagnetic coupling constant(s) operative in the [Fe₄S₄]²⁺ cluster (Blondin and Girerd 1990). Therefore, the choice of the parameters to input in the Solomon equation to predict the behavior of R₂ vs H-Fe distance in [Fe₄S₄]²⁺ clusters is not obvious (Bertini et al. 1997): if we consider that each iron ion will relax with the same electronic relaxation time of a High Spin Fe²⁺ ion (τ_e = 5*10^–12), and that paramagnetism at room temperature arises from the population of the first excited state of the electron spin energy ladder, characterized by S = 1, we obtain, as shown in Fig. 1C, a behavior somehow intermediate between the two cases considered here for iron ions, with expected values for the blind sphere and for the PRE sphere of about 6 Å and 13 Å. This makes PioC an ideal test case for the optimization of sequences aiming at measuring R₂ rates in the proximity of the cluster.

Pulse sequence description

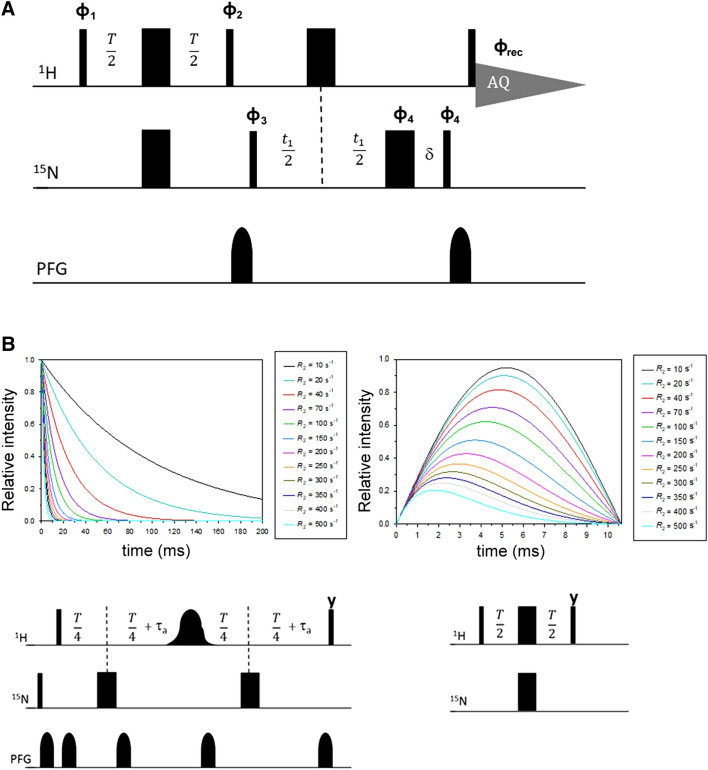
Here we propose a novel pulse sequence, shown in Fig. 2a, in which the relaxation delay is embedded within the INEPT evolution, the refocusing INEPT is removed and signal is acquired as antiphase doublet as soon as the H_yN_z magnetization is created by the last ¹H 90° pulse. We called the experiment ¹H R₂-weighted ¹⁵N-HSQC-AP because the INEPT period, typically 1/(2J_HN), is replaced here by a variable relaxation delay T. In this very simple sequence, ¹H transverse relaxation is active only during the delay T, when the 2H_xN_z coherence evolves from H_y as H_xN_zsin(πJ_HNT). The relaxation rate of the 2H_xN_z antiphase term is a combination of ¹⁵ N R₁ and ¹H R₂ relaxation rates; paramagnetic relaxation rates have a γ² dependence from the observed nucleus (Solomon 1955; Bertini 1986), therefore the contribution of ¹⁵N R₁ can be neglected and the observed rates are fully due to ¹H R₂ relaxation (Iwahara et al. 2007). Also cross correlation between ¹H Curie Spin Relaxation and HN dipole–dipole relaxation is not contributing to the observed rates (Pintacuda et al. 2003; Mori et al. 2010). In order to sample ¹H relaxation rates also at T values of a few μs, we avoid using pulsed field gradients, generally applied during the INEPT period. The delay T can then be arrayed from zero to 10 ms to sample the evolution of H_y → 2H_xN_z coherence transfer for half a sinusoidal period (1/J), during which ¹H R₂ relaxation is active. To avoid signal losses due to ¹H R₂ relaxation, the inverse INEPT block is removed and the 2H_yN_z coherence, created by the two 90° pulses at the end of ¹⁵N evolution, is acquired in antiphase without ¹⁵N decoupling. Removing the ¹⁵N decoupling also rules out duty cycle problems: without decoupling, one can safely use very short recycle delays in order to increase S/N of fast relaxing signals and to suppress water signal via progressive saturation (Camponeschi et al. 2019). This may affect the observed relaxation rates of H_N signals; however, when the observed values in Eq. (1) are dominated by R_2para, water saturation should not play a significant role. Another very important feature of this sequence is the suitability for cryo-probes, because there are no risks associated to coil heating due to an excess of RF power (Helms and Satterlee 2013). The use of a refocusing INEPT and ¹⁵N decoupling during acquisition is indeed a severe limiting factor for the recycle delay that, by no means, could have been as short as we used in our experiments.

Fig. 2.

The ¹H R₂ weighted ¹⁵N HSQC-AP pulse experiment. a Pulse sequence used for the experiment. Hard 90° and 180° pulses are used for both ¹H and ¹⁵N channels, using phase x when undefined. Phase cycling: φ₁ = x, −x, y, −y; φ₂ = 2(y), 2(x); φ₃ = 2(x), 2(−x); φ₄ = 4(x), 4(−x); φ_rec = x, −x, −x, x, −x, x, x, −x. PFG gradients of 200 μs were used, with 100 μs for gradient recovery. Standard parameters to measure fast relaxing nuclei as follows: aq = 47 ms, T = ranging from 200 μs to 10 ms, recycle delay = 150 ms. b Comparison between different R₂ relaxation building blocks. Considering the relaxation building block shown on the left panel (Donaldson 2001; Iwahara et al. 2007), using τ_a = 2.65 ms and T/4 = 1.8 ms as shortest possible delay, the exponential decay can be measured from about 12.5 ms. Signals with R₂ values over 70 s⁻¹ will be lost or detected at very weak intensities for few points. In the R₂-weighted building block shown in the right panel, they could be easily measured for a sufficient number of time delays in the range 0–10 ms, provided signals have enough S/N. The time scales of the two curves highlight the complementarity of the two experiments

The R₂-weighted HSQC-AP is essentially the simplest possible scheme for measuring ¹H R₂ relaxation with an HSQC-type experiment. Figure 2b shows the features of the R₂-weighted building block with respect to the relaxation building block commonly used (Donaldson 2001). For the latter, the relaxation delay T must accommodate the selective ¹H 180° pulse, the Pulsed Field Gradients, the INEPT transfer period 2τ_a. The shortest possible value of the relaxation delay T is set to about 12 ms, indeed this is why very fast relaxing signals are not observed with this approach. The removal of the ¹H 180° selective pulse and shorter gradients allow one to decrease this value, even though it can’t be below 6.5 ms. As shown in Fig. 2b, for an R₂ rate of 70 s⁻¹ signals will be already at 50% of the initial intensity at the first time point of the series, while those exceeding 150 s⁻¹ will be beyond detection after two time points of the R₂ series, for all these situations the exponential decay could not be properly analyzed. On the other hand, the R₂-weighted INEPT building block is highly complementary to this approach, because it will monitor the evolution of signal intensities during the first 10 ms of the relaxation recovery, starting from T period as small as 100 μs, therefore being able to monitor also very fast relaxing signals. Another interesting feature of the R₂-weighted HSQC is that fast and slow relaxing resonances will be measured with comparable precision.

As expected, the most representative spectra of the two R₂ series are rather different. In Fig. 3a, the first time point of the exponential decay of the in-phase experiment is superimposed to the spectrum of the R₂-weighted HSQC-AP series, recorded with T = 2.4 ms. Several signals, such as those of residues 22, 27–28, 36–37, 47–51, are indeed observable only in the R₂-weighted HSQC-AP, while other residues are only barely visible in the first point of the exponential decay (e.g. residues 25 and 35). Fast relaxing signals are much better observed in the R₂ weighted experiment, although signals are much broader than in the in-phase experiment, because they have been acquired as HN antiphase doublets. Like homonuclear ¹H and ¹³C cases, a dispersion phase mode of the antiphase doublets produces the sum of the two dispersive components of opposite phase, thus giving rise to a pseudo-singlet with the maximum of signal intensity (Turner 1993; Bertini et al. 1994, 2005a). As an example, Fig. 3b shows selected rows for His7 and Asn27. In the case of His7, which has a negligible R_2para contribution, we observe that, when the signal linewidth is smaller than the splitting of the HN doublet, the typical pattern of an antiphase doublet phased in dispersion mode is observed; when signals are broader than the scalar coupling constant, like the case of Asn27 (R₂ = 221 s⁻¹), the doublet splitting is lost and the dispersive component of the doublet give rise to a well pseudo observable pseudo singlet. The removal of the inverse INEPT prevents transverse relaxation to be operative before ¹H detection. Indeed, an additional refocusing would prevent the observation of signals characterized by T₂ shorter than the INEPT period.

Fig. 3.

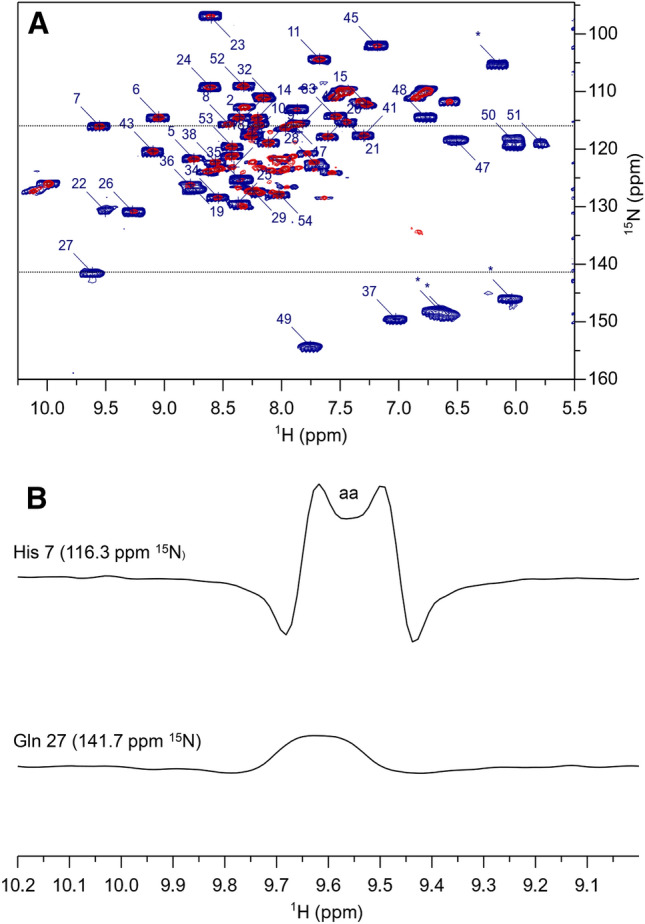
a ¹⁵N HSQC spectra of PioC obtained with an R₂-weighted ¹⁵N-HSQC-AP experiment collected with T = 2.4 ms (blue) and the first point of the R₂ series collected with the standard experiment with an overall relaxation delay = 12.5 ms (red). Experiments were recorded using a 500 MHz NEO-Avance Bruker spectrometer equipped with Triple resonances inverse cryoprobe (CP-TXI). R₂-weighted ¹⁵N-HSQC-AP was recorded with 256 scans each fid using an overall recycle delay of 200 ms, the in-phase experiment with 16 scans each fid and 4 s as recycle delay. Folded peaks are marked with an asterisk. b Expanded plot of selected rows of R₂-weighted ¹⁵ N-HSQC-AP, corresponding to His7 and Asn27

Fitting of R₂ values. The intensity of observed signals in the R₂-weighted HSQC-AP can be analyzed according to:

$$\text{I}\left(\text{t}\right)={\mathbf{I}}_{\mathbf{0}}sin(\text{p}TJ)exp\left(-T{\mathbf{R}}_{\mathbf{2}}\right)$$ 2

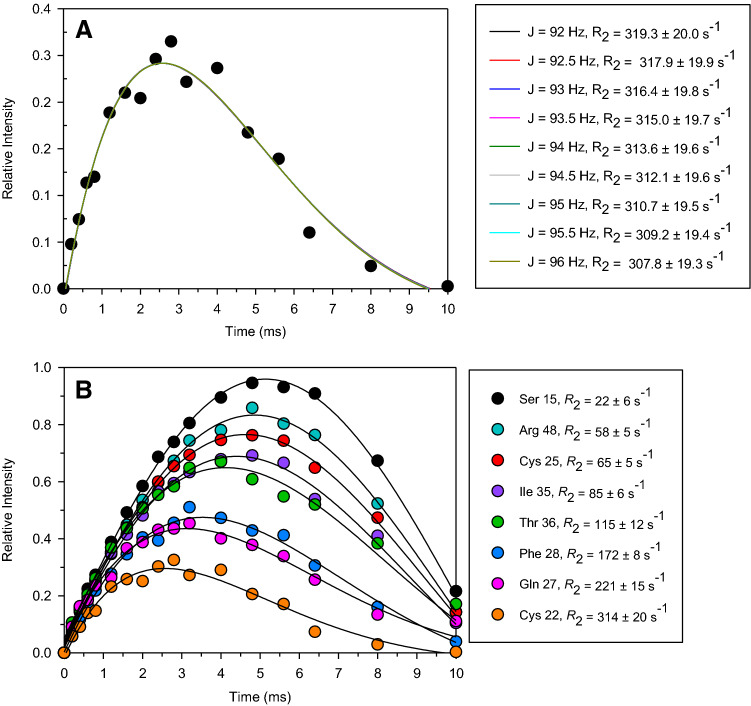
where T is the variable delay. In principle, a three-parameter fitting will provide values for I₀, J and R₂, respectively representing the initial signal intensity, the ¹J_HN scalar coupling constant, and the ¹H R₂ relaxation rate. However, the interplay between the two parameters J and R₂ is such that a three parameters fitting of the buildup curves tends either to over-estimate J and then compensate it with an under-evaluation of R₂ values or the other way around (smaller J and higher R₂ values). We therefore used a two-parameter fitting for Eq. (2), with constant J values. As shown in Fig. 4a, for J values in the range 92–96 Hz, i.e. the range of admissible values for ¹J_HN scalar coupling at 500 MHz (residual dipolar couplings are expected to be negligible at 500 MHz for a protein of this size containing a [Fe₄S₄]²⁺ cluster), the deviations among calculated R₂ values were much smaller than the errors observed in each two-parameters fitting. We therefore decided to consider values and uncertainties taken from the two-parameter fitting obtained using J = 94 Hz as a fixed value. Some representative build-up curves are reported in Fig. 4b. The R₂-weighted, ¹⁵ N-HSQC-AP experiment is able to measure R₂ values for all HN signals of the protein, including those belonging to residues of the iron-bound cysteines, to residues H-bonded to cluster sulfide ions, and those spatially close to the 4Fe-4S cluster although not in direct electronic contact with the prosthetic group.

Fig. 4.

Peak intensities in the R₂-weighted ¹⁵N-HSQC-AP experiment. Relative intensity are expressed with respect to I₀ term of Eq. (2). a Buildup curves obtained with a two-parameter fitting of Eq. (2) using fixed J values. Fitted intensities are those of the R₂-weighted ¹⁵N-HSQC-AP experiment for the case of Cys22 HN signal. When J was varied from 92 to 96 Hz, the interplay between J and R₂ provide essentially the same best fitting curve, with R₂ values in the range 308–319 s⁻¹. The uncertainty of R₂ due to the admissible values of J is smaller than the standard error (± 19.6 s⁻¹) of each individual fitting. b Experimental build-up curves of some selected signals. Curve fitting using a two-parameter fit and J = 94 Hz give R₂ values as indicated in Figure

Data evaluation and assessment

The R₂ values obtained with the R₂-weighted HSQC-AP experiments are summarized in Table 1, together with those measured using the standard sequence. A data assessment is reported in Fig. 5, where, for both series, the value of the relative error (ΔR₂/R₂) vs R₂ is shown. When R₂ values are lower than 45 s⁻¹, the accuracy of the sequence based on exponential decay and in-phase acquisition is much higher than that of the R₂-weighted-HSQC-AP. Indeed, when INEPT (2τ_a) and R₂ relaxation (T) evolve into separate building blocks, a single exponential decay is measured and several methods allow one to measure R₂ values with very good precision and accuracy (Iwahara et al. 2007). However, in the range 45–80 s⁻¹ the relative errors become larger than those obtained with the R₂-weighted-AP and, above 80 s⁻¹, R₂ values are measurable only (with the experimental conditions we used to perform the experiments) with the R₂-weighted-AP sequence, up to R₂ rates as large as 310 s⁻¹. This indicates that, for signals with R₂ rates larger than ca. 50 s⁻¹, the R₂-weighted-AP sequence should be the preferred method to measure relaxation rates, while the standard approach should be used in all other cases. Because all backbone HN signals of PioC have been identified and assigned and this was the fastest rate among them, it is not possible to set the upper limit threshold of the R₂-weighted-HSQC-AP experiment. In principle (see Fig. 2b), one should be able to measure R₂ values up to 400–500 s⁻¹, provided that very broad signals do not fall within a crowded spectral region.

Table 1.

500 MHz, 298 K, observed transverse relaxation rates for PioC HN amide protons

δ1H (ppm)	δ15 N (ppm)	residue		R2 (s−1) AP	error (s−1) AP	R2 (s−1) IP	error (s−1) AP
		VAL	1
8.26	117.2	THR	2			11.1	0.4
8.42	123.7	LYS	3			15.4	1.3
8.43	121.8	LYS	4	23.0	6.9	19.1	1.5
8.76	122.3	ALA	5	25.8	7.3	23.4	0.8
9.08	115.2	SER	6	38.8	5.2	17.8	0.6
9.64	116.3	HIS	7	37.8	4.4	21.3	0.8
8.49	116.5	LYS	8	52.9	19.1	32.8	2.2
8.13	119.5	ASP	9	35.3	5.3	16.9	0.7
8.23	118.2	ALA	10	34.6	4.3	19.6	0.8
7.69	105.0	GLY	11	46.8	3.9	20.0	1.4
8.19	116.3	TYR	12	36.6	3.8	29.9	1.5
8.67	124.5	GLN	13	54.3	3.8	46.4	4.1
8.22	115.2	GLU	14			19.4	1.1
7.29	112.8	SER	15	21.9	5.8	21.6	1.0
		PRO	16
7.92	116.4	ASN	17	31.2	4.4	22.8	1.1
8.17	111.6	GLY	18	43.5	5.2	25.1	1.5
8.78	126.9	ALA	19	52.6	12.0	44.4	2.8
7.62	118.4	LYS	20	41.8	10.9	17.8	0.8
7.47	115.9	ARG	21	38.0	2.8	44.4	3.1
9.47	131.4	CYS	22	313.6	19.6	n.o
8.62	97.5	GLY	23	60.3	6.2	48.8	6.3
8.62	109.8	THR	24	45.9	4.1	42.0	2.8
8.36	130.0	CYS	25	65.0	5.1	44.1	7.5
9.28	131.4	ARG	26	47.9	4.9	55.5	5.3
9.62	141.7	GLN	27	221.0	15.1	n.o
7.72	123.4	PHE	28	172.3	8.4	n.o
8.19	128.2	ARG	29	39.2	5.2	44.9	3.0
		PRO	30
		PRO	31
8.15	111.8	SER	32	43.5	5.2	25.1	1.5
7.55	114.9	SER	33	43.4	4.3	24.2	0.8
8.55	129.0	CYS	34	37.5	3.9	42.5	3.7
8.36	126.0	ILE	35	84.5	5.9	65.6	26
8.75	127.6	THR	36	115.0	12.3	n.o
7.00	149.9	VAL	37	161.5	10.7	n.o
8.61	122.8	GLU	38	43.0	4.0	24.2	0.8
8.43	115.7	SER	39	35.2	8.3	19.7	1.0
		PRO	40
7.28	118.2	ILE	41	25.4	7.5	27.7	1.3
7.84	116.4	SER	42	36.7	3.8	42.8	2.4
9.12	121.2	GLU	43	24.1	3.4	19.2	0.5
7.98	116.8	ASN	44	25.7	5.2	27.4	1.5
7.20	102.6	GLY	45	55.5	3.8	46.2	6.5
7.86	113.7	TRP	46	73.1	5.0	54.8	14.8
6.47	118.9	CYS	47	182.7	11.0	n.o
6.79	115.2	ARG	48	57.9	5.3	74.0	28.6
7.74	154.7	LEU	49	168.4	12.4	n.o
6.02	119.5	TYR	50	56.6	14.3	n.o
5.46	119.0	ALA	51	216.6	42.0	n.o
8.33	109.7	GLY	52	39.4	4.4	23.0	1.3
8.43	120.2	LYS	53	24.9	5.0	18.0	0.9
8.04	128.5	ALA	54			7.7	0.3
8.53	124,0	TRP sc	46	53.1	4.2	33.9	2.1

Columns 5–6 refer to values observed with the R₂-weighted HSQC-AP experiment, columns 7–8 to values observed with an in-phase HSQC experiment with a single exponential T₂ decay prior to INEPT

Fig. 5.

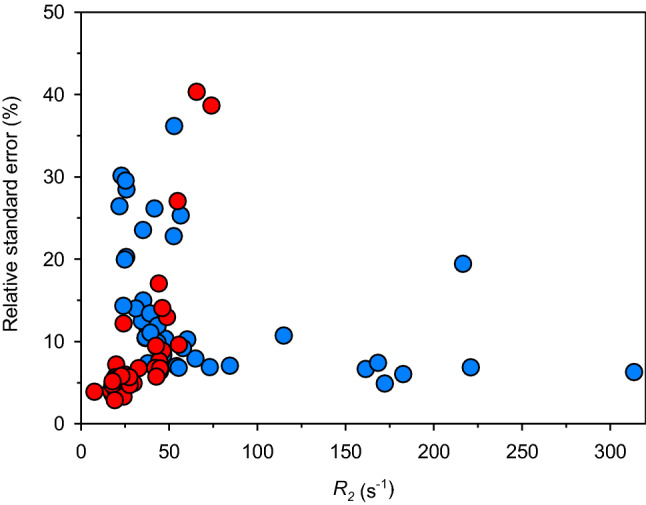
Transverse relaxation rates percentage errors (ΔR₂/R₂) obtained with the two series of experiments discussed in Fig. 2: (red) in-phase detected HSQC with relaxation delay preceding INEPT; (blue) R₂-weighted HSQC-AP. The recycle delays for the two series were 4 s and 200 ms, respectively. For R₂ values under 40 s⁻¹, data from the in-phase experiment have much smaller errors than those from the R₂-weighted HSQC-AP experiment. For R₂ values over 50 s⁻¹, the R₂-weighted-HSQC-AP has much better performances. For R₂ values above 80 s⁻¹, only the R₂-weighted-HSQC-AP provided reliable R₂ measurements

The poor agreement between the two sets of values obtained with the two experiments and reported in Table 1 also deserves a comment. Indeed, the R₂-weighted HSQC-AP experiment has been optimized to measure R₂ rates of fast relaxing signals, which are the target of this experiment. To this end, we have used, for the R₂-weighted HSQC-AP, recycle delays that are a factor 20 shorter than those used in the in-phase sequence (200 ms vs 4 s). Due to the fast repetition of the experiment, signals with R₂ < 35 s⁻¹ suffer from partial saturation. As a matter of speculation, it would always be possible to perform the R₂-weighted HSQC-AP experiment with longer recycle delays to properly fit R₂ values of slower relaxing signals. However, the obvious complementarity between the two experiments, given by the time scale of the recoveries measurable with the two experiments, and the intrinsic higher precision of the in phase experiment provided by the single exponential dependence, suggest that a combination of two R₂ measurements, respectively optimized for the quantification of small and large PREs would be, by far, the most efficient approach.

Conclusions

In summary, the R₂-weighted HSQC-AP experiment, proposed here, is the simplest experiment for R₂ relaxation, in which ¹H magnetization is kept along the transverse plane only during the relaxation delay and t₂ acquisition and all periods of J_HN evolution/refocusing are removed. This simplified scheme not only detects signals that escape detection in a conventional HSQC experiment, but measures R₂ values that are fully reliable, in the range of rates 50–400 s⁻¹. This is extremely important for metalloproteins, where the first coordination sphere of the metal ion(s) and its immediate neighboring regions can be identified, characterized and, finally, restrained into NMR structure calculations only when it is possible to obtain paramagnetism-based structural restraints such as PREs. The small HiPIP protein PioC is a challenging and significant example of the application of this experiment, where this objective was achieved and the R₂ could be measured for all four cysteines coordinating the paramagnetic cluster. Finally, it is worth noting that this approach can be useful in all other cases where R₂ is larger than 50 s⁻¹: conformation dynamics and exchange phenomena often increase relaxation rates above this threshold also in diamagnetic systems, thus extending the potential applications of this approach.

Compliance with ethical standards

Conflict of interest

The authors declare that they have no conflict of interest.

Availability of data and material:

Complete protein NMR Assignment reported in BMRB ID-34487. Pulse sequences and NMR data sets available upon request.