Abstract
As the second most common transition metal in the human body, zinc is of great interest to research but has few viable routes for its direct structural study in biological systems. Herein, Zn valence-to-core X-ray emission spectroscopy (VtC XES) and Zn K-edge X-ray absorption spectroscopy (XAS) are presented as a means to understand the local structure of zinc in biological systems through the application of these methods to a series of biologically relevant molecular model complexes. Taken together, the Zn K-edge XAS and VtC XES provide a means to establish the ligand identity, local geometry, and metal–ligand bond lengths. Experimental results are supported by correlation with density-functional-theory-based calculations. Combining these theoretical and experimental approaches will enable future applications to protein systems in a predictive manner.
Short abstract
Zinc is a biologically prevalent transition metal but is largely silent to spectroscopic techniques. Zn K-edge X-ray absorption (XAS) and valence-to-core X-ray emission (VtC XES) spectroscopies offer a unique chance to probe the local structure of zinc proteins and molecules. Herein, a series of biologically relevant zinc complexes were studied using XAS and VtC XES, in combination with DFT calculations. The presented approach should provide a powerful means to characterize zinc active sites in proteins.
1. Introduction
Present in an estimated 3000 human proteins, zinc is essential for the majority of cellular function.1−4 It is widely biologically available and plays a multitude of roles, in part due to its redox stability and its flexible coordination sphere.5 As such, biological zinc is always found in the Zn2+ state. It is most often coordinated by proteins using anywhere from four to six ligands (four being most typical), which may include histidine, cysteine, glutamate, and aspartate.2,6 There are several avenues of continued study of zinc-containing proteins, in particular, and biological zinc, in general, including investigating the role of zinc-containing antisigma factors in thiol-induced oxidative stress.7 Zinc has been implicated in amyloid plaque buildups, which are known to be a significant part of Alzheimer’s disease.8,9 Levels of zinc in the brain (both high and low) have been implicated in a series of neurological disorders, including Parkinson’s Disease, traumatic brain injury, depression, and schizophrenia.9 The role of zinc in many of these illnesses is unclear, and experts continue to argue about the benefit/harm that neurological zinc has in each of these.10,11 How zinc is managed in biological systems is not yet well understood, and studies following zinc homeostasis and dynamics in cells are ongoing.12−14 Additionally, protein design based on Zn2+ binding sites is used to introduce or alter catalytic activity.3,4
Zn2+ is not easily studied, since it is a diamagnetic ion with a filled 3d shell. This means that techniques often used to study other transition metals, such as ultraviolet–visible spectroscopy, magnetic circular dichroism (MCD), or electron paramagnetic resonance (EPR), generally fall short.15 Metal substitution with cobalt or cadmium was common in previous studies, but there is no guarantee that these complexes will be isostructural.1,16−1867Zn nuclear magnetic resonance (NMR) has also been used with some success, but the technique is hindered by the low natural abundance and small magnetic moment of 67Zn, as well as a large quadrupole moment.19 In isotropic solution, rapid relaxation further broadens spectra, making solution 67Zn NMR impractical, limiting its application in protein studies. The most common X-ray technique, X-ray crystallography, suffers from requiring protein crystallization to create the long-range order and from relatively modest accuracy (∼0.1 Å or worse), that is often insufficient to distinguish, e.g., water from hydroxide ligands. Additionally, X-ray crystallography is unable to distinguish between similar scatterers, such as C, N, and O, and has limited spatial resolution. Therefore, applications of crystallography are not well suited for following chemical reactions or other kinetic changes that require structural flexibility.
X-ray absorption and emission spectroscopies (XAS and XES, respectively) provide element-specific structural and electronic insight into the local structure and are applicable to both solid and solution samples.20−24 K-edge XAS, both in the edge region and the extended X-ray absorption fine structure (EXAFS) region, is well established as a means to obtain detailed local geometric and electronic structure information. K-edge XAS occurs when the absorption of a photon leads to a removal of an electron from the 1s orbital. The rise in absorption cross section at the Zn K-edge is due to promoting a 1s electron into an unoccupied 4p level via a dipole allowed transition. Pre-edge features are due to a 1s to 3d transition and, as the 3d orbitals are filled in Zn2+, are not observed in Zn K-edge XAS spectra.15
In some cases, XAS can also be used for ligand identification.25−28 Unfortunately, the spectral changes vary rather slowly with atomic number, and like XRD, this technique suffers from being unable to distinguish similar scatterers. Even the presence and number of nitrogen and sulfur ligands can appear ambiguous in XAS spectra.29 This is due to the characteristic phase shifts of nitrogen and sulfur, which are approximately π apart. This phase relation results in destructive interference in the EXAFS and results in the absence of resolvable peaks in the Fourier Transform. Despite these limitations, XAS in conjunction with density functional theory (DFT) calculations has the potential to assign ligand identity and protonation state (albeit somewhat indirectly) and is an extremely good indicator of local geometry.30−33
Valence-to-core X-ray emission spectroscopy (VtC XES) occurs when an electron from a valence orbital refills the 1s core hole created by absorption of a photon above the K-edge. The VtC XES spectral features have been shown to arise largely from ligand np and ns molecular orbitals. Hence, both the energies and the intensities of the VtC spectral features depend strongly on ligand identity and, as such, are incredibly useful for determining the identity of coordinated ligands.23,34−38 To date, very little research on VtC XES of zinc compounds has been reported,39 although VtC XES of other metals has led to a wide range of discoveries, including the identification of the interstitial carbon in the active site of molybdenum40 and vanadium41 nitrogenases, detection of bridging oxygen ligands and assessment of protonation states in an oxygen evolving complex and in related structural models,42,43 and as a means to assess O–O and N–N bond activation.44,45
Herein, both Zn K-edge XAS and VtC XES of a series of biologically relevant zinc complexes were examined to assess the viability of these spectroscopies to study oxygen-, nitrogen-, and sulfur-bound zinc in biological systems. Ligands were chosen for their similarity to relevant amino acids: benzoate (BzO) to mimic aspartate/glutamate, 1-methylimidazole (MeIm) and 2-aminopyridine (pyNH2) for histidine, and thiourea (SC(NH2)2) and thiophenol (SPh) for cysteine. In addition, two complexes, [Zn(MeIm)6]2+ and [Zn(MeIm)4]2+, were selected for gaining comparative insight into how local geometry and coordination number affect both absorption and emission spectra (Figure 1). To obtain a deeper understanding of the observed trends in the experimental spectra, we performed density functional theory (DFT) based spectral calculations. The complementarity of the two spectroscopic approaches for maximizing our understanding of the geometric and electronic structure of zinc complexes is emphasized. The approaches established here will allow for future application to zinc-proteins.
Figure 1.
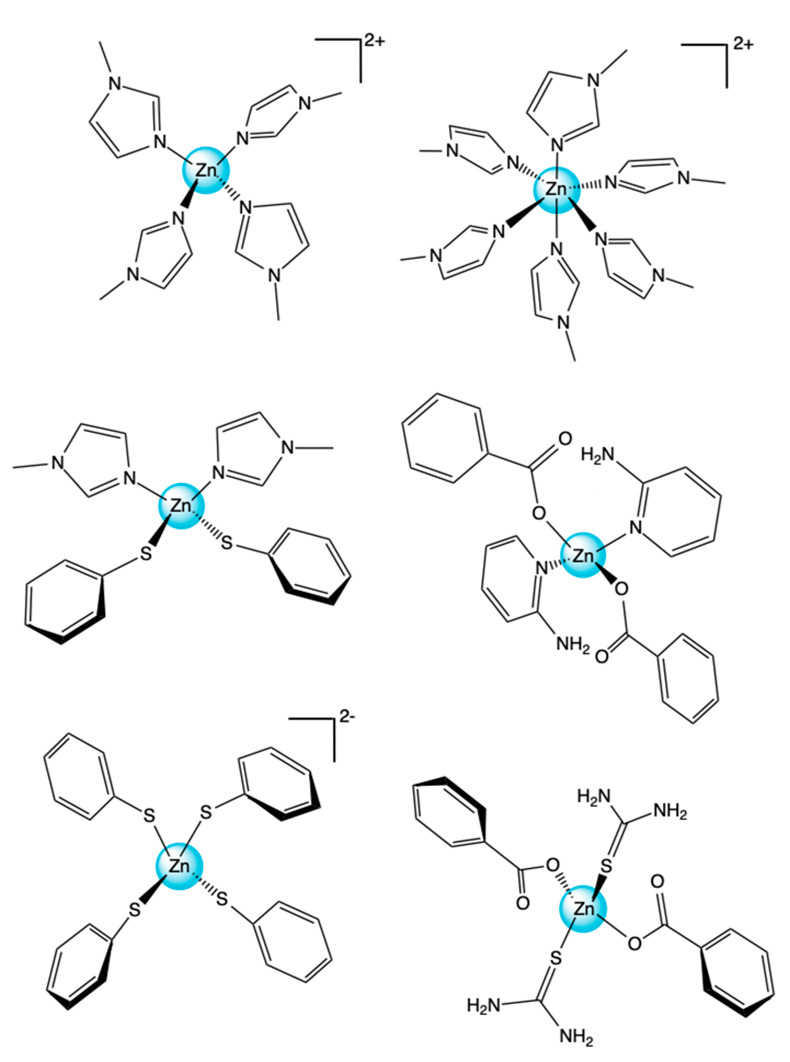
[Zn(MeIm)4]2+ top left, [Zn(MeIm)6]2+ top right, [Zn(MeIm)2(SPh)2] center left, and [Zn(BzO)2(pyNH2)2] center right, [Zn(SPh)4]2– bottom left, and [Zn(BzO)2(SC(NH2)2)2] bottom right.
2. Experimental Section
2.1. Sample Preparation
Bis(2-aminopyridine-N)bis(benzoate-O)zinc ([Zn(BzO)2(pyNH2)2]),46 tetrakis(1-methylimidazole-N3)zinc(II) diperchlorate ([Zn(MeIm)4]2+),47 bis(benzoate-O)bis(thiourea-S)zinc(II) ([Zn(BzO)2(SC(NH2)2)2]),48 tetraethylammonium tetrathiolphenolatozinc(II) ([Zn(SPh)4]2–),49 and bis(1-methylimidazole-N)bis(thiophenol-S)zinc(II) ([Zn(MeIm)2(SPh)2])50 were all synthesized according to literature procedures. Hexakis(1-methylimidazole-N3)zinc(II) diperchlorate ([Zn(MeIm)6]2+) was synthesized according to a procedure for the analogous cobalt complex.51 For XAS experiments, samples were diluted 10-fold with boron nitride, then packed into aluminum spacers, and sealed with 38 μm Kapton tape. For XES experiments, undiluted powder samples of all complexes were packed into aluminum spacers and sealed with 38 μm Kapton tape.
2.2. XAS Data Collection
XAS spectra were collected at SSRL beamline 9-3, with SPEAR operating at 3 GeV electron energy and 100 mA current. A Si(220) monochromator was used to scan from 9430 to 10325 eV, and a Rh-coated mirror with an energy cutoff of 10.4 keV was used for harmonic rejection. The incident energy was calibrated using a Zn foil between the second and third ion chambers, with a first inflection point defined as 9659 eV. XAS was measured in transmission mode using nitrogen filled ion chambers. The data are the averaged result of 2–3 individual scans. The pre-edge region (9430 eV–9630 eV) was scanned in 10 eV steps, the edge region (9630 eV–9690 eV) was scanned in 0.35 eV steps, and the EXAFS region (1.62–13 Å–1) was scanned in 0.05 Å–1 steps. Samples were positioned at 90 deg with respect to the incident beam and were maintained at a temperature of 12 K using a He-cooled cryostat.
2.3. XES Data Collection
XES spectra were collected at SSRL beamline 6-2 (54-Pole wiggler, 1T). The incident beam was tuned to 10.4 keV using a Si(111) monochromator. Vertical and horizontal focusing mirrors were used to achieve a beam size of (∼200 μm × ∼800 μm) and a flux of 3.8 × 1012 photons/s at 100 mA ring current. The energy of the incident beam was calibrated with Zn foil, setting the first inflection point to 9534.92 eV.
To collect the fluorescence spectra, three spherically curved Ge(555) analyzer crystals were used in a geometry with 1-m Rowland circles intersecting on a Si drift detector with a 3 mm vertical slit. The analyzer resolution is estimated to be 1.2 eV full width at half-maximum (fwhm) by Gaussian deconvolution of the measured elastic peak widths of 1.6 eV fwhm and an estimated Si(111) monochromator resolution of 1.1 eV fwhm. Samples were positioned at 45 deg with respect to the incident beam and maintained at room temperature. Radiation damage studies were performed for all samples to establish the maximum exposure time per spot. Scans were also performed in alternating directions (from 9616.8 to 9674.4 eV, then from 9674.4 to 9616.8 eV) to determine the extent of radiation damage. No significant differences were observed. Examples of the single scans collected in both directions are shown in Figure S1. As the sample area was not limited, fresh spots on the sample were used for each scan, and the averaged data showed no signs of radiation damage.
2.4. Data Processing
Fourier transforms and normalization of XAS experimental spectra were conducted using SamView from SixPACK.52 XES data processing was performed utilizing in-house Python scripts. VtC XES experimental spectra were normalized by integrating the full spectral energy range (including the Kβ main line) and setting the area to 1000. This is equivalent to the edge-jump normalization in XAS, as the integrated Kβ mainline intensity (which provides the predominant signal) is independent of the Zn chemical environment. The Kβ mainline and VtC regions were fit separately using the Lmfit package in Python 3.53 The fits of the experimental VtC spectra are shown in Figure S2.
2.5. Calculations
All calculations were performed using the ORCA 4.2.0 electronic structure program package from Neese and co-workers.54 Cartesian coordinates for all complexes were built using Avogadro55 and then geometry optimized using a B3LYP functional56−59 with a ZORA-def2-TZVP basis set60 and Sarc/J auxiliary basis set.61 Scalar relativistic effects were introduced using ZORA (zeroth-order regular approximation).62 Dispersion effects were accounted for using D3BJ.63,64 MOAnalyzer was used as an aid in the quantitative analysis of ORCA output files.65 Chemdraw was used for the visualization of molecular orbitals and for bond length adjustments. XES and XAS calculations were performed using previously established protocols, with a simple ground state DFT approach for the former36 and a time-dependent DFT approach for the latter.66,67 Example input files for the geometry optimization and XES and XAS calculations are provided in the SI. In all cases, electric dipole, magnetic dipole, and quadrupole contributions were allowed for in spectral calculations, but no significant magnetic dipole contributions were observed. TDDFT calculated spectra (K edge XAS) were shifted −16.5 eV to align with experimental energies. This shift was determined by finding the average difference (standard deviation of 0.49) of the calculated and experimental whiteline. XAS calculated spectra were broadened differentially by a factor of 0.03*(Energy)2 to account for the diffuse (experimental) and less rigorously defined (calculated) unoccupied states that tend to broaden experimental XAS data toward higher energies above the edge. DFT calculated spectra (VtC XES) were shifted −14.7 eV to align with VtC experimental energies, as determined by the average energy difference (standard deviation 0.25) between the most intense VtC peak in experiment and calculation. The correlation between the calculated VtC XES area and the experimental area was found to have a scaling factor of 2.05 ± 0.15. Calculated XES spectra were broadened by 2.25 eV.
3. Results and Discussion
3.1. XAS of Tetradentate Zinc Complexes
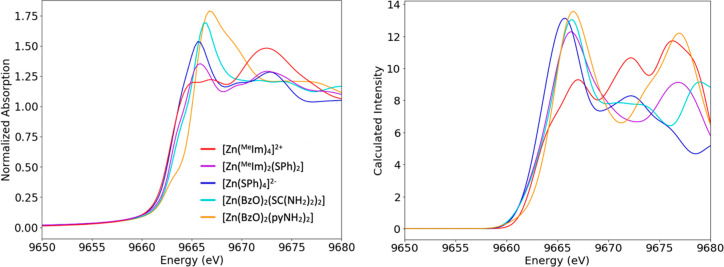
In order to determine the sensitivity of Zn K-edge XAS to ligand identity, the spectra of five tetradentate complexes were collected. The rise of intensity at the Zn K-edge is due to an absorption of a photon, and the resultant dipole allowed 1s to 4p transition. In this case, where the oxidation state of zinc is 2+ and the geometry is approximately tetrahedral in all included compounds, the energy of the edge is not expected to shift dramatically. However, some changes can occur due to the relative electronegativity of various ligands or the deviation from a perfectly tetrahedral symmetry. Pre-edge features occur due to a 1s to 3d transition and are theoretically not possible with a filled 3d orbital, as is the case for Zn2+. We note, however, pre-edges can occur in formally d10 complexes as a result of metal to ligand charge transfer, as has been observed for Cu(I) complexes.68,69 To our knowledge, no pre-edge features have ever been observed in Zn K-edge XAS spectra. Figure 2 (left) shows the normalized experimental Zn K-edge XAS data for the five tetradentate complexes. As expected, the majority of the spectra rise dramatically at ∼9662 eV. [Zn(pyNH2)2(BzO)2] has an immediately visible low energy shoulder superimposed on the rising edge, and both [Zn(MeIm)2(SPh)2] and [Zn(pyNH2)2(SC(NH2)2)2] have a shoulder at higher intensity along the edge at ∼9663 eV. By contrast, the complexes with only one ligand type, [Zn(SPh)4]2– and [Zn(MeIm)4]2+, rise monotonously without apparent shoulders. Within the set of 1-methylimidazole and thiophenol complexes, an increase in edge intensity at 9665 eV occurs with increasing sulfur ligation; sulfur-free [Zn(MeIm)4]2+ has a lower intensity than the doubly thiolate-ligated [Zn(MeIm)2(SPh)2], both of which are lower than the fully thiolate-ligated [Zn(SPh)4]2–.
Figure 2.
Experimental (left) and calculated (right) Zn K-edge XAS spectra.
To better understand the experimental data and to assign trends to specific ligands, TDDFT calculated spectra were calculated for all complexes. The experimental trends for edge position are well mimicked by the calculations, as can be seen in Figure 2 (right). The calculated edge intensity also generally follows the experimental trends. The largest discrepancy between calculated and experimental edge data is an increased calculated intensity in the two thiophenol-containing compounds relative to experiment. All three shoulders along the edge seen in the experiment are present in calculated data. At lower energies, intensity is predominately due to 4p transitions, while at higher energies, discrete orbitals cannot be readily assigned, and diffuse Rydberg orbitals dominate the high energy region.
3.2. Kβ Mainline of Tetradentate Zinc Complexes
K XES occurs after the ionization of a 1s electron, where the core hole is filled by another electron from a higher orbital. The strongest emission line is Kα, where the 1s core hole is filled with a 2p electron. There are two distinct sections of Kβ XES spectra: the Kβ mainline region, where the electron filling the core hole originates from a metal 3p orbital, and the VtC region, where the electron originates from the filled valence orbitals. The spectral shape of the Kβ mainline for first row transition metals usually consists of two peaks, a splitting that occurs because of 3p-3d exchange coupling.70−73 This splitting allows mainlines to provide insight into spin state and metal–ligand covalency. However, similar to what has been found for Cu(I) Kβ mainlines,74 which also have a d10 configuration, the zinc Kβ mainlines for all six complexes studied here are superimposable, and no spectral changes due to the differences in ligand coordination are observed. An overlay of the Kβ mainlines is shown in the SI (Figure S3). The Kβ mainlines for all compounds presented have an intense peak at 9572.6 eV, two shoulders to lower energies at 9565.7 and 9569.7 eV, and one shoulder to higher energy at 9574.8 eV. For zinc, where 3p-3d exchange contribution is absent due to the closed 3d shell configuration, the observed splitting is at least in part attributed to 3p spin–orbit coupling. For Zn, this is estimated to be 2.8 eV. However, the presence of four discrete features in the zinc mainlines (Figure 3 and SI) indicates that there must be additional factors contributing to the observed spectral shape. Previously unassigned transitions arising for copper75 and other 3d transition metals76 were determined to be spectator transitions. It is likely that this is also true for zinc. However, due to this insensitivity of the Kβ mainline to changes in ligation, a further investigation of this spectral region has not been pursued.
Figure 3.
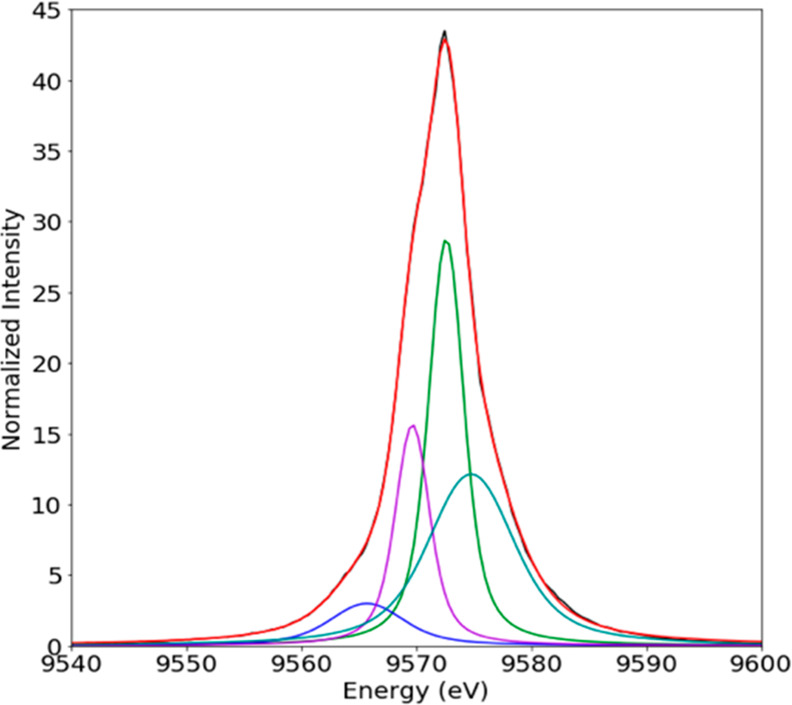
Experimental Kβ XES spectra of [Zn(BzO)2(pyNH2)2] fit with four distinct peaks.
3.3. VtC of Tetradentate Zinc Complexes
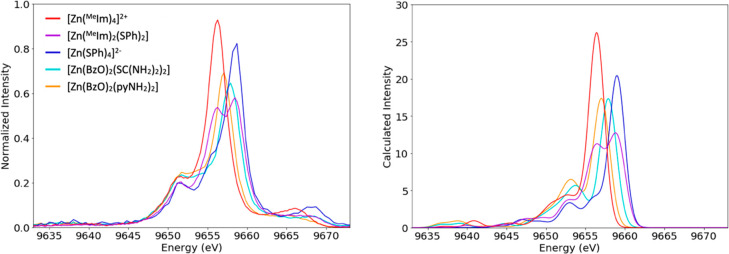
The experimental VtC spectra for the five tetradentate complexes can be seen in Figure 4, left. VtC spectra arise from electrons in valence orbitals transitioning to refill the Zn 1s core hole, and since these valence molecular orbitals have a mixture of metal and ligand character, VtC is particularly sensitive to ligand identity.20,23 In general, two sets of peaks are found that correlate to ligand s and p contributions at lower and higher energies, respectively. Lower energy peaks in the “Kβ″ region” correspond to orbitals dominated by ligand s character and would likely be found around 9635–9645 eV. They are largely absent in our spectra. All spectra exhibit rich features in the “Kβ2,5 region”, the region related to molecular orbitals with high ligand p character that is here found between 9647 and 9662 eV. For all samples, there is a peak at 9652 eV, the energy of which appears largely unaffected by changes in ligation.
Figure 4.
Experimental (left) and calculated (right) VtC XES spectra of tetradentate zinc(II) complexes.
At higher energies (9655 to 9662 eV) dramatic changes occur with variation in ligand identity. All spectra but [Zn(MeIm)2(SPh)2] present one major peak in this region. This peak occurs at lowest energy (9656 eV) for [Zn(MeIm)4]2+, which has four nitrogen donors. The two benzoate complexes are somewhat higher in energy; [Zn(BzO)2(pyNH2)2] has the most intense peak at 9657 eV, and [Zn(BzO)2(SC(NH2)2)2] has its most intense peak at 9658 eV. [Zinc(SPh)4]2– has the highest energy for this peak (9659 eV), and the mixed N/S ligated [Zn(MeIm)2(SPh)2] has two distinct peaks in this region at 9656 and 9659 eV. The systematic variation in the energy of the ligand p-related peak found between 9655 and 9660 follows the following pattern: aromatic nitrogen rings < carboxylates < thiones/thiolates. The hydrogen bonding or orbital overlap of aromatic nitrogen rings/carboxylates or carboxylate/thione pairs allows for complexes with these ligand mixtures to appear as a single peak. In contrast, aromatic nitrogen rings and thiolates have orbitals that are far enough apart in energy, such that compounds ligated by a combination of these ligands should have two well separated peaks. However, we note that the exact position of the Kβ2,5 also is dependent on the extent of covalent interactions with zinc, which is modulated by factors like distance and secondary coordination effects. Hence, one cannot generalize that there is a specific energy where the Kβ2,5 peak will always occur for a specific type of ligand.
To more closely examine the origin of these VtC peaks, we performed DFT calculations of VtC spectra shown in Figure 4, right panel. The calculations show some very weak ligand s features that we do not observe experimentally, possibly because of our limited data quality in that spectral region. Between 9655 and 9660, the calculated spectra produce trends very similar to those found experimentally. The calculations show that these peaks are due to orbitals with majority ligand p character. Dipole contributions account for the majority (92.4%) of VtC spectral intensity throughout the valence to core region, with the caveat of a relatively intense calculated quadrupole peak at 9652 eV, which is largely insensitive to changes in ligation and seen in all spectra. Based on the calculated orbital content, this ever-present peak at 9652 eV is primarily related to Zn 3d character. An example spectrum of calculated dipole and quadrupole contributions to the VtC spectrum is shown in Figure 5. The position of the blue quadrupole feature clearly indicates that the Zn 3d levels are below the filled ligand orbitals and is consistent with previous photoelectron spectroscopy studies.77 This has been attributed to the high effective nuclear charge on Zn2+ which results in an inverted ligand field.
Figure 5.
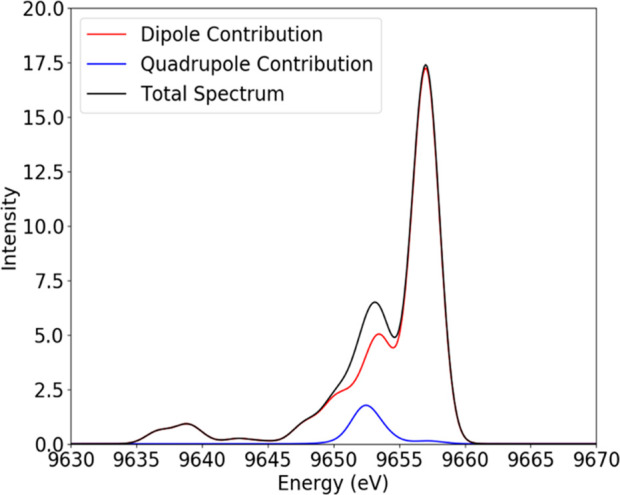
Calculated VtC XES spectrum of [Zn(BzO)2(pyNH2)2] with dipole and quadrupole contributions.
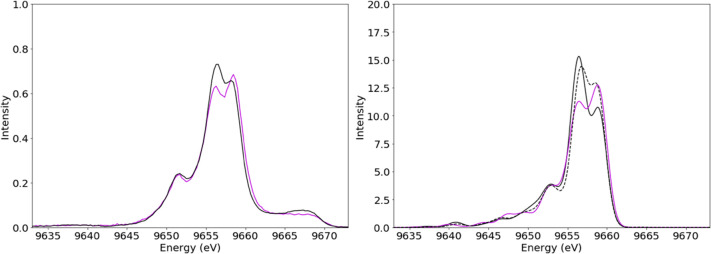
Having established that VtC XES is dominated by contributions from ligand valence orbitals, it is useful to explore both how generally transferable these observations are and to what extent VtC XES can be utilized for the extraction of further structural information. An investigation into the effects of ligand–metal bond length on the VtC spectra was performed by more closely examinining the spectra of [Zn(MeIm)4]2+, [Zn(SPh)4]2–, and [Zn(MeIm)2(SPh)2]. The geometry-optimized molecular models of these complexes vary in bond length, with a Zn–N bond length of 2.01 Å for [Zn(MeIm)4]2+, a Zn–S bond length of 2.39 Å for [Zn(SPh)4]2–, and a Zn–N bond length of 2.08 Å and a Zn–S bond length of 2.31 Å for [Zn(MeIm)2(SPh)2]. If the VtC spectrum for [Zn(MeIm)2(SPh)2] was simply a 50/50 sum of the other two spectra, this would suggest insensitivity to metal–ligand bond length and overall geometry. However, as shown in Figure 6 (right), the spectrum for [Zn(MeIm)2(SPh)2] differs from a 50/50 sum of the two homogeneously ligated complexes.
Figure 6.
Experimental (left) and calculated (right) VtC spectra of [Zn(MeIm)2(thio)2] in violet and an averaged spectrum of [Zn(MeIm)4]2+ and [Zn(thio)4]2– in black. The dashed line represents the average calculated spectra with adjusted bond lengths for [Zn(MeIm)4]2+ and [Zn(thio)4]2–.
To better analyze these changes, we calculated the spectra of model complexes with fixed bond lengths of 2.08 Å (Zn–N) for [Zn(MeIm)4]2+ and 2.31 Å (Zn–S) for [Zn(SPh)4]2–. The sum of the calculated optimized [Zn(MeIm)4]2+ and [Zn(SPh)4]2–, as well as the sum of these two complexes with adjusted bond lengths, is compared to the calculated spectrum of [Zn(MeIm)2(SPh)2] in Figure 6 (right). By decreasing the Zn–S bond length and increasing the Zn–N bond length, the peaks at 9656 and 9659 eV in the 50/50 composite spectra, respectively, decrease and increase in intensity, thus, more closely approximating the calculated spectrum of geometry optimized [Zn(MeIm)2(SPh)2]. As such, bond length plays a clear role in the intensities of the VtC XES features.
The bond length adjusted 50/50 composite spectrum and the spectrum of [Zn(MeIm)2(SPh)2] still differ somewhat, suggesting that other factors such as ligand–ligand interaction may also affect the spectrum. The geometric coordinates of [Zn(MeIm)2(SPh)2], as visualized in Figure S4a, show pi-stacking between the MeIm and SPh groups. A series of calculations varying the angle of the SPh groups to vary the separation from the MeIm ligands were performed. This resulted in a dramatic decrease of intensity at 9656 and an increase in intensity at 9659 eV, along with a slight shift toward higher energy (see Figure S4b). Since the experimental and calculated spectra match so well, it is suggested that VtC is sensitive not only to ligand identity and metal–ligand bond length but also to the subtle geometric structural changes that occur between a homogeneously ligated complex and a complex with mixed ligation.
3.4. Undefined Peaks above K-Edge in Tetradentate Zinc Complexes
Also of interest are the weak features at ∼9665 eV and higher, which are observed in the experimental VtC XES spectra but are absent in the calculations. The high energy features indicate that they do not correspond to a simple valence to core de-excitation. Emission spectra, in general, are the result of an electron from some filled higher orbital filling some hole (here, the 1s). Since these peaks are above the absorption K-edge energy, the transition from which these peaks result must be from an initial higher energy state than the valence orbitals in the ground state. There are two ways to accomplish this: a double excitation or temporary filling of an assumed empty orbital during the initial excitation process.
In a previous zinc VtC XES study, these features were briefly mentioned but empirically subtracted in order to better compare experimental VtC and DFT-based calculations, which do not account for multielectron excitations, among other things.39 However, the change in both intensity and position of these high energy peaks with ligand identity is, to our knowledge, a novel observation. In fact, these peaks appear to approximately mimic the trends of the Kβ2,5 features seen 10 eV lower, suggesting that they too are influenced by some valence related transition.
A 2017 paper by Valenza et. al discussed double ionization satellites in nickel metal that appear incredibly similar in both positioning and relative intensity to what can be seen in this zinc data.78 The more commonly known isothermal double ionization requires that the incident photon be well above the KL3 double-excitation threshold (10.6 keV for Zn): with an incident energy of 10.4 keV, it is unreasonable to attribute these peaks to isothermal double ionization. Another, less commonly discussed and harder to model double ionization process is the adiabatic ionization process, which occurs at lower energy than the double-excitation threshold. The process for accounting for these double excitations in calculations, while technically possible, is rather arduous and beyond the scope of this current work. Another possible explanation relates to the lowest unoccupied zinc p shell above the filled zinc d shell, which is predicted at approximately 9665 eV. It is possible that, while in the excited state, these p orbitals are also temporarily occupied and that transition of an electron from this orbital to refill the 1s core hole could account for these peaks. The experimental observation of these peaks make an important statement: although current DFT methods, both simple and complex, often work wonderfully for modeling the trends in VtC XES data, they can miss the spectroscopic effects of more electronically complex scenarios. Understanding why these peaks occur in some metal complexes but not in others could lead to further insight into transition metal electronic structure and bonding, as they could be the result mixing of the filled 3p/3d zinc orbitals with higher energy empty orbitals, such as zinc 4s or 4p. However, a clear understanding of these features is hindered by their energetic overlap with the rise of the absorption edge, which changes the escape probability of emitted photons and thus affects spectral shape. Further insight into the origin of these peaks might be obtained through resonant XES experiments.
3.5. Comparison of Geometry in Zinc 1-Methylimidazole Complexes
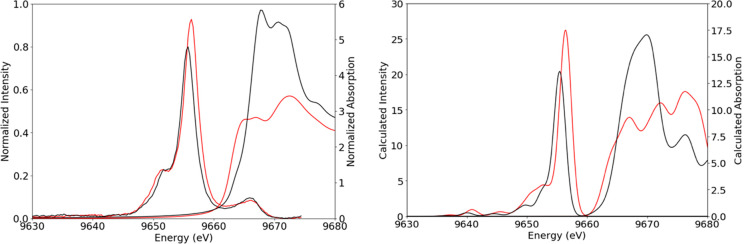
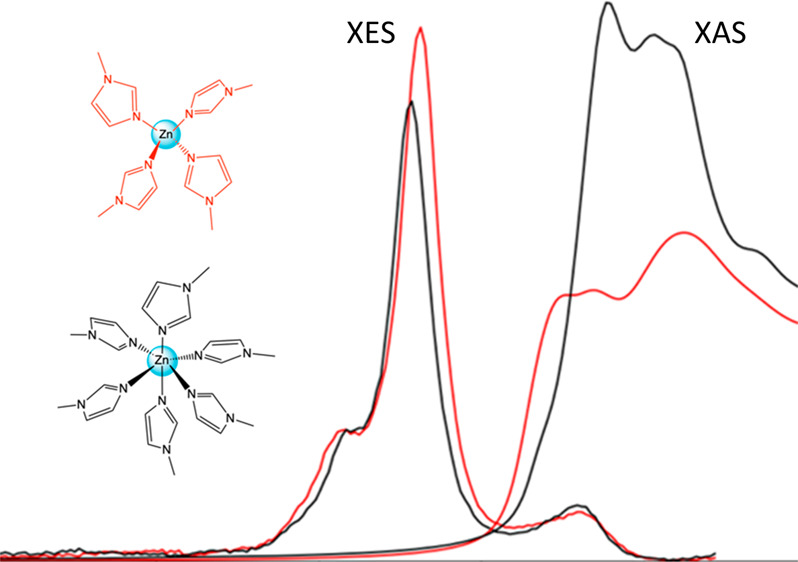
For a fair comparison of K-edge XAS and VtC XES spectroscopies and to continue to illustrate ways in which they collaborate to form a full picture of local geometry, electronic structure, and ligand identity, a second zinc methyl imidazole complex [Zn(MeIm)6]2+ was also characterized for comparison to the [Zn(MeIm)4]2+ complex, already presented above. The XES and XAS experimental spectra of these two complexes are shown in Figure 7 (left). The Zn K-edges change dramatically between the two complexes, both in edge energy and in intensity.
Figure 7.
Experimental (left) and calculated (right) Zn VtC XES and K-edge spectra of [Zn(MeIm)4]2+ in red and [Zn(MeIm)6]2+ in black.
Following simple electrostatic considerations, the shift of the edge to higher energy on going from [Zn(MeIm)4]2+ at 9662 eV to [Zn(MeIm)6]2+ at 9664 eV is likely due to the destabilization of metal 4p orbitals upon increasing coordination number. This effect is mirrored in the VtC XES spectra, which clearly show that in the 6-coordinate complex the filled orbitals are stabilized to deeper binding energy than those of the 4-coordinate complex. Within the VtC XES spectra, one also observes modulations in the intensities, with the 4-coordinate complex exhibiting higher VtC XES intensities than the 6-coordinate complex. This observation suggests that the shorter Zn–N(MeIm) bond lengths in the 4-coordinate complex (2.01 Å for [Zn(MeIm)4]2+ and 2.20 Å for [Zn(MeIm)6]2+) make a more significant contribution to the observed intensity than the increased coordination number. The calculated spectra (Figure 7, right) clearly reproduce the general trends observed in the experimental data for both the VtC XES and Zn K-edges.
Given the good agreement between the experimental and calculated spectra, we can now use the calculations to obtain further insight into the contributions of local site symmetry (Oh vs Td) and metal–ligand bond length. As noted above, the XES and XAS spectra in Figure 7 were calculated first using their optimized geometry, which had metal–ligand bond lengths of 2.01 Å for [Zn(MeIm)4]2+ and 2.20 Å for [Zn(MeIm)6]2+. To separate the effect of geometry from the effect of bond length, a separate calculation was run with a constant bond length of 2.10 Å for both complexes. The calculated VtC XES and K-edge XAS spectra of these four models are shown in Figure 8. As the 6-coordinate models maintain the significantly higher edge intensity compared to their 4-coordinate counterparts, the dramatic difference in white line intensity can be considered an effect of coordination number/site symmetry. Similarly, regardless of bond length, the 6-coordinate complexes show edges that are higher in energy (pointing to greater destabilization of the empty orbitals) and VtC XES spectra that are lower in energy (pointing to greater stabilization of the filled orbitals). In both cases, the highest VtC XES intensity is observed for the shortest [Zn(MeIm)x]2+ bond lengths. Taken together, these data show that the VtC XES and Zn K-edge XAS can provide a comprehensive picture of the Zn local site symmetry and coordination number, while also providing insight into metal–ligand bond lengths.
Figure 8.
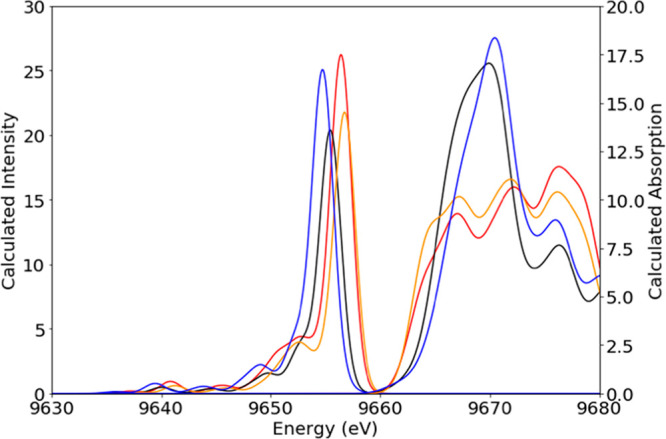
Calculated Zn VtC XES and K-edge spectra of [Zn(MeIm)4]2+ red (optimized) and orange (adjusted bond length of 2.1 Å). Calculated spectra of [Zn(MeIm)6]2+ are shown in black (optimized) and blue (adjusted bond length of 2.1 Å).
4. Conclusion
This work illustrates the great potential and complementary nature of Zn K-edge XAS and VtC XES for the structural characterization of zinc complexes. Both Zn K-edge XAS and VtC XES are sensitive to the local electronic structure. While the former shows a more pronounced sensitivity to local site symmetry (which manifests in the increased white line intensity for 6- vs 4-coordiante complexes), the latter is more sensitive to ligand identity. The sensitivity of VtC XES to ligand identity and also metal–ligand distance could serve as an important complement to EXAFS studies. Previous EXAFS studies have shown that it is often difficult to separate N and S contributions in zinc complexes with mixed ligation due to the unfavorable phase relation between Zn–N and Zn–S EXAFS contributions. In practice, this means that EXAFS is often unable to differentiate ZnS4 from ZnS3N sites.29 Herein, the demonstrated sensitivity of VtC XES spectra with regard to mixed S/N ligation could be used to complement EXAFS data and gain a more holistic structural view of studied zinc sites. VtC sensitivity to metal–ligand bond length and ligand interactions, such as hydrogen bonding, allows the technique to potentially provide complementary structural information for both EXAFS and crystallographic analyses, which would be particularly useful in protein studies where a high-resolution picture of the local changes at zinc sites may be important. These spectroscopies in combination with calculations provide a powerful way to characterize biological zinc, a very important and notoriously difficult-to-probe metal.
Acknowledgments
O.M.S. and S.D. acknowledge the Max Planck Society for funding. J.P.H. and J.W. received funding from the National Institutes of Health (NIH R01 GM038047). SSRL is acknowledged for allocation of beam time. Use of SSRL is supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences, under Contract DE-AC02-76SF00515. Dr. Matthew Latimer, Allyson Aranda, and Dr. Erik Nelson at SSRL 9-3 are gratefully acknowledged for their technical assistance. Dr. Vlad Martin-Diaconescu is acknowledged for helpful discussions.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.inorgchem.0c01931.
Additional computational and experimental details (PDF)
Author Present Address
∥ PNNL, Richland, WA 99354, United States.
The authors declare no competing financial interest.
Supplementary Material
References
- Parkin G. Synthetic Analogues Relevant to the Structure and Function of Zinc Enzymes. Chem. Rev. 2004, 104 (2), 699–767. 10.1021/cr0206263. [DOI] [PubMed] [Google Scholar]
- Krezel A.; Maret W. The Biological Inorganic Chemistry of Zinc Ions. Arch. Biochem. Biophys. 2016, 611, 3–19. 10.1016/j.abb.2016.04.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zastrow M. L.; Pecoraro V. L. Designing Hydrolytic Zinc Metalloenzymes. Biochemistry 2014, 53 (6), 957–978. 10.1021/bi4016617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu F. T.; Cangelosi V. M.; Zastrow M. L.; Tegoni M.; Plegaria J. S.; Tebo A. G.; Mocny C. S.; Ruckthong L.; Qayyum H.; Pecoraro V. L. Protein Design: Toward Functional Metalloenzymes. Chem. Rev. 2014, 114 (7), 3495–3578. 10.1021/cr400458x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lim N. C.; Freake H. C.; Bruckner C. Illuminating Zinc in Biological Systems. Chem. - Eur. J. 2005, 11 (1), 38–49. 10.1002/chem.200400599. [DOI] [PubMed] [Google Scholar]
- Patel K.; Kumar A.; Durani S. Analysis of the Structural Consensus of the Zinc Coordination Centers of Metalloprotein Structures. Biochim. Biophys. Acta, Proteins Proteomics 2007, 1774 (10), 1247–1253. 10.1016/j.bbapap.2007.07.010. [DOI] [PubMed] [Google Scholar]
- Heo L.; Cho Y. B.; Lee M. S.; Roe J. H.; Seok C. Alternative Zinc-Binding Sites Explain the Redox Sensitivity of Zinc-Containing Anti-Sigma Factors. Proteins: Struct., Funct., Genet. 2013, 81 (9), 1644–1652. 10.1002/prot.24323. [DOI] [PubMed] [Google Scholar]
- Bush A. I. The Metallobiology of Alzheimer’s Disease. Trends Neurosci. 2003, 26 (4), 207–214. 10.1016/S0166-2236(03)00067-5. [DOI] [PubMed] [Google Scholar]
- Portbury S. D.; Adlard P. A. Zinc Signal in Brain Diseases. Int. J. Mol. Sci. 2017, 18 (12), 2506. 10.3390/ijms18122506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atrian-Blasco E.; Gonzalez P.; Santoro A.; Alies B.; Faller P.; Hureau C. Cu and Zn Coordination to Amyloid Peptides: from Fascinating Chemistry to Debated Pathological Relevance. Coord. Chem. Rev. 2018, 371, 38–55. 10.1016/j.ccr.2018.04.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valko M.; Jomova K.; Rhodes C. J.; Kuca K.; Musilek K. Redox- and Non-Redox-Metal-Induced Formation of Free Radicals and Their Role in Human Disease. Arch. Toxicol. 2016, 90 (1), 1–37. 10.1007/s00204-015-1579-5. [DOI] [PubMed] [Google Scholar]
- Han Y.; Sanford L.; Simpson D. M.; Dowell R. D.; Palmer A. E. Remodeling of Zn2+ Homeostasis Upon Differentiation of Mammary Epithelial Cells. Metallomics 2020, 12 (3), 346–362. 10.1039/C9MT00301K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carter K. P.; Young A. M.; Palmer A. E. Fluorescent Sensors for Measuring Metal Ions in Living Systems. Chem. Rev. 2014, 114 (8), 4564–4601. 10.1021/cr400546e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dittmer P. J.; Miranda J. G.; Gorski J. A.; Palmer A. E. Genetically Encoded Sensors to Elucidate Spatial Distribution of Cellular Zinc. J. Biol. Chem. 2009, 284 (24), 16289–16297. 10.1074/jbc.M900501200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penner-Hahn J. E. Characterization of ″Spectroscopically Quiet″ Metals in Biology. Coord. Chem. Rev. 2005, 249 (1–2), 161–177. 10.1016/j.ccr.2004.03.011. [DOI] [Google Scholar]
- Bertini I.; Luchinat C. An Insight on the Active-Site of Zinc Enzymes through Metal Substitution. Metal Ions in Biological Systems 1983, 15, 101–156. [Google Scholar]
- Ryde U.; Hemmingsen L. The Active-Site Metal Coordination Geometry of Cadmium-Substituted Alcohol Dehydrogenase - A Theoretical Interpretation of Perturbed Angular Correlation of Gamma-Ray Measurements. JBIC, J. Biol. Inorg. Chem. 1997, 2 (5), 567–579. 10.1007/s007750050171. [DOI] [Google Scholar]
- Gatjens J.; Mullins C. S.; Kampf J. W.; Thuery P.; Pecoraro V. L. Corroborative Cobalt and Zinc Model Compounds of α-Amino-β-Carboxymuconic-Epsilon-Semialdehyde Decarboxylase (ACMSD). Dalton Transactions 2009, (1), 51–62. 10.1039/B809453E. [DOI] [PubMed] [Google Scholar]
- Mroue K. H.; Power W. P. High-Field Solid-State Zn-67 NMR Spectroscopy of Several Zinc-Amino Acid Complexes. J. Phys. Chem. A 2010, 114 (1), 324–335. 10.1021/jp908325n. [DOI] [PubMed] [Google Scholar]
- Glatzel P.; Bergmann U. High Resolution 1s Core Hole X-Ray Spectroscopy in 3d Transition Metal Complexes - Electronic and Structural Information. Coord. Chem. Rev. 2005, 249 (1–2), 65–95. 10.1016/j.ccr.2004.04.011. [DOI] [Google Scholar]
- Glatzel P.; Alonso-Mori R.; Sokaras D.. Hard X-Ray Photon-In/Photon-Out Spectroscopy: Instrumentation, Theory and Applications. In X-Ray Absorption And X-Ray Emission Spectroscopy, 1st ed. Ed.; Van Bokhoven J. A., Lamberti C., Eds.; John Wiley and Sons, Ltd.: United Kingdom, 2016; Vol. 1, pp 125–153, 10.1002/9781118844243.ch6. [DOI] [Google Scholar]
- Kowalska J. K.; Lima F. A.; Pollock C. J.; Rees J. A.; DeBeer S. A Practical Guide to High-Resolution X-Ray Spectroscopic Measurements and Their Applications in Bioinorganic Chemistry. Isr. J. Chem. 2016, 56 (9–10), 803–815. 10.1002/ijch.201600037. [DOI] [Google Scholar]
- Pollock C. J.; DeBeer S. Insights into the Geometric and Electronic Structure of Transition Metal Centers from Valence-to-Core X-ray Emission Spectroscopy. Acc. Chem. Res. 2015, 48 (11), 2967–2975. 10.1021/acs.accounts.5b00309. [DOI] [PubMed] [Google Scholar]
- Bauer M. HERFD-XAS and Valence-to-Core-XES: New Tools to Push the Limits in Research with Hard X-Rays?. Phys. Chem. Chem. Phys. 2014, 16 (27), 13827–13837. 10.1039/C4CP00904E. [DOI] [PubMed] [Google Scholar]
- Garcia G. A.; Tierney D. L.; Chong S. R.; Clark K.; Pennerhahn J. E. X-Ray Absorption Spectroscopy of the Zinc Site in Trna-Guanine Transglycosylase from Escherichia Coli. Biochemistry 1996, 35 (9), 3133–3139. 10.1021/bi952403v. [DOI] [PubMed] [Google Scholar]
- Peariso K.; Zhou Z. H. S.; Smith A. E.; Matthews R. G.; Penner-Hahn J. E. Characterization of The Zinc Sites in Cobalamin-Independent and Cobalamin-Dependent Methionine Synthase Using Zinc and Selenium X-ray Absorption Spectroscopy. Biochemistry 2001, 40 (4), 987–993. 10.1021/bi001711c. [DOI] [PubMed] [Google Scholar]
- Tobin D. A.; Pickett J. S.; Hartman H. L.; Fierke C. A.; Penner-Hahn J. E. Structural Characterization of the Zinc Site in Protein Farnesyltransferase. J. Am. Chem. Soc. 2003, 125 (33), 9962–9969. 10.1021/ja035927o. [DOI] [PubMed] [Google Scholar]
- Herbst R. W.; Perovic I.; Martin-Diaconescu V.; O’Brien K.; Chivers P. T.; Pochapsky S. S.; Pochapsky T. C.; Maroney M. J. Communication between the Zinc and Nickel Sites in Dimeric Hypa: Metal Recognition and pH Sensing. J. Am. Chem. Soc. 2010, 132 (30), 10338–10351. 10.1021/ja1005724. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark-Baldwin K.; Tierney D. L.; Govindaswamy N.; Gruff E. S.; Kim C.; Berg J.; Koch S. A.; Penner-Hahn J. E. The Limitations of X-Ray Absorption Spectroscopy for Determining the Structure of Zinc Sites in Proteins. When is a Tetrathiolate not a Tetrathiolate?. J. Am. Chem. Soc. 1998, 120 (33), 8401–8409. 10.1021/ja980580o. [DOI] [Google Scholar]
- Krewald V.; Lassalle-Kaiser B.; Boron T. T.; Pollock C. J.; Kern J.; Beckwith M. A.; Yachandra V. K.; Pecoraro V. L.; Yano J.; Neese F.; DeBeer S. The Protonation States of Oxo-Bridged Mn-IV Dimers Resolved by Experimental and Computational Mn K Pre-Edge X-Ray Absorption Spectroscopy. Inorg. Chem. 2013, 52 (22), 12904–12914. 10.1021/ic4008203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westre T. E.; Kennepohl P.; Dewitt J. G.; Hedman B.; Hodgson K. O.; Solomon E. I. A Multiplet Analysis of Fe K-Edge 1s->3d Pre-Edge Features of Iron Complexes. J. Am. Chem. Soc. 1997, 119 (27), 6297–6314. 10.1021/ja964352a. [DOI] [Google Scholar]
- Chandrasekaran P.; Stieber S. C. E.; Collins T. J.; Que L.; Neese F.; DeBeer S. Prediction of High-Valent Iron K-Edge Absorption Spectra by Time-Dependent Density Functional Theory. Dalton Transactions 2011, 40 (42), 11070–11079. 10.1039/c1dt11331c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin-Diaconescu V.; Bellucci M.; Musiani F.; Ciurli S.; Maroney M. J. Unraveling the Helicobacter Pylori Ureg Zinc Binding Site Using X-Ray Absorption Spectroscopy (XAS) and Structural Modeling. JBIC, J. Biol. Inorg. Chem. 2012, 17 (3), 353–361. 10.1007/s00775-011-0857-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollock C. J.; DeBeer S. Valence-to-Core X-Ray Emission Spectroscopy: A Sensitive Probe of the Nature of a Bound Ligand. J. Am. Chem. Soc. 2011, 133 (14), 5594–5601. 10.1021/ja200560z. [DOI] [PubMed] [Google Scholar]
- Smolentsev G.; Soldatov A. V.; Messinger J.; Merz K.; Weyhermuller T.; Bergmann U.; Pushkar Y.; Yano J.; Yachandra V. K.; Glatzel P. X-Ray Emission Spectroscopy to Study Ligand Valence Orbitals in Mn Coordination Complexes. J. Am. Chem. Soc. 2009, 131 (36), 13161–13167. 10.1021/ja808526m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee N.; Petrenko T.; Bergmann U.; Neese F.; DeBeer S. Probing Valence Orbital Composition with Iron Kβ X-Ray Emission Spectroscopy. J. Am. Chem. Soc. 2010, 132 (28), 9715–9727. 10.1021/ja101281e. [DOI] [PubMed] [Google Scholar]
- Beckwith M. A.; Roemelt M.; Collomb M. N.; Duboc C.; Weng T. C.; Bergmann U.; Glatzel P.; Neese F.; DeBeer S. Manganese Kβ X-Ray Emission Spectroscopy as a Probe Of Metal-Ligand Interactions. Inorg. Chem. 2011, 50 (17), 8397–8409. 10.1021/ic200970t. [DOI] [PubMed] [Google Scholar]
- Swarbrick J. C.; Kvashnin Y.; Schulte K.; Seenivasan K.; Lamberti C.; Glatzel P. Ligand Identification in Titanium Complexes using X-Ray Valence-to-Core Emission Spectroscopy. Inorg. Chem. 2010, 49 (18), 8323–8332. 10.1021/ic100755t. [DOI] [PubMed] [Google Scholar]
- Mortensen D. R.; Seidler G. T.; Kas J. J.; Govind N.; Schwartz C. P.; Pemmaraju S.; Prendergast D. G. Benchmark Results and Theoretical Treatments for Valence-to-Core X-Ray Emission Spectroscopy in Transition Metal Compounds. Phys. Rev. B: Condens. Matter Mater. Phys. 2017, 96 (12), 125136. 10.1103/PhysRevB.96.125136. [DOI] [Google Scholar]
- Lancaster K. M.; Hu Y. L.; Bergmann U.; Ribbe M. W.; DeBeer S. X-Ray Spectroscopic Observation of an Interstitial Carbide in Nifen-Bound Femoco Precursor. J. Am. Chem. Soc. 2013, 135 (2), 610–612. 10.1021/ja309254g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rees J. A.; Bjornsson R.; Schlesier J.; Sippel D.; Einsle O.; DeBeer S. The Fe-V Cofactor of Vanadium Nitrogenase Contains an Interstitial Carbon Atom. Angew. Chem., Int. Ed. 2015, 54 (45), 13249–13252. 10.1002/anie.201505930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pushkar Y.; Long X.; Glatzel P.; Brudvig G. W.; Dismukes G. C.; Collins T. J.; Yachandra V. K.; Yano J.; Bergmann U. Direct Detection of Oxygen Ligation to the Mn4Ca Cluster of Photosystem II by X-Ray Emission Spectroscopy. Angew. Chem., Int. Ed. 2010, 49 (4), 800–803. 10.1002/anie.200905366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathe Z.; Pantazis D. A.; Lee H. B.; Gnewkow R.; Van Kuiken B. E.; Agapie T.; DeBeer S. Calcium Valence-To-Core X-Ray Emission Spectroscopy: A Sensitive Probe of Oxo Protonation in Structural Models of the Oxygen-Evolving Complex. Inorg. Chem. 2019, 58 (23), 16292–16301. 10.1021/acs.inorgchem.9b02866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cutsail G. E.; Gagnon N. L.; Spaeth A. D.; Tolman W. B.; DeBeer S. Valence-to-Core X-Ray Emission Spectroscopy as a Probe of O-O Bond Activation in Cu2O2 Complexes. Angew. Chem., Int. Ed. 2019, 58 (27), 9114–9119. 10.1002/anie.201903749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pollock C. J.; Grubel K.; Holland P. L.; DeBeer S. Experimentally Quantifying Small-Molecule Bond Activation Using Valence-to-Core X-Ray Emission Spectroscopy. J. Am. Chem. Soc. 2013, 135 (32), 11803–11808. 10.1021/ja3116247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raj S. S.; Raj S. Bis (2-Aminopyridine-N) Bis (Benzoato-O) Zinc. Acta Crystallographica. Section C, Crystal Structure Communications 2000, 56 (7), 742. 10.1107/S0108270100003462. [DOI] [PubMed] [Google Scholar]
- Chen X. M.; Huang X. C.; Xu Z. T.; Huang X. Y. Tetrakis (1-Methylimidazole-N3) Zinc (II) Diperchlorate. Acta Crystallogr., Sect. C: Cryst. Struct. Commun. 1996, 52 (10), 2482. 10.1107/S0108270196007706. [DOI] [Google Scholar]
- Cernak J.; Adzimova I.; Gerard F.; Hardy A. M. Bis (Benzoato-O) Bis (Thiourea-S) Zinc (II). Acta Crystallogr., Sect. C: Cryst. Struct. Commun. 1995, 51 (3), 392. 10.1107/S0108270194004075. [DOI] [Google Scholar]
- Wilker J. J.; Lippard S. J. Alkyl Transfer to Metal Thiolates: Kinetics, Active Species Identification, and Relevance to the DNA Methyl Phosphotriester Repair Center of Escherichia Coli Ada. Inorg. Chem. 1997, 36 (6), 969. 10.1021/ic961082o. [DOI] [PubMed] [Google Scholar]
- Wilker J. J. Modeling The DNA Methylphosphotriester Repair Site in Escherichia Coli Ada. Why Zinc and Four Cysteines?. J. Am. Chem. Soc. 1995, 117 (33), 8682. 10.1021/ja00138a031. [DOI] [Google Scholar]
- Marzotto A.; Bianchi A.; Valle G.; Clemente D. A. Structure of Hexakis (Methylimidazole) Cobalt (II) Dichloride Dihydrate,[Co (CH3-C3H3N2) 6] Cl2. 2H2O. Acta Crystallogr., Sect. C: Cryst. Struct. Commun. 1989, 45 (4), 582. 10.1107/S0108270188011795. [DOI] [Google Scholar]
- Webb S. M. Sixpack: A Graphical User Interface for XAS Analysis Using IFEFFIT. Phys. Scr. 2005, T115, 1011–1014. 10.1238/Physica.Topical.115a01011. [DOI] [Google Scholar]
- Newville M.; Stensitzki T.; Allen D. B.; Ingargiola A.. LMFIT: Non-Linear Least-Square Minimization and Curve-Fitting for Python, 2014.
- Neese F. The ORCA Program System. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012, 2 (1), 73–78. 10.1002/wcms.81. [DOI] [Google Scholar]
- Hanwell M. D.; Curtis D. E.; Lonie D. C.; Vandermeersch T.; Zurek E.; Hutchison G. R. Avogadro: an Advanced Semantic Chemical Editor, Visualization, and Analysis Platform. J. Cheminf. 2012, 4, 17. 10.1186/1758-2946-4-17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becke A. D. Density-Functional Exchange-Energy Approximation with Correct Asymptotic-Behavior. Phys. Rev. A: At., Mol., Opt. Phys. 1988, 38 (6), 3098–3100. 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
- Stephens P. J.; Devlin F. J.; Chabalowski C. F.; Frisch M. J. Ab-Initio Calculation Of Vibrational Absorption and Circular-Dichroism Spectra Using Density-Functional Force-Fields. J. Phys. Chem. 1994, 98 (45), 11623–11627. 10.1021/j100096a001. [DOI] [Google Scholar]
- Lee C. T.; Yang W. T.; Parr R. G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron-Density. Phys. Rev. B: Condens. Matter Mater. Phys. 1988, 37 (2), 785–789. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- Vosko S. H.; Wilk L.; Nusair M. Accurate Spin-Dependent Electron Liquid Correlation Energies for Local Spin-Density Calculations - A Critical Analysis. Can. J. Phys. 1980, 58 (8), 1200–1211. 10.1139/p80-159. [DOI] [Google Scholar]
- Weigend F.; Ahlrichs R. Balanced Basis Sets of Split Valence, Triple Zeta Valence And Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7 (18), 3297–3305. 10.1039/b508541a. [DOI] [PubMed] [Google Scholar]
- Weigend F. Accurate Coulomb-Fitting Basis Sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8 (9), 1057–1065. 10.1039/b515623h. [DOI] [PubMed] [Google Scholar]
- Pantazis D. A.; Chen X.-Y.; Landis C. R.; Neese F. All-Electron Scalar Relativistic Basis Sets for Third-Row Transition Metal Atoms. J. Chem. Theory Comput. 2008, 4 (6), 908–919. 10.1021/ct800047t. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Antony J.; Ehrlich S.; Krieg H. A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132 (15), 154104. 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
- Grimme S.; Ehrlich S.; Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32 (7), 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- Delgado-Jaime M. U.; DeBeer S. Expedited Analysis of DFT Outputs: Introducing Moanalyzer. J. Comput. Chem. 2012, 33 (27), 2180–2185. 10.1002/jcc.23028. [DOI] [PubMed] [Google Scholar]
- DeBeer George S.; Petrenko T.; Neese F. Prediction of Iron K-Edge Absorption Spectra using Time-Dependent Density Functional Theory. J. Phys. Chem. A 2008, 112 (50), 12936–12943. 10.1021/jp803174m. [DOI] [PubMed] [Google Scholar]
- DeBeer George S.; Petrenko T.; Neese F. Time-Dependent Density Functional Calculations of Ligand K-Edge X-Ray Absorption Spectra. Inorg. Chim. Acta 2008, 361 (4), 965–972. 10.1016/j.ica.2007.05.046. [DOI] [Google Scholar]
- Tomson N. C.; Williams K. D.; Dai X. L.; Sproules S.; DeBeer S.; Warren T. H.; Wieghardt K. Re-Evaluating the Cu K Pre-Edge XAS Transition in Complexes with Covalent Metal-Ligand Interactions. Chemical Science 2015, 6 (4), 2474–2487. 10.1039/C4SC03294B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walroth R. C.; Lukens J. T.; Macmillan S. N.; Finkelstein K. D.; Lancaster K. M. Spectroscopic Evidence For A 3d10 Ground State Electronic Configuration and Ligand Field Inversion in Cu(CF3)41-. J. Am. Chem. Soc. 2016, 138 (6), 1922–1931. 10.1021/jacs.5b10819. [DOI] [PubMed] [Google Scholar]
- Pollock C. J.; Delgado-Jaime M. U.; Atanasov M.; Neese F.; DeBeer S. Kβ Mainline X-Ray Emission Spectroscopy as an Experimental Probe of Metal-Ligand Covalency. J. Am. Chem. Soc. 2014, 136 (26), 9453–9463. 10.1021/ja504182n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gamblin S. D.; Urch D. S. Metal Kβ X-Ray Emission Spectra Of First Row Transition Metal Compounds. J. Electron Spectrosc. Relat. Phenom. 2001, 113 (2–3), 179–192. 10.1016/S0368-2048(00)00416-3. [DOI] [Google Scholar]
- Tsutsumi K. The X-Ray Non-Diagram Lines Kβ′ of Some Compounds of the Iron Group. J. Phys. Soc. Jpn. 1959, 14 (12), 1696–1706. 10.1143/JPSJ.14.1696. [DOI] [Google Scholar]
- Wang X.; Grush M. M.; Froeschner A. G.; Cramer S. P. High-Resolution X-Ray Fluorescence and Excitation Spectroscopy of Metalloproteins. J. Synchrotron Radiat. 1997, 4, 236–242. 10.1107/S0909049596015440. [DOI] [PubMed] [Google Scholar]
- Martin-Diaconescu V.; Chacon K. N.; Delgado-Jaime M. U.; Sokaras D.; Weng T. C.; DeBeer S.; Blackburn N. J. Kβ Valence to Core X-Ray Emission Studies of Cu(I) Binding Proteins with Mixed Methionine-Histidine Coordination. Relevance to the Reactivity of the M- and H-Sites of Peptidylglycine Monooxygenase. Inorg. Chem. 2016, 55 (7), 3431–3439. 10.1021/acs.inorgchem.5b02842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deutsch M.; Holzer G.; Hartwig J.; Wolf J.; Fritsch M.; Forster E. Kα And Kβ X-Ray-Emission Spectra of Copper. Phys. Rev. A: At., Mol., Opt. Phys. 1995, 51 (1), 283–296. 10.1103/PhysRevA.51.283. [DOI] [PubMed] [Google Scholar]
- Holzer G.; Fritsch M.; Deutsch M.; Hartwig J.; Forster E. Kα1,2 And Kβ1,3 X-Ray Emission Lines of the 3d Transitions Metals. Phys. Rev. A: At., Mol., Opt. Phys. 1997, 56 (6), 4554–4568. 10.1103/PhysRevA.56.4554. [DOI] [Google Scholar]
- Didziulis S. V.; Cohen S. L.; Butcher K. D.; Solomon E. I. Variable Photon Energy Photoelectron Spectroscopic Studies of Covalent Bonding in 3d10 Transition-Metal Compounds. Inorg. Chem. 1988, 27 (13), 2238–2250. 10.1021/ic00286a008. [DOI] [Google Scholar]
- Valenza R. A.; Jahrman E. P.; Kas J. J.; Seidler G. T. Double-Ionization Satellites in the X-Ray Emission Spectrum of Ni Metal. Phys. Rev. A: At., Mol., Opt. Phys. 2017, 96 (3), 032504. 10.1103/PhysRevA.96.032504. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.