Abstract
COVID-19 is a deadly viral infection that has brought a significant threat to human lives. Automatic diagnosis of COVID-19 from medical imaging enables precise medication, helps to control community outbreak, and reinforces coronavirus testing methods in place. While there exist several challenges in manually inferring traces of this viral infection from X-ray, Convolutional Neural Network (CNN) can mine data patterns that capture subtle distinctions between infected and normal X-rays. To enable automated learning of such latent features, a custom CNN architecture has been proposed in this research. It learns unique convolutional filter patterns for each kind of pneumonia. This is achieved by restricting certain filters in a convolutional layer to maximally respond only to a particular class of pneumonia/COVID-19. The CNN architecture integrates different convolution types to aid better context for learning robust features and strengthen gradient flow between layers. The proposed work also visualizes regions of saliency on the X-ray that have had the most influence on CNN’s prediction outcome. To the best of our knowledge, this is the first attempt in deep learning to learn custom filters within a single convolutional layer for identifying specific pneumonia classes. Experimental results demonstrate that the proposed work has significant potential in augmenting current testing methods for COVID-19. It achieves an F1-score of 97.20% and an accuracy of 99.80% on the COVID-19 X-ray set.
Keywords: COVID-19, Deep learning, CNN, Chest X-ray, Pneumonia
1. Introduction
The novel SARS-CoV-2 (COVID-19) virus comes from the coronavirus family. The coronavirus cause ailments ranging from the common cold, fever to severe difficulty in breathing, and respiratory illness. COVID-19 is a novel coronavirus that was first reported in Wuhan, China, in December 2019 and is now affecting the countries across the world. The coronavirus outbreak was officially declared as a pandemic by WHO on Mar 11, 2020.
The COVID-19 coronavirus has left a devastating effect on the people’s livelihood and the healthcare sector worldwide. According to the latest reports (as of July 2020), the US is the most affected country with 3.48M confirmed cases, and the global death toll has surpassed 578K [1]. More importantly, over 7.37M have recovered from the infection. Lockdown of the state has been imposed in most countries to prevent the virus from spreading among the population. COVID-19 affected patients can be both symptomatic and asymptomatic [2]. While it is important to test people showing symptoms of the infection, it is also equally necessary to test people in contact with the affected person, even though they may not show symptoms in the initial stages.
COVID-19 is a droplet infection and spreads from human to human by the means of cough, sneeze, or any other form of physical contact through which the virus can enter the host body [3]. The COVID-19 virus affects people regardless of any age group but the most susceptible targets are the older fraction of people and patients with respiratory illness, cancer, diabetes, and cardiovascular diseases. The symptoms of the disease include dry cough, fever, body pain, and exhaustion. The symptoms are usually mild and commonly start to develop only around 5–6 days after acquiring the virus. The most serious manifestation of the symptom is breathing difficulty and high fever. To date, no antiviral drugs are clinically proven to fight COVID-19, though possible vaccines, plasma-therapy, and specific drugs (hydroxychloroquine) treatment are being investigated and administered on trial subjects [4]. Recovery from the virus is highly dependent on the immunity of the affected host [5]. WHO advisories for the prevention of the virus include social distancing and following personal hygiene [6].
Currently, for the diagnosis of COVID-19, WHO recommends Real-time PCR (Polymerase Chain Reaction) testing that detects the presence of antigen from the respiratory samples [7]. From a clinical study on a trial group of 64 patients, the RT-PCR test is shown to have a sensitivity of 91% in a confidence interval of 81%–96% [8]. The results are generally obtained within a few hours to 2 days, which is a critical phase as per treatment protocols. A new line of rapid diagnostic tests (RPT) is being used to detect the presence of viral proteins expressed by COVID-19 from respiratory samples. These tests have shown sensitivity ranging from 34% to 80% and give results in 10–30 min [9]. But the results highly depend on the concentration of the antigen in the sample, time from the onset, and several other factors. Serological testing techniques detect antibodies in the blood of affected people, formed in response to fighting the virus. But since for the majority of people, the anti-bodies develop only 2 weeks after contracting the virus, these tests cannot be used for early diagnosis.
Medical imaging can serve as an effective screening aid for pneumonia detection. It can be combined with Artificial Intelligence to investigate the nature of pneumonia. Chest X-ray has already been shown to be a fundamental indicator of pneumonia and severe lung infection [10]. It is also the first-line imaging modality used for studying the complications in patients suspected with COVID-19 [8]. Airspace opacities are the most common find in the chest X-rays that suggest pneumonia. Since COVID-19 can lead to pneumonia and manifests in the lungs, medical imaging (chest X-rays and CT scans) can be mined for patterns that can provide such distinguishable factors for the identification of the virus. Deep learning technology can enable drawing a clear distinction of the non-tangible elements in the X-ray that can expose the infection. The proposed work is an effort made towards addressing the extent to which deep Convolutional Neural Network (CNN) can learn that pattern from the radiological data.
Being a contagious disease, early detection of the virus can not only help to save the affected but also to avoid community spread. Treatment in the early stages is also shown to reduce the mortality rate. Chest X-rays are inexpensive and can be readily obtained in a period of 15 to 20 min. If sufficient evidence of the virus can be spotted on the X-ray, then the sample can be classified immediately. The presence of the infection can be addressed in a more informed way by automating the final step to save time and add value to the decision process.
In this work, we propose a channel-shuffled dual-branched CNN architecture for accurately detecting COVID-19 from chest X-rays. To effectively learn salient features that capture class-discriminatory information towards the final layers of the CNN, a novel distinctive filter learning paradigm has also been proposed. The network design is mainly composed of two tightly coupled functional blocks that are bound by feature channel shuffling and dual residual connectivity spanning across the blocks. The proposed distinctive filter learning approach constrains a subset of convolutional filters to uniquely learn X-ray patterns that characterize a particular class. It learns dedicated filter-sets for COVID-19/pneumonia by exploiting the filters’ gradient response towards that target class.
The proposed work effectively addresses the following research challenges in COVID-19 detection.
-
•
Transfer learning and custom CNN models still follow the conventional loss optimization, which can just fit any data distribution. Any additional value that can be derived from these models should come from enhancing the base learning paradigm to capture more latent patterns.
-
•
While most of the existing research in COVID-19 detection explores standard CNN architectures and transfer learning methods, customized architectural design specific to data and task tends to generalize well to real-world samples.
-
•
The literature on COVID-19/pneumonia detection does not provide any additional insights into the CNN, in terms of the filter properties and response to a target class. Examining these patterns can provide the much needed human-level understanding for interpretation of the virus from X-rays.
The main contributions of the proposed work are three-fold.
-
•
The proposed learning paradigm is an algorithm that exclusively learns distinctive convolutional filters for every target label. It is done by restricting certain filters to maximally respond only to a particular class of pneumonia/COVID-19.
-
•
The proposed CNN architecture integrates different convolutional types along residual links to aid better context for learning robust features. The architectural design regulates information flow by aggregating variably sized receptive fields and sustaining steady gradient flow between layers.
-
•
The proposed work provides visualizations of the top-k filters that are learned to identify specific target classes. Also, the salient regions on the X-ray that influence CNN class prediction are presented to aid better context for infection localization.
The rest of the manuscript is organized as follows. In Section 2, related works in pneumonia and COVID-19 detection are reviewed. Section 3 describes the proposed CNN architectures and its various components in detail. Section 4 provides a comprehensive analysis of the results of model training and validation. The manuscript concludes with a summary of the key findings of the work.
2. Related works
Diagnosis of COVID-19 from Chest X-rays is associated with the symptoms of pneumonia. Thus, it should be possible to distinguish between the manifestations exhibited by COVID-19 from other pneumonia on the chest X-ray modality. The traces of COVID-19 on chest X-ray needs to be uniquely identified against patterns observed in other forms of pneumonia. A wide array of research works uncovers the discriminatory information that best expresses pneumonia from normal samples on chest X-rays. The methods employed in the research of pneumonia/COVID-19 classification from chest X-rays fall into these categories: Machine learning (ML) methods [11], [12], [13], statistical approaches [14], CNN architectures [15], [16], [17], [18], [19], [20], [21], [22], transfer learning [23], [24], [25], [26], [27], [28], [29], [30], [31], [32], [33], [34], complex CNN models [35], [36], [37], [38], [39], [40], [41], [42] and adversarial networks [43].
2.1. Pneumonia detection methods
Machine learning-based approaches define feature extraction techniques that can effectively exploit features of interest from the chest X-rays. These features are typically classified on a ML algorithm. Chandra et al. propose a three-step solution for automatic detection of pneumonia [11]. Regions of the X-rays enclosing the lungs are extracted and quantified using first-order statistical features like mean, kurtosis, etc. These feature encodings are distinguished using logistic regression, MLP, random forests to obtain classification labels. Ambita et al. proposed an approach for pneumonia detection from chest X-rays using adaptive regression kernel descriptors and Support Vector Machine (SVM) [12]. Santos et al. proposed a methodology that exploits texture-based statistical features from the Gray Level Co-occurrence Matrix (GLCM) for classifying chest X-rays with Neural Networks [13].
Statistical techniques model the distribution of a random variable as a feature to be used for classification. Khatri et al. used the Earth Mover’s Distance (EMD), to measure the difference between intensity spread for pneumonia affected and non-pneumonia X-rays [14]. Based on the variation in EMD values, thresholds are identified to categorize X-rays as having pneumonia/not.
CNN based approaches efficiently learn the underlying latent feature representations, that can discriminate between pneumonia affected and normal samples. Sharma et al. proposed a custom CNN for pneumonia classification [15]. The performance of the trained network was studied under different settings to validate the inclusion of dropout layers and data augmentation. Wu et al. proposed a CNN based approach for deep feature extraction from denoised X-rays to detect pneumonia [16]. Adaptive median filtering is used for denoising, and a random forest classifier is fit over the extracted CNN features. Fathurahman et al. used the Histogram of Oriented Gradient (HOG) and GCLM features extracted from the chest X-ray to train a one-dimensional convolutional network [17]. Nakrani et al. introduced a 19-layer custom CNN to identify pneumonia from chest X-rays [18]. The approach presented in [19] employs MLP and CNN for classifying chest X-rays. It compares the performance of MLP and CNN with four convolutional layers for pneumonia detection. Stephen et al. developed a feed-forward CNN model with few convolutional layers and a fully connected layer for classifying pneumonia [20]. Chakraborty et al. used a 17-layer CNN with 3 convolutional layers and 5 dense layers for viral/bacterial pneumonia identification from chest X-rays [21]. Li et al. proposed a custom CNN for pneumonia detection, which is experimented under a range of convolutional layers [22].
Transfer learning is a technique that reuses existing weights from a model, pre-trained on a larger database. By replacing and retraining only the last few layers of the pre-trained model, the modified CNN derives all of the architectural advantages from the base CNN. The work by Rahman et al. used four existing deep architectures: AlexNet, ResNet18, DenseNet201, and SqueezeNet, to detect bacterial and viral pneumonia from chest X-rays [23]. Chouhan et al. applied transfer learning on five deep neural architectures to form an ensemble classifier for the task of pneumonia classification [24]. In the work presented by Chhikara et al. Google’s InceptionV3 model was utilized for deep transfer learning by adding on dropout, average pooling, and fully connected layers at the end of the network [25]. Chen et al. proposed to apply transfer learning on deep architectures like Inception ResNet, NASNet, etc [26]. In [27], 11 ImageNet pre-trained models like AlexNet, SqueezeNet, GoogLenet, were retrained on the chest X-ray dataset using transfer learning. Narayanan et al. proposed a two-level CNN for pneumonia classification [28]. In the first stage, samples are broadly classified as having pneumonia or not, of which the pneumonia samples are further categorized to viral/bacterial in the second stage. Bhandary et al. utilized deep features from the modified AlexNet, Harlick features, and Hu moments to render an ensemble feature-set for Deep Learning-based classification [29].
Advanced CNN models precisely learn specific aspects of pneumonia, that distinctly capture the infection. For instance, Mittal et al. Proposed a method that combines multi-layered capsules from the CapsuleNet architecture with convolutions to form an ensemble network for pneumonia detection [35]. Archarya et al. proposed a deep Siamese network to compare the symmetry between the left and the right lung segments [36]. Sarkar et al. employed residual CNN with separable convolutions for pneumonia detection from X-rays [37]. Jaiswal et al. proposed to identify potential pneumonia from X-rays using a Mask-RCNN [38]. Regions of interest were drawn around the predicted bounding boxes and the lung opacity was quantified within these regions to generate pixel-wise infection segmentation.
GAN is an adversarial pair of networks that optimize a shared objective in min–max fashion. Bhagat et al. presented an approach to augment chest X-ray data using GAN [43]. The augmented dataset with new samples from the GAN is classified on a variant of the AlexNet to result in samples’ class predictions.
2.2. COVID-19 detection methods
Since research in COVID-19 detection from radiographs has just begun to gain traction, the diversity of methods that explore Machine learning and Deep learning for identifying COVID-19 are limited. This section covers key findings from the recent COVID-19 works.
Transfer learning has been the most popular area of study for detecting COVID-19. These works probe the levels of model fitting that can be achieved by customizing standard deep architectures, for the task of COVID-19 detection. Farooq and Hafeez presented a fine-tuning of the ResNet50 by altering the training settings [30]. In this transfer learning approach, the ResNet was trained with X-ray images of different sizes and under different learning rates for the network head & backbone. Apostolopoulos and Mpesiana tested five standard architectures under different hyperparameter settings for COVID-19 detection from chest X-rays [31]. Five standard CNN architectures that include, VGG19, InceptionNet, MobileNetV2, XceptionNet, Inception ResNetV2 have been experimented for the X-ray classification task under different hyperparameter (number of untrainable layers, choice of the top layer neural network classifier, etc.) settings. Apostolopoulos et al. proposed a transfer learning approach that uses off-the-shelf features from the standard MobileNetV2 for deep classification of chest X-rays into target classes consisting of COVID-19, pneumonia and 5 other pulmonary diseases [32]. The MobileNetV2 was also trained from scratch on these classes. Khan et al. had used transfer learning on Xception net CNN for COVID-19 classification from chest X-rays [33]. The approach modified the base Xception model by adding a dropout layer and a fully connected layer at the end of the network with a residual connection. Mangal et al. proposed to use CheXNet CNN for COVID-19 detection [34]. The work applies transfer learning on CheXNet by utilizing DenseNet121 as the backbone network.
Researches in COVID-19 identification have also employed complex CNNs to learn mappings that can capture specific aspects unique to COVID-19. Ozturk et al. proposed a modified form of the DarkNet-19 model that is used in object detection systems (like YOLO) [39]. The custom DarkCovidNet CNN comprised of 17 convolutional layers stacked sequentially along the cross-section of the CNN. Saiz et al. proposed to utilize the single-shot multi-detector (SSD) CNN. It generates objectness scores for patches sampled from different parts of the X-ray (having larger IoU with ground truth object) and classifies them to one of the normal or COVID-19 classes [40]. Pereira et al. attempted a multi-class classification for pneumonia using texture-based feature descriptors and deep CNN features [41]. The early and late fusion techniques were employed to group feature sets for training and combine prediction results from different feature sets. Wang and Wong proposed a custom CNN architecture built with projection and expansion convolutional layers [42]. The network design pattern was architecturally enhanced with depth-wise convolutions, different kernel sizes, and selective long-range connectivity across the layers. The model was reported to perform better than standard VGG-16 and ResNet-50 on the same dataset.
3. Proposed work
The proposed work consists of two CNN architectures: (1) Channel-Shuffled Dual-Branched (CSDB) CNN (2) CSDB CNN augmented with Distinctive Filter Learning (DFL) paradigm. The motivation behind the CSDB CNN is to present a network design that benefits from (1) dual residual connectivity across blocks, (2) coupled network paths, (3) channel-shuffling and (4) correlation of variably sized receptive fields. The DFL module is a network learning strategy that learns unique class-identifying filters in a single convolutional layer. The idea behind DFL is to quantify a measure of the filters’ response to a target pneumonia class and introduce this factor into the network loss optimization.
3.1. Channel-shuffled dual-branched CNN
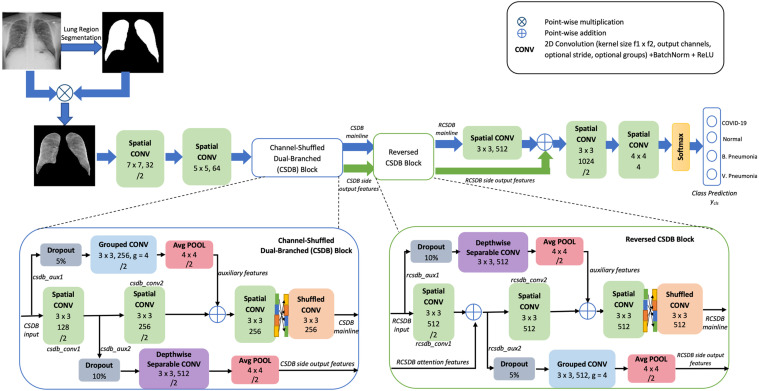
The architecture of the proposed system is presented in Fig. 1. The CNN operates on input dimensions of 256 ×256. Along with CNN, the feature depth increases by a factor of 2, i.e., starting from 32, 64, 128, 256, 512 to 1024 channels in the penultimate layer. The lung regions segmented from the base chest X-ray is used for model training and prediction. This ensures that only the data from the masked lung regions guide the learning algorithm and prevent unwarranted interferences from other regions from being correlated by the model. The augmented lung segments samples are propagated across the various convolutional layers to wrap with a final softmax activated feature map in four classes. To keep the network size low with as few parameters as possible, we employ three other types of convolutions that can save the cost of additional computation: (1) depth-wise separable convolution, (2) grouped convolution, (3) shuffled grouped convolution. The advantages derived from these individual convolutions are multi-fold: (1) they reduce the number of learnable parameters, minimize computation costs, but still provide optimal performance (2) they can be easily parallelized over multiple GPUs. (3) they can provide much better contextual information and are shown to strengthen gradient flow between adjacent layers. (4) by using them as residual links to the main branch, their capabilities are enhanced, as information flow is aided by aggregation of multi-scale features.
Fig. 1.
Schematic diagram of the proposed Channel Shuffled Dual-Branched CNN.
The network architecture presented in Fig. 1 is mainly composed of two CSDB blocks stacked in succession. The convolutional function on the residual branches in the second block is switched, resulting in Reversed CSDB. In a broad view, the spatial convolutional layers progressively extract mainline features along the cross-section of the network, while residual connections from auxiliary convolutional layers are utilized to raise more context for feature learning. The dual residual links across the CSDB and reversed CSDB complement each other by providing multiple network paths for information flow.
The initial two convolutional layers with kernel size 7 ×7 and 5 ×5 extract preliminary low-level features from the chest X-ray. Large-sized kernels in the first few CNN layers incorporate maximal spatial information to successive layers, as the receptive fields grow along with the CNN. The low-level X-ray features are passed onto the first CSDB block.
At the inception of the first CSDB block, the network forks into mainline and sideline paths. The side output branch (csdb_aux1) is a result of grouped convolution with four groups and average pooling. Using grouped convolution for building feature map outputs with multiple kernels leaves a regularization effect. It is also shown to learn filters that highly correlate with those in the adjacent layers. Thereby it binds and develops robust links for every filter group with surrounding layers. The csdb_aux1 connection jumps over the two mainstream Convolutional layers (csdb_conv1, csdb_conv2) and the auxiliary features fuse at the main branch. This fused feature map is spatially filtered by a convolutional layer. The output from this layer is acted upon by the channel shuffle layer and then by grouped convolution, both of which together make up the shuffled convolution. Shuffled convolution is shown to strengthen gradient flow between adjacent layers. Especially in the context of CSDB, it forms strong bindings between features propagated out of this block and the ensuing RCSDB block. Besides the mainline features, additional side-attention features are obtained from the csdb_aux2 branch. The csdb_aux2 branch extends from the output of the csdb_conv1 layer and is a result of depth-wise separable convolution followed by average pooling. The depth-wise separable convolutions on the residual link enable the network to observe more contextual information at a much lower computation cost. It is highly efficient, as the operations are dense. The features computed at csdb_aux2 serve as implicit prior attention cues for guided feature extraction at the RCSDB block.
The RCSDB block is inherently the same as the CSDB block, except for a few architectural changes. The convolutional layers on the dual branches are reversed, concerning preceding CSDB as shown in Fig. 1. The motivation for functionally reversed residual branches comes from the fact that RCSDB input is the result of shuffled convolution that employs filter groups. Since convolution with grouped filters explores only subsets of modalities, the resulting maps need to be aggregated over all channels. Depth-wise separable and spatial convolutions in the rcsdb_aux1 and rcsdb_conv1 branches achieve exactly this. Also, the rcsdb_aux2 grouped convolutional branch learns specialized filter groups for distinct sets of feature channels in the input map. This strategy effectively complements the learning at depth-wise separable convolution (in csdb_aux2 branch) that draws correlations over all the feature channels, offering dense pixel connectivity. Overall, the dual residual connections spanning the two blocks function as coupled modules that yield multiple network paths for information flow. That is, the input features can trace any of these paths: csdb_conv1- rcsdb_conv1, csdb_conv1- rscdb_conv2, csdb_conv2- rcsdb_conv2. In all these possible paths, the modules aggregate & disseminate contextual feature information over multiple channels and provide regularization capabilities (with dropout layers).
The RCSDB features are processed and consolidated through a series of convolutions. The stream ends at a final classification layer that maps these large sets of features to class-wise probabilities. On the whole, the proposed CNN utilizes only 15.6M parameters for accurately mapping the decision space.
The network parameters are learned by optimizing the log-likelihood loss of the predicted class probabilities with target class , given by Eq. (1).
| (1) |
where denotes the sample in the batch and {‘healthy’, ‘COVID-19’, ‘bacterial pneumonia’, ‘viral pneumonia’} indicates the four classes modeled by the CNN.
3.2. CSDB CNN augmented with distinctive filters learning (DFL) paradigm
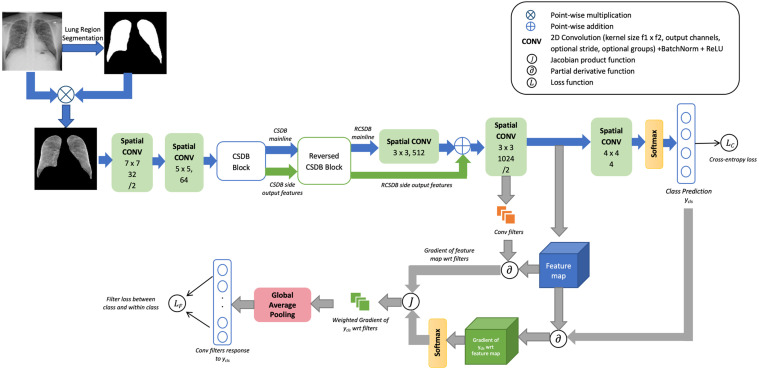
To learn filters that can accurately observe discriminating characteristics for specific classes, the formulation of a novel secondary loss function is proposed. The proposed loss strategy is applied to the CSDB CNN as shown in Fig. 2.
Fig. 2.
Architectural sketch of the proposed CSDB CNN with Distinctive Filter Learning (DFL).
The proposed approach utilizes the weighted gradients of filters for the target class to identify the set of filters that respond maximally to a particular class. Such filters (that capture differentiating factors for a particular class) can be determined for every output class. The additional loss function proposed, will aim to minimize the distance between the maximally activated filters within the same class and maximize the dissimilarity of filters between different classes. This technique is applied to the penultimate layer of CNN so that the shared features learned until then can be distinctively associated with respective classes.
Let denote the target class. For a spatial convolutional layer yielding activated feature map fm, let denote learnable weights/filters of with dimensions [out_channels in_channels filter_size filter_size]. The gradient of the feature map at layer , fm, for a particular class is a mode-3 tensor given by Eq. (2).
| (2) |
where are the gradient matrices for channel 1 to out_channels, i.e., the gradients are computed for every feature channel in the output feature map.
A spatial softmax activation is applied along the depth axis, over every h w pixel on the gradient map to obtain as shown in Eq. (3).
| (3) |
is a weighted distribution of the layer ’s feature map gradients for the output class. Indirectly is a manifestation of the relative importance of features obtained at a layer that responds the most to a target class. The significance of the output features from a convolutional layer can be quantified by encoding it this way.
Let denote the vectorizer function that unfolds the elements of a tensor into a flat vector. Let indicate the vectorized form of the mode-4 weights tensor . Similarly, let denote the linear vector of the feature map fm. Let and be the total number of elements in the vectors and . Then, the gradient of the activated feature map for layer weights can be encoded into a Jacobian matrix , as given by Eq. (4).
| (4) |
The vector–Jacobian product between the Jacobian matrix in Eq. (4) and the vectorized form of , i.e., in Eq. (3) is shown in Eq. (5). This resultant are the gradients of filters for , weighted by the maximally activated output at that layer’s feature map, i.e. .
| (5) |
The values in in the vectorized form can be wrapped back to the original dimensions of , that is [out_channels in_channels filter_size filter_size]. From the formulation, holds these gradient weights in the base dimensions. A global average pooling of window size (filter_size, filter_size) is applied over the last two dimensions of to render a matrix of gradient values, . Each cell in this matrix of shape (out_channels in_channels) corresponds to a filter learned by layer . The values in represent a single weighted gradient value for a filter for the target class and is a measure of the contribution of the filter towards that class.
To enable comparison of the filters at a layer that maximally respond to samples from different output classes, an encoding vector is constructed from to represent that information. The resultant is normalized between 0 to 1 and a boolean vector is framed such that values more than 90th percentile are set to 1 while the rest are 0s. The Eq. (6) gives the construction of from .
| (6) |
This representational encoding of the set of filters that respond the most to a target class, , can be obtained by a single backward gradient step. The computed gradients can be completely reused for updating the gradients against the loss function defined in Eq. (1). The proposed secondary loss function for updating the gradients of layer C and preceding layers is given in Eq. (9). This function maximizes the dice similarity coefficient between the encodings of samples x and y from the same class Eq. (7) and minimizes the dice score between samples x and z of different classes Eq. (8). The dice distance was employed so that the intersecting filters (between samples in the same/different classes) is effectively capturing the overall maximal filters. The dice distance is an accurate measure of distortedness between two boolean representations, especially here, as the minor case (filter gradient values 90th percentile) is only 10% of all filters.
| (7) |
| (8) |
| (9) |
It can be observed from Eq. (9) that the loss formulation has included a factor (in ), which is a particular convolutional layer on CNN. It is essential to choose , as it will determine the model’s learning curve to a large extent. For the proposed architecture, , 10, i.e., the two penultimate layers from the last. Learning distinct filters that can be associated with individual classes can only be achieved in the final few layers. This is because, after the computation of intricate and complicated features in the mid-layers, CNN tries to learn discriminatory features only towards the end. Until the final layers, most of the features are shared in ways that can efficiently represent all possible latent modes in chest X-rays. The last layer is not chosen, as the immediate softmax cross-entropy function updates those weights. Also, by learning the penultimate filters this way, makes it very easy for the last layer to discern differences in samples from different classes.
To show an example of the proposed filter loss, the filter encoding for the 10th spatial convolutional layer (penultimate layer) is derived from the layer weights of dimensions 1024 ×512 ×3 ×3. is an encoding in 1024 ×512 524 288 filters, where each value is a boolean representing a maximal response or not.
A similar effect (of learning filters for particular classes) can also be achieved by spawning explicit sub-networks for each class, that branch off the shared backbone. But the proposed technique not only learns unique class identifying filters, but also accomplishes these key points of saliency: (1) it has converted a single convolutional layer as a dual purpose learner, i.e. learning to extract representational features, learning them in a distinguishable way by tuning the filters. (2) it has performed class discrimination with the least number of parameters (hardly 10% filters for each class) that capture most significant neuronal spikes leading to a target class classification. (3) during predictions, classical CNN approaches correlate neuronal patterns from all the channels in the feature map to arrive at the target class. But the proposed technique learns a few robust spatial filters that only observe certain channel slices of the feature map, and is still able to provide discerning factors for multiple classes. (4) the proposed approach can be easily introduced into any CNN architecture. It offers performance enhancements over the classical CNN paradigm by boosting class discriminability with dedicated filter-sets for each target class.
4. Results and discussions
This section presents a comprehensive view of the dataset, experimentation, model training, and validation. A performance comparison of the proposed approach with the existing works has been presented in the final sub-section.
4.1. Data acquisition
The dataset was prepared from the frontal view of chest X-rays. The X-rays for different classes of pneumonia were acquired from multiple sources. The details of the data sources are presented in Table 1. These sources collectively yielded a set of 558 COVID-19 Chest X-rays.
Table 1.
Data collection from different sources. Provided are the count of patients studied and samples curated in each category of pneumonia.
| S.No | Source | Details | Category | Number of patients | Sample count |
|---|---|---|---|---|---|
| 1 | Joseph Cohen Dataset [44] | Open-source data maintained by the University of Montreal | COVID-19 | 227 | 356 |
| 2 | Radiopaedia [45] | An open database compiled by radiologists and clinicians | COVID-19 | 35 | 61 |
| 3 | AG Chung Dataset [46] | University of Waterloo, Canada | COVID-19 | 31 | 35 |
| 4 | ActualMed Dataset [47] | University of Waterloo, Canada | COVID-19 | 51 | 58 |
| 5 | SIRM [48] | Italian Society of Medical and Interventional Radiology | COVID-19 | 48 | 48 |
| 6 | RSNA Challenge [49] | Public data provided by the National Institutes of Health Clinical Center | Normal | 8851 | 8851 |
| 7 | Paul Mooney dataset [50] | Guangzhou Women and Children’s Medical Centre, Guangzhou | Normal |
584 |
1583 |
| Bacterial Pneumonia |
1437 |
2780 |
|||
| Viral Pneumonia | 1216 | 1493 | |||
4.2. Lung region segmentation
From chest X-ray samples, the lungs regions were segmented by applying a pre-trained algorithm [51]. These lung segments are subjected to augmentation and fed as input to the CNN.
4.3. Data augmentation
COVID-19 chest X-ray databases are continually sourced from community contributions that are not sufficient for training complex models like CNN. This work adopts a lossless augmentation technique that can multiply the sample count as well as preserve the inherent property of the infection in the samples.
To enable model fitting on a sufficiently large number of samples, the lung segments in the base dataset were augmented by applying four random affine transformations: horizontal flipping, rotation, translation, shearing. The affine transformation functions for rotation, translation, shear, horizontal flip are parameterized as follows: is the angle of counter-clockwise rotation about the origin; and are the translations along x and y directions; and are the horizontal and vertical shear factors. For generating diverse samples, the transformations are randomly seeded with parameter values in the specified range: ‘ is between to ; and are within 0.1 of the height and width of the image respectively; and are in the range of to units of and for the shear angle in the range [; flipping is performed randomly with a probability of 0.5. The augmentation was online, i.e., performed on batches sampled during training. The four transformations were applied in succession to render the augmented samples.
4.4. Experimental setup
The proposed network was trained on two 12 GB NVIDIA Tesla K80 GPUs on Google Cloud VM. The proposed learning paradigm was implemented in PyTorch. The data parallelism module built into the Torch framework was exploited to generate gradients for multiple data batches simultaneously on different GPUs. The system specifications are Ubuntu 18.04, 2vCPUs, and 13 GB RAM. The model was trained with Adam optimizer, with a learning rate of 0.002. The data was trained in batches of 512 images with a roughly equal number of samples under every class in a training batch, with over 24 steps per epoch. As the dataset sample counts were skewed towards certain classes, the augmentation trick and weighted-class batch sampling compensate for the data imbalance. The stratified data sampling approach was employed to result in an equal number of samples from each class in every training batch. The proposed CNN was trained for 75 epochs, and it converged well.
4.5. Hyperparameter tuning
Hyperparameter tuning was performed using Grid search on the RayTune framework. The experiment was set up with three hyperparameters in the model: (1) dropout rate in the dropout layer (2) multiplicative factor of learning rate decay (3) gradient update optimization algorithms. Optimal tuning was attained by searching for the parameter values in the specified range: dropout factor is between 5% to 20% in steps of 5%; exponential decay rate is either of discrete values 0.01 or 0.02; gradient optimizers is one of ADAM or SGD. It was found that dropout probabilities of 5% and 10% resonated well with the grouped and separable convolutional branches respectively. The decay parameter yielded optimal network convergence at a value of 0.01 and the ADAM optimizer gave better results over SGD.
Table 3.
Observations of the cross-validation process (learning curves) recorded by the CSDB CNN with the DFL model. The rows present the evolution of prediction accuracy with epochs, degeneration of model loss, ROC curve respectively.
 |
4.6. Model training and validation
The proposed models were trained on the augmented chest X-ray lung region data and evaluated on a set of hold-out real X-ray samples. To prove model convergence on a limited test dataset, the proposed CNN is evaluated on k-fold cross-validation (k 5 folds). Of all the collected samples in Table 1, the distribution of samples into training-validation sets under each fold across target classes is split in the ratio of 4:1. The models were evaluated on various ML classification metrics, that include accuracy, precision, recall, specificity, area under ROC (AUC), and F1-score. The experimental results of the proposed CSDB CNN model are tabulated in Table 2.
Table 2.
Performance of the CSDB CNN on each validation fold.
| Folds | Precision | Recall | F1-score | Accuracy | Specificity | AUC |
|---|---|---|---|---|---|---|
| Fold1 | 90.46 | 93.53 | 91.73 | 93.94 | 97.78 | 95.66 |
| Fold2 | 88.90 | 91.97 | 90.03 | 92.47 | 97.22 | 94.60 |
| Fold3 | 89.34 | 92.69 | 90.65 | 93.09 | 97.52 | 95.10 |
| Fold4 | 89.58 | 94.63 | 91.87 | 94.07 | 97.88 | 96.25 |
| Fold5 | 88.60 | 94.06 | 91.07 | 93.55 | 97.66 | 95.86 |
| Overall Average | 89.38 | 93.38 | 91.07 | 93.42 | 97.61 | 95.49 |
The proposed CSDB CNN attained an average accuracy of 93.42% in classifying the four target classes. Particularly for the COVID-19 class, the model achieved precision, recall, F1-score, accuracy values of 95.93%, 92.50%, 94.10%, 99.57% respectively. CNN has shown good results on all the metrics with values of over 90%. A modest recall score of 93.38% asserts the reliability of the model’s predictions on unseen data. Besides, the macro AUC of 95.49% suggests a minimal classification error rate and is indicative of the model’s class distinguishability.
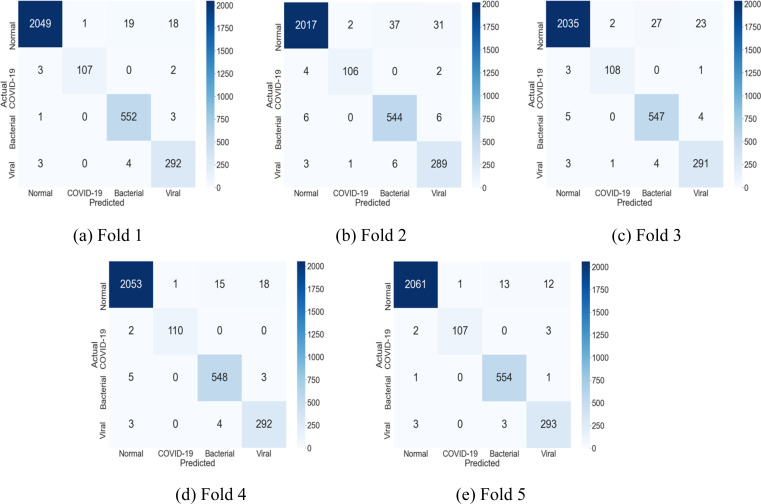
While the CSDB model qualifies well as a ML classifier, AI-assisted diagnosis and prognosis in medicine demand accurate detection and localization of the infection for clinical analysis. To enable precise detection of the infection traces on the chest X-ray modality, the DFL strategy has been proposed for the CSDB CNN. The DFL algorithm learns distinct spatial filters that are affine towards particular classes of COVID-19 or pneumonia. The results of model training and validation for the DFL-enhanced CSDB CNN are presented in Table 3, Table 4. Of the curves in Table 3, the degeneration of the loss values, and the predictive accuracy over epochs were recorded during training. The Receiver operating characteristic (ROC) curve was sketched post-training on the respective validation sets. Table 4 gives fold-wise quantitative values of accuracy, the loss for training, and validation. It also lists the area under ROC for COVID-19 class and macro-average across all target classes under each validation fold. Fig. 3 provides the confusion matrices obtained on the validation sets in the 5 folds.
Table 4.
Accuracy, Loss values for the proposed DFL embedded CSDB CNN observed on the training and validation data across 5 folds. Also, the Macro averaged Area under ROC (AUC) and AUC for the COVID-19 class are shown for each fold.
| Fold | Accuracy |
Loss |
Area under ROC (%) |
|||
|---|---|---|---|---|---|---|
| Training | Validation | Training | Validation | COVID-19 | Macro-average | |
| Fold1 | 99.70 | 98.23 | 0.0667 | 0.167 | 98.51 | 97.75 |
| Fold2 | 99.88 | 96.79 | 0.0512 | 0.237 | 97.65 | 97.27 |
| Fold3 | 99.34 | 97.61 | 0.082 | 0.179 | 98.26 | 98.16 |
| Fold4 | 99.50 | 98.33 | 0.088 | 0.159 | 98.77 | 99.09 |
| Fold5 | 99.81 | 98.72 | 0.0710 | 0.127 | 98.75 | 97.75 |
Fig. 3.
Fold-wise Confusion Matrix for the proposed DFL-enabled CSDB CNN. The values were recorded on the validation set under each fold.
From Table 3, it is clear that the model had converged well in all the 5 folds and displays an average accuracy of over 97% on the validation sets. The ROC curve measures the extent of separability of classes by drawing a trade-off between the positive class (true positive rate) and negative class (false positive rate). In a multi-class setting, ROC can be plotted for each target class by considering the non-class samples to be the negative class (one vs rest strategy). The macro average ROC curve represents all four classes and is obtained by averaging ROC values from each target class. The fold-wise macro average ROCs in Table 4 demonstrate a minimal overlap in the predictions amongst classes (lesser false positives and false negatives). The area under the ROC curve (AUC) quantifies the classifier’s ability to correctly distinguish between classes. The proposed approach has learned precise decision boundaries for the target COVID-19, which is evident from the 5-fold AUC values for the COVID-19 class. The proposed classifier’s performance was evaluated comprehensively under various ML classification metrics. Table 5 presents these evaluation metrics with values aggregated from the 5 folds.
Table 5.
Proposed DFL augmented CSDB CNN performance on the validation set for the four target classes (values are averaged across 5 folds). Also, the macro-averaged scores for each metric (computed from all classes per validation fold) are aggregated over all 5 folds.
| Classes | Precision | Recall | F1-score | Accuracy | Specificity | AUC |
|---|---|---|---|---|---|---|
| COVID-19 | 98.36 | 96.07 | 97.20 | 99.80 | 99.94 | 98.01 |
| Normal | 99.54 | 97.89 | 98.71 | 98.25 | 99.03 | 98.46 |
| Bacterial Pneumonia | 95.43 | 98.74 | 97.05 | 98.91 | 98.94 | 98.84 |
| Viral Pneumonia | 92.03 | 97.46 | 94.66 | 98.92 | 99.08 | 98.27 |
| Macro scores | 96.34 | 97.54 | 96.90 | 97.94 | 99.25 | 98.39 |
From Table 5, it can be observed that the proposed model performs excellently in detecting the COVID-19 samples as testified by the precision, recall, and F1-scores of over 95%. A high recall value is usually the desired outcome in medical applications as it can pose a bigger risk if a real infected patient is not detected. For the three pneumonia classes, the recall scores are sufficiently high to capture any possibility of the predicted sample being infected. On the other hand, the model has shown a higher precision in identifying normal (pneumonia-free) samples, which indicates that the model seldom emits fake ‘normal’ alerts. It classifies a sample to be normal only when there is very little evidence for the sample to express any pneumonia. The specificity values for COVID-19 and viral pneumonia is high, signifying the classifier’s precision in identifying samples outside the target class. The accuracy is measured in a one vs rest fashion, by deemed the samples outside a given class to be a negative sample. Considering the F1-score as an overall projection of the classifier’s performance given the trade-offs between recall and precision, the model has displayed good results for all classes.
4.7. Ablation study
To prove the effectiveness of the proposed architectures i.e. CSDB CNN and the DFL module, the methods were evaluated with reference to a baseline CNN architecture that comprises of 7 feedforward convolutional layers. Several experiments carried out as a part of ablation studies are presented in Table 6. These experimental studies investigate the individual performance enhancements offered by the CSDB and the DFL components over conventional CNN layers.
Table 6.
Classification performance of the CSDB CNN and DFL over a baseline CNN with 7 convolutional layers connected in a feedforward manner. Class-wise F1-scores and AUC values are reported for the ablation experiments. It is assumed that ‘n’ denotes the number of convolutional layers on CNN.
| Experiments | F1-score |
AUC |
Accuracy | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| COVID-19 | Normal | Bacterial Pneumonia | Viral Pneumonia | Macro average | COVID-19 | Normal | Bacterial Pneumonia | Viral Pneumonia | Macro AUC | ||
| Baseline 7-layer feedforward CNN | 73.60 | 84.48 | 69.26 | 64.78 | 73.56 | 90.29 | 84.49 | 84.75 | 83.62 | 85.78 | 79.96 |
| Baseline CNN with DFL at n-1 conv layer | 81.78 | 89.90 | 76.02 | 72.89 | 80.14 | 94.51 | 88.16 | 88.45 | 88.24 | 89.84 | 84.87 |
| CSDB CNN | 94.26 | 95.62 | 90.15 | 83.18 | 76.85 | 95.21 | 94.88 | 95.60 | 94.78 | 87.81 | 93.42 |
| CSDB CNN with DFL at n-2, n-1 conv layers | 96.86 | 98.28 | 95.50 | 94.74 | 96.34 | 98.16 | 97.99 | 97.93 | 99.10 | 98.23 | 97.35 |
| CSDB CNN with DFL at n-1 conv layer | 97.20 | 98.71 | 97.05 | 94.66 | 96.90 | 98.01 | 98.46 | 98.84 | 98.27 | 98.39 | 97.94 |
From the results presented in Table 6, the network performance gains from the two contributions can be assessed as follows:
4.7.1. Effectiveness of the CSDB CNN architecture
To validate the efficacy of the CSDB block, it is compared against a baseline CNN with seven sequentially stacked convolutional layers. X-ray features are propagation through the baseline model in a simple feedforward fashion and classified. This base model is around 80% accurate on a randomized test set. By accounting for 80% accuracy as the baseline for comparison of CNN works on the COVID-19 X-ray data, the CSDB CNN improves this score by a factor of 16.83%, purely from the architectural design perspective. The CSDB block also improves the F1-scores for all classes (esp. COVID-19) by many folds, over the baseline scores.
4.7.2. Effectiveness of the DFL module
The DFL module was tested under multiple different experimental settings. When applied to the penultimate convolutional layer in the baseline CNN, the DFL strategy boosted native CNN performance by 6.14%. It is to be noted that DFL loss can be set to optimize single or multiple Convolutional layers in the CNN. While DFL can be set on any convolutional layer in the CNN, it yields the best results when tried on the final few layers. The last layer is not chosen, as the immediate cross-entropy function updates those weights. Since CNN learn shared high-level features until the last few layers, the final layers ideally learn class distinguishing features that work well with DFL. The number of final layers to which DFL can be applied without affecting CNN’s feature mining has to be determined empirically. In the case of CSDB CNN, the DFL applied to the last (n−2)th and (n−1)th convolutional layer gave almost the same results as DFL applied to just the (n−1)th layer. For this CNN, the performance saturates when DFL is set to the utmost one convolutional layer from the last. For other very deep networks, DFL applied to multiple final layers can provide optimal performance. From the observations, it is evident that DFL has improved the CSDB model by 4.84% to attain the state of the art performance for COVID-19 detection from chest X-ray. It has also boosted the macro F1-score by 6.40%. The DFL has augmented the capabilities of the CSDB CNN by adding more discriminatory power for learning patterns unique to pneumonia classes.
4.8. Comparison with standard CNNs
Table 7 presents a comparison of the proposed work with standard CNN architectures. Extensive experiments were performed to validate the enhancements from DFL over standard architectures. Five CNN architectures listed in Table 7 were re-implemented and trained on the COVID-19 X-ray data. Further, performance improvements from DFL were studied by integrating it with the penultimate layer for each CNN. For the architectures that had utilized fully connected layers for classification, those layers were compensated with 1 x 1 convolutions. DFL was shown to improve the performance over all the backbone architectures. The DFL had brought about large leaps inaccuracy, F1 value for some models (Squeezenet, DenseNet161, VGG16), and relatively smaller gains in other cases (ResNeXt32, ResNet50).
Table 7.
Quantitative performance validation results of multiple standard CNN architectures on the COVID-19 X-ray dataset. The enhancements from DFL are evaluated by applying it to the penultimate Convolutional layer for each CNN.
| Methods | Number of parameters | Macro average precision | Macro average recall | Macro average F1-score | Accuracy | AUC |
|---|---|---|---|---|---|---|
| SqueezeNet | 728K | 67.33 | 76.91 | 70.26 | 74.92 | 84.00 |
| SqueezeNet + DFL | 72.15 | 81.10 | 75.16 | 79.34 | 86.85 | |
| VGG16 | 134M | 73.06 | 84.17 | 77.13 | 81.40 | 88.79 |
| VGG16 + DFL | 77.49 | 84.86 | 80.11 | 85.20 | 89.77 | |
| ResNet50 | 23M | 85.50 | 91.68 | 88.03 | 90.93 | 94.25 |
| ResNet50 + DFL | 91.49 | 95.15 | 93.15 | 94.79 | 96.62 | |
| ResNeXt 32 × 4d | 23M | 86.91 | 92.87 | 89.46 | 92.24 | 95.07 |
| ResNeXt 32 × 4d + DFL | 91.69 | 95.35 | 93.34 | 94.96 | 96.76 | |
| DenseNet161 | 26M | 88.96 | 93.64 | 90.98 | 93.25 | 95.62 |
| DenseNet161 + DFL | 95.11 | 97.04 | 96.03 | 97.15 | 97.99 | |
| CSDB CNN | 15M | 82.97 | 89.28 | 85.37 | 88.42 | 92.57 |
| CSDB CNN + DFL | 96.34 | 97.54 | 96.90 | 97.94 | 98.39 | |
Of all the compared CNNs, DenseNet161 results were the closest to the CSDB model, but it had utilized a far bigger number of parameters in contrast. This large performance margin can be attributed to the dense connectivity pattern and strengthened flow of gradients in DenseNets. With DFL, DenseNet results were advanced by a factor of 4.18%. The Squeezenet model had under fitted the X-ray data (failed to converge on the training set), which led to a sub-optimal performance on the test set. But with DFL enabled, the model’s class separability was enhanced and resulted in 5.9% better scores. VGG16 on the other hand had overfitted the X-ray data and gave rise to 85% accuracy on the validation set. DFL had positively impacted the model fitting to an extent and improved VGG16 validation results by 4.67%. The ResNet and ResNeXt models yielded equivalent F1-scores of 88% and 89.5%. The ResNeXt model utilized 32 convolutional skip connection paths between blocks with an internal channel dimension of 4 in each path. By integrating DFL onto the model architecture, ResNeXt produced marginally better F1 than DFL enabled ResNet. The DFL boosted F1-scores for ResNeXt and ResNet was enhanced by 4.34% and 5.82% respectively. On the whole, the proposed CSDB CNN augmented with DFL achieved the best overall performance under reduced parameters.
4.9. Visual interpretation of the trained model features
Table 8 presents three gradient-based visual representations that show chest X-ray regions weighed by their propensity towards the target classes: (1) class saliency maps (2) guided backpropagation (3) Grad-CAM [52]. These techniques capture regions of saliency, as pixel response to class outcome is quantified by its gradient.
Table 8.
Visualization of the most salient regions on the X-ray using three gradient-based input response weighing methods. Samples on the top left, top right, bottom left, bottom right correspond to COVID-19, normal, bacterial, and viral pneumonia classes respectively. The color bars were suitably chosen to best project the sensitivities of these heat maps in the most characteristic way.
The saliency map is formed by calculating the gradient of the target class probability for spatial pixels on the input image . It can be observed that the COVID-19 X-ray sample in Table 8 has registered the most impact in the central region of the lung. In the normal sample case, CNN had attended to almost all regions of the X-ray to look for regions that can pose defects. In the other two pneumonia cases, the regions are spread out in different parts of the lungs.
In the guided backpropagation approach, neurons that produce no effects or negative effects against a target class are masked out. It is achieved by refining the feature flow during the forward pass (ReLU activated feature maps) and gradient flow in the backward pass (clipping gradients to the positive range), thereby resulting in lesser noisy gradients. For the specific COVID-19 sample in Table 8, guided backpropagation has suggested precise infection hotspots, explicitly pointing to top areas in the lungs. For the normal X-ray, most of the gradients had zeroed out during the backpropagation, so it did not trace any identifiable region on the input X-ray. For viral and bacterial pneumonia, regions around the center and corner of the lungs are marked to have produced a positive gradient response towards the target class.
The gradient class-activation map (Grad-CAM) is a channel-wise weighted averaging of feature map gradients at a convolutional layer. The channel weights are determined by average pooling spatial gradient values at that channel. The representational Grad-CAM maps in Table 8 were computed at the penultimate convolutional layer. The COVID-19 map shows an intense band of activations in regions roughly aligning with the saliency map. For the normal sample, gradient weighted features are mild and are uniformly spread in all directions of the X-ray. The bacterial and viral pneumonia hotspots are shown to occur around the mid regions and the lower zones in the lungs.
Thus, the visual modes are inter-related to an extent but are uniquely characterized in their approach towards finding regions of saliency.
To verify if the proposed methodology has mapped dedicated filter sets for specific classes, the top responding 10% filters (524 K out of 524 288 filters) in the penultimate layer are identified for every chest X-ray sample in the validation set. When compared across samples in the same class, it was observed that intersection over union (IoU) values of the all the filter sets within the class was 0.985, 0.971, 0.963 and 0.930 for the COVID-19, normal, bacterial and viral pneumonia classes respectively. It was also seen that between classes, the intersection of filters was minimal for all the classes: 0.017, 0.037, 0.063, 0.036 respectively. Hence it is evident that the model has converged well in learning unique filter sets for each class. The top 500 such 3-by-3 filters (sorted by weighted gradient response) are shown for each class in Fig. 4. COVID-19 filters appear to be subtly oriented around the tainted regions of the X-ray. Filters from normal class samples seem to be neutrally responsive overall X-ray regions. Bacterial and viral pneumonia filters respond to input templates that seem to vary widely over different parts of the X-ray.
Fig. 4.
Visualization of the template patterns captured by a distinct set of filters for each class. (For visual purposes, top 500 filters are shown for every target class).
4.10. Performance analysis
Table 9 presents a performance comparison of the proposed work with existing works. To draw a valid comparison between the proposed study and other COVID-19 studies, the related works should have performed multi-class (COVID-19/pneumonia) classification on the same/similar chest X-ray dataset with AI techniques. Only works that have experimented on the same COVID-19/pneumonia datasets as the current work (listed in Table 1) are compared. The compared works have performed classification in three classes (COVID-19, normal, pneumonia) or four classes (COVID-19, normal, bacterial, viral pneumonia). By limiting to these classes, the works share more or less the same level of complexity. The proposed work has yielded the best F1-score and accuracy for COVID-19 detection as well as overall pneumonia detection compared to most of the existing works. This is due to the result of learning patterns to identify class samples uniquely.
Table 9.
Performance Analysis of the proposed work with current research works that have utilized the same chest X-ray data sources for COVID-19, Pneumonia images as the current work.
| S No | Source | Methodology | Class | Number of COVID-19 Test samples | Approx. parameters | Overall F1-score (%) |
Overall accuracy (%) | F1-score for COVID-19 (%) |
COVID-19 class accuracy (%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | Ozturk et al. [39] | DarkNet-19 based CNN | 3 | 25 | 1.164M | 87.40 | 87.02 | 88.00 | 87.02 |
| 2 | Mangal et al. [34] | CheXNet based CNN | 4 | 30 | 26M | 92.30 | 87.2 | 96.77 | 99.6 |
| 3 | Khan et al. [33] | Transfer learning with Xception net | 4 | 70 | 33M | 89.8 | 89.6 | 95.61 | 96.6 |
| 4 | Wang and Wong [42] | Customized CNN architecture | 3 | 100 | 11.75M | 93.13 | 93.33 | 94.78 | 96.67 |
| 5 | Apostolopoulos and Mpesiana [31] | Transfer learning with MobileNetV2 | 4 | 222 | 3.4M | 93.80 | 94.72 | 90.50 | 96.80 |
| 6 | Farooq and Hafeez [30] | ResNet50 based CNN | 4 | 8 | 25.6M | 96.88 | 96.23 | 100.0 | 100.0 |
| 7 | Proposed Work | Customized CNN with distinctive filter learning module | 4 | 112 | 15.6M | 96.90 | 97.94 | 97.20 | 99.80 |
It is to be noted that Farooq and Hafeez [30] had reported 100% COVID-19 detection results only on a small test set size of 8 COVID-19 samples and displayed an overall accuracy of 96.23%. In contrast, the proposed work has validated on 112 samples robustly under 5-fold cross-validation and has shown better 4-class accuracy. Though [31] has tested with more samples, the proposed work has outperformed [31] by a large margin in terms of F1-score and accuracy. Of all the compared works, the proposed work achieves the best trade-off between network size (characterized by several learnable parameters) and performance (in terms of accuracy and F1-score).
5. Conclusion
In this work, a novel CNN architecture and a network learning paradigm were proposed for classifying COVID-19 from chest X-rays. CNN uses channel-shuffling and dual residual skip connections for learning robust features. It also integrates dual branching with multiple convolutional layers with for raising diverse contextual features. The CNN architecture efficiently aggregates variably sized receptive fields and sustains stable gradient flow across blocks. The proposed distinctive convolutional filter learning module utilizes the softmax weighing over the first-order gradients of the activated feature map to derive significant features. By considering weighted gradients as a measure of filter’s affinity towards the predicted class, different sets of filters are optimized to learn unique patterns for each pneumonia class. To alleviate the problem of the smaller available dataset, the proposed system trains on augmented samples of lung segments. The presented CSDB and DFL components were subjected to ablation studies under different experimental settings to validate the effectiveness of the proposed approaches. The efficiency of the DFL module was also evaluated on five standard CNN backbone architectures. From the results, it is evident that the model has converged optimally and has learned differentiating patterns for each pneumonia class. As future work, the model can be extended to work with sub-types of pneumonia, other lung diseases to learn definitive patterns that can help radiologists.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- 1.Coronavirus disease . WHO; 2019. (COVID-19) Situation Report – 176. https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200714-covid-19-sitrep-176.pdf?sfvrsn=d01ce263_2. (Accessed 15 July 2020) [Google Scholar]
- 2.Coronavirus disease . WHO; 2019. (COVID-19) Situation Report – 73. https://www.who.int/docs/default-source/coronaviruse/situation-reports/20200402-sitrep-73-covid-19.pdf. (Accessed 24 April 2020) [Google Scholar]
- 3.2020. WHO Q & A On coronaviruses (COVID-19) https://www.who.int/news-room/q-a-detail/q-a-coronaviruses. (Accessed 24 April 2020) [Google Scholar]
- 4.2020. Landscape analysis of therapeutics. https://www.who.int/blueprint/priority-diseases/key-action/Table_of_therapeutics_Appendix_17022020.pdf?ua=1.(Accessed 9 May 2020) [Google Scholar]
- 5.2020. Immunity passports in the context of COVID-19. https://www.who.int/news-room/commentaries/detail/immunity-passports-in-the-context-of-covid-19. (Accessed 9 May 2020) [Google Scholar]
- 6.WHO; 2020. Coronavirus Disease (COVID-19) Advice for Public. https://www.who.int/emergencies/diseases/novel-coronavirus-2019/advice-for-public .(Accessed 9 May 2020) [Google Scholar]
- 7.2020. WHO Lists two COVID-19 tests for emergency use. https://www.who.int/news-room/detail/07-04-2020-who-lists-two-covid-19-tests-for-emergency-use. (Accessed 2 June 2020) [Google Scholar]
- 8.Wong H.Y.F. Frequency and distribution of chest radiographic findings in COVID-19 positive patients. Radiology. 2019 doi: 10.1148/radiol.2020201160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.2020. Advice on the use of point-of-care immunodiagnostic tests for COVID-19. https://www.who.int/news-room/commentaries/detail/advice-on-the-use-of-point-of-care-immunodiagnostic-tests-for-covid-19. (Accessed 2 June 2020) [Google Scholar]
- 10.Wootton D., Feldman C. The diagnosis of pneumonia requires a chest radiograph (x-ray)–yes, no or sometimes? Pneumonia. 2014;5(S1):1–7. doi: 10.15172/pneu.2014.5/464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Chandra Tej Bahadur, Verma Kesari. Proceedings of 3rd International Conference on Computer Vision and Image Processing. Springer; Singapore: 2020. Pneumonia detection on chest X-ray using machine learning paradigm. [Google Scholar]
- 12.Ambita A.A.E., Boquio E.N.V., Naval P.C., Jr. Intelligent Information and Database Systems. Springer International Publishing; 2020. Locally adaptive regression kernels and support vector machines for the detection of pneumonia in chest X-ray images; pp. 129–140. [Google Scholar]
- 13.Varela-Santos S., Melin P. Intuitionistic and Type-2 Fuzzy Logic Enhancements in Neural and Optimization Algorithms: Theory and Applications. Springer International Publishing; 2020. Classification of x-ray images for pneumonia detection using texture features and neural networks; pp. 237–253. [Google Scholar]
- 14.Archit Khatri. Trends in Communication, Cloud, and Big Data. Springer; Singapore: 2020. Pneumonia identification in chest X-ray images using EMD; pp. 87–98. [Google Scholar]
- 15.H. Sharma, J.S. Jain, P. Bansal, S. Gupta, Feature Extraction and Classification of Chest X-ray Images Using CNN to Detect Pneumonia, in: 2020 10th International Conference on Cloud Computing, Data Science & Engineering (Confluence), Noida, India, 2020, pp. 227–231.
- 16.Wu H., Xie P., Zhang H., Li D., Cheng M. IFS; 2020. Predict Pneumonia with Chest X-Ray Images Based on Convolutional Deep Neural Learning Networks; pp. 1–15. [Google Scholar]
- 17.Fathurahman M., Fauzi S.C., Haryanti S.C., Rahmawati U.A., Suherlan E. Advances in Intelligent Systems and Computing. Springer International Publishing; 2019. Implementation of 1D-convolution neural network for pneumonia classification based chest X-ray image; pp. 181–191. [Google Scholar]
- 18.Nakrani N.P., Malnika J., Bajaj S., Prajapati H., Jariwala V. Advances in Intelligent Systems and Computing. Springer Singapore; 2020. Pneumonia identification using chest X-ray images with deep learning; pp. 105–112. [Google Scholar]
- 19.Saraiva A.A. 2019. Models of learning to classify X-ray images for the detection of pneumonia using neural networks. [Google Scholar]
- 20.Stephen Okeke. An efficient deep learning approach to pneumonia classification in healthcare. J. Healthcare Eng. 2019;2019 doi: 10.1155/2019/4180949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Sabyasachi Chakraborty, et al. Detection of Pneumonia from Chest X-rays using a Convolutional Neural Network Architecture. in: International conference on future information & communication engineering., Vol .11, No. 1, 2019.
- 22.Z. Li, et al. PNet: An Efficient Network for Pneumonia Detection, 2019 12th International Congress on Image and Signal Processing, in: BioMedical Engineering and Informatics, CISP-BMEI, Suzhou, China, 2019, pp. 1–5.
- 23.Rahman Tawsifur. Transfer learning with deep convolutional neural network (CNN) for pneumonia detection using chest X-ray. Appl. Sci. 2020;10(9):3233. [Google Scholar]
- 24.Chouhan Vikash. A novel transfer learning based approach for pneumonia detection in chest X-ray images. Appl. Sci. 2020;10(2):559. [Google Scholar]
- 25.Chhikara Prateek. Advances in Bioinformatics, Multimedia, and Electronics Circuits and Signals. Springer; Singapore: 2020. Deep convolutional neural network with transfer learning for detecting pneumonia on chest X-rays; pp. 155–168. [Google Scholar]
- 26.Chen X. PIN92 pediatric bacterial pneumonia classification through chest x-rays using transfer learning. Value Health. 2019;22:S209–S210. [Google Scholar]
- 27.Kh Tohidul Islam, et al. A Deep Transfer Learning Framework for Pneumonia Detection from Chest X-ray Images.
- 28.Narayanan Barath Narayanan, Davuluru Venkata Salini Priyamvada, Hardie Russell C. Medical Imaging 2020: Imaging Informatics for Healthcare, Research, and Applications, Vol. 11318. International Society for Optics and Photonics; 2020. Two-stage deep learning architecture for pneumonia detection and its diagnosis in chest radiographs. [Google Scholar]
- 29.Bhandary Abhir. Deep-learning framework to detect lung abnormality–A study with chest X-ray and lung CT scan images. Pattern Recognit. Lett. 2020;129:271–278. [Google Scholar]
- 30.Farooq Muhammad, Hafeez Abdul. 2020. Covid-resnet: a deep learning framework for screening of covid19 from radiograph. arXiv preprint arXiv:2003.14395. [Google Scholar]
- 31.Apostolopoulos I.D., Mpesiana T.A. Covid-19: automatic detection from X-ray images utilizing transfer learning with convolutional neural networks. Phys. Eng. Sci. Med. 2020 doi: 10.1007/s13246-020-00865-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Apostolopoulos I.D., Aznaouridis S.I., Tzani M.A. Extracting possibly representative COVID-19 biomarkers from X-ray images with deep learning approach and image data related to pulmonary diseases. J. Med. Biol. Eng. 2020;40(3):462–469. doi: 10.1007/s40846-020-00529-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Khan A.I., Shah J.L., Bhat M.M. Coronet: A deep neural network for detection and diagnosis of COVID-19 from chest x-ray images. Comput. Methods Programs Biomed. 2020 doi: 10.1016/j.cmpb.2020.105581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mangal A., Kalia S., Rajgopal H., Rangarajan K., Namboodiri V., Banerjee S., Arora C. 2020. CovidAID: COVID-19 detection using chest X-ray. arXiv preprint arXiv:2004.09803. [Google Scholar]
- 35.Mittal A. Detecting pneumonia using convolutions and dynamic capsule routing for chest X-ray images. Sensors. 2020;20(4):1068. doi: 10.3390/s20041068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kumar Acharya A., Satapathy R. A deep learning based approach towards the automatic diagnosis of pneumonia from chest radio-graphs. Biomed. Pharmacol. J. 2020;13(1):449–455. [Google Scholar]
- 37.Sarkar R., Hazra A., Sadhu K., Ghosh P. Computer Vision and Machine Intelligence in Medical Image Analysis. Springer Singapore; 2019. A novel method for pneumonia diagnosis from chest X-ray images using deep residual learning with separable convolutional networks; pp. 1–12. [Google Scholar]
- 38.Jaiswal Amit Kumar. Identifying pneumonia in chest X-rays: A deep learning approach. Measurement. 2019;145:511–518. [Google Scholar]
- 39.Ozturk T., Talo M., Yildirim E.A., Baloglu U.B., Yildirim O., Rajendra Acharya U. Automated detection of COVID-19 cases using deep neural networks with X-ray images. Comput. Biol. Med. 2020;121 doi: 10.1016/j.compbiomed.2020.103792. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Saiz F., Barandiaran I. COVID-19 detection in chest X-ray images using a deep learning approach. Int. J. Interact. Multimed. Artif. Intell. 2020;6(2):4. [Google Scholar]
- 41.Pereira R.M. Covid-19 identification in chest X-ray images on flat and hierarchical classification scenarios. Comput. Methods Programs Biomed. 2020;194 doi: 10.1016/j.cmpb.2020.105532. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Wang L., Wong A. 2020. COVID-Net: A tailored deep convolutional neural network design for detection of COVID-19 cases from chest radiography images. arXiv preprint arXiv:2003.09871. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Bhagat Vedant, Bhaumik Swapnil. Augmentation using Generative Adversarial Networks for Pneumonia classification in chest xrays. 2019 Fifth International Conference on Image Information Processing; ICIIP; IEEE; 2019. [Google Scholar]
- 44.Cohen J.P., Morrison P., Dao L. 2020. COVID-19 image data collection. arXiv:2003.11597, https://github.com/ieee8023/covid-chestxray-dataset. (Accessed 3 June 2020) [Google Scholar]
- 45.2020. COVID-19 Radiopaedia. https://radiopaedia.org/articles/covid-19-3?lang=us. (Accessed 3 June 2020) [Google Scholar]
- 46.Chung A.G. 2020. COVID CHest X-ray dataset. https://github.com/agchung/Figure1-COVID-chestxray-dataset. (Accessed 3 June 2020) [Google Scholar]
- 47.2020. Actualmed COVID-19 chest X-ray dataset. https://github.com/agchung/Actualmed-COVID-chestxray-dataset. (Accessed 12 July 2020) [Google Scholar]
- 48.2020. Italian Society of medical and interventional radiology (SIRM) https://www.sirm.org/en/category/articles/covid-19-database/page/1/. (Accessed 3 June 2020) [Google Scholar]
- 49.2020. RSNA Pneumonia Detection challenge. https://www.kaggle.com/c/rsna-pneumonia-detection-challenge/data. (Accessed 3 June 2020) [Google Scholar]
- 50.2020. Chest X-ray images (Pneumonia) https://www.kaggle.com/paultimothymooney/chest-xray-pneumonia/version/1. (Accessed 3 June 2020) [Google Scholar]
- 51.2020. Lung fields segmentation on CXR images using CNN. https://github.com/imlab-uiip/lung-segmentation-2d. (Accessed 3 June 2020) [Google Scholar]
- 52.Selvaraju R.R., Cogswell M., Das A., Vedantam R., Parikh D., Batra D. Grad-CAM: Visual explanations from deep networks via gradient-based localization. Int. J. Comput. Vis. 2019;128(2):336–359. [Google Scholar]