Abstract
Diffuse optical imaging and tomography based upon frequency-domain near-infrared spectroscopy (fdNIRS) is used to noninvasively measure tissue structure and function through quantitative absolute measurements of tissue optical absorption and scattering. Here we describe how utilizing a silicon photomultiplier (SiPM) detector for fdNIRS improves performance. We discuss the operation of SiPMs, how they differ from other fdNIRS photodetectors, and show theoretically that SiPMs offer similar sensitivity to photomultiplier tube (PMT) detectors while having a higher dynamic range and lower cost, size, and operating voltage. With respect to avalanche photodiode (APD) detectors, theoretical and experimental data shows drastically increased signal to noise ratio performance, up to 25dB on human breast, head, and muscle tissue. Finally, we extend the dynamic range (∼10dB) of the SiPM through a nonlinear calibration technique which reduced absorption error by a mean 16 percentage points.
1. Introduction
Frequency-domain near infrared spectroscopy (fdNIRS) provides measurements of tissue optical absorption and scattering properties which have been used extensively to characterize tissue structure and function in preclinical and clinical studies [1–4]. Unlike continuous-wave NIRS, fdNIRS yields quantitative absolute tissue optical properties that can be compared between and within subjects over time. Furthermore, the additional information afforded by the phase of the photon density waves (PDWs) that interrogate tissue in fdNIRS can theoretically lead to deeper depth penetration [5,6]. However, because fdNIRS photodetectors (PD) require sufficient sensitivity and bandwidth (BW) of at least 50 MHz to measure the highly attenuated intensity-modulated light remitted from tissue, maximum source-detector separations (SDS) in fdNIRS are typically lower compared to both continuous-wave and time-domain NIRS methods. This results in shallower depth sensitivity for fdNIRS and can negate the increased depth afforded by phase information [6–10]. Improving fdNIRS depth sensitivity will not only lead to more applications of this promising modality, but improve performance in established areas such as interrogating deeper neurocortical layers for functional NIRS (fNIRS) and improving sensitivity to deeper and smaller tumors for breast cancer diagnosis and treatment monitoring [5,11].
We have recently shown that fdNIRS with silicon photomultiplier (SiPM) detectors increases sensitivity to low light levels by 1.5-2 orders of magnitude thus enabling longer SDS in phantoms and human tissue compared to a similarly-sized avalanche photodiode (APD) [12–14]. However, SiPMs operate in a fundamentally different manner compared to traditional fdNIRS PDs. They are composed of up to thousands of individual detector pixels or microcells that are operated above avalanche breakdown in Geiger mode. The two-terminal SiPM output signal is a sum of the individual microcell responses. Therefore, the SiPM introduces two practical complications: 1) a choice of detector characteristics (e.g. pixel size and number as well as recovery time) that will have a significant effect on fdNIRS sensitivity and BW and 2) lower-than-typical linear dynamic range which can negatively impact measurements of tissue with varying attenuation [14]. Although our previous work showcased some of the advantages of using SiPMs in fdNIRS, the ways in which SiPM characteristics and nonlinearity affect fdNIRS performance and optical property recovery is largely unexplored.
Therefore, in this work, we present the first systematic study of the challenges and optimization of SiPM use in fdNIRS, including theoretical analysis, tissue-simulating phantom validation, and in vivo proof of performance. We first describe PD detector choice in fdNIRS and how fundamental SiPM characteristics (i.e. microcell size, microcell number, recovery time, and dark count rate) affect fdNIRS performance (i.e. SNR and BW). We then analyze non-linear SiPM response to high level fdNIRS intensity-modulated light, and demonstrate a calibration approach that extends SiPM usable dynamic range for accurately recovering optical properties. Finally, we show that SiPM-based fdNIRS offers superior sensing performance including higher SNR and SDS in phantom and in vivo human studies.
2. fdNIRS detectors
fdNIRS relies on measuring the amplitude and phase of highly-attenuated intensity-modulated light in the radio frequency (RF) range (50-1000MHz). In a typical noninvasive implementation, light emitted from the source on the skin is multiply scattered through tissue and a small (<∼10−6) fraction is collected by a detector some distance away (∼30mm). Higher SDS leads to increased depth sensitivity since longer pathlength photons are more likely to be scattered to greater depths. The resulting low detected optical power (µW to pW) makes it difficult to precisely resolve the amplitude and especially the phase of the modulated signal. Because source power is limited by safety concerns, fdNIRS system performance is typically limited by PD sensitivity.
Photomultiplier tubes (PMTs) and avalanche photodiodes (APDs) are commonly employed as fdNIRS detectors due to their intrinsic amplification. PMTs offer extremely high intrinsic gain (104-109) and low dark current, but they are relatively large, sensitive to magnetic fields, and require very high reverse bias (∼1kV). Linear-mode APDs have a lower gain (∼100x), but are much smaller, exhibit high linear dynamic range, and require somewhat lower bias (∼200-500V). Both PD types require a large (>7cm3) high voltage converter limiting practicality in handheld, wearable, or high-density fdNIRS configurations, which are emerging as the frontier in tissue optical spectroscopy applications [9,15].
SiPM (also known as multi-pixel photon counter, MPPC) is a more recently developed PD technology [16–18] that has been evaluated for use in positron emission tomography and spectroscopy applications [19–21], among others. SiPMs are composed of a parallel-connected array of microcell APDs operated in Geiger mode (i.e. each microcell is a single photon avalanche diode, SPAD). SiPMs offer high intrinsic gain ∼105-107 resulting in SNR performance similar to that of PMTs, but at a much lower reverse bias (∼20-50V). This allows for extremely small high voltage modules (∼0.1cm3) and represent an enabling technology for ultra-small fdNIRS systems. The primary drawbacks of SiPMs include a lower BW compared to a similarly-sized photoactive area APDs and PMTs and nonlinear response at high signal levels, which is described in detail in the next section. A comparison of PD technologies and their associated general characteristics is shown in Table 1. Further, although SiPM bandwidth appears insufficient for fdNIRS operation, we demonstrate that its extremely high gain extends its usable bandwidth to approximately 200 MHz. Table 1 also provides rough costs for only the PD sensors while complete PD modules are much more expensive (s) depending on the detector type and module type (e.g. cooled vs un-cooled). PMT modules tend to be the most expensive, followed by APD modules and SiPM modules.
Table 1. Comparison of fdNIRS photodetectors with approximate specifications.
| SiPM | PMT | APD | |
|---|---|---|---|
| Photosensitivity @ SNR=20 (W) | 10f | 10f | 10p |
| Dynamic Range (dB) | 50 | 80 | 90 |
| Bandwidth, 3dB a (MHz) | 10 | 100-500 | 100-1000 |
| Detector Cost, Sensor Only () | 50 | 500 | 100 |
| Detector Size (mm3) | 5-100 | 5-80k | 5-100 |
| Bias Voltage (V) | 50 | 1000 | 250 |
| HVPS Cost () | 50 | 200 | 200 |
| HVPS Size (mm3) | 100 | 7000 | 7000 |
3. SiPM operation and characteristics
3.1. Basic structure and operation
SiPMs are two terminal devices that operate as a single-pixel detector due to the parallel connection of all individual SPAD microcells. SiPM microcells are typically square with side lengths on the order of 10-100m. Due to the necessity to isolate the individual microcells, in addition to the limitations of fabrication, SiPMs contain dead space between microcells. The resulting ratio of photoactive area to total area is described by the fill-factor (FF), which correlates with microcell size. The number of microcells which can be fabricated in a given SiPM photoactive area is therefore related to both microcell size and fill factor. Microcell size affects electrical characteristics as the surface area determines microcell capacitance. This is important because the recovery time of a microcell after photon activation is limited by the RC time constant of the microcell and quenching resistor.
Each photon absorbed by a microcell results in an electrical output pulse whose amplitude is determined by the SiPMs overvoltage, gain, and output resistance. Microcells which are biased (VBias) above its breakdown voltage (VBr) by an overvoltage (VOV) such that are called Geiger-mode APDs (GM-APD). In this condition, a photoelectron will initiate a self-sustained avalanche process until quenched by a resistor placed in series with the GM-APD [23,24]. The quenching resistor reduces the voltage across the GM-APD to extinguish the avalanche process. GM-APD output pulses are characterized by an initial fast rise—due to the rapid discharge of stored charge through the quenching resistor—followed by the much slower RC-mediated decay back to zero as the capacitor recharges [25]. When a microcell is fully recharged, a photon detection event is complete and the voltage across the GM-APD is returned to the bias voltage. At this point a generated photoelectron is capable of producing a full amplitude output pulse. However, if the process of recharging the GM-APD is interrupted by a photoelectron prior to a complete recharge, the resulting output pulse will have a reduced amplitude according to the lower overvoltage in the GM-APD at the time of the photon’s arrival. If multiple microcells absorb photons simultaneously then the SiPM output signal is the sum of each individual pulse due to the parallel connection of all microcells in an array. In this way, SiPMs may be used as an analog PD to detect time varying signals.
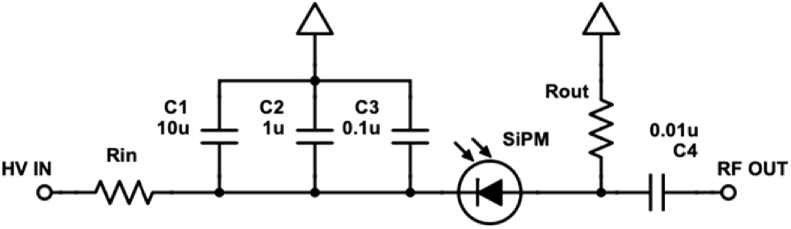
In addition to the quenching resistor, external circuit elements such as input and output resistors (Fig. 2) can impact the SiPMs output. Input resistors are used to limit the maximum current delivered but can reduce the overvoltage, and thus photon detection efficiency and gain. A series output resistance is also commonly used to convert SiPM current pulses into a detectable voltage. The output resistance adds series resistance to the SiPMs microcells which further reduces the time-varying overvoltage and increases microcell recovery time.
Fig. 2.
SiPM bias and fdNIRS interface circuit.
3.2. Photon detection efficiency
Photon detection efficiency (PDE) is the probability that a photon impinging upon an SiPM produces a photoelectron that results in an output pulse. PDE is a function of fill factor and quantum efficiency (QE), which are static properties of the SiPM, as well as the triggering probability, which is the probability that a photoelectron initiates an output pulse. The triggering probability, and thus PDE, is a strong and complicated function of overvoltage [26]. PDE tends to zero at 0V overvoltage because there is no avalanche process and saturates at an upper limit equal to the product of FF and QE at sufficiently high overvoltage.
3.3. Noise
Sources of noise in an SiPM are either uncorrelated or correlated with respect to arriving photons [27]. Uncorrelated noise is caused by thermally generated carriers that produce a dark count rate or dark current. Noise of the correlated type includes afterpulsing and optical crosstalk [28]. Afterpulsing is the result of trapped charge that is released after a current pulse is initially generated. This produces yet another current pulse unrelated to a photon detection event, although recent advancements in fabrication techniques have reduced afterpulsing to <1%. Optical crosstalk is the process by which a single photon causes more than one microcell to generate an output pulse. The probability of optical crosstalk varies depending upon microcell size and tends to have probabilities of occurrence between 1-10%. The excess noise factor (F) is a metric which describes these noise sources. In SiPMs, excess noise results largely from crosstalk events and has an extremely low value as compared to APDs and PMTs (see Table 2).
Table 2. Physical and optical characteristics of PDs used in analytical comparison. All models are manufactured by Hamamatsu Photonics (Shizuoka Japan).
| Type/Model #: | SiPM | SiPM | SiPM | SiPM | PMT | APD |
|---|---|---|---|---|---|---|
| S13360-3025 | S13360-1325 | S13360-1350 | S13360-1375 | R928 | S2384 | |
| Photosensitive Area (mm2) | 4.2 | 0.8 | 1.3 | 1.4 | 6.0 a | 7.1 |
| Microcell Size (µm) | 25 | 25 | 50 | 75 | - | - |
| Microcell Number | 14,400 | 2,668 | 667 | 285 | - | - |
| Fill Factor (%) | 47 | 47 | 74 | 82 | - | - |
| Recovery Time (ns) | 40 | 40 | 120 | 160 | - | - |
| Operating Voltage (V) | 58 | 58 | 56 | 56 | 1250 | 150 |
| Temp. Coeff. of Vbr (V/°C) | 0.054 | 0.054 | 0.054 | 0.054 | - | 0.65 |
| PDE 650/850nm (%) | 13/4 | 13/4 | 20/6 | 25/7 | 8/0.5 | 82/70 |
| Gain | 0.7 × 106 | 0.7 × 106 | 1.7 × 106 | 4 × 106 | 1 × 106 | 60 |
| Dark Current (nA) | 45 | 8 | 25 | 62 | 1 | 1 |
| Excess Noise Factor | 1.01 | 1.01 | 1.03 | 1.07 | 1.2 b | 3.98 |
3 mm fiber bundle (0.85 fill factor)
[27]
4. Theoretical and experimental evaluation of fdNIRS photodetectors
4.1. Theoretical evaluation
In this section we theoretically evaluate SNR, the most critical metric for fdNIRS, for a typical PMT, APD (linear-mode), and proposed SiPM. SNR is accurately described by an analytic equation which accounts for PD gain and noise [27–33]:
| (1) |
where is the photocurrent generated by a signal, is dark current, M is gain, F is the excess noise factor, B is the measurement bandwidth, T is temperature, is the load resistance, q is the charge of an electron, and k is the Boltzmann constant. Signal current takes the form:
| (2) |
where is the optical power associated with the wavelength () of incident light, is photon detection efficiency, h is Planck’s constant, and c is the speed of light. Minor differences in SNR for each PD type are attributed to dark current:
| (3) |
| (4) |
This is generally due to which type of dark current is predominant in a given PD and whether the dark current is subject to multiplication via the avalanche region. One critical assumption in using Eq. (1) is that the PD being analyzed is operating within its bandwidth and can respond to the modulation without incurring loss.
We used this framework to compare performance for a typical PD of each type commonly employed in fdNIRS. These PDs are described in Table 2. In Fig. 1(A-B), the SNR of each PD was calculated across a wide range of optical input power, beyond what is typical in an fdNIRS measurement (∼10−12-10−6W). For the SiPM and PMT, the calculation was limited to a maximum detectable optical power. For the PMT, the maximum optical power is dictated by the maximum allowable anode current. For the SiPM, we restricted this initial analysis to the linear dynamic range (i.e. ∼1 × 10−7W, Fig. 4(A)), which is discussed further in section 6. In order to make a realistic comparison that reflects typical fdNIRS instrument, the APD and SiPM were assumed to be in direct contact with the tissue, while the PMT was coupled with a 3mm fiber bundle assuming 0.85 fill factor. SNR was determined for two wavelengths, 650 and 850nm, representing a range utilized in fdNIRS for hemodynamic measurements. Because the SiPM has a lower bandwidth than typically used for fdNIRS (Table 1) and Eq. (1) assumes that each PD is operated within its BW, SiPM SNR was reduced by 5dB in Fig. 1(A-B) which corresponds to a frequency of 50MHz [12]. This factor depends greatly on the specific SiPM and frequency being considered. With this in mind, Fig. 1(A-B) shows that the SiPM has similar SNR to the PMT both of which are superior to the APD at low optical powers relevant in fdNIRS. The APD gains an SNR advantage at optical powers above ∼10−9W.
Fig. 1.
Analytical models comparing SNR of common PDs used in fdNIRs. (A)-(B) SNR at 50 MHz for each PD type versus incident light power at 650 and 850 nm respectively. The SiPM has 25m microcells (S13360-3025). (C)-(D) SNR versus incident light power for a 1s light pulse demonstrating the range of linearity for 3 SiPMs with different microcell sizes (S13360-30XX).
Fig. 4.
Output signal as a function of input light power and bandwidth for SiPMs with varied microcell sizes (A-B) as well as input and output resistances (C-D). Vertical lines in (A) and (C) indicate where the ND filter was changed.
Next, we examined SiPM saturation at high optical power. After a microcell has been activated by photon absorption, the microcell requires time to restore overvoltage and produce another equal amplitude output pulse. When a microcell is struck with another photon before this recovery time, a diminished pulse is produced by the microcell due to decreased overvoltage and therefore PDE and gain. Therefore, SiPM response becomes nonlinear beyond a given incident photon rate, due to the combination of finite recovery time and a limited number of microcells. This phenomenon is described by simple analytical equations for a pulsed light source which cover two distinct cases:1) when the pulse width is less than the recovery time of a microcell and 2) when the pulse width is greater than the recovery time of a microcell [25,32,34]. The models are:
| (5) |
| (6) |
where is the number of pixels that produce an output pulse, is the total number of microcells, is the number of impinging photons, is the photon detection efficiency, is the pulse width in seconds, and is the microcell recovery time.
Although pulsed light is different than the sinusoidal signals encountered in fdNIRS, these simple analytical equations provide useful insight into SiPM performance and allows us to compare SiPM characteristics. Further justification for this approximation is found in Ref. [14]. Figure 1(C-D) compares three SiPM detectors with different microcell sizes exposed to a 1s light pulse. As expected, SiPMs with larger microcell sizes have a greater SNR across the linear range. This results from an increase in gain and PDE associated with a higher FF. However, a simultaneous increase in dark current partially negates the SNR improvement resulting in an SNR advantage of only ∼1dB for each 25m step in microcell size. Furthermore, we see that the linear range increases with decreasing microcell size. This is due to the higher number of microcells in the smaller microcell devices (for the same overall area). In other words, there are more available microcells able to respond to subsequent photons with maximum gain. The optical power at saturation is ∼14x higher for 25m microcells as compared to 50m microcells and ∼60x greater as compared to 75m microcells. Overall this data suggests that, for a given active area, choosing a smaller microcell size maximizes dynamic range with little tradeoff in SNR at fdNIRS power levels.
4.2. Experimental evaluation
We evaluated a family of three SiPMs with different microcell size (S13360-13xx, Table 2) for their SNR and BW in fdNIRS. By using a single family of related SiPMs, other variations in design and fabrication which may impact performance are minimized. From our theoretical analysis, we expected that different microcell sizes would impact SNR and BW through its effect on total microcell number, recovery time, PDE, gain, and dark count rate.
The bias circuit design used in this work is shown in Fig. 2. Standard 50Ω connectors/cabling are used to directly connect the RF output to a miniature fdNIRS system described previously [35]. It is important to note that the design of this circuit can greatly impact SiPM performance. The input resistor (Rin) is placed in series with the SiPM in order to limit maximum current draw through the device to prevent damage and can have an impact on SNR and BW by reducing applied high voltage (HV) to the SiPM. The capacitors C1-C3 serve as filtering capacitors to reduce ripple and voltage spikes resulting from the HV power supply. The output resistor (Rout) serves to convert PD signal current into a detectable voltage and can also impact SNR and BW by affecting microcell recovery time via an altered RC time constant. C4 is a blocking capacitor used to allow only RF signal to reach the fdNIRS measurement unit.
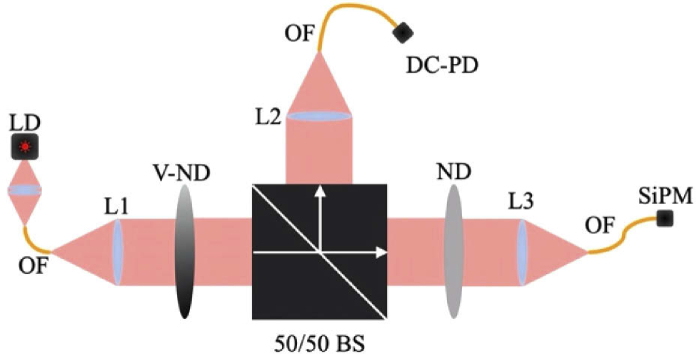
The custom optical set-up used to evaluate SiPM performance is shown in Fig. 3. The measurement unit was designed to control and monitor the RF modulated light power incident on the SiPM. A 660nm laser diode (L660P120, Thorlabs) was driven via a DC current source and modulated using a network analyzer (TR1300, Copper Mountain Technologies). Fiber-coupled laser light was collimated with an aspheric lens, passed through a motor-driven variable attenuation wheel (NDC-50C-4, Thorlabs) and a 50/50 beam splitter, and directed to either a reference photodiode (DC-PD-S150C, Thorlabs) or an SiPM. The reference PD was used for measuring absolute optical power providing linear data for comparison to nonlinear SiPM data. The light was fiber-coupled again using aspheric lenses to easily deliver it to the detectors. Because of the high SiPM gain (compared to none on the DC-PD), light in the SiPM arm was first passed through an additional neutral density filter. The variable and fixed neutral density (ND) filters were chosen to evaluate a range of optical powers commensurate with fdNIRS. However, because of the difference in gain between the reference photodiode and the SiPM, three data sets were taken for each SiPM using a different fixed ND filter for each to avoid SiPM overcurrent while remaining above the noise floor of the DC-PD. The data presented is therefore a fusion of 3 individual data sets per device, resulting in a slight discontinuity at the interface of optical power ranges.
Fig. 3.
Custom optical measurement apparatus used to measure SiPM performance. LD – laser diode, OF – optical fiber, L – lens, V-ND – variable neutral density filter, DC-PD –direct current photodiode, 50/50 BS – 50/50 beam splitter, ND – neutral density filter.
Figures 4(A and B) compare the SiPM signal output as a function of optical power and modulation frequency. As expected from the analytical results, larger microcell sizes provide a larger output signal at low optical powers but exhibit a reduced linear dynamic range. SiPMs with smaller microcell sizes have a superior BW, which is attributed to their shorter recovery times. The results in Fig. 4(A) (particularly for the 25m SiPM) show similar trends to what was predicted in Fig. 1(C). Both show saturation effects occurring near 10nW with noise floors near 1pW with the experimental values diminished as expected. A stark difference from theory is the gradual trend towards saturation observed experimentally compared to abrupt saturation. This difference comes from limitations of the analytic model which does not account for microcells’ ability to produce attenuated output pulses before the complete recovery time is passed. From this data, we conclude that SiPMs with smaller microcell sizes are more favorable for fdNIRS despite a lower signal amplitude at lower optical powers. This is because the increased linearity and BW are preferred to accommodate different probe configurations. However, one may choose the higher sensitivity SiPM (larger microcell size) if it is known the signal level will remain low due to long SDS or high tissue attenuation.
Figures 4(C) and (D) compare the effect of input and output resistance on signal output for a single SiPM (75m microcell size). As expected, a larger output resistance resulted in a larger output signal, while reducing BW. A smaller input resistor increased SiPM overvoltage, thus marginally increasing output signal and BW. For this reason, going forward in this work we choose to use zero input resistance with a ∼50 output resistor to provide a larger output signal, minimize BW reduction, and simplify impedance matching.
5. Extending SiPM dynamic range
A challenge of using SiPMs for fdNIRS is their nonlinear response at high optical powers. If not properly identified and/or accounted for, this nonlinearity could translate into significant errors in optical property estimation. There are two primary ways to overcome this limitation: 1) identify the onset of signal saturation (i.e. monitoring amplitude) and respond accordingly by reducing source power, increasing SDS, or discarding the data; or 2) apply a nonlinear calibration technique to “correct” the data and extend the dynamic range. Although simple, the first approach may not be feasible in some fdNIRS applications. For example, it is common to use a calibration phantom with known optical properties to correct for the fdNIRS instrument response function (IRF) [36,37]. With an SiPM, one would have to be careful to match phantom attenuation closely to the measurement target. This may not be possible for measurements taken continuously over time where significant variations in tissue optical attenuation are expected, such as during a vascular occlusion. Similarly, multi-distance fdNIRS measurements require a PD (or multiple PDs) that can respond accurately over a large dynamic range.
Therefore, we evaluated how nonlinear calibration of SiPM response can extend its dynamic range and improve fdNIRS measurement accuracy. This requires recording the SiPMs amplitude response over its entire operating range from the noise floor to saturation and then applying a nonlinear correction on subsequent data. Phase is not affected and does not need correction. This characterization could be accomplished with the experimental setup in Fig. 3, but requires careful attention to optical coupling such that light fills the SiPM active area and activates a similar number of microcells that would be used in the fdNIRS implementation. Instead, we sampled the SiPM nonlinearity by measuring eight tissue-simulating phantoms at four wavelengths (660, 690, 785, and 830nm) and 5 SDSs (22, 28, 36, 42, and 48mm) which offered wide and detailed sampling of attenuation. Some data points are excluded due to poor SNR. This was carried out with both the SiPM and a highly-linear APD (C5658 module with S12060-10, Hamamatsu Photonics) to generate the calibration curve in Fig. 5. For this work, we chose to fit a simple 2nd order polynomial function to the data to generate an analytical relationship that qualitatively fit the data well. However, in future work, we will investigate a functional form that better fits SiPM behavior approaching the expected linear response at low optical power. The inverse of this function is used to correct subsequent raw amplitude data from an fdNIRS measurement, effectively translating non-linear SiPM amplitude into linear APD amplitude. When using phantom-based calibration for the IRF, both the calibration phantom data and the sample data are corrected. This technique assumes that SiPM response does not change over time, which is the same assumption commonly applied to single phantom-based “linear” calibration for the IRF. Additionally, any linear PD, regardless of responsivity or gain, can be used as the reference because fdNIRS measurements, whether phantom calibration-based or multi-distance, are inherently relative. In other words, the y-axis in Fig. 5 is arbitrary. This also practically means that a calibration curve generated with one source wavelength can be applied to other wavelengths because the wavelength dependence of detector responsivity does not affect the correction. Finally, it is important to note that this approach cannot overcome the intrinsic reduction of amplitude precision that occurs when operating in the nonlinear region. One may be able to practically “undo” a nonlinear response at its onset, but the measurement will lose precision as the detector response saturates (though the phase will still be accurate).
Fig. 5.
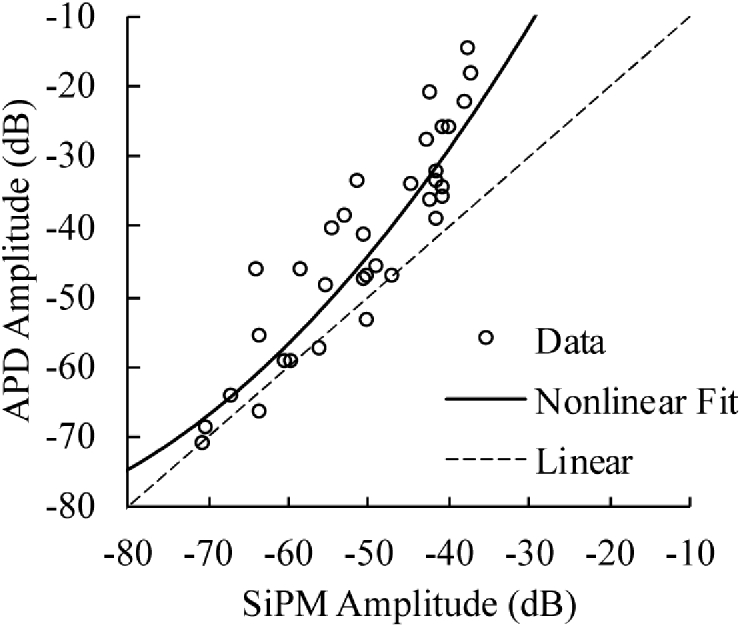
Nonlinear calibration curve extracted from multiple tissue simulating phantom measurements. Dashed line indicates what would be a perfectly linear device.
To evaluate this approach, the multi-wavelength optical properties of multiple silicone-based tissue-simulating phantoms were measured using both an SiPM and APD PD. The 3 × 3mm 10m microcell SiPM (S12572-010P, Hamamatsu Photonics) was biased to 65V per Fig. 2 without further amplification. SiPM internal gain is 1.35 × 105. The APD module (C5658 module with S12060-10 APD, Hamamatsu Photonics) included 40 dB preamplification and was biased for an intrinsic gain of 100 resulting in a total APD gain of 1 × 104. The PDs were connected to a custom fdNIRS device developed at the University of California Irvine [35] equipped with four excitation wavelengths (659, 687, 786, 829nm). Optical properties were calculated by fitting (nonlinear corrected and uncorrected) IRF-calibrated fdNIRS amplitude and phase, for all frequencies (50-500MHz) where SNR >3dB, to the P1 semi-infinite approximation of the radiative transport equation [38,39] using Levenberg-Marquardt least squares minimization. Due to a limited number of available phantoms, the target phantoms were included in the set that was used to generate the calibration curve. However, the generation of the nonlinear calibration curve did not consider the optical properties of the phantoms, and here we are evaluating the accuracy of the downstream optical property recovery. The nonlinear correction was only applied to the initial raw amplitude data.
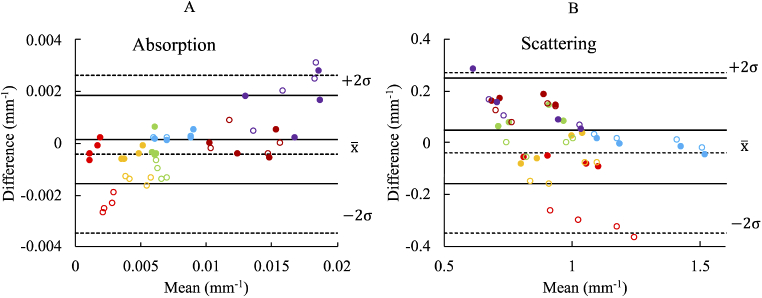
Optical property recoveries at a fixed SDS of 28mm are compared in Bland-Altman format (Fig. 6) with the compounded results tabulated in Table 3 wherein the SiPM has been calibrated in two ways: 1) standard IRF-calibration (uncorrected) and 2) with nonlinear plus IRF correction. Overall, six tissue simulating phantoms at four discrete wavelengths were measured resulting in a total of 24 independent data points covering a wide range of optical properties. The corrected data shows significant improvements in both absorption and scattering accuracy for phantoms with lower absorption (indicated by red and yellow on /Fig. 6), where detector signals are in the highly nonlinear range. Mid-range absorption phantoms (blue and red) do not need much correction since they already fall within the linear range. Figure 6(A) uncorrected absorption data suggests that there is a systematic bias in the SiPM measured optical properties (i.e. a linear dependence of absorption difference with the mean absorption). This is because absorption is underestimated by the SiPM at lower absorptions due to high signal saturation and the increasing effects of noise are apparent at high absorption. This trend largely disappears in the corrected case, because the low attenuation results are corrected, while the high attenuation deviations remain because of the low SNR. Overall, the corrected absorption data has a mean absolute value of the difference of 10.0% / 0.0006mm−1 compared to 26.0% / 0.0013mm−1 without correction. Reduced scattering exhibits a more modest improvement (11.0% / 0.09mm−1 corrected vs. 12.2% / 0.12mm−1 uncorrected) because it is more sensitive to phase, which is not adjusted with the nonlinear calibration technique. More variation is observed in the phantom with the highest attenuation (purple), but this is primarily due to low SNR, and not the nonlinear calibration. When the “purple” phantom is removed, the mean absolute vale of the absorption difference improves to 8.4% / 0.0003mm−1 and 7.7% / 0.07mm−1 for absorption and reduced scattering, respectively.
Fig. 6.
Bland-Altman comparison of measured optical absorption and reduced scattering coefficients for SiPM and APD. Colors represent a single tissue simulating phantom of six in total. Filled circles (solid lines) represent corrected SiPM data based on our nonlinear calibration method while unfilled circles (dashed lines) represent SiPM data based on a standard linear calibration. is the sample mean, while is the mean plus or minus two standard deviations (95% confidence interval). Each data point is the mean of ten measurements; standard deviations are not shown as the error bars lie within the data markers.
Table 3. Compounded results of Bland-Altman PD comparison.
| Corrected | Uncorrected | ||||
|---|---|---|---|---|---|
| Mean |Diff.| | STD |Diff.| | Mean |Diff.| | STD |Diff.| | ||
| µa | (%) | 10.0 | 12.2 | 26.0 | 33.1 |
| (mm−1) | 0.0006 | 0.0006 | 0.0013 | 0.0009 | |
| µs’ | (%) | 11.0 | 10.1 | 12.2 | 10.2 |
| (mm−1) | 0.09 | 0.07 | 0.12 | 0.11 | |
6. Improved in vivo fdNIRS performance with SiPM detectors
We evaluated fdNIRS SNR resulting from SIPM use for noninvasive measurements of several human tissue types in vivo. Measurements were acquired with the same fdNIRS system used to acquire data for Fig. 6 with the addition of an amplifier (ZX60-3018G-S+, Mini-Circuits) while using the SiPM which places the signal level within the dynamic range for the fdNIRS system. We used the system separately with the APD and SiPM to measure the breast and forehead (over the right prefrontal cortex) of a 28 year old healthy female adult and the gastrocnemius calf muscle of a 28 year old healthy male adult. These tissue sites were chosen because of their different composition. In particular, the gastrocnemius muscle of the male volunteer was well-developed with minimal subcutaneous fat and therefore exhibited extreme optical attenuation. Ethical approval for this study was obtained from the Institutional Review Board of the University of Notre Dame, and the participants gave written informed consent prior to the study.
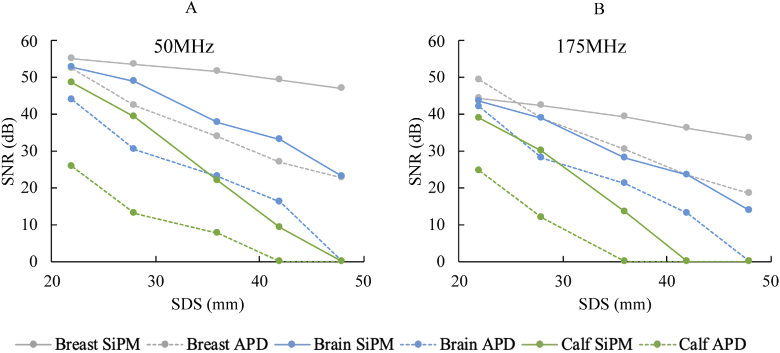
In vivo SNR analysis as a function of SDS are shown in Fig. 7. To assure a fair comparison, an offset in SNR (11.55dB) was subtracted from the SiPM data to account for its larger photoactive area equal to , where A is the photoactive area of the detector. At 50MHz, the SiPM has an SNR advantage on all tissue types and at all SDSs ranging up to 25dB. We expect, from our theoretical analysis, that an SiPM with larger microcells would lead to even greater SNR advantage. At 175MHz, we observe the tradeoff between sensitivity and bandwidth for each detector. The SiPM excels at long SDS and over the highly attenuating calf due its higher gain. However, at short SDS in less-attenuating breast and brain tissue, the SiPM is inferior because its lower bandwidth offsets the advantage in gain. Nonetheless there is ample signal available to make robust, accurate optical property measurements.
Fig. 7.
In vivo SNR as a function of SDS comparing an APD (dashed) and SiPM (solid). SNR is taken on three tissue types common to fdNIRS measurements: breast (grey), brain (blue), and calf muscle (green). Multiple frequencies are taken with 50 and 175 MHz shown in (A) and (B) respectively.
7. Discussion and conclusion
In this work we conducted a systematic theoretical and experimental investigation into the use of SiPM detectors for fdNIRS. We explored how characteristics unique to SiPM design such as microcell size and number of microcells, and bias circuit design affects fdNIRS performance. We also developed a simple-to-apply technique to extend the linear dynamic range of SiPM response in fdNIRS. We hope that this work provides useful guidance to others hoping to integrate SiPM technology in fdNIRS systems.
The intensity-modulated signals associated with fdNIRS makes the SiPM detector an unexpected choice since SiPMs are typically used in single-photon counting and other applications requiring extremely low light level detection. Furthermore, at first consideration, SiPM recovery time and resulting BW appears to be insufficient for fdNIRS though our previous and current findings prove this to be untrue [12]. Indeed, SiPMs have been explored for use in time-domain [40–43] and continuous-wave NIRS [8] which require sensitive single-photon counting and low-BW detection, respectively. Zimmerman et al. found that SiPMs resulted in a drastic increase in SNR that led to >2x increase in measurable SDS in a continuous-wave device [8]. Similarly, Dalla Mora et al. found that SiPMs incorporated into a time-domain system exhibited superior timing resolution that led to improved optical property recoveries and increased depth sensitivity [44]. SiPMs have also been demonstrated to have similar or greater sensitivity than PMTs in laser scanning microscopy [44].
Our work shows that, despite a lower overall BW and noticeable nonlinear response at higher power levels, SiPMs can provide significant advantages for fdNIRS use compared to APDs and PMTs. We showed that SiPM gain is high enough to overcome loss resulting from operating above its intended BW. Specifically, SiPMs provide up to 25dB more SNR than APDs on highly-attenuating human tissue, which allows for longer SDSs and increased depth sensitivity in vivo. Our simulations suggest that they will yield similar performance to PMTs at a fraction of the size, cost, and bias voltage. Furthermore, we demonstrate that non-linearities can be corrected to improve the dynamic range of the overall system by ∼10dB, though operating too far into this regime limits measurement precision as signal saturation occurs.
Our study has led us to the following conclusions for SiPM use in fdNIRS. First, for general fdNIRS instrumentation intended to be used on various tissue types and with probe designs, SiPMs with smaller and more numerous microcells are favorable because of their larger dynamic range at the expense of a slightly reduced SNR. However, if sensitivity to low optical power is paramount, then a larger microcell size should be considered. Second, one should be aware of the nonlinear SiPM response possible at higher fdNIRS optical powers. SiPMs should be thoroughly characterized to identify at what power level (i.e. fdNIRS amplitude) the nonlinear response becomes unacceptable. The nonlinear effects can be mitigated by reducing the signal level (e.g. decreasing optical power or increasing SDS) or through the nonlinear calibration technique we described in this work. We demonstrated that the nonlinear calibration technique could improve accuracy of optical absorption estimation, but, as expected, has less of an effect on reduced scattering. Since fdNIRS phase is not affected by the nonlinear response, phase-only measurement approaches could be considered. Finally, the size of the SiPM and ancillary power supply makes it well-suited for use in compact and wearable fdNIRS systems. Since these applications present other challenges not investigated here (e.g. varying temperature and optical coupling), we plan to develop new fdNIRS probes to assess SiPM performance in these exciting applications.
Acknowledgments
The authors would like to acknowledge SensL and Hamamatsu Photonics for technical discussions on SiPMs and their implementation in biomedical sensing applications.
Funding
Advanced Diagnostics and Therapeutics (AD&T) Discovery Fund, University of Notre Dame (Notre Dame, IN).
Disclosures
VJK and TDO disclose patents related to fdNIRS technology. TDO discloses ownership of NearWave, Inc, which is producing a commercial fdNIRS device.
VJK: University of Notre Dame (P), TDO: NearWave, Inc. (I, E, P)
References
- 1.O’Sullivan T. D., Leproux A., Chen J.-H., Bahri S., Matlock A., Roblyer D., McLaren C. E., Chen W.-P., Cerussi A. E., Su M.-Y., Tromberg B. J., “Optical imaging correlates with magnetic resonance imaging breast density and reveals composition changes during neoadjuvant chemotherapy,” Breast Cancer Res. 15(1), R14 (2013). 10.1186/bcr3389 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Taroni P., Quarto G., Pifferi A., Ieva F., Paganoni A. M., Abbate F., Balestreri N., Menna S., Cassano E., Cubeddu R., “Optical identification of subjects at high risk for developing breast cancer,” J. Biomed. Opt. 18(6), 060507 (2013). 10.1117/1.JBO.18.6.060507 [DOI] [PubMed] [Google Scholar]
- 3.Eggebrecht A. T., Ferradal S. L., Robichaux-Viehoever A., Hassanpour M. S., Dehghani H., Snyder A. Z., Hershey T., Culver J. P., “Mapping distributed brain function and networks with diffuse optical tomography,” Nat. Photonics 8(6), 448–454 (2014). 10.1038/nphoton.2014.107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.O’Sullivan T. D., Cerussi A. E., Cuccia D. J., Tromberg B. J., “Diffuse optical imaging using spatially and temporally modulated light,” J. Biomed. Opt. 17(7), 0713111 (2012). 10.1117/1.JBO.17.7.071311 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Doulgerakis M., Eggebrecht A. T., Dehghani H., “High-density functional diffuse optical tomography based on frequency-domain measurements improves image quality and spatial resolution,” Neurophotonics 6(03), 1 (2019). 10.1117/1.NPh.6.3.035007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fantini S., Sassaroli A., “Frequency-Domain Techniques for Cerebral and Functional Near-Infrared Spectroscopy,” Front. Neurosci. 14, 1–18 (2020). 10.3389/fnins.2020.00300 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Veesa J. D., Dehghani H., “Functional near infrared spectroscopy using spatially resolved data to account for tissue scattering: A numerical study and arm-cuff experiment,” J. Biophotonics 12(10), e201900064 (2019). 10.1002/jbio.201900064 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Zimmermann R., Braun F., Achtnich T., Lambercy O., Gassert R., Wolf M., “Silicon photomultipliers for improved detection of low light levels in miniature near-infrared spectroscopy instruments,” Biomed. Opt. Express 4(5), 659–666 (2013). 10.1364/BOE.4.000659 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Pifferi A., Contini D., Mora A. D., Farina A., Spinelli L., Torricelli A., “New frontiers in time-domain diffuse optics, a review,” J. Biomed. Opt. 21(9), 091310 (2016). 10.1117/1.JBO.21.9.091310 [DOI] [PubMed] [Google Scholar]
- 10.Torjesen A., Istfan R., Roblyer D., “Ultrafast wavelength multiplexed broad bandwidth digital diffuse optical spectroscopy for in vivo extraction of tissue optical properties,” J. Biomed. Opt. 22(3), 036009 (2017). 10.1117/1.JBO.22.3.036009 [DOI] [PubMed] [Google Scholar]
- 11.Tromberg B. J., Shah N., Lanning R., Cerussi A., Espinoza J., Pham T., Svaasand L., Butler J., “Non-invasive in vivo characterization of breast tumors using photon migration spectroscopy,” Neoplasia 2(1-2), 26–40 (2000). 10.1038/sj.neo.7900082 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kitsmiller V. J., O’Sullivan T. D., “Next-generation frequency domain diffuse optical imaging systems using silicon photomultipliers,” Opt. Lett. 44(3), 562–565 (2019). 10.1364/OL.44.000562 [DOI] [PubMed] [Google Scholar]
- 13.Kitsmiller V. J., Campbell C., O’Sullivan T. D., “Silicon Photomultipliers Increase Signal to Noise Ratio in Frequency Domain Diffuse Optical Spectroscopy of Human Muscle,” in Biophotonics Congress: Biomedical Optics 2020 (Translational, Microscopy, OCT, OTS, BRAIN) (2020), Paper TTh4B.3 (The Optical Society, 2020), p. TTh4B.3. [Google Scholar]
- 14.Kitsmiller V. J., O’Sullivan T. D., “Fundamental considerations for integrating silicon photomultipliers in frequency domain diffuse optical spectroscopy,” in Proceedings of SPIE 11274, Physics and Simulation of Optoelectronic Devices XXVII (SPIE-Intl Soc Optical Eng, 2020). [Google Scholar]
- 15.Zhao H., Cooper R. J., “Review of recent progress toward a fiberless, whole-scalp diffuse optical tomography system,” Neurophotonics 5(01), 1 (2017). 10.1117/1.NPh.5.1.011012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Renker D., “New trends on photodetectors,” Nucl. Instrum. Methods Phys. Res., Sect. A 571(1-2), 1–6 (2007). 10.1016/j.nima.2006.10.016 [DOI] [Google Scholar]
- 17.Dolgoshein B., Balagura V., Buzhan P., Danilov M., Filatov L., Garutti E., Groll M., Ilyin A., Kantserov V., Kaplin V., Karakash A., Kayumov F., Klemin S., Korbel V., Meyer H., Mizuk R., Morgunov V., Novikov E., Pakhlov P., Popova E., Rusinov V., Sefkow F., Tarkovsky E., Tikhomirov I., “Status report on silicon photomultiplier development and its applications,” Nucl. Instrum. Methods Phys. Res., Sect. A 563(2), 368–376 (2006). 10.1016/j.nima.2006.02.193 [DOI] [Google Scholar]
- 18.Buzhan P., Dolgoshein B., Filatov L., Ilyin A., Kantzerov V., Kaplin V., Karakash A., Kayumov F., Klemin S., Popova E., Smirnov S., “Silicon photomultiplier and its possible applications,” Nucl. Instrum. Methods Phys. Res., Sect. A 504(1-3), 48–52 (2003). 10.1016/S0168-9002(03)00749-6 [DOI] [Google Scholar]
- 19.Cates J. W., Bieniosek M. F., Levin C. S., “Highly multiplexed signal readout for a time-of-flight positron emission tomography detector based on silicon photomultipliers,” J. Med. Imaging 4(1), 011012 (2017). 10.1117/1.JMI.4.1.011012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Il Kwon S., Ferri A., Gola A., Berg E., Piemonte C., Cherry S. R., Roncali E., “Reaching 200-ps timing resolution in a time-of-flight and depth-of-interaction positron emission tomography detector using phosphor-coated crystals and high-density silicon photomultipliers,” J. Med. Imaging 3(4), 043501 (2016). 10.1117/1.JMI.3.4.043501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zhang C., Zhang L., Yang R., Liang K., Han D., “Time-Correlated Raman and Fluorescence Spectroscopy Based on a Silicon Photomultiplier and Time-Correlated Single Photon Counting Technique,” Appl. Spectrosc. 67(2), 136–140 (2013). 10.1366/12-06736 [DOI] [PubMed] [Google Scholar]
- 22.Biggio I. J., Fantini S., Quantitative Biomedical Optics, 1st ed. (Cambridge University Press, 2016). [Google Scholar]
- 23.AdvanSiD , “Introduction to SiPMs, Rev 2,” (2014).
- 24.Piemonte C., Gola A., “Overview on the main parameters and technology of modern Silicon Photomultipliers,” Nucl. Instrum. Methods Phys. Res., Sect. A 926, 2–15 (2019). 10.1016/j.nima.2018.11.119 [DOI] [Google Scholar]
- 25.Jha A. K., Van Dam H. T., Kupinski M. A., Clarkson E., “Simulating silicon photomultiplier response to scintillation light,” IEEE Trans. Nucl. Sci. 60(1), 336–351 (2013). 10.1109/TNS.2012.2234135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Buzhan P., Dolgoshein B., Ilyin A., Kantserov V., Kaplin V., Karakash A., Pleshko A., Popova E., Smirnov S., Volkov Y., Filatov L., Klemin S., Kayumov F., “An Advanced Study of Silicon Photomultiplier,” ICFA Instrum. Bull. 717–728 (2001).
- 27.Retière F., “MPPC response simulation and high speed readout optimization,” IEEE Nucl. Sci. Symp. Conf. Rec. 2197–2200 (2009). [Google Scholar]
- 28.Serra N., Ferri A., Gola A., Pro T., Tarolli A., Zorzi N., Piemonte C., “Characterization of new FBK SiPM technology for visible light detection,” J. Instrum. 8(03), P03019 (2013). 10.1088/1748-0221/8/03/P03019 [DOI] [Google Scholar]
- 29.Saleh B. E. A., Teich M. C., Fundamentals of Photonics, Third (Wiley, 2019). [Google Scholar]
- 30.Adamo G., Parisi A., Stivala S., Tomasino A., Agrò D., Curcio L., Giaconia G. C., Busacca A., Fallica G., “Silicon photomultipliers signal-to-noise ratio in the continuous wave regime,” IEEE J. Sel. Top. Quantum Electron. 20(6), 284–290 (2014). 10.1109/JSTQE.2014.2346489 [DOI] [Google Scholar]
- 31.Sensl and ON Semiconductor Application Note , “Silicon PhotoMultiplier (SiPM) Signal to Noise Ratio,” (2018). https://www.onsemi.com/pub/Collateral/AND9794-D.PDF
- 32.Ghassemi A., Sato K., Kobayashi K., Ohashi Y., Enomoto Y., Adachi Y., “Hamamatsu Photonics Technical Note: MPPC,” (n.d.).
- 33.Hamamatsu Photonics , “Photomultiplier Tubes Basics and Applications Third Edition,” (2007).
- 34.Pulko J., Schneider F. R., Velroyen A., Renker D., Ziegler S. I., “A Monte-Carlo model of a SiPM coupled to a scintillating crystal,” J. Instrum. 7(02), P02009 (2012). 10.1088/1748-0221/7/02/P02009 [DOI] [Google Scholar]
- 35.No K.-S., Kwong R., Chou P. H., Cerussi A., “Design and testing of a miniature broadband frequency domain photon migration instrument,” J. Biomed. Opt. 13(5), 050509 (2008). 10.1117/1.2998473 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Fishkin J. B., Coquoz O., Anderson E. R., Brenner M., Tromberg B. J., “Measurements of Normal and Malignant Tissue Optical Properties in a Human Subject,” Appl. Opt. 36(1), 10–20 (1997). 10.1364/AO.36.000010 [DOI] [PubMed] [Google Scholar]
- 37.Pham T. H., Coquoz O., Fishken J. B., Anderson E., Tromberg B. J., “Broad bandwidth frequency domain instrument for quantitative tissue optical spectroscopy,” Rev. Sci. Instrum. 71(6), 2500–2513 (2000). 10.1063/1.1150665 [DOI] [Google Scholar]
- 38.Fishkin J. B., Fantini S., VandeVen M. J., Gratton E., “Gigahertz photon density waves in a turbid medium: Theory and experiments,” Phys. Rev. E 53(3), 2307–2319 (1996). 10.1103/PhysRevE.53.2307 [DOI] [PubMed] [Google Scholar]
- 39.Haskell R. C., Svaasand L. O., Tsay T.-T., Feng T.-C., McAdams M. S., Tromberg B. J., “Boundary conditions for the diffusion equation in radiative transfer,” J. Opt. Soc. Am. A 11(10), 2727–2741 (1994). 10.1364/JOSAA.11.002727 [DOI] [PubMed] [Google Scholar]
- 40.Di Sieno L., Zouaoui J., Hervé L., Pifferi A., Farina A., Martinenghi E., Derouard J., Dinten J.-M., Mora A. D., “Time-domain diffuse optical tomography using silicon photomultipliers: feasibility study,” J. Biomed. Opt. 21(11), 116002 (2016). 10.1117/1.JBO.21.11.116002 [DOI] [PubMed] [Google Scholar]
- 41.Re R., Martinenghi E., Mora A. D., Contini D., Pifferi A., Torricelli A., “Probe-hosted silicon photomultipliers for time-domain functional near-infrared spectroscopy: phantom and in vivo tests,” Neurophotonics 3(4), 045004 (2016). 10.1117/1.NPh.3.4.045004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Puszka A., Di Sieno L., Dalla Mora A., Pifferi A., Contini D., Boso G., Tosi A., Hervé L., Planat-Chrétien A., Koenig A., Dinten J.-M., Hebden J. C., Varela M., Magazov S., Everdell N., Gibson A., Meek J., Austin T., Yusof R. M., Hillman E. M. C, Delpy D. T., Arridge S. R., Meek J. H., Wyatt J. S., “Time-resolved diffuse optical tomography using fast-gated single-photon avalanche diodes,” J Biophotonics 1(170), 200–203 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Dalla Mora A., Martinenghi E., Contini D., Tosi A., Boso G., Durduran T., Arridge S., Martelli F., Farina A., Torricelli A., Pifferi A., Dolgoshein B., Balagura V., Buzhan P., Danilov M., Filatov L., Garutti E., Groll M., Ilyin A., Kantserov V., Kaplin V., Karakash A., Kayumov F., Klemin S., Korbel V., Meyer H., Mizuk R., Morgunov V., Novikov E., Pakhlov P., Popova E., Rusinov V., Sefkow F., Tarkovsky E., Tikhomirov I., Kantzerov V., Smirnov S., Eggebrecht A. T., Ferradal S. L., Robichaux-Viehoever A., Hassanpour M. S., Dehghani H., Snyder A. Z., Hershey T., Culver J. P., “Fast silicon photomultiplier improves signal harvesting and reduces complexity in time-domain diffuse optics,” Nucl. Instruments Methods Phys. Res. Sect. A Accel. Spectrometers, Detect. Assoc. Equip 563(2), 6–27 (2006). [DOI] [PubMed] [Google Scholar]
- 44.Giacomelli M. G., “Evaluation of silicon photomultipliers for multiphoton and laser scanning microscopy,” J. Biomed. Opt. 24(10), 1 (2019). 10.1117/1.JBO.24.10.106503 [DOI] [PMC free article] [PubMed] [Google Scholar]