Abstract
Light sheet fluorescence microscopy (LSFM) has become an indispensable tool in biomedical studies owing to its depth-sectioning capability and low photo-bleaching. The axial resolution in LSFM is determined mainly by the thickness of the illumination sheet, and a high numerical-aperture lens is thus preferred in the illumination to increase the axial resolution. However, a rapid divergence of the illumination beam limits the effective field-of-view (FoV), that provides high-resolution images. Several strategies have been demonstrated for FoV enhancement, which involve the use of Bessel or Airy beams, for example. However, the generation of these beams requires complicated optical setup or phase filters with continuous phase distributions, which are difficult to manufacture. In contrast, a binary phase filter (BPF) comprising concentric rings with 0 or π phases produces a response similar to its continuous original and is easy to realize. Here, we present a novel form of LSFM that integrates BPFs derived from two representative axi-symmetric aberrations, including phase axicon and spherical aberrations, to improve the imaging performance. We demonstrate that these BPFs significantly increase the FoV, and those derived from axicon generate self-reconstructing beams, which are highly desirable in imaging through scattering specimens. We validate its high-contrast imaging capability over extended FoV by presenting three-dimensional images of microspheres, imaginal disc of Drosophila larva, and Arabidopsis.
1. Introduction
Light sheet fluorescence microscopy (LSFM), a recently re-discovered technique since its first inception by Siedentopf and Zsigmondy [1], has been highlighted as a suitable technology for three-dimensional (3D) fluorescence imaging, owing to its superior depth-sectioning ability and low photo-toxicity [2,3]. The depth-sectioning of LSFM is attributed to its unique configuration, i.e., orthogonally placed illumination optics relative to the imaging setup. Such a configuration enables full-field detection of fluorescence coming from the focal plane that is illuminated by the “sheet” of light. The axial resolution in LSFM is thus determined mainly by the thickness of the illumination sheet. Therefore, it is desirable to employ a high numerical-aperture () focusing lens in the illumination to obtain high axial resolution. However, the effective field-of-view (FoV) decreases in such cases, as the illumination beam with the high NA lens diverges rapidly. This leads to a trade-off between the depth-sectioning capability (or axial resolution) and lateral FoV.
Non-diffracting beams, such as Bessel [4,5] and Airy beams [6], have been exploited to extend the FoV in LSFM. Such beams are characterized by their elongated sharp focus, which significantly enlarges the FoV, while maintaining the high axial resolution or depth-sectioning ability. However, the generation of these beams require pupil filters of complex and continuous phase distributions, which are difficult and expensive to manufacture, or involve complicated optical setup with low light throughput. Several other approaches for FoV extension have been developed, which involve the use of aspheric lenses [7] and tiling multiple light sheets [8,9]. However, implementation of these strategies may increase the complexity and cost of the LSFM setup.
The binary phase filter (BPF) [10,11] represents a specialized class of optical elements used for improving three-dimensional focal behaviors in diverse applications. These optical structures are characterized by their unique configuration of alternating 0-π phases arranged in concentric rings. As light transmits these specially configured rings, the resulting phase distribution generate complex light interactions in the focal plane of the lens, which can be tuned to enhance the resultant beam behavior, such as maximizing the axial depth-of-focus (DoF). BPFs provide several advantages over other alternatives, such as axicon [12], annular aperture [13], and cubic phase masks [6], especially because discrete 0-π configurations of BPFs enable better manufacturable fabrication processes such as photo-lithography, wet-etching, and thin-film deposition [14,15]. Owing to its manufacturability and tunabilty, the use of a BPF can be considered a desirable approach to improve the FoV [16]. Here, we present specially designed axi-symmetric BPFs as critical elements that can significantly improve the LSFM performance. It has been suggested that the binarization of axi-symmetric optical aberrations produces a group of BPFs that generate elongated foci [17]. We employ a spatial light modulator (SLM) to implement various BPFs, and integrate these BPFs into LSFM (BPF-LSFM) to demonstrate high-resolution fluorescence imaging with significantly improved FoV. In addition, we note that the BPFs derived from phase axicon produce self-reconstructing beams, which is highly desirable for imaging through scattering media. The proposed BPF-LSFM prototype enables high-resolution fluorescence imaging over 7.7x and 11x larger FoV than the clear pupil. Resistance to scattering in some forms of BPF-LSFM is also demonstrated through experiments by presenting the images of microspheres, Drosophila larva imaginal disc, and Arabidopsis.
2. Results
2.1. BPFs derived from axicon and spherical aberrations
Our BPFs are designed via binarization of defocused axicon and spherical aberrations [17]. Unlike previously reported design methodologies, this design strategy does not require any pre-conditions, such as the number of rings, and an optimum solution can be obtained using a direct search for two design variables. In brief, this method is based on the observation that the binarization of continuous pupil functions produces two complementary focal responses, which are positioned symmetrically relative to the focal plane of the lens. Each of the focal responses replicates the response of its continuous original. It is thus predicted that the shift and superposition of the two foci in optical axis would result in an elongated focus. The shift of the two foci can be readily handled by incorporating the defocus term or quadratic phase function into the pupil function. The BPF transmission functions derived from the axicon (BPF-AXI) and spherical aberrations (BPF-SA) can be described as follows:
| (1) |
where is the radial coordinate in the pupil plane that is normalized with () ( is the wavelength of light, and is the numerical-aperture of the lens). , and are the parameters related to defocus, axicon slope, and spherical aberration, respectively. The binarization operator () and defocus parameter () are defined as:
| (2) |
| (3) |
where denotes the real part of a complex number, is the defocus length relative to the focal plane, and n is the refractive index of the medium. As can be inferred from Eq. (1), the BPFs with a desired focal response can be obtained by searching for two parameters for each filter. These include the axicon slope () and defocus () parameters for BPF-AXIs, and spherical aberration () and defocus () parameters for BPF-SAs. Detailed BPF design procedures for a specific DoF gain are described in [17].
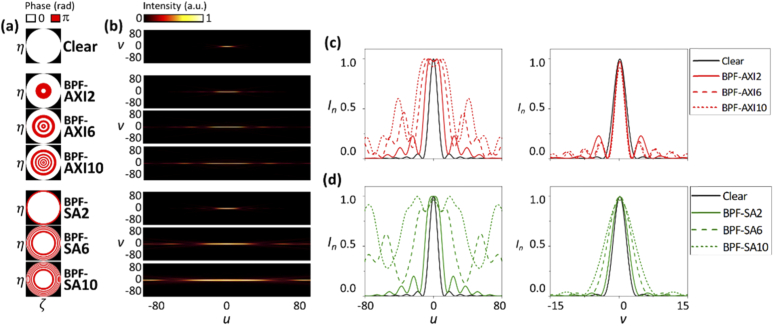
Figure 1(a) presents exemplary BPF designs that are derived from representative complex-valued originals, i.e., phase axicons and spherical aberrations. We set the axicon and spherical parameters for the continuous functions, and sought for the defocus parameter to combine the foci in the proximal to the focal plane. Several BPF designs were considered, and their respective design parameters are provided in Tables 1 and 2. Note that the numeric at the end of each BPF denotes the axicon slope and spherical aberration parameters of the complex-valued original pupils. The ring (phase transition) positions of the designed BPFs are normalized with. It can be observed that as the parameters related to axicon slope () and spherical aberration () increase, the corresponding defocus parameters and the number of rings also increase for FoV extension. This can be accounted for by the fact that the high values of axicon slope and spherical aberration lead to a large separation between the two foci, and thus, the shift by along the optical axis should be increased accordingly to combine the two symmetric foci. Figure 1(b–d) shows the 3D focal responses of the BPFs. and v denote the optical units in the axial and lateral directions as defined in Ref. [10]. While BPFs provide elongated focal responses in the axial direction, the corresponding lateral focal responses exhibit different behaviors. The lateral focal responses of the BPF-AXIs exhibit smaller mainlobes than those obtained with the clear aperture, whereas the sidelobes are more pronounced. This feature is similar to that of the Bessel beam. In contrast, the lateral responses of the BPF-SAs present significantly reduced sidelobes; however, their widths are larger than those from BPF-AXIs and clear aperture. The DoFs using BPF-AXI10 and BPF-SA10 are estimated to be respectively 7.7x and 11x larger than that obtained with a clear aperture. The BPFs with larger axicon slope and spherical aberration parameters enable further DoF improvement. However, these filters exhibit phase rings with smaller widths, which may be difficult to fabricate using conventional manufacturing processes.
Fig. 1.
(a, b) Computer-generated transmission functions and corresponding focal responses of clear aperture and representative binary phase filters (BPFs). The pupil coordinates and are the spatial frequencies normalized with NA/λ. The design parameters of the BPFs are provided in Table 1 and Table 2. It can be noted that the focus is elongated significantly as the number of rings in the BPFs increases. u and v are the axial and lateral coordinates in optical units, respectively [10]. (c, d) Comparisons of axial and lateral focal responses of the BPFs against those of a clear aperture. The BPFs with a large number of rings provide elongated focal responses with broader widths. The lateral responses of BPF-AXI filters exhibit narrower mainlobes than those of clear aperture, but with pronounced sidelobes. The lateral responses of BPF-SA filters, however, are characterized by broader mainlobes with reduced sidelobes.
Table 1. Design parameters for axicon-derived BPFs (BPF-AXI).
| Filter | Slope parameter (α) | Defocus parameter (ψ) |
|---|---|---|
| BPF-AXI2 | 2 | 0.761 |
| BPF-AXI4 | 4 | 1.755 |
| BPF-AXI6 | 6 | 2.750 |
| BPF-AXI8 | 8 | 3.801 |
| BPF-AXI10 | 10 | 4.808 |
Table 2. Design parameters for spherical aberration derived BPFs (BPF-SA).
| Filter | Strength of spherical aberration (γ) | Defocus parameter (ψ) |
|---|---|---|
| BPF-SA2 | 2 | 1.374 |
| BPF-SA4 | 4 | 1.476 |
| BPF-SA6 | 6 | 1.548 |
| BPF-SA8 | 8 | 1.475 |
| BPF-SA10 | 10 | 1.488 |
2.2. BPF-LSFM implementation
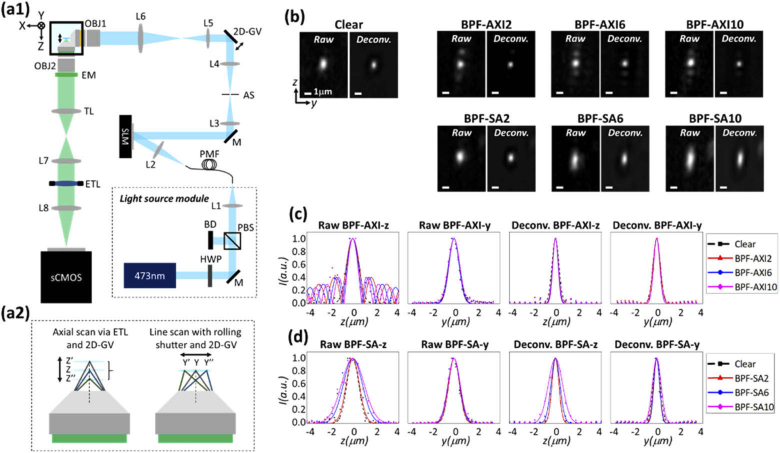
We implemented a BPF-LSFM system to validate high-resolution imaging over an extended FoV via the BPF-generated elongated focus (Fig. 2(a)). The BPF-LSFM is similar to the system used in previous publication [18], except that a spatial light modulator (SLM, P512-0532-C, Meadowlark Optics, CO, USA) and two-dimensional galvanometric beam scanners (2D-GV) are additionally employed for the implementation and imaging with various BPFs designed herein. A 473-nm light from a light source module illuminated the SLM that was placed in the conjugate location of back focal plane of an illumination objective (OBJ1, UMPLFLN 10XW, 10x/0.3 , Olympus, Japan). The phase-modulated light was then focused via the illumination objective and scanned through a specimen with a galvanometric scanner in Y- and Z- directions (refer to the coordinate system in Fig. 2(a)). In the detection path, fluorescence emission from a specimen was collected using a detection objective (OBJ2, UMPLFLN 20XW, 20x/0.5 , Olympus, Japan). An electrical tunable lens (ETL) was placed in the Fourier plane of the detection system to produce quadratic phase delay, thereby axially scanning the detection focal plane. This axial focus scanning via the ETL was performed in sync with the 2D-GV and image sensor (sCMOS, Orca flash 4.0 V3, Hamamatsu Corporation, Japan). We implemented the confocal slit detection scheme using the rolling shutter of sCMOS sensor to further reject the fluorescence background from the out-of-focal region and sidelobes generated by the BPF-AXIs [19]. The rolling shutter of the sCMOS sensor was configured to scan along the Y-axis synchronously with the scanning of the elongated focus. We set the slit width of the rolling shutter to be 0.5 Airy units for achieving optimal signal-to-noise ratio (SNR) and resolution [19]. Detailed information on our BPF-LSFM is provided in the Materials and Methods section.
Fig. 2.
(a1) Schematic of BPF-LSFM. A 473-nm light illuminated a spatial light modulator (SLM) that was employed to implement various BPF designs. The light was then imaged into the back focal plane of illumination objective (OBJ1) to generate elongated focus, which scanned through a specimen via a two-dimensional galvanometric scanner (2D-GV). The fluorescence emission was imaged by an imaging setup comprising the detection objective (OBJ2), emission filter (EM), and relay lenses. ETL: electrical tunable lens, sCMOS: scientific CMOS camera, M: mirror, HWP: half-wave plate, BD: beam dump, PBS: polarizing beam splitter, PMF: polarization-maintaining fiber, AS: aperture stop. (a2) Axial focal plane scanning was performed with ETL, which operated synchronously with the 2D-GV. The rolling shutter of sCMOS scanned synchronously with Y-directional scanned focus. (b) Raw and post-processed Y-Z images of 100-nm fluorescent beads. The scale bar denotes 1 µm. (c-d) Raw and deconvolved point-spread functions along the Y- and Z-directions.
The spatial resolution of BPF-LSFM is determined mainly by the detection objective and confinement of the BPF-generated beam focus. The resolution in the X-direction is mainly set by the diffraction limit of the detection optical system, while the confocal slit detection scheme improves the resolutions in the Y- and Z-dimensions. To examine the effect of the BPFs and confocal slit detection on the spatial resolution in the Y- and Z-directions, we measured the point-spread functions (PSFs) of BPF-LSFM by imaging fluorescent beads (G100, Thermo Fisher Scientific, MA, USA) with a nominal diameter of 100 nm. A total of 1 wt% of stock solution of the microbeads was diluted in the ratio of 50:1 in 1% agarose gel solution and prepared for imaging after solidification in a glass capillary. The glass tube was positioned into a custom-built imaging chamber, and the 3D image of the beads was acquired by BPF-LSFM with various BPFs. The representative raw and post-processed images of the beads along the Y- and Z-directions are shown in Fig. 2(b). We employed the Lucy–Richardson (LR) deconvolution algorithm for post-processing, which effectively deduced the maximum-likelihood estimation of high-resolution images [20,21]. The de-convolution significantly alleviated the artifact caused by the BPF-generated focus. In our imaging studies (that are described later), we mainly utilized BPF-AXI10 and BPF-SA10, as they provided the largest FoV among all the considered designs. The full-widths at half-maximum (FWHMs) of the PSFs in the Y- and Z-directions were measured to be 0.62 µm and 0.53 µm for BPF-AXI10 and 0.89 µm and 1.45 µm for BPF-SA10, respectively, after the LR deconvolution.
2.3. Improved FoV with BPFs
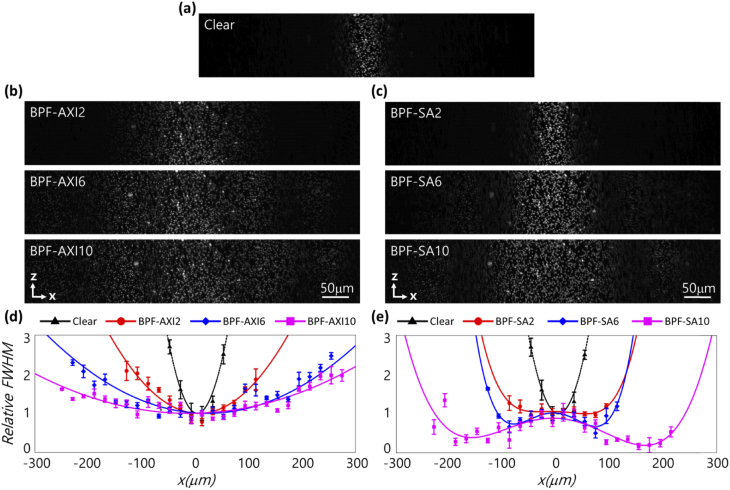
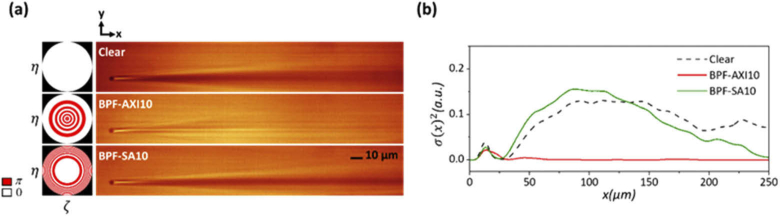
To validate BPF-enabled FoV extension, we performed imaging and FoV analysis with a sample of 100-nm diameter fluorescent beads (G100, Thermo Fisher Scientific, MA, USA) embedded in a 1% agarose gel (Fig. 3). For these measurements, the LSFMs with clear aperture, BPF-AXIs, and BPF-SAs with the same effective NA of 0.3 were considered. Figures 3(a-c) show the XZ maximum intensity projection (MIP) images of the beads obtained with clear aperture, BPF-AXIs, and BPF-SAs, respectively. It can be observed that the FoV is increased significantly when using the BPFs in comparison to that obtained with the clear aperture (Figs. 3(b, c)). In order to quantify FoV enhancement with the BPFs, we examined YZ slices at 20 µm intervals in the X direction, and evaluated the axial PSFs of 20 beads in each image. (Figures 3(d, e)). For each YZ slice, the baseline was first determined by evaluating the average of the pixel values over 21 × 11 pixels in the background (i.e., the region without the microbeads), and was subtracted from the image. The FWHM was then computed from each PSF that corresponded to the microbead. We define the effective FoV as the lateral extent along the X-direction, over which the measured axial FWHM is smaller than z (z denotes the axial FWHM measured at X = 0). We observed that BPF-AXI10 and BPF-SA10 provided, respectively, 7.7x and 11x larger FoV than that obtained with the clear aperture of a similar effective . It should be noted, though, that for the BPF-SA, the axial resolution at the central part of the FoV (X = 0 position) is inferior to that with the clear aperture.
Fig. 3.
XZ maximum intensity projection (MIP) images generated from raw 3D datasets of 100-nm fluorescent beads obtained with clear aperture (a), BPF-AXIs (b), and BPF-SAs (c). (d–e) The measured FWHMs of the axial PSFs (relative to that at X=0) for clear aperture, BPF-AXIs and BPF-SAs. It is clearly observed that BPF-AXI and BPF-SA filters provide extended FoV along the X direction.
2.4. Self-reconstruction of BPF-generated beams
One of the most important and desirable properties of LSFM illumination light is its “self-healing” or “self-reconstruction,” which represents the regeneration or reconstruction of a light wavefront to its original shape, even after the light is partially obstructed [19]. It has been recognized that all forms of non-diffractive beams exhibit self-reconstruction characteristics to some extent [22]; a Gaussian beam also regenerates after being partially blocked [23], though the distance that it requires to be completely recovered is much longer than those of non-diffracting beams [24]. The self-reconstruction property of the beams has been investigated in fluorescence imaging. For instance, Rohrbach et al. exploited the self-reconstruction ability of Bessel beam for biological imaging [25] and demonstrated that the use of a Bessel beam could reduce artifacts and shadows caused by scatterers in biological specimens [19,26].
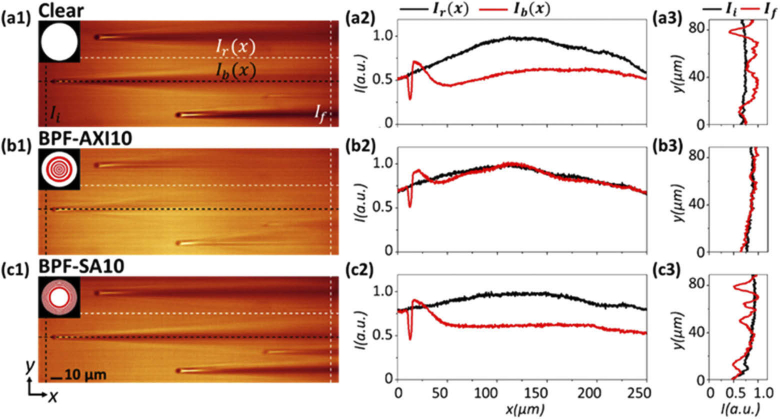
We investigated the self-reconstruction characteristics of our BPF-generated beams. A fluorescent specimen was prepared by mixing 5-µm silica beads and fluorescein dyes in agarose gel. Figures 4(a1), 4(b1), and 4(c1) show the XY slice fluorescence images of specimens acquired with the clear aperture, BPF-AXI10, and BPF-SA10, respectively. In this experiment, the illumination were adjusted to = 0.11, 0.17, and 0.17 to match the effective FoVs in all the cases. It is observed that the silica beads generate the shadow artifacts behind the particles in the clear aperture and BPF-SA10 cases (Figs. 4(a1, c1)). The illumination beams are observed to have scattered and spread to form a shadow artifact. In contrast, this artifact rapidly disappears in the BPF-AXI10 case. To quantitatively compare the self-reconstruction abilities, the intensity distributions along the lines that do and do not cross the beads were examined (Figs. 4(a2, b2, c2)). The corresponding intensity profiles are denoted by and , respectively. The intensity was rapidly restored after ∼50 µm behind the particles in the BPF-AXI10 case; however, it was not recovered for the cases with clear aperture and BPF-SA10. We also examined the intensity distributions along the Y-direction before () and after ) the beads for the three filters (Figs. 4(a3, b3, c3)). The illumination light was recovered after the particles for BPF-AXI10, although the shadows did not disappear for the other two cases. Fahrbach et al. [26] proposed a quantitative metric for the self-reconstruction abilities of the beams, which essentially computes the difference between the non-scattered and scattered light intensities along the propagation distance, i.e.,
| (4) |
where and are the unperturbed and perturbed illumination beam intensities, respectively, and b is the lateral coordinate along Y-direction. Figure 5 shows the results of Eq. (4) for the clear aperture, BPF-AXI10, and BPF-SA10. It is evident that BPF-AXI10 provides more resistance toward scattering, while the response of BPF-SA10 to obstruction is similar to that of the clear aperture, i.e., rapid and distinct recovery of focal response cannot be observed. The self-healing ability of BPF-AXI generated light beam may be partly attributed to its transversal modes that correspond to the sidelobes. These modes circumvent the scatterers, propagate with minimal disturbance, and converge onto deeper regions. This self-healing phenomenon can be beneficial for the imaging of 3D inhomogeneous samples [19].
Fig. 4.
(a1, b1, c1) XY slice images of 5-µm silica microspheres embedded in fluorescent gels, obtained with the clear aperture, BPF-AXI10, and BPF-SA10. The illumination beams propagated from left to right. (a2, b2, c2) Corresponding intensity profiles along the black and white dashed lines in the X direction in (a1, b1, c1). The black and white dashed lines represent the cases where the illumination beams do and do not cross the microspheres, respectively. (a3, b3, c3) Intensity distributions along the black and white dashed lines in the Y direction in (a1, b1, c1), which correspond to the intensity profiles before and after the microspheres. The beam from BPF-AXI10 recovers rapidly after the microspheres, while other beams spread after the scatterers.
Fig. 5.
(a) XY slice images of 5-µm silica beads embedded in fluorescing gel obtained with clear aperture, BPF-AXI10, and BPF-SA10. (b) Evaluation results of Eq. (4) for the three pupil filters. It is evident that the scattered light from the bead rapidly recovers and returns to its original unperturbed light for BPF-AXI10, while it deviates significantly from the unperturbed light for clear aperture and BPF-SA10.
2.5. BPF-LSFM imaging of the Drosophila imaginal disc
To demonstrate the high-contrast imaging capability of our proposed prototype over extended FoV, we performed BPF-LSFM imaging of Drosophila larva imaginal disc. The imaginal disc is a part of the insect larva that becomes a part of the adult insect during pupal transformation [27]. Numerous discoveries in developmental and cellular biology have been achieved by studying the Drosophila imaginal disc, especially on organ growth [28], cellular interactions, [29] and tissue regeneration [30].
For imaging, imaginal discs dissected from the Drosophila larva was stained with Fasciclin III, which compose septate junction in Drosophila, and positioned in a custom-made imaging chamber that was designed to securely position a specimen in the focal volume of illumination ( = 0.3) and detection objectives ( = 0.5). The imaging volume was set to 665(X) x 665(Y) x 284(Z) µm3 with its pixel number of 2048(X) x 2048(Y) x 720(Z), respectively. Other imaging procedures are detailed in the Materials and Methods section.
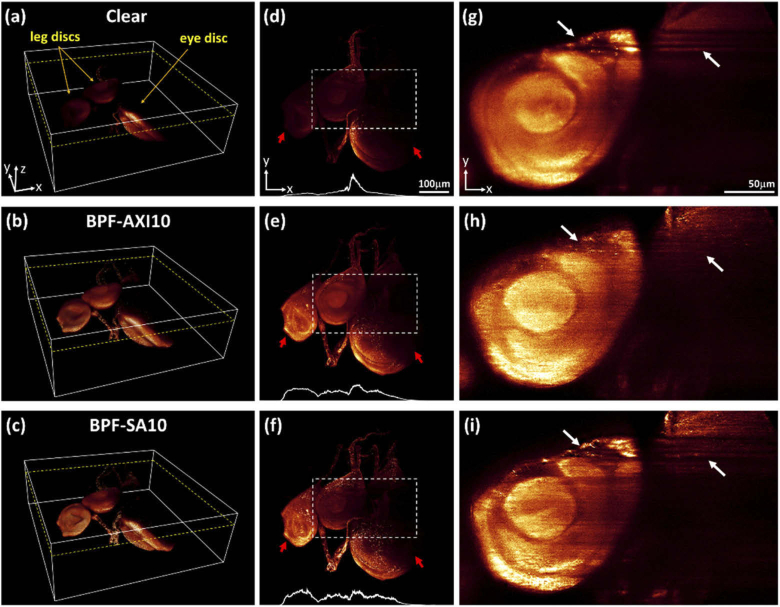
Figures 6(a–f) present the 3D rendered images of the imaginal disc and the corresponding maximum intensity projection (MIP) images along the Z-direction acquired with the clear aperture, BPF-AXI10, and BPF-SA10, respectively. The discs, which represent the structures that will be transformed into organs such as eyes and legs, are indicated by the arrows in Fig. 6(a). Note that the effective NAs of the BPFs and clear aperture were set to 0.3. A significant degradation of image contrast can be observed in the out-of-focus region (marked with red arrow) of the illumination beam in the clear aperture case (Figs. 6(d)). In contrast, for BPF-AXI10 and BPF-SA10 (Figs. 6(b, e) and 6(c, f)), the discs can be visualized over the extended volume. Imaging over extended FoV with the BPFs is well illustrated in the inset line profiles of Figs. 6(d–f), which show the averaged fluorescence signal as a function of the propagation distance. It is observed that the discs can be resolved up to ∼65 µm in the clear aperture case, while the use of BPF-AXI10 and BPF-SA10 provided structural imaging up to ∼400 µm. Visualization 1 (26.9MB, mpeg) and Visualization 2 (42.1MB, mpeg) show the 3D deconvolved and raw Z-stack images, and manifest the imaging capability of BPF-LSFMs over the extended volume compared to LSFM with the clear aperture. Figures 6(g–i) show the zoom-in XY slice images of the regions marked with dashed white rectangles at the position of 72.9 µm from the bottom of imaging volumes. The images obtained with the clear aperture and BPF-SA10 exhibit pronounced artifacts in the form of stripes. The scattering caused by the left discs in the illumination beam path leads to deviation and beam spreading, and thus, the structures in the right part of the images can hardly be illuminated (refer to the regions in the white arrows). In contrast, BPF-AXI10 provides significant reduction of this shadow artifact.
Fig. 6.
(a–c) 3D-rendered and (d–f) maximum intensity projection (MIP) images along the Z-direction of a Drosophila imaginal disc acquired with the clear aperture, BPF-AXI10, and BPF-SA10. The illumination beams propagate from left to right in the X-direction. The insets in (d–f) show the averaged intensity profiles as a function of propagation distance. High-contrast imaging over extended volumes is achieved with BPF-AXI10 and BPF-SA10. (g–i) Magnified XY slice images of the regions marked with dashed white rectangles in (d-f). The images correspond to the XY plane at the position of 72.9 µm from the bottom of imaging volumes. It is evident that the use of BPF-AXI10 enables imaging with significant reduction of the shadow artifacts. Visualization 1 (26.9MB, mpeg) and Visualization 2 (42.1MB, mpeg) demonstrate the imaging capability of BPF-LSFMs over the extended volume.
2.6. BPF-LSFM imaging of Arabidopsis
We further imaged Arabidopsis seedling with its tubulin expressing green fluorescence protein (GFP). In this case, the imaging volume was set to 665 (X) x 665 (Y) x 180 (Z) µm3 with the corresponding pixel numbers of 2048(X) x 2048(Y) x 425(Z).
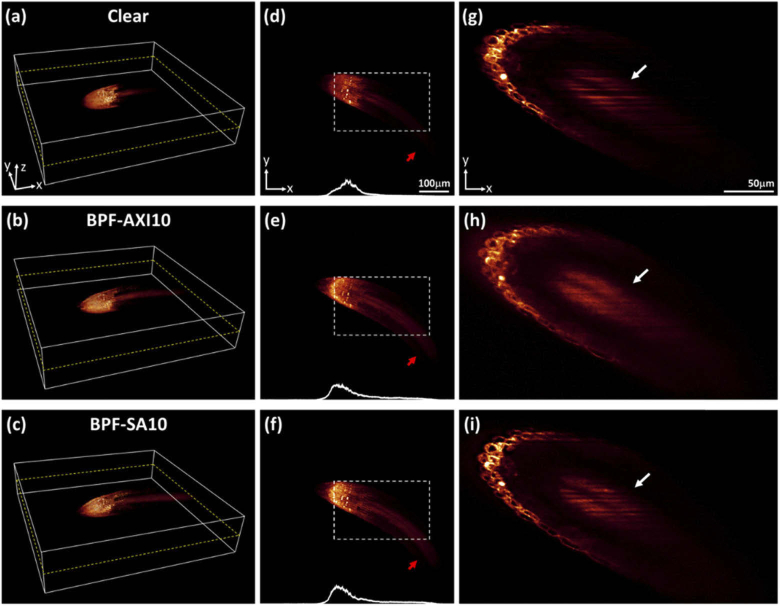
Figures 7(a–f) present 3D perspectives and the corresponding MIP images along the Z-direction of the vascular tissue of Arabidopsis root, which were acquired using the clear aperture, BPF-AXI10, and BPF-SA10, respectively. The cells and root structures can be clearly visualized over extended FoV for the images with BPF-AXI10 and BPF-SA10 (Figs. 7(b–c) and 7(e–f)), while the LSFM with the clear aperture provides limited FoV and cannot visualize the root structures that are located far from the illumination objective (marked with red arrow). The inset intensity profiles are also included for a clear demonstration of extended FoV via BPF-AXI and BPF-SA filters. The 3D deconvolved and raw Z-stack images are provided in Visualization 3 (26.9MB, mpeg) and Visualization 4 (41.8MB, mpeg) , respectively, to demonstrate high-contrast imaging capability of BPF-LSFMs over extended volume. Figures 7(g–i) show the XY slice images acquired at the position of 93.6 µm from the bottom of imaging volume. The image with BPF-AXI10 exhibits significant reduction of the shadow artifact, enabling visualization of the features behind the scatterers along the illumination beam path. The images with the clear aperture and BPF-SA10, however, exhibit pronounced artifacts in the form of stripes, as the beam scatters and spreads due to the scatterers.
Fig. 7.
(a–c) 3D-rendered and (d–f) MIP images of the Arabidopsis root meristem along the Z-direction, acquired with the clear aperture, BPF-AXI10, and BPF-SA10. It is evident that imaging over extended volumes can be achieved through BPF-AXI and BPF-SA. The insets in (d–f) show the averaged intensity profiles as a function of propagation distance. Figures (g–i) present the corresponding XY slice images acquired at 93.6 µm from the bottom of the imaging volumes, which clearly demonstrate the dramatic reduction of shadow artifact in the image with BPF-AXI10. Visualization 3 (26.9MB, mpeg) and Visualization 4 (41.8MB, mpeg) manifest high-contrast imaging capability of BPF-LSFMs over extended volume.
3. Discussion
Our BPF-LSFM is based on the BPFs derived from axi-symmetric aberrations (e.g., axicon and spherical aberration) to build a viable LSFM imaging platform capable of high-contrast imaging with improved FoV. We examined the FoV extension and self-reconstruction abilities of the BPF-generated beams, and presented quantitative analysis and experimental validations by imaging several 3D samples. For many years, various pupil designs for achieving improved 3D microscopy have been presented. The BPFs, among those pupil designs, are particularly desirable as they can easily control the focal responses and are inexpensive to manufacture at a large scale.
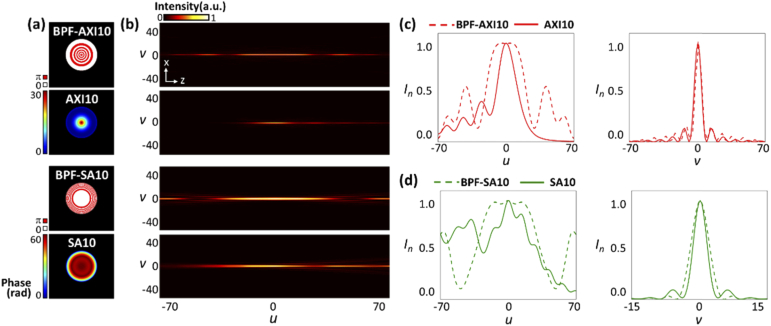
The binary optical structures (either in amplitude and phase) can be regarded as discrete (or stepped) approximations to ideal continuous optical functions. As such, their responses approximate to those from continuous originals [31]. Fresnel amplitude and phase lenses, for instance, have been extensively utilized as a suitable replacement for refractive lenses in diverse imaging and focusing applications [32,33]. Similarly, BPF-SA and BPF-AXI can be considered as binarized approximations to spherical aberration and phase axicon, and thus, their responses are expected to be similar to those from continuous originals. We performed numerical simulations to examine the 3D focal responses of BPF-AXI10, BPF-SA10, and their continuous originals (Fig. 8). Note that quadratic phase (defocus) terms of ψ = 3.98 and ψ = 5.08 have been multiplied to the continuous transmission functions of axicon (AXI10) and spherical aberration (SA10), respectively, so that their respective focal responses are centered at the focal plane of the lens. As can be noted, the DoFs from the BPF-AXI10 and BPF-SA10 are approximately 2.5x and 2.2x larger than those from their continuous originals. This can be accounted for by that the binarization of a complex-valued pupil function results in two focal responses that are similar to that from its continuous original but separated by a certain distance. We combine these two foci by incorporating the defocus term, thereby elongating the focal responses. The lateral responses, on the other hand, are found to be similar to those from continuous originals. The beams generated from BPF-AXI10 exhibits the sidelobes in its lateral response, which accounts for the self-reconstructing behaviors similar to its continuous counterpart, i.e., Bessel beams. This observation is of great importance, as it suggests that any type of non-diffracting and self-reconstructing beams generated by the complex phase filters can be obtained by BPFs that approximate their continuous originals. For example, the Airy beam demonstrates non-diffracting and self-healing behaviors; however, its generation requires phase filters of a cubic function, which are expensive to realize. Our results indicate that the binarization of cubic phase filters with appropriate defocus term could potentially generate Airy-like beam with non-diffracting and self-constructing properties. In addition, such filters are thin and involve a cost-effective fabrication process. In a recent study, aspheric lenses were utilized in an ultramicroscope [7] to generate extended light sheet with minimal or no enlargement of lateral extent. The axial resolution of the ultramicroscope was reported to be ∼4 µm, and it provided a FoV of ∼6000 µm. The generation of such thin and long light sheets can be achieved through binarization of aspheric illumination optics, which may enable fast imaging of large samples, such as mouse brain and entire embryo/larvae of animal development models.
Fig. 8.
(a) Pupil transmission functions of BPF-AXI10, BPF-SA10, and their respective continuous counterparts (i.e., AXI10 and SA10). The BPFs are generated from the continuous pupil functions with the same axicon (α=10) and spherical aberration (γ=10) parameters, with the proper incorporation of defocus parameters to combine two foci in the optical axis. (b) 3D focal responses from the BPFs and their respective originals. Note that quadratic phase terms have been multiplied to the continuous pupil functions to locate their focal responses proximal to the focal plane of a lens. (c, d) Comparisons of the axial and lateral focal responses of the BPF-AXI10 and BPF-SA10 against those of their continuous originals.
It should be noted that other axi-symmetric BPFs may also be considered to improve the imaging performance of LSFM. For example, Sheppard [10] presented several BPF designs with maximally-flat axial responses. Our numerical analysis with 3-element BPFs indicates that the BPFs in [10] provide 1.3x larger DoFs compared to our BPFs, while their lateral responses exhibit similar or broader mainlobes than those of our BPFs. In some BPF designs, the sidelobes in the lateral responses were also observed, as in our BPFs derived from axicon. It would be of great interest to examine other characteristics such as self-reconstruction abilities of the beams generated by those BPFs.
In the present work, we employed an SLM to examine the focal responses from various BPF structures considered in this study and their applicability in LSFM imaging. As noted in [34], SLM typically exhibits a crosstalk between adjacent pixels, which results in a spatial low-pass filtering of the phase map expected for an SLM with no pixel crosstalk. The transmission function from SLM can thus be modeled as the convolution of the original phase map with a point spread function, which is typically expressed by a Gaussian function. The SLM employed in our BPF-LSFM was found to exhibit a crosstalk of <0.2 pixel in standard deviation of Gaussian PSF (refer to [34] for detailed expression). Our analysis revealed that such pixel-crosstalk does not cause significant discrepancy in the 3D focal responses, with <5% DoF difference. In BPF-LSFM, FoV can be further improved by using BPFs with a larger number of rings. The BPFs with a large number of rings, however, is accompanied by the reduction of optical energy for fluorescence excitation, as the energy is distributed all over the elongated focus. Specifically, the Strehl ratio, which is the ratio of the maximum intensities obtained with the BPFs and clear aperture, was estimated as 0.039 and 0.127 for BPF-SA10 and BPF-SA10, respectively. In our case, the finite pixel size of the employed SLM and limited optical power of the excitation laser limited the exploration of BPFs with a larger number of rings. However, BPFs with a larger number of rings can be designed and manufactured with high-resolution fabrication methods, such as E-beam lithography or nanoimprinting. These filters can then be installed in a conventional scanning microscope, thereby transforming the conventional LSFM into BPF-LSFM that can provide a much larger FoV.
In addition, it is important to note that the current BPF-LSFM is not optimized for imaging speed and resolution. The use of high-power lasers and high frame rate image sensor can improve the imaging speed. The illumination beam multiplexing combined with multiple rolling shutters in the state-of-the-art sCMOS camera or multiple image sensors can further increase the imaging speed. Various super-resolution techniques can be implemented in BPF-LSFM to improve the spatial resolution. For instance, structured illumination (SI) can be implemented by the modulated illumination of BFP-generated beams as the beam scans across the lateral plane, which results in patterned illumination over XY plane. Rapid modulation of the elongated focus can be achieved by the high-speed beam modulators such as acousto-optic modulator. The acquired images can then be used to construct super-resolution images using conventional SI algorithms [35,36]. Image scanning microscopy doubles the spatial resolution of confocal microscopy by re-scanning the fluorescence emission on two-dimensional image sensor [37,38]. The de-coupling of magnification in scanning and de-scanning optical architectures enables lateral super-resolution, with improved light collection efficiency. Similar strategy can be implemented in our BPF-LSFM by properly designed de-scanning mechanism.
Our BPFs can also be extended for multi-color or multi-photon imaging. However, in such cases, the BPF structures must be designed properly according to the wavelengths used. In our numerical simulation, however, we observed that the elongation of the focal responses did not change significantly, while the corresponding PSFs and efficiency needed to be carefully characterized. In such cases, a new PSF characterization and subsequent deconvolution should be performed to achieve an optimal performance.
4. Materials and methods
4.1. BPF-LSFM setup
A schematic of BPF-LSFM is depicted in Fig. 2(a). A 473-nm light from a diode-pumped solid-state laser (MBL-III-473, CNIlaser, China) transmitted through an optical setup comprising a half-wave plate (HWP) and a polarizing beamsplitter (PBS), and subsequently coupled into a polarization-maintaining fiber (PMF, P3-488PM-FC-2, Thorlabs, Inc., NJ, USA). This optical system was constructed for achieving efficient power control of the 473-nm light delivered to the LSFM illumination system. The light from the PMF was then collimated and reflected by the SLM (P512-0532-C, Meadowlark Optics, CO, USA), which was positioned in the conjugate location of the back focal plane of the illumination objective (OBJ1, UMPLFLN 10XW, 10x/0.3 , water immersion, Olympus, Japan). The angle of the PMF was aligned to match the SLM polarization requirement. A 1D blazed grating was superimposed onto the BPF function in SLM to reject the unmodulated light generated due to the SLM fill factor. An aperture (AS) placed at the focal plane of the lens (L3) blocked all but the first-order diffraction from the SLM. Then the light was re-collimated by a lens (L4, f = 200 mm), scanned by the 2D-GV (GVS202, Thorlabs, Inc., NJ, USA), and expanded by a telescope with lenses (L5, f = 50 mm and L6, f = 100 mm) to obtain the required for appropriate illumination. The light was then focused onto the specimen through an illumination objective (OBJ1).
The fluorescence emission was collected by the detection objective (OBJ2, UMPLFLN 20XW, 20x/0.5 , water immersion, Olympus, Japan) and transmitted through an emission filter (EM, ET525/50 m, Chroma technology, VT, USA) to finally form an image in the intermediate image plane via the tube lens (TL). The image was further relayed by a pair of lenses (L7-L8, f = 180 mm) and recorded by a scientific CMOS camera (sCMOS, Orca Flash 4.0 V3, Hamamatsu Corporation, Japan). An ETL was placed in the Fourier plane of the imaging system to induce quadratic phase delay, thereby axially scanning the focal plane in sync with the 2D-GV and sCMOS camera.
For image construction, we employed confocal slit detection using the rolling shutter of the sCMOS sensor to effectively reject the fluorescence background. The rolling shutter of the sCMOS sensor scanned along the Y-axis synchronously with the scanning of the elongated focus. As the slit width determines the SNR and spatial resolution, we examined the resultant SNR and spatial resolution by varying the effective slit width of the rolling shutter. We observed that the use of the slit with four adjacent pixels provided the optimum SNR and resolution, while effectively rejecting the fluorescence from the sidelobes. The slit width of four pixels corresponded to 0.5 Airy units. In our case, it is estimated that 41∼47% of fluorescence emission is rejected by the confocal slit, but the SNR is found to be improved by 2x. Unless specified otherwise, the illumination optical power was set to 1.8 mW at the back aperture of the illumination objective, and the exposure time for each slit was set to 400 µs.
4.2. Image deconvolution
The acquired fluorescence images were post-processed with LR deconvolution algorithm, which iteratively computes the image and PSF, leading to a maximum-likelihood estimation of high-resolution image. For the acquired image and a PSF of h, the iteration can be performed using
| (5) |
where denotes the image obtained through the -th iteration deconvolution, is convolution, and ∗ operator represents the flipping of the image. Note that . In practice, the PSF is FoV-dependent, and thus, the measured PSFs along various X positions (37 positions in our case) were utilized for deconvolution. The PSFs for de-convolution were experimentally obtained from YZ slices at 20 µm intervals along the X direction from the 3D dataset of fluorescent microbeads (Sec. 2.3). For de-convolution, volumetric dataset from a specimen was first segmented at 20 µm intervals along the X direction. The YZ slice images in each segment were then deconvolved using the corresponding PSF acquired in Sec. 2.3., and the background averaged over 21 × 11 pixels in fluorescence-free region was subtracted. The number of iterations in the LR deconvolution was 10 per image. The experimental validation of our deconvolution is provided in Fig. 2.
4.3. Sample preparation
Two biological specimens (i.e., Drosophila imaginal discs and Arabidopsis) were prepared and imaged to demonstrate the improved 3D imaging capability of BPF-LSFM. The imaginal discs extracted from Drosophila larva were stained for the cell junction protein FasIII using Alexa Fluor 488, and the beta tubulin of Arabidopsis cell was tagged with GFP using Arabidopsis UBQ1 promoter.
For imaging of the fluorescent specimens, 1 wt% of low melting agarose gel was prepared, and the stained samples were immersed in the gel. Then, the sample and gel were loaded together into a glass capillary and mounted in a custom-made imaging chamber that was designed and fabricated to securely position the specimen in the focal volume of illumination and detection objectives. The chamber was then filled with water for achieving the refractive index match. Prior to image acquisition, the gel immersed sample was forced out of the capillary using a plunger to avoid aberration due to the presence of a glass layer in the detection path.
Funding
National Research Foundation of Korea10.13039/501100003725 (2020R1A2C2012061, 2015R1A5A1037668).
Disclosures
The authors declare no conflicts of interest.
References
- 1.Siedentopf H., Zsigmondy R., “Uber Sichtbarmachung und Größenbestimmung ultramikoskopischer† Teilchen, mit besonderer Anwendung auf Goldrubingläser,” Ann. Phys. 315(1), 1–39 (1902). 10.1002/andp.19023150102 [DOI] [Google Scholar]
- 2.Huisken J., Swoger J., Bene F. D., Wittbrodt J., Stelzer E. H. K., “Optical sectioning deep inside live embryos by selective plane illumination microscopy,” Science 305(5686), 1007–1009 (2004). 10.1126/science.1100035 [DOI] [PubMed] [Google Scholar]
- 3.Huisken J., Stainier D. Y. R., “Selective plane illumination microscopy techniques in developmental biology,” Development 136(12), 1963–1975 (2009). 10.1242/dev.022426 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.McGloin D., Dholakia K., “Bessel beams: diffraction in a new light,” Contemp. Phys. 46(1), 15–28 (2005). 10.1080/0010751042000275259 [DOI] [Google Scholar]
- 5.Planchon T. A., Gao L., Milkie D. E., Davidson M. W., Galbraith J. A., Galbraith C. G., Betzig E., “Rapid three-dimensional isotropic imaging of living cells using Bessel beam plane illumination,” Nat. Methods 8(5), 417–423 (2011). 10.1038/nmeth.1586 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Vettenburg T., Dalgarno H. I. C., Nylk J., Coll-Lladó C., Ferrier D. E. K., Čižmár T., Gunn-Moore F. J., Dholakia K., “Light-sheet microscopy using an Airy beam,” Nat. Methods 11(5), 541–544 (2014). 10.1038/nmeth.2922 [DOI] [PubMed] [Google Scholar]
- 7.Pende M., Becker K., Wanis M., Saghafi S., Kaur R., Hahn C., Pende N., Foroughipour M., Hummel T., Dodt H.-U., “High-resolution ultramicroscopy of the developing and adult nervous system in optically cleared Drosophila melanogaster,” Nat. Commun. 9(1), 4731 (2018). 10.1038/s41467-018-07192-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wang D., Jin Y., Feng R., Chen Y., Gao L., “Tiling light sheet selective plane illumination microscopy using discontinuous light sheets,” Opt. Express 27(23), 34472–34483 (2019). 10.1364/OE.27.034472 [DOI] [PubMed] [Google Scholar]
- 9.Gao L., “Extend the field of view of selective plan illumination microscopy by tiling the excitation light sheet,” Opt. Express 23(5), 6102–6111 (2015). 10.1364/OE.23.006102 [DOI] [PubMed] [Google Scholar]
- 10.Sheppard C. J. R., “Binary phase filters with a maximally-flat response,” Opt. Lett. 36(8), 1386–1388 (2011). 10.1364/OL.36.001386 [DOI] [PubMed] [Google Scholar]
- 11.Zlotnik A., Yaish S. B., Yehezkel O., Lahav-Yacouel K., Belkin M., Zalevsky Z., “Extended depth of focus contact lenses for presbyopia,” Opt. Lett. 34(14), 2219–2221 (2009). 10.1364/OL.34.002219 [DOI] [PubMed] [Google Scholar]
- 12.Zhai Z., Ding S., Lv Q., Wang X., Zhong Y., “Extended depth of field through an axicon,” J. Mod. Opt. 56(11), 1304–1308 (2009). 10.1080/09500340903082689 [DOI] [Google Scholar]
- 13.Vetter C., Steinkopf R., Bergner K., Ornigotti M., Nolte S., Gross H., Szameit A., “Realization of Free-Space Long-Distance Self-Healing Bessel Beams,” Laser Photonics Rev. 13(10), 1900103 (2019). 10.1002/lpor.201900103 [DOI] [Google Scholar]
- 14.Morrison R. L., Walker S. L., Cloonan T. J., “Beam array generation and holographic interconnections in a free-space optical switching network,” Appl. Opt. 32(14), 2512–2518 (1993). 10.1364/AO.32.002512 [DOI] [PubMed] [Google Scholar]
- 15.Barlev O., Golub M. A., “Multifunctional binary diffractive optical elements for structured light projectors,” Opt. Express 26(16), 21092–21107 (2018). 10.1364/OE.26.021092 [DOI] [PubMed] [Google Scholar]
- 16.Wilding D., Pozzi P., Soloviev O., Vdovin G., Sheppard C. J., Verhaegen M., “Pupil filters for extending the field-of-view in light-sheet microscopy,” Opt. Lett. 41(6), 1205–1208 (2016). 10.1364/OL.41.001205 [DOI] [PubMed] [Google Scholar]
- 17.Ryu S., Joo C., “Design of binary phase filters for depth of focus extension via binarization of axisymmetric aberrations,” Opt. Express 25(24), 30312–30326 (2017). 10.1364/OE.25.030312 [DOI] [PubMed] [Google Scholar]
- 18.Pitrone P. G., Schindelin J., Stuyvenberg L., Preibisch S., Weber M., Eliceiri K. W., Huisken J., Tomancak P., “OpenSPIM: an open-access light-sheet microscopy platform,” Nat. Methods 10(7), 598–599 (2013). 10.1038/nmeth.2507 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Fahrbach F. O., Rohrbach A., “Propagation stability of self-reconstructing Bessel beams enables contrast-enhanced imaging in thick media,” Nat. Commun. 3(1), 632 (2012). 10.1038/ncomms1646 [DOI] [PubMed] [Google Scholar]
- 20.Richardson W. H., “Bayesian-based iterative method of image restoration,” J. Opt. Soc. Am. 62(1), 55–59 (1972). 10.1364/JOSA.62.000055 [DOI] [Google Scholar]
- 21.Lucy L. B., “An iterative technique for the rectification of observed distributions,” Astron J. 79, 745 (1974). 10.1086/111605 [DOI] [Google Scholar]
- 22.Mazilu M., Stevenson D. J., Gunn-Moore F., Dholakia K., “Light beats the spread: “non-diffracting” beams,” Laser Photonics Rev. 4(4), 529–547 (2010). 10.1002/lpor.200910019 [DOI] [Google Scholar]
- 23.Aiello A., Agarwal G. S., Paúr M., Stoklasa B., Hradil Z., Řeháček J., Hoz P. d. l., Leuchs G., Sánchez-Soto L. L., “Unraveling beam self-healing,” Opt. Express 25(16), 19147 (2017). 10.1364/OE.25.019147 [DOI] [PubMed] [Google Scholar]
- 24.Wen W., Chu X., “Quantitative comparison of self-healing ability between Bessel–Gaussian beam and Airy beam,” Ann. Phys. 360, 549–555 (2015). 10.1016/j.aop.2015.05.024 [DOI] [Google Scholar]
- 25.Rohrbach A., “Artifacts resulting from imaging in scattering media: a theoretical prediction,” Opt. Lett. 34(19), 3041–3043 (2009). 10.1364/OL.34.003041 [DOI] [PubMed] [Google Scholar]
- 26.Fahrbach F. O., Simon P., Rohrbach A., “Microscopy with self-reconstructing beams,” Nat. Photonics 4(11), 780–785 (2010). 10.1038/nphoton.2010.204 [DOI] [Google Scholar]
- 27.Beira J. V., Paro R., “The legacy of Drosophila imaginal discs,” Chromosoma 125(4), 573–592(2016). 10.1007/s00412-016-0595-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Shearn A., Garen A., “Genetic control of imaginal disc development in Drosophila,” Proc. Natl. Acad. Sci. 71(4), 1393–1397 (1974). 10.1073/pnas.71.4.1393 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Spradling A. C., Rubin G. M., “Transposition of cloned P elements into Drosophila germ line chromosomes,” Science 218(4570), 341–347 (1982). 10.1126/science.6289435 [DOI] [PubMed] [Google Scholar]
- 30.Bryant P. J., “Regeneration and duplication following operations in situ on the imaginal discs of Drosophila melanogaster,” Dev. Biol. 26 (4), 637–651(1971). 10.1016/0012-1606(71)90146-1 [DOI] [PubMed] [Google Scholar]
- 31.Goodman J. W., Introduction to Fourier Optics, 3 ed. (Roberts and Company Publishers, 2004). [Google Scholar]
- 32.Li X., Wei L., Poelma R. H., Vollebregt S., Wei J., Urbach H. P., Sarro P. M., Zhang G. Q., “Stretchable Binary Fresnel Lens for Focus Tuning,” Sci. Rep. 6(1), 25348 (2016). 10.1038/srep25348 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hain M., Spiegel W. v., Schmiedchen M., Tschudi T., Javidi B., “3D integral imaging using diffractive Fresnel lens arrays,” Opt. Express 13(1), 315–326 (2005). 10.1364/OPEX.13.000315 [DOI] [PubMed] [Google Scholar]
- 34.Persson M., Engström D., Goksör M., “Reducing the effect of pixel crosstalk in phase only spatial light modulators,” Opt. Express 20(20), 22334–22343 (2012). 10.1364/OE.20.022334 [DOI] [PubMed] [Google Scholar]
- 35.Gustafsson M. G. L., “Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy,” J. Microsc. 198(2), 82–87 (2000). 10.1046/j.1365-2818.2000.00710.x [DOI] [PubMed] [Google Scholar]
- 36.Chen B.-C., Legant W. R., Wang K., Shao L., Milkie D. E., Davidson M. W., Janetopoulos C., Wu X. S., Hammer J. A., Liu Z., English B. P., Mimori-Kiyosue Y., Romero D. P., Ritter A. T., Lippincott-Schwartz J., Fritz-Laylin L., Mullins R. D., Mitchell D. M., Bembenek J. N., Reymann A.-C., Böhme R., Grill S. W., Wang J. T., Seydoux G., Tulu U. S., Kiehart D. P., Betzig E., “Lattice light-sheet microscopy: Imaging molecules to embryos at high spatiotemporal resolution,” Science 346(6208), 1257998 (2014). 10.1126/science.1257998 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Müller C. B., Enderlein J., “Image Scanning Microscopy,” Phys. Rev. Lett. 104(19), 198101 (2010). 10.1103/PhysRevLett.104.198101 [DOI] [PubMed] [Google Scholar]
- 38.De Luca G. M., Breedijk R. M., Brandt R. A., Zeelenberg C. H., de Jong B. E., Timmermans W., Azar L. N., Hoebe R. A., Stallinga S., Manders E. M., “Re-scan confocal microscopy: scanning twice for better resolution,” Biomed. Opt. Express 4(11), 2644–2656 (2013). 10.1364/BOE.4.002644 [DOI] [PMC free article] [PubMed] [Google Scholar]