Abstract
In this work, we revise the preparation procedure and conduct an in depth characterization of optical properties for the recently proposed silicone-based tissue-mimicking optical phantoms in the spectral range from 475 to 925 nm. The optical properties are characterized in terms of refractive index and its temperature dependence, absorption and reduced scattering coefficients and scattering phase function related quantifiers. The scattering phase function and related quantifiers of the optical phantoms are first assessed within the framework of the Mie theory by using the measured refractive index of SiliGlass and size distribution of the hollow silica spherical particles that serve as scatterers. A set of purely absorbing optical phantoms in cuvettes is used to evaluate the linearity of the absorption coefficient with respect to the concentration of black pigment that serves as the absorber. Finally, the optical properties in terms of the absorption and reduced scattering coefficients and the subdiffusive scattering phase function quantifier γ are estimated for a subset of phantoms from spatially resolved reflectance using deep learning aided inverse models. To this end, an optical fiber probe with six linearly arranged optical fibers is used to collect the backscattered light at small and large distances from the source fiber. The underlying light propagation modeling is based on the stochastic Monte Carlo method that accounts for all the details of the optical fiber probe.
1. Introduction
Tissue-mimicking phantoms simulate the properties of human or animal tissues and are designed for a specific diagnostic modality or therapeutic intervention. Their main purposes are testing and evaluation of new medical devices and protocols, performance optimization of the existing devices and protocols, routine quality control, and performance comparison of different systems [1]. While tissue phantoms are well established, routinely used in standard clinical diagnostic and therapeutic procedures (e.g., CT, MRI, radiotherapy) and regulated by medical physics associations and other regulatory bodies, standardization and regulation of the tissue-mimicking phantoms are still needed in the field of biomedical optics.
Numerous optical phantom recipes are found in the literature, ranging from liquid [2,3] to hydrogel-based [4] and solid phantoms [5]. A comprehensive review of the optical phantoms was provided by Pogue and Patterson [1]. The liquid tissue phantoms, especially Intralipid suspensions, have become the most widely used reference materials in the biomedical optics community. These phantoms have been thoroughly studied in the past years, which includes characterization of their optical properties for multiple combinations of scatterer and absorber concentrations, scattering phase function measurements, and determination of suspension stability with time and temperature [6]. However, Bodenschatz et al., [6] reported a formation of a highly scattering surface layer in these phantoms giving rise to a measurement error of up to 10%. The drawbacks of the liquid phantoms are their relatively low-term stability (hours to days), water evaporation, inability to produce complex multilayer phantoms, and necessary containers [1].
The hydrogel-based phantoms are commonly used when imitation of biological tissues is required over a broad range of physical properties in addition to the optical properties, i.e., thermal, elastic properties [1,7,8]. These phantoms allow for the construction of multiple layer and arbitrary phantom shapes with different properties, including water soluble chromophores and fluorophores typical for biological tissues. The main weaknesses of these phantoms are short-term stability and water evaporation.
The solid phantoms are made of polymers (typically, PDMS, polyacryl, wax). They allow for the construction of long-term stable inhomogeneous phantoms involving multiple layers, arbitrary shapes, and different optical properties [1,9,10]. In addition, it has been recently demonstrated that these phantoms can be 3D printed, thus making fabrication of arbitrary geometry objects possible [8,11,12]. Their main disadvantages are that they do not typically model the chemical composition of tissues and hydrophobicity.
The limiting factors of the majority of the reported phantom recipes, as pointed out by Konugolu Venkata Sekar et al., [13], are that they are (a) not providing a detailed manufacturing procedure (e.g., temperatures, time intervals, stirring, environmental conditions), (b) not systematically studying the phantom behavior over a wide range of absorber and scatterer concentrations, (c) not covering broad spectral ranges for optical characterization, and (d) not testing the phantoms in terms of reproducibility, shelf life, and homogeneity. Therefore, research groups are still wasting effort in redesigning the optical phantoms instead of using the phantoms that have already been well designed and characterized by other groups.
Konugolu Venkata Sekar et al., [13] developed a solid phantom based on black silicone pigment (absorber), silica microspheres (scatterer) and silicone rubber (PlatSil SiliGlass, bulk material) bearing in mind the aforementioned limiting factors. The advantage of the SiliGlass silicone rubber over other silicone based rubbers is that it is a clear medium instead of becoming bluish or turbid on curing. This is important for better control of absorption and scattering properties in the produced phantoms. In general, silicon rubbers feature lower intrinsic absorption and longer shelf life compared to other solid phantom substrates [10,12].
The optical characterization was performed over a broadband spectrum (from 600 to 1100 nm) using a time-of-flight (TOF) diffuse optical spectrometer. The resulting optical properties of the phantoms cover a wide range (absorption coefficient from 0.1 to 1 cm−1 and reduced scattering coefficient from 5 to 25 cm−1) that is relevant to human tissues. The samples were tested for reproducibility and spatial homogeneity, which was found to be within 4%. Such phantoms are stable, homogenous, robust, and allow for selection of both absorption and reduced scattering coefficients. In addition, the authors demonstrated that the phantoms can also be 3D printed, which makes them extremely versatile.
The above study characterized the phantoms in a broad range of optical properties, and demonstrated their reproducibility and homogeneity. Moreover, the authors provided analytical expressions for estimation of ingredients based on the desired scattering and absorption coefficients, and thoroughly documented the recipe, thus allowing for easy production of the phantoms by other research groups. Therefore these phantoms are good candidates for an independent reproduction and re-evaluation.
Yet, the SiliGlass tissue-mimicking phantoms must be further characterized to fulfill the needs of the wider biomedical optics community. Among others the refractive index was not reported. The refractive index is needed for estimation of light reflection and transmission at the boundaries. If the subdiffusive regime is involved, the scattering phase function parameters (anisotropy g and subdiffusive quantifiers such as γ or σ [14–17]) are required. To improve the understanding of the scattering properties, the spheres size and wall thickness distribution must be determined and used within the framework of the Mie theory [18]. Furthermore, the relation between the pigment concentration, absorption coefficient and pigment scattering component should be found by measuring optical properties of the pure pigment. In our opinion, determination of these additional parameters would significantly increase the usefulness of the phantoms.
The main aim of this study was to reproduce the phantoms and characterize them with a complementary measurement technique (spatially resolved reflectance), so that the recipe and the optical properties would be independently confirmed. The next aim was to additionally characterize the phantoms by measuring the refractive index, scattering phase function parameters, and obtain more information about the pure absorbing and scattering components allowing for better understanding of the optical properties and proper light propagation modeling by well-established methods, such as the stochastic Monte Carlo (MC) method.
2. Materials and methods
2.1. Preparation of the SiliGlass optical phantoms
The SiliGlass phantoms were prepared using a slightly modified version of the procedure reported by Konugolu Venkata Sekar et al., [13], taking into account the inconsistencies discovered during the preparation. The constituents were the same as in the original recipe, namely silicone rubber (Parts A and B of PlatSil SiliGlass, Polytek, USA), silicone pigment (Polycraft Black Silicone Pigment, MB Fibreglass, UK), and silica microspheres (No. 440345, Sigma-Aldrich, USA). The black silicone pigment was initially diluted in part A to match the dilution ratio of 1 (pigment):2272 (Part A) as specified in [13] and stirred with a magnetic stirrer (AREC Digital Ceramic Hot Plate Stirrer, Italy) for 10 minutes. To break the microsphere clusters, the spheres were first stirred in a cup using a magnetic stirrer for 2 min and later thoroughly shaken by hand. At the end they were mixed with a glass rod.
Mass of each part was calculated according to the selected mass of part A (mA) using the following equations:
| (1) |
where mabs, msc and mB stand for masses of the diluted absorber, scatterer and part B, respectively. Note that mabs is not the actual mass of the absorber but the mass of the 1:2272 diluted absorber solution. Cabs and Csc represent the selected percent concentrations of the absorber and scatterers according to Fig. 1 in [13]. Because some of the material remains on the container walls, after combining both parts together, the mass mB was increased by 1.0 g, which was found by comparing the mass of an empty container and the part B container after the contents were removed during the mixing procedure. msc was increased accordingly to maintain the same concentration of the scatterers.
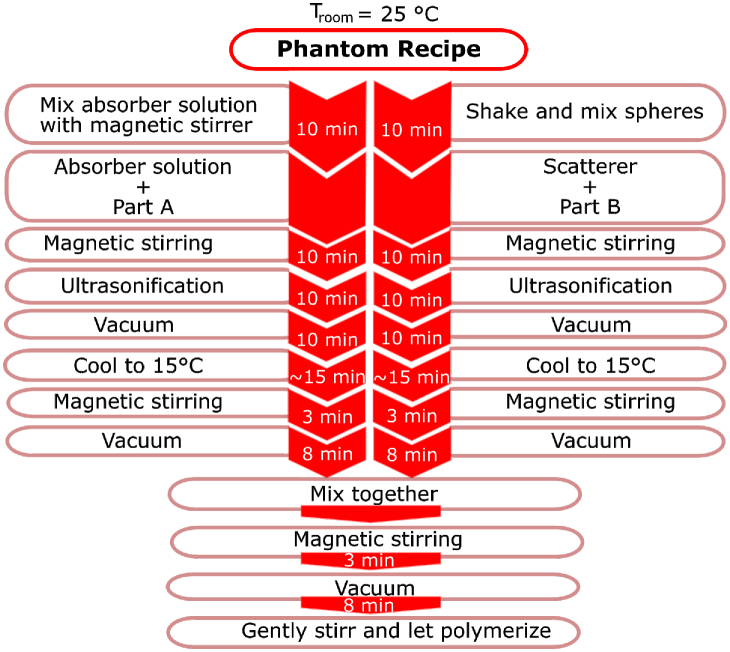
Fig. 1.
SiliGlass phantom preparation procedure diagram.
The recipe used in this study also differs from the original recipe in the ratio of mA and mB. In the original recipe, the mass of part B is expressed as mB = mA + mabs, which can be found in Fig. 1 in [13]. However, in our recipe, the expression is modified by including msc, i.e. mB + msc = mA + mabs. The difference in mA and mB could potentially affect the refractive index and the intrinsic absorption of the pure SiliGlass phantom. However, as we show later, the refractive index remains the same regardless of the concentration of black silicone pigment or hollow silica spheres. Likewise, the intrinsic absorption of pure SiliGlass is small compared to the absorption of the black silicone pigment. It should be noted that Cabs and Csc and the corresponding absorption and reduced scattering coefficients remain the same as in the original recipe since both concentrations are the target values.
Part A was mixed with the diluted silicone pigment, and part B with the silica microspheres in 120 ml plastic Urine Cups (A5-50.20.18APL, Mikro + Polo, Slovenia). The concentrations of the black pigment and silica spheres were selected according to the desired optical properties [13]. Each solution was first stirred with the stirring rod for 1 minute and then by the magnetic stirrer for 10 minutes. Both solutions were then ultrasonicated (ASonic PRO 08, Slovenia) for 10 minutes and afterwards vacuumed in a custom build vacuum desiccator at a pressure of 4 millibar for 10 minutes in order to remove air bubbles from the solutions. The temperature of solution was found to rise considerably during the ultrasonication, which lead to significantly faster polymerization after mixing both solutions. To prevent the rapid polymerization and consequential inadequate mixing, the solutions were cooled down to 15 °C before mixing. The cooled solutions were stirred with the magnetic stirrer for 3 minutes to minimize the sedimentation of particles, and again vacuumed for 5 minutes. Afterwards both solutions were combined by pouring dilution of part B with the scatterers into the cup of part A with the absorber dilution. The resulting mixture was stirred for 3 minutes. Subsequently the mixture was vacuumed for 8 minutes and at the end gently stirred with the stirring rod to ensure homogeneity of the SiliGlass phantom. Multiple degassing steps were necessary to prevent the final degassing step becoming excessively long. We found that if the final degassing step is too long, the resin begins to polymerize before all gas bubbles are removed. The room temperature was kept constant at 25 °C, which is 4°C higher than reported in [13]. While the whole phantom preparation procedure was carried out at the reported room temperature, an intermediate step involved the refrigeration and cooling of the mixture components to a temperature of 15°C. The SiliGlass phantom preparation procedure is depicted step by step in Fig. 1.
To provide adequate repeatability a reader should be particularly careful at (a) weighing and diluting the ingredients, (b) mixing of the microspheres before and after adding them to the part B to prevent clumps, (c) sufficient degassing to remove all air bubbles, and (d) mixing both resin parts before final degassing to ensure homogeneity of the phantom.
In total, four different SiliGlass phantoms reported in [1] were prepared using the original labelling. The first one was Cc (13.14% of absorber and 5.43% of spheres). The rest of the SiliGlass phantoms were Da, Dc and Df. Small letters denote the concentration of the absorber and capital letters the concentration of scattering particles. The accurate concentrations were recalculated by measuring the masses of every component and are presented in Table 1. Final concentrations deviate less than 2% from the original concentrations.
Table 1. Absorber and scatterers concentrations in Da – Df SiliGlass phantoms.
| ID | Absorber concentration (%) | Scatterer concentration (%) |
|---|---|---|
| Cc | 13.32 | 5.37 |
| Da | 3.51 | 7.14 |
| Dc | 13.12 | 7.08 |
| Df | 31.96 | 7.07 |
A separate set of SiliGlass phantoms without the spheres was prepared for collimated transmittance measurements. The absorber concentrations as given in Table 2 approximately correspond to the original absorber series (a, b, c, d, e, f) in [13]. Each absorbing mixture of parts A and B was poured into five polystyrene 1-cm path length cuvettes (Q-VETTES, Ratiolab GmbH, Germany) and was let to polymerize in the vacuum desiccator. In addition to the absorbing set, a transparent SiliGlass phantom without any pigment and spheres was also prepared and poured into five cuvettes, which served as a reference in the collimated transmittance measurements. In total, 35 cuvettes were prepared, 5 for each SiliGlass phantom type.
Table 2. Absorber concentrations of the diluted purely absorbing SiliGlass phantoms used for the collimated transmittance measurements.
| ID | Concentration (%) |
|---|---|
| a | 3.98 |
| b | 7.46 |
| c | 14.42 |
| d | 21.19 |
| e | 27.79 |
| f | 33.94 |
2.2. Refractive index measurement of the SiliGlass optical phantoms
The refractive indices of SiliGlass phantoms were measured using a commercial certified refractometer (Abbemat MW, Anton Paar GmbH, Austria) with an accuracy of ± 0.00004. The refractive index of each optical phantom was measured at eight wavelengths including 436.3, 480.3, 514.2, 533.1, 546.1 589.3, 633.7 and 657.2 nm and at three temperatures, namely 20.0 °C, 25.0 °C and 30.0 °C. A one-term Sellmeier equation (Eq. (2)) with parameters λ0, a0 and a1 was fit to the measured data at each of the three listed temperatures. In this way, a continuous description of the refractive index n as a function of wavelength λ was obtained.
| (2) |
The value of the reference wavelength λ0 was set to 436.3 nm.
2.3. Scattering phase function calculation of the PlatSil SiliGlass optical phantoms
To better understand and properly model the optical properties of the optical phantoms in MC simulations of reflectance, the scattering phase function of hollow silica spherical particles (No. 440345, Sigma-Aldrich, USA) suspended in SiliGlass was studied. The scattering phase function was characterized through the anisotropy factor g and subdiffusive quantifier γ [14] that is defined as , where g and g2 correspond to the first and second Legendre moments of the scattering phase function. The scattering phase functions were calculated with the help of a publicly available library scattnlay (available from https://github.com/ovidiopr/scattnlay under the GPL v3+ license), a numerical implementation of the analytical Mie solution for scattering of light by layered spherical particles [19]. The provided numerical solutions were extended in a way that allowed computation of scattering phase functions for arbitrary size distributions of hollow spherical particles.
2.4. Spatially resolved reflectance measurements
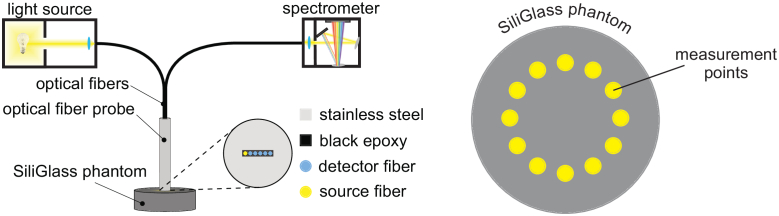
The light backscattered from the SiliGlass phantoms was collected with a 6 mm stainless steel optical fiber probe (custom solution, Fibertech Optica Inc., Canada) that included 6 linearly placed optical fibers with a center-to-center distance of 220 µm, fiber core diameter 200 µm and a numerical aperture of 0.22. The first fiber was used to illuminate the sample by a fiber-coupled broadband tungsten-halogen light source (SLS201/M, Thorlabs Inc., USA). The remaining five optical fibers were used to collect the spatially resolved reflectance (SRR) through the use of a spectrograph-based (V10E, Specim, Finland) multichannel spectrometer. Each acquired spectrum was corrected for the dark response of the sensor array and normalized to the dark response corrected reflectance of a standard reflectance target (WS-2, Avantes, The Netherlands). The left side of Fig. 2 illustrates the measurement setting.
Fig. 2.
(left) Spatially resolved reflectance measurement setting and (right) reflectance measurement sites that were used to study the surface and volume homogeneity of SiliGlass phantoms.
The reflectance measurements of SiliGlass phantoms were performed in two steps. In the first step, we have measured the reflectance of SiliGlass phantoms repeatedly 12 times at a single measurement site to study the effect of the optical coupling between the optical fiber probe and the solid phantom. In the second step, we have measured the reflectance of SiliGlass phantoms in 12 different measurement sites to study the surface and volume homogeneity of the fabricated solid phantoms. The right side of the Fig. 2 shows the layout of the measurement sites used during the second measurement step.
2.5. Collimated transmittance measurements
The collimated transmittance signal of 35 cuvettes (1-cm path length Q-VETTES, Ratiolab, Germany) containing the absorbing SiliGlass phantoms was measured using a cuvette holder (CUV-UV/VIS, Avantes, The Netherlands), two 200-µm optical fibers connecting the broadband tungsten-halogen light source (SLS201/M, Thorlabs Inc., USA) and a spectrograph-based (V10E, Specim, Finland) multichannel spectrometer. Collimated transmittance was defined as a ratio between the dark corrected collimated transmittance signal of an absorbing phantom and dark corrected collimated transmittance signal of a reference transparent phantom without the added absorber. Note that the transparent phantom was used as a reference to maintain the same refractive index mismatch as for the absorbing phantoms. Finally, the measured collimated transmittance was turned into the attenuation coefficient through the Beer-Lambert law.
2.6. Estimation of optical properties by inverse models
The optical properties of SiliGlass phantoms were estimated from the measured SRR by utilizing deep artificial neural network (ANN) inverse models. The preparation of ANN inverse models followed the procedure described in [20]. Briefly, the ANN topology included five layers with 35, 25, 15, 5 and 1 nodes, respectively. Each of the nodes also included an additional bias term, leading to a network with a total of 1586 trainable parameters. The activation functions used in the individual layers were a linear on the input layer, a hyperbolic tangent on the hidden layers and a hard sigmoid on the output layer. Each optical property was estimated by a dedicated deep ANN network. The network inputs were formed by the 5 reflectance values of the measured SRR and the output represented the estimated optical property. The input reflectances were logarithmically scaled and passed through a standard normal variate (SNV) correction. The output was linearly scaled to the [0, 1] range.
The network was trained by MC-simulated SRR for a range of optical properties that included absorption coefficients from 0.0 to 3.0 cm−1, reduced scattering coefficients from 5.0 to 35 cm−1 and subdiffusive quantifier γ from 1.7 to 2.3. The medium was treated as semi-infinite with a refractive index of SiliGlass. A Gegenbauer kernel (GK) scattering phase function [21] was used to calculate the scattering angles. The MC simulations were based on a realistic description of the optical fiber probe tip-sample interface following the details outlined in [22]. Two sets of SRR were prepared. The larger training dataset included about 150,000 SRR and a smaller validation dataset that was used to monitor the quality of the network and stop the training process included about 20,000 SRR.
Prior to the estimation of optical properties the measured SRR, which is normalized to a standard reflectance target, has to be multiplicatively mapped to the MC-simulated SRR by a calibration coefficient. The calibration coefficients were obtained by dividing the measured and simulated SRR acquired from water-based polystyrene microsphere suspension with a diameter of 1.01 µm (MicroParticles GmbH, Germany).
The prepared inverse models were validated on water-based polystyrene microsphere suspensions with a diameter of 0.525 µm and an additional molecular absorber (Live Line Green) with an absorption peak at approximately 630 nm. The root mean square error of the absorption and reduced scattering coefficients, and subdiffusive quantifier γ resulted in 0.022 cm−1, 0.30 cm−1 and 0.027, respectively. More details on the validation of our recent ANN-based inverse model can be found in [23].
It should also be noted that the use of GK scattering phase function is required to describe the backscattered light due to the small source-detector separation of the utilized optical fiber probe and the resulting subdiffusive regime. We have thoroughly investigated the subdiffusive regime in previous publications [24,25]. Further details on the efficient and accurate sampling of the scattering angles in MC simulations from scattering phase functions with no analytical inverse cumulative distribution function, such as the Mie scattering phase function of microspheres, can be found in [26].
3. Results and discussion
3.1. Refractive index of SiliGlass phantoms
The measured refractive indices of SiliGlass phantoms were consistent and did not depend on the amount of black silicone pigment or hollow silica spheres included in the optical phantom.
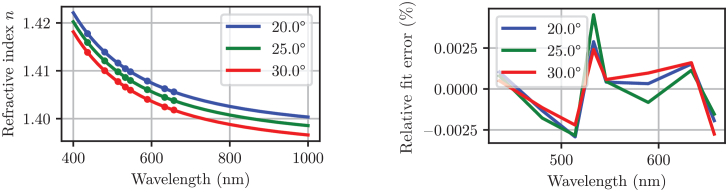
As shown in Fig. 3, the variability of the measured refractive indices was within 0.02% of the average calculated across all the SiliGlass phantoms at a given temperature. Consequently, a single one-term Sellmeier equation was fit to all the refractive indices that were measured at a particular temperature. Table 3 summarizes the obtained parameters of the one-term Sellmeier equations and Fig. 4 shows the corresponding relative fit errors. We can see that a one-term Sellmeier equation nicely fits the measured refractive indices resulting in a small relative error that is within 0.003% of the measured values.
Fig. 3.
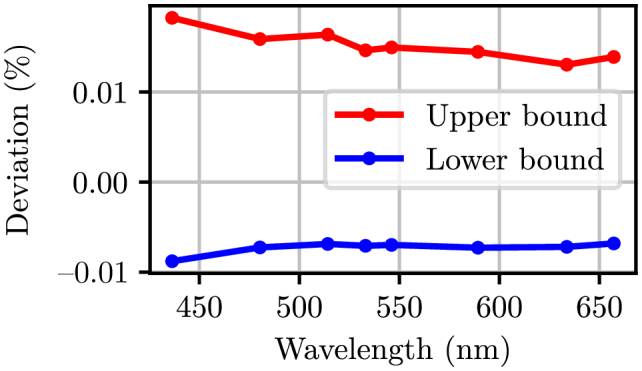
Maximum and minimum relative deviation of the measured refractive indices from the average refractive index at three temperatures (20°, 25° and 30°) computed across all the SiliGlass phantoms.
Table 3. Parameters of a one-term Sellmeier equation (Eq. (2)) for the refractive index of SiliGlass at three temperatures.
| Parameter | 20.0 °C | 25.0 °C | 30.0 °C |
|---|---|---|---|
| a 0 | 0.95007197 | 0.94511839 | 0.93973639 |
| a 1 | 0.05943376 | 0.05944601 | 0.05930627 |
| λ0 | 436.4 nm | 436.4 nm | 436.4 nm |
Fig. 4.
(left) Refractive index of SiliGlass phantoms estimated by a one-term Sellmeier equation. The measured values are denoted by a dot. (right) Relative fit error of the one-term Sellmeier equation.
3.2. Scattering phase function of SiliGlass phantoms
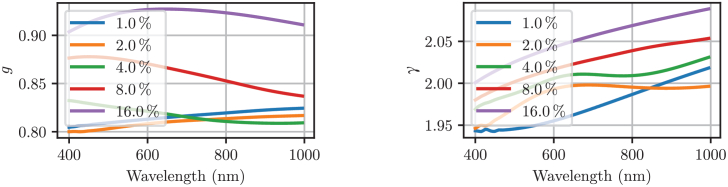
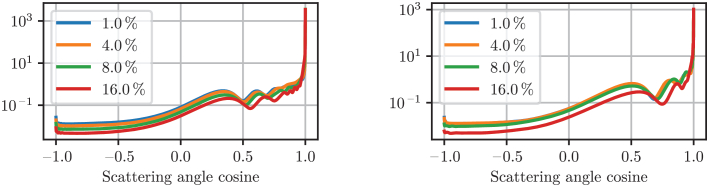
The values required for numerical calculations of the scattering phase function anisotropy g and subdiffusive quantifier γ were selected following the information available from the supplier. The scattering phase functions were computed using a normal size distribution of hollow spheres with an average diameter of d = 11 µm and a standard deviation of σ = 1.5 µm (according to the specifications given for the hollow silica spherical particles). The distribution was cut off at d ± 5σ to exclude physically meaningless negative diameters and large diameters for which the numerical solutions are not accurate. A wide range of wall thickness was investigated for the hollow spheres. The values were normalized by the outer sphere diameter and ranged from 1 to 16%. The numerical calculations presumed that the wall thickness linearly scales with the outer diameter of the sphere. The refractive index of fused silica was taken from [27]. The values of the anisotropy factor g and subdiffusive quantifier γ as a function of the wall thickness are summarized in Fig. 5. The results show that the values of g and γ do not significantly change with wavelength. The wall thickness of the hollow spherical particles does not significantly affect g or γ if under 4% of the sphere diameter. However, increasing the wall thickness beyond 4% of the sphere diameter leads to increasing g values that converge towards 0.99. This observation is expected, since the refractive indices of the SiliGlass and silica are similar and hence once the hollow volume of the sphere is reduced, the scattering becomes increasingly forward directed.
Fig. 5.
(left) Anisotropy g of the scattering phase function and (right) subdiffusive quantifier γ calculated for hollow silica spherical particles suspended in SiliGlass as a function of the wall thickness expressed in terms of the particle diameter (%). A normal size distribution with an average of 11 µm and a standard deviation of 1.5 µm was used in the calculations.
Finally, the scattering phase functions of the optical phantoms were computed for the lower 475 nm and upper 922 nm end of the investigated spectral range. The results presented in Fig. 6 reveal the unique angular features of the scattering phase function for different wall thicknesses.
Fig. 6.
Scattering phase function of normally distributed (average diameter d = 11 µm, standard deviation σ = 1.5 µm, clipped to d ± 5σ) hollow silica spherical particles suspended in SiliGlass at 475 nm (left) and 925 nm (right) as a function of the wall thickness expressed in terms of the particle diameter (%).
3.3. Reflectance measurements
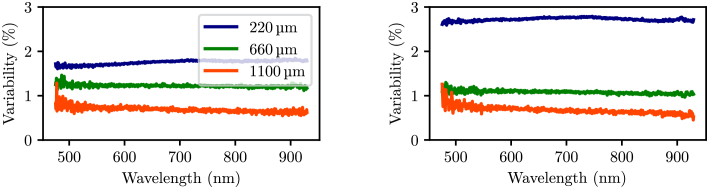
The variability of the reflectance acquired at the same or different measurement sites (as suggested by Fig. 2) for 220, 660 and 1100 µm source-detector separations on the SiliGlass phantom Cc is demonstrated in Fig. 7. The variability is expressed as a ratio between the standard deviation and the mean of the 12 acquired reflectance spectra at each available wavelength. While only data from SiliGlass phantom Cc is presented, other phantoms exhibited similar or even lower reflectance variabilities. Note that the variability of reflectance acquired from a single measurement site on the SiliGlass phantom mainly corresponds to the repeatability of optical contact between the optical probe and the phantom, whereas the variability of reflectance acquired from multiple measurement sites can arise from the repeatability of the optical contact, and surface and volume inhomogeneities of the phantoms.
Fig. 7.
Variability of reflectance acquired from a single (left) and from multiple (right) measurement sites on the SiliGlass phantom Cc demonstrated for three out of five source detector separations (see the legend).
Variability of reflectance acquired from a single measurement site on the phantom is below 2% for all SDSs (Fig. 7), which is considered satisfactory. The variability improves with increasing SDSs and for 1100 µm falls below 1% suggesting that longer SDSs are less sensitive to the positioning of the probe and optical contact.
While the variability of reflectance acquired from multiple measurement sites on the phantom increases from the previous example, the worst variability observed for the 220 µm SDS is still below 3%. Note that for longer SDSs this effect is not as apparent and again suggests that longer SDSs are less sensitive to uncertainties arising from the optical contact, and surface and volume inhomogeneities. We attribute this finding to the fact that the sampling volume increases with the distance from the source fiber and thus averages out local non-homogeneities of the SiliGlass phantoms.
3.4. Collimated transmittance measurements and total attenuation coefficient
Before the 35 cuvettes were filled with the absorbing SiliGlass phantoms, collimated transmittance of empty cuvettes was measured to investigate the collimated transmittance variability due to potential differences in cuvettes. The collimated transmittance variability at a given wavelength was calculated as a ratio between the standard deviation and mean of the collimated transmittance collected from 35 cuvettes. Figure 8 shows the mean collimated transmittance accompanied by a green stripe representing the standard deviation. Pale red region represents the calculated relative variability with the corresponding y-axis on the right hand side of the Fig. 8. Note that the collimated transmittance variability is less than 0.5% across the utilized wavelength range indicating the collimated transmittance measurements are highly repeatable. Five cuvettes filled with a transparent SiliGlass phantom served as a reference for the remaining cuvettes filled with absorbing SiliGlass phantoms. The resulting normalized collimated transmittance can be directly converted to the total attenuation coefficient by the Beer-Lambert law. However, it is important to realize that while such an approach eliminates issues arising from the refractive index mismatch, it also eliminates the intrinsic absorption of the transparent SiliGlass phantom.
Fig. 8.
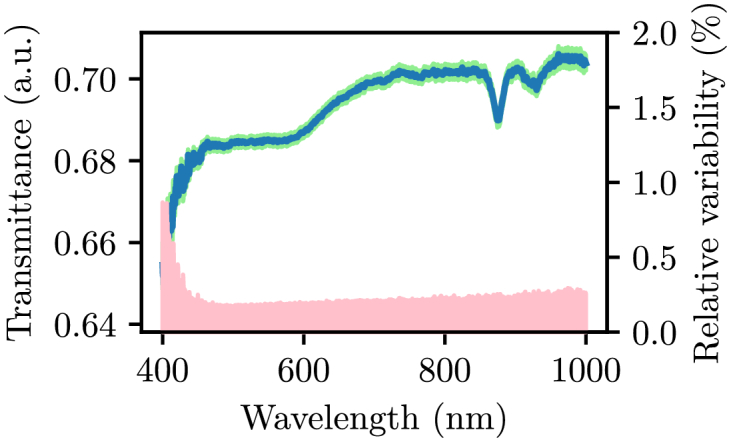
Mean collimated transmittance (blue line) of 35 empty cuvettes accompanied by the standard deviation interval (green region) and relative variability (pale red region, y-axis to the right).
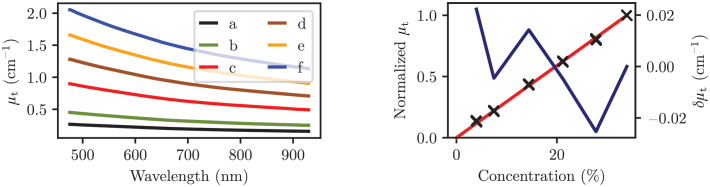
The left side of Fig. 9 shows the mean total attenuation coefficient of absorbing SiliGlass phantoms (a, b, c, d, e, f – increasing in concentration), each calculated from measured collimated transmittance through 5 cuvettes. The standard deviation of the total attenuation coefficient is less than the thickness of the lines and therefore it is not shown.
Fig. 9.
(left) Measured total attenuation coefficients µt of absorbing SiliGlass phantoms from series a, b, c, d, e, f (increasing in concentration and absorption). (right) Normalized total attenuation coefficient µt (see text for details) as a function of concentration in the absorbing SiliGlass phantoms (black crosses represent measured normalized µt and red line the ideal linear relationship with the concentration). The navy blue line shows the absolute deviation δµt of the total attenuation coefficient from the ideal linear relationship at a single wavelength point (633 nm).
One of the most important properties of an absorbing agent is the linearity with increasing concentration. The right side of Fig. 9 shows the concentration dependence of the total attenuation coefficient µt normalized to its highest µt value at each wavelength. Each concentration point therefore comprises a group of normalized µt points (shown with black crosses) that should in principle follow the ideal linear relationship represented with the red line. The navy blue line shows the absolute deviation from the ideal linear relationship for total attenuation coefficient at 633 nm. Note that the absolute value of the deviation hardly exceeds 0.02 cm−1, suggesting a highly linear relationship between the concentration and the total attenuation coefficient.
It should be noted that the total attenuation coefficient as calculated through the measured transmittance is almost twice the absorption coefficient as measured on the turbid SiliGlass phantoms (see Section 3.5). We believe that the rationale for the observed discrepancy is the significant scattering component of the black silicone pigment. Scanning electron microscope image indeed reveals that the pigment exhibits lumps in sizes between 0.1 and 1 µm (Fig. 10, left). To this ends, we have qualitatively investigated the scattering intensity from several samples including blue molecular fountain pen dye, deionized water, absorbing and transparent SiliGlass phantom (Fig. 10, right). It is apparent that the absorbing SiliGlass phantom (third cuvette from left) is qualitatively significantly more scattering than the other samples. For this demonstration we used the absorbing SiliGlass phantom of the type f, i.e. with the highest absorption coefficient.
Fig. 10.
(left) Scanning electron microscope image of the absorbing agent. (right) Qualitative demonstration of the scattering component in the absorbing agent of the SiliGlass phantom. From left to right: molecular water-based absorber, transparent SiliGlass phantom, absorbing SiliGlass phantom and water.
According to these results, we have therefore shown that the black silicone pigment cannot be easily characterized through collimated transmittance, which would yield an independent estimate of the absorption coefficient. Moreover, according to the results obtained in Section 3.5, the contribution of the scattering coefficient to the total attenuation coefficient is approximately 1 cm−1 or less at the highest concentration of the black silicone pigment.
3.5. Estimation of SiliGlass phantom optical properties by inverse model
Optical properties of SiliGlass phantoms Da, Dc and Df were estimated from reflectance acquired at 12 points distributed on the surface of the phantoms as shown in Fig. 2. We utilized only a subset of SiliGlass phantoms in order to study the trend in the absorption coefficient and to compare it to the collimated transmittance measurements in Sect. 3.4. Moreover, optical fiber probes with small SDS are very sensitive to the scattering phase function especially at lower reduced scattering coefficients. Therefore, we have opted for type “D” SiliGlass phantoms with the highest possible reduced scattering coefficient.
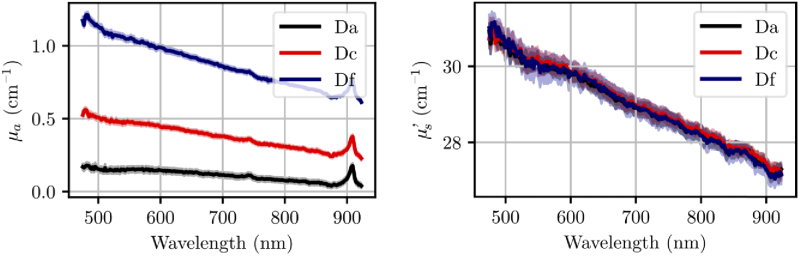
The left side of Fig. 11 shows the mean estimated absorption coefficients and the right side of Fig. 11 the mean estimated reduced scattering coefficients for the SiliGlass phantoms Da, Dc and Df with the standard deviation presented as a lighter region. The mean and the standard deviation were calculated amongst the 12 different measurements performed on each phantom. It can be observed that the absorption coefficients are approximately half of the total attenuation coefficient shown in Fig. 9. As already pointed out in Section 3.4, the black silicone pigment exhibits a significant scattering component. This scattering component amounts to approximately 1 cm−1 scattering coefficient at the lower wavelengths. For anisotropy factors of approximately 0.8 for the black pigment, this would result in 0.2 cm−1 reduced scattering coefficient. Such a value would hardly be noticeable for type “D” SiliGlass phantoms. Of course, the anisotropy factor for the black pigment is not known and could be less than 0.8 based on the SEM image in Fig. 10. In this case, the reduced scattering coefficient would be higher and would also significantly contribute to the total reduced scattering coefficient of the SiliGlass phantoms. However, we can see that for all three SiliGlass phantoms Da, Dc and Df, the reduced scattering coefficients overlap and there is no obvious trend with the concentration of the black silicone pigment.
Fig. 11.
Absorption coefficient (left) and reduced scattering coefficient (right) of phantoms Da, Dc and Df as estimated by our ANN inverse model. The shaded areas correspond to the spread of parameters (one standard deviation) estimated among the 12 different measurement sites.
In comparison to the measurements of Konugolu Venkata Sekar et al., that reported a reduced scattering coefficient of 25.2 cm−1 at 600 nm for phantom Da, our estimation of the reduced scattering coefficient is 30.0 cm−1. Similar observations can be made for the absorption coefficient, where our values again somewhat exceed the values reported by Konugolu Venkata Sekar et al.
There can be numerous reasons for the observed discrepancies. For example, the anisotropy factor g of the hollow silica spheres used in the two studies might be different, since the hollow spherical particles are not fully characterized by the supplier. Similar conclusions could be made about the absorption coefficient of the black pigment. Next, during the mixing of components A and B, some of the material will inevitably stick to the container wall and not make it into the phantom. If this is not properly measured and subsequently used to correct the composition of the mixture, significant errors can be introduced.
In addition to the described differences in the phantom preparation procedure, we would also like to point out the difference in the methodology of our study and the study by Konugolu Venkata Sekar et al. It should be noted that we utilized spatially resolved reflectance spectroscopy with small source-detector separations that is particularly useful for determination of scattering phase function related subdiffusive parameters such as γ. While the estimated optical properties should in principle be independent of the utilized methodology, inherent differences such as source-detector arrangement could render deviations in the estimated optical properties, especially if the optical phantom is not completely homogeneous. For example, while our study utilized a reflectance setup with small source-detector separations, Konugolu Venkata Sekar et al., utilized a transmittance setup with larger source-detector separations. Therefore, different sampling volumes could yield optical properties of different parts of the phantom. Furthermore, our inverse model is based on MC modeling (numerical solution of RTE) that accounts for the sample refractive index and scattering phase function variability, while Konugolu Venkata Sekar et al., used a diffusion approximation to estimate the optical properties. For a complete validation of our revised phantom recipe, we would additionally have to perform time-of-flight measurements with a similar geometry as used in the study by Konugolu Venkata Sekar et al.
Figure 12 shows the subdiffusive quantifier γ of SiliGlass phantoms Da, Dc and Df as estimated by our ANN inverse model. The subdiffusive quantifier γ for the SiliGlass phantoms should be the same regardless of the concentration of the absorbers and scatterers, since it is a property of the scattering phase function, and the latter, the property of the shape and size of the scatterers. We can see that this is in fact the case and that the subdiffusive quantifier γ slightly increases with the wavelength. The standard deviation of the subdiffusive quantifier γ is approximately ± 0.05 or ± 2.5%. Remarkably, the obtained values also very much agree with the prediction made by our numerical calculations in Fig. 5. However, it should be noted, that the numerical calculations show a relatively small variability of the subdiffusive quantifier γ for a wide range of wall thicknesses from 1% to 16%.
Fig. 12.
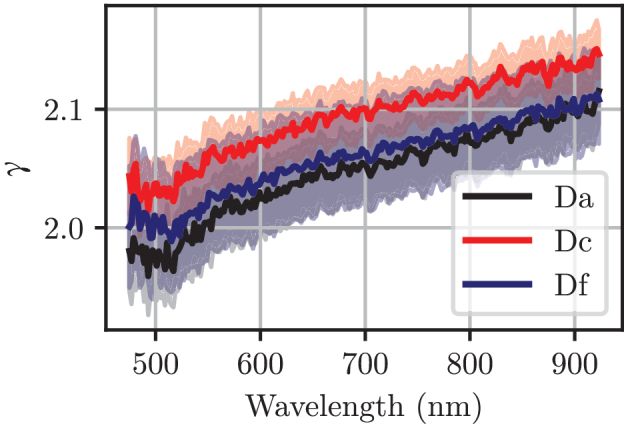
The subdiffusive quantifier γ of phantoms Da, Dc and Df as estimated by our ANN inverse model. The shaded areas correspond to the spread of parameters estimated from the 12 different measurement sites.
3.6. Potential limitations of the SiliGlass phantom recipe and utilized methodology for estimation of optical properties
While the SiliGlass phantom recipe and the protocol itself should guarantee a high level of reproducibility within a single-batch of phantom constituents, batch-to-batch variations of the constituents could still pose a problem, since they are not standardized and lack information on the quality control. Konugolu Venkata Sekar et al., [13] have studied the batch-to-batch variations and found a 4% coefficient of variation. A more thorough study would be welcome, ideally in various laboratories within the biomedical optics community.
In terms of the utilized methodology, two main limitations can be put forth that can interfere with the accuracy of the estimated optical properties. First, the optical contact between the fibers and the SiliGlass phantom is assumed as ideal in the Monte Carlo method that is used to build the inverse model. Any deviations from such an assumption could degrade the accuracy of the estimated optical properties. The amplitude of the negative impact on the accuracy would have to be studied separately. However, while optical probes can be problematic when phantoms are completely solid, it should be noted that in the case of SiliGlass phantoms, we have observed highly repeatable reflectance measurements and excellent optical contact, which can be attributed to the soft and elastic physical properties of the SiliGlass phantoms that form a tight contact with the optical fiber probe tip.
Second limitation of our methodology are short source-detector separations which render lower sensitivity to the absorption coefficient. Consequently, lower absorption coefficients, especially for the Da phantom, are expected to have higher relative error. Short source-detector separations have also influenced our selection of the phantom set, which included only the highest scattering ones (Da, Dc, Df). Reflectance at short source-detector separations is highly sensitive to the shape of the scattering phase function, since light is only weakly scattered prior to detection. Therefore, potential uncertainty can also arise from the influence of the scattering phase function. However, in one of our publications we have shown that our initial methodology yields accurate results for reduced scattering coefficients above 15 cm−1 [24]. Moreover, in recent publications that summarize the improved methodology used in this work, we have markedly improved the imposed limit [23,25].
4. Conclusions
We have conducted a detailed characterization of the optical properties for PlatSil SiliGlass tissue-mimicking optical phantoms. The original preparation procedure of optical phantoms was slightly modified by cooling down the two components of SiliGlass before mixing and thereby prolonging the polymerization process, which allowed easier handling, improved mixing, and better degassing of the phantoms. Furthermore, it is essential to weigh the individual ingredients and components and the final mixture, since some of the material will inevitably stick to the container wall. The collected data can then be backtracked and used to accurately compute the parameters of optical phantoms. The results show that the refractive index of phantoms is independent of the content of hollow silica spheres and black pigment. The attenuation coefficient exhibits highly linear relationship with the concentration of the black pigment. However, we have found that the scattering component of the black pigment particles also contributes to the total attenuation coefficient. This contribution amounts to about 1 cm−1 at the lower end of the investigated spectral range. The scattering phase function anisotropy of phantoms was found to largely depend on the wall thickness of the hollow spheres and is expected to range between 0.8 and 0.9. In contrast, the subdiffusive scattering phase function quantifier γ is much less sensitive to the wall thickness and is expect to range from 1.9 to 2.1 with a small positive slope as a function of wavelength. Given the above conclusions and the fact that the hollow spherical particles and black pigment are not fully characterized by the manufacturers and are also very likely subject to inter-batch variability, the prepared optical phantoms should be characterized by alternative means to independently verify the optical properties.
Funding
Javna Agencija za Raziskovalno Dejavnost RS10.13039/501100004329 (J2-7118, J2-7211, J2-8171, J2-8173, P1-0389, P2-0232); European Regional Development Fund10.13039/501100008530 (SME 2/17-19/2017); Republic of Slovenia.
Disclosures
The authors declare that there are no conflicts of interest.
References
- 1.Pogue B. W., Patterson M. S., “Review of tissue simulating phantoms for optical spectroscopy, imaging and dosimetry,” J. Biomed. Opt. 11(4), 041102 (2006). 10.1117/1.2335429 [DOI] [PubMed] [Google Scholar]
- 2.Ninni P. D., Martelli F., Zaccanti G., “The use of India ink in tissue-simulating phantoms,” Opt. Express 18(26), 26854–26865 (2010). 10.1364/OE.18.026854 [DOI] [PubMed] [Google Scholar]
- 3.Spinelli L., Botwicz M., Zolek N., Kacprzak M., Milej D., Sawosz P., Liebert A., Weigel U., Durduran T., Foschum F., Kienle A., Baribeau F., Leclair S., Bouchard J.-P., Noiseux I., Gallant P., Mermut O., Farina A., Pifferi A., Torricelli A., Cubeddu R., Ho H.-C., Mazurenka M., Wabnitz H., Klauenberg K., Bodnar O., Elster C., Benazech-Lavoue M., Berube-Lauziere Y., Lesage F., Khoptyar D., Subash A. A., Andersson-Engels S., Di Ninni P., Martelli F., Zaccanti G., “Determination of reference values for optical properties of liquid phantoms based on Intralipid and India ink,” Biomed. Opt. Express 5(7), 2037–2053 (2014). 10.1364/BOE.5.002037 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ninni P. D., Martelli F., Zaccanti G., “Intralipid: towards a diffusive reference standard for optical tissue phantoms,” Phys. Med. Biol. 56(2), N21–N28 (2011). 10.1088/0031-9155/56/2/N01 [DOI] [PubMed] [Google Scholar]
- 5.Hull E. L., Nichols M. G., Foster T. H., “Quantitative broadband near-infrared spectroscopy of tissue-simulating phantoms containing erythrocytes,” Phys. Med. Biol. 43(11), 3381–3404 (1998). 10.1088/0031-9155/43/11/014 [DOI] [PubMed] [Google Scholar]
- 6.Bodenschatz N., Krauter P., Foschum F., Nothelfer S., Liemert A., Simon E., Kröner S., Kienle A., “Surface layering properties of Intralipid phantoms,” Phys. Med. Biol. 60(3), 1171–1183 (2015). 10.1088/0031-9155/60/3/1171 [DOI] [PubMed] [Google Scholar]
- 7.Leh B., Siebert R., Hamzeh H., Menard L., Duval M.-A., Charon Y., Haidar D. A., “Optical phantoms with variable properties and geometries for diffuse and fluorescence optical spectroscopy,” J. Biomed. Opt. 17(10), 108001 (2012). 10.1117/1.JBO.17.10.108001 [DOI] [PubMed] [Google Scholar]
- 8.Nivetha K. B., Sujatha N., “Development of thin skin mimicking bilayer solid tissue phantoms for optical spectroscopic studies,” Biomed. Opt. Express 8(7), 3198–3212 (2017). 10.1364/BOE.8.003198 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Saager R. B., Quach A., Rowland R. A., Baldado M. L., Durkin A. J., “Low-cost tissue simulating phantoms with adjustable wavelength-dependent scattering properties in the visible and infrared ranges,” J. Biomed. Opt. 21(6), 067001 (2016). 10.1117/1.JBO.21.6.067001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Jones C. J. M., Munro P. R. T., “Stability of gel wax based optical scattering phantoms,” Biomed. Opt. Express 9(8), 3495–3502 (2018). 10.1364/BOE.9.003495 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Ghassemi P., Wang J., Melchiorri A. J., Ramella-Roman J. C., Mathews S. A., Coburn J. C., Sorg B. S., Chen Y., Pfefer T. J., “Rapid prototyping of biomimetic vascular phantoms for hyperspectral reflectance imaging,” J. Biomed. Opt. 20(12), 121312 (2015). 10.1117/1.JBO.20.12.121312 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Dempsey L. A., Persad M., Powell S., Chitnis D., Hebden J. C., “Geometrically complex 3D-printed phantoms for diffuse optical imaging,” Biomed. Opt. Express 8(3), 1754–1762 (2017). 10.1364/BOE.8.001754 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sekar S. K. V., Pacheco A., Martella P., Li H., Lanka P., Pifferi A., Andersson-Engels S., “Solid phantom recipe for diffuse optics in biophotonics applications: a step towards anatomically correct 3D tissue phantoms,” Biomed. Opt. Express 10(4), 2090 (2019). 10.1364/BOE.10.002090 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Bevilacqua F., Depeursinge C., “Monte Carlo study of diffuse reflectance at source–detector separations close to one transport mean free path,” J. Opt. Soc. Am. A 16(12), 2935–2945 (1999). 10.1364/JOSAA.16.002935 [DOI] [Google Scholar]
- 15.Bodenschatz N., Krauter P., Liemert A., Kienle A., “Quantifying phase function influence in subdiffusively backscattered light,” J. Biomed. Opt 21(3), 035002 (2016). 10.1117/1.JBO.21.3.035002 [DOI] [PubMed] [Google Scholar]
- 16.McClatchy D. M., Rizzo E. J., Wells W. A., Cheney P. P., Hwang J. C., Paulsen K. D., Pogue B. W., Kanick S. C., “Wide-field quantitative imaging of tissue microstructure using sub-diffuse spatial frequency domain imaging,” Optica 3(6), 613–621 (2016). 10.1364/OPTICA.3.000613 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kanick S. C., McClatchy D. M., Krishnaswamy V., Elliott J. T., Paulsen K. D., Pogue B. W., “Sub-diffusive scattering parameter maps recovered using wide-field high-frequency structured light imaging,” Biomed. Opt. Express 5(10), 3376–3390 (2014). 10.1364/BOE.5.003376 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bohren C. F., Huffman D. R., Absorption and Scattering of Light by Small Particles (John Wiley & Sons, 2008). [Google Scholar]
- 19.Ladutenko K., Pal U., Rivera A., Peña-Rodríguez O., “Mie calculation of electromagnetic near-field for a multilayered sphere,” Comput. Phys. Commun. 214, 225–230 (2017). 10.1016/j.cpc.2017.01.017 [DOI] [Google Scholar]
- 20.Ivančič M., Naglič P., Pernuš F., Likar B., Bürmen M., “Efficient estimation of subdiffusive optical parameters in real time from spatially resolved reflectance by artificial neural networks,” Opt. Lett. 43(12), 2901–2904 (2018). 10.1364/OL.43.002901 [DOI] [PubMed] [Google Scholar]
- 21.Reynolds L. O., McCormick N. J., “Approximate two-parameter phase function for light scattering,” J. Opt. Soc. Am. 70(10), 1206 (1980). 10.1364/JOSA.70.001206 [DOI] [Google Scholar]
- 22.Naglič P., Pernuš F., Likar B., Bürmen M., “Limitations of the commonly used simplified laterally uniform optical fiber probe-tissue interface in Monte Carlo simulations of diffuse reflectance,” Biomed. Opt. Express 6(10), 3973–3988 (2015). 10.1364/BOE.6.003973 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Zelinskyi Y., Naglič P., Pernus F., Likar B., Burmen M., “Fast and accurate Monte Carlo simulations of subdiffusive spatially resolved reflectance for realistic optical fiber probe tip model aided by deep neural networks,” Biomed. Opt. Express 11(6) 108720R (2020). 10.1364/BOE.391720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Naglič P., Pernuš F., Likar B., Bürmen M., “Estimation of optical properties by spatially resolved reflectance spectroscopy in the subdiffusive regime,” J. Biomed. Opt. 21(9), 095003 (2016). 10.1117/1.JBO.21.9.095003 [DOI] [PubMed] [Google Scholar]
- 25.Naglič P., Pernuš F., Likar B., Bürmen M., “Adopting higher-order similarity relations for improved estimation of optical properties from subdiffusive reflectance,” Opt. Lett. 42(7), 1357–1360 (2017). 10.1364/OL.42.001357 [DOI] [PubMed] [Google Scholar]
- 26.Naglič P., Pernuš F., Likar B., Bürmen M., “Lookup table-based sampling of the phase function for Monte Carlo simulations of light propagation in turbid media,” Biomed. Opt. Express 8(3), 1895–1910 (2017). 10.1364/BOE.8.001895 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Malitson I., “Interspecimen Comparison of Refractive Index of Fused Silica,” J. Opt. Soc. Am. 55(10), 1205 (1965). 10.1364/JOSA.55.001205 [DOI] [Google Scholar]