Categorical rhythms are shared between songbirds and humans

Summary

Rhythm is a prominent feature of music. Of the infinite possible ways of organizing events in time, musical rhythms are almost always distributed categorically. Such categories can facilitate the transmission of culture – a feature that songbirds and humans share. We compared rhythms of live performances of music to rhythms of wild thrush nightingale and domestic zebra finch songs. In nightingales, but not in zebra finches, we found universal rhythm categories, with patterns that were surprisingly similar to those of music. Isochronous 1:1 rhythms were similarly common. Interestingly, a bias towards small ratios (around 1:2 to 1:3), which is highly abundant in music, was observed also in thrush nightingale songs. Within that range, however, there was no statistically significant bias toward exact integer ratios (1:2 or 1:3) in the birds. High-ratio rhythms were abundant in the nightingale song and are structurally similar to fusion rhythms (ornaments) in music. In both species, preferred rhythms remained invariant over extended ranges of tempos, indicating natural categories. The number of rhythm categories decreased at higher tempos, with a threshold above which rhythm became highly stereotyped. In thrush nightingales, this threshold occurred at a tempo twice faster than in humans, indicating weaker structural constraints and a remarkable motor proficiency. Together, the results suggest that categorical rhythms reflect similar constraints on learning motor skills across species. The saliency of categorical rhythms across humans and thrush nightingales suggests that they promote, or emerge from, the cultural transmission of learned vocalizations.

Introduction

Musical rhythms consist mostly of a few distinct classes of intervals. A particularly prominent class are isochronous rhythms, in which approximately identical intervals are repeated [1]. In non-isochronous rhythms, the ratio between intervals often forms a simple integer ratio such as 1:2 or 1:3. Consistent with this, Western musical notation reflects the prominence of small-integer rhythms [2]. Other types of music, however, deviate from integer ratios [3–6]. Notably, Malian Jembe drummers perform ratios smaller than 1:1.5 which are maintained during tempo changes [4,7]. The extent to which simple integer ratios are universal is therefore controversial [8–12]. A third common type of musical rhythms are fast transitions that “ride” on slower (often isochronous) rhythms. These are sometimes referred to as “ornaments” or “grace notes”. Ornaments are typically applied on top of the regular beat structure, their time being “stolen” from adjacent notes instead of adding to the beat [13][14]. Such “fused” rhythms (with high interval ratios) are often generated with a single gesture exploiting biomechanics (for example, creating a slight phase shift between hands generating a “flam”, a near-unison double stroke, or by “flutter-tonguing” on a wind instrument) [3,13,15,16]. Fused rhythms are associated with perceptual constraints: Humans can perceive tempos as a “regular” beat with an upper bound of about 100–200 ms (5–10 Hz) [17,18]. Therefore, they usually avoid producing faster tempos, with the exception of fused rhythms. Here we test if these rhythm types – isochronous, small-integer ratio, and fused rhythms –, form distinct clusters in naturally occurring song of two songbird species: wild thrush nightingales (Luscinia luscinia) and domesticated zebra finches (Taeniopygia guttata).

Among songbirds, thrush nightingales produce particularly elaborated and stereotyped rhythms in their song [19–21]. Songs are composed of sub-phrases with repetitive one- to five-interval patterns spanning a wide range of tempos and note types (Figure 1A). Thrush nightingales form local song dialects by imitating and sharing each others’ repertoires [19]. In contrast to the complexity of the nightingale song, zebra finches sing a single rhythmic phrase type called ‘motif’, which is repeated without much variation and remains largely stable throughout life (Figure 2A). Zebra finch songs include stable, ‘metronomic’ rhythms [22], but as opposed to nightingales, there is no evidence for stable song dialects in either wild or domesticated zebra finches [23]. We compared song rhythms in these two species to those of live musical performances and to finger tapping experiments, using similar methods. Restricting our rhythm analysis to ratios of adjacent onset-to-onset intervals (first order dyadic rhythms) allows us to focus on patterns that are well-studied across different human rhythmic behaviors and comparable across species. Analysis of amplitude envelopes allowed us to extract syllable onsets from a collection of single- and multiple-instrument musical corpora, matching seven musical traditions from around the world: Western classical piano, Indian Raga, Cuban Salsa, Malian Jembe, Uruguayan Candombe, Tunisian Stambeli and Persian Zarb. For multi-instrument music (all corpora except Western piano and Persian Zarb), we extracted two-interval rhythms in two manners: for each instrument separately, and for the surface rhythm of multi-instrument music combined.

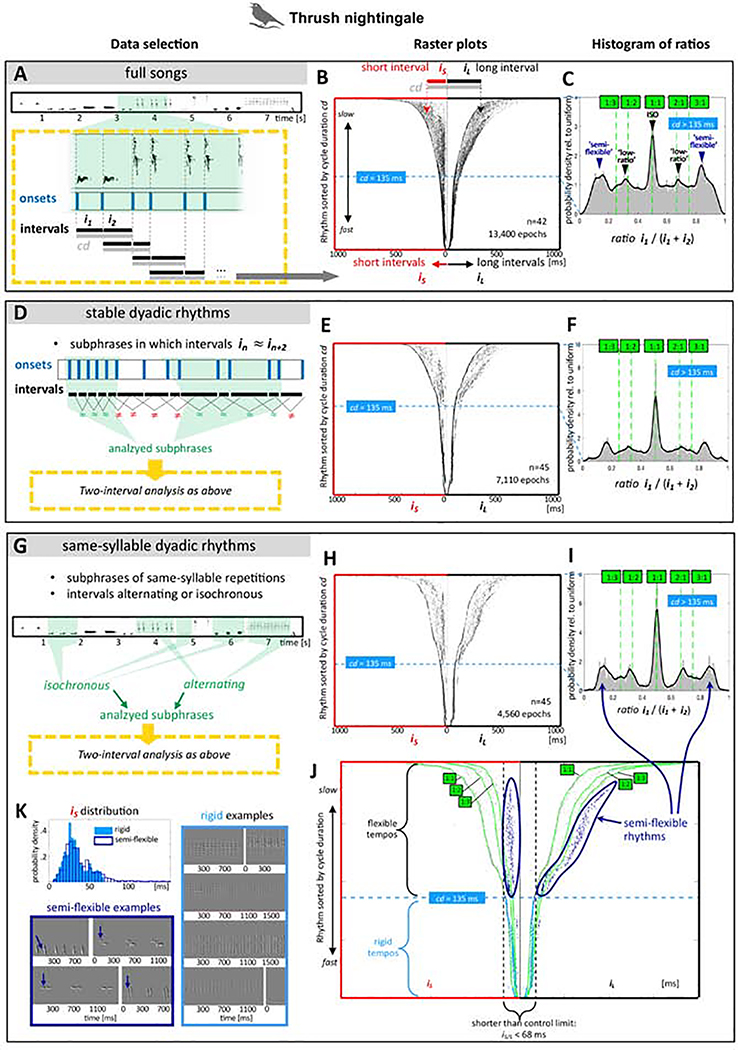
Figure 1. Rhythms of wild thrush nightingale song.

A-C: Rhythm analysis of the entire song database (unfiltered). D-F: Rhythm analysis of stable rhythm intervals. G-J: Rhythm analysis of same-syllable rhythms. Left panels (A,D,G): Schematics depicting extraction of two-interval rhythms. Middle column (B,E,H): Raster plots of pooled rhythms (across birds), sorted by cycle duration (cd). Each two-interval segment is represented by a pair of horizontally aligned markers. The short interval i_S is represented by a marker on the left and the long interval i_L by a marker on the right (highlighted in B). Note that each interval thus occurs twice in the raster plot, namely once with its preceding and once with its subsequent interval. Narrow ‘stems’ outlined by dotted lines (at cd=135 ms) indicate a boundary: Rhythms that are faster than this are mostly unimodal (i.e., inflexible). Fanning-out ‘petals’ above the boundary indicate a diversity of rhythms at slower tempos. J: Annotated raster plot (same as in H), outlining three distinct clusters at slow tempos: An isochronous cluster (symmetric lines at equal distance from y axis), a semi-flexible (‘ornament’ or ‘fused’ rhythm) cluster marked navy blue, with a pair of a tight short interval, and a variably long interval. A low-ratio cluster can be seen around the 1:2 and 1:3 ratio lines. Right column (C, F, I): Histograms of rhythm ratios (first interval/cycle duration) at the slow tempo range (cd>135 ms). Peaks correspond to rhythm clusters in the raster plots: isochronous (ISO), semi-flexible, and low-ratio rhythms. K: Histograms of short intervals in semi-flexible rhythms (corresponding to navy blue markers on the left side of K), vs. short intervals in inflexible rhythms (below 135ms, corresponding to azure markers on the left side of K), and spectral derivatives of examples. Arrows point to first note in semi-flexible rhythms (‘ornament’).

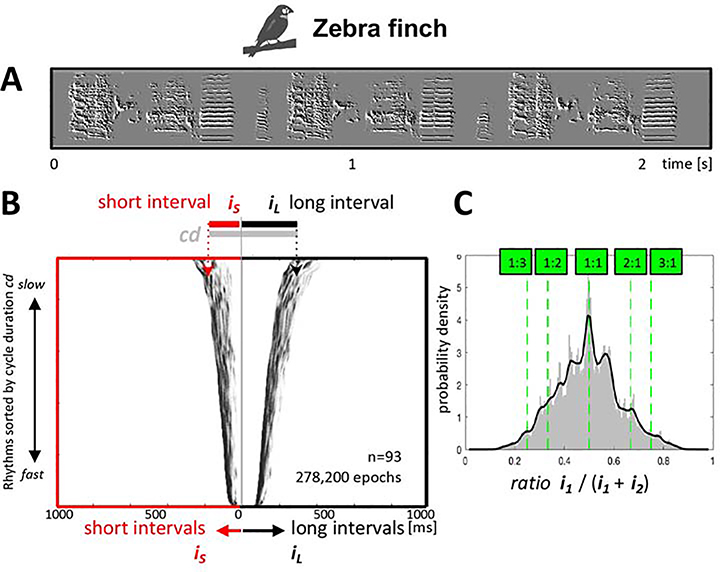
Figure 2. Zebra finch rhythms.

A: a sonogram with spectral derivatives of a zebra finch song showing three repetitions of the bird’s motif. B: Two-interval raster plots of pooled rhythms of 93 zebra finches (as in Figure 1B). C: Histogram with probability density of rhythm ratios pooled across 93 zebra finches.

Results

Rhythm raster plots and histograms of birdsong

We first analyzed songs from 42 individual wild thrush nightingales from the xeno-canto birdsong library (http://www.xeno-canto.org). In each song, we detected syllable onsets and measured the time intervals between onsets (onset-to-onset intervals, Figure 1A). We estimated rhythm structure by comparing the durations of consecutive intervals in pairs (dyadic rhythms). For each pair of consecutive (back-to-back) intervals we evaluate three measures (Figure 1A): The duration of the shorter interval i_S, the duration of the longer interval i_L, and the cycle duration i_S + i_L. Note that in many cases, i_S and i_L were of nearly identical length. We next pooled the data across birds and sorted rhythms by cycle duration to generate a sorted raster plot (Figure 1B). In this plot, we represent each dyadic rhythm by a pair of horizontally aligned markers. The short interval i_S is represented by a marker on the left and the long interval i_L by a marker on the right. Each interval is thus plotted twice, once with its preceding and once with its subsequent interval. In isochronous rhythms, i_S ≈ i_L, and markers appear at similar distances from the central Y axis. Note that corresponding short and long intervals are located on the same horizontal plane.

Figure 1B shows several concentrations of markers (potential rhythm categories). In order to improve signal-to-noise ratio and remove artifacts, we filtered the data using two approaches: In Figure 1D-F, we automatically excluded epochs in which rhythms were unstable (see METHOD DETAILS, ‘Creating three thrush nightingale datasets’ & ‘Obtaining ‘stable-rhythm’ epochs from thrush nightingale songs’). In Figure 1G-I, we present 607 hand-curated epochs in which a single syllable type was repeated rhythmically (see METHOD DETAILS ‘Creating three thrush nightingale datasets’ & ‘Extracting a ‘same-syllable type’ (trill) dataset’). Analysis of these renditions of a single syllable type allows us to test for variation in rhythm ratios that may exist while syllable durations are kept constant.

Despite differences in signal-to-noise ratio, the three raster plots (Figure 1B, E, H) are fairly similar in structure. The symmetrical appearance of the raster plot mirrors the prevalence of isochronous rhythms across a wide range of tempos. An empty gap can be seen next to the isochronous lines, indicating that isochrony is a natural category. This can be seen most clearly in the filtered plots (Figure 1E & H), but a trough surrounding the isochronous peak can be seen in all histograms (Figures 1C, 1F & 1I, for statistical analysis see Figure 3). The raster plots have a flower-like shape, with a narrower ‘stem’, and a top of ‘petals’ that is fanning out. We identified the transition point between ‘stem’ and ‘petals’ by partitioning the data into tempo bins (see QUANTIFICATION AND STATISTICAL ANALYSIS, section ‘Raster plots’), and automatically detecting rhythm peaks in each bin. We found a transition from multiple rhythm peaks to a single stable peak of isochronous rhythms at a cycle duration of 135 ms. It is interesting that this transition can be seen across songs of 42 birds recorded in different regions in Middle, Eastern, and Northern Europe.

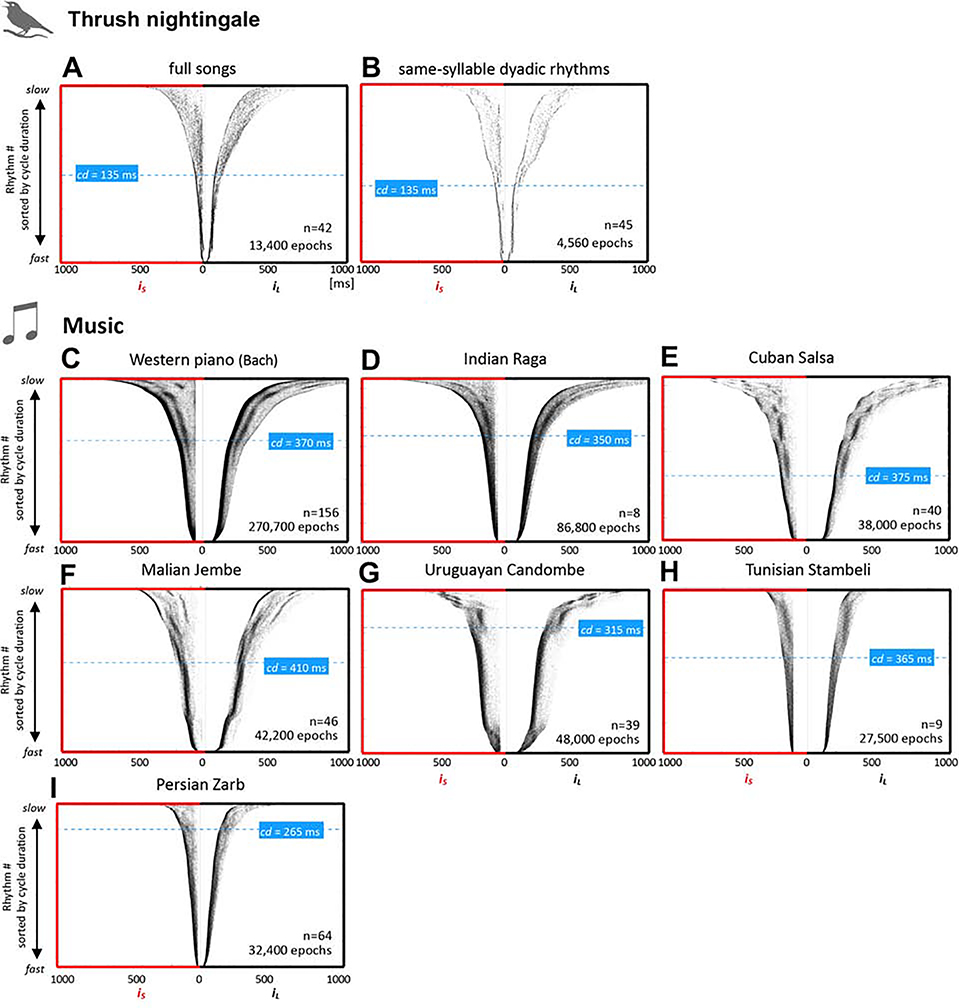
Figure 3: Thrush nightingale song vs. music rhythm structure.

A, B: same sorted raster plots of dyadic rhythm epochs as in Figure 1B & H, for easier interspecies comparison, C-I, sorted raster plots for seven musical corpora from different musical cultures. For multi-instrument music (D-H), rhythms were extracted from each instrument and then pooled together (for surface rhythm across instruments see Figure S1). Dashed blue lines indicate the transition point between stem and petals, blue boxes tempo at transition (as cycle duration [cd]).

Other than isochrony, in cycle durations longer than 135 ms (the ‘petal’ area of the raster plots), we see concentrations of markers (clusters), suggesting additional rhythm categories. The most apparent non-isochronous cluster is marked by navy-blue markers in Figure 1J. Note that as in isochronous rhythms, a clear gap separates this cluster from the rest of the data (Figure 1H & J). Rhythms in this category are highly asymmetric, including one very short interval and one highly variable long interval: The long intervals cover a broad range, but interestingly, the short intervals are invariant to tempo and narrowly distributed (34 ± 11ms). That is, the navy-blue cluster on the left side of Figure 1J appears to be equidistant from the Y axis across the entire tempo range that it covers (between about 500–135 ms cycle duration). Note that invariance to tempo is also a feature of musical fused rhythms [13]. We will refer to this category as ‘semi-flexible rhythms’ (Figure 1K). Importantly, the distribution of these short intervals of semi-flexible rhythms is similar to that of short intervals of inflexible (unimodal) rhythms below the 135 ms threshold (Figure 1K). Further, the upper bound of short intervals in semi-flexible rhythms is about 70 ms, which is about half of the 135 ms tempo threshold (which includes two intervals). Together, these observations suggest that dyadic rhythms below 135 ms and semi-flexible rhythms might reflect the same biophysical constraints.

Finally, there are sparse concentrations of rhythms in the area between isochronous and semi-flexible rhythms, mostly around ratios of 1:2 and 1:3 (Figure 1B,E,H). We will examine these in detail later on, and will refer to them as low-ratio rhythms.

These three rhythm categories - isochronous, semi-flexible, and low-ratio rhythms - can be visualized by plotting histograms of rhythm ratios within the flexible rhythm range (above 135 ms; Figure 1C,F,I). Comparing these histograms across the entire song data (Figure 1C) and stable rhythms (Figure 1F) indicate that these three rhythm categories are similarly apparent regardless of data filtering. Further, these three categories can be seen most clearly in single-syllable type trills (Figure 1I) indicating that these categories cannot be explained by differences in syllable durations. Hereafter, we will therefore look at unfiltered data across species.

We next analyzed songs from 93 domesticated zebra finches (Rockefeller University birdsong library, see EXPERIMENTAL MODEL AND SUBJECT DETAILS & METHOD DETAILS, ‘Extracting onsets from birdsong data’). The zebra finch is an important comparison because its songs are relatively simple, consisting of a single repeated motif, without complex transitions between rhythms as in the thrush nightingale (Figure 2A). Indeed, in the zebra finch, we see a roughly unimodal distribution of rhythms, with a prominent mode at 1:1 ratio (see stats in Figure 4). There is a distinct trough surrounding isochrony but no other clusters can be seen, either in the raster plot or in the rhythms histogram. Finally, there is no apparent transition between flexible and inflexible rhythms (Figure 2B,C).

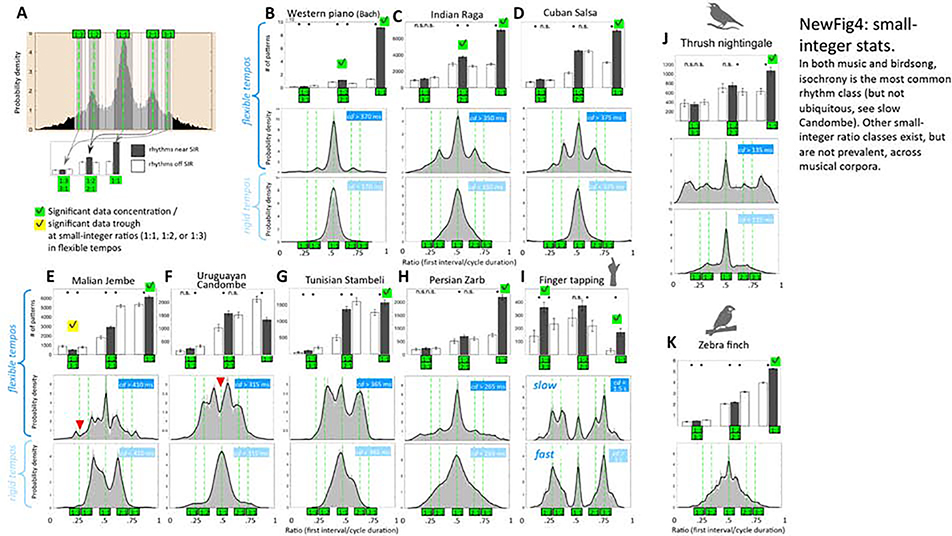
Figure 4: Testing for isochronous & small integer ratio rhythms.

A: schematic of statistical testing for concentration of rhythm frequencies at small-integer ratios (SIR). Histogram presents an example of probability densities of rhythm ratios (first interval/cycle duration) in the Indian Raga corpus. Dashed green lines mark small-integer ratios (1:1, 1:2, 1:3, 2:1, 3:1). Bar plot underneath indicates abundance of near-integer rhythms (gray bars) vs. adjacent off-integer rhythms (white bars), as counted in the gray and white shaded areas on the histogram. For statistical analysis, short-long and long-short rhythms were pooled (e.g. 1:2 and 2:1 ratios were combined). Error bars present 95% bootstrap confidence intervals. B-I: Top rows present statistical tests for concentration of rhythm frequencies at SIRs 1:1, 1:2 & 1:3 ratios in the flexible tempo range for music (C-H), and finger tapping (I). Instruments were analyzed separately for the multi-instrument music (C-G); for surface rhythm across instruments see Figure S1. A SIR was considered statistically significant (checkmark) only if 95% confidence intervals were non-overlapping between on- and off-integer areas, and if trends were consistent on both sides (either both lower [green check mark] or higher [yellow check mark]). P-values were Bonferroni adjusted for multiple comparisons. Middle rows: histograms of rhythm ratios at flexible tempos (corresponding to petals area in Figure 1), with smoothed kernel density estimates in black (see QUANTIFICATION AND STATISTICAL ANALYSIS, section ‘Histograms of ratios’). SIRs that were significantly avoided are marked by a red arrowhead. Bottom rows: similar histograms & density estimates of rhythm ratios at rigid tempos (corresponding to stem area in Figure 1). J: similar SIR visualization for thrush nightingale, and K, for zebra finch song. The zebra finch ratio histogram is for all tempos combined since there is no distinction of a flexible vs. rigid tempo range.

Transition from unimodal to flexible rhythms in music vs. birdsong

We next compared birdsong rhythms to music performances from different cultures. Figure 3C-H presents raster plots for rhythms extracted from each instrument separately in recordings of music performances. A transition from ‘stem’ to ‘petals’, similar to that observed in thrush nightingales, can be seen in most of the musical performances. As with the birds, we identified this transition by partitioning the data into tempo bins (QUANTIFICATION AND STATISTICAL ANALYSIS, section ‘Raster plots’) and automatically detecting rhythm peaks in each bin. The transition to stem was estimated by the tempo below which only a single peak could be detected. In Malian Jembe, this single peak occurred at a ratio of about 1:1.5 [24]. In all other cases, including birdsong, the single peak ratio was 1:1, namely isochronous. An abrupt transition from unimodal to flexible rhythms can be seen in the Western piano performances, Cuban Salsa, Uruguayan Candombe, and Malian Jembe (Figure 3C,E,F,G). But the transition is less abrupt in Indian Raga, Tunisian Stambeli, and Persian Zarb music (Figure 3D,H,I). Interestingly, in the thrush nightingale, flexible rhythms appear at cycle durations of about 135 ms, whereas in music, thresholds occur at much slower tempo ranges, between 265 and 410 ms. Note that in music, in addition to production constraints, the transition to a single mode could also reflect the need to coordinate events and synchronize musical performances between performers [10,17].

Isochronous rhythms in music vs. birdsong

Isochrony is a common mode underlying rhythmic behaviors in many species, and it plays a particularly strong role in music [25]. Indeed, as shown in Figure 3, all rhythm raster plots are highly symmetric, indicating high occurrence of isochronous rhythms. We first compared the abundance of isochrony between corpora, focusing on the flexible rhythm range. Isochronous (1:1) rhythms are the most common rhythm class in most corpora, forming particularly high peaks in the histograms (Figure 4). We tested for statistical significance of isochronous rhythms using a bootstrap analysis, comparing the rhythm frequency between the 1:1 ratio and its neighborhood (see QUANTIFICATION AND STATISTICAL ANALYSIS, ‘Quantifying isochrony and small-integer bias’ & Figure 4A). With the exception of Uruguayan Candombe, isochronous rhythms were significantly more frequent in all performances, as well as in the thrush nightingale and zebra finch song (p<0.05, Bonferroni corrected). The abundance of isochronous rhythms in the thrush nightingale songs was 38 ± 4%, which is within the error margin of the 45 ± 6% isochronous rhythm frequencies we observed across musical performances. In contrast, isochrony was less common in the zebra finches (18.8 ± 0.12%). Note that isochronous rhythms were strictly avoided in the flexible tempo range of Uruguayan Candombe (p<0.05 for integer ratio avoidance, in line with previous findings by Jure and Rocamora [24]). This is the case also at the multi-instrument (surface rhythm) level of Uruguayan Candombe, except that in the fast ‘stem’ area, all rhythms collapse into a single isochronous peak (Supplemental Figure S1D).

We next compared rhythm performances with an additional type of rhythmic behavior: finger tapping [26] (Figure 4I). Participants finger-tapped a heard two-interval repeated rhythm and replicated it from memory. Experiments started with a random ratio, but progressively adapted to the participant’s tapped rhythm. This way, rhythms gradually converged on ratios that reveal participants’ perceptual priors [27]. The advantage of this method is that it can provide access to internal representation (priors) of rhythms. That is, it estimates the perceptual saliency of different rhythms. We asked participants to tap either with a slow or with a fast tempo (cycle durations of 1000 and 1500 ms, respectively). In the finger tapping experiment too, isochrony was strongly favored over adjacent non-isochronous ratios (p<0.05, Figure 4). However, the frequency of isochronous rhythms in finger tapping was lower than in musical performance and nightingale song, accounting for 11 ± 2.3% of tapping at the slow tempo, and more similar to the 18.8% isochrony ratio in zebra finch songs. Together, results further suggest that the abundance of isochrony in the nightingale song, but not in the zebra finch, is comparable to that observed in musical performances.

Small-ratio rhythms in music vs. birdsong

Figure 4 presents histograms of rhythm ratios, separately for flexible (petals) and inflexible (stem) ranges, for different music corpora, finger tapping, thrush nightingale and zebra finch song. Green lines represent small-integer ratios: 1:1, 1:2, 2:1, 1:3, and 3:1. Several rhythm peaks are apparent in the flexible rhythm range of music corpora. As expected, in the stem (Figure 4, bottom panels), there is only a single isochronous peak, except for Malain Jembe where the stem contains two regions of non-isochronous rhythms. Analysis of surface rhythm (of several instruments combined) shows an even stronger collapse of rhythms into a single peak in the stem range (Supplemental Figure S1). Further investigation therefore focuses on the flexible rhythm range.

In both thrush nightingale song and music performances, there was an abundance of non-isochronous rhythms in the small-ratio range around 1:2 and 1:3. We tested whether the tendency to produce rhythms at these small-integer ratios (SIR) is greater than expected by chance. As with isochronous rhythms, we performed a bootstrap analysis to test for concentration of rhythms at 1:2 and 1:3 integer ratios (Figure 4A). In order to simplify the analysis, we pooled short-long with long-short ratios (such that 1:2 & 2:1 SIRs regarded as a single category, as were 1:3 & 3:1 SIRs). A peak at a SIR was considered statistically significant if the 95% confidence intervals were non-overlapping between pre-defined on- and off-integer areas (Figure 4A). We also required that trends must be consistent on both sides (either both lower or higher). A statistically significant tendency to produce 1:2 ratios was detected only in Western piano and Indian Raga performances (Figure 4B & C). No significant tendency to produce 1:2 or 1:3 ratios was detected in any other music, but in Malian Jembe, we found a significant tendency to avoid 1:3 rhythms and favor non-SIRs instead (Figure 4E), consistent with previous analyses of this music that found deviation from integer ratio proportions at the subdivision level [3]. Thrush nightingales showed no significant tendency to produce either 1:2 or 1:3 ratios, even though they produced an abundance of rhythms in that region (Figure 4J). Note also that thrush nightingales produced many high-ratio rhythms (Figure 4J, Figure 1C, F & I) forming a distinct peak at the range of 1:7–1:9. No such peak is apparent in any of the musical performances.

We finally tested for SIRs in finger tapping [26]. Comparing rhythm histograms in slow vs. fast tapping, we observed a similar differentiation of rhythms in the slow range as in thrush nightingale song and music (Figure 4I, middle vs. bottom panel): Two SIRs, 1:1 and 1:3 rhythms, were produced at the faster tapping speed, but an additional class of 1:2 rhythms was added at slower tapping speed. While at the 1:2 ratio, concentration of rhythms did not reach statistical significance, the concentration of rhythms at the 1:3 ratio was statistically significant (p<0.05, Bonferroni corrected, Figure 4I). Note, however, that other analytic methods [26] did reveal significance at the 1:2 ratio in finger tapping, indicating that the statistical approach used here is more conservative, being sensitive to small deviations from perfect integer ratios. In the next section, we take a more liberal approach for identifying rhythm peaks a posteriori across tempos.

Rhythm stability across tempos in music vs. birdsong

We next compared the stability of rhythm categories across birdsong and musical performances. To do so, we calculated probability densities in tempo-ratio space (Figure 5). This analysis shows the ratio histogram across tempos. We divided the space of cycle durations into overlapping bins, or tempo “slices”, and normalized the histogram of ratios separately for each slice (see QUANTIFICATION AND STATISTICAL ANALYSIS, section ‘Heat maps’). This affords tracking the abundance of the different ratios even in the case the overall number of samples for a given duration is small. The heat maps of ratio-tempo space reveal distinct rhythm classes sorted by tempo. Peaks in interval ratios are plotted as black markers which form lines across adjacent tempos (Figure 5A, left panel). This representation reveals additional structure by allowing better detection of rhythms that are common in only a subset of the tempos, and rhythms that change dynamically with tempo. This approach is particularly useful for detecting high-ratio (ornament) rhythms. In contrast to the rhythm histograms (Figure 4) where a peak in the high-ratio range can only be seen in thrush nightingales, we can easily detect similar peaks in the tempo-ratio space maps across all human musical performances (Figure 5) as this method normalizes for the overall low probability of fast rhythms in human performances.

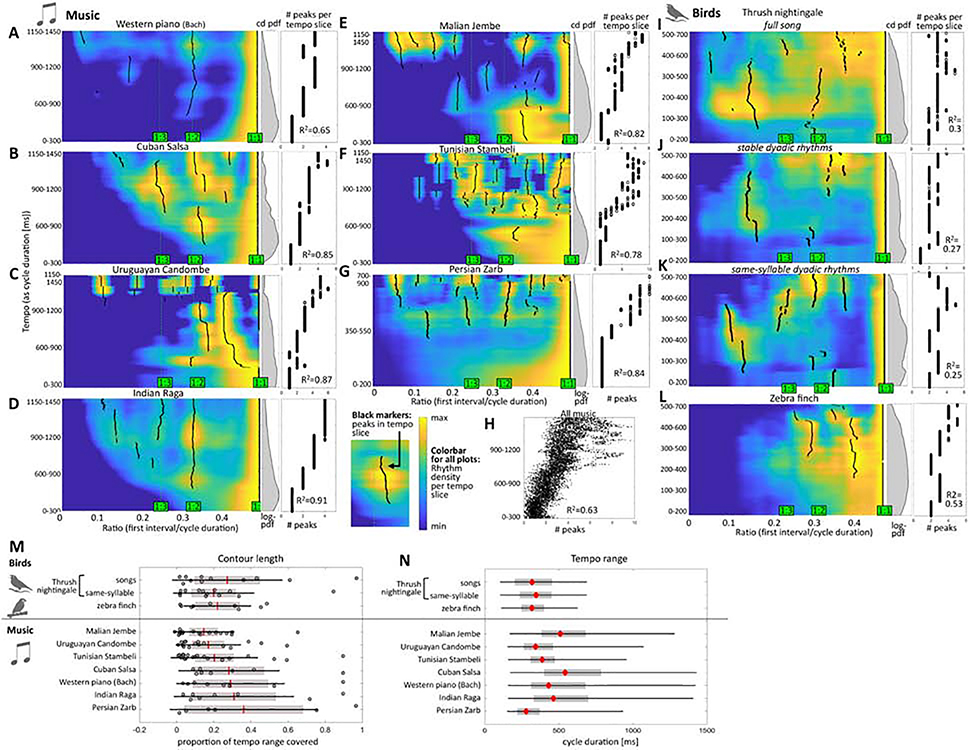
Figure 5: Probability densities of rhythms in tempo-ratio space.

Heat maps are for musical corpora (A-G), thrush nightingales (I-K), and zebra finches (L)). Probability densities are normalized per row (i.e. per tempo “slice” on the Y axes). Black markers indicate peaks in probability density. Middle panels show histograms of the tempo range abundance (same Y-axis) as log of probability density. Right panels present the number of peaks per tempo (same Y-axis as in heat maps) with coefficients of determination for number of peaks vs. tempo. Note the different y-scale between music (A-G) and birds (I-L), as birds use faster tempos. H: number of peaks vs. tempo for all musical corpora combined (peak number jittered). M: length of the peak ‘contours’ as indicated by the black markers (relative to tempo range used and shown in the heat maps). N: tempo ranges used by birdsong and music corpora as density of cycle duration [ms]. Red markers=median, gray boxes=quartiles, black lines=0.5th to 99.5th percentile.

The stability of rhythms across tempos can be judged by measuring the lengths of the vertical rhythm contours. We found that the length of rhythm contours (relative to the range of tempos/cycle durations used) is similar between birdsong and different musical corpora (Figure 5M). Rhythm contours were particularly long in Zarb drumming, Indian Raga and Western piano performances, which all feature fewer distinct rhythm classes in comparison with the other music. Note, however, that both bird species produce a narrower tempo range compared to music (Figure 5N; also visible as narrower raster plots for birds than music, Figure 1 & 2). It is within their own tempo production range that the birds keep their rhythms as stable over tempo as humans do in music (Figure 5M). Moreover, birdsong tends to be faster than most music (Figure 5N), with only the exceptionally high-tempo Zarb drumming being faster (this style is characterize by virtuosic fast drumming strokes).

The continuous ratio-tempo space also allows us to quantitatively estimate how the number of rhythm contours increases with cycle duration (right panels in Figure 5A-G & I-L). In the thrush nightingale songs, only about 30% of the variance in the number of rhythm contours can be explained by tempo Figure 5I-K, right panels). In music performances and in zebra finch songs (Figure 5L), R²s were higher, explaining 67–91% of the variance. Pooling peaks-vs.-tempo data across musical performances (Figure 5H), tempo can still explain about 63% of the variance in number of rhythm contours, indicating strong consistency across musical styles.

Finally, thrush nightingales produced many high-ratio (semi-flexible) rhythms, with ratios around 1:7–1:9, covering a broad tempo range (17 ± 3 % of all rhythms; Figures 1 & 4). These rhythms form a distinct peak in the ratio histogram of thrush nightingale rhythms, but not in any of the musical corpora (Figure 4). The tempo-ratio space, however, which is more sensitive to rare events, reveals similar high-ratio rhythm (presumably fused rhythms) in most music performances (e.g., in Malian Jembe, Figure 5E). As opposed to the thrush nightingale, where fused rhythms persist over a remarkably broad tempo range, high-ratio rhythms in musical performances are limited to slow tempos at least in the music genres that we tested.

Discussion

We observed categorical rhythms across songs pooled over a wide range of thrush nightingale populations in Middle, Eastern, and Northern Europe, indicating a species-wide phenomenon. In contrast, in domesticated zebra finches, whose songs are highly rhythmic, we only found discretization of isochronous rhythms. Other than that, rhythms were not discretized across zebra finches even within a colony. Comparing thrush nightingale rhythmic structure to music performances, we observed several similarities and a few differences. In both human music and thrush nightingales songs, rhythms were strongly categorical with a similar preference for producing isochronous (1:1) rhythms. Isochronous rhythms, however, were less common in zebra finches, who do not discretize other rhythms. Further, abundance of isochrony in zebra finches was similar to that of the finger tapping experiment in humans where rhythms were presented evenly. This outcome is consistent with the notion that the cultural evolution of categorical rhythms may promote isochrony, which is a fundamental attribute of rhythmic processing across species [1, 25,28–32].

In music, the prevalence of isochrony may reflect the need to coordinate events and synchronize musical performances between performers. To our knowledge, however, thrush nightingales do not sing in unison and do not coordinate their vocalization like musicians do. This could suggest that the cultural evolution of categorical rhythms may promote isochrony regardless of synchronization. Future studies could test if the similarity in the abundance of isochrony between human music and birdsong would generalize across songbird species who show discretization of rhythms and song dialects. It would also be interesting to compare the abundance of isochrony we observed to animal species such as the white-browed sparrow-weaver [33], seals [34] and plain-tailed wrens [35] who does coordinated group singing.

Related to that, we found that in the thrush nightingale, the transition to unimodal, isochronous rhythm occurs at a remarkably fast tempo threshold of 135ms, which can be at least partially explained by agility due to their smaller size. This transition point is associated with the median duration of short semi-flexible rhythm intervals (Figure 1K), suggesting that nightingales produce non-isochronous rhythms as fast as biomechanical constraints allow them to. This is certainly not the case in music, where the transitions to isochrony we observed (stem vs. petals in Figure 2) occurred in much slower tempos, between 315–410 ms, which are all slower than human production control limits [17,18]. Variation in the transition point across performances can be explained by two factors:

First, it may reflect different bio-musical constraints due to different modes of sound production: While the birds rely on two coupled sound sources – their vocal organ, the syrinx [36][37] – the different musical corpora vary in number of instruments and in gestures for sound generation (usage of sticks for some drums, fingers for piano playing, etc. ). The way each of these instruments is played is likely to affect the transition point from rigid to flexible rhythms, as the control of fingers, hands, feet, tongue, voice, and breath is likely to underlie different production limits.

Second, in musical performances, the transition to isochrony in fast tempos may correspond to the fastest unit in the musical meter (subdivision rate) [17][18]. Therefore, it is important to distinguish between abundance of isochrony within the flexible tempo range, which is similar across thrush nightingales and music, as opposed to the transition point from multiple rhythms to isochronous rhythms, which occurs at much slower tempos in musical performances, in part due to the need to synchronize across musicians. A particularly interesting case is Uruguayan Candombe drumming, where non-isochronous modes appear in fast tempos produced by each musician, but across musicians, fast rhythm are isochronous (Figure 4 & Supplemental Figure S1). Here, the overall duration of the pattern selects a consecutive rhythm at the subdivision level, namely the fastest unit of the musical meter. This unit is typically dividing the beat (the main element of the meter) to 2, 3, or 4 nearly equal units, therefore generating an isochronous fast rhythm. Slower patterns could contain multiple fast units herby generating higher ratio rhythms. Overall, our results further demonstrate similarities in how human music and birdsong cultures prefer isochrony. Further, the structural similarity between fused-rhythms (ornaments) in music and semi-flexible rhythms in the thrush nightingale suggests that expressive deviations from simple isochrony are not unique to human cultural productions.

Rhythms of thrush nightingale songs did not gravitate toward the small-integer ratios 1:2 and 1:3. Despite the prominence of 1:2 and 1:3 ratios in music [8,26,38–42], analysis of superficial rhythms in musical performances gave mixed results. For example, a bias toward 1:2 ratios was only observed in Western piano and Indian Raga performances. The failure to detect small-integer ratios in some performances can be attributed, at least in part, to limitations of analysis at the level of the surface rhythm. Beyond this, the expressive human musical performance is known to deviate from small-integer ratios across a wide range of tempos, except for the slowest ones [42][43]. Within these limitations, we conclude that the lack of apparent bias toward 1:2 and 1:3 integer ratios in the thrush nightingale song does not firmly distinguish them from most of the musical performances we analyzed. In addition, our results demonstrate that on the surface level, thrush nightingales’ temporal flexibility is on par with the expressivity found in human performances.

Another shared feature of thrush nightingale songs and human music performances is the tendency to produce discretized rhythms in a tempo-dependent manner. In all musical performances analyzed, the number of categories decreased with increasing tempo. A similar, but much weaker effect was observed in the thrush nightingale. It is trivial that as tempos get slower, more options are exploited, but these options are, interestingly, discretized. Further, the tempo-ratio space is remarkably similar across species: In slow tempos, the typical number of rhythm peaks ranged between 4–6, whereas in fast tempos, the typical range was 1–2. This result suggests that both species exploit their available tempo/rhythm space extensively, including patterns whose temporal properties they can only partly control.

Finally, thrush nightingales showed a marked preference for alternating rhythms with high ratios (1:7–1:9). Such rhythms can be seen in tempo-ratio space of musical performances but not in the overall rhythm histograms. This is because the birds performed these alternating rhythms frequently across a broad range of tempos, whereas musicians performed them mostly at slow tempos.

The discretized nature of rhythms might be related to the nature of birdsong as culturally transmittable communication. Like music and language, the song of many bird species is culturally transmitted through learning, and it forms dialects reminiscent of local musical traditions, or different languages. We do not know if birdsong rhythm templates might be shared across individuals in the same way as, say, syntactic rules in language, or rhythm patterns in musical cultures [44][45]. However, it is conceivable that this discreteness of syntactic categories and rhythmic timing patterns is a generic signature of cultural communication: Discrete entities might be easier to share and learn than entities from a continuous range, as only a limited number of classes need to be learned, produced, and decoded for successful communication [46]. This way, rhythm templates may facilitate song processing and song learning in the thrush nightingales given production and memory constraints. The fact that birdsong – like music and language – is culturally transmitted may play an additional role. Categorization can be used to increase communication efficiency in a noisy communication channel [48]. Therefore, it is conceivable that the shared function of both music and birdsong – namely to attract and hold the attention of conspecific listeners [49] – would result in similar usage of categories.

While comparisons between animals and human behaviors can help with studying mechanisms and origins of behaviors [49][50], different traditions for descriptive models across disciplines can be difficult to reconcile. When comparing music with animal vocalizations, this is especially challenging: The rich scholarly tradition of musical analysis cannot be easily applied to birdsong [51][52]. We therefore took a step back and used a very simple analysis of rhythmic structure that is applicable to both. We found that on this simple level, musical and birdsong rhythms are fairly similar. Our findings can only serve as a first step into a species comparison of rhythm: Both musical and birdsong rhythms feature multi-level organizational structure not captured in our dyadic rhythms analysis. For example, in the thrush nightingale songs we found that rhythmic events usually start with a short interval, suggesting a higher order organization that is not captured by histograms of consecutive events. Similarly, musical meters and musical grouping contains complex structures [1,53–54] that have no trivial or direct relation to our two-interval ratios. Future species comparisons of such structure are needed to reveal at which point the similarity breaks down.[22].

STAR Methods

RESOURCE AVAILABILITY

Lead Contact

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Tina Roeske (tina.roeske@ae.mpg.de).

Materials Availability

This study did not generate new unique reagents.

Data and Code Availability

Thrush nightingale corpus

The thrush nightingale corpus contained songs from 45 recordings obtained from the publicly available birdsong library xeno-canto (http://www.xeno-canto.org).

Xeno-canto recording IDs of the thrush nightingale recordings, recordists, and countries were the following: XC100481, XC41054, XC100008, XC134265 (Jarek Matusiak, Poland), XC101771 (Alan Dalton, Sweden), XC106840, XC270075, XC199691, XC342316, XC270075/XC270077 (the last two are recordings from the same individual, as reported by recordist Albert Lastukhin, Russian Federation), XC120947, XC245720 (Lars Lachmann, Lithuania and Poland), XC178834, XC178964 (David M., Poland), XC247794 (Pawel Bialomyzy, Poland), XC281394 (Peter Boesman, Netherlands), XC30133 (Ruud van Beusekom, Netherlands), XC36746 & XC75409 (Tomas Belka, Poland), XC49642 (Niels Krabbe, Denmark), XC83219 (Jelmer Poelstra, Sweden), XC110336, XC186525, XC27289, XC327878 (Patrik Aberg, Sweden), XC246863 (Piotr Szczypinski, Poland), XC374235 (Roland Neumann, Germany), XC368725, XC371264, & XC371254 (Annette Hamann, Germany), XC381335 (Romuald Mikusek, Poland), XC376998 (Antoni Knychata, Poland), XC370813 (Mike Ball, Estonia), XC322370 (Jens Kirkeby, Denmark), XC319730 (Jerome Fischer, Finland), XC316444 (Tim Jones, UK), XC315914, XC370927, & XC314699 (Krysztof Deoniziak, Poland), XC373585 (Uku Paal, Estonia), XC372102 (Ola Moen, Norway), XC178832 (Christoph Bock, Germany), XC370955 (Eetu Paljakka, Finland), XC315973 (Espen Quinto-Ashman, Romania), XC247473 & XC247477 (Mikael Litsgard, Sweden).

We used a subset of songs from these recordings to extract onset-onset intervals (see METHOD DETAILS). The interval data are available via Mendeley Data [DOI: 10.17632/zhb728dc4z.2].

Zebra finch songs

The extracted onset-onset intervals from zebra finch song recordings from the Rockefeller University Field Research Center are available at Mendeley Data [DOI: 10.17632/zhb728dc4z.2].

Musical corpora

Five of the seven musical corpora used in this study (North Indian Raga, Cuban Salsa, Uruguayan Candombe, Malian Jembe, Tunisian Stambeli) are part of the Interpersonal Entrainment in Music Performance (IEMP) corpus [55][56]. The original data are available at https://osf.io/37fws/.

The Western piano (Bach) corpus used in this study consists of all Bach performances from a large Western piano corpus. The original corpus is available at https://arxiv.org/abs/1810.12247 [57].

The Persian Zarb corpus used in this study consists of commercial recordings which are not publicly available for copyright reasons.

All extracted onset-onset intervals are available via Mendeley Data [doi:10.17632/s4cjj7h5sv.1].

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Thrush nightingale song data

Thrush nightingale recordings were from wild birds recorded at different sites in Middle, Northern, and Eastern Europe, as well as Russia (information on exact locations are available at http://www.xeno-canto.org. under the above recording numbers).

We extracted from each of the recordings a subset of songs (a song being 3–20 seconds of uninterrupted singing, flanked by silence). The total number of interval pairs was 13,366.

Zebra finch song data

We recorded undirected songs from 93 adult male zebra finches at the Rockefeller field center in Millbrook, NY. Audio data include at least 1000 song syllables per birds.

Music data

Our set of musical corpora comprised seven musical styles, including both Western and non-Western ones, as well as solo- and multi-instrument performances. Beyond comprehensive cross-cultural coverage, the following considerations determined our selection: First, as we wanted to compare birds and humans’ precise timing of rhythmic events, we could not use musical notation, which provides only approximate temporal durations [2]. In addition, as the birds produce highly precise temporal onsets, we could not use data from performances of instruments that provide imprecise onsets such as human vocalization and string instruments (their tones have relatively long “attacks”, making it difficult to determine onset times precisely). We therefore focused on music that includes mainly percussion or keyboard instruments, which are characterized by crisp onsets.

Five non-Western, multi-instrument corpora were obtained from the Interpersonal Entrainment in Music Performance (IEMP) corpus [55,56] (see also https://osf.io/37fws/): North Indian (Hindustani) Raga, Cuban Salsa, Uruguayan Candombe, Malian Jembe, and Tunisian Stambeli (see Table ‘Corpus sample sizes’). The IEMP corpus also includes a European string quartet corpus that we did not analyze because of the string instruments’ imprecise onsets.

Multi-instrument music (obtained from the IEMP corpus):

The Cuban Salsa corpus consists of recordings by the group Asere, a Havana based group of seven musicians (for detailed information see the website of the IEMP corpus: https://osf.io/8hmtn/).

The Malian Jembe corpus contains 15 pieces played by 3–5 performers (for a detailed description, see https://osf.io/y5ixm/).

The North Indian (Hindustani) Raga corpus contains eight pieces played by 2–3 performers, recorded in India and the UK (see https://osf.io/3cmg4/ for details).

The Tunisian Stambeli corpus is of four pieces by a group of four performers (for details, see https://osf.io/qaxdv/).

The Uruguayan Candombe corpus comprises 12 performances by 3–4 players (for details, see https://osf.io/4q9g7/).

Single-instrument music:

We chose the Western piano (Bach) corpus as an example of Western art music that was likely to feature some ornamentation, affording the comparison of fused rhythms (ornaments) across species. It contains 156 Bach piano recordings by 50 pianists from a large corpus of Western piano performances [57].

The Persian Zarb corpus includes 64 pieces of Zarb solo playing by 5 performers from commercial recordings (Djamchid Chemirani, Keyvan Chemirani, Khaladj Madjid, Pablo Cueco and Jean-Pierre Lafitte).

Corpus Sample Sizes.

Musical style	Note onsets	Pieces / performances	solo or multi-instrument
North Indian Raga	86,822	8	multi-instrument
Cuban Salsa	38,056	40	multi-instrument
Uruguayan Candombe	47,998	39	multi-instrument
Malian Jembe	42,195	46	multi-instrument
Tunisian Stambeli	27,451	9	multi-instrument
Persian Zarb	32,416	64	solo
Western piano (Bach)	260,653	156	solo

Tapping experiment subjects

The tapping experiment was conducted at Columbia University with participants recruited from the NYC area. Participants generally had little musical experience (i.e., they were usually non-musicians), though some had up to 10 years of musical experience, based on self-report. Experiment 1 (cycle duration 1000 ms) had 24 participants (7 female, mean age = 30.3 years, SD=8.12, range 21–49). Mean musical experience was 2.75 years; SD=2.9; range 0–10 years. Experiment 2 (cycle duration 1500 ms) had 24 participants (11 female, mean age=29.0 years, SD=7.25, range 21–45). 19 participants of these 24 also participated in experiment 1 (in cases where someone participated in both experiments, the order was randomized). In this experiment, mean musical experience was 2.91; SD=2.8; range 0–10.

METHOD DETAILS

Birdsong processing

Creating three thrush nightingale datasets

We segmented and extracted onsets (details below) from the thrush nightingale song data, creating three separate datasets (corresponding to Figure 1A, D & G):

1. a full-song dataset (comprising the entire corpus)

2. a ‘stable rhythm’ dataset (a subset of 1) containing song epochs with stably repeated interval dyads (for details, see section “Obtaining ‘stable-rhythm’ epochs from thrush nightingale songs”)

3. a ‘same-syllable’ dataset containing epochs of same-syllable repetitions, which we manually extracted from the original sound files (for details, see section ‘Extracting a ‘same-syllable type’ (trill) dataset).

Supplemental Figure S2 illustrates the workflow for creating the three datasets.

Extracting onsets from birdsong data

Amplitude envelopes were extracted from the sound files in 10 ms time windows and steps of 1 ms using SoundAnalysisPro 2011 [58–59].

Segmentation of the thrush nightingale song was performed semi-automatically. At the first stage, each song epoch was segmented automatically using an adaptive threshold (amplitude smoothing Hodrick-Prescott (HP) filter with coefficient = 50; dynamic threshold filter with coefficient = 5 · 10⁷). The difference between the smoothed amplitude envelope and the adaptive filter provided robust segmentation in most song segments. At the second stage, we automatically excluded note onset times that occurred within 12 ms or less, as those usually indicate a complex two-peaked note rather than two notes. Finally, we visually inspected the segmented sonograms, and in cases of failure, we manually outlined notes onset using SoundAnalysisPro manual segmentation. In the same syllable dataset, which is already curated, we followed the same procedure, but no manual corrections were required.

Zebra finch data were analyzed as described for thrush nightingales, except that segmentation was performed using a simple amplitude threshold using SoundAnalysisPro default settings.

Calculation of dyadic rhythm features

For each song epoch, we first calculated onset-to-onset time intervals, for each back-to-back note pair (Figure 1). Dyadic rhythms were defined as two consequent intervals (including 3 back-to-back notes). For example, given the notes sequence {N₁, N₂, N₃}, we calculate the interval i₁ between the onsets of N₁ & N₂, and interval i₂ between the onset of notes N₂ & N₃. With the two intervals {i₁, i₂ } defining the first dyadic rhythm, we proceed to calculate the second dyadic rhythm {i₂, i₃ } between notes {N₂, N₃, N₄ } and so forth. This way, each interval occurs twice in our raster plots (Figures 1–3), namely once with its preceding and once with its subsequent interval. For each dyadic rhythm {i_n ,i_n+1 }, we calculate the cycle duration, cd_n = i_n + i_n+1, and rhythm ratio = i_n/(i_n + i_n+1). We also identify the short interval as i_S, and the long interval as i_L.

Obtaining ‘stable-rhythm’ epochs from thrush nightingale songs

For each consecutive pair of dyadic rhythms {i_n ,i_n+1 } and {i_n+1 ,i_n+2 }, we compared the durations of i_n and i_n+2. We then filtered out pairs of dyadic rhythms where duration differences exceeded 25%. This way, the filtered dataset included only epochs where those intervals are similar in duration. For example, this sequence of dyadic rhythms:

$$\left\{i_n=50,i_{n+1}=200\right\},\left\{i_{n+1}=200,i_{n+2}=53\right\},\left\{i_{n+2}=53,i_{n+3}=205\right\}$$

would survive because i_n & i_n+2 (50 & 53) are similar, and also i_n+1 & i_n+3 (200 & 205) are similar (Figure 1D).

Extracting a ‘same-syllable type’ (trill) dataset

In order to explore rhythm patterns in cases where note durations are nearly identical (epochs with constant note lengths), we used the sound editor GoldWave v6.18 (GoldWave Inc., St. Johns, Canada), to manually identify epochs in which a single syllable type was repeated rhythmically (Figure 1G). We filtered out the following sub-phrases:

• sub-phrases containing less than three notes

• non-repetitive sub-phrases

• repetitive sub-phrases that contain more than one note type

• repetitive sub-phrases in which each cycle contains more than two notes.

This filtering was performed on the original sound files, and followed by amplitude envelope extraction with SoundAnalysisPro [59] and segmentation as described below.

Processing of music data

Extracting onsets from music corpora

Onset extraction from musical performances were as similar as possible to those we used for birdsong. For Persian Zarb, which is the most challenging to segment, we segmented the audio data using an adaptive threshold approach, as with the thrush nightingale songs (see ‘Extracting onsets from birdsong data’ above), except that thresholds were determined separately for each performance based on visual inspection of the sonograms. The Western piano music corpus is provided as MIDI data and therefore contains onset information. Onsets were directly recorded as MIDI information, but the corpus also includes audio recordings of the same performances. This way, MIDI data was further validated and compared with the audio using dynamic warping methods, a process that guaranteed that onsets in the MIDI were aligned with the audio recordings [57]. Since It has been verified that the audio segmentation closely matches the MIDI onset extraction, we used the MIDI onsets. The IEMP corpus [55,56] provides onsets that were extracted using onset extraction methods: it was initially recorded as a multichannel audio recording. The onsets from each channel were extracted using an amplitude threshold method. The success of the onset extraction method was supervised by musical experts that checked the automatic onset /extractions worked well and provided manual corrections in a small fraction of cases (< 1 % of the onsets in all corpora). The detailed information about the techniques used can be found under DOI 10.17605/OSF.IO/NVR73, (https://osf.io/nvr73/).

Rhythm extraction from music corpora

The musical corpora include performances in which several instruments played simultaneously. In these cases, we analyzed each instrument separately, and aggregated the resulting two-interval ratios across instruments as a second step. We compared these results to a different type of analysis that also started by extracting onsets from each instrument individually, but we combined these onsets before calculating ratios, to generate the instrument-combined histograms in Supplemental Figure S1. This combined method was also used for the analysis of the Western piano corpus in which the instrument is a piano that usually produces a number of simultaneous notes (“chords”). To avoid counting onsets that are musically simultaneous (“chords”) but performed with some small timing deviation on the different instruments (“asynchronies”), we clustered sound events that are less than 25 ms apart and treated them as a single onset positioned at the first onset of the cluster. We chose a threshold that is well below the threshold for “simultaneity” (estimated at about 100 ms, though this value may be smaller for certain cultures, see Polak [7]) based on the music cognition literature [17]. We also selected a value that will not eliminate ornaments (typically with inter-onset-intervals around 50 ms). Overall the two types of extraction (separate for each instrument and simultaneous for combined “surface” rhythm) produced similar results (see Supplemental Figure S1). We added the Zarb corpus as control in order to provide a dataset that is a) non-Western, and b) played by a single player (not an ensemble, so similar in nature to piano playing). In this database we also performed onset extraction ourselves fully equating the processing steps in humans and birds.

Tapping experiment

The aim of the tapping experiment was to characterize the perceptual priors of the rhythmic representation of two-interval rhythms based on a paradigm described in McDermott and Jacoby [26]. We probed rhythmic representations at two tempos, namely a cycle duration of 1000 ms and of 1500 ms. In the original design in McDermott and Jacoby [26] who limited the fastest interval to 15% of the overall duration (150 ms in the case of a cycle duration of 1000 ms). If participants tried to reproduce a faster rhythm, the rhythm was marked as an error (bad trial). Here we allowed participants to reproduce faster rhythms (up to 70 ms in duration). This was done in order to probe fused rhythms (critical to the analysis of this paper).

Ethics for tapping experiment

The study received ethical approval from the Columbia University Institutional Review Board, under Protocol AAAR1677.

Apparatus for tapping experiment

The apparatus used in this experiment was identical to the one used by McDermott and Jacoby [26]. All stimuli were presented through Sennheiser HD 280 Pro headphones at a comfortable level chosen by the participant. Tapping responses were recorded with a designated sensor constructed from soft material so as to provide minimal auditory feedback. A microphone was installed within the sensor in order to be sensitive to the lightest touch. To account for the recording latency, data was acquired with a Focusrite Scarlett 2i2 USB sound card, which simultaneously recorded the microphone output and a split of the headphone signal. Stimulus and response onsets were extracted from the audio signal using a Matlab script, and the overall latency and jitter obtained this way was about 1 ms.

Stimuli for tapping experiment

Rhythmic patterns consisted of short percussive sounds that were a burst of filtered white noise lasting 55 ms with an attack time of 5 ms.

Onset extraction of tapping

The onsets were extracted directly after each recording of the stimulus. Considering the high signal-to-noise ratio that the sensor provides, it was sufficient to extract onsets by a simple heuristic, namely measuring audio onsets that exceeded a threshold of 2.25% of the maximal power of the sound waveform in a window of 15 s. More details of the extraction algorithm are described by Jacoby and McDermott [26].

Tapping experiment procedure

The experiment was a variant of experiment 3 of Jacoby and McDermott [26]. The main difference between this paradigm and the one reported there is that we enabled the presentation and production of much faster intervals. The limit for the fastest interval was 142.5 ms in Jacoby and McDermott’s study [26] and only 70 ms here.

In each block, we set the seed to an initial uniformly distributed random ratio. I.e., if the pattern duration was T (T=1000 ms and 1500 ms for experiment 1 and 2, respectively), we randomized the first interval (S₁) to a random value sampled from the uniform distribution S₁~U(L,T-L) where L=70 ms was the fastest interval presented. Note that in this case, S₂~U(L,T-L) and S₁+S₂=T. We then presented the pattern (S₁, S₂) 3 times cyclically, forming 7 onsets. Participants were instructed to replicate the pattern they heard from memory, forming 7 onsets (6 inter-onset intervals R’₁,R’₂,..,R’₆). To ensure that participants provided responses that could be analyzed, we provided feedback directly after each response delivered via headphones. If the number of response onsets exceeded 7 onsets, the feedback was the short (English) text “too many taps”. If the number of taps was less than 7 onsets, the feedback was “not enough taps”. In these cases, the seed was not changed and the participant received an identical stimulus as the next iteration. In all other cases, we computed the average inter-response pattern over the 3 repetitions (forming the two-interval rhythm R₁,R₂). We then normalized it so that the overall duration remained unchanged. Namely, the new stimulus for the next iteration was (R₁,R₂)* (T/(R₁+R₂)). Additionally, we provided feedback indicating the proximity of the response and stimulus intervals. For experiment 1, the feedback was “excellent” if |S₁-R₁|<50 ms; the feedback was “good” if |S₁-R₁| <150 ms; and “OK” otherwise. For experiment 2, the thresholds were 75 and 225 for “excellent” and “good”, respectively. The process was repeated 5 times, as Jacoby and McDermott [26] showed that a stationary distribution is obtainable at approximately this number of iterations. Note that under some experimentally verifiable assumptions discussed in Jacoby and McDermott [26], the process converges to samples from the perceptual priors over rhythms. To obtain an estimate of the underlying distribution from tapping data, we used kernel density estimates, identical to the process applied for corpus analysis.

QUANTIFICATION AND STATISTICAL ANALYSIS

Unless stated otherwise, all analyses were carried out in Matlab_R2018b (The MathWorks, Inc., Natick, Massachusetts, United States).

Data visualization

Raster plots

To visualize the data from each corpus in its entirety, we developed a sorted raster plot that reveals patterns of systematic tempo/ratio use. To this end, we first sorted all two-interval patterns by their cycle duration. Then, the short and long intervals of every pattern, i_S and i_L, were represented by two markers on the same horizontal plane, i_S to the left and i_L to the right (Figure 1–3), resulting in the “flower-shaped” raster plots. Cycle duration of a rhythm corresponds to the horizontal distance between the i_S and i_L markers.

The threshold between unimodal and flexible rhythms that becomes apparent as transition from ‘stem’ to ‘petals’ in the raster plots was identified as follows: The two-interval data were partitioned into overlapping tempo bins (i.e. cycle duration bins) of 50 ms width. We automatically detected rhythm peaks in each bin using Matlab’s findpeaks function. The transition to stem was estimated by the tempo below which only a single peak could be detected. Matlab code for the raster plots is provided together with the music corpora interval data under Mendeley Data (http://dx.doi.org/10.17632/s4cii7h5sv.2).

Histograms of ratios

Ratio histograms were generated using Matlab’s ‘histogram’ function, as probability density (‘normalization’ option set to ‘pdf’). Gray histogram is in bins with values $v_i=\frac{c_i}{N\cdot w_i}$, with c_i the number of elements in bin i, N total number of ratios in the input data, and w_i the bin width. Black density estimate of ratios was calculated with Matlab’s ‘ksdensity’ function which provides a kernel smoothing function estimate. The Matlab code for the ratio histograms is provided together with the music corpora interval data under Mendeley Data (http://dx.doi.org/10.17632/s4cii7h5sv.2).

Heat maps

To compute heat maps (Figure 5) showing rhythms in tempo-ratio space, we divided the space of cycle durations into overlapping bins, or tempo “slices” (for music: cycle duration range of 1 to 1300 ms, bins of 300 ms width, with the exception of the fast Persian Zarb for which we cycle duration range was 1 to 800 ms and bin width 200 ms; for birdsong: cycle duration range of 1 to 620 ms, bins of 200 ms width). The bins were therefore for musical corpora (except Zarb): b_n= [l_n,h_n]=[n,n+300] ms, where 0<n<1300 (with l_n lower boundary and h_n upper boundary of the bin b_n). We then divided the interval pairs in the corpus (i₁, i₂) such that their cycle duration (cd=i₁ + i₂) lies within all bins for which l_n < cd <h_n. In the case of the birds, we had 525 bins with bin width of 200 ms b_n= [n,n+200] where 0<n<525. The overlapping bins were essential for accommodating different amounts of patterns within each duration. Note that each pattern was counted multiple times (once for each relevant bin). We then calculated the ratio of the short interval for each pattern and computed the ratio between this interval and the pattern duration (r_i=min( i₁, i₂)/(i₁ + i₂)). We computed a kernel density estimate of the ratios within each bin: for the kernel width, we used a Gaussian with fixed standard deviation of 1%. Namely, we computed a kernel density estimate ${\text{Q}}_n(\text{x})={\sum }_i\text{G}(\text{x};{\text{r}}_i,{\mathrm{\sigma }}^2)$ where σ=0.01 and $\text{G}(\text{x};\mathrm{\mu },{\mathrm{\sigma }}^2)=\exp (-{(\text{x}-\mathrm{\mu })}^2/(2{\mathrm{\sigma }}^2)))/\mathrm{sqrt}(2\mathrm{\pi }{\mathrm{\sigma }}^2)$. This distribution was then normalized by dividing Q_n(x) by its maximal value (P_n(x)=Q_n(x)/max(Q_n(x))); this procedure was done separately for each bin. To adjust the dynamic ranges of the values so they are more clearly visible using Matlab default colormap, we applied compression: we presented a heat map with log(P_n(x)+0.01) for music data and log2(P_n(x)+0.051) for birds.

Quantifying isochrony and small-integer bias

To quantify occurrence of particular rhythm ratios (e.g. isochrony) and small-integer bias, we first aggregated short-long and long-short rhythms such that all ratios were < 0.5. We then divided the ratio space into on-integer vs. off-integer ratio ranges in the following way: On-integer ratio ranges were centered around $\frac{1}{2}$ (i.e. 0.5, isochrony, or “1:1” rhythms in terms of short:long interval), $\frac{1}{3}$ (i.e. 0.33, or “1:2” rhythms in terms of short:long interval), and $\frac{1}{4}$ (i.e. 0.25, or “1:3” rhythms in terms of short:long interval; see Figure 3A). Off-integer ratio ranges were centered around $\frac{1}{2.5}$, $\frac{1}{3.5}$ and $\frac{1}{4.5}$. The boundaries of all on- and off-integer ratio ranges were: $\frac{1}{2.25}$, $\frac{1}{2.75}$, $\frac{1}{3.25}$, $\frac{1}{3.75}$, $\frac{1}{4.25}$, $\frac{1}{4.75}$. Rhythms in each on- and off-integer ratio range were counted, and counts were weighted according to the size of the respective range they fell into, before comparing each on-integer range with the two adjacent off-integer ranges (Figure 3A). To determine statistical significance of the count difference, a bootstrap was performed as described below.

The percentage of isochronous rhythms was determined as the percentage of two-interval patterns with ratios between $\frac{1}{2.25}$ and $\frac{1}{2}$.

Bootstrapping

To obtain statistical significance of integer ratios, we used bootstrapping. For each corpus, we sampled ratios with replacement. We repeated this process 1000 times. Direct p-values were determined based on 95% confidence intervals of bootstrapped data. Statistical significance was assumed if the 95% confidence intervals (Bonferroni-adjusted for multiple comparisons) were non-overlapping between the on- and off-integer range.

A second bootstrapping procedure was performed on the bird and the Western piano corpora to quantify discretization of rhythm space, see below (section Entropy and tempo-dependency of peak distribution).

Peak distribution

Peaks were computed for each heat map bin b_n separately. For each bin, we used Matlab’s ‘findpeaks’ function to allocate peaks in the distribution with parameter “MinPeakProminence” set to 0.07.

KEY RESOURCES TABLE.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
Musical rhythm: Onsets/intervals of seven music corpora	Mendeley Data: Roeske, Tina; Jacoby, Nori (2020), “Musical rhythm: Onsets/intervals of seven music corpora”, Mendeley Data, V2, doi: 10.17632/s4cjj7h5sv.2	DOI: http://dx.doi.org/10.17632/s4cjj7h5sv.2
xeno-canto birdsong library	Xeno-canto open access birdsong library, run by xeno-canto foundation, Netherlands.	http://www.xeno-canto.org
Interpersonal Entrainment in Music Performance (IEMP) corpus [55,56]	Clayton, M., Eerola, T., Tarsitani, S., Jankowsky, R., Jure, L., Poole, A., … Jakubowski, K. (2019, December 9). Interpersonal Entrainment in Music Performance.	https://osf.io/37fws/
MAESTRO (MIDI and Audio Edited for Synchronous TRacks and Organization) dataset of Western piano music [57]	Hawthorne, Curtis, et al. “Enabling factorized piano music modeling and generation with the MAESTRO dataset.” arXiv preprint arXiv:1810.12247 (2018)	https://arxiv.org/abs/1810.12247
Birdsong rhythm: Onsets/intervals of a zebra finch song corpus and 3 thrush nightingale song corpora	Mendeley Data: Tina, Roeske; Tchernichovski, Ofer (2020), “Birdsong rhythm: Onsets/intervals of a zebra finch song corpus and 3 thrush nightingale song corpora”	DOI: http://dx.doi.org/10.17632/zhb728dc4z.2
Software and Algorithms
Matlab R2014b, R2018b	The MathWorks, Inc., Natick, Massachusetts, United States	https://www.mathworks.com/
GoldWave v6.18	GoldWave Inc., St. Johns, Canada	https://www.goldwave.com
Sound Analysis Pro 2011 [59]	Tchernichovski, O., Nottebohm, F., Ho, C.E., Bijan, P., Mitra, P.P. (2000). A procedure for an automated measurement of song similarity. Animal Behaviour 59, 1167–1176	http://soundanalysispro.com/
Matlab code for dyadic rhythm visualization (ratio histogram & dyadic interval raster plot)	Mendeley Data: Roeske, Tina; Jacoby, Nori (2020), “Musical rhythm: Onsets/intervals of seven music corpora”	DOI: http://dx.doi.org/10.17632/s4cjj7h5sv.2#folder-b79a7c77–20ba-48d4-ade9–38e02d8e24fd