Abstract

Mactanamide (MA) is a diketopiperazine isolated from marine fungi of the genus Aspergillus. This compound is known as a natural antioxidant from experimental studies, yet this activity has not been successfully modeled thus far. In this work, the hydroperoxyl radical scavenging activity of MA was evaluated in the gas phase and physiological environments by thermodynamic and kinetic calculations. The results revealed that the HOO• radical scavenging of MA in the lipid media follows the formal hydrogen transfer mechanism via hydrogen abstraction at the O11–H bond. In the aqueous solution, however, the antioxidant activity follows the sequential proton loss electron transfer mechanism. The rate constant of the HOO• scavenging of MA in the polar environment is about 1045 times (koverall = 2.23 × 106 M–1 s–1) higher than that in the lipid medium (koverall = 2.20 × 103 M–1 s–1). In polar media, the HOO• radical scavenging activity of MA is therefore 18 times higher than that of Trolox, the reference compound when assessing antioxidant activity. The results presented here align well with the experimental data, validating the mechanistic pathways and thus providing useful insights into the antioxidant activity of MA.
1. Introduction
Mactanamide (MA, Figure 1) is a diketopiperazine that was isolated from marine fungi of the genus Aspergillus.1,2 In experimental studies, MA exhibited good radical scavenging activity in 2,2-diphenyl-1-picrylhydrazyl (DPPH) and 2,2′-azino-bis(3-ethylbenzothiazoline-6-sulfonic acid) (ABST) assays with IC50 values of 138.12 ± 0.34 and 1.72 ± 0.01 μM, respectively, which reveals better antioxidant activity than a range of other natural products of marine fungal origin including chraceopone F, aspertetranone D, cycloechinulin, wasabidienone E, and even the reference antioxidant Trolox (IC50 = 5.52 ± 0.41 μM).2
Figure 1.
Structure of MA.
However, computational results reported in the same study suggested that MA is a weaker radical scavenger than the other natural products (the overall rate constants koverall = 1.11 × 10–3 and 2.39 × 10–1 M–1 s–1 in pentyl ethanoate and water solvents, respectively, for MA vs koverall = 1.16–2.60 × 104 M–1 s–1 for the other compounds).2 While the calculations were performed for HOO• scavenging that was not assessed experimentally, based on the results of DPPH and ABST assays that are good predictors of overall antioxidant activity, it is expected that MA is a better radical scavenger, and therefore, there is a conflict between the reported experimental data and the calculated results.
It is important to note that in the computational study, the contribution of the O11(15)–H bond of MA was ignored in the evaluation of the HOO• radical scavenging activity. However, several previous studies showed that phenolic alcohol groups can also contribute to the antioxidant activity, and hence, the site of hydrogen abstraction has to be established for each compound individually.3−7 The phenolic alcohol groups played an important role in the antioxidant activity of phenolic compounds such as flavonoids, stilbenes, lignans, anthocyanins, and phenolic acids.8,9 The computational study also omitted the acid–base equilibrium of the phenolic O11–H bond of MA, even though it was shown before that the dissociated form, even if only present in trace amounts, may dominate the antiradical activity of phenolic compounds3,5 in aqueous solutions. Hence, there is scope for improving the computational analysis of the radical scavenging activity of MA.
This study is aimed at accurate computational evaluation of the HOO• radical scavenging activity of MA by using thermodynamic and kinetic calculations including the consideration of all important structural and environmental factors. The obtained results will provide reliable and accurate data on HOO• radical scavenging activity of MA to inform the use of this compound in practice.
2. Results and Discussion
2.1. Radical Scavenging in the Gas Phase
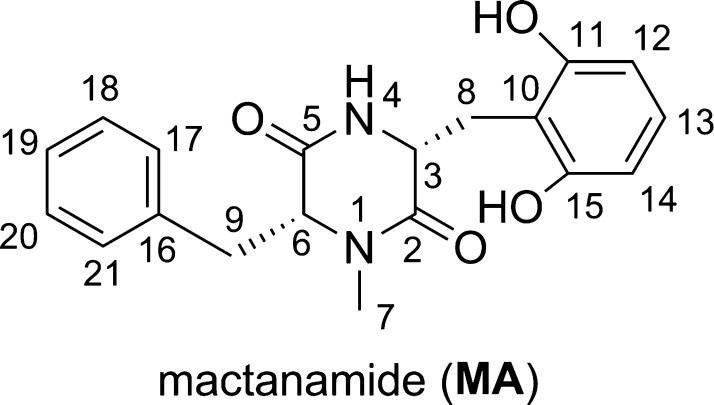
Study on the MA structure indicated that the aromatic rings can rotate around the single bonds (C6–C9, C3–C8 bonds) to form a range of conformers. Thus, in the initial step, the possible conformers of MA were screened10 and the six lowest electronic energy conformers were then analyzed at the M06-2X/6-311++G(d,p) level of theory (Figure 2). The hindered internal rotation treatment was also applied to the single bonds to ensure that the obtained conformer has the lowest electronic energy.11,12 As shown in Figure 2, MA has the lowest ΔGo value in all of the studied conformers. MA1–MA5 have 3.7–6.4 kcal/mol higher free energy than MA. Using the Maxwell–Boltzmann distribution to estimate the relative populations of tautomers13,14 indicated that MA is the dominant conformer (>99%), and therefore, this conformer was used in further studies.
Figure 2.
Typical conformers of MA and the relative free energies ΔGo (in kcal/mol) compared with the MA conformer.
Antioxidant activity is usually evaluated by thermodynamic calculations based on three typical radical scavenging mechanisms: (i) formal hydrogen transfer (FHT), (ii) single electron transfer–proton transfer (SETPT), and (iii) sequential proton-loss electron-transfer (SPLET).15 Which of these three mechanism is the dominant one depends on both the antioxidant structure and the radical; previous studies showed that the SETPT and SPLET mechanisms do not take place in HOO• radical scavenging in the gas phase.3,5 Thus, in this study, the HOO• radical scavenging of MA in the gas phase was only assessed via the FHT mechanism, and hence, bond dissociation energy (BDE) values were calculated for all bonds. The results are presented in Table 1.
Table 1. Calculated BDEs and ΔGo Values (in kcal/mol) of the Reactions of MA with HOO• Following the FHT Mechanism in the Gas Phase.
| position | BDE | ΔGo |
|---|---|---|
| C3 | 77.2 | –8.3 |
| C6 | 86.0 | 0.6 |
| C7 | 93.4 | 7.8 |
| C8 | 89.3 | 4.3 |
| C9 | 101.4 | 15.7 |
| N4 | 111.2 | 25.4 |
| O11 | 84.8 | –0.8 |
It is clear from Table 1 that the BDEs of MA are in the range of 77.2–111.2 kcal/mol. The lowest BDE value is observed at the C3–H bond with BDE = 77.2 kcal/mol. The BDE(O11–H) is the second lowest at 84.8 kcal/mol. The N4–H bond has the highest BDE at 111.2 kcal/mol.
The calculation of ΔGo values of the reactions of MA with HOO• revealed that the H-abstraction was only spontaneous (ΔGo < 0) at the C3–H and O11–H bonds, while the reactions at other positions were not spontaneous, and therefore, these positions can be disregarded in the following kinetic modeling.
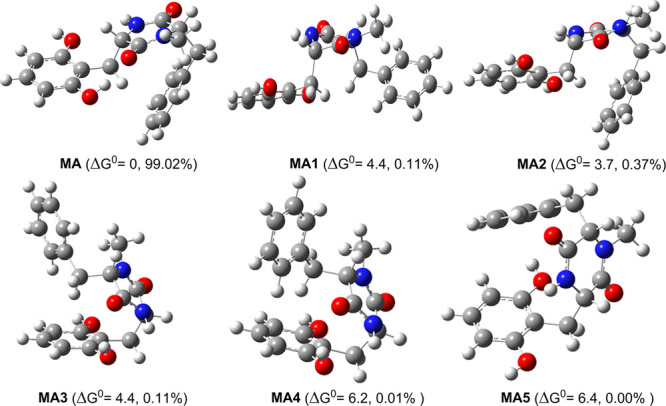
The results of kinetic calculations for the HOO• radical scavenging of MA are presented in Table 2 and optimized transition state (TS) structures are shown in Figure 3. The higher rate constant was predicted for the H-abstraction of the O11–H bond with kEck = 1.02 × 106 M–1 s–1. The activity at the C3–H bond is 27.3 times lower, even though the BDE value of the C3–H bond (BDE(C3–H) = 77.2 kcal/mol) is lower than that of O11–H bond (BDE(O11–H) = 84.8 kcal/mol) and tunneling correction value of the M–C3–H + HOO• reaction (κ(C3–H) = 444.5) is higher than that of the M–O11–H + HOO• reaction (κ(O11–H) = 18.0). Thus, the H-abstraction occurs at the O11–H bond and not the C3–H bond, as suggested in the former study.2 This may explain that H abstraction at the O11–H occurs via proton coupled electron transfer mechanism, while abstraction at the C3–H bond occurs via hydrogen atom-transfer pathway.16 The HOO• radical scavenging of MA in the gas phase is lower than that of Trolox (kEck = 1.87 × 107 M–1 s–1).3
Table 2. Calculated ΔG⧧ (in kcal/mol), Tunneling Corrections (κ), and kEck (M–1 s–1) for the HOO• Scavenging of the MA in the Gas Phase at 298.15 K.
| comp. | position | ΔG⧧ | κ | kEck |
|---|---|---|---|---|
| MA | C3 | 14.8 | 444.5 | 3.73 × 104 |
| O11 | 11.4 | 18.0 | 1.02 × 106 | |
| koverall | 1.06 × 106 | |||
| Trolox | OH | 9.7 | 36.7 | 1.87 × 107 |
Figure 3.
Optimized geometries and imaginary frequencies (ν) of the typical TSs according to the FHT mechanism between the MA and HOO• radicals.
2.2. Radical Scavenging in Physiological Environments
To identify the possible radical scavenging pathways, the protonation state of MA has to be evaluated at physiological pH. The MA structure allows protonation at the N1 and N4 positions following reactions 1a and 1b and deprotonation of the alcohol moiety at O11–H position following reaction 2. The pKa for the deprotonation of N4 is trivially seen to be too high for consideration. Thus, the pKa values of MA were calculated based on the model reactions 1a, 1b and 2(17) according to eq 2.3,18
| 1a |
| 1b |
| 2 |
| 3 |
| 4 |
where ΔGBA° was obtained from reactions 1a, 1b, and 2 following eq 3; m and C0 are fitted parameters directly obtained from ref (17).
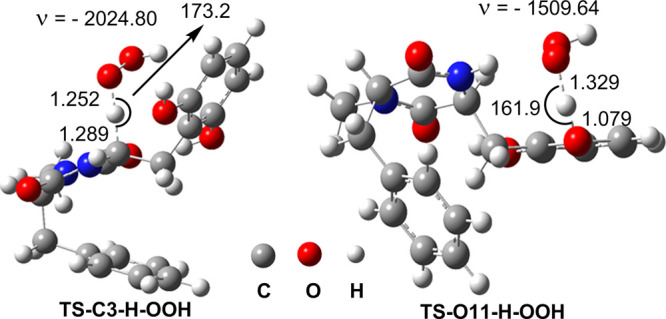
The calculated pKa values for the amines were <1, whereas that for the O11–H bond was 9.34. Therefore, in pH = 7.4 aqueous solution there is a non-negligible population of the monoanionic state (MA–O11–, 1%) (Figure 4). Hence, both the neutral and anionic states were used in the kinetic evaluation of the HOO• radical scavenging of MA in water at pH = 7.4. The antiradical activity of MA against HOO• radical in water can follow the following mechanisms:3,19
Figure 4.
Acid dissociation equilibrium of MA at pH = 7.4.
Single electron transfer (SET)
| 5 |
| 6 |
FHT that was introduced above for the gas-phase calculations
| 7 |
where R• = HOO•.
The results of the calculations are presented in Table 3. The H-abstraction of the O11–H bond in the HOO• radical scavenging of MA in lipid media yielded koverall = 2.20 × 103 M–1 s–1, while in the aqueous solution, the dominant mechanism was SPLET with koverall = 2.23 × 106 M–1 s–1. Thus, the HOO• antiradical activity of MA in the polar environment is about 1045 times higher than that in the lipid medium. The results suggest that the anionic state (MA–O11–) plays a dominant role in the HOO• radical scavenging of MA in the aqueous solution, despite the fact that this state is only present in 1% under the given conditions. Therefore, omitting this state in the evaluation of the antioxidant activity in polar solvents leads to inaccurate results, explaining the discrepancy between experimental and computational data in the above-described study.2 In a comparison with the reference antioxidant Trolox,3 the HOO• radical scavenging of MA is slightly lower in the lipid medium; however, in polar solvent it is about 18 times higher. Thus, MA is a promising antioxidant in physiological environments, in particular in aqueous media.
Table 3. Gibbs Free Energies of Activation (ΔG⧧, kcal/mol) and Rate Constants (kapp, kf, M–1 s–1) at 298.15 K in the MA Oxidation by HOO• Radicals in Water and Pentyl Ethanoate Solvents.
| pentyl
ethanoate |
water |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| mechanism | ΔH | ΔG⧧ | κ | kapp | ΔG⧧ | κ | kapp | f | kfb | |
| SET | ∼0 | 0.990 | ||||||||
| SPLET | 6.1 | 16.3a | 2.20 × 108 | 0.010 | 2.23 × 106 | |||||
| FHT | O11 | 6.0 | 15.9 | 74.0 | 2.20 × 103 | 17.8 | 56.4 | 3.16 × 101 | 0.990 | 3.13 × 101 |
| koverall | 2.20×103 | 2.23×106 | ||||||||
The nuclear reorganization energy (λ).
kf = f·kapp.
3. Conclusions
The hydroperoxyl radical scavenging activity of MA in the gas phase as well as in physiological environments was investigated by thermodynamic and kinetic calculations. It was found that the H-abstraction at the O11–H bond defined the HOO• radical scavenging of MA in lipid media with koverall = 2.20 × 103 M–1 s–1, while in aqueous solution radical scavenging followed the SPLET mechanism with koverall = 2.23 × 106 M–1 s–1. Compared with Trolox, the HOO• radical scavenging activity of MA is slightly lower in the lipid medium and 18 times higher in water than that of Trolox. Thus, MA is a promising antioxidant in an aqueous environment.
4. Computational Methods
In this study, the M06-2X/6-311++G(d,p) level of theory, which is proven to be highly accurate for computing both thermodynamic and kinetic parameters,20−24 was used to computed thermochemical properties [proton affinities (PAs), BDEs and ionization energies (IEs)] and kinetic parameters [activation energies ΔG⧧ (kcal/mol), tunneling corrections (κ), and rate constants (k)] in the gas phase and in physiological environments (water for the aqueous solution and pentyl ethanoate for the lipid medium).21−24 BDE, PA, and IE were calculated as follows4,7,8
| 8 |
| 9 |
| 10 |
where H(MA), H(MA•), H(H•), H(MA+•), H(e–), and H(H+) are enthalpies of the neutral molecule, radical, radical cation, electron, and proton, respectively.
The kinetic calculations were performed following the quantum mechanics-based test for overall free-radical scavenging activity (QM-ORSA) protocol with the solvation model density method that is widely used for evaluating the radical scavenging activity of antioxidants with low errors compared to experimental data (kcalc/kexp ratio = 1–2.9).18,20,25,26
The rate constant (k) was calculated by using the conventional TS theory and 1M standard state at 298.15 K according to eq 10(20,27−33)
| 11 |
where σ is the reaction symmetry number,34,35 κ stands for tunneling corrections which were calculated using the Eckart barrier,36kB is the Boltzmann constant, h is the Planck constant, and ΔG⧧ is Gibbs free energy of activation. The details of the method are shown in Table S1.33 The calculations were performed with the Gaussian 16 suite of programs.37 The conformers were screened by the Spartan software.10
Acknowledgments
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 104.06-2020.17 (P.C.N.).
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.0c03646.
Cartesian coordinates, frequency and energies of all of the precomplexes, TSs, and postcomplexes in the studied environments (PDF)
The authors declare no competing financial interest.
Supplementary Material
References
- Lorenz P.; Jensen P. R.; Fenical W. Mactanamide, a new fungistatic diketopiperazine produced by a marine Aspergillus sp. Nat. Prod. Lett. 1998, 12, 55–60. 10.1080/10575639808048871. [DOI] [Google Scholar]
- Dao D. Q.; Phan T. T. T.; Nguyen T. L. A.; Trinh P. T. H.; Tran T. T. V.; Lee J. S.; Shin H. J.; Choi B.-K. Insight into Antioxidant and Photoprotective Properties of Natural Compounds from Marine Fungus. J. Chem. Inf. Model. 2020, 60, 1329–1351. 10.1021/acs.jcim.9b00964. [DOI] [PubMed] [Google Scholar]
- Vo Q. V.; Tam N. M.; Hieu L. T.; Van Bay M.; Thong N. M.; Le Huyen T.; Hoa N. T.; Mechler A. The antioxidant activity of natural diterpenes: theoretical insights. RSC Adv. 2020, 10, 14937–14943. 10.1039/d0ra02681f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vo Q. V.; Van Gon T.; Van Bay M.; Mechler A. Antioxidant Activities of Monosubstituted Indolinonic Hydroxylamines: A Thermodynamic and Kinetic Study. J. Phys. Chem. B 2019, 123, 10672–10679. 10.1021/acs.jpcb.9b08912. [DOI] [PubMed] [Google Scholar]
- Vo Q. V.; Cam Nam P.; Bay M. V.; Minh Thong N.; Hieu L. T.; Mechler A. A theoretical study of the radical scavenging activity of natural stilbenes. RSC Adv. 2019, 9, 42020–42028. 10.1039/c9ra08381b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Galano A.; Raúl Alvarez-Idaboy J. Computational strategies for predicting free radical scavengers’ protection against oxidative stress: Where are we and what might follow?. Int. J. Quantum Chem. 2019, 119, e25665 10.1002/qua.25665. [DOI] [Google Scholar]
- Wright J. S.; Carpenter D. J.; McKay D. J.; Ingold K. U. Theoretical Calculation of Substituent Effects on the O–H Bond Strength of Phenolic Antioxidants Related to Vitamin E. J. Am. Chem. Soc. 1997, 119, 4245–4252. 10.1021/ja963378z. [DOI] [Google Scholar]
- Leopoldini M.; Russo N.; Toscano M. The molecular basis of working mechanism of natural polyphenolic antioxidants. Food Chem. 2011, 125, 288–306. 10.1016/j.foodchem.2010.08.012. [DOI] [Google Scholar]
- Galano A.; Mazzone G.; Alvarez-Diduk R.; Marino T.; Alvarez-Idaboy J. R.; Russo N. Food antioxidants: chemical insights at the molecular level. Annu. Rev. Food Sci. Technol. 2016, 7, 335–352. 10.1146/annurev-food-041715-033206. [DOI] [PubMed] [Google Scholar]
- Hehre W.; Yu J.; Klunzinger P.; Lou L.. Spartan Software; Wavefunction Inc.: Irvine, 2000.
- Mai T. V.-T.; Duong M. v.; Le X. T.; Huynh L. K.; Ratkiewicz A. Direct Ab Initio Dynamics Calculations of Thermal Rate Constants For The CH4+ O2= CH3+ HO2 Reaction. Struct. Chem. 2014, 25, 1495–1503. 10.1007/s11224-014-0426-2. [DOI] [Google Scholar]
- Le T. H. M.; Tran T. T.; Huynh L. K. Identification of Hindered Internal Rotational Mode for Complex Chemical Species: A Data Mining Approach with Multivariate Logistic Regression Model. Chemom. Intell. Lab. Syst. 2018, 172, 10–16. 10.1016/j.chemolab.2017.11.006. [DOI] [Google Scholar]
- Galano A.; Alvarez-Idaboy J. R. Glutathione: mechanism and kinetics of its non-enzymatic defense action against free radicals. RSC Adv. 2011, 1, 1763–1771. 10.1039/c1ra00474c. [DOI] [Google Scholar]
- Vo Q. V.; Tam N. M.; Bay M. V.; Mechler A. The radical scavenging activity of natural ramalin: A mechanistic and kinetic study. Chem. Phys. Lett. 2020, 739, 137004. 10.1016/j.cplett.2019.137004. [DOI] [Google Scholar]
- Ingold K. U.; Pratt D. A. Advances in radical-trapping antioxidant chemistry in the 21st century: a kinetics and mechanisms perspective. Chem. Rev. 2014, 114, 9022–9046. 10.1021/cr500226n. [DOI] [PubMed] [Google Scholar]
- Muñoz-Rugeles L.; Galano A.; Raúl Alvarez-Idaboy J. Non-covalent π–π stacking interactions turn off non-adiabatic effects in proton-coupled electron transfer reactions. Phys. Chem. Chem. Phys. 2017, 19, 6969–6972. 10.1039/c6cp08610a. [DOI] [PubMed] [Google Scholar]
- Galano A.; Pérez-González A.; Castañeda-Arriaga R.; Muñoz-Rugeles L.; Mendoza-Sarmiento G.; Romero-Silva A.; Ibarra-Escutia A.; Rebollar-Zepeda A. M.; León-Carmona J. R.; Hernández-Olivares M. A.; Alvarez-Idaboy J. R. Empirically Fitted Parameters for Calculating p K a Values with Small Deviations from Experiments Using a Simple Computational Strategy. J. Chem. Inf. Model. 2016, 56, 1714–1724. 10.1021/acs.jcim.6b00310. [DOI] [PubMed] [Google Scholar]
- Galano A.; Alvarez-Idaboy J. R. A Computational Methodology for Accurate Predictions of Rate Constants in Solution: Application to the Assessment of Primary Antioxidant Activity. J. Comput. Chem. 2013, 34, 2430–2445. 10.1002/jcc.23409. [DOI] [PubMed] [Google Scholar]
- Boulebd H.; Amine Khodja I.; Bay M. V.; Hoa N. T.; Mechler A.; Vo Q. V. Thermodynamic and Kinetic Studies of the Radical Scavenging Behavior of Hydralazine and Dihydralazine: Theoretical Insights. J. Phys. Chem. B 2020, 124, 4123. 10.1021/acs.jpcb.0c02439. [DOI] [PubMed] [Google Scholar]
- Dzib E.; Cabellos J. L.; Ortíz-Chi F.; Pan S.; Galano A.; Merino G. Eyringpy: A program for computing rate constants in the gas phase and in solution. Int. J. Quantum Chem. 2019, 119, e25686 10.1002/qua.25686. [DOI] [Google Scholar]
- Zhao Y.; Schultz N. E.; Truhlar D. G. Design of Density Functionals by Combining the Method of Constraint Satisfaction with Parametrization for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Theory Comput. 2006, 2, 364–382. 10.1021/ct0502763. [DOI] [PubMed] [Google Scholar]
- Galano A.; Alvarez-Idaboy J. R. Kinetics of radical-molecule reactions in aqueous solution: A benchmark study of the performance of density functional methods. J. Comput. Chem. 2014, 35, 2019–2026. 10.1002/jcc.23715. [DOI] [PubMed] [Google Scholar]
- Zhao Y.; Truhlar D. G. How Well Can New-Generation Density Functionals Describe the Energetics of Bond-Dissociation Reactions Producing Radicals?. J. Phys. Chem. A 2008, 112, 1095–1099. 10.1021/jp7109127. [DOI] [PubMed] [Google Scholar]
- Carreon-Gonzalez M.; Vivier-Bunge A.; Alvarez-Idaboy J. R. Thiophenols, Promising Scavengers of Peroxyl Radicals: Mechanisms and kinetics. J. Comput. Chem. 2019, 40, 2103–2110. 10.1002/jcc.25862. [DOI] [PubMed] [Google Scholar]
- Alvarez-Idaboy J. R.; Galano A. On the Chemical Repair of DNA Radicals by Glutathione: Hydrogen Vs Electron Transfer. J. Phys. Chem. B 2012, 116, 9316–9325. 10.1021/jp303116n. [DOI] [PubMed] [Google Scholar]
- Vo Q. V.; Van Bay M.; Nam P. C.; Mechler A. Is Indolinonic Hydroxylamine a Promising Artificial Antioxidant?. J. Phys. Chem. B 2019, 123, 7777–7784. 10.1021/acs.jpcb.9b05160. [DOI] [PubMed] [Google Scholar]
- Evans M. G.; Polanyi M. Some Applications of the Transition State Method to the Calculation of Reaction Velocities, Especially in Solution. Trans. Faraday Soc. 1935, 31, 875–894. 10.1039/tf9353100875. [DOI] [Google Scholar]
- Eyring H. The Activated Complex in Chemical Reactions. J. Chem. Phys. 1935, 3, 107–115. 10.1063/1.1749604. [DOI] [Google Scholar]
- Truhlar D. G.; Hase W. L.; Hynes J. T. Current Status of Transition-State Theory. J. Phys. Chem. 1983, 87, 2664–2682. 10.1021/j100238a003. [DOI] [Google Scholar]
- Furuncuoğlu T.; Ugur I.; Degirmenci I.; Aviyente V. Role of Chain Transfer Agents in Free Radical Polymerization Kinetics. Macromolecules 2010, 43, 1823–1835. 10.1021/ma902803p. [DOI] [Google Scholar]
- Vélez E.; Quijano J.; Notario R.; Pabón E.; Murillo J.; Leal J.; Zapata E.; Alarcón G. A Computational Study of Stereospecifity in the Thermal Elimination Reaction of Menthyl Benzoate in the Gas Phase. J. Phys. Org. Chem. 2009, 22, 971–977. 10.1002/poc.1547. [DOI] [Google Scholar]
- Dzib E.; Cabellos J. L.; Ortiz-Chi F.; Pan S.; Galano A.; Merino G.. Eyringpy 1.0.2; Cinvestav: Mérida, Yucatán, 2018.
- Boulebd H.; Mechler A.; Hoa N. T.; Vo Q. V. Thermodynamic and Kinetic Studies of the Antiradical Activity of 5-Hydroxymethylfurfural: Computational Insights. New J. Chem. 2020, 44, 9863. 10.1039/D0NJ01567A. [DOI] [Google Scholar]
- Pollak E.; Pechukas P. Symmetry Numbers, not Statistical Factors, Should be used in Absolute Rate Theory and in Broensted Relations. J. Am. Chem. Soc. 1978, 100, 2984–2991. 10.1021/ja00478a009. [DOI] [Google Scholar]
- Fernández-Ramos A.; Ellingson B. A.; Meana-Pañeda R.; Marques J. M. C.; Truhlar D. G. Symmetry Numbers and Chemical Reaction Rates. Theor. Chem. Acc. 2007, 118, 813–826. 10.1007/s00214-007-0328-0. [DOI] [Google Scholar]
- Eckart C. The Penetration of a Potential Barrier by Electrons. Phys. Rev. 1930, 35, 1303. 10.1103/physrev.35.1303. [DOI] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.; Nakatsuji H.; Caricato M.; Li X.; Hratchian H. P.; Izmaylov A. F.; Bloino J.; Sonnenberg J. L.; Hada M.; Ehara M.; Toyota K.; Fukuda R.; Hasegawa J.; Ishida M.; Nakajima T.; Honda Y.; Kitao O.; Nakai H.; Vreven T.; Montgomery J. A.; Peralta J. E. Jr.; Ogliaro F.; Bearpark M.; Heyd J. J.; Brothers E.; Kudin K. N.; Staroverov V. N.; Keith T.; Kobayashi R.; Normand J.; Raghavachari K.; Rendell A.; Burant J. C.; Iyengar S. S.; Tomasi J.; Cossi M.; Rega N.; Millam J. M.; Klene M.; Knox J. E.; Cross J. B.; Bakken V.; Adamo C.; Jaramillo J.; Gomperts R.; Stratmann R. E.; Yazyev O.; Austin A. J.; Cammi R.; Pomelli C.; Ochterski J. W.; Martin R. L.; Morokuma K.; Zakrzewski V. G.; Voth G. A.; Salvador P.; Dannenberg J. J.; Dapprich S.; Daniels A. D.; Farkas O.; Foresman J. B.; Ortiz J. V.; Cioslowski J.; Fox D. J.. Gaussian 16, Revision B.01; Gaussian, Inc.: Wallingford CT, 2016.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.