Creating and applying SIR modified compartmental model for calculation of COVID-19 lockdown efficiency

Highlights

• •SIR compartmental model of COVID-19 spread may help to evaluate efficiency of lockdown measures.
• •Epidemiological data collected in fifteen european countries, are taken as input parameters.
• •Herd immunity level and the time of its formation are considered as factors indicating efficiency of lockdowns.
• •Lockdown and no-lockdown mode of containment lead to roughly similar results. Lockdowns do not stop COVID-19 spread.
• •Rationale for lockdowns is avoidance of healthcare system overburdening.
• •Reliance on lockdowns as the only administrative measures that may contain a pandemic, is a misstep that should be avoided in the future.

Abstract

We propose a Susceptible–Infected–Recovered (SIR) modified model for Coronavirus disease – 2019 (COVID-19) spread to estimate the efficacy of lockdown measures introduced during the pandemic. As input data, we used COVID-19 epidemiological information collected in fifteen European countries either in private surveys or using official statistics. Thirteen countries implemented lockdown measures, two countries (Sweden, Iceland) not. As output parameters, we studied herd immunity level and time of formation. Comparison of these parameters was used as an indicator of effectiveness / ineffectiveness of lockdown measures. In the absence of a medical vaccine, herd immunity may be regarded as a factor of population adaptation to severe acute respiratory syndrome-related coronavirus-2, the viral pathogen causing COVID-19 disease (SARS-CoV-2), and hence COVID-19 spreading stop. We demonstrated that there is no significant difference between lockdown and no-lockdown modes of COVID-19 containment, in terms of both herd immunity level and the time of achieving its maximum. The rationale for personal and business lockdowns may be found in the avoidance of healthcare system overburdening. However, lockdowns do not prevent any virus with droplet transmission (including SARS-CoV-2) from spreading. Therefore, in case of a future viral pathogen emergence, lockdown measures efficiency should not be overestimated, as it was done almost universally in the world during COVID-19 pandemic.

1. Introduction

Efficiency and necessity of lockdown measures implemented on a scale of the whole world, cause much controversy [1], [2], [3]. In the current paper, we analyse whether total lockdowns are helpful in stopping spread of Coronavirus disease – 2019 (COVID-19) and future similar global diseases, by means of investigating herd immunity formation to Severe acute respiratory syndrome-related coronavirus-2, the viral causative agent of COVID-19 disease (SARS-CoV-2). In the current absence of a vaccine, herd immunity remains the only way to stabilise human population reaction to the novel viral pathogen.

It was repeatedly emphasised that creating of so-called herd (population, block, natural) immunity is important for slowing down the rate of COVID-19 spread in population and, actually, for stopping the pandemic [4], [5], [6], [7], [8], [9], [10]. However, as of 25 June 2020, not many official investigations of SARS-CoV-2 dissemination in the whole ecosystems and populations (e.g. random mass testing, representative sample screening, closed ecosystem studies, etc.) have been performed and reported, that would allow us to estimate the level of herd immunity formation. Henrik Jarlov collected the most comprehensive list of all programmes of COVID-19 population mass screening, including RT-PCR tests and immunoglobulin tests [11].

The evaluation of herd immunity formation may be highly important in clinical treatment of COVID-19 patients for several reasons. First, it may help to avoid excessive loads related to COVID-19 suspicious cases, on healthcare systems, by differentiating COVID/non-COVID cases. This knowledge is relevant even in September 2020 (the time of the final revision of the article), as a second COVID-19 wave is not impossible. A threat of healthcare system overheat has been already reported for a number of countries [12], [13], [14], [15]. Second, it may give a more realistic picture of COVID-19 spread in the population and, therefore, provide more dependable statistical data on the number of the infected, symptomatic and asymptomatic patients at a given time point. Third, it can be used for elaborating the general rules of identifying and classifying the patients. And most importantly, herd immunity may be a means of assessing the efficiency of lockdown measures.

Used as an epidemiological instrument initially, notorious and much talked-about lockdowns unfortunately transformed to the means of social control and political compelling/blackmailing in many parts of the world. Excepting a very limited number of countries, the almost global and universal governmental response to COVID-19 pandemic evidently put the world on the verge of the Orwell's 1984 scenario. Now, in September 2020, when media and many politicians do not stop to speculate about second and consecutive waves of SARS-CoV-2 pandemic, lockdown measure are looming on the horizon again. In UK, in the small city of Aberdeen in Scotland, exceeding the acceptable SARS-CoV-2 infection limits defined by the government merely by fifty humans, plunged the city in the full lockdown of indefinite length again. The Brazilian population vast in size continues to suffer from incessant lockdowns. In USA, each state administration regards COVID-19 differently and the country remains severely split in terms of the SARS-CoV-2 containment strategy. In Russia, all governmental media do not cease to intimidate people by a possibility that soon everybody will be locked again and every citizen will pay for his/her relaxed summer rest (basically, normal mode of life without coercive deprivation of personal freedoms). Is the time not come when we should critically evaluate with the help of mathematical models backed by experimental epidemiological information collected thus far, to which extent the lockdown measures and strategies should be used again, if used at all?

Currently, a lot of mathematical models of SARS-CoV-2 spread have been elaborated, both theoretical [16], [17] and computational, many of them already described in Special Issues of Chaos, Solitons and Fractals journal “Modeling and forecasting of epidemic spreading: the case of Covid-19 and beyond” [18], [19]. By dint of our model, we hope to contribute to our mutual understanding of the lockdown measures efficacy.

2. Materials and methods

2.1. Methodology

We propose a Susceptible–Infected–Recovered (SIR) modified compartmental model. Using epidemiological data as input parameters for the model, we calculate times and levels of herd immunity formation for different modes of containment (lockdown and no-lockdown). Finally, we evaluate the efficiency of lockdown measures.

2.2. Open-Source primary epidemiological data

The statistical data on COVID-19 random testing were used: Diamond Princess cruise ship [20], [21], [22], [23], evacuation flights data in Japan [24], Japan [25], Republic of Korea [26], Taiwan [27], Austria [28], Germany [29], Iceland [30], Lombardy (Italy) [31]; Portugal [32]; Russia [33]; and United Kingdom [34].

2.3. Privately collected primary epidemiological data

COVID-19 primary statistical data sets were collected since 2 March to 21 April 2020. In May-August 2020, additional data have been collected that changed our understanding of SARS-CoV-2 spread substantially. The Acknowledgement section contain a number of names of people who assisted in collecting the data and expressed their explicit consent for their contribution to be noted.

The primary information and its sources are summarised in Table 1 for the initial period (March-April 2020).

Table. 2.

Estimation of herd immunity formation in Europe (95% confidence interval) during the “first wave” of SARS-CoV-2 according to our SIR modified modelling with the privately collected input data on different European countries, for different possible basic reproduction numbers r₀.

Mode of containment	Full-lockdown						No-lockdown
Basic reproduction number r0	r0 = 1.6			r0 = 5.6			r0 = 1.6			r0 = 5.6
Scenario*	a	b	c	a	b	c	a	b	c	a	b	c
Total herd immunity achievable, per cent of population	3.31	4.78	5.24	3.63	5.17	6.02	4.40	4.65	5.11	4.77	5.56	6.42
Estimated time of achieving maximal rate of herd immunity growth, weeks	7.2	–5.7; 6.6	–16.3	6.9	–13.3; 5.8	–23.6	3.1	–5.7; 2.7	–16.3	3.0	–13.3; 2.4	–23.6
Estimated time of achieving 95% herd immunity, weeks	14.0	12.8	11.5	13.2	11.5	10.0	47.3	45.2	42.8	45.0	43.6	40.4

Negative time values stand for the time before the beginning of the infection process in a given community.

* Scenarios:.

^aworld disease peak (“first wave” of SARS-CoV-2) has not yet been passed on 11 March 2020 (announcement of the pandemic by World Health Organisation (WHO));.

^bthere are two peaks a and c; a current situation is their overlapping;.

^cdisease peak has been already passed unnoticed before the pandemic was announced by WHO.

Table. 1.

Sources of private and publicly available data sets on COVID-19 statistics in some European countries obtained in time interval 2 March – 21 April 2020.

Countries (in the alphabetical order)	Number of venues surveyed		Total number of tests made, available for our analysis*	Percentage of the population tested,%	Number of time snapshots available*	Availability of data	Official mass screening procedures taking place as of 25 April 2020
	Medical institutions and ambulance (hospital and field tests)	Commercial and non- commercial test labs
Austria (official)			156,800	1.742	10	Public	Yes
Austria	3	2	26,608	0.296	14	Private
Denmark	3	4	21,782	0.376	12	Private	No
Finland	2	2	3081	0.056	6	Private	No
Germany (official)			2320,415	2.800	16	Public	Yes
Germany	10	18	224,220	0.271	34	Private
Iceland (official)			4197**	1.183	1	Public	Yes
Iceland	1	1	10,102	2848	2	Private
Italy (official)			234,870***	0.389	1	Public	No
Italy	3	5	5702	0.009	12	Private
Norway	4	4	42,147	0.795	16	Private	No
Poland	8	2	4262	0.012	8	Private	No
Portugal (official)			208,314	2.027	15	Public	Yes
Portugal	4	6	48,188	0.469	18	Private
Russia (official)			2142,600	1.459	22	Public	Yes
Russia	2	1	37,205	0.025	2	Private
Spain	4	5	9322	0.020	10	Private	No
Sweden	2	3	42,163	0.409	27	Private	Yes
Switzerland	3	6	8014	0.094	12	Private	No
The Netherlands	2	8	87,341	0.501	27	Private	No
United Kingdom (official)			386,044****	0.579	1	Public	No
United Kingdom	7	12	62,254	0.094	20	Private	No
Total	58	79	> 4500,000

* As of 21 April 2020. We have no information about the total number of COVID-19 tests made on a scale of a whole country, if the information is not disclosed publicly.

** As of 21 March 2020.

*** In Lombardy only.

**** In-patient (hospital only) PHE statistics, as of 21 April 2020.

2.4. Modelling the COVID-19 spread in population

We assume that the dissemination of COVID-19 may be explained by a continuous-time Markov process model [35], [36]. This process can be generally described by a Susceptible–Infected–Recovered (SIR) compartmental model [37], [38]. Some authors used Susceptible–Exposed–Infected–Recovered (SEIR) model for their calculations [39], [40], [41]. We chose to use a common SIR compartmental model altered by introducing several significant modifications to the corresponding Markov process structure.

Regarding lockdown measures imposed on citizens, we used two models: a) common; b) Swedish. In the former, full lockdown measures were implemented during the surge of COVID-19 disease (only Home – Pharmacy – Grocery Store – Walk with an Animal (e.g. dog) – Hospital possibilities), in the latter no lockdowns were in force. Most of countries followed the lockdown way. Very few countries implemented no lockdowns, e.g. Sweden, Iceland, Belarus, Japan, Taiwan, Republic of Korea. The Swedish model is more complex, and the corresponding Markov process includes 13 knots (in our modelling). The knots (states) of the Markov processes of people relocation in a community, are shown in Fig. 1 .

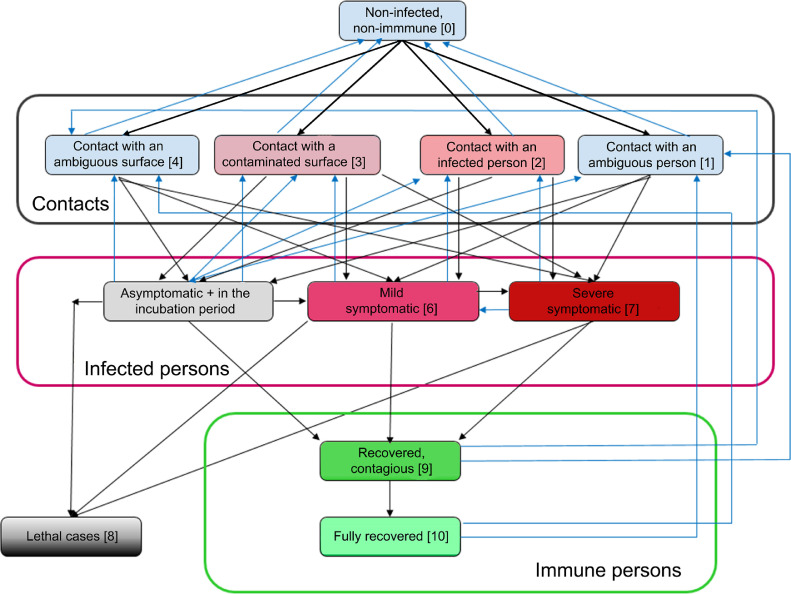
Fig. 1.

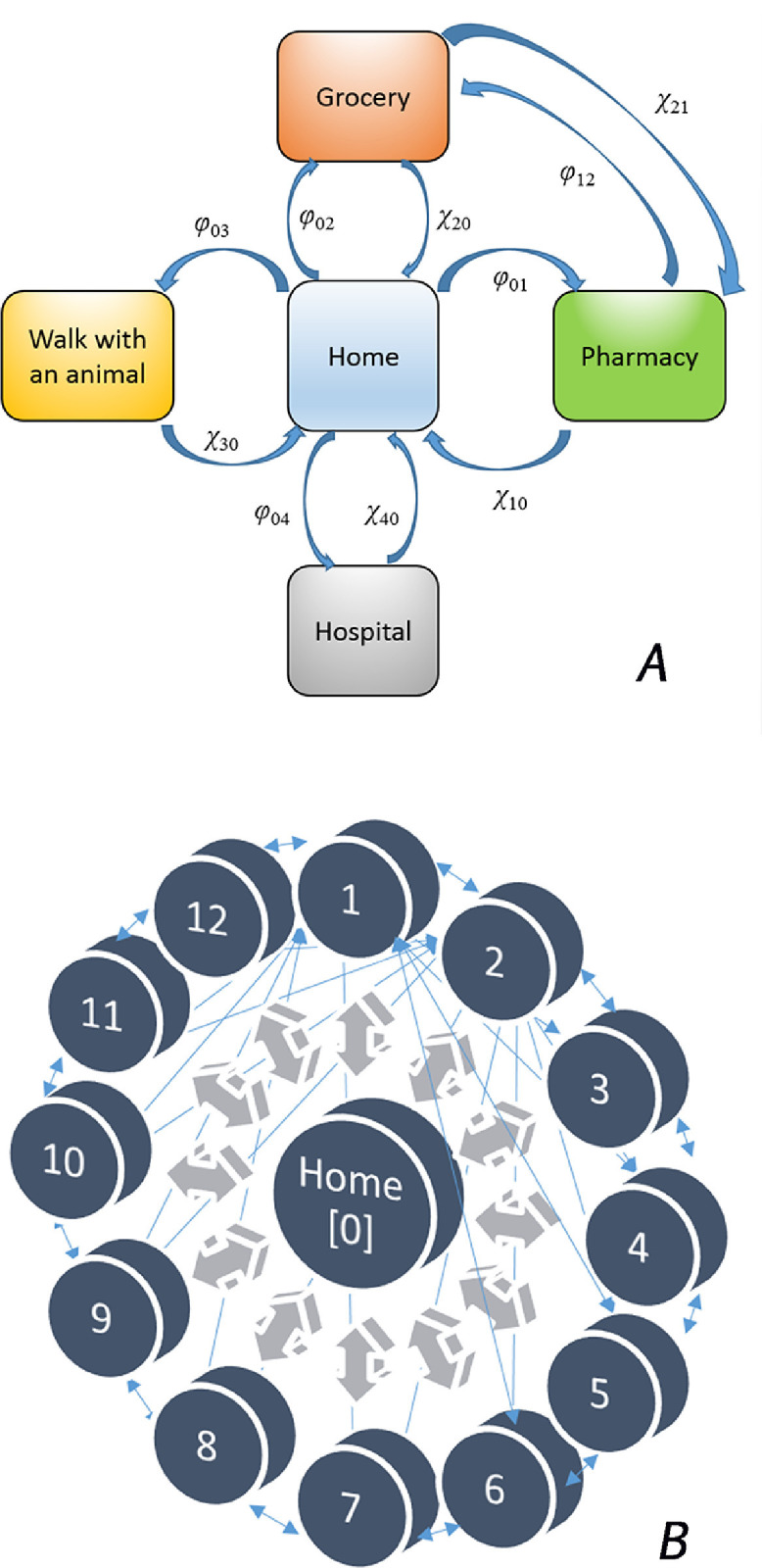
Two public policies of SARS-CoV-2 containment: full lockdown (A) and no-lockdown (B). The latter represents a “bicycle wheel” where every knot (state) is connected with all other knots (states), with intensity coefficients λ_ij, i and j are running from 0 to 12: Home {0} – Pharmacy {1} – Grocery store {2} – Walk with an animal {3} – Walk anywhere with several people together {4} – Public transport {5} – Public gatherings, excluding mass gatherings {6} – Cafés, restaurants {7} – Hospitals, medical institutions {8} – Offices, working places {9} – Asylums, orphanages, hospices {10} – Weekend limited gatherings, camps on nature (e.g. school, university, corporate etc.) {11} – Educational institutions (schools, universities, training programmes etc.) [12}. For simplicity of the figure, full sets of arrows are shown only for knots 1 and 2.

Fig. 2 demonstrates our SIR modified compartmental model as a continuous-time Markov process modelling the infection transmission, with the knots (states) corresponding to different possible situations of a human in regard to the disease.

Fig. 2.

Schematics of a continuous-time Markov process describing SARS-CoV-2 transmission (SIR modified compartmental model).

2.5. Distribution and relocation of population in space and time in two different modes of containment

Let us consider a human who may be in any of the five places in a full lockdown mode of life. Then the probabilities of his/her stay in these five places are p ₀ (home), p ₁ (pharmacy), p ₂ (grocery store), p ₃ (street saunter with an animal, most commonly a dog), p ₄ (hospital / any other medical institution, in inpatient / outpatient modes of treatment). It is obvious that

$$\sum _{i=0}^4{p}_i\left(t\right)=1$$ (1)

First, let us write a system of Kolmogorov linear differential (2), (3), (4), (5), (6) for the movement of a human in Model 2 (in a country with a full lockdown mode). For the considerations of simplicity, we assume that a hospitalisation may be made only from his/her home, and intensities are not functions of t:

$$\{\begin{array}{c}\frac{d{p}_0\left(t\right)}{dt}\left(Home\right)={\chi }_{10}{p}_1\left(t\right)+{\chi }_{20}{p}_2\left(t\right)+{\chi }_{30}{p}_3\left(t\right)+{\chi }_{40}{p}_4\left(t\right)-\hfill \\ \left({\phi }_{01}+{\phi }_{02}+{\phi }_{03}+{\phi }_{04}\right)p_0\left(t\right),\hfill \end{array}$$ (2)

$$\{\frac{d{p}_1\left(t\right)}{dt}\left(Pharmacy\right)={\phi }_{01}{p}_0\left(t\right)+{\chi }_{21}{p}_2\left(t\right)-\left({\chi }_{10}+{\phi }_{12}\right)p_1\left(t\right),$$ (3)

$$\{\frac{d{p}_2\left(t\right)}{dt}\left(Grocery\right)={\phi }_{02}{p}_0\left(t\right)+{\phi }_{12}{p}_1\left(t\right)-\left({\chi }_{20}+{\chi }_{21}\right)p_2\left(t\right),$$ (4)

$$\{\frac{d{p}_3\left(t\right)}{dt}\left(Saunter\right)={\phi }_{03}{p}_0\left(t\right)+{\chi }_{30}{p}_3\left(t\right)$$ (5)

$$\{\frac{d{p}_4\left(t\right)}{dt}\left(Hospital\right)={\phi }_{04}{p}_0\left(t\right)+{\chi }_{40}{p}_4\left(t\right)$$ (6)

For the second model (Swedish), we have fourteen Kolmogorov equations. Taking into account that Markov process in the Swedish model is ergodic, in comparison with the full lockdown Markov process, we receive the following system of Kolmogorov equations:

$$\frac{d{p}_i\left(t\right)}{dt}=\sum _{\begin{array}{c}j=0\\ j\ne i\end{array}}^{13}{\phi }_{ji}{p}_j\left(t\right)-p_i\left(t\right)\sum _{\begin{array}{c}j=0\\ j\ne i\end{array}}^{13}{\phi }_{ij},i=\overline{\left(0;12\right)}$$ (7)

Typical values of λ _ij and μ _ij are taken from the similar models of human relocation, as described in the works [42], [43], [44], [45].

To estimate the number of the immune people and, therefore, the level of herd immunity created thus far, we have to observe how Kolmogorov equation systems 2–6 and 7, and the corresponding master equations behave (how the solutions p_i(t) change) on varying the epidemiologic and demographic parameters. The solutions, i.e. probability functions p_i(t) are complex functions of t, and they have these parameters as variables:

$$p_i=p_i\left(t,r_0,c_{drop.},c_{surf.},N_{imm}\left(t\right)\right),$$ (8)

where r ₀ is basic reproduction number, c_drop contagiousness coefficient of droplet transmission, c_surf contagiousness coefficient of touching surface transmission, N the total number of humans in a community, N_imm the number of people in the community who already have the immunity to SARS-CoV-2.

Using coefficients of transmission is a rather new concept. In fact, these coefficients represent probabilities of a non-immune person of becoming infected through a direct contact with a person already infected or a contaminated surface: $c=\frac{N_{infectedaftercontact}}{N_{totalcontacts}}$, and, therefore, 0 ≤ c_drop. + c_surf. ≤ 1. In a more broad sense, 0 ≤ c_drop. + c_surf. ≤ 2, but the value 2 for the sum is not achievable even for the most contagious diseases known to humanity thus far (e.g. varicella for droplet transmission or Ebola haemorrhagic fever for body liquids transmission).

Basic reproduction number r ₀ is estimated differently by different research groups. The difference is tremendous, from 1.6 [36] or 2.6 [46] to 5.6 as a median with 6.7 as the maximal value [47] and even almost 15 for the virus spread estimations on Diamond Princess cruise ship [20]. In its report of 17 and 24 April 2020, Robert Koch Institute made evaluations of r ₀ as low as 0.5–0.6 [29]. Such enormous difference in evaluating basic reproduction number may result from the fact that various research groups studied different samplings incomparable with each other in terms of closeness and rate of human contacts. We will use r ₀ = 1.6 and 5.6 as reference points.

The sum c_drop + c_surf was initially estimated in 0.3–0.4 range (nearly 3 or 4 of 10 persons directly contacting an infected individual of surfaces with a full virus titre, will be infected by SARS-CoV-2 virus) [48], [49], [50], where c_drop may be 0.1–0.2 [50]. Values of N for different communities are taken from various demographic sources publicly available over the Internet. $h\left(t\right)=\frac{N_{imm.}\left(t\right)}{N}$ is required to be assessed in our model.

2.6. The model of the virus transmission

To perform estimations of N_imm(t), an additional Kolmogorov equation system should be included in our analysis. Within our SIR modified compartmental model, this system of linear differential equations describes intensities and directions of flows in the transmission model (Fig. 2). Analysing the behaviour of Markov process that describes the virus spread, along with the behaviour of systems 2–6 and 7 of space-time population distribution, enabled us to evaluate the level and time of herd immunity formation in the countries studied.

A non-infected person may contact with: a) an ambiguous person (he/she may be either infected or non-infected) (knot 1); b) a proven SARS-CoV-2 carrier (knot 2); c) a contaminated surface (knot 3); d) an ambiguous surface (a virus amount may be present or may not) (knot 4). The knots 5–7 correspond to the virus carriers proven by an RT-PCR or RT-LAMP test: asymptomatic OR those in the incubation period (knot 5); mild symptomatic (knot 6) and severe symptomatic with atypical pneumonia clinical picture (knot 7). Finally, the outcomes are either decease (knot 8) or recovery (knots 9–10). amongst the recovered patients, there may be the contagious ones (knot 9) and completely recovered ones without active virions in their bodies, and therefore, without any SARS-CoV-2 contagiousness (knot 10). The Markov process is non-ergodic, non-stationary. We are interested in the characteristics of the final state of this process. Potentially, with relatively large time values, the Markov process described will reach a stationary state of the maximal herd immunity formation (one global spike of disease) or several quasi-stationary states of local herd immunity plateaus formation (two or more local spikes of disease), with the last plateau being the global maximum of herd immunity achievable in population. The stationary state of the Markov process discussed will not change over time any longer; the quasi-stationary states will not change over some time. These states correspond with herd immunity global and local plateaus. We shall find the times and values of these plateaus by finding the inflection points of herd immunity dependence on time, that coincide with extremum points of herd immunity first time derivative.

The system of Kolmogorov equations for this SIR modified disease transmission compartmental model is the following (9-19):

$$\begin{array}{c}\hfill \{\begin{array}{c}\frac{d{p}_0\left(t\right)}{dt}\left(\begin{array}{c}non-infected\\ persons,non-immune\end{array}\right)={\mu }_{10}{p}_1\left(t\right)+{\mu }_{20}{p}_2\left(t\right)\hfill \\ +{\mu }_{30}{p}_3\left(t\right)+{\mu }_{40}{p}_4\left(t\right)-\left({\lambda }_{01}+{\lambda }_{02}+{\lambda }_{03}+{\lambda }_{04}\right)p_0\left(t\right),\hfill \end{array}\end{array}$$ (9)

$$\begin{array}{c}\hfill \{\begin{array}{c}\frac{d{p}_1\left(t\right)}{dt}\left(\begin{array}{c}non-infectedperson\\ contactsambiguousperson\end{array}\right)={\lambda }_{01}{p}_0\left(t\right)\hfill \\ +{\mu }_{51}{p}_5\left(t\right)+{\mu }_{91}{p}_9\left(t\right)+{\mu }_{10,1}{p}_{10}\left(t\right)\hfill \\ -\left({\lambda }_{15}+{\lambda }_{16}+{\lambda }_{17}+{\mu }_{10}\right)p_1\left(t\right),\hfill \end{array}\end{array}$$ (10)

$$\begin{array}{c}\hfill \{\begin{array}{c}\frac{d{p}_2\left(t\right)}{dt}\left(\begin{array}{c}non-infectedperson\\ contactsinfectedperson\end{array}\right)={\lambda }_{02}{p}_0\left(t\right)+{\mu }_{52}{p}_5\left(t\right)\hfill \\ +{\mu }_{62}{p}_6\left(t\right)+{\mu }_{72}{p}_7\left(t\right)\hfill \\ -\left({\lambda }_{25}+{\lambda }_{26}+{\lambda }_{27}+{\mu }_{20}\right)p_2\left(t\right),\hfill \end{array}\end{array}$$ (11)

$$\begin{array}{c}\hfill \{\begin{array}{c}\frac{d{p}_3\left(t\right)}{dt}\left(\begin{array}{c}non-infectedperson\\ touchescontaminatedsurface\end{array}\right)={\lambda }_{03}{p}_0\left(t\right)\hfill \\ +{\mu }_{53}{p}_5\left(t\right)+{\mu }_{63}{p}_6\left(t\right)+{\mu }_{73}{p}_7\left(t\right)\hfill \\ -\left({\lambda }_{35}+{\lambda }_{36}+{\lambda }_{37}+{\mu }_{30}\right)p_3\left(t\right),\hfill \end{array}\end{array}$$ (12)

$$\begin{array}{c}\hfill \{\begin{array}{c}\frac{d{p}_4\left(t\right)}{dt}\left(\begin{array}{c}non-infectedperson\\ touchesambiguoussurface\end{array}\right)={\lambda }_{04}{p}_0\left(t\right)\hfill \\ +{\mu }_{54}{p}_5\left(t\right)+{\mu }_{94}{p}_9\left(t\right)+{\mu }_{10,4}{p}_{10}\left(t\right)-\hfill \\ -\left({\lambda }_{45}+{\lambda }_{46}+{\lambda }_{47}+{\mu }_{40}\right)p_4\left(t\right),\hfill \end{array}\end{array}$$ (13)

$$\{\begin{array}{c}\frac{d{p}_5\left(t\right)}{dt}\left(\begin{array}{c}asymptomatic\\ \begin{array}{c}carrierstate\\ ORincubationperiod\end{array}\end{array}\right)={\lambda }_{15}{p}_1\left(t\right)+{\lambda }_{25}{p}_2\left(t\right)+{\lambda }_{35}{p}_3\left(t\right)+{\lambda }_{45}{p}_4\left(t\right)\hfill \\ -\left({\mu }_{51}+{\mu }_{52}+{\mu }_{53}+{\mu }_{54}+{\lambda }_{56}+{\lambda }_{58}+{\lambda }_{59}\right)p_5\left(t\right),\hfill \end{array}$$ (14)

$$\{\begin{array}{c}\frac{d{p}_6\left(t\right)}{dt}\left(\begin{array}{c}mildsymptomatic\\ carrierstate\end{array}\right)={\lambda }_{16}{p}_1\left(t\right)+{\lambda }_{26}{p}_2\left(t\right)\hfill \\ +{\lambda }_{36}{p}_3\left(t\right)+{\lambda }_{46}{p}_4\left(t\right)+{\lambda }_{56}{p}_5\left(t\right)-\left({\mu }_{62}+{\mu }_{63}+{\lambda }_{67}+{\lambda }_{68}+{\lambda }_{69}\right)p_6\left(t\right),\hfill \end{array}$$ (15)

$$\{\begin{array}{c}\frac{d{p}_7\left(t\right)}{dt}\left(\begin{array}{c}severesymptomatic\\ carrierstate\end{array}\right)={\lambda }_{17}{p}_1\left(t\right)+{\lambda }_{27}{p}_2\left(t\right)\hfill \\ +{\lambda }_{37}{p}_3\left(t\right)+{\lambda }_{47}{p}_4\left(t\right)+{\lambda }_{67}{p}_6\left(t\right)-\left({\mu }_{72}+{\mu }_{73}+{\mu }_{76}+{\lambda }_{78}+{\lambda }_{79}\right)p_7\left(t\right),\hfill \end{array}$$ (16)

$$\{\frac{d{p}_8\left(t\right)}{dt}\left(\begin{array}{c}deceased\\ persons\end{array}\right)={\lambda }_{58}{p}_5\left(t\right)+{\lambda }_{68}{p}_6\left(t\right)+{\lambda }_{78}{p}_7\left(t\right),$$ (17)

$$\{\begin{array}{c}\frac{d{p}_9\left(t\right)}{dt}\left(\begin{array}{c}recovered,immune,\\ contagious\end{array}\right)={\lambda }_{59}{p}_5\left(t\right)+{\lambda }_{69}{p}_6\left(t\right)+{\lambda }_{79}{p}_7\left(t\right)\hfill \\ -\left({\lambda }_{9,10}+{\lambda }_{9,1}+{\lambda }_{9,4}\right)p_9\left(t\right),\hfill \end{array}$$ (18)

$$\{\frac{d{p}_{10}\left(t\right)}{dt}\left(\begin{array}{c}completelyrecovered,\\ immune\end{array}\right)={\lambda }_{9,10}{p}_9\left(t\right)-\left({\lambda }_{10,1}+{\lambda }_{10,4}\right)p_9\left(t\right),$$ (19)

where probability changes (first derivatives) in the left parts of the equations are calculated by means of separate probabilities p_i and current intensities λ_ij. A separate probability p_i stands for a description that in moment t a human being will be in state S_i (one of the described states). A major assumption of the model that oversimplifies it is that a said human cannot be in two states simultaneously. Plus signs are for straight direction (from initial events in the disease to further events, i.e. classical progression of the infection) (black arrows in Fig. 2) and minus signs for backward events that return a human to previous states (blue arrows in Fig. 2). The exact structure of possible connections and, therefore, currents, were taken from the book of Karin VanMeter and Robert Hubert [35].

Besides, the condition (1) is met for this system, as $\sum _{\begin{array}{c}m\\ m\ne 8\end{array}}{N}_m=N$, where m is the number of Markov process knots, in our case 11, and we consider that the number of deaths is small.

Several obvious border conditions and definitions may be further explicated, such as

p ₀(0) = N(0) / N < 1; the inequality assumes that at the initial moment of time there is a portion of persons that already have the immunity to SARS-CoV-2.

p ₁₀(T) + p ₉(T) = N_immune(T) / N, where T >> t (in fact, we may take T → ∞ for the simplicity), is the final herd immunity level; while p ₁₀(t) + p ₉(t) may be not equal to N_immune(t) / N for any moment of time. For any t the intermediary herd immunity level may be measured as

$${\nu }_{immune}\left(t\right)=\frac{N_9\left(t\right)+N_{10}\left(t\right)}{N}$$ (20)

Likewise, p ₈(T) = N_d(T) / N, is total population fatality rate (TPFR). For any t we use

$${\nu }_{deseased}\left(t\right)=\frac{N_8\left(t\right)}{N}$$ (21)

instead. It is population fatality rate (PFR) that shows the percentage of the deceased in the total population.

$$p_5\left(t\right)=p_{5,incubation}\left(t\right)+p_{5,asymptomatic}\left(t\right)foranyt;$$ (22)

$$PIR=p_5\left(t\right)+p_6\left(t\right)+p_7\left(t\right)=\frac{N_{infected}}{N},$$ (23)

for any t, is population infection rate (PIR);

$$p_{5,asymptomatic}\left(T\right)=N_{asymptomatic}\left(T\right)/N;$$ (24)

and

$$\frac{p_8\left(t\right)}{p_5\left(t\right)+p_6\left(t\right)+p_7\left(t\right)+p_8\left(t\right)}=\frac{N_{deceased}\left(t\right)}{N_{infected}\left(t\right)}$$ (25)

is the infection fatality rate (IFR).

We composed the system (9–19) just for one person. Solving the system numerically for each person for each state in (2–6) and 7 with a subsequent averaging, and observing how the solutions would change on varying epidemiological parameters, is not a best algorithm. In a community there are N people, and this number is constant (the number of deaths is small in regard to the total population size). Therefore, we have a multinomial distribution. We may assume that the time of a contact with a carrier is negligibly small in comparison with other times (e.g. the time of self-isolated life or a stay in a hospital). Then, according to Sanov theorem about large deviations for a multinomial distribution [51] further explicated by Borovkov [52], we receive the equation:

$$\begin{array}{c}\hfill \frac{N!}{{\prod }_{\begin{array}{c}m\in M,\\ m=0\end{array}}^{10}\left(N_m\left(t\right)!\right)}{p}_0^{N_0\left(t\right)}\left(t\right)·\dots ·p_{10}^{N_{10}\left(t\right)}\left(t\right)\\ \hfill =exp\left(-N·\sum _{\begin{array}{c}m\in M,\\ m=0\end{array}}^{10}{\nu }_m\left(t\right)\text{ln}\frac{{\nu }_m\left(t\right)}{p_m\left(t\right)}+R\right),\end{array}$$ (26)

where $\left(m=\overline{1;10)}\cap (m\in M\right);M=\left\{0;5;6;7;8;9;10\right\}$, i.e. m is an index from set M, running through the chosen integer values from 0 to 10. It means that we take into account only non-immune non-infected people; all types of carriers (asymptomatic, mild symptomatic and severe symptomatic), immune contagious recovered persons and fully recovered and immune persons. Further, ${\nu }_m=\frac{N_m}{N}$, and R is a compensating term:

$$R\le \frac{7}{2}\left(\ln N+1\right).$$ (27)

Indeed, (26) can be obtained for our case in such a way. Infection process development may be described as a continuous Ehrenfests’ chain [44], [53], [54]. Let ξ(t) stand for these Ehrenfest chain within our virus spread system. ν_m and ν_m+1 are parts (proportions) of Markov chains η_i that in time moment t are in states m and m + 1, i.e. they can be defined as Ehrenfest frequencies:

$${\nu }_m\left(t\right)=1-\frac{\xi \left(t\right)}{N}$$ (28a)

and

$${\nu }_{m+1}\left(t\right)=1-\frac{\xi \left(t\right)}{N}$$ (28b)

Then, as explained by A. Gasnikov in details in his work [54], let us express the probability of these frequencies being probabilities p ₁ and p ₂ (later we may transfer similarly to all our probabilities p_m):

$$\begin{array}{c}\mathbb{P}\left(v_m\left(t\right)=p_1,v_{m+1}\left(t\right)=p_2\right)=\hfill \\ =\frac{N!}{\left(N{p}_1\right)!\left(N{p}_2\right)!}\mathbb{P}{\left({\eta }_m\left(t\right)=m\right)}^{N{p}_1}\mathbb{P}{\left({\eta }_m\left(t\right)=m+1\right)}^{N{p}_2}\hfill \end{array}$$ (29)

Indeed, Ehrenfest chain ξ(t) with N + 1 knots may be expressed via N independent or dependant Markov chains η_i with only one border condition $\mathbb{P}\left({\eta }_0\left(t\right)=0\right):$ (in conditional designation)

$$\xi \left(t\right)\genfrac{}{}{0pt}{}{\Delta }{=}\sum _{i=1}^m{\eta }_i\left(t\right).$$ (30)

Hence we have

$$\mathbb{P}\left(\xi \left(t\right)=0\right)=\prod _{i=1}^m\mathbb{P}\left({\eta }_i\left(t\right)=0\right)$$ (31)

Switching in (29) to the limit at t → ∞ (we assume that the virus spread may be as prolonged as we prefer and not restricted by time), we receive

$$\underset{t\to \infty }{lim}\mathbb{P}\left(v_m\left(t\right)=p_1,v_{m+1}\left(t\right)=p_2\right)=\frac{N!}{\left(N{p}_1\right)!\left(N{p}_2\right)!}\frac{1}{2^N}$$ (32)

After that, we proceed to the limit at N → ∞ (the human population size where SARS-CoV-2 is spreading may be as large as we prefer). Using Stirling formula for factorial approximation

$$n!=n^n{e}^{-n}\sqrt{2\pi n}\left(1+\mathcal{O}\left(\frac{1}{n}\right)\right),$$ (33)

we obtain (with compensating $\mathcal{O}\left(\frac{1}{n}\right)$ with an approximate equality and simplifying it)

$$\underset{t\to \infty }{lim}\mathbb{P}\left(v_m\left(t\right)=p_1,v_{m+1}\left(t\right)=p_2\right)\approx \frac{1}{\sqrt{N}}\frac{2^{-N}}{\sqrt{2\pi p_1{p}_2}}\frac{1}{p_1^{N{p}_1}{p}_2^{N{p}_2}}$$ (34)

It is obvious that the right part may be re-written using logarithmic functions of probabilities ψ(p_i) = – p₁lnp₁ – p₂lnp₂ and exponent, and then we have:

$$\begin{array}{c}\hfill \underset{t\to \infty }{lim}\mathbb{P}\left(v_m\left(t\right)=p_1,v_{m+1}\left(t\right)=p_2\right)\approx \frac{1}{\sqrt{N}}\frac{2^{-N}}{\sqrt{2\pi p_1{p}_2}}\\ \hfill \exp \left(-N\left(--p_{1}ln{p}_1--p_{2}ln{p}_2\right)\right)\end{array}$$ (35)

We investigate our system of SARS-CoV-2 dissemination for stability – precisely what we do with studying the behaviour of its Lyapunov functions. Here the stability may be defined as Sanov [51], Borovkov [52] and Gasnikov [54] define it, viz. a stable state of virus spread system (p ₁, p _2, …, p_m) in whose little neighbourhood stationary measure (probability of frequencies ν_m receiving values m, m + 1, m + 2, …) is being concentrated, independently of t. It is simpler to consider stationary states with t → ∞, but non-stationary states may be obtained as easily. Maximising $\mathbb{P}\left(v_m\left(t\right)=p_1,v_{m+1}\left(t\right)=p_2\right)$ on condition that p ₁ + p ₂ = 1, or ultimately $\sum _{i=1}^m{p}_i=1,$ is the same as minimising ψ(p_i). Differentiating ψ(p_i) by t, we receive

$$\frac{d{p}_i\left(t\right)}{dt}=\sum _{\begin{array}{c}j=1,\\ j\ne i\end{array}}^m{\lambda }_j{p}_j-{\lambda }_i{p}_i$$ (36)

It is not difficult to see that we received exactly our system of Eqs. (9-19) with Lyapunov functions ψ(p_i), Q.E.D. The same procedure may be carried out first for considering limit at N → ∞ and only after that at t → ∞. In such a case, the completely similar result may be received using the theorem formulated by Thomas G. Kurtz [53].

Now, having assured ourselves that system (36) is in fact system (9–19), we can analyse the behaviour of our multinomial distribution (26) without solving system (9–19) for each state in (2–6) and 7. We can vary r _0, c_drop + c_surf and compare the outcome. A proprietary C# algorithm was written for estimating levels and times of herd immunity formation in the countries studies. We observed the stability of the multinomial distribution of virus spread in the population (26) by analysing the behaviour of Lyapunov functions of master equation corresponding to the process (9–19) in the non-negative orthant ${\mathbb{R}}^{n+}$(all probabilities and herd immunity levels are non-negative real numbers from 0 to 1; times are non-negative real numbers). Finding the attractors (if any) by means of analysing Lyapunov functions behaviour in the orthant ${\mathbb{R}}^{n+}$ would allow us to determine the most probable values of the projected herd immunity and the times of its formation.

2.7. Software packages

Microsoft Visual Studio 2010, OriginLab OriginPro 8.1 and PTC Mathcad 6.0 were used.

2.8. Time of preparing the paper

The paper was prepared in its initial state in April 2020 and was re-considered several times in May, June and August with serious corrections of the model proposed. The final revision was completed by 24 September 2020.

3. Results and discussion

3.1. Change of population infection rate over time

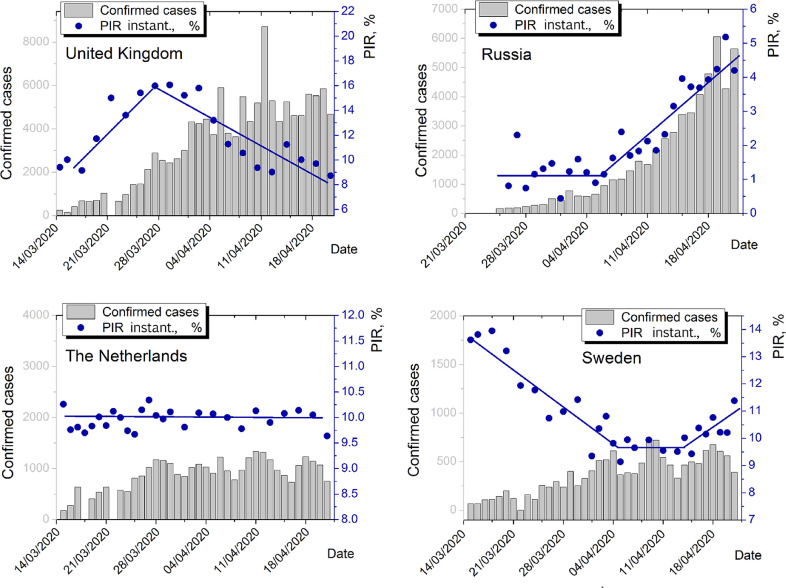
In addition to the mean population infection rate (PIR) level, its change over time is of importance. In Fig. 3 , the time dependence of instantaneous PIR is shown for United Kingdom, Russia, the Netherlands (lockdowns) and Sweden (no lockdown). Instantaneous PIR is calculated as $PI{R}_{inst.}=\frac{\Delta N_{newpos.cases}}{\Delta N_{newtestsmade}}$, i.e. the ratio of daily increase of positive cases to daily increase of the tests performed.

Fig. 3.

Dynamics of instantaneous PIR for UK, Russia, the Netherlands and Sweden for late April 2020. Except Russia, all instantaneous PIRs are calculated on the basis of privately collected data. For Russia, official statistics is used, since no sufficient snapshot amount is present in the private data set. Grey columns represent daily change of confirmed positive cases. Blue dots are instantaneous PIRs calculated. Blue polylines are parts of linear piecewise approximations.

We observed mixed dependency on time here. By 21 April 2020, symbate dynamics of instantaneous PIR and daily increment of positive cases is observed only for Russia. For UK, there is a maximum of instantaneous PIR that does not coincide with the maximum of confirmed positive cases. For the Netherlands, the approximation is very close to a constant line. For Sweden, we may localise a decay, low plateau and growth. On the whole, for the four countries concerned, instantaneous PIR as a function of time does not correlate with confirmed cases dynamics.

Asymbate dynamics of instantaneous PIR and confirmed positive cases at the initial stages of the pandemic may be generally explained by three factors. First, the samplings in at least one case (confirmed positive cases measurements or mass screening procedures) may be not fully representative on a scale of a population. Second, the change in new tests performed on a daily basis may grow with different speed than the infection dissemination, e.g. faster constant growth of number of tests made than the disease spread may result in an instantaneous PIR decay on growing confirmed cases dynamics. Third, several spikes of disease may be present of which we are currently detecting only one. Along with relatively low values of PIRs, it enables us to suggest that three scenarios for European countries studied are possible, regarding real (not observed) disease spread extremums:

• adisease peak has not yet been passed on 21 April 2020;
• bthere may be several disease peaks, and different European countries may be situated in different time places regarding the peaks (e.g. between them); a current situation may be an overlapping of different peaks;
• cdisease peak has been already passed unnoticed by the world community, by the moment of the pandemic announcement (early March 2020).

Taking into account these three scenarios, creating herd immunity may become an even more important factor for population adaptation to COVID-19. It was so in April and continues to be in August 2020.

3.2. Herd immunity formation under lockdowns and without lockdowns

To estimate times and values of maximums of herd immunity formation in the countries studied, PC numerical solving the Kolmogorov equation systems described in Materials and Methods section with modelling the Lyapunov functions behaviour for the corresponding master equations (finding global attractors) has been performed for the three scenarios described above, for full-lockdown and no-lockdown modes of SARS-CoV-2 containment.

On maximising herd immunity first derivative

$$\frac{dh\left(t\right)}{dt}=\frac{d{N}_{immune}\left(t\right)}{Ndt},$$ (37)

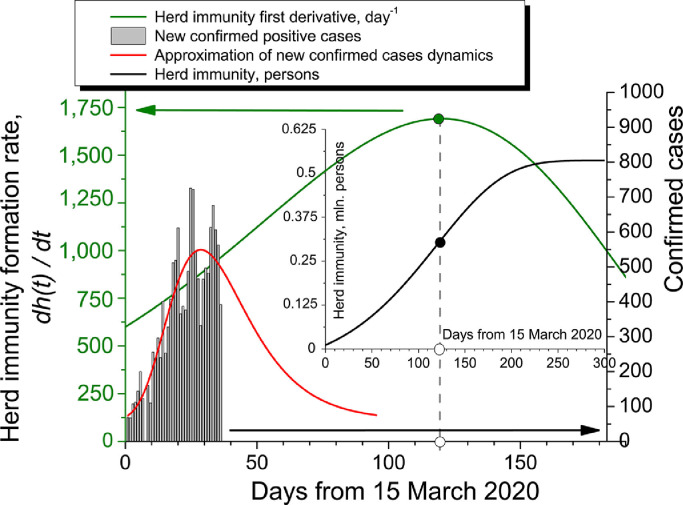
we receive the inflection points for herd immunity curves. The schematics for Sweden is shown in Fig. 4 . For the interval 0–120 days from Day Zero, confirmed positive cases dynamics (official WHO data) may be approximated by an extreme function

$$N_{confirmed}=N_0+A{e}^{-e^{\frac{t-t_{max}}{w}}-\frac{t-t_{max}}{w}+1},$$ (38)

and for Sweden the coefficients are:

Fig. 4.

Calculation of herd immunity formation for Sweden. Day Zero is 15 March 2020. The inflection point of herd immunity is the maximum of its first derivative.

N ₀ = 60.30 persons;

A = 488.79 persons;

t_max = 30.07 days;

w = 15.63 days.

Different peak functions may be used for confirmed cases dynamics approximation [53], [54], [55], [56]. The extreme function provided above was chosen of the list of the most widely used functions by criterion of achieving the best approximation results (the lowest χ_dim. ² and highest R_adj. ²), where the parameters were calculated as follows:

$${\chi }_{\dim }^2=\frac{{\chi }^2}{n-1},$$ (39)

$${\chi }^2=\sum _i\frac{{\left(x_i-C_i\right)}^2}{{\sigma }^2},$$ (40)

$${\sigma }^2=\frac{\sum _{q=1}^m{\left(x_q-\overline{x}\right)}^2}{m},$$ (41)

m is the numbers of points; n – 1 is the number of degrees of freedom; x_i are experimental epidemiological data; C_i are approximated values; and σ ² is variance.

The adjusted coefficient of determination

$$R_{adj}^2=1-\frac{\left(1-R^2\right)\left(1-n\right)}{n-k-1},$$ (42)

where R is Pearson correlation coefficient between experimental data and the approximation and k is the number of explanatory terms (descriptors). Of course, another approximation could be used instead of the proposed one.

Using private data on Sweden PIR, taking into account its no-lockdown mode of containment, r ₀ = 5.6 and maximising herd immunity first time derivative by Lyapunov function analysis in the positive quadrant, give us a double exponential function $\frac{dh\left(t\right)}{dt}$ (green curve in Fig. 4):

$$\frac{dh\left(t\right)}{dt}=D{e}^{\left(-e^{{\left(\frac{t-t_z}{q}\right)}^p}+{\left(\frac{t-t_z}{v}\right)}^u\right)},$$ (43)

The coefficients:

D = 3417.46 days^–1

t_z = 62 days

p = 1.6

q = 150.0 days

u = 1

v = 50.50 days

Finally, integrating $\frac{dh\left(t\right)}{dt}$ over t, we receive a sigmoidal function of h(t) (black curve in the inset in Fig. 4), with its maximum value of approximately 540,000 people (based on the epidemiological data collected for Sweden in June 2020). That means the overall herd immunity rate. Taking into consideration the population of Sweden (currently 10,319,600 people), it gave 20.80 per cent of population in April and 5.20 per cent in June 2020. Thus, we see a dramatic correction of the model to be discussed below.

3.3. Iteration-based correcting and refining the model

SARS-CoV-2 is an evolving process that change our understanding on a constant basis. Obviously, SARS-CoV-2 has not yet reached limits of its dissemination. In our truly global world without any fixed cultural boundaries that might help to slow down tourism and migrant currents, spreading a new virus will continue till a stable co-existence with homo sapiens population has been attained [57], [58], [59], [60], [61]. Recently, Oleg Donskikh [62] and Alexandre Gnes [63] demonstrated the influence of cultural implications on epidemiological situation. As Wolfgang Sassin evidently showed in his modelling human evolutionary processes, in the global open world with population more than 1.2–1.5 billion people, even a local viral pathogen outbreak with 100–150 humans infected may hit the whole world in two-three months and the process of its dissemination will not be stopped by any restrictive means until a new evolutionary niche with co-existence of homo and the virus has been created [59], [60], [64], [65]. Regarding SARS-CoV-2, this niche is not created yet. New data on SARS-CoV-2 situation are appearing incessantly that help to improve the model by the possibility to input the most novel and relevant epidemiological information.

Four major iterations of model correction/refinement have been made (mid-March prediction of April, mid-April prediction of May, mid-May prediction of June, and mid-June prediction of further SARS-CoV-2 spread). It is very important that the newest epidemiological information on the pandemic changed the model dramatically since March 2020, when Europe had entered the first SARS-CoV-2 wave. Additionally, different type of information has emerged since that time, viz. antibody testing programmes have been launched in many European countries, that are auxiliary sources of our knowledge about the virus spread.

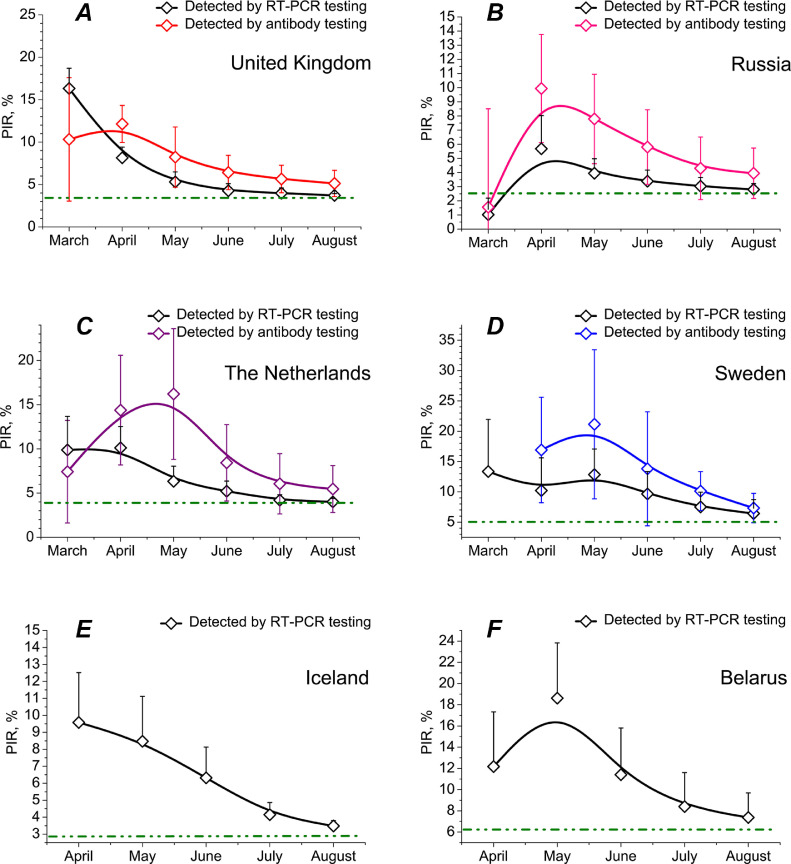
Fig. 5 demonstrates that now, much later after SARS-CoV-2 initial outbreak in China, PIR diminished significantly, reaching a lower plateau independently of the country or mode of containment (full lockdown / partial lockdown / no lockdown) concerned. Of six states the data on which are presented in Fig. 5, UK and Russia chose full lockdown mode, the Netherlands partial lockdown while Sweden, Iceland and Belarus no lockdown at all. Surprisingly, since May 2020, a clear trend of PIR decrease was observed everywhere. In most of countries, PIR can be estimated now as some 2–4 per cent, in Sweden and Belarus 6–7 per cent, whereas initial March and April numbers were substantially higher. It may be possibly explained by improving representativeness of the virus (RT-PCR) and antibody testing programmes. At the beginning of the pandemic, only people who were seriously ill with COVID-19 got into the focus of the tests, whether official, government-sponsored or commercial. This fact unfolds a likely origin of highly overstated epidemiological figures for UK and Belgium in Match-April (PIR of nearly 35–40 per cent). Later milder symptomatic patients were included in the tests too. But only since May and especially in summer 2020, a broad and much more representative cohort of European population commenced to be tested [66], [67], [68], [69], [70]. Using the May and June data as input parameters for the model enabled us to augment its quality and predicting force. June iteration based on June European epidemiological situation resulted in the herd immunity level prediction for August approximately four times less than the April prediction.

Fig. 5.

Epidemiological data on population infection rate (PIR) collected for various countries in different months since the beginning of SARS-CoV-2 pandemic in Europe. Whiskers show estimations of false positive and false negative test results for antibody testing programmes and false negative estimations for RT-PCR tests. Confidence interval (CI) is 95%. Full containment until late May 2020: United Kingdom (A). Full lockdown until mid-June 2020: Russia (B). Partial lockdown for April 2020 and full for May 2020: the Netherlands (C). No lockdowns ever: Sweden (D), Iceland (E) and Belarus (F).

3.4. Statistical treatment

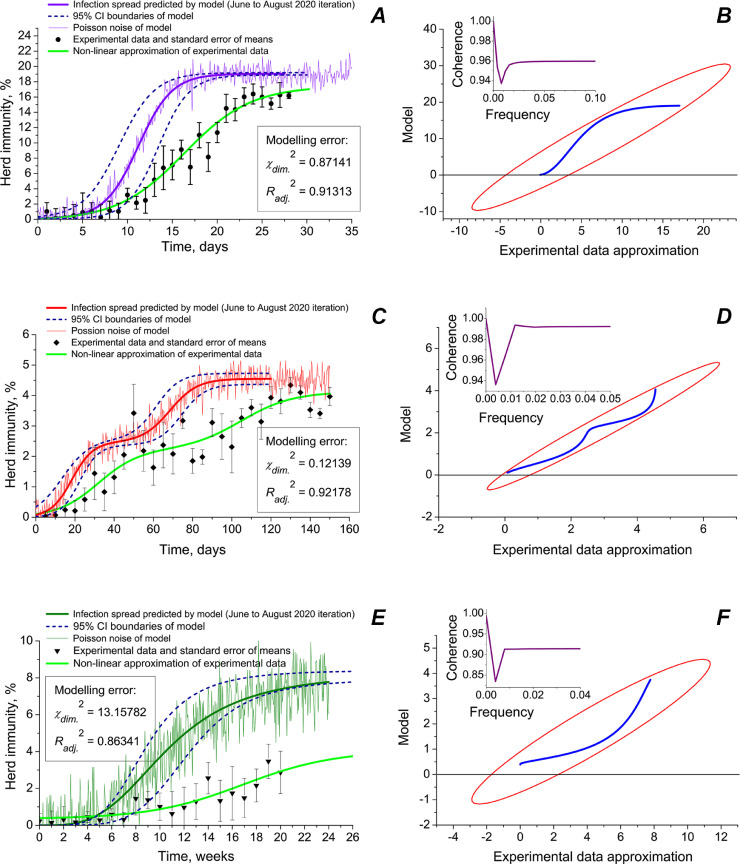
Different predicting force of the model has been observed for different types of ambience: closed communities, semi-open premises and open space (Fig. 6 ). In Fig. 6, the June modelling iteration is provided that was performed at the time when the paper was returned for revision. It was based on the data collected by us during surveillance procedures in UK, Russia, the Netherlands and Sweden. As modelling error estimations show (χ_dim. ² and R_adj. ²), the model allowed to receive the best coincidence of predicted herd immunity with the experimental data for semi-open premises (multi-storey living houses, condominiums, fenced living districts, large offices, trading floors, warehouse premises, etc.), where lowest χ_dim. ² and highest R_adj. ² were achieved within apartments and small houses) gave less exact results (Fig. 6, panels C and D). A biphasic structure of the virus spread predicted by the model was in a satisfactory agreement with the experimental epidemiological data. Modelling spreading SARS-CoV-2 in closed communities (family environments within apartments and small houses) gave less exact results (Fig. 6, panels A and B). Predicting the virus dissemination in open spaces was the least precise (Fig. 6, panels A and B).

Fig. 6.

Modelling herd immunity, real epidemiological data and statistical treatment of the model for different types of environments: closed communities (A, B), semi-open premises (C, D) and open spaces (E, F). Pearson correlations coefficients between simulated curve and epidemiological data approximation: 0.95882 (p ≤ 0.00183) (A); 0.96290 (p ≤ 0.00072); and 0.93733 (p ≤ 0.01274). In right panes (B, D and F), scatter matrices (blue lines) and 95% correlation CI ellipses (red) are shown. In the insets, coherence vs frequency of signal plots are provided. Coherence between simulated curve and real data is calculated as$C_{ab}\left(f\right)=\frac{{|P_{ab}\left(f\right)|}^2}{P_{aa}\left(f\right)P_{bb}\left(f\right)},$ where P_ab the cross power spectral density, and P_aa and P_bb are power spectral densities of simulated curve and experimental data means. Estimations of Poisson noise of the model: 5.12% (A); 6.68% (C); and 14.47% (E).

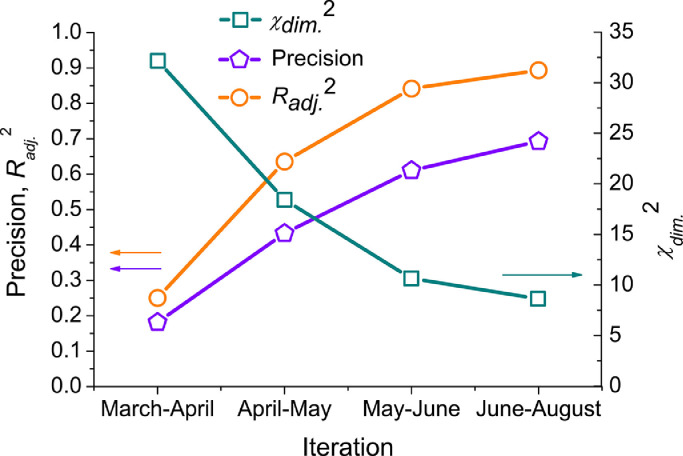
In Fig. 7 , the comparison of the model precision is given for the four main iterations of correcting the model. Precision coefficient is calculated as the mean of precision factors for each point i of n:

$$Prec=\frac{1}{n}\sum _{i=1}^n\frac{\left|C_{modi}-C_{reali}\right|}{\left|C_{xi}\right|},$$ (44)

where C_{x i} is the largest by module of {C_{mod i;} C_{real i}}; C_{mod i} is a modelled value in point i; and C_real i is an observed value in this point. In Fig. 7, one can see that the model changed essentially since the beginning of the pandemic.

Fig. 7.

Model precision statistical estimations at every iteration (see text for detailed description).

In March 2020, PIR = 19.19% was taken as the maximum of herd immunity that may be achieved without any lockdown and restrictive measures. In August 2020, it is already becoming clear that value is the maximum only for closed communities (Fig. 6, panel A). The fact is not very surprising, as such places with interlinked ventilation as Diamond Princess cruise ship may be considered a completely closed ecosystem [20], [21], [22], [23], [71], [72], [73], [74], [75]. An opener ambience leads to much less PIRs (Fig. 6, panels C and E).

Current improving the model does not mean, however, that we achieved a desired level of precision. A possible surge of SARS-CoV-2 infected humans’ figures in autumn 2020 and winter 2020–2021 may introduce further significant corrections.

4. Conclusions

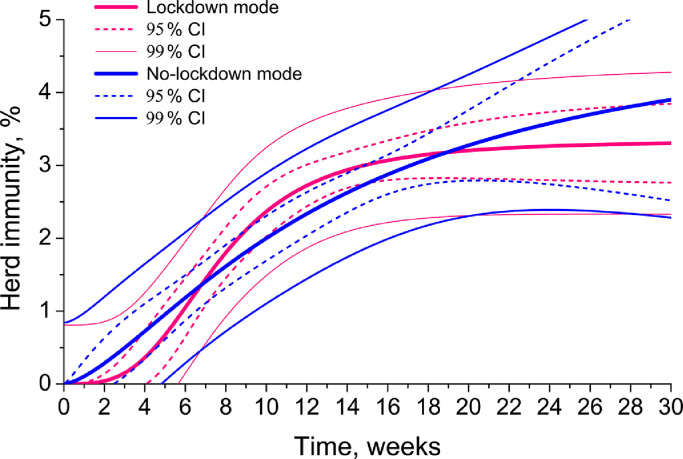
The analysis of both epidemiological data and simulation results indicates that the initially anticipated herd immunity level for SARS-CoV-2 of nearly two thirds of a population or even higher, is hardly ever achievable. The real herd immunity for the current virus is three-six times as less. Therefore, COVID-19 contagiousness is not so high as it was initially thought in January-March 2020. Almost universal and worldwide implementation of lockdown measures and complete switching off the economies, as it has been done in Germany, France, Russia or UK, may be reckless. Despite some governmental and administrative assumptions that only strict quarantine might lead to diminishing SARS-CoV-2 spread, our study does not confirm it. Neither modelling, nor PIR statistical data on the European countries collected and studied by us so far, may corroborate that full-lockdown modes are any better than the Swedish no-lockdown mode in terms of the virus dissemination (Fig. 8 , Table 2). Fig. 8 demonstrates the June prediction iteration with 95% and 99% CI. According to the model, only at the very beginning of the epidemic, the lockdown mode may demonstrate better results in containment of the virus than no-lockdown one (pink line is lower than blue line). After 7–8 weeks of the virus spread, both modes start to give similar outcomes. This simulation is corroborated sufficiently by the experimental data obtained. Countries with full lockdowns and no lockdowns reached very similar results in PIR and herd immunity, viz. 3–5 per cent predicted by the model after the June iteration (Fig. 8) and 3–7 per cent of the total population observed in reality (Fig. 5). The basic reproduction numbers are also similar [75], [76].

Fig. 8.

The most recent modelling herd immunity formation in lockdown and no-lockdown modes of SARS-CoV-2 containment (August 2020 iteration).

Why so? First, during lockdowns people were still allowed to go outside, e.g. to grocery stores and saunter with pets. Meetings that caused reciprocal infection in elevators, on streets and in close premises, were imminent. Second, ventilation system in large multi-storey buildings disseminated the virus further. Third, public transport was still on, where cross-infection possibility was high.

Was any sense in lockdowns at all? We think yes. They helped to avoid healthcare system collapse in many countries. However, their near and distant harm to health of different groups of population, economies, business and world supply chains is still to be assessed in the future.

We suppose that a real hazard of COVID-19 lockdowns is associated with the common governmental belief backed by several World Health Organisation's announcements that it is the lockdowns that saved humanity from excessive mortality connected with COVID-19. Our research proves that it is a very dangerous misbelief with far-reaching consequences. It is SARS-CoV-2 relatively low contagiousness and case fatality rate that led to avoidance of millions of deaths, not lockdowns. We agree with the Editors that the health consequences of the pandemic are devastating [77]. However, non-evidence-based reliance of governments just on total lockdown as a universal measure of the pandemic containment may be much more devastating in the future, in case of possible consecutive waves of SARS-CoV-2 or any other viral pathogen. Governments should not use simplest lockdown ways of “containment” the virus with an obvious threat to the democracy and human rights in the whole world instead of elaborating complex and effective epidemiological and social strategies.

Why may the belief in lockdowns as the only means of pandemic containment be harmful? In our truly global world with global tourism and transport routes, an emergence and possible immediate worldwide spread of a new viral pathogen, much more dangerous than SARS-CoV-2, may be only a matter of time. In case this virus may have a mortality of Ebola, contagiousness of varicella and worldwide spread, governmental and administrative reliance just on lockdowns may cost hundred millions of human lives.

In the end, lockdowns may be ineffective because they do not and potentially cannot stop a respiratory virus spread [78], [79]. Instead, effective healthcare and public policy containment measures must be depended upon, such as strictest epidemiological surveillance in airports, international railways and bus stations; managing tourist routes at the very beginning of early epidemic warnings; applying antiviral cleansing and sanitation of publicly accessible territories, especially in urban environment; habitual wearing individual protective units in places of mass congestion of people and during seasonal respiratory disease surges (e.g., according to Japanese positive experience); and preparedness of medical care systems for global pandemics and other “Black Swan” emergencies. All these measures can be much more effective than lockdowns.

Funding

This work has been funded by Government program of basic research in Koltzov Institute of Developmental Biology, Russian Academy of Sciences in 2020, No. 0108–2019–0002.

Credit author statement

KSS is the sole author

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper..