Welfare Analysis in a Two-Stage Inverse Demand Model: An Application to Harvest Changes in the Chesapeake Bay

Abstract

Like many agricultural commodities, fish and shellfish are highly perishable and producers cannot easily adjust supply in the short run to respond to changes in demand. In these cases it is more appropriate to conduct welfare analysis using inverse demand models that take quantities as given and allow prices to adjust to clear the market. One challenge faced by economists conducting demand analysis is how to limit the number of commodities in the analysis while accounting for the relevant substitutability and complementarity among goods. A common approach in direct demand modeling is to assume weak separability of the utility function and apply a multi-stage budgeting approach. This approach has not, however, been applied to an inverse demand system or the associated welfare analysis. This paper develops a two-stage inverse demand model and derives the total quantity flexibilities which describe how market clearing prices respond to supply changes in other commodity groups. The model provides the means to estimate consumer welfare impacts of an increase in finfish and shellfish harvest from the Chesapeake Bay while recognizing that harvests from other regions are potential substitutes. Comparing the two-stage results with single-stage analysis of the same data shows that ignoring differentiation of harvests from different regions, or the availability of substitutes not affected by a supply shock, can bias welfare estimates.

Introduction

Casual observation that seafood menus list both the prices and the origin of their fare is evidence that patrons care about the source of their seafood. Empirical studies support the notion that location matters to consumers and that some will seek out and pay a premium for seafood from a specific region (Stiles et al. 2013). We also know that a consumer looking to purchase grouper could be convinced to buy seabass instead if the price is right. When analyzing the demand for seafood, inverse demand systems are often used to capture consumer preferences and substitution possibilities such as these. Barten and Bettendorf (1989) make the case that demands for perishable goods like produce, meat, and seafood should be examined using inverse demand equations in which supply is treated as exogenous and price adjusts to clear the market. In addition to perishability, seafood harvest is often limited by gear and effort restrictions and depends in a large part on capital investments that are made long before the boat leaves the dock. For these reasons, inverse demand systems have been the preferred approach to analyze the demand for seafood, regulation of commercial fisheries, and welfare impacts of changes in seafood harvests (e.g. Holt and Bishop 2002; Park et al. 2004).

The capability of these models to capture preferences between source regions and substitution possibilities is limited, however, by the size of the demand system which would require an equation for every species and every region from which those species are harvested. As such, analyses of this sort tend to focus on a single harvest region, ignoring substitution possibilities from other sources (e.g. Beach and Holt 2001; Holt and Bishop 2002) or summing regional harvests into an aggregate supply thereby assuming away preferences between regions (e.g. Eales et al. 1997; Wong and McLaren 2005). When faced with a large number of commodities analysts estimating direct demands have instead invoked weak separability and used multi-stage budgeting to model consumer choice in a series of steps (Strotz 1959; Gorman 1959; Brown and Heien 1972; Fan et al. 1995; Edgerton 1997). In the first step consumers allocate expenditures among commodity groups and then further divide those expenditures between the elementary commodities in subsequent steps.

This paper is the first to develop a two-stage inverse demand system and derive the total quantity flexibilities that describe how the market clearing price for one good is affected by a supply shock of another good in a different commodity group.¹ We show how the utility parameters estimated in the two stages can be used to estimate consumer welfare impacts of a change in supply by expanding upon a distance function approach developed in a single-stage framework by Kim (1997). To demonstrate the contribution of a two-stage model we compare the welfare estimates with those estimated by single-stage alternatives.

To examine how regional preferences and the availability of substitutes affect consumer welfare estimates we consider recent regulations intended to reduce excess nutrient and sediment loads to the Chesapeake Bay. Excess nitrogen and phosphorous loadings to the Bay are fueling the growth of algae blooms which lead to areas of low dissolved oxygen and in extreme cases create dead zones in which oxygen levels are so low that fish and shellfish that are unable to escape them die. Algae blooms also harm the aquatic grasses that juvenile fish and crabs rely on for habitat. Sediment pollution blocks sunlight when suspended in the water and can smother grasses and oyster beds when it comes to rest on the bottom. In January 2013, a panel of experts was convened by the US Environmental Protection Agency (EPA) and asked how the populations of 14 different species in the Chesapeake Bay would respond to the nutrient and sediment reductions required by the new regulations (the details of which are reported by Newbold, Massey, and Moore, 2017). We use the expert predictions for commercially harvested species, including the iconic striped bass, blue crab, and eastern oyster, to estimate the resulting consumer welfare impacts. Our results show that limiting the scope to one harvest region or aggregating harvests across regions will produce biased estimates of welfare impacts from harvest changes.

Consumer Welfare Estimation in Quantity Space

The distance function is dual to the expenditure function and can be considered a normalized money metric utility function (Kim 1997) that measures how the quantity vector must be scaled in order to reach a reference utility level. Given the quantity vector X and a direct utility function U = U X, the distance function D U, X is defined as

$$DU,\mathit{X}=\underset{t}{\max }t>0:U\mathit{X}/t>0,$$ (1)

which gives the maximum amount, t, by which the quantity vector must be divided in order to just reach the indifference surface.

Exact measures of consumer welfare can be calculated from the distance function by finding the difference between D(U,X) evaluated at different quantity vectors, say X⁰ and X¹, given a reference utility level U⁰ and U¹. Specifically, the normalized compensating and equivalent surplus from exogenous quantity changes are

$$cs=D{U}^0,{\mathit{X}}^1-D{U}^0,{\mathit{X}}^0$$ (2)

$$es=D{U}^1,{\mathit{X}}^1-D{U}^1,{\mathit{X}}^0$$ (3)

Since (2) and (3) are normalized by total expenditures, the non-normalized, or absolute, consumer welfare measures are found by multiplying by total expenditures Y. Utility is not observable so the distance function cannot be estimated directly. To estimate the parameters of the distance function it is necessary to choose a functional form and derive the resulting system of inverse demands. These demands can be estimated empirically and are then used to recover the parameters needed for welfare analysis.

A number of functional forms for the distance function and associated inverse demand system have been used in the literature (see Brown et al. 1995 for a review). A popular choice is the Inverse Almost Ideal (IAI) specification (Eales and Unnevher 1994; Moschini and Vissa 1992). We adopt the version used by Moschini and Vissa 1992.²

$$\ln [DU,\mathit{X}]=a\mathit{X}-Ub\mathit{X}$$ (4)

where, $a(\mathit{X})={\alpha }_0+{\sum }_{\mathit{i}}{\alpha }_{i}ln{X}_i+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\sum }_{\mathit{i}}{\sum }_{\mathit{j}}{\gamma }_{ij}ln{X}_{i}ln{X}_j$, $bX={\beta }_0{\prod }_{\mathit{i}}{X}_i^{{\beta }_i},i=(1,\dots ,N)$ and j=(1,…,N) index goods in the demand system, and X_i are elements of the quantity vector X. Because D(U,X) is homogeneous of degree one in X, the following restrictions apply: ${\sum }_{\mathit{i}}{\alpha }_i=1$, ${\sum }_{\mathit{i}}{\gamma }_{ij}={\sum }_{\mathit{j}}{\gamma }_{ij}=0$, and ${\sum }_{\mathit{i}}{\beta }_i=0$. The symmetry property further requires ${\gamma }_{ij}={\gamma }_{ji}$.

According to Shephard’s theorem, the first derivatives of the distance function with respect to the quantities yield normalized compensated (Hicksian) inverse demands. For a specific market, i, the compensated inverse demand, H_i(U,X), is $\frac{\partial D(U,\mathit{X})}{\partial X_i}=H_i(U,\mathit{X})=\frac{P_i(U,\mathit{X})}{Y}$, where P_i (U, X) /Y is the price normalized by income. Applying Shephard’s theorem to the IAI form of the distance function, recognizing that $\frac{\partial \ln [D(U,\mathit{X})]}{\partial \ln \left[X_j\right]}=\frac{\partial D(U,\mathit{X})}{\partial X_j}\cdot \frac{X_j}{D(U,\mathit{X})}$, and that utility maximization requires that D = 1, yields the compensated (or Hicksian, denoted by the superscript h) inverse demand system in expenditure share form

$$W_i^h={\alpha }_i+{\sum }_j{\gamma }_{ij}ln\left(X_j\right)-U{\beta }_{j}b(\mathit{X}).$$ (4)

Using D = 1, inverting the distance function in (4), yielding U(X) = a(X)/b(X), and plugging it into the inverse demands, yields

$$W_i=\frac{X_i{P}_i}{Y}={\alpha }_i+{\sum }_j{\gamma }_{ij}ln\left(X_j\right)-{\beta }_i\ln Q$$ (7)

Where lnQ is a “quantity index,” ln Q ≡ a(X). Expression (7) represents a non-linear system with cross-equation restrictions on the parameters to satisfy homogeneity and symmetry.

A single-stage model such as (7) could be used to capture the substitution patterns between multiple species harvested from multiple regions by estimating an inverse demand equation for each species from each region. Such a model quickly becomes intractable, however, as the number of species and regions increases. Many of the species in this analysis are harvested in four or five different regions which would create a demand system with 80 equations or more and thousands of parameters in order to account for cross-quantity effects.

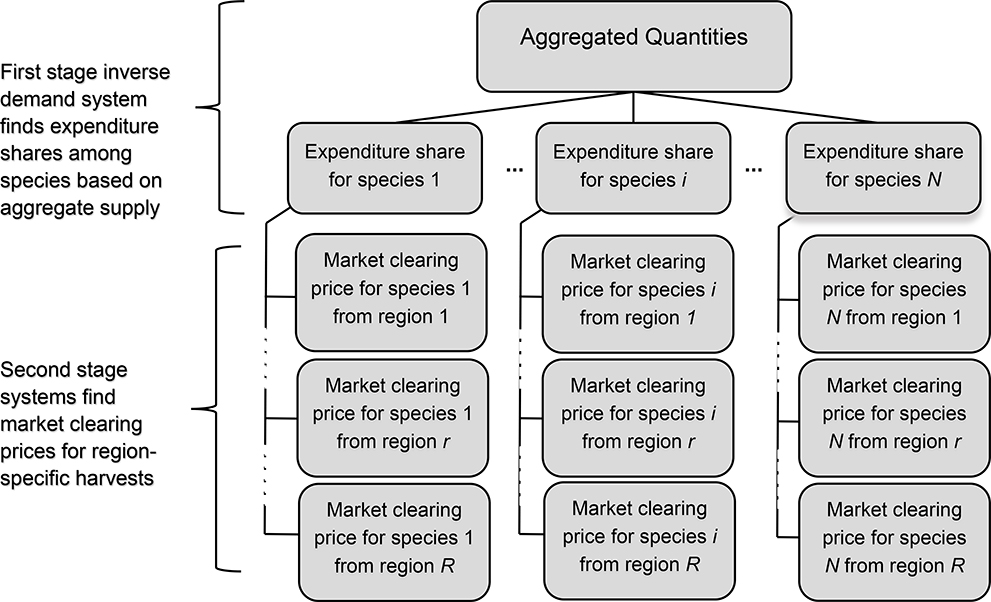
A more tractable alternative is to use a two-stage budgeting approach such as the one applied by Edgerton (1997) to a direct demand model. In a two-stage direct demand model, consumers allocate total expenditure among broad categories of goods and then further divide those expenditures among the elementary goods in the groups. Consumers take prices as given and quantity demanded adjusts to exogenous price shocks. In an inverse demand model, quantities of the elementary goods are determined exogenously and prices adjust to clear the market. In the first stage allocation of the inverse demand model, the exogenous supplies of the elementary goods determine the aggregate quantities, X_i, and the aggregate quantity index, lnQ. This change in lnQ affects all normalized prices and budget shares among the commodity groups. Market clearing prices for elementary goods are determined in the second stage conditional on the aggregate quantity allocations of the first stage.

The two-stage budgeting approach requires that we assume weak separability between harvests of different species. That is to say, a change in harvest of a given species, i, from a particular region, r, can affect the market clearing price for a different species, j, but only through the effect that the supply shock has on the aggregate quantity and the normalized prices and, thus, the expenditure shares determined in the first stage. ³ The welfare impact of a change in the quantity of species i in region r, x _(i)r will depend on the new normalized market clearing price for that species and changes in the supply of other species to the extent that there are cross-quantity effects. The two-stage demand system allows us to account for the availability of substitutes - different types of fish and/or harvests from other regions - while recognizing that they may not be perfect substitutes. In the model description that follows time subscripts have been omitted but estimation relies on monthly harvest and dockside value data.

Substitution between different types of fish is captured by the first stage system which includes an inverse demand equation for each species. If a supply shift for one species has an effect on the market clearing price, and thus the expenditure share for another species, this information is required to project welfare changes based on the results of the second stage. A first stage IAI demand system with an equation for each species i = (1,…,N) will provide estimates of expenditure shares given harvest levels

$$W_i={\alpha }_i+{\sum }_{\mathit{j}}{\gamma }_{ij}ln\left(X_j\right)-{\beta }_i\ln Q.$$ (8)

Evaluating expression (8) at the new quantity vector will provide the expected market clearing prices on all species of interest via the new expenditure shares W_i.

The second stage will estimate an inverse demand system for each species with an equation for each region that the species is harvested. This stage will capture the substitutability between harvests of the same species from different regions, r = (1,…, R). For example, if blue crabs harvested from any region other than the Chesapeake Bay are poor substitutes for Chesapeake Bay blue crab then welfare impacts from a change in Chesapeake Bay harvest will be larger than if very close substitutes were available. In fact, if consumers were completely indifferent regarding the source of the commodity, only the first stage inverse demand system would be necessary to estimate welfare impacts of a change in Chesapeake harvest because all that would matter to consumers is the change in total supply of that species. For species i, expenditure shares for region r will be estimated with the same IAI demand system described for the first stage

$$w_{(i)r}={\alpha }_{(i)r}+{\sum }_{\mathit{s}}{\gamma }_{(i)rs}ln\left(x_{(i)s}\right)-{\beta }_{(i)r}\ln Q_{(i)}$$ (9)

The two-stage inverse demand system captures substitution patterns between fish species and harvest regions while keeping estimation tractable. The results of both stages enter the calculation of consumer welfare impacts from the expected supply changes. Equations (2) and (3) provide normalized welfare impacts, however, monetized impacts require forecasts of expenditures on each species. In this case, parameters estimated in the first stage allow us to estimate changes in the expenditures among species as a result of the changes in aggregate supply of each fish type. The baseline and post-policy expenditure shares for species i are

$$W_i^0={\alpha }_i+{\sum }_{\mathit{j}}{\gamma }_{i\mathit{j}}ln\left(X_j^0\right)-{\beta }_i\ln Q^0,$$ (10)

$$W_i^1={\alpha }_i+{\sum }_j{\gamma }_{ij}\ln \left(X_j^1\right)-{\beta }_i\ln Q^1,$$ (11)

$W_i^0$ and $W_i^1$ are multiplied by total expenditures Y to provide estimates of baseline and post-policy expenditure allocations $Y_i^0$ and $Y_i^1$.

The coefficients estimated in the second stage provide the utility parameters to calculate welfare impacts from changes in regional harvests of a given species. Non-normalized, or absolute, compensating and equivalent surplus are calculated using

$$CS={\sum }_i\left[Y_i^0{D}_i{U}^0,{\mathit{X}}_i^1-D_i{U}^0,{\mathit{X}}_i^0-Y_i^1-Y_i^0\right],$$ (12)

$$ES={\sum }_i\left[Y_i^1{D}_i{U}^1,{\mathit{X}}_i^1-D_i{U}^1,{\mathit{X}}_i^0-Y_i^1-Y_i^0\right],$$ (13)

where

${\mathit{X}}_i^0$= baseline supply vector of species i

${\mathit{X}}_i^1$= post-policy supply vector of species i

$U_i^0$ = baseline utility for species i

$U_i^1$= post-policy utility for species i.

So by appealing to weak separability we are able to forecast changes in market clearing prices of each fish type, estimate the welfare effects of regional supply changes, and sum the welfare impacts across fish types for total welfare changes.

Partial and Total Flexibilities

In an inverse demand system, quantity flexibilities are analogous to the price elasticities of a direct demand system and can be interpreted in similar ways. A quantity flexibility represents the change in the market clearing price of a particular good given a change in the supply of that good (in the case of own-quantity flexibilities) or another good (in the case of cross-quantity flexibilities). Similar to their direct demand counterparts, own-quantity flexibilities will be negative for normal goods.

For the IAI demand model, the first stage uncompensated partial own- and cross-quantity flexibility for species, i and j, ∂ln[P_i]/∂ln[X_j], is given by

$$E_{ij}=\frac{\partial \ln \left[P_i\right]}{\partial \ln \left[X_j\right]}=-{\delta }_{ij}+\left\{{\gamma }_{ij}-{\beta }_i\left(W_j+{\beta }_j\ln Q\right)\right\}\left(\frac{1}{W_j}\right)$$ (14)

where δ_ij is a Kronecker delta such that δ_ij=1 if i = j and δ_ij=0 otherwise. The second stage partial own- and cross-quantity flexibilities for two regions, r and s, supplying the same species, i, would be

$${\epsilon }_{(i)rs}=\frac{\partial \ln \left[p_{(i)r}\right]}{\partial \ln \left[x_{(i)s}\right]}=\left\{{\gamma }_{(i)rs}-{\beta }_{(i)r}\left(w_{(i)s}+{\beta }_{(i)s}\ln Q_{(i)}\right)\right\}\left(\frac{1}{w_{(i)r}}\right)$$ (15)

The total quantity flexibility would be the percent change in the second stage price of a species, i, in some region, r, given a percent change in the quantity of any species, j, harvested in any region, r. This is analogous to Edgerton’s (1993) uncompensated total price elasticity for the direct almost ideal demand model. For the IAI model, the total quantity flexibility, ∂ln[p_(i)r]/∂ln[x_(j)s], is given by

$$\begin{gathered} {\epsilon }_{(i)r,(j)s}={\delta }_{ij}\left[-{\delta }_{rs}+\left\{{\gamma }_{(i)rs}-{\beta }_{(i)r}\left(w_{(i)s}+{\beta }_{(i)s}\ln Q_{(i)}\right)\right\}\left(\frac{1}{w_{(i)r}}\right)\right] \\ +\left[\left\{{\gamma }_{ij}-{\beta }_i\left(W_j+{\beta }_j\ln Q\right)\right\}\left(\frac{1}{W_i}\right)\right]\left(\frac{x_{(j)s}}{X_j}\right) \end{gathered}$$ (16)

The derivation of these flexibilities is given in the appendix. While the estimated flexibilities will not be used in the welfare analysis directly, prior expectations on their signs and magnitudes provide a theoretical check on the estimated inverse demand parameters.

Data

To better represent consumers’ substitution patterns and simplify estimation, the Chesapeake species are divided into three groups: high value fish, low value fish, and shellfish. Other popular species that are not harvested from the Chesapeake but could substitute for Chesapeake species are included in each group (table 1). High value fish are finfish with an average dockside price greater than $1 per pound while low value fish have a dockside price of less than $1 per pound and are generally harvested for uses other than human consumption. A two-stage inverse demand system is estimated for each group. The presumption here is that changes in the supply of Chesapeake species will affect demand for other species within that group but not across groups. Total expenditures on each group are held constant.

Table 1.

Baseline Harvest and Projected Change after Water Quality Improvements (tons per year)

	Baseline Harvest (1990–2012 Averagea)		Projected Change in Chesapeake Harvestc
	Chesapeake Bay	Combined Rest of Regionsb
High Valued
Flounder	1,504	4,580	65
Striped Bass	2,358	2,248	101
Black Sea Bass	171	955	0
Eel	315	163	7
Cod		15,782	-
Grouper		3,043	-
Low Valuee
Spot	1,588	485	90
Perch	824	186	24
Croaker	4,771	466	138
Menhaden	199,200	538,470	−14,140
Herring		15,782	-
Mackerel		19,170	-
Shellfish
Blue Crab	44,382	51,287	7,280
Oyster	710	10,569	117
Clam		26,640	-
Scallop		20,240	-
Shrimp		9,863	-
Lobster		39,250	-

^aBased on NOAA National Marine Fisheries Service (NMFS) landings and ex-vessel value data for all commercial fisheries.

^bThe other regions are New England, the Mid-Atlantic, the South Atlantic, and the Gulf of Mexico.

^cProjected harvest changes are based on the best professional judgments of seven experts panelists in January 2013 on the potential changes in Chesapeake Bay species’ stock sizes under the required reductions in nutrient and sediment pollution relative to current water quality conditions and assuming that harvest changes will be proportional to the projected changes in stock sizes.

^dFinfish with an average dockside price greater than $1 per pound.

^eFinfish with a dockside price of less than $1 per pound and generally harvested for uses other than human consumption.

NOAA National Marine Fisheries Service (NMFS) compiles landings and ex-vessel value data for all commercial fisheries. Both stages of the demand model are estimated with monthly harvest and dockside price data from the years 1990 to 2012. None of the species harvested commercially in the Chesapeake Bay is harvested from the Pacific so only Atlantic regions and Gulf of Mexico are included in the analysis. Not all species are harvested to a significant degree in all regions.

To project changes in supply, seven experts on fisheries and water quality in the Chesapeake Bay participated in a workshop in January, 2013. The panelists were asked to provide their best professional judgments of potential changes in Chesapeake Bay species’ stock sizes under the required reductions in nutrient and sediment pollution relative to current water quality conditions, holding all other influences constant. The qualitative conclusions of each panelist were converted to percentages by EPA analysts and averaged to generate a single projection for each species. For this analysis we assume harvest changes will be proportional to the projected changes in stock sizes and report the results in table 1. It is worth noting that one Chesapeake stock, Menhaden, is expected to decrease as a result of the water quality improvements. Menhaden feed on the microalgae that benefit from excess nutrient pollution so reducing nitrogen and phosphorus loads to the Bay will likely decrease menhaden harvest. Also worth noting are the relatively large expected increases in blue crab and oyster harvests. In addition to management practices that will reduce nutrient and sediment pollution plans for cleaning up the Chesapeake Bay, plans include actively expanding oyster beds and restoring eel grass beds that protect juvenile crabs from predation. Members of the expert panel providing these projections were asked to consider those features of the implementation plans as well.

Results

The first and second stage systems of the inverse demand model are estimated via non-linear seemingly unrelated regression. Estimation is performed using Stata’s nonlinear seemingly unrelated regression (nlsur) routine which relies on iterative feasible nonlinear generalized least squares. The singularity of the cross-equation covariance matrix requires dropping one of the equations from the system and relying on the adding up condition to identify the parameters. The stability of the parameters using this approach was confirmed by reestimating each of the inverse demand systems, omitting a different equation, and reproducing the same results. Homogeneity and symmetry restrictions are imposed by estimating a subset of the model parameters and solving for the remaining restricted parameters.

With eighteen equations in the first stage and ten systems of three to five equations each in the second stage, hundreds of individual parameters are estimated in the three two-stage models. To present those results in a more manageable and meaningful way we report the partial first and second stage own-quantity flexibilities alongside total own-quantity flexibilities for comparison in tables 2 through 4. Numerical simulations of the complex non-linear flexibilities provide the standard deviations reported on the right-hand side of the tables⁴. For all 56 equations (18 in the first stages and 38 in the second) the estimated partial own-quantity flexibilities lie below zero, which is what one would expect for normal goods. Only species harvested from the Chesapeake require second stage inverse demand systems for welfare estimation so second stage flexibilities for other species are not estimated. Tables 2 through 4 also contain the expected change in market clearing prices given the expert panel’s projection of harvest changes. Price changes are calculated by using the first and second stage model results to find the baseline and policy expenditure shares and then dividing by the exogenously determined supply vectors to find market clearing prices under each scenario. Something to note in table 2 is that since black sea bass harvests were not projected to change the only impact to market clearing price for that species is through the cross-quantity effects of the first stage. An implication of weak separability is that the prices for all black sea bass harvests are affected proportionally, hence identical percentage changes in price for all regions. Likewise, market clearing prices for each of the non-Chesapeake species would be expected to change by the same proportion regardless of harvest region and so reporting only one percentage change for each species is sufficient.

Table 2.

Own-quantity flexibilities and changes to market clearing prices for high value^a finfish

	Own-Quantity Flexibilities			Standard Deviations			Percentage Change in Priceb
	First Stage	Second Stage	Total	First Stage	Second Stage	Total
Flounder	−0.612			0.011
Chesapeake		−0.4720	−0.3775		0.0209	0.0212	−2.25%
New England		−0.6452	−0.5472		0.0134	0.0135	−0.84%
Mid-Atlantic		−0.6143	−0.5167		0.0144	0.0147	−0.67%
South Atlantic		−0.4949	−0.3970		0.0129	0.0133	0.12%
Striped Bass	−0.3842			0.0184
Chesapeake		−0.8186	−0.3683		0.0371	0.0386	−1.62%
New England		−0.4479	−0.2735		0.1726	0.1727	1.01%
Mid-Atlantic		−0.7519	−0.6620		0.0468	0.0469	0.15%
South Atlantic		−0.6291	−0.5372		0.0759	0.0759	0.98%
Black Sea Bass	−0.3351			0.0205
Chesapeake		−0.6840	−0.5262		0.0155	0.0164	−0.49%
New England		−0.2334	−0.1243		0.0184	0.0188	−0.49%
Mid-Atlantic		−0.5675	−0.3873		0.0191	0.0199	−0.49%
South Atlantic		−0.5976	−0.4269		0.0150	0.0161	−0.49%
Gulf		−0.4068	−0.3546		0.0597	0.0597	−0.49%
Eel	−0.7295			0.0552
Chesapeake		−0.7141	−0.5306		0.0200	0.0425	−1.02%
Mid-Atlantic		−0.6381	−0.5698		0.0284	0.0321	−0.08%
South Atlantic		−0.5968	−0.5639		0.0309	0.0318	−0.34%
Cod	−0.5880			0.0162			−0.37%
Grouper	−0.6224			0.0143			−0.56%

^aFinfish with an average dockside price greater than $1 per pound.

^bPredicted change in market clearing prices given the expert panel’s projection of Chesapeake Bay species’ stock sizes and assuming proportional harvest changes. Price changes are calculated by using the first and second stage model results to find the baseline and policy budget allocations and then dividing by the exogenously determined harvest vectors to find market clearing prices under each scenario.

Table 4.

Own-quantity flexibilities and changes to market clearing prices for shellfish

	Own-Quantity Flexibilities			Standard Errors			Percentage Change in Pricea
	First Stage	Second Stage	Total	First Stage	Second Stage	Total
Blue crab	−0.4022			0.0402
Chesapeake		−0.5186	−0.2962		0.0123	0.0191	−5.48%
Mid-Atlantic		−0.2611	−0.2345		0.0364	0.0366	−0.34%
South Atlantic		−0.4831	−0.3171		0.0177	0.0211	0.05%
Gulf		−0.5945	−0.4072		0.0162	0.0211	−2.11%
Oyster	−0.6780			0.0447
Chesapeake		−0.2802	−0.2570		0.0236	0.0239	−8.07%
Mid-Atlantic		−0.5734	−0.5645		0.0261	0.0262	−1.98%
South Atlantic		−0.5515	−0.5409		0.0256	0.0256	−2.78%
Gulf		−0.9772	−0.6967		0.0040	0.0392	−3.77%
Clam	−0.1051			0.0833			−3.43%
Scallop	−0.3461			0.0281			−0.22%
Shrimp	−0.5741			0.0217			−0.28%
Lobster	−0.3863			0.0219			−0.11%

^aPredicted change in market clearing prices given the expert panel’s projection of Chesapeake Bay species’ stock sizes and assuming proportional harvest changes. Price changes are calculated by using the first and second stage model results to find the baseline and policy budget allocations and then dividing by the exogenously determined harvest vectors to find market clearing prices under each scenario.

In order to evaluate consumer welfare, we first have to forecast the new expenditures on each species, $Y_i^1$, using the results of the first stage expenditure share equations and the post-policy quantity vectors based on the expert panel’s projections. Table 5 shows the baseline expenditure share and the predicted change based on the new quantity vectors for each of the species groups.

Table 5.

Impact of harvest changes^a on average expenditures

Group	Species	Average Annual Expenditure Share 1990–2012b	Average Annual Expenditure 1990–2012b (thousands 2012$)	Change in Expenditure Sharec	Change in Annual Species Expenditure (thousands 2012$)
High Valued	Flounder	0.2634	22,952	0.0003	31
	Striped Bass	0.1985	9,998	0.0021	211
	Black Sea Bass	0.0630	5,638	−0.0003	−28
	Eel	0.0562	4,496	0.0001	15
	Grouper	0.1544	12,356	−0.0005	−49
	Cod	0.2646	32,077	−0.0018	−180
Low Valuee	Spot	0.0197	2,846	0.0001	88
	Perch	0.0295	1,161	−0.0004	127
	Croaker	0.0185	7,518	−0.0008	295
	Menhaden	0.6267	95,883	0.0017	−601
	Herring	0.1355	19,084	−0.0007	91
	Mackerel	0.1702	5,823	0.0001	1
Shellfish	Crab	0.1109	136,800	0.0049	7,359
	Oyster	0.0542	64,998	−0.0017	−2,523
	Clam	0.0105	29,588	−0.001	−1,558
	Scallop	0.2286	248,400	−0.0006	−833
	Shrimp	0.302	418,800	−0.0013	−1,849
	Lobster	0.2938	273,600	−0.0004	−597

^aProjected harvest changes are based on the best professional judgments of seven experts panelists in January 2013 on the potential changes in Chesapeake Bay species’ stock sizes under the required reductions in nutrient and sediment pollution relative to current water quality conditions, holding all other influences constant, and assuming that harvest changes will be proportional to the projected changes in stock sizes.

^bBased on NOAA National Marine Fisheries Service (NMFS) data.

^cChanges in expenditure shares are found by evaluating the estimated expenditure equations at the post-policy harvest vectors and differencing the result with the baseline expenditure shares.

^dFinfish with an average dockside price greater than $1 per pound.

^eFinfish with a dockside price of less than $1 per pound and generally harvested for uses other than human consumption.

These expenditure shares are sufficient to calculate the new market clearing prices since we hold total expenditures on the high value, low value, and shellfish categories constant. The change in expenditure shares shows the value of including substitute species that are not directly affected by the policy so far as cross-quantity effects cause market clearing prices on fish like cod, mackerel, and lobster to change despite no changes in their harvest. This implies welfare impacts in those markets that should also be accounted for.

Table 6 shows the compensating variation resulting from the expected changes in harvest for each of the species groups. Consumer welfare gains in the market for high value fish are relatively modest, about $800,000 per year. This is an expected result since the projected harvest increases for Chesapeake species are also modest – none greater than 5% of current levels. The impacts in the market for low value fish are in the opposite direction and somewhat larger, a loss of almost $2 million per year. The negative impacts are driven by the expected decline in menhaden harvest. The Chesapeake Bay catch of menhaden amounts to about 37% of the U.S. supply so one would expect the direct impact and the increase in the prices of substitutes to be substantial. The vast majority of consumer welfare impacts, however, are in the shellfish market. The expected increase in the supply of the iconic Chesapeake blue crab provides the largest increase in welfare, about $4.6 million per year, followed closely by that of Chesapeake Bay oysters, about $4.1 million per year. Consumers substituting toward these two species, which are relatively cheaper now because of the supply increases, decreases demand for substitutes harvested elsewhere and consequently lowers the market clearing price for other shellfish yielding additional consumer welfare gains. The total welfare gains in the shellfish market are $13.5 million per year. The estimated net welfare impact in all markets from the reduced sediment and nutrients is about $12.4 million per year.

Table 6.

Annual compensating surplus from harvest increases^a

Group	Species	Annual Compensating Surplus (thousands 2012$)	Standard Deviation
High Valueb	Flounder	209	9.09
	Striped Bass	296	32.34
	Seabass	28	4.03
	Eel	44	8.89
	Grouper	49	6.24
	Cod	180	9.46
	High Value Total	806	33.52
Low Valuec	Spot	32	1.84
	Perch	−36	22.10
	Croaker	−246	37.16
	Menhaden	−1,644	85.27
	Herring	−91	15.40
	Mackerel	−1	15.00
	Low Value Total	−1,985	90.64
Shellfish	Crab	4,646	610.72
	Oyster	4,078	268.63
	Clam	1,558	243.49
	Scallop	833	366.47
	Shrimp	1,849	480.83
	Lobster	597	274.72
	Shellfish Total	13,561	324.85
All Species Groups		12,383	342.04

^aProjected harvest changes are based on the best professional judgments of seven expert panelists in January 2013 on the potential changes in Chesapeake Bay species’ stock sizes under the required reductions in nutrient and sediment pollution relative to current water quality conditions, holding all other influences constant, and assuming that harvest changes will be proportional to the projected changes in stock sizes.

^bFinfish with an average dockside price greater than $1 per pound.

^cFinfish with a dockside price of less than $1 per pound and generally harvested for uses other than human consumption.

To demonstrate the value of the two-stage approach in this particular case the same data and harvest forecasts are used in two separate single-stage approaches to compare welfare estimates. Estimating a single-stage model forces the analysts to make one of two implicit assumptions that are not required in a multi-stage model. One option is to capture a large part of the market by aggregating the supply of each species into a single national supply (e.g. Nielsen et al. 2012; Cheng and Capps 1988). In this case the implicit assumption is that harvests from all regions are perfect substitutes and when faced with a change in supply consumers are indifferent about where the change in harvest occurred. If, on the other hand, the analyst wants to capture the value of a regional fishery and estimates an inverse demand system focusing on that single region or, alternatively, multiple regions but for one type of fish (e.g. Lee and Thunberg 2013; Hilmer et al. 2011; Park et al. 2004) then the availability of substitutes and associated cross-price effects are not being captured. The direction of the bias introduced by each of these approaches is ambiguous and will depend on a number of factors including the substitutability of aggregated or omitted harvests. Table 7 presents the results of the single-stage welfare models and shows the differences with the two-stage results in percentage terms.

Table 7.

Annual compensating surplus estimates from harvest increases^a using single-stage models

Aggregated Supplies Modelb			Chesapeake Only Modelc
Group	Compensating Surplus (thousands 2012$)	% Difference from two-stage model results	Compensating Surplus (thousands 2012$)	% Difference
High Valued	817	1.28%	633	−21.52%
Low Valuee	−1,505	−24.18%	−1,416	−28.64%
Shellfish	13,464	−0.72%	9,965	−26.52%
Total	12,775	3.17%	9,182	−25.85%

^aProjected harvest changes based on the best professional judgments of seven experts panelists in January 2013 on the potential changes in Chesapeake Bay species’ stock sizes under the required reductions in nutrient and sediment pollution relative to current water quality conditions, holding all other influences constant, and assuming that harvest changes will be proportional to the projected changes in stock sizes.

^bThe Aggregated Supplies Model is a single-stage IAI demand system using an aggregate national supply of each species to estimate the compensating surplus.

^cThe Chesapeake Only Model is a single-stage IAI demand system using only Chesapeake harvests to estimate the Compensating Surplus.

^dFinfish with an average dockside price greater than $1 per pound.

^eFinfish with a dockside price of less than $1 per pound and generally harvested for uses other than human consumption.

In some cases the single-stage estimates are very similar to the two-stage estimates. Such is the case with high value fish and shellfish when all regional supplies are aggregated into a homogeneous national supply. The single-stage model deviates from the two-stage model by about 1% for both species groups. There is a large difference, however, in the market for low value fish. The single-stage model produces a 24% lower estimate of the welfare impact from the projected harvest changes. This is an unexpected result since one might expect the source of the harvest to matter least for these types of fish. It’s hard to draw general conclusions from these results however because the expected harvest changes examined here vary in direction and magnitude across species so the cross-quantity effects are complex. When only Chesapeake harvests are included in the analysis, excluding substitutes harvested outside the Chesapeake (right-hand side of table 7), the differences from the two-stage model are similar across groups and rather large. Again, we should resist drawing broad conclusions from these results but when only the region in which the harvest increases occur is considered, the welfare effects are between 21% and 29% smaller in magnitude than the two-stage model that includes harvests from other regions. The smaller welfare impacts could be explained in part by the omission of price effects for non-Chesapeake species. In the two-stage model and in the aggregated single-stage model changes in Chesapeake harvest affect prices for species harvested elsewhere leading to larger welfare gains in the high value and shellfish market and larger losses in the low value market. These impacts are not captured when the analysis is restricted to Chesapeake harvests.

Conclusion

There are several features of the two-stage model that allow us to capture consumers’ preferences and substitution patterns among a large number of species harvested from four regions on the Atlantic coast and the Gulf of Mexico. First, species that are commercially harvested from the Chesapeake Bay were divided into three groups between which cross-quantity effects are expected to be negligible. Then species that are not harvested from the Chesapeake Bay but serve as substitutes for those that are were added to each of the groups. A first stage inverse demand model was estimated for each of the groups that captured substitution patterns between species but aggregated regional harvests into a single supply. Then a second stage was estimated for each of the Chesapeake species with an inverse demand equation for each harvest region. The results of the first stage were used to forecast market clearing prices and expenditure shares among species after the increase in Chesapeake harvests. The second stage expenditure shares, regional supply vectors, and the utility parameters estimated in the second stage were used to estimate compensating variation for the harvest increase using a distance function approach.

In addition to developing the welfare model we have derived expressions for the total flexibilities of the two-stage IAI demand model that describe how market clearing prices respond to supply changes in other commodity groups. These total flexibilities account for within-group substitution and changes in relative prices between commodity groups. We have calculated the partial flexibilities from the first and second stages to show how they differ from the total flexibilities when both stages of budgeting are accounted for. Visual inspection of tables 2 through 4 show that the total own-quantity flexibilities tend to be smaller in magnitude than the second stage flexibilities. This suggests that after a regional supply shift cross-species substitution helps to redistribute demand and dampen the impact on prices.

We apply the two-stage welfare model to estimate compensating variation from increased commercial harvests in the Chesapeake Bay resulting from pollution reduction programs recently put in place there. The anticipated harvest increases for high value finfish are modest and the estimated welfare impacts are accordingly small in magnitude. The large menhaden fishery in the Chesapeake Bay and the judgement of experts that populations of menhaden would fall as a result of reducing nutrient pollution lead to consumer welfare losses in the low value finfish market. The high value of the blue crab and oyster fisheries in the Bay combined with optimistic projections for their population and harvest lead to welfare gains that are an order of magnitude larger than the other two markets. When two alternative single-stage approaches are used to estimate the welfare impacts - one equivalent to the first stage, the other focusing on Chesapeake harvests only - we find some significant differences when compared with the two-stage model.

Figure 1:

Diagram of two-stage inverse demand system for seafood

Table 3.

Own-quantity flexibilities and changes to market clearing prices for low value^a finfish

	Own-Quantity Flexibilities			Standard Errors			Percentage Change in Priceb
	First Stage	Second Stage	Total	First Stage	Second Stage	Total
Spot	−0.4124			0.0482
Chesapeake		−0.7335	−0.3434		0.0083	0.0332	−1.16%
Mid-Atlantic		−0.6017	−0.5881		0.0468	0.0468	3.09%
South Atlantic		−0.6135	−0.3719		0.0191	0.0283	0.95%
Gulf		−0.0626	−0.0501		0.1188	0.1167	0.93%
Perch	−0.7806			0.0759
Chesapeake		−0.7980	−0.6199		0.0092	0.0175	1.33%
Mid-Atlantic		−0.2601	−0.2473		0.0229	0.0229	1.86%
South Atlantic		−0.2063	−0.1784		0.0437	0.0437	2.01%
Croaker	−0.5963			0.0283
Chesapeake		−0.9024	−0.6936		0.0092	0.0175	2.16%
Mid-Atlantic		−0.7064	−0.7064		0.0229	0.0229	4.27%
Gulf		−0.4376	−0.4017		0.0437	0.0437	3.99%
Menhaden	−0.7524			0.0081
Chesapeake		−0.7520	−0.6821		0.0117	0.0119	3.92%
Mid-Atlantic		−0.1915	−0.1859		0.0930	0.0930	2.01%
South Atlantic		−0.7055	−0.6991		0.0245	0.0245	1.74%
Gulf		−0.7941	−0.6278		0.0073	0.0094	−0.13%
Herring	−0.7755			0.225			0.66%
Mackerel	−0.7187			0.202			0.06%

^aFinfish with a dockside price of less than $1 per pound and generally harvested for uses other than human consumption.

^bPredicted change in market clearing prices given the expert panel’s projection of Chesapeake Bay species’ stock sizes and assuming proportional harvest changes. Price changes are calculated by using the first and second stage model results to find the baseline and policy budget allocations and then dividing by the exogenously determined harvest vectors to find market clearing prices under each scenario.

Appendix: Two-Stage Inverse Almost Ideal (IAI) Demand System Derivation

The logarithmic distance function analogous to Deaton and Muellbauer’s (1980) Almost Ideal Demand System model as specified by Moschini and Vissa (1992)¹ is

$$ln[D(U,\mathit{X})]=a(\mathit{X})-U\cdot b(\mathit{X})$$ (A.1)

$$\text{where}a(\mathit{X})={\alpha }_0+{\sum }_{\mathbf{i}}{\alpha }_{i}ln\left(X_i\right)+\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right){\sum }_{\mathbf{i}}{\sum }_{\mathbf{j}}{\gamma }_{ij}ln\left(X_i\right)ln\left(X_j\right)$$ (A.2)

$$b(\mathit{X})={\beta }_0{\Pi }_{\mathbf{i}}{X}_i^{\beta i}$$ (A.3)

X is the quantity vector, X={X₁,…,X_i,…,X_N}, and U is utility. The distance function measures how this quantity vector must be scaled in order to achieve the utility level, U. The following restrictions ensure that D(U,X) is homogenous of degree one

$${\sum }_{\mathit{i}}{\mathrm{\alpha }}_{\mathrm{i}}=1{\sum }_{\mathit{i}}{\gamma }_{\mathrm{ij}}={\sum }_{\mathit{j}}{\gamma }_{\mathrm{ij}}=0{\sum }_{\mathit{i}}{\beta }_i=0{\gamma }_{\mathrm{ij}}={\gamma }_{\mathrm{ji}}$$

If we evaluate our quantity vector, X at its optimum, X^* for utility level U, then D(U,X^*)=1 and ln[D(U,X^*)]=0. This implies that direct utility at the optimum is

$$U\left({\mathit{X}}^{*}\right)=a(\mathit{X})/b(\mathit{X})$$ (A.4)

One property of the distance function is that the differentiation with respect to the quantity for a given sector, i, gives the compensated (Hicksian) inverse demand function of prices in that sector, P_i, normalized by expenditure, Y, as a function of utility and quantity supplied (Deaton 1979),

$$\frac{\partial D(U,\mathit{X})}{\partial X_i}=H_i(U,\mathit{X})=\frac{P_i(U,\mathit{X})}{Y}$$ (A.5)

Substituting in direct utility, equation (A.4), gives the uncompensated (Marshallian) inverse demand of prices for that sector normalized by expenditure as a function of quantity,

$$M_i(\mathit{X})=\frac{P_i(\mathit{X})}{Y}$$ (A.6)

The compensated (Hicksian, denoted by the superscript h) inverse budget share in terms of utility and quantities, W^h_i, for sector i evaluated at X^* so that D(U,X^*)=1 is

$$\frac{\partial \ln [D(U,\mathit{X})]}{\partial \ln \left[X_i\right]}=\frac{\partial D(U,\mathit{X})}{\partial X_i}\cdot \frac{X_i}{D(U,\mathit{X})}=\frac{P_i(U,\mathit{X})}{Y}\cdot X_i=W_i^h$$ (A.7)

Two-stage budgeting

First stage

In our two-stage IAI model, the first stage (group level) is the fish species, indexed over i=(1,…,N) and j=(1,…,N).² The distance function is ln[D(U,X)] = a(X) – U·b(X), where X={X₁,…,X_i,…,X_N}. Capital letters are used for first stage variables. Using the functional forms given in equations (A.2) and (A.3) and taking the derivative of equation (A.1), the compensated budget share for species i is ³

$$\begin{gathered} W_i^h=\frac{\partial \ln [D(U,\mathit{X})]}{\partial \ln \left[X_i\right]}={\alpha }_i+\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right){\sum }_{\mathit{i}}{\gamma }_{ij}ln\left(X_i\right)+\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right){\sum }_{\mathit{j}}{\gamma }_{ij}ln\left(X_j\right)-U{\beta }_0\left[{\beta }_i{\mathrm{\Pi }}_{\mathit{j}}{X}_j^{{\beta }_j}\frac{1}{X_i}\right]X_i \\ ={\alpha }_i+{\sum }_{\mathit{j}}{\gamma }_{ij}ln\left(X_j\right)-U{\beta }_0{\beta }_k{\mathrm{\Pi }}_{\mathit{j}}{X}_j^{{\beta }_j}={\alpha }_i+{\sum }_{\mathit{j}}{\gamma }_{ij}ln\left(X_j\right)-U{\beta }_{j}b(\mathit{X}) \end{gathered}$$ (A.8)

Substituting in direct utility, equation (A.4), gives the uncompensated budget share

$$\begin{gathered} W_i=\frac{X_i{P}_i}{Y}={\alpha }_i+{\sum }_{\mathit{j}}{\gamma }_{ij}ln\left(X_j\right)-\left[\frac{a(\mathit{X})}{b(\mathit{X})}\right]{\beta }_0{\beta }_i{\mathrm{\Pi }}_{\mathit{j}}{X}_j^{{\beta }_j}={\alpha }_k+{\sum }_{\mathit{j}}{\gamma }_{ij}ln\left(X_j\right)-{\beta }_{i}a(\mathit{X}) \\ ={\alpha }_i+{\sum }_{\mathit{j}}{\gamma }_{ij}ln\left(X_j\right)-{\beta }_i\ln Q \end{gathered}$$ (A.9)

where lnQ is a “quantity index”

$$\ln Q\equiv a(\mathit{X})={\alpha }_0+{\sum }_{\mathit{i}}{\alpha }_{i}ln\left(X_i\right)+\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right){\sum }_{\mathit{i}}{\sum }_{\mathit{j}}{\gamma }_{ij}ln\left(X_i\right)ln\left(X_j\right)$$ (A.10)

For any species, i, the group level, uncompensated inverse demand is

$$M_i(\mathit{X},Y)=P_i=\left(\frac{Y}{X_i}\right)W_i=\left(\frac{Y}{X_i}\right)\left\{{\alpha }_i+{\sum }_{\mathit{j}}{\gamma }_{ij}ln\left(X_j\right)-{\beta }_i\ln Q\right\}$$ (A.11)

The group level expenditure on species i is

$$Y_i=X_i\cdot P_i=Y\cdot W_i=(Y)\left\{{\alpha }_i+{\sum }_{\mathit{j}}{\gamma }_{ij}ln\left(X_j\right)-{\beta }_i\ln Q\right\},$$ (A.12)

$$ln\left(Y_i\right)=ln\left(X_i\right)+ln\left(P_i\right)$$ (A.13)

Second stage

An analogous set of calculations can be done for the second stage (within-group) IAI, which are regions in our model, indexed over r=(1,…, R) and s=(1,…,R).⁴ The second stage distance function for species, i, is ln[D_i(U_i,x_i)] = a(x_i) – U_i·b(x_i), where x_i is the quantity vector for species i, x_i={x_(i)1,…,x_(i)r,…,x_(i)R}. Small letters are used for second stage variables and the first stage subscript is written in parentheses when it appears with a second stage subscript. The within-group budget share, quantity index, and uncompensated inverse demand for any specific species, i, in region, r, are

$$w_{(i)r}=\frac{x_{(i)r}{p}_{(i)r}}{Y_i}={\alpha }_{(i)r}+{\sum }_{\mathit{s}}{\gamma }_{(i)rs}ln\left(x_{(i)s}\right)-{\beta }_{(i)r}\ln Q_{(i)},$$ (A.14)

$$\ln Q_{(i)}\equiv {\alpha }_{(i)0}+{\sum }_{\mathit{r}}{\alpha }_{(i)r}ln\left(x_{(i)r}\right)+\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right){\sum }_{\mathit{r}}{\sum }_{\mathit{s}}{\gamma }_{(i)rs}ln\left(x_{(i)r}\right)ln\left(x_{(i)s}\right)$$ (A.15)

$$m_{(i)r}\left({\mathit{x}}_i,Y_i\right)=p_{(i)r}=\left(\frac{Y_i}{x_{(i)r}}\right)w_{(i)r}=\left(\frac{Y_i}{x_{(i)r}}\right)\left\{{\alpha }_{(i)r}+{\sum }_{\mathit{s}}{\gamma }_{(i)rs}ln\left(x_{(i)s}\right)-{\beta }_{(i)r}\ln Q_{(i)}\right\}$$ (A.16)

In the two-stage budgeting context, equations (A.14)–(A.16) are conditional on the first stage budgeting allocation, given by Y_i. For this to be appropriate, the conditional, within-group inverse demand function for species i in region r must yield the same result as an unconditional demand function for that species and region. (Deaton and Muellbauer 1980; Edgerton 1997)

$$p_{(i)r}=m_{(i)r}\left({\mathit{x}}_i,Y_i\right)=m_{(i)r}\left({\mathit{x}}_i,Y_i(\mathit{X},Y)\right)=M_{(i)r}(\mathit{X},Y),$$ (A.17)

To maintain consistency with the first stage quantity totals, the group level quantity, measured in pounds harvested for any given species, i, is the sum of all regional level harvests of that species, also measured in pounds,

$$X_i={\sum }_r{x}_{(i)r}$$ (A.18)

Flexibilities

Quantity flexibilities

To evaluate the effect of a quantity shock of species i in region r, we define the quantity flexibility as the percentage change in price associated with a one percent change in quantity.⁵ This is analogous to a price elasticity in a direct demand model. The within-group own-quantity flexibility is the percentage change in the price of species i in region r given a one percent change in the quantity of that species, i, in that region, r.⁶

$$\begin{gathered} {\epsilon }_{(i)rr}=\frac{\partial \ln \left[p_{(i)r}\right]}{\partial \ln \left[x_{(i)r}\right]}=\left[\frac{\partial p_{(i)r}}{\partial x_{(i)r}}\right]\left(\frac{x_{(i)r}}{p_{(i)r}}\right)=\left[\frac{\partial \left\{w_{(i)r}\left(\frac{Y_i}{x_{(i)r}}\right)\right\}}{\partial \left[x_{(i)r}\right]}\right]\left(\frac{x_{(i)r}}{p_{(i)r}}\right) \\ =\left[\frac{-w_{(i)r}{Y}_i}{{\left(x_{(i)r}\right)}^2}+\frac{\partial \left\{{\alpha }_{(i)r}+{\sum }_{\mathit{s}}{\gamma }_{(i)rs}ln\left(x_{(i)s}\right)-{\beta }_{(i)r}\ln Q_{(i)}\right\}\left(\frac{Y_i}{x_{(i)r}}\right)}{\partial \left[x_{(i)r}\right]}\right]\left(\frac{x_{(i)r}}{p_{(i)r}}\right) \\ =\left[\frac{-w_{(i)r}{Y}_i}{{\left(x_{(i)r}\right)}^2}+\left\{\frac{{\gamma }_{(i)m}}{x_{(i)r}}-{\beta }_{(i)r}\left(\frac{{\alpha }_{(i)r}}{x_{(i)r}}+\frac{{\sum }_{\mathit{s}}{\gamma }_{(i)rs}ln\left(x_{(i)s}\right)}{x_{(i)r}}\right)\right\}\left(\frac{Y_i}{x_{(i)r}}\right)\right]\left(\frac{x_{(i)r}}{p_{(i)r}}\right) \\ =-1+\left\{{\gamma }_{(i)m}-{\beta }_{(i)r}\left(w_{(0)r}+{\beta }_{(i)r}\ln Q_{(i)}\right)\right\}\left(\frac{1}{w_{(i)r}}\right) \end{gathered}$$ (A.19)

The within-group cross-quantity flexibility – the effect on the price of species i in region r given a change in the quantity of species i in some other region s – is similar but lacks the first term.

$${\epsilon }_{(i)rs}=\frac{\partial \ln \left[p_{(i)r}\right]}{\partial \ln \left[x_{(i)s}\right]}=\left\{{\gamma }_{(i)rs}-{\beta }_{(i)r}\left(w_{(i)s}+{\beta }_{(i)s}\ln Q_{(i)}\right)\right\}\left(\frac{1}{w_{(i)r}}\right)$$ (A.20)

The generic within-group quantity flexibility would then be

$${\epsilon }_{(i)rs}=\frac{\partial \ln \left[p_{(i)r}\right]}{\partial \ln \left[x_{(i)s}\right]}=-{\delta }_{rs}+\left\{{\gamma }_{(i)rs}-{\beta }_{(i)r}\left(w_{(i)s}+{\beta }_{(i)s}\ln Q_{(i)}\right)\right\}\left(\frac{1}{w_{(i)r}}\right)$$ (A.21)

Where δ_rs is a Kronecker delta equal to 1 if r=s and equal to zero otherwise.

A similar set of quantity flexibilities can be derived for the first stage inverse demands. The generic, group level quantity flexibility is the percentage change in the first stage price of species i given a one percent change in the first stage, total quantity of species j.

$$E_{ij}=\frac{\partial \ln \left[P_i\right]}{\partial \ln \left[X_j\right]}=-{\delta }_{ij}+\left\{{\gamma }_{ij}-{\beta }_i\left(W_j+{\beta }_j\ln Q\right)\right\}\left(\frac{1}{W_j}\right)$$ (A.22)

It is important to recognize that the partial (within-group) quantity flexibility derived above, ε_(i)rs, is conditional on the first stage budgeting allocation in the same way as was discussed for equations (A.14)–(A.16). The total quantity flexibility, ε_(i)r,(j)s, would be the percentage change in the price of species i in region r given a one percent change in the price of any species, j, in any region, s. In other words, it is the change in the second stage price of a species in some region given a change in the quantity of any species harvested in any region. This is analogous to Edgerton’s (1997) uncompensated total price elasticity for the direct Almost Ideal specification model. Deriving this total flexibility requires an estimation of the effect of a second stage quantity change on the first stage expenditures and is derived in detail below.

Expenditure flexibilities

In the direct Almost Ideal specification models, the expenditure elasticity – the effect on quantity given a change in expenditure – is (∂ln[X_i]/∂ln[Y]) = 1 + (β_i/W_i) (see Eales and Unnevher 1994). The first term on the right-hand side is the direct effect of expenditure on quantity while the second term is the effect of income as it affects the expenditure share. The second term appears because expenditure is an explicit argument in the share equation in the direct Almost Ideal specification model. In the IAI model, expenditure, Y, is not an argument in the share equation, W_i. Therefore, the second term is not present in the analogous expenditure flexibility for the IAI model.

The group level expenditure flexibility is

$${\mathrm{\Upsilon }}_i=\frac{\partial \ln \left[P_i\right]}{\partial \ln [Y]}=\left[\frac{\partial P_i}{\partial Y}\right]\left(\frac{Y}{P_k}\right)=\left[\frac{\partial \left\{W_i\left(\frac{Y}{X_i}\right)\right\}}{\partial Y}\right]\left(\frac{Y}{P_i}\right)=\left(\frac{W_i}{X_i}\right)\left(\frac{Y}{P_i}\right)=1$$ (A.23)

Similarly, the within-group expenditure flexibility (conditional on Y_i) is

$${\psi }_{(i)}=\frac{\partial \ln \left[p_{(i)r}\right]}{\partial \ln \left[Y_i\right]}=\left[\frac{\partial p_{(i)r}}{\partial Y_i}\right]\left(\frac{Y_i}{p_{(i)r}}\right)=\left[\frac{\partial \left\{w_{(i)r}\left(\frac{Y_i}{x_{(i)r}}\right)\right\}}{\partial \left[Y_i\right]}\right]\left(\frac{Y_i}{p_{(i)r}}\right)=\left(\frac{w_{(i)r}}{x_{(i)r}}\right)\left(\frac{Y_i}{p_{(i)r}}\right)=1$$ (A.24)

Scale flexibilities

The expenditure flexibility derived above is the analog to the expenditure elasticity. However, in the inverse demand literature, the scale flexibility is sometimes conflated with this analog.⁷ In fact, the scale flexibility is something different. In an inverse demand system, the scale flexibility measures the change in the price of a good given a change in all quantities. This is related to the distance function which measures how much the full quantity vector, X, must be scaled in order to achieve a given utility level, U. If λ is this scaling factor, then the scale flexibility is the percent change in the price of a good given a one percent change in this scaling factor.

The scale flexibility can be derived by first multiplying all of our quantities by λ. Our first stage share equation and Marshallian demand would be

$$W_i^{*}={\alpha }_i+{\sum }_{\mathit{j}}{\gamma }_{ij}ln\left(\lambda X_j\right)-{\beta }_i\ln \lambda Q$$ (A.25)

$$\ln \lambda Q={\alpha }_0+{\sum }_{\mathit{i}}{\alpha }_{i}ln\left(\lambda X_i\right)+\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right){\sum }_{\mathit{i}}{\sum }_{\mathit{j}}{\gamma }_{ij}ln\left(\lambda X_i\right)ln\left(\lambda X_j\right)$$ (A.26)

$$M_i^{*}(\lambda \mathit{X},Y)=P_i^{*}(\lambda \mathit{X})=\left(\frac{Y}{\lambda X_i}\right)W_i^{*}$$ (A.27)

λ=1 is the special case, assumed in our derivations above, in which the quantity vector is just sufficient to produce the utility level implied by equation (A.4).

The first stage scale elasticity is then^8,9

$$\begin{gathered} {\mathrm{\Phi }}_i=\frac{\partial \ln \left[P_i^{*}(\lambda \mathit{X})\right]}{\partial \ln [\lambda ]}=\frac{\partial \ln \left[M_i^{*}(\lambda \mathit{X},Y)\right]}{\partial \ln [\lambda ]}=\left[\frac{\partial M_i^{*}(\lambda \mathit{X},Y)}{\partial \lambda }\right]\left(\frac{\lambda }{M_i^{*}}\right)=\left[\frac{\partial \left\{W_i^{*}\left(\frac{Y}{\lambda {\mathit{X}}_i}\right)\right\}}{\partial \lambda }\right]\left(\frac{\lambda }{M_i^{*}}\right) \\ =\left[\frac{-W_i^{*}Y}{{\lambda }^2{X}_i}+\left\{{\sum }_{\mathit{j}}\frac{{\gamma }_{ij}}{\lambda }-{\beta }_i\left({\sum }_{\mathit{i}}\frac{{\alpha }_i}{\lambda }+{\sum }_{\mathit{i}}{\sum }_{\mathit{j}}\frac{{\gamma }_{ij}\ln \left(X_i\right)}{\lambda }\right)\right\}\left(\frac{Y}{\lambda X_i}\right)\right]\left(\frac{\lambda }{M_i^{*}}\right) \\ =\left[-W_i^{*}+\left\{{\sum }_{\mathit{j}}{\gamma }_{ij}-{\beta }_i\left({\sum }_{\mathit{i}}{\alpha }_i+{\sum }_{\mathit{i}}{\sum }_{\mathit{j}}{\gamma }_{ij}ln\left(X_i\right)\right)\right\}\right]\left(\frac{Y}{M_i^{*}\lambda X_i}\right) \\ =-1-\left(\frac{{\beta }_i}{W_i^{*}}\right) \end{gathered}$$ (A.28)

The second stage scale flexibility gives the percentage change in the price of species i in region r given a one percent change in the scale parameter in region r.

$${\varphi }_{(i)r}=\frac{\partial \ln \left[m_{(i)r}^{*}\right]}{\partial \ln [\lambda ]}=-1-\left(\frac{{\beta }_{(i)r}}{w_{(i)r}^{*}}\right)$$ (A.29)

A scale flexibility might be appropriate to measure the effect of a shock in a region that affects all species in that region by the same percentage.

Aggregate quantity flexibilities

The final elasticity that we will need to derive the total quantity flexibility is the percent change in first stage aggregate quantity of some species, i, given a one percent change in quantity of that species in a single region, r.¹⁰

$${\xi }_{(i),(i)r}=\frac{\partial \ln \left[X_i\right]}{\partial \ln \left[x_{(i)r}\right]}=\frac{\partial X_i}{\partial x_{(i)r}}\left(\frac{x_{(i)r}}{X_i}\right)=\frac{\partial \left({\sum }_{\mathit{s}}{x}_{(i)s}\right)}{\partial x_{(i)r}}\left(\frac{x_{(i)r}}{X_i}\right)=\left(\frac{x_{(i)r}}{X_i}\right)$$ (A.30)

It should be obvious that a change in the quantity of one species, j, in some region, r, does not affect the aggregate quantity of a different species, i. That is ξ_(i),(j)r = ∂ln(X_i)/∂ln(x_(j)r) = 0.

Total, flexibility

The total flexibility, ε_(i)r,(j)s, is then the percent change in the price of species i in region r given a one percent change in the quantity of any species j in any region s. We refer to this as the total flexibility because it includes the effect of the change in expenditures for each species. As we mentioned before for equation (A.17), for two-stage budgeting to be appropriate, the conditional, within-group inverse demand function for species i in region r must yield the same result as an unconditional demand function for that species and region.

$$p_{(0)r}=m_{(i)r}\left({\mathit{x}}_i,Y_i\right)=m_{(i)r}\left({\mathit{x}}_i,Y_i(\mathit{X},Y)\right)=M_{(0)r}(\mathit{X},Y).$$

So, ¹¹

$$\begin{gathered} {\epsilon }_{(i)r,(j)s}=\frac{\partial \ln \left[M_{(i)r}(\mathit{X},Y)\right]}{\partial \ln \left[x_{(j)s}\right]}=\frac{\partial \ln \left[m_{(i)r}\left({\mathit{x}}_i,Y_i(\mathit{X},Y)\right)\right]}{\partial \ln \left[x_{(j)s}\right]}=\frac{\partial \ln [p_{(i)r}\left({\mathit{x}}_i,Y_i(\mathit{X},Y)\right]}{\partial \ln \left[x_{(j)s}\right]} \\ =\frac{\partial \ln \left[p_{(i)r}\right]}{\partial \ln \left[x_{(j)s}\right]}+\frac{\partial \ln \left[p_{(i)r}\right]}{\partial \ln \left[Y_i\right]}\frac{\partial \ln \left[Y_i\right]}{\partial \ln \left[x_{(j)s}\right]} \\ ={\delta }_{ij}\left[{\epsilon }_{(i)rs}\right]+\frac{\partial \ln \left[p_{(i)r}\right]}{\partial \ln \left[Y_i\right]}\left[\frac{\partial \ln \left[X_i\right]}{\partial \ln \left[x_{(j)s}\right]}+\frac{\partial \ln \left[P_i\right]}{\partial \ln \left[x_{(j)s}\right]}\right] \\ ={\delta }_{ij}\left[{\epsilon }_{(i)rs}\right]+{\psi }_i\left[{\delta }_{ij}{\xi }_{(j),(j)s}+\frac{\partial \ln \left[P_i\right]}{\partial \ln \left[X_j\right]}\frac{\partial \ln \left[X_j\right]}{\partial \ln \left[x_{(j)s}\right]}\right] \\ ={\delta }_{ij}\left[{\epsilon }_{(i)rs}\right]+{\psi }_i\left[{\delta }_{ij}{\xi }_{(j),(j)s}+E_{ij}{\xi }_{(j),(j)s}\right] \\ ={\delta }_{ij}\left[{\epsilon }_{(i)rs}\right]+{\psi }_i\left[{\delta }_{ij}+E_{ij}\right]{\xi }_{(j),(j)s} \end{gathered}$$ (A.31)

Substituting in the IAI functional forms for these flexibilities, the resulting total, unconditional, within-group flexibility is

$$\begin{gathered} {\epsilon }_{(i)r,(j)s}={\delta }_{ij}\left[-{\delta }_{rs}+\left\{{\gamma }_{(i)rs}-{\beta }_{(i)r}\left(w_{(i)s}+{\beta }_{(i)s}\ln Q_{(i)}\right)\right\}\left(\frac{1}{w_{(i)r}}\right)\right] \\ +\left[\left\{{\gamma }_{ij}-{\beta }_i\left(W_j+{\beta }_j\ln Q\right)\right\}\left(\frac{1}{W_i}\right)\right]\left(\frac{x_{(j)s}}{X_j}\right) \end{gathered}$$ (A.32)