Photothermal Conversion of Gold Nanoparticles for Uniform Pulsed Laser Warming of Vitrified Biomaterials

Abstract

Pulsed laser (ms, 1064 nm) gold nanoparticle (GNP) heating has been used recently to achieve fast (> 10,000,000 °C min⁻¹) warming of vitrified droplets using gold nanorods (GNRs) as photon-absorbers. To maximize the viability of biomaterials in vitrified droplets, the droplets must be warmed as uniformly as possible. A potential approach to such warming is to use an appropriate combination of photon-absorption and -scattering to distribute heat more uniformly throughout a droplet. To investigate this, 2 plasmonic gold nanorods (GNRs), 1 hollow gold nanoshell, and 2 silica-core gold nanoshells (GNSs) were synthesized and characterized under 1064 nm laser irradiation in water, propylene glycol, and protein-rich (egg white) solutions. Using a modified laser cuvette heating experiment with complementary Monte Carlo modeling, the GNSs were found to have higher per-particle absorption and scattering cross sections, while the GNRs had higher photothermal conversion efficiency, absorption efficiency, and Au mass normalized absorption cross sections. In the characterization, the GNSs with larger scattering-to-absorption ratios could have ~30% over-estimation of photothermal conversion efficiency if scattering and reabsorption inside the solution were not considered, while GNRs with lower ratios were less impacted. Combined Monte Carlo and COMSOL simulations were used to predict the specific absorption rate (Wm⁻³) and heating behavior of GNP-loaded hemispherical droplets, thereby demonstrating that the GNS case with higher scattering-to-absorption ratio achieved more uniform heating than the GNR case. Interestingly, further tuning of the scattering and absorption coefficients of the hemispherical GNP-loaded droplet within the model suggests the ability to obtain an optimal scattering-to-absorption ratio for uniform heating. These results show the importance of considering the reabsorption of scattered light to accurately characterize the photothermal conversion efficiency of GNP solutions during laser irradiation. We also show that the relative scattering and absorption properties of the nanoparticles can be designed to promote both rapid and uniform rewarming of vitrified droplets for application in cryopreservation.

Graphical Abstract

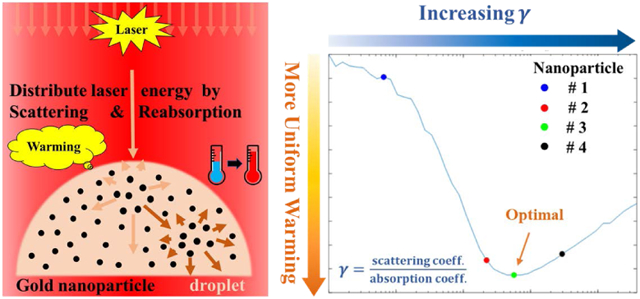
The gold nanoparticles’ ratio of light scattering to absorption can be designed to more uniformly distribute the absorbed energy during rapid pulsed laser warming of vitrified biomaterials in droplets.

1. Introduction

Gold nanoparticles (GNPs) are increasingly used in laser heating biomedical applications due to their high biocompatibility¹, ease of chemical functionalization,² and tunable localized surface plasmon resonance (LSPR) absorption band^3-5. For instance, laser heating of GNPs has been widely applied in photothermal cancer therapies such as the use of gold nanoshells (GNSs) as NIR laser absorbers.^{6, 7} More recent work uses photosensitizer-loaded GNPs for photothermal/photodynamic therapy^{8, 9}, drug-loaded GNPs for thermo-chemotherapy^{10, 11}, and engineered GNSs for imaging coupled photothermal therapy.¹² GNPs have also been used for the selective killing of pathogenic bacteria^{13, 14} and viruses^{15, 16}, neuron stimulation^{17, 18}, and wound healing¹⁹. The present work focuses on the promising applications of fast laser GNP heating for warming of vitrified biomaterials from cryopreservation^{20, 21} such as fish embryos^{22, 23} and coral larvae²⁴, which is an evolution from the use of black India ink to warm vitrified mammalian embryos and oocytes^{25, 26}. For successful droplet rewarming, the warming rate should exceed the rate of ice formation and/or growth inside the droplets which otherwise would be lethal to the loaded biomaterials^{25, 27}. Thus, ms pulse laser has been used to rapidly rewarm the GNP loaded droplets at warming rates > 10,000,000 °C min⁻¹ warming rate^{22, 23}. In this study, we show the ability to achieve both speed and uniformity of rewarming through nanoparticle design.

GNPs have optical properties that are a function of their size and shape, and it is important to select a GNP that has scattering and absorption properties that maximize photothermal performance in the target system. Gold nanorods (GNRs) have the highest photothermal efficiency and mass averaged absorption cross section compared to other nanostructures, including nanostars, nanoshells, and nanocages within the first near infra-red (NIR) biological window (~ 650 - 950 nm).²⁸ By adjusting the particle geometry, GNRs^29-31 and nanoechinus³² can be tuned to absorb well in the second NIR window (1000 – 1350 nm).³³ While it is straightforward to measure particle’s extinction property, separating the scattering and absorption components of nanoparticles is more challenging. Theoretical calculations provide the relative contributions of scattering and absorption but plasmonic nanoparticles such as GNRs^{30, 34, 35} and GNSs^{34, 36}, are very sensitive to geometric polydispersity that can cause discrepancies between experimental and theoretical predictions.³⁷ Among experimental approaches, monitoring the temperature of a solution of GNPs that are illuminated with a concentrated light source is a direct method of measuring photothermal properties.^37-39 However, in the NIR range, water’s absorbance is non-negligible and needs to be accounted for despite some studies that neglect^{37, 39} or do not accurately account³⁸ for it. Finally, even though many studies have coupled optical and thermal simulations to study laser-gold-tissue interactions^{40, 41}, we are unaware of similar studies that account for absorption, scattering, and reabsorption of scattered light to characterize GNPs during laser heating in solutions. This is important as it suggests earlier work^37-39 based on absorption only may over-estimate photothermal conversion efficiency, especially for larger GNPs (i.e. GNS) with significant scattering properties³⁴.

The design and use of GNPs as effective heaters⁴² in laser warming of vitrified droplets are critical to the success of the warming event (Fig. 1(a)), thus impacting the survival rate of the loaded biomaterials. For instance, failed rewarming can lead to partial boiling and/or ice crystallization (devitrification) inside the droplets due to non-uniform heating as shown in Fig. 1(b and d) from the preliminary experiments (detailed in section S5). However, by matching the GNP type and concentration to the laser irradiation, successful rewarming of droplets can be achieved without the failure modes highlighted above, as shown in Fig. 1(c). The goal of this work is to provide a systematic approach to characterizing the optical properties of GNPs for the application of fast and uniform (1064 nm) laser warming of vitrified biomaterials. To this end, the optical absorption and scattering properties of silica-core GNSs, hollow gold nanoshells (HGNSs), and GNRs were quantitatively characterized and compared using a previously reported cuvette calorimetry approach which is able to measure GNPs’ per-particle optical properties from their bulk solutions.³⁷ For improved accuracy in the characterization of photothermal conversion, we also accounted for the scattering and reabsorption of light within the bulk solution by adopting Monte Carlo simulations as shown in Fig. 2(b). The impact of solution media, including cryoprotectant solutions (propylene glycol, PG) and protein-rich biological medium (egg white) on the optical properties was also studied, as it is critical to understand the effect of photothermal heating within biomaterials such as embryos. Finally, GNP optical properties were applied to a droplet system as a model to optimize nanoparticle property design for more uniform laser warming from vitrification. Monte Carlo modeling was also used and coupled with numerical simulation to assess the heating profiles of different GNP-loaded (GNR vs. GNS) small hemispherical droplets (mm scale) during laser heating. Optimization was conducted to achieve more uniform heating profiles of the vitrified droplets by designing the optical absorption and scattering properties of the system.

Fig.1.

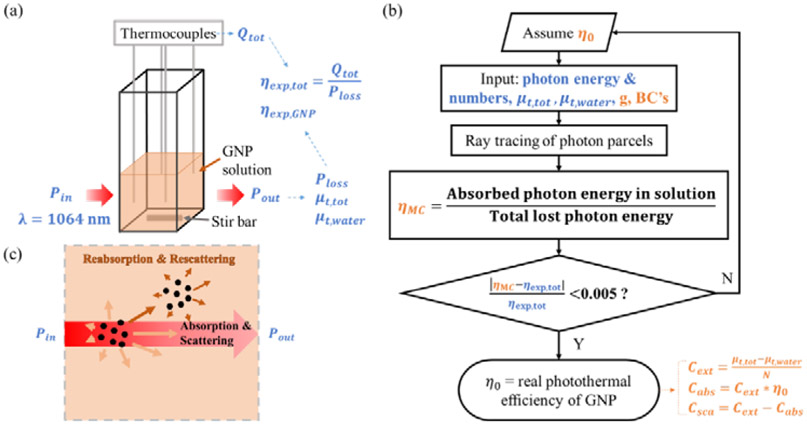
(a) Laser warming of vitrified GNP-loaded droplets. The scattering of the GNPs helps to distribute the absorbed laser energy for uniform heating. (b-c) The recorded photos of hemispherical droplets before and after laser warming from vitrification. (b) The droplets were under-warmed with significant ice crystallization; (c) The droplet was successfully rewarmed; (d) The droplet was over-warmed with boiling. The bright white spots remained in the droplets both before and after laser heating were the images of bulbs due to mirroring effects.

Fig. 2.

Cuvette heating experiment supplemented with Monte Carlo modeling to characterize GNPs’ absorption and scattering properties in water solutions. (a) Scheme of the experimental setup. The inlet (P_in) and outlet (P_out) laser power was measured. The total power loss of the laser beam (P_loss), GNP solution’s (μ_t,tot) and water’s (μ_t,water) extinction coefficients are then determined. The total heat generation of the solution (Q_tot) is obtained by temperature measurement via thermocouples. The experimental photothermal conversion efficiencies of the GNP solution (η_exp,tot) and single GNP (η_exp,GNP) can thus be derived. (b) Monte Carlo modeling was used to study the effects of reabsorbing the scattered light in the GNP solution to predict the real photothermal conversion efficiency of the single GNP, η₀. The input parameters include both measured optical properties (in blue) and assumed constants (in brown) with details shown in Table 3 in Methods. The absorption cross sections (C_abs), scattering cross sections (C_sca), and extinction cross section (C_ext) for single GNP can be predicted after calculating η₀ (correlations in Table 2). (c) Scheme of ray tracing of photons that can either be absorbed, scattered, reabsorbed, or re-scattered when traveling through the GNPs’ solution during cuvette heating experiments. Abbreviation and nomenclature: BC’s, Boundary conditions; g, scattering anisotropy factor. Variables in blue color: measured; Variables in brown color: assumed or predicted.

2. Results & Discussion

2.1. Gold nanoparticle type and geometry

The GNSs (hollow and silica-core) and GNRs used in this study were custom synthesized by nanoComposix Inc (San Diego, CA, USA) with absorption peaks close to 1064 nm. Their batch numbers, concentration, and geometric information were provided by the company and are summarized in Table 1. The concentration of the GNPs was determined by the gold mass concentration from ICP-MS measurement and the averaged geometric dimensions from TEM imaging, which was conducted by nanoComposix, Inc. All the GNPs were surface-functionalized with 5 kDa polyethylene glycol (PEG) with a methyl end group except GNR-1 which had a carboxyl end group.

Table 1.

GNP type and geometry.

GNPs	Name	Batch No.	Concentration (particles mL−1)	2R1, L (nm)	2R2, W (nm)	R2/R1, L/W	Peak Wavelength (nm)	Geometry Scheme
Hollow Nanoshells	HGNS	JCP1612	1.2E10	~ 195	225 ± 28	0.87 (R2/R1)	987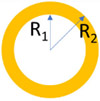
Nanoshells (Silica-core)	GNS-1	BAM0089	2.1E11	198 ± 10	242 ± 10	0.82	988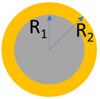
	GNS-2	KJW2253	1.7E10	198 ± 10	240 ± 10	0.83	987
Nanorods	GNR-1	ALJ0045	4.67E13	86.5 ± 11.9	14 ± 1.9	6.18 (L/W)	1019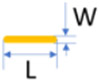
	GNR-2	BAM0278	1.4E13	93.1 ± 9.8	15.4 ±1.5	6.05	1014

^*Dimensions obtained from TEM measurement.

2.2. Optical properties of GNRs and GNSs in aqueous solutions

The UV-vis-NIR extinction spectra and TEM images provided by nanoComposix are shown in Fig. S1. The extinction spectra show that all GNSs and GNRs have a surface plasmon resonance peak near 1064 nm. However, the extinction spectra do not provide the GNPs’ absorption and scattering optical properties. Further characterizing GNPs is thus needed, which was performed by cuvette heating experiments supplemented with Montel Carlo modeling. The scheme of the experimental setup and modeling are provided in Fig. 2 and detailed in the Methods.

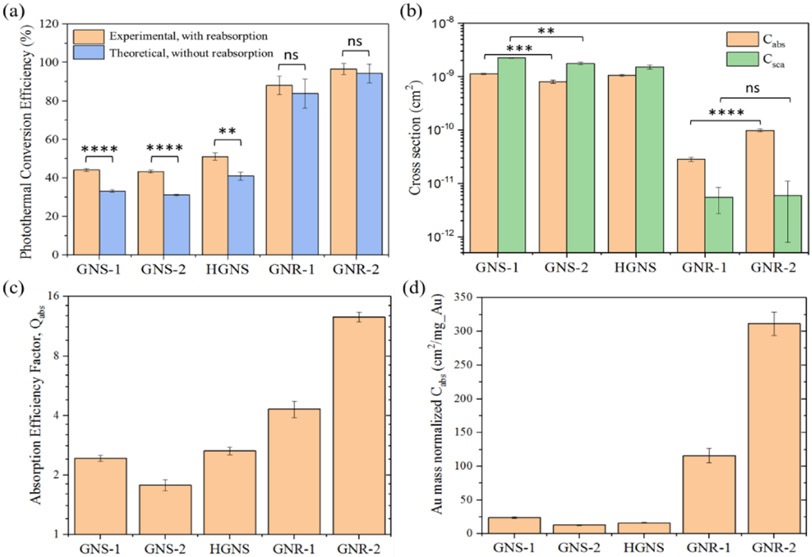
The predicted single GNP’s absorption (C_abs) and scattering (C_sca) cross sections and photothermal efficiencies (η) are shown in Fig. 3 and their correlations to the optical properties of the bulk solution are summarized in Table 2. Fig. 3(a) compares the photothermal conversion efficiencies of different GNP types in the aqueous medium. The photothermal conversion efficiencies without reabsorption of scattered light were obtained by using Monte Carlo modeling (denoted as “predicted”), while those with the reabsorption effect were directly obtained from measurement (denoted as “measured”). As is shown, GNRs have much greater photothermal conversion efficiencies (predicted: 84%-94%) than all the other GNSs (predicted: under 50%). These photothermal conversion efficiencies can be related to absorption and scattering cross sections (Equations (8-9) in Table 2):

$$\eta =\frac{C_{abs}}{C_{abs}+C_{sca}}$$ (17)

Fig. 3.

(a) Comparison of the photothermal conversion efficiencies of GNPs in water solutions with (measured) and without (predicted) the influence of the reabsorption of scattering. (b) Predicted absorption (C_abs) and scattering (C_sca) cross sections for the different GNPs. (c) Predicted absorption efficiency factor, Q_abs, and (d) predicted Au mass normalized absorption cross sections of the different GNPs. Q_abs is the normalized C_abs by the geometric cross-sectional area of GNPs. The effective cross-sectional area of a GNR is calculated from their volume-equivalent nanospheres. Statistical significance is indicated with asterisks: * p < 0.05; ** p < 0.01; *** p < 0.001 **** p < 0.0001; ns: p > 0.05.

Table 2.

The corresponding optical properties between the single nanoparticle and the bulk solution.

Optical properties	Bulk solution		Single GNP		Correlations (from bulk solution to single GNP)
Absorption	μa,tot	$$\begin{gathered} \text{Absorption coefficient} \\ =N\ast C_{abs}+{\mu }_{a,medium} \end{gathered}$$ (1)	Cabs	Absorption cross section	$$C_{abs}=C_{ext}\ast {\eta }_0$$ (14)
Scattering	μs,tot	$$\begin{gathered} \text{Scattering coefficient} \\ =N\ast C_{sca}+{\mu }_{s,medium} \end{gathered}$$ (2)	Csca	Scattering cross section	$$C_{sca}=C_{ext}-C_{abs}$$ (15)
Extinction	μt,tot	$$\begin{gathered} \text{Extinction coefficient} \\ =N\ast C_{ext}+{\mu }_{t,medium} \end{gathered}$$ (3) $$={\mu }_{a,tot}+{\mu }_{s,tot}$$ (4)	Cext	$$\begin{gathered} \text{Extinction cross section} \\ =C_{abs}+C_{sca} \end{gathered}$$ (8)	$$C_{ext}=({\mu }_{t,tot}-{\mu }_{t,medium})∕N$$ (16)
	AGNP	Extinction of GNPs (UV-vis-NIR) = N * Cext * L * log10 e (S28)
Photothermal efficiency	ηtot	$$\text{Photothermal converesion efficiency}={\mu }_{a,tot}∕{\mu }_{s,tot}$$ (5)	η	$$\begin{gathered} \text{Photothermal conversion efficiency} \\ =C_{abs}∕C_{ext} \end{gathered}$$ (9)	η0: Predicted by Monte Carlo modeling
			Qabs	$$\begin{gathered} \text{Absorption efficiency factor} \\ =C_{abs}∕A_{geom} \end{gathered}$$ (10)
			$\frac{C_{abs}}{m_{Au}}$	$$\begin{gathered} \text{Au mass normalized}{\mathrm{C}}_{\text{abs}} \\ =C_{abs}∕m_{Au} \end{gathered}$$ (11)
Ratio of scattering to absorption	γtot	$${\mu }_{s,tot}∕{\mu }_{a,tot}$$ (6)	γ	$$=C_{sca}∕C_{abs}$$ (12)
Heat generation	Qtot	$$\begin{gathered} \text{Direct absorption}({\mu }_{a,tot}\ast I_{laser})+ \\ \text{reabsorption of scattered light} \end{gathered}$$ (7)	Q′GNP	$$=C_{abs}\ast I_{laser}$$ (13)

^*I_laser is the flux of laser irradiation, W m⁻². N is the concentration of the nanoparticles in the solution, number of particles mL⁻¹. A_geom is the geometric cross-sectional area of the GNPs, m². For the GNRs, the effective cross-sectional area is calculated from their volume-equivalent nanospheres. m_Au is the average Au mass consumed in an individual GNP, mg.

This is important since heat generation (C_abs*I_laser) in the droplet will be directly related to C_abs of the different GNPs, although reabsorption after scattering implies a dependence on C_sca as well. As shown in Fig. 3(b), both types of GNSs have significantly higher C_abs than the tested GNRs (difference: 8-40 fold). In addition, GNSs have a much higher C_sca than the GNRs (difference: 250-400 fold). One reason for the higher C_abs and C_sca for GNSs is their much larger size (over 200 nm in diameter) which is ~10 times larger than the GNRs’ (effective diameter smaller than 20 nm).³⁴ Clearly, on a per-particle basis, the GNS is the highest absorber and scattering particle tested. Nevertheless, in Fig. 3(c) and (d), GNRs have an over 3-fold larger absorption efficiency and a 50-fold greater Au mass normalized C_abs than GNS. Thus, for photothermal applications at 1064 nm, GNRs are excellent candidate photon-absorbers for localized heating while GNSs are highly efficient at scattering and potentially distributing light in a bulk solution.

Importantly, the absorption properties of both the GNSs’ and GNRs’ can be affected by geometric polydispersity. As indicated in Fig. 3(c) and (d), GNR-2 has significantly higher normalized C_abs than GNR-1, although they have close absorption peaks and geometries. This is probably because the geometric polydispersity (the ratio of the standard deviation to the mean value, σ/μ) of GNR-2 (10.53% in length and 9.74% in width) is smaller than that of GNR-1(13.76% in length and 13.57% in width). Our previous study³⁷ supports this, as geometric polydispersity of the GNRs can lower and broaden the peak in the extinction spectrum of their bulk solution, thus adversely affecting the heat generation during laser heating. GNS-1 and GNS-2 also have a noticeable difference in both C_abs and C_sca as shown in Fig. 3(b) (ANOVA, p ≤ 0.01) and normalized C_abs in Fig. 3(c) and (d). But compared to the GNR-1 and GNR-2, the difference in the normalized C_abs between GNS-1 and GNS-2 is much smaller, which means GNSs are less sensitive to geometry variations than GNRs at 1064 nm light excitation.

For all the GNPs studied, there is a drop in the photothermal conversion efficiency when reducing the reabsorption of scattering in the solutions. This can be best appreciated by introducing the ratio of scattering to absorption, γ:

$$\gamma =\frac{C_{sca}}{C_{abs}}$$ (18)

a derivative optical property as shown in Equation (12) in Table 2. For instance, in the low scattering nanoparticles (e.g. GNRs with predicted γ from 0.060-0.192), there is a limited difference between the results with and without reabsorption (ANOVA, p > 0.05). However, for the high scattering nanoparticles (e.g. GNSs with predicted γ from 2.003-2.205), the disparity becomes especially significant and accounts for more than a 30% over-estimation of photothermal conversion efficiency for GNS-2. It suggests that for the high scattering GNPs, there will be a large portion of laser energy scattered by the GNPs and later reabsorbed both by the GNPs and the solvent medium in the cuvette (loaded with 1 mL solution), thus introducing a higher steady-state temperature increase during measurement. Therefore, Monte Carlo modeling analysis of the cuvette heating experiment enables us to more accurately characterize the optical absorption and scattering properties for both high-absorbing and high-scattering nanoparticles at a specific wavelength.

2.3. Photothermal performance of GNPs in CPA and protein-rich media

In laser warming of vitrified droplets, cryoprotective agent (CPA) and GNPs are directly injected into the zebrafish embryo²². Importantly, both the CPA and the protein-rich media in the vitrified biomaterial can potentially change the dielectric environment surrounding the GNPs, thus affecting the surface plasmon resonance and ultimately absorption and scattering.⁴³ For a better understanding of this, one specific GNP, GNR-2, was picked to study photothermal performance further in CPA and protein-rich media.

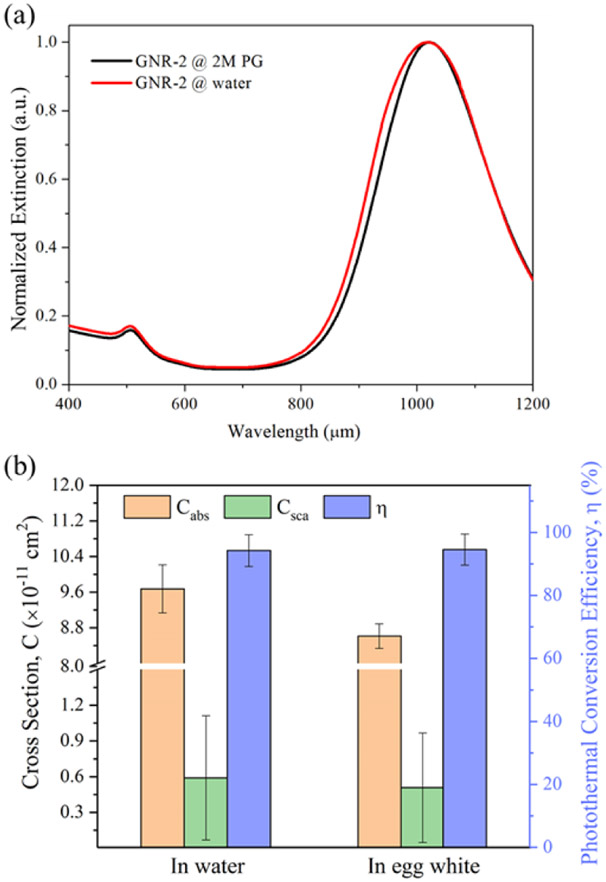
Fig. 4(a) shows the similar UV-vis-NIR extinction spectra of GNR-2 in water and 2M PG (CPA). Comparable results for other GNPs are summarized in Fig. S5. The dispersion stability of the GNRs in the CPA solutions was tested and detailed in section S4, which demonstrated that aggregation of GNRs is not a factor. All the comparison results suggest that the 2M PG has a minor effect on the extinction spectra of all tested GNP types in terms of peak wavelength and broadening. Introducing PG into the water will slightly change the dielectric constant of the medium⁴⁴, which minimally shifts the oscillation frequency of surface electron charges of GNRs. However, surface coatings can be more important in determining the surface plasmon resonance of GNRs than the medium⁴⁵, thus tending to maintain the photothermal properties of the GNRs. Given that the extinction curves of GNPs in aqueous and CPA solutions overlap strongly, this suggests that the change in medium does not appreciably impact the photothermal properties of the GNPs.

Fig. 4.

(a) Comparison of the UV-vis-NIR extinction spectra of GNR-2 suspended in water and 2M PG solutions. The extinction spectra were normalized by the peak extinction. (b) Comparison of the predicted light-absorbing and light-scattering properties of the GNR-2 at 1064 nm in the water and protein-rich medium.

The effects of the protein-rich biological medium, egg white, on the heat generation performance of GNR-2 was also investigated. Fig. S6 shows that, near the plasmon resonance peak (900-1100 nm wavelength range), the extinction curves of the GNR-2 in different egg white solutions generally match with that for GNR-2 in aqueous solution. But there was a large variation in the extinction curves outside of this wavelength range (data not shown). Further testing done by cuvette heating and Monte Carlo modeling is shown in Fig. 4(b) where C_abs and C_sca of GNR-2 in water and egg white medium is reported. As shown in Fig. 4(b), the photothermal conversion efficiency (η) of the GNR-2 remains consistent across the media. However, the egg white medium lowered the C_abs and C_sca of the GNR-2 at 1064 nm by roughly 10% compared with the aqueous case. This is possibly due to the high concentration of proteins in the solution that could cause a change in both the real and imaginary parts of the dielectric function of the medium.⁴³ So the GNR-2 could possibly experience peak shift and shielding effects. Other reports^46-48 support that protein corona can form around the GNPs through chemical and physical interactions, thus changing the surface plasmon resonance. The above results suggest that 2M PG CPA solutions will minimally affect the photothermal properties of the PEGylated GNPs while proteins can lead to a drop in photothermal conversion performance.

2.4. Laser warming of GNP-loaded droplets from vitrification

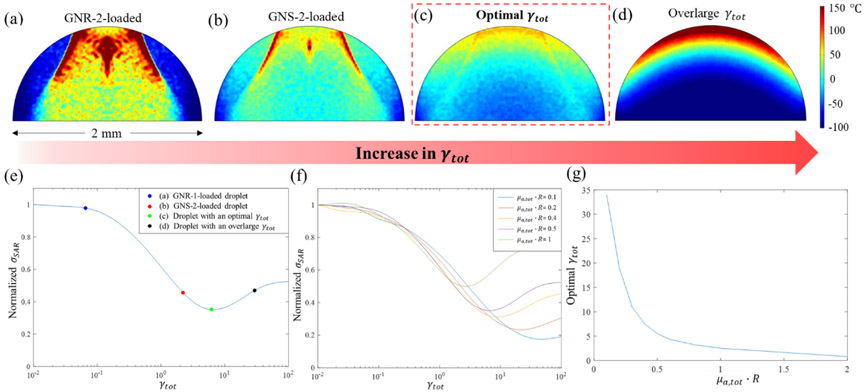
As indicated in previous studies, both rapid and uniform heating is critical to vitrified droplet laser rewarming.⁴⁹ To illustrate the importance of our findings for vitrified system rewarming, two extreme rewarming cases, with relatively absorbing (GNR-2) and relatively scattering (GNS-2) GNP-loaded hemispherical droplets, were simulated. Results of distributions of temperature increase and specific absorption rate (SAR, W m⁻³) for the laser energy are compared and discussed below.

Fig. 5 (a) and (b) show similarities, but also clear and important differences in the heating profiles of these cases at the end of the ms laser pulse. For instance, there is an area around the bottom corners of the droplet that is under warmed due to what we believe is the lensing of the light by the droplet in both cases. The total energy absorption in the GNS-loaded droplet was nearly identical to the GNR loaded droplet, 56.3% vs. 53.5%. However, the temperature profile is much more uniform in the GNS-loaded droplet than the GNR case. In the GNR case, the most absorbed laser energy is deposited into the central top half of the droplet, resulting in an extremely locally heated region. The GNR case has a very low γ_tot, which prevents the distribution of the laser energy to all parts of the droplet. Further, each droplet acts as a lens thereby refracting, reflecting, and focusing light on the focal point (“hot spot”) near the top of the droplet. While this occurs in both cases, it is less pronounced in the GNS case as photons are much more likely to be scattered from their incident trajectory. The larger μ_s,tot and γ_tot (Table 3) in the GNSs-loaded droplet serves to diffuse the inlet laser beam and produce a more uniform temperature profile in the bottom half of the droplet. Thus, there may exist an optimal γ_tot that could enable optimal uniform heating and largely eliminate locally overheating spots.

Fig. 5.

Predicted temperature profiles of the vertical central cross-sections in the laser-warmed 2 mm-diameter hemispherical droplets at the end of the 0.5 ms laser pulse irradiation from the top of the droplet. (a) The temperature profile in the droplet loaded with GNR-2 at the end of the pulse with μ_a,tot = 5 cm⁻¹, γ_tot 0.06. (b) The temperature profile in the droplet loaded with GNS-2 at the end of the pulse with μ_a,tot = 5 cm⁻¹, γ_tot = 2.2. (c) The temperature profile in the droplet at the end of the pulse assumed with an optimal γ_tot where μ_a,tot = 5 cm⁻¹, γ_tot = 5.5. (d) The temperature profile in the droplet at the end of the pulse with an overlarge γ_tot where μ_a,tot = 5 cm⁻¹, γ_tot = 30. (e) Normalized σ_SAR, as an indicator of the uniformity of laser warming, changes with the optical γ_tot of the droplet with the μ_a,tot set constantly at 5 cm⁻¹. The σ_SAR was normalized by the value at γ_tot = 0.01. (f) Normalized σ_SAR changes with the optical properties γ_tot and μ_a,tot · R of the hemispherical droplet. The σ_SAR was normalized by the value at γ_tot = 0.01. (g) The optimal γ_tot of the hemispherical droplet for each μ_a,tot · R to achieve the lowest normalized σ_SAR (i.e., the most uniform heating temperature profile).

Table 3.

A summary of input parameters in the two Monte Carlo models for the cuvette experimental data analysis and laser warming of a GNP-loaded droplet simulation.

Parameters		Cuvette experimental data analysis	Laser warming of droplets
nd	Refraction index of solutions	1.333 (water); 1.35553 (egg white)	1.3554, 55 (droplet)
na	Refraction index of air	1.00	1.00
ra	1/e2 radius of Gaussian beam (mm)	0.562 mm *	1 *
Io	Laser energy density (W m−2)	$P_{in}∕\pi r_a^2$ *	1.83×109 *
PW	Pulse width of laser beam (ms)	−	0.5*
Ep	Photon energy at 1064 nm (eV)	1.211	1.211
Nphotons	Flux of photons $(\frac{\#}{{\mathrm{m}}^2\cdot \mathrm{s}})$	I0/Ep	I0/Ep
μt,medium	Extinction coefficient of medium	$\frac{1}{L}\text{ln}\left(\frac{P_{out}}{P_{in}}\right)$, Eq. (S9) without GNPs *	−
μs,medium	Scattering coefficient of medium	0 (water); or characterized same as GNPs	−
μt,tot	Attenuation coefficient of GNP solutions	$\frac{1}{L}\text{ln}\left(\frac{P_{out}}{P_{in}}\right)$, Eq. (S9) with GNPs *	μa,tot + μs,tot
μa,tot	Absorption Coefficient of GNP solutions	N * Cabs + μa,medium, Eq. (1)	5 cm−1**
μs,tot	Scattering Coefficient of GNP solutions	N * Csca + μs,medium, Eq. (2)	0.3 cm−1 (GNR) **, 11 cm−1 (GNS) **, or other assume values
η0	Photothermal conversion efficiency of GNP	Varied to find experimental fit **	−
g	Scattering anisotropy factor	0 (GNS)56 **; 0.25 (GNR)57 **	0 (GNS)56 **; 0.25 (GNR)57 **

^*Measured values

^**Assumed values. The other unmarked values are either known constants or derived from the measured or assumed values. The choice of scattering anisotropy factors for different GNPs is explained in section S2.2 Part (1).

To explore this possibility for optimization, the specific absorption rate (SAR, W m⁻³) across the laser warmed droplet was calculated for different γ_tot and the standard deviation of SAR (σ_SAR) was compared as a metric of heating uniformity. During laser heating, the thermal diffusion length is $L_{thermal}\sim \sqrt{\alpha t}$, where α is the thermal diffusivity of the medium (2M PG: 1. 3E-7 m² s⁻¹) and t is the pulse width. In the case of 0.5 ms pulse laser heating, the L_thermal during warming is about 8.0 μm, which is much less than the scale of the droplet (2 mm in diameter). Thus, the distribution of SAR mainly determines the temperature distribution of the droplet during laser warming. A smaller σ_SAR corresponds to better uniformity of laser heating. Fig. 5 (e) shows the optimization of γ_tot of the droplet to achieve minimal σ_SAR during warming with the same μ_a,tot (5 cm⁻¹). It is shown that the uniformity increases with increasing γ_tot to an optimal condition (green dot), and then decreases with even larger γ_tot. The γ_tot for the GNR-2 (0.06) and GNS-2 (2.2) cases in Fig. 5(a-b) are all suboptimal and are shown as blue and red dots in Fig. 5(e). However, for an optimal case (γ_tot = 5.5) corresponding to the green dot in Fig. 5(e), the temperature profile of the droplet at the end of the laser pulse in Fig. 5(c) shows a much more uniform profile than those in any of the previous cases (Fig. 5(a) and (b)). To verify that an overlarge γ_tot can adversely impact the uniform warming, an extreme scattering case (γ_tot = 30) was modeled and shown in Fig. 5(d). In this temperature profile, the top is extremely overheated and the bottom is under-warmed, suggesting that the droplet-light interaction mainly occurs in the top part of the droplet. This is due to too high scattering (μ_s = 150 cm⁻¹) and extinction (μ_t = 180 cm⁻¹) coefficients, such that little light can transmit through the droplet.

In cryopreservation and rewarming of different systems (e.g. zebrafish embryo, pancreatic islets, etc.), different sized droplets loaded with various concentrations of GNP and CPA may be needed due to their varied and complex biological properties (e.g. varied toxicity tolerance, etc.). To achieve a general solution for optimal uniform warming in different sized hemispherical droplets with different concentration of GNPs, the dimensionless characteristic parameter, μ_a,tot · R is used for the optimization, where R is the radius of the droplet and μ_a,tot is related to GNP concentration by Equation (1) in Table 2. Details on justifying this dimensionless parameter are provided in Section S2.2 Part (3). Fig. 5(f) shows that for different μ_a,tot · R, the normalized σ_SAR changes similarly with increasing γ_tot. But Fig. 5(g) suggests that the optimal γ_tot is inversely related to the μ_a,tot · R for the best uniform temperature increase in the laser warmed hemispherical droplet. For instance, low μ_a,tot · R tends to make the droplet system prone to the lensing effect, like the GNR case in Fig. 5(a) where μ_a,tot · R=0.5. To reduce this a very high γ_tot is needed to enhance the scattering portion of the transmitted light and distribute absorbed laser energy over the droplet. In contrast, a very large μ_a,tot · R leads to a strong exponential decay in the absorbed laser energy like Fig. 5(d). In such a case, a large γ_tot would make the exponential decay even steeper or worse in terms of uniform rewarming. Thus, for a large μ_a,tot · R, γ_tot should be relatively small to achieve more uniform warming.

Therefore, optimized scattering and absorbing properties can help homogenize the temperature increase inside the droplet, which is critical for a high survival rate of the rewarmed biological system held in the droplet. This can likely be achieved by loading specially designed GNPs with tailored optical properties or a combination of nanoparticles with varied optical properties.

3. Conclusion

This study provides a framework for characterization and selection of GNPs for laser warming of mm-scale droplets loaded with biological systems such as cells, islets, and aquatic embryos. Specifically, the optical absorption and scattering properties were tested for GNRs and hollow and silica-core GNSs. It was found that GNRs convert light into heat more efficiently than both types of GNSs, though the GNSs generally have higher absolute absorption and scattering cross sections. While the GNRs are more efficient for localized heating, the GNSs are better at scattering and distributing light energy which can lead to an overestimation of photothermal conversion efficiency in GNS when the reabsorption of scattering is not accounted for in the characterization of photothermal conversion, although not in GNRs. During fast laser warming, 2M PG (CPA) solution has a limited effect on the extinction spectra of the nanoparticles, while a protein-rich medium (i.e. egg white) can lower the heat generation in GNR solutions by roughly 10%. During the simulated warming of mm-scale droplets, the GNSs produced a much more uniform heating profile than GNRs. To achieve optimal uniform rewarming, further optimization of light scattering and absorption properties for specific applications will be key to achieving uniform SAR and fewer overheated local regions. This may be possible by selecting a GNP or GNP combinations with the desired optical properties. The characterization framework of this study, using a simple cuvette system to obtain GNPs’ light absorbing and scattering properties with Monte Carlo modeling analysis, can be extended to photothermal conversion in cancer therapy, drug delivery, diagnostics, and other biomedical applications.

4. Methods

4.1. Photothermal conversion experiment analyzed with Monte Carlo modeling

GNPs in aqueous solutions:

The as-received GNPs were diluted in Milli-Q treated ultrapure water (18.0 mΩ cm) that was also used in all the other experiments. Their photothermal conversion properties (including reabsorption) were measured using a previously reported cuvette heating system³⁷, which is shown in Fig. 2(a). Briefly, 1 mL of GNP solution was pipetted into a polystyrene cuvette, whose temperature was recorded by 4 T-type, 40-gauge thermocouples placed away from the laser beam. After the first steady-state temperature was achieved with the stir bar turned on, the solution was then irradiated by a continuous wave (CW) laser (1064 nm Spectrum Stabilized Laser Module, Model #: I1064SR0300B, Innovative Photonic Solutions Inc.) until another steady state was reached. The temperature change of the solution and laser power loss were recorded. The inlet and outlet power of the laser beam going through the GNP solution were measured by a power meter.³⁷ The size of the beam was measured by the knife-edge method.⁵⁰ An example of the solution’s temperature change as a function of time is shown as the black line in Fig. S2. Further details of this method are reported in the previous work³⁷.

Details about how to obtain the photothermal conversion efficiencies of the GNPs (η_exp,GNP) and the bulk solution (η_exp,tot) from measurement are provided in section S2.1. In brief, η_exp,tot can be estimated by dividing the total heat generation of the GNPs’ bulk solution (Q_tot) obtained via temperature recording over the total power loss of the laser beam (P_loss) (Equation (S13)). η_exp,GNP was estimated by reducing the effects of light-water interactions, including both laser power loss and heat generation due to water.

However, both η_exp,GNP and η_exp,tot are over-estimated when reabsorption of scattered light occurs in the GNP solutions (Fig. 2(c)). To address this, we improved upon our previous work³⁷ by incorporating Monte Carlo modeling using ray tracing of the laser beam inside the GNPs’ bulk solution, thereby accounting for both absorption and the reabsorption of scattered light. The Monte Carlo modeling was taken from A. Welch et al.⁴¹ and written in Matlab. As shown in Fig. 2(b), we assumed the photothermal conversion efficiency of the single GNP, η₀, as an input. The measured extinction coefficients (details in Section 2.1) of water (μ_t,water) and GNP solutions (μ_t,tot) were also input into the model along with other assumed constants in Table 3 (column: Cuvette experimental data analysis). The boundary conditions followed Fresnel’s law between the liquid and air (Table 3). We neglected the small mismatch of the refractive index between the liquid and the non-absorbing thin cuvette’s wall (polystyrene: 1.516), which had little impact on the modeling results. Based on the above parameters and boundary conditions, the model was able to simulate the total laser energy lost (P_loss,MC) between the beam inlet and outlet and the total absorption of laser energy (Q_MC) by both direct absorption of incident light and reabsorption of scattered light in the solution for assumed η₀. Thus, the bulk solution’s photothermal conversion efficiency (η_MC) was computed by the ratio of Q_MC/P_loss,MC as shown in Fig. 2(b). Here it was necessary to vary η₀ until the difference between η_MC and η_exp,tot was less than 0.5%. At this point the assumed η₀ is reported as the predicted photothermal conversion efficiency of the GNP without scattering and reabsorption. Upon knowing the η₀, other predicted optical properties of extinction, absorption, and scattering cross sections of the single GNP were calculated according to their correlations to bulk solution properties, shown as Equations (14-16) in Table 2.

For a better understanding of characterizing the GNPs’ optical properties from laser heating their bulk solutions, a comparison of the methods from this study and literature^37-39 is provided in section S2.3.

GNR-2 in CPA and protein-rich solutions:

The same procedure as above in water was repeated in egg white solutions (protein-rich solution). GNR-2s were mixed with egg white to model a protein-rich medium. The egg was randomly chosen from a supermarket and the egg white was carefully extracted to avoid yolk contamination prior to addition. The GNR-2s were then added from stock solution into the pure egg white solution at a dilution ratio of 1:1000 and vortexed. Due to this much less volume of GNR-2s compared with the egg white medium in preparation of the solution, the egg white concentration in the medium was approximate 100%. Before measurement, the solution was kept in the refrigerator (4 °C) for 2 hours to remove air bubbles. Briefly, the optical absorption and scattering properties of the egg white medium were characterized separately and then with GNPs to extract the nanoparticle photothermal properties in this medium, both of which are similar to characterizing GNPs in aqueous solutions. The operating temperature of the solutions during measurement was kept less than 37 °C to prevent the denaturation of proteins. Due to too high scattering, the egg yolk was not fit for the characterization methods in this study where the test solution was loaded in the cuvette.

4.2. Measuring UV-vis-NIR extinction spectra

The as-received GNPs were diluted in water, 2M PG (Acros Organics, ≥ 99.5%), and pure egg white media. The extinction spectra of these media with and without GNPs were measured using a UV–vis–NIR spectrophotometer (Cary 7000 UV–vis–NIR spectrophotometer, Agilent Technologies). The extinction of GNPs (A_GNP) was obtained by reducing the background caused by pure medium’s extinction from the total solution’s (Equation S24). The GNP’s extinction spectra plot was normalized by dividing the one at the peak extinction. For more details the correlations between A_GNP, the extinction coefficient of GNP solutions (μ_t,tot), and the extinction cross section of individual GNP (C_ext) are discussed further in section S2.4.

4.3. Modeling laser warming of vitrified droplets

To assess the ability of GNR and GNS to perform laser warming, another Monte Carlo model was constructed. In brief, a simulation was carried on laser warming of a vitrified (77 K) hemispherical droplet containing GNPs on a holder called a cryotop. The droplet was assumed to have a diameter at 2 mm, which is large enough to encapsulate a zebrafish embryo (~0.8 mm in diameter) or other biological materials such as coral larvae and cells.^{23, 24} The Monte Carlo model generated a distribution of SAR (W m⁻³) in the droplet. These results for SAR were then used as a heat source profile input in the heat transfer module of COMSOL, along with appropriate thermal properties (Table S1) of the droplet, to calculate the temperature profile in the droplet during the laser pulse heating.

In the Monte Carlo modeling, the cryotop was assumed to be highly reflective (95%) to maximize laser absorption in the droplet. The other boundary conditions at the water-air interface followed Fresnel’s law. In this modeling, due to the singularities at the corners of the hemispherical droplets on the cryotop, the hop steps to trace photons were broken into smaller values; an overview of the code is shown in Fig. S3. The optical properties (μ_t,tot, μ_a,tot, and μ_s,tot) of the GNP-loaded droplets are necessary inputs in the Monte Carlo modeling. Since the GNPs’ C_abs, C_sca and C_ext have been characterized, those optical properties of the GNP-loaded droplets can be calculated by Equations (1-3) in Table 2 by knowing the number concentration of GNPs and the medium’s optical properties. But to properly compare the GNR-loaded and GNS-loaded cases in this study, the μ_a,tot was assumed and kept the same as 5 cm⁻¹ for all the droplets. The water medium’s absorption coefficient (0.147 cm⁻¹) was much less than that assumed μ_a,tot and thus neglected in the modeling. Since water has no scattering, γ_tot was approximately equal to γ of the single GNP. According to Equations (4) and (6) in Table 2, the μ_s,tot and μ_t,tot for the GNR-2-loaded and GNS-2-loaded droplets can be calculated respectively. The optical properties of the GNP droplets were assumed to remain consistent during laser warming from glassy state to liquid. Other input parameters in this model are also found in Table 3 (column: Laser warming of droplets). Details about optimizing the optical properties of the droplets for more uniform heating by Monte Carlo modeling is provided in S2.2 Part (3). An important note is that our modeling did not include simulation with regard to the formation of bubbles and their influence on the optical and thermal properties of the medium during laser heating. While bubble formation is an interesting and impactful phenomenon in increasing the light scattering and/or modifying the heat transfer rate⁵¹ we regarded any manifest bubble formation as an indication of boiling and therefore a failure with regards to successful rewarming. Thus, our modeling prediction for over-heated regions (i.e. > 100 °C) during failures where boiling might occur should be regarded as qualitative, not quantitative in their prediction of absolute temperature values.

In the COMSOL simulation, we assumed that the convection heat transfer coefficient around the droplet surfaces was 50 W · m⁻²K⁻¹ with ambient room temperature at 20 °C. No phase change (i.e. boiling) or volume expansion was included in the COMSOL model as we aimed to understand the trend of temperature distribution for the different cases rather than absolute accuracy.

It is noted that optical (Monte Carlo) and thermal simulations have been used in the past to predict the photothermal effects of laser-excited GNPs that were loaded in tumors^{40, 52}. However, due to substantial differences in temporal, spatial, and optical conditions, the results for the droplet rewarming reported here are expected to be quite different to those for tumors under photothermal therapy. Nevertheless, these studies serve to highlight the importance of the careful study of photothermal conversion in biomedical applications. The validation of the Monte Carlo model used in this study is provided in S2.2 Part(4).