MEDT study of the 1,3-DC reaction of diazomethane with Psilostachyin and investigation about the interactions of some pyrazoline derivatives with protease (M^pro) of nCoV-2

Abstract

The molecular electronic density theory (MEDT) was invested to elucidate the chemo-, regio- and stereo-selectivity of the 1,3-dipolar cycloaddition between Diazomethane (DZM) and Psilostachyin (PSH). The DFT method at B3LYP/6-31 + G (d,p) level of theory was used. Reactivity indices, transition structures theory, IGM and ELF analysis were employed to reveal the mechanism of the reaction. The addition of DZM to PSH takes place through a one-step mechanism and an asynchronous transition states. Eight possible addition channels of reaction were investigated (addition of C (sp2) to Diazomethane at C4, C5, C6 or C7). The addition of C (sp2) at C5 leading to P1 product is the preferred channel. The addition of ether does not affect the chemo-, regio- and stereo-selectivity of the reaction. Analysis of transfer of charges along the IRC path associated with the P1 product shows a polar character for the studied reaction. We have also used the noncovalent interaction (NCI) which is very helpful to reveal the most favored addition channel of the reaction, by analyzing the weak interactions in different TSs. Finally, we investigate about the potential of inhibition of some pyrazoline compounds against COVID-19-M^pro by performing a molecular docking calculations.

Graphical abstract

Highlights

• •The 1,3-DC reaction between Diazomethane and Psilostachyin has been investigated by MEDT.
• •The asynchronicity of TSs has been revealed by IGM and Wiberg indices.
• •The electronic description of mechanism of reaction has been performed by ELF analysis.
• •The NCI analysis allow a deep description of weak interactions.
• •The pyrazolines products possess a potential effect against COVID-19.

1. Introduction

1,3-Dipolar cycloaddition reactions play a key role in organic chemistry [1]. They are routes for the synthesis of a considerable diversity of functionalized five-membered heterocyclic systems, which present a perfect compounds of “non heterocyclic” derivatives [2]. The effect of the 1,3-dipolar cycloaddition reactions in domain of heterocyclic synthesis is comparable to that of Diels–Alder reactions on synthesis of carbocyclic products [3,4]. In fact, the abundance of various classes of dipoles and dipolarophiles offer a lot of perspectives. Indeed, the dipolar cycloaddition reactions serve as main key in the total synthesis of natural products or analogues [5]. 1,3-Dipolar cycloaddition is a main synthesis strategy to the regio- and stereoselective of five membered heterocycles and their ring opened acyclic derivatives, more than that, it serves as a chemical test [6]. Indeed, the 1,3-dipolar cycloaddition of Diazomethane (DZM) leading to pyrazolines, was used to test the presence of an exocyclic methylene α, β-unsaturated-γ-lactone functionality [7]. Large experimental and theoretical studies focused at understanding the reaction mechanism and the origin of the observed chemo-, regio- and stereo-selectivity observed in many reactions. The earlier work of Huisgen and coworkers revealed that the mechanism of 1,3-dipolar cycloadditions which lead to 5-membered rings are managed by the stereoselectivity of dipolarophiles, the nature of solvent and substituents, the activation parameters, and by orientation phenomena [[8], [9], [10]]. Whereas Houk et al. [11,12] explain that the frontier orbital energies and coefficients allow a specific qualitative treatment of reactivity of individual 1,3 dipoles. Recently, molecular electronic density theory (MEDT) accompagnied with the IGM and ELF analysis have been invested with a great success to reveal the mechanism of many reactions [[13], [14], [15], [16], [17]]. In the present work, we have used the MEDT, IGM and ELF tools to study the 1,3-dipolar cycloaddition reaction between Diazomethane (DZM) and Psilostachyin (PSH). This reaction has been realized by the Adriana Ortiz-León group [7] in ether solution, leading to mexicanin I acetate pyrazoline product (Scheme 1 ). However, to date, the stereochemistry of this reaction has not been explained nor a mechanism associated with the previous reaction had been elaborated. The DZM, known as a 1,3-dipole of the propargyl/allenyl anion type presents an electron donating capacity of the C-atom with double Carbone-Carbon bonds in dipolarophile, involving its highest occupied molecular orbital (HOMO).

Scheme 1.

Synthesis of mexicanin I acetate pyrazoline by the reaction of Diazomethane with the PSH reagent.

Theoretically, there are eight possibilities for the C-atom of DZM to add up at the double Carbone-Carbon bonds of PSH reagent (addition of C (sp2) of DZM at C4, C5, C6 or C7). So, this interaction leads a priori to eight products: P1, P2, P3, P4, P5, P6, P7 and P8 (Scheme 2 ). This reaction evolves through the pathways specified, where eight transition states (TS1, TS2, TS3, TS4, TS5, TS6, TS7 and TS8) are involved. So, our goal in this work is to investigate the different possibilities of addition between the two reagents, to detect the different transition structures, to predict the more favored channel of addition, in order to reveal the mechanism of reaction with a good electronic density description.

Scheme 2.

The different possibilities of addition of Diazomethane to carbon-carbon double bonds of PSH reagent leading to eight possible products.

The obtained products P1, P2, P3, P4, P5, P6, P7 and P8 belong to a large family of pyrazoline derivatives (pseudoguaianolide pyrazolines). These compounds are an important biological agents and many studies in literature have been focused on this class, due to their relevant biological properties, that include antiviral, antibacterial, antitumor, anti-tubercular, antifungal, antiparasitic, anti-inflammatory, anti-diabetic, anaesthetic, analgesic and insecticidal agents [[18], [19], [20], [21], [22], [23], [24], [25], [26], [27]]. Considering the large anti-viral properties of pyrazoline products [[28], [29], [30], [31]], they deserve to be tested against COVID-19, seen till this date, there is no vaccine and no antiviral for the treatment of this virus [32,33]. The appearance of new structural data of key proteins associated with SARSCoV-2 and the host, such as the main protease (M^pro) [34], the RNA-dependent RNA polymerase (RdRp) [35], human angiotensin-converting enzyme 2 (hACE2) [36] and spike glycoprotein (S) [37], make the operation of search of the drug against COVID-19 from the knowledge of the three-dimensional structure of the protein targets and to identify small molecules that exhibit the desired chemical characteristics wanted to bind to the proteins targeted by molecular docking. This should be promising [[38], [39], [40]]. In this context, The last part of this work aims to investigated about the potential of inhibition of some derivatives of the family of pyrazoline products against COVID-19, by performing a molecular docking calculations. In this paper, we have focused on main protease protein (M ^pro) who intervenes at viral replication and transcription, as key to inhibit this virus [[41], [42], [43], [44], [45], [46]]. Indeed, the M ^pro possesses an important role in cutting down polyproteins into functional pieces. Thus, we have targeted this protein in the docking calculations in order to check the ability of our pyrazoline products to inhibit the activity of M ^pro which could block the replication of the SARS-COV virus.

2. Theoretical tools

2.1. Quantum chemical details

The Density functional theory (DFT) has become a useful tool with a notable successes in most branches of chemistry [[47], [48], [49]]. Indeed, many theoretical works on chemical reactivity have adopted this theory for their calculations to providing theoretical insights for chemo-, regio- and stereo-selectivity. In this work, we have performed our DFT calculations by using the GAUSSIAN 09 [50] set of programs along with the graphical interface GaussView-5.0. Geometry optimization of different stationary points were performed at DFT/B3LYP/6-31 + G (d,p) level and visualized by CYLview program [51]. Calculations of frequencies have been performed at 298.15 K and 1.0 atm, in order to verify that the transition structures (TSs) possess one imaginary frequency and that the minima have no imaginary frequency [52]. The energy profiles have been developed by the IRC calculation. The electronic structures of stationary points and the Wiberg bond indices [53] were analyzed through the natural bond orbital (NBO) method [54]. The solvent effects of ether were considered using a self-consistent reaction field (SCRF) based on the polarizable continuum model (PCM) of Thomasi [55]. The local and global reactivity have been analyzed through the Parr function using population analysis (NPA) [56]. The reactivity of molecular systems has been unveiled through several concepts [13,57,58] the electronic chemical potential μ, the chemical hardness η, the global electrophilicity ω and global nucleophilicity N. The previous global indices in the framework of the conceptual Density Functional Theory, are calculated by the next expressions, μ = (ε_HOMO+ε_LUMO)/2, η = ε_LUMO - ε_HOMO and ω = μ²/2 η. The global nucleophilicity N, is calculated referring to tetracyanoethylene, N = E _{HOMO (nucleophile)} – E _{HOMO (TCE).} The local indices ω_k, N_k at atomic site K are obtained using Parr functions, respectively P⁺(r) and P⁻(r), as follows ω_k = ωP⁺(r) and N_k = NP⁻(r). P⁺(r) = ρ_s ^ra(r) and P⁻(r) = ρ_s ^rc(r). ρ_s ^rc(r) and ρ_s ^ra(r) are respectively the atomic spin density (ASD) of the radical cation and anion. According to Hohenberg-Kohn [59], the total molecular information is in the electron density (ED) and the models based on the ED are more physically significant for chemical bonding analysis. Indeed, the independent gradient model approach (IGM) [60], is more efficient to evaluate the evolution of the formation of new bonds. The IGM is more qualified for description of the covalent bonding pattern and revealing the weak interactions where other tools were obviously failing. It offers direct 3-D depiction in the form of closed domains associated with the spatial localization of the interactions. This is done through the mono determinantal wave functions of the ground state (GS) and that of the transition structures calculated at B3LYP/6-31 + G (d,p) level, using the Multiwfn software and visualized by the VMD program [61]. The physical descriptor associated with IGM [60] is symbolized by δg, δg = |∇ρ^IGM|-|∇ρ|. ρ represents the electron density (it’s a local function), and is an experimentally accessible scalarfield, |∇ρ^IGM| represents the virtual upper limit of the electron density gradient and |∇ρ| represents a non-interacting system electron density gradient. δg is a measure of the ED gradient collapse caused by electron sharing between contra gradient ED sources present in the chemical system. The ELF calculation [56,62,63] has been adopted, in order to realize a good description of the electronic structures of our molecular systems and reveal the mechanism of the favored addition along the IRC path. The ELF analysis had a great success in literature. It’s defined as follow, ELF = 1/(1+[D(r)/D₀(r)]²) with $\text{D}(\text{r})=\frac{1}{2}\sum {\eta }_i|\nabla {\varphi }_i(r){|}^2-\frac{1}{8}\frac{|\nabla \rho (r){|}^2}{\rho (r)}$ and ${\text{D}}_{\text{0}}(\text{r})=\frac{3}{10}{(3{\pi }^2)}^{\frac{2}{3}}\rho {(r)}^{\frac{5}{3}}$. The D(r) reveals the excess kinetic energy density caused by Pauli repulsion. The D₀(r) can be interpreted as Thomas-Fermi kinetic energy density, which is the exact kinetic energy density of non-interacting, uniform electron gas. Hence D₀(r) is introduced as a reference. A large ELF value means that electrons are greatly localized, indicating that there is a covalent bond, a lone pair or inner shells of the atom involved. Finally, we have used the noncovalent interaction (NCI) method [64], which is also known as reduced density gradient (RDG) method. It will be very helpful to reveal the most favored addition channel, by analyzing the weak interactions in different TSs.

The expression relative to RDG is $\text{RDG}(\text{r})=\frac{1}{{2(3{\pi }^2)}^{\frac{1}{3}}}\frac{|\nabla \rho (r)|}{\rho {(r)}^{\frac{4}{3}}}$, it is dimensionless. ρ(r) (the electron density) and ∇ρ(r) (non-interacting system electron density gradient). The region where the electron density is small, reveals the presence of weak interaction region [65].

2.2. Molecular docking details

Concerning the docking part, the biological activity of our compounds has been evaluated by using Maestro software (Schrödinger, LLC, New York, NY, 2018) [66], Against Main protease (M^pro) of SARS-CoV2 (DOI: https://doi.org/10.2210/pdb6LU7/pdb) [66] which is a potential target of COVID-19 disease. Our compounds were initially docked to the binding site Main protease receptor using Glide SP (Schrödinger Suite 2018) [66] with standard settings. The procedure was composed of the preparation of the ligand and receptor, grid generation, and docking. The binding pocket of the proteins was predicted as to be the nearest space with distance less than 3 Å from ligand crystallized in the Main protease (N3). Concerning the preparation of the ligand in the Schrodinger software, we have used the LigPrep [66] to optimize the geometry of ligand and offer its three dimensional structure with correct chiralities. The LigPrep can also produce a number of structures from each input structure with various ionization states, tautomers, stereochemistry, and ring conformations.

3. Results and discussion of reactivity study

The presentation of the results concerning the reactivity study will be structured as follows. We start byan analysis of the conceptual DFT (CDFT) reactivity indices [67] and a topological analysis of ELF. Secondly, we present a mechanistic study for the eight competitive reaction paths associated with the 1,3-dipolar cycloaddition between DZM and PSH (Scheme 2). In the next we will be focused on analysis of the asynchronicity of the formation of the new sigma bonds using Wiberg bond order and IGM analysis [13]. Then, we show the ELF topological analysis along the IRC path associated with the favored product. This allows an accurate description for the mechanism of our reaction. Finally, we mention an analysis of non conventional interactions (NCI) in the different TSs associated with the addition of DZM at the C4=C5 double bond area, which will be very helpful to reveal the most favored path for addition by analyzing the weak interactions.

3.1. CDFT reactivity indices

To investigate the local atomic properties of reagents we will start by CDFT reactivity indices. Thus, the global reactivity indices defined via the CDFT are a useful theoretical tool to explain the reactivity in cycloaddition reactions [67,68]. In Table 1 are displayed the global properties of the different reagents, the values of the electronic chemical potential, μ, the chemical hardness, η, electrophilicity, ω, and nucleophilicity, N, for the different reagents.

Table 1.

HOMO, LUMO energies (eV), electronic chemical potential (μ,eV), chemical hardness (η,eV), global electrophilicity (ω,eV) and global nucleophilicity (N,eV) at B3LYP/6-31 + G (d,p).

	HOMO	LUMO	μ	Η	ω	N
DZM	−6.34	−1.69	−4.015	4.65	1.73	3.07
PSH	−7.14	−2.13	−4.635	5.01	2.14	2.27

E_HOMO (TCE) = −9.41 eV at B3LYP/6-31 + G(d,p).

As presented in Table 1, the electronic chemical potential of DZM (−4.015eV) is higher than that of dipolarophile PSH (−4.635eV), consequently, the transfer of charge will be more favored from dipole to dipolarophile (NED: Normal Electronic Demand). The values of η for the two reagents confirm the previous results of μ, indeed the PSH (η = 5.01 eV) is more hard to give electrons than DZM (η = 4.65 eV). The electrophilicity ω scale, permits to classifying the organic compounds as strong electrophiles if ω > 1.5 eV, moderate electrophiles with 0.8 < ω < 1.5 eV and marginal electrophiles if ω < 0.8 eV [67]. According to Domingo, the scale of nucleophilicity N index is as follows, N > 3ev strong nucleophile, 2 eV < N < 3eV moderate nucleophile and N < 2 eV marginal nucleophile [67]. Therefore, the values of (ω; Ν) related to the dipolarophile: PSH (2.14;2.27) and dipole DZM (1.73;3.07) indicate that the dipolarophile will act as a strong electrophile and for DZM will act as powerful nucleophile, in agreement with other previous parameters. When a nucleophile approaches an electrophile along a polar procedure, a specific electron density is moved from the nucleophile to the electrophilic species. As a result, the nucleophilic reagent loses a certain electronic density, while the electrophilic reagent gains this electronic density. These changes require a reorganization of the electronic density in two frames. In this case, the electrophilic and nucleophilic Parr functions have proved to be the most precise and insightful tools for studying the redistribution of electron density along polar processes, and are widely used to analyze localities in polar processes reactivity. The electrophilic Parr function of PSH and the nucleophilic Parr function of DZM are represented in Fig. 1 .

Fig. 1.

3D representations of the Mulliken atomic spin densities of the anionic DZM and of the radical cation PSH, as well as, the electrophilic Parr functions of PSH and of the nucleophilic Parr function of DZM.

Analysis of nucleophile Parr function of DZM shows that C1 is the most active center (0.71) and this carbon is the most nucleophilic center of DZM. The presence of the ethanoate group between the ketone and ester in the PSH molecule making the value of the Parr electrophilic functions of carbon C6 (0.45) greater than the center C5 (0.31); the most favorable regioisomeric channel will be linked with the two-center interaction between the most nucleophilic center in the DZM framework, the C1 carbon, and the most electrophilic center of electrophilic PSH C6 carbon, in disagreement with the experimental results and energetic analysis of the different competitive reaction paths. The failure of the Parr indices to predict the more favored zone of addition is explained by the fact that these indices are obtained from separated reagents without any consideration of energetic profile (TSs and products), and the interaction between the two reagents (steric effects and weak interactions). For these reasons we investigate in the next, the mechanistic factors beside the steric effects and the weak interactions associated with our reaction (NCI analysis).

3.2. Topological analysis of ELF and NPA of reagents

For more details and deep investigation about the local atomic properties of reagents we have realized a topological analysis of ELF and NPA of reagents. Thus, the quantum-chemical evaluation of ELF is an attractive procedure, that provides a simple link between the chemical structures and the distribution of electron density. To describe the simplest electronic structure of reagents, and determine their reactivity in 1,3-dipolar cycloaddition reactions, a topological evaluation of the ELF was first carried out. The ELF basin attractor positions, ELF localization domains as well as the populations of the valence basin, together with the Lewis type structures proposed and the natural atomic charges are illustrated in Fig. 2 .

Fig. 2.

B3LYP/6-31 + G (d,p) ELF basin attractor positions, as well as the valence basin populations together with the Lewis type structures of Diazomethane (DZM) and Psilostachyin (PSH). ELF valence basin populations are given in average number of electrons.

The topological analysis of the ELF of diazomethane DZM demonstrate the presence of two monosynaptic basins V(C1) and V′ (C1) integrating a total population of 1.06e, two monosynaptic basins V(N3) and V′ (N3) integrating a total population of 3.86e, a disynaptic basin V (C1,N2) integrating 3.06e, and two disynaptic basins V (N2,N3) and V′ (N2,N3) integrating a total population of 3.60e. These ELF valence basin populations make it possible to link the monosynaptic basins V(C1) and V′ (C1) to a sp2 pseudoradical carbon, the monosynaptic basins V(N3) and V′ (N3) to a non-bonding N3 electron density, the disynaptic basin V(C1,N2) to an under populated C1–N2 double bond and the two V(N2,N3) and V′ (N2,N3) disynaptic basin to an N2–N3 double bond (see the proposed Lewis-like structure of DZM in Fig. 2). Consequently, the topological analysis of the ELF of diazomethane DZM indicates that this TAC has an allenic pseudoradical electronic structure. The topological analysis of the lactone framework of Psilostachyin (PSH) shows that there are two disynaptic basins V(C4, C5) and V′ (C4, C5) with a total population of 3.49 e, a V (C4, C8) diynaptic basin integrating 2.30 e, a disynaptic basin V(C8, O9) integrating 2.42 e and two monosynaptic basins V(O9) and V′ (O9) integrating total population 5.29e. On the other hand, the ELF topological evaluation of the enone framework of the Psilostachyin (PSH) shows that there are two synaptic basins V(C6, C7) and V′ (C6, C7) integrated 3.36e, a disynaptic basin V(C7,C10) integrating a total population of 2.26 e, and a V(C10,O11) disynaptic basin integrating 2.34e. Finally, there are two monosynaptic basins V(O11) and V’ (O11) integrating a total population of 5.28e (Fig. 2). After realizing an investigation about the local atomic properties of reagents by CDFT and ELF analysis, we have investigated about the kinetic and thermodynamic factors which influence our reaction. Thus we have performed a mechanistic study of our reaction.

3.3. Mechanistic study and geometries of TSs

Analysis of the mechanistic results in gas-phase indicates that the reaction between DZM and PSH occur along asynchronous concerted processes, therefore the different products (P1, P2, P3, P4, P5, P6, P7 and P8) and their corresponding TSs (TS1, TS2, TS3, TS4, TS5, TS6, TS7 and TS8) were obtained and verified. The total and relative energies are presented in table S1. The geometries of the different TSs are depicted in figure S1. The structure of the transition states are characterized by a vibrational frequency analysis. Indeed each transition state possess a single imaginary frequency.

3.3.1. Mechanistic study

According to the relative energies values in gas-phase summarized in Table S1, Scheme 3 a and Scheme 3 b, the activation barriers associated with the different possible products P1; P2; P3; P4; P5; P6; P7 and P8 are equals to 13,29; 13,77; 19,09; 24,18; 18,64; 18,61; 18,90 and 17.92 (Kcal/mol) respectively. Consequently, the P1 product has the lowest value of the activation barrier. Kenetically, the P1 product is slightly favored than P2 product, but much more favored than the rest of products, in agreement with the experimental outcomes [7]. Thermodynamically, the most stable product is P2. The difference of stability between P2 (−27,12 kcal/mol) and P1 (-23.29 kcal/mol) is equal to 3.93 kcal/mol. Hence, the studied reaction is controlled by the kinetic factors. To test the solvent effect in reaction, we have performed a total optimization of all stationary points in ether at the B3LYP/6–31 + G (d,p) level by using the self-consistent reaction field (SCRF) model based on the polarizable continuum model (PCM) of Tomasi [55]. All the results of energies are collected in table S1. The addition of ether causes an increase of activation barrier energy for the different products by 0.48–2.30 kcal/mol. The difference between the activation barrier energies of TS1 (13.77 kcal/mol) and TS2 (15.39 kcal/mol) in ether, increase to 1.62 kcal/mol, so the addition of ether is helpful for the formation of P1 product. The stability of the products in ether, decreases slightly by 0.124–1.67 kcal/mol (Scheme 3a, Scheme 3b). In summary, we can conclude that the addition of ether has a weak influence on the kinetic and thermodynamic factors, without any influence on chemo-, regio- and stereo-selectivity of reaction.

Scheme 3a.

The stereo- and regio-isomeric reaction paths associated with the addition of Diazomethane to carbon-carbon double bonds (C4=C5) of PSH. Reagent relative energies at B3LYP/6-31 + G (d,p) level, in gaz phase and in ether (in parentheses), are given in Kcal/mol relative to the separated reagents.

Scheme 3b.

The stereo- and regioisomeric reaction paths associated with the addition of Diazomethane to carbon-carbon double bonds (C6=C7) of PSH reagent. Relative energies at B3LYP/6-31 + G (d,p), in gaz phase and in ether (in parentheses), are given in Kcal/mol relative to the separated reagents.

The thermodynamic factors associated with the reaction of DZM with PSH in ether had been studied at B3LYP/6-31 + G (d,p) level by calculating the thermal enthalpy (H) and the thermal free energy (G). The different results of G and H have been mapped at Table S2. The enthalpy profiles of the reaction paths associated with the 1,3-dipolar cycloaddition of Diazomethane to the PSH reagent, in ether at B3LYP/6-31 + G (d,p) (Fig. 3 ), show that the P1 product need a lowest energy than other products. Indeed it need only 14.96 kcal/mol as energy for activation and release a low energy of −18.98 kcal/mol. Generally, all possibilities of reaction leading to different products P1; P2; P3; P4; P5; P6; P7 and P8 release energy in favor of the exterior, which shows that the 1,3-dipolar cycloaddition of Diazomethane to PSH reagentis exothermic. The energy released for different products varies from 16.99 kcal/mol to 22.02 kcal/mol.

Fig. 3.

Enthalpy profiles, in Kcal/mol, for the examined reaction paths associated with the 1,3-dipolar cycloaddition of Diazomethane to PSH reagent, in ether at B3LYP/6-31 + G (d,p) level.

3.3.2. Geometry of TSs, transition vectors and frequency analysis

• a.Geometry analysis of TSs

The optimized geometries of the TSs corresponding to the eights channels of reaction (Scheme 2) are reported in figure S1. The length of the new sigma bonds in evolution C1–C5 and N3–C4 at TS1 (lowest value of activation barrier) are 2.1223 Å and 2.5766 Å respectively. The degree of synchronicity (Δd, in Å) can be measured as the difference between the lengths of the two new sigma bonds in evolution. The value of Δd between the C1–C5 and N3–C4 bonds in evolution of TS1 is equal to 0.4543 Å, indicating that the process of formation of the new sigma bonds in evolution occurs asynchronously. For TS2, the values of length of the new bonds in evolution are d (C1–C5) = 2.24399 Å and d (N3–C4) = 2.25172 Å, hence the formation of the two bonds is more or less synchronous. For more details about the degree of synchronicity Δd for the rest of TSs, see Table S3. To confirm the previous results we use, in the next, the Wiberg bond indices and IGM analysis.

• b.Transition vectors (TVs) and frequency analysis

The results of TVs allow us to collect useful information about the chemical process linked to the different transition structures detected in the studied reactions. The imaginary frequencies, the main TVs components and their corresponding geometric parameters for TSs are presented in Table 2 .

Table 2.

Imaginary frequency (cm⁻¹), Hessian unique eigenvalue (a.u), main components of the transition vector (a.u) and corresponding geometric parameters (lengths in Angstrom and angles in °) for the different TSs.

The dominant TVs components are associated with the evolution of the formation of new sigma bonds N3–C4; C4 –C5 for TS1 and N3–C4; C1–C5 for TS2. N3–C5; C1–C4 for TS3 and TS4. N3–C6; C1–C7 for TS5 and TS6. N3–C7; C1–C6 for TS7 and TS8. During the interaction between the two reagents, DZM undergo a distortion, hence, the angle (C1,N2,N3) also participates in the transition vectors for different TSs associated with the hybridization change at nitrogen center N2 of DZM from sp to sp2 and C1 of DZM from sp2 to sp3. The imaginary frequency values of different TSs are between −432.72 cm⁻¹ and -470.16 cm⁻¹, inferior than those for the Diels Alder cycloadditions (500 cm⁻¹), indicating that these processes are associated with the motions of the heavy atoms and are also related to the earlier transition states.

3.4. Wiberg bond indices and IGM analysis

Beside the wiberg bond indices which have been computed by using the NBO population analysis, the novel IGM descriptor δg = |∇ρ^IGM|-|∇ρ|, can be also invested as a real and an effective physical index, based on the electron density to obtain a deep analysis of the evolution of the cycloadducts process. The IGM analysis can be obtained by evaluating the electron density using the corresponding mono-determinantal wave functions of the ground state, corresponding to the TSs. The δg descriptor measures the interaction between atoms in the system, so we have focused on the atoms that will participate in the formation of the new bonds. The different results of Wiberg bond indices and IGM descriptor are reported in table S4 and Fig. 4a, Fig. 4b . The values of the percentage of the new sigma bonds (N3–C4; C1 –C5) for TS1 and TS2 are (24.05%; 47.82%) and (13.08%; 41.47%) respectively, so the bond C1–C5 in evolution is more advanced than N3–C4, consequently the formation of the two bonds is asynchronous. For the rest of TSs the formation of the new sigma bonds appears also asynchronous. The IGM analysis (δg) of the new sigma bonds in evolution (N3–C4; C1–C5) for TS1 and TS2 gives the following values (0.19; 0.40) and (0.19; 0.35) respectively, consequently the bond C1–C5 is more advanced than N3–C4 in TS1 and TS2. For the rest of TSs, the IGM values confirm the asynchronicity of the formation of the new sigma bonds, in agreement with the Wiberg bond analysis.

Fig. 4a.

Distances (Å) (bold), IGM indices (italic), Wiberg bond indices (between two brackets) for TS1, TS2, TS3 and TS4.

Fig. 4b.

Distances (Å) (bold), IGM indices (italic), Wiberg bond indices (between two brackets) for TS5, TS6, TS7 and TS8.

After detecting the different TSs and analyzing their geometries and frequencies, we have then elaborate the mechanism of our reaction. Hence the necessity to an ELF topological analysis along the IRC path associated with the favored product (P1).

3.5. ELF topological analysis along the IRC path associated with the P1 product

3.5.1. ELF topological analysis

The ELF topological analysis of sorted structures along the IRC profile are listed in table S5. The most significant points of the IRC path were throughout analyzed and characterized, which lead to obtaining an important information concerning the mechanism of the reaction. The absence of an intermediate complex along IRC (Scheme S1), indicates that the formation of the new sigma bonds N3–C4 and C1–C5 takes place through a one-step molecular mechanism. Topological analysis of the ELF highlight that the formation of the N3–C4 and C1–C5 bonds is done in two stages and one-step. The ELF analysis reveals an interesting valence basins from S0 to S18 (see supplementary).

The topological analysis of the ELF of the first structure of the IRC (S0), displays similar bonding pattern to those of the separated reagents. Indeed, at S0 there are two important disynaptic basins V(C,C) = 8 and V(C,C) = 9 with a sum of electronic population equal to 3.45e, indicating that C4–C5 is a double bond, in front of this, we have two other disynaptic basins V(N,N) = 3 and V(N–N) = 4 integrating a total of population of 3.59e, which indicates a double bond between the two N atoms of DZM fragment. Furthermore, we have a disynaptic basin V(N,C) = 5 between N atom and C atom of DZM integrating 3.09e which implied a pseudo double bond between the two previous atoms. Concerning the most important monosynaptic basins we have V(N) = 1; V(N) = 2; V(C) = 6 and V(C) = 7 which integrate 2.04e; 1.83e; 0.50e; 0.47e respectively. The values of V(N) = 1; V(N) = 2 indicate the existence of a lone pair and negative charge (−1.83e) on N atom. The change in basins is more remarkable at the structure S3, where we observe the disappearance of V(C) = 6 and V(C) = 7 basins and appearance of a novel basin V(C) = e with 0.72e, which increases to 1.49e at S6. In the same time the two disynaptic basins V(C–C) = 8 and V(C–C) = 9 disappear leading to a novel disynaptic basin V(C–C) = 13 at S4 including 3.36e. At S11 we notice the formation of the novel C–C sigma bond (1.75e) which increases its electronic population to 1.85e at S18. Consequently the C–C bond is more advanced than the N–C sigma bond. The next novel sigma bond (N–C) begin to be formed at S15 by the appearance of monosynaptic basin V(C) = 17 integrating 0.75e, which increases to 0.87e at S16, leading then to appearance of monosynaptic basin V(C) = 14 and a disynaptic basin V(C–C) = 18 at S17 integrating 1.58e as electronic population which increases to 1.71e at S18 leading to the formation of the second new sigma bond N3–C4.

3.5.2. Charge transfer

Analysis of charge transfer along the IRC path associated with the P1 product, indicates that it takes place from DMZ fragment to PSH fragment in conformity with the results of CDFT reactivity indices, so we confirm the NED character of the reaction. The values of global electronic density (table S5) transferred from DZM to PSH varied between 0.044e and 0.205e, which indicates the polar process of our reaction.

3.6. Non-covalent interactions analysis (NCI)

As we have already reported the local indices have failed to predict the more favored zone of addition. This could been explained by the fact that these indices are obtained from separated reagents without any consideration of steric effects and weak interactions. For these reasons we have investigated about the steric effects and the weak interactions associated with our reaction by realizing a non covalent interactions analysis. Thus, the NCI index developed by Yang’s group using quantum-mechanical electron density [69] is a visualization index, which allow an identification of non-covalent interactions (favorable and unfavorable interactions). It provides a rich representation of the weak interactions where other methods fail to describe them. The visualization for different intramolecular and intermolecular interactions (attractive and repulsive forces) is performed by coloration (Fig. 5 ). The more blue implies the stronger attractive interaction, the interaction region marked by green can be identified as VdW interactions region and the regions marked by red, implied a zone of strong repulsion effect [58].

Fig. 5.

Color-coded bar associated with the NCI visualization. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

In our case, we have focused on the impact of the weak interactions on the regio- and stereo-selectivity at C4=C5 double bond area, so we have performed the NCI calculations with NCI plot [70] for the different TSs,TS1; TS2;TS3 and TS4 (Fig. 6 ). The visualization has been realized by the VMD program [61]. Herein, the 2D scatter graph and 3D RDG isosurface for the different TSs are represented in Figs. 6 and 7 . The RDG and sign (λ₂)ρ are a pair of very important functions for revealing weak interaction regions, they are collectively employed in NCI method. The scatter plots of RDG versus the second largest eigenvalue of the Hessian matrix of electron density functions are obtained by using Multiwfn 3.6 program [71], based on the obtained wave functions calculated at the B3LYP/6-31 + G (d,p) level and plotted using gnuplot program [72]. Fig. 6 presented the different scatter graphs associated with the eight TSs. These scatter graphs, inform us about the type of dominant interactions by calculation of RDG in function with the sign (λ₂)ρ. According to the obtained Scatter graphs, it exists tree type of interactions: strong attractions (blue area), Van Der Waals interactions (VdW) (green area) and strong repulsion (red area). The scatter graph of TS1 presents a large blue area (−0.05 a.u to −0.02 a.u), a narrow green area (−0.02 a.u to 0.01 a.u) and a red area (0.01 a.u to 0.05 a.u). Generally, for the rest of scatter graphs associated with other TSs we remark that the green area expands slightly at the expense of blue area, furthermore the red area gets slightly bigger. The analysis of color-mapped RDG isosurfaces (Fig. 7) show a strong attraction (blue color) of N and C atoms of DZM with the two C atoms (Double bond C C) of PSH in different TSs. However, the addition approach associated withTS1 is more favored because the DZM fragment can get near the double bond easily without any other effects that can hinder it. On the other hand, for the rest of the TSs we can observe more VdW interactions (green color) which weaken the forces of addition on the double bond. So, the approach of DZM to the double bond of PSH in these cases is more difficult for the rest of the TSs. Consequently, the P1 pathway is more favored than the other products in conformity with the experimental outcomes [7].

Fig. 6.

Plots of the reduced density gradient versus the electron density multiplied by the sign of the second Hessian eigenvalue for TS1,TS2,TS3 and TS4.

Fig. 7.

Three-dimensional (3D) colour-filled RDG isosurfaces for TS1,TS2,TS3 and TS4. (For interpretation of the references to color in this figure legend, the reader is referred to the Web version of this article.)

4. Investigation about the interactions of pyrazoline compounds with COVID-19 main protease (M^pro)

The outbreak of the novel coronavirus disease COVID-19, caused by the SARS-CoV-2 virus, has spread rapidly around the world, the epidemiological characteristics of this virus allow it a high contagiousness risks. This invincible virus, causes enormous damage every day across the globe, and destabilize the human society and economy. As today, there is no vaccine and no antiviral for the treatment of this virus. However, some compounds can been promising for treatment, as pyrazoline molecules. So, we have tested some compounds of pyrazoline family (Table 3 ) with the Main protease (M ^pro) of SARS-CoV2 which is an essential protein for the proteolytic maturation of the virus. Indeed, it has been examined as a potential target protein to prevent the spread of infection by inhibiting the cleavage of the viral polyprotein [73].

Table 3.

Chemical formulae of pseudoguaianolide pyrazolines tested on the Main Protease (M^pro) of SARS-CoV2.

Molecular docking study is a helpful cheminformatics tool [[41], [42], [43]] that gives compounds interacting with the protein (M ^pro), related to a specific biological activity, the manner in which they interact, and also the way a ligand (pyrazoline compounds) and M ^pro protein can bind. The crystal structure of COVID-19 main protease in complex with an inhibitor N3 has been realized by Jin Zheming et al. [46] the global symmetry of the complex is Cyclic-C2 and its global stoichiometry is Homo 2-mer-A2 (Fig. 8 ).

Fig. 8.

The crystal structure of COVID-19 main protease in complex with an inhibitor N3, with a resolution of 2.16 Å, characterised by X-RAY DIFFRACTION [46].

The biological activity of our pyrazoline compounds has been evaluated using Maestro software (Schrödinger, LLC, New York, NY, 2018), Against M ^proof SARS-CoV2. The compounds were initially docked to the binding site Main protease receptor using Glide SP (Schrödinger Suite 2018) [66] with standard settings. We choose the compounds who have a binding affinity higher than -5 kcal/mol for further analysis. We evaluate their interaction with the binding site of the target.

The 3D interacting site of the ligands with the binding site of the protein are in Fig. 9a, Fig. 9b , the Hydrogen bond interactions for all the compounds who have a binding activities less than -5 kcal/mol with the protein are shown in Fig. 10a, Fig. 10b . The molecular docking scores of the compounds and the amino acids found in the active site pockets of M ^pro protein are showed in Table 4 . Main protease has the hydrogen bond attractors and hydrogen bond donors with the amino acids in the binding site at a distance less than 2.73 Å. The 2D structure of the most active compounds interacting with the amino acids in the binding site of the Main protease show for complex Spiro G-M^pro a hydrogen bond donor between oxygen atom of Spiro-G and CYS145, GLU166, hydrogen bond acceptor with the hydoxyd group (OH) of Spiro-G and ASN142. For Spiro-F, there are two hydrogen bonds donors with oxygen atom and CYS145, GLN189, hydrogen bond donor between nitrogen atom and GLY143. For the Spiro C there are two hydrogen bonds between oxygen atom and SER144, THR26. Concerning the P1 compound there are three hydrogen bonds donors between oxygen atom and GLN189, GLY143, GLU 166. Finally, for P3, there are two hydrogen bonds donors between oxygen atom and GLU166, CYS145. We noted also, that the most common amino acids in the binding site for the different complexes are CYS145, GLU166 and GLY143. The comparison of the binding energy of our products (Spiro-C, Spiro G and P3) is greater than that of Lopinavir and the mixture of Lopinavir + Oseltamivir which have been used to cure MERS and SARS [73].

Fig. 9a.

3D structure of P1, P3, Spiro G and Spiro F compounds in the binding site.

Fig. 9b.

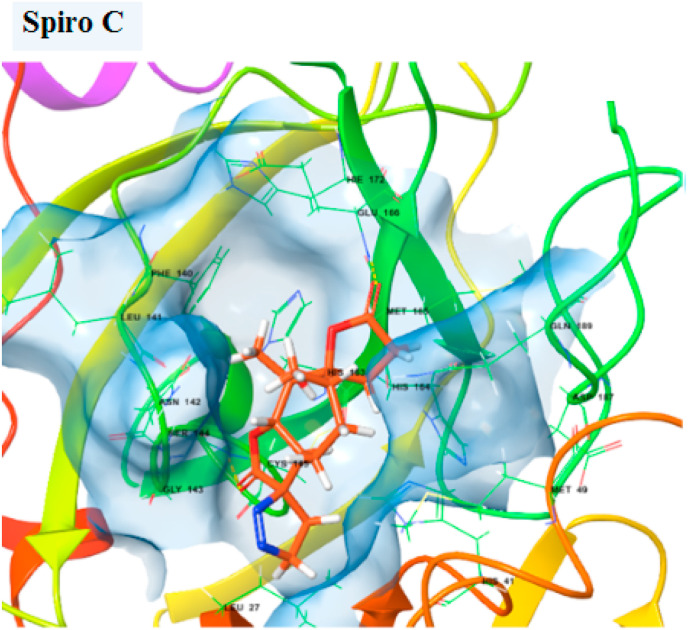
3D structure of Spiro C compound in the binding site.

Fig. 10a.

2D structure of the P1, P3, Spiro G and Spiro F compounds interacting with the amino acids in the binding site of the Main protease.

Fig. 10b.

2D structure of the Spiro C compound interacting with the amino acids in the binding site of the Main protease.

Table 4.

Binding energy (Kcal/mol) and the most promising active site (Amino acids) for hydrogen bond interactions.

compound	Binding energy	Amino acids
P1	−5.044	GLY143, CYS145, GLN189
P 3	−5.75	GLY143, GLN189
P 5	−4,81	GLY143, GLN189
P 7	−4.31	GLN189
Spiro-A	−3.64	ASN142, GLN189
Spiro-B	−4.41	CYS145
Spiro-C	−6.18	THR26, SER144
Spiro-D	−4.75	CYS145, GLU166
Spiro-E	−4.28	GLY143, GLN189
Spiro-F	−5.07	GLY143, CYS145, GLN189
Spiro-G	−5.46	ASN142, CYS145,166
Lopinavir [73]	−4.10	LEU287
Mixture [73] a	−5.40	LEU287, ASP33, TYR101

^aLopinavir + Oseltamivir.

For all these compounds must be predicted their toxicity, druglikness and ADME (Data of ADME/ToX) using the preADMET server [74]. According to results associated with toxicity, druglikness and ADME we note the following. For the different pyrazolline products the Ames_test is non-mutagen. The risk associated with the hERG_inhibition is low and their CMC_like_Rule is qualified. The solubility of P1, P3, spiro-C, spiro-F and spiro-G in pure water is between 71 and 144 mg/l. The value of binding with the plasma protein is from 69.94 to 76.80, consequently, these products possess a good absorption. For more details about the prediction of ADME/Tox see supplementary (Data of ADME/ToX). In summary, the pyrazoline compounds may act as inhibitors of the COVID-M^pro, and they deserve more investigations.

5. Conclusion

The B3LYP/6-31 + G (d,p) level of computation was used to study the 1,3-DC reaction of diazomethane to PSH. The kinetic, thermodynamic and geometrical parameters associated with the formation of the different possible products were analyzed in the gas phase and ether. The global and local reactivity indices at the ground state of the reagents were evaluated to understand the reactivity in the polar processes. Whereas the electrophilic and nucleophilic character of the reagents is are responsible for the high polar character of this 1,3-DC reaction, the energetic results for 1,3-DC reaction of diazomethane to PSH, indicate that the reaction path, leading to P1 product, is kinetically preferred. The addition of ether as a solvent has a weak influence on the kinetic and thermodynamic of the studied reaction without any influence on the chemo-, regio- and stereo-selectivity. ELF calculations reveal that the formation of the N3–C4 and C1–C5 bonds is done in two stages and one-step and the C1–C5 bond is more advanced than N3–C4 bond. The weak interactions associated with the VdW forces unfavored the addition of DZM in the cumbersome zone by weakening the forces of addition, leading to the formation of P1 product. Finally, the investigation about the inhibition of Mpro-COVID-19 by pyrazoline products have given encouraging results. More accurate researches on this family of products are worth undertaking for the struggle against COVID-19 virus.

Declaration of competing interest

No conflict to declare.

Appendix A. Supplementary data

The following is the Supplementary data to this article: