Trade disruptions, behavioral biases, and social influences: Can luxury sporting goods supply chains be immunized?

Highlights

• •A dual channel supply chain with multi-tiered products experiencing trade disruption and market volatility is studied.
• •A flexible trade credit contract with minimum order quantity (MOQ) is devised.
• •A coordination mechanism under social influences and behavioral biases is established.
• •Impacts of trade disruptions, social influences, and loss-aversion on channel coordination are studied.

Abstract

This paper studies a luxury sporting goods supply chain (LSGSC) experiencing trade disruption and market volatility. We propose a flexible trade credit contract with minimum order quantity (MOQ) and design a coordination mechanism between a supplier and a loss-averse wholesaler. We extend our study to a multi-tiered product setting and examine the impacts of social influences and loss aversion on SC decisions and channel coordination. Given the gloomy post-Covid-19 economic prospects in an era of reglobalization, this study urges trade associations and business leaders to immunize their SCs by considering behavioral biases and social influences and revisiting their contractual obligations.

1. Introduction

Rapid economic growth and increased consumer affordability has resulted in a global shift in societal values and a commensurate growth of global Luxury Supply Chains (LSC). For some people at least, the globalized world is a more luxurious world. The aggregate revenue of the top 100 global luxury brands has increased by US$30 billion, with almost 35% of these companies reporting double-digit growth in annual sales (Deloitte, 2019). Motivated by this global trend and consumer interest in active luxury lifestyles, some traditionally non-luxury sporting and athleisure (i.e., a portmanteau of “athletic” and “leisure”) brands have started to market luxury sporting goods2 (LSG) through co-branding with eminent fashion designers3 , putting them in competition with emergent athleisure brands (e.g., DYNE, Castore, and Monreal London) as well as active-casual clothing marketed by luxury fashion brands (e.g., Giorgio Armani, Canada Goose, and Moncler) (Segreti, 2018, Achim, 2019, HHS, 2019). These developments, combined with the democratization of luxury, have resulted in a 46% increase in consumer spending towards established and emerging LSG brands (Yeoman and McMahon-Beattie, 2018, BCG-A, 2019).

Product counterfeiting is illegal, unethical and an all-too-common problem for the LSG industry. To deal with counterfeiting and compete against their gray market counterparts, luxury brands usually employ an umbrella branding strategy by adding a lower-tier product to their portfolio (Amaldoss and Jain, 2015). Implementing a multi-tiered product strategy creates a “social influence” effect, which refers to how a consumer’s choice of a certain LSG brand (lower or higher tier) is affected by the choices of other consumers (Chiu et al., 2018, Choi and Liu, 2019). Some leading LSG brands have leveraged the power of social influence and online e-commerce platforms to create omnichannel business models, enabling them to offer multi-tiered products concurrently via traditional wholesale and direct-to-consumer (DTC) channels (Canada Goose, 2019, Moncler, 2020). This strategy not only enables the LSG brands to boost their market demand and ameliorate counterfeiting, but also helps them eliminate unnecessary supply chain (SC) elements and create early-to-market advantages (Wei et al., 2020, Javadi et al., 2019).

Despite the growth in LSG and concomitant expansion of global luxury sporting goods supply chains (LSGSC), the market demands for LSG are known to be highly vulnerable to market fluctuation, consumer behavior, and macroeconomic shocks. Leading LSG brands are impacted negatively by their wholesalers’ cyclical behavior and substantial trade disruptions across their SC (Deloitte, 2018). For instance, in the first quarter of 2020 alone, Adidas and Moncler reported a revenue decline of 19% and 18% respectively due to the Covid-19 outbreak (Adidas, 2020, Moncler, 2020). Another example is the escalation of the trade war between the USA and China that could drastically affect USA’s US$52 billion sporting goods industry (Chad and Moon, 2019). This unpromising prospect for LSGSC may become even darker when the side effects of decision biases and social influences occur, causing further changes to the ordering and/or purchasing behavior of capital-constrained wholesalers and end consumers in an era of reglobalization (Asian et al., 2020, Evenett, 2020, Reza-Gharehbagh et al., 2020).

To mitigate possible trade disruptions and hedge against the negative impacts of deteriorating market conditions, some leading LSG brands have recently started to offer innovative contractual mechanisms to their wholesalers. For instance, due to their risk-sharing and channel coordinating properties (Chod, 2017, Yang and Birge, 2018, Mathis, 2018), trade credit contracts have been widely used as an important source of external financing in the LSG industry (Adidas, 2019, Canada Goose, 2019, Moncler, 2019)4 . While theoretically efficient, if not devised and implemented appropriately, trade credit contracts may impose a considerable amount of financial burden on the suppliers and overlook the negative impacts of social influences and wholesalers’ behavioral biases, especially in the event of trade disruptions (Yang and Birge, 2018, Tang and Yang, 2020). For example, unlike a few global brands who have been commended for fulfilling their commitments during the Covid-19 pandemic, several leading Australian wholesalers attempted to cancel and/or hold their confirmed orders, while delaying payments and asking for substantial discounts (Bainbridge and Vimonsuknopparat, 2020). Adidas and Canada Goose had reduced their trade credit offering limit even before the Covid-19 outbreak and increased their credit collection efforts to improve their financial and operational flexibility (Adidas, 2020, Canada Goose, 2020). Reinforcing such behavior will make suppliers more cautious and reluctant to extend trade credit to their wholesalers and have a catastrophic impact on the livelihood of low-paid LSG workforces in developing countries.

Several extensions to the earlier version of trade credit contracts have already been developed by researchers, aiming to add a higher level of flexibility to its functionality and coordination features (Zhang et al., 2014, Li et al., 2016). All extensions, however, mainly focused on protecting the downstream wholesaler without considering behavioral biases and social influences, making it difficult to achieve win–win coordination, particularly when both demand fluctuation and trade disruption risks exist. Although the theoretical value of trade credit contracts in improving the SC performance has been widely investigated, to the best of our knowledge, the impacts of trade disruption, social influences, and behavioral biases on channel coordination and associated challenges in immunizing a dual-channel multi-tiered product SC are rather unexplored.

To bridge the gap, this study develops a new flexible contractual mechanism by coupling the basic trade credit with the minimum order quantity (MOQ) contract, which is widely used in B2B and e-commerce environments (e.g., alibaba.com) due to its simple structure and flexible features (Tuncel et al., 2019). Using a Stackelberg game theoretical framework with a supplier-dominant power structure (Asian et al., 2019), this paper characterizes the sequential decision making of an LSG supplier and a loss-averse wholesaler under trade disruption, examining how the proposed contract can help the LSGSC partners proactively mitigate their trade risks and achieve channel coordination in the presence of behavioral biases and social influences. We extend our basic models to a multi-tiered product setting and analytically examine the separate and joint impacts of social influence and loss-aversion on the optimal decisions and win–win coordination within an LSGSC. Finally, recognizing the possibility of conflict within the proposed trade credit contracts (i.e., risk-sharing vs. MOQ), we investigate how the decentralized LSGSC can achieve win–win coordination. The key research questions of this study are:

• • Mechanism design: Given the cyclical nature of the luxury industry and the potential high impact of trade disruptions on the SC performance, how can a flexible trade credit contract with MOQ achieve Pareto (i.e., win–win) coordination?
• • Behavioral biases in decision making (i.e., loss aversion): What are the consequences of wholesaler’s loss-aversion on the performance of LSGSC and channel coordination under trade disruptions?
• • Social influences: In a dual channel multi-tiered product setting, how does the social influence affect the performance of LSGSC as well as the channel coordination under trade disruption? What are the joint impacts of loss aversion, social influences, and trade disruptions?

Given the gloomy economic prospects in an era of reglobalization, our results enable trade associations and business leaders to revisit their contractual agreements and immunize their SCs by considering the possibility of trade disruptions, and consequent impacts of behavioral and social influences.

The remainder of this paper is organized as follows. Section 2 reviews the relevant studies. Problem description, model assumptions, and benchmark models are provided in Section 3. In Section 4, we present a flexible trade credit contract with MOQ and investigate the impact of wholesaler’s loss aversion. In Section 5, we extend our model to a multi-tiered product setting and study the joint impact of social influence and decision bias. Finally, Section 6 draws concluding remarks, managerial insights and suggests future research directions. All mathematical proofs are provided in the Appendix.

2. Literature review

This review examines three streams of literature, namely luxury supply chains (LSC), SC disruptions, and trade credit contracts.

2.1. Luxury supply chains

The success of the luxury industry is increasingly reliant on the overall performance of their SC strategy (Brun et al., 2008). The majority of the rapidly growing LSC literature focuses on critical success factors and their relationship with corresponding SC strategies (Caniato et al., 2011, Castelli and Sianesi, 2015, Brun et al., 2017). Using an exploratory approach to understand demand management of jewelry, Brun and Moretto (2012) highlight the importance of contract design in LSC. Although there is a broad range of LSC studies, only a few examine the impact of social influence on channel coordination and optimal decisions (Shen et al., 2017, Chiu et al., 2018, Choi, 2019, Choi and Liu, 2019, Wang et al., 2020). For instance, Shen et al. (2017) examine how online retail services that are associated with social influence in an LSC can achieve channel coordination. Similarly, Choi and Liu (2019) explore the optimal advertisement budget allocation strategy and discuss coordination conditions in LSC with multiple brand-tier products.

Our work can be distinguished from previous studies in three aspects. First, we propose a flexible trade credit contract that incorporates an MOQ condition which can achieve win–win coordination within an LSGSC. Second, instead of using a deterministic linear model, our flexible contract is built on a newsvendor model with stochastic demand under trade disruption. Third, under an omnichannel system of multi-tiered products, we simultaneously consider the joint impacts of social influence and wholesaler’s loss aversion on channel coordination under trade disruption.

2.2. Supply chain disruption

SC disruption has recently emerged as an important topic in SC management. Existing studies on SC disruption can be classified according to the origin of disruption, namely supply disruptions and demand disruptions (e.g., Asian and Nie, 2014, Snyder et al., 2016). Because of its focus on demand fluctuation and vulnerability of the market to external trade disruptions, our research is more closely aligned to the demand disruption literature. Qi et al. (2004) were among the first to investigate SC coordination under demand disruption. Extending their work, Chen and Xiao (2009) suggest that the profit allocation among SC members is influenced significantly by the proportion of disrupted demand. In another attempt, Huang et al. (2012) focused on a dual-channel SC and studied joint pricing and production decisions under demand disruptions. Focusing on online demand disruptions, Hosseini-Motlagh et al. (2019) propose a three-sided coordination mechanism for a reverse SC. Advancing the research on SC resilience and disruption recovery (e.g., Lu et al., 2018, Paul et al., 2018, Paul et al., 2019), this paper takes a proactive approach and presents a flexible contractual mechanism that not only incentivizes the SC members to enhance their trade participation, but also mitigates the negative impacts of both demand fluctuation and trade disruption prior to its occurrence.

2.3. Trade credit contracts

Trade credit is a risk-sharing and coordination mechanism that is widely offered by a dominant supplier to empower downstream wholesalers that commonly suffer from capital shortages (Yang and Birge, 2018, Devalkar and Krishnan, 2019). Lee and Rhee’s (2011) seminal study on SC coordination via trade credit examines channel coordination from a supplier’s perspective. Zhang et al. (2014) examine how channel coordination is impacted by the simultaneous use of trade credit and a quantity discount contract. Focusing on moral hazards and working capital financing costs, Devalkar and Krishnan (2019) study a two-echelon SC and examine channel coordination. They find that reverse factoring programs combined with trade credit can improve SC efficiency. Phan et al. (2019) investigate a retailer’s role in coordinating the capital-constrained SC via trade credit.

Trade credit is also studied extensively in risk management literature (Tsao, 2017, Wang et al., 2018, Kouvelis and Zhao, 2018, Yang and Birge, 2018). Yang and Birge (2018) investigate trade credit as a risk sharing mechanism in SC and examine its influence on SC performance. Their results reveal that trade credit can successfully share risk among SC players, encourage the retailer to order larger quantities, and minimize the impact of financial distress costs. A few studies also consider the impact of decision bias (e.g., wholesaler’s balking and loss aversion behaviors) on trade credit terms and SC performance (Zhang et al., 2018, Yan et al., 2019). For example, Yan et al. (2019) show how firms’ loss aversion influence SC decisions and suggest that a retailer’s loss aversion may significantly impact both the retailer’s order quantity and the supplier’s pricing decisions. Advancing the ideas of Yan et al. (2019), this paper develops a flexible trade credit contract with MOQ and examines the impacts of decision bias (i.e., loss aversion) and social influence on a wholesaler’s ordering, supplier’s trade credit terms, and SC coordination in both single product and multi-tiered product setting.

While motivating the channel members to participate, the basic SC contract may not be able to fairly share the risk among members and coordinate the channel. Benefitting from its simplicity and ease of implementation, MOQ is prevalent in the fashion industry. Focusing on a U.S. fashion skiwear manufacturer (Sport Obermeyer), a seminal case study by Hammond and Raman (1996) demonstrates the value of an MOQ within the apparel SC. Since then, several studies have explored how an MOQ contract can balance supplier stability and wholesaler flexibility (Chow et al., 2012, Cai et al., 2015, Yuan et al., 2015, Chintapalli et al., 2017). For example, Chow et al. (2012) investigate the coordination of a two-echelon SC by introducing a hybrid mechanism of MOQ and quick response contracts. Similarly, Chintapalli et al. (2017) design a combined coordinating contract consisting of advanced-order discounts and an MOQ, where the MOQ is defined as a qualifier to receive advanced-order discounts.

In responding to the research gap identified in the literature above, we focus on the application of flexible trade credit contracts with MOQ in the LSGSC and investigate the separate and joint impacts of trade disruption, wholesaler’s loss aversion, and social influence on LSGSC players’ optimal decisions and channel coordination. Table 1 shows the positioning of the present study with respect to the most relevant papers.

Table 1.

A summary of relevant papers.

Reference	Demand disruption	Trade credit	MOQ	Loss aversion	Social influence	Newsvendor model	Channel coordination
Chow et al. (2012)			√			√	√
Chintapalli et al. (2017)			√			√	√
Shen et al. (2017)	√				√		√
Yang and Birge (2018)		√				√	√
Yan et al. (2019)		√		√		√
Choi and Liu (2019)					√		√
Hosseini-Motlagh et al. (2019)	√						√
This study	√	√	√	√	√	√	√

3. Problem description and benchmark models

This paper considers a LSGSC, wherein a supplier (hereafter referred to as “she”) sells LSG to a wholesaler (hereafter referred to as “he”). Our models are built based on the classic newsvendor model with a single product type. The realized market demand follows a general probability distribution with $f\left(x\right)$ as PDF and $F\left(x\right)$ as CDF. To capture the existing uncertainty, trade disruption is assumed to follow a Bernoulli distribution, implying that the wholesaler financially defaults and the market demand for LSG disappears with probability $\beta$. With probability $1-\beta$, there is no trade disruption and the market follows its normal pattern (i.e., $x\in \left[0,+\infty \right]$). This assumption is extensively used in the SC disruption literature (e.g., Tomlin, 2009, Dong and Tomlin, 2012, Asian and Nie, 2014, Snyder et al., 2016, Devalkar and Krishnan, 2019, Hosseini-Motlagh et al., 2019). Table 2 provides a complete list of notations used throughout this paper.

Table 2.

Notation.

Notation	Description
$\beta$	Probability of a trade disruption
$x$	Realized demand$x\in \left[0,+\infty \right]$
c	Unit production cost of LSG supplier
w	Unit wholesale price of LSG supplier
k	Production capacity of LSG supplier (i.e., MOQ)
$\pi$	Unit emergency production cost of LSG supplier
p	Unit selling price of wholesaler
$q$	Order quantity of wholesaler
$q_c^{\ast }$	Optimal production quantity in the centralized LSGSC
$q_d^{\ast }$	Optimal order quantity of risk-neutral wholesaler in the decentralized LSGSC
$q_{\mathit{tc}}^{\ast }$	Optimal order quantity of risk-neutral wholesaler under flexible trade credit contract
$\theta$	Proportion of order quantity that is eligible for early-payment discount
$\delta$	LSG supplier’s early-payment discount under trade credit flexible trade credit contract
${\mathrm{\Pi }}_w$	Expected profit function of wholesaler
${\mathrm{\Pi }}_s$	Expected profit function of LSG supplier
${\mathrm{\Pi }}_{\mathit{sc}}^c$	The centralized LSGSC’s total expected profit
${\mathrm{\Pi }}_{\mathit{sc}}^d$	The LSGSC’s total expected profit under a wholesale price contract
${\mathrm{\Pi }}_{\mathit{sc}}^{\mathit{tc}}$	The LSGSC’s total expected profit under a flexible trade credit contract
$\mathrm{\Delta }\mathrm{\Pi }$	Transfer payment made by LSG supplier to wholesaler
$\lambda$	Wholesaler’s loss aversion coefficient,$\lambda \ge 1$
${\gamma }_i$	Sensitivity of higher-tier and lower-tier LSG demands to social influence, $\forall i\in \left(h,l\right)$
${\epsilon }_i$	Independent random variable of higher-tier and lower-tier LSG demands,$\forall i\in \left(h,l\right)$
$D_i$	Market demand for higher-tier and lower-tier LSGs,$\forall i\in \left(h,l\right)$
$k_i$	Production capacity of the higher-tier and lower-tier LSGs,$\forall i\in \left(h,l\right)$
$q_i$	Order quantity of higher-tier and lower-tier LSGs,$\forall i\in \left(h,l\right)$

Prior to the selling season, the LSG supplier builds its initial production capacity $k$ at unit cost $c$ and receives an order quantity $q$ from the wholesaler. For any order above $k$, the supplier must use its urgent capacity at a higher production cost $\pi$. It is assumed, when demand exceeds the placed order quantity $\left(x>q\right)$, the wholesaler is unable to place a second emergency order. Unsold products are assumed to have negligible salvage value (here, 0). This assumption is consistent with real-world practice, where unsold stocks from past seasons are usually destroyed or recycled to maintain the scarcity and exclusivity of luxury products and prevent counterfeiting (Lieber, 2018).

In the following subsections, two benchmark models, namely centralized and decentralized LSGSC with a wholesale price contract are presented.

3.1. Centralized supply chain: Benchmark model 1

To construct our first-best solution, we first study a centralized structure where a supplier manages the entire LSGSC. Considering the possibility of a trade disruption and the initial capacity constraint, the centralized planner’s expected profit can be formulated as follows:

$${\mathrm{\Pi }}_{\mathit{sc}}^c=\left(1-\beta \right)\mathbb{E}\left[p.\mathit{min}\left(x,q\right)\right]-\mathbb{E}\left[c.\mathit{min}\left(q,k\right)+\pi .\mathit{max}\left(q-k,0\right)\right]$$ (1)

which can be rewritten as follows:

$${\mathrm{\Pi }}_{sc}^c=\left\{\begin{array}{cc}\left(1-\beta \right)p{\int }_0^q\overline{F}\left(x\right)dx-ck-\pi \left(q-k\right)\hfill & ifq>k\hfill \\ \left(1-\beta \right)p{\int }_0^q\overline{F}\left(x\right)dx-cq\hfill & ifq\le k\hfill \end{array}\right)$$ (2)

The optimal solution for an LSGSC under a centralized setting is provided in the following theorem.

Theorem 1.

The expected profit of a centralized SC in the presence of trade disruption is concave and the optimal production quantity can be obtained as follows:

$$q_c^{\ast }=\left\{\begin{array}{cc}{F}^{-1}\left(1-\frac{\pi }{p(1-\beta )}\right)\hfill & ifq>k\hfill \\ F^{-1}\left(1-\frac{c}{p(1-\beta )}\right)\hfill & ifq\le k\hfill \end{array}\right)$$ (3)

Theorem 1 states that $q_c^{\ast }$ always increases as $p$ increases and decreases with respect to $\beta$. Moreover, $q_c^{\ast }$ decreases with respect to $\pi$ (only when $q>k)$ and $c$ (only when $q\le k$). Moreover, there is a non-negativity threshold for the trade disruption probability ($0\le \beta <{\overline{\beta }}_c$), which reflects the maximum risk tolerance of the centralized LSGSC to trade disruption. The upper-bound can be derived as follows:

$${\overline{\beta }}_c=\left\{\begin{array}{cc}1-\frac{\pi }{p}\hfill & ifq>k\hfill \\ -\frac{c}{p}+1\hfill & ifq\le k\hfill \end{array}\right)$$ (4)

3.2. Decentralized supply chain with a wholesale price contract: Benchmark model 2

In this subsection, we consider a decentralized SC model with a wholesale price contract, where both the LSG supplier and wholesaler are risk neutral.

Prior to the selling season, the LSG supplier announces a wholesale price $w$, based on which the wholesaler determines his order quantity $q$ . The wholesaler receives the products from the supplier, makes full payment $\mathit{wq}$, and sells them to the market at unit price p. The wholesaler’s expected profit under a wholesale price contract can be derived as follows:

$${\mathrm{\Pi }}_w^d\left(q|w\right)=\left(1-\beta \right)\mathbb{E}\left[p.\min \left(x,q\right)-wq\right]-\beta wq$$ (5)

which can be rewritten as follows:

$${\mathrm{\Pi }}_w^d\left(q|w\right)=\left(1-\beta \right)\left[p{\int }_0^q\overline{F}\left(x\right)dx\right]-wq$$ (6)

Theorem 2 characterizes the wholesaler’s optimal ordering decision in the decentralized setting utilizing a wholesale price contract.

Theorem 2.

Under a wholesale price contract, the wholesaler’s expected profit function is concave, and the optimal order quantity can be obtained as follows:

$$q_d^{\ast }=F^{-1}\left(1-\frac{w}{p(1-\beta )}\right)$$ (7)

As expected, the wholesaler’s optimal order quantity increases as the retail price $p$ increases and decreases with respect to wholesale price $w$ and trade disruption probability $\beta$. Given the wholesaler’s optimal solution, we derive a non-negativity condition for $q_d^{\ast }$, denoting the maximum risk tolerance of the wholesaler to trade disruption $(0\le \beta <{\overline{\beta }}_d)$ in the decentralized SC:

$${\overline{\beta }}_d=1-\frac{w}{p}$$ (8)

After characterizing the wholesaler’s optimal solution, the expected profit of the supplier can be derived as follows:

$${\mathrm{\Pi }}_s^d\left(q_d^{\ast }\right)=w{q}_d^{\ast }-\mathbb{E}\left(c.\mathrm{m}\mathrm{i}\mathrm{n}(q_d^{\ast },k)+\pi .\max \left(q_d^{\ast }-k,0\right)\right)$$ (9)

As can be seen, the LSG supplier’s profit is independent of the realized market demand. This is because, participating in a wholesale price contract, the wholesaler undertakes the full risk of trade disruption and possible mismatch between order quantity and demand realization. However, when $q>k$, the supplier is obliged to build an emergency capacity $q-k$ at unit cost $\pi$ and fulfil the order.

Theorem 3.

Under a wholesale price contract, the optimal order quantity is strictly less than that of the centralized SC, i.e. $q_d^{\ast }<q_c^{\ast }$ . Moreover, the total expected profit of the decentralized SC is strictly less than that of the centralized setting, i.e. ${\mathrm{\Pi }}_{\mathit{sc}}^d<{\mathrm{\Pi }}_{\mathit{sc}}^c$ . Finally, the maximum tolerance to trade disruption is weaker than that in the centralized model, i.e. ${\overline{\beta }}_d<{\overline{\beta }}_c$ .

As shown in Theorem 3, due to the double marginalization effect and the lack of risk-sharing arrangements, the wholesale price contract cannot maximize the performance of the entire LSGSC. In the next section, we propose a flexible contract that can eliminate existing inefficiencies and achieve channel coordination by effectively sharing the risks between LSGSC members.

4. Flexible trade-credit contract with MOQ

While incentivizing the capital-constrained wholesalers to participate in trade and positively influencing their ordering decisions, the classic trade credit contract makes the supplier undertake a large proportion of demand risk, exposing her expected profit to larger fluctuations. The situation can worsen when the market demand is not only subject to typical fluctuations but may even —temporarily or permanently— disappear due to trade disruptions, mainly caused by uncontainable external factors. Motivated by the real-world operations of fashion and apparel industries (Chow et al., 2012, Omotoso, 2018), in this section we present a flexible trade credit contract with an MOQ and investigate how such a contract can effectively share demand uncertainty and trade disruption risk between SC members and help coordinate the channel.

Our key assumptions, mechanism design, and the sequence of events are presented in Section 4.1. We examine the channel members’ decision making under a flexible trade credit contract with an MOQ and discuss win–win coordination in the presence of trade disruption in Section 4.2. We extend our analysis in Section 4.3 and discuss impacts of behavioral bias on LSGSC members’ optimal decisions and channel coordination.

4.1. Mechanism design and key assumptions

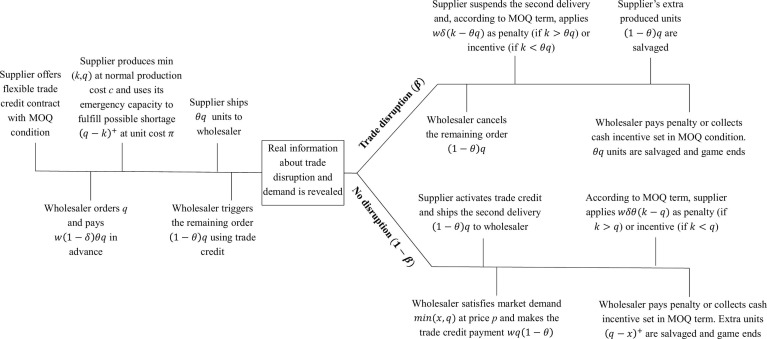
Given the actual business practice of trade credit contracts in the LSG industry and using a Stackelberg game approach, we consider a contract design problem where a wholesaler seeks trade credit from a supplier at the beginning of the season. In this section, we outline our mechanism design and demonstrate how a supplier (i.e., the game leader) and a wholesaler (i.e., the game follower) interact via a flexible trade credit contract with an MOQ, in the presence of demand uncertainty and the possibility of a trade disruption. The sequence of events and the key features of the proposed contract are summarized in Fig. 1 and Table 3 .

Fig. 1.

Sequence of events under a flexible trade credit contract with an MOQ.

Table 3.

Summary of the flexible trade credit contract with an MOQ.

Possible scenarios	Actual traded quantity	Trade credit		MOQ proportional penalty (or incentive)
		Early-payment discounts	Risk-sharing
Disruption ($\beta$)	$\theta q$	$w\delta \theta q$	$w\left(1-\theta \right)q$	$w\delta (k-\theta q)$
No disruption ($1-\beta$)	$q$	$w\delta \theta q$	0	$w\delta \theta (k-q)$

(1) Before starting the selling season, the supplier builds its initial capacity $k$ and offers a flexible trade credit with an MOQ to the wholesaler $\left(w,\delta ,\theta ,k\right)$. As part of her contract design process, the supplier (as game leader) determines an optimal proportion of order quantity $\theta$ that is eligible for early-payment discount.

(2) Upon receiving the offer, the wholesaler either rejects the contract or accepts it. If accepted, the wholesaler must decide on his order quantity $q$ and transfer an advanced discounted payment of $\left(1-\delta \right)w\theta q$ to the supplier. Given the flexibility of the proposed trade credit contract, the wholesaler is not bounded to meet the MOQ threshold and may decide to order less or more than $k$. Doing so, however, triggers an MOQ penalty (or incentive) which should be paid (or collected) as a separate transaction at the end of the selling season.

(3) The supplier produces $\min \left(q,k\right)$ units at normal unit cost $c$ and utilizes its emergency capacity to fulfill any possible shortages ${\left(q-k\right)}^{+}$ at unit cost $\pi$. Once produced, $\theta q$ units will be shipped to the wholesaler.

(4) Real information about the trade disruption and demand is revealed and one of the following two scenarios may take place:

(4.1) When a trade disruption occurs (with probability $\beta$), the wholesaler instantly cancels the remaining order $\left(1-\theta \right)q$. According to the MOQ term, the supplier suspends the second delivery and applies a proportional penalty $w\delta (k-\theta q)$, if $k>\theta q$. When $k<\theta q$, however, the same amount $w\delta (k-\theta q)$, will be transferred as an MOQ incentive to the wholesaler. The wholesaler pays the penalty or collects the cash incentive set in the MOQ term at the end of the selling season. Extra units are salvaged and the game ends.

(4.2) When no trade disruption occurs (with probability $1-\beta$), the supplier delivers $\left(1-\theta \right)q$ units to the wholesaler with an original unit price $w$ set in the contract. The wholesaler satisfies market demand $\mathit{min}(x,q)$ at price p and clears the second payment $wq\left(1-\theta \right)$ . Like the disruption scenario, the supplier applies $w\delta \theta (k-q)$ as the MOQ proportional penalty (if $k>q$) or incentive (if $k<q$). Extra units are salvaged and the game ends.

As mentioned before, the MOQ term of the proposed contract may result in a one-time penalty (or incentive) payment. This additional transaction is derived by the total discounts attributed by trade credit $\delta w\theta q$ and is applied in proportion to the actual traded quantity of LSG between the supplier and wholesaler. As can be seen, the MOQ term of the proposed contract results in two asymmetric penalty (or incentive) rates. When a trade disruption occurs, the wholesaler cancels the remaining order and only exercises the first order $\theta q$. Given a lower traded quantity $\theta q$ and the costs of the risk-sharing mechanism $w\left(1-\theta \right)q$, the supplier would apply a penalty (or incentive) of $w\delta \left(\theta q-k\right)$ to punish (or compensate) the wholesaler’s underordering (or overordering).

It is assumed that the MOQ $k$, early-payment discount $\delta$, wholesale price $w,$ and other exogenous cost and revenue parameter values are given. Without loss of generality and to avoid trivial cases, we assume $c<\pi <w(1-\delta )\le w<p$, $0\le \theta \le 1$, and $0\le \delta \le 1$ hold throughout the paper. Hence, when $\theta =0$, the supplier offers an interest-free loan without early-payment discount ($\delta =0$), commonly referred to as net-terms trade credit (Yang and Birge, 2018). In this case, the supplier shares the demand uncertainty risk with the wholesaler and knowingly bears the full risk of trade disruption. When $\theta =1\mathrm{a}\mathrm{n}\mathrm{d}\delta =0$, on the other hand, the flexible trade credit reduces to a wholesale price contract (see Section 3.2), where the wholesaler concurrently undertakes the full risk of both trade disruption and demand fluctuation. In the next subsections, we focus on general cases, where $0<\theta <1\mathrm{a}\mathrm{n}\mathrm{d}\delta >0$.

4.2. Channel members’ optimal decision making

Given the power structure within the LSGSC, the supplier’s expected profit function can be derived as follows:

$${\mathrm{\Pi }}_s^{\mathit{tc}}\left(\theta \right)=-\mathbb{E}\left(c.\min \left(q,k\right)+\pi .{\left(q-k\right)}^{+}\right)+\left(1-\beta \right)\mathbb{E}\left(\left(1-\delta \right)w\theta q+wq\left(1-\theta \right)-w\delta \theta \left(q-k\right)\right)+\beta \mathbb{E}\left(\left(1-\delta \right)w\theta q-w\delta \left(\theta q-k\right)\right)$$ (10)

As can be seen, the supplier’s expected profit consists of three components. The first term refers to the expected production costs, which includes normal production and contingent emergency production costs. The second term represents the supplier’s expected revenue under a normal scenario and includes discounted early-payment and trade credit repayment, as well as applied proportional MOQ penalty (or incentive). The last term refers to the supplier’s expected revenue under disruption and includes discounted early-payment and applied proportional MOQ penalty (or incentive). Clearly, when $\theta =1\mathrm{a}\mathrm{n}\mathrm{d}\delta =0$, the supplier’s expected profit is identical to that of the wholesale price contract (see Eq. (9)).

We next derive the wholesaler’s expected profit function under the flexible trade credit with an MOQ:

$${\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right)=\left(1-\beta \right)\mathbb{E}\left(p.\min \left(x,q\right)-\left(1-\delta \right)w\theta q-wq\left(1-\theta \right)-w\delta \theta \left(k-q\right)\right)+\beta \mathbb{E}\left(-\left(1-\delta \right)w\theta q-w\delta \left(k-\theta q\right)\right)$$ (11)

The first component in Eq. (11) refers to the “no disruption” scenario and includes four terms: the expected revenue, discounted early-payment, trade credit repayment, and the incurred proportional MOQ penalty (or incentive). The second component refers to the scenario where a trade disruption occurs and includes two terms: the realized trade credit payment and the incurred proportional MOQ penalty (or incentive).

We can rewrite Eq. (11) as follows:

$${\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right)=\left(1-\beta \right)\left[p{\int }_0^q\overline{F}\left(x\right)dx-wq\left(1-\delta \theta \right)-w\delta \theta \left(k-q\right)\right]+\beta \left[-\left(1-\delta \right)w\theta q-w\delta \left(k-\theta q\right)\right]$$ (12)

Following a backward induction approach, anticipating the supplier’s best response, the wholesaler’s optimal order quantity is characterized in Theorem 4.

Theorem 4.

Under the flexible trade credit contract with an MOQ, the wholesaler’s expected profit function is concave, and the optimal order quantity can be obtained as follows:

$$q_{\mathit{tc}}^{\ast }=F^{-1}\left(1-\frac{w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)}{p(1-\beta )}\right).$$ (13)

From Theorem 4 we observe that the wholesaler is motivated to place an order quantity, $q_{\mathit{tc}}^{\ast }\ge 0$, only if the probability of trade disruption is not higher than that of a certain range, $\beta \le {\overline{\beta }}_{\mathit{tc}}$, where we have:

$${\overline{\beta }}_{\mathit{tc}}=\frac{p-w+2w\delta \theta }{p-w(1-\theta )}.$$ (14)

Compared with the wholesale price contract (illustrated in Theorem 2), it is easy to prove $q_{\mathit{tc}}^{\ast }>q_d^{\ast }$ and ${\overline{\beta }}_{\mathit{tc}}>{\overline{\beta }}_d$. This implies that the proposed flexible trade credit improves the wholesaler’s tolerance to trade disruption risk and encourages him to increase his order quantity.

Corollary 1.

Under the flexible trade credit contract with an MOQ, we have $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \delta }>0$ ; $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \beta }<0$ ; $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial p}>0$ , $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial w}<0$ ; if $2\delta -\beta >0,\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \theta }>0$ , otherwise, $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \theta }\le 0$ .

Corollary 1 has several implications: First: it states that the optimal order quantity $q_{\mathit{tc}}^{\ast }$ increases with respect to the early-payment discount $\delta$, implying that by offering a higher early-payment discount, the supplier can motivate the wholesaler to increase his order quantity. Second: as the trade disruption probability $\beta$ increases, the wholesaler’s order quantity decreases. Third: when trade disruption probability is high, $2\delta <\beta <{\overline{\beta }}_{\mathit{tc}}$, $q_{\mathit{tc}}^{\ast }$ decreases with respect to $\theta$. When trade disruption probability is low ($\beta <2\delta$), however, $q_{\mathit{tc}}^{\ast }$ increases with respect to $\theta$. This is an important finding and indicates that, to maximize its expected profit, the wholesaler will balance between the overage loss resulted from trade disruption and the benefits of early-payment discount offered by the trade credit contract. Fourth: $q_{\mathit{tc}}^{\ast }$ decreases with respect to the wholesale price $w$ and increases with respect to the selling price $p$. This finding suggests that LSG with higher profit margins increase the risk tolerance of the wholesaler to trade disruption and overstock, encouraging him to order more without being directly affected by the MOQ condition set by the supplier.

With an understanding of the wholesaler’s best response strategy, we next investigate the supplier’s optimal flexible trade credit contract design under the MOQ condition.

The supplier’s expected profit (Eq. (10)) can be rewritten as follows:

$${\mathrm{\Pi }}_s^{tc}\left(\theta \left|q_{tc}^{\ast }\right)\right)=\left\{\begin{array}{cc}{q}_{tc}^{\ast }\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-\pi \right]+w\delta k\left(\beta +\left(1-\beta \right)\theta \right)+\left(\pi -c\right)k\hfill & ifq>k\hfill \\ q_{tc}^{\ast }\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-c\right]+w\delta k\left(\beta +\left(1-\beta \right)\theta \right)\hfill & ifq\le k\hfill \end{array}\right)$$ (15)

To ensure that the supplier does not offer early-payment discount at a loss, we assume $\delta \in \left(0,r_s\right)$, where $r_s$ can be found as follows:

$$r_s=\left\{\begin{array}{cc}\frac{w-\pi }{w}\hfill & ifq>k\hfill \\ \frac{w-c}{w}\hfill & ifq\le k\hfill \end{array}\right)$$ (16)

Theorem 5 characterizes the LSG supplier’s optimal decision in different scenarios.

Theorem 5.

Under the flexible trade credit contract with an MOQ, the supplier’s expected profit is concave in $\theta$ when the following conditions are satisfied:

(i) For $q>k$, $\frac{f^{\text{'}}\left(q_{\mathit{tc}}^{\ast }\right)\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-\pi \right]}{f^2\left(q_{\mathit{tc}}^{\ast }\right)p\left(1-\beta \right)}+2>0$;

(ii) For $q\le k$, $\frac{f^{\text{'}}\left(q_{\mathit{tc}}^{\ast }\right)\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-c\right]}{f^2\left(q_{\mathit{tc}}^{\ast }\right)p\left(1-\beta \right)}+2>0$.

Hence, the optimal proportion of the order that is eligible for early-payment discount exists and can be obtained as follows:

$${\theta }^{\ast }=\left\{\begin{array}{cc}\frac{p\left(1-\beta \right)f\left(q_{tc}^{\ast }\right)\left[\left(1-\beta \right)w\delta k+\rho q_{tc}^{\ast }\right]-\rho \left(\left(1-\beta \right)w-\pi \right)}{{\rho }^2}\hfill & ifq>k\hfill \\ \frac{p\left(1-\beta \right)f\left(q_{tc}^{\ast }\right)\left[\left(1-\beta \right)w\delta k+\rho q_{tc}^{\ast }\right]-\rho \left(\left(1-\beta \right)w-c\right)}{{\rho }^2}\hfill & ifq\le k\hfill \end{array}\right)$$ (17)

where $\rho =w\left(\beta -2\delta \right)$.

Corollary 2.

Under the optimal flexible trade credit contract with an MOQ, tightening the MOQ condition always increases ${\theta }^{\ast }$ , that is $\frac{\partial {\theta }^{\ast }}{\partial k}>0$ .

As expected, Corollary 2 shows that ${\theta }^{\ast }$ always increases with respect to $k$. This is in line with the main principal of the proposed flexible SC contract and confirms that, before making an offer, the LSG supplier would be able to analyze the situation and make a tradeoff between the key terms of the trade credit contract (i.e., ${\theta }^{\ast }\mathrm{a}\mathrm{n}\mathrm{d}k$). In other words, regardless of the situation, the flexible trade credit contract enables the supplier to incentivize the wholesaler to place a larger order quantity while balancing her exposure to trade disruption risk as well as market demand uncertainty.

After studying the LSGSC members’ optimal decisions under a flexible trade credit with MOQ conditions, we examine whether the proposed mechanism could coordinate the channel. For this purpose, we identify conditions under which: (i) the total expected profit of the decentralized system is equal to the centralized expected profit (i.e., channel coordination); (ii) both members are incentivized and prefer to take part in the contract (i.e., Pareto improvement). A win-win coordination occurs only when both conditions (i) and (ii) are satisfied (Chow et al., 2012, Asian and Nie, 2014).

Theorem 6 provides the necessary and sufficient channel coordination conditions.

Theorem 6.

The channel coordination can be achieved if and only if the supplier’s early-payment discount, $\delta$ satisfies the following condition:

$${\delta }_c^{\ast }=\frac{\beta q_c^{\ast }}{2q_c^{\ast }-\left(1-\beta \right)k},$$ (18)

where $\delta \in \left(0,r_s\right)$, that is $k<\min \left(\frac{2q_c^{\ast }}{1-\beta },\frac{q_c^{\ast }\left(2r_s-\beta \right)}{r_s\left(1-\beta \right)}\right)$.

Also, the early-payment discount has the following properties:

• (i) For any given trade disruption probability $\beta$ , ${\delta }_c^{\ast }$ increases as $k$ increases, but decreases with respect to $q_c^{\ast }$ ;
• (ii) When $q>k$ , ${\delta }_c^{\ast }$ always increases as $\beta$ increases;
• (iii) When $q\le k$ , ${\delta }_c^{\ast }$ increases with respect to $\beta$ , if and only if $k<\min \left(\frac{2q_c^{\ast }}{1-\beta },\frac{q_c^{\ast }\left(2r_s-\beta \right)}{r_s\left(1-\beta \right)},\frac{2p\left(1-\beta \right)q_c^{\ast 2}f\left(q_c^{\ast }\right)}{p\left(1-\beta \right)q_c^{\ast }f\left(q_c^{\ast }\right)-\beta c}\right)$ .

Theorem 6 has three important implications: First, our proposed flexible trade credit could coordinate the LSGSC by adjusting the early-payment discount. Second, under channel coordination, the early-payment discount ${\delta }_c^{\ast }$ increases with respect to $k$, implying that when the supplier has a larger initial capacity level, offering more attractive early-payment discount by tightening MOQ condition can encourage the wholesaler to order more and achieve channel coordination. Third, at feasible intervals of the supplier’s initial capacity $k$, the early-payment discount ${\delta }_c^{\ast }$ always increases as the trade disruption probability $\beta$ increases. In other words, when the channel is coordinated, increasing trade disruption risk motivates the supplier to offer a more generous discount but set a higher penalty (incentive) rate to ensure that the wholesaler would stick to the MOQ term of the contract.

Corollary 3.

Under the channel coordination, the optimal proportion of order with advance payment reduces to:

$${\theta }_c^{\ast }=\frac{r_s-\beta }{2{\delta }_c^{\ast }-\beta }$$ (19)

wherein, for any given trade disruption probability $\beta$, ${\theta }_c^{\ast }$ always decreases as ${\delta }_c^{\ast }$ increases but increases with respect to $r_s$.

In the trade credit literature, early-payment discount is commonly used to incentivize the wholesalers to voluntarily increase their payments in advance (Yang and Birge, 2018). Corollary 3 presents a seemingly counterintuitive result, arguing that for any given trade disruption probability $\beta$, ${\theta }_c^{\ast }$ always decreases with respect to ${\delta }_c^{\ast }$. This can be explained by the fact that in addition to discounting the wholesaler’s early-payment, $\delta$ is a determinant factor in our proposed flexible trade credit contract and increases the MOQ penalty (incentive) term (see Section 4.1). In such a flexible framework, $\delta$ plays the dual role of early payment incentive and MOQ enforcement, enabling the LSGSC to achieve channel coordination in different conditions.

We next examine if the proposed contract under coordination condition could incentivize both SC members to participate in the contract and achieve Pareto improvement.

Theorem 7.

There is an interval of $\delta \in \left(\frac{\beta }{2},min\left(\frac{1}{2},r_s\right)\right)$ within which the proposed flexible trade credit contract with an MOQ can achieve win–win coordination if $\delta ={\delta }_c^{\ast }$ and transfer payment 5 $(\mathrm{\Delta }\mathrm{\Pi })$ satisfies the following condition:

$$\left\{\begin{array}{cc}p\left(1-\beta \right)\left({\int }_0^{q_d^{\ast }}\overline{F}\left(x\right)dx-{\int }_0^{q_c^{\ast }}\overline{F}\left(x\right)dx\right)+w\left(q_c^{\ast }-q_d^{\ast }\right)<\mathrm{\Delta \Pi }<\left(w-\pi \right)\left(q_c^{\ast }-q_d^{\ast }\right)\hfill & ifq>k\hfill \\ p\left(1-\beta \right)\left({\int }_0^{q_d^{\ast }}\overline{F}\left(x\right)dx-{\int }_0^{q_c^{\ast }}\overline{F}\left(x\right)dx\right)+w\left(q_c^{\ast }-q_d^{\ast }\right)<\mathrm{\Delta \Pi }<\left(w-c\right)\left(q_c^{\ast }-q_d^{\ast }\right)\hfill & ifq\le k\hfill \end{array}\right)$$

where $\mathrm{\Delta }\mathrm{\Pi }=\beta w{\delta }_c^{\ast }k\left(\frac{1-2{\delta }_c^{\ast }}{2{\delta }_c^{\ast }-\beta }\right)$. When $q\le k$, the following additional conditions must be also satisfied:

• (i) If $r_s>\frac{1}{2},$ then $q_c^{\ast }\le k<2q_c^{\ast };$
• (ii) If $r_s\le \frac{1}{2},then$ $q_c^{\ast }\le k<\frac{q_c^{\ast }\left(2r_s-\beta \right)}{r_s\left(1-\beta \right)}.$

As shown in Theorem 7, Pareto improvement can be achieved if the total transfer payment offered by the LSG supplier is less than her profit increase, while greater than the wholesaler’s profit loss. This condition ensures that, instead of using an optimal order quantity determined under the wholesale price contract $q_d^{\ast }$, the wholesaler can achieve a higher profit by ordering $q_c^{\ast }$. This also enables the supplier to offset the total transfer payment and achieve a higher profit than that of the wholesale price contract. Also note that when the wholesaler orders less than the MOQ threshold, there is a necessary condition (i or ii) that urges the supplier to limit her MOQ condition contingent on her profit margin.

Corollary 4.

If the win–win coordination condition is satisfied, for any given trade disruption probability, the transfer payment made by supplier increases with respect to $w$ and $k$ , but decreases as ${\delta }_c^{\ast }$ increases.

Corollary 4 has two key implications. First, when offering an LSG with a large production capacity and/or high wholesale price, the supplier needs to consider a higher transfer payment to the wholesaler to maintain Pareto coordination. Second, setting a higher ${\delta }_c^{\ast }$ under win–win coordination, on the other hand, would increase the MOQ penalty (or incentive) and makes the supplier reduce her transfer payment.

4.3. Impact of wholesaler’s loss aversion

In contrast to the assumption of the decision-makers’ risk neutrality (see Section 4.2), in this subsection we regard the wholesaler as a loss-averse LSG sales agent with a preference to avoid losses than gain equivalent profits (Schweitzer and Cachon, 2000, Wang and Webster, 2007, Wang and Webster, 2009). We investigate how the wholesaler’s loss aversion influences his ordering behavior and impacts the supplier’s possible reactions. We also examine if the proposed flexible trade credit contract with an MOQ (see Section 4.1) can still lead to channel coordination when the loss aversion of the wholesaler is taken into consideration.

Given the loss aversion consideration, the wholesaler’s expected profit (Eq. (11)) can be rewritten as follows:

$${\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right)=\left\{\begin{array}{cc}\left(1-\beta \right)\left[px-wq+w\delta \theta \left(2q-k\right)\right]-\beta w\left[\left(1-2\delta \right)\theta q-\delta k\right]\hfill & ifx\le q\hfill \\ \left(1-\beta \right)\left[\left(p-w\right)q+w\delta \theta \left(2q-k\right)\right]-\beta w\left[\left(1-2\delta \right)\theta q-\delta k\right]\hfill & ifx>q\hfill \end{array}\right)$$ (20)

Lemma 1.

The wholesaler’s realized profit is negative, ${\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right)<0$ , if and only if $x<\underset{\_}{x}\left(q\right)$ , where:

$$\underset{\_}{x}\left(q\right)=\frac{wq\left(1-\beta +\left(\beta -2\delta \right)\theta \right)+w\delta k\left(\left(1-\beta \right)\theta +\beta \right)}{p\left(1-\beta \right)}$$ (21)

As suggested in Lemma 1, the wholesaler only faces an overage loss if the realized demand drops below the breakeven selling quantity $\underset{\_}{x}\left(q\right)$. It can be also observed that tightening the MOQ condition (i.e., increasing $k$) increases the breakeven selling quantity $\underset{\_}{x}\left(q\right)$, making the wholesaler more vulnerable to negative demand shocks. In the following, a piecewise-linear form of the loss-averse wholesaler’s utility function is presented:

$$U\left({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right)\right)=\left\{\begin{array}{cc}{\mathrm{\Pi }}_w^{tc}\left(q\left|\theta \right)\right)-{\mathrm{\Pi }}_0\hfill & if{\mathrm{\Pi }}_w\left(q\left|\theta \right)\right)>{\mathrm{\Pi }}_0\hfill \\ \lambda \left({\mathrm{\Pi }}_w^{tc}\left(q\left|\theta \right)\right)-{\mathrm{\Pi }}_0\right)\hfill & if{\mathrm{\Pi }}_w\left(q\left|\theta \right)\right)<{\mathrm{\Pi }}_0\hfill \end{array}\right)$$ (22)

Note that $\lambda \ge 1$ denotes the wholesaler’s loss aversion coefficient. So, the higher the value of $\lambda$, the more loss-averse the wholesaler will become. For $\lambda =1$, the wholesaler becomes risk-neutral and the above model reduces to the earlier model discussed in Section 4.1. Without loss of generality, we normalize the wholesaler’s reference level to zero, that is ${\mathrm{\Pi }}_0=0$. Thus, the loss-averse wholesaler’s expected utility can be derived as follows:

$$U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right))={\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right)+(\lambda -1){\int }_0^{\underset{\_}{x}(q)}{\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right)f(x)dx$$ (23)

Theorem 8.

The loss-averse wholesaler’s expected utility is concave. An optimal order quantity $q_{\lambda }^{\ast }$ exists and must satisfy the following condition:

$$C_u\overline{F}\left(q_{\lambda }^{\ast }\right)-C_{o}F\left(q_{\lambda }^{\ast }\right)-\left(\lambda -1\right)\left(C_{o}F\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)\right)=0$$ (24)

where $C_u$ refers to the unit underage cost i.e., $C_u=\left(1-\beta \right)\left(p-w\right)+w\theta \left(2\delta -\beta \right)>0$, and $C_o$ refers to the unit overage cost i.e., $C_o=w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)>0$. When $\lambda =1$, the wholesaler is risk-neutral, and we always have $q_{\lambda }^{\ast }=q_{\mathit{tc}}^{\ast }$.

As shown in Theorem 8, the wholesaler’s optimal order quantity depends on the marginal overage loss $C_{o}F\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)$ and loss aversion coefficient $\lambda$. We next examine how the optimal order quantity $q_{\lambda }^{\ast }$ is influenced by the loss aversion coefficient and other key model parameters.

Corollary 5.

For any $\lambda >1$ , $q_{\lambda }^{\ast }<q_{\mathit{tc}}^{\ast }$ and $\frac{\partial q_{\lambda }^{\ast }}{\partial \lambda }<0$ , that is, the loss aversion of the wholesaler negatively impacts his ordering decision.

Results presented in Corollary 5 are consistent with the findings suggested by Schweitzer and Cachon, 2000, Wang and Webster, 2007, Wang and Webster, 2009, confirming that when facing a high-impact trade disruption in addition to demand uncertainty, the loss-averse wholesaler always orders less than the risk-neutral newsvendor.

Corollary 6.

For any $\lambda >1$ , $q_{\lambda }^{\ast }$ has the following properties:

• (i) $q_{\lambda }^{\ast }$ increases with respect to $p$ , but decreases as $k$ , $w$ and $\beta$ increase.
• (ii) If $2w\theta \left[1+\left(\lambda -1\right)F\left(\underset{\_}{x}\left(q_{\lambda }^{\ast }\right)\right)\right]+\frac{w\left(\lambda -1\right)}{p\left(1-\beta \right)}{C}_{o}f\left(\underset{\_}{x}\left(q_{\lambda }^{\ast }\right)\right)\left[2\theta q_{\lambda }^{\ast }-k\left(\left(1-\beta \right)\theta +\beta \right)\right]>0$ , then $\frac{\partial q_{\lambda }^{\ast }}{\partial \delta }>0$ ; otherwise, $\frac{\partial q_{\lambda }^{\ast }}{\partial \delta }\le 0$ .
• (iii) If $w\left(\beta -2\delta \right)+\left(\lambda -1\right)\left(w\left(\beta -2\delta \right)F\left(\underset{\_}{x}\left(q_{\lambda }^{\ast }\right)\right)+\frac{C_{o}f\left(\underset{\_}{x}\left(q_{\lambda }^{\ast }\right)\right)\left[w{q}_{\lambda }^{\ast }\left(\beta -2\delta \right)+w\delta k\left(1-\beta \right)\right]}{p\left(1-\beta \right)}\right)>0$ , then $\frac{\partial q_{\lambda }^{\ast }}{\partial \theta }<0$ ; otherwise, $\frac{\partial q_{\lambda }^{\ast }}{\partial \theta }\ge 0$ .

Corollary 6 states that: (i) similar to the risk-neutral case in Corollary 1, the LSG wholesaler’s optimal order quantity always increases with respect to his profit margins but decreases as the trade disruption probability increases. Another interesting finding is that the supplier’s initial capacity (i.e., MOQ) negatively impacts the loss-averse wholesaler’s optimal order quantity. This is because tightening the MOQ condition increases the breakeven selling quantity $\underset{\_}{x}\left(q\right)$ of the wholesaler, making him reduce his order quantity to mitigate the risk associated with trade disruption and market fluctuation; (ii) the early-payment discount positively impacts the loss-averse wholesaler’s optimal order quantity under some necessary conditions; (iii) For $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \theta }<0$, we always have $\frac{\partial q_{\lambda }^{\ast }}{\partial \theta }<0$. For $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \theta }>0$, $\frac{\partial q_{\lambda }^{\ast }}{\partial \theta }>0$ is not guaranteed. This finding is in line with Corollary 5 and reveals that the loss aversion makes the wholesaler more sensitive to trade disruption risks.

We next investigate the supplier’s best decision in Theorem 9.

Theorem 9.

For any $\lambda >1$ , the supplier’s expected profit function is concave in $\theta$ , if the following conditions are satisfied:

(i) When $q>k$, $\frac{f^{\text{'}}\left(q_{\lambda }^{\ast }\right)\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-\pi \right]}{f^2\left(q_{\lambda }^{\ast }\right)p\left(1-\beta \right)}+2>0$;

(ii) When $q\le k$, $\frac{f^{\text{'}}\left(q_{\lambda }^{\ast }\right)\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-c\right]}{f^2\left(q_{\lambda }^{\ast }\right)p\left(1-\beta \right)}+2>0$.

Hence, ${\theta }_{\lambda }^{\ast }$ can be derived as follows:

$${\theta }_{\lambda }^{\ast }=\left\{\begin{array}{cc}\frac{f\left(q_{\lambda }^{\ast }\right)p\left(1-\beta \right)\left[\left(1-\beta \right)w\delta k+\rho q_{\lambda }^{\ast }\right]-\rho \left(\left(1-\beta \right)w-\pi \right)}{{\rho }^2}\hfill & ifq>k\hfill \\ \frac{f\left(q_{\lambda }^{\ast }\right)p\left(1-\beta \right)\left[\left(1-\beta \right)w\delta k+\rho q_{\lambda }^{\ast }\right]-\rho \left(\left(1-\beta \right)w-c\right)}{{\rho }^2}\hfill & ifq\le k\hfill \end{array}\right)$$ (25)

where $\rho =w\left(\beta -2\delta \right)$.

Corollary 7.

Under the optimal flexible trade credit contract, tightening the MOQ condition (i.e., increasing $k)$ increases ${\theta }_{\lambda }^{\ast }$ only if the following condition is satisfied:

$$\frac{\partial q_{\lambda }^{\ast }}{\partial k}{f}^{\text{'}}\left(q_{\lambda }^{\ast }\right)\left[\left(1-\beta \right)w\delta k+\rho q_{\lambda }^{\ast }\right]+f\left(q_{\lambda }^{\ast }\right)\left[\left(1-\beta \right)w\delta +\rho \frac{\partial q_{\lambda }^{\ast }}{\partial k}\right]>0$$

Unlike the loss-neutral case, where ${\theta }^{\ast }$ always increases with respect to $k$ (see Corollary 2), Corollary 7 states there are some scenarios where ${\theta }_{\lambda }^{\ast }$ may decrease as $k$ increases. To ensure the loss-averse wholesaler’s participation in the contract and maintain her profit margin, the supplier may decide to undertake a higher risk and simultaneously increase $k$ and $(1-{\theta }_{\lambda }^{\ast })$. This is an interesting finding and implies that, dealing with a loss-averse wholesaler, the LSG supplier takes a riskier approach in balancing the two conflicting terms of her flexible trade credit contract with an MOQ, i.e., $k\mathrm{and}\theta$.

Corollary 8.

For any $\lambda >1$ , the wholesaler’s loss aversion will negatively impact the optimal proportion of order quantity that is eligible for supplier’s early-payment discount ${\theta }_{\lambda }^{\ast }$ . In other words, ${\theta }_{\lambda }^{\ast }<{\theta }^{\ast }$ , when the following conditions are satisfied:

$f^{\text{'}}\left(q_{\lambda }^{\ast }\right)\left[\left(1-\beta \right)w\delta k+\rho q_{\lambda }^{\ast }\right]+\rho f\left(q_{\lambda }^{\ast }\right)>0$ .

Corollary 8 indicates that, under some necessary conditions, ${\theta }_{\lambda }^{\ast }$ decreases as the wholesaler’s loss aversion coefficient $\lambda$ increases. This is consistent with Corollary 7 and implies that, dealing with a more loss-averse wholesaler, the LSG supplier needs to offer more attractive trade credit to positively influence the wholesaler’s order quantity.

Theorem 10.

The LSGSC with a loss-averse wholesaler can be coordinated via a flexible trade credit contract with an MOQ if and only if the supplier’s early-payment discount satisfies the following condition:

$${\delta }_{\lambda }^{c\ast }=\left\{\begin{array}{cc}\frac{\beta \pi v+\left(v+1\right)q_c^{\ast }f\left(q_c^{\ast }\right)p\left(1-\beta \right)\beta }{2\pi v+\left(v+1\right)f\left(q_c^{\ast }\right)p\left(1-\beta \right)\left(2q_c^{\ast }-k\left(1-\beta \right)\right)}\hfill & ifq>k\hfill \\ \frac{\beta cv+\left(v+1\right)q_c^{\ast }f\left(q_c^{\ast }\right)p\left(1-\beta \right)\beta }{2cv+\left(v+1\right)f\left(q_c^{\ast }\right)p\left(1-\beta \right)\left(2q_c^{\ast }-k\left(1-\beta \right)\right)}\hfill & ifq\le k\hfill \end{array}\right)$$ (26)

where $v=\left(\lambda -1\right)F\left(\underset{\_}{x}\left(q_c^{\ast }\right)\right)$, denoted as an indicator of the decision bias contributed by the wholesaler’s loss aversion. When $\lambda =1,v=0$, ${\delta }_{\lambda }^{c\ast }={\delta }_c^{\ast }=\frac{\beta q_c^{\ast }}{2q_c^{\ast }-\left(1-\beta \right)k}$.

As Theorem 10 shows, to coordinate a LSGSC with a loss-averse wholesaler, the supplier needs to consider not only her flexible trade credit contract term (i.e., ${\delta }_{\lambda }^{c\ast }$ and $k$) , the wholesaler’s optimal order quantity $q_c^{\ast }$, and trade disruption probability $\beta$, but also the decision bias contributed by wholesaler’s loss aversion.

Corollary 9.

For any $\lambda >1$ , under the coordinated flexible trade credit with an MOQ, the early-payment discount decreases with respect to the wholesaler’s loss aversion, $\frac{\partial {\delta }_{\lambda }^{c\ast }}{\partial \lambda }<0$ .

As Corollary 9 shows, under channel coordination, as his degree of loss aversion increases, the wholesaler becomes more sensitive to negative demand shocks. To incentivize the wholesaler and achieve coordination, the supplier needs to make more transfer payment by reducing her early-payment discount.

5. A multi-tiered product setting: an extension

In this section, we extend our model to a multi-tiered product setting and investigate how social influence and behavioral bias jointly impact the optimal decisions of the SC members and channel coordination.

To benefit from a dual-channel SC setting, leading luxury brands can choose to produce and sell lower-tier products in conjunction with their traditional higher-tier products. This strategy enables LSG brands to not only diversify their product portfolio, but also mitigate the negative impacts of counterfeiting and better compete with their unlicensed market counterparts (Chiu et al., 2018, Choi and Liu, 2019). Motivated by this strategy, and consistent with the omnichannel concept that is commonly implemented in the LSG industry (Moncler, 2020, Adidas, 2020), we extend our basic models (see Section 4) by studying a dual-channel setting where a brand owner (here, the supplier) produces and sells higher-tier and lower-tier products simultaneously. Prior to the selling season, the supplier offers a flexible trade credit contract with an MOQ to the wholesaler that represents its higher-tier products in the market. In parallel, the supplier utilizes an online DTC channel and directly sells its lower-tier products to the market (see Fig. 2 ).

Fig. 2.

A dual channel setting with multi-tiered LSG.

Following Chiu et al., 2018, Choi and Liu, 2019, the market demands of the higher-tier and lower-tier products can be derived as follows:

$$D_h=-{\gamma }_h\mathbb{E}\left(D_l\right)+{\epsilon }_h$$ (27)

$$D_l={\gamma }_l\mathbb{E}\left(D_h\right)+{\epsilon }_l$$ (28)

where ${\gamma }_i\left(i\in \left(h,l\right)\right)$ represents the sensitivity of demand functions to social influence and is always between 0 and 1. In other words, ${\gamma }_i$ captures the degree to which the lower-tier and higher-tier LSG demands are affected by each other. ${\epsilon }_i\left(i\in \left(h,l\right)\right)$ is an independent random variable defined on the range of $\left[A_i,B_i\right]$, with ${\mu }_i(i\in \left(h,l\right))$ as the mean and ${\sigma }_i\left(i\in \left(h,l\right)\right)$ as standard deviation respectively. To ensure the nonnegativity of demand values, it is assumed that ${\epsilon }_i\left(i\in \left(h,l\right)\right)$ always satisfies $A_h\ge {\gamma }_h\mathbb{E}\left(D_l\right)$, $A_l\ge 0$.

The expected demand of the higher-tier and lower-tier products can be represented as follows:

$$\mathbb{E}\left(D_h\right)=\frac{{\mu }_h-{\gamma }_h{\mu }_l}{1+{\gamma }_h{\gamma }_l}$$ (29)

$$\mathbb{E}\left(D_l\right)=\frac{{\mu }_l+{\gamma }_l{\mu }_h}{1+{\gamma }_h{\gamma }_l}$$ (30)

To maintain the scarcity and exclusivity of her LSG, it is assumed that the supplier invests in small runs of higher-tier production capacity, making her bear a higher emergency production cost to handle the wholesaler’s overordering. In contrast, for lower-tier products, the supplier always builds enough capacity and, where necessary, incurs a lower emergency production cost.

Prior to the selling season, the LSG supplier should select a production quantity for lower-tier products ($q_l$) and simultaneously decide what proportion of the wholesaler’s order for higher-tier products ($\theta$) is eligible for early-payment discounts. The total expected profit function of the supplier under the dual channel setting with social influence considerations can be derived as follows:

$${\mathrm{\Pi }}_s\left(\theta ,q_l\right)={\mathrm{\Pi }}_s^{\mathit{tc}}\left(\theta \right)+{\mathrm{\Pi }}_s\left(q_l\right)$$ (31)

The first component in Eq. (31) refers to the expected profit for the supplier from selling the lower-tier products via DTC channel. The second component refers to the supplier’s expected profit from the higher-tier products under the flexible trade credit contract with an MOQ.

As illustrated in Fig. 2, the wholesaler is only responsible for selling the higher-tier products under the proposed flexible trade credit contract with an MOQ. Similar to Eq. (11), the wholesaler’s expected profit with social influence considerations, can be derived as follows:

$${\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_h\left|\theta \right)\right)=\left(1-\beta \right)\mathbb{E}\left(\left(p_h.\min \left(D_h,q_h\right)-\left(1-\delta \right)w_h\theta q_h-w_h{q}_h\left(1-\theta \right)+w_h\delta \theta \left(q_h-k_h\right)\right)\right)+\beta \left(w_h\delta \left(\theta q_h-k_h\right)-\left(1-\delta \right)w_h\theta q_h\right)$$ (32)

Following Petruzzi and Dada (1999), let $D_h=y_h+{\epsilon }_h$ and $z_h=q_h-y_h$, where $y_h=-{\gamma }_h\mathbb{E}\left(D_l\right)$. Thus, the wholesaler’s expected profit (see Eq. (32)) can be transformed as follows:

$${\mathrm{\Pi }}_w^{\mathit{tc}}\left(z_h\left|\theta \right)\right)=\left(1-\beta \right)\left[p_h\left({\int }_{A_h}^{z_h}\left(y_h+{\epsilon }_h\right)f\left({\epsilon }_h\right)d{\epsilon }_h+{\int }_{z_h}^{B_h}\left(y_h+z_h\right)f\left({\epsilon }_h\right)d{\epsilon }_h\right)\right]-\left(1-\beta \right)\left[w_h\left(y_h+z_h\right)\left(1-\delta \theta \right)+w_h\delta \theta \left(\left(y_h+z_h\right)-k_h\right)\right]+\beta \left(w_h\delta \left(\theta \left(y_h+z_h\right)-k_h\right)-\left(1-\delta \right)w_h\theta \left(y_h+z_h\right)\right)$$ (33)

As shown in Eq. (33), this transformation offers an alternative interpretation of the wholesaler’s ordering decision $q_h=z_h+y_h$, that is, for a given negative impact of social influence $y_h$, if $z_h$ is larger than the realized value of ${\epsilon }_h$, then $q_h>D_h$. Otherwise, the wholesaler can partially satisfy the demand, that is $q_h\le D_h$.

Anticipating the supplier’s joint decisions, the wholesaler’s optimal solution is characterized in Theorem 11.

Theorem 11.

Considering the social influence in LSG markets, the wholesaler’s optimal order quantity for higher-tier products can be obtained as follows:

$$q_h^{\mathit{tc}\ast }=z_h^{\mathit{tc}\ast }-{\gamma }_h\frac{{\mu }_l+{\gamma }_l{\mu }_h}{1+{\gamma }_h{\gamma }_l}$$ (34)

where $z_h^{\mathit{tc}\ast }{=F}^{-1}\left(1-\frac{w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)}{p_h(1-\beta )}\right)$.

As can be seen in Eq. (34), the first term $z_h^{\mathit{tc}\ast }$ is equal to the wholesaler’s optimal order quantity in a single channel model (see Theorem 4). The second term reflects the impact of social influence in the dual channel LSG market.

Corollary 10.

The wholesaler’s optimal order quantity for higher-tier products decreases with respect to the degree of social influence, that is, $\frac{\partial q_h^{\mathit{tc}\ast }}{\partial {\gamma }_h}<0$ , $\frac{\partial q_h^{\mathit{tc}\ast }}{\partial {\gamma }_l}<0$ .

Corollary 10 states that as the degree of social influence increases, the wholesaler reduces his optimal order quantity for higher-tier products. This is an intuitive result and means that the negative impact of social influence always reduces the actual demand for higher-tier products. (see Eq. (27)).

After characterizing the wholesaler’s optimal order quantity for higher-tier products, we next examine the supplier’s problem. For the sake of clarity, we first simplify and transform the key elements of the supplier’s total expected profit (Eq. (31)).

$${\mathrm{\Pi }}_s^{\mathit{tc}}=-\mathbb{E}\left(c_h.\min \left(q_h,k_h\right)+{\pi }_h.\max \left(q_h-k_h,0\right)\right)+\left(1-\beta \right)\mathbb{E}\left(\left(1-\delta \right)w_h\theta q_h+w_h{q}_h\left(1-\theta \right)-w_h\delta \theta \left(q_h-k_h\right)\right)+\beta \mathbb{E}\left(\left(1-\delta \right)w_h\theta q_h-w_h\delta \left(\theta q_h-k_h\right)\right)$$ (35)

Given different scenarios, Eq. (35) can be further simplified as follows:

$${\mathrm{\Pi }}_s^{\mathit{tc}}\left(\theta \left|q_h^{\mathit{tc}\ast }\right)\right)=\left\{\begin{array}{cc}{q}_h^{tc\ast }\left[w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-{\pi }_h\right]+w_h\delta k_h\left(\beta +\left(1-\beta \right)\theta \right)+\left({\pi }_h-c_h\right)k_h\hfill & if{q}_h>k_h\hfill \\ q_h^{tc\ast }\left[w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-c_h\right]+w_h\delta k_h\left(\beta +\left(1-\beta \right)\theta \right)\hfill & if{q}_h\le k_h\hfill \end{array}\right)$$ (36)

Following a centralized decision-making concept, the second term of supplier’s total expected profit (Eq. (31)) can be derived as follows:

$${\mathrm{\Pi }}_s\left(q_l\right)=-\mathbb{E}\left(c_l.\min \left(q_l,k_l\right)+{\pi }_l.\max \left(q_l-k_l,0\right)\right)+\left(1-\beta \right)\mathbb{E}\left[p_l.\min \left(D_l,q_l\right)\right]$$ (37)

Using $D_l=y_l+{\epsilon }_l$ and $z_l=q_l-y_l$, where $y_l={\gamma }_l\mathbb{E}\left(D_h\right)$, Eq. (37) can be transformed as follows:

$${\mathrm{\Pi }}_s\left(z_l\right)=\left\{\begin{array}{cc}\left(1-\beta \right)\left[p_l\left({\int }_{A_l}^{z_l}\left(y_l+{\epsilon }_l\right)f\left({\epsilon }_l\right)d{\epsilon }_l+{\int }_{z_l}^{B_l}\left(y_l+z_l\right)f\left({\epsilon }_l\right)d{\epsilon }_l\right)\right]-c_l{k}_l-\pi \left(q_l-k_l\right)\hfill & if{q}_l>k_l\hfill \\ \left(1-\beta \right)\left[p_l\left({\int }_{A_l}^{z_l}\left(y_l+{\epsilon }_l\right)f\left({\epsilon }_l\right)d{\epsilon }_l+{\int }_{z_l}^{B_l}\left(y_l+z_l\right)f\left({\epsilon }_l\right)d{\epsilon }_l\right)\right]-c_l{q}_l\hfill & if{q}_l\le k_l\hfill \end{array}\right)$$ (38)

Substituting Eq. (36) and Eq. (38) into Eq. (31), we characterize the supplier’s joint decisions in Theorem 12.

Theorem 12.

In the presence of social influence, the supplier’s expected profit is jointly concave in $\theta$ and $z_l$ when the following conditions are satisfied:

(i) For $q_h>k_h$, $\frac{f^{\text{'}}\left(q_{\mathit{tc}}^{\ast }\right)\left[w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-{\pi }_h\right]}{f^2\left(q_{\mathit{tc}}^{\ast }\right)p_h\left(1-\beta \right)}+2>0$;

(ii) For $q_h\le k_h$, $\frac{f^{\text{'}}\left(q_{\mathit{tc}}^{\ast }\right)\left[w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-c_h\right]}{f^2\left(q_{\mathit{tc}}^{\ast }\right)p_h\left(1-\beta \right)}+2>0$.

Hence, the optimal proportion of order quantity eligible for early-payment discount can be obtained as follows:

$${\theta }_{\gamma }^{\ast }=\left\{\begin{array}{cc}\frac{p_h\left(1-\beta \right)f\left(q_{tc}^{\ast }\right)\left[\left(1-\beta \right)w_h\delta k_h+\rho q_h^{tc\ast }\right]-\rho \left(\left(1-\beta \right)w_h-{\pi }_h\right)}{{\rho }^2}\hfill & if{q}_h>k_h\hfill \\ \frac{p_h\left(1-\beta \right)f\left(q_{tc}^{\ast }\right)\left[\left(1-\beta \right)w_h\delta k_h+\rho q_h^{tc\ast }\right]-\rho \left(\left(1-\beta \right)w_h-c_h\right)}{{\rho }^2}\hfill & if{q}_h\le k_h\hfill \end{array}\right)$$ (39)

where $\rho =w\left(\beta -2\delta \right)$, $q_{\mathit{tc}}^{\ast }=z_h^{\mathit{tc}\ast }$.

The optimal production quantity of lower-tier products can be obtained as follows:

$$q_l^{\ast }=z_l^{\ast }{+\gamma }_l\frac{{\mu }_h-{\gamma }_h{\mu }_l}{1+{\gamma }_h{\gamma }_l},$$ (40)

where $z_l^{\ast }=\left\{\begin{array}{cc}{F}^{-1}\left(1-\frac{{\pi }_l}{p_l(1-\beta )}\right)\hfill & if{q}_l>k_l\hfill \\ F^{-1}\left(1-\frac{c_l}{p_l(1-\beta )}\right)\hfill & if{q}_l\le k_l\hfill \end{array}\right)$.

Having $q_h^{\mathit{tc}\ast }<q_{\mathit{tc}}^{\ast }$, it is easy to show that ${\theta }_{\gamma }^{\ast }<{\theta }^{\ast }$, if $\beta >2\delta$. Otherwise, we have ${\theta }_{\gamma }^{\ast }>{\theta }^{\ast }.$ This means that when trade disruption risk is high, the early-payment discount will be unattractive to the wholesaler, encouraging the supplier to relax her advance order condition (i.e., reducing $\theta$) and thus improving the risk-sharing effect of flexible trade credit. By contrast, when facing a lower trade disruption risk, the supplier is likely to reduce her risk-sharing role (i.e., increasing $\theta$) and further rely on the early-payment discount to enhance the wholesaler’s participation in trade.

As explained before, the LSG supplier decides the optimal production quantity of the lower-tier products that are sold directly to the market via the DTC channel. Hence, to coordinate the dual channel setting (see Fig. 2), it suffices to examine the optimal decisions of the wholesaler and supplier regarding the higher-tier products.

Theorem 13.

In the presence of social influence, the flexible trade credit contract with an MOQ can coordinate the LSGSC, if and only if:

$${\delta }_{\gamma }^{c\ast }=\frac{\beta q_h^{c\ast }}{2q_h^{c\ast }-\left(1-\beta \right)k_h}$$ (41)

where $q_h^{c\ast }=z_h^{c\ast }-{\gamma }_h\frac{{\mu }_l+{\gamma }_l{\mu }_h}{1+{\gamma }_h{\gamma }_l}$ , $z_h^{c\ast }=\left\{\begin{array}{cc}{F}^{-1}\left(1-\frac{{\pi }_h}{p_h(1-\beta )}\right)\hfill & if{q}_h>k_h\hfill \\ F^{-1}\left(1-\frac{c_h}{p_h(1-\beta )}\right)\hfill & if{q}_h\le k_h\hfill \end{array}\right)$.

Under the channel coordination, both ${\theta }_{\gamma }^{c\ast }$ and the transfer payment ($\mathrm{\Delta }{\mathrm{\Pi }}_{\gamma }$) decrease with respect to the social influence.

As illustrated in Theorem 13, the demand for higher-tier products and the wholesaler’s order quantity reduce by increasing the degree of social influence (i.e., ${\gamma }_h$ and ${\gamma }_l$). When the channel is coordinated, high social influence is more likely to reduce the optimal order quantity $q_h^{c\ast }$ and trigger MOQ penalties. Theorem 13 also implies that, in the presence of high social influence and trade disruption, the LSG supplier is willing to offer a higher early-payment discount and relax the payment condition to maintain the attractiveness of flexible trade credit. As a result, the wholesaler receives more trade credit when there is no disruption. However, when disruption occurs, the wholesaler may incur penalties for failing to satisfy the MOQ condition.

Table 4 illustrates the impact of social influence on the performance of the proposed flexible trade credit contract with an MOQ. Theorem 14 demonstrates the joint impacts of social influence and wholesaler’s loss-aversion on the LSGSC members’ optimal decisions and channel coordination.

Theorem 14.

Considering the joint impacts of social influence and wholesaler’s loss aversion, we have:

Table 4.

Impacts of social influence.

Social influence	$D_h$	$q_h^{\mathit{tc}\ast }$	${\theta }_{\gamma }^{\ast }$	Channel coordination terms
				$q_h^{c\ast }$	${\delta }_{\gamma }^{c\ast }$	${\theta }_{\gamma }^{c\ast }$	$\mathrm{\Delta }{\mathrm{\Pi }}_{\gamma }$
${\gamma }_h$↑	↑	↓	↓ if $\beta >2\delta$ ↑ if $\beta <2\delta$	↓	↑	↓	↓
${\gamma }_l$↑	↓	↓	↓if $\beta >2\delta$ ↑ if $\beta <2\delta$	↓	↑	↓	↓

(i) Wholesaler’s optimal order quantity:

$$q_{h,\lambda }^{\mathit{tc}\ast }=z_{h,\lambda }^{\mathit{tc}\ast }-{\gamma }_h\frac{{\mu }_l+{\gamma }_l{\mu }_h}{1+{\gamma }_h{\gamma }_l}$$ (42)

(ii) Optimal proportion of order quantity that is eligible for early-payment discount:

$${\theta }_{\lambda \gamma }^{\ast }=\left\{\begin{array}{cc}\frac{p_h\left(1-\beta \right)f\left(q_{\lambda }^{\ast }\right)\left[\left(1-\beta \right)w_h\delta k_h+\rho q_{h,\lambda }^{tc\ast }\right]-\rho \left(\left(1-\beta \right)w_h-{\pi }_h\right)}{{\rho }^2}\hfill & if{q}_h>k_h\hfill \\ \frac{p_h\left(1-\beta \right)f\left(q_{\lambda }^{\ast }\right)\left[\left(1-\beta \right)w_h\delta k_h+\rho q_{h,\lambda }^{tc\ast }\right]-\rho \left(\left(1-\beta \right)w_h-c_h\right)}{{\rho }^2}\hfill & if{q}_h\le k_h\hfill \end{array}\right)$$ (43)

where $\rho =w_h\left(\beta -2\delta \right)$, $q_{\lambda }^{\ast }=z_{h,\lambda }^{\mathit{tc}\ast }$. If $q_h>k_h$, $\frac{f^{\text{'}}\left(q_{\lambda }^{\ast }\right)\left[w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-{\pi }_h\right]}{f^2\left(q_{\lambda }^{\ast }\right)p_h\left(1-\beta \right)}+2>0$; otherwise, $\frac{f^{\text{'}}\left(q_{\lambda }^{\ast }\right)\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-c_h\right]}{f^2\left(q_{\lambda }^{\ast }\right)p_h\left(1-\beta \right)}+2>0$. If $\beta >2\delta$, ${\theta }_{\lambda \gamma }^{\ast }<{\theta }_{\lambda }^{\ast }$; if $\beta <2\delta$, ${\theta }_{\lambda \gamma }^{\ast }>{\theta }_{\lambda }^{\ast }$.

(iii) The channel coordination can be achieved if and only if ${\delta =\delta }_{\lambda \gamma }^{c\ast }$, where

$${\delta }_{\lambda \gamma }^{c\ast }=\left\{\begin{array}{cc}\frac{\beta {\pi }_{h}v+\left(v+1\right)q_h^{c\ast }f\left(q_c^{\ast }\right)p_h\left(1-\beta \right)\beta }{2{\pi }_{h}v+\left(v+1\right)f\left(q_c^{\ast }\right)p_h\left(1-\beta \right)\left(2q_h^{c\ast }-k_h\left(1-\beta \right)\right)}\hfill & if{q}_h>k_h\hfill \\ \frac{\beta c_{h}v+\left(v+1\right)q_h^{c\ast }f\left(q_c^{\ast }\right)p_h\left(1-\beta \right)\beta }{2c_{h}v+\left(v+1\right)f\left(q_c^{\ast }\right)p_h\left(1-\beta \right)\left(2q_h^{c\ast }-k_h\left(1-\beta \right)\right)}\hfill & if{q}_h\le k_h\hfill \end{array}\right)$$ (44)

and $v=\left(\lambda -1\right)F\left(\underset{\_}{x}\left(q_h^{c\ast }\right)\right)$, $q_c^{\ast }=z_h^{c\ast }$ , $q_{h,\lambda }^{\mathit{tc}\ast }=q_h^{c\ast }$.

Theorem 14 has three important implications (summarized in Table 5 ): First, confronted with the reduction in demand for higher-tier products caused by social influence, the loss-averse wholesaler reduces his order quantity to avoid further losses in the event of trade disruption. Second, encountering the loss-averse wholesaler’s order quantity reduction under high trade disruption risk ($\beta >2\delta$), the supplier enhances her risk-sharing role by relaxing the early-payment condition of the trade credit contract (i.e., reducing ${\theta }_{\lambda \gamma }^{\ast }$). Third, compared to the separate impact of wholesaler’s loss aversion, achieving channel coordination in the multi-tiered product setting is more likely in the presence of both social influence and the wholesaler’s loss aversion.

Table 5.

Joint impacts of social influence and wholesaler’s loss aversion.

	Loss aversion	Social influence	Joint impacts
	$\lambda$↑	${\gamma }_h,{\gamma }_l$↑	$\lambda ,{\gamma }_h,{\gamma }_l$↑ ${\gamma }_h,{\gamma }_l$$.$↑
$D_h$	–	↓	↓
$q_{h,\lambda }^{\mathit{tc}\ast }$	↓	↓	↓
${\theta }_{\lambda \gamma }^{\ast }$	↓	↓ if $\beta >2\delta$ ↑ if $\beta <2\delta$	↓ if $\beta >2\delta$ ↑ if $\beta <2\delta$
$q_h^{c\ast }$	–	↓	↓
${\delta }_{\lambda \gamma }^{c\ast }$	↓	↑	↓↑

6. Conclusion and future research

6.1. Concluding remarks and managerial implications

The LSG industry is clearly vulnerable to demand shocks and trade disruptions such as those created by the Covid-19 pandemic. Although there is some evidence that recessions can stimulate demand for luxury goods (Bradshaw et al., 2019), this argument is highly nuanced. The rapidly evolving politico-economic developments and trade tensions may further deepen the economic fallout of Covid-19 and disrupt international trade more frequently. Such disruptions have the potential to damage the profits of global LSG brands and wholesalers, and also materially worsen the efficiency of their SC (Adidas, 2020, Moncler, 2020, Canada Goose, 2020). Confronting these hard challenges, the leading LSG brands should rethink their approach towards the prospect of trade disruptions, consequential negative demand shocks, and possible mitigation strategies in an era of reglobalization.

Inspired by the actual business operations of the LSG industry, this paper employed a game theoretical approach and investigated the risk-sharing and coordinating roles of flexible trade credit contracts with an MOQ in the event of trade disruptions. Following a bi-level optimization approach, we investigated the channel members’ equilibrium decisions and identified win–win coordination conditions. We first developed two benchmark models, namely a centralized and a decentralized system with a wholesale price contract. Considering a risk-neutral LSGSC scenario, we then proposed a flexible trade credit contract with an MOQ and characterized the optimal decisions of a wholesaler and an LSG supplier. These findings were then compared with the benchmark models and win–win coordination conditions were derived. Furthermore, to capture the behavioral characteristics of the wholesaler’s decision-making, the impacts of a wholesaler’s loss aversion on individual members’ optimal decisions as well as channel coordination were also examined. Finally, we extended our model to a multi-tiered product setting, where higher-tier products are distributed by the wholesaler with trade credit, while lower-tier products are sold on the online DTC channel. In such an environment, the separate and joint impacts of social influence and the wholesaler’s loss aversion on the channel members’ optimal decisions and the LSGSC channel coordination were examined. An extensive analytical sensitivity analysis was also conducted. In line with findings of a recent experimental study conducted by Tuncel et al. (2019), our results revealed that, owing to its simple yet efficient structure, the proposed flexible trade credit contract with an MOQ enables the LSGSC players to proactively mitigate the trade disruption and market volatility risks and successfully achieve channel coordination in the presence of behavioral bias and social influences. Our key findings and notable managerial insights are summarized below.

• • Optimal decision making and win–win coordination

To optimize its decision and minimize the overstock risk, the wholesaler trades off the average loss resulting from trade disruption with the benefits of early-payment discounts and risk-sharing offered by the flexible trade credit contract (Theorem 4 and Corollary 1). This finding suggests that when facing lower trade disruption risk, the capital-constrained wholesaler should take full advantage of early-payment discounts by increasing his order quantity, rather than prioritizing trade credits. In contrast, when the possibility of trade disruption is higher, the wholesaler should pursue additional trade credits, and in doing so, benefit from the risk-sharing role of the flexible trade credit contract.

On the other hand, by leveraging the MOQ term and adjusting her trade credit offering, the LSG supplier could incentivize the wholesaler to place a larger order quantity while balancing her exposure to trade disruption risk as well as market fluctuation (see Corollary 2). More importantly, flexible trade credit could enable the LSG supplier (i.e., the channel leader) to create win–win coordination by adjusting the early-payment discount (see Theorem 6., Theorem 7.). One counterintuitive finding is that the optimal proportion of order with advance payment decreases with respect to the early-payment discount. This contradicts the common argument supporting the use of early-payment discounts as leverage to incentivize wholesalers to voluntarily increase advance payments (e.g., Yang and Birge, 2018). We also found that the operational characteristics of an LSGSC significantly affect the channel members’ decisions and win–win coordination.

• • Impacts of wholesaler’s loss aversion

Increasing the degree of loss-aversion makes the wholesaler reduce his optimal order quantity (see Corollary 5). Tightening the MOQ condition could further impact the loss-averse wholesaler’s ordering decision (see Corollary 6). Hence, to enhance the wholesaler’s participation, the LSG supplier is urged to increase her risk-sharing role and offer more attractive trade credit (see Corollary 7., Corollary 8.). To ensure the loss-averse wholesaler’s participation in the contract and maintain her profit margin, the LSG supplier may even take a riskier approach in balancing the determinant terms of the flexible trade credit contract with an MOQ (see Corollary 7). While increasing the degree of loss aversion discourages the wholesaler’s participation, the supplier may still be able to create channel coordination by reducing her MOQ penalty (or incentive) rate (see Theorem 10 and Corollary 9).

• • Separate and joint impacts of social influences and behavioral biases

Our results revealed that, in a multi-tiered product setting, social influence could negatively impact the demand of higher-tier products and discourage the wholesaler from placing a larger order quantity (see Corollary 10). When the channel is coordinated, high social influence is more likely to reduce the optimal order quantity and trigger MOQ penalties (Theorem 13). In the presence of high social influence and trade disruption, the LSG supplier is suggested to offer a higher early-payment discount and relax the advance payment condition to maintain the attractiveness of flexible trade credit. We further investigated the joint impacts of social influence and loss aversion and found that, due to double negative impacts on the order decision, the loss-averse wholesaler will further reduce his optimal order quantity (Theorem 14). Encountering the loss-averse wholesaler’s order quantity reduction under high trade disruption risk, the supplier is suggested to increase her risk-sharing role by relaxing the early-payment conditions. Interestingly, achieving channel coordination in the multi-tiered product setting is found to be more possible when both social influence and the behavioral bias factors are considered.

6.2. Future directions

Given the gloomy post-Covid-19 economic prospects in an era of reglobalization, this paper urges trade associations and business leaders to immunize their SCs by rethinking contractual obligations and considering behavioral biases and social influences. Considering the limitations of this study, several extensions could be applied as future research. Future research may consider a single-supplier, multi-wholesaler setting, where loss-averse wholesalers compete on market share but can collaborate to hedge against the trade disruption. Simultaneous examination of SC immunization, risk mitigation, and resiliency strategies by incorporating strategic decisions, such as SC restructure and network reconfiguration is another challenging yet promising direction. Researchers are also encouraged to incorporate tariff uncertainties and trade renegotiation factors into the current model.

CRediT authorship contribution statement

Sobhan Asian: Investigation, Supervision, Validation, Writing - original draft, Formal analysis, Project administration. Jian Wang: Investigation, Formal analysis, Validation, Writing - original draft. Geoff Dickson: Validation, Writing - review & editing.

Appendix A.

Proof of Theorem 1

To prove the concavity of expected profit function in the centralized SC setting (Eq. (2)), we have:

$$\frac{\partial {\mathrm{\Pi }}_{\mathit{sc}}^c}{\partial q}=\left\{\begin{array}{c}\left(1-\beta \right)\left(p-pF\left(q\right)\right)-\pi ifq>k\hfill \\ \left(1-\beta \right)\left(p-pF\left(q\right)\right)-cifq\le k\hfill \end{array}\right)$$ (A.1)

and $\frac{{\partial }^2{\mathrm{\Pi }}_{\mathit{sc}}^c}{\partial q^2}=-\left(1-\beta \right)pf\left(q\right)<0$.

Setting $\frac{\partial {\mathrm{\Pi }}_{\mathit{sc}}^c}{\partial q}=0$, the optimal production quantity in the centralized setting can be obtained:

$$q_c^{\ast }=\left\{\begin{array}{c}{F}^{-1}\left(1-\frac{\pi }{p(1-\beta )}\right)ifq>k\hfill \\ F^{-1}\left(1-\frac{c}{p(1-\beta )}\right)ifq\le k\hfill \end{array}\right)$$ (A.2)

To guarantee the non-negativity of $q_c^{\ast }$, it suffices to show the following condition holds:

$$\left\{\begin{array}{c}0<1-\frac{\pi }{p\left(1-\beta \right)}<1ifq>k\hfill \\ 0<1-\frac{c}{p\left(1-\beta \right)}<1ifq\le k\hfill \end{array}\right)$$ (A.3)

As such, an upper bound on the trade disruption probability can be found:

$${\overline{\beta }}_c=\left\{\begin{array}{c}1-\frac{\pi }{p}ifq>k\hfill \\ 1-\frac{c}{p}ifq\le k\hfill \end{array}\right)$$ (A.4)

To show the monotonicity of $q_c^{\ast }$ with respect to retail price $p$, emergency production cost $\pi$ and trade disruption probability $\beta$, we have:

if $q>k$,

$$\frac{\partial q_c^{\ast }}{\partial p}=\frac{1}{f\left(q_c^{\ast }\right)}.\frac{\pi }{p^2\left(1-\beta \right)}>0$$ (A.5)

$$\frac{\partial q_c^{\ast }}{\partial \pi }=-\frac{1}{f\left(q_c^{\ast }\right)}.\frac{1}{p\left(1-\beta \right)}<0$$ (A.6)

$$\frac{\partial q_c^{\ast }}{\partial \beta }=\frac{1}{f\left(q_c^{\ast }\right)}.\frac{-\pi }{p{\left(1-\beta \right)}^2}<0$$ (A.7)

if $q\le k$,

$$\frac{\partial q_c^{\ast }}{\partial p}=\frac{1}{f\left(q_c^{\ast }\right)}\bullet \frac{c}{p^2\left(1-\beta \right)}>0$$ (A.8)

$$\frac{\partial q_c^{\ast }}{\partial c}=-\frac{1}{f\left(q_c^{\ast }\right)}\bullet \frac{1}{p\left(1-\beta \right)}<0$$ (A.9)

$$\frac{\partial q_c^{\ast }}{\partial \beta }=\frac{1}{f\left(q_c^{\ast }\right)}\bullet \frac{-c}{p{\left(1-\beta \right)}^2}<0$$ (A.10)

(Q.E.D).

Proof of Theorem 2

To show the concavity of wholesaler’s expected profit function in the decentralized SC setting (Eq. (6)), we have:

$$\frac{\partial {\mathrm{\Pi }}_w^d\left(q|w\right)}{\partial q}=\left(1-\beta \right)\left[p-pF\left(q\right)\right]-w$$ (A.11)

and $\frac{{\partial }^2{\mathrm{\Pi }}_w^d\left(q|w\right)}{\partial q^2}=-(1-\beta )pf\left(q\right)\le 0$ . Thus, the optimal order quantity in the decentralized setting can be obtained by setting $\frac{\partial {\mathrm{\Pi }}_w^d\left(q|w\right)}{\partial q}=0$:

$$q_d^{\ast }=F^{-1}\left(1-\frac{w}{p(1-\beta )}\right)$$ (A.12)

To guarantee the non-negativity of $q_d^{\ast }$, an upper bound on trade disruption probability can be derived as follows:

$${\overline{\beta }}_d=1-\frac{w}{p}$$ (A.13)

To show the monotonicity of $q_d^{\ast }$ with respect to retail price $p$, wholesale price $w,$ and trade disruption probability $\beta$, we have:

$$\frac{\partial q_d^{\ast }}{\partial p}=\frac{1}{f\left(F^{-1}\left(\frac{p\left(1-\beta \right)-w}{p(1-\beta )}\right)\right)}\bullet \frac{w}{p^2\left(1-\beta \right)}>0$$ (A.14)

$$\frac{\partial q_d^{\ast }}{\partial w}=\frac{1}{f\left(F^{-1}\left(\frac{p\left(1-\beta \right)-w}{p(1-\beta )}\right)\right)}\bullet \frac{-1}{p\left(1-\beta \right)}<0$$ (A.15)

$$\frac{\partial q_d^{\ast }}{\partial \beta }=\frac{1}{f\left(F^{-1}\left(\frac{p\left(1-\beta \right)-w}{p(1-\beta )}\right)\right)}\bullet \frac{-w}{p{\left(1-\beta \right)}^2}<0$$ (A.16)

(Q.E.D).

Proof of Theorem 3

Following the basic assumption, $c<\pi <w<p$, we can easily show,

$$1-\frac{w}{p\left(1-\beta \right)}<1-\frac{\pi }{p\left(1-\beta \right)}<1-\frac{c}{p\left(1-\beta \right)}$$ (A.17)

Hence, we always have $q_d^{\ast }<q_c^{\ast }$.

Using Eqs. (6) and (9), the optimal total expected profit of decentralized SC can be derived as follows:

$${\mathrm{\Pi }}_{\mathit{sc}}^d=\left\{\begin{array}{c}\left(1-\beta \right)\left[p{\int }_0^{q_d^{\ast }}\overline{F}\left(x\right)dx\right]-ck-\pi \left(q_d^{\ast }-k\right)ifq>k\hfill \\ \left(1-\beta \right)\left[p{\int }_0^{q_d^{\ast }}\overline{F}\left(x\right)dx\right]-c{q}_d^{\ast }ifq\le k\hfill \end{array}\right)$$ (A.18)

Given $q_d^{\ast }<q_c^{\ast }$, it is easy to prove ${\mathrm{\Pi }}_{\mathit{sc}}^d{<\mathrm{\Pi }}_{\mathit{sc}}^c$.

Finally, comparing Eq. (A.4) with Eq. (A.13), we have ${\overline{\beta }}_d<{\overline{\beta }}_c$.

(Q.E.D).

Proof of Theorem 4

Taking the first-order derivative of ${\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right)$ (Eq. (12)) with respect to $q$ , we have:

$$\frac{\partial {\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right)}{\partial q}=\left(1-\beta \right)\left[p\left(1-F\left(q\right)\right)-w\left(1-\delta \theta \right)+w\delta \theta \right]+\beta \left[-\left(1-\delta \right)w\theta +w\delta \theta \right]$$ (A.19)

Taking the second-order derivative of ${\mathrm{\Pi }}_w\left(q\left|\theta \right)\right)$ respect to $q,$ we have:

$$\frac{{\partial }^2{\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right)}{\partial q^2}=-\left(1-\beta \right)pf(q)<0$$ (A.20)

Thus, the optimal order quantity can be obtained by setting $\frac{\partial {\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right)}{\partial q}=0$:

$$q_{\mathit{tc}}^{\ast }=F^{-1}\left(1-\frac{w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)}{p(1-\beta )}\right)$$ (A.21)

To guarantee the non-negativity of $q_{\mathit{tc}}^{\ast }$, it suffices to show that $0<1-\frac{w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)}{p(1-\beta )}<1$. Hence, an upper bound on trade disruption probability can be derived as follows:

$${\overline{\beta }}_{\mathit{tc}}=\frac{p-w+2w\delta \theta }{p-w\left(1-\theta \right)}$$ (A.22)

Comparing Eq. (A21) with Eq. (A.12), we have $\frac{\left(1-\beta \right)\left(p-w\right)+w\left(2\delta -\beta \right)\theta }{p\left(1-\beta \right)}-\frac{p\left(1-\beta \right)-w}{p\left(1-\beta \right)}=\frac{w\left[\beta \left(1-\theta \right)+2\delta \theta \right]}{p\left(1-\beta \right)}>0$. Hence, it is easy to show that, $q_{\mathit{tc}}^{\ast }>q_d^{\ast }$. Using Eq. (A.13) and Eq. (A.22), we always have ${\overline{\beta }}_{\mathit{tc}}>{\overline{\beta }}_d$.

(Q.E.D).

Proof of Corollary 1.

To show the monotonicity of $q_{\mathit{tc}}^{\ast }$ with respect to $\delta$, $\theta$, $p$, $w$, and $\beta$, we have:

$$\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \delta }=\frac{1}{f\left(q_{\mathit{tc}}^{\ast }\right)}.\frac{2w\theta }{p\left(1-\beta \right)}>0$$ (A.23)

suggesting that if the LSG supplier offers more early-payment discount, the wholesaler will increase his order quantity.

$$\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \beta }=\frac{1}{f\left(q_{\mathit{tc}}^{\ast }\right)}.\frac{-w\theta \left(1-2\delta \right)}{p{\left(1-\beta \right)}^2},$$ (A.24)

From Theorem 4 and Eq. (A.21), we have $0<1-\beta +\left(\beta -2\delta \right)\theta \le 1-2\delta$. Thus, we have $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \beta }<0$.

$$\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \theta }=\frac{1}{f\left(q_{\mathit{tc}}^{\ast }\right)}.\frac{w\left(2\delta -\beta \right)}{p\left(1-\beta \right)},$$ (A.25)

If $2\delta -\beta >0$, $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \theta }>0$, if $2\delta -\beta <0$, $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \theta }<0$.

$$\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial p}=\frac{1}{f\left(q_{\mathit{tc}}^{\ast }\right)}.\frac{w\left[1-\beta +\left(\beta -2\delta \right)\theta \right]}{p^2\left(1-\beta \right)},$$ (A.26)

Having $1-\beta +\left(\beta -2\delta \right)\theta >0$, we always have $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial p}>0$.

$$\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial w}=\frac{1}{f\left(q_{\mathit{tc}}^{\ast }\right)}.\frac{-\left[1-\beta +\left(\beta -2\delta \right)\theta \right]}{p\left(1-\beta \right)}<0$$ (A.27)

In summary, $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \delta }>0$, $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \beta }<0$, $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial p}>0$, and $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial w}<0$. If $2\delta -\beta >0$, $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \theta }>0$; otherwise, $\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \theta }\le 0$.

(Q.E.D).

Proof of Theorem 5.

To find the optimal trade credit, we first prove the concavity of ${\prod }_s\left(\theta \left|q_{\mathit{tc}}^{\ast }\right)\right)$ (Eq. (15)) with respect to $\theta$:

(i) If $q>k$

Taking the first-order derivative of ${\prod }_s\left(\theta \left|q_{\mathit{tc}}^{\ast }\right)\right)$ with respect to $\theta$, we have:

$$\frac{\partial {\prod }_s\left(\theta \left|q_{\mathit{tc}}^{\ast }\right)\right)}{\partial \theta }=\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-\pi \right]\frac{1}{f\left(q_{\mathit{tc}}^{\ast }\right)}.\frac{w\left(2\delta -\beta \right)}{p\left(1-\beta \right)}+w{q}_{\mathit{tc}}^{\ast }\left(\beta -2\delta \right)+\left(1-\beta \right)w\delta k$$ (A.28)

Taking the second-order derivative of ${\prod }_s\left(\theta \left|q_{\mathit{tc}}^{\ast }\right)\right)$ respect to $\theta$, we have:

$$\frac{{\partial }^2{\prod }_s\left(\theta \left|q_{\mathit{tc}}^{\ast }\right)\right)}{\partial {\theta }^2}=-\frac{2}{f\left(q_{\mathit{tc}}^{\ast }\right)}\frac{w^2{\left(\beta -2\delta \right)}^2}{p\left(1-\beta \right)}-\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-\pi \right]\frac{w^2{\left(\beta -2\delta \right)}^2}{p\left(1-\beta \right)}\bullet \frac{f^{\text{'}}\left(q_{\mathit{tc}}^{\ast }\right)}{f^2\left(q_{\mathit{tc}}^{\ast }\right)}\frac{1}{f\left(q_{\mathit{tc}}^{\ast }\right)p\left(1-\beta \right)}=-\frac{w^2{\left(\beta -2\delta \right)}^2}{p\left(1-\beta \right)f\left(q_{\mathit{tc}}^{\ast }\right)}\left(\frac{f^{\text{'}}\left(q_{\mathit{tc}}^{\ast }\right)\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-\pi \right]}{f^2\left(q_{\mathit{tc}}^{\ast }\right)p\left(1-\beta \right)}+2\right)$$ (A.29)

Thus, the expected profit of the LSG supplier is concave if

$$\frac{f^{\text{'}}\left(q_{\mathit{tc}}^{\ast }\right)\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-\pi \right]}{f^2\left(q_{\mathit{tc}}^{\ast }\right)p\left(1-\beta \right)}+2>0$$ (A.30)

Setting $\frac{\partial {\prod }_s\left(\theta \left|q_{\mathit{tc}}^{\ast }\right)\right)}{\partial \theta }=0$, the optimal proportion of order quantity that is eligible for supplier’s early-payment discount can be obtained as follows:

$${\theta }^{\ast }=\frac{p\left(1-\beta \right)f\left(q_{\mathit{tc}}^{\ast }\right)\left[\left(1-\beta \right)w\delta k+{\rho q}_{\mathit{tc}}^{\ast }\right]-\rho \left(\left(1-\beta \right)w-\pi \right)}{{\rho }^2}$$ (A.31)

where $\rho =w\left(\beta -2\delta \right)$.

(ii) If $q\le k$,

Similar to the scenario (i) proofs, we have:

$$\frac{\partial {\prod }_s\left(\theta \left|q_{\mathit{tc}}^{\ast }\right)\right)}{\partial \theta }=\left(1-\beta \right)w\delta k+w{q}_{\mathit{tc}}^{\ast }\left(\beta -2\delta \right)+\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-c\right]\frac{1}{f\left(q_{\mathit{tc}}^{\ast }\right)}.\frac{w\left(2\delta -\beta \right)}{p\left(1-\beta \right)}$$ (A.32)

$$\frac{{\partial }^2{\prod }_s\left(\theta \left|q_{\mathit{tc}}^{\ast }\right)\right)}{\partial {\theta }^2}=-\frac{1}{f\left(q_{\mathit{tc}}^{\ast }\right)}.\frac{w^2{\left(\beta -2\delta \right)}^2}{p\left(1-\beta \right)}.\left[\frac{f^{\text{'}}\left(q_{\mathit{tc}}^{\ast }\right)\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-c\right]}{f^2\left(q_{\mathit{tc}}^{\ast }\right)p\left(1-\beta \right)}+2\right]$$ (A.33)

Thus, the expected profit of the LSG supplier is concave, if

$$\frac{f^{\text{'}}\left(q_{\mathit{tc}}^{\ast }\right)\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-c\right]}{f^2\left(q_{\mathit{tc}}^{\ast }\right)p\left(1-\beta \right)}+2>0$$ (A.34)

Setting $\frac{\partial {\prod }_s\left(\theta \left|q_{\mathit{tc}}^{\ast }\right)\right)}{\partial \theta }=0$, the optimal proportion of order quantity that is eligible for the supplier’s early-payment discount can be obtained as follows:

$${\theta }^{\ast }=\frac{f\left(q_{\mathit{tc}}^{\ast }\right)p\left(1-\beta \right)\left[\left(1-\beta \right)w\delta k+{\rho q}_{\mathit{tc}}^{\ast }\right]-\rho \left(\left(1-\beta \right)w-c\right)}{{\rho }^2}$$ (A.35)

where $\frac{f^{\text{'}}\left(q_{\mathit{tc}}^{\ast }\right)\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-c\right]}{f^2\left(q_{\mathit{tc}}^{\ast }\right)p\left(1-\beta \right)}+2>0$.

Above results can be summarized as follows:

$${\theta }^{\ast }=\left\{\begin{array}{c}\frac{p\left(1-\beta \right)f\left(q_{\mathit{tc}}^{\ast }\right)\left[\left(1-\beta \right)w\delta k+{\rho q}_{\mathit{tc}}^{\ast }\right]-\rho \left(\left(1-\beta \right)w-\pi \right)}{{\rho }^2}ifq>k\hfill \\ \frac{p\left(1-\beta \right)f\left(q_{\mathit{tc}}^{\ast }\right)\left[\left(1-\beta \right)w\delta k+{\rho q}_{\mathit{tc}}^{\ast }\right]-\rho \left(\left(1-\beta \right)w-c\right)}{{\rho }^2}ifq\le k\hfill \end{array}\right)$$ (A.36)

where $\rho =w\left(\beta -2\delta \right).$

If $q>k$, $\frac{f^{\text{'}}\left(q_{\mathit{tc}}^{\ast }\right)\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-\pi \right]}{f^2\left(q_{\mathit{tc}}^{\ast }\right)p\left(1-\beta \right)}+2>0$; and if $q\le k$, $\frac{f^{\text{'}}\left(q_{\mathit{tc}}^{\ast }\right)\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-c\right]}{f^2\left(q_{\mathit{tc}}^{\ast }\right)p\left(1-\beta \right)}+2>0$.

(Q.E.D).

Proof of Corollary 2.

To prove the monotonicity of ${\theta }^{\ast }$ with respect to $k$, we always have:

$$\frac{\partial {\theta }^{\ast }}{\partial k}=\frac{pw\delta {\left(1-\beta \right)}^{2}f\left(q_{\mathit{tc}}^{\ast }\right)}{{\rho }^2}>0$$ (A.37)

where $\rho =w\left(\beta -2\delta \right)$.

(Q.E.D).

Proof of Theorem 6.

Using Eqs. (12) and (15), the total expected profit of LSGSC under the flexible trade credit contract can be derived as follows:

$${\mathrm{\Pi }}_{\mathit{sc}}^{\mathit{tc}}=\left\{\begin{array}{c}\left(1-\beta \right)p{\int }_0^q\overline{F}\left(x\right)dx-ck-\pi \left(q-k\right)ifq>k\hfill \\ \left(1-\beta \right)p{\int }_0^q\overline{F}\left(x\right)dx-cqifq\le k\hfill \end{array}\right)$$ (A.38)

Comparing Eqs. (A.38), (2), we always have ${\mathrm{\Pi }}_{\mathit{sc}}^{\mathit{tc}}={\mathrm{\Pi }}_{\mathit{sc}}^c$, if and only if $q_{\mathit{tc}}^{\ast }=q_c^{\ast }$. To achieve this, we need to find the conditions under which the LSGSC can be coordinated via the flexible trade credit contract in different scenarios.

When $q>k$:

Setting $q_{\mathit{tc}}^{\ast }=q_c^{\ast }$, we have:

$$F^{-1}\left(\frac{\left(1-\beta \right)\left(p-w\right)+w\theta \left(2\delta -\beta \right)}{p(1-\beta )}\right)=F^{-1}\left(\frac{p\left(1-\beta \right)-\pi }{p(1-\beta )}\right)$$ (A.39)

After simplification, we have

$$w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)=\pi$$ (A.40)

Substituting ${\theta }^{\ast }$ (derived in Eq. (A.36)) into Eq. (A.40), we have:

$$p\left(1-\beta \right)f\left(q_{\mathit{tc}}^{\ast }\right)\left[w{q}_{\mathit{tc}}^{\ast }\left(\beta -2\delta \right)+\left(1-\beta \right)w\delta k\right]=0$$ (A.41)

Since $p\left(1-\beta \right)f\left(q_{\mathit{tc}}^{\ast }\right)>0$, we have

$$w{q}_{\mathit{tc}}^{\ast }\left(\beta -2\delta \right)+\left(1-\beta \right)w\delta k=0$$ (A.42)

Following some simplifications, we can derive the channel coordination condition as follows:

$${\delta }_c^{\ast }=\frac{\beta q_{\mathit{tc}}^{\ast }}{2q_{\mathit{tc}}^{\ast }-\left(1-\beta \right)k}=\frac{\beta q_c^{\ast }}{2q_c^{\ast }-\left(1-\beta \right)k}$$ (A.43)

When $q\le k$, setting $q_{\mathit{tc}}^{\ast }=q_c^{\ast }$, we have

$$F^{-1}\left(\frac{(1-\beta )(p-w)+w(2\delta -\beta )\theta }{p(1-\beta )}\right)=F^{-1}\left(\frac{p\left(1-\beta \right)-c}{p(1-\beta )}\right)$$ (A.44)

which can be further simplified to

$$w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)=c$$ (A.45)

Substituting ${\theta }^{\ast }$ (Eq. (A.36)) into Eq. (A.45), we have:

$${\delta }_c^{\ast }=\frac{\beta q_{\mathit{tc}}^{\ast }}{2q_{\mathit{tc}}^{\ast }-\left(1-\beta \right)k}=\frac{\beta q_c^{\ast }}{2q_c^{\ast }-\left(1-\beta \right)k}$$ (A.46)

In summary, the LSGSC can be coordinated under the flexible trade credit, if and only if:

$${\delta }_c^{\ast }=\frac{\beta q_c^{\ast }}{2q_c^{\ast }-\left(1-\beta \right)k}$$ (A.47)

Considering the participation condition of supplier (Eq. (16)), $0<{\delta }_c^{\ast }<r_s$, we have $k<\min \left(\frac{2q_c^{\ast }}{1-\beta },\frac{q_c^{\ast }\left(2r_s-\beta \right)}{r_s\left(1-\beta \right)}\right)$.

We next analyze the impacts of $k$, $q_c^{\ast }$, $\beta$ on LSGSC’s coordination condition:

$$\frac{\partial {\delta }_c^{\ast }}{\partial k}=\frac{\beta {\left(1-\beta \right)q}_c^{\ast }}{{\left(2q_c^{\ast }-\left(1-\beta \right)k\right)}^2}>0$$ (A.48)

$$\frac{\partial {\delta }_c^{\ast }}{\partial q_c^{\ast }}=\frac{-\beta \left(1-\beta \right)k}{{\left(2q_c^{\ast }-\left(1-\beta \right)k\right)}^2}<0$$ (A.49)

As can be seen in Eq. (3), $q_c^{\ast }$ is a function of $\beta$. Taking the first derivative of ${\delta }_c^{\ast }$ with respect to $\beta$, we have:

$$\frac{\mathrm{d}{\delta }_c^{\ast }}{\mathrm{d}\beta }=\frac{\partial {\delta }_c^{\ast }}{\partial q_c^{\ast }}\frac{\partial q_c^{\ast }}{\partial \beta }+\frac{\partial {\delta }_c^{\ast }}{\partial \beta }=\left\{\begin{array}{c}\frac{2q_c^{\ast 2}f\left(q_c^{\ast }\right)p(1-\beta )-k\left[q_c^{\ast }f\left(q_c^{\ast }\right)p\left(1-\beta \right)-\beta \pi \right]}{{\left(2q_c^{\ast }-\left(1-\beta \right)k\right)}^{2}f\left(q_c^{\ast }\right)p(1-\beta )}ifq>k\hfill \\ \frac{2q_c^{\ast 2}f\left(q_c^{\ast }\right)p(1-\beta )-k\left[q_c^{\ast }f\left(q_c^{\ast }\right)p\left(1-\beta \right)-\beta c\right]}{{\left(2q_c^{\ast }-\left(1-\beta \right)k\right)}^{2}f\left(q_c^{\ast }\right)p(1-\beta )}ifq\le k\hfill \end{array}\right)$$ (A.50)

To prove $\frac{\mathrm{d}{\delta }_c^{\ast }}{\mathrm{d}\beta }>0$ when $q>k$, it suffices to show that $2q_c^{\ast 2}f\left(q_c^{\ast }\right)p(1-\beta )-k\left[q_c^{\ast }f\left(q_c^{\ast }\right)p\left(1-\beta \right)-\beta \pi \right]>0$, that is $k<\frac{2p\left(1-\beta \right)q_c^{\ast 2}f\left(q_c^{\ast }\right)}{p\left(1-\beta \right)q_c^{\ast }f\left(q_c^{\ast }\right)-\beta \pi }$. Since $k<q_c^{\ast }<2q_c^{\ast }<\frac{2p\left(1-\beta \right)q_c^{\ast 2}f\left(q_c^{\ast }\right)}{p\left(1-\beta \right)q_c^{\ast }f\left(q_c^{\ast }\right)-\beta \pi }$, we always have $\frac{\mathrm{d}{\delta }_c^{\ast }}{\mathrm{d}\beta }>0$.

There are two scenarios when $q\le k.$ If $q_c^{\ast }<k<2q_c^{\ast }<\frac{2p\left(1-\beta \right)q_c^{\ast 2}f\left(q_c^{\ast }\right)}{p\left(1-\beta \right)q_c^{\ast }f\left(q_c^{\ast }\right)-\beta c}$, we have$\frac{\mathrm{d}{\delta }_c^{\ast }}{\mathrm{d}\beta }>0$. If $q_c^{\ast }<2q_c^{\ast }<\frac{2p\left(1-\beta \right)q_c^{\ast 2}f\left(q_c^{\ast }\right)}{p\left(1-\beta \right)q_c^{\ast }f\left(q_c^{\ast }\right)-\beta c}<k$, we have $\frac{\mathrm{d}{\delta }_c^{\ast }}{\mathrm{d}\beta }<0$, where the penalty from breaching the MOQ condition outweighs the total trade credit discounts, that is $\left(1-\beta \right)w\delta \theta \left(2q_c^{\ast }-k\right)+\beta w\delta \left(2\theta q_c^{\ast }-k\right)<0$. In the luxury industry, LSG suppliers usually keep small runs rather than massive production capacity. Thus, this scenario is purposefully eliminated from our analysis. Together with the supplier’s participation condition of $k<\min \left(\frac{2q_c^{\ast }}{1-\beta },\frac{q_c^{\ast }\left(2r_s-\beta \right)}{r_s\left(1-\beta \right)}\right),$ we have $\frac{\mathrm{d}{\delta }_c^{\ast }}{\mathrm{d}\beta }>0$, if and only if $k<\min \left(\frac{2q_c^{\ast }}{1-\beta },\frac{q_c^{\ast }\left(2r_s-\beta \right)}{r_s\left(1-\beta \right)},\frac{2p\left(1-\beta \right)q_c^{\ast 2}f\left(q_c^{\ast }\right)}{p\left(1-\beta \right)q_c^{\ast }f\left(q_c^{\ast }\right)-\beta c}\right)$.

(Q.E.D).

Proof of Corollary 3.

Combining Eqs. (A.36), (A.40) and (A.45), we have:

$${\theta }_c^{\ast }=\left\{\begin{array}{c}\frac{w\left(1-\beta \right)-\pi }{w\left(2{\delta }_c^{\ast }-\beta \right)}ifq>k\hfill \\ \frac{w\left(1-\beta \right)-c}{w\left(2{\delta }_c^{\ast }-\beta \right)}ifq\le k\hfill \end{array}\right)$$ (A.51)

Substituting $r_s$ (Eq. (16)) into Eq. (A.51), we have:

$${\theta }_c^{\ast }=\frac{r_s-\beta }{2{\delta }_c^{\ast }-\beta }$$ (A.52)

where ${\delta }_c^{\ast }=\frac{\beta q_c^{\ast }}{2q_c^{\ast }-\left(1-\beta \right)k}$.

From Eq. (A.52), we can easily show that, $2{\delta }_c^{\ast }-\beta >0$ and $k<\frac{2q_c^{\ast }}{1-\beta }$. Hence, to ensure that ${\theta }_c^{\ast }$ is nonnegative, it suffices to show $r_s>\beta$.

For the monotonicity of ${\theta }_c^{\ast }$ with respect to $r_s$ and ${\delta }_c^{\ast }$, we have:

$$\frac{\partial {\theta }_c^{\ast }}{\partial r_s}=\frac{1}{2{\delta }_c^{\ast }-\beta }>0$$ (A.53)

$$\frac{\partial {\theta }_c^{\ast }}{\partial {\delta }_c^{\ast }}=\frac{-2\left(r_s-\beta \right)}{{\left(2{\delta }_c^{\ast }-\beta \right)}^2}<0$$ (A.54)

(Q.E.D).

Proof of Theorem 7.

For the wholesale price contract, the maximum expected profit for both parties can be presented as follows:

$${\mathrm{\Pi }}_{\mathrm{s}}^d\left(q_d^{\ast }\right)=\left\{\begin{array}{c}\left(w-\pi \right)q_d^{\ast }+\left(\pi -c\right)kifq>k\hfill \\ \left(w-c\right)q_d^{\ast }ifq\le k\hfill \end{array}\right)$$ (A.55)

$${\mathrm{\Pi }}_w^d\left(q_d^{\ast }\right)=\left(1-\beta \right)\left[p{\int }_0^{q_d^{\ast }}\overline{F}\left(x\right)dx-w{q}_d^{\ast }\right]-\beta w{q}_d^{\ast }$$ (A.56)

Under channel coordination, the optimal expected profit of individual players can be derived as follows:

$${\mathrm{\Pi }}_s^{\mathit{tc}}\left(q_c^{\ast }\right)=\left\{\begin{array}{c}{q}_c^{\ast }\left[w\left(1-\beta +\left(\beta -2{\delta }_c^{\ast }\right){\theta }_c^{\ast }\right)-\pi \right]+w{\delta }_c^{\ast }k\left(\beta +\left(1-\beta \right){\theta }_c^{\ast }\right)+\left(\pi -c\right)kifq>k\hfill \\ q_c^{\ast }\left[w\left(1-\beta +\left(\beta -2{\delta }_c^{\ast }\right){\theta }_c^{\ast }\right)-c\right]+w{\delta }_c^{\ast }k\left(\beta +\left(1-\beta \right){\theta }_c^{\ast }\right)ifq\le k\hfill \end{array},\right)$$ (A.57)

$${\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_c^{\ast }\right)=\left(1-\beta \right)\left[p{\int }_0^{q_c^{\ast }}\overline{F}\left(x\right)dx-w{q}_c^{\ast }+2w{\delta }_c^{\ast }{\theta }_c^{\ast }{q}_c^{\ast }-w{\delta }_c^{\ast }{\theta }_c^{\ast }k\right]+\beta \left[w{\delta }_c^{\ast }\left({\theta }_c^{\ast }{q}_c^{\ast }-k\right)-w\left(1-{\delta }_c^{\ast }\right){\theta }_c^{\ast }{q}_c^{\ast }\right]$$ (A.58)

To guarantee the LSG supplier’s participation in the flexible trade credit contract with MOQ and achieve channel coordination, it suffices to prove,

$${\mathrm{\Pi }}_s^{\mathit{tc}}\left(q_c^{\ast }\right)-{\mathrm{\Pi }}_{\mathrm{s}}^d\left(q_d^{\ast }\right)>0$$ (A.59)

When $q>k$ ,

$${\mathrm{\Pi }}_s^{\mathit{tc}}\left(q_c^{\ast }\right)-{\mathrm{\Pi }}_{\mathrm{s}}^d\left(q_d^{\ast }\right)=\left(w-\pi \right)\left(q_c^{\ast }-q_d^{\ast }\right)-{\mathit{wq}}_c^{\ast }\left[\beta -\left(\beta -2{\delta }_c^{\ast }\right){\theta }_c^{\ast }\right]+w{\delta }_c^{\ast }k\left(\beta +\left(1-\beta \right){\theta }_c^{\ast }\right)>0$$ (A.60)

After some algebraic simplifications, Eq. (A.60) can be further reduced to:

$$\begin{gathered} \left(w-\pi \right)\left(q_c^{\ast }-q_d^{\ast }\right)>{\mathit{wq}}_c^{\ast }\left[\beta -\left(\beta -2{\delta }_c^{\ast }\right){\theta }_c^{\ast }\right]-w{\delta }_c^{\ast }k\left(\beta +\left(1-\beta \right){\theta }_c^{\ast }\right) \\ =\left(1-\beta \right)w{\delta }_c^{\ast }{\theta }_c^{\ast }\left(2q_c^{\ast }-k\right)+\beta w{\delta }_c^{\ast }\left(2{\theta }_c^{\ast }{q}_c^{\ast }-k\right)+\beta w{q}_c^{\ast }\left(1-{\theta }_c^{\ast }\right) \end{gathered}$$ (A.61)

Rearranging the right-hand side of Eq. (A.61), we can derive the transfer payment made by the supplier, including the early-payment discounts, incentive (penalty) payments, and cost incurred by risk-sharing of trade disruption (see Table 3).

Under channel coordination (see Eq. (A.42)), we have:

$$q_c^{\ast }=q_{\mathit{tc}}^{\ast }=\frac{\left(1-\beta \right){\delta }_c^{\ast }k}{2{\delta }_c^{\ast }-\beta }$$ (A.62)

Substituting Eq. (A.62) into Eq. (A.61), we have ${\mathrm{\Pi }}_s^{\mathit{tc}}\left(q_c^{\ast }\right)-{\mathrm{\Pi }}_{\mathrm{s}}^d\left(q_d^{\ast }\right)>0$, if:

$$\left(w-\pi \right)\left(q_c^{\ast }-q_d^{\ast }\right)>\beta w{\delta }_c^{\ast }k\left(\frac{1-2{\delta }_c^{\ast }}{2{\delta }_c^{\ast }-\beta }\right)$$ (A.63)

Similarly, when $q\le k$, we have ${\mathrm{\Pi }}_s^{\mathit{tc}}\left(q_c^{\ast }\right)-{\mathrm{\Pi }}_{\mathrm{s}}^d\left(q_d^{\ast }\right)>0$, if:

$$\left(w-c\right)\left(q_c^{\ast }-q_d^{\ast }\right)>\beta w{\delta }_c^{\ast }k\left(\frac{1-2{\delta }_c^{\ast }}{2{\delta }_c^{\ast }-\beta }\right)$$ (A.64)

To guarantee wholesaler’s participation in the flexible trade credit contract with MOQ and achieve channel coordination, it suffices to prove ${\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_c^{\ast }\right)-{\mathrm{\Pi }}_w^d\left(q_d^{\ast }\right)>0$. That is:

$$\begin{gathered} \left(1-\beta \right)\left[p{\int }_0^{q_c^{\ast }}\overline{F}\left(x\right)dx-w{q}_c^{\ast }+2w{\delta }_c^{\ast }{\theta }_c^{\ast }{q}_c^{\ast }-w{\delta }_c^{\ast }{\theta }_c^{\ast }k\right] \\ +\beta \left[w{\delta }^{\ast }\left({\theta }^{\ast }{q}_c^{\ast }-k\right)-w\left(1-{\delta }^{\ast }\right){\theta }^{\ast }{q}_c^{\ast }\right]-\left(1-\beta \right)\left[p{\int }_0^{q_d^{\ast }}\overline{F}\left(x\right)dx-w{q}_d^{\ast }\right]+\beta w{q}_d^{\ast }>0 \end{gathered}$$ (A.65)

After simplification, we have:

$$w{q}_c^{\ast }\left[\left(2{\delta }_c^{\ast }-\beta \right){\theta }_c^{\ast }+\beta \right]-w{\delta }_c^{\ast }k\left[\left(1-\beta \right){\theta }_c^{\ast }+\beta \right]>\left(1-\beta \right)p\left({\int }_0^{q_d^{\ast }}\overline{F}\left(x\right)dx-{\int }_0^{q_c^{\ast }}\overline{F}\left(x\right)dx\right)+w\left(q_c^{\ast }-q_d^{\ast }\right)$$ (A.66)

Substituting Eq. (A.62) into Eq. (A.66), we have ${\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_c^{\ast }\right)-{\mathrm{\Pi }}_w^d\left(q_d^{\ast }\right)>0$, if:

$$\beta w{\delta }_c^{\ast }k\left(\frac{1-2{\delta }_c^{\ast }}{2{\delta }_c^{\ast }-\beta }\right)>\left(1-\beta \right)p\left({\int }_0^{q_d^{\ast }}\overline{F}\left(x\right)dx-{\int }_0^{q_c^{\ast }}\overline{F}\left(x\right)dx\right)+w\left(q_c^{\ast }-q_d^{\ast }\right)$$ (A.67)

Using Eqs. (A.63), (A.64), and (A.67), we can derive the condition under which the flexible trade credit contract with MOQ condition can achieve win–win coordination:

$$\left\{\begin{array}{c}p\left(1-\beta \right)\left({\int }_0^{q_d^{\ast }}\overline{F}\left(x\right)dx-{\int }_0^{q_c^{\ast }}\overline{F}\left(x\right)dx\right)+w\left(q_c^{\ast }-q_d^{\ast }\right)<\mathrm{\Delta }\mathrm{\Pi }<\left(w-\pi \right)\left(q_c^{\ast }-q_d^{\ast }\right)ifq>k\hfill \\ p\left(1-\beta \right)\left({\int }_0^{q_d^{\ast }}\overline{F}\left(x\right)dx-{\int }_0^{q_c^{\ast }}\overline{F}\left(x\right)dx\right)+w\left(q_c^{\ast }-q_d^{\ast }\right)<\mathrm{\Delta }\mathrm{\Pi }<\left(w-c\right)\left(q_c^{\ast }-q_d^{\ast }\right)ifq\le k\hfill \end{array}\right)$$ (A.68)

where $\mathrm{\Delta }\mathrm{\Pi }=\beta w{\delta }_c^{\ast }k\left(\frac{1-2{\delta }_c^{\ast }}{2{\delta }_c^{\ast }-\beta }\right)$ refers to the supplier’s transfer payment to the wholesaler.

From Eq. (A52), we always have $1-2{\delta }_c^{\ast }>0$. To ensure the nonnegativity of $\mathrm{\Delta }\mathrm{\Pi }$, we also need to prove ${\delta }_c^{\ast }>\frac{\beta }{2}$. Considering the supplier’s participation condition $\overline{{\delta }_c^{\ast }}=r_s$ (derived in Theorem 6), we can derive a feasible interval of early-payment discount, ${\delta }_c^{\ast }\in \left(\frac{\beta }{2},min\left(\frac{1}{2},r_s\right)\right)$, that concurrently guarantees the supplier’s participation and ensures the nonnegativity of $\mathrm{\Delta }\mathrm{\Pi }$. We next examine the feasibility of MOQ condition given the derived interval of early-payment discount.

When $r_s>\frac{1}{2}$, the feasible interval of early-payment is ${\delta }_c^{\ast }\in \left(\frac{\beta }{2},\frac{1}{2}\right)$, where $k<min\left(\frac{{2q}_c^{\ast }}{1-\beta },{2q}_c^{\ast }\right)$. According to the supplier’s participation condition (derived in Theorem 6), we have $\frac{q_c^{\ast }\left(2r_s-\beta \right)}{r_s\left(1-\beta \right)}>2q_c^{\ast }$, if $r_s>\frac{1}{2}$. Thus, when $r_s>\frac{1}{2}$, $k<2q_c^{\ast }$.

When $r_s\le \frac{1}{2}$, we have ${\delta }_c^{\ast }\in \left(\frac{\beta }{2},r_s\right)$, where $k<min\left(\frac{{2q}_c^{\ast }}{1-\beta },\frac{q_c^{\ast }\left(2r_s-\beta \right)}{r_s\left(1-\beta \right)}\right)$. Therefore, when $r_s\le \frac{1}{2}$, $k<\frac{q_c^{\ast }\left(2r_s-\beta \right)}{r_s\left(1-\beta \right)}$.

The above conditions always hold when $q>k$. However, if $q\le k$, the following additional conditions must be also satisfied:

• (i)If $r_s>\frac{1}{2}$ , then $q_c^{\ast }\le k<2q_c^{\ast };$
• (ii)If $r_s\le \frac{1}{2}$ , then $q_c^{\ast }\le k<\frac{q_c^{\ast }\left(2r_s-\beta \right)}{r_s\left(1-\beta \right)}.$

(Q.E.D).

Proof of Corollary 4.

Using Theorem 7, we can prove the following properties:

$$\frac{\partial \mathrm{\Delta }\mathrm{\Pi }}{\partial w}=\beta {\delta }_c^{\ast }k\left(\frac{1-2{\delta }_c^{\ast }}{2{\delta }_c^{\ast }-\beta }\right)>0$$ (A.69)

$$\frac{\partial \mathrm{\Delta }\mathrm{\Pi }}{\partial k}=\beta w{\delta }_c^{\ast }\left(\frac{1-2{\delta }_c^{\ast }}{2{\delta }_c^{\ast }-\beta }\right)>0$$ (A.70)

$$\frac{\partial \mathrm{\Delta }\mathrm{\Pi }}{\partial {\delta }_c^{\ast }}=\frac{\beta wk\left[4{\delta }_c^{\ast }\beta -4{{\delta }_c^{\ast }}^2-\beta \right]}{{\left(2{\delta }_c^{\ast }-\beta \right)}^2}<\frac{\beta wk\left[4{\delta }_c^{\ast }\beta -4{{\delta }_c^{\ast }}^2-{\beta }^2\right]}{{\left(2{\delta }_c^{\ast }-\beta \right)}^2}=-\beta wk<0$$ (A.71)

(Q.E.D).

Proof of Lemma 1.

For any realized demand $x\le q$ in Eq. (20), setting ${\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right)=0$, we have:

$${\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right)=\left(1-\beta \right)\left[px-wq\left(1-\delta \theta \right)+\theta \delta w\left(q-k\right)\right]+\beta \left[-\left(1-\delta \right)w\theta q+\delta w\left(\theta q-k\right)\right]=p\left(1-\beta \right)x-wq\left[1-\beta +\left(\beta -2\delta \right)\theta \right]-w\delta k\left[\left(1-\beta \right)\theta +\beta \right]=0$$ (A.72)

After some simplification, the breakeven point of realized demand can be shown as follows,

$$\underset{\_}{x}\left(q\right)=\frac{wq\left(1-\beta +\left(\beta -2\delta \right)\theta \right)+w\delta k\left(\left(1-\beta \right)\theta +\beta \right)}{p\left(1-\beta \right)}$$ (A.73)

When $x\le q$, ${\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right)$ is strictly increasing in $x$. Hence, if $x<\underset{\_}{x}\left(q\right)$, ${\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right)<0$.

(Q.E.D).

Proof of Theorem 8.

To prove the concavity of the loss-averse wholesaler’s expected utility function $U({\mathrm{\Pi }}_w\left(q\left|\theta \right)\right))$ (Eq. (23)), the first order and second order derivative of $U({\mathrm{\Pi }}_w\left(q\left|\theta \right)\right))$ with respect to $q$ are derived as follows:

$$\frac{\partial U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right))}{\partial q}=\left(1-\beta \right)\left[p\left(1-F\left(q\right)\right)-w\left(1-\delta \theta \right)+w\delta \theta \right]+\beta \left[-\left(1-\delta \right)w\theta +w\delta \theta \right]-\left(\lambda -1\right)w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)F\left(\underset{\_}{x}\left(q\right)\right)$$ (A.74)

$$\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right))}{\partial q^2}=-p\left(1-\beta \right)f\left(q\right)-\left(\lambda -1\right)w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)f\left(\underset{\_}{x}\left(q\right)\right)$$ (A.75)

Eq. (13) (see Theorem 4) can be rewritten as follows:

$$q_{\mathit{tc}}^{\ast }=F^{-1}\left(\frac{C_u}{C_u+C_o}\right),$$ (A.76)

where $C_u=\left(1-\beta \right)\left(p-w\right)+w\theta \left(2\delta -\beta \right)>0$, $C_o=w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)>0$.

Substituting $C_o$ into Eq. (A.75), we have:

$$\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right))}{\partial q^2}=-p\left(1-\beta \right)f\left(q\right)-\left(\lambda -1\right)C_{o}f\left(\underset{\_}{x}\left(q\right)\right)<0$$ (A.77)

Therefore, the loss-averse wholesaler’s expected utility function $U({\mathrm{\Pi }}_w\left(q\left|\theta \right)\right))$ is concave. Setting $\frac{\partial U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right))}{\partial q}=0$, we have:

$$\frac{\partial U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial q}=\left(1-\beta \right)p\overline{F}\left(q_{\lambda }^{\ast }\right)-w\left[1-\beta +\left(\beta -2\delta \right)\theta \right]-\left(\lambda -1\right)w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)F\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)=0$$ (A.78)

Substituting $C_u$ and $C_o$ into Eq. (A.78), we have:

$$C_u\overline{F}\left(q_{\lambda }^{\ast }\right)-C_{o}F\left(q_{\lambda }^{\ast }\right)-\left(\lambda -1\right)\left(C_{o}F\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)\right)=0$$ (A.79)

where $C_{o}F\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)$ refers to the marginal overage loss of the loss-averse wholesaler. So, when the wholesaler is risk neutral, the first order condition reduces to:

$$C_u\overline{F}\left(q_{\lambda }^{\ast }\right)-C_{o}F\left(q_{\lambda }^{\ast }\right)=0$$ (A.80)

which suggests that when $\lambda =1$, we always have $q_{\lambda }^{\ast }=q_{\mathit{tc}}^{\ast }$.

(Q.E.D).

Proof of Corollary 5.

Substituting $q_{\mathit{tc}}^{\ast }$ into Eq. (A.74), we have:

$$\frac{\partial U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\mathit{tc}}^{\ast }\left|\theta \right)\right))}{\partial q}=-\left(\lambda -1\right)C_{o}F\left({\underset{\_}{x}(q}_{\mathit{tc}}^{\ast })\right)<0$$ (A.81)

As shown in the Proof of Theorem 8, $U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q\left|\theta \right)\right))$ is concave. Hence, we always have $q_{\lambda }^{\ast }<q_{\mathit{tc}}^{\ast }$. According to the implicit function theorem, we have:

$$\frac{\partial q_{\lambda }^{\ast }}{\partial \lambda }=\frac{\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial \mathrm{q}\partial \lambda }}{-\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial q^2}}=\frac{-C_{o}F\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)}{p\left(1-\beta \right)f\left(q_{\lambda }^{\ast }\right)+\left(\lambda -1\right)C_{o}f\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)}<0$$ (A.82)

(Q.E.D).

Proof of Corollary 6.

To prove monotonicity of $q_{\lambda }^{\ast }$ with respect to $\delta$, $\theta$, $\beta$,$p$, $w$ and $k$, we take the first-order partial derivatives of $q_{\lambda }^{\ast }$.

$$\frac{\partial q_{\lambda }^{\ast }}{\partial \delta }=\frac{\frac{{\partial }^{2}U\left({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right)\right)}{\partial \mathrm{q}\partial \delta }}{-\frac{{\partial }^{2}U\left({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right)\right)}{\partial q^2}}=\frac{2w\theta \left[1+\left(\lambda -1\right)F\left(\underset{\_}{x}{(q}_{\lambda }^{\ast })\right)\right]+\frac{w\left(\lambda -1\right)}{p\left(1-\beta \right)}{C}_{o}f\left(\underset{\_}{x}{(q}_{\lambda }^{\ast })\right)\left[2\theta q_{\lambda }^{\ast }-k\left(\left(1-\beta \right)\theta +\beta \right)\right]}{-\frac{{\partial }^{2}U\left({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right)\right)}{\partial q^2}}\mathrm{A}.83$$

If $2w\theta \left[1+\left(\lambda -1\right)F\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)\right]+\frac{w\left(\lambda -1\right)}{p\left(1-\beta \right)}{C}_{o}f\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)\left[2\theta q_{\lambda }^{\ast }-k\left(\left(1-\beta \right)\theta +\beta \right)\right]>0$, then we have $\frac{\partial q_{\lambda }^{\ast }}{\partial \delta }>0$. When $\lambda =1$, $\frac{\partial q_{\lambda }^{\ast }}{\partial \delta }=\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \delta }=\frac{1}{f\left(q_{\mathit{tc}}^{\ast }\right)}\frac{2w\theta }{p\left(1-\beta \right)}>0$.

$$\frac{\partial q_{\lambda }^{\ast }}{\partial \theta }=\frac{\frac{{\partial }^{2}U\left({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right)\right)}{\partial q\partial \theta }}{-\frac{{\partial }^{2}U\left({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right)\right)}{\partial q^2}}=\frac{-\left[w\left(\beta -2\delta \right)+\left(\lambda -1\right)\left(w\left(\beta -2\delta \right)F\left(\underset{\_}{x}{(q}_{\lambda }^{\ast })\right)+\frac{C_{o}f\left(\underset{\_}{x}{(q}_{\lambda }^{\ast })\right)\left[w{q}_{\lambda }^{\ast }\left(\beta -2\delta \right)+w\delta k\left(1-\beta \right)\right]}{p\left(1-\beta \right)}\right)\right]}{-\frac{{\partial }^{2}U\left({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right)\right)}{\partial q^2}}\mathrm{A}.84$$

If $w\left(\beta -2\delta \right)+\left(\lambda -1\right)\left(w\left(\beta -2\delta \right)F\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)+\frac{c_{o}f\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)\left[w{q}_{\lambda }^{\ast }\left(\beta -2\delta \right)+w\delta k\left(1-\beta \right)\right]}{p\left(1-\beta \right)}\right)>0$, then we have $\frac{\partial q_{\lambda }^{\ast }}{\partial \theta }<0$; otherwise, $\frac{\partial q_{\lambda }^{\ast }}{\partial \theta }\ge 0$. When $\lambda =1$, $\frac{\partial q_{\lambda }^{\ast }}{\partial \theta }=\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \theta }=\frac{1}{f\left(q_{\mathit{tc}}^{\ast }\right)}\frac{w\left(2\delta -\beta \right)}{p\left(1-\beta \right)}$.

Similarly,

$$\frac{\partial q_{\lambda }^{\ast }}{\partial \beta }=\frac{\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial \mathrm{q}\partial \beta }}{-\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial q^2}}=\frac{-\left[p\overline{F}\left(q_{\lambda }^{\ast }\right)+w\left(-1+\theta \right)+w\left(\lambda -1\right)\left(-1+\theta \right)F\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)+C_o\left(\lambda -1\right)f\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)\frac{w\left(1-2\delta \right)\theta +w\delta k}{p{\left(1-\beta \right)}^2}\right]}{-\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial q^2}}$$ (A.85)

Using Eq. (A.78), we have $\left(1-\beta \right)p\overline{F}\left(q_{\lambda }^{\ast }\right)=w\left[1-\beta +\left(\beta -2\delta \right)\theta \right]+\left(\lambda -1\right)w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)F\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)$, then we have

$$\frac{\partial q_{\lambda }^{\ast }}{\partial \beta }=\frac{-\left[\frac{w\theta \left(1-2\delta \right)}{1-\beta }\left[1+\left(\lambda -1\right)F\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)\right]+C_o\left(\lambda -1\right)f\left(x\left(q_{\lambda }^{\ast }\right)\right)\frac{w\left(1-2\delta \right)\theta +w\delta k}{p{\left(1-\beta \right)}^2}\right]}{-\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial q^2}}$$ (A.86)

Having $0<1-\beta +\left(\beta -2\delta \right)\theta \le 1-2\delta$, we can show $\frac{w\theta \left(1-2\delta \right)}{1-\beta }\left[1+\left(\lambda -1\right)F\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)\right]+C_o\left(\lambda -1\right)f\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)\frac{w\left(1-2\delta \right)\theta +w\delta k}{p{\left(1-\beta \right)}^2}>0$. Hence, we have $\frac{\partial q_{\lambda }^{\ast }}{\partial \beta }<0$. When $\lambda =1$, $\frac{\partial q_{\lambda }^{\ast }}{\partial \beta }=\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial \beta }=\frac{1}{f\left(q_{\mathit{tc}}^{\ast }\right)}\frac{-w\theta \left(1-2\delta \right)}{p{\left(1-\beta \right)}^2}<0$.

$$\frac{\partial q_{\lambda }^{\ast }}{\partial p}=\frac{\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial q\partial p}}{-\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial q^2}}=\frac{\left(1-\beta \right)\overline{F}\left(q_{\lambda }^{\ast }\right)+C_o\left(\lambda -1\right)f\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right){\underset{\_}{x}(q}_{\lambda }^{\ast })/p}{-\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial q^2}}>0$$ (A.87)

when $\lambda =1$, $\left(1-\beta \right)\overline{F}\left(q_{\lambda }^{\ast }\right)=w\left[1-\beta +\left(\beta -2\delta \right)\theta \right]$, then we have $\frac{\partial q_{\lambda }^{\ast }}{\partial p}=\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial p}=\frac{1}{f\left(q_{\mathit{tc}}^{\ast }\right)}\frac{w\left[1-\beta +\left(\beta -2\delta \right)\theta \right]}{p^2\left(1-\beta \right)}>0$.

$$\frac{\partial q_{\lambda }^{\ast }}{\partial w}=\frac{\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial q\partial w}}{-\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial q^2}}=\frac{-\left(1-\beta +\left(\beta -2\delta \right)\theta \right)\left[1+\left(\lambda -1\right)\left[F\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)+\frac{C_{o}f\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)q_{\lambda }^{\ast }}{p\left(1-\beta \right)}\right]\right]}{-\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial q^2}}<0$$ (A.88)

when $\lambda =1$, $\frac{\partial q_{\lambda }^{\ast }}{\partial w}=\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial w}=\frac{1}{f\left(q_{\mathit{tc}}^{\ast }\right)}\frac{-\left[1-\beta +\left(\beta -2\delta \right)\theta \right]}{p\left(1-\beta \right)}<0$.

$$\frac{\partial q_{\lambda }^{\ast }}{\partial k}=\frac{\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial q\partial k}}{-\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial q^2}}=\frac{-C_o\left(\lambda -1\right)f\left({\underset{\_}{x}(q}_{\lambda }^{\ast })\right)\frac{w\delta \left(\left(1-\beta \right)\theta +\beta \right)}{p\left(1-\beta \right)}}{-\frac{{\partial }^{2}U({\mathrm{\Pi }}_w^{\mathit{tc}}\left(q_{\lambda }^{\ast }\left|\theta \right)\right))}{\partial q^2}}<0$$ (A.89)

when $\lambda =1$, $\frac{\partial q_{\lambda }^{\ast }}{\partial k}=0$.

(Q.E.D).

Proof of Theorem 9.

In the presence of wholesaler’s loss aversion, the expected profit function of LSG supplier remains unchanged, and therefore, the proof is identical to Theorem 5.

Substituting $q_{\lambda }^{\ast }$ into Eq. (A.36), we have:

$${\theta }_{\lambda }^{\ast }=\left\{\begin{array}{c}\frac{f\left(q_{\lambda }^{\ast }\right)p\left(1-\beta \right)\left[\left(1-\beta \right)w\delta k+\rho q_{\lambda }^{\ast }\right]-\rho \left(\left(1-\beta \right)w-\pi \right)}{{\rho }^2}ifq>k\hfill \\ \frac{f\left(q_{\lambda }^{\ast }\right)p\left(1-\beta \right)\left[\left(1-\beta \right)w\delta k+\rho q_{\lambda }^{\ast }\right]-\rho \left(\left(1-\beta \right)w-c\right)}{{\rho }^2}ifq\le k\hfill \end{array}\right),$$ (A.90)

where $\rho =w\left(\beta -2\delta \right)$. If $q>k$, $\frac{f^{\text{'}}\left(q_{\lambda }^{\ast }\right)\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-\pi \right]}{f^2\left(q_{\lambda }^{\ast }\right)p\left(1-\beta \right)}+2>0$; if $q\le k$, $\frac{f^{\text{'}}\left(q_{\lambda }^{\ast }\right)\left[w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-c\right]}{f^2\left(q_{\lambda }^{\ast }\right)p\left(1-\beta \right)}+2>0$.

(Q.E.D).

Proof of Corollary 7.

To prove the monotonicity of ${\theta }_{\lambda }^{\ast }$ with respect to $k$, we always have:

$$\frac{\partial {\theta }_{\lambda }^{\ast }}{\partial k}=\frac{p\left(1-\beta \right)\left(f^{\text{'}}\left(q_{\lambda }^{\ast }\right)\frac{\partial q_{\lambda }^{\ast }}{\partial k}\left[\left(1-\beta \right)w\delta k+\rho q_{\lambda }^{\ast }\right]+f\left(q_{\lambda }^{\ast }\right)\left[\left(1-\beta \right)w\delta +\rho \frac{\partial q_{\lambda }^{\ast }}{\partial k}\right]\right)}{{\rho }^2}$$ (A.91)

If $\frac{\partial q_{\lambda }^{\ast }}{\partial k}{f}^{\text{'}}\left(q_{\lambda }^{\ast }\right)\left[\left(1-\beta \right)w\delta k+\rho q_{\lambda }^{\ast }\right]+f\left(q_{\lambda }^{\ast }\right)\left[\left(1-\beta \right)w\delta +\rho \frac{\partial q_{\lambda }^{\ast }}{\partial k}\right]>0$, then we have $\frac{\partial {\theta }_{\lambda }^{\ast }}{\partial k}>0$; otherwise, $\frac{\partial {\theta }_{\lambda }^{\ast }}{\partial k}<0$. When $\lambda =1$, we have $\frac{\partial q_{\lambda }^{\ast }}{\partial k}=\frac{\partial q_{\mathit{tc}}^{\ast }}{\partial k}=0$, $\frac{\partial {\theta }_{\lambda }^{\ast }}{\partial k}=\frac{\partial {\theta }^{\ast }}{\partial k}=\frac{pw\delta {\left(1-\beta \right)}^{2}f\left(q_{\lambda }^{\ast }\right)}{{\rho }^2}>0$.

(Q.E.D).

Proof of Corollary 8.

According to the chain rule of derivative, we have,

$$\frac{\partial {\theta }_{\lambda }^{\ast }}{\partial \lambda }=\frac{\partial {\theta }_{\lambda }^{\ast }}{\partial q_{\lambda }^{\ast }}\bullet \frac{\partial q_{\lambda }^{\ast }}{\partial \lambda }=\frac{\partial q_{\lambda }^{\ast }}{\partial \lambda }\bullet \frac{p\left(1-\beta \right)}{{\rho }^2}\left(f^{\text{'}}\left(q_{\lambda }^{\ast }\right)\left[\left(1-\beta \right)w\delta k+\rho q_{\lambda }^{\ast }\right]+\rho f\left(q_{\lambda }^{\ast }\right)\right)$$ (A.92)

Using Eq. (A.92) and having $\frac{\partial q_{\lambda }^{\ast }}{\partial \lambda }<0$ (see Corollary 5), it is easy to show that when $f^{\text{'}}\left(q_{\lambda }^{\ast }\right)\left[\left(1-\beta \right)w\delta k+\rho q_{\lambda }^{\ast }\right]+\rho f\left(q_{\lambda }^{\ast }\right)>0$, we have $\frac{\partial {\theta }_{\lambda }^{\ast }}{\partial q_{\lambda }^{\ast }}>0$, $\frac{\partial {\theta }_{\lambda }^{\ast }}{\partial \lambda }<0$, and ${\theta }_{\lambda }^{\ast }<{\theta }^{\ast }$ (for $\lambda >1$); otherwise ${\theta }_{\lambda }^{\ast }\ge {\theta }^{\ast }$.

(Q.E.D).

Proof of Theorem 10.

Similar to the proof of Theorem 6, we can prove ${\mathrm{\Pi }}_{\mathit{sc}}^{\mathit{tc}}={\mathrm{\Pi }}_{\mathit{sc}}^c$, if $q_{\lambda }^{\ast }=q_c^{\ast }$.

When $q>k$,

Using Eq. (A1) and Eq. (A.78), and setting $q_{\lambda }^{\ast }=q_c^{\ast }$, we have:

$$\left(1-\beta \right)p\overline{F}\left(q_{\lambda }^{\ast }\right)-w\left[1-\beta +\left(\beta -2\delta \right)\theta \right]-\left(\lambda -1\right)w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)F\left(\underset{\_}{x}{(q}_{\lambda }^{\ast })\right)=\left(1-\beta \right)p\overline{F}\left(q_c^{\ast }\right)-\pi \mathrm{A}.93$$

which can be further simplified to

$$\pi =w\left[1-\beta +\left(\beta -2\delta \right)\theta \right]+\left(\lambda -1\right)w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)F\left({\underset{\_}{x}(q}_c^{\ast })\right)$$ (A.94)

Substituting ${\theta }_{\lambda }^{\ast }$ (see Eq. (A.90)) into Eq. (A.94) and after some simplifications, we have:

$${\delta }_{\lambda }^{c\ast }=\frac{\beta \pi v+\left(v+1\right)q_{\lambda }^{\ast }f\left(q_{\lambda }^{\ast }\right)p\left(1-\beta \right)\beta }{2\pi v+\left(v+1\right)f\left(q_{\lambda }^{\ast }\right)p\left(1-\beta \right)\left(2q_{\lambda }^{\ast }-k\left(1-\beta \right)\right)}$$ (A.95)

where $v=\left(\lambda -1\right)F\left(\underset{\_}{x}\left(q_c^{\ast }\right)\right)$.

Similarly, when $q\le k$, let $q_{\lambda }^{\ast }=q_c^{\ast }$, we have:

$$c=w\left[1-\beta +\left(\beta -2\delta \right)\theta \right]+\left(\lambda -1\right)w\left(1-\beta +\left(\beta -2\delta \right)\theta \right)F\left(\underset{\_}{x}\left(q_c^{\ast }\right)\right)$$ (A.96)

Substituting ${\theta }_{\lambda }^{\ast }$ (see Eq. (A.90)) into Eq. (A.96) and after some simplifications, we have:

$${\delta }_{\lambda }^{c\ast }=\frac{\beta cv+\left(v+1\right)q_c^{\ast }f\left(q_c^{\ast }\right)p\left(1-\beta \right)\beta }{2cv+\left(v+1\right)f\left(q_c^{\ast }\right)p\left(1-\beta \right)\left(2q_c^{\ast }-k\left(1-\beta \right)\right)}$$ (A.97)

where $v=\left(\lambda -1\right)F\left(\underset{\_}{x}\left(q_c^{\ast }\right)\right)$.

Thus, the LSGSC with a loss-averse wholesaler can be coordinated via a flexible trade credit contract if and only if the LSG supplier’s early-payment discount satisfies the following condition:

$${\delta }_{\lambda }^{c\ast }=\left\{\begin{array}{c}\frac{\beta \pi v+\left(v+1\right)q_c^{\ast }f\left(q_c^{\ast }\right)p\left(1-\beta \right)\beta }{2\pi v+\left(v+1\right)f\left(q_c^{\ast }\right)p\left(1-\beta \right)\left(2q_c^{\ast }-k\left(1-\beta \right)\right)}ifq>k\hfill \\ \frac{\beta cv+\left(v+1\right)q_c^{\ast }f\left(q_c^{\ast }\right)p\left(1-\beta \right)\beta }{2cv+\left(v+1\right)f\left(q_c^{\ast }\right)p\left(1-\beta \right)\left(2q_c^{\ast }-k\left(1-\beta \right)\right)}ifq\le k\hfill \end{array}\right)$$ (A.98)

where $v=\left(\lambda -1\right)F\left({\underset{\_}{x}(q}_c^{\ast })\right)$. When $\lambda =1$,$v=0$, ${\delta }_{\lambda }^{c\ast }={\delta }_c^{\ast }=\frac{\beta q_c^{\ast }}{2q_c^{\ast }-\left(1-\beta \right)k}$.

(Q.E.D).

Proof of Corollary 9.

In the following, we will analyze the impact of loss-aversion of wholesaler on the coordination condition. The first order partial derivative of ${\delta }_{\lambda }^{\ast }$ respect to $\lambda$ can be derived as follows:

$$\frac{\partial {\delta }_{\lambda }^{c\ast }}{\partial \lambda }=\frac{\partial {\delta }_{\lambda }^{c\ast }}{\partial v}\bullet \frac{\partial v}{\partial \lambda }=F\left(\underset{\_}{x}\left(q_c^{\ast }\right)\right)\frac{\partial {\delta }_{\lambda }^{c\ast }}{\partial v}$$ (A.99)

$$\frac{\partial {\delta }_{\lambda }^{c\ast }}{\partial v}=\frac{\left(\beta \pi +{\beta mq}_c^{\ast }\right)\left[2\pi v+\left(v+1\right)m\left(2q_c^{\ast }-k\left(1-\beta \right)\right)\right]-\left(\beta \pi v+\beta m\left(v+1\right)q_c^{\ast }\right)\left(2\pi +m\left(2q_c^{\ast }-k\left(1-\beta \right)\right)\right)}{{\left[2\pi v+\left(v+1\right)m\left(2q_c^{\ast }-k\left(1-\beta \right)\right)\right]}^2}=\frac{-\beta \pi mk\left(1-\beta \right)}{{\left[2\pi v+\left(v+1\right)m\left(2q_c^{\ast }-k\left(1-\beta \right)\right)\right]}^2}<0$$ (A.100)

where $v=\left(\lambda -1\right)F\left(\underset{\_}{x}\left(q_c^{\ast }\right)\right)$, $m=f\left(q_c^{\ast }\right)p\left(1-\beta \right)$.

Hence, we always have ${\delta }_{\lambda }^{c\ast }<{\delta }_c^{\ast }$, if $\lambda >1$.

(Q.E.D).

Proof of Theorem 11.

To prove the concavity of wholesaler’s expected profit function and obtain the optimal order quantity in the presence of social influence, the first order and second order derivatives of ${\mathrm{\Pi }}_w\left(z_h\left|\theta \right)\right)$ (see Eq. (33)) with respect to $z_h$ are derived as follows:

$$\frac{\partial {\mathrm{\Pi }}_w\left(z_h\left|\theta \right)\right)}{\partial z_h}=\left(1-\beta \right)\left[p_h\left(1-F\left(z_h\right)\right)-w_h\left(1-\delta \theta \right)+w_h\delta \theta \right]+\beta \left[w_h\delta \theta -\left(1-\delta \right)w_h\theta \right]$$ (A.101)

$$\frac{{\partial \mathrm{\Pi }}_w\left(z_h\left|\theta \right)\right)}{\partial z_h^2}=-\left(1-\beta \right)p_{h}f\left(z_h\right)<0$$ (A.102)

Let $\frac{\partial {\mathrm{\Pi }}_w\left(z_h\left|\theta \right)\right)}{\partial z_h}=0$, we have

$$z_h^{\mathit{tc}\ast }=F^{-1}\left(1-\frac{w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)}{p_h(1-\beta )}\right)$$ (A.103)

Therefore, the optimal order quantity for higher-tier products can be obtained as follows:

$$q_h^{\mathit{tc}\ast }=z_h^{\mathit{tc}\ast }-{\gamma }_h\frac{{\mu }_l+{\gamma }_l{\mu }_h}{1+{\gamma }_h{\gamma }_l}$$ (A.104)

As can be seen, the optimal order quantity consists of two components: the first term equates to the optimal order quantity in the basic model, that is $z_h^{\mathit{tc}\ast }=q_{\mathit{tc}}^{\ast }$ (shown in Theorem 4), and the second term denotes the impact of social influence.

(Q.E.D).

Proof of Corollary 10

To examine how the social influence impacts the ordering behavior of wholesaler, we have

$$\frac{\partial q_h^{\mathit{tc}\ast }}{\partial {\gamma }_h}=\frac{-\left({\mu }_l+{\gamma }_l{\mu }_h\right)}{{\left(1+{\gamma }_h{\gamma }_l\right)}^2}<0$$ (A.105)

$$\frac{\partial q_h^{\mathit{tc}\ast }}{\partial {\gamma }_l}=\frac{-{\gamma }_h\left({\mu }_h-{\gamma }_h{\mu }_l\right)}{{\left(1+{\gamma }_h{\gamma }_l\right)}^2}<0$$ (A.106)

From Eq. (A.105), (A.106), we can easily show that the optimal order quantity of wholesaler decreases as the degree of social influence increases.

(Q.E.D).

Proof of Theorem 12.

Substituting Eq. (36) and Eq. (38) into Eq. (31), the expected profit of supplier can be rewritten as

$${\mathrm{\Pi }}_s\left(\theta ,q_l\right)={\mathrm{\Pi }}_s\left(\theta ,z_l\right)={\mathrm{\Pi }}_s^{\mathit{tc}}\left(\theta \left|z_h^{\mathit{tc}\ast }\right)\right)+{\mathrm{\Pi }}_s\left(z_l\right)$$ (A.107)

To prove the concavity of ${\mathrm{\Pi }}_s\left(\theta ,z_l\right)$ with respect to $\theta$ and $z_l$, we have:

when $q_h>k_h$,

$$\frac{\partial {\mathrm{\Pi }}_s\left(\theta ,z_l\right)}{\partial \theta }=\left[w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-{\pi }_h\right]\frac{1}{f\left(z_h^{\mathit{tc}\ast }\right)}\frac{w_h\left(2\delta -\beta \right)}{p_h\left(1-\beta \right)}+w_h{q}_h^{\mathit{tc}\ast }\left(\beta -2\delta \right)+\left(1-\beta \right)w_h\delta k_h\mathrm{A}.108$$

$$\frac{{\partial }^2{\mathrm{\Pi }}_s\left(\theta ,z_l\right)}{\partial {\theta }^2}=-\frac{2}{f\left(z_h^{\mathit{tc}\ast }\right)}\frac{w_h^2{\left(\beta -2\delta \right)}^2}{p_h\left(1-\beta \right)}-\left[w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-{\pi }_h\right]\frac{w_h^2{\left(\beta -2\delta \right)}^2}{p_h\left(1-\beta \right)}\bullet \frac{f^{\text{'}}\left(z_h^{\mathit{tc}\ast }\right)}{f^2\left(z_h^{\mathit{tc}\ast }\right)}\frac{1}{f\left(z_h^{\mathit{tc}\ast }\right)p_h\left(1-\beta \right)}=-\frac{2}{f\left(z_h^{\mathit{tc}\ast }\right)}\frac{w_h^2{\left(\beta -2\delta \right)}^2}{p_h\left(1-\beta \right)}\left(\frac{f^{\text{'}}\left(z_h^{\mathit{tc}\ast }\right)\left[w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-{\pi }_h\right]}{f^2\left(z_h^{\mathit{tc}\ast }\right)}+2\right)$$ (A.109)

$$\frac{{\partial }^2{\mathrm{\Pi }}_s\left(\theta ,z_l\right)}{\partial \theta \partial z_l}=0$$ (A.110)

$$\frac{\partial {\mathrm{\Pi }}_s\left(\theta ,z_l\right)}{\partial z_l}=\left\{\begin{array}{c}{p}_l\left(1-\beta \right)\left(1-F\left(z_l\right)\right)-{\pi }_{l}if{q}_l>k_l\hfill \\ p_l\left(1-\beta \right)\left(1-F\left(z_l\right)\right)-c_{l}if{q}_l\le k_l\hfill \end{array}\right)$$ (A.111)

$$\frac{{\partial }^2{\mathrm{\Pi }}_s\left(\theta ,z_l\right)}{\partial z_l^2}=\left\{\begin{array}{c}-p_l\left(1-\beta \right)f\left(z_l\right)if{q}_l>k_l\hfill \\ -p_l\left(1-\beta \right)f\left(z_l\right)if{q}_l\le k_l\hfill \end{array}\right)$$ (A.112)

Therefore, the Hessian matrix is negative definite, implying that ${\mathrm{\Pi }}_s\left(\theta ,z_l\right)$ is jointly concave in $\theta$ and $z_l$, as shown in (A.113).

$$H=\left|\begin{array}{cc}\frac{{\partial }^2{\mathrm{\Pi }}_s\left(\theta ,z_l\right)}{\partial {\theta }^2}\hfill & \frac{{\partial }^2{\mathrm{\Pi }}_s\left(\theta ,z_l\right)}{\partial z_l\partial \theta }\hfill \\ \frac{{\partial }^2{\mathrm{\Pi }}_s\left(\theta ,z_l\right)}{\partial \theta \partial z_l}\hfill & \frac{{\partial }^2{\mathrm{\Pi }}_s\left(\theta ,z_l\right)}{\partial z_l^2}\hfill \end{array}\right|>0$$ (A.113)

Setting $\frac{\partial {\prod }_s\left(\theta \left|z_h^{\mathit{tc}\ast }\right)\right)}{\partial \theta }=0$, we have:

$${\theta }_{\gamma }^{\ast }=\frac{p_h\left(1-\beta \right)f\left(z_h^{\mathit{tc}\ast }\right)\left[\left(1-\beta \right)w_h\delta k_h+\rho q_h^{\mathit{tc}\ast }\right]-\rho \left(\left(1-\beta \right)w_h-{\pi }_h\right)}{{\rho }^2}$$ (A.114)

where $\rho =w\left(\beta -2\delta \right)$, $\frac{f^{\text{'}}\left(z_h^{\mathit{tc}\ast }\right)\left[w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-{\pi }_h\right]}{f^2\left(z_h^{\mathit{tc}\ast }\right)p_h\left(1-\beta \right)}+2>0$.

Similarly, setting $\frac{\partial {\mathrm{\Pi }}_s\left(\theta ,z_l\right)}{\partial z_l}=0$, we have

$$z_l^{\ast }=\left\{\begin{array}{c}{F}^{-1}\left(1-\frac{{\pi }_l}{p_l(1-\beta )}\right)if{q}_l>k_l\hfill \\ F^{-1}\left(1-\frac{c_l}{p_l(1-\beta )}\right)if{q}_l\le k_l\hfill \end{array}\right)$$ (A.115)

Therefore, the optimal production quantity of lower-tier products can be derived as follows:

$$q_l^{\ast }={z_l^{\ast }+\gamma }_l\frac{{\mu }_h-{\gamma }_h{\mu }_l}{1+{\gamma }_h{\gamma }_l}$$ (A.116)

Similarly, when $q_h\le k_h$, we have

$${\theta }_{\gamma }^{\ast }=\frac{p_h\left(1-\beta \right)f\left(z_h^{\mathit{tc}\ast }\right)\left[\left(1-\beta \right)w_h\delta k_h+\rho q_h^{\mathit{tc}\ast }\right]-\rho \left(\left(1-\beta \right)w_h-c_h\right)}{{\rho }^2}$$ (A.117)

where $\rho =w\left(\beta -2\delta \right)$, $\frac{f^{\text{'}}\left(z_h^{\mathit{tc}\ast }\right)\left[w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-c_h\right]}{f^2\left(z_h^{\mathit{tc}\ast }\right)p_h\left(1-\beta \right)}+2>0$.

Substituting $z_h^{\mathit{tc}\ast }=q_{\mathit{tc}}^{\ast }$ into Eq. (A.114) and Eq. (A.117), we have

$${\theta }_{\gamma }^{\ast }=\left\{\begin{array}{c}\frac{p_h\left(1-\beta \right)f\left(q_{\mathit{tc}}^{\ast }\right)\left[\left(1-\beta \right)w_h\delta k_h+\rho q_h^{\mathit{tc}\ast }\right]-\rho \left(\left(1-\beta \right)w_h-{\pi }_h\right)}{{\rho }^2}if{q}_h>k_h\hfill \\ \frac{p_h\left(1-\beta \right)f\left(q_{\mathit{tc}}^{\ast }\right)\left[\left(1-\beta \right)w_h\delta k_h+\rho q_h^{\mathit{tc}\ast }\right]-\rho \left(\left(1-\beta \right)w_h-c_h\right)}{{\rho }^2}if{q}_h\le k_h\hfill \end{array}\right)$$ (A.118)

where $\rho =w\left(\beta -2\delta \right),$ if $q_h>k_h,$ $\frac{f^{\text{'}}\left(q_{\mathit{tc}}^{\ast }\right)\left[w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-{\pi }_h\right]}{f^2\left(q_{\mathit{tc}}^{\ast }\right)p_h\left(1-\beta \right)}+2>0;$ otherwise $\frac{f^{\text{'}}\left(q_{\mathit{tc}}^{\ast }\right)\left[w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-c_h\right]}{f^2\left(q_{\mathit{tc}}^{\ast }\right)p_h\left(1-\beta \right)}+2>0$. Since $q_h^{\mathit{tc}\ast }<z_h^{\mathit{tc}\ast }=q_{\mathit{tc}}^{\ast }$, if $\beta >2\delta$, we have ${\theta }_{\gamma }^{\ast }<{\theta }^{\ast }$; if $\beta <2\delta$,${\theta }_{\gamma }^{\ast }>{\theta }^{\ast }.$

(Q.E.D).

Proof of Theorem 13.

The total expected profit of SC in the centralized setting can be written as follows:

$${\mathrm{\Pi }}_{\mathit{sc}}^c\left(q_h,q_l\right)=\left(1-\beta \right)\mathbb{E}\left[p_h\bullet \min \left(D_h,q_h\right)\right]-c_h\bullet \min \left(q_h,k_h\right)-{\pi }_h\bullet \max \left(q_h-k_h,0\right)+\left(1-\beta \right)\mathbb{E}\left[p_l\bullet \min \left(D_l,q_l\right)\right]-c_l\bullet \mathrm{m}\mathrm{i}\mathrm{n}(q_l,k_l)-{\pi }_l\bullet \max \left(q_l-k_l,0\right)$$ (A.119)

Let $D_i=y_i+{\epsilon }_i$, and further defining $z_i=q_i-y_i$, $i\in \left(h,l\right)$.

$${\mathrm{\Pi }}_{\mathit{sc}}^c\left({z_h,z}_l\right)=\left(1-\beta \right)\mathbb{E}\left[p_h\bullet \min \left(y_h+{\epsilon }_h,y_h+z_h\right)-c_h\bullet \min \left(y_h+z_h,k_h\right)-{\pi }_h\bullet \max \left(y_h+z_h-k_h,0\right)\right]+\left(1-\beta \right)\mathbb{E}\left[p_l\bullet \min \left(y_l+{\epsilon }_l,y_l+z_l\right)-c_l\bullet \min \left(y_l+z_l,k_l\right)-{\pi }_l\bullet \max \left(y_l+z_l-k_l,0\right)\right]$$ (A.120)

It is easy to show that the Hessian Matrix is negative definite and jointly concave in $z_h$ and $z_l$:

$$H=\left|\begin{array}{cc}\frac{{\partial }^2{\mathrm{\Pi }}_s\left(z_l,z_h\right)}{\partial z_h^2}\hfill & \frac{{\partial }^2{\mathrm{\Pi }}_s\left(z_l,z_h\right)}{\partial z_l\partial z_h}\hfill \\ \frac{{\partial }^2{\mathrm{\Pi }}_s\left(z_l,z_h\right)}{\partial z_h\partial z_l}\hfill & \frac{{\partial }^2{\mathrm{\Pi }}_s\left(z_l,z_h\right)}{\partial z_l^2}\hfill \end{array}\right|>0$$ (A.121)

In a similar vein, we can obtain the optimal $z_i^{c\ast },i\in \left(h,l\right)$ for higher-tier products and lower-tier products in the centralized LSGSC setting:

$$z_i^{c\ast }=\left\{\begin{array}{c}{F}^{-1}\left(1-\frac{{\pi }_i}{p_i(1-\beta )}\right)if{q}_i>k_i\hfill \\ F^{-1}\left(1-\frac{c_i}{p_i(1-\beta )}\right)if{q}_i\le k_i\hfill \end{array}\right)$$ (A.122)

where $i\in \left(h,l\right).$

The optimal production quantity of higher-tier and lower-tier products in centralized setting can be shown as follows:

$$q_h^{c\ast }=z_h^{c\ast }-{\gamma }_h\frac{{\mu }_l+{\gamma }_l{\mu }_h}{1+{\gamma }_h{\gamma }_l}$$ (A.123)

$$q_l^{c\ast }={z_l^{c\ast }+\gamma }_l\frac{{\mu }_h-{\gamma }_h{\mu }_l}{1+{\gamma }_h{\gamma }_l}$$ (A.124)

Comparing $q_l^{\ast }$ (Eq. (A.116)) with $q_l^{c\ast }$ (Eq. (A.124)), we can show $q_l^{c\ast }=q_l^{\ast }$.

Similar to the proof of Theorem 6, to achieve channel coordination, it suffices to show that $q_h^{\mathit{tc}\ast }=q_h^{c\ast }$ and $z_h^{\mathit{tc}\ast }=z_h^{c\ast }$.

When $q_h>k_h$, we have:

$$w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)={\pi }_h$$ (A.125)

Substituting ${\theta }_{\gamma }^{\ast }$ (Eq. (A.118)) into Eq. (A.125) and with some algebra, we have:

$${\delta }_{\gamma }^{c\ast }=\frac{\beta q_h^{\mathit{tc}\ast }}{2q_h^{\mathit{tc}\ast }-\left(1-\beta \right)k_h}=\frac{\beta q_h^{c\ast }}{2q_h^{c\ast }-\left(1-\beta \right)k_h}$$ (A.126)

When $q_h\le k_h$, Eq. (A.126) holds. This suggests that the channel coordination condition derived in the Theorem 6 holds in the multi-tiered products setting.

Comparing Eq. (A.123) with Eq. (A.2), we can easily show that $q_h^{c\ast }<q_c^{\ast }$. Together with $\frac{\partial {\delta }_{\gamma }^{c\ast }}{\partial q_h^{c\ast }}<0$, we have ${\delta }_{\gamma }^{c\ast }>{\delta }_c^{\ast }$. Following Corollary 3 and Corollary 4, we can show that both ${\theta }_{\gamma }^{c\ast }$ and transfer payment $\mathrm{\Delta }{\mathrm{\Pi }}_{\gamma }$ decrease with respect to ${\delta }_{\gamma }^{c\ast }$. Hence, we always have ${\theta }_{\gamma }^{c\ast }<{\theta }_c^{\ast }$ and $\mathrm{\Delta }{\mathrm{\Pi }}_{\gamma }<\mathrm{\Delta }\mathrm{\Pi }$.

(Q.E.D).

Proof of Theorem 14.

(i) Following the Theorem 11 proof, the optimal order quantity of wholesaler in presence of social influence and loss aversion can be derived as follows,

$$q_{h,\lambda }^{\mathit{tc}\ast }=z_{h,\lambda }^{\mathit{tc}\ast }-{\gamma }_h\frac{{\mu }_l+{\gamma }_l{\mu }_h}{1+{\gamma }_h{\gamma }_l}$$ (A.127)

As shown in Eq. (A127), the intercept term $-{\gamma }_h\frac{{\mu }_l+{\gamma }_l{\mu }_h}{1+{\gamma }_h{\gamma }_l}$ is negatively influenced by social influence, while the random term $z_{h,\lambda }^{\mathit{tc}\ast }$ decreases with respect to the degree of wholesaler’s loss aversion (see Proof of Corollary 5). Therefore, as the degree of social influence and loss aversion increase, the wholesaler will reduce his optimal order quantity.

(ii) Similar to the proof of Theorem 9., Theorem 12., when the impact of social influence and wholesaler’s loss aversion are jointly taken into consideration, the optimal decision of supplier can be derived as follows:

$${\theta }_{\lambda \gamma }^{\ast }=\left\{\begin{array}{c}\frac{p_h\left(1-\beta \right)f\left(q_{\lambda }^{\ast }\right)\left[\left(1-\beta \right)w_h\delta k_h+\rho q_{h,\lambda }^{\mathit{tc}\ast }\right]-\rho \left(\left(1-\beta \right)w_h-{\pi }_h\right)}{{\rho }^2}if{q}_h>k_h\hfill \\ \frac{p_h\left(1-\beta \right)f\left(q_{\lambda }^{\ast }\right)\left[\left(1-\beta \right)w_h\delta k_h+\rho q_{h,\lambda }^{\mathit{tc}\ast }\right]-\rho \left(\left(1-\beta \right)w_h-c_h\right)}{{\rho }^2}if{q}_h\le k_h\hfill \end{array}\right)$$ (A.128)

where $\rho =w_h\left(\beta -2\delta \right)$,$q_{\lambda }^{\ast }=z_{h,\lambda }^{\mathit{tc}\ast }$. If $q_h>k_h$, $\frac{f^{\text{'}}\left(q_{\lambda }^{\ast }\right)\left[w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-{\pi }_h\right]}{f^2\left(q_{\lambda }^{\ast }\right)p_h\left(1-\beta \right)}+2>0$; otherwise, $\frac{f^{\text{'}}\left(q_{\lambda }^{\ast }\right)\left[w_h\left(1-\beta +\left(\beta -2\delta \right)\theta \right)-c_h\right]}{f^2\left(q_{\lambda }^{\ast }\right)p_h\left(1-\beta \right)}+2>0$.

From Eq. (A.127), we have $q_{h,\lambda }^{\mathit{tc}\ast }<q_{\lambda }^{\ast }$. Also note that $\frac{\partial {\theta }_{\lambda \gamma }^{\ast }}{\partial q_{h,\lambda }^{\mathit{tc}\ast }}<0$, if $\beta >2\delta$. Hence, we have ${\theta }_{\lambda \gamma }^{\ast }<{\theta }_{\lambda }^{\ast }$. Similarly, we have ${\theta }_{\lambda \gamma }^{\ast }>{\theta }_{\lambda }^{\ast }$, if $\beta <2\delta$.

(iii) Similar to the proof of Theorem 10., Theorem 13., when the impact of social influence and wholesaler’s loss aversion are jointly taken into consideration, the channel coordination could be achieved if and only if:

$${\delta }_{\lambda \gamma }^{c\ast }=\left\{\begin{array}{c}\frac{\beta {\pi }_{h}v+\left(v+1\right)q_h^{c\ast }f\left(q_c^{\ast }\right)p_h\left(1-\beta \right)\beta }{2{\pi }_{h}v+\left(v+1\right)f\left(q_c^{\ast }\right)p_h\left(1-\beta \right)\left(2q_h^{c\ast }-k_h\left(1-\beta \right)\right)}if{q}_h>k_h\hfill \\ \frac{\beta c_{h}v+\left(v+1\right)q_h^{c\ast }f\left(q_c^{\ast }\right)p_h\left(1-\beta \right)\beta }{2c_{h}v+\left(v+1\right)f\left(q_c^{\ast }\right)p_h\left(1-\beta \right)\left(2q_h^{c\ast }-k_h\left(1-\beta \right)\right)}if{q}_h\le k_h\hfill \end{array}\right)$$ (A.129)

where $v=\left(\lambda -1\right)F\left({\underset{\_}{x}(q}_h^{\mathrm{c}\ast })\right)$, $q_c^{\ast }=z_h^{c\ast }$, $q_h^{c\ast }=q_{h,\lambda }^{\mathit{tc}\ast }$. When $\lambda =1$,$v=0$, ${\delta }_{\lambda \gamma }^{c\ast }={\delta }_{\gamma }^{c\ast }=\frac{\beta q_h^{c\ast }}{2q_h^{c\ast }-\left(1-\beta \right)k_h}$.

Similar to the proof of Corollary 9, for a given degree of social influence, it is easy to show that $\frac{\partial {\delta }_{\lambda \gamma }^{c\ast }}{\partial \lambda }<0$, which means that ${\delta }_{\lambda \gamma }^{c\ast }<{\delta }_{\gamma }^{c\ast }$. Also note that, $\frac{\partial {\delta }_{\lambda \gamma }^{c\ast }}{\partial v}<0$. The reason can be explained by the fact that, for a given degree of wholesaler’s loss-aversion, the reduction of $q_h^{c\ast }$ will lower $v=\left(\lambda -1\right)F\left({\underset{\_}{x}(q}_h^{\mathrm{c}\ast })\right)$ and further increase ${\delta }_{\lambda \gamma }^{c\ast }$, that is, the early-payment discount increases with respect to the degree of social influence. In summary, compared with the separate impact of wholesaler’s loss aversion, achieving channel coordination in the multi-tiered product setting is more likely when both social influence and the wholesaler’s loss aversion are present.

(Q.E.D).