Abstract
This paper investigated the behavior of the two-dimensional magnetohydrodynamics (MHD) nanofluid flow of water-based suspended carbon nanotubes (CNTs) with entropy generation and nonlinear thermal radiation in a Darcy–Forchheimer porous medium over a moving horizontal thin needle. The study also incorporated the effects of Hall current, magnetohydrodynamics, and viscous dissipation on dust particles. The said flow model was described using high order partial differential equations. An appropriate set of transformations was used to reduce the order of these equations. The reduced system was then solved by using a MATLAB tool bvp4c. The results obtained were compared with the existing literature, and excellent harmony was achieved in this regard. The results were presented using graphs and tables with coherent discussion. It was comprehended that Hall current parameter intensified the velocity profiles for both CNTs. Furthermore, it was perceived that the Bejan number boosted for higher values of Darcy–Forchheimer number.
Keywords: entropy generation, nonlinear thermal radiation, energy conservation, magnetohydrodynamic, nanofluid, thin needle
1. Introduction
The novel idea to reduce entropy generation in heat transfer convective processes was floated by Bejan [1]. In thermodynamic systems, this notion is employed to enhance the efficiency of thermal engineering gadgets [2]. Indeed, entropy generation is used to gauge the molecular chaos or disorder in a thermodynamic system. Thermodynamics’ second law states that higher molecular disorder is inversely proportional to the quality of energy reduction. It has been examined that energy dissipation and heat transfer owing to differences in temperatures are the key factors for entropy generation. That is why special attention is given for the enhancement of heat transfer in varied engineering applications. The average internal heat loss because of entropy generation in a titanium dioxide (TiO2) suspended in a water-based nanofluid Poiseuille flow with the impact of mixed convection and thermal radiation in a wavy channel is discussed by Zeeshan et al. [3]. The 2nd law of thermodynamics is betrothed for the entropy generation model erection. It is reported that the pressure gradient is the key factor for a rise in the average energy loss. Further, it is noted that the entropy generation for the radiation parameter is more near walls in comparison to the middle of the channel. The study of entropy generation in the nanofluid thin-film flow, containing a suspension of both types of carbon nanotubes (CNTs) with Cattaneo-Christov heat flux, magnetohydrodynamics, and variable source/sink, is studied by Lu et al. [4]. Numerical simulations with the erected mathematical model are found by the bvp4c function of MATLAB software (University of New Mexico, New Mexico). It is witnessed that entropy generation is larger for higher estimates of the magnetic parameter for a thin film flow. The entropy generation analysis during the heat transfer process in the flow of Ferrofluid with low oscillating magnetic field past a stretched rotating disk is deliberated by Hassan et al. [5]. The analytical solution of the problem is attained via Mathematica-based bvp 2.0 based on the homotopy analysis method. It is comprehended that total entropy is boosted with the dispersion of nanoparticles. Further, it is noted that the irreversibility of the fluid flow is enhanced by the strong magnetic impact. Some recent literature about entropy generation may be found in references [6,7,8,9,10].
CNTs are cylindrical type carbon allotropes. These were first exposed in the form of multi-walled carbon nanotubes (MWCNTs) by Iijima [11] in 1991. This was followed by another study by Bethune et al. [12] who introduced the idea of single-walled carbon nanotubes (SWCNTs) in 1993. In today’s era, a good number of applications involving CNTs may be found, like in health care, energy, electronics, etc. [13,14,15]. It is now a well-established theory that snags with the materials possessing low thermal conductivity are removed with the introduction of nanofluids. Nanofluids holds nanoparticles with a size of <100 nm. These nanoparticles are made up of copper, metal oxides, alumina, nanomaterials, nitrides, and carbides [16]. The concept of nanofluids was the first time floated by Choi and Eastman [17]. A substantial number of studies have been carried out since its inception [18,19,20]. Recently, Sheikholeslami and Shehzad [21] numerically examined the flow of nanofluid comprising Fe3O4-H2O solution in a permeable cavity under the influence of a variable magnetic field using Control Volume Finite Element Method (CVFEM). They observed the highest heat transfer rate in the case of the platelet-shaped nanoparticles. It was further witnessed by them that the velocity of the nanofluid was on the decline once the strong magnetic field was applied. Entropy optimization for the flow of Carreau nanofluid flow with cubic auto-catalysis chemical reaction was studied by Khan et al. [22] analytically. They noticed that the sturdier magnetic field boosted the entropy generation. Sheikholeslami [23] found a numerical solution of nanofluid flow under the influence of the magnetic field in a permeable medium via the CVFEM scheme. He analyzed the influences of entropy and exergy on the presented model and reported that entropy loss enhanced in attendance of stronger magnetic field. Khan et al. [24] examined the numerical solution of 3D cross nanofluid with activation energy and binary chemical reaction with zero mass flux and convective boundary conditions. They noticed that higher estimates of activation energy boosted the concentration of the cross nanofluid. Hosseini and Sheikholeslami [25] analyzed the thermal competence of a convective nanofluid flow with entropy generation inside a microchannel under the influence of the magnetic field. Between two phases, non-equilibrium condition for a permeable media is engaged. They noticed that the entropy generation enhanced with an increase in fluid friction irreversibility. Some recent studies have also highlighted the concept of carbon nanotubes [26,27,28,29,30,31,32,33] and many therein.
Abundant applications focusing on Cattaneo-Christov heat flux amalgamated with thermal radiation may be found in missiles, air crafts, nuclear power plants, space vehicles’ propulsion gadgets, etc. Keeping in view these interesting applications, scientists and researchers [34,35,36,37,38,39,40] are motivated to look for fluid behavior in attendance of thermal radiation and Cattaneo-Christov heat flux.
Motivated from the above literature, our objective was to find the water-based CNTs dusty nanofluid flow over a moving thin needle. The analysis was performed in the presence of Hall current and nonlinear thermal radiation in a Darcy–Forchheimer porous media. The thermal efficacy of the system was analyzed by employing entropy analysis. A numerical solution of the envisaged inimitable mathematical model was found. To our information, no such study has been conducted so far in the literature. This model was unique in its category. Endorsement of the outcomes of the existing study was done by comparing with a published article in limiting case. Graphical sketches and tables were also part of this study.
2. Mathematical Modeling
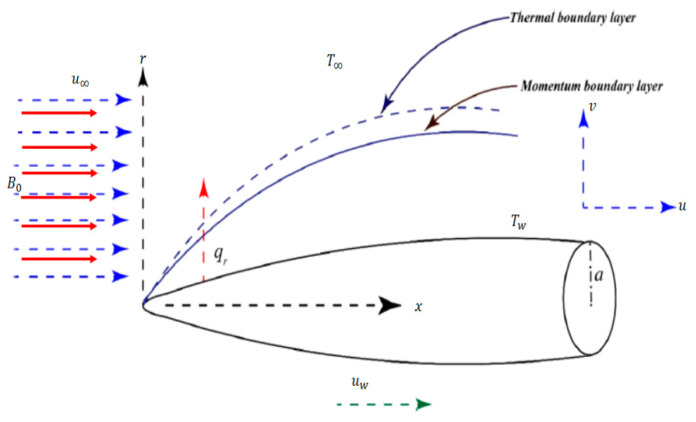
Let us assume an H2O-CNTs-based nanofluid flow with Hall current over a moving slender needle having speed and radius “a” (Figure 1). The speed of fluid far away from the surface is taken as The cylindrical coordinates (x, r) are taken in such a way that is along the axis of the needle and normal to the axis. The flow containing dust particles is generated in a non-Darcy absorbent media. The associated impacts affecting the flow in the heat equation are viscous dissipation and nonlinear thermal radiation. Furthermore, and are the constant temperatures at the wall and far off from the wall with A magnetic field with magnetic strength is applied with the low Reynold number assumption [41], which eventually results in the induced magnetic field to be neglected. Two types of the equations, i.e., fluid phase and particle phase, comprising the envisioned mathematical model fulfilling laws of conservation are also laid down as given below:
Figure 1.
The physical design of the flow problem.
The above flow theory gives rise to the following boundary layer equations [41,42,43,44,45]:
-
Continuity equation:
Fluid phase(1) -
Momentum equation:
Fluid phase(2) -
Continuity equation:
Particle phase(3) -
Momentum equation:
Particle phase(4) -
Energy equation:
Fluid phase(5) -
Energy equation:
Particle phase(6)
with the boundary conditions
| (7) |
| (8) |
The heat flux in simplified form after considering Rosseland approximation is:
| (9) |
where is the mean absorption coefficient, and is the Stephen–Boltzman constant. For a planer boundary layer flow, the above equation can be written as:
| (10) |
The mathematical model proposed by Xue [46] for the CNTs is given in Table 1. The thermo-physical traits of the CNTs of both types and H2O are appended in Table 2.
Table 1.
Properties of the nanofluid defined for the presented model [46].
| Properties | Nano-Fluid |
|---|---|
| Density | |
| Heat capacity | |
| Viscosity | |
| Thermal conductivity |
Table 2.
Thermo-physical features of the base fluid H2O and CNTs [46].
| Thermo-Physical Properties | H2O | SWCNT | MWCNT |
|---|---|---|---|
| Cp (j/kg)K | 425 | 796 | |
| ρ (kg/m3) | 997.1 | 2600 | 1600 |
| k (W/mK) | 0.613 | 6600 | 3000 |
| Prandtl number (Pr) |
3. Similarity Transformation
The similarity variables are introduced as follows,
| (11) |
The resulting non-dimensional Ordinary differential equations (ODEs) system after referring to similarity variables:
-
Momentum equation:
Fluid phase(12) -
Momentum equation:
Particle phase(13) -
Energy equation:
Fluid phase(14) -
Energy equation:
Particle phase
associated with boundary conditions(15) (16)
Here, prime represents derivative with respect to . The dimensionless physical parameters are defined as follows:
| (17) |
4. Nusselt Number and Skin Friction Coefficient
The skin friction coefficients and the local Nusselt number in dimensional form are given by:
| (18) |
where and are defined as below:
| (19) |
By using Equations (11), (18) and (19) we get
| (20) |
| (21) |
with
| (22) |
5. Entropy Generation
Entropy generation analysis is much important to study the thermal energy irreversibility of a particular system.
| (23) |
Equation (23), after employing Equation (11), in dimensionless form is
| (24) |
Here, the characteristic entropy generation is given by:
| (25) |
In non-dimensional form, heat transfer irreversibility is given by:
| (26) |
The fluid friction irreversibility is defined by:
| (27) |
and the porous medium and magnetic field irreversibility are represented by:
| (28) |
The Bejan number Be in dimensional form is defined as:
| (29) |
In dimensionless form, after consulting (11) is:
| (30) |
6. Numerical Scheme
The system with high nonlinearity comprising Equations (12)–(15) with the support of Equation (16) is numerically solved by bvp4c MATLAB function. The following code transforms the given model into the 1st order system of ODEs.
| (31) |
| (32) |
| (33) |
| (34) |
With boundary conditions
| (35) |
Table 3 depicts the validation of the obtained results by comparing with already published articles in limiting case. This endorses the truthfulness of the presented mathematical model.
Table 3.
Validation of the existing model for the values of when
Table 4 illustrates the numerically calculated values of the skin friction coefficient for numerous estimates of , , , and It is noticed that value of the drag force coefficient is higher for , and but it declines for estimates of and for both types of CNTs. Likewise, Table 5 portrays the Nusselt number for , , , , and . It is comprehended that heat transfer rate is higher in case of and but converse behavior is seen for , , , and for SWCNTs and MWCNTs.
Table 4.
Skin friction coefficient against different parameters.
| Skin Friction Coefficient | |||||||
|---|---|---|---|---|---|---|---|
| SWCNT | MWCNT | ||||||
| 0.001 | 0.00184647 | 0.00184157 | |||||
| 0.01 | 0.00583012 | 0.00581468 | |||||
| 0.2 | 0.02591430 | 0.02584880 | |||||
| 0.1 | 0.00583012 | 0.00581468 | |||||
| 2.0 | 0.00583276 | 0.00581722 | |||||
| 3.5 | 0.00583491 | 0.00581927 | |||||
| 0.10 | 0.00583012 | 0.00581468 | |||||
| 0.25 | 0.00644651 | 0.00640784 | |||||
| 0.4 | 0.00706302 | 0.00700110 | |||||
| 1.0 | 0.00583012 | 0.00581468 | |||||
| 2.0 | 0.00582586 | 0.00581043 | |||||
| 3.0 | 0.00582165 | 0.00580623 | |||||
| 0.2 | 0.00583012 | 0.00581468 | |||||
| 0.3 | 0.00711701 | 0.00710157 | |||||
| 0.4 | 0.00840431 | 0.00838888 | |||||
| 1.0 | 0.00583012 | 0.00581468 | |||||
| 1.4 | 0.00499559 | 0.00498015 | |||||
| 1.8 | 0.00447082 | 0.00445537 | |||||
Table 5.
Numerical values of Nusselt number against different parameters.
| Nusselt Number | |||||||
|---|---|---|---|---|---|---|---|
| SWCNT | MWCNT | ||||||
| 0.10 | 1.10739 | 1.05489 | |||||
| 0.25 | 1.12048 | 1.06695 | |||||
| 0.40 | 1.13570 | 1.08087 | |||||
| 1.0 | 1.10739 | 1.05489 | |||||
| 2.0 | 1.28855 | 1.22836 | |||||
| 3.0 | 1.44647 | 1.37965 | |||||
| 0.3 | 1.12089 | 1.06788 | |||||
| 0.5 | 1.10739 | 1.05489 | |||||
| 0.9 | 1.09958 | 1.04738 | |||||
| 1.0 | 1.10739 | 1.05489 | |||||
| 1.4 | 1.09857 | 1.04640 | |||||
| 1.8 | 1.09329 | 1.04131 | |||||
| 6.0 | 1.10739 | 1.05489 | |||||
| 9.0 | 0.80951 | 0.77264 | |||||
| 15.0 | 0.59158 | 0.56589 | |||||
| 1.1 | 1.10739 | 1.05489 | |||||
| 1.4 | 0.80635 | 0.77013 | |||||
| 1.7 | 0.71356 | 0.68292 | |||||
7. Results and Discussion
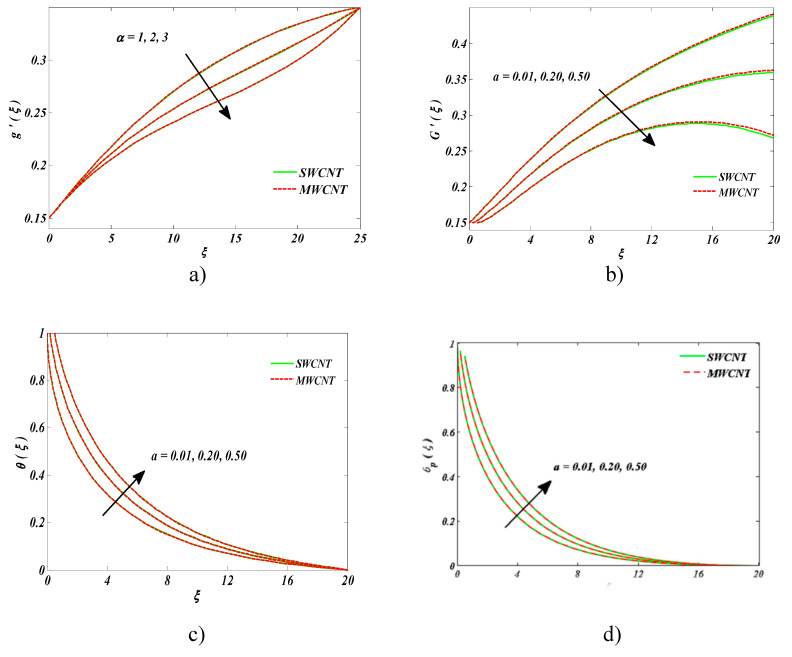
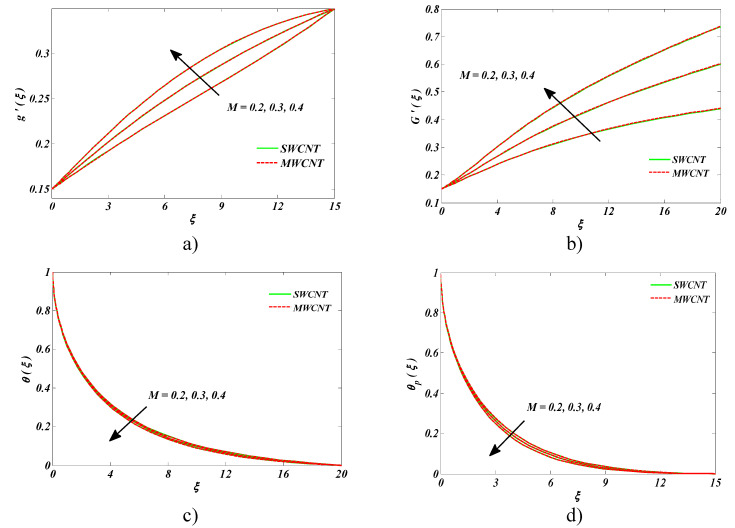
This segment was devoted to envisioning the physical insight for graphical illustration Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9 and Figure 10. We took the fixed values of the parameters throughout the study as (α = 0.01, ε = 0.3, ϕ = 0.04, ϕd = Fr = λ = Ec = 0.1, α = m = γ = 1, β = βT = 0.5, M = 0.2, Nr = 6, θr = 1.1,) and Figure 2a,b exemplify the impacts of needle’s size “” on the nanofluid velocity and velocity of the dust phase, respectively. It was comprehended that velocities were declining functions of the needle size in the case of CNTs of both types. Physically speaking, both velocities were highly dependent on the size of the needle. Increasing the needle’s size lowered the velocities, which was obvious. An opposite trend was witnessed in the case of Figure 2c,d. It was witnessed that temperature was dominant in the case of SWCNTs as compared to MWCNTs. This was because MWCNTs have lower thermal conductivity than SWCNTs.
Figure 2.
Impact of on (a) nanofluid velocity, (b) the velocity of the dust phase, (c) nanofluid temperature, and (d) temperature of the dust phase.
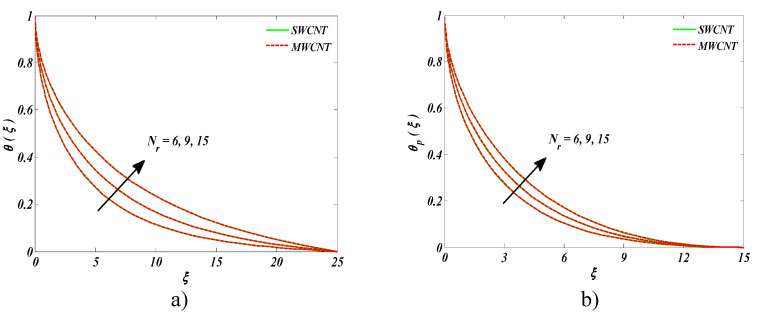
Figure 3.
Impact of on (a) nanofluid temperature and (b) temperature of the dust phase.
Figure 4.
Impact of on (a) nanofluid temperature and (b) temperature of the dust phase.
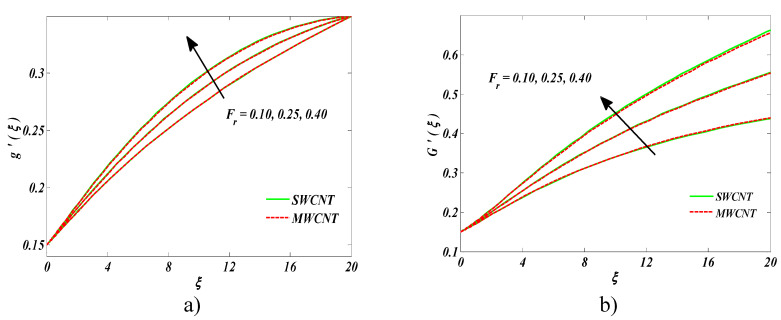
Figure 5.
Impact of on (a) nanofluid velocity and (b) the velocity of the dust phase.
Figure 6.
Impact of on (a) nanofluid velocity, (b) the velocity of the dust phase, (c) nanofluid temperature, and (d) temperature of the dust phase.
Figure 7.
Impact of on (a) nanofluid velocity and (b) the velocity of the dust phase.
Figure 8.
Impact of on (a) entropy generation number and (b) Bejan number.
Figure 9.
Impact of on (a) entropy generation number and (b) Bejan number.
Figure 10.
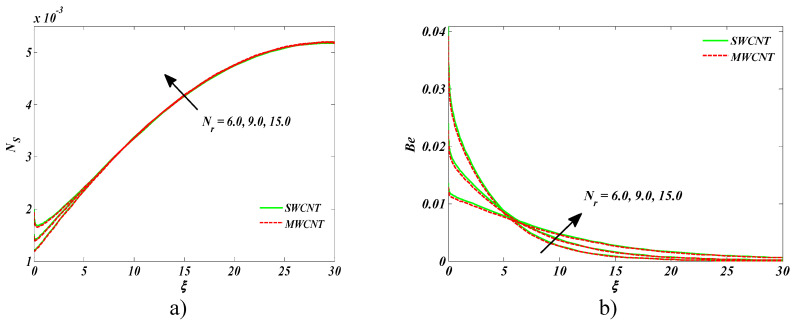
Impact of on (a) entropy generation number and (b) Bejan number.
The impact of radiation parameter Nr on the nanofluid temperature and temperature of the dust phase could be seen in Figure 3a,b. Owing to higher radiation, more heat was transmitted to both nanofluid and the dust phase. Eventually, the augmented temperature in both cases, i.e., nanofluid and dust fluid, was witnessed.
Variation in temperature ratio parameter on temperatures of the nanofluid and dust fluid is depicted in Figure 4a,b, respectively. is the quotient of the wall temperature to ambient temperature. Larger values of meant sturdier wall temperature than the ambient temperature. Higher estimates of resulted in a rise in the temperature of both fluids in the case of both CNTs.
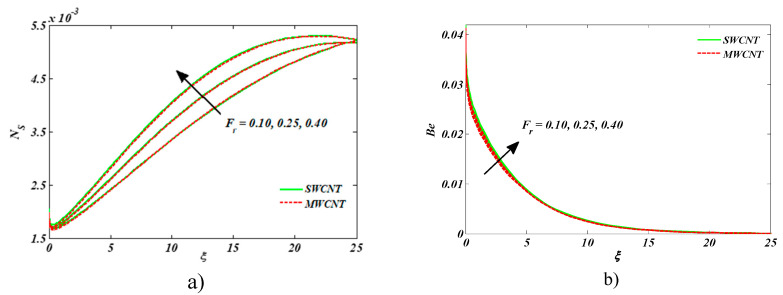
Figure 5a,b revealed the nanofluid velocity and dust phase for the Darcy–Forchheimer parameter Fr. It is learned that both velocity functions are diminishing for the growing values of Fr [29]. Actually, higher estimates of Fr produced resistance in nanofluid motion for both CNTs that ultimately dropped nanofluid and dust fluid velocities.
The upshot of magnetic parameter M on associated distributions is described in Figure 6a–d. Upon increasing the number of dust particles into the fluid, the drag force was strengthened, and more resistance to the fluid flow was experienced, and, eventually, a decrease in both velocities was witnessed. An opposing trend was identified for the temperature field and the dust fluid temperature, which was obviously owing to sturdier M.
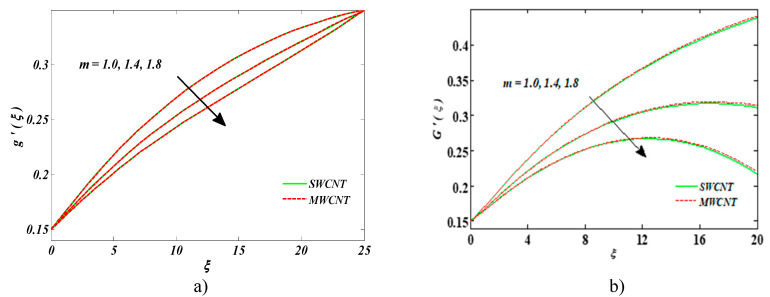
Figure 7a,b are outlined to perceive the impact of Hall current parameter m on both velocities. It was detected that velocities were mounting functions of m. Larger estimates of m enforced the damping force, and, eventually, velocities were strengthened.
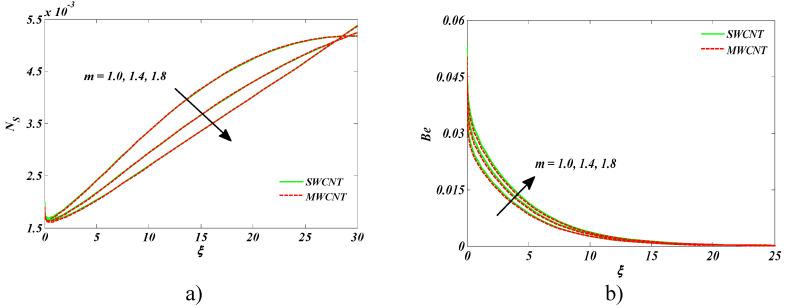
The impression of Hall current m on entropy generation and the Bejan number is shown in Figure 8a,b. Larger values of m lowered the temperature that resulted in a drop of entropy generation as well. An inverse behavior was seen for the Bejan number against m.
Figure 9a,b is plotted for entropy generation and Bejan number for Forchheimer parameter Fr. An upsurge was visualized in both cases. Larger estimates of the inertial coefficient boosted the disorderliness and caused it to intensify Ns and Be.
Figure 10a,b is sketched to comprehend the upshot of radiation parameter Nr on entropy generation and the Bejan number, respectively. An enhancement in both entropy generation and the Bejan number was witnessed versus the radiation parameter. This was all because of the heightened energy systems, owing to larger estimates of Nr.
8. Final Remarks
In the present exploration, Hall current sequel on the Darcy–Forchheimer H2O-CNTs dusty nanofluid solution over a thin needle was investigated numerically. The novelty impacts of nonlinear thermal radiation with other effects were accompanied by entropy analysis. The leading outcomes of the investigation are appended as follows:
-
⮚
Bejan number increased for larger values of Darcy–Forchheimer number.
-
⮚
Velocity was on the decline once the size of the needle and Darcy–Forchheimer parameter’s values were enhanced.
-
⮚
Higher estimates of Hall current parameter escalated the velocity profiles for both CNTs.
-
⮚
An upsurge in entropy generation and the Bejan number was witnessed versus the radiation parameter.
-
⮚
Sturdier magnetic field diminished the velocity of the fluid.
-
⮚
Skin friction coefficient declined for growing estimates of dust particles’ mass concentration.
Nomenclature
| Coordinate measured in radial direction | |
| Velocity components along and directions | |
| Effective dynamic viscosity of nanofluid | |
| Density of nanofluid | |
| Kinematic viscosity of nanofluid | |
| Darcy-permeability of the porous medium | |
| Drag coefficient | |
| Volume fraction of dust particles | |
| Stokes resistance | |
| Number density of dust particles | |
| Electric conductivity | |
| Applied magnetic field | |
| Hall parameter | |
| md | Mass concentration of the dust particles |
| knf | Effective thermal conductivity of the nanofluid |
| (ρCp)nf | Effective heat capacitance of the nanofluid |
| N 1 | Density of the particle phase |
| τv | Relaxation time of dust particles |
| τT | Thermal equilibrium time |
| τw | Shear stress at the surface |
| Entropy generation rate per unit volume | |
| Velocity components of particle phase in x and r directions | |
| Specific heat of the dust particles | |
| Velocity of the moving needle | |
| Velocity outside the boundary layer | |
| Dimensional temperature of the nanofluid | |
| Temperature of the dust particle | |
| Constant surface temperature of the thin needle | |
| Ambient temperature | |
| Porosity parameter | |
| Forchheimer parameter | |
| Dust particles mass concentration | |
| Fluid particle interaction parameter for velocity | |
| Magnetic field parameter | |
| Prandtl number | |
| Nonlinear radiation parameter | |
| Temperature ratio parameter | |
| Eckert number | |
| Fluid particle interaction parameter for temperature | |
| Ratio of specific heat | |
| Surface heat flux | |
| Entropy generation number |
Author Contributions
Methodology, I.T.; Conceptualization, Project Administration, Writing—Original Draft, M.R.; Software, S.K.; Validation, H.-W.K.; Funding Acquisition, Writing—review and Editing, Y.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Bio & Medical Technology Development Program of the NRF funded by the Korean government, MSIP(NRF-2015M3A9D7067219) and also supported by the Soonchunhyang University Research Fund.
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Bejan A. A study of entropy generation in fundamental convective heat transfer. J. Heat Transf. 1979;101:718–725. doi: 10.1115/1.3451063. [DOI] [Google Scholar]
- 2.Rehman A.U., Mehmood R., Nadeem S. Entropy analysis of radioactive rotating nanofluid with thermal slip. Appl. Therm. Eng. 2017;112:832–840. doi: 10.1016/j.applthermaleng.2016.10.150. [DOI] [Google Scholar]
- 3.Zeeshan A., Shehzad N., Abbas T., Ellahi R. Effects of radiative electro-magnetohydrodynamics diminishing internal energy of pressure-driven flow of titanium dioxide-water nanofluid due to entropy generation. Entropy. 2019;21:236. doi: 10.3390/e21030236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lu D., Ramzan M., Mohammad M., Howari F., Chung J.D. A Thin Film Flow of Nanofluid Comprising Carbon Nanotubes Influenced by Cattaneo-Christov Heat Flux and Entropy Generation. Coatings. 2019;9:296. doi: 10.3390/coatings9050296. [DOI] [Google Scholar]
- 5.Hassan M., Mohyud-Din S.T., Ramzan M. Study of heat transfer and entropy generation in ferrofluid under low oscillating magnetic field. Indian J. Phys. 2019;93:749–758. doi: 10.1007/s12648-018-1328-8. [DOI] [Google Scholar]
- 6.Suleman M., Ramzan M., Zulfiqar M., Bilal M., Shafee A., Chung J.D., Lu D., Farooq U. Entropy analysis of 3D non-Newtonian MHD nanofluid flow with nonlinear thermal radiation past over exponential stretched surface. Entropy. 2018;20:930. doi: 10.3390/e20120930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Ramzan M., Sheikholeslami M., Chung J.D., Shafee A. Melting heat transfer and entropy optimization owing to carbon nanotubes suspended Casson nanoliquid flow past a swirling cylinder-A numerical treatment. AIP Adv. 2018;8:115130. doi: 10.1063/1.5064389. [DOI] [Google Scholar]
- 8.Li Z., Hedayat M., Sheikholeslami M., Shafee A., Zrelli H., Tlili I., Nguyen T.K. Numerical simulation for entropy generation and hydrothermal performance of nanomaterial inside a porous cavity using Fe3O4 nanoparticles. Phys. A. 2019;524:272–288. doi: 10.1016/j.physa.2019.04.146. [DOI] [Google Scholar]
- 9.Khan M.I., Shah F., Hayat T., Alsaedi A. Transportation of CNTs based nanomaterial flow confined between two coaxially rotating disks with entropy generation. Phys. A. 2019;527:121154. doi: 10.1016/j.physa.2019.121154. [DOI] [Google Scholar]
- 10.Abbas S.Z., Khan W.A., Sun H., Ali M., Irfan M., Shahzed M., Sultan F. Mathematical modeling and analysis of Cross nanofluid flow subjected to entropy generation. Appl. Nanosci. 2019:1–2. doi: 10.1007/s13204-019-01039-9. [DOI] [Google Scholar]
- 11.Iijima S. Helical microtubules of graphitic carbon. Nature. 1991;354:56. doi: 10.1038/354056a0. [DOI] [Google Scholar]
- 12.Bethune D.S., Kiang C.H., De Vries M.S., Gorman G., Savoy R., Vazquez J., Beyers R. Cobalt-catalysed growth of carbon nanotubes with single-atomic-layer walls. Nature. 1993;363:605. doi: 10.1038/363605a0. [DOI] [Google Scholar]
- 13.Baughman R.H., Zakhidov A.A., De Heer W.A. Carbon nanotubes--the route toward applications. Science. 2002;297:787–792. doi: 10.1126/science.1060928. [DOI] [PubMed] [Google Scholar]
- 14.Dresselhaus M.S., Dresselhaus G., Eklund P.C. Science of Fullerenes and Carbon Nanotubes: Their Properties and Applications. ACADEMIC PRESS; New Yourk, NY, USA: 1996. [Google Scholar]
- 15.De Volder M.F., Tawfick S.H., Baughman R.H., Hart A.J. Carbon nanotubes: Present and future commercial applications. Science. 2013;339:535–539. doi: 10.1126/science.1222453. [DOI] [PubMed] [Google Scholar]
- 16.Chamkha A.J., Abbasbandy S., Rashad A.M., Vajravelu K. Radiation effects on mixed convection about a cone embedded in a porous medium filled with a nanofluid. Meccanica. 2013;48:275–285. doi: 10.1007/s11012-012-9599-1. [DOI] [Google Scholar]
- 17.Choi S.U., Eastman J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles. Argonne National Lab; Du Page County, IL, USA: 1995. [Google Scholar]
- 18.Eastman J.A., Choi U.S., Li S., Thompson L.J., Lee S. Enhanced thermal conductivity through the development of nanofluids. MRS Online Proc. Libr. Arch. 1996 doi: 10.1557/PROC-457-3. [DOI] [Google Scholar]
- 19.Keblinski P., Phillpot S.R., Choi S.U., Eastman J.A. Mechanisms of heat flow in suspensions of nano-sized particles (nanofluids) Int. J. Heat Mass Transf. 2002;45:855–863. doi: 10.1016/S0017-9310(01)00175-2. [DOI] [Google Scholar]
- 20.Makinde O.D., Aziz A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 2011;50:1326–1332. doi: 10.1016/j.ijthermalsci.2011.02.019. [DOI] [Google Scholar]
- 21.Sheikholeslami M., Shehzad S.A. Numerical analysis of Fe3O4–H2O nanofluid flow in permeable media under the effect of external magnetic source. Int. J. Heat Mass Transf. 2018;118:182–192. doi: 10.1016/j.ijheatmasstransfer.2017.10.113. [DOI] [Google Scholar]
- 22.Khan M.I., Kumar A., Hayat T., Waqas M., Singh R. Entropy generation in flow of Carreau nanofluid. J. Mol. Liq. 2019;278:677–687. doi: 10.1016/j.molliq.2018.12.109. [DOI] [Google Scholar]
- 23.Sheikholeslami M. New computational approach for exergy and entropy analysis of nanofluid under the impact of Lorentz force through a porous media. Comput. Method Appl. M. 2019;344:319–333. doi: 10.1016/j.cma.2018.09.044. [DOI] [Google Scholar]
- 24.Khan W.A., Sultan F., Ali M., Shahzad M., Khan M., Irfan M. Consequences of activation energy and binary chemical reaction for 3D flow of Cross-nanofluid with radiative heat transfer. J. Braz. Soc. Mech. Sci. 2019;41:4. doi: 10.1007/s40430-018-1482-0. [DOI] [Google Scholar]
- 25.Hosseini S.R., Sheikholeslami M. Investigation of the nanofluid convective flow and entropy generation within a microchannel heat sink involving magnetic field. Powder Technol. 2019;351:195–202. doi: 10.1016/j.powtec.2019.04.022. [DOI] [Google Scholar]
- 26.Ahmed J., Khan M., Ahmad L. MHD swirling flow and heat transfer in Maxwell fluid driven by two coaxially rotating disks with variable thermal conductivity. Chin. J. Phys. 2019;60:22–34. doi: 10.1016/j.cjph.2019.02.010. [DOI] [Google Scholar]
- 27.Cheng B., Yang S., Liu H., Zhang L., Wang F. Investigation of the interaction between carbon nanotube tip and silicon sample through molecular dynamic simulation. Chin. J. Phys. 2019;60:407–415. doi: 10.1016/j.cjph.2019.05.022. [DOI] [Google Scholar]
- 28.Talla J.A., Alsalieby A.F. Effect of uniaxial tensile strength on the electrical properties of doped carbon nanotubes: Density functional theory. Chin. J. Phys. 2019;59:418–425. doi: 10.1016/j.cjph.2019.01.022. [DOI] [Google Scholar]
- 29.Bilal M., Ramzan M. Hall current effect on unsteady rotational flow of carbon nanotubes with dust particles and nonlinear thermal radiation in Darcy–Forchheimer porous media. J. Therm. Anal. Calorim. 2019;138:3127–3137. doi: 10.1007/s10973-019-08324-3. [DOI] [Google Scholar]
- 30.Nadeem S., Abbas N., Elmasry Y., Malik M.Y. Numerical analysis of water based CNTs flow of micropolar fluid through rotating frame. Comput. Methods Programs Biomed. 2020;186:105194. doi: 10.1016/j.cmpb.2019.105194. [DOI] [PubMed] [Google Scholar]
- 31.Ibrahim M., Khan M.I. Mathematical modeling and analysis of SWCNT-Water and MWCNT-Water flow over a stretchable sheet. Comput. Methods Programs Biomed. 2019;187:105222. doi: 10.1016/j.cmpb.2019.105222. [DOI] [PubMed] [Google Scholar]
- 32.Shahzadi I., Sadaf H., Nadeem S., Saleem A. Bio-mathematical analysis for the peristaltic flow of single wall carbon nanotubes under the impact of variable viscosity and wall properties. Comput. Methods Programs Biomed. 2017;139:137–147. doi: 10.1016/j.cmpb.2016.10.016. [DOI] [PubMed] [Google Scholar]
- 33.Maleki R., Afrouzi H.H., Hosseini M., Toghraie D., Piranfar A., Rostami S. pH-sensitive loading/releasing of doxorubicin using single-walled carbon nanotube and multi-walled carbon nanotube: A molecular dynamics study. Comput. Methods Programs Biomed. 2020;186:105210. doi: 10.1016/j.cmpb.2019.105210. [DOI] [PubMed] [Google Scholar]
- 34.Zheng S., Liang W., Chu H., Zhou H. Effects of radiation reabsorption of C1-C6 hydrocarbon flames at normal and elevated pressures. Fuel. 2020;266:117061. doi: 10.1016/j.fuel.2020.117061. [DOI] [Google Scholar]
- 35.Khan M.I., Qayyum S., Hayat T., Waqas M., Khan M.I., Alsaedi A. Entropy generation minimization and binary chemical reaction with Arrhenius activation energy in MHD radiative flow of nanomaterial. J. Mol. Liq. 2018;259:274–283. doi: 10.1016/j.molliq.2018.03.049. [DOI] [Google Scholar]
- 36.Ramzan M., Mohammad M., Howari F., Chung J.D. Entropy analysis of carbon nanotubes based nanofluid flow past a vertical cone with thermal radiation. Entropy. 2019;21:642. doi: 10.3390/e21070642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sheikholeslami M., Behnoush R., Milad D., Ahmad S., Zhixiong Li., Truong K.N. Application of nano-refrigerant for boiling heat transfer enhancement employing an experimental study. Int. J. Heat Mass Transfer. 2019;141:974–980. doi: 10.1016/j.ijheatmasstransfer.2019.07.043. [DOI] [Google Scholar]
- 38.Ramzan M., Riasat S., Kadry S., Long C., Nam Y., Lu D. Numerical simulation of 3D condensation nanofluid film flow with Carbon nanotubes on an inclined rotating disk. Appl. Sci. 2020;10:168. doi: 10.3390/app10010168. [DOI] [Google Scholar]
- 39.Ramzan M., Mohammad M., Howari F. Magnetized suspended carbon nanotubes based nanofluid flow with bio-convection and entropy generation past a vertical cone. Sci. Rep. 2019;9:1–5. doi: 10.1038/s41598-019-48645-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Karvelas E., Liosis C., Benos L., Karakasidis T., Sarris I. Micromixing efficiency of particles in heavy metal removal processes under various inlet conditions. Water. 2019;11:1135. doi: 10.3390/w11061135. [DOI] [Google Scholar]
- 41.Fragkou A.D., Karakasidis T.E., Sarris I.E. Recurrence quantification analysis of MHD turbulent channel flow. Phys. A Stat. Mech. Appl. 2019;531:121741. doi: 10.1016/j.physa.2019.121741. [DOI] [Google Scholar]
- 42.Chen J.L., Smith T.N. Forced convection heat transfer from nonisothermal thin needles. J. Heat Transf. 1978;100:358–362. doi: 10.1115/1.3450809. [DOI] [Google Scholar]
- 43.Afridi M.I., Tlili I., Qasim M., Khan I. Nonlinear Rosseland thermal radiation and energy dissipation effects on entropy generation in CNTs suspended nanofluids flow over a thin needle. Bound Value Probl. 2018;2018:148. doi: 10.1186/s13661-018-1062-3. [DOI] [Google Scholar]
- 44.Sulochana C., Prakash J., Sandeep N. Unsteady MHD flow of a dusty nanofluid past a vertical stretching surface with non-uniform heat source/sink. Int. J. Sci. Eng. 2016;10:1–9. [Google Scholar]
- 45.Raju C.S., Saleem S., Al-Qarni M.M., Upadhya S.M. Unsteady nonlinear convection on Eyring–Powell radiated flow with suspended graphene and dust particles. Microsyst. Technol. 2019;25:1321–1331. doi: 10.1007/s00542-018-4076-y. [DOI] [Google Scholar]
- 46.Xue Q.Z. Model for thermal conductivity of carbon nanotube-based composites. Phys. B. 2005;368:302–307. doi: 10.1016/j.physb.2005.07.024. [DOI] [Google Scholar]
- 47.Ishak A., Nazar R., Pop I. Boundary layer flow over a continuously moving thin needle in a parallel free stream. Chin. Phys. Lett. 2007;24:2895. doi: 10.1088/0256-307X/24/10/051. [DOI] [Google Scholar]