Scalable Bayesian Nonparametric Clustering and Classification

Abstract

We develop a scalable multi-step Monte Carlo algorithm for inference under a large class of nonparametric Bayesian models for clustering and classification. Each step is “embarrassingly parallel” and can be implemented using the same Markov chain Monte Carlo sampler. The simplicity and generality of our approach makes inference for a wide range of Bayesian nonparametric mixture models applicable to large datasets. Specifically, we apply the approach to inference under a product partition model with regression on covariates. We show results for inference with two motivating data sets: a large set of electronic health records (EHR) and a bank telemarketing dataset. We find interesting clusters and competitive classification performance relative to other widely used competing classifiers. Supplementary materials for this article are available online.

1. Introduction

We propose a distributed Monte Carlo algorithm for Bayesian nonparametric clustering and classification methods that is suitable for large sample sizes. The algorithm is applicable for both conjugate and non-conjugate structures, and consists of K computationally efficient steps, where K is dynamically determined and is typically less than four. In each of the first (K − 1) steps, we divide the data into multiple shards and run Markov chain Monte Carlo (MCMC) simulations in each shard. The algorithm is run in parallel without any communication between the parallel jobs. Schemes with such zero communication cost are known as “embarrassingly parallel” algorithms, a term that first appeared in Moler (1986). In the last step, MCMC is run again to generate approximate samples from the full posterior. We apply the algorithm for inference in a product partition model with regression on covariates (PPMx, Müller et al. 2011), and show results for a large electronic health records (EHR) dataset and a telemarketing dataset. The method is scalable, shows competitive performance compared to state-of-the-art classifiers and generates interpretable partitions of the data.

Classification and clustering.

We consider Bayesian nonparametric (BNP) methods for clustering and classification. Classification aims to assign observations into two or more categories on the basis of training data with known categories. Widely used classification algorithms include logistic regression (LR), naive Bayes, neural networks, k-nearest neighbors, support vector machines (SVM, Cortes and Vapnik 1995), decision trees, random forests (RF, Ho 1995), classification and regression trees (Breiman et al. 1984), Bayesian additive regression trees (BART, Chipman et al. 2010), and mixture models based on BNP priors. Some recent examples for the latter are Cruz-Mesía et al. (2007) who use a dependent Dirichlet process prior, Mansinghka et al. (2007) who model the distribution within each subpopulation defined by the class labels using a Dirichlet process mixture model, or Gutiérrez et al. (2014) who use a geometric-weights prior instead. For more examples, see a recent review by Singh et al. (2016) and references therein.

In contrast to supervised learning in classification, clustering methods partition the observations into latent groups/clusters in an unsupervised manner, with the aim of creating homogeneous groups such that observations in the same cluster are more similar to each other than to those in other clusters. Widely used clustering methods include hierarchical clustering, k-means, DBSCAN (Ester et al., 1996) and finite mixture models. Posterior simulation for finite mixtures was first discussed in Richardson and Green (1997) and extended to multivariate mixtures in Dellaportas and Papageorgiou (2006). See, for example, Jain (2010) and Fahad et al. (2014) for recent reviews. BNP (Hjort et al., 2010) clustering methods offer particularly flexible alternatives to the earlier mentioned clustering algorithms. Examples include Dirichlet process mixtures (DPM, Lo, 1984; MacEachern, 2000; Lau and Green, 2007) and variations with different data structures, such as Rodriguez et al. (2011) for a mixture of graphical models, Pitman-Yor process (PY) mixtures (Pitman and Yor, 1997; Ni et al., 2018), normalized inverse Gaussian process mixtures (Lijoi et al., 2005), normalized generalized Gamma process mixtures (Lijoiet al., 2007), and more general classes of BNP mixture models (Barrioset al., 2013; Favaro and Teh, 2013; Argiento et al., 2010).

Scalable methods.

Datasets that are too large to be analyzed on a single machine increasingly arise in many applications. Many of the earlier mentioned classification or clustering methods do not easily scale to large datasets, partly due to lack of straightforward parallelization. Below, we briefly review some recently proposed computation efficient strategies.

Zhang et al. (2012) developed two algorithms for parallel statistical optimization based on averaging and bootstrapping. Kleiner et al. (2014) developed a scalable bootstrap to evaluate the uncertainty of estimators. Bayesian methods naturally provide uncertainty quantification of estimators but are in general computation-intensive. Huang and Gelman (2005) proposed consensus Monte Carlo algorithms that distribute data to multiple machines running separate MCMC simulations in parallel. Various ways of eventually consolidating simulations from these subset posteriors have been proposed (Neiswanger et al., 2013; Wang and Dunson, 2013; Whiteet al., 2015; Minsker et al., 2014; Scott et al., 2016). An alternative strategy for scalable Bayesian computation is based on approximating the full likelihood/posterior using subsampling techniques (Welling and Teh, 2011; Korattikara et al., 2014; Bardenet et al., 2014; Quiroz et al., 2018); see Bardenet et al. (2015) for a review of related recent MCMC approaches. Alternatively to MCMC, Bayesian inference can be carried out by using approximation such as variational Bayes (Jaakkola and Jordan, 2000; Ghahramani and Beal, 2001; Broderick et al., 2013; Hoffman et al., 2013). For a grand overview of Bayesian computation, see also Green et al. (2015). Although variational inference is scalable to large-scale datasets and usually yields good approximations to the marginal posterior, MCMC algorithms tend to better approximate the joint posterior, due to their nature as simulation-exact methods.

Scalable classification and clustering.

Some classical classifiers like logistic regression are scalable to large datasets and easy to interpret. However, logistic regression tends to be not as accurate as other “black box” classifiers. Ideally, a good classifier should not need to sacrifice its predictive performance for interpretability and scalability. This is what we aim to achieve in this paper.

Some work has been done in this area. Payne and Mallick (2018) developed a two-stage Metropolis-Hastings algorithm for logistic regression to avoid the need for exact likelihood computation. The first stage, based on an approximate likelihood, is used to determine whether a full likelihood evaluation is necessary in the second stage. Combined with consensus Monte Carlo, the proposed method scales well to datasets with large samples. Rebentrost et al. (2014) implemented SVM on a quantum computer and showed exponential speed-up compared to classical sampling algorithms.

For clustering, Pennell and Dunson (2007) developed a two-stage approach for fitting random effects models to longitudinal data with large sample size. They first cluster subjects using a deterministic algorithm and then cluster the group-specific random effects using a DPM model. Zhao et al. (2009) proposed a parallel k-means clustering algorithm using the MapReduce framework (Dean and Ghemawat 2008). Wang and Dunson (2011) developed a single-pass sequential algorithm for conjugate DPM models. In each iteration, they deterministically assign the next subject to the cluster with the highest probability conditional on past cluster assignments and data up to the current observation. The algorithm is repeated for multiple permutations of the samples. Lin (2013) proposed a one-pass sequential algorithm for DPM models. The algorithm utilizes a constructive characterization of the posterior distribution of the mixing distribution given data and a partition. Variational inference is adopted to sequentially approximate the marginalization. Williamson et al. (2013) introduced a parallel MCMC for DPM models which involves iteration over local updates and a global update. For the local update, they exploit the fact that a Dirichlet mixtures of Dirichlet processes (DP) again defines a DP, if the parameters of Dirichlet mixture are suitably chosen. Geet al. (2015) used a similar characterization of the DP as in Lin (2013). But instead of a variational approximation, they adapted the slice sampler for parallel computing under a MapReduce framework. Tank et al. (2015) developed two variational inference algorithms for general BNP mixture models.

The method that is most similar to the approach in this paper is the subset nonparametric Bayesian (SNOB) clustering of Zuanetti et al. (2018), a computation-efficient alternative for model-based clustering under a DPM model with conjugate priors. SNOB is a two-step approach. It first splits data into shards and computes clusters locally in parallel. A second step combines the local clusters into global clusters. All steps are carried out using MCMC simulation under a common DPM model. All cluster-specific parameters are marginalized out in the second step in order to merge local clusters. The latter requires conjugate models and limits its applicability in a wide range of applications where non-conjugate models are desired. In addition, for large datasets, the number of local clusters may still be too large to process in a single machine. This motivates the construction of a more general multi-step algorithm that allows for possibly non-conjugate models.

Proposed method.

Inspired by the Algorithm 8 in Neal (2000) for inference in DPM models, we extend SNOB to clustering under non-conjugate BNP models, and propose a multi-step algorithm for subset inference of general nonparametric Bayesian methods (SIGN). The algorithm is a K-step approach (K is dynamically determined and will be introduced in Section 2). Each step requires clustering on small subsets only. The number of required subsets grows linearly with the sample size n, making it possible to implement posterior inference also for data that is too large for full MCMC simulation. SIGN can be applied with a large class of BNP mixture models. Particularly, we show how SIGN is implemented for inference under the PPMx model to simultaneously cluster and classify patients from a large Chinese EHR dataset with 85,021 samples and customers from a bank telemarketing dataset with 37,078 records. SIGN relies on a notion of “clustering of clusters” which, in different contexts, has been successfully used in the literature before. For example, Argiento et al. (2014) and Malsiner-Walli et al. (2017) developed clustering-of-clusters models for clustering non-Gaussian or non-convex data. In the upcoming discussion, we use the same notion to greatly reduce the computation cost of clustering large datasets.

In the context of a classification problem, SIGN still requires that all data can be accessed. This is not an inherent constraint of the proposed algorithm; rather it is due to the lack of sufficient/summary statistics for general classification models (such as probit regression). Whenever such statistics exist, SIGN does not need to access the entire dataset.

The remainder of this paper is organized as follows. In Section 2, we introduce the proposed SIGN algorithm which is applied for inference under the PPMx model in Section 3. The SIGN algorithm is evaluated with simulation studies in Section 4 and applied to EHR and bank telemarketing data in Section 5. We conclude with a discussion in Section 6.

2. The proposed SIGN algorithm

2.1. BNP clustering

We propose an algorithm for posterior inference on random partitions under BNP mixture models. To state the general model, we need some notation. A partition ρ = {S₁,…,S_C} of an index set [n] ={1,…,n} is a collection of nonempty, disjoint and exhaustive subsets S_c⊆[n]. The partition can alternatively be represented by a set of cluster membership indicators s = (s₁,…,s_n) with s_i = c if i ∈ S_c. Throughout the paper, we will use superscript – i to represent the appropriate quantity with the ith sample or the ith item (defined later) removed. For instance, s⁻ⁱ = s\s_i and ${\rho }^{-i}=\left(\rho \backslash S_{s_i}\right)\cup \left(S_{s_i}\backslash i\right)$ are the cluster memberships and partition after removing index i.

In what follows we consider a random partition ρ with prior probability distribution p(ρ). Let n_c =| S_c| denote the cardinalities of the partitioning subsets. Let n = (n₁, …, n_C) and let n^j+ denote with the jth element incremented by 1, with the convention that n^{(C + 1)+} = (n₁, …,n_C,1). A random partition is called exchangeable if p(ρ) = f(n) for a symmetric (in its arguments) function f (n) and if $f(n)=\sum _{j=1}^{C+1}f\left(n^{j+}\right)$. The function f(n) is known as the exchangeable partition probability function (EPPF). By Kingman’s representation theorem (Kingman, 1978), any exchangeable random partition can be characterized as the groups formed by ties under i.i.d. sampling from a discrete probability measure $G=\sum _{h=1}^{\infty }{w}_h{\delta }_{m_h}$. That is, ρ is determined by the ties among θ_i ~ G, i = 1,…,n. We denote the unique values of θ_i’s by ${\theta }_1^{\star },\dots ,{\theta }_C^{*}$, implying i ∈ S_c if ${\theta }_i={\theta }_c^{\star }$. See, for example, Lee et al. (2013) for a discussion. It follows that a prior probability model for an exchangeable random partition ρ can always be defined as a prior p(G) on a random discrete distribution $G=\sum _{h=1}^{\infty }{w}_h{\delta }_{m_h}$. This implicit definition of p(ρ) by a BNP prior p(G) on the random probability measure G is a commonly used specification of random partition models. The construction already includes cluster-specific parameters ${\theta }_c^{\star }$ which are useful for the construction of a sampling model conditional on the partition. We use it in the next step of the model construction.

The model on G and θ_i is completed with a sampling model for the observed data conditional on ρ. For example, the θ_i could index a sampling model p(y_i | θ_i), implying that all observations in a cluster share the same sampling model. In summary,

$$y_i|{\theta }_i\stackrel{ind}{~}p\left(y_i|{\theta }_i\right),{\theta }_i|G\stackrel{ind}{~}G,G~H,$$

where G is a discrete prior distribution for θ_i and H is the BNP prior for the random probability measure G.

There are a number of options for H. A popular choice is the DP, which yields an EPPF of the form $p(\rho )\propto {\alpha }^{C-1}\prod _{c=1}^C\left(n_c-1\right)!$ where α is known as the concentration parameter. Other choices include the PY process, the normalized inverse Gaussian process and the normalized generalized gamma process. In many applications, the focus is on the posterior distribution of the random partition ρ. The posterior distribution on ρ can be approximated by various MCMC algorithms, including Escobar (1994), MacEachern and Müller (1998), Neal (2000) and Walker (2007) in the case of the DP prior, and, for more general models, Barrios et al. (2013), Favaro and Teh (2013) or Argiento et al. (2010). However, MCMC is only practicable for small to moderate datasets. Directly applying MCMC to large datasets is very costly because the algorithm has to scan through all observations at each iteration, each requiring likelihood and prior evaluations.

2.2. SIGN algorithm

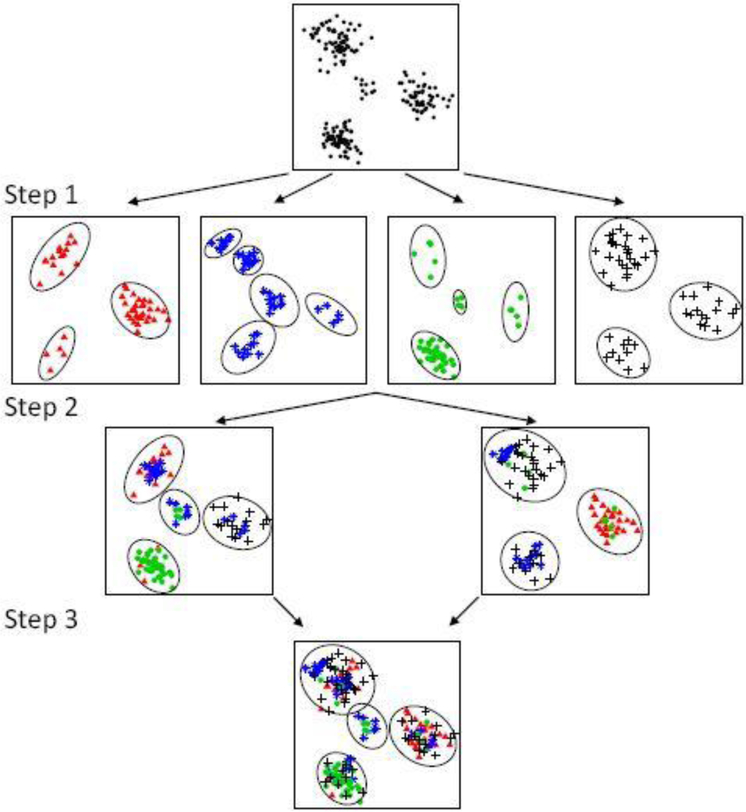
The proposed SIGN algorithm proceeds in steps. For illustration, an example workflow of SIGN with K = 3 steps is shown in Figure 1. Importantly, across all steps of the algorithm, all updates of cluster configurations (initially of observations, and of sets of observations in later steps) are based on a single underlying BNP mixture model for the data. Details of the implied probabilities for clustering sets of obserations are given later.

Fig. 1.

Example workflow of a 3-step SIGN algorithm. Step 1: the dataset is randomly distributed into 4 shards, each denoted by a unique type (color) of marker and observations are partitioned into local clusters (represented by the ellipses) within each shard in parallel. Step 2: local clusters are collected, randomly distributed into M₂ = 2 shards, and then partitioned into regional clusters within each shard. Step 3: regional clusters are aggregated and partitioned into global clusters.

Step 1. In the first step, the full dataset is randomly split into M₁ shards, M₁ = 4 in Figure 1; the observations from each shard are denoted by a distinct symbol in the figure. A clustering method is then applied (in our implementation, using the algorithm 8 in Neal (2000) for posterior simulation) to cluster the items (initially, in the first step, the observations) in each shard separately, and can be implemented in parallel. We refer to the estimated clusters, represented by the ellipses, as “local” clusters. These local clusters are frozen, meaning that the observations within each cluster will never be divided in the subsequent steps, although merging is possible.

Step 2. The local clusters estimated from the previous step become the items to be clustered in this step. The items are distributed into M₂ shards (M₂ = 2 in Figure 1). We still use the same underlying BNP mixture model to cluster the items. See later for a statement of the relevant probabilities to cluster the items. At the end of the second step, the estimated clusters are again frozen as “regional” clusters.

Step 3. At the last step, all regional clusters are collected to form the items for the next, third, step. Again items are split into M₃ shards and clustered within each shard. In the example of Figure 1, M₃ =1 and iteration stops.

In general, iteration continues until the number of items is sufficiently small to be clustered in a single shard. Importantly, at each step one need to only scan through a small number of items (created by previous steps), instead of all observations in a large dataset. Each step can be implemented in parallel using instances of the same MCMC algorithm which takes as input a set of (current) items, generically denoted by $\tilde{y}=\left\{{\tilde{y}}_1,\dots ,{\tilde{y}}_B\right\}$ and outputs estimated clusters of these items. Those clusters then define the items for the next step of the algorithm. Initially, in step 1, ${\tilde{y}}_i=y_i$ are the original data. Let $r_i=|{\tilde{y}}_i|$, i = 1,…,B denote the size of each item, in terms of the number of original data that form ${\tilde{y}}_i$, and let r ={r₁,…,r_B}. In the following, we describe the posterior probabilities for clustering items, i.e., sets of original observations, in any of the steps k = 1,…,K. To simplify notation we do not include an index for steps.

2.2.1. MCMC

In each of the K steps, MCMC simulation iterates between (i) updating the cluster membership, and (ii) updating cluster-specific parameters given the cluster membership. The key quantity in updating the cluster membership is the conditional probability

$$p\left({\tilde{s}}_i=c|{\tilde{s}}^{-i},\tilde{y},{\theta }^{\star }\right)\propto p\left({\tilde{s}}_i=c|{\tilde{s}}^{-i}\right)p\left({\tilde{y}}_i|{\theta }_c^{*}\right)$$ (1)

for i = 1,…,B and c = 1,…,C⁻ⁱ + 1 where ${\tilde{s}}_i=c$ means that item i is in cluster c, i.e., all observations in ${\tilde{y}}_i$ are assigned to cluster c. The definition of the items ${\tilde{y}}_i$ and the number of items, B, changes across steps. Initially, ${\tilde{y}}_i$ are the original data, and B = n is the sample size. In step 2, the items ${\tilde{y}}_i$ are the local clusters and B is the total number of local clusters, etc. Importantly, the probabilities that are evaluated under (1) and used for clustering in steps 1 through 3 are all based on the same BNP mixture model for the original observations.

Equation (1) states the probabilities for combining clusters of observations into larger clusters. The first factor can be evaluated as

$$p\left({\tilde{s}}_i=c|{\tilde{s}}^{-i}\right)\propto \frac{p\left({\rho }^{+c}\right)}{p\left({\rho }^{-i}\right)}$$ (2)

where ${\rho }^{+c}=\left({\rho }^{-i}\backslash S_c^{-i}\right)\cup \left(S_c^{-i}\cup \tilde{i}\right)$ is the new partition that assigns the ith item to cluster c (that is, all original data points that make up ${\tilde{y}}_i$). The partition probabilities on the right-hand side of (2) depend on r n and the BNP prior H. For example, using H = PY,(d,G₀) with concentration parameter α, discount parameter d, and baseline probability measure G₀, implies the random prior partition:

$$p(\rho )\propto {(\alpha |d)}_C\prod _{c=1}^C{(1-d)}_{n_c-1},$$ (3)

where (x)n = x(x+1)…(x+n-1) denotes the Pochhammer symbol of a rising factorial, and (x | y)_n = x(x + y)…(x + (n −1)y) denotes the Pochhammer symbol with increment y. Substituting (3) into (2) yields

$$p\left({\tilde{s}}_i=c|{\tilde{s}}^{-i}\right)\propto \{\begin{array}{cc}\frac{\text{Γ}\left(n_c^{-i}+r_i-d\right)}{\text{Γ}\left(n_c^{-i}-d\right)}& \text{ if }c=1,\dots ,C^{-i}\\ \frac{\left(\alpha +d{C}^{-i}\right)\text{Γ}\left(r_i-d\right)}{\text{Γ}(1-d)}& \text{ if }c=C^{-i}+1\end{array},$$ (4)

where $n_c^{-i}$ is the size of the cth cluster after removing the ith item ${\tilde{y}}_i$ (recall that size is recorded in original data units). In the special case when $r_i=|{\tilde{y}}_i|=1$ for all i, equation (4) reduces to the Pólya urn representation of the PY.

The second factor in (1) is the sampling model evaluated for ${\tilde{y}}_i$ given the cluster-specific parameters, which is straightforward to compute except for the missing ${\theta }_c^{\star }$ for c = C⁻ⁱ + 1, which could be avoided by marginalizing with respect to ${\theta }_c^{\star }$. In general, this marginalization is analytically intractable and we use instead the Algorithm 8 in Neal (2000). The algorithm includes a temporary model augmentation with m latent variables ${\theta }_c^{\star }$,c = C⁻ⁱ + 1,…,C⁻ⁱ + m which serve as potential new cluster parameters, and are generated from the prior for unique atoms of the BNP prior (base measure in the DP or PY prior). The prior probability for a new cluster in (4) is split equally among the m potential values. The case when resampling ${\tilde{s}}_i$ removes a current cluster, say S_c, by re-assigning the only element of a singleton cluster, needs careful attention. In that case, ${\theta }_c^{\star }$ becomes ${\theta }_{C^{-i}+1}^{\star }$ and only the remaining latent variables are sampled from the prior. The only remaining parameters to be sampled in the MCMC are the cluster-specific parameters ${\theta }_j^{\star }$, which are updated using a suitable MCMC transition probability. At the end of each MCMC pass, we compute a least-squares estimate of the partition (Dahl, 2006). An alternative method of summarizing partitions is also considered in Section 4.1. Algorithm 1 summarizes the MCMC simulation.

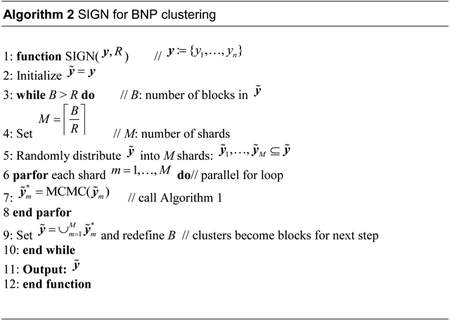
2.2.2. The complete scheme

The complete SIGN algorithm simply repeatedly distributes the items (i.e., blocked observations) into shards and applies Algorithm 1 to each shard in parallel. The number K of steps is dynamically determined by specifying a maximum number R (typically a few hundred) of items that can be clustered in one processor. Simulation terminates when the total number of items is less than R. For example, suppose we set R = 200 and we obtain 600 local clusters from the first step. Since 600 > R, we decide to distribute the local clusters into 3 shards each with 200 blocked observations. If 30 regional clusters are returned from the second step, we will in a final step cluster the regional clusters in one shard. Since 30 < R, there is no need for a further split and iteration stops. Hence in this example K = 3. The complete scheme is summarized in Algorithm 2. SIGN implements approximate posterior inference under the BNP mixture model. The approximation arises from the fact that observations in the same item at any step will not be split in any of the subsequent steps. See the following discussion for more details.

The SIGN algorithm can be applied with a wide range of BNP mixture models. The key step is deriving the prior probabilities for combining clusters. If an EPPF for the underlying BNP prior is available, it is simply evaluated as the ratio of two EPPFs as shown in Equation (2). Combined with the sampling model, the cluster membership of each item can be drawn from its full conditional.

2.2.3. Approximation

The described update for ρ involves an approximation of the target distribution p(ρ | y). The SIGN algorithm reduces computation time by replacing the problem of clustering n items by essentially M₁ problems of clustering n / M₁ items. The nature of the involved approximation is similar in flavor to a variational Bayes approximation. This is seen in a simplified setup assuming M₁ = 2 shards, say A₁ and A₂, and assuming that iteration stops after K = 2 steps. Let d_ij denote co-clustering indicators d_ij = I(s_i = s_j), and let d₁ = (d_ij; i, j ∈A₁), and similarly for d₂ and d₁₂ = (d_ij; i ∈A₁, j ∈A₂). Then (d₁,d₂,d₃) is an alternative representation of a partition ρ. Let y₁ denote the data in A₁ and similarly for y₂. If SIGN is implemented by generating one (approximate) posterior draw of d₁ and d₂ in each shard, then the algorithm p(d₁,d₂,d₁₂ | y) q(d₁,d₂,d₁₂) = p(d₁ | y₁) p(d₂ | y₂) p(d₁₂ | d₁,d₂, y), that is, a distribution that is independent in d₁,d₂, but with each factor defined by the original target distribution. In contrast to a variational Bayesian approach there is no notion of optimizing the approximation.

Based on these considerations we propose a simple diagnostic to summarize the level of approximation. Select any two of the M₁ shards in step 1, say A₁ and A₂. We then carry out Steps 1a and 2a like Steps 1 and 2 before, but restricted to the two selected shards only. Alternatively we implement (simulation exact) posterior MCMC simulation in

A₁ ∪ A₂. For any pair (i, j) in A₁ ∪ A₂, let p_ij = E(d_ij | y) denote the posterior co-clustering probabilities let ${\tilde{p}}_{ij}$ denote the estimate based on Steps 1a and 2a, and let ${\widehat{p}}_{ij}$ denote the same based on the MCMC simulation. We summarize the level of the approximation in SIGN by reporting the histogram of ${\tilde{p}}_{ij}-{\widehat{p}}_{ij}$ and the proportion F_0.1 of pairs (i, j) with $\left|{\tilde{p}}_{ij}-{\widehat{p}}_{ij}\right|<0.1$. For the simulations and examples discussed in later sections, we find the histogram is concentrated around zero and F_0.1 > 70%.

3. Clustering and classification with PPMx

Clustering is often carried out to find more homogeneous subpopulations that can then be used, for example, to derive improved classification and prediction. One example of such approaches is the PPMx model, which allows for simultaneously partitioning of heterogeneous samples and predicting outcomes on the basis of covariates. To fix notation, let z_i ∈{0,1} denote a binary outcome (reserving notation y_i for a later introduced augmented response). Let

x_i ={w_i,u_i} denote a set of continuous covariates w_i = (w_i1,…, w_ip) and categorical covariates u_i = (u_i1,…,u_iq) for experimental units i =1,…,n. Let z = {z₁,…, z_n} and x ={x₁,…, x_n}. A product partition model (PPM) (Hartigan, 1990) assumes $p(\rho )\propto \prod _{c=1}^{C}h\left(S_c\right)$, where h(·) is a non-negative cohesion function that quantifies the tightness of a cluster. For example, the prior distribution on partitions that is induced under i.i.d. sampling from a DP-distributed random measure with concentration parameter α is a PPM with h(S_c) = α × (|S_c| − 1)!. Müller et al. (2011) define the PPMx as a variation of the PPM by introducing prior dependence on covariates by augmenting the random partition to

$$p(\rho |x)\propto \prod _{c=1}^{C}h\left(S_c\right)g\left(x_c^{\star }\right),$$ (5)

with a nonnegative similarity function g(·) indexed by covariates where $x_c^{\star }=\left\{x_i|i\in S_c\right\}$ are the covariates of observations in the cth cluster. The similarity function measures how similar the covariates are thought to be. A computationally convenient default way to define a similarity function uses the marginal probability in an auxiliary probability model q on x:

$$g\left(x_c^{\star }\right)=\int \prod _{i\in S_c}{q}_x\left(x_i|{\xi }_c\right)q_{\xi }\left({\xi }_c\right)d{\xi }_c.$$

The important feature here is that the marginal distribution has higher density value for a set of very similar x_i than for a very diverse set. For continuous covariates, we use an independent normal-normal-gamma auxiliary model. Let N(x | m,v) denote the evaluation of a normal density with moments (m, v), evaluated at x, and similar for a gamma density, Ga(x | a,b) and other distributions. We use $q_x\left(w_{ij}|{\mu }_c,{\lambda }_c\right)=\text{N}\left(w_{ij}|{\mu }_c,{\lambda }_c^{-1}\right)$ and $q_{\xi }\left({\mu }_c,{\lambda }_c\right)=\text{N}\left({\mu }_c|{\mu }_0,{\left(v_0{\lambda }_c\right)}^{-1}\right)\times Ga\left({\lambda }_c|a_{\lambda },b_{\lambda }\right)$. In this case, ξ_c = (μ_c,λ_c). Let Cat(x|π) indicate a discrete r.v. x with probabilities p(x,=l) = π_l. For categorical covariates with r categories, we use a categorical-Dirichlet auxiliary model, q_x(u_ij | π_c) = Cat(u_ij | π_c) and q_ξ (π_c) = Dir(π_c | a_π,…,a_π) with π_c = (π_c1,…,π_cr). The prior p(ρ | x) introduces the desired covariate-dependent prior on the clusters ${\mathcal{S}}_c$.

Conditional on ρ we introduce cluster-specific parameters β_c and complete the model with a probit sampling model,

$$p(z|\rho ,\beta ,x)=\prod _{c=1}^C\prod _{i\in S_c}p\left(z_i|x_i,{\beta }_c\right)=\prod _{c=1}^C\prod _{i\in S_c}{p}_i^{z_i}{\left(1-p_i\right)}^{1-z_i}$$ (6)

with p_i = Φ(x_i β_c) and a centered multivariate normal prior on β_c ~ N(0,τ_βI).

A practical advantage of the PPMx is its simple implementation. The posterior defined by models (5) and (6) becomes

$$p(\rho ,\beta ,\xi |\mathit{z},x)\propto \prod _{c=1}^C\left[\left\{\prod _{i\in S_c}p\left(z_i|x_i,{\beta }_c\right)q_x\left(x_i|{\xi }_c\right)\right\}p\left({\beta }_c\right)q_{\xi }\left({\xi }_c\right)h\left(S_c\right)\right].$$

Letting $y_i=\left\{z_i,x_i\right\},{\theta }_c^{\star }=\left\{{\beta }_c,{\xi }_c\right\}$,$q_y\left(y_i|{\theta }_c^{\star }\right)=p\left(z_i|x_i,{\beta }_c\right)q_x\left(x_i|{\xi }_c\right)$, $q_{\theta }\left({\theta }_c^{\star }\right)=p\left({\beta }_c\right)q_{\xi }\left({\xi }_c\right)$ and $q_{\rho }(\rho )=\prod _{c=1}^{C}h\left(S_c\right)$ one can rewrite the posterior distribution as

$$p(\rho ,\beta ,\xi |z,x)\propto \prod _{c=1}^c\prod _{i\in S_c}{q}_y\left(y_i|{\theta }_c^{\star }\right)\times \prod _{c=1}^C{q}_{\theta }\left({\theta }_c^{\star }\right)\times q_{\rho }(\rho ).$$ (7)

That is, posterior inference can proceed as if y_i were sampled from Equation (7). For example, in our application, we choose q_ρ(·) to be the random partition that is induced by a PY prior. The PY generalizes the DP and is more flexible in modeling the number of clusters (De Blasi et al., 2015). Posterior inference under (7) can then be carried out using Equation (2.1) (and hence Algorithms 1 and 2) with p(y_i |·) = q_y(y_i |·), H = PY(α,d,G₀) and G₀ = q_θ (·). Note how (7) is identical to the posterior in a model with data y_i cluster-specific parameters θ*_c and prior q_ρ(ρ), allowing for easy posterior simulation.

One of the goals in our later applications is to classify a new subject, i.e., predict the binary outcome z_n+1, on the basis of covariates x_n+1. It is straightforward to predict z_n+1 using posterior averaging with respect to partitions, cluster allocation and model parameters. Let $q\left(x_{n+1}|x_c^{\star }\right)=g\left(x_c^{\star },x_{n+1}\right)/g\left(x_c^{\star }\right)$. The posterior predictive distribution is given by

$$\begin{gathered} p\left(z_{n+1}|x_{n+1},z,x\right)\propto \int \{\left(n_c-d\right)\sum _{c=1}^{C}p\left(z_{n+1}|x_{n+1},{\beta }_c,s_{n+1}=c\right)q\left(x_{n+1}|x_c^{\star }\right) \\ +(\alpha +dC)p\left(z_{n+1}|x_{n+1},{\beta }_{C+1}\right)g\left(x_{n+1}\right)\}p(\rho |z,x)d\rho , \end{gathered}$$

which can be approximated by

$$\begin{gathered} p\left(z_{n+1}|x_{n+1},z,x\right)\propto \frac{1}{T}\sum _{t=1}^T\{\left(n_c^{(t)}-d\right)\sum _{c=1}^{C^{(t)}}p\left(z_{n+1}|x_{n+1},{\beta }_c^{(t)},s_{n+1}^{(t)}=c\right)q\left(x_{n+1}|x_c^{\star }\right) \\ +\left(\alpha +d{C}^{(t)}\right)p\left(z_{n+1}|x_{n+1},{\beta }_{C+1}^{(t)}\right)g\left(x_{n+1}\right)\}, \end{gathered}$$

with superscript (t) indexing the tth MCMC samples t = 1,…,T, and ${\beta }_{C+1}^{(t)}$ is drawn from its prior.

4. Simulation

We conduct four simulation studies. The first two simulations focus on clustering. We use a PY mixture (PYM) model. The last two simulations consider clustering and classification based on the PPMx. We use relatively small datasets with n = 800 in the simulations, so that we can compare with standard MCMC implementations of inference under the PYM and PPMx models. Scalability is later explored, in two case studies. We report frequentist summaries based on 50 repetitions. For each repeat simulation, MCMC is run for 10,000 iterations, discarding the first 50% of MCMC samples as burn-in and thinning the chain by keeping every 5th sample.

4.1. Simulation I: Mixture of five normals

The first simulation considers a SIGN approximation of posterior inference in a PYM model for a p = 5 dimensional outcome y_i:

$$y_i|{\mu }_i,{\Sigma }_i\stackrel{\text{ ind }}{~}p\left(y_i|{\mu }_i,{\Sigma }_i\right),{\mu }_{\text{i}},{\Sigma }_{\text{i}}|\text{G}\stackrel{\text{ ind }}{~}\text{G},\text{G}~\text{PY}\left(\alpha ,\text{d},{\text{G}}_0\right),$$

where G₀(μ, Σ) = N_p(μ|0,Σ/κ₀) × IW(Σ|b, I_p). The hyperparameters are α =1, d = 0.5, κ₀ = 0.01, b = p.

We construct a simulation truth with C₀ = 5 true clusters with equal sizes. We generate s_i using p(s_i = l) = 1/5, and data y_i|s_i = c ~ N_p(μ_c, Σ_c), i = 1,…,n. where μ₁ = (−2,1.5,0,0,0)^T, μ₂ = (0,3,0,0,0)^T, μ₃ = (0,0,0,1, −2)^T, μ₄ = (1,2,0,0,0)^T, μ₅ = (0,0,0, −2, −2)^T, Σ₁= diag(0.25,0.1,1,1,1), Σ₂= diag(1.25²,0.1,1,1,1), Σ₃= diag(1,1.1,0.1,0,0.25), ${\Sigma }_4=blkdiag\left(\left[\begin{array}{cc}0.1& 0.05\\ 0.05& 0.1\end{array}\right],I_3\right)$ and ${\Sigma }_5=\text{ blkdiag }\left({\text{I}}_3,\left[\begin{array}{cc}0.25& 0.125\\ 0.125& 0.25\end{array}\right]\right)$.

In words, clusters 1, 2, and 4 are characterized by a shift in the distribution for the first two variables y_i1 and y_i2 with different correlation structures, whereas clusters 3 and 5 are characterized by a shift in the third and fourth variables y_i4 and y_i5. And y_i3 plays the role of a “noisy” response with the same distribution across all clusters. Variables that do not characterize clusters (such as y_i3, y_i4, y_i5 in clusters 1, 2 and 4) are independently sampled from standard normal distributions. The data of one randomly selected simulation is shown in Supplementary Materials (Figure 1).

We implement SIGN for approximate posterior inference, using K = 2 steps. In the first step, the data are randomly split into M₁ = 4 shards with each shard processing 200 samples. We compare the SIGN approximation with a (simulation exact) MCMC implementation for PYM and with DBSCAN (Ester et al. 1996). DBSCAN is a clustering-algorithm designed to discover clusters of arbitrary shape. It has two tuning parameters: neighborhood size ϵ and the minimum number m of points in the ϵ-neighborhood. We use the default choice m = 5 as implemented in the R package ”dbscan” (Hahsler and Piekenbrock 2018). The value of ϵ is set to 1, which gives the best performance in the spiral data (Section 4.2), a typical example showcasing the strength of DBSCAN. We will also examine a couple of other values of ϵ. In addition, we include a variation of SIGN with a different loss function instead of squared error loss (to summarize the partition at the end of each MCMC pass). Specifically, we use variation of information loss (Meilă 2007; Wade and Ghahramani 2018; Rastelli and Friel 2018), and refer to this variation as SIGN-VI.

The average estimated number of clusters, C, and the misclustering rate are reported in Table 1. SIGN and SIGN-VI slightly underestimate C (relative to the posterior mean under full MCMC simulation). In terms of the misclustering rate, full MCMC posterior inference is closely matched by SIGN and SIGN-VI. DBSCAN shows a 41% misclustering rate. A similar comparison holds for parameter estimation: SIGN and SIGN-VI closely match the average mean squared error for cluster-specific means μ that is reported under full posterior MCMC, which in turn is lower than under DBSCAN (Table 1).

Table 1.

Clustering performance of the methods used for Simulation I. The table reports the average estimated number of clusters (C), misclustering rate (MISC) and mean squared error in estimating cluster-specific means μb (MSE) for inference under SIGN, SIGN with variation of information loss (SIGN-VI), standard implementation of Pitman-Yor process mixture (PYM) and DPSCAN. Numerical errors (as standard deviations over repeat simulation) are given within the parentheses.

	SIGN	SIGN-VI	PYM	DBSCAN
C	4.94 (0.31)	4.90 (0.30)	5.08 (0.27)	3.64 (1.63)
MISC	0.08 (0.03)	0.09 (0.03)	0.04 (0.01)	0.41 (0.11)
MSE	0.01 (0.01)	0.01 (0.01)	0.01 (0.00)	0.49 (0.18)

To further evaluate the approximation accuracy of SIGN relative to full posterior simulation for the PYM, we evaluate the posterior co-clustering probabilities p_ij = p(s_i = s_j | y), i < j, using SIGN and full posterior MCMC in the PYM, and then take the differences between the two estimates across all pairs (i, j) of observations. The histogram of the differences across 50 simulations (Supplementary Material, Figure 2) indicates good approximation accuracy of SIGN.

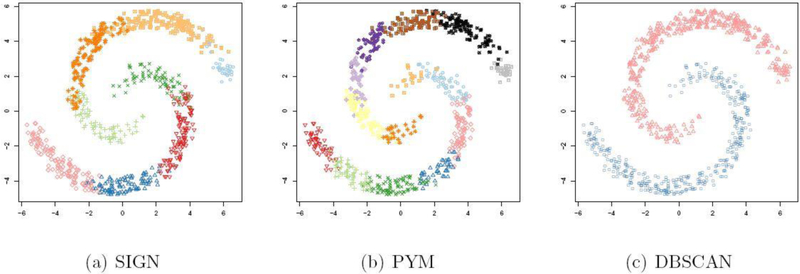
Fig. 2.

Two-spiral data. One randomly selected simulation result for inference under (a) SIGN, (b) standard implementation of PYM, and (c) DBSCAN. Marker types indicate clusters.

Sensitivity analysis.

Next, we evaluate the sensitivity of the SIGN approximation with respect to different random splits of the data in the first step. We randomly pick one simulation and run SIGN 50 times, each time with a different initial split. The average estimated number of clusters is 4.96 with standard deviation 0.20 and misclustering rate 0.09 with standard deviation 0.03. The small standard deviations indicate stable performance of SIGN under different splits of the data.

To assess sensitivity with respect to the local sample size in each shard in the first step, we increase the sample size to n = 4000 and compare with full posterior MCMC under the PYM and with DBSCAN. Full posterior inference finds 21.8 clusters on average. As expected, larger total sample size gives rise to more clusters, a typical property of many BNP mixture models. DBSCAN finds 126.38 clusters on average using ϵ = 1. DBSCAN is quite sensitive to the choice of ϵ. For example, in a randomly selected simulation, the estimated numbers of clusters are 123, 77 and 5 for ϵ = 1.0,1.1,1.7. However, we note that DBSCAN is particularly designed to work well with unusual clusters, as we shall see later, in Section 4.2.

We then run SIGN with M₁ = 4,8,10,20 corresponding to 1000,500,400,200 data points per shard. The average (over repeat simulations) estimated numbers of clusters are 8.54,6.46,5.74,5.44 with standard deviations 1.76,1.03,0.75,0.70 The average misclustering rates are 0.06,0.05,0.05,0.09 with standard deviations 0.02,0.01,0.01,0.02. In summary, the SIGN approximation tends to under-estimate the number of clusters relatively to full MCMC. This is probably due to the fact that local clusters in earlier steps are frozen and can only grow by later merging, but can never shrink. This biases the number of estimated clusters toward smaller numbers. However, in most applications the many small and singleton clusters that are generated by some BNP mixture models are not of interest, making this approximation error less critical.

4.2. Simulation II: Two spirals

The main strength of DBSCAN is its flexibility to adjust to clusters of different shapes. Here, we consider data with two highly non-convex clusters. A typical view of the data is shown in Figure 2. Applying full MCMC for the PYM model, the SIGN approximation, and DBSCAN for 50 randomly generated two-spiral datasets, we find the average (over the repeat simulations) estimated number of clusters to be 14.10,9.28,1.98 with standard deviations 1.37,0.93,0.14 for full posterior inference, the SIGN approximation, and for DBSCAN, respectively. However, the tuning parameter ϵ of DBSCAN is tuned in an “oracle” way, that is, we set

ϵ = 1 so that the average number of clusters is close to the truth C₀ = 2. Not surprisingly, due to the convexity of normal density/contours, the PYM model requires more clusters to compensate the non-convex shape of the true clusters, using both, full posterior MCMC as well as using the SIGN approximation. The estimated clusters for one simulation are shown in Figure 2.

4.3. Simulation III: cluster-specific probit regression

Next we assess the performance of the SIGN implementation for inference in the PPMx. We first consider a scenario where the simulation truth includes underlying clusters. We assume a simulation truth with C₀ = 5 clusters, p = q = 5 continuous and discrete covariates, and all clusters having the same size. Discrete covariates u_i are generated as u_ij ~ Cat(1/ 3,1/ 3,1/ 3), independently, j =1,…,q. Continuous covariates w_i are generated in the same way as y_i in Simulation I. The binary response z_i is generated from a cluster-specific probit regression, z_i ~ Bernoulli(p_i) with

$${\Phi }^{-1}\left(p_i\right)=\{\begin{array}{ccc}-\text{1}-w_{i\text{5}}& \text{if}& s_i\text{ = 1}\\ -\text{1+2}{w}_{i\text{3}}& \text{if}& s_i\text{ = 2}\\ -\text{1+}{w}_{i\text{4}}& \text{if}& s_i\text{ = 3}\\ -1+1.5w_{i1}-I\left(u_{i1}=2\right)+I\left(u_{i1}=3\right)& \text{if}& s_i\text{ = 4}\\ -1-1-1.5w_{i1}-I\left(u_{i2}=2\right)+I\left(u_{i3}=3\right)& \text{if}& s_i\text{ = 5}.\end{array}$$

We fix the hyperparameters as

α =1,d = 0.5,τ_β =1,μ₀ = 0,v₀ = a_λ = b_λ = 0.01,a_π =1/ r, and carry out inference under the PPMx model using the default similarity functions (simply PPMx hereafter). For comparison, we also carry out inference using k-means (Hartigan and Wong, 1979) for the continuous covariates (which define the clusters) with k = 5 (the true number of clusters) and 20 random starting points. PPMx is always able to correctly identify the number of clusters with 2.5% average misclustering rate (with respect to cluster assignment). The SIGN approximation selects the correct number of clusters in 48 (out of 50) simulations, with average misclustering rate 7.5%. In contrast, with k-means we find a misclustering rate of 25.5%.

To assess the out-of-sample predictive performance, that is, prediction of z_n+1, we compute the area under the ROC curve (AUC) based on 50 independent test samples generated from the same simulation truth as the training data. In addition to the previous comparison, we also benchmark against four more alternative classifiers: sparse LR with lasso (R package ”glmnet”, Friedman et al., 2010), SVM (”e1071”, Meyer et al., 2018), RF (”randomForest”, Liaw and Wiener, 2002), and BART (”BayesTree”, Chipman and McCulloch, 2016). For SVM, we transform the discrete covariates using dummy variables, fit with linear, cubic and Gaussian radial bases and report the best performance of the three. We grow 50,000 trees for RF and 200 trees for BART. For a fair comparison, we run BART using the same MCMC configuration as ours (i.e. 10,000 iteration, 50% burn-in and save every 5th sample). The results are reported in the first column of Table 2, where we find that full posterior inference in the PPMx and the SIGN approximation have almost the same AUC’s and both compare favorably with the competing classifiers.

Table 2.

Performance of the methods used for Simulations III and IV, and the two case studies. The table reports AUC for inference under the SIGN approximation, (standard implementation of) PPMx, BART, RF, LR and SVM. Numerical errors (as standard deviations over repeat simulation) are given within the parentheses.

	Simulation III	Simulation IV	EHR	Bank
SIGN	0.808 (0.067)	0.838 (0.067)	0.880	0.825
PPMx	0.824 (0.060)	0.841 (0.063)	-	-
BART	0.755 (0.062)	0.866 (0.050)	0.867	0.792
RF	0.793 (0.059)	0.838 (0.067)	0.869	0.786
LR	0.600 (0.091)	0.524 (0.073)	0.856	0.781
SVM	0.622 (0.077)	0.585 (0.077)	0.856	0.761

4.4. Simulation IV: non-linear probit regression

The favorable results for SIGN and PPMx in simulation III may be partially due to the chosen simulation truth. For an alternative comparison, in this example we use a simulation truth different from the PPMx model. Particularly, we assume a simulation truth without an underlying clustering structure, generating the binary response by a nonlinear probit regression, z_i ~ Bernoulli(p_i) with

$${\Phi }^{-1}\left(p_i\right)=-1+w_{i1}^2-w_{i2}^2+\text{sin}\left(w_{i3}{w}_{i4}\right)+I\left(u_{i1}=2\right)-I\left(u_{i1}=3\right)-I\left(u_{i2}=2\right)+I\left(u_{i2}=3\right).$$

The AUC summaries for the classification are shown in the second column of Table 2. SIGN, PPMx and RF have the same AUC, AUC = 0.84, which is slightly lower than the AUC of BART, AUC = 0.87. LR and SVM do not perform well in both simulations possibly due to the parametric (linear or cubic) decision boundary in LR, and the use of SVM with linear and cubic bases, and the difficulty in tuning the model parameters in SVM with radial bases.

5. Case studies

5.1. Electronic health records data: detecting diabetes

The emergence of EHR data gives rise to great opportunities as well as challenges for data-driven approaches in early disease detection. Large sample sizes allow more efficient statistical inference but at the same time impose computational challenges, especially for flexible but computation-intensive BNP models.

We consider EHR data for n = 85, 021 individuals in China. The dataset is based on a physical examination of residents in some districts of a major city in China conducted in 2016. We use the data to develop a model for chronic disease prediction, specifically for diabetes. We extract data on diabetes from the items “medical history” and “other current diseases” in the physical examination form. If either of the two items of a subject mention diabetes, that subject is considered as having diabetes. We denote the diabetes status by z_i (1: diabetic and 0: normal) for subjects i =1,…,n. Blood samples were drawn from each subject and sent to a laboratory for subsequent tests. We consider test results that are thought to be relevant to diabetes. These include white blood cell count (WBC), red blood cell count (RBC), hemoglobin (HGB), platelets (PLT), fasting blood glucose (FBG), low density lipoproteins (LDL), total cholesterol (TC), triglycerides (Trig), triketopurine (Trik), high density lipoproteins (HDL), serum creatinine (SCr), serum glutamic oxaloacetic transaminase (SGOT), and total bilirubin (TB). We also include 5 additional covariates: gender, height, weight, blood pressure, and waist. Our goal is twofold: (1) predicting diabetes; and (2) clustering a heterogeneous population into homogeneous subpopulations.

To comply with Chinese policy, we report inference for data generated by a Generative Adversarial Network (GAN, Goodfellow et al. 2014), which replicates the distribution underlying the raw data. GAN is a machine learning algorithm which simultaneously trains a generative model and a discriminative model on a training dataset (in our case, the raw EHR dataset). The generative model simulates the training data distribution in order to simulate hypothetical additional data, which is then merged with the original data. Meanwhile, the discriminative model learns to optimally distinguish between original and simulated data. During training, the generative model uses gradient information from the discriminative model to produce better simulations. After training, the generative model can be used to generate an arbitrary number of simulations which are similar in distribution to the original dataset. In our case, we generate a simulated dataset of the same size as the raw EHR dataset.

For this application, we train on a dataset where columns of continuous variables are standardized, and corresponding output are then re-scaled at simulation time. To accommodate binary variables, we allow the GAN to simulate continuous values, and round corresponding outputs to 0 or 1. We use the architecture of MMD-GAN (Li et al., 2017), which uses maximum mean discrepancy (MMD, Gretton et al., 2012), a distributional distance, to compare real data and simulations. Our implementation uses encoder and decoder networks each containing three layers of 100 nodes, connected by a bottleneck layer of 64 nodes, and with exponential linear unit activations. In the optimization, we use RMSProp with a learning rate of 0.001, and we weight the MMD in our discriminator loss function by 0.1.

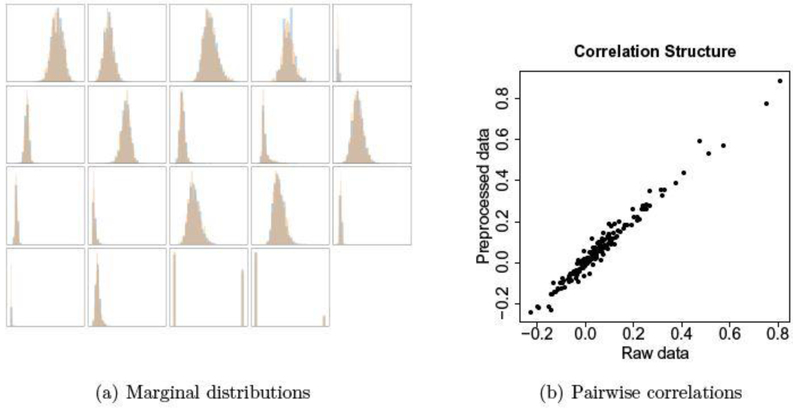
Our model reaches a stable point, where both marginal distributions and pairwise correlations agree with the raw data (see Figure 3). Moreover, the classifiers we consider have similar prediction performance on the two datasets. Therefore, we only report the results based on the replicated EHR data (referred to as EHR data hereafter). To the extent to which the preprocessed data set retains all information and structure of the original data, any inference other than subject-specific summaries remains practically unchanged. See the Appendix for more details.

Fig. 3.

GAN-preprocessed EHR data versus raw EHR data. (a) Marginal distribution of each variable. For each variable, the two overlaid histograms show the agreement between the preprocessed and the raw data. (Variable names and ranges are deliberately not shown.) (b) Correlation of each pair of variables. Each dot represents the Pearson correlation coefficients of one pair of variables in the raw EHR data (x-axis) versus the same in the GAN-preprocessed EHR data (y-axis). In total, we have $\left(\begin{array}{c}19\\ 2\end{array}\right)$ pairs/dots.

Results.

We randomly sample 84,750 subjects as training data and use the remaining 271 subjects as test data to evaluate out-of-sample classification performance. We implement inference under the PPMx model using the proposed SIGN algorithm. In the implementation, we use 250 compute cores (equivalent to 11 compute nodes with 24 cores per node) at the Texas Advanced Computing Center (TACC, http://www.tacc.utexas.edu) for computation. In the first step, the training data are randomly split into M₁ = 250 compute cores/shards with 339 samples in each shard. Across all shards, we obtain 1351 local clusters. In the second step, the 1351 local clusters are distributed to M₂ = 5 shards with each shard taking about 270 items. In step 2, the local clusters are grouped into 25 regional clusters. Iteration stops there since 25 items need not be further split, i.e., K = 3. In a final step, the 25 regional clusters are merged to 5 global clusters with sizes 26892, 26453, 18778, 11474, and 1153, respectively.

The AUC summaries based on the test dataset are provided in Table 2. SIGN reports the highest AUC (0.880), followed by RF, and BART. As expected, the most important covariate for predicting diabetes is FBG. Regressing on FBG alone achieves AUC = 0.829. In terms of computation time, SIGN, BART, RF and SVM take 0.9, 18.7, 3.5 and 2.5 hours with 2.6 GHz Xeon E5–2690 v3 CPU, respectively, whereas LR is several magnitude faster at the price of accuracy. We do not implement PPMx with standard MCMC, as this is not feasible with the large sample size. The good performance of SIGN may be explained by its ability to explicitly accommodate the heterogeneous nature of the subject population and allow for cluster-specific probit models in each subpopulation, while leveraging model averaging to classify new subjects. For example, the estimated intercept is −1.5 for cluster 2 and −0.95 for cluster 4. The coefficient of the important covariate FBG also exhibits heterogeneity, 0.97 for cluster 3 and 0.76 for cluster 4.

Finally, we evaluate the F_0.1 diagnostic proposed in Section 2.2.3. Specifically, we sample m = 4 out of the M₁ = 250 shards. We then run the SIGN approximation as well as full MCMC posterior simulation on the merged dataset of the 4 selected shards. Repeating the same procedure 62 times, we find an average F_0.1 value of 0.73.

5.2. Predicting the success of telemarketing

Direct marketing is a form of advertising where the salesperson directly communicates with the customers to promote business. In 2011, marketers are estimated to have spent $163 billion on direct marketing which accounted for 52.1% of total US advertising expenditures in that year (Direct Marketing Association INC., 2012). A common direct marketing practice is by phone, known as telemarketing. In this study, we focus on predicting the success of telemarketing in selling long-term bank deposits.

We analyze a dataset collected from a Portuguese retail bank (Moro et al., 2014) with n = 41, 188 records. The outcome of interest is whether the customer eventually subscribed a long-term deposit: z_i = 1 if yes, and z_i = 0 otherwise, i =1,…,n. Associated with each record/customer are 20 covariates which are listed in Table 3. We follow Moro et al. (2014) and remove the covariate “last contact duration,” since the duration is unknown before a call is performed and therefore can not be used to predict the outcome of the next customer. After removing records that are inconsistent with the data description, the resulting dataset contains 37,078 records. We randomly sample n = 36, 750 as training data and use the remaining 328 for testing purpose. Similarly to the analysis in Section 5.1, we apply PPMx using SIGN with K = 3 steps. In the first step, we randomly split the training data into M₁ = 150 shards (distributed on 7 compute nodes) with each shard taking 245 samples. We find 1,474 local clusters in the first step. Next, the 1,474 local clusters are then split to M₂ = 5 shards, with each shard processing about 295 blocks of customers. In this step, the local clusters are merged into 64 regional clusters. Finally, the 64 regional clusters are grouped into 14 global clusters with cluster sizes 7,687, 6,042, 5,725, 5,130, 3,950, 2,815, 2,101, 1,484, 975, 689, 56, 48, 26 and 22.

Table 3.

20 Covariates in the long-term deposit data. For categorical covariates, the number within the parentheses indicates the number of categories.

Covariate name	Type
Type of job	Categorical (12)
Marital status	Categorical (4)
Education	Categorical (8)
Default or not	Categorical (3)
Housing loan or not	Categorical (3)
Contact communication type	Categorical (2)
Last contact month of year	Categorical (12)
Last contact day of the week	Categorical (5)
Outcome of the previous campaign	Categorical (3)
Age	Continuous
Last contact duration	Continuous
Number of contacts	Continuous
Number of days from a previous campaign	Continuous
Number of contacts before this campaign	Continuous
Employment variation rate	Continuous
Consumer price index	Continuous
Consumer confidence index	Continuous
Euribor 3 month rate	Continuous
Number of employees	Continuous

The classification performance evaluated on the testing dataset is reported in the last column of Table 2 for SIGN, BART, RF, LR and SVM. We find SIGN outperforms all other methods with AUC = 0.825. The second best algorithm is BART with AUC = 0.792.

6. Discussion

We have introduced SIGN as a scalable algorithm for inference on clustering under BNP mixture models. SIGN can be thought of as a parallelizable extension of the Algorithm 8 in Neal (2000), which is applicable to both conjugate and non-conjugate models. We use SIGN to implement inference under a PPMx model for a Chinese EHR dataset with 85,021 individuals and a bank telemarketing dataset with 37,078 customers. We find good classification performance compared with state-of-the-art competing methods. For the EHR study, we find five meaningful clusters in the study population. We anticipate that this study will continue to collect many more subjects over the coming years. The use of algorithms that are scalable to millions of observations in terms of both, computing time and memory is therefore imperative. The computing time for the proposed algorithm remains practicable with increasing sample size, as long as enough computing resources are available. For example, with 1,000,000 observations, SIGN runs for about 1 hour on 2,000 cores or equivalently on 80 compute nodes. This is feasible on many high performance computing centers such as TACC. Memory is less of a critical limitation. If needed, one can use one large-memory compute node (192GB on TACC) in the last step where we have to access the entire dataset.

In this paper, we only consider “large n, small p” problems. The two motivating applications include only p = 18 and p = 19 covariates. Extension to “large n, large p” problems is of practical interest for other potential applications. Another limitation of inference for the PPMx model with the current SIGN implementation is the need to access the entire dataset in the last step, which becomes computationally prohibitive for big n or p. For the PPMx, one possible strategy is to replace the cluster-specific probit model by a simpler cluster-specific Bernoulli model with the binary response. The desired dependence between response and covariate is introduced marginally, after marginalizing with respect to the partition. Under this construction the algorithm depends on the data only through low dimensional summary statistics and could handle arbitrarily large data. A similar strategy was explored in Zuanetti et al. (2018). However, introducing the dependence between response and covariates through the partition only, we find less favorable classification performance than in the current implementations (results not shown).

Appendix: GAN preprocessing details

To evaluate the privacy of the simulated set, we measure two types of risk: presence disclosure and attribute disclosure (Choi et al., 2017). Presence disclosure is the ability to determine whether a candidate point was included in the training dataset. Attribute disclosure is the ability to predict other attributes of a candidate point, given partial information about that point. For both settings, we choose three sets of equal size – 5% of the training data, a heldout set for testing, and a heldout set for baseline comparison – then estimate the sensitivity and precision of classification schemes.

For presence disclosure, we sample a candidate from the union of training and testing sets, and classify whether the candidate was included in the training set based on the presence of an ϵ-close neighbor in the simulated set. For large ϵ, the notion of ϵ-closeness is not informative, since many points are returned as neighbors, and precision scores hover around 50% – no better than random guessing. For small ϵ, few points are returned as neighbors, and neighbors are more likely to be correctly guessed, since the requirement is for a neighbor to be nearly identical to the candidate point. To reflect the optimal privacy standard, we report scores using the largest ϵ for which precision exceeds 55%. This yields the largest sensitivity under nontrivial risk, where a higher sensitivity indicates greater ability to identify a participant. At ϵ = 9.5, the sensitivity of this classification is 0.0005, indicating that compromised training points would be identifiable only 0.05% of the time.

For attribute disclosure, we sample as above, and classify whether unknown features of a candidate point can be correctly estimated to within 5% of the true value, by averaging each feature over the candidate’s five nearest neighbors in the simulated set. We report values for the case in which half of the candidate’s features are known, and the other half are imputed, and note that performance did not change significantly when the percentage of known values differed. The sensitivity and precision scores of this classification are 0.31 and 0.72, respectively, indicating that unknown features would be correctly guessed 31% of the time, and features claiming to be within 5% of the true value would in fact be 72% of the time.

We note that privacy and accuracy goals are inherently opposed. An increase in privacy corresponds to a simulated set with less information about individual data points, and vice versa. As a general guideline, we aim to satisfy privacy requirements while preserving as much as possible the utility of the simulations. In the specific case of attribute risk, we recognize that scores depend on the correlation structure of the data, where highly correlated features are more susceptible to attribute disclosure. As a baseline, we compared attribute risk scores of simulations to those of the final heldout set, and found that both were approximately 30% and 70%, respectively.