Dynamic Visualization and Fast Computation for Convex Clustering via Algorithmic Regularization

Abstract

Convex clustering is a promising new approach to the classical problem of clustering, combining strong performance in empirical studies with rigorous theoretical foundations. Despite these advantages, convex clustering has not been widely adopted, due to its computationally intensive nature and its lack of compelling visualizations. To address these impediments, we introduce Algorithmic Regularization, an innovative technique for obtaining high-quality estimates of regularization paths using an iterative one-step approximation scheme. We justify our approach with a novel theoretical result, guaranteeing global convergence of the approximate path to the exact solution under easily-checked non-data-dependent assumptions. The application of algorithmic regularization to convex clustering yields the Convex Clustering via Algorithmic Regularization Paths (CARP) algorithm for computing the clustering solution path. On example data sets from genomics and text analysis, CARP delivers over a 100-fold speed-up over existing methods, while attaining a finer approximation grid than standard methods. Furthermore, CARP enables improved visualization of clustering solutions: the fine solution grid returned by CARP can be used to construct a convex clustering-based dendrogram, as well as forming the basis of a dynamic path-wise visualization based on modern web technologies. Our methods are implemented in the open-source R package clustRviz, available at https://github.com/DataSlingers/clustRviz.

1. Introduction

Clustering, the task of identifying meaningful sub-populations in unlabelled data, is a fundamental problem in applied statistics, with applications as varied as cancer subtyping, market segmentation, and topic modeling of text documents. A wide range of methods for clustering have been proposed and we do not attempt to make a full accounting here, instead referring the reader to the recent book of Hennig et al. (2015). Perhaps the most popular clustering method, however, is hierarchical clustering (Ward, 1963). Hierarchical clustering derives its popularity from an intuitive formulation, efficient computation, and powerful visualizations. Dendrogram plots, which display the family of clustering solutions simultaneously, provide an easily-understood summary of the global structure of the data, allowing the analyst to visually examine the nested group structure of the data. Despite its popularity, hierarchical clustering has several limitations: it is highly sensitive to the choice of distance metric and linkage used; it is a heuristic algorithm which lacks optimality guarantees; and the conditions under which hierarchical clustering recovers the true clustering are unknown.

To address these limitations, several authors have recently studied a convex formulation of clustering (Pelckmans et al., 2005; Hocking et al., 2011; Lindsten et al., 2011; Chi and Lange, 2015). This convex formulation provides guarantees of global optimality of a clustering solution and allows analysis of its theoretical properties (Tan and Witten, 2015; Zhu et al., 2014; Radchenko and Mukherjee, 2017; Chi and Steinerberger, 2018). Despite these advantages, convex clustering has not yet achieved widespread popularity, due to its computationally intensive nature and lack of dendrogram-based visualizations. In this paper, we address these problems with a efficient algorithm for computing convex clustering solutions with sufficient precision to construct interpretable accurate dendrograms and dynamic path-wise visualizations, thereby making convex clustering a practical tool for applied data analysis.

Our main theoretical contribution is the concept of Algorithmic Regularization, a novel computationally efficient approach for obtaining high-quality approximation of regularization paths. We provide a theoretical justification for our proposed approach, showing that we can obtain a high-quality approximation simultaneously at all values of the regularization parameter. While we focus on the convex clustering problem, our proposed approach can be applied to a much wider range of problems arising in statistical learning.

Using algorithmic regularization, we make two methodological contributions related to clustering: first, we propose an efficient algorithm, carp, for computing convex clustering solutions, carp is typically over one-hundred times faster than existing approaches, while simultaneously computing a much finer set of solutions than commonly used in practice. Secondly, we propose new visualization strategies for convex clustering based on carp: a new dendrogram construction based on convex clustering paths and a novel “ path-wise” visualization, which provides more information about the structure of the estimated clusters. We hope that, thanks to our proposed computational and visualization strategies, convex clustering will become a viable tool for exploratory data analysis, carp and our proposed visualizations are implemented in our clustrviz r package, available at https://github.com/DataSlingers/clustRviz.

The remainder of this paper is organized as follows: Section 2 reviews convex clustering in more detail and discusses the difficulties entailed in producing dendrograms from convex clustering. Section 3 introduces the concept of “Algorithmic Regularization,” uses it to develop the carp clustering algorithm, and gives theoretical guarantees of global convergence. Section 4 compares carp with existing approaches for convex clustering, demonstrating its impressive computational and statistical performance on several data sets. Section 5 describes several novel visualizations made possible by the carp algorithms in the context of an extended text-mining example. Finally, Section 6 concludes the paper with a discussion and proposes possible future directions for investigation.

2. Convex Clustering and Dendrograms

We seek to represent the convex clustering solution path as a dendrogram, and in this section, discuss both the theoretical conditions and computational considerations for this task. We first review the basic properties of convex clustering in Section 2.1 and then discuss dendrogram construction from convex clustering in Section 2.2.

2.1. Convex Clustering

Let $\mathit{X}\in {\mathbb{R}}^{n\times p}$ denote a data matrix, consisting of n observations (rows of the matrix) in p dimensions. The convex clustering problem, first discussed by Pelckmans et al. (2005) and later explored by Hocking et al. (2011) and Lindsten et al. (2011), is a convex relaxation of the general clustering problem:

$$\underset{\mathit{U}\in {\mathbb{R}}^{n\times p}}{\mathrm{argmin}}\frac{1}{2}\Vert \mathit{X}-\mathit{U}{\Vert }_F^2\text{subject to}\sum _{1\le i<j\le n}{1}_{{\mathit{U}}_{i\cdot }\ne {\mathit{U}}_{j\cdot }}\le t,$$

where U_i· is the i^th row of U. Replacing the non-convex indicator function with an ℓ_q-norm of the difference, we obtain the convex clustering problem:

$${\mathit{U}}_{\lambda }=\underset{\mathit{U}\in {\mathbb{R}}^{n\times p}}{\mathrm{argmin}}\frac{1}{2}\Vert \mathit{X}-\mathit{U}{\Vert }_F^2+\lambda \left(\sum _{1\le i<j\le n}{w}_{ij}\Vert {\mathit{U}}_{i\cdot }-{\mathit{U}}_{j\cdot }{\Vert }_q\right).$$ (1)

Note that we have included non-negative fusion weights {w_ij} in our convex relaxation. We will say more about the computational and statistical roles played by these weights below.

The squared Frobenius norm loss function favors solutions which minimize the Euclidean distance between observations and their estimated centroids, while the fusion penalty term, p(U; w, q), encourages the differences in columns of U_λ to be shrunk to zero. We interpret the solution U_λ as a matrix of cluster centroids, where each observation X_i. belongs to a cluster with centroid (U_λ)_i·. For sufficiently large values of λ, the columns of U_λ will be shrunk together by the penalty term. We say that points with the same centroid belong to the same cluster; that is, the observations X_i· and X_j· are assigned to the same cluster if (U_λ)_i = (U_λ)_j·

A major advantage of convex clustering is that the solution U_λ smoothly interpolates between clustering solutions, yielding a continuous path of solutions indexed by λ. At λ = 0, U_λ=0 = X, resulting in a solution of n distinct clusters, with each observation as the centroid of its own cluster. As λ is increased, the fusion penalty encourages the columns of U_λ to merge together, inducing a clustering behavior. Finally, when λ is large, all columns of U_λ are fully merged, yielding a single cluster centroid equal to the grand mean of the columns of X. Thus, the penalty parameter λ determines both the number of clusters and the cluster assignments.

The choice of the fusion weights $\mathit{w}\in {\mathbb{R}}_{\ge 0}^{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}$ has a large effect on the statistical accuracy and computational efficiency of convex clustering. When uniform weights are used, convex clustering has a close connection to single-linkage hierarchical clustering, as shown by Tan and Witten (2015). More commonly, weights inversely proportional to the distances between observations are used, and have been empirically demonstrated to yield superior performance (Hocking et al., 2011; Chi and Lange, 2015; Chi et al., 2017). Furthermore, setting many of the weights to zero dramatically reduces the computational cost associated with computing the convex clustering solution. We typically prefer using the rotation-invariant ℓ₂-norm in the fusion penalty (q = 2), but one could employ ℓ₁ or ℓ_∞ norms as well.

By formulating clustering as a convex problem, it becomes possible to analyze its theoretical properties using standard techniques from the highdimensional statistics literature. Tan and Witten (2015) show a form of prediction consistency and derive an unbiased estimator of the effective degrees of freedom associated with the solution. Zhu et al. (2014) give sufficient conditions for exact cluster recovery at a fixed value of λ (“sparsistency”). Like us, Radchenko and Mukherjee (2017) are interested in properties of the entire solution path and give conditions under which convex clustering solutions (1) asymptotically yield the true dendrogram.

2.2. Constructing Dendrograms from Convex Clustering Paths

In this paper, we propose to represent the convex clustering solution path as a dendrogram, an example of which is shown in Figure 1. The convex clustering dendrogram is interpreted in much the same way as the classical dendrogram. As individual observations or groups of observations are fused together by the fusion penalty, they are denoted by merges in the tree structure. The height of the merge in the tree structure is given by the value of the regularization parameter, λ, or more precisely log(λ), at which the fusion occurred. Thus, observations that fuse at small values of λ are denoted by merges at the bottom of the dendrogram structure. As with hierarchical clustering, one can cut the dendrogram horizontally at a specific height to yield the associated clusters, and we can interpret the tree height at which merges occur as indicative of the similarity between groups. Before proceeding, however, it is natural to ask whether it is even possible to represent the convex clustering solution path as a dendrogram. This simple question turns out to have a rather subtle answer.

Fig. 1.

A convex clustering dendrogram, displaying the 44 U.S. presidents. The interpretation of this dendrogram is discussed in more detail in Section 5.

There are two possible impediments to finding the desired dendrogram representation: i) it may be impossible to represent the exact solution path as a dendrogram; and ii) it may be unrealistic to compute the solution path with enough precision to form a dendrogram. We first consider the question of whether the exact solution path admits a dendrogram representation. It is easy to observe that the exact solution path can only be written as a dendrogram if it is agglomerative, i.e., if the solution path consists of only fusions and no fissions. Hocking et al. (2011) showed that if an ℓ₁-norm is used for the fusion penalty and the weights are uniform then the solution path is agglomerative, but their analysis does not generalize to arbitrary norms or arbitrary weight schemes. Chi and Steinerberger (2018) showed that it is possible to select weights to yield a agglomerative path, but their analysis applies only to a specific weighting scheme. In general, for an arbitrary data-driven choice of weights, there is no theoretical guarantee that the solution path will be agglomerative. In our experience, however, the solution path is agglomerative except in pathological situations.

Assuming that the exact solution path is agglomerative, we still must determine whether the solution path, as calculated, is agglomerative. While, in theory, this poses no additional challenge as the solution path is a continuous function of λ, in practice this poses a nearly insurmountable computational challenge. To construct a dendrogram, we require the exact values of λ at which each fusion occurs. Since these values of λ are not known a priori, we are faced with a double burden: we must identify a critical set of values of λ and solve the convex clustering problem (1) at those values. There are two widely-used approaches to finding the critical set of λ’s, path-wise algorithms and grid search, but, as we will show below, neither approach is sufficient in this case.

Path-wise algorithms, such as those proposed for the Lasso (Osborne et al., 2000; Efron et al., 2004) or generalized Lasso (Tibshirani and Taylor, 2011) problems, compute the entire solution path exactly, identifying each value of λ at which a sparsity event, equivalent to a fusion in our case, occurs. These algorithms are typically based on piece-wise linearity of the underlying solution path, which allows for smooth interpolation between sparsity events. Rosset and Zhu (2007) studied the conditions under which solution paths are piece-wise linear and hence under which path-wise algorithms can be developed. It is easy to verify that these conditions do not hold with our preferred ℓ₂-norm fusion penalty, so the solution path is not piece-wise linear and hence a path-wise algorithm cannot be employed for the convex clustering problem (1). We note that several authors have proposed path-wise algorithms which can theoretically handle non-piece-wise-linear paths, but require solving an ordinary differential equation exactly (Wu, 2011; Zhou and Wu, 2014; Xiao et al., 2015); in practice, these methods are computationally intensive and only approximate the path at a series of grid points, similar to the iterative methods we discuss next. For the ℓ₁-norm fusion case, it is possible to apply path-wise algorithms for weights with specific graphical structures (see the discussion in Hocking et al. (2011) or the examples considered in Tibshirani and Taylor (2011)), but not for arbitrary graph structures with arbitrary weights, again eliminating the possibility of a general-purpose path-wise algorithm.

Since there exists no exact path-wise algorithm, we might instead compute the convex clustering solution at a series of discrete points corresponding to a regular grid of λ’s. As we will show in Section 4, however, this strategy is still computationally burdensome even using state-of-the-art algorithms and warm-start techniques. For example, the fastest algorithm considered by Chi and Lange (2015), an Accelerated Alternating Minimization Algorithm, takes 6.87 hours and 19.81 hours to compute the solution path at 100 and 1000 regularly spaced λ’s, respectively, on a relatively small data set of dimension n = 438 and p = 353. Furthermore, a grid of 100 or 1000 λ’s does not give us the value of λ at which each fusion event occurs, which we need to construct a dendrogram. Even if one wants to construct a dendrogram using the order in which each fusion event occurs and their associated approximate values of λ, computing the path along a grid of 100 or 1000 λ’s only uniquely resolves 11.4% or 37.44% respectively of the fusion events needed to construct a dendrogram. (See Table 1 in Section 4 for complete results.)

Table 1.

Proportion of dendrogram recovered by carp, carp–viz, and standard fixed-grid methods. The back-tracking employed by carp–viz is necessary for exact dendrogram recovery, but fixed step-size carp is still able to recover the dendrogram more accurately than standard fixed-grid approaches.

Method	TCGA (n = 438, p = 353)	Authors (n = 841, p = 69)
carp (t = 1.1)	5.93%	4.40%
carp (t = 1.05)	11.18%	8.09%
carp (t = 1.01)	41.55%	22.71%
carp (t = 1.005)	60.27%	30.56%
carp–viz	100%	100%
100-Point Grid	11.42%	5.00%
1000-Point Grid	37.44%	—

In general, the computational cost of performing convex clustering is so high that it precludes its use as a practical tool for clustering and exploratory data analysis. Further, computing the entire convex clustering solution path with fine enough precision to construct a dendrogram is an all but insurmountable task given existing computational algorithms for convex clustering. We seek to address this problem in this paper, using a novel computational technique which provides a fine grid of high-quality estimates of the regularization path. We introduce our approach and the clustering algorithm it suggests, carp, in the next section.

3. carp: Convex Clustering via Algorithmic Regularization Paths

We now turn our attention to efficiently computing solutions to the convex clustering problem (1) for a fine grid of λ, with a goal of dendrogram construction. Like many problems in the “loss + penalty” form, the convex clustering problem is particularly amenable to operator-splitting schemes such as the Alternating Direction Method of Multipliers (ADMM) (Boyd et al., 2011). In statistical learning, we are often interested in the solution to a regularized estimation problem at a large number of values of λ. In this context, the performance of ADMMs is increased further by the use of “warm-starts:” if the ADMM is initialized near the solution, usually the solution at the previous value of λ, only a few iterations are typically required to obtain a solution which is accurate up to the statistical uncertainty inherent in the problem.

We propose an extreme version of this approach which we call Algorithmic Regularization. Instead of running the ADMM to convergence, we take only a single ADMM step, after which we move to the next value of λ. By taking only a single ADMM step, we can significantly reduce the computational cost associated with estimating a regularization path. We can then use these computational savings to solve for a much finer grid of λ’s than we would typically use if employing a standard scheme. In essence, Algorithmic Regularization allows us to exchange computing an exact solution for a small set of λ’s for calculating a highly accurate approximation at a large set of λ’s. Usefully, we can now use a λ grid with sufficiently fine resolution that we can fully capture the desired dendrogram structure in a reasonable amount of time.

Chi and Lange (2015) first considered the use of the ADMM to solve the convex clustering problem (1). To apply the ADMM, we introduce D, the directed difference matrix used to calculate to the pairwise differences of rows of U, and an auxiliary variable V, corresponding to the matrix of between-observation differences:

$$\underset{\begin{array}{c}\hfill \mathit{U}\in {\mathbb{R}}^{n\times p}\hfill \\ \hfill \mathit{V}\in {\mathbb{R}}^{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)\times p}\hfill \end{array}}{\mathrm{argmin}}\frac{1}{2}\Vert \mathit{X}-\mathit{U}{\Vert }_F^2+\lambda \underset{P(\mathit{V};\mathit{w},q)}{\underbrace{\sum _{k=1}^{\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}{w}_k\Vert {\mathit{V}}_{k\cdot }{\Vert }_q}}\text{subject to}\mathit{V}=\mathit{DU}.$$

Applying the ADMM with warm-starts to the above, we obtain the following algorithm:

Algorithm 1 Warm-Started ADMM for the Convex Clustering Problem (1)
Initialize l = 0, λl = ϵ, V(0) = Z(0) = DX
Repeat until ∥V(k)∥=0:
•  Repeat until convergence:
(i) U(K+1) = L−T L−1 (X + DT (V(k) − Z(k)))
(ii) V(k+1) = proxλlp(·;w,q) (DU(k+1) + Z(k))
(iii) Z(k+1) = Z(k) + DU(k+1) − V(k+1)
(iv) k := k + 1
•  Store U λl = U(k)
• Update regularization: l := l + 1 ; λl := λl−1 * t
Return {U λ} as the regularization path

where Z is the dual variable with the same dimensions as V, L is Cholesky factorization of I + D^T D, and ${\text{prox}}_{f(\cdot )}(\mathit{x})={\text{argmin}}_{\mathit{z}}\frac{1}{2}\Vert \mathit{x}-\mathit{z}{\Vert }_2^2+f(\mathit{z})$ is the proximal mapping of a general function f. Note that, if sparse weights are used, the corresponding rows of D,V, and Z may be omitted, yielding more efficient updates. Additionally, note that, because we use a multiplicative update for λ, we must initialize at λ = ϵ, for some small ϵ, rather than at λ = 0. A derivation and more detailed statement of this algorithm are given in Section A of the Supplementary Materials.

We now take Algorithm 1 as the basis for our extreme early stopping strategy of Algorithmic Regularization. Removing the the inner loop, we obtain the following scheme, which we refer to as carp–Convex Clustering via Algorithmic Regularization Paths:

Algorithm 2 carp: Algorithmic Regularization for the Convex Clustering Problem (1)
Initialize k = 0, γ(k) = ϵ, V(0) = Z(0) = DX
Repeat until ∥V(k)∥=0 :
(i) U(k+1) = L−T L−1 (X + DT (V(k) − Z(k)))
(ii) V(k+1) = proxγ(k)p(·;w,q) (DU(k+1) + Z(k))
(iii) Z(k+1) = Z(k) + DU(k+1) − V(k+1)
(iv) k := k + 1, γ(k) = γ(k−1) * t
Return {U(k)} as the carp path.

The fundamental difference between Algorithm 1 and Algorithm 2 is that Algorithm 2 does not have an “inner loop” in which ADMM iterates are repeated until convergence to the exact solution for a fixed value of the regularization parameter. As such, the carp iterates {U^(k)} are not exact solutions to the convex clustering problem (1) for any value of λ, though they are typically accurate approximations in a sense that Theorem 1 below makes precise. Our notation reflects this distinction and replaces λ_l with γ^(K) in the V-update to avoid suggesting any false equivalence. A more detailed formulation of the carp algorithm is given in Section A of the Supplementary Materials.

The role of the step-size parameter t in Algorithm 2 is particularly important in understanding carp. The step size t controls the fineness of the {ɣ^(K)} grid used internally by carp and, as such, serves as a computational tuning parameter controlling how well the carp path approximates the true convex clustering path. Decreasing t therefore has benefits for both local and global accuracy of the carp path: a smaller value of t yields an approximate solution path which has a finer set of grid points {γ^(K)} (improved global accuracy) and more accurate approximations {U^(k)} at each of those grid points (improved local accuracy). This is in contrast to standard approaches where the user has to pre-specify the {λ_l} grid used and the stopping tolerance of the iterative algorithm to strike a balance between local accuracy and global accuracy. As we will see in Section 4, the Algorithmic Regularization strategy of replacing an iterative algorithm with a one-step approximation thereof allows us to improve both local and global accuracy at a fraction of the cost of competing methods.

While this may all seem rather fishy, the following theorem shows that, in the limit of small changes to the regularization level (i.e., (t,ϵ)→(1,0)), there is indeed no loss in accuracy induced by the one-step approximation. In fact, we are able to show a very strong form of convergence, so-called Hausdorff convergence, in both the primal and dual variables. Hausdorff convergence implies two different convergence results hold simultaneously for both the primal and dual variables. The first, $\underset{\lambda }{\text{sup}}\underset{k}{\text{inf}}\Vert {\mathit{U}}^{(k)}-{\mathit{U}}_{\lambda }\Vert \to 0$, implies every convex clustering solution will be recovered by carp as (t,ϵ)→(1,0). The second, $\underset{k}{\text{sup}}\underset{\lambda }{\text{inf}}\Vert {\mathit{U}}^{(k)}-{\mathit{U}}_{\lambda }\Vert \to 0$, implies that any clustering produced by carp as (t,ϵ)→(1,0) is a valid convex clustering solution for some λ. More memorably, Theorem 1 shows that asymptotically carp produces “the whole regularization path and nothing but the regularization path:”

Theorem 1. As (t,ϵ)→(1,0) , where t is the multiplicative step-size update and ϵ is the initial regularization level, the primal and dual carp paths converge to the primal and dual convex clustering paths in the Hausdorff metric: that is,

$$d_H(\{{\mathit{U}}^{(k)}\},\{{\mathit{U}}_{\lambda }\})\equiv \max \left\{\underset{\lambda }{\text{sup}}\underset{k}{\text{inf}}\Vert {\mathit{U}}^{(k)}-{\mathit{U}}_{\lambda }\Vert ,\underset{k}{\text{sup}}\underset{\lambda }{\text{inf}}\Vert {\mathit{U}}^{(k)}-{\mathit{U}}_{\lambda }\Vert \right\}\stackrel{(t,ϵ)\to (1,0)}{\to }0$$

$$d_H(\{{\mathit{Z}}^{(k)}\},\{{\mathit{Z}}_{\lambda }\})\equiv \max \left\{\underset{\lambda }{\text{sup}}\underset{k}{\text{inf}}\Vert {\mathit{Z}}^{(k)}-{\mathit{Z}}_{\lambda }\Vert ,\underset{k}{\text{sup}}\underset{\lambda }{\text{inf}}\Vert {\mathit{Z}}^{(k)}-{\mathit{Z}}_{\lambda }\Vert \right\}\stackrel{(t,ϵ)\to (1,0)}{\to }0$$

where U^(k),Z^(k) are the values of the K^th carp iterate and U_λ, Z_λ are the exact solutions to the convex clustering problem (1) and its dual at λ.

A full proof of Theorem 1 is given in Section B of the Supplementary Materials, but we highlight the three essential elements here: i) we obtain a high-quality initialization at the first step by setting U⁽⁰⁾ = X which is the exact solution at λ = 0 (U_λ=0 = X); ii) the convex clustering problem (1) is strongly convex due to the squared Frobenius norm loss, so the ADMM converges quickly (linearly); and iii) the solution path is Lipschitz as a function of λ, so U^λ does not vary too quickly. Putting these together, we show that carp can “track” the exact solution path closely, with the approximation error at each step decreasing at a faster rate than the exact solution changes. We emphasize that both strong convexity and Lipschitz solution paths are features of the optimization problem, not the specific data, and are easily checked in practice. A careful reading of the proof of Theorem 1 will reveal that our analysis applies to a much wider class of problems than convex clustering. We consider the application of algorithmic regularization to the closely related problem of convex bi-clustering (Chi et al., 2017) in Section C of the Supplementary Materials, where we develop the cbass (Convex Bi-Clustering via Algorithmic Regularization with Small Steps) algorithm, but we leave examination of the more general phenomenon of Algorithmic Regularization to future work.

While Theorem 1 implies that a sufficiently small choice of step size t allows for exact dendrogram recovery, in practice it is often challenging to select t sufficiently small without requiring excessive computation. Instead, we take a small, but not infinitesimal, value of t and add a back-tracking step to ensure that fusions necessary for dendrogram construction are exactly identified. We refer to the back-tracking version of carp as carp–viz, for reasons which will be clarified in Section 4. Furthermore, a post-processing step can be used to find fusions that back-tracking is unable to isolate. Details of the back-tracking and post-processing rules, as implemented in clustrviz, are given in Section E of the Supplementary Materials.

Algorithmic Regularization, as used here, was first discussed in Hu et al. (2016) without theoretical justification and was successfully applied to unmixing problems in hyperspectral imaging by Drumetz et al. (2017). We emphasize that, while grounded in standard optimization techniques, algorithmic regularization takes a different perspective than other commonly-used computational approaches, more akin to function approximation than standard optimization. The algorithmic regularization perspective is principally concerned with recovering the overall structure of the solution path than with obtaining the most accurate solution possible at a fixed value of λ. As such, our Theorem 1 is of a different character than similar results appearing in the optimization literature, making a claim of global path-wise convergence rather than local point-wise convergence. This “holistic” viewpoint is necessary to recover dendrograms, a major goal of this paper, but has also recently been found useful for choosing tuning parameters in penalized regression problems (Chichignoud et al., 2016).

3.1. Related Work

Several authors have considered path approximation algorithms not unlike carp, often in the context of boosting algorithms. Rosset et al. (2004), Zhao and Yu (2007), and Friedman (2012) all consider iterative algorithms which approximate solution paths of regularized estimators. Of these, the approach of Zhao and Yu (2007), who consider a path approximation algorithm for the Lasso, is most similar to our own. Assuming strong convexity, their blasso algorithm exactly recovers the lasso solution path as the step-size goes to zero. Their algorithm can be viewed as an application of algorithmic regularization to greedy coordinate descent with an additional back-tracking step to help isolate events of interest (variables entering or leaving the active set). Our algorithmic regularization strategy is simpler than their approach, as it does not require the back-tracking step, and can be applied to more general penalty functions.

Clarkson (2010) and Giesen et al. (2012) consider the problem of obtaining approximate solutions for a set of parameterized problems subject to a simplex constraint, though their approach still requires running an optimization step until approximate convergence at each step, Building on this, Tibshirani (2015) proposes a general framework for constructing “stagewise” solution paths, which can be interpreted as an application of algorithmic regularization to the Frank-Wolfe algorithm (Jaggi, 2013). He shows that the stagewise estimators achieve the optimal objective value as the step-size is taken to zero; if a strong convexity assumption is added, it is not difficult to extend his Theorem 2 to recover a result similar to our Theorem 1. Our framework is more general than his, as we do not require require the gradient of the loss function to be Lipschitz and we admit more general regularizers.

4. Numerical and Timing Comparisons

Having introduced carp and given some theoretical justification for its use, we now consider its performance on representative data sets from text analysis and genomics. As we will show, carp achieves the superior clustering performance of convex clustering at a small fraction of the computational cost. Throughout this section, we use two example data sets: TCGA and Authors. The TCGA data set (n = 438, p = 353) contains log-transformed Level III RPKM gene expression levels for 438 breast-cancer patients from The Cancer Genome Atlas Network (2012). The Authors data set (n = 841, p = 69) consists of word counts from texts written by four popular English-language authors (Austen, London, Shakespeare, and Milton). For all comparisons, we use clustrviz’s default sparse Gaussian kernel weighting scheme described in the package documentation. For timing comparisons, the Accelerated ADMM and AMA proposed by Chi and Lange (2015) and implemented in their cvxclustr package was used; our clustrviz package was used for carp and carp-viz. All comparisons were run on a 2013 iMac with a 3.2 GHz Intel i5 processor and 16 GB of 1600 MHz DDR3 memory.

While Theorem 1 strictly only applies for asymptotically small values of t, carp paths are high-quality approximations of the exact convex clustering solution path, even at moderate values of t. We assess accuracy of the carp paths by considering the normalized relative Hausdorff distance between the primal carp path (U^(k)) and the exact solution (U_λ)

$$d_H(\{{\mathit{U}}^{(k)}\},\{{\mathit{U}}_{\lambda }\})=\frac{\max \left\{\underset{\lambda }{\text{sup}}\underset{k}{\text{inf}}{\Vert {\mathit{U}}^{(k)}-{\mathit{U}}_{\lambda }\Vert }_2,\underset{k}{\text{sup}}\underset{\lambda }{\text{inf}}{\Vert {\mathit{U}}^{(k)}-{\mathit{U}}_{\lambda }\Vert }_2\right\}}{n^{\ast }{p}^{\ast }\Vert \mathit{DX}{\Vert }_{2,\infty }}$$

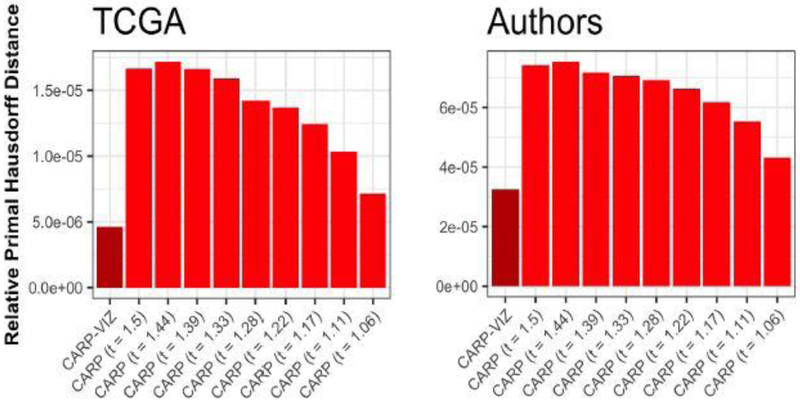
where ∥·∥_2,∞ is the maximum of the ℓ₂-norms of the rows of a matrix. (We include the normalization constants in the denominator so that our distance measure does not depend on the size or numerical scale of the data.) In order to calculate the Hausdorff distance, the carp path with a very small step-size t was used in lieu of the exact solution {U_λ}. As can be seen in Figure 2, the carp path is highly accurate even at moderate values of t and converges quickly to the exact solution as t→1. carp–viz, which uses an adaptive choice of t to isolate each individual fusion, performs even better than the fixed step-size carp, attaining a very accurate approximation of the true clustering path.

Fig. 2.

Normalized Relative Primal Hausdorff Distance between the exact convex clustering solution and carp Paths for various values of t. As t decreases, the carp Paths converge to the exact convex clustering solution path, consistent with Theorem 1.

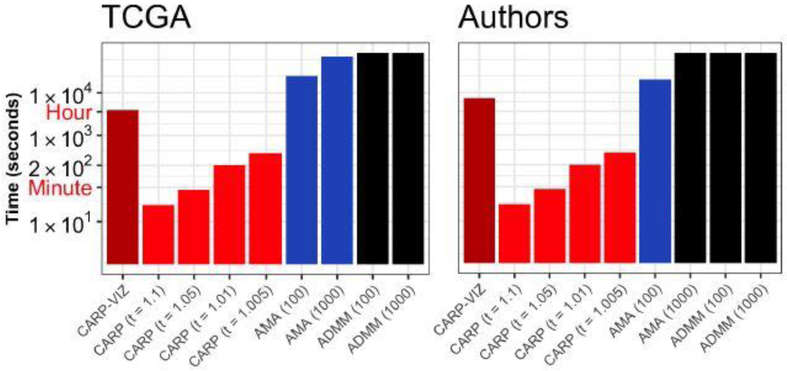
Even though they are highly accurate, carp paths are relatively cheap to compute. In Figure 3, we compare the computational cost of carp with the algorithms proposed in Chi and Lange (2015). As shown in Figure 3, carp significantly outperforms the Accelerated AMA and ADMM algorithms. At large step-sizes (t = 1.1,1.05), carp terminates in less than a minute and, even at finer grid-sizes (t = 1.01,1.005), carp takes only a few minutes to run. The carp-viz variant takes significantly longer than standard carp, though it still outperforms the AMA, taking about an hour for TCGA, rather than the six and a half hours required to solve the AMA at 100 grid points. This improvement in computational performance is even more remarkable when we note that carp and carp-viz produce a fine grid of solutions by default: on the TCGA data, carp with t = 1.01 produces over 2047 distinct grid points in under five minutes.

Fig. 3.

Time required to compute clustering solution path (logarithmic scale). carp produces high-quality path approximations in a fraction of the time of standard iterative algorithms. Timings in black indicate calculations that took more than 24 hours to complete.

The fine grid of solutions returned by carp and carp-viz result in much improved dendrogram recovery, as measured by the fraction of unique clustering assignments each method returns. Table 1 shows recovery results for carp (at several values of t), carp–viz, and standard fixed-grid methods. It is clear that back-tracking employed by carp–viz is necessary for exact dendrogram recovery and that carp–viz should be used if the exact dendrogram recovery is required for visualization. Even with moderate step-sizes (t = 1.1,1.05), however, carp is still able to estimate the dendrogram far more accurately and more rapidly than standard iterative methods, making it a useful alternative for exploratory work.

On the TCGA data, carp with t = 1.05 is able to recover the dendrogram with the same accuracy in a minute that the AMA attains in six and a half hours. With t = 1.01, carp recovers the dendrogram more accurately in under five minutes than the AMA does in nineteen hours (1000 grid points), carp achieves these improvements by using its computation efficiently: while a standard optimization algorithm may spend several hundred iterations at a single value of the regularization parameter, carp only spends a single iteration. By reducing the number of iterations at each grid point, it can take examine a much finer grid in less time. This trade-off is particularly well-suited for our goal of dendrogram recovery, which requires a fine grid of solutions to assess the order of fusions, but does not depend on the exact values of the estimated centroids. While not a primary focus of this paper, the high-quality dendrogram estimation allowed by carp translates into improved statistical performance as well. We compare the statistical performance of carp with other clustering methods in Section D of the Supplementary Materials.

5. Visualization of carp Results

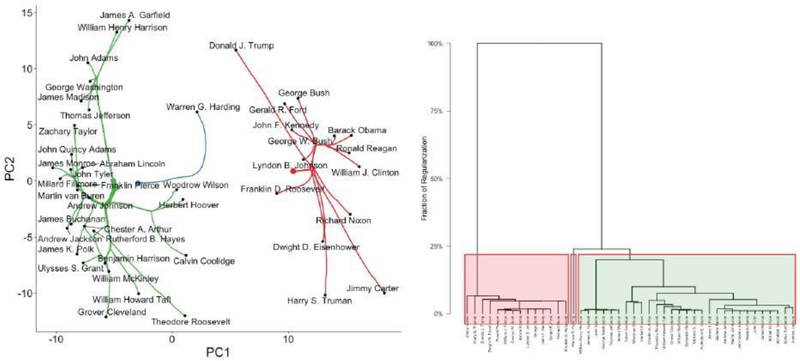
In this section, we discuss visualization of convex clustering results, emphasizing the role that carp can play in exploratory data analysis. The visualizations illustrated in this section can all be produced using our clustrviz r package. Throughout this section, we will use the Presidents data set, (n = 44, p = 75) which contains log-transformed word counts of the 75 most variable words taken from the aggregated major speeches (primarily Inaugural and State of the Union Addresses) of the 44 U.S. presidents through mid-2018. (We consolidate the two non-consecutive terms of Grover Cleveland.)

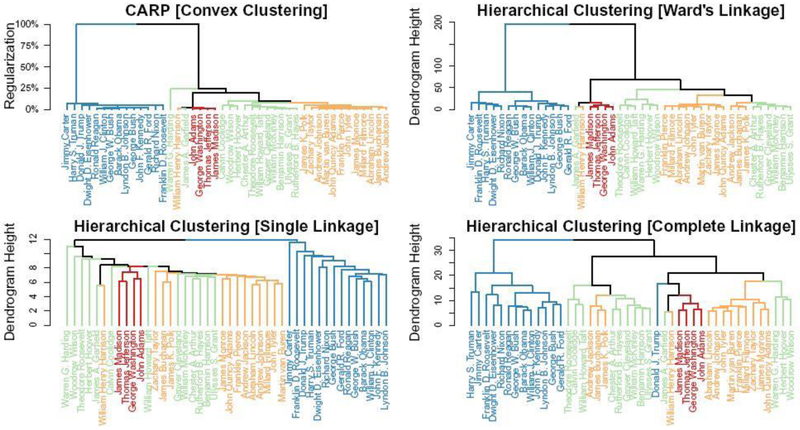
We begin by considering a dendrogram representation of this data, as shown in Figure 4. For each dendrogram, we have colored the observations by historical period: Founding Fathers, pre-Civil War, pre-World War II, and modern. Given the evolution of the English language and the changing political concerns of these periods, we would expect clustering methods to group the presidents according to historical period. With three exceptions, carp clearly identifies the four historical periods, with the modern period being particularly well-separated. The performance of hierarchical clustering is highly sensitive to the choice of linkage: Ward’s linkage (Ward, 1963) does almost as well as carp, but does not clearly separate the pre-Civil War and pre-World War II periods. Single linkage correctly identifies the modern period, but otherwise does not separate the pre-modern presidents. Complete linkage performs the worst, clustering Donald Trump with the Founding Fathers, Garfield, and Harrison instead of with other modern presidents. We note that Harrison is consistently misclustered by all methods considered: we believe this is due to the fact he died thirty-one days into his first term and did not leave a lengthy textual record.

Fig. 4.

Comparison of carp (top left) and Euclidean-distance Hierarchical Clustering dendrograms on the data. The presidents are colored according to historical period: Founding Fathers (pink, 1789–1817, Washington to Madison, n = 4); pre-Civil War (gold, 1817-1869, Monroe to Johnson, n = 13); pre-World War II (teal, 1869-1933, Grant to Hoover, n = 13); and modern (purple, 1933-present, F.D. Roosevelt to Trump, n = 14). We consider Johnson to be a pre-Civil War president as he ascended to the presidency following the assassination of Lincoln rather than being directly elected.

Beyond allowing accurate dendrogram construction, the carp paths are themselves interesting to visualize. By plotting the path traced by the carp iterates U^(k), we can observe exactly how carp forms clusters from a given data set. For dimension reduction, we typically plot the projection of U^(k) onto the principal components of X, though clustrviz allows visualization of the raw features as well. Unlike the carp-dendrogram, the path plot allows examination of the structure of the estimated clusters and not just their membership. By displaying the original observations on the path plot, we also enable comparison of the estimated centroids with the original data. Modern web technologies allow us to display these path plots dynamically, forming a movie with each carp iterate as a separate frame. The fine solution grid returned by carp is especially relevant here, enabling us to construct movies in which the observations move smoothly. We have found that the smoothness of the movie is a useful heuristic to asses whether a small enough step-size t was used: if the paths “jump” conspicuously from one frame to the next, one should consider re-running carp with a smaller step-size.

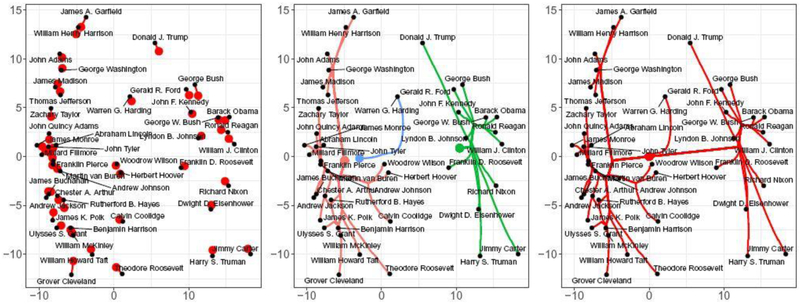
Figure 5 shows three frames of such a movie: in each frame, on the left side, we see the Founding Fathers cluster being merged to the other pre-modern presidents, while on the right, we see a clear cluster of modern presidents. A closer examination of the central frame reveals additional information not visible in the carp-dendrogram: Harding, the last president to join the pre-modern cluster, is an outlier lying between two clusters rather than far to one side.

Fig. 5.

Direct visualization of the solution paths produced by carp on the Presidents data, corresponding to unclustered (left), partially clustered (middle), and fully clustered (right) solutions. In each panel, the clusters of pre-modern and modern presidents are clearly visible, as is the outlier status of Harding.

Because both the dendrogram and path visualizations are indexed by the regularization level, γ^(k), it is possible to display them in a “linked” fashion, highlighting clusterings on the dendrogram as they are fused in the path plot. Particularly when rendered dynamically, this combination gives the best of both visualizations, combining the global structure visible in the dendrogram with the structural information visible in the path plot. An example of this “linked” visualization is shown in Figure 6.

Fig. 6.

Linked simultaneous visualization of the carp dendrogram and path plots. As clusters are formed in the path plot (left), they are highlighted on the dendrogram (right). The clusters of pre-modern and modern presidents are clearly visible, as is the outlier status of Warren G. Harding.

6. Discussion

We have introduced Algorithmic Regularization, an iterative one-step approximation scheme which can be used to efficiently obtain high-quality approximations of regularization paths. Algorithmic regularization focuses on accurate reconstruction of an entire regularization path and is particularly useful when for obtaining path-wise information, such as a dendrogram or the order in which variables leave the active set in sparse regression. We have focused on the application of the ADMM to convex clustering, but the technique of iterative one step-approximations can be applied to any problem which lacks an efficient algorithm. We believe that algorithmic regularization can be fruitfully applied to a broader range of statistical learning problems and expect that similar computational improvements can be achieved for other difficult optimization problems.

Theorem 1 is a novel global convergence result, guaranteeing high-quality approximation at each point of the exact solution path. Despite this, there are still many open questions in the analysis of algorithmic regularization. We are particularly interested in determining optimal convergence rates for global path-wise approximation problems and showing that algorithmic regularization can attain those rates. Our proof of Theorem 1 depends on the strong convexity of the convex clustering problem to ensure linear convergence of the underlying ADMM steps. It would be interesting to explore the interplay between algorithmic regularization and optimization schemes which are linearly convergent without strong convexity, as this may extend the applicability of algorithmic regularization even further.

Using algorithmic regularization, we have introduced the carp and cbass algorithms for convex clustering and bi-clustering. On moderately sized problems, carp and cbass reduce the time necessary to obtain high-quality regularization paths from several hours to only a few minutes, typically attaining over one-hundred-fold improvements over existing algorithms. Because carp and cbass return solutions at a fine grid of the regularization parameter, they can be used to construct accurate convex (bi-)clustering dendrograms, particularly if the back-tracking carp–viz and cbass–viz variants are employed. Additionally, the fine-grained carp and cbass solution paths allow for path-wise dynamic visualizations, allowing the analyst to observe exactly how the estimated clusters are formed and structured.

We anticipate that the computational and visualization techniques proposed in this paper will make convex clustering and bi-clustering an attractive option for applied data analysis. Both carp and cbass, as well as the proposed visualizations, are implemented in our clustrviz software, available at https://github.com/DataSlingers/clustRviz.