The nested joint clustering via Dirichlet process mixture model

Abstract

This article focuses on the clustering problem based on Dirichlet process (DP) mixtures. To model both time invariant and temporal patterns, different from other existing clustering methods, the proposed semi-parametric model is flexible in that both the common and unique patterns are taken into account simultaneously. Furthermore, by jointly clustering subjects and the associated variables, the intrinsic complex shared patterns among subjects and among variables are expected to be captured. The number of clusters and cluster assignments are directly inferred with the use of DP. Simulation studies illustrate the effectiveness of the proposed method. An application to wheal size data is discussed with an aim of identifying novel temporal patterns among allergens within subject clusters.

1. Introduction

In this paper, motivated by an epidemiological study we examine different allergic sensitization temporal patterns among subjects with different asthma statuses. Of interest is whether allergic sensitization to a set of indoor and outdoor allergens changes across different time points from infant to pre-adolescence, and to young adulthood, and if it does, then whether there exist systematic temporal patterns for different groups of subjects and for different groups of allergens. Compared to cross-sectional data, longitudinal data like this contains in depth information and provides us a unique opportunity to detect effective biomarkers for disease manifestations. For applications like this, cluster analyses aiming to detect the similarity between subjects are commonly implemented. In general, all clustering methods are either non-parametric, e.g., the k-means approach, or model-based (semi-)parametric approaches [5]. In this article, we focus on model-based semi-parametric clustering methods in the Bayesian framework.

Many model-based clustering methods group subjects based on the means, for instance, the method built upon a mixture of density functions [5,17]. Some approaches cluster subjects based on associations of a dependent variable with independent variables [10]. The clustering process is to identify groups of subjects with each group (cluster) representing a unique association and such association can be longitudinal [10]. Model-based clustering methods have also been proposed to cluster variables, which are beneficial to studies with interest on grouped patterns of variables, e.g., different temporal expression patterns for genes in different pathways. One such a method is proposed by Qin and Self [15], in which a maximum likelihood-based approach via an estimation-maximization algorithm is applied to infer variable clusters and regression coefficients. However, all these methods either cluster subjects or variables but not both.

Biclustering is more recognized recently with its concept dated back to the 1970’s[11]. The biclustering scheme simultaneously clusters both subjects and variables and tries to optimize a pre-specified objective function. There are two main classes of bi-clustering algorithms: systematic search algorithms and stochastic search algorithms [6]. Some of the methods are proposed under the Bayesian framework, e.g., the parametric Bayesian BiClustering model (BBC) [9] performing clustering for both genes and experimental conditions and the non-parametric Bayesian methods [12,13]. Bi-clustering focuses on coherence of rows and columns in the data. Since the technique is not model-based, it is restricted to profiles in the variables and external variables do not have any contribution to the evaluation of similarity between different variables. Furthermore, in variable clustering, it seems no methods available to handle variables with longitudinal measurements, as in the data motivating our study.

In this article, we propose a Bayesian nested joint clustering method to identify joint clusters based on temporal trends of a set of variables with background pattern adjusted. An underlying background pattern refers to a pattern shared by all subjects and variables. For instance, in our motivating example, the background pattern refers to a temporal allergic sensitization trend in the general population across all allergens. Subjects and variables with a pattern different from the background pattern will be included in a unique cluster. The proposed approach is a substantial extension to the method by Han et al. [10], where the focus is on clustering subjects only via longitudinal patterns of a variable of interest.

The road map for the remaining of the article is as follows. In Section 2, we present model specification, including model assumptions, parameter priors and posteriors. Numeric studies are in Section 3 and we present an application example in Section 4. Finally, a summary and discussion are included in Section 5.

2. Model Specification

2.1. Model

Suppose there are I subjects, and each subject is associated with H variables, measured at T time points. Let Y_i, a T × H matrix, denotes a measure of response for subject I with Y_i = (Y_i1,⋯, Y_iH), Y_ih = (y_ih1,⋯, y_ihT)^T, h = 1,⋯ , H, a T × 1 vector being the observation of hth variable for subject i over T time ·units and Y = {Y₁,⋯, Y_I} denoting all the observations. Clearly, each subject i has a data matrix Y_i of the dimension T × H.

We assume that Y_ih is associated with time invariant covariates X_i, a T × C matrix with C being the number of covariates via the following function,

$${\mathit{Y}}_{ih}={\mathit{X}}_i{\mathit{\beta }}_0+f_1\left(t_i;{\mathit{\gamma }}_0,{\mathit{b}}_0\right)+{\mathit{X}}_i{\mathit{\beta }}_{ih}+f_2\left(t_i;{\mathit{\gamma }}_{ih},{\mathit{b}}_{ih}\right)+{\mathit{s}}_i+{\mathit{ϵ}}_{ih},$$ (1)

where f₁(·) is an unknown function describing the temporal pattern applicable to all subjects (background pattern) and all variables, f₂(·) is for temporal pattern specific to subject i for variable h (with background adjusted), s_i represents subject random effects, and ϵ_ih is measurement error. Model (1) is for subject i and variable h and is in the same spirit as in Han et al. [10]. We assume independence among variables Y_i and also between random noise and independent variables. Model (1) consists of two parts. The first part X_iβ₀ + f₁(t_i; γ₀, b₀) describes background pattern common to all subjects and variables, and X_iβ_ih +f₂(t_i; γ_ih, b_ih) describes the pattern specifically for subject i and variable h. Assuming ϵ_ih ~ N(0,τI) and $s_i~N\left(0,{\sigma }_s^{2}I\right)$ with I being the identity matrix, we have

$${\mathit{Y}}_{ih}|{\mathit{\theta }}_0,{\mathit{\theta }}_i~N\left({\mathit{M}}_{ih},\Sigma \right),$$ (2)

with M_ih = X_iβ₀ + f₁(t_i; γ₀, b₀) + X_iβ_ih + f₂(t_i; γ_ih, b_ih), a T × 1 vector, Σ being a T ×T matrix with ${\sigma }_s^2+\tau$ on the diagonal and ${\sigma }_s^2$ off diagonal, θ =(β₀, γ₀, b₀)^T denoting common parameters in the background, θ_ih = (β_ih; γ_ih, b_ih)^T being the collection of parameters unique (unique parameters) to subject i and variable h, i = 1, 2,⋯ , I,h = 1, 2,⋯ , H. As seen in the construction of (1), θ_ih is added onto θ₀ and θ_ih = 0 if subject i in variable h does not have a unique temporal trend.

We take Bayesian P-splines [2] with order l (l = 2) for functions f₁(·) and f₂(·) to estimate the unknown common and subject specific temporal trends. Specifically, we define

$$\begin{gathered} f_1\left(t_i,{\mathit{\gamma }}_0,{\mathit{b}}_0\right)={\gamma }_{00}+{\gamma }_{01}{t}_{il}+{\gamma }_{02}{t}_{il}^2+\sum _{j=1}^N{b}_{0j}{\left(t_{il}-t_{ij}^{*}\right)}_{+}^2, \\ {f}_2\left(t_i,{\mathit{\gamma }}_{ih},{\mathit{b}}_{ih}\right)={\gamma }_{ih0}+{\gamma }_{ih1}{t}_{il}+{\gamma }_{ih2}{t}_{il}^2+\sum _{j=1}^N{b}_{ihj}{\left(t_{il}-t_{ij}^{*}\right)}_{+}^2, \end{gathered}$$ (3)

where ${\left(x\right)}_{+}^2=x^{2}I(x\ge 0)$ and N is the number of knots.

2.2. Nested joint clustering Scheme

We are interested in detecting two features, features in subjects indexed by i and features in variables indexed with h, represented by θ_ih in (4). To reach the goal, we propose a nested joint clustering plan with variable clusters nested in subject clusters. The clustering process is unified, but to ease the understanding, we present the process in two steps: subject clustering and nested variable clustering.

To cluster subjects, we group θ_1·,⋯, θ_I· (each of the H variables in θ_i· has repeated measures) based on overall pattern in the H variables. Next the clustering will be performed on the variables within each identified subject cluster, i.e., clustering θ_·1,⋯, θ_·H. Under this context, variable clustering is nested in subject clustering. By performing the nested joint clustering, we are able to capture overall subject cluster trends and variable heterogeneity (distinct variable clusters) in each subject cluster.

$$\begin{gathered} \left(\begin{array}{ccc}{\mathit{\theta }}_{11}& \cdots & {\mathit{\theta }}_{1\mathit{H}}\\ ⋮& \ddots & ⋮\\ {\mathit{\theta }}_{\mathit{I}1}& \cdots & {\mathit{\theta }}_{\mathit{I}\mathit{H}}\end{array}\right)\triangleq \left({\mathit{\theta }}_{1\cdot },\cdots ,{\mathit{\theta }}_{\mathit{i}\cdot },\cdots ,{\mathit{\theta }}_{\mathit{I}\cdot }\right)(\text{features in subjects}) \\ \triangleq \left({\mathit{\theta }}_{\cdot 1},\cdots ,{\mathit{\theta }}_{\cdot \mathit{h}},\cdots ,{\mathit{\theta }}_{\cdot \mathit{H}}\right)\text{ (features in variables within subject cluster}) \end{gathered}$$ (4)

2.3. Parameter Priors

A fully Bayesian approach is used to infer the parameters and clusters. We start from the construction for the prior of θ_ih, then discuss prior distributions of θ_i and θ_·h. For subject i with a background pattern for variable h, θ_ih = 0, otherwise, the subject has a unique pattern different from that in the background for that variable. To incorporate both unique and background patterns into the construction of prior distribution of θ_ih, we use a mixture of distribution G and point mass δ(θ_ih = 0),

$${\mathit{\theta }}_{ih}|G,\omega ~\omega G+(1-\omega )\mathit{\delta }\left({\mathit{\theta }}_{ih}=0\right),$$

with G generated from a Dirichlet Process (DP), G ~ DP (α, G₀), where G₀ is the base distribution and assumed to be G₀ = N(μ₀, Σ₀). Parameter in G is a precision parameter that controls the distance between G and G₀. Details of DP can be found in [1,3,4], among others. We assume Σ₀ is a diagonal matrix composed of variance parameters corresponding to β_ih, γ_ih, and b_ih in θ_ih (Section 2.1). Parameter ω is the probability that subject i with variable h has a unique longitudinal trend different from the background.

To fit in the nested joint clustering scheme proposed in Section 2.2, in the following, we discuss the prior distributions of θi. and θ_·h, along with other hyper-prior distributions.

2.3.1. Subject clustering

The parameters to be clustered to form subject clusters are θ_i ‘s. When clustering subjects, we focus on overall longitudinal patterns across all the variables and group subjects into clusters based on unique temporal patterns. For a subject with a background pattern only, i.e., the longitudinal pattern across all the H variables for that subject follows the pattern in the general population, we have θ_i = 0. Based on the prior distribution of θ_ih, we have,

$${\mathit{\theta }}_{i\cdot }|G,{\omega }_1~\omega \prod _{h=1}^{H}G+(1-\omega )\delta \left({\mathit{\theta }}_{i\cdot }=0\right).$$

Having G generated from DP equipped G an ability to describe skewed distributions. Since our goal is to assess overall patterns across all H variables, flexibility of G is essential. Furthermore, the inherent clustering property of samples drawn from a distribution with DP prior ensures the formation of clusters among θ_i·. Thus, using DP as part of the mixture is critical for the process of clustering subjects. The conditional prior distribution for θ_i with (·) denoting all other parameters and data is then defined as,

$${\mathit{\theta }}_{i\cdot }|(\cdot )~\omega \prod _{h=1}^H\left(\frac{1}{I-1+\alpha }\sum _{j\ne i}\delta \left({\mathit{\theta }}_{j\cdot }\right)+\frac{\alpha }{I-1+\alpha }N\left({\mathit{\mu }}_0,{\Sigma }_0\right)\right)+\left(1-{\omega }_1\right)\delta \left({\mathit{\theta }}_{i\cdot }=0\right),$$ (5)

which assumes that subjects not following the temporal trend in a general population (determined by θ₀) are grouped into clusters with each cluster having one unique temporal pattern on average across all H variables. Parameter α in G controls cluster sizes. A larger value of α leads to a larger number of clusters. Since we do not expect many levels of discrepancy among subjects with respect to overall longitudinal patterns for the H variables, the value of α is chosen to be relatively small, e.g., α = 0.01, although we can choose α by optimizing the deviance information criterion (DIC) [7,16].

2.3.2. Nested variable clustering

To cluster variables within each subject cluster, θ_·h is used. Note that conditional on T time units, the distribution of Y_ih is exchangeable with respect to i and h. This property of exchangeability eases the difficulty of clustering the H variables within each subject cluster and makes it comparable to the process of clustering subjects. To achieve this, we treat measures on H variables as observations on H “subjects” and, each having I_k (number of subjects in kth subject cluster, k = 1,⋯ , K) “variables” and each “variable” has T repeated measures. With this “modified” structure of data, for θ_·h within each subject cluster, we further examine their heterogeneity. In this sense, the prior distribution of θ_·h is conditional on all other parameters as well as the clustering of θ_i·,

$${\mathit{\theta }}_{\mathit{\cdot }\mathit{h}}|{\mathit{\theta }}_{\mathit{i}\cdot },(\cdot )~\omega \prod _{i=1}^{I_k}\left(\frac{1}{I-1+\alpha }\sum _{g\ne h}\delta \left({\mathit{\theta }}_{\cdot g}\right)+\omega \frac{\alpha }{I-1+\alpha }N\left({\mathit{\mu }}_0,{\Sigma }_0\right)\right)+(1-\omega )\delta ({\mathit{\theta }}_{\cdot h}=0).$$ (6)

It is worth noting that in expressions (5) and (6), we assume the probability that subject i has a unique overall longitudinal trend across the H variables is the same as that for the pattern of variable h being in the background across all I_k subjects. This assumption is acceptable in that in both situations we are interested in the probability that a longitudinal trend is coincident with a pattern in the background.

2.4. Prior distributions for other parameters

For the hyper-prior distributions of μ₀ and Σ₀ in the base distribution G₀, and the distribution of weight parameter ω, we propose vague or non-informative priors. For μ₀, we choose a multivariate normal distribution with mean 0 and known large diagonal covariance matrix ${\Sigma }_{{\mu }_0}$. For all the parameters in Σ₀, we take inverse gamma (IG) as the prior distributions with shape and scale parameters are known and chosen small. For the weight parameter ω, we assume ω ~ Beta(2, 2), which is a symmetric distribution within interval (0,1). For the prior distributions of θ₀, a multivariate normal is chosen with mean 0 and covariance ${\Sigma }_{{\theta }_0}$, a known diagonal matrix with large components. For variance parameter τ in ϵ_ih and variance parameter ${\sigma }_s^2$ in random subject effects, an inverse gamma distribution with small shape and scale parameters are used.

2.5. Joint and conditional posterior distributions

Let $\mathcal{A}=\left\{{\mathit{\theta }}_{ih},i=1,\cdots ,I,h=1,\cdots ,H,\mathit{\zeta }\right\}$, where $\mathit{\zeta }=\left({\mathit{\mu }}_0,{\Sigma }_0,\omega ,{\mathit{\theta }}_0,\tau ,{\sigma }_s^2\right)$, denote all parameters, the joint posterior distribution is, up to a normalization constant,

$$\begin{gathered} P(\mathcal{A}|\mathit{Y})\propto \prod _i\prod _{h}p\left(\mathit{Y}|{\mathit{\theta }}_{ih},{\mathit{\theta }}_0,\tau ,{\sigma }_s^2\right)p\left({\mathit{\theta }}_{i.},{\mathit{\theta }}_{.h}|G,\omega \right)p\left(G|G_0,\alpha \right)p\left({\mathit{\mu }}_0\right)p\left({\Sigma }_0\right)p(\omega )p\left({\mathit{\theta }}_0\right)p(\tau )p\left({\sigma }_s^2\right), \\ \text{with }{G}_0=N\left({\mathit{\mu }}_0,{\Sigma }_0\right). \end{gathered}$$ (7)

Note that the joint posterior distribution reduced to the distribution in Han et al. [10] if we only have one variable, and nested joint clustering becomes clustering subjects only. Posterior inference of $\mathcal{A}$ is obtained by successively simulating values from their full conditional posterior distributions through the Gibbs sampling scheme. We included the conditional posterior distributions as well as the sampling scheme in the Appendix. Derivations of these distribution are similar in spirit to those given in Han et al. [10].

3. Simulated Experiments

For methods clustering subjects based on longitudinal patterns with background patterns adjusted, Han et al. [10] via simulations compared with a non-parametric approach implemented in an R package kml [8], and demonstrated the advantage of their proposed method. The proposed method performs joint clustering and reduces to [10] when there is one variable. We expect that the advantage of adjusting background while clustering still holds. As for methods with the ability of jointly clustering subjects and variables under a longitudinal setting, we have not identified comparable methods. To demonstrate the effectiveness of the method, we thus implemented simulated data sets generated under different scenarios. Different sample sizes and different number of variables are considered. We take sample size I = 200, 400, 600 and number of variables H = 10, 20. The background pattern is assumed to be linear as

$$f_1=p_0+p_{1}t$$

where p₀, and p₁ are generated from N(0, 0.1). The number of subjects with background only is I/2. Two subject clusters are considered and each subject cluster is with size of I/4. Within each subject cluster, variables are further grouped into two clusters. Thus in total, we have four clusters. The patterns of these four distinct variable clusters are

$$\begin{gathered} clust11:f_2=7-23t \\ clust12:f_2=2 \\ clust21:f_2=-3 \\ clust22:f_2=-27+3t-6t^2, \end{gathered}$$

where clust11 denotes the first variable cluster in subject cluster 1. We consider one covariate, X_i ~ N(0, 1), and coefficient for X_i in the background is β₀ = 20. The coefficient of X_i for each subject cluster is generated from N(0, 10), which is shared for all subject in this cluster, i.e. subject cluster specific. Random subject effect s_i, and random error ϵ_ih are both generated from N(0, 0.5) and they are independent of each other.

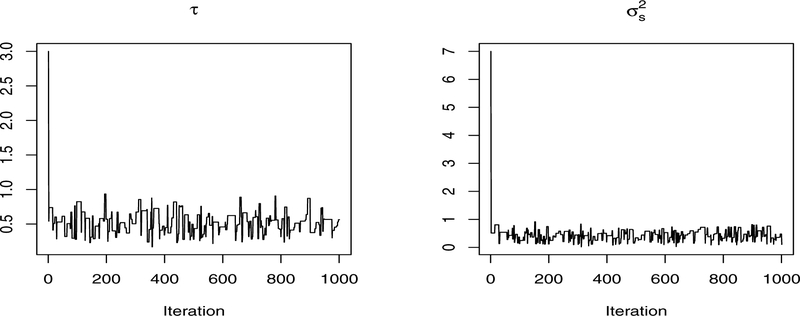
For each setting in terms of sample size and the number of variables, we generated 100 Monte Carlo (MC) replicates. We then applied our method to each MC replicate. The precision parameter α is set at 0.01. Fast convergence of MCMC chains are observed. In general, the chains converge within the first 500 iterations (Figure 1), after which the chains become very stable and the sampled values are around the true values. We also calculated the potential scale reduction statistics $\widehat{R}$ suggested by [7], which supports the fast convergence observed in Figure 1. In particular, for τ, ${\sigma }_s^2$, R_τ = 1.0018, $R_{{\sigma }_S^2}=1.0017$ calculated based on multiple MCMC chains, are both close to 1, indicating potential convergence of the sampling sequences.

Figure 1.

Trace plots of one chain of MCMC simulations for the two scale parameters, τ (left) and ${\sigma }_s^2$ (right). The x-axis represents the number of iterations and values on the y-axis are the sampled values of each parameter in the MCMC simulation process.

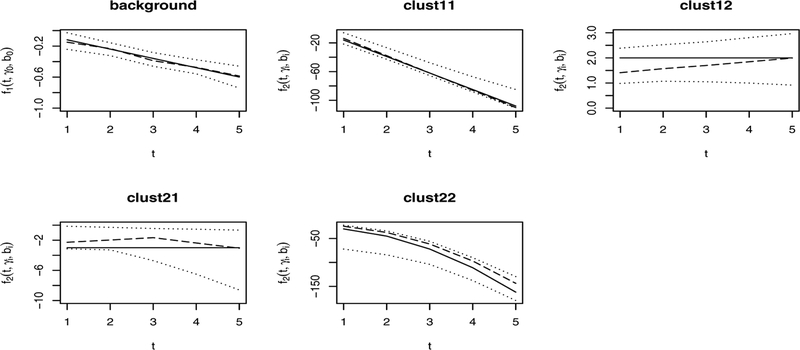
Figure 2 demonstrates the fit of the model to the data. The true patterns, fitted curves, and 95% empirical bands are displayed for data set with the sample size of 600 and 20 variables. The fitted curves are closer to the true patterns and confidence bands are narrower in the background than in other unique clusters. This is likely due to the larger sample size as well as the larger number of variables in the background. Similar results are observed in other settings of sample size and number of variables.

Figure 2.

True curve (solid lines), fitted curve (dashed lines) and confidence bands (dotted lines) with sample size of 600 and 20 variables.

To assess the overall performance of the method, we present the clustering sensitivity and specificity in different scenarios in Table 1 and Table 2. Sensitivity and specificity in background are expectedly higher than in unique clusters because of the larger sample size. Overall sensitivity and specificity for subject clusters are clearly increased as the sample size increases. When the number of variables is increased from 10 to 20, both sensitivity and specificity in unique clusters are improved, indicating stronger underlying clustering information as the number of variables increases.

Table 1.

Summary of sensitivity and specificity across 100 MC replicates for both subject clusters and variable clusters with varying subject sample sizes. The number of variables is 10. Background: background patterns applied to all subjects and variables. sub.clust1: subject cluster 1, sub.clust2: subject cluster 2, clustij: variable cluster j in subject cluster i, i, j = 1, 2.

			Subject 200	Sample 400	Size 600
Background	Sensitivity	Mean	0.9539	0.9775	0.9898
		SD	0.0990	0.0617	0.0375
	Specificity	Mean	0.9870	0.9891	0.9930
		SD	0.0556	0.0370	0.0180
sub.clust1	Sensitivity	Mean	0.7494	0.8631	0.9161
		SD	0.2760	0.2315	0.1912
	Specificity	Mean	0.9539	0.9659	0.9731
		SD	0.0648	0.0512	0.0437
sub.clust2	Sensitivity	Mean	0.7761	0.8730	0.9089
		SD	0.2331	0.2017	0.1702
	Specificity	Mean	0.9753	0.9816	0.9916
		SD	0.0582	0.0411	0.0217
clust11	Sensitivity	Mean	0.6904	0.7168	0.7407
		SD	0.2472	0.2447	0.2445
	Specificity	Mean	0.6250	0.6225	0.7004
		SD	0.3339	0.2742	0.2244
clust12	Sensitivity	Mean	0.6738	0.7071	0.7218
		SD	0.2103	0.2061	0.2123
	Specificity	Mean	0.7640	0.7658	0.7531
		SD	0.3254	0.2347	0.2617
clust21	Sensitivity	Mean	0.6992	0.6787	0.6699
		SD	0.2333	0.2339	0.2458
	Specificity	Mean	0.6711	0.6596	0.6771
		SD	0.2789	0.2943	0.2911
clust22	Sensitivity	Mean	0.6718	0.6690	0.6800
		SD	0.2117	0.2105	0.1956
	Specificity	Mean	0.7060	0.7212	0.7834
		SD	0.3035	0.2886	0.2584

Table 2.

Summary of sensitivity and specificity across 100 MC replicates for both subjects clusters and variable clusters with varying subject sample sizes. The number of variables is 20. Background: background patterns applied to all subjects and variables. sub.clust1: subject cluster 1, sub.clust2: subject cluster 2, clustij: variable cluster j in subject cluster i, i, j = 1, 2.

			Subject 200	Sample 400	Size 600
Background	Sensitivity	Mean	0.9763	0.9848	0.9916
		SD	0.0658	0.0483	0.0433
	Specificity	Mean	0.9891	0.9943	0.9902
		SD	0.0265	0.0130	0.0397
sub.clust1	Sensitivity	Mean	0.8005	0.8579	0.9217
		SD	0.2652	0.2383	0.1874
	Specificity	Mean	0.9575	0.9659	0.9745
		SD	0.0663	0.0559	0.0423
sub.clust2	Sensitivity	Mean	0.8134	0.8825	0.9318
		SD	0.2260	0.1924	0.1557
	Specificity	Mean	0.9810	0.9817	0.9911
		SD	0.0669	0.0350	0.0211
clust11	Sensitivity	Mean	0.8028	0.8351	0.8567
		SD	0.2504	0.2323	0.2264
	Specificity	Mean	0.6612	0.7464	0.7087
		SD	0.2787	0.2356	0.2273
clust12	Sensitivity	Mean	0.8072	0.8092	0.8271
		SD	0.1878	0.2051	0.1890
	Specificity	Mean	0.8654	0.8424	0.8725
		SD	0.2057	0.2209	0.1800
clust21	Sensitivity	Mean	0.8064	0.7865	0.8598
		SD	0.2438	0.2502	0.2153
	Specificity	Mean	0.7417	0.6572	0.7422
		SD	0.2733	0.2750	0.1658
clust22	Sensitivity	Mean	0.7745	0.7697	0.8169
		SD	0.2195	0.2075	0.1953
	Specificity	Mean	0.8518	0.8143	0.8366
		SD	0.2588	0.2310	0.1904

Results displayed in Table 1 and Table 2 are for variable clusters such that the number of variables in each variable cluster is the same. We also considered unevenly distributed variables in each variable cluster. To demonstrate the performance of the method under this setting, we simulated 100 MC replicates such that variables in subject cluster 1 are unequally split into two variables clusters, with one cluster of 8 variables and the other of 12. The sample size is set at I = 600. Other settings are the same as before. Results of summary statistics for sensitivity and specificity are included in Table 3. As expected, the overall clustering accuracy is slightly reduced compared to balanced cases. This is due to the stronger uncertainty in the smaller variable clusters. Overall, results from the simulations provide an evidence that the proposed method is capable of jointly clustering both subjects and variables.

Table 3.

Sample size 600, 20 variables: Unevenly distributed variables, in subject clust1, there are 8, 12 variables in variable cluster 1, and 2 respectively, and in subject cluster 2, there are 10, 10 variables in variable cluster 1 and 2 respectively. Background: background patterns applied to all subjects and variables. sub.clust1: subject cluster 1, sub.clust2: subject cluster 2, clustij: variable cluster j in subject cluster i, i, j = 1, 2.

	Mean (SD)
	Sensitivity	Specificity
Background	0.9785 (0.0537)	0.9883 (0.0301)
sub.clust1	0.9143 (0.1995)	0.9530 (0.0641)
sub.clust2	0.9278 (0.1556)	0.9808 (0.0382)
clust11	0.7961 (0.2476)	0.8039 (0.1566)
clust12	0.8672 (0.1565)	0.7409 (0.2130)
clust21	0.8335 (0.2360)	0.6571 (0.2422)
clust22	0.7393 (0.1607)	0.8433 (0.2211)

4. Real Data Applications

We apply the proposed method to an epidemiology data collected from 595 subjects, each having wheal sizes measured at ages 4, 10, and 18 years in reaction to 11 allergens (Grass, Dog, Cat, House dust mite [HDM], peanut, soy, cod, egg, milk, Alternaria, Cladosporium). Our goal is to detect clusters of subjects sharing similar overall temporal wheal size patterns across the allergens, and within each subject cluster, we would like to detect clusters of allergens sharing similar temporal patterns. The underlying motivation is that some subjects may react to certain allergens different from other subjects.

Without loss of generality, we standardized the age variable before analyzing to avoid potential bias in clustering caused by heterogeneous scale.

We set α as 0.01, assuming small numbers of clusters in subjects as well as variables. We run one long chain with 10,000 iterations in total, among which 8,000 iterations are for burn in, and the posterior inferences are based on the remaining 2,000 iterations.

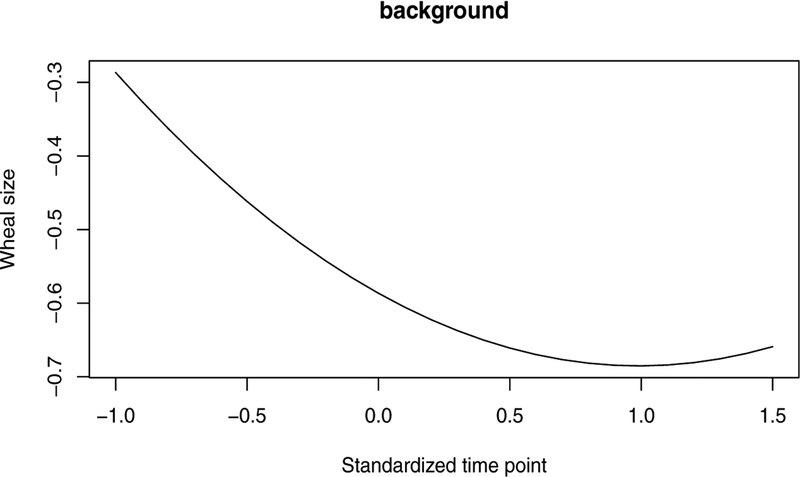
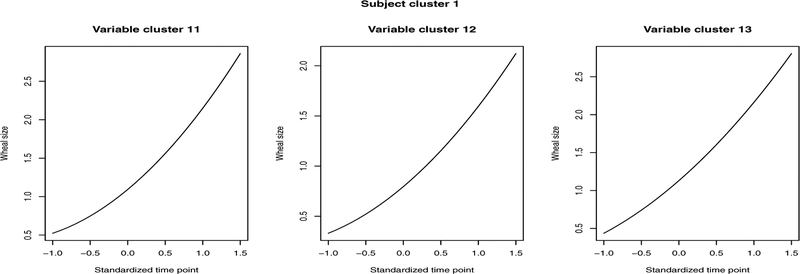
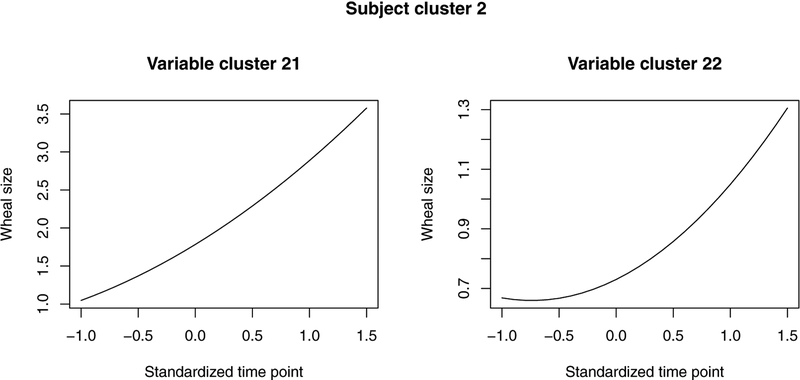
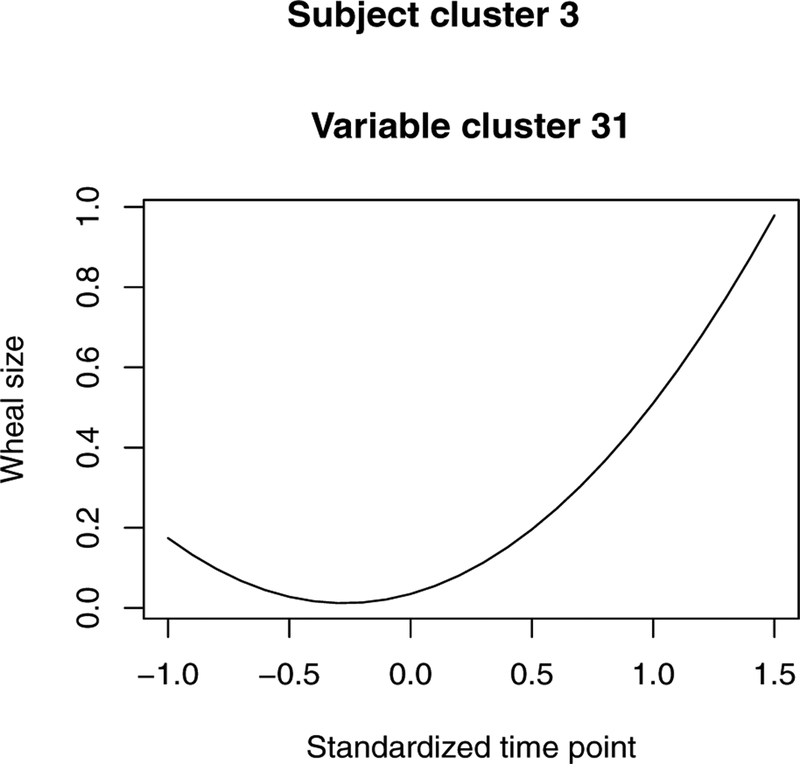
On top of background patterns (i.e., patterns in the general population), three unique subject clusters are identified, in which unique variable clusters with respect to longitudinal wheal size patterns are further detected. As shown in Figure 3, the wheal sizes in the general population are overall close to zero. Wheal size longitudinal patterns with respect to allergens soy, cod, egg, milk, Alternaria, and Cladosporium are in the background, implying an extremely low prevalence of allergic sensitization to these allergens. Wheal sizes in the unique clusters are clearly much larger, but show different temporal patterns in different clusters of allergens. In the first subject cluster, the unique patterns are brought by allergens Grass, Dog, Cat, and House dust mite and the pattern of the remaining 7 allergens are constant with patterns in general population. In particular, wheal sizes against Cat allergen are smaller and increase more slowly over time compared to the wheal sizes against the other three allergens. Among Grass, Dog, and HDM, wheal sizes in reaction to Grass and Dog follow similar temporal trend, increasing over time and increasing faster compared to the trend for HDM. In subject cluster 2, compared to allergens in unique clusters of subject cluster 1, Peanut allergen joins in. For subjects in this cluster, wheal sizes for allergens Grass, Dog, HDM, and Peanut increases quickly over time to an expected wheal size larger than 3.5mm. On the other hand, wheal sizes in reaction to Cat for subjects in this cluster are much smaller. Wheal sizes are small at an earlier age (around 4 years, unstandardized age) and start to increase around 10 years of age. In the last subject cluster, wheal sizes for all the allergens except for HDM and Milk follow a pattern as in the background. Wheal sizes for HDM and Milk are small in expectation and share similar patterns.

Figure 3.

Background pattern.

Because sizes of wheals reflect a potential severity of allergic sensitization (atopy) and atopy is linked to asthma, we further examined whether subjects in each of the clusters ever had asthma. The prevalence of asthma ever in each unique subject cluster and among the subjects with a background pattern is recorded in Table 4. Linking the prevalence of asthma to the longitudinal patterns in each unique cluster, subjects with larger wheal sizes increasing over time certainly have a higher risk of having asthma compared to those in the background. However, two points may deserve a further consideration. Firstly, among subjects allergic to the four allergens, Grass, Dog, Cat, and HDM, wheal size in reaction to Cat allergen seems to play a role in the prevalence of asthma. If wheal sizes for Cat allergen are relatively small compared to reaction to the other three allergens, even though a subject is allergic to peanut as well, the risk of having asthma can be smaller compared to subjects with large wheal sizes for Cat allergen (cluster 1 and 2 in Table 4). Secondly, there exists a group of subjects such that they have a slight reaction to a small number of allergens, in our case, HDM and Milk. For those subjects, the prevalence of asthma (13.6%) is slightly lower but similar to that in the general population (16.4%). It is unclear whether a small reaction to a small number of allergens is actually protective and surely deserves further investigation.

Table 4.

Asthma prevalence in each subject cluster and background.

Unique Subject Cluster/Background	Size	% asthma
Cluster 1	43	29.4
Cluster 2	84	22.2
Cluster 3	31	13.6
Background	437	16.4

5. Summary

We proposed a nested joint clustering method built upon Dirichlet process to jointly cluster longitudinal data. Under the proposed mechanism, variables are clustered within each subject cluster based on their agreement in possibly non-linear temporal trends and associations with external variables. Dirichlet process (DP) is implemented in the clustering of subjects as well as in the jointed clustering of variables nested within each subject cluster.

To our knowledge, methods with the ability to jointly cluster longitudinal data are not available. In the absence of competitive methods, we evaluated the proposed methods via simulations under different settings defined by sample sizes and numbers of variables. Results from simulations demonstrate the effectiveness of the proposed approach with respect to sensitivity and specificity in clustering. As expected, sensitivities and specificities improve with the increase of sample sizes and with the increase of number of variables. The application of the method to the longitudinal wheal size assessment of children at ages 4, 10, and 18 years detected 6 unique clusters with each showing a different temporal pattern of wheal size for different groups of allergens and subjects. After connecting the features of the unique clusters to the proportions of ever having asthma among the children, it was found that being allergic to Cat allergen (but not other allergens) in addition to other common allergens (Dog, Grass, and House dust mite) can potentially increase the risk of asthma.

Common to all analytical methods, the proposed nested joint clustering approach has its limitations. The sensitivity and specificity of variable clusters require improvement when the number of variables is small. This is likely due to the characteristics of DP, e.g., producing clusters with a small number of observations. Another limitation is in the assumption of independence between variables. With variables being dependent, the likelihood constructed under the independence assumption can be treated as a composite likelihood. Since the goal is clustering, we do not expect this assumption will deteriorate the ability of cluster detections; rather, the dependency among the variables is expected to have the underlying variable clusters emerge more easily, and subsequently benefit the clustering and improve the quality of clustering.

Figure 4.

Pattern of allergen variables in subjects cluster 1 which has 43 subjects. Variable cluster 11: Grass, Dog; Variable cluster 12: Cat; Variable cluster 13: HDM.

Figure 5.

Pattern of allergen variables in subject cluster 2 with 84 subjects. Variable cluster 21: peanut, Grass, Dog, HDM; Variable cluster 22: Cat.

Figure 6.

Pattern of allergen variables in subject cluster 3 with 31 subjects. Variable cluster 31: milk, HDM.

6. Appendix

In the following, we present the conditional posterior distributions, followed by the sampling scheme used to draw posterior samples for posterior inferences.

6.1. Derivations of conditional posterior probabilities for key parameters

We present below conditional posterior distributions for two key parameters θ₀, θ_i· in the step of clustering subjects and omit the posterior distributions for parameters θ_·h for clustering variables as its posterior can be derived in the same way as θ_i·. Analogously, μ₀, Σ₀ have standard posteriors with similar derivations as for θ₀. However, for τ, ${\sigma }_s^2$, we use M-H sampling to draw samples based on the joint posterior probabilities in (7).

1. Conditional posterior of θ₀,

   $$P\left({\mathit{\theta }}_0|\mathit{Y},{\mathit{\theta }}_{\mathit{i}\mathit{h}},i=1,2,\cdots ,I,h=1,\dots ,H;\mathit{\zeta }\backslash {\mathit{\theta }}_0\right)\propto exp\left\{-\frac{1}{2}{\left({\mathit{\theta }}_0\right)}^T{\left({\Sigma }_{\mathit{\theta }0}\right)}^{-1}{\theta }_0\right\}\times exp\left\{-\frac{1}{2}\sum _{i=1}^I\sum _{h=1}^H{\left({\mathit{Y}}_{\mathit{i}\mathit{h}}-{\mathit{M}}_{\mathit{i}\mathit{h}}\right)}^T{(\Sigma )}^{-1}\left({\mathit{Y}}_{\mathit{i}\mathit{h}}-{\mathit{M}}_{\mathit{i}\mathit{h}}\right)\right\}$$

   where θ₀ = (β₀, γ₀, b₀). Because Σ_θ0 is a diagonal matrix, let ${\mathbf{\Sigma }}_{\mathit{\theta }0}=diag\left\{{\Sigma }_{{\mathit{\beta }}_0},{\Sigma }_{{\mathit{\gamma }}_0},{\Sigma }_{b_0}\right\},{\mathit{R}}_{\mathit{i}\mathit{h}}\left({\mathit{\beta }}_0\right)={\mathit{Y}}_{\mathit{i}\mathit{h}}-f\left(t_i;{\mathit{\gamma }}_0,b_0\right)-X_i{\mathit{\beta }}_{\mathit{i}\mathit{h}}-f\left({\mathbf{t}}_i;{\mathit{\gamma }}_{\mathit{i}\mathit{h}},{\mathit{b}}_{\mathit{i}\mathit{h}}\right)$, which does not involve β₀ any more. The conditional posterior of β₀ is proportional to Analogously, the posterior probability of β₀ is proportional to

   $$\begin{gathered} exp\left\{-\frac{1}{2}{\left({\mathit{\beta }}_0\right)}^T{\left({\mathbf{\Sigma }}_{{\mathit{\beta }}_0}\right)}^{-1}{\mathit{\beta }}_0\right\}\times exp\left\{-\frac{1}{2}\sum _{i=1}^I\sum _{h=1}^H{\left({\mathit{R}}_{\mathit{i}\mathit{h}}\left({\mathit{\beta }}_0\right)-X_i{\mathit{\beta }}_0\right)}^T{(\mathbf{\Sigma })}^{-1}\left({\mathit{R}}_{\mathit{i}\mathit{h}}\left({\mathit{\beta }}_0\right)-X_i{\mathit{\beta }}_0\right)\right\} \\ =exp\{-\frac{1}{2}{\left({\mathit{\beta }}_0\right)}^T\left[{\left({\Sigma }_{{\mathit{\beta }}_0}\right)}^{-1}+H\sum _{i=1}^I{X}_i^T{(\Sigma )}^{-1}{X}_i\right]{\mathit{\beta }}_0 \\ +\left[\frac{1}{2}\sum _{i=1}^I\sum _{h=1}^H{\mathit{R}}_{\mathit{i}\mathit{h}}{\left({\mathit{\beta }}_0\right)}^T{(\Sigma )}^{-1}{X}_i\right]{\mathit{\beta }}_0+{\left({\mathit{\beta }}_0\right)}^T\left[\frac{1}{2}\sum _{i=1}^I\sum _{h=1}^H{X}_i^T{(\Sigma )}^{-1}{\mathit{R}}_{\mathit{i}\mathit{h}}\left({\mathit{\beta }}_0\right)\right]\}+c \end{gathered}$$

   $$\begin{gathered} {\mathit{\beta }}_0|(.)~MN(\mathit{\mu },\mathrm{\Delta }),with \\ \mathit{\mu }=\mathrm{\Delta }\sum _{i=1}^I\sum _{h=1}^H{X}_i^T{\left(\Sigma \right)}^{-1}{\mathit{R}}_{\mathit{i}\mathit{h}}\left({\mathit{\beta }}_0\right), \\ \mathrm{\Delta }={\left[{\left({\Sigma }_{{\mathit{\beta }}_0}\right)}^{-1}+H\sum _{i=1}^I{X}_i^T{(\Sigma )}^{-1}{X}_i\right]}^{-1}. \end{gathered}$$
   Analogously, the posterior probability of γ₀ is proportional to

   $$exp\left\{-\frac{1}{2}{\left({\mathit{\gamma }}_0\right)}^T{\left({\mathbf{\Sigma }}_{\mathit{\gamma }0}\right)}^{-1}{\gamma }_0-\frac{1}{2}\sum _{i=1}^I\sum _{h=1}^H{\left[{\mathit{R}}_{\mathit{i}\mathit{h}}\left({\mathit{\gamma }}_0\right)-\left({\mathit{I}}_{\mathit{T}\times \mathit{T}}\otimes {\left({\mathit{\gamma }}_0\right)}^{\mathit{T}}\right){\mathit{T}}_i\right]}^T{(\mathbf{\Sigma })}^{-1}\left[{\mathit{R}}_{\mathit{i}\mathit{h}}\left({\mathit{\gamma }}_0\right)-\left({\mathit{I}}_{\mathit{T}\times \mathit{T}}\otimes {\left({\mathit{\gamma }}_0\right)}^{\mathit{T}}\right){\mathit{T}}_i\right]\right\}$$

   where ⊗ is the outer product, ${\mathit{R}}_{\mathit{i}\mathit{h}}\left({\mathit{\gamma }}_0\right)=Y_{ih}-X_i{\mathit{\beta }}_0-{\left({\mathit{b}}_0^T\nabla {\mathit{T}}_{1\mathbf{*}}^{(\mathit{i})},\cdots ,{\mathit{b}}_0^{\mathit{T}}\nabla {\mathit{T}}_{\mathit{T}*}^{(\mathit{i})}\right)}^T-X_i{\mathit{\beta }}_{\mathit{i}\mathit{h}}-f\left(t_i;{\mathit{\gamma }}_{\mathit{i}\mathit{h}},b_{ih}\right)$, T_i = (T_i1,⋯, T_iT)^T, $\nabla {\mathit{T}}_{\mathit{l}\mathbf{*}}^{(\mathit{i})}=\left({\left(t_{il}-t_{i1}^{*}\right)}_{+}^2,\cdots ,{\left(t_{il}-t_{iN}^{*}\right)}_{+}^2\right),l=1,2,\cdots ,T$. After simplifications,

   $$\begin{gathered} {\gamma }_{0j}|(.)~N\left(\frac{\Pi }{2}\left(\mathrm{\Delta }+\frac{1}{{\sigma }_{{\gamma }_{0i}}^2}\right),\frac{1}{\mathrm{\Delta }+{\frac{1}{{\sigma }_{\gamma 0i}}}^1}\right),with \\ \mathrm{\Delta }=\sum _{i=1}^I\sum _{h=1}^H\sum _{t=1}^T\sum _{k=1}^T{(\Sigma )}_{kt}^{-1}{t}_{ik}^{2j}, \\ \Pi =\sum _{i=1}^T\sum _{h=1}^H\sum _{t=1}^T\sum _{k=1}^T\left(R_{ih}{\left({\gamma }_{0i}\right)}_k+R_{ih}{\left({\gamma }_{0i}\right)}_t\right){\left(\Sigma \right)}_{kt}^{-1}{t}_{ik}^j, \\ j=\mathrm{0,1,2}. \end{gathered}$$
   Similarly,

   $$\begin{gathered} b_{0j}|(.)~N\left(\frac{\Pi }{2}\left(\mathrm{\Delta }+\frac{1}{{\sigma }_{b_{0j}}^2}\right),\frac{1}{\mathrm{\Delta }+\frac{1}{{\sigma }_{b_i}^2}}\right),with\mathrm{\Delta }=\sum _{i=1}^I\sum _{h=1}^H\sum _{t=1}^T\sum _{k=1}^T{(\Sigma )}_{kt}^{-1}{\left(t_{ik}-t_{ij}\right)}_{+}^4, \\ \Pi =\sum _{i=1}^I\sum _{h=1}^H\sum _{t=1}^T\sum _{k=1}^T\left(R_{ih}{\left(b_{0j}\right)}_k+R_{ih}{\left(b_{0j}\right)}_t\right){\left(\Sigma \right)}_{kt}^{-1}{\left(t_{ik}-t_{ij}\right)}_{+}^2, \\ j=1,2,\cdots ,N, \end{gathered}$$

   where R(*)_k is the kth element of the “residual” of *.

2. Conditional posterior of θ_i·,

   Following the same way, it is straightforward to derive the conditional posterior for θ_i·. As for β_i,

   $$\begin{gathered} {\mathit{\beta }}_i|(\cdot )~MN(\mathit{\mu },\mathrm{\Delta }),with \\ \mathit{\mu }=\mathrm{\Delta }\left[{\left({\mathbf{\Sigma }}_{{\mathit{\beta }}_i}\right)}^{-1}{\mathit{\mu }}_{{\mathit{\beta }}_i}+\sum _{\mathit{i}=1}^I\sum _{h=1}^H{\mathbf{\text{X}}}_i^T{(\mathbf{\Sigma })}^{-1}{\mathit{R}}_{\mathit{i}\mathit{h}}\left({\mathit{\beta }}_{\mathit{i}}\right)\right], \\ \mathrm{\Delta }={\left[{\left({\mathbf{\Sigma }}_{{\mathit{\beta }}_i}\right)}^{-1}+H\sum _{i=1}^I{X}_i^T{(\Sigma )}^{-1}{X}_i\right]}^{-1}, \end{gathered}$$

   where R_ih(β_i) = Y_ih − X_iβ₀ − f(t_i; β₀, b₀) − f(t_i; γ_i, b_i).
   For γ_i,

   $$\begin{gathered} {\gamma }_{is}|(.)~N(\mu ,\mathrm{\Delta }),with \\ \mu =\mathrm{\Delta }\left(\frac{\Pi }{2}+\frac{{\mu }_{{\gamma }_{is}}}{{\sigma }_{{\gamma }_{is}}^2}\right), \\ \mathrm{\Delta }=\frac{1}{\Phi +\frac{1}{{\sigma }_{{\gamma }_{is}}^2}}, \\ \Phi =\sum _{j:subjectj has{\theta }_{i\cdot }}\sum _{t=1}^T\sum _{k=1}^T{(\Sigma )}_{kt}^{-1}{t}_{ik}^{2s}, \\ \Pi =\sum _{i=1}^I\sum _{h=1}^H\sum _{t=1}^T\sum _{k=1}^T\left(R_{ih}{\left({\gamma }_{is}\right)}_k+R_{ih}{\left({\gamma }_{is}\right)}_t\right){\left(\Sigma \right)}_{kt}^{-1}{t}_{ik,}^s \\ s=\mathrm{0,1,2}. \end{gathered}$$

   Finally, for b_i,

   $$\begin{gathered} b_{is}|(.)~N(\mu ,\mathrm{\Delta }),with \\ \mu =\mathrm{\Delta }\left(\frac{\Pi }{2}+\frac{\mu b_{is}}{{\sigma }_{b_{is}}^2}\right), \\ \mathrm{\Delta }=\frac{1}{\Phi +\frac{1}{{\sigma }_{b_{is}}^2}}, \\ \Phi =\sum _{j:subjectjhas{\theta }_{i\cdot }}\sum _{t=1}^T\sum _{k=1}^T{(\Sigma )}_{kt}^{-1}{\left(t_{ik}-t_{is}\right)}_{+}^4, \\ \Pi =\sum _{i=1}^I\sum _{h=1}^H\sum _{t=1}^T\sum _{k=1}^T\left(R_{ih}{\left(b_{is}\right)}_k+R_{ih}{\left(b_{is}\right)}_t\right){\left(\Sigma \right)}_{kt}^{-1}{\left(t_{ik}-t_{is}\right)}_{+}^2, \\ s=1,2,\cdots ,N. \end{gathered}$$

6.2. Overall sampling procedure

In this section, we present details about how the overall sampling procedure proceeds and we use algorithm 8 in [14] to sample unique parameters. At every full iteration, we start from clustering subjects. Suppose currently we have k subject clusters for all I subjects.

• Step 1 Update cluster assignment: Use DP to reassign all I subjects into different clusters. Subject i will be assigned into one of the existing k clusters with some probability, or into one extra cluster with the remaining probability, i = 1, 2,⋯ , I, resulting in new cluster assignments such that all I subjects are re-distributed into new k* clusters.

• Step 2 Sampling unique parameters: Based on new assignments of all subjects, draw posterior samples of unique parameters θ_i·, i = 1, 2,⋯, k* (could be different from k). Information on subjects in cluster i is used for sampling θ_i·, i = 1, 2,⋯ k*.

• Step 3 Sampling common parameters: Draw posterior samples of common parameters.

• Step 4 Nested variables clustering: Within each subject cluster i, i = 1, 2,⋯ , k* concluded in Step 2, cluster variables as in Steps 1–3, but with subject index i replaced by variable index h.

• Step 5 Repeat Steps 1–4: One full iteration is finished. Go back to step 1 to start the next iteration.