Selective Influence and Sequential Operations: A Research Strategy for Visual Search

Abstract

We discuss the problem of elucidating mechanisms of visual search. We begin by considering the history, logic, and methods of relating behavioral or cognitive processes with neural processes. We then survey briefly the cognitive neurophysiology of visual search and essential aspects of the neural circuitry supporting this capacity. We introduce conceptually and empirically a powerful but underutilized experimental approach to dissect the cognitive processes supporting performance of a visual search task with factorial manipulations of singleton-distractor identifiability and stimulus-response cue discriminability. We show that systems factorial technology can distinguish processing architectures from the performance of macaque monkeys. This demonstration offers new opportunities to distinguish neural mechanisms through selective manipulation of visual encoding, search selection, rule encoding, and stimulus-response mapping.

INTRODUCTION

This introduction surveys the literature on visual search in the context of describing the underlying neuro-computational mechanisms and motivating a new experimental approach. To understand the neural mechanisms of visual search requires discovering the mapping between neural processes and visual, attention, and motor processes. Neural processes supporting visual search have been investigated in human studies using noninvasive measures of EEG and fMRI and in nonhuman primates using invasive sampling of neural discharges. Hence, to understand the neural mechanisms of visual search requires building a conceptual and empirical bridge between levels of explanation, neural measures, and species. This paper will situate the problem more definitely, briefly survey relevant performance and neural data, and introduce a program of research that can elucidate more specifically how neural circuits accomplish visual search.

Seeking to understand the relationship between neural and mental processes is hardly a new problem. For example, in 1865 Ernst Mach explained, “To every psychical there corresponds a physical, and conversely. Like psychical processes correspond to like physical, unlike to unlike. If a psychical process can be resolved, in a purely psychological manner, into a multiplicity of qualities, a, b, c, then to these there correspond an equal number of different physical processes, α, β, γ. Particulars of the physical correspond to all the particulars of the psychic.” (Boring, 1942). In 1970 Donald Davidson wrote, “… mental characteristics are in some sense dependent, or supervenient, on physical characteristics. Such supervenience might be taken to mean that there cannot be two events alike in all physical respects but differing in some mental respects, or that an object cannot alter in some mental respect without altering in some physical respect.” (Davidson 1970). These axioms frame cognitive neurophysiology research.

The relationship between mental and physical descriptions can be articulated through linking propositions that specify the nature of the mapping between particular behaviors or cognitive states and associated neural states (Brindley 1970; Teller & Pugh 1983; Teller 1984). Different kinds of linking propositions can be distinguished, e.g., identity, similarity, and analogy (Teller 1984). To illustrate, consider this linking proposition: the nerve impulse is an action potential. The nerve impulse is an event that caused muscle contraction after nerve irritation that was discovered by Galvani and characterized by Swammerdam (McComas 2011). Its speed was first measured by Helmholtz in 1850. The action potential (or nerve current) was first measured by du Bois-Reymond in 1848 and its ionic nature was first described by Bernstein and Lillie and elucidated by Hodgkin and Huxley. How do we know that the behavioral nerve impulse is the ionic action potential? This may seem obvious today, but it was not always. Indeed, the identity was established beyond doubt only by Huxley and Stämpfli (1949). They reported, “It was found that the muscle twitched when the nerve was stimulated if, but only if, the thread connecting the fluids on the two sides of the gap was in place. … This demonstrates that the transmission of the nervous impulse depends on currents flowing outside the myelin sheath…”

What linking propositions are necessary to explain how the brain does visual search? How should such linking propositions be articulated and tested? Adopting Marr’s hierarchy of computational theory, algorithm, and implementation, it seems clear that explaining how the brain does visual search requires translating between these levels of explanation. Several complementary and competing computational theories of visual search and attention have been formulated. These include the Theory of Visual Attention (Bundesen 1990), COntour DEtector (Logan 1996), Feature Gate (Cave 1999), and Guided Search (Wolfe et al. 1989; Wolfe 1994; Wolfe 2007; Wolfe et al. 2015). Other computational approaches are designed to solve pragmatic, real-world search problems (e.g., Itti & Koch 2000; Bruce et al. 2015). Some of these computational models have been articulated in terms of neural circuits at various levels of specificity from identification with specific brain structures and circuits (e.g., Bundesen et al. 2011; Schwemmer et al. 2015; Adeli et al. 2017; Murray et al. 2017) to microcircuitry of a cortical area (Heinzle et al. 2007) and with convolutional neural networks (e.g., Adeli & Zelinsky, 2018). Another approach has embedded neural signals measured during visual search performance into the stochastic accumulator framework (Purcell et al. 2010, 2012b).

These diverse computational and algorithmic approaches offer tools appropriate to translate between the neural and cognitive processes producing an observed pattern of performance. They serve another scientific function too. The literature on visual search and selective attention is governed by ambiguous and vague terms such as attention (both as cause and as effect), capacity, capture, disengage, efficiency, engage, map, priority, salience, selection, and shift. Formal models are needed to explain what these terms mean by identifying them with specific components, processes, or outputs.

Human and nonhuman primate visual search performance

Visual search has been investigated in many laboratories in many ways. Nevertheless, some general attributes have been established in human studies and replicated in macaque studies. The first key attribute is this: visual search takes time. A minimal amount of time is needed for visual encoding and response preparation. Not much more time is needed if the sought for object is easily discriminated from distracting objects, but progressively more time is needed if the distracting objects are more visually similar to the sought for target object and there are more such distracting objects (e.g, Treisman & Gelade 1980; Duncan & Humphreys 1989). Additional time may be taken if one of the non-target items is especially conspicuous (e.g., Theeuwes 1994; Bacon & Egeth 1994) or if the target item is in the same location as a previously attended target (Posner & Cohen 1984; Klein 2000). More time is needed if the response to the target object requires any kind of arbitrary mapping from stimulus location or property to response.

To investigate mechanisms of visual search at the neural circuit level requires systematic testing in nonhuman primates. For such studies to be relevant for understanding human performance, we must verify that nonhuman primates exhibit chronometric characteristics of search performance corresponding to humans. Fortunately, when sought, this confirmation has been found. Macaque monkeys exhibit dependence of visual search on target-distractor similarity and set size during singleton search (e.g., Azzato & Butter 1984; Buracas & Albright 1999; McPeek & Keller 2001; Sato et al. 2001; Arai et al. 2004; Camalier et al. 2007; Motter & Holsapple 2000, 2007; Balan et al. 2008; Song et al. 2008; Cohen et al. 2009; Nothdurft et al. 2009; Lee & McPeek 2013) and conjunction search (Motter & Belky 1998; Bichot & Schall 1999; Shen & Paré 2006). They can exhibit feature search asymmetries (Nakata et al. 2014). They can exhibit inhibition of return (Bichot & Schall, 2002; Fecteau & Munoz 2003; Torbaghan et al. 2012). Visual search is guided by memory as well as sensation. On the shortest time scale, performance of popout search varies if the search feature dimensions change (Malkovic & Nakayama, 1994). Called priming of popout, this demonstrated the limits of automaticity in visual search. Monkeys also exhibit priming of pop out (Bichot & Schall 2002; Purcell et al. 2012a). Macaque monkeys can also perform visual search filtering tasks that require search on one feature dimension and response according to another (Sato & Schall, 2003; Katnani & Gandhi 2013). Most recently, we have shown that monkeys also show contingent capture of attention by conspicuous non-target items (Cosman et al. 2018). Hence, macaque monkeys are a valid model of human visual search.

Nonhuman primate visual search neurophysiology

Establishing that macaque monkeys perform visual search like humans provides the opportunity to investigate at the neurophysiological level the various operations, processes, and stages supporting visual search. To orient the reader to this literature, we offer a selective survey of the neurophysiological correlates of visual search.

The first such studies were published by Chelazzi et al. (1993) in inferotemporal cortex and Schall and Hanes (1993) in frontal eye field. Both studies found that neurons that initially did not distinguish the target from distractors eventually came to discharge more spikes when the target relative to a distractor was in the response field. Subsequent studies across numerous laboratories have replicated and extended the original observations during visual search tasks in frontal eye field (Schall et al. 1995; Thompson et al. 1996, 1997; Bichot et al. 2001a,b, 2002; Sato & Schall 2003; Sato et al. 2001, 2003; Schall et al. 2004; Thompson et al. 2005a,b; Cohen et al., 2007; Monosov et al. 2008; Trageser et al. 2008; Woodman et al. 2008; Cohen et al. 2009; Murthy et al. 2009; Monosov & Thompson 2009; Phillips & Segraves 2010; Zhou & Desimone 2011; Heitz & Schall 2012; Purcell et al. 2013; Miller & Buschman 2013; Costello et al. 2013; Nelson et al. 2016; Ramkumar et al. 2016; Mirpour et al. 2018; Sapountzis et al. 2018), in other prefrontal regions (Hasegawa et al. 2000; Iba & Sawaguchi 2003; Bichot et al. 2015), in extrastriate visual areas like MT (Buracas & Albright 2009) and V4 (Motter 1994; Chelazzi et al. 2001; Mazer & Gallant 2003; Bichot et al. 2005; Ogawa & Komatsu 2006; Gee et al. 2010; Zhou & Desimone 2011; Ipata et al. 2012; Arcizet et al., 2018), as well as areas in the temporal lobe (Chelazzi et al. 1998; Mruczek & Sheinberg 2007a,b, 2012; Monosov et al. 2010) and the parietal lobe (Constantinidis & Steinmetz 2001; Ipata et al. 2006a,b; Thomas & Paré 2007; Balan et al. 2008; Ogawa & Komatsu 2009; Mirpour et al. 2009, 2010, 2013; Nishida et al. 2013, 2014; Steenrod et al. 2013; Tanaka et al. 2015; Meyers et al. 2017; Arcizet et al. 2018; Sapountzis et al., 2018) as well as subcortically in the superior colliculus (McPeek & Keller 2002; Shen & Paré 2007, 2014; Song & McPeek 2015; Lovejoy & Krauzlis 2017; White et al. 2009, 2017; Reppert et al. 2018), substantia nigra of the basal ganglia (Basso & Wurtz 2002), and central thalamus (Costello et al. 2016).

Viewing these diverse results with a goal of formulating a mechanistic model of visual search, we must appreciate that each of these cortical areas and subcortical structures is comprised of a diversity of neurons distinguished by morphology and connectivity. Only some of the neurons in these various neural loci contribute to visual search. The detailed connectivity of this network has yet to be worked out, but some results point toward nuances that will constrain such a mechanistic model. For example, different neurons in FEF project to V4 and to MT, and the two pools of neurons have different frontal lobe inputs (Ninomiya et al. 2012). Also, FEF is connected with at least 80 cortical areas (e.g. Schall et al. 1993, 1995b; Markov et al. 2014). Similarly, the superior colliculus receives inputs from effectively as many cortical areas (Fries 1984; Cerkevich et al. 2014). Crucially, pyramidal neurons in the cerebral cortex do not project to more than one cortical area (Markov et al. 2014). Likewise, pyramidal neurons in layer 5 that project to the superior colliculus do not also project to cortical areas (Pouget et al. 2009). Hence, if each pyramidal neuron projecting to a different target conveys a different signal, then a cortical area like FEF must have dozens of distinct types of pyramidal neurons. The extent of this functional variability has only recently been investigated quantitatively (Lowe and Schall 2018).

Research has demonstrated that different neurons support different operations. For example, the target selection process manifest by visually responsive neurons is distinct from saccade production. For example, in FEF the target selection process happens if no saccade to the target is made (Thompson et al. 1997; Thompson et al. 2005b) or if the endpoint of the saccade is not at the search target (Sato & Schall 2003; Murthy et al. 2009). Moreover, the target selection process does not automatically produce saccade preparation (Juan et al 2004; cf. Katnani and Gandhi 2013). Corrective saccades are produced by FEF (and related) movement neurons independent of state of the visual neurons (Murthy et al. 2007).

The claim that anatomically and functionally different populations of neurons accomplish visual search requires an explanation of the relationship between those populations. One approach was formalized in the Gated Accumulator Model (Purcell et al. 2010, 2012b). This model explains the relationship between visual target selection and saccade preparation by using the observed responses of FEF visual neurons as inputs to a network of accumulators. The salience evidence that is accumulated is just the spike trains recorded from visually responsive neurons in FEF. Accumulated variability in the firing rates of these neurons explains choice probabilities and the distributions of correct and error response times with search arrays of different set sizes if the accumulators are mutually inhibitory. The dynamics of the stochastic accumulators quantitatively predict the activity of presaccadic movement neurons that initiate eye movements if gating inhibition prevents accumulation before the representation of stimulus salience emerges. This formal modeling approach demonstrates the viability of combining neurophysiological data and computational models to identify neural substrates of visual attention and to formalize the otherwise vague concepts and terms listed above.

Human and nonhuman primate visual search electrophysiology

Establishing similarities between macaque and human measures of visual search is necessary to enable mapping between monkey neurophysiology and human cognition. We reviewed similarities of macaque and human performance above. Here, we briefly summarize another empirical bridge, recording event-related potentials in nonhuman primates to obtain measures parallel to those of human studies. First, the ERP signature known as contralateral delay activity has been measured in macaque monkeys (Reinhart et al. 2012), so the contribution of working memory in guiding search can be investigated with macaque monkeys in parallel to human studies (e.g., Woodman, Luck, and Schall 2007). Next, the allocation of visual attention during visual search is indexed by an event-related potential known as the N2pc (e.g., Luck & Hillyard 1994; Liesefeld et al. 2017; McCants et al. 2018). Also, the suppression of salient distractors is indexed by an event-related potential known as the Pd (e.g., Hickey et al. 2009; Sawaki & Luck 2010; Liesefeld et al. 2017). Previous research has confirmed that macaque monkeys manifest the N2pc (Woodman et al. 2007; Cohen et al. 2009; Heitz et al., 2010; Purcell et al., 2013). Recent work has also demonstrated monkeys manifest the Pd component associated with suppression of salient distractors (Cosman et al. 2018). The relationship of intracranial single-unit signals and extracranial EEG signals requires much further investigation, because for unknown reasons the neural events signaling search target location arise in FEF before the N2pc (Cohen et al. 2009). To understand these timing relationships, data from a likely generator of the N2pc, such as area V4, is needed (e.g., Hopf 2000).

Linking propositions through combined neural and mental chronometry

To claim that we understand the neural mechanisms of visual search, we will need to explain the neural processes that occupy the different amounts of time taken during visual search under various conditions. As visual search time increases, do a fixed number of neuro-computational processes just take longer? Or does an increase of visual search time happen because additional neuro-computational processes are inserted between encoding and responding? If additional processes are invoked, how do the multiple processes interact?

We believe that the answers to these questions will end with neurophysiological data, but they must begin with a clear appreciation of the psychological perspective on visual search and the history of response time models. A conceptually and historically foundational hypothesis posited that response time (RT) in complex tasks is the summation of functionally distinct stages (Donders 1868). This stage assumption is foundational to the predominant model of “decision-making”, which consists of a single stochastic sequential-sampling process following an uninteresting visual encoding stage and preceding a delayed response production stage (Ratcliff et al. 2016; Shadlen & Kiani 2013). Such models explain performance and account for neural activity in visual discrimination tasks as well as visual search with direct stimulus-response mapping (Purcell et al. 2010, 2012b). But, if RT is not comprised of dissociable stages, or if RT is comprised of multiple stochastic sequential-sampling processes, then models like drift diffusion seem disqualified. If that is so, then alternative models must be considered. One possibility is a cascade architecture in which multiple levels of processing are arranged serially with information continuously propagating from one level to the next (e.g., McClelland 1979). Another, intermediate possibility is known as asynchronous discrete flow in which the processing of multiple features is accomplished discretely, independently but in parallel and finishing at different times (Miller 1988). These qualitatively different mechanisms with aspects of simultaneity of processing have been overlooked in the canonical literature on the neural mechanisms of decision making.

Crucially, models with a single stochastic decision process cannot explain tasks that require multiple, sequential operations. Consider a visual search filtering task like the one used in this study. In the vernacular of this literature, accomplishing such a task requires a “decision” about the location of a color singleton, a “decision” about the shape of the singleton, a “decision” about the shapes of distractors, a “decision” about the congruency of the singleton and distractor shapes, a “decision” about the instructed stimulus-response mapping, a “decision” about the correct endpoint of the saccade, and a “decision” about when to initiate the saccade. This confusion can be eliminated by using the term “decision” to describe the deliberations and actions of agents but not to characterize particular neuro-computational processes (Schall 2001).

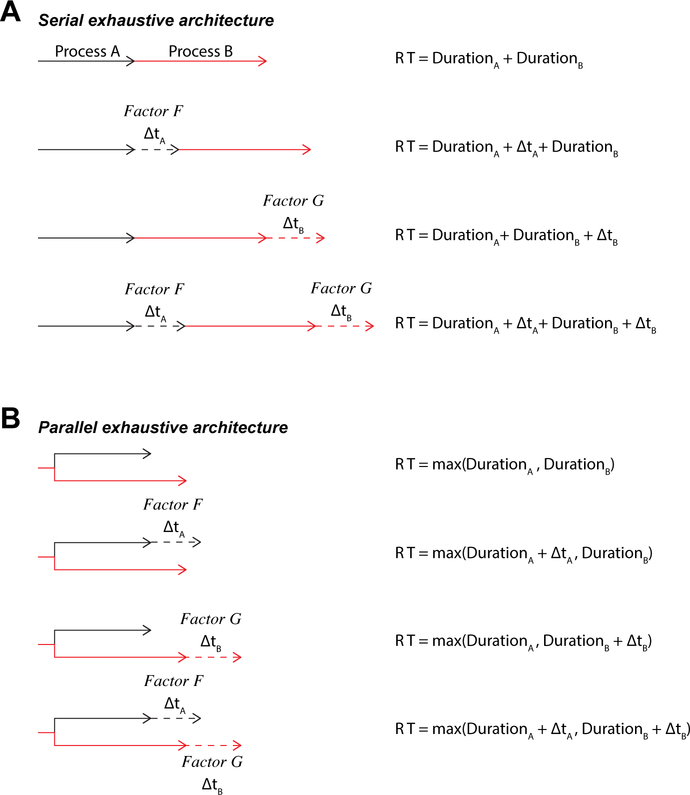
If neuro-computational modules are distinct and independent, then it should be possible to change one process without changing another. This idea underlies the logic of separate modifiability formulated by Saul Sternberg (1969, 2001). If mental modules are distinct and independent, then it should be possible to change one process without changing the other. The logical, mathematical, and statistical formulation developed by Sternberg specifies how to interpret the effects of specific causal manipulations on performance and neural measures. For example, if factors F (e.g, singleton-distractor identifiability) and G (stimulus-response cue discriminability) influence two sequential processes, A and B, selectively, then RT = Duration_A(F) + Duration_B(G). If A and B are distinct, sequential processes, then in an F x G factorial experiment, changes of RT over variation of F will be independent of changes of RT over variation of G (Figure 1). This approach has already revealed additivity and mutual invariance of singleton-distractor similarity and response interference in monkey cognitive neurophysiology studies (Mouret & Hasbrouq 2000; Sato et al. 2001) and human ERP studies (e.g., Osman et al. 1992; Smulders et al. 1995; Servant et al. 2015; see also Liesefeld 2018).

Figure 1.

Two alternative architectures for the interaction of two distinct processes. (A) Serial exhaustive architecture. Both processes must complete before a response can be initiated. The durations of the two stages of processing, A and B, are under the selective influence of factors, F and G. Mutual invariance is satisfied when manipulation of factor F (or G) alters the duration of stage A (or B) but not B (or A). Additivity is satisfied when the total RT equals the sum of the durations of the separate processes. (B) Parallel exhaustive architecture. The two processes operate concurrently but both must complete before a response can be initiated. Manipulation of factor F (or G) alters the duration of stage A (or B) but not B (or A). The variation of RT across the two manipulations is additive or under-additive.

Although this approach has proven effective, distinct and independent modules need not result in total additivity. If factors F and G selectively influence distinct but simultaneous processes, A and B, then RT < Duration_A(F) + Duration_B(G) (Figure 1). The literature is divided on how filtering tasks, like the one we used, are performed. The most common view is that selection and categorization of an object are separate sequential stages (Figure 1A) (e.g., Broadbent 1971; Hoffman, 1978; Treisman 1988; Wolfe et al. 2015). An alternative view is that objects are selected and categorized through parallel processes (Figure 1B) (e.g., Bundesen 1990; Logan 2002).

The fundamental problem of distinguishing serial from parallel processing has proven challenging because particular serial and parallel architectures can be mathematically indistinguishable (e.g, Townsend 1972, 1990). However, a mathematically rigorous approach to investigating alternative process architectures was developed by James Townsend and colleagues, known as systems factorial technology (Townsend & Nozawa, 1995; Houpt et al., 2014; Harding et al. 2016). Based on mathematical axioms, postulates, and theorems, systems factorial technology offers strong tests of alternative architectures. Under conditions of selective influence, distinct predictions about response time dynamics are made for serial and parallel models with different decision stopping rules. Through a series of specific analyses of response time distributions, systems factorial technology can discriminate between five types of information processing architectures that could accomplish a task. These are (1) serial self-terminating, (2) serial exhaustive, (3) parallel self-terminating, (4) parallel exhaustive, and (5) coactive. Of course, distinguishing serial from parallel processing in visual search has a long and some may say discouraging history (e.g., Treisman & Gelade 1980; Townsend 1990; see also Thornton & Gilden, 2007; Moran et al. 2016; Liesefeld & Müller 2019); yet, progress on this issue remains possible. Through systems factorial technology, when selective influence is applied effectively in visual search, predictions of serial and parallel models and their stopping rules are mathematically distinct and experimentally discriminable (Fifić et al. 2008b).

Prerequisites for linking neurophysiology and systems factorial technology

The integration of neurophysiology and systems factorial technology has three prerequisites: (1) the existence of distinct operations or stages that can be selectively influenced by experimental manipulations; (2) a factorial task design that selectively influences these distinct operations or stages; and (3) evidence that macaque monkeys can perform such a factorial experiment in a manner that can be analyzed by SFT. For perspective, prerequisites like this had to be satisfied when this laboratory began using the stop signal saccade countermanding task (Hanes & Schall 1995).

The first prerequisite has already been satisfied empirically. During cognitive neurophysiological experiments, RT can be divided into distinct processing stages during visual search (Thompson et al. 1996; cf. Costello et al. 2013). The singleton selection stage takes longer during less efficient search when the target is more similar to distractors (Sato et al. 2001). Saccade preparation is delayed in less efficient relative to more efficient visual search (Woodman et al. 2008). Requiring arbitrary stimulus-response mapping reveals more neuro-computational processes because it requires more operations that occupy different intervals including singleton selection, encoding the stimulus-response rule, and saccade endpoint selection (Sato and Schall 2003; Schall 2004).

Here, we present the second and third prerequisites. We have developed a filtering task that requires search on color and response on shape with factorial manipulations of singleton selection through singleton-distractor chromatic similarity and of stimulus-response mapping through stimulus elongation. We then provide the first demonstration that such tasks can be performed by macaque monkeys. We also show that performance can be analyzed using the methods of systems factorial technology producing results that support substantive inferences about the processing architectures underlying the performance. Importantly, the processing architectures discovered for two monkeys differed. We regard this as a positive indication about the utility of systems factorial technology to discriminate different strategies. Using the large datasets provided through cognitive testing of macaque monkeys, we addressed other questions that have not been possible using systems factorial technology with the smaller datasets typical of human studies. These include relating processing architecture to the quality of performance and to the production of error responses. These novel results establish a foundation for neurophysiological investigation using the logic of separate modifiability and the tools of systems factorial technology, which will provide unprecedented insights into the neuro-computational mechanisms of visual search.

METHODS

Subjects, surgical procedures, and gaze acquisition

All procedures were approved by the Vanderbilt Institutional Animal Care and Use Committee in accordance with the United States Department of Agriculture and Public Health Service Policy on Humane Care and Use of Laboratory Animals.

Behavioral data were collected from two macaque monkeys, Macaca mulatta and M. radiata, identified as Le and Da. The monkeys weighed approximately 12 kg (Le) and 8 kg (Da) and were aged 6 years (Le) and 12 years (Da) at the time of the study. Monkeys were surgically implanted with a headpost affixed to the skull via ceramic screws under aseptic conditions with isoflurane anesthesia. Antibiotics and analgesics were administered postoperatively. Monkeys were allowed at least 6 weeks to recover following surgery before being placed back on task. Gaze was tracked using an Eyelink 1000 system (SR Research; sampling rate = 1,000 Hz).

Task design and protocol

Monkeys performed 30 sessions of a go-nogo visual search task in which response was cued by the shape of a color singleton. Trials began with the monkey fixating a central stimulus for 800–1200 ms, after which eight iso-eccentric, isoluminant stimuli were presented with eccentricity = 6.0 deg. Stimuli were either square or rectangular. All eight stimuli had the same shape on each trial. If the singleton and distractors were square, cueing a no-go trial, monkeys were rewarded for maintaining fixation at the central spot for 1000 ms. No-go trials comprised ~20% of all trials in each session. If stimuli were rectangular, monkeys were rewarded for shifting gaze to the singleton and maintaining fixation for 800 ms (monkey Le) or 1000 ms (monkey Da). The inter-trial interval was fixed at 2 sec.

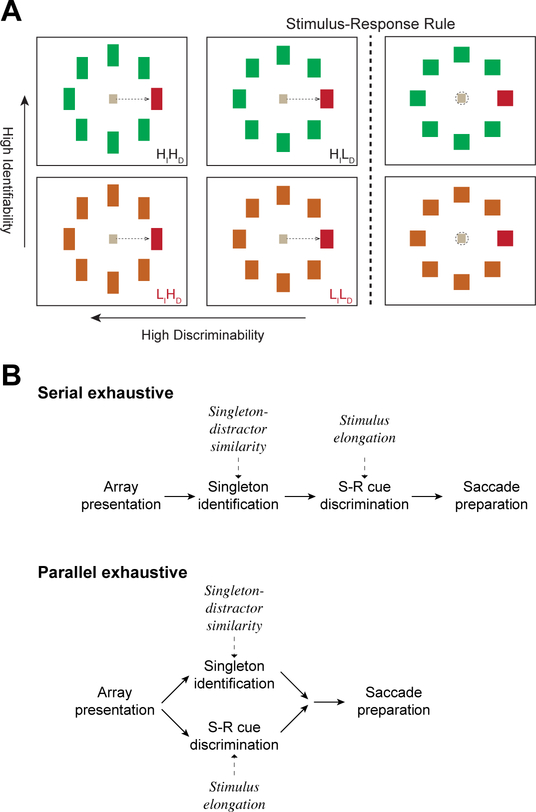
Task difficulty varied along two dimensions (Figure 2): singleton-distractor color similarity and stimulus elongation. Singleton-distractor color similarity manipulated singleton identifiability. Stimulus elongation manipulated cue discriminability. All stimuli had four possible colors: red (CIE x 628, y 338, Y 4.4 or x 604, y 339, Y 5.2), off-red (CIE x 552, y 399, Y 4.5 or x 520, y 405, Y 6.6), green (CIE x 280, y 610, Y 4.6 or x 292, y 575, Y 6.1), and off-green (CIE x 322, y 558, Y 4.6 or x 364, y 426, Y 6.8) presented on a gray background (CIE x 275, y 228, Y 0.54 or x 334, y 375, Y 0.6). Stimuli had three possible aspect ratios: square for nogo trials, and either 1.4 or 2.0 for go trials. The orientation of elongation was counterbalanced between the two monkeys; for monkey Da a vertical rectangle signaled go, whereas for monkey Le a horizontal rectangle signaled go.

Figure 2.

Visual search task designed to elucidate distinct operations. (A) Visual search task with go-nogo stimulus-response mapping. Six representative trial types are depicted. Correct gaze behavior is illustrated with dotted arrows for go trial saccades or dotted circle for nogo maintained fixation. The singleton is illustrated as always red and located on the right for purposes of illustration. Singleton shape cued the response rule. If the singleton was square (right), it cued withholding of the saccade. If the singleton was elongated (left and middle), it cued a pro-saccade. Two factors were manipulated independently. Stimulus-response cue discriminability was either High (aspect ratio = 2.0, H_Discrim or H_D) or Low (aspect ratio = 1.4, L_Discrim or L_D). On each trial, all distractors shared the degree of elongation with the color singleton. Singleton identifiability was either High (larger chromatic difference between singleton and distractors, H_Ident or H_I) or Low (smaller chromatic difference between singleton and distractors, L_Ident or L_I). The task offered 4 basic types of trials: High Identifiability and High Discriminability (H_IdentH_Discrim), Low Identifiability and High Discriminability (L_IdentH_Discrim), High Identifiability and Low Discriminability (H_IdentL_Discrim), and Low Identifiability and Low Discriminability (L_IdentL_Discrim). To assess the additivity and mutual invariance of these factors, trial types were interleaved in a 2×2 design. (B) Alternative processing architectures for the double factorial visual search task. Singleton identification is influenced by target-distractor similarity but not singleton elongation. Stimulus-response cue discrimination is affected by singleton elongation, but not target-distractor similarity. Under the serial exhaustive architecture (top), singleton identification is completed before cue discrimination, which must then be completed before production of the response. Under the parallel exhaustive architecture (bottom) singleton identification and cue discrimination operate concurrently and must both finish before production of the response.

Assessment of operations, stages and strategies

To assess alternative process architectures supporting performance of this task, we applied systems factorial technology (Townsend & Nozawa, 1995; Houpt et al., 2014; Harding et al. 2016). Statistical details of systems factorial technology and reporting conventions can be found in these references. Systems factorial technology typically requires a 2×2 manipulation of factors that selectively influence distinct processing operations (cf. Yang et al. 2014). As illustrated in Figure 2, the first manipulation was singleton identifiability through interleaved presentation of search arrays with low singleton-distractor similarity (e.g., red among green) (High Identifiability, H_Ident) and search arrays with high singleton-distractor similarity (e.g., red among off-red) (Low Identifiability, L_Ident). The second manipulation was cue discriminability through interleaved presentation of array items with higher aspect ratio (High Discriminability, H_Discrim.) and array items with lower aspect ratio (Low Discriminability, L_Discrim.). The cue discrimination was enforced by interleaving 20% nogo trials. This 2×2 design results in four types of trial. The easiest were High Identifiability with High Discriminability (H_IdentH_Discrim.). The most difficult were Low Identifiability with Low Discriminability (L_IdentL_Discrim). The two intermediate difficulty were Low Identifiability with High Discriminability (L_IdentH_Discrim) and High Identifiability with Low Discriminability (H_IdentL_Discrim).

Statistical analyses

All t-tests presented are two-sided, unless otherwise stated. ANOVA were calculated on across-session mean response times and accuracy rates. Also, to account for incidental variation across sessions while preserving relative relationships between conditions, ANOVA were repeated with per-session response times after subtracting the session mean from each response time (adjusted session means). To avoid edge effects, accuracy rates were transformed using the logit transformation (Wharton & Hui, 2011).

RESULTS

Each monkey performed 30 sessions of the search task. On average, Da performed 649 correct trials per session providing a total of 19470 correct trials, and Le performed 642 correct trials per session, providing a total of 19260 correct trials.

Monkeys are sensitive to cue discriminability and singleton identifiability

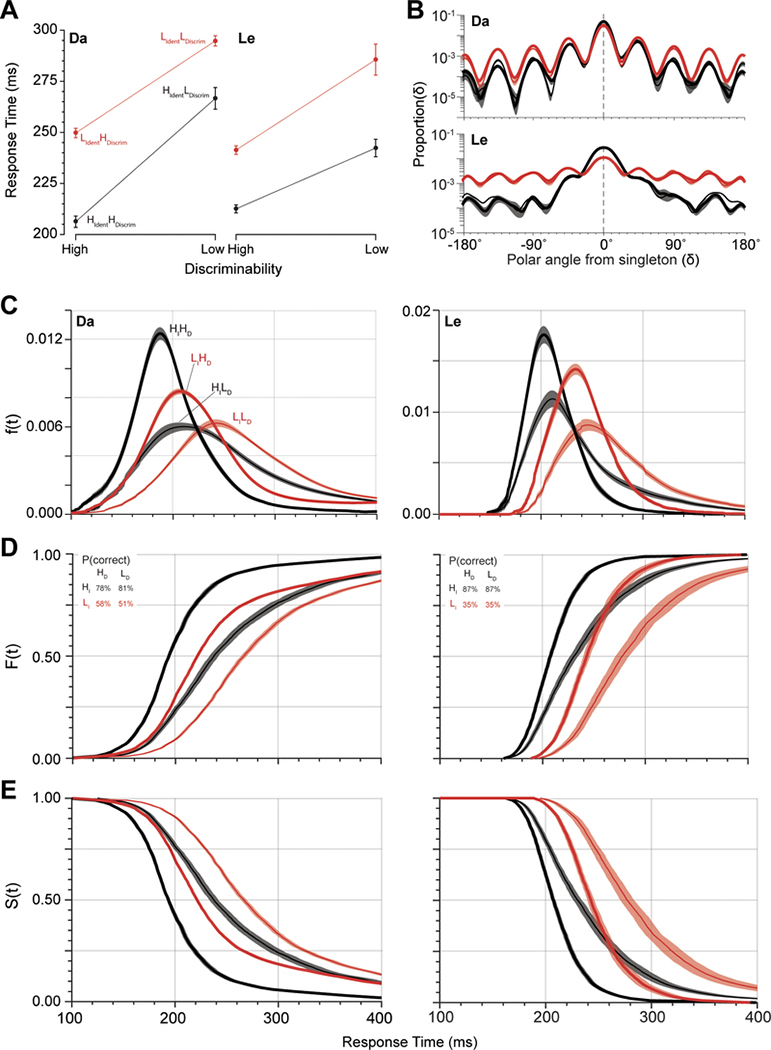
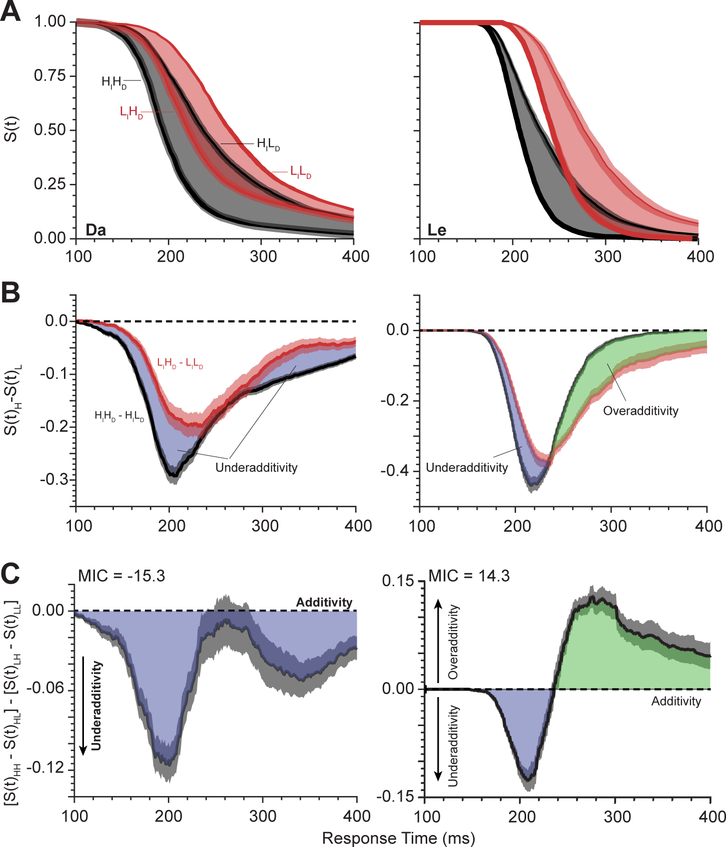
Response times (RT) of both monkeys were affected by both task manipulations. The RTs for each condition are plotted in Figure 3A and listed in Table 1. As expected, response times were longer for trials in which the singleton was more chromatically similar to distractors and thus harder to identify. Likewise, response times were longer when the cue was less discriminable. These differences were statistically significant when evaluated as simple session means or when accounting for variation in means across sessions (Table 1). In session means we found a significant interaction of the factors for monkey Da but not Le. In adjusted session mean values, the interaction was evident for both monkeys.

Figure 3.

Basic performance measures. (A) Mean RT ± SEM for each trial type of the double factorial paradigm. There were four trial types: H_IdentH_Discrim, H_IdentL_Discrim, L_IdentH_Discrim, and L_IdentL_Discrim Trials with High and Low singleton identifiability are shown in black and red, respectively. Monkey Da exhibited under-additivity of RT, whereas monkey Le exhibited over-additivity of RT across the two manipulations. (B) Log plot of the probability density of saccade endpoints relative to singleton location for High (black) and Low (red) singleton identifiability and High (bold) and Low (thin) cue discriminability. Spacing between search stimuli was 45° in polar angle. Both monkeys exhibited higher incidence of error saccades to the location adjacent to the singleton. Error bands are SE across sessions. (C) Probability density of RT, f(t). (D) Cumulative distribution of RT, F(t). Percent correct for each trial type is inset. (E) Survivor function of RT, S(t) = 1 – F(t).

TABLE 1.

Response time mean ± SD (ms) and associated ANOVA table.

Monkey Da					Session Mean
					Predictor	Sum of squares	df	Mean square	F	p
		Cue discrimiminability			Discriminability	83468.7	1	83468.7	234.6	0.000
		High	Low		Identifiability	38471.7	1	38471.7	108.1	0.000
Singleton identifiability	High	206 ± 15	266 ± 29		Discriminability x Identifiability	1754.7	1	1754.7	4.93	0.028
	Low	249 ± 13	295 ± 14		Error	41274	116	355.8
					Adjusted Session Mean
					Predictor	Sum of squares	df	Mean square	F	p
					Discriminability	83468.7	1	83468.7	535.1	0.000
					Identifiability	38471.7	1	38471.7	246.6	0.000
					Discriminability x Identifiability	1754.7	1	1754.7	11.25	0.001
					Error	18094.8	116	155.98966
Monkey Le					Session Mean
					Predictor	Sum of squares	df	Mean square	F	p
		Cue discriminability			Discriminability	41155	1	41155	65.28	0.000
		High	Low		Identifiability	38966.6	1	38966.6	61.81	0.000
Singleton identifiability	High	213 ± 11	242 ± 23		Discriminability x Identifiability	1577.8	1	1577.8	2.5	0.116
	Low	241 ± 11	286 ± 42		Error	73131.6	116	630.4
					Adjusted Session Mean
					Predictor	Sum of squares	df	Mean square	F	p
					Discriminability	41155	1	41155	170.2	0.000
					Identifiability	38966.6	1	38966.6	161.1	0.000
					Discriminability x Identifiability	1577.8	1	1577.8	6.52	0.012
					Error	28054.8	116	241.85172

The endpoints of errant saccades were not distributed randomly and were thus informative. Both monkeys made false alarm saccades toward the color singleton when it was a square (Da: 11.5 ± 5.2% H_Ident, 11.3 ± 3.3% L_Ident; Le: 26.7 ± 15.0% H_Ident, 7.2 ± 7.1% L_Ident). This demonstrates that squares and the less elongated rectangles were sufficiently similar to invoke cue discriminability confusion.

Saccade endpoint was affected more by singleton identifiability than by shape discriminability (Figure 3B, Table 2). As expected, accuracy was significantly higher under high identifiability relative to low identifiability for both monkeys. However, the effect of cue discriminability on saccade endpoint accuracy was different for the two monkeys. Monkey Le was equally accurate when stimulus shape was more or less discriminable. Curiously, monkey Da was more accurate when stimulus shape was less discriminable. Finally, as observed previously (e.g., Findlay 1997), on error trials both monkeys more commonly shifted gaze to a distractor adjacent to the color singleton (Figure 3B).

TABLE 2.

Percent correct mean ± SD (%) and associated ANOVA table.

Monkey Da				Logit Transformation
				Predictor	Sum of squares	df	Mean square	F	p
		Cue discrimiminability		Discriminability	1.2597	1	1.2597	9.25	0.000
		High	Low	Identifiability	42.9175	1	42.9175	315.26	0.003
Singleton identifiability	High	78.3 ± 4.4	80.6 ± 4.2	Discriminability x Identifiability	0.1234	1	0.1234	91	0.343
	Low	51.2 ± 10.0	57.6 ± 11.4	Error	15.7915	116	0.1361
Monkey Le				Logit Transformation
				Predictor	Sum of squares	df	Mean square	F	p
		Cue discriminability		Discriminability	0.009	1	556.1	0.04	0.850
		High	Low	Identifiability	209.5	1	0.04	843.65	0.000
Singleton identifiability	High	87.2 ± 5.4	86.9 ± 5.6	Discriminability x Identifiability	0	1	< 0.001	< 0.001	0.968
	Low	35.1 ± 7.2	35.5 ± 10.0	Error	28.813	116	66.6

The average trends are commonly all that is reported. However, the approach we will use begins with recognizing that singleton identifiability and cue discriminability influenced the shape of the RT distributions. To prepare for the systems factorial analysis, we illustrate the variation of the RT distributions in three formats. The first is the simple probability density (f(t) = Prob(t < RT < t+Δt)), which is the probability of a response at a given time (Figure 3C). The second is the cumulative distribution (F(t) = ∫f(t)dt = Prob(RT≤t)), which is the probability of a response being produced at a time less than or equal to t (Figure 3D). The third is the survivor function (S(t) = Prob(RT > t) = 1 – F(t)), which is the probability that a response has not yet been produced by time t (Figure 3E). The influence of both factors on the shape of these distributions is clear for both monkeys. However, much deeper computational insights are available through the next analytical steps.

Systems factorial technology-based assessment of visual search performance

Systems factorial technology is used to assess processing stage architecture and performance strategy by analyzing the RT distributions of each condition within a 2×2 factorial design (Townsend and Nozawa 1995; Houpt and Townsend 2010; Houpt et al. 2014; Harding et al. 2016). Given that each factor (singleton identifiability and cue discriminability) affected RT, we assessed the manner in which one factor affected RT while the other factor was fixed. In other words, how stimulus shape affects RT on trials with dissimilar singleton and distractors may or may not be the same as how shape affects RT on trials with similar singleton and distractors.

To illustrate the rationale and implementation of systems factorial technology, we performed a system of simple simulations (Figure 4). The 5 alternative architectures were simulated with pairs of linear accumulators embodying two processes, designated A and B (Carpenter & Williams 1995; Brown & Heathcote, 2008). The finishing times of the accumulators were determined by four parameters: threshold, drift rate, drift rate variability, and non-decision time. To simplify, both accumulators shared an equivalent arbitrary threshold and a non-decision time of zero. An arbitrary mean drift rate was assigned for the more efficient condition of each factor, and a slower drift rate was assigned for the less efficient condition of each factor. Each manipulation was also assigned identical drift rate variability. For the combined manipulation, the drift rate effects were added. Each replicate for each condition had a drift rate sampled from a normal distribution centered on the assigned mean drift rate and with a standard deviation of the assigned drift rate variability. The parameters of each simulation were adjusted to produce similar ranges of RT. The resultant process durations were assessed by 10000 random samples defined by each manipulation’s drift rate parameterization.

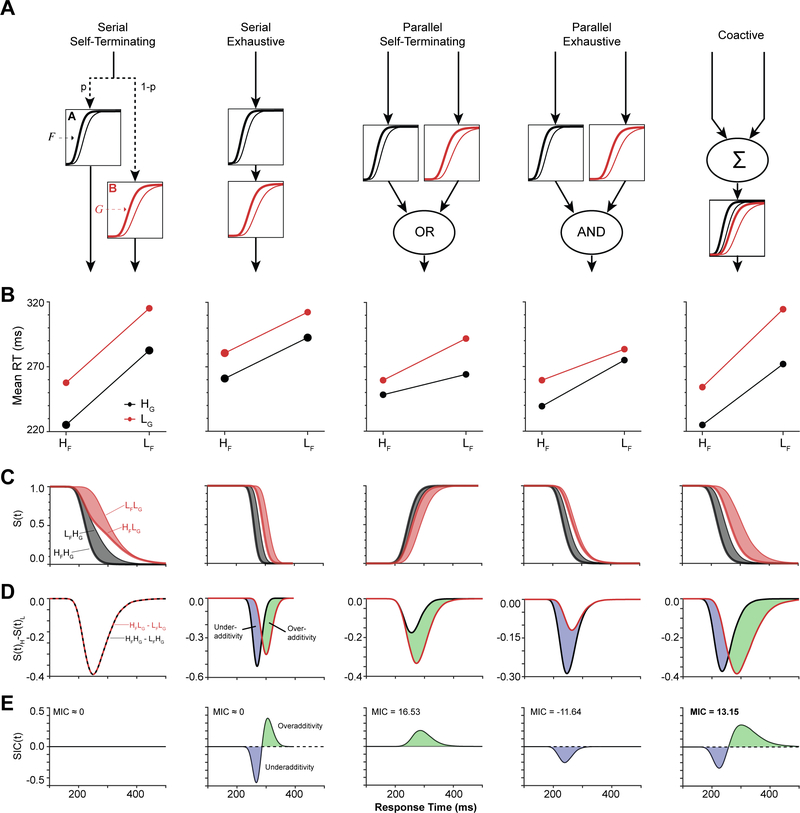
Figure 4.

Systems factorial technology simulations. (A) Each of five processing architectures were modeled using two simple linear accumulator models, each representing an independent operation or stage. The two operations, A and B, were assumed to be under the selective influence of Factors F and G. Stage A varied with Factor F (but not G), and Stage B varied with Factor G (but not F). Essential features of each architecture are shown with depictions of relative stage durations. (B) Mean interaction contrast. Plots of mean RT for each trial type of the double factorial setup. Lines in red and black refer to Low and High levels of Factor G. (C) Survivor function S(t) for each trial type. The gray and red shadings highlight the effects of Factor F on S(t) at fixed levels of Factor G. (D) Difference in survivor function S(t) for fixed levels of Factor G. Regions of blue and green denote intervals of underadditivity and overadditivity, respectively. (E) Survivor interaction contrast S(t). The serial self-terminating architecture produced a SIC that did not differ from 0.0 for all time. The serial exhaustive architecture produced a SIC that deviated to under-additivity followed by over-additivity, with equal area under each region. The parallel self-terminating architecture produced a SIC with overadditivity. The parallel exhaustive architecture produced a SIC with underadditivity. The coactive architecture produced a SIC that deviated to underadditivity followed by overadditivity, with greater area under the overadditive region for net overadditivity.

We explore the influence of two factors, designated F and G, either of which can cause higher (H) or lower (L) efficiency. For example, factor F could be identified with singleton-distractor similarity that influences the duration of singleton identification (process A), and factor G could be identified with singleton elongation that influences the duration of response cue discrimination (process B). Importantly, depending on task demands not all processing architectures are candidates for task performance. For example, if a response is specified by a conjunction of two features, self-terminating architectures will result in high error rates. Conversely, if a response can be determined from a single source of information and not necessarily both, exhaustive architectures will result in inefficient performance. Nevertheless, because no particular task is being modeled in these simulations, SFT can be applied to simulated outcomes produced by all 5 architectures. We present these simulations to aid in conceptualizing the differences in the architecture details and in recognizing how the signatures of each architecture are produced. We now present the 5 possible processing architectures resolved by SFT.

Consider first processes A and B as serial self-terminating processes (Figure 4A). The two processes are queued sequentially, but only one needs to be completed for the overt response to be produced. Formally, the order of sub-processes is unknown and random. The two levels of factor F result in two distributions of process finishing times that overlap but have different modal values. Similarly, the two levels of factor G result in two distributions of finishing times that overlap but have different modal values. In this architecture, RT on each trial corresponds to the finishing time of the fastest process. Of course, process A or B might finish first on a given trial, but on average the systematic variation of RT will depend on the influence of the respective factors on each process. Crucially, under this architecture the influence of each factor on each process is independent. This results in mutually invariant, additive differences in average RT (<RT>) of both processes across both factors. In other words, a plot of average RT produced for each combination of the 2×2 design will produce parallel relations with no interaction across factors. The nature of the interaction across factors can be summarized by a value known as the Mean Interaction Contrast (MIC), which is calculated as

$$\mathrm{MIC}=\left(<\mathrm{RT}{>}_{\mathrm{HH}}-<\mathrm{RT}{>}_{\mathrm{HL}}\right)–\left(<\mathrm{RT}{>}_{\mathrm{LH}}-<\mathrm{RT}{>}_{\mathrm{LL}}\right).$$

In this formula <RT>_HH is the mean RT on trials with both factors allowing high efficiency for their respective processes, which tends to make it the smallest value. In comparison, <RT>_LL is the mean RT on trials with both factors allowing low efficiency for their respective processes, which tends to make it the largest value. Likewise, <RT>_HL and <RT>_LH are the mean RT on trials with one factor allowing high efficiency for its process with the other factor allowing only low efficiency for its process, which tends to make these intermediate values.

For the serial self-terminating processes, MIC = 0, which indicates perfect additivity of the underlying processes. Non-zero values of MIC signify an interaction among the processes. Such an interaction can be underadditive (MIC < 0) or overadditive (MIC > 0). MIC > 0 identifies either parallel self-terminating or coactive process architectures, and MIC < 0 identifies parallel exhaustive processes. Thus, the MIC offers some insight into the nature of the interaction between sub-processes. However, MIC cannot discriminate between the self-terminating or exhaustive stopping rules for serial architectures or discriminate between coactive and parallel self-terminating architectures (Townsend and Nozawa 1995).

Further insight is available through examination of the production of responses through time across conditions. The effects of the combination of conditions can be assessed as a function of time over the production of the responses by measuring the difference of the survivor functions. The justification and rationale for this approach is detailed by Townsend and colleagues (Townsend and Nozawa 1995; Houpt and Townsend 2010; Houpt et al. 2014). The purpose of the analysis is to determine the extent to which the two levels of each factor influence the rate of response production through time. This is quantified by measuring the difference between response production when one factor is highly efficient (H_F) and when it is less efficient (L_F), while the other factor is more (H_G) or less (L_G) efficient.

The interaction between the two manipulations is known as the survivor interaction contrast (SIC). The SIC is a distribution-free measure for assessing the architecture (i.e., serial or parallel) and stopping rule (i.e., race minimum time or exhaustive maximum time) of information processing, which indexes the difference in levels of G between the levels of F, is calculated similar to the MIC by subtracting the two resulting difference functions over time:

$$\mathrm{SIC}\left(\mathrm{t}\right)=\left[{\mathrm{S}}_{\mathrm{HH}}\left(\mathrm{t}\right)–{\mathrm{S}}_{\mathrm{HL}}\left(\mathrm{t}\right)\right]–\left[{\mathrm{S}}_{\mathrm{LH}}\left(\mathrm{t}\right)–{\mathrm{S}}_{\mathrm{LL}}\left(\mathrm{t}\right)\right]$$

where S_HH(t) is the value of the survivor function at time t when both factors are more efficient (H_FH_G), S_LL(t) is the value of the survivor function at time t when both factors are less efficient (L_FL_G), S_HL(t) is the value of the survivor function at time t when factor F is more efficient and factor G is less efficient (H_FL_G), and S_LH(t) is the value of the survivor function at time t when factor F is less efficient and factor G is more efficient (L_FH_G). These operations are commutative thus the effect of varying G with respect to varying F is expected to be equivalent. The SIC measures the interaction contrast throughout the duration of all processes. The basic concepts of additivity, underadditivity, and overadditivity apply to the SIC; they just apply through time. Under the assumptions of systems factorial technology (e.g., stochastic independence of the processes), the form of SIC(t) is diagnostic of the 5 processing architectures. The statistical issues involved in evaluating SIC curves have been detailed (Houpt and Townsend 2010).

The purely additive influence of factors in the serial self-terminating architecture result in SIC values that do not vary over time. However, the SIC produced by the other 4 architectures varies through time, each producing a different pattern of variation. Accordingly, the pattern of variation of the SIC curves can diagnose which underlying architecture produced a given pattern of RTs in the 2×2 factorial experimental design.

Consider next the serial exhaustive architecture. The processes are queued sequentially and the overt response is produced only when both processes have finished. Formally, the order of processes is unknown and SFT is unable to identify which one acted first. The mean RTs across factors exhibit no sign of interaction, so the MIC = 0 for this architecture as well. However, through time this architecture produces first underadditivity then overadditivity. That is, the SIC exhibits a negative-going followed by a positive-going deflection. Importantly, to satisfy the requirement that MIC = 0, the areas under the negative-going and positive-going deflections are equivalent. This time varying SIC is then used to resolve ambiguities when MIC = 0.

Consider next the parallel self-terminating architecture. Both processes operate simultaneously, so a stopping rule must be specified. Specifically, if a response can be made when one stage is complete, then the combined process is parallel self-terminating. In this architecture, the overt response is produced as soon as either process finishes. This architecture is also known as a race and predicts overadditivity. Thus, MIC > 0, and the SIC curve deviates only positively.

Consider next the parallel exhaustive architecture in which a response can only be made when both stages are complete. Both processes operate simultaneously, but the overt response is produced only after both processes have finished. This architecture predicts underadditivity. Thus, MIC < 0, and the SIC curve deviates only negatively. The performance of one of the monkeys will have this appearance.

Consider finally the coactive architecture. While more complex and less explicit in form, it can be distinguished in function through these methods. In this architecture processes interact in a manner that can be characterized as finer grain coordination such as summation of the respective states through time. This can be realized if neither of the two processes A nor B produce the overt response but instead provide activations to a third process that sums the activations from A and B and thereby produces the overt response. This architecture, like a serial exhaustive architecture, predicts first underadditivity and then overadditivity. However, unlike a serial exhaustive architecture, for the co-active architecture, MIC > 0. Therefore, the area under the positive-going, over-additive deflection is greater than the area under the negative-going under-additive deflection and the architecture predicts a net overadditivity. Accordingly, although this architecture has an initial negative dip and a positive deflection (like serial processing) and has an MIC greater than 0 (like parallel self-terminating), the combination of SIC and MIC differentiates it from either of these other architectures. The performance of another monkey will have this appearance.

Processing architectures supporting visual search

We applied systems factorial technology to the visual search data obtained from two macaque monkeys. Figure 5A presents mean survivor functions for each level of the 2×2 factorial design for each monkey. At a fixed level of singleton identifiability, the difference between survivor functions represents the effect of shape discriminability. Figure 5B plots the difference in survivor functions for each level of singleton identifiability. The shape of these differences reveals the effect of the separate factors on response production through time. Figure 5C plots the difference of these differences, which is the survivor interaction contrast (SIC). The SIC summarizes the influence of the two factors through time. We will report SIC results by first describing the shape of the curve, then reporting the MIC, then reporting the inferred architecture.

Figure 5.

Systems factorial analysis of RT distributions from the double factorial visual search task. (A) Survivor functions S(t) for each combination of singleton identifiability and cue discriminability. Black and red lines depict High and Low singleton identifiability. Thick and thin lines depict High and Low cue discriminability. The difference between survivor functions for High and Low cue discriminability is shaded in black (High singleton identifiability) and red (Low singleton identifiability). (B) Difference between survivor functions for High and Low cue discriminability, computed at fixed levels of singleton identifiability. Shaded regions represent period of underadditivity (blue) and overadditivity (green) for Low (red) and High (black) singleton identifiability. Error regions are SE across sessions. (C) Survivor interaction contrast curves. The SIC curve for monkey Da was exclusively sub-additive, consistent with the parallel exhaustive architecture. The SIC curve for monkey Le exhibited a change from under- to over-additivity, consistent with the parallel coactive architecture.

For monkey Le, the SIC exhibited a pronounced period of underadditivity followed by a prolonged period of overadditivity. The integral of the period of overadditivity exceeded that of the underadditivity, indicative of a positive mean interaction contrast (MIC = 14.3). This outcome is characteristic of the coactive processing architecture (Figure 4, fifth architecture).

For monkey Da, the SIC exhibited only a prolonged underadditive deflection with MIC = −15.3. This outcome is characteristic of the parallel exhaustive architecture (Figure 4, fourth architecture). Note that neither monkey exhibited a self-terminating architecture. This is reassuring because a correct response requires both singleton identification and cue discrimination. Either serial or parallel self-terminating architectures would produce a response with only half of the necessary information and thus nearly chance performance.

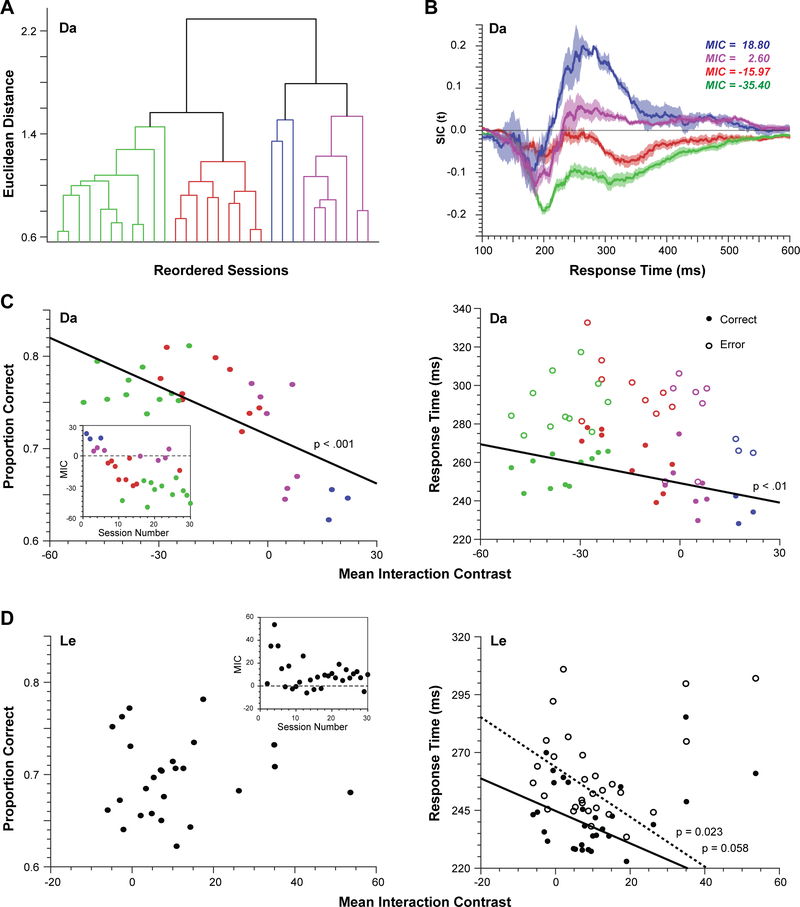
SFT analyses are typically performed on a per-subject basis rather than the present repeated testing across many sessions that can be done with monkeys. Thus, it is possible that the performance strategy associated with different processing architectures or dynamics varies across sessions. If so, then the multiphasic SIC curves could be artifacts of averaging sessions performed with different strategies. To assess whether the average SIC curve is a mixture of multiple architectures across different sessions, we performed a hierarchical agglomerative cluster analysis of SIC curves. We contrasted the use of Euclidean distance, which emphasizes the magnitudes of the SIC curves, and correlation distance, which emphasizes the shapes of the SIC curves, as similarity metrics.

For monkey Da, using Euclidean distance as the similarity metric, we identified four clusters (Figure 6A). Using correlation distance as a similarity metric was less discriminating. We believe this indicates that the major differences in SIC are in magnitude rather than shape. To examine the systematic variability across sessions, we plotted the SIC for each cluster (Figure 6B). With MIC > 0 and a later overadditive deflection exceeding the early underadditive deflection of the SIC, two of the clusters identified the coactive architecture. With MIC < 0 and only underadditive SIC deflections, the other two clusters identified the parallel exhaustive architecture. Notably, the biphasic SIC was evident in individual clusters. Even the most clearly underadditive SIC cluster had bimodal characteristics.

Figure 6.

Variation of performance across sessions. (A) Dendrogram resulting from clustering of SIC curves across sessions for monkey Da based on Euclidean distance. Four clusters were evident, suggesting the use of different strategies. (B) Form of the four clusters of SIC curves. Two (blue, magenta) corresponded to the co-active architecture, and two (red, green) were unlike the SIC of any architecture. (C) (left) Proportion correct as a function of MIC across sessions for monkey Da. A strong correlation was observed. MIC across session number inset. Points are colored in accordance with their cluster identity. (right) Mean RT for correct (filled) and error (open) trials as a function of MIC across sessions. Error RT were longer than correct RT, and a strong correlation with MIC was observed for correct but not error RT. (D) (left) Proportion correct as a function of MIC across sessions for monkey Le. MIC across session number inset. A significant correlation was not observed. (right) Mean RT for correct (filled) and error (open) trials as a function of MIC across sessions. Error RT were longer than correct RT, and a correlation with MIC was observed for error RT and a trend toward correlation with MIC was observed for correct RT.

For monkey Le, neither Euclidean nor correlation distance yielded distinct clusters. The coactive architecture was identified by the MIC values and SIC forms from each session, although MIC magnitude varied across sessions.

The variation in MIC values across sessions offers a unique opportunity to assess whether qualitative or quantitiative differences in processing strategies result in predictable differences in performance. Hence, we examined the relationship between the per-session MIC, accuracy and response times (Figure 6C). For monkey Da, we found a significant negative correlation between percent correct and MIC (r = −0.69, p < 0.001). We also found a significant negative correlation between RT of correct responses and MIC (r = −0.49, p < 0.01). However, we found no relationship between MIC and RT on error trials (r = −0.30, p = 0.11).

For monkey Le, some early sessions had MICs much greater than the majority of sessions. Treating these as outliers, we found no relationship between percent correct and MIC (r = −0.21, p = 0.32), but RT and MIC trended toward a significant negative correlation for correct RTs (r = −0.38, p = 0.058) and were significantly negatively correlated for error trials (r = −0.45, p = −0.022). Relationships like these have not been reported before.

Processing architectures for correct and error performance

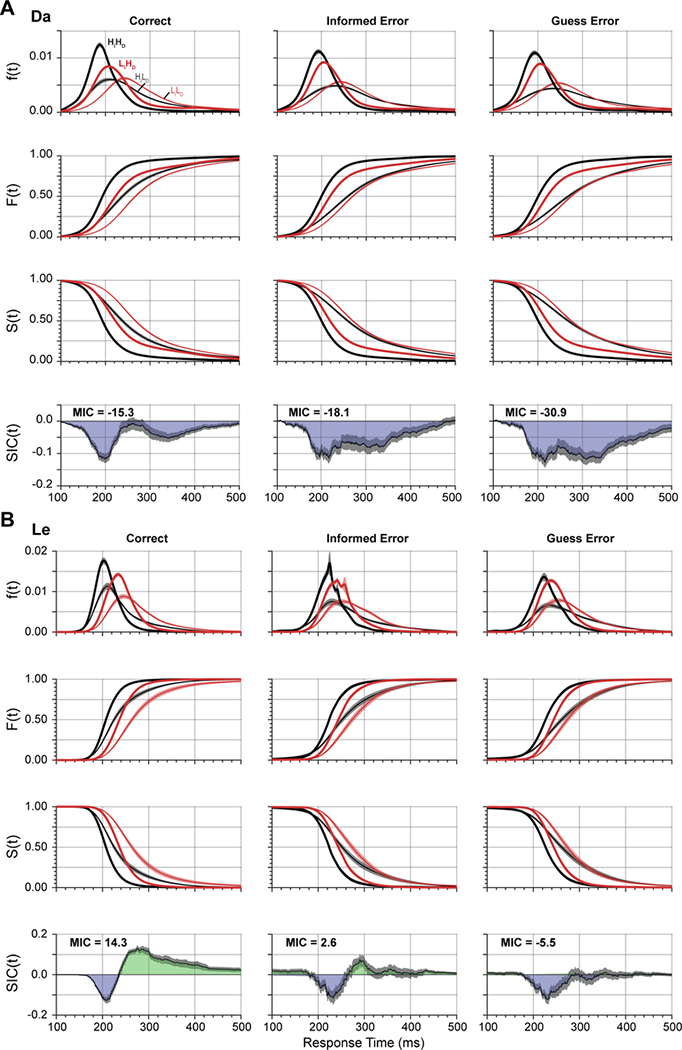
SFT analyses commonly assume a low error rate (Townsend and Nozawa 1995). The performance of our monkeys had relatively high error rates. However, other investigators have demonstrated that conclusions from SFT are reliable in spite of error rates approximating what we obtained (Fifić et al. 2008a). We utilized the large amount of data obtained across sessions to investigate for the first time whether performance strategies differed between correct trials and errors. Given the prevalence of erroneous saccades to the distractor adjacent to the singleton, we distinguished two categories of errors. First, we will examine informed errors made to the stimulus adjacent to the singleton. Second, we will examine guess errors made to any other location.

Figure 7 illustrates the progression of distributions used for the SFT analysis for correct responses, informed errors, and guesses for both monkeys. The factorial manipulation trial types were assigned according to the configuration of the search array and not saccade endpoint. That is, H_I, L_I, H_D, and L_D were assigned with respect to the identifiability and discriminability of the singleton.

Figure 7.

SFT analysis for different trial outcomes. (A) SIC curves derived from monkey Da performance on correct (left), informed errors adjacent to the singleton (middle) and guess errors (right). SIC curves for informed and guess errors exhibit more underadditivity relative to correct trials. All three SIC curves resemble that of the parallel exhaustive architecture. (B) SIC curves derived from monkey Le performance on correct (left), informed errors adjacent to the singleton (middle) and guess errors (right). SIC curves for errors exhibit more underadditivity (less overadditivity) relative to correct trials. The SIC curve for guess errors resembles the parallel exhaustive architecture, for informed errors, the serial exhaustive architecture, and for correct trials, the coactive architecture.

For monkey Da, both informed errors and guesses were generated with SIC deflecting only in the underadditive direction (MIC < 0), like the correct responses. Hence, like correct responses, errors were identified with the parallel exhaustive architecture. In other words, qualitatively a single architecture produced both correct and error responses. However, quantitatively, MIC for guesses was more underadditive than MIC for informed errors, which was more underadditive than MIC for correct responses. Also, the SIC for error responses was prolonged but lacked the pronounced multiphasic pattern obtained from correct trials. Thus, the evidence suggested that monkey Da employed similar architectures on both error and correct trials.

For monkey Le, we observed qualitative variation in MIC and SIC for error relative to correct trials. As noted, correct trial performance produced MIC and SIC values that identified the coactive architecture. However, for guess errors, the SIC deviated only in the underadditive direction (MIC < 0), which identify the parallel exhaustive architecture. Meanwhile, for the informed errors, the SIC deflected more in the under- than overadditive direction (MIC slightly greater than zero). This pattern seems to approximate at least the parallel exhaustive architecture. Thus, for monkey Le, errors may originate from a processing architecture different from that resulting in correct trials.

For both monkeys, although their overall SIC curves have different shapes, the MIC for correct responses (Da: MIC = −15.3; Le: MIC = 14.3) was more positive than the MIC for informed errors (Da: MIC = −18.1; Le: MIC = 2.6), which was more positive than the MIC for guess errors (Da: MIC = −30.8; Le: MIC = −5.5). It should be noted that for both monkeys this difference appears most pronounced around the time of the second negative peak in Da’s biphasic SIC curve.

DISCUSSION

Through the present results, we have demonstrated the ability of monkeys to perform a speeded response task with 2×2 factorial manipulations of difficulty. To our knowledge, this is a first application of this experimental design in nonhuman primate research. We have also demonstrated the utility of systems factorial technology in assessing behavioral responses to infer underlying processing architectures. These findings pave the way for developing studies in monkeys that are directly comparable to studies in humans and to extend investigation to the neurophysiology producing the performance. We discuss two potential limitations of these current results: inter-monkey differences and error-prone performance. We conclude that neither of these considerations undermines the utility of this new experimental approach for nonhuman primate cognitive neurophysiology. In fact, the inter-monkey differences highlight the utility of systems factorial technology in diagnosing visual search strategy. We then situate this work in the context of related research using other approaches.

Individual differences between monkeys

We identified a plausible processing architecture for both monkeys. Technically, it should be noted that the approach could have resulted in implausible architectures. Interestingly, the results differed, indicating that the two monkeys used different strategies. While such lack of replication invites further research with more subjects, we believe useful insights are still available for two reasons. First, although both monkeys showed the same main effects of the factorial manipulations, subtle differences in RT distributions were evident across monkeys. However, in and of themselves, these differences offer no insights into the source of those differences. The use of systems factorial technology provided distinctively different results for both monkeys. This outcome offers additional inferences about the mechanisms producing the RT distributions.

Second, these different inferences provide starkly contrasting predictions for the neurophysiological underpinnings of this behavior. For example, for monkey Da, whose RT distributions suggest a parallel exhaustive processing architecture, separate populations of neurons may carry signals related to singleton identifiability or cue discriminability. In contrast, for monkey Le, whose RT distributions suggest a coactive processing architecture, one population of neurons may carry signals related to singleton identifiability and cue discriminability. These are just two of multiple alternatives that can be formulated but are beyond the scope of this paper. Further insights are available through quantifying the degree and timing of saccade preparation assessed through the activity of movement neurons (e.g., Hanes and Schall 1996; Bichot et al. 2001a; Woodman et al. 2008).

The differences across monkeys could be due to one of two differences in the task. First, the two monkeys were required to fixate the search stimuli for different amounts of time. We doubt that this modest difference in fixation duration can explain the major difference in strategy. Because the fixation interval follows both array presentation and response time and are identical for all go-trial conditions, we do not see a mechanism by which this post-response fixation interval would affect the processing of the array during the trial. Still, further research can verify this supposition. Second, the elongated stimuli seen by Da were vertical whereas those seen by Le were horizontal. The orientations of the stimuli result in different edge-to-edge distances of stimulus pairs which may influence stimulus salience. We doubt that stimulus shape explains the difference in strategy. This rotation of the stimuli would be balanced across the two monkeys, where the edge-to-edge distance of the stimuli on the left and right for monkey Da would be the same as the edge-to-edge distance of the stimuli on the top and bottom for monkey Le. Similarly, the stimuli on the top and bottom for Da have the same edge-to-edge distance as the stimuli on the left and right for Da. If this did explain the difference in processing architectures, then these stimulus location sets (Da: left/right, Le: top/bottom and Da: top/bottom, Le: left/right) should also be systematically different. We have compared results across these stimulus configurations and found no differences. Therefore, differences in array configuration cannot explain the differences in inferred processing architectures.

Further, the dissociation between parallel exhaustive and coactive architectures has been described previously. Fifić and colleagues (2008a) had human participants perform a multidimensional classification task for stimuli with dimensions that were either separable or integral. Performance during classification of separable-dimension stimuli was marked by the use of a parallel exhaustive architecture whereas performance during classification of integral-dimension stimuli was marked by the use of a coactive architecture. This performance strategy difference, revealed only through systems factorial technology, resembles the performance strategy difference identified here. Because the shape and chromatic dimensions of the current stimuli are different, they could be treated as separable dimensions. However, because both dimensions are carried by the same object they could be seen as integral. Monkey Da had performed several visual search tasks prior to this study in which shape and color cue different aspects of the response rules (e.g., Heitz & Schall, 2012; Reppert et al., 2018). This experience may enable the parallel exhaustive strategy by treating these feature dimensions separately. Monkey Le, on the other hand, had not performed other tasks prior to this study and thus may integrate the two feature dimensions through a coactive strategy. Alternatively, monkey Le may have analyzed the distractors, or the whole array holistically, to determine the stimulus-response rule. If he did not individuate stimuli, this may also explain the coactive processing strategy, pooling all sources of information.

Many other investigators have addressed the problem of the architecture underlying visual search. All now agree that the slope of RT with set size is not an effective criterion. More complex tasks are needed. For example, previous work studying a wide variety of visual search displays with multiple targets concluded that whereas most search conditions are accomplished through parallel limited-capacity process, a few conditions require serial search (Thornton & Gilden, 2007; see also Moran et al. 2016). A previous investigation of visual search with manipulation of target-distractor similarity employed systems factorial technology (Fifić et al. 2008b). These authors reported systematic departure from parallel or serial processing and concluded that the results were consistent with co-active processing.

Potential problems of error-prone performance

Systems factorial technology generally assumes perfect or near-perfect performance, because errors can contaminate RT distributions through speed accuracy tradeoffs. However, performance was not perfect in the data presented here. Thus, it is valid to wonder whether the SIC calculations and processing architecture inferences are invalidated by contamination of errors. This seems unlikely for two reasons. First, the SIC curves for both monkeys are qualitatively similar to those obtained in several other studies in humans with low error rates. Thus, the inferences supported by the findings are sensible in the context of separable and integral feature dimensions as discussed above.

Second, simulation approaches that are allowed to produce errors have shown that the MIC and SIC signatures are robust with moderately high error rates (Fifić et al., 2008; Townsend & Wenger, 2004). Specifically, only the coactive architecture signatures degrade with errors by losing their overadditivity. However, such an outcome means that a coactive architecture would be mistakenly identified as serial exhaustive. Hence, if performance supports the inference of the coactive architecture in spite of high error rates, then this should only increase confidence in the validity of the inference. If anything, we suspect that the high error rate may have resulted in the uncharacteristic bimodality of the SIC curve for monkey Da, but the nature of this bimodality is not at odds with the overall inference of a parallel exhaustive architecture.

Further evidence that errors do not prevent interpretation of system factorial results is found in the interesting relationships we discovered between MIC and SIC values and error production. For monkey Da, although both error and correct responses arose from the same parallel exhaustive architecture, the magnitude of additivity assessed through MIC values was lower for errors relative to correct trials. This indicates that errors arose from quantitative, not qualitatively different processing. In contrast, for monkey Le, errors arose from qualitatively different processing. Correct trials arose from the coactive architecture, but errors arose from the parallel exhaustive architecture. We surmise, therefore, that rather than system factorial technology being challenged by errors, with large enough samples, errors can be interpreted by systems factorial technology. This is an innovative extension.

The logic of selective influence, additivity, race inequalities, and systems factorial technology

As noted above, the overall goal of applying the logic of selective influence is to distinguish cognitive, motor, and sensory, or, more generally, computational processes. The experimental approach of creating dissociations to discover separable processes is well-known in ocular motor and visual neuroscience. For example, memory-guided saccades were devised to dissociate visual processing from saccade production (Hikosaka and Wurtz, 1983; Bruce and Goldberg, 1985). Double-step saccades were devised to dissociate retinal location and eye position in saccade production (Hallett and Lightstone 1976). Anti-saccades are contrasted with pro-saccades to distinguish contributions of voluntary stimulus-response mapping (Hallett and Adams 1980). Bistable visual stimuli afford a distinction between explicitly perceiving an object from simply responding to stimuli (Logothetis and Schall 1989; Blake and Logothetis 2002). Visual search was used to dissociate presentation of a stimulus in a neurons response field from that stimulus being the target of a saccade (Schall and Hanes 1993). And so on.

The straightforward framing hypothesis that RT is the summation of functionally distinct stages (Donders 1868) was challenged on multiple grounds during the early years of experimental psychology. Indeed, in the 1938 edition of his textbook Experimental Psychology, Robert S. Woodworth wrote, “If we cannot break up the reaction into successive acts and obtain the time of each act, of what use is the reaction time?” (page 310). However, this pessimistic conclusion was removed from a revised edition (Woodworth and Schlosberg 1954). Further progress on inferring processing architecture from systematic variation of RT was sparked by the formulation of the additive factors method (Sternberg 1969). To determine whether two factors affect the same or separate stages, the method assesses additivity of mean response times and of their variances. When response times from two or more factors are additive, the factors are taken to affect separate independent stages.

The formulation of critiques (Townsend 1972) and extensions (e.g., Taylor 1976; Schweickert 1978; Ashby and Townsend, 1980; Townsend 1984) energized more sophisticated approaches to decomposing RT. For example, additive factors assumes a strictly serial architecture. As demonstrated in Figure 1, though, in a parallel architecture two factors can independently affect processing stages without affecting response times in an additive fashion. Today, the theoretical foundation and empirical effectiveness of the approach has been established in multiple research domains of experimental psychology and cognitive neuroscience (e.g., Townsend and Ashby, 1983; Sternberg, 2001).

Today, systems factorial technology offers the most complete method to infer processing architectures from performance of a double-factorial task (Townsend and Nozawa 1995). Here, we manipulated singleton identifiability by varying singleton-distractor similarity and cue discriminability by varying singleton elongation. Other factors can be manipulated, of course. Indeed, the selective influence approach enables discovery of which factors influence common or different sub-ordinate processes. In the context of visual search, additional factors that merit investigation include set size, feature conjunctions, inhibition of return, priming of popout, attentional capture, and stimulus-response mapping difficulty. For example, the relationship between singleton-distractor similarity and stimulus-response mapping could be assessed by adding an additional stimulus-response mapping rule, e.g. instructing pro-saccades or anti-saccades (Sato & Schall, 2003). By iteratively and systematically testing the independence and interactions of pairs of factors, we will gain a deeper understanding of the existence of and relationships among the computational processes accomplishing visual search. Further validation would entail simulation as illustrated in Figure 4 and identification of neural signaling corresponding to the timing of the hypothetical constituent processes.

We should note that other, more specific approaches to inferring processing architecture and duration have been developed. For example, Miller (1982) described the race model inequality to distinguish between parallel channels and coactive processing. In this conception, if two sources of information are in separate parallel channels, then the probability of responding to two sources of information at a given time t must be less than the probability of responding to either individual source alone at time t. Otherwise, processing must be coactive. This model holds for self-terminating architectures, such as a race model, because it assumes that either piece of information can elicit a response. However, if both pieces of information are needed to produce a response, then this assumption does not hold and violations of the inequality do not necessarily indicate coactivity.

Similarly, Logan and Cowan (1984) used the race model formulation to explain performance of the stop signal (countermanding) task. This model affords estimation of the duration of a covert stopping process that happens to correspond precisely to the moment of modulation of particular sensory-motor neurons (Hanes et al. 1998; Paré and Hanes 2003; Murthy et al. 2009; Costello et al. 2013; Mallet et al. 2016). The relationship between the abstract race model and the neurophysiological findings was elucidated through development and validation of the interactive race model (Boucher et al. 2007; Logan et al. 2015).

Systems factorial technology improves upon both of these methods by distinguishing self-terminating and exhaustive stopping rules and is not limited to additivity which allows the assessment of both serial and parallel processing architectures. Thus, if an experiment can be designed such that the response times are amenable to systems factorial technology, it is the more powerful method because it can differentiate all possibilities. Ultimately, we believe that similar mappings between abstract model architectures and neural processes can be achieved using the logic of selective influence and the tools of systems factorial technology.

Conclusions

RT in complex tasks is the summation of functionally distinct operations or stages. While not emphasized, the stage assumption is fundamental to the predominant model of “decision- making” – a single sequential-sampling process intervening between uninteresting visual encoding and response production stages. Such models explain performance and account for neural activity in visual discrimination tasks as well as visual search with direct stimulus-response mapping. But, if RT is not comprised of dissociable stages, then models like drift diffusion may be disqualified and alternative models are endorsed, such as cascade (e.g., McClelland 1979) or asynchronous discrete flow (Miller 1988), which are qualitatively different mechanisms.

The most effective and perhaps only method for assessing the existence and characterizing the properties of modules or stages is the logic of separate modifiability. Crucially, single-stage decision-making models cannot explain tasks that require multiple, sequential operations. The term “decision” is hopelessly ambiguous when applied to a task that requires a “decision” about the location of a color singleton, a “decision” about the shape of the singleton, a “decision” about the shapes of distractors, a “decision” about the congruency of the singleton and distractor shapes, a “decision” about the instructed stimulus-response mapping, a “decision” about the correct endpoint of the saccade, and a “decision” about when to initiate the saccade. We have established that macaque monkeys can perform a task with simultaneous, independent factorial manipulations, producing performance measures that produce interpretable outcomes using the most advanced computational analytical approaches. This paves the way for a next step in cognitive neurophysiology of visual search by providing the ability to assess whether individual neural processes are prolonged, more numerous, or interacting.