Abstract
Although COVID-19 has been spreading throughout Belgium since February, 2020, its spatial dynamics in Belgium remain poorly understood, partly due to the limited testing of suspected cases during the epidemic’s early phase. We analyse data of COVID-19 symptoms, as self-reported in a weekly online survey, which is open to all Belgian citizens. We predict symptoms’ incidence using binomial models for spatially discrete data, and we introduce these as a covariate in the spatial analysis of COVID-19 incidence, as reported by the Belgian government during the days following a survey round. The symptoms’ incidence is moderately predictive of the variation in the relative risks based on the confirmed cases; exceedance probability maps of the symptoms’ incidence and confirmed cases’ relative risks overlap partly. We conclude that this framework can be used to detect COVID-19 clusters of substantial sizes, but it necessitates spatial information on finer scales to locate small clusters.
Keywords: COVID-19, Disease mapping, Spatially correlated random effects, Integrated nested Laplace approximation, Self-reporting
2020 MSC: 00-01, 99-00
1. Introduction
COVID-19 is a respiratory disease caused by a highly infectious single-stranded RNA corona virus, SARS-CoV-2 (Chen, Zhou, Dong, Qu, Gong, Han, et al., 2020, Wu, Zhao, Yu, Chen, Wang, Song, et al., 2020). It was first observed in Wuhan, the capital of the Hubei province in the People’s Republic of China, in December 2019 (Zhu et al., 2020). The virus most likely has a zoonotic origin, but human-to-human transmission, which happens mainly via droplets and fomites, combined with a high basic reproductive number, has caused the disease to rapidly spread across continents. It has been declared a global pandemic on March 11, 2020 (World Health Organization, 2020).
The first imported COVID-19 case in Belgium was reported on February 4, 2020, in Brussels; this case did not lead to further infections. Due to various further introductions, the disease spread throughout the country. The Belgian government has undertaken several measures to slow down community transmission, the most notable of which has been the implementation of a lockdown of the country on March 18, 2020. Due to limited capacity, only a fraction of suspected Belgian COVID-19 patients has been tested to confirm SARS-CoV-2 infection. These are primarily severe cases, which has complicated the assessment of the true extent of the disease’s spatio-temporal spread.
The University of Antwerp, in collaboration with Hasselt University and KU Leuven, has designed an ethically approved weekly online COVID-19 survey (https://www.uantwerpen.be/en/projects/corona-study/), which is open to the general Belgian public. A key objective of the survey is to collect information on COVID-19 symptoms from the general public. The weekly number of participants has been large; during its first four rounds, the survey reached 537,172; 334,935; 397,529; and 215,138 respondents, respectively, with complete residential and personal information to conduct a spatial analysis. However, as the survey may not reach all segments of society equally (Alessi, Martin, 2010, Andrews, Nonnecke, Preece, 2003), it remains unclear whether sampling bias invalidates statistical inference on the spatial dynamics of COVID-19-like symptoms as a proxy for the distribution of COVID-19.
Geostatistical models are often applied to analyse and predict disease risk in a population (Diggle and Ribeiro, 2007). Using methods for spatially discrete outcomes (Besag, York, Mollié, 1991, Lawson, 2013, Leroux, Lei, Breslow, 1999), we can predict COVID-19 incidence via crowd-sourced data of symptoms obtained by self-reporting in the online survey. We can use these predictions to optimally model the geographical risk distribution of confirmed COVID-19 cases, as reported by the Belgian government. This additionally allows to investigate routes to develop an early-warning framework aimed at detecting COVID-19 cases by self-reporting citizens, when large-scale testing and tracing of the general public is not feasible, and to supplement information obtained from testing and tracing otherwise.
In this study, we fit spatial models to data obtained during the third round of the online survey, conducted on March 31, 2020, and data of confirmed cases, as reported by the Belgian population health institute (Sciensano) between April 7 and April 9, 2020. We use approximate Bayesian estimation methods to spatially analyse self-reported COVID-19 symptoms. We then use mean incidence predictions as a plug-in covariate in a spatial model to analyse confirmed cases. Our aim is to investigate whether symptoms that are reported in an online survey, which is ordinarily subject to sampling bias, are useful to predict the spatial spread of detected COVID-19 disease approximately one week later.
2. Methodology
2.1. Data
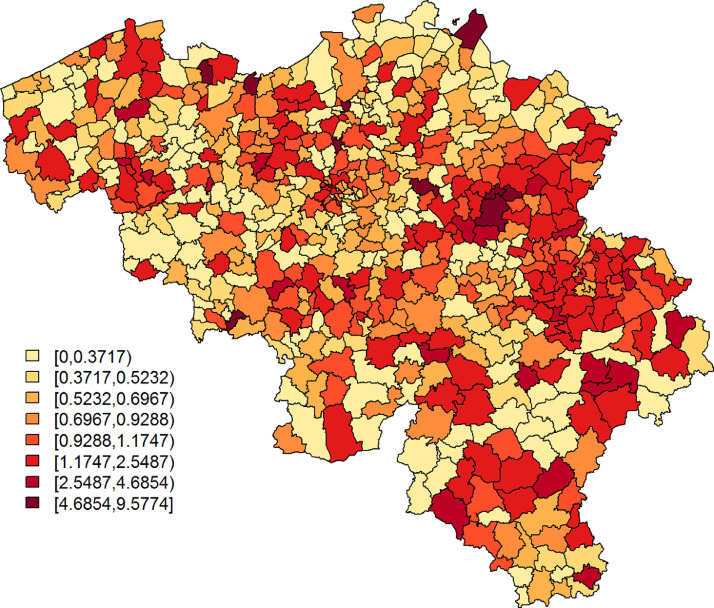
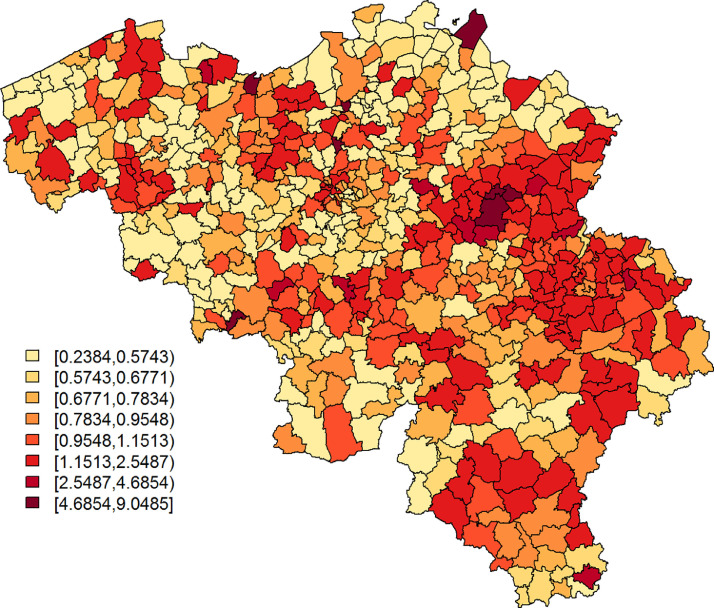
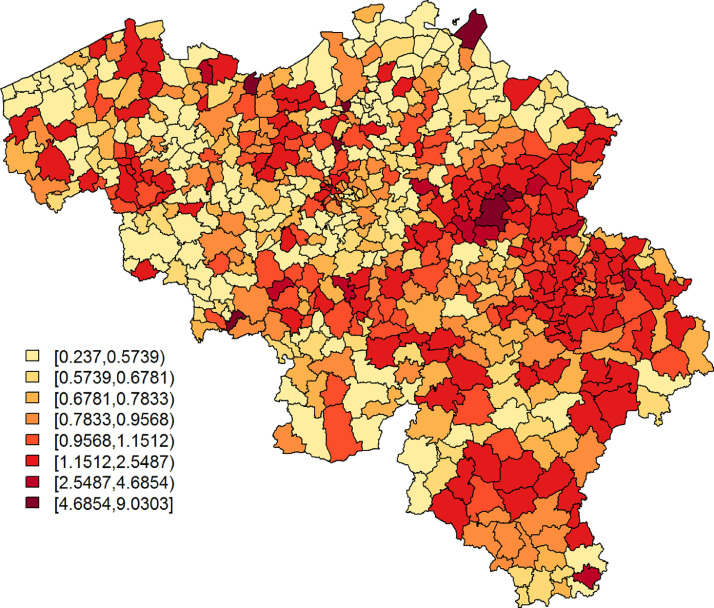
The Belgian population health institute (Sciensano) collects daily numbers on confirmed cases in Belgium, an aggregated version of which is made publicly available (https://epistat.wiv-isp.be/covid/). We make use of the raw, publicly unavailable, data of 5183 individuals with known residential, age, and gender information, who were diagnosed with COVID-19 on April 7, April 8, or April 9, 2020 (henceforth, covid data). Fig. 1 depicts the standardized incidence rates, with Oi and Ei the observed number of cases and the internally age-gender standardised expected counts, respectively, for municipality with . We use age groups in the standardisation process, more specifically the age intervals, 0–24, 25–44, 45–64, and years old. The widths of the age intervals are based on considerations related to the online survey data set; more information is provided in Section 2.2. Note that on Jan 1, 2019, a number of Belgian municipalities have been geographically and administratively united, which reduced the total number of Belgian municipalities from 589 to 581. We use the Belgian municipality structure of 2018 to improve spatial resolution, along with demographical information from the same year, which differs only minimally from the demography in 2020.
Fig. 1.
SIR of COVID-19 cases per municipality, based on all confirmed cases between April 7 and April 9, 2020.
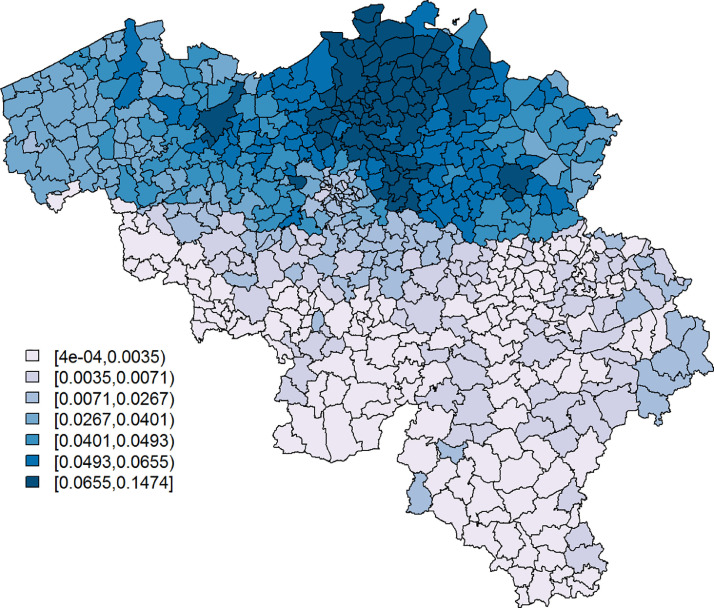
Secondly, we use data on COVID-19 symptoms, as self-reported by participants in the third round of the online COVID-19 survey (March 31, 2020; henceforth, symptoms data), for which all necessary ethical approvals have been obtained. The survey can be filled in by all members of the public and is designed to collect data about spatial trends in COVID-19 symptoms within Belgium, the extent to which members of the public adhere to measures taken by the government, contact behaviour, and mental health dynamics, among others. We investigate data of the third round in the main analysis presented here, since (i) the survey in round 1 only contained one general question that gauged whether individuals experienced any flu-like symptoms. From round 2 onwards, this question was replaced by thirteen separate questions regarding specific COVID-19 symptoms; (ii) of the remaining surveys, round 3 had the largest sample size and the best coverage in Wallonia, the southern part of Belgium; (iii) during rounds 1 and 2, there was considerable overlap with the end of the influenza season, while exploratory analyses of symptom shifts through time signal the start of the pollen allergy season in round 4. We provide analysis results of survey rounds 2 and 4 as an Appendix (Section A.3). We use data of males and females - not intersex due to the category’s limited sample size - with available age and residential information. This yields 397,529 data records, with at least one respondent from each of the 589 Belgian municipalities. The majority of the respondents comes from Flanders, the northern part of Belgium (Fig. 2 ). All participants were asked to indicate which of the following COVID-19-like symptoms they experienced during the week preceding the online survey (March 2020), if any: (i) a rapidly increasing fever, (ii) a high fever, (iii) a dry cough, (iv) shortness of breath, (v) chest pain, (vi) muscle pain, (vii) exhaustion, (viii) chills, (ix) nausea, (x) painful eyes, (xi) a sore throat, (xii) a rattling cough, and/or (xiii) a running nose. A binary variable Yij takes a value 1 when person in municipality i experienced at least one of the most typical symptoms, which we define as symptoms (i)-(iv), based on Jiang et al. (2020), Yang et al. (2020), and World Health Organization (2020); otherwise, .
Fig. 2.
The proportion of the population per municipality taking the survey on March 31, 2020.
2.2. Statistical methods
We fit models for spatially discrete data to the symptoms and covid data, using integrated nested Laplace approximation (INLA, (Rue et al., 2009)). INLA is a convenient approximate Bayesian estimation method that computes approximations of posterior marginal distributions for latent Gaussian models. We apply it in R 4.0.0 (RCoreTeam, 2020), through the package R-INLA.
For the symptoms data, the model structure is defined by
| (1) |
where single denotes a binary variable taking the value 1 when a participant is the only member of a household and 0 otherwise; agecat 1, agecat 2, and agecat 3 are dummy variables that indicate whether participants belong to the age groups 25–44, 45–64, and respectively, the interval widths of which we have chosen to categorise the data into groups expected to showcase different social behaviour, while maintaining balanced sample sizes among these categories; for males, 0 for females; z 1i is a term that corrects for spatially correlated heterogeneity (CH) and/or uncorrelated heterogeneity (UH) at the municipality level. We apply and compare three approaches; (i) the convolution model (Besag et al., 1991), where with v 1i defined as a normally distributed random effects term to capture UH,
| (2) |
CH is accommodated by u 1i, an intrinsic conditional autoregressive (CAR) random effects term,
| (3) |
| (4) |
| (5) |
Here, if areas i and k are adjacent and 0 otherwise; as an alternative, we fit (ii) the Leroux model (Leroux et al., 1999), where
| (6) |
| (7) |
Here, Ω1 is the precision matrix of an intrinsic CAR process, such as introduced in (3)–(5). The parameter λ 1 controls how strong the spatial dependence attributes to the extra-variability; when there is no spatial heterogeneity, when all heterogeneity can be linked to spatial dynamics. The Leroux latent model is not provided as a standard option in INLA, but it can be implemented by specifying the variance-covariance matrix as suggested by Ugarte et al. (2014) and applied by Adin et al. (2019); (iii) we compare both spatial models with a non-spatial log-normal model, where with v 1i parametrised similarly as in (2).
We perform model selection using the Deviance Information Criterion (DIC, Spiegelhalter et al., 2002) and the Watanabe-Akaike Information Criterion (WAIC, Watanabe, 2010) goodness-of-fit criteria. We then estimate the predicted probability of a municipality’s inhabitant to experience at least 1 typical COVID-19 symptom, which is corrected for the age, gender, and single households dynamics of the municipality.
For the covid data, we fit a spatial Poisson model with a full model structure that is defined as,
where Ri denotes the relative risk for municipality i. We again use the convolution, Leroux, and log-normal modelling approaches to define z 2i. In the convolution and log-normal models, v 2i and u 2i are defined similarly as v 1i and u 1i in (2)–(5), respectively, but with different separate heterogeneity terms denoted by and instead of and respectively. For the Leroux model, we use similar parametrisations as in (6)–(7), but with Σ2, σ 2, λ 2, and Ω2 instead of resp. Σ1, σ 1, λ 1, and Ω1. We include as predicted by (1), as a risk factor in the model, but in its standardised form, which we denote as . We compare results with those coming from convolution, Leroux, and log-normalmodels without the symptoms’ incidence covariates. Model selection is based on the joint investigation of DIC and WAIC statistics and the effect of .
We use vague priors: N(0, 1000) for all covariate effects, logit(λ) ~ beta(1, 1) for the control parameters in the Leroux models, and penalised complexity (PC) priors (Simpson et al., 2017) for the precision parameters of the random effects. PC priors for a precision parameter, are defined by two parameters, σ 0 and ξ, such that . We set and for and . A sensitivity analysis for the choice of the prior distribution, where we use Gamma(1, 0.0005), here parametrised with a shape and rate parameter, as a prior for the precision parameters, and logit(λ) ~ N(0, 10), has been documented in the Appendix (Section A.1). Note that precision, control, and covariate estimates, along with the maps displaying predictions and exceedance probabilities, remain almost unchanged in the sensitivity analysis. We denote covariate effects as significant, when their associated 95% credible interval does not include 0.
Note that the online survey collected residential information at the postal code area level, a subdivision of the municipality level. Since this yielded at least one data record for 1083 out of these 1133 Belgian postal code areas, the symptoms data can be investigated on this finer scale as well. We provide this analysis as an Appendix (Section A.2). We have chosen to report the data on a coarser spatial scale in the main manuscript due to two main reasons: (i) the gain of working at the postal code area level is limited in the context of predictions, since demographic information at the postal code area level is currently not at our disposal. This means that predicting spatial symptom probabilities necessitates the use of covariate information at the municipality level, which is not optimal; (ii) predictions at the postal code area level need to be aggregated within the municipality level to be used as a covariate in the analysis of the covid data. Hence, working at the municipality level in the symptoms data analysis allows us to provide these predictions in a more direct way.
3. Results
In the analysis of the symptoms data, the convolution and Leroux models provide very similar parameter estimates and goodness-of-fit statistics, while they outperform the log-normal model (Table 1 ). This is in line with the observation that most extra-variability can be attributed to unobserved spatial phenomena; in the Leroux model, lies close to 1; furthermore, we see that the largest part of the uncorrelated extra-variability in the log-normal model is attributed to spatial dynamics when extending the model to the convolution model. One can argue to fit a CAR model without an UH term as an alternative, but we decide against that approach, since we would then assume that there is no small-scale extra-variability. Note that the unexplained variability in all three models is arguably small, with its estimated standard deviation fluctuating around 0.1. We proceed with the Leroux model, since the convolution model can suffer from identifiability problems in its random effects structure (Leroux et al., 1999), while noting that the final results remain largely unaffected by this choice.
Table 1.
symptoms data analysis: estimation results and goodness-of-fit statistics..
| Effect | Parameter | Convolution model |
Leroux model |
Log-normal model |
|||
|---|---|---|---|---|---|---|---|
| Estimate | 95% credible interval | estimate | 95% credible interval | Estimate | 95% credible interval | ||
| Intercept | α0 | −1.6084 | [ −1.6418,−1.5752] | −1.6106 | [−1.7080,−1.5102] | −1.6304 | [−1.6604,−1.6004] |
| single | α1 | −0.0553 | [−0.0827,−0.0280] | −0.0551 | [−0.0825,−0.0278] | −0.0555 | [−0.0830,−0.0282] |
| agecat1 | α2 | 0.1770 | [0.1454,0.2087] | 0.1771 | [0.1455,0.2088] | 0.1783 | [0.1466,0.2100] |
| agecat2 | α3 | −0.0941 | [−0.1284,−0.0598] | −0.0941 | [−0.1284,−0.0598] | −0.0945 | [−0.1288,−0.0602] |
| agecat3 | α4 | −0.6692 | [−0.7334,−0.6055] | −0.6691 | [−0.7334,−0.6055] | −0.6707 | [−0.7349,−0.6071] |
| male | α5 | −0.1009 | [−0.1573,−0.0448] | −0.1009 | [−0.1573,−0.0447] | −0.1016 | [−0.1580,−0.0454] |
| agecat1*male | α6 | 0.0731 | [0.0116,0.1348] | 0.0731 | [0.0116,0.1348] | 0.0734 | [0.0119,0.1351] |
| agecat2*male | α7 | 0.0934 | [0.0288,0.1581] | 0.0934 | [0.0288,0.1582] | 0.0948 | [0.0302,0.1595] |
| agecat3*male | α8 | 0.0113 | [−0.0890,0.1114] | 0.0113 | [−0.0890,0.1114] | 0.0136 | [−0.0867,0.1137] |
| st. dev. UH | σv1 | 0.0138 | [0.0029,0.0297] | – | – | 0.0763 | [0.0627,0.0905] |
| st. dev. CH | σu1 | 0.0943 | [0.0733,0.1200] | – | – | – | – |
| st. dev. | σ1 | – | – | 0.1006 | [0.0785,0.1257] | – | – |
| control par. | λ1 | – | – | 0.9655 | [0.8780,0.9973] | – | – |
| DIC | – | 22863.96 | – | 22864.11 | – | 22935.75 | – |
| WAIC | – | 22866.28 | – | 22866.67 | – | 22944.69 | – |
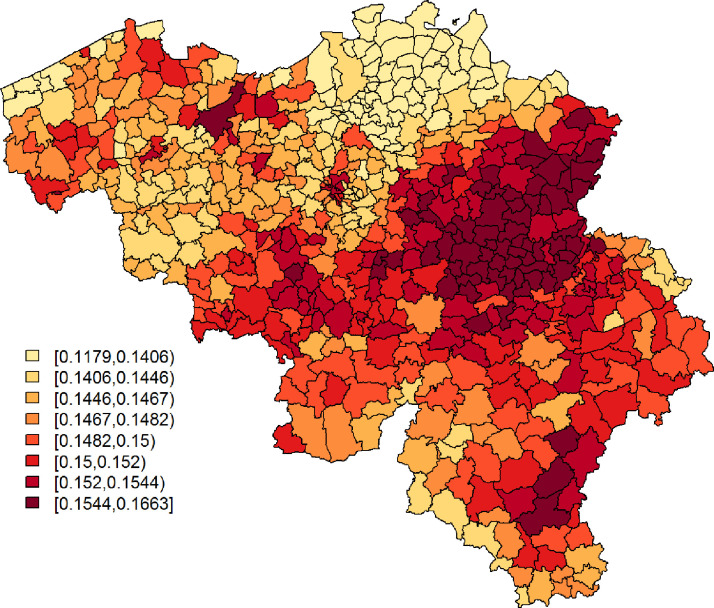
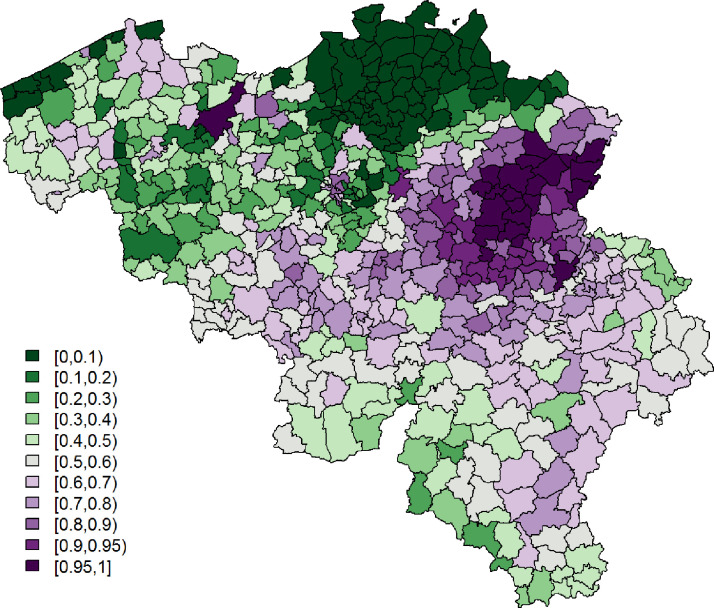
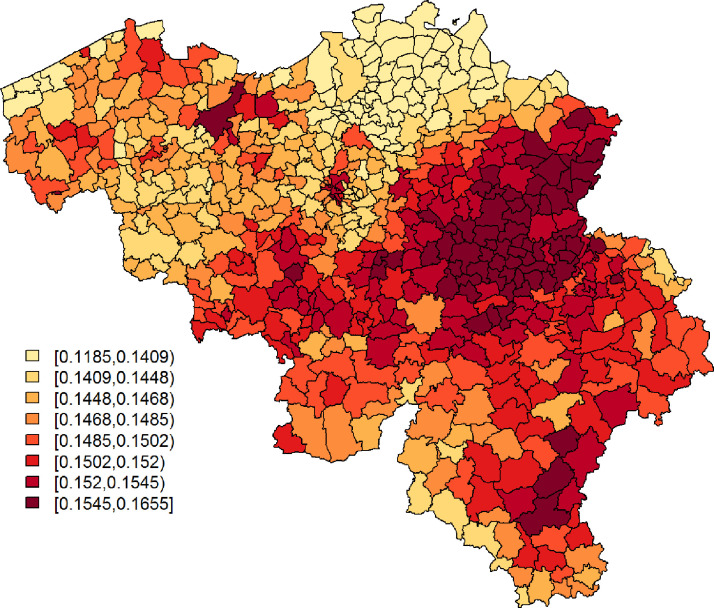
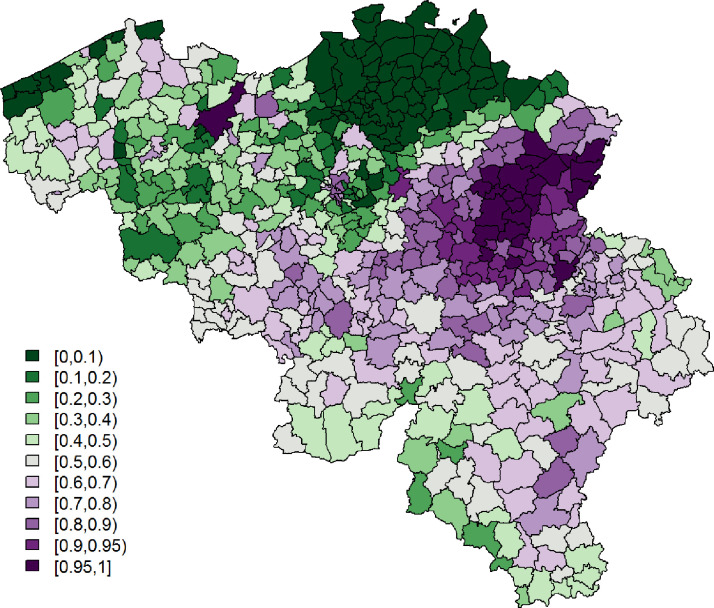
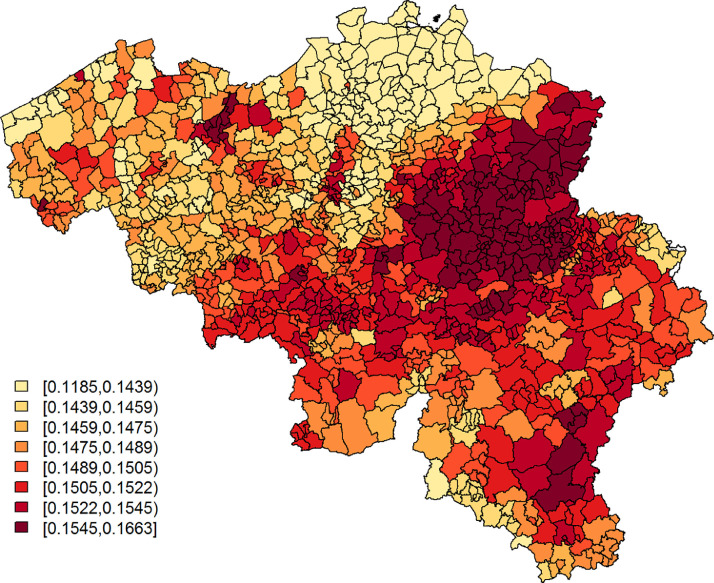
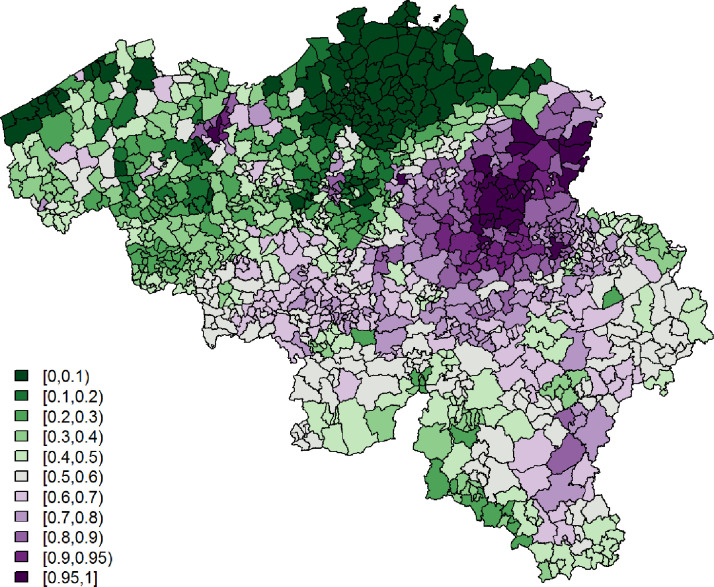
Being single is significantly associated with a lower probability to report at least 1 typical COVID-19 symptom. However, its effect is small. Age and gender have significant interaction effects; we see the largest probability among non-single females between 25 and 44 years old, while the lowest probability is seen in single elderly males. Figs. 3 and 4 show, respectively, after correcting for demographic variation in age, gender, and household, i.e., singles vs. non-singles, and the exceedance probabilities, .
Fig. 3.
Leroux model: predicted probabilities for a citizen to experience at least 1 of 4 typical COVID-19 symptoms per municipality.
Fig. 4.
Leroux model: exceedance probabilities per municipality for the predicted probability for a citizen to experience at least 1 of 4 typical COVID-19 symptoms, with threshold .
Table 2 presents parameter estimates and goodness-of-fit statistics for the covid data analyses. Again, the convolution and Leroux models outperform the log-normal model in terms of DIC and WAIC. These statistics are almost identical for both spatial models that include the symptoms’ incidence covariate and for the convolution model without the covariate. Estimates of β 0 and β 1 are similar across the three models.
Table 2.
covid data analysis: estimation results and goodness-of-fit statistics.
| Effect | Parameter | Convolution model |
Leroux model |
Log-normal model |
|||
|---|---|---|---|---|---|---|---|
| Estimate | 95% credible interval | Estimate | 95% credible interval | Estimate | 95% credible interval | ||
| covariate | |||||||
| Intercept | β0 | -0.2874 | [−0.3567,−0.2198] | −0.2917 | [−0.3878,−0.1982] | −0.2865 | [−0.3589,−0.2160] |
| β1 | 0.2022 | [0.0949,0.3041] | 0.1966 | [0.1085,0.2818] | 0.2204 | [0.1521,0.2890] | |
| st. dev. UH | σv2 | 0.6270 | [0.5575,0.7013] | – | – | 0.6792 | [0.6231,0.7393] |
| st. dev. CH | σu2 | 0.4254 | [0.2193,0.7156] | – | – | – | – |
| st. dev. | σ2 | – | – | 0.9001 | [0.7550,1.0616] | – | – |
| control par. | λ2 | – | – | 0.1973 | [0.0764,0.3830] | – | – |
| DIC | – | 2832.51 | – | 2832.58 | – | 2837.58 | – |
| WAIC | – | 2762.97 | - | 2763.59 | – | 2768.42 | – |
| no covariate | |||||||
| Intercept | β0 | −0.2912 | [−0.3582,−0.2261] | −0.2983 | [−0.4202,−0.1784] | −0.2992 | [−0.3741,−0.2263] |
| st. dev. UH | σv2 | 0.5836 | [0.5063,0.6768] | – | – | 0.7144 | [0.6561,0.7769] |
| st. dev. CH | σu2 | 0.6503 | [0.4403,0.8935] | – | – | – | – |
| st. dev. | σ2 | – | – | 1.0729 | [0.9045,1.2470] | – | – |
| control par. | λ2 | – | – | 0.3623 | [0.1818,0.5606] | – | – |
| DIC | – | 2832.94 | – | 2835.58 | – | 2848.66 | – |
| WAIC | – | 2763.84 | – | 2769.19 | – | 2779.38 | – |
With regards to the symptoms’ incidence’s usefulness as a predictor for the relative incidence risk of the confirmed cases, we list a number of observations: (i) goodness-of-fit statistics point towards improved model fits when the symptoms’ predicted incidence is used as a covariate, except for the convolution model; (ii) parameter estimates in the upper panel of Table 2 indicate a relatively small, but significantly positive association between the symptoms’ incidence and the relative incidence risk based on the confirmed cases; (iii) however, in all models, the extra-variability’s parameter estimates do not increase substantially when the covariate is left out of the linear predictor; (iv) when we predict relative risks from a spatial model, e.g., the Leroux model, without the covariate, the Kendall correlation of those relative risks and is significantly different from 0, but its point estimate is small (; pvalue ); (v) unlike in the symptomsdata analysis, the majority of the extra-variability is attributed to small-scale spatial variation (e.g., for the Leroux model, ). This is partly due to the fact that the symptoms’ incidence, which predominantly shows spatial and little non-spatial dynamics, captures mostly spatial variation in the confirmed cases’ incidence risk. The results from the Lerouxmodel without the covariate confirm this, as increases to 0.3627.
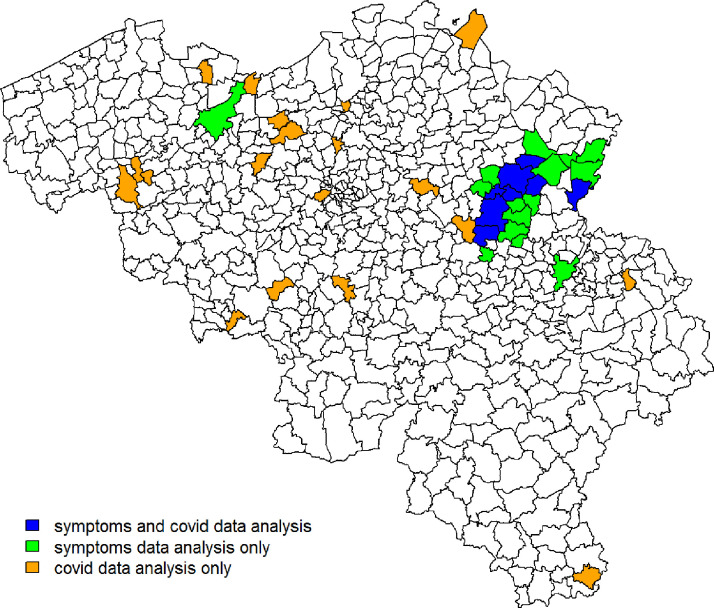
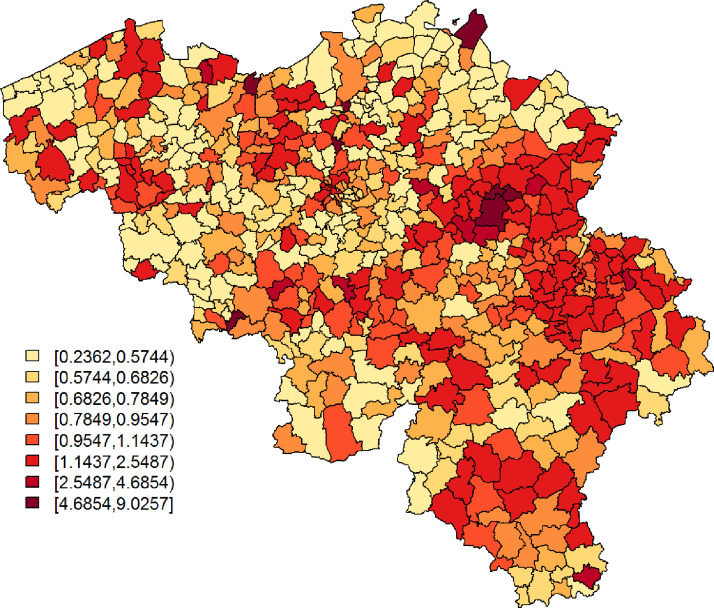
From the observations listed above, we learn that (i) explains a small, yet arguably significant, proportion of variability in the confirmed cases’ relative incidence risk. We will denote this as moderately predictive; (ii) mostly explains spatially correlated variation in the confirmed cases’ and is best at pinpointing large disease clusters. This is also seen in Figs. 5 and 6 , which depict, respectively, and the exceedance probabilities, based on the Leroux model with as a covariate. The region with elevated predicted incidence of typical COVID-19 symptoms in the central-east of Belgium, situated around the city of Sint-Truiden, in Fig. 4, overlaps well with the cluster of municipalities in Fig. 6 that has a high probability, i.e., larger than 95%, to have at least a 150% increase in relative incidence risk (Fig. 7 ). This region is known, as it had the largest local COVID-19 outbreak in Belgium. Other smaller outbreaks could however not be predicted by . Increased risk in these locations is likely accounted for in the model by the spatially uncorrelated heterogeneity term.
Fig. 5.
Leroux model: predicted COVID-19 relative risk per municipality, based on data of confirmed cases between April 7 and April 9, 2020.
Fig. 6.
Leroux model: exceedance probabilities for the relative risk per municipality, based on data of confirmed cases between April 7 and April 9, 2020, with relative risk threshold .
Fig. 7.
Map depicting locations where and/or .
Based on these considerations, we decide to leave the covariate in the model, but note that its explanatory power is limited. We proceed with the Leroux model that includes the covariate, again due to possible identifiability issues in the convolution model. Note that the symptoms that were self-reported to be experienced during the period of March 24–30, have similar, moderately predictive, effects on the incidence risk of confirmed cases within a period that spans more days than the period of April 7–9 (Table 3 ). We find significant results for the effect of on the incidence risk of confirmed cases for almost all three-day periods throughout March 31 and April 22, as well as a significant effect when analysing all cases that were confirmed between March 31 and April 22 together. Based on the effect size and the credible intervals’ widths, the optimal predictive performance is suggested for the period between April 7 and April 9. Although it is uncommon to consider traditional issues related to multiple testing in the context of a Bayesian analysis, we note that for a number of three-day periods, lower limits of 95% credible intervals often lie close to zero, which might reflect spurious correlations.
Table 3.
Estimation results for β1, the effect of when investigating different time periods of confirmed cases. An asterisk (*) denotes a significant effect on a 5% significance level.
| Period | Estimate | 95% credible interval | No. cases |
|---|---|---|---|
| March 31 – April 2 | 0.1454 | [0.0490,0.2394]* | 4565 |
| April 1 – April 3 | 0.1477 | [0.0533,0.2378]* | 4567 |
| April 2 – April 4 | 0.1973 | [0.1091,0.2825]* | 3989 |
| April 3 – April 5 | 0.1988 | [0.1087,0.2860]* | 3205 |
| April 4 – April 6 | 0.1703 | [0.0907,0.2474]* | 3415 |
| April 5 – April 7 | 0.1839 | [0.1015,0.2618]* | 3977 |
| April 6 – April 8 | 0.1548 | [0.0661,0.2381]* | 4881 |
| April 7 – April 9 | 0.1966 | [0.1085,0.2818]* | 5183 |
| April 8 – April 10 | 0.1873 | [0.0870,0.2842]* | 5990 |
| April 9 – April 11 | 0.1985 | [0.0782,0.3161]* | 5446 |
| April 10 – April 12 | 0.1602 | [0.0216,0.2953]* | 3768 |
| April 11 – April 13 | 0.1614 | [0.0141,0.3067]* | 2020 |
| April 12 – April 14 | 0.1347 | [-0.0065,0.2691] | 2473 |
| April 13 – April 15 | 0.1980 | [0.0666,0.3245]* | 3543 |
| April 14 – April 16 | 0.1971 | [0.0714,0.3205]* | 4643 |
| April 15 – April 17 | 0.1754 | [0.0513,0.2977]* | 4532 |
| April 16 – April 18 | 0.1558 | [0.0298,0.2786]* | 3652 |
| April 17 – April 19 | 0.2151 | [0.0723,0.3481]* | 2468 |
| April 18 – April 20 | 0.2236 | [0.0895,0.3542]* | 2345 |
| April 19 – April 21 | 0.1772 | [0.0593,0.2941]* | 2867 |
| April 20 – April 22 | 0.1410 | [0.0277,0.2511]* | 3179 |
| March 31 – April 22 | 0.1465 | [0.0685,0.2198]* | 29405 |
4. Discussion and conclusion
Our study shows that, when using geographical crowd-sourced information on COVID-19 that is obtained by self-reporting in the Big Corona Study, a large-scale online survey study, model-based symptom incidence predictions are capable of explaining a (borderline) significant, yet limited, proportion of the heterogeneity that is seen in the number of confirmed COVID-19 cases, as reported by the government, within 1 to 28 days after these symptoms were experienced. Exceedance probabilities, based on the analysis of the symptoms data, pinpoint an important cluster of elevated COVID-19 risk around the city of Sint-Truiden in central eastern Belgium, which aligns well with a region that has since then received increased attention, due to a number of local outbreaks. However, the symptoms analysis’ exceedance probabilities do not detect disease clusters that occur very localised and that manifest themselves in the data as small-scale spatial variation, i.e., spatially uncorrelated overdispersion.
Note that we have conducted the same analyses, using symptoms data from rounds 2 and 4 of the online survey, which we document as an appendix (Section A.3). Similarly as in the analysis based on survey 3, the predictive means of the symptoms’ incidence (borderline) significantly explain variation in the number of confirmed cases. Note however that for survey round 2, these effects are seen for a more restricted set of three-day periods within a 21-day time span after the day of the respective surveys. As explained in Section 2.1, These weaker predictive performances are likely due to a combination of the overlapping influenza season during round 2 and a lower amount of participants from Wallonia, which may obstruct the detection of all spatial dynamics of COVID-19 symptoms in Belgium. Note that the symptoms data reflect symptoms that were experienced during the week preceding the respective rounds of the survey. This period does not necessarily reflect the moment of the symptoms’ onsets, which may have taken place earlier. Future studies will investigate how data of COVID-19 symptoms’ onsets can be optimally linked to data of confirmed cases.
One limitation of the current modelling framework, is that not all high-risk areas in Fig. 6 could be detected by the symptoms data analysis (Fig. 4). We believe that this is at least partly due to a considerably large amount of small-scale variation in virus transmission, such that our model is currently best at pinpointing clusters that are occurring on a moderately large scale. This might be explained by the quarantine measures that obstruct typical transmission routes, such that infection mostly occurs very localised (Ganyani et al., 2020). However, the definition of small-scale spatial variation is study-specific and depends on the spatial resolution of data; in order to develop COVID-19 monitoring tools, analysts will need spatial information on finer scales than the municipality (or postal code area) level. Another reason for the limited predictive capabilities of the symptoms data is that there might still be considerable overlap with other common illnesses that have similar symptoms and occur in the same season, such as influenza or pollen allergy. Because of this, we might currently only detect signals in regions that are severely hit by COVID-19. Considering the objective to use online surveys in large-scale COVID-19 monitoring, this prompts the need for more research into symptoms definitions, particularly when information on their incidence is collected through self-reporting. Furthermore, similarly to the previous conclusions with respect to rounds 2 of the survey, the relatively small sample sizes in the southern part of Belgium for the symptoms data likely hamper the detection of high-incidence areas in the analysis of round 3 as well. This highlights the need for investments in monitoring tools, and promotional campaigns to engage the general public throughout the whole region to participate in these online surveys, in combination with such other measures as, for example, tracing strategies.
With respect to demographic heterogeneity in typical COVID-19 symptoms, the analysis results report the lowest symptoms’ incidence for elderly, while symptoms occur mostly among persons between 25 and 44 years old, especially females with at least one additional household member. These differences might be a result of variation in the social distancing behaviour between age groups. Preliminary analyses of contact behaviour, based on the online survey data (not shown), suggest that Belgian elderly started to engage in social distancing significantly sooner than younger individuals during the COVID-19 outbreak; among individuals who are younger than 65 years, those younger than 25 are suggested to be the slowest to adapt to social distancing measures. A plausible reason why the latter is not reflected in the symptoms data analysis results, is that among COVID-19 patients, children and adolescents in general are less likely to experience typical COVID-19 symptoms (Dong et al., 2020).
This study can be improved by investigating the outcomes spatio-temporally. However, the correct extraction of the specific day of the symptoms’ onset from the online survey data should be undertaken with care and will be investigated in the future. We have therefore analysed symptoms data that were aggregated in time. Moreover, we plan to develop a joint modelling framework in which we simultaneously model symptoms and confirmed cases, e.g., by extending correlated random-effects models proposed by Neyens et al. (2016). This will allow us to exploit spatial dependence that is likely to occur between symptoms’ incidence and the confirmed cases’ disease risk. This can improve the current two-step approach where we use model-based symptom predictions as a plug-in covariate to model the spatial dynamics of the confirmed cases’ disease risk. Furthermore, this modelling framework will allow us to optimally model uncertainty in the symptoms’ incidence predictions, which is now left unaccounted for when using these as a covariate in the covid data analysis. Ultimately, our goal is to develop a model that forecasts spatio-temporal dynamics in COVID-19 incidence, based on self-reporting of symptoms in addition to other data sources, such as absenteeism, mobility of individuals, etc., to act as an early warning system for surges in disease risk.
Funding
This research received funding from the Flemish Government (AI Research Program). Authors NH and PB acknowledge funding from the European Union’s Horizon 2020 research and innovation programme - project EpiPose (No. 101003688). Authors TN, NH, PVD, and PB acknowledge funding from the Research Foundation Flanders (No. G0G1920N).
Data availability statement
The covid data, as analysed in this study, are confidential. They are available in an aggregated format on https://epistat.wiv-isp.be/covid/. The symptoms data are confidential, but can be accessed after approval by the Corona Study steering committee.
Ethics statement
All data were collected in ethically approved studies.
CRediT authorship contribution statement
Thomas Neyens: Conceptualization, Methodology, Software, Writing - original draft. Christel Faes: Methodology, Writing - review & editing. Maren Vranckx: Formal analysis, Software. Koen Pepermans: Investigation, Resources, Writing - review & editing. Niel Hens: Supervision, Writing - review & editing. Pierre Van Damme: Resources, Writing - review & editing. Geert Molenberghs: Conceptualization, Writing - review & editing. Jan Aerts: Data curation, Writing - review & editing. Philippe Beutels: Investigation, Resources, Supervision, Writing - review & editing.
Declaration of Competing Interest
The authors declare no conflicts of interest.
Acknowledgements
We thank Herman Van Oyen and Toon Braeye from the Belgian population health institute (Sciensano) for reading and commenting on our manuscript.
Appendix A
A1. Sensitivity analysis
In the sensitivity analysis (Fig. 8, Fig. 9, Fig. 10, Fig. 11; Table 4), we refit the Leroux models, using a Gamma(1, 0.0005) prior instead of a PC prior for the precision parameters of the random effects term, and logit(λ) ~ N(0, 10) instead of logit(λ) ~ beta(1, 1) for the control parameter.
Table 4.
Sensitivity analysis: estimation results.
| Effect | Parameter | Estimate | 95% credible interval |
|---|---|---|---|
| Symptoms data | |||
| Intercept | α0 | −1.6094 | [−1.7971,−1.4197] |
| single | α1 | −0.0550 | [−0.0825,−0.0277] |
| agecat1 | α2 | 0.1771 | [0.1455,0.2088] |
| agecat2 | α3 | −0.0942 | [−0.1284,−0.0599] |
| agecat3 | α4 | −0.6692 | [−0.7334,−0.6056] |
| male | α5 | −0.1009 | [−0.1573,−0.0448] |
| agecat1*male | α6 | 0.0731 | [0.0117,0.1348] |
| agecat2*male | α7 | 0.0934 | [0.0289,0.1582] |
| agecat3*male | α8 | 0.0113 | [−0.0890,0.1114] |
| st. dev. | σ1 | 0.0943 | [0.0730,0.1188] |
| control par. | λ1 | 0.9844 | [0.9301,0.9996] |
| DIC | – | 22863.23 | – |
| WAIC | – | 22865.60 | – |
| Covid data | |||
| Intercept | β0 | −0.2901 | [−0.3816,−0.2013] |
| β1 | 0.2005 | [0.1156,0.2827] | |
| st. dev. | σ2 | 0.8673 | [0.7289,1.0195] |
| control par. | λ2 | 0.1678 | [0.0594,0.3423] |
| DIC | – | 2832.79 | – |
| WAIC | – | 2763.75 | – |
Fig. 8.
Sensitivity analysis - Leroux model: predicted probabilities for a citizen to experience at least 1 of 4 typical COVID-19 symptoms per municipality.
Fig. 9.
Sensitivity analysis - Leroux model: exceedance probabilities per municipality for the predicted probability for a citizen to experience at least 1 of 4 typical COVID-19 symptoms, with threshold .
Fig. 10.
Sensitivity analysis - Leroux model: predicted COVID-19 relative risk per municipality, based on data of confirmed cases between April 7 and April 9, 2020.
Fig. 11.
Sensitivity analysis - Leroux model: exceedance probabilities for the relative risk per municipality, based on data of confirmed cases between April 7 and April 9, 2020, with relative risk threshold .
A2. Postal code area analysis
In the postal code area analysis, we analyse the symptoms data with a Leroux model, but at the postal code area level. The postal code area is a subdivision of a municipality, such that each municipality with consists of Ni postal code areas. We define Ylm as a binary variable that takes a value 1 when person in postal code area with experienced at least one of the most typical symptoms. From the analysis of these data we calculate symptoms’ incidences at the postal code area level, which we subsequently aggregate within the municipality level. These are used as a covariate in a Leroux model for the analysis of the covid data, which are available on the municipality level. The methodology remains similar to the one introduced in the main text:
For the symptoms data, the model structure is then defined by
with the same parameter interpretations as presented in the main text. We fit the Leroux model, such that
again with the same parameter interpretations as given in the main text. The probability of a municipality’s inhabitant to experience at least 1 typical COVID-19 symptom is calculated as,
with the predictive mean of the symptoms’ incidence for postal code area l. We include again in the linear predictor in its standardised form, .
For the covid data, we fit a Leroux Poisson model with the same parametrisation as presented in the main text,
with the Leroux residual term Σ2, σ 2, λ 2, and Ω2 instead of resp. Σ1, σ 1, λ 1, and Ω1.
We use N(0, 1000) as a prior for all covariate effects, logit(λ) ~ beta(1, 1) for the control parameters, and penalised complexity (PC) priors (Simpson et al., 2017) for the precision parameters of the random effects, where we again set and . Table 5 and Fig. 12, Fig. 13, Fig. 14, Fig. 15 present the analysis results, which lie very close to the ones obtained in the analysis in the main text.
Table 5.
Estimation results.
| Effect | Parameter | Estimate | 95% credible interval |
|---|---|---|---|
| Symptoms data | |||
| Intercept | α0 | −1.6038 | [−1.6892,−1.5152] |
| single | α1 | −0.0552 | [−0.0826,−0.0279] |
| agecat1 | α2 | 0.1787 | [0.1472,0.2104] |
| agecat2 | α3 | −0.0919 | [−0.1261,−0.0577] |
| agecat3 | α4 | −0.6647 | [−0.7288,−0.6013] |
| male | α5 | −0.0980 | [−0.1544,−0.0420] |
| agecat1*male | α6 | 0.0686 | [0.0072,0.1302] |
| agecat2*male | α7 | 0.0882 | [0.0237,0.1528] |
| agecat3*male | α8 | 0.0039 | [−0.0961,0.1039] |
| st. dev. | σ1 | 0.0956 | [0.0749,0.1189] |
| control par. | λ1 | 0.9784 | [0.9219,0.9983] |
| DIC | – | 30331.12 | – |
| WAIC | – | 30333.03 | – |
| Covid data | |||
| Intercept | β0 | −0.2918 | [−0.3905,−0.1959] |
| β1 | 0.1552 | [0.0631,0.2418] | |
| st. dev. | σ2 | 0.9239 | [0.7722,1.0966] |
| control par. | λ2 | 0.2161 | [0.0830,0.4177] |
| DIC | – | 2835.97 | – |
| WAIC | – | 2767.52 | – |
Fig. 12.
Postal code area analysis - Leroux model: predicted probabilities for a citizen to experience at least 1 of 4 typical COVID-19 symptoms per postal code area.
Fig. 13.
Postal code area analysis - Leroux model: exceedance probabilities per postal code area for the predicted probability for a citizen to experience at least 1 of 4 typical COVID-19 symptoms, with threshold .
Fig. 14.
Postal code area analysis - Leroux model: predicted COVID-19 relative risk per municipality, based on data of confirmed cases between April 7 and April 9, 2020. The model includes symptoms’ incidence predictions, based on the postal code area analysis of the symptoms data, which were aggregated within the municipality level.
Fig. 15.
Postal code area analysis - Leroux model: exceedance probabilities for the relative risk per municipality, based on data of confirmed cases between April 7 and April 9, 2020, with relative risk threshold . The model includes symptoms’ incidence predictions, based on the postal code area analysis of the symptomsdata, which were aggregated within the municipality level.
A3. Analyses of rounds 2 and 4
Table 6, Table 7 depict estimation results with regards to the predictive ability of the symptoms' incidences, based on rounds 2 and 4 of the online survey.
Table 6.
Estimation results for β1, the effect of obtained from the analysis via a Leroux model of 341,320 respondents in the second round of the online survey, when investigating different time periods of confirmed cases. An asterisk (*) denotes a significant effect on a 5% significance level.
| period | estimate | 95% credible interval | no. cases |
|---|---|---|---|
| March 24 - March 26 | 0.1182 | [0.0356,0.2003]* | 3705 |
| March 25 - March 27 | 0.0701 | [-0.0173,0.1563] | 4016 |
| March 26 - March 28 | 0.0806 | [-0.0142,0.1752] | 3663 |
| March 27 - March 29 | 0.0906 | [-0.0083,0.1891] | 2987 |
| March 28 - March 30 | 0.1225 | [0.0308,0.2130]* | 3206 |
| March 29 - March 31 | 0.1390 | [0.0432,0.2334]* | 4039 |
| March 30 - April 1 | 0.1026 | [0.0029,0.2011]* | 4848 |
| March 31 - April 2 | 0.1300 | [0.0301,0.2285]* | 4565 |
| April 1 - April 3 | 0.1073 | [0.0078,0.2036]* | 4567 |
| April 2 - April 4 | 0.1453 | [0.0488,0.2384]* | 3989 |
| April 3 - April 5 | 0.1740 | [0.0790,0.2652]* | 3205 |
| April 4 - April 6 | 0.1284 | [0.0414,0.2122]* | 3415 |
| April 5 - April 7 | 0.1444 | [0.0543,0.2313]* | 3977 |
| April 6 - April 8 | 0.1010 | [0.0046,0.1926]* | 4881 |
| April 7 - April 9 | 0.1561 | [0.0626,0.2470]* | 5183 |
| April 8 - April 10 | 0.1409 | [0.0347,0.2448]* | 5990 |
| April 9 - April 11 | 0.1667 | [0.0396,0.2933]* | 5446 |
| April 10 - April 12 | 0.0933 | [-0.0547,0.2380] | 3768 |
| April 11 - April 13 | 0.0534 | [-0.1089,0.2091] | 2020 |
| April 12 - April 14 | 0.1339 | [-0.0149,0.2732] | 2473 |
| April 13 - April 15 | 0.2118 | [0.0773,0.3393]* | 3543 |
Table 7.
Estimation results for β1, the effect of obtained from the analysis via a Leroux model of 217,877 respondents in the fourth round of the online survey, when investigating different time periods of confirmed cases. An asterisk (*) denotes a significant effect on a 5% significance level..
| period | estimate | 95% credible interval | no. cases |
|---|---|---|---|
| April 7 - April 9 | 0.2191 | [0.1331,0.3035]* | 5183 |
| April 8 - April 10 | 0.2309 | [0.1342,0.3260]* | 5990 |
| April 9 - April 11 | 0.2267 | [0.1040,0.3470]* | 5446 |
| April 10 - April 12 | 0.1942 | [0.0502,0.3328]* | 3768 |
| April 11 - April 13 | 0.1812 | [0.0281,0.3299]* | 2020 |
| April 12 - April 14 | 0.1726 | [0.0288,0.3087]* | 2473 |
| April 13 - April 15 | 0.1691 | [0.0274,0.3027]* | 3543 |
| April 14 - April 16 | 0.1668 | [0.0322,0.2982]* | 4643 |
| April 15 - April 17 | 0.1862 | [0.0589,0.3128]* | 4532 |
| April 16 - April 18 | 0.2051 | [0.0801,0.3290]* | 3652 |
| April 17 - April 19 | 0.2992 | [0.1682,0.4243]* | 2468 |
| April 18 - April 20 | 0.2871 | [0.1581,0.4162]* | 2345 |
| April 19 - April 21 | 0.1886 | [0.0694,0.3093]* | 2867 |
| April 20 - April 22 | 0.1784 | [0.0666,0.2911]* | 3179 |
| April 21 - April 23 | 0.1717 | [0.0509,0.2922]* | 2893 |
| April 22 - April 24 | 0.2316 | [0.1023,0.3637]* | 2452 |
| April 23 - April 25 | 0.2716 | [0.1315,0.4170]* | 2078 |
| April 24 - April 26 | 0.2620 | [0.1166,0.4166]* | 1340 |
| April 25 - April 27 | 0.1553 | [0.0196,0.3038]* | 1288 |
| April 26 - April 28 | 0.0233 | [-0.0847,0.1406] | 1448 |
| April 27 - April 29 | 0.0284 | [-0.0810,0.1466] | 1743 |
References
- Adin A., Goicoa T., Ugarte M.D. Online relative risks/rates estimation in spatial and spatio-temporal disease mapping. Comput. Methods Programs Biomed. 2019;172:103–116. doi: 10.1016/j.cmpb.2019.02.014. [DOI] [PubMed] [Google Scholar]
- Alessi E.J., Martin J.I. Conducting an internet-based survey: benefits, pitfalls, and lessons learned. Soc. Work Res. 2010;34:122–128. [Google Scholar]
- Andrews D., Nonnecke B., Preece J. Electronic survey methodology: a case study in reaching hard-to-involve internet users. Int. J. Hum. Comput. Interact. 2003;16:185–210. [Google Scholar]
- Besag J., York J., Mollié A. Bayesian image restoration with two applications in spatial statistics. Ann. Inst. Stat. Math. 1991;43:1–59. [Google Scholar]
- Chen N., Zhou M., Dong X., Qu J., Gong F., Han Y. Epidemiological and clinical characteristics of 99 cases of 2019 novel coronavirus pneumonia in wuhan, china: a descriptive study. Lancet. 2020;395:507–513. doi: 10.1016/S0140-6736(20)30211-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Diggle, P. J., Ribeiro, Jr., P. J., 2007. Model-based Geostatistics. Springer, New York (USA).
- Dong Y., Mo X., Hu Y., Qi X., Jian F., Jiang F., Tong S. Epidemiology of COVID-19 among children in china. Pediatrics. 2020:e20200702. doi: 10.1542/peds.2020-0702. [DOI] [PubMed] [Google Scholar]
- Ganyani, T., Kremer, C., Chen, D., Torneri, A., Faes, C., Wallinga, J., Hens, N., 2020. Estimating the generation interval for COVID-19 based on symptom onset data. Preprint. 10.1101/2020.03.05.20031815 [DOI] [PMC free article] [PubMed]
- Jiang F., Deng L., Zhang L., Cai Y., Cheung C.W., Xia Z. Review of the clinical characteristics of coronavirus disease 2019 (COVID-19) J. Gen. Intern. Med. 2020;35:1545–1549. doi: 10.1007/s11606-020-05762-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lawson A.B. second ed. Chapman & Hall; Boca Rotan: 2013. Bayesian Disease Mapping: Hierarchical Modeling in Spatial Epidemiology. [Google Scholar]
- Leroux B., Lei X., Breslow N. Estimation of disease rates in small areas: a new mixed model for spatial dependence. In: Halloran M., Berry D., editors. Statistical Models in Epidemiology, the Environment and Clinical Trials. Springer-Verlag; New York: 1999. pp. 135–178. [Google Scholar]
- Neyens T., Lawson A.B., Kirby R.S., Faes C. The bivariate combined model for spatial data analysis. Stat. Med. 2016;35 doi: 10.1002/sim.6914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- R Core Team . R Foundation for Statistical Computing. 2020. R: A language and environment for statistical computing. [Google Scholar]; Vienna, Austria. https://www.R-project.org/
- Rue H., Martino S., Chopin N. Approximate bayesian inference for latent gaussian models by using integrated nested laplace approximations. J. R. Stat. Soc. 2009;71:319–392. [Google Scholar]
- Simpson D.P., Rue H., Riebler A., Martins T.G., Sørbye S.H. Penalising model component complexity: a principled, practical approach to constructing priors. Stat. Sci. 2017;32(1):1–28. [Google Scholar]
- Spiegelhalter D.J., Best N.G., Carlin B.P., Van Der Linde A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. 2002;64:583–639. doi: 10.1111/1467-9868.00353. [DOI] [Google Scholar]
- Ugarte M.D., Adin A., Goicoa T., Militino A.F. On fitting spatio-temporal disease mapping models using approximate bayesian inference. Stat. Methods Med. Res. 2014;23:507–530. doi: 10.1177/0962280214527528. [DOI] [PubMed] [Google Scholar]
- Watanabe S. Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. J. Mach. Learn. Res. 2010;11:3571–3594. [Google Scholar]
- World Health Organization (WHO), 2020. Health organization (WHO). https://www.who.int/dg/speeches/detail/who-director-general-s-opening-remarks-at-the-media-briefing-on-covid-19—11-march-2020.
- Wu F., Zhao S., Yu B., Chen Y.-M., Wang W., Song Z.G. A new Coronavirus associated with human respiratory disease in china. Nature. 2020;579:265–269. doi: 10.1038/s41586-020-2008-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang W., Cao Q., Qin L., Wang X., Cheng Z., Pan A., Dai J., Sun Q., Zhao F., Qu J., Yan F. Clinical characteristics and imaging manifestations of the 2019 novel Coronavirus disease (COVID-19):a multi-center study in Wenzhou City, Zhejiang, China. J. Infect. 2020;80:388–393. doi: 10.1016/j.jinf.2020.02.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu N., Zhang D., Wang W., Li X., Yang B., Song J. A novel Coronavirus from patients with pneumonia in China, 2019. N. Engl. J. Med. 2020;382:727–733. doi: 10.1056/NEJMoa2001017. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The covid data, as analysed in this study, are confidential. They are available in an aggregated format on https://epistat.wiv-isp.be/covid/. The symptoms data are confidential, but can be accessed after approval by the Corona Study steering committee.