Handling Imbalanced Medical Image Data: A Deep-Learning-Based One-Class Classification Approach

Abstract

In clinical settings, a lot of medical image datasets suffer from the imbalance problem which hampers the detection of outliers (rare health care events), as most classification methods assume an equal occurrence of classes. In this way, identifying outliers in imbalanced datasets has become a crucial issue. To help address this challenge, one-class classification, which focuses on learning a model using samples from only a single given class, has attracted increasing attention. Previous one-class modeling usually uses feature mapping or feature fitting to enforce the feature learning process. However, these methods are limited for medical images which usually have complex features. In this paper, a novel method is proposed to enable deep learning models to optimally learn single-class-relevant inherent imaging features by leveraging the concept of imaging complexity. We investigate and compare the effects of simple but effective perturbing operations applied to images to capture imaging complexity and to enhance feature learning. Extensive experiments are performed on four clinical datasets to show that the proposed method outperforms four state-of-the-art methods.

Graphical Abstract

1. Introduction

Computer-aided diagnosis is an important research field in medical imaging, where the goal of a majority of task is to differentiate malignancy from normal (i.e., benign or negative) findings [36, 47, 48]. With the development of deep learning, medical image classification has achieved remarkable progress [7, 47, 48]. Usually the training of deep learning models need plenty of labeled samples that belong to different classes. However, in many medical and clinical cases, it can be hard to collect a balanced dataset for training since some diseases have a low prevalence. This leads to the data imbalance problem, namely, the number of samples in different classes is not balanced.

Imbalanced data can negatively affect the performance of models significantly. Many models that perform well on balanced datasets cannot achieve good performances when it comes to their imbalanced counterparts [23]. To address this challenge, Anomaly Detection (AD) is proposed to learn models from samples that belong to the majority class and take samples that belong to the minority class as anomalies [29, 38]. Such method is also called One-Class Classification (OCC) [4], which focuses on learning models from samples belonging to a single class. Unlike multi-class classification tasks where the key is to learn discriminative features by comparing the samples from multiple different classes, the critical problem for one-class classification is how to effectively capture the single-class-relevant features. In previous work, there are many efforts on one-class learning and anomaly detection [2, 29, 38], which usually focus on feature fitting [9] or feature mapping [33]. For example, One-Class Support Vector Machine (OCSVM) works by mapping features from the given space to a new feature space. Based on OCSVM, many feature mapping methods have been proposed to form constraints in feature spaces. Another scheme of one-class learning is to train models that only respond to samples from a given single class. Deep neural networks have been widely employed in this scheme because of their powerful feature learning ability [15, 40, 51]. Examples include Convolutional Autoencoders (CAE) [9, 49] and Generative Adversarial Networks (GAN) based models [32, 42]. Researchers also propose end-to-end methods by adding other factors such as entropy-based loss and Gaussian Mixture to make positive and negative samples distinguishable [49, 51]. However, the performance of these works is still limited, especially for complex clinical image datasets.

How to learn discriminative clinical imaging features from a single class is an essential challenge for machine learning models. Generally, the features of medical images can be summarized into the following categories: (1) shape features; (2) texture features; (3) intensity features and (4) high-level statistical features [1, 19, 24]. For medical images, feature learning is challenging because of the large intra-class variance and the small scale of data samples. This becomes even more challenging when only samples from a single class are given to learn features.

In this work, a novel method, namely Image Complexity based One-Class Classification (ICOCC), is proposed to optimally learn single-class-relevant imaging features by leveraging the concept of image-complexity. Our method is inspired by the measure of image complexity [41]. Perturbed images reflect the complexity and discriminability within the class. If a model can perform well on classifying a set of perturbed images generated by given samples, it most likely has learned informative and inherent features of the given class. The intuition is that perturbing parts of an image will lead to the change of key features that are relevant to image classification. By training a classifier to distinguish the original and the perturbed images, the classifier can learn discriminative features of the given class and distinguish samples of other classes. The proposed method is implemented in a Convolutional Neural Network (CNN) framework and evaluated on four different biomedical imaging datasets, with a comparison with other previous related methods. The contributions of this paper are as follows:

1. A novel deep-learning-based model is proposed to address the dataimbalance problem in medical image datasets by leveraging imaging complexity.

2. Simple but effective perturbing operations are investigated to capturesingle-class-relevant features in medical images.

3. Extensive experiments are performed on four medical image datasetsto demonstrate that ICOCC outperforms the state-of-the-art methods.

2. Related Work

Imbalanced data classification can be handled using binary classification models or one-class classification models. We briefly summarize related work in the following.

Binary classification

The strategy behind this approach is to artificially balance the effects of model training [20]. A straightforward way is to balance the sample numbers by oversampling/undersampling [17, 28, 39]. For instance, [28] utilizes the extrapolation method to sample new minority class samples from the boundary area. Oversampling performance can also be improved through undersampling the minority class [8]. In addition, cost-sensitive learning [3, 26, 43] has been proposed to balance the influence of samples based on certain cost. For example, cost-sensitive SVM [20] focuses on integrating probability elicitation into the risk minimization procedure to minimize the prediction risk. Focal loss [25] can be used to add weights on the loss to make the network focus on samples with large loss values. [50] proposes to move the threshold to balance the margin between different classes. In general, these methods aim to balance the effects of the majority and minority class samples and show improved performance in some tasks.

One-class classification

There is a relatively small body of work in the one-class classification for medical images. Based on the feature learning methods, previous work can be summarized into two main schemes.

The first scheme aims to map the features of given samples to a new feature space in the training process. Then in the process of testing, the samples belonging and not belonging to the training class will be mapped into the same and different feature space respectively, making them distinguishable. A representative method is OCSVM [33], which tries to map features to a new feature space by kernel functions. OCSVM has been widely applied in the one-class classification task and has achieved remarkable performance in a variety of fields, especially with small scale datasets [22, 27]. For example, OCSVM is employed to identify the deterioration of patients in vital-sign data [6] and detect seizures in the human electroencephalogram (EEG) series [13]. Weighted OCSVM is designed to detect tumors in brain CT images [16]. Based on OCSVM, Support Vector Data Description (SVDD) is proposed to map the original images into a hypersphere instead of a hyperplane. Deep SVDD [31] replaces kernel functions with neural networks to extend SVDD to deep learning-based models. It proposes a new quadratic loss function to prompt the representation of samples into a minimum volume. As much as the advancement in some clinical datasets, these kernel based methods are still limited in complex clinical datasets.

The second scheme attempts to build models which only respond to the features of a given class. Thus these models can “recognize” samples belonging to the given class but fail to “recognize” those belonging to other classes, making the samples distinguishable. In that regard, autoencoders and adversarial training have been applied widely. For instance, [37] uses the reconstruction loss of autoencoder to remove noised samples and outliers from the training dataset, then gradually obtains a cleaner training dataset to train a one-class classification model. Some works further enhance the performance of autoencoders by employing adversarial learning [9, 42]. ADGAN [9] firstly trains a generative adversarial network, then attempts to generate a fake sample similar to the given image. The given class sample is easy to find such representation while the other classes are not. Using that, the algorithm is able to distinguish the abnormal samples. DAOL [42] employs autoencoder to reconstruct an image and encodes the generated images again to enhance performance. EGAN [45] replaces the generator with an autoencoder and employs both the reconstruction loss of autoencoder and the classification results of the discriminator to score samples. When it comes to application in clinical dataset, AnoGAN [32] employs GAN to learn normal optical coherence tomography (OCT) images of the retina to detect abnormal retina. However, all those autoencoder-based methods can not fully capture the features of images due to their limited learning ability.

Some methods also combine these two schemes by integrating CAE and OCSVM to extract single-class-relevant features. For example, to identify unhealthy regions in OCT images, [34] firstly employs a CAE to learn features of healthy images, and then uses the bottleneck features of CAE to train the OCSVM. Still, there is more to be done for image feature capturing.

In general, previous OCC methods are limited in learning discriminative class-relevant features, especially for images with complex features. How to optimally learn inherent features when only one-class samples are given is still an open and challenging research question. The proposed method provides a new approach that falls under the second scheme, as we propose to learn inherent image features by leveraging imaging complexity.

3. A Novel Framework for One-Class Classification

In this section, we formulate the one-class classification problem and elucidate the pipeline of our proposed method.

3.1. Definition and formulation

One-class classification (OCC) task aims to learn classification models when only samples belonging to one-class are given. The problem is formulated as follows. For a given class C and training samples$\mathcal{Y}$, the aim is to learn a scoring function $F(\mathcal{Y}):\mathcal{Y}\to R$. In R, a higher value indicates that a sample of $\mathcal{Y}$ is more likely to belong to C. Thus, for a testing sample X, we can compute its score F(X) and determine whether it belong to class C or not, based on a series of assessments.

3.2. One-class training and testing pipeline

Figure 1 depicts the pipeline of the proposed framework. To enable the model to effectively learn features of the given class, a key component of ICOCC lies in the novel mechanism of identifying perturbed samples to capture the inherent features of images. Because the classification of perturbed images is a highly complex task, discriminative and unique features of the given class can be learned if a machine learning model can effectively distinguish these perturbed images. The pipeline of our method includes three steps:

Figure 1:

The pipeline of the proposed one-class framework. In the training phase, perturbed images x = {x₁; ⋯; x_n} generated from a sample X are used to train a classifier to classify them into n sub-classes. In the testing phase, we perturb a testing sample and input into the classifier to obtain the prediction matrix, then we calculate the score and classify it into the corresponding class.

First, model the complexity of training samples by generating their perturbed counterparts. The perturbation can be defined as:$\mathcal{T}=\left\{{\mathcal{T}}_1,\dots ,{\mathcal{T}}_n\right\}$, ${\mathcal{T}}_c$ represents a perturb way with corresponding label c ∈ {1,…,n}. Inspired by data augmentation [35] and unsupervised representation learning [14], the perturbing operations mainly include displacement (shift), rotation, flipping, color transform, etc. All those operations can potentially be applied to perturb an original image. Rotation and flipping are suitable to learn the contour information [14], while the contour of medical images is usually round, making them less sensitive to rotation and/or flipping operations. The shift operation is suitable to learn texture and structure features [10, 11]. When we shift a patch, the texture (e.g., the density of tumor) and structure (e.g., the position of nucleus and cytoplasm) features can be changed, thus be identified by the classifier. In this way, the shift is used in this paper to generate multiple perturbed images. Specifically, the perturbation is defined as:

$$\begin{gathered} \mathcal{T}={\mathcal{T}}_x\cup {\mathcal{T}}_y \\ =\left\{T_x^1,\dots ,T_x^p\right\}\times \left\{T_y^1,\dots ,T_y^p\right\} \end{gathered}$$ (1)

${\mathcal{T}}_x^t$,${\mathcal{T}}_y^t$ represent shifting t times in x, y direction. p is the number of displacement operation in each direction. In the experiments, we shift {0, i, 2·i, ⋯·, (p-1)·i} pixels each in x and y direction, i is the pixel number we shift each time. Thus, each original image is enriched to $n=\left|{\mathcal{T}}_x\right|\times \left|{\mathcal{T}}_y\right|=\text{p}\times \text{p}$ perturbed images (including the original image itself). Figure 2 is an example to show how to perturb one sample into n=9 images when p=3. Through the displacement, the shape, texture, intensity and high-level statistical features will be perturbed. At the conceptual level, these perturbed images contain discriminative features that reflect the class complexity. It should be noted the difference between the proposed perturbation method and the common definition of data augmentation. The perturbation aims to construct a multi-class classification task for the given samples of a single class, while usually data augmentation aims to augment the samples from the same class to enhance generalization.

Figure 2:

Demonstration of image perturbations with the shift operation on a nature image (a) and a cell image (b) selected from our experimented datasets. Assume the perturbation number p=3, then the sample X is perturbed into n=p×p=9 images {x₁; ⋯ x_g}, with corresponding pseudo labels 1 ~ 9. To show the perturbation more clear, here we insert white lines in each perturbed image, which are not exist in the experiments. As shown in this demo, the texture and structure features are perturbed.

Second, use the perturbed images to train a classifier that can distinguish corresponding perturbations (i.e., classifying into the sub-classes as referred in the above paragraph). The classifier will learn the original and perturbed features when classifying them into corresponding perturbed classes. The proposed framework allows a variety of classification models to be integrated into this method to classify perturbed images into corresponding sub-classes. Here the Wide Residual Network (WRN) [44] is employed as the CNN classifier in the pipeline. The structure of the network is shown in Figure 3. For each sample X, the CNN classifier outputs a matrix of size n × n by classifying n perturbed images into n sub-classes.

Figure 3:

The structure of the deep learning classifier used in ICOCC. Each dashed block is composed of three convolutional layers (blue box), three blocks are utilized for images of size 32×32, and four blocks for images of size 64×64. Each blue box represents a Convolution/Add/Dense layer, a batch normalization layer and an activation layer. For all convolutional layer, ReLU is used as the activation function, the kernel size is set to 3×3, and the kernel number in each dashed block is 16, 64, 128 and 256 respectively. For all ADD layers, the number represents the shape of the feature map. Skip connection layer is also used to convert more features between different layers.

The third step is to classify a test sample using the trained one-class model. Given a testing image, we can obtain a n×n matrix P = {p₁₁,·⋯ ,p_nn} by applying the same perturbation operations and input them into the learned classifier. p(i, j) represents the probability of image x_i belonging to sub-class y_j. Because the classifier is trained by perturbed positive samples, it will be able to classify positive samples into corresponding sub-classes. In this way, for a positive sample, P is more likely a unit diagonal matrix. While for a negative sample, P is more likely a random matrix because the classifier can not classify the sub-class images into corresponding sub-classes. Thus the positive and negative samples can be distinguished by observing the diagonal elements of P. Inspired by the cross-entropy calculation [15, 30], the score s of each sample X in ICOCC can be calculated by the following formula:

$$s(X)=\sum _{i=0}^{n-1}\text{log}p\left(y\left(x_c\right)\mid c\right)$$ (2)

where c ∈{0, ⋯·, n-1} is the class of a perturbed image x. p(y(x_c)| c) is the probability of classifying x_c into class c.

3.3. Evaluation

After obtaining the scores of testing samples, both the Area Under receiver operating characteristic Curve (AUC) and the Area Under Precision-Recall curve (AUPR) are used as evaluation metrics. The AUPR metric is calculated in two ways: AUPR-NP (samples from the given class are considered positive) and AUPR-AP (samples from the other classes are considered positive).

4. Experiments

The proposed method is extensively evaluated in three aspects: 1) comparing ICOCC to other existing one-class learning methods to show its superior performance (Section 4.2); 2) comparing to previous methods implemented using perturbation-based data augmentation (Section 4.3). 3) comparing the effects of different perturbing operations (displacement vs. displacement+rotation) to show its robustness (Section 4.4); 4) showing the converging speed of ICOCC (Section 4.5); and 5) comparing to a binary classification method with data oversampling (Section 4.6).

4.1. Experimental settings and datasets

In all experiments, the number of shift operation p is set to 6, which means that each sample is perturbed into $\text{n}=\Vert {\mathcal{T}}_x\Vert \times \Vert {\mathcal{T}}_y\Vert =\text{p}\times \text{p}=36$ images. For an image of size 32×32, we shift $\text{i}=\frac{32}{6}\approx 5$ pixels each time, for an image of size 64×64, we set $\text{i}=\frac{64}{6}\approx 10$ pixels. Keras [5] is employed with an NVIDIA TITAN GPU to conduct the experiments. Adam [21] is adopted as the optimizer, with the learning rate of 0.0002 and the batch size of 128. These parameters are fixed across all the experiments in this study.

Our experiments include four different imaging datasets of different modalities, as briefly described in Table 1. We use two breast screening datasets with segmented regions: MRI and FFDM for breast tumor diagnosis, in which a majority of them are confirmed as tumors while a minority of them are suspicious but normal tissues. We use a public cytopathologic image dataset: Human Epithelial Type 2 Cell (Hep-2)¹, which is used for autoimmune disease diagnosis. The image examples of each dataset are shown in Figures 4, 5, 6 and 7. The proportion of normal class is 67.8%, 82.3%, 81.8%, and 44.4%, for the MRI, FFDM, SOKL, and Hep-2 dataset, respectively. Note that in the HEp-2 dataset, there are 6 classes and the sum of the five abnormal classes accounts to 55.6%. The details are as follows.

Table 1:

Statistics of the four imbalanced datasets. The proportion of normal class is 67.8%, 82.3%, 81.8%, and 44.4%, for the MRI, FFDM, SOKL, and Hep-2 dataset, respectively. Note that in the HEp-2 dataset, there are 6 classes and the sum of the five abnormal classes accounts to 55.6%. In the MRI and FFDM datasets, tumor images (positive) are utilized to train the model because the normal class (negative) is difficult to define.

Dataset	Class	Dimension	Training (positive)	Testing	Positive in testing	Total
MRI	2	32×32×1	1000	1872	946	2872
FFDM	2	64×64×1	200	104	52	304
SOKL	2	64×64×3	115	66	33	181
HEp-2	6	64×64×1	1000	2000	333	8000

Figure 4:

Samples of the breast tumor MRI dataset.

Figure 5:

Samples of the FFDM dataset.

Figure 6:

Samples of the space-occupying kidney lesion dataset.

Figure 7:

Samples of the HEp-2 dataset. The first two rows come from training data, while the last two rows come from testing data.

Breast Magnetic Resonance Imaging (MRI) dataset:

This dataset has 1946 tumor images (positive samples) and 926 normal (suspicious) images. The image size ranges from 8 to 125 pixels, with a mean size of 31 pixels. We resize all the images to 32×32 pixels.

Breast Full-Field Digital Mammography (FFDM) dataset:

This dataset includes 252 tumor images and 52 normal (suspicious) images for testing. The image size ranges from 100 to 500 pixels, we resize all the images to 64×64 pixels.

Space-occupying kidney lesion (SOKL) dataset:

The type of lesion is the most important prognostic factor that affects patients’ survival and management [18]. This is a dataset aims to distinguish benign lesion samples from malignant (renal cell carcinoma) samples. It includes 33 benign cases (negative) and 148 malignant cases (positive). We use 115 malignant cases for training, 33 benign and malignant cases for testing.

HEp-2 Cell Image dataset:

This is a publicly available dataset provided by the International Conference on Image Processing (ICIP) 2013 [12] for HEp-2 cell image classification competition. It consists of images of 6 categories corresponding to 6 stages of mitosis. The whole dataset contains more than 60,000 images. Here we select 1000 images in each of the 6 categories/classes for training, and another 2000 images (333 different samples from the same training category and 1667 negative samples from the other categories) for testing. All images are resized from approximately 80×80 pixels to 64×64.

4.2. Comparison with four previous OCC methods

The proposed method is compared with four previous one-class classification algorithms: OCSVM [33], COCSVM [15], DSEBM [46], and DAGMM [51]. All deep learning methods are trained for 200 epochs. Since ICOCC augments each sample into 36 images, it is trained for $\frac{200}{6}\approx 6$ epochs, where all methods keep comparable calculation consumption. We run each algorithm for 4 times and report the average of the performance. The code of all methods will be available online when the paper is accepted.

OCSVM

One-Class SVM [33] attempts to learn a mapping to project the original samples into a new feature space by kernel functions (e.g., linear, RBF). Here RBF kernel is used and each original image is reshaped into a vector as the feature input into the algorithm. We grid search the parameters slack variable c ∈{0.01, 0.02, ⋯·, 0.09} and regularization parameter g ∈{2⁻⁷, 2⁻⁶, ⋯ ·,2²} respectively, then report the best performance of the model. Note that for OCSVM the ground truth labels of the testing set are accessed to select the best performance.

COCSVM

This method is a two-stage combination of CAE and OCSVM. Firstly an autoencoder is trained with training samples, then the bottleneck features are used to train the OCSVM. Similar to the discriminator and generator of DCGAN [30], for images of size 64×64, a ten-layer network is used with 256 bottleneck nodes; for images of size 32×32, an eight-layer network is used with 256 bottleneck nodes. The parameter settings of OCSVM are the same as the OCSVM method.

DSEBM

Deep structured energy-based Model (DSEBM) [46] directly models the data distribution with deep architecture and uses an energy function as the output of the model. It uses the score matching method which connects an EBM with a regularized autoencoder to train the model. Here the discriminator of DCGAN [30] is utilized as the basic model.

DAGMM

Deep Autoencoding Gaussian Mixture Model (DAGMM) [51] employs an autoencoder to compress data and obtain a reconstruction loss, which is further fed into a Gaussian Mixture Model (GMM). By jointly training with GMM, the autoencoder can escape from local optima and further reduce reconstruction errors, thus compress normal samples while deconstructing abnormal samples. Here the autoencoder is set to have the same structure as the CAE in COCSVM.

All the related experiment results are shown in Table 2 and Figure 8. As can be seen, ICOCC outperforms the four traditional models by a noticeable margin, indicating an overall superiority of the proposed framework. Note that there are certain classes in the HEp-2 dataset that ICOCC performs lower, which is mostly because the cellular shapes in these classes present greater intra-class variations. Also, note that previous methods exhibit overall lower performance on the classification of the 6th class in the HEp-2 dataset. This is probably because of the large variation within this class (see Figure 7), especially the extracellular matrix.

Table 2:

Comparison of ICOCC to four other previous methods. Note that “—“ indicates the performance metric values are meaningless when AUC=0.5.

Data	Methods	c	OCSVM	COCSVM	DAGMM	DSEBM	ICOCC
MRI	AUC	1	0.855	0.883	0.629	0.764	0.969
	AUPR-NP	1	0.861	0.895	0.545	0.759	0.972
	AUPR-AP	1	0.858	0.870	0.722	0.773	0.949
FFDM	AUC	1	0.753	0.680	0.563	0.737	0.924
	AUPR-NP	1	0.819	0.670	0.563	0.633	0.947
	AUPR-AP	1	0.668	0.665	0.660	0.633	0.916
SOKL	AUC	1	0.657	0.621	0.5	0.506	0.703
	AUPR-NP	1	0.618	0.658	—	0.475	0.692
	AUPR-AP	1	0.646	0.590	—	0.523	0.662
	AUC	1	0.785	0.662	0.556	0.779	0.941
		2	0.824	0.819	0.520	0.499	0.810
		3	0.602	0.639	0.497	0.710	0.825
		4	0.386	0.529	0.469	0.490	0.595
		5	0.546	0.452	0.527	0.687	0.710
		6	0.190	0.253	0.499	0.228	0.618
		avg	0.556	0.559	0.511	0.565	0.750
HEP-2	AUPR-NP	1	0.444	0.217	0.260	0.520	0.819
		2	0.529	0.513	0.311	0.225	0.324
		3	0.182	0.251	0.235	0.247	0.619
		4	0.128	0.184	0.118	0.150	0.186
		5	0.193	0.134	0.167	0.536	0.409
		6	0.098	0.107	0.458	0.108	0.242
		avg	0.262	0.234	0.258	0.298	0.433
	AUPR-AP	1	0.932	0.921	0.914	0.924	0.987
		2	0.955	0.956	0.918	0.863	0.962
		3	0.907	0.898	0.915	0.931	0.941
		4	0.828	0.880	0.885	0.870	0.898
		5	0.827	0.859	0.873	0.867	0.907
		6	0.701	0.734	0.917	0.726	0.896
		avg	0.858	0.875	0.904	0.863	0.932

Figure 8:

The ROC and PR (Precision-Recall) curves on the MRI dataset.

4.3. Comparing to previous methods implemented using perturbation-based data augmentation

In this comparison, we implement previous methods using augmented number of samples generated by the perturbation operation. For the HEp-2 data, we use class 1 as an example. As shown in Table 3, perturbation-based data augmentation increases the AUCs (comparing to Table 2) for some of these related methods on some datasets. It appears that the deep learning-based methods (e.g. DAGMM and DSEBM) mostly benefit from this data augmentation but others not, indicating that the perturbation operation may not be an effective data augmentation strategy for non-deep learning-based methods (this observation merits further investigation in future work). But overall, our proposed method shows highest performance when compared to others (regardless using or not using perturbation-based data augmentation).

Table 3:

The AUCs of previous methods implemented using perturbation-based data augmentation and the comparison to the ICOCC method.

Data	OCSVM	COCSVM	DAGMM	DSEBM	ICOCC
MRI	0.727	0.611	0.716	0.691	0.969
FFDM	0.823	0.633	0.651	0.825	0.924
SOKL	0.615	0.658	0.5	0.677	0.703
HEp-2	0.7 2	0.713	0.510	0.682	0.941

4.4. Comparison of different perturbation operations

The image perturbation is the core of ICOCC and different perturbation operations reflect different ways to increase the image complexity. We mainly use the displacement operation in all the above-presented experiments. Here we further compare the experiment effects by incorporating rotation as the additional perturbation operation. Here T36 denotes the 6×6 displacement operations as described in Section 3.2; R1T36 denotes adding an additional rotation over the T36.

As shown in Table 4, both the T36 and R1T36 perturbations achieve remarkable performance on the four datasets, where T36 performs better than R1T36. This demonstrates that ICOCC is relatively steady for these two perturbation operations; it also indicates that on these datasets the rotation is less effective than displacement in changing imaging complexity, which makes sense according to the nature of these medical images.

Table 4:

Comparison of different imaging perturbation operations. T36 denotes the 6×6 displacement operations and R1T36 denotes adding an additional rotation over the T36.

Dataset	MRI		FFDM		SOKL		HEp-2
Perturbation	T36	R1T36	T36	RIT36	T36	R1T36	T36	R1T36
AUC	0.969	0.953	0.924	0.914	0.703	0.642	0.941	0.939
AUPR-NP	0.972	0.960	0.947	0.938	0.692	0.593	0.829	0.803
AUPR-AP	0.949	0.945	0.916	0.871	0.662	0.612	0.988	0.986

To show the effectiveness of ICOCC, we also plot the converge curves of ICOCC. Figure 9 shows the accuracy of distinguishing perturbed testing positive/negative samples of the classifier. We can see that the accuracy on perturbed positive samples is much higher than that of the negative samples. Figure 10 shows the loss value of the classifier when training the classification model to identify the perturbed images into the corresponding sub-classes. We can see that the classifier can converge relatively fast among different datasets.

Figure 9:

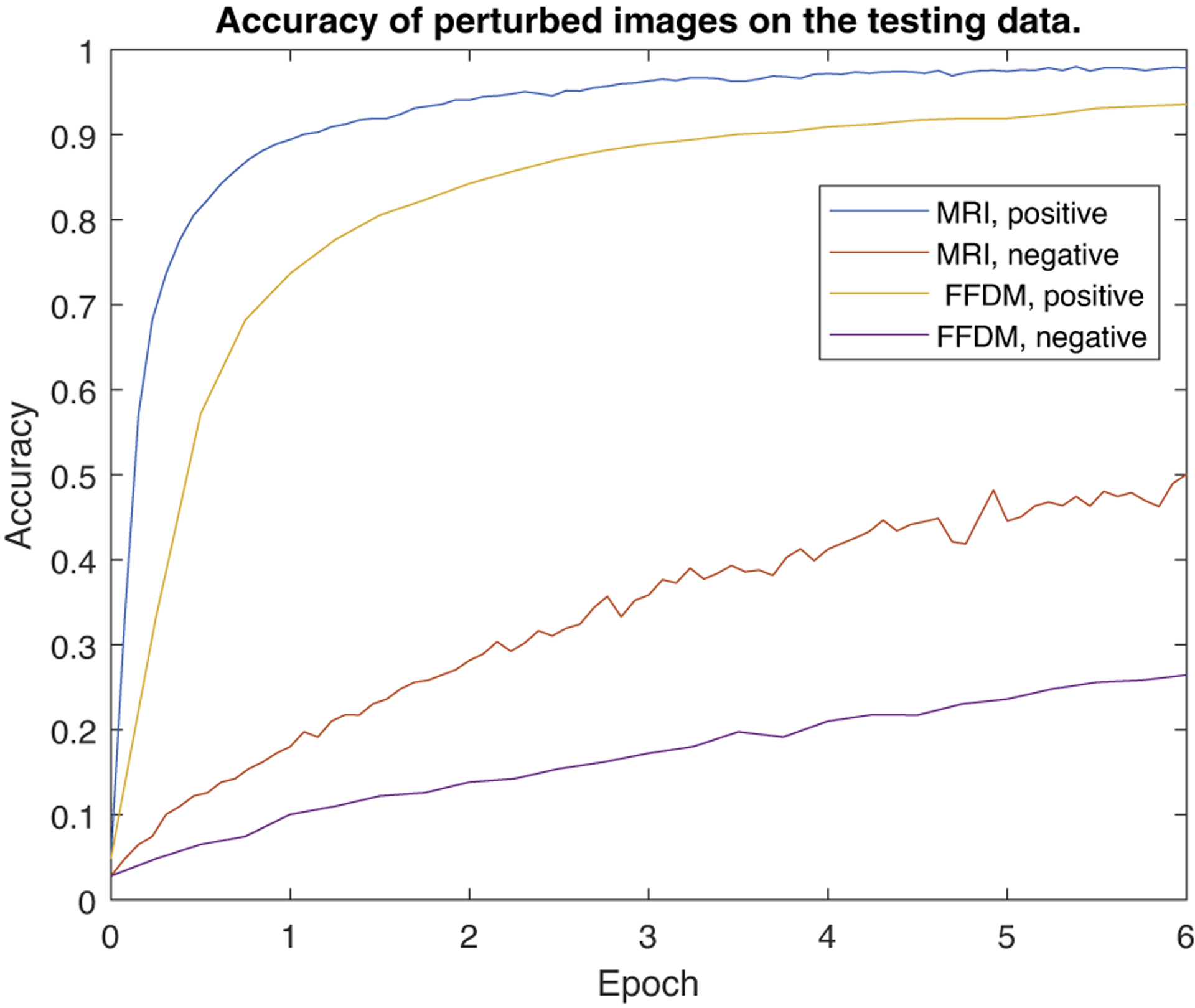
The accuracy curve of the classification task where perturbed images are classified into corresponding sub-classes for positive/negative samples of testing data. The classifier can distinguish perturbed positive samples efficiently, while can’t distinguish perturbed negative samples, making them distinguishable.

Figure 10:

The loss curve when training the model to classify images into corresponding sub-classes for training data. The proposed method converges in three epochs for these four datasets.

4.5. Converge speed

To show the effectiveness of the proposed method, we also plot the converge curves of ICOCC. Figure 9 shows the accuracy of distinguishing perturbed testing positive/negative samples of the classifier. We can see that the accuracy on perturbed positive samples is much higher than that of the negative samples. Figure 10 shows the loss value of the classifier when training the classification model to identify the perturbed images into the corresponding sub-classes. We can see that the classifier can converge relatively fast among different datasets.

4.6. Comparison to a binary classification method with data oversampling

This experiment is to compare our method to a binary classification method that uses data oversampling to deal with imbalanced data. Here we use the WRN model [44] to implement the binary classifier, where the structure of the model is the same to the classifier used in the ICOCC, except that the last layer is changed to two nodes for binary classification. Because there are only 52 and 33 negative cases in the FFDM and SOKL datasets, it limits the number of samples for training a binary classifier and thus we skip the experiment on these two datasets. As the HEp-2 dataset has 6 classes, we simplify the multi-class tasks into a binary classification by labelling the samples of the first class as positive and all other classes as negative. For training on the MRI and Hep-2 datasets, we use 1000 positive samples and 200 negative samples, and the negative class is augmented to 1000 samples by oversampling. For testing, we maintain the test data used in Section 4.2 except the 200 negative samples moved to the training set to train the binary classifier. As shown in Table 5, the oversampling technique improves the classification when compared to without using the oversampling, but the improved performance is still lower than our proposed method.

Table 5:

Comparison of our one-class model to a binary classifier using data oversampling. Our method (ICOCC) uses 1000 positive (pos) and 0 negative (neg) samples. For binary classification, we use 1000 positive samples and 200 negative samples and ”200ov” denotes the negative class is augmented to 1000 samples by oversampling.

		MRI			HEp-2
Train	Pos neg	1000 200	1000 200ov	ICOCC	1000 200	1000 200ov	ICOCC
AUC		0.957	0.961	0.969	0.839	0.850	0.941
AUPR-NP		0.951	0.959	0.972	0.360	0.431	0.829
AUPR-AP		0.955	0.965	0.949	0.843	0.891	0.988

5. Conclusion

In this work, a novel pipeline is proposed for the one-class classification task. We leverage the concept of image complexity to train the CNN models by capturing discriminative and inherent imaging features through selfperturbation of the given samples from a single class. The proposed method is extensively evaluated on both public and internal datasets and has shown superior performance on all of them when compared with other one-class models. Promising results are shown in datasets from cellar level to tissue level as well as different image modalities. We also look into the effects of different perturbation operations to gain insights on how different perturbation methods perform differently in feature capturing. Going forward, we envision our method to be applied to more clinical and medical applications for one-class classification and anomaly detection. Also, perturbation methods tailored to specific tasks or to work on high-resolution images where anomalies are locally located merit further investigation in future work.

Highlights.

• A novel deep-learning-based model for the data imbalance problem.

• Effective perturbing operations to capture single-class-relevant features.

• State-of-the-art performance on four imbalanced medical image datasets.