Evolution of the Kondo lattice electronic structure above the transport coherence temperature

Significance

The temperature ($T$)-dependent evolution of the Kondo lattice electronic structure is a long-standing topic of theoretical and experimental investigation, still lacking a truly microscopic theory that agrees with a full experimental characterization. Here multiple characteristic $T$ scales of the interaction of localized $f$ moments with conduction electrons in the Kondo lattice CeCo${\mathrm{I}\mathrm{n}}_5$ are identified and investigated using angle-resolved photoemission measurements that substantiate dynamical mean-field theory which newly includes the full realism of crystalline electric-field (CEF) $f$ splittings. Thereby errors in the itinerant versus localized $f$-state classification from standard density functional theory are corrected, microscopic insight into the broad $T$-range crossover of $f$-hybridization effects is gained, and a prediction of CEF degeneracy crossover below the lattice coherence $T$ is made.

Abstract

The temperature-dependent evolution of the Kondo lattice is a long-standing topic of theoretical and experimental investigation and yet it lacks a truly microscopic description of the relation of the basic $f$-$c$ hybridization processes to the fundamental temperature scales of Kondo screening and Fermi-liquid lattice coherence. Here, the temperature dependence of $f$-$c$ hybridized band dispersions and Fermi-energy $f$ spectral weight in the Kondo lattice system CeCoIn₅ is investigated using $f$-resonant angle-resolved photoemission spectroscopy (ARPES) with sufficient detail to allow direct comparison to first-principles dynamical mean-field theory (DMFT) calculations containing full realism of crystalline electric-field states. The ARPES results, for two orthogonal (001) and (100) cleaved surfaces and three different $f$-$c$ hybridization configurations, with additional microscopic insight provided by DMFT, reveal $f$ participation in the Fermi surface at temperatures much higher than the lattice coherence temperature, $T^{*}\approx 45$ K, commonly believed to be the onset for such behavior. The DMFT results show the role of crystalline electric-field (CEF) splittings in this behavior and a $T$-dependent CEF degeneracy crossover below $T^{*}$ is specifically highlighted. A recent ARPES report of low $T$ Luttinger theorem failure for CeCoIn₅ is shown to be unjustified by current ARPES data and is not found in the theory.

In heavy fermion systems, understanding the nature of heavy fermion states and associated metallic states with strong electron correlation is of prime importance to clarify emergent exotic phenomena, such as unconventional superconductivity and quantum criticality. This class of materials exhibits at low temperature ($T$) an itinerant Fermi liquid due to Kondo screening that arises from hybridization of $f$ and conduction band ($c$) states and emerges from an $f$ local moment regime at high $T$ (1–3). The $f$ electrons are predicted (3, 4) to be included in a “large” Fermi surface (FS) for the former and excluded from a “small” FS for the latter. One of the key unsolved problems is finding what determines the $T$ scale(s) for the evolution of this behavior for the dense periodic “Kondo lattice” of $f$ moments. Theoretical models of the Kondo lattice involve two basic temperature scales, the single-impurity Kondo temperature ($T_{\text{K}}$) and the lattice coherence temperature ($T^{*}$). There has been debate as to the relative magnitudes of the two $T$ scales (5, 6) and whether only one $T$ scale is relevant to the lattice problem (7, 8). Although there have been intensive studies on the Kondo breakdown of $f$-$c$ hybridization and consequent abrupt changes of the FS size at low $T$ or with variation of a tuning parameter near a quantum critical point (9, 10), there have been few studies on the microscopic understanding of $f$-$c$ hybridization $T$ scales extending to high $T$ (5). Previous theoretical studies, with a focus on large-to-small FS changes with $T$, include two-dimensional (2D) lattice model calculations (11, 12) and, aimed at CeCo${\mathrm{I}\mathrm{n}}_5$, density functional theory plus dynamical mean-field theory (DFT+DMFT) calculations (4, 13) with single or multiple $f$ orbitals. A commonly held belief that $f$-$c$ hybridization occurs only below $T^{*}$ is not citable in any microscopic description, but is codified in a universal scaling formula of the 4$f$ density of states (DOS) proposed for the phenomenological two-fluid model (14).

On the experimental side, the issue of the FS size $T$ evolution has recently been highlighted in two angle-resolved photoelectron spectroscopy (ARPES) measurements. YbRh₂Si₂ provides a hole analog to Ce heavy fermion materials and is the only system where the large (hole) FS has been observed at low $T$ by ARPES (15). In the most recent study (16) which includes a well-cited discussion of the general theoretical issues of the T evolution of heavy fermion materials, this large FS was found to extend to higher $T$ than expected, and the transition to the small FS is yet to be observed. [The large FS has also been observed in low T de Haas van Alphen (dHvA) experiments, e.g., CeCoIn₅ (17) and YbRh₂Si₂ (18), but which are not easily extended to high T.] For the Kondo lattice system CeCo${\mathrm{I}\mathrm{n}}_5$, a more recent ARPES study (19) was somewhat similar in finding that the transition from localized to itinerant behavior begins at unexpectedly high $T$, but was quite different in reporting that the $f$ electrons are still mostly localized even at low $T$; i.e., the applicability of the Luttinger theorem for CeCo${\mathrm{I}\mathrm{n}}_5$ was challenged. It was suggested that both these findings might arise somehow from crystal-field excitations.

In the present work, we use both ARPES and DFT+DMFT calculations, including both spin–orbit and crystalline electric-field (CEF) splittings of the $f$ states, to investigate the $T$-dependent electronic structure of the Kondo lattice system CeCo${\mathrm{I}\mathrm{n}}_5$. Resonant enhancement of the ARPES Ce 4$f$ spectral weight is used to highlight Fermi-level ($E_{\text{F}}$) participation of $f$ electrons in the three-dimensional (3D) FS, whose detailed topology is revealed using measurement from two orthogonal (001) and (100) surfaces. Experimentally we confirm, but in much greater detail, the general sense of previous ARPES findings of $f$-electron participation in the FS to temperatures much higher than $T^{*}$, far into the logarithmic $T$ regime of “incoherent” Kondo spin–flip scattering. The DFT+DMFT calculations agree with this finding and elucidate the role(s) of CEF $f$ states in this high-$T$ behavior. Specifically, the DFT+DMFT spectral functions explicitly show and confirm the concept (20) of a $T$-dependent crossover of the Kondo resonance effective degeneracy of the two lowest CEF $f$ states. However, our DMFT results show that crystal-field excitations do not lead to a failure of the Luttinger theorem at low $T$ and we show that none of the current ARPES data for CeCo${\mathrm{I}\mathrm{n}}_5$, including our own, can support such a dramatic claim.

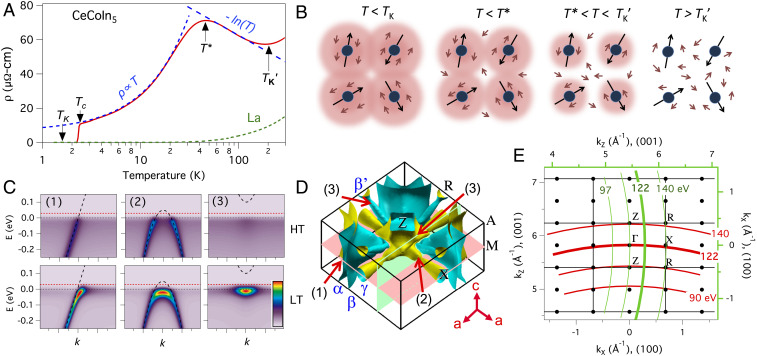
The $T$ scales specific to CeCo${\mathrm{I}\mathrm{n}}_5$ are illustrated in relation to its resistivity profile in Fig. 1A with schematic images of the Kondo lattice screening $T$ regimes in Fig. 1B. First, the single impurity Kondo temperature $T_{\text{K}}$ corresponds to the crossover from a logarithmic regime (extending far above $T_{\text{K}}$) of incoherent spin–flip scattering with antiferromagnetic Kondo coupling (described by perturbation theory) to a nonperturbative strong Kondo coupling regime that ultimately leads to a fully screened Kondo singlet ground state (well below $T_{\text{K}}$). The high-temperature onset appearance of the –ln($T$) Kondo scattering regime, for which we introduce the label $T_{\text{K}}^{\prime }$, is roughly estimated by the resistivity minimum crossover ($\sim$200 K) from the lattice phonon scattering contribution to the electrical resistivity (21). The true mathematical onset of logarithmic Kondo scattering is in fact infinity. In dilute $f$ moment systems, the resistivity profile eventually plateaus to a constant value below $T_{\text{K}}$. Resistivity profile scaling behavior in a La dilution study of CeCo${\mathrm{I}\mathrm{n}}_5$ has determined a very small value of $T_{\text{K}}$ $\approx 1.7$ K (22), and $T_{\text{K}}$ $\approx 5$ K was also estimated from the temperature at which the entropy obtained from specific heat measurements (23) reaches a value of $\frac{1}{2}R$ln2.

Fig. 1.

Kondo lattice hybridization concepts and $f$-$c$ hybridization configurations. (A) Identification of the Kondo temperature $T_{\text{K}}$, lattice coherence temperature $T^{*}$, and other $T$ transitions (main text) relative to the temperature-dependent resistivity of CeCo${\mathrm{I}\mathrm{n}}_5$. (B) Schematics of four different Kondo screening temperature regimes. (C) Schematic spectral image plots of three different $f$-$c$ hybridization configurations found in CeCo${\mathrm{I}\mathrm{n}}_5$ shown for low and high temperatures. (D) Bulk Brillouin zone and localized DFT FS of CeCo${\mathrm{I}\mathrm{n}}_5$ and high-symmetry points. Resonance photon energy cuts at 122 eV for the two cleave directions is indicated by transparent planes. (E) Constant photon energy arcs for normal emission relative to the bulk Brillouin zone for the two different orthogonal cleave surfaces: (001), red lines; and (100), green lines.

For a dense periodic array of $f$ magnetic moments, intersite coupling between $f$ electrons (schematically represented by overlapping Kondo screening clouds in Fig. 1B) leads to coherence of the $f$-$c$ scattering and a downturn in the resistivity. Hence the transport lattice coherence temperature $T^{*}$ is identified experimentally as the resistivity maximum, $\sim$45 K in CeCo${\mathrm{I}\mathrm{n}}_5$. Partial screening of the $f$ moments in the two intermediate $T$ regimes in Fig. 1B and partial coherence below $T^{*}$ are important concepts for our understanding, which naturally allow for $T_{\text{K}}<T^{*}<T_{\text{K}}^{\prime }$. The broad crossover behavior and $T$-scale definitions are further discussed in SI Appendix, section S.1.

A final low $T$ scale specific to CeCo${\mathrm{I}\mathrm{n}}_5$ derives from its proximity to a nearby antiferromagnetic quantum critical point in Ce(Co,Rh)${\mathrm{I}\mathrm{n}}_5$. Its unusual $T$-linear resistivity profile below 20 K is thought to be a signature of this quantum criticality. Additionally, analyses of two other spectroscopic signatures of quantum criticality, $T$ linearity of the Kondo $f$-peak width and $E/T$ scaling of the Kondo $f$-peak lineshape, have recently been performed on CeCo${\mathrm{I}\mathrm{n}}_5$ using scanning tunneling microscopy (STM) (24) and ARPES (19).

Three-Dimensional Fermi Surface k Locations

The temperature dependences of three different $f$-$c$ hybridization configurations, schematically shown in Fig. 1C, are studied. Their $k$ locations relative to the experimentally determined FS topology (25) are indicated in Fig. 1D. The $E_{\text{F}}$ crossing of the quasi-2D $\alpha$ band (and also the $\beta$ band) corresponds to the configuration 1, where the low $T$ $f$-$c$ hybridization causes a heavy mass dispersion of the $d$ band near $E_{\text{F}}$ with enhanced $f$ weight in the dispersion kink. In configuration 2, two $c$-band dispersions form a narrow hole pocket at high $T$ and induce even greater $f$ weight below $E_{\text{F}}$ at low $T$ with possible removal of the $E_{\text{F}}$ crossings. This configuration arises at the tip of the diamond-shaped $\gamma$ sheet near the zone center. In configuration 3, an unoccupied electron-like $c$-band minimum exists above $E_{\text{F}}$, invisible to ARPES at high $T$. At low $T$ its hybridization with the flat $f$ band just above $E_{\text{F}}$ creates a strong $f$-weight “hotspot” corresponding to a very shallow electron $E_{\text{F}}$ crossing. This configuration 3 occurs at multiple points in the Brillouin zone (BZ), including the edge of $Z$-point hole-like $\gamma$-band FS indicated in Fig. 1D.

The ARPES study of the $f$-weight $T$ dependence is assisted by the 4$d$-4$f$ resonant enhancement of the 4$f$ photoionization cross-section at 122 eV photon energy. Fig. 1E shows a 2D schematic of the cross-section of the bulk tetragonal BZ with Fermi-energy $k$-space arcs for photon energies in the range of 90 to 140 eV. Two different orthogonal cleave surfaces of CeCo${\mathrm{I}\mathrm{n}}_5$ were measured with ARPES. For the (001) cleave surface, the photon energy range spans $\sim$1.5 BZs along the $c$ axis with high-symmetry $\mathrm{\Gamma }$ and $Z$ points occurring at $\approx$90, 105, 122, and 140 eV. Thus, the resonant energy of 122 eV cuts very close to the high-symmetry $\mathrm{\Gamma }$ plane. In contrast, for the orthogonal (100) cleave surface, the same photon energy range covers less than a full BZ along the $x$ axis with high-symmetry $\mathrm{\Gamma }$ and $X$ planes at $\approx$110 and 140 eV, respectively, and the resonant energy of 122 eV cuts midway between $\mathrm{\Gamma }$ and $X$.

Earlier ARPES studies of CeIr${\mathrm{I}\mathrm{n}}_5$ (26, 27) and CeCo${\mathrm{I}\mathrm{n}}_5$ (28, 29) have essentially concluded that those systems are “nearly localized” even down to low $T$ from comparison to DFT band calculations (26, 29), yet have a “small itinerant” low energy-scale component as revealed also by $f$-resonant ARPES along $\mathrm{\Gamma }$-$X$ (27) or along $X$-$M$ (28). Such seemingly contradictory localized yet itinerant character in the ARPES measurement is a natural consequence of 1) the weak $f$-$c$ hybridization for a low $T_{\text{K}}$ system, 2) experimental ARPES resolution limitations, and 3) the well-known $f$-bandwidth deficiencies of DFT. More sophisticated theoretical treatments such as “renormalized band theory” (30, 31) or DFT+DMFT (4, 32) include the necessary ingredients of electron correlation and dynamical screening for proper description of the low energy-scale physics. DMFT additionally provides single-particle excitation spectral function results that are directly comparable to ARPES spectra.

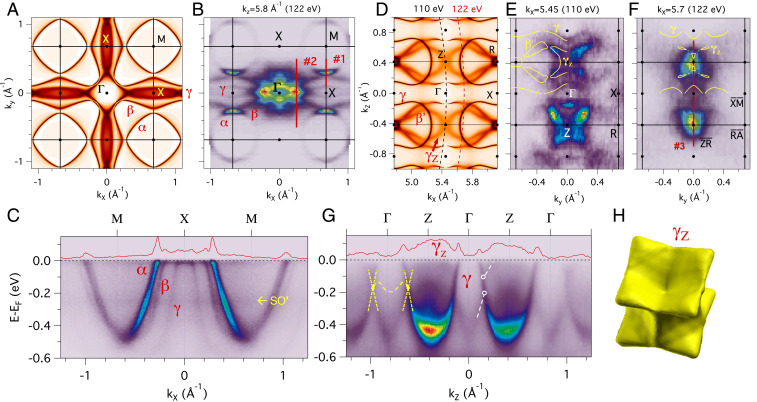
Theoretical and experimental slices of the 3D FS, presented in Fig. 2, highlight the three specific $k$ locations for subsequent $T$-dependent study. Fig. 2A shows the DMFT spectrum of the FS in the high-symmetry $\mathrm{\Gamma }$ plane with labeling of $M$-centered $\alpha$ and $\beta$ electron sheet contours and also hole-like $\gamma$ tube FS along $\mathrm{\Gamma }$-$X$ that connects to a diamond-shaped FS centered on the $\mathrm{\Gamma }$ point. In Fig. 2B, we show a resonant energy Fermi-edge intensity map from the (001) cleave surface, symmetrized about $k_x$ = 0 to remove a geometrical matrix element asymmetry in the central region. Good agreement with the DMFT $\mathrm{\Gamma }$-$X$ contours along the horizontal $k_y$ = 0 axis is observed, while orbital and polarization dependence of the matrix elements appears to suppress those $X$-point intensities along the vertical $k_x$ = 0 axis. More detailed off-resonance high-symmetry $\mathrm{\Gamma }$- and $Z$-plane FS map comparisons are given elsewhere (25). The $s$ polarization of the incident light used for the FS map in Fig. 2B advantageously enables distinct enhancement of $f$ weight at the edges of the $\alpha$ band along $X$-$M$ (cut 1), compared to $p$ polarization. This $E_{\text{F}}$ enhancement is also visible in the corresponding 122-eV wide-energy band dispersions along $M$-$X$-$M$, shown in Fig. 2C, which illustrates the electron or hole character of the $\alpha$, $\beta$, and $\gamma$ conduction bands. Another even stronger $f$ hotspot enabled by the $s$ polarization is visible at the tip of the $\mathrm{\Gamma }$-centered diamond-shaped FS (cut 2). Line cuts 1 and 2 through these two $k$ points are used for the $T$-dependent measurements presented later.

Fig. 2.

$k$-space locations of $T$-dependent measurements for the (001) and (100) surfaces of CeCo${\mathrm{I}\mathrm{n}}_5$. (A) DMFT (T = 10 K)-calculated $k_x$-$k_y$ FS spectral function in the $\mathrm{\Gamma }$ plane. (B) On-resonance 122-eV ARPES (001) $E_{\text{F}}$ intensity map using linear vertical ($s$-) polarization. (C) On-resonance 122-eV valence band dispersion image along $M$-$X$-$M$ (cut 1) with a Fermi-edge intensity profile (red line) and identification of a weak-intensity spin–orbit sideband excitation (SO^′). (D) DMFT $k_x$-$k_z$ FS spectral image for $k_y$ = 0, with the $k_x$ axis corresponding to ARPES (100) surface normal emission photon dependence. (E) High-symmetry 110-eV ARPES (100) $E_{\text{F}}$ intensity map imaging the ${\beta }^{\prime }$, $\gamma$, and ${\gamma }_Z$ FS structures. (F) On-resonance 122-eV ARPES (100) $E_{\text{F}}$ intensity map highlighting $f$ hotspots at the $k_z$ BZ boundary and $k_x$ edge of the ${\gamma }_Z$ FS. DMFT (T = 10 K) FS contours are overplotted in experimental ARPES panels. Numbered red line momentum cuts correspond to $T$-dependent measurements presented in Figs. 3 and 4. (G) High-symmetry valence band dispersion images for the (100) cleave surface at $h\nu$ = 110 eV at normal emission. (Left, in yellow) Overplotted schematic of topological surface state dispersion (dashed) connecting single Dirac-like band dispersion (dashed) crossing points (solid), all as predicted in DFT. (Right) Locations of two separated band crossing points actually observed in experiment (white circles). Related, as discussed in text, the predicted surface state dispersion is not observed. (H) Theoretical 3D shape of the ${\gamma }_Z$ hole FS.

A DMFT Fermi-energy spectral image of the orthogonal $\mathrm{\Gamma }$-$X$-$Z$-$R$ plane in Fig. 2D highlights the existence of a $Z$-centered hole FS (labeled ${\gamma }_Z$) and its separated relation to the tubular $\gamma$ sheet along $\mathrm{\Gamma }$-$X$. Diagonal features along $R$-$\mathrm{\Gamma }$ are associated with the finger-shaped ${\beta }^{\prime }$ FS represented in Fig. 1D and imaged in the high-symmetry 110-eV angle-dependent map of an orthogonally cleaved (100) surface shown in Fig. 2E. The $Z$-centered hole FS has a theoretical “X”-shaped $E_{\text{F}}$ contour that outlines a similar-shaped high-intensity spectral weight feature (Fig. 2E). Additionally the triangular lobes of the ${\gamma }_Z$ FS along the diagonal $Z$-$A$ directions are imaged in (001)-cleaved ARPES in SI Appendix, Fig. S2. Hence with consideration of experimental $k_z$-broadening effects perpendicular to the experimental angle maps, ARPES is consistent with the same size and shape of the DMFT-predicted $Z$-centered hole FS represented in Fig. 2H.

An angle-dependent map at the $f$-resonance energy of 122 eV for the (100) surface, shown in Fig. 2F, is then observed to be dominated by two bright $f$ hotspots at the BZ boundaries where the $k_x$ location is at the edge of the ${\gamma }_Z$ FS where the curvature becomes concave (electron-like). A line cut (no. 3) through these two hotspots is used for $T$-dependent measurements (see Fig. 4).

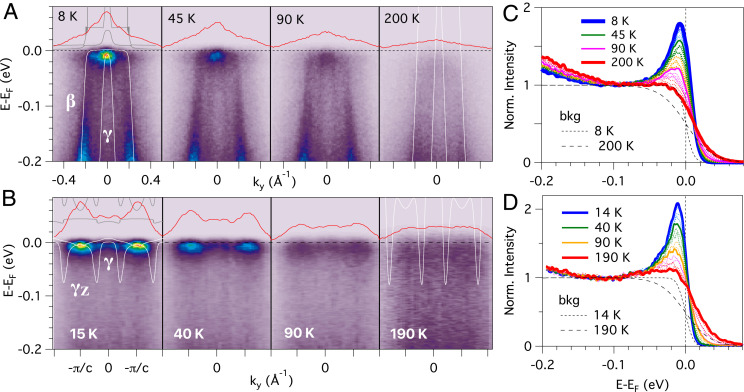
Fig. 4.

Temperature dependence of Ce 4$f$ states for two hotspot locations of CeCo${\mathrm{I}\mathrm{n}}_5$. (A and B) Selected spectral images for the $T$ series of (A) (001) surface central diamond-shaped $f$ hotspot (line cut 2), and (B) (100) surface $Z$-hole FS $f$ hotspot (line cut 3). Low and high $T$ DMFT bands are overplotted in the selected spectral images illustrating the different hole and electron $f$-$c$ hybridization configurations. $E_{\text{F}}$ momentum-dependent profiles (red) also illustrate the relative intensity decay with $T$ and the existence of $\gamma$-band $E_{\text{F}}$ crossing between the two hotspots in B. (C and D) Line spectra for the complete $T$ series for two hotspots. Low and high $T$ Fermi–Dirac distribution profiles (dashed) for background subtraction are also shown.

The corresponding (100) surface high-symmetry normal emission valence band dispersion image at 110 eV, shown in Fig. 2G spanning multiple $c$-axis BZs, also highlights the $k_z$ separation of the $\gamma$ and ${\gamma }_Z$ FS where the hole-like dispersions result in an accidental band crossing at a shallow binding energy. Recently the Dirac-like band crossing along $\mathrm{\Gamma }$-$Z$ has been identified in uncorrelated DFT calculations as a fourfold degenerate quadratic band crossing point arising from the C_4v rotational symmetry of the $c$ axis (33). Furthermore, surface state arcs connecting the two crossing points per Brillouin zone (schematic lines in Fig. 2G) are theoretically predicted for the (100) surface. Closer inspection of the ARPES dispersions reveals two separated crossing points (circles in Fig. 2G) and the absence of any surface state band. This is suggestive of the influence of electron correlations, in particular the effect of the spin–orbit side band (SO^′ in Fig. 2C), in disrupting the simple single DFT band crossing point. As further discussed in SI Appendix, section S.14, DMFT calculations provide some support for this understanding.

The existence of complex shape of the $Z$-centered hole-FS with evidence of strong $f$ participation identified here in DMFT and ARPES is notable in that it also exists in localized ($f$-core) DFT calculations, inherently without any $f$ contribution, and yet is completely absent in itinerant DFT calculations (34, 35). This highlights the artificial and sometimes misleading conclusions derived from the standard “itinerant-versus-localized” DFT theory comparison. While simple postfacto energy-scale renormalization of itinerant DFT can be a sufficient correction in the cases of isolated $\alpha$ or $\beta$ FS band crossings, the low energy-scale complexity of the non-$f$ $\gamma$-band structure along $\mathrm{\Gamma }$-$Z$ in CeCo${\mathrm{I}\mathrm{n}}_5$ is a prime example where the itinerant DFT large $f$-bandwidth disruption is too great.

A comparison of the Fig. 1D ARPES- and DMFT-derived FS sheets ($\alpha$, $\beta$, $\gamma$) to itinerant DFT and localized DFT FS calculations, highlighting their differences, is further detailed in SI Appendix, Fig. S3. Another recent $T$-dependent DFT+DMFT calculation of CeCo${\mathrm{I}\mathrm{n}}_5$ (13) also exhibits low $T$ deviations from $f$-itinerant DFT, including the presence of the diagonal finger-shaped $\beta$’ FS along $R$-$\mathrm{\Gamma }$ instead of multiple shallow electron FS sheets along $R$-$Z$, but still exhibits the same incorrect DFT-like complete disappearance of the ${\gamma }_Z$ FS sheet at low $T$.

Large-to-Small Fermi Surface T Dependence

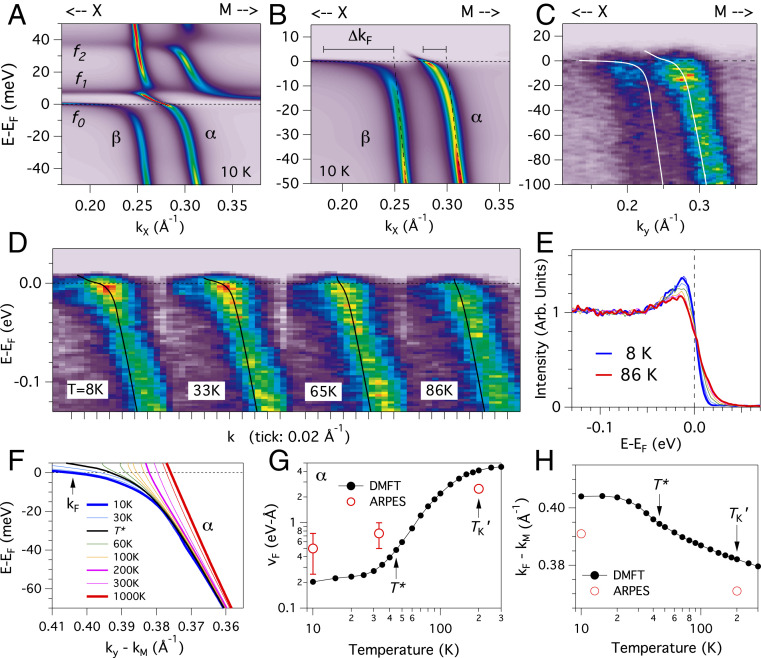
In this section we focus attention on the low energy-scale $f$-$c$ hybridization modification of the $\alpha$ and $\beta$ bands along $X$-$M$ (line cut 1) to highlight the large-to-small FS size change with temperature. The DMFT spectral function at 10 K for this $k$ cut, shown in Fig. 3A, shows the $f$-$c$ hybridization interaction between two $d$ bands and three CEF split $f$ levels, with a rich complexity of connectivity and selectivity that arises from the close proximity of the $d$ bands and the relative symmetries of the $f$ and $d$ states. The three 4$f_{5/2}$ CEF doublets, labeled $f_0$, $f_1$, and $f_2$, correspond to ${\mathrm{\Gamma }}_7^{\left(1\right)}$, ${\mathrm{\Gamma }}_7^{\left(2\right)}$, and ${\mathrm{\Gamma }}_6$ orbitals, respectively, and their relative energies of $\sim E_{\text{F}}$, +8 meV and +40 meV, are in good agreement with neutron scattering measurements of the first and second excited states at +8 and +25 meV (36, 37). Whereas the hybridized outer $\beta$ band connects with very heavy mass dispersion to the $f_0$ ground-state level, the close proximity of the $\alpha$ band requires its hybridized dispersion to immediately connect to the first excited $f_1$ level, thereby giving it an order-of-magnitude larger Fermi velocity ($v_{\text{F}}$ $\approx$ 0.2 eV-Å) compared to the $\beta$ band ($\approx$0.02 eV-Å). This close proximity effect, specific for this $k$ region, contributes to the much smaller average effective mass ($m^{*}<18$) for the $\alpha$-sheet orbits in dHvA compared to the $\beta$-sheet orbits ($m^{*}>48$) (16).

Fig. 3.

Temperature dependence of $\alpha$-band Ce 4$f$ states for the CeCo${\mathrm{I}\mathrm{n}}_5$ (001) cleaved surface. (A and B) DMFT $A\left(k,\omega \right)$ spectral image at 10 K for cut 1 in Fig. 2 through both $\alpha$ and $\beta$ $E_{\text{F}}$ crossings without (A) and with (B) a Fermi–Dirac thermal distribution cutoff. (C) Experimental $\alpha$- and $\beta$-band crossings at 8 K for a similar momentum cut. (D and E) ARPES $T$ dependence of the $\alpha$-band $E_{\text{F}}$ crossing including selected spectral images (D) and $k_{\text{F}}$ line spectra (E). (F–H) DMFT $T$ dependence of the $\alpha$-band dispersion (F) and quantitative analysis of the Fermi velocity (G) and Fermi momentum (H).

The differences in the occupied $\alpha$ and $\beta$ dispersions are also visualized in Fig. 3B where the DMFT spectral function has been multiplied by the 10-K Fermi–Dirac cutoff. In addition to the very different $\mathrm{\Delta }{k}_{\text{F}}$ shifts relative to the extrapolated $d$-band dispersion Fermi wave-vector ($k_{\text{F}}$) values, the relatively weak $f$ weight at $k_{\text{F}}$ in the $\alpha$ band is further diminished for the even heavier $\beta$-band dispersion. An experimental 122-eV resonance energy cut through the $\alpha$ and $\beta$ bands, slightly displaced from the $X$-$M$ line, is shown in Fig. 3C with overplotted DMFT dispersions. While quantification of the $\beta$ band is limited by the resolution of $\sim$15 meV, a relatively stronger $f$ weight in the $\alpha$ band, similar to that of the DMFT calculation, is present for both $s$ and $p$ polarization of the incident light.

Fig. 3D shows $\alpha$-band energy dispersion images for the line cut 1 for four temperatures selected out of a $T$ series measured from 8 K up to 86 K. The enhanced $f$ weight near $E_{\text{F}}$ is observed to diminish simultaneously with the low energy kink becoming less visible. The overplotted DMFT dispersion at 86 K shows still a small dispersion kink at this temperature. The weak $f$-weight enhancement and $T$ dependence are also shown in the $k_{\text{F}}$ line spectra in Fig. 3E. A previous resonant ARPES analysis of $k$-integrated windows just inside and outside the $\alpha$-band dispersion at three temperatures has also reported a weakened but still discernible low energy-scale $f$ peak at 105 K in comparison to 20 and 180 K (28).

Confident that the signatures of the large-to-small FS have been observed experimentally with basic agreement to the DMFT result, we go beyond the ARPES resolution and $T$-range limitations and additionally analyze the DMFT spectral functions to extract the peak dispersion, Fermi velocity, and Fermi momentum of the $\alpha$ band for many intermediate and high temperatures in Fig. 3 F–H. Upon cooling from 1,000 to 200 K, Fig. 3F shows a gradual $k_{\text{F}}$ shift resulting from a near linear band velocity change extending to 100 meV below $E_{\text{F}}$. Then below 200 K ($\approx T_{\text{K}}^{\prime }$) a weak kink in the dispersion develops around −20 meV and the Fermi velocity begins to decrease more rapidly. Upon further cooling, the rapid $v_{\text{F}}$ change is observed to slow down around 50 K (near $T^{*}$) and then becomes constant below 30 K where $k_{\text{F}}$ also stops changing. ARPES $v_{\text{F}}$ and $k_{\text{F}}$ Fig. 3 G and H also show the comparison of the predicted $T$ dependence from DMFT to experimental $v_{\text{F}}$ and $k_{\text{F}}$ values at high and low $T$. The high binding-energy ARPES band velocity of 2.5 eV-Å is compared to the DMFT at high $T$, whereas at low $T$, the ARPES $v_{\text{F}}$ and $k_{\text{F}}$ values are estimated from a visual triangular fit of the dispersion kink near $E_{\text{F}}$. We do not claim to experimentally verify the detailed DMFT $v_{\text{F}}$ and $k_{\text{F}}$ $T$-dependent profile(s), but we note that the 33-K spectrum bears greater resemblance to the 8-K spectrum than to the 86-K spectrum, indicating that the FS evolution is not just beginning at $T^{*}$.

Thus a central finding, so far, is that the resistivity downturn temperature $T^{*}$, associated with lattice coherence, does not signify the onset of the heavy effective mass $f$-$c$ hybridization dispersion curvature or the onset of FS size changes indicated by $k_{\text{F}}$ changes. A very similar conclusion was drawn for $T$-dependent ARPES data of YbRh₂Si₂ (16). Previous DMFT calculations, without the inclusion of CEF states, have similarly predicted dHvA orbit FS size changes occurring as high as 130 K ($>$2.5 $T^{*}$) for CeIr${\mathrm{I}\mathrm{n}}_5$ (4) and near vertical kinks in the non-$f$ dispersive states in CeCoGe₂ as high as $\sim$200 K prior to the formation of heavy mass band dispersion below $\sim$90 K (38). The additional presence of the CEF states in the DMFT calculations here may be responsible for the even higher onsets of the heavy mass $v_{\text{F}}$ changes and FS size $k_{\text{F}}$ shifts (up to 1,000 K) theoretically observed in Fig. 3. Similar analysis of the DMFT $\beta$-band dispersion, in SI Appendix, Fig. S8, indicates that the transport coherence temperature in CeCo${\mathrm{I}\mathrm{n}}_5$ is more closely associated with the most rapid $T$-dependent changes of $v_{\text{F}}$ and $k_{\text{F}}$.

STM quasiparticle interference (QPI) measurements of the Ce-In terminated surface have also observed a heavy mass band dispersion kink along the (100) direction of CeCo${\mathrm{I}\mathrm{n}}_5$ at 20 K with a scattering $q$ vector of 0.2$\cdot \left(2\pi /a\right)$ that is consistent with $\alpha$-sheet FS nesting in the $Z$ plane (24). Hence those results can be directly compared to the $\alpha$-band ARPES measurements in Fig. 3. At 70 K, the STM-QPI observes the linear light mass dispersion above $E_{\text{F}}$, without the heavy mass dispersion kink, but with still a weak hybridization intensity dip.

Hotspot f-Weight T Dependence

Next we turn our attention from $T$-dependent dispersion analysis to the $T$-dependent $f$-weight signatures of $f$ participation in the FS for Fig. 1C $f$-$c$ hybridization configurations 2 and 3, where the stronger $f$ weight allows experimental analysis up to temperatures as high as 200 K. Fig. 4 A and B shows 122-eV energy dispersion images for selected temperatures for (001) and (100) cleave surface line cuts 2 and 3 in Fig. 2, respectively. Overplotted DMFT bands (white lines) at low and high $T$ illustrate the $f$-$c$ hybridization configuration of $f$ weight being pulled below $E_{\text{F}}$ at the center of a narrow hole-like $d$-band dispersion in Fig. 4A and a very shallow electron-like $f$ dispersion at the zone boundaries being induced by a non-$f$ electron-like band minimum farther above $E_{\text{F}}$ in Fig. 4B.

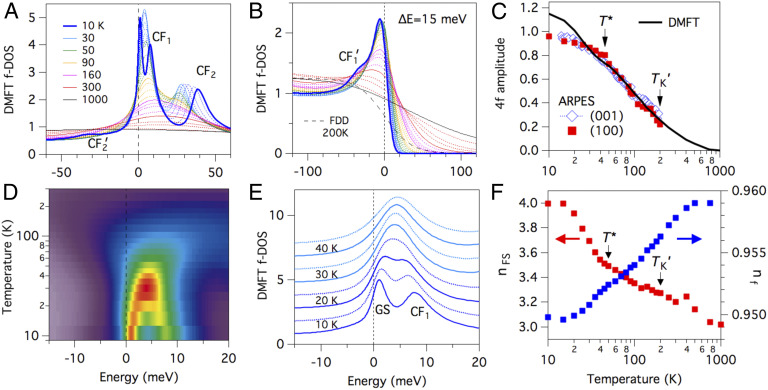
The $T$-dependent line spectra at the (001) $f$ hotspot and at one of the two (100) hotspots are shown in Fig. 4 C and D, respectively. The hotspot $f$-peak width is visibly narrower for the (100) surface as compared to the (001) surface, consistent with the different $f$-$c$ hybridization configuration schematic simulations in Fig. 1C. In both cases, while the $f$ peak appears to be suppressed in the energy dispersion images at 190 to 200 K, the line spectra reveal a continuous decrease of the peak amplitude all of the way up to the highest measured temperature. A $T$-dependent Fermi–Dirac distribution (FDD) function convolved with a Gaussian instrumental broadening of 15 meV, illustrated for low and high $T$ in Fig. 4 C and D, is used for background subtraction (39) for the extraction of the normalized 4$f$ amplitude $T$ profiles in Fig. 5C. Note that this implies a finite 4$f$ DOS even for a flat line spectrum that does not exhibit a visual peak. The sensitivity to different background subtraction methods is discussed in SI Appendix, Fig. S5.

Fig. 5.

DMFT $k$-integrated temperature dependence of Ce 4$f$ states for CeCo${\mathrm{I}\mathrm{n}}_5$. (A and B) $T$-dependent $k$-integrated DMFT 4$f$-DOS spectra with (B) a Fermi-edge cutoff and experimental energy broadening of 15 meV. (C) Comparison of experimental and simulated $T$ dependences of $f$-peak amplitudes after background subtraction. (D and E) Spectral weight image and stack plot of the $T$-dependent merging of the ground state and first excited CEF peaks. (F) (left) $T$ dependence of the DMFT total FS volume converted to electron occupation ($n_{FS}$) exhibiting an $\sim$1-electron gain at low $T$ and (right) the DMFT total localized-$f$ occupation ($n_f$) exhibiting a tiny 0.01-electron loss at low $T$. Crystalline electric-field levels (CF^1,2) and their crystal field sideband peaks (${\text{CF}}_{\mathrm{1,2}}^{\prime }$) are labeled.

For theoretical comparison, DMFT $k$-integrated $f$-DOS spectral weights were calculated from 10 to 1,000 K, shown in Fig. 5A for only the Kondo resonance and CEF-split states. The DMFT spectra were then multiplied by the FDD function and convolved with a Gaussian instrumental broadening of 15 meV, to simulate the photoemission measurements, and are plotted in Fig. 5B. Using the 750-K spectrum for background subtraction, the $T$-dependent Fermi-edge weight is plotted in Fig. 5C with comparison to the ARPES $f$-peak amplitudes. The experimental results for the two $f$ hotspots are very comparable with each other, despite the different $f$-$c$ hybridization configurations and $f$-peak widths. A reasonable agreement of the approximate logarithmic $T$ dependence between 40 and 200 K is found for normalization of the DMFT $T$ profile to 1.2 at low $T$. Both experiment and theory agree to the existence of a long $f$-weight tail extending to high $T$ far above $T^{*}$. A reason for the low $T$ discrepancy and saturation of the ARPES $T$ profile is the instrumental resolution suppression of the low $T$ peak amplitude.

CEF Effects

It is important to carefully delineate the various effects that contribute to the high $T$ extension of the $f$ weight in Fig. 5C. First, analysis of the full-range $k$-integrated DMFT spectra, presented and discussed in SI Appendix, Fig. S4, reveals that the large residual high $T$ $f$-DOS in the Kondo resonance (KR) region (including CEF and spin–orbit excitations) does not result from a strong spectral weight transfer (it is $<$10%) from the KR region to the higher $f^2$ energy range above 2 eV. Rather, the primary $T$ dependence in the KR region is that of peak broadening of spectral weight from the peak center(s) to the peak tails. This leads to a number of generic effects which contribute to the appearance of relatively enhanced $E_{\text{F}}$ $f$ weight at higher temperatures, even with background subtraction of the high $T$ $f$ weight: 1) The key notable effect is that of broadening of CEF weight into the KR peak and $E_{\text{F}}$ energy windows. Their $T$-dependent profiles will then include the $T$ dependence of the tail of the CEF peak. Such CEF broadening origin of enhanced $E_{\text{F}}$ $f$ weight at high $T$ has been noted before (39, 40) within single-impurity noncrossing approximation (NCA) calculations (41). 2) Similarly the $E_{\text{F}}$ weight will inherently have a weaker $T$ profile than the KR peak because it exists in the KR tail with a smaller low $T$ amplitude and a similar high $T$ amplitude. 3) Finally, large energy-window area analyses will generally have weaker $T$ dependences than narrow energy-window amplitudes.

Another important CEF effect concerns the $T$-dependent effective $f$ degeneracy as discussed in the early theoretical perturbation theory calculations of resistivity profiles of Ce heavy fermion compounds (20). The effect leads to a larger effective Kondo temperature and an extended high $T$ logarithmic resistivity regime relative to the n = 2 doublet ground-state Kondo effect. The degeneracy crossover effect was initially predicted to manifest as a thermal depopulation hump(s) in the resistivity profile around the CEF energy-level splitting temperatures (20), e.g., 100 and 300 K for CeCo${\mathrm{I}\mathrm{n}}_5$. However, a theoretical treatment going beyond third-order perturbation theory and including Kondo broadening of the CEF levels predicts a modification to the resistivity profile at much lower $T$s than the nominal CEF splittings (42). The KR and CEF peak broadening within single-impurity NCA calculations of the $f$-DOS, discussed above, does in general lead to indistinguishability of CEF peaks at temperatures below the actual CEF splitting energies.

CeCo${\mathrm{I}\mathrm{n}}_5$ experimentally exhibits only a single resistivity maximum (at 45 K) whose downturn is firmly associated with lattice coherence from La-dilution studies (22), with no apparent additional secondary humps that one might associate with the CEF merging effect. An enhanced n = 6 Kondo temperature due to both CEF excitations was estimated to be $T_{\text{K}}^{\left(6\right)}$ $\approx$ 35 K (22, 43) relative to $T_{\text{K}}$ = 1.7 K for the dilute system, and so the coherence downturn below 45 K could possibly be masking the CEF degeneracy crossover(s).

The manifestation of such a CEF $f$-degeneracy crossover of the two lowest CEF levels is observed in the $k$-integrated DFT+DMFT spectral function $T$ dependence shown in Fig. 5 D and E. While single-impurity NCA calculations exhibit broadening and monotonic decline of fixed-energy KR and CEF $f$ peaks, here both the ground-state ${\mathrm{\Gamma }}_7^{\left(1\right)}$ and first-excited ${\mathrm{\Gamma }}_7^{\left(2\right)}$ CEF peaks are observed to shift toward each other and merge into a single enhanced-amplitude peak as early as 30 K, before the subsequent monotonic broadening decline to higher $T$. This is suggestive of the crossover from a narrow $N$ = 2 degeneracy KR peak ($\approx$1-meV center with 3-meV width) at 10 K to a new $N$ = 4 degeneracy KR peak ($\approx$4-meV center with 9-meV width) in which the ${\mathrm{\Gamma }}_7^{\left(1\right)}$ and ${\mathrm{\Gamma }}_7^{\left(2\right)}$ states are indistinguishable. The higher peak energy above $E_{\text{F}}$ plus the broader width and enhanced amplitude of the new KR peak are all consistent with the crossover to a larger Kondo temperature.

Direct experimental verification of this CEF degeneracy crossover of two peaks at 1 and 8 meV merging into a single peak at $\sim$30 K is in principle possible by photoemission spectroscopy of electrons thermally excited into these low energy states. However, in addition to direct energy resolution limits, it is challenging due to the low thermal occupation of the first excited CEF state (CF₁) at low $T$ where the peaks are sharpest and most resolvable. Also, the common data analysis recovery procedure of the division of the spectra by a resolution-convolved FDD lineshape is based on an approximation that breaks down at low $T$ in relation to the energy resolution, thereby creating energy shifts and quantitative artifacts as discussed in SI Appendix, section S.12. Another possible method is to probe the $T$-dependent behavior of the virtual excitations into the CF₁ states that produced the ${\text{CF}}_1^{\prime }$ sideband peak, but they appear only as a weak shoulder on the KR tail in the $k$-integrated DMFT spectral function shown in Fig. 5B. Another challenge (or opportunity) is the complex $k$-dependent variation of the KR and CF₁ levels as they hybridize with the conduction bands. A $k$-resolved DFT+DMFT band image view of this CEF merging effect for the $\alpha$- and $\beta$-band crossings is shown in SI Appendix, Fig. S9. Another experimental example of this $k$-dependent complexity of the lowest CEF levels comes from the (100) surface $f$ hotspot spectrum probed in Fig. 4B, where the FDD recovery procedure is able to visualize the central $\gamma$ bands forming a third $f$ hotspot above $E_{\text{F}}$ closer to the CF₁ energy. This result, specifically enabled by 30-K thermal excitation, and consistent with the overplotted theoretical DMFT band structure in Fig. 4A, is presented in SI Appendix, Fig. S2E.

The closeness of this CEF degeneracy crossover temperature in the DFT+DMFT result to the resistivity maximum $T^{*}$ suggests that lattice coherence may be intimately involved in the more rapid CEF merging effect and that a clean separation of the $T^{*}$ and CEF $T$ scales is not realized in CeCo${\mathrm{I}\mathrm{n}}_5$, resulting in only a single resistivity peak and downturn. A related $T$-dependent DFT+DMFT study of Ce₂IrIn₈ uses tuning of the CEF splittings to reveal CEF effects on the $f$-orbital anisotropy, the relative Fermi-edge scattering coherence, and the appearance of secondary humps in calculated resistivity profiles (44).

Discussion

The ARPES and DMFT demonstrations of $f$-$c$ hybridization effects well above $T^{*}$ are supported by several other experimental spectroscopy and scattering measurements of CeCo${\mathrm{I}\mathrm{n}}_5$, including the signature of a hybridization gap in early optical spectroscopy (45) and in STM spectroscopy (24), which decreases for increasing $T$, but are still very much present at 70 to 100 K ($\approx$2$T^{*}$). Similarly, resonant elastic X-ray scattering at the Ce 3$d$-4$f$ $M_5$ edge has recently demonstrated a $q$-dependent sensitivity to bulk $f$ states along the (110) direction (46), with the $f$-resonant peak intensity exhibiting a logarithmic dependence persisting up to at least 150 K ($\approx$3$T^{*}$). Further discussion and comparison of this $T$ profile are provided in SI Appendix, Fig. S6.

Another recent purely experimental ARPES study of CeCo${\mathrm{I}\mathrm{n}}_5$ by Chen et al. (19) has also shown similar $T$-dependent $f$ weight above $T^{*}$. Differences in the results, methods, and interpretations with the current study are discussed below and in SI Appendix, section S.7. Also a recent angle-integrated photoemission study of YbNiSn reports a $T$-linear behavior of a $<$35% variation of the Yb 4$f$ intensity, in the range of 1 to 100 K, that also extends far above its transport signature of coherence below $\sim$10 K (47). In that case, the occupied Yb 4$f$ spectral peak inherently contains multiple CEF levels which contribute to its broad $\sim$80-meV width. This T-linear dependence, different from the $T$-logarithmic behavior observed here for CeCo${\mathrm{I}\mathrm{n}}_5$, was described there by a non-Fermi liquid-like $T$-linear damping in the self-energy of the periodic Anderson model, proposed as accounting phenomenologically for effects of feedback from closely spaced CEF-split bands.

The small to large FS crossover can be additionally visualized from the DMFT calculation by the total FS volume as a function of temperature, as plotted in Fig. 5f with conversion to electron occupation, $n_{FS}$, e.g., 2 electrons per Brillouin Zone volume. It is observed that $n_{FS}\sim$3 at high $T$ increases to $n_{FS}=4$ at 15 K where one $f$ electron fully participates in the FS. In this case, $T^{*}$ appears to be associated with the onset of a more rapid change in FS size, while surprisingly $\sim$0.5 electron are already gradually incorporated from high $T$ down to $T^{*}$. Similarly, the small to large FS transition of the $\alpha$ and $\beta$ sheets can be analyzed by the cross-sectional FS area, provided in SI Appendix, Fig. S11, with comparison to Ce versus La dHvA orbits (34). Note that the large FS volume $f$-occupation increase to low $T$ should be distinguished from the few percent decrease of the local $f$ occupation from $n_f\sim$ 1, also plotted in Fig. 5F, which is consistent with recent analysis of Ce 3$d$ hard X-ray core-level photoemission obtaining $n_f$ = 0.97 at 20 K (48).

In their ARPES study of CeCo${\mathrm{I}\mathrm{n}}_5$, Chen et al. (19) have estimated that the net FS volume change from 145 to 17 K is rather small, corresponding to only 0.2 $f$-electrons incorporation. In their discussion this estimate is contrasted with an expected change of 1 electron, i.e., a discrepancy as large as 0.8 electrons, and it is speculated that the presence of CEF levels may be responsible in some way for such a large discrepancy. Our Fig. 5F shows what is actually expected quantitatively in a DMFT calculation that includes the CEF splittings. As we have already seen, their major effect is to extend the Kondo regime to much higher temperature than would be obtained considering only the lowest level. Thus we see that 0.3 electrons are already incorporated in the FS from the highest $T$ down to 200 K (outside the scope of the experiment) via $k_{\text{F}}$ shifts originating from high energy $v_{\text{F}}$ slope changes (Fig. 3F). The $f$-electron participation in the FS becomes $>$0.9 electrons by 20 K, i.e., at most a net 0.6 electron change from 145 to 17 K. So the difference between the 0.2 estimate of Chen et al. (19) and the DMFT prediction is actually no more than 0.4 electrons, and this much smaller difference could easily be within the large uncertainties involved in their estimate. That estimate is based on a single $\mathrm{\Gamma }$-$M$ cut for the $\alpha$ and $\gamma$ sheets only, coupled with the assumption that the $k_{\text{F}}$ changes along this single line can be used to compute the volume changes of both of the sheets. In contrast to the situation for the roughly cylindrical $\alpha$ sheet, this assumption is very questionable for the complex shape of the $\gamma$ sheet. It is also assumed that the volume change of the $\beta$ sheet is approximately equal to the sum of the $\alpha$ and $\gamma$ contributions. However, its $\approx$2$\times$ larger total FS size and its significantly heavier effective mass likely make this a considerable underestimation of the $\beta$-sheet contribution to the $f$ occupation at low $T$ (see additional discussions in SI Appendix, sections S.8 and S.10). Finally, the ${\beta }^{\prime }$ and the ${\gamma }_Z$ sheets, newly identified and characterized here, are not included in this estimate. Unfortunately we also do not have sufficiently detailed experimental knowledge to specify the $T$ dependences of these complex volumes well enough to test the theory quantitatively. A future experimental effort with this level of detail would be greatly aided by a future full theoretical calculation of the separate $T$ dependences of each of the five FS sheets. However, in our opinion, at the moment there is no experimental reason to doubt the DMFT result in Fig. 5F or the validity of the Luttinger theorem at sufficiently low $T$ for CeCo${\mathrm{I}\mathrm{n}}_5$.

Theoretical efforts to compute the lattice coherence scale (4, 5, 38, 49–52) rely on a variety of definitions including onset of Fermi-liquid transport coefficients, comparison of single-impurity Anderson model and periodic Anderson model properties (51), effective mass scaling (4, 38), and others, with unclear relation to the experimental CeCo${\mathrm{I}\mathrm{n}}_5$ resistivity maximum $T^{*}$. In addition, while the proposed two-fluid model universal scaling formula for the $f$-DOS (14) contains a logarithmic term that extends out to $\approx$2.7 $T^{*}$, a multiplying “order parameter” term defines a sharp termination of the $f$-DOS at $T^{*}$, as illustrated in SI Appendix, Fig. S7. CEF effects are not discussed within the two-fluid model.

The low $T$ discrepancy between the ARPES and DMFT $f$ spectral weight profiles in Fig. 5C, ascribed to instrumental resolution limitations, is also in the $T$ regime of the $T$-linear resistivity below 20 K and thus is suggestive of a possible role of quantum criticality in this discrepancy. Hence this motivates an exploration of the power law $T$ dependences of the amplitude, width, and peak energy of our (100) and (001) $f$-hotspot lineshapes in SI Appendix, section S.13, to look for possible $E/T$ scaling behavior, similar to that of the previous ARPES $T$-dependent study (19). What we discover instead is that, intimately related to the $f$-weight analyses leading to Fig. 5C, the instrumental resolution and choice of background also play key roles in deviations at low and high $T$ from uniform power law scaling of the $f$ lineshape and provide a natural explanation for the “intermittent” scaling behavior previously reported (19).

In summary, we have presented a detailed view of the experimental 3D FS of CeCo${\mathrm{I}\mathrm{n}}_5$, including the complex-shaped hole-like $Z$ sheet, using ARPES measurements from two orthogonal (001) and (100) cleave surfaces. We have used an $f$-resonant photon energy to highlight the $k$ locations of the enhanced $f$ weight corresponding to three different $f$-$c$ hybridization configurations, including the well-known $\alpha$-band crossing, and have measured the $T$ dependence of these $f$ weights. We find declining, but finite $f$ weight extending up to $\sim$200 K, surprisingly far above the transport coherence temperature of $\sim$45 K.

Theoretical $k$-resolved DFT+DMFT calculations confirm the experimental 3D FS topology and provide $T$-dependent $f$-spectral functions that predict both dispersion and $f$-weight changes that extend even higher than the ARPES measurements. The inclusion of CEF states in the DMFT provides a glimpse of the complexity of $k$-resolved $f$-$c$ hybridization interactions above $E_{\text{F}}$, origins of the disparity in effective masses of $\alpha$- and $\beta$-band crossings, and an explicit spectral function view of a $T$-dependent crossover of the Kondo resonance effective degeneracy involving the two lowest CEF $f$ states. These CEF effects may explain much of the long high $T$ tail of KR $f$ weight, but the role of CEF states in the observed DMFT high $T$ onset of the effective mass and large-to-small FS size $T$ evolution still needs to be elucidated. A mismatch between the transport-defined coherence temperature and the higher $T$ onset of signatures of $f$-$c$ hybridization and coherence-related effective mass changes, as observed here for CeCo${\mathrm{I}\mathrm{n}}_5$, is also the framework put forth (16) to account for the absence thus far of an observation of the small FS in high $T$ ARPES studies of YbRh₂Si₂.

Materials and Methods

Experimental.

Temperature-dependent ARPES measurements were performed at the MERLIN beamline 4.0.3 of the Advanced Light Source (ALS) employing both linear horizontal and linear vertical polarizations from an elliptically polarized undulator. A Scienta R8000 electron spectrometer with 2D parallel detection of electron kinetic energy and angle was used in combination with a six-axis helium cryostat goniometer with 6 K base temperature and $<5\times 10^{-11}$ torr base pressure. Total energy resolution of approximately 15 meV was used for measurements at h$\nu$ = 122 eV corresponding to the Ce 4$d$-4$f$ resonant enhancement of the $f$ photoionization cross-section. Temperature-dependent procedures typically progressed from sample alignment and optimization at 20 to 40 K, to brief cooling to the lowest $T$, to full range warming to the highest $T$ (SI Appendix, Fig. S5).

Single crystal samples of CeCo${\mathrm{I}\mathrm{n}}_5$ were grown with a molten indium flux technique (23). The (001) surface was cleaved in vacuum using the top-post method. Orthogonal (100) surfaces were similarly fractured using side mounting of platelet samples with narrow $c$-axis thickness. Optimal regions of the cleaved surfaces excited by a 50-$\mathrm{\mu }$m beam spot were selected which exhibit maximal Fermi-edge 4$f$ weight at 122 eV. Also, special attention was given to avoid a common (001) surface state originating from In termination that obscures the normal emission details of the ${\gamma }_Z$ FS (SI Appendix, Fig. S2). This previously observed surface state (28) corresponds to the third “type C” surface observed by STM (24).

Theory.

The correlation effect of the Ce 4$f$ orbital is treated by the charge self-consistent DFT+DMFT method (53, 54). The WIEN2k package was used for the DFT part, which is based on the full potential linearized augmented plane-wave+local orbitals (FP-LAPW+lo) method (55). The Perdew–Burke–Ernzerhof generalized gradient approximation (PBE-GGA) is employed for exchange-correlation potential (56). Ce 4$f$ electrons are treated dynamically with the DMFT local self-energy, where the full atomic interaction matrix is taken into account to describe the crystal field splitting at low temperature. We used previously determined Coulomb and exchange interaction parameters of 5.0 and 0.68 eV, respectively (32), in which the occupation of the Ce 4$f$ orbital was estimated to be 0.96 at 20 K. For the impurity solver in the DMFT step, the NCA is used.

In the description of the spin–orbit interaction (SO) and CEF splittings of the Ce 4$f$ states under the tetragonal symmetry, both the diagonal basis and the simple atomic $jj$ basis of the interaction matrix were tested, and give similar results. The CEF energy-level splittings are first calculated ab initio on the level of the lattice (i.e., in the DFT part) and then they are renormalized inside the impurity solver. Because the atomic $jj$ basis has quite small off-diagonal components, it was used inside the impurity solver. There are three doubly degenerate $J$ = 5/2 CEF states with ground state ${\mathrm{\Gamma }}_7^{\left(1\right)}$ = $\alpha |5/2,\pm 5/2⟩-\sqrt{1-{\alpha }^2}|5/2,\mp 3/2⟩$, first excited state ${\mathrm{\Gamma }}_7^{\left(2\right)}$ = $\sqrt{1-{\alpha }^2}|5/2,\pm 5/2⟩+\alpha |5/2,\mp 3/2⟩$, and second excited state ${\mathrm{\Gamma }}_6$ = $|5/2,\pm 1/2⟩$, using $|J,J_z⟩$ state notation. In CeCo${\mathrm{I}\mathrm{n}}_5$, the calculated ${\alpha }^2$ ($\sim$0.25) value is similar to X-ray absorption results that report a high portion of $|5/2,\pm 3/2⟩$ states for ${\mathrm{\Gamma }}_7^{\left(1\right)}$ and $|5/2,\pm 5/2⟩$ states for ${\mathrm{\Gamma }}_7^{\left(2\right)}$ (53, 57). The CEF splittings are estimated to be $\sim$8 and $\sim$40 meV, which are consistent with other Ce$M{\mathrm{I}\mathrm{n}}_5$ ($M$ = Rh and Ir) compounds (37).

Data Availability.

All study data are included in this article and SI Appendix.