Scaling relationships for the elastic moduli and viscosity of mixed lipid membranes

Significance

Life requires a delicate balance between cell membrane rigidity and fluidity to define cell boundaries yet enable cell deformation, growth, and division. Here, we bridge the molecular and macroscopic scales with neutron scattering techniques to demonstrate how the material properties of model lipid membranes are readily tuned by the constituent lipid composition. Mixing lipids leads to softer and less viscous membranes than predicted a priori from the pure component membrane properties. Instead, the dynamics are linked to the membrane structure and follow simple scaling relationships with the area per molecule. These results emphasize the importance of lipid packing and reveal the interwoven relationship between lipid membrane structure and dynamics.

Abstract

The elastic and viscous properties of biological membranes play a vital role in controlling cell functions that require local reorganization of the membrane components as well as dramatic shape changes such as endocytosis, vesicular trafficking, and cell division. These properties are widely acknowledged to depend on the unique composition of lipids within the membrane, yet the effects of lipid mixing on the membrane biophysical properties remain poorly understood. Here, we present a comprehensive characterization of the structural, elastic, and viscous properties of fluid membranes composed of binary mixtures of lipids with different tail lengths. We show that the mixed lipid membrane properties are not simply additive quantities of the single-component analogs. Instead, the mixed membranes are more dynamic than either of their constituents, quantified as a decrease in their bending modulus, area compressibility modulus, and viscosity. While the enhanced dynamics are seemingly unexpected, we show that the measured moduli and viscosity for both the mixed and single-component bilayers all scale with the area per lipid and collapse onto respective master curves. This scaling links the increase in dynamics to mixing-induced changes in the lipid packing and membrane structure. More importantly, the results show that the membrane properties can be manipulated through lipid composition the same way bimodal blends of surfactants, liquid crystals, and polymers are used to engineer the mechanical properties of soft materials, with broad implications for understanding how lipid diversity relates to biomembrane function.

The material properties of biological membranes are essential to cell function. The lipid bilayer that forms the basis of these membranes has a thickness, elasticity, and viscosity that influence biological processes from protein conformational changes on the molecular scale to large-scale membrane deformations in events like endocytosis and cell division. In turn, the lipid bilayer properties are determined by the characteristics of the hundreds of chemically distinct lipid molecules that make up the membrane. Thousands of chemically unique lipids have been identified to date, and lipid composition is known to vary not only among different cell types but also among organelles within the cell (1). Viral infection has been connected to specific membrane lipids, and changes in membrane lipid composition also have been associated with Alzheimer’s disease, cystic fibrosis, and cancer (2, 3). However, a long-standing challenge in biophysics is to link this complex and highly regulated lipid diversity to the membrane biophysical properties and ultimately cell function.

Changes in membrane properties with changing lipid composition are often described qualitatively in terms of “fluidity” or “softness” without a good understanding of the underlying molecular mechanisms. Our quantitative understanding of membrane mechanics stems from significant efforts to measure the elastic and viscous properties in model membranes composed of a single lipid of interest. However, far less is known about how mixing different lipids together affects these properties. Further adding to the challenge, even taking a minimalist bottom-up approach has proven to be difficult, and simple binary lipid mixtures may have dramatically different properties than either of the constituent single-component membranes. For instance, the effects of cholesterol on the bilayer thickness (4, 5), stiffness (quantified as the bending modulus, κ) (4–7), and curvature modulus (8) are all highly dependent on the lipid species. Experimental and computational studies further suggest that some lipid mixtures show nonlinear trends in thickness with lipid composition in binary mixtures (9, 10). Recently, we showed that mixing lipid species with different tail lengths, dimyristoylphosphatidylcholine (DMPC) (14:0 diC) and distearoylphosphatidylcholine (DSPC) (18:0 diC), significantly increased the thickness fluctuation dynamics compared to either DMPC or DSPC alone (11). These nonadditive changes are compounded by the limited data on lipid mixtures and make it difficult to predict the properties of mixed lipid membranes.

In the present work, we show that the unexpected, nonlinear compositional dependence of the dynamics in mixed DMPC/DSPC lipid membranes can be directly correlated with structural changes in the membrane and ultimately the lipid packing efficiency. We measure both the collective bending and thickness fluctuations to quantify the enhanced dynamics in the mixed bilayers as a reduction in the bending modulus, κ, area compressibility modulus, K_A, and membrane viscosity, η_m. Moreover, by measuring these dynamics at different mixing ratios and across a wide range of temperatures in the fluid phase, we show that the measured κ, K_A, and η_m, for both the mixed and the pure component bilayers, collapse onto master curves that scale with the area per lipid. These scaling relationships draw a direct link between the membrane structure and dynamics and establish a framework toward predicting both the elastic and viscous properties of more complex membrane compositions, with broad implications for understanding the biological role of lipid diversity.

Results

DMPC and DSPC differ in acyl chain length by four methylene groups, and binary mixtures of DMPC and DSPC have been used extensively as a model system of chain length mismatch. The phase behavior has been well documented with a number of techniques (9, 12–19), which provides a solid foundation for the present work. Here, we focus on the fluid phase at temperatures well above the miscibility transition. Both simulation and experiment show that the lipids form a randomly mixed fluid phase at temperatures >57 °C regardless of the composition (14, 15, 18). All presented data correspond to temperatures where the lipids are reported to be randomly mixed.

There are also outstanding questions as to whether it is more appropriate to compare lipid mixtures at the same experimental temperature or the same relative temperature to the miscibility transition. A survey of literature shows that both comparisons are used, and the appropriate temperature reference may depend on the membrane property (6, 17, 20–23). For example, Small proposed that it is best to compare different lipid compositions at the same relative temperature (24), while more recent work suggests that it is better to compare lipid volumes at the same absolute temperature (23). Here, we present structural data for both the same relative (Fig. 1) and experimental temperature (Fig. 2) and emphasize that the properties of mixed DMPC/DSPC membranes are not a linear function of their composition regardless of the temperature reference. Meanwhile, studies of the membrane elastic properties indicate that the moduli show anomalous behavior near the phase transition (6, 22). We will focus on the dynamics at the same relative temperature in the second half of Results, but as with the membrane structure, the elastic and viscous properties do not follow linear trends regardless of the temperature reference.

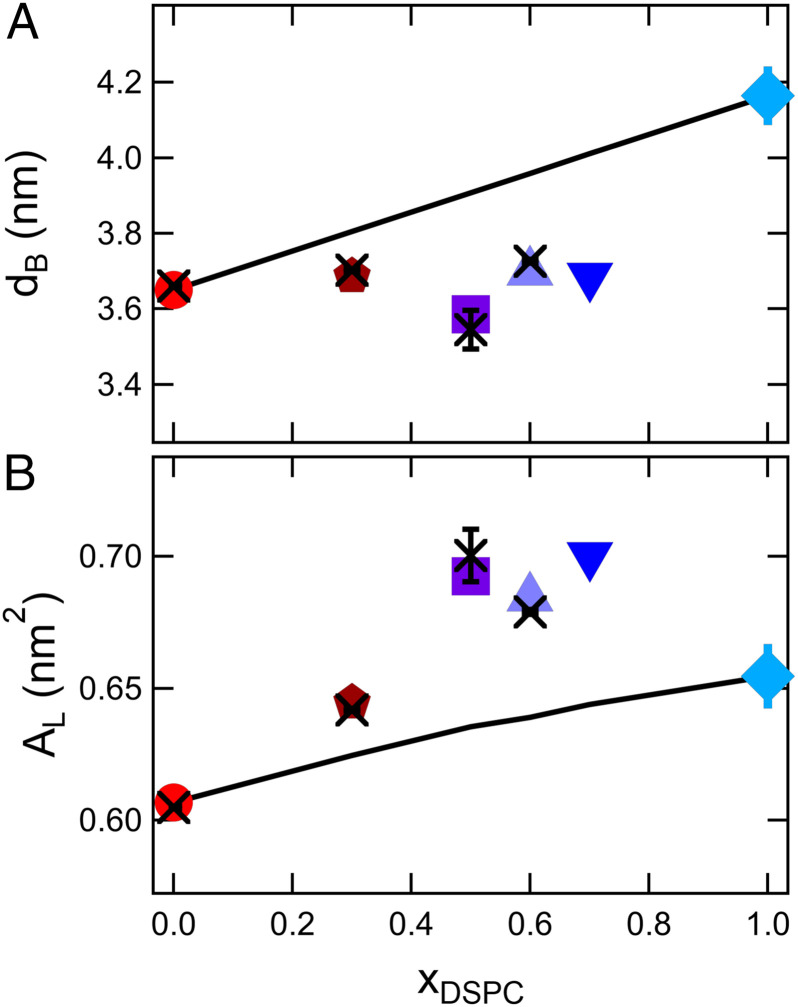
Fig. 1.

Bilayer structure as a function of DSPC mole fraction (x_DSPC-d70) in the mixture. (A) Bilayer thickness, d_B, and (B) area per lipid, A_L, in mixed lipid bilayers at a constant relative temperature, T – T_m = 20 °C. Crosses are values determined from SANS experiments at the specified temperature, and the symbols are values calculated from the thermal expansivities listed in SI Appendix, Table S4. The solid lines represent the calculated thickness assuming a composition-weighted average of the pure component bilayer thickness (A) and the corresponding areas per lipid (B). Error bars represent 1 SD throughout the manuscript and in some cases are smaller than the symbols.

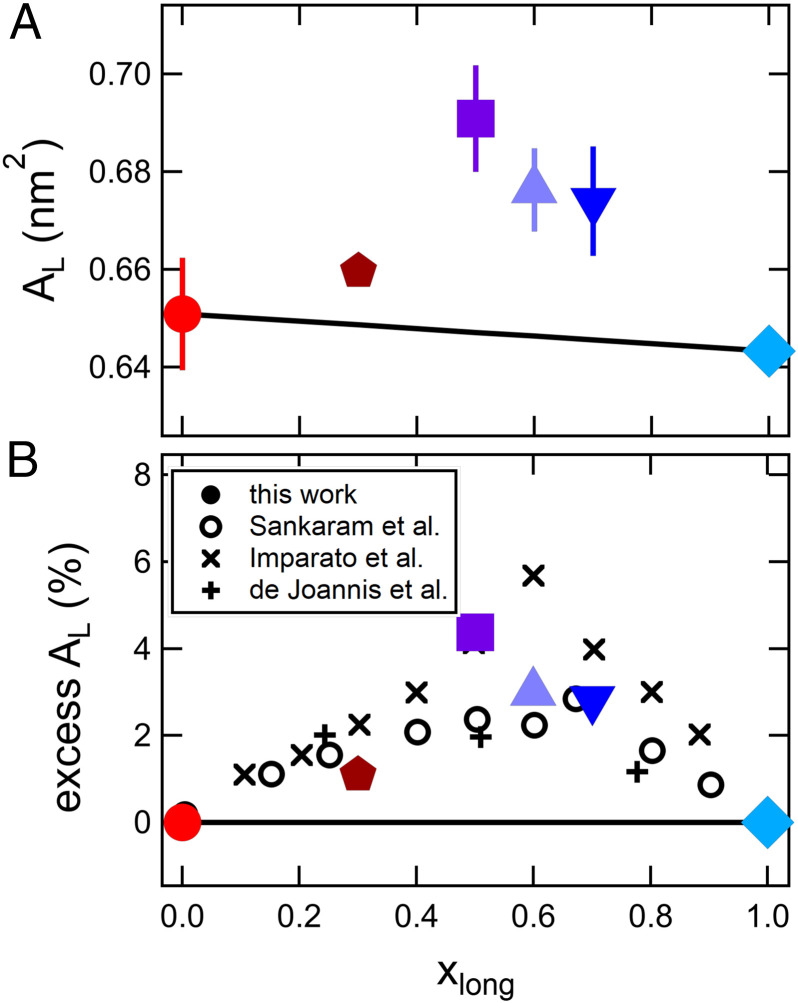
Fig. 2.

Area per lipid (A_L) as a function of bilayer composition at the same experimental temperature. (A) A_L vs. x_DSPC for DMPC/DSPC at T = 60 °C and (B) the same data for DMPC/DSPC plotted as excess area per lipid as a function of the mole fraction of long-tail lipid to compare with other mixtures of short- and long-tail lipids in literature (open symbols and crosses). The solid line represents the expected area per lipid if the mixtures followed a composition-weighted sum of the pure component A_L. Open symbols are areas for DMPC/DSPC mixtures at 55 °C calculated from bilayer thicknesses measured by Sankaram and Thompson (9) using deuterium NMR. Crosses are calculated from coarse grain molecular dynamics simulations of long and short lipids by Imparato et al. (25) and atomistic simulations of dilaurylphosphatidylcholine (DLPC) (12:0 diC) and dipalmitoylphosphatidylcholine (DPPC) (16:0 diC) by de Joannis et al. (10) as indicated in the legend.

Nonlinear Trends in the Mixed Membrane Structure.

The bilayer thickness of saturated lipids in the fluid phase is known to increase by ≈0.19 nm for each additional methylene in the lipid tail (26–28). Accordingly, the thickness of DSPC membranes is expected to be ≈0.8 nm thicker than DMPC, and mixing the two lipids should be a convenient means of tuning the bilayer thickness. Presented in Fig. 1A are the thicknesses measured for the mixed DMPC/DSPC bilayers. The pure DSPC bilayer thickness, d_B, is ≈0.5 nm thicker than pure DMPC bilayer; however, the mixed bilayer thicknesses show only minor changes with composition compared to pure DMPC at the same relative temperature, T – T_m, where T_m is the melting transition of the single component bilayers and the miscibility transition or onset of phase separation in the mixed lipid bilayers. The data in Fig. 1A also show that the thicknesses calculated from the measured thermal expansivities (see SI Appendix, Table S4, symbols in Fig. 1A) are in good agreement with the thicknesses determined from small angle neutron scattering (SANS) measurements at corresponding temperatures (crosses).

The measured d_B values are less than estimated from a composition-weighted sum of the thickness of the single component membranes (11). If there is no change in lipid volume or packing (e.g., tilt or leaflet interdigitation), then the mixed bilayer thicknesses should be an additive sum of the constituent properties, i.e., d_B,mix = x_DSPCd_B,DSPC + x_DMPCd_B,DMPC, shown as the solid line in Fig. 1A. All of the mixtures fall below this line and are ≈ 3 to 8% thinner than expected if the single component membrane thicknesses were additive.

Measurements of the lipid volume, V_L, with densitometry indicated that there is no change in lipid volume upon mixing (i.e., ΔV_mix = 0, see SI Appendix, Table S3), which are in good agreement with published V_L values for DMPC/DSPC mixtures (29, 30). The lipid volume measurements suggest that the observed deviations in mixed bilayer thickness are due to a change in lipid packing. The values of d_B and V_L can be used to calculate the area per lipid, A_L = 2V_L/d_B, which is presented in Fig. 1B (26, 31). The effective A_L of the mixtures are greater than the values from the expected composition-weighted trends (solid line) and greater than either of the pure component lipid membranes.

The increase in A_L of the mixed DMPC/DSPC membranes is also seen at a constant experimental temperature, confirming that the nonideality is not due to the choice of temperature for comparison (Fig. 2). The data also are presented in Fig. 2B as an excess area compared to the expected values from simple mixing rules (i.e., $A_{L,mix}=\sum x_i{A}_{L,i}$, where i refers to the different components of the mixture) to facilitate comparison of our results with other measurement techniques and mixed lipid systems in literature. Our scattering results are qualitatively consistent with work by Sankaram and Thompson (9), who determined the thickness of DMPC/DSPC mixtures using deuterium NMR. While the authors did not calculate A_L in their original work, combining their reported values for the bilayer thickness with our and others’ measurements of V_L shows qualitatively similar trends in the area per lipid (open circles in Fig. 2B). Moreover, results in literature suggest that the nonlinearity is not unique to DMPC/DSPC mixtures and has also been seen in other mixtures of long and short lipids (10, 25). Given that the area per lipid is a measure of the lateral organization of the membrane, our observations suggest that the mixed bilayers are less ordered than the single-component membranes, further emphasizing the nonadditive effects of mixing lipids on the molecular packing and corresponding bilayer structure.

Nonadditivity of Bending and Thickness Fluctuation Dynamics.

In this section, we focus on dynamics at the same relative temperature T – T_m because previous work in literature has found that single-component lipid membranes soften near the phase transition due to changes in the bending (6) or tilt moduli (22). However, the reported increase in dynamics in single-component membranes are found at temperatures less than ∼5 °C above T_m and here the presented data are for single-component and mixed lipid membranes at T – T_m > 10 °C. Similarly, phase separation in the mixed lipid bilayers would significantly affect the dynamics; however, the formation of small gel domains in a fluid matrix should lead to an increase in the effective rigidity not the measured decrease (32–34). We recently showed that effective bending modulus of phase separated DMPC/DSPC membranes follows theoretical predications and increases with the area fraction of gel phase (35). Moreover, the measurements in the present work were conducted at temperatures where the lipids are known to be randomly mixed (14, 15, 18). We also note that the data show nonlinear trends with composition at the same experimental temperature well above the miscibility transition (SI Appendix, Fig. S4).

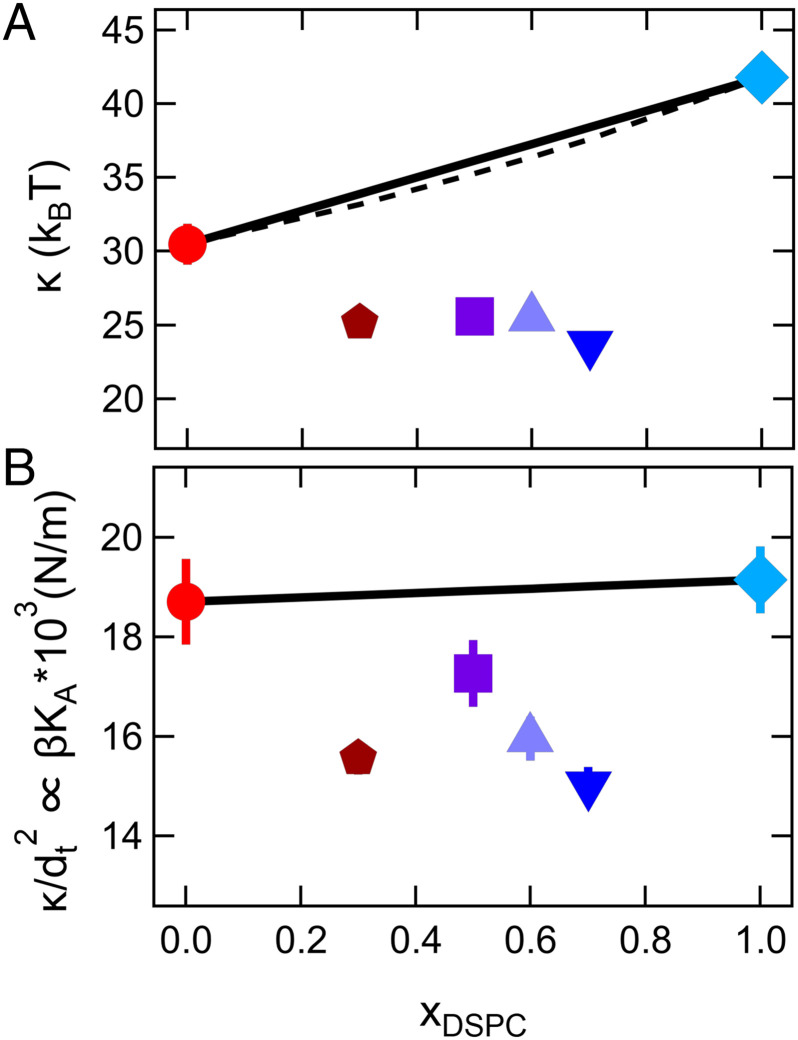
Literature reports often assume that the moduli of mixed lipid membranes are a simple additive function of the constituent component values (32–34). Our measurements of mixed DMPC/DSPC membrane dynamics demonstrate that this assumption is not always true. Shown in Fig. 3A are the bending moduli, κ, determined from neutron spin echo spectroscopy (NSE) measurements of the thermally excited bending fluctuations plotted vs. x_DSPC at a constant relative temperature. Remarkably, the data for the fluid DMPC/DSPC mixtures show that all of the mixtures are softer than either of the single-component membranes.

Fig. 3.

Bending and compressibility moduli determined from measurements of the membrane bending fluctuations. Measured (A) bending moduli, κ, and corresponding (B) values normalized by the bilayer thickness, κ/d_t² = βK_A, plotted vs. mole fraction of DSPC in the membrane at a constant relative temperature, T – T_m = 15 °C. The solid line corresponds to an arithmetic average of the measured κ for pure component membranes, while the dashed line is a harmonic average as predicted in literature (32–34).

Incorporating a mole fraction of 30% short-tail DMPC lipids into a majority DSPC membrane (x_DSPC = 0.7) reduced the effective rigidity by almost a factor of 2 compared to the pure DSPC membrane. Comparing the bending moduli for x_DSPC = 0.7 and x_DSPC = 0.3 to the pure component membranes further suggests that incorporating a small amount of short-tail lipid into a majority long-tail membrane has a much more dramatic effect than incorporating a small amount of long-tail lipid into a majority short-tail membrane.

Interestingly, the reduction in κ is not due to the measured decrease in membrane thickness discussed above. The bending modulus quadratically depends on the bilayer thickness according to the well-established relation $\kappa =\beta K_{\mathrm{A}}{d}_t^2$, in which β is a constant that describes the degree of coupling between the leaflets, K_A is the area compressibility modulus, and d_t is the hydrophobic thickness of the bilayer (31, 36). Replotting the results for κ normalized by the hydrocarbon thickness d_t², i.e., κ/d_t² = βK_A as shown in Fig. 3B, suggests that the βK_A values of the mixtures are still less than the single lipid bilayers and that the ∼5% decrease in bilayer thickness does not fully describe the decrease in κ seen in the mixtures.

Instead, the trends in κ/d_t² suggest that the decrease in κ is related to either a decrease in β or K_A in the mixtures. Work by Rawicz et al. (36) showed that for single-component phosphatidylcholine (PC) lipid membranes β = 1/24. Taking this value of β as well as the thickness and κ values measured for the DMPC and DSPC membranes gives K_A values on the order of ≈0.3 to 0.4 N/m for the single lipid bilayers. However, it is not clear that the assumption of β = 1/24 would still hold true for mixed lipid bilayers. Values of β range from 1/12 in the limit of complete coupling between the leaflets where the bilayer behaves as a single slab to 1/48 in the limit of no coupling where the leaflets freely slide past each other for the same total membrane thickness (37). If we assume that the K_A values for the mixtures are the same as for the single components, then the trends in Fig. 3B would suggest the β values for the mixtures approach 1/48 and that the leaflets are less coupled in the mixed lipid bilayers than in the single-component lipid bilayers. Alternatively, if the value of β is the same between the pure and mixed bilayers, then the decrease in κ is due to a reduction in K_A. Determining the origins of the enhanced bending dynamics of the mixed lipid bilayers therefore requires another independent measurement of K_A or β.

We recently showed that, in addition to the bending fluctuations, NSE can also be used to measure the membrane thickness fluctuations (11, 38, 39) and that the amplitude of these fluctuations $\left({\sigma }_d=\mathrm{\Delta }d/d\right)$ are related to K_A (40). Assuming the bilayer volume compressibility is negligible, any change in thickness is compensated for by a change in area, i.e., ${\sigma }_d^2={\sigma }_A^2$ in which ${\sigma }_A=\mathrm{\Delta }A/A$ (41–43). The change in area is governed by the area compressibility modulus according to the following:

$${\sigma }_A^2=\frac{k_{b}T}{K_A{A}_L}={\sigma }_d^2,$$ [1]

in which A_L is the area per lipid discussed above (40, 42). It follows that the thickness fluctuation amplitude will be large when K_A is low. More importantly, Eq. 1 means that we can use the thickness fluctuation amplitude as an additional measure of the membrane compressibility modulus, K_A.

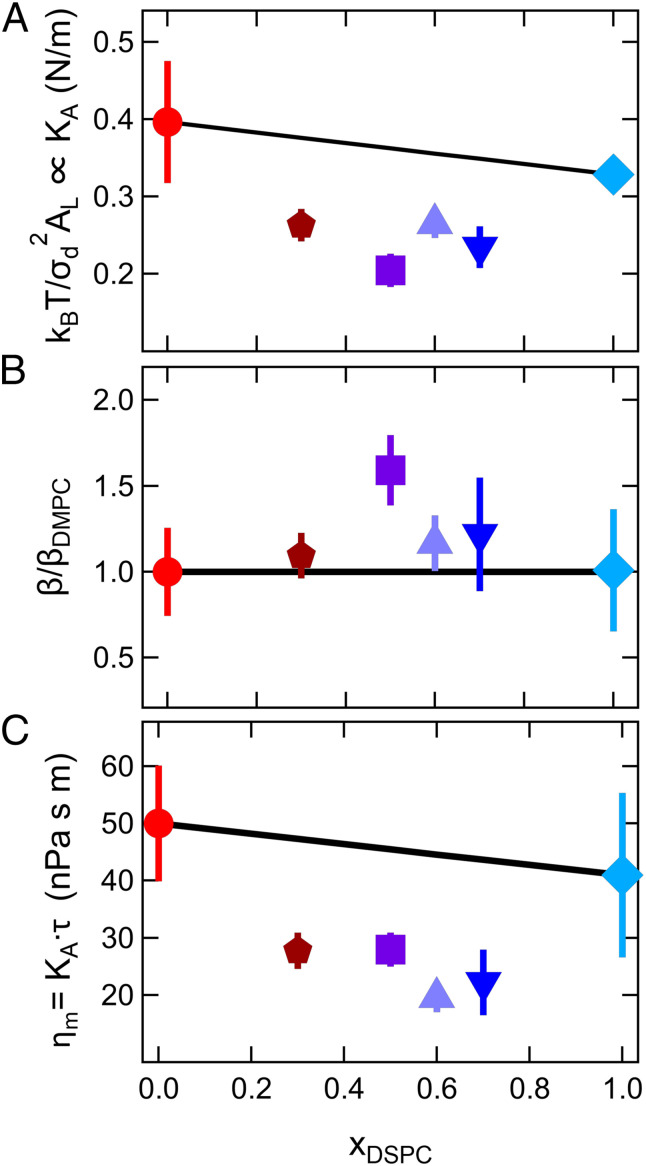
Calculating K_A values from the measured thickness fluctuation amplitude shows that K_A of the mixed bilayers are ≈20% lower than the single-component bilayers at the same relative temperature. As seen in Fig. 4A, the trends in K_A with x_DSPC calculated from σ_d are qualitatively similar to the nonmonotonic trends in βK_A determined from the bending modulus (Fig. 3B). Together, the bending and thickness fluctuation data suggest that the decrease in κ for the mixed bilayers reflects a decrease in K_A and not a change in the degree of coupling between leaflets (β). We can combine the values for βK_A from the bending fluctuations (Fig. 3B) and K_A values from the thickness fluctuations (Fig. 4A) to estimate a normalized value of β/β_DMPC, which is plotted in Fig. 4B.

Fig. 4.

Membrane elastic and viscous properties determined from measurements of the collective thickness fluctuations. (A) Relative area compressibility moduli for the mixed and pure lipid bilayers calculated from the thickness fluctuation amplitude (B) normalized coupling constant (β/β_DMPC) calculated by combining the results for the bending modulus and thickness fluctuation amplitude, and (C) calculated membrane viscosity from the compressibility moduli and thickness fluctuation relaxation time τ. Data are at the same relative temperature, T – T_m = 20 °C. The values for x_DSPC = 1.0 at T – T_m = 20 °C were extrapolated from the temperature-dependent data. All other compositions were measured at the specified temperature. Solid lines are the arithmetic average of the corresponding properties measured for the single-component membranes.

While the membrane compressibility modulus controls the thickness fluctuation amplitude, recent theoretical and experimental work show that the timescale of these fluctuations (τ) are related to the membrane viscosity (η_m) (44). Theoretical work by Bingham et al. (44) suggests that the membrane thickness fluctuations are damped by the membrane and solvent viscosities. In the limit of small-scale fluctuations that fall within the Saffman–Delbrück length scales (45), such as expected here, $\tau \approx {\eta }_m/K_A$ (44). Using this theoretical framework and using β = 1/24 to calculate K_A, the membrane viscosity is estimated to be ≈45 to 50 nPa⋅s⋅m for the pure component membranes and ≈20 nPa⋅s⋅m for the mixtures. Plotting the membrane viscosity as a function of x_DSPC highlights that the membrane viscosity is reduced by more than a factor of 2 in the mixed membranes compared to the DMPC membranes (Fig. 4C) and further reiterates that the mixed DMPC/DSPC bilayers have dramatically different properties compared to either of the constituent lipid membranes.

Correlating Membrane Structure and Dynamics.

The data presented above show that the mixed lipid membranes are easier to bend and compress and are less viscous than either of the single-component membranes at the same relative temperature. These enhanced dynamics are surprising without context. However, taking a holistic view of the data presented here reveals that the changes in both the membrane structure and dynamics show qualitatively similar trends and suggests that they are directly linked. The direct correlation between the membrane structure and dynamics is clearly seen from how the membrane fluctuations measured with NSE (see SI Appendix, Fig. S7) as well as the extracted mechanical properties in Fig. 5, in which κ, K_A, and η_m for all lipid compositions across a wide range of temperatures, collapse onto their respective master curves, all of which scale with the area per lipid (A_L).

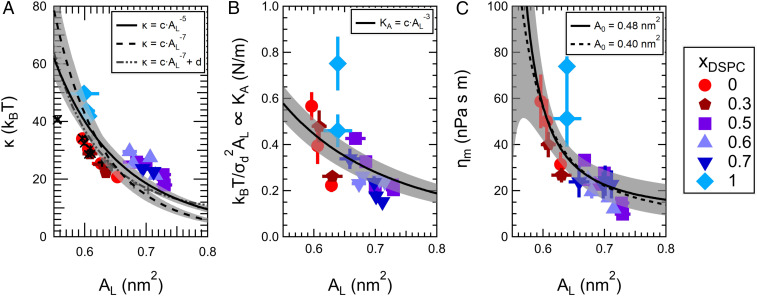
Fig. 5.

The elastic and viscous properties are linked to the membrane structure and scale with the area per lipid, A_L. Bending modulus (A), compressibility modulus (B), and viscosity (C) vs. A_L for all lipid compositions measured at various temperatures in the lipid fluid phase. The points are the measured data, and the lines are the expected scaling for the respective properties indicated in the legend where c and d are constants. See text for details. Crosses in A correspond to bending modulus values from simulations by Doktorova et al. of $(+)$ pure phosphatidylcholine lipid membranes and $(\times )$ mixtures of zwitterionic monounsaturated phosphatidylcholine (PC) and phosphatidylethanolamine (PE) lipids with charged phosphatidylserine (PS) and phosphatidylglycerol (PG) lipids (46). Values of A_L and κ were taken from tables 1 and 2 in the reference, respectively. The mixtures include 1-palmitoyl-2-oleoyl phosphatidylethanolamine (POPE) with 1-palmitoyl-2-oleoyl phosphatidylglycerol (POPG) (POPE/POPG 70:30) and 1-palmitoyl-2-oleoyl phosphatidylserine (POPS) (POPE/POPS 70:30) as well as mixtures of 1-palmitoyl-2-oleoyl phosphatidylcholine (POPC) with POPS (POPC/POPS 70:30) and palmitoyl sphingomyelin (PSM) (POPC/PSM 70:30). All points were weighted equally for the fits, and shaded areas represent the 95% confidence bands.

Fig. 5A suggests that the bending modulus decays strongly with area per lipid for small changes in lipid area, especially given that the total range of A_L varies by only ∼20%. The steep dependence seen here is in good agreement with theory that predicts κ strongly depends on A_L and is related to the conformational entropy of the tails (47, 48). As the area per chain in the bilayer increases, the number of conformations accessible to the tail increases, and the membrane is easier to bend. Accordingly, any change in the membrane structure or composition that increases the conformational degrees of freedom should decrease the bending rigidity of the bilayer (48).

Several theoretical studies have shown that mixing long- and short-tailed amphiphiles is an effective means of increasing the conformational entropy of the tails and thereby decrease κ in mixed bilayers (49–51). Moreover, work by Szleifer et al. (49) and Safran et al. (51) suggest that κ of the mixtures is further reduced if the mixed bilayers have a greater area per lipid than the pure component membranes, such as seen here experimentally. Subsequent theoretical studies showed that the compositional degree of freedom introduced by mixing lipids with different tail lengths will also lead to a reduction in κ, as the lipid composition can adjust to the local curvature (52, 53). Our measured softening of mixed DMPC/DSPC lipid bilayers at the same relative temperature are in excellent agreement with these predictions (49–51, 53) as well as several computational studies (25, 54, 55) that show mixed tail length bilayers are softer than the single-component bilayers. Moreover, the theoretical and computational studies suggest that the measured softening is not unique to DMPC/DSPC mixtures, but a generic feature of mixed tail length bilayers that disrupt the lipid packing.

The bending modulus is most often plotted as a function of the bilayer thickness using the well-established polymer brush model developed by Rawicz and colleagues (36), $\kappa =\beta K_A{d}_t^2,$ discussed above. While the decrease in membrane thickness did not fully account for the decrease in κ, our NSE measurements also indicated that K_A decreases in the mixed lipid bilayers. The polymer brush model also predicts that K_A will depend on A_L⁻³ as indicated in Fig. 5B and discussed below, which when combined with $d_t^2\propto A_L^{-2}$, suggests $\kappa \propto A_L^{-5}$. This scaling is shown as the solid line in Fig. 5A and captures the overall trend in the experimental data, with a steep dependence at small A_L that decays with increasing A_L. At the same time, theoretical mean field calculations by Szleifer et al. predict an even stronger $\kappa \propto A_L^{-7}$ dependence, shown as the dashed line. The $\kappa \propto A_L^{-7}$ scaling was also recently seen in all-atom simulations performed by Doktorova et al. (46), where the constants c and d in $\kappa \propto c\cdot A_L^{-7}+d$ (dot-dash curve in Fig. 5A) are directly taken from their best fit for structurally distinct phosphatidylcholine lipid membranes (shown as the $+$ symbols in Fig. 5A). Not only does the curve from Doktorova et al. reasonably describe the experimental measurements for DMPC/DSPC reported here, but it also seems to fit the trends in their simulations of mixtures of zwitterionic and charged lipids that are shown as the $\times$ symbols in Fig. 5A.

While there are not enough data to distinguish between the different forms of the predicted scaling relationships, they do support the hypothesis that A_L is a more relevant variable than membrane composition when it comes to predicting the behavior of more complex lipid mixtures. Looking at the bending modulus as a function of A_L suggests that the increase in dynamics is influenced mainly by the disrupted packing of the lipid tails and associated disordering of the membrane (i.e., increase in A_L) in the mixed lipid bilayers studied here. While recent work by Steinkühler et al. showed that biological membranes are softer than model lipid membranes, the measured κ for plasma membrane extracts still directly correlated with the local membrane order measured with environment-sensitive dyes (56). In another example, work by Boscia et al. (57) investigated the properties of multicomponent HIV and T-cell fluid-phase membrane models containing mixtures of 10 lipids with varying saturation and headgroup chemistries. Interestingly, while the bending modulus of the T-cell membrane mimic was comparable to single-component bilayers of the same thickness, the HIV membrane mimic was significantly softer than single-component membranes of the same thickness, suggesting changes in thickness alone cannot describe the differences in elastic properties between the complex membrane mimics. Moreover, coarse-grained simulations of lipid membranes by Cooke and Deserno (58) showed that both A_L and κ scale with interaction potential between lipid tails, and by extension, κ will increase with decreasing A_L for a range of tail–tail attractions. Together with our work on model lipid mixtures, these results point toward a promising relationship between bending rigidity and lipid order that may extend to more complex membrane systems.

The scaling of membrane area compressibility with the area per lipid is perhaps the most intuitive, i.e., membranes with a larger A_L will be easier to compress (Fig. 5B). As suggested above, the Rawicz et al. (36) derivation assumed K_A = 6Π, where Π is the surface pressure, and that Π (and by extension K_A) scale with $\text{Π}\propto K_A\propto A_L^{-3}$ in their development of the polymer brush model. The best fit to this scaling is shown as the solid line in Fig. 5B. In modeling the lipid membrane as a polymer brush, Rawicz et al. assumed that surface pressure, and therefore K_A, were dominated by the chain extension and ultimately the chain confinement entropy. As with the bending modulus, K_A should decrease as the area per lipid increases and the tails are less extended and able to adopt more configurations.

In addition to the elastic properties, η_m decreases with increasing area per lipid and corresponding increasing temperature (Fig. 5C). The temperature dependence of the viscosity in three-dimensional (3D) bulk liquids and polymers is explained by the free volume theory according to the Doolittle equation, in which the viscosity decreases with increasing temperature as the free volume increases (59, 60). The Doolittle equation has been extended to 2D fluid lipid membranes in terms of the free area model, in which the membrane viscosity is related to the free area per molecule in the bilayer, according to the following:

$${\eta }_m=j\exp \left[k\frac{A_L}{A_L-A_0}\right]\hspace{1em},$$ [2]

in which A₀ is the area per molecule in the crystalline condition at 0 K and j and k are constants (61–63). The excluded area for all trans hydrocarbon chains at 0 K (A_c) is ∼0.19 nm², which would give A₀ = 2A_c ∼ 0.4 nm² (36, 62, 64). However, studies of gel-phase phosphatidylcholine (PC) lipid membranes suggest there is a strong repulsion between PC headgroups below 0.472 nm², which has been used as the limiting area per lipid in literature (65–67). While our data show excellent agreement with the scaling predicted by Eq. 2, they are not sensitive to differences between A₀ = 0.40 nm² vs. A₀ = 0.48 nm² represented by the dashed and solid lines in Fig. 5C, respectively. Accurately determining A₀ would require accessing a larger range of A_L. The reduced viscosity of mixed tail length bilayers is opposite to the effects of adding cholesterol to saturated phospholipid bilayers, which is known to increase the membrane packing order and thereby decrease the area per lipid and increase the membrane viscosity (63, 68). More importantly, contextualizing our results in the frame of free area highlights the importance of lipid packing and the associated membrane structure in also regulating the membrane viscosity.

The results in Fig. 5 emphasize that membranes with mixed lipid tail lengths become more dynamic as the lipids are less ordered. For a given composition, the dynamics can be manipulated by changing temperature as the trans-gauche isomerization of the tails increases with increasing temperature, leading to a decrease in the lipid order and packing efficiency and an increase in the area per lipid. The effect of mixing lipid tail lengths is akin to increasing temperature in that it disrupts the lipid packing, suggesting that lipid composition can be used to control the membrane properties without changing the temperature. This compositional control over the membrane structure and dynamics is especially relevant for biological membranes where physiological temperature is highly constrained. For instance, this control would allow cells to tune the membrane fluidity by simply changing the local membrane composition. The importance of compositional control over membrane viscosity is best illustrated by homeoviscous adaptation, a phenomenon in which cells are known to manipulate their lipid composition according to their growth temperature (69). A recent study demonstrated that membrane viscosity directly impacts cellular respiration in Escherichia coli (70), and our results for model systems confirm that membrane composition is an efficient means to control membrane viscosity for a given temperature.

Another interesting implication of the results in Fig. 5 is that mixing long- and short-tail lipids does not seem to significantly affect the bilayer mechanical thickness and/or coupling between leaflets (β, Fig. 4B) in these membranes. If either of these parameters were significantly different between the mixed and single-component bilayers, then κ and K_A would not scale with the changes in A_L. The relationship between κ and K_A is derived from thin elastic sheet theory, where β = 1/12 for a fully coupled bilayer behaving as a single slab and β = 1/48 for a bilayer behaving as two independent sheets (37). In other words, for the same total thickness, a completely coupled membrane will be four times stiffer than an uncoupled bilayer. The polymer brush model developed by Rawicz et al. gives an intermediate value of β = 1/24 by assuming the elastic properties were governed by a mechanical thickness that depends on the stress distribution across the bilayer. The polymer brush model has been shown to work for a number of single-component lipid membranes where the mechanical thickness is taken as the hydrocarbon thickness of the bilayer (d_t). However, this assumption has not worked well for membranes composed of lipids with multiple degrees of unsaturation or membranes containing additives. It has been suggested in literature that changing the physical interactions between leaflets by incorporating lipids with asymmetric tail lengths (71, 72), long chain linear alkanes (73), or a peptide (74) that spans both leaflets could change the value of β. Other works suggest that incorporating stiff bulky molecules like cholesterol changes the mechanical thickness of the bilayer and therefore the relationship between κ and K_A (4, 75).

The scaling of the membrane elastic properties with A_L in the mixed DMPC/DSPC bilayers further emphasizes that the lipid order is the main determinant of the membrane elastic moduli in these systems. In fact, deviations from the scaling relationships seen in Fig. 5 would point to a different mechanism through which membrane composition can influence the elastic properties. For example, significant changes in the membrane elastic properties but not the membrane order may indicate a change in the coupling constant (β) or effective mechanical thickness of the bilayer (57, 74). Or the proportionality factors (c and d in Fig. 5) may change with lipid chemistry (36, 50). The theoretical mean field calculations by Szleifer et al. (50) that predict $\kappa \propto A_L^{-7}$ also show that the values of κ (and therefore the proportionality factor) significantly depend on whether or not the individual lipids are allowed to rapidly rearrange within the bilayer. Similarly, the polymer brush model that predicts $K_A\propto A_L^{-3}$ assumes that the surface pressure is dominated by the chain entropy and neglects specific headgroup interactions; therefore, the scaling factors for K_A may be different for other groups of headgroups than those studied here (36). Nevertheless, while other factors may come into play, the link between the membrane structure and dynamics in Fig. 5 highlights that understanding and predicting the elastic properties of more complex membrane compositions will require understanding more than just the properties of membranes composed of the constituent lipids.

Discussion and Summary

The detailed structural and dynamical characterization presented here shows that mixing lipids with different tail lengths disrupts the lipid packing, and, as a result, the mixed membrane morphology and collective dynamics are not additive properties of the single-component bilayer properties. We take advantage of the unique capabilities of NSE to show that mixed DMPC/DSPC membranes are more dynamic than their single-component analogs, as evidenced by the reduction in the bending modulus, κ, area compressibility modulus, K_A, and membrane viscosity, η_m. Importantly, we show that κ, K_A, and η_m measured at different temperatures collapse onto master curves and scale with the changes in area per lipid and associated lipid order. The direct scaling suggests that it is not the chemistry of the individual lipids, as much as how the molecular structure affects the lipid packing, that governs the macroscopic membrane properties in these mixtures. Moreover, the linkage between structure and dynamics and the simple scaling relationships presented here provide a path toward predicting the dynamics of more complex and biologically relevant mixtures.

From a fundamental soft matter engineering perspective, the results presented here are a prime example of introducing new properties by manipulating the molecular composition. There are numerous examples of blending long and short molecules to tune the mechanical properties of soft materials from small-molecule surfactants to high–molecular-weight polymers. Blending long and short surfactants molecules has been shown to soften microemulsions (76) and worm-like micelles (77) often used in household and personal care products. Work by Yamamoto et al. (78) also took advantage of molecular composition to tune the compressibility and therefore the phase behavior of liquid crystal mixtures. They showed that mixing long (twin) and short (monomer) liquid crystal molecules stabilized a novel “blue phase” because the mixtures were drastically softer. Similarly, bimodal blends of high–molecular-weight (long) and low–molecular-weight (short) polyolefins simultaneously enhance the mechanical properties and improve the processability of polymer products for commercial applications (79, 80). In each example, the macroscopic mechanical properties were controlled by the microscopic molecular composition, like the mixed lipid membrane studied here; suggesting cells may exploit the same tools scientists and engineers use to control the mechanical properties of soft materials.

From a biological perspective, these results have important implications for understanding the role of lipid diversity in biological functions. The biological relevance of lipid diversity is often considered in the context of lateral membrane organization and the formation of raft domains. Our results highlight that even in a homogenously mixed fluid membrane, lipid composition can significantly influence the structural, elastic, and viscous properties of biological membranes. These are the same membrane properties that are essential to protein and cell functions, which has important ramifications for designing model membrane systems and understanding the role of the highly regulated lipid composition in biological membranes.

Experimental Procedures

Materials.

Mixtures of tail deuterated (DMPC-d₅₄ or DSPC-d₇₀) and protiated lipids were used to vary the neutron scattering contrast and highlight specific structural and dynamical features discussed in more detail below. The membrane compositions are summarized in SI Appendix (SI Appendix, Tables S1 and S2), and the nomenclature x_DSPC refers to the mole fraction of long-tailed DSPC in the mixture. Lipid mixtures were prepared by dissolving the desired amounts of the dry lipid powders in a small volume of chloroform. The chloroform was removed under a stream of nitrogen gas followed by drying under vacuum at 60 °C for at least 12 h. The dry lipid films were rehydrated to the desired concentration with D₂O, and then incubated at 60 °C overnight, producing multilamellar vesicle suspensions. Unilamellar vesicles were prepared by sequentially extruding the vesicle suspension through filters with pore diameters of 400 nm (21 passes), 200 nm (21 passes), and finally 100 nm (41 passes). All extrusions were performed at temperatures corresponding to the bilayer fluid phase, typically between 55 and 65 °C. The final concentration of the vesicle solutions was 100 mg/mL lipid in D₂O. All samples were stored in the lipid fluid phase before analysis, and experiments were performed upon cooling.

Densitometry.

Lipid vesicle samples for densitometry were diluted to 20 mg/mL with D₂O. Densitometry measurements were made in the temperature range of 70 to 15 °C with temperature steps of 0.2 °C. The densitometry data were analyzed following literature (81–83), and the analysis is discussed in detail in SI Appendix (SI Appendix, section S2). The measured and calculated lipid volumes (V_L) are also presented in SI Appendix (SI Appendix, Table S3).

Differential Scanning Calorimetry.

Vesicle samples for differential scanning calorimetry (DSC) were diluted with D₂O to concentrations ranging from 5 to 20 mg/mL. Samples were equilibrated in the fluid phase, and at least two cooling and heating cycles were measured using a scan rate of 0.5 °C/min. Corresponding heating and cooling cycles were also measured for the D₂O to correct the sample data for the solvent baseline. DSC data were used to determine the phase transition temperatures presented in SI Appendix (SI Appendix, Table S3).

Small-Angle X-Ray Scattering.

Small-angle X-ray scattering (SAXS) experiments were performed on the 12-ID-B beamline at the Advanced Photon Source at Argonne National Laboratory. SAXS experiments were performed using a flow cell and the temperature was maintained within ± 2 °C. SAXS data were collected using an X-ray wavelength of 0.9 Å (corresponding X-ray energy of 14 keV) with a sample to detector distance of 2 m to measure a scattering vector, q, range of 0.004 Å⁻¹ ≤ q ≤ 1 Å⁻¹. The scattering vector is defined as q = (4π/λ)sin(θ/2), in which θ is the scattering angle. Data were collected using 2-s acquisitions times and averaged over 30 acquisitions. The data were reduced and background scattering from D₂O was subtracted using the software packages provided by the beamline (SI Appendix, Fig. S1C). X-ray scattering experiments were performed with the same mixture of tail-deuterated and protiated lipids (SI Appendix, Table S2) in D₂O as used for NSE at a concentration of 20 mg/mL.

SANS.

SANS experiments were performed on the NG7 and NGB 30m SANS instruments at the National Institute of Standards and Technology (NIST) Center for Neutron Research (NCNR) (84). Experiments were performed using a neutron wavelength, λ, of 6 Å and sample to detector distances of 1 and 4 m to probe a q range of 0.01 Å⁻¹ < q < 0.4 Å⁻¹. The temperature was controlled with a water bath within an accuracy of ±0.2 °C, and all data were acquired on cooling the sample. The raw SANS data were reduced to 1D data using the reduction procedures provided by NIST (85). The scattering data for all samples were checked to ensure that the vesicles were unilamellar before further characterization with NSE or detailed data analysis (86). Data for the tail-deuterated lipid mixtures were fit with a bilayer form factor model described in literature (86, 87); details of the SANS data analysis are discussed in SI Appendix (SI Appendix, section S3).

For temperatures at which SANS data were not collected, the bilayer thickness was calculated from the measured bilayer expansivity, ${\alpha }_{d_B}=\left(1/d_B\right)\left(\partial d_B/\partial T\right)$ (SI Appendix, Table S4), and the presented error represents the propagated uncertainty in the calculated value. The area per lipid, A_L, was calculated from the bilayer thickness determined from the SANS data analysis according to A_L = 2V_L/d_B in which V_L is the volume per lipid molecule (SI Appendix, Table S3) (26, 27). The hydrocarbon tail thickness, d_t, was calculated as d_t = d_B – 10.0 Å, based on results for d_B – d_t for published for saturated phosphatidylcholine lipids (26–28).

NSE.

NSE experiments were performed on the NGA-NSE Spectrometer at the NCNR (88). The NSE experiments used λ of 6, 8, and 11 Å with a wavelength spread Δλ/λ ∼ 0.18, providing access to q values ranging from 0.04 Å⁻¹ < q < 0.18 Å⁻¹ and Fourier times ranging from 0.01 to 100 ns. Temperature was controlled with a recirculation bath within an accuracy of ±1 °C. All experiments were performed on cooling the sample. The NSE data were corrected for the instrument resolution and solvent background to give the intermediate scattering function using the DAVE software package (89).

To measure the bending fluctuations, protiated lipids were mixed at the desired molar ratio (SI Appendix, Table S1) and prepared in D₂O according to the procedure above. To measure the thickness fluctuations, the dynamic contributions from the headgroups were emphasized by minimizing the scattering from the lipid tails using mixtures of tail-deuterated and protiated lipids (SI Appendix, Table S2) in D₂O (11, 38). The NSE data were analyzed following established procedures in literature (11, 38, 40, 90–93), and the details of the NSE data analysis are described in SI Appendix (SI Appendix, section S4).

Data Availability.

All raw SANS and NSE data are publicly available in the NCNR data repository (DOI: 10.18434/T4201B). All data discussed in the paper are also available upon request.