Mechanical design of the highly porous cuttlebone: A bioceramic hard buoyancy tank for cuttlefish

Significance

Cellular solids, or foams, are an important class of structural materials for packaging, transportation, and infrastructure due to their mechanical efficiency. Current foams are primarily made of metallic or polymeric materials, while ceramics could potentially serve this goal better, as they have higher specific stiffness and strength, and are chemically more stable. What limits the application of ceramic cellular solids as structural components are their brittleness and flaw sensitivity. Overcoming the fragile nature of ceramic foams, making them lighter while reaching higher stiffness, strength, and energy absorption is challenging but critical toward many applications. In this study, we elucidate how cuttlebone overcomes its intrinsic brittleness through the “wall–septa” microstructure, which could inspire the development of lightweight ceramic cellular solids.

Abstract

Cuttlefish, a unique group of marine mollusks, produces an internal biomineralized shell, known as cuttlebone, which is an ultra-lightweight cellular structure (porosity, ∼93 vol%) used as the animal’s hard buoyancy tank. Although cuttlebone is primarily composed of a brittle mineral, aragonite, the structure is highly damage tolerant and can withstand water pressure of about 20 atmospheres (atm) for the species Sepia officinalis. Currently, our knowledge on the structural origins for cuttlebone’s remarkable mechanical performance is limited. Combining quantitative three-dimensional (3D) structural characterization, four-dimensional (4D) mechanical analysis, digital image correlation, and parametric simulations, here we reveal that the characteristic chambered “wall–septa” microstructure of cuttlebone, drastically distinct from other natural or engineering cellular solids, allows for simultaneous high specific stiffness (8.4 MN⋅m/kg) and energy absorption (4.4 kJ/kg) upon loading. We demonstrate that the vertical walls in the chambered cuttlebone microstructure have evolved an optimal waviness gradient, which leads to compression-dominant deformation and asymmetric wall fracture, accomplishing both high stiffness and high energy absorption. Moreover, the distribution of walls is found to reduce stress concentrations within the horizontal septa, facilitating a larger chamber crushing stress and a more significant densification. The design strategies revealed here can provide important lessons for the development of low-density, stiff, and damage-tolerant cellular ceramics.

Cuttlefish is a fascinating group of marine organisms that has attracted broad interest from both scientists and the public because of its remarkable intelligence (1), extreme camouflage (2), and unique visual system (3). The earliest interest in studying cuttlefish dates back to the Greek philosopher Aristotle almost 2,500 y ago, who was intrigued by the unique anatomy of cuttlefish (4). Although named as a fish, cuttlefish is in fact a mollusk of the order Sepiida with over 120 different species. Together with squid, octopuses, and nautiluses, cuttlefish belongs to the class Cephalopoda, which represents a special group of mollusks capable of swimming. Unlike most mollusks with hard shells covering their body exterior for protection, the “shell” of cuttlefish is internal and highly porous (porosity, ∼93 vol%) (5), commonly known as cuttlebone. This allows cuttlefish to adjust its buoyancy by regulating the gas-to-liquid ratio within the shell, similar to nautiluses (6, 7). Unlike the soft swim bladders for buoyancy-regulating purposes in fishes, cuttlebone is a stiff structure composed of >90% aragonite (8), a common mineral found in many mollusk shells (9). It has been demonstrated that cuttlefish controls the concentration of salt ions of the fluid inside cuttlebone and hence the fluid’s osmotic pressure, which then regulates the charge and discharge of the fluid for buoyancy adjustment (10).

Although most cuttlefishes live in shallow waters, some species are known to inhabit as deep as 600 m (11, 12). This requires the cuttlebone to sustain extreme external water pressure as high as 60 atm and to avoid catastrophic failure (10, 13–15), which entails the cuttlebone to be both stiff and damage tolerant. Previous studies show that some cuttlefish can survive with partially damaged cuttlebone because the damage is progressive and localized, which can be repaired subsequently (5, 6, 16). This is remarkable given the fact that the cuttlebone is primarily composed of intrinsically brittle aragonite (8). Moreover, the active fluid exchange for buoyancy control requires the structure to be open and bicontinuous, whereas the closed cell design of many natural cellular structures, such as bird feathers, porcupine quills and cork, cannot achieve such function (17). Although the functional requirement of cuttlebone is clearly recognized in the biology field, the underlying material design strategies for achieving such remarkable mechanical performance with extreme lightweight are yet to be established (5, 6, 18).

Recently, mechanical metamaterials (materials that possess unusual mechanical properties primarily resulting from their microstructure instead of the constituent materials) with ultrahigh specific stiffness have been developed (19, 20). The high specific stiffness in these metamaterials is achieved through a compression/stretching-dominant deformation mechanism, where their structural elements are dominantly under compression or stretching instead of bending (21). However, these ultrastiff metamaterials suffer from catastrophic failure, due to the lack of an effective damage arresting mechanism (22–24). Therefore, learning how cuttlebone achieves high specific stiffness, progressive failure, and light weight simultaneously can provide new insights to improve the damage tolerance of mechanical metamaterials. Researchers have tried to mimic the geometry of cuttlebone (25–28), but tough ceramic lattices comparable to cuttlebone have not been accomplished, limited by the incomplete understanding of the structural design and deformation mechanism in cuttlebone.

In this work, we seek to establish the structural designs of cuttlebone utilizing complementary three-dimensional (3D) structural and four-dimensional (4D) mechanical analysis combined with parametric mechanical modeling. With in situ synchrotron-based microcomputed tomography (µ-CT) coupled with mechanical testing, we visualize and quantify the detailed failure process of cuttlebone. The 3D structural quantification further allows us to parametrically establish biomimetic models to investigate the mechanical performance and design trade-offs across different length scales, which is correlated with the in situ results and digital image correlation (DIC). Our results reveal that the cuttlebone has evolved an optimal chambered “wall–septa” microstructure that achieves high stiffness as well as graceful failure.

Results

Structure of Cuttlebone: The Chambered Wall–Septa Design.

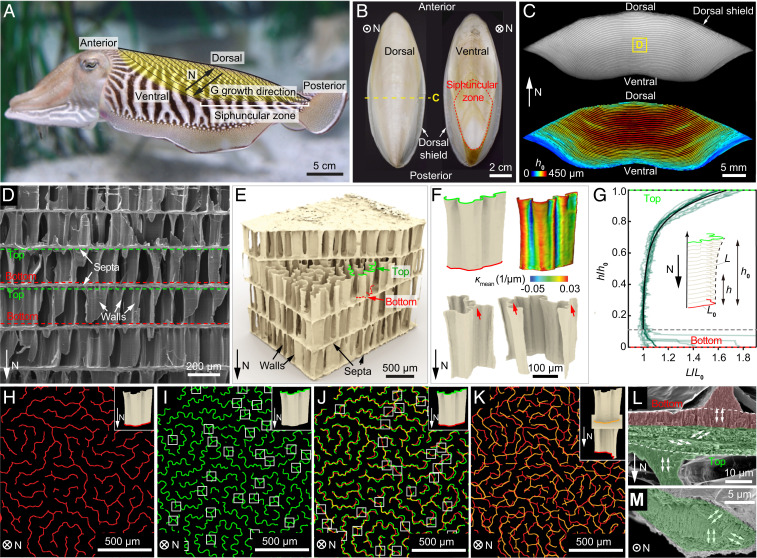
As illustrated schematically in Fig. 1A, the cuttlebone is located toward the dorsal side of the cuttlefish body. In this study, the species Sepia officinalis was used as a model system, which can survive 200 m under water, corresponding to an external water pressure of ∼20 atm (16). The dorsal side of the rigid cuttlebone is covered with a thick and tough layer (∼0.5 mm) known as the dorsal shield (5), under which a porous chambered structure is placed ventrally (Fig. 1 B and C and SI Appendix, Fig. S1). The posterior end of the chambers forms the siphuncular zone, through which the fluid can flow in and out for buoyancy control (Fig. 1 A and B) (13). In the transverse view along the normaldirection "N" (defined as the direction pointing from the ventral to the dorsal side, Fig. 1A), individual chambers can be seen clearly and their heights gradually decrease from the center toward the ventral side (Fig. 1C). Note that new chambers are added at the ventral side (15); therefore, the growth direction (“G”) is opposite to the normal direction (“N”) of cuttlebone.

Fig. 1.

The chambered wall–septa structure of cuttlebone. (A) A cuttlefish with the cuttlebone highlighted in yellow. “N” direction points from the ventral to the dorsal side. “G” denotes the growth direction. Siphuncular zone is the striated area on the posterior-ventral part of the shell. (B) Dorsal and ventral views of the cuttlebone. (C) A transverse view of the cuttlebone (Top) and corresponding chamber height map (Bottom). (D) A scanning electron microscopy (SEM) image of the chambers with walls and septa indicated by white arrows. The top and bottom of the walls are highlighted by green and red dashed lines, respectively. (E) A 3D µ-CT reconstructed wall–septa structure. The walls have wavier top profiles (green) compared to the bottom profiles (red). (F) Representative reconstructed individual walls. The red arrows indicate the triple joints. The contour represents the corresponding mean curvature distribution. (G) Normalized wall length $L/L_0$ plotted against normalized height $h/h_0$ of 11 walls. Eq. 1 is plotted as the solid black line. The labyrinthine pattern of walls near the (H) bottom and (I) top of the chamber. The white boxes in I indicate triple junctions. (J) Overlay of H and I, where the white boxes indicate the splitting locations of the walls. (K) Overlay of the wall bottoms from two adjacent chambers. (L) Side-view and (M) top-view SEM images showing the microstructure of septum. The lower portion of the septum possesses a rotating plywood structure (green), while the crystallites of the upper portion (red) are aligned vertically with the wall.

The chambered cuttlebone structure is based on a characteristic wall–septa design as revealed by the scanning electron microscopy (SEM) (Fig. 1D) and 3D µ-CT reconstruction (Fig. 1E). The horizontal septa (thickness, 7 to 15 µm) separate the cuttlebone into individual chambers, which are supported by numerous vertical walls. The wall thickness is measured as 4 to 7 µm, where variations may exist among individuals (12, 18, 29). Moreover, no significant changes in wall thickness between wet and dry samples have been observed (SI Appendix, Fig. S2). This wall–septa design results in an extremely high porosity of cuttlebone (∼93 vol%) (5). The walls have corrugated morphologies and become wavier from the bottom to the top of the chamber (along the growth direction), which is also consistent with the increase in the absolute values of mean curvature (Fig. 1F and SI Appendix, Fig. S3). Due to this gradual morphological variation, the cross-sectional profile of an individual wall is found to follow this relationship (based on the measurements of 11 walls):

$$L/L_0=0.998+0.002e^{6.55\left(h/h_0-0.11\right)},$$ [1]

where $h_0$ represents the chamber height, $L_0$ is the cross-sectional length close to the bottom, and L is the cross-sectional length at a height h (Fig. 1G). Note that in the region with h < 50 μm $\left(h/h_0<0.11\right)$, some walls split into multiple segments, which are not included in the model for simplicity. This mathematical description of the wall profile allows parametric investigations of the wall mechanics later.

On a larger length scale, the vertical walls within one chamber are organized in a labyrinthine pattern (Fig. 1 H and I) (29). The spacing between adjacent walls is roughly constant at specific heights: 88.7 ± 15.6 and 67.0 ± 15.7 μm at the wall bottom and top, respectively (SI Appendix, Fig. S4). Moreover, the gradual increase in waviness from the wall bottom to top is clearly visualized by overlaying the cross-sectional profiles from the same projected region in the chamber, which also reveals the splitting of some walls (white boxes in Fig. 1J). The density of wall splitting is estimated to be 14/mm² (46% of the walls split). Approximately one-half of the walls possess one to two triple junctions, and walls with triple junctions tend to be longer compared to those without such junctions (Fig. 1I and SI Appendix, Fig. S5). Overlay of the patterns of wall bottoms from adjacent chambers shows that the vertical walls from adjacent chambers are not aligned exactly in the same position (Fig. 1K).

It is known that cuttlebone is composed of aragonite (one polymorph of calcium carbonate) (30) as the only mineral phase and a small amount of organic materials (∼9.8 wt% for the whole cuttlebone and ∼5 wt% for the chambered structure) consisting of β-chitin and proteins (5, 8, 31, 32). Previous studies have also shown that the walls have a higher mineral content than the septa (18). A careful examination of the microstructure revealed that each septum consists of two sublayers (33). The upper sublayer and the wall share the same vertically aligned aragonite crystallites along their [001] directions (red shaded region in Fig. 1L) (8), whereas the nanorod-like crystallites in the lower sublayer rotate their orientations gradually, forming a rotating plywood structure (green shaded regions in Fig. 1 L and M and see SI Appendix, Fig. S6 for magnified SEM images) (18, 34).

Graceful Failure for High Energy Absorption.

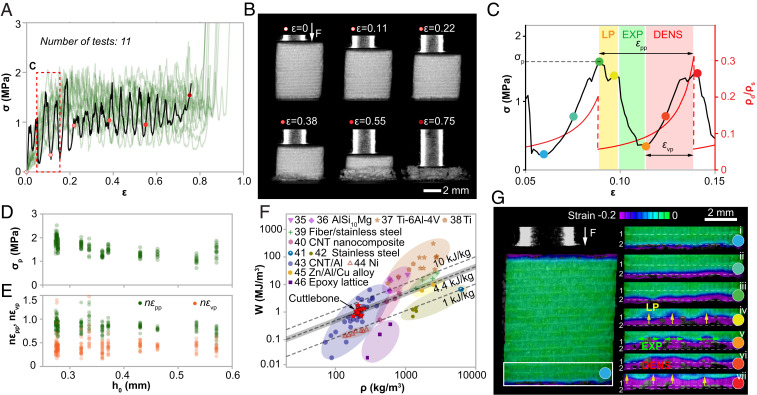
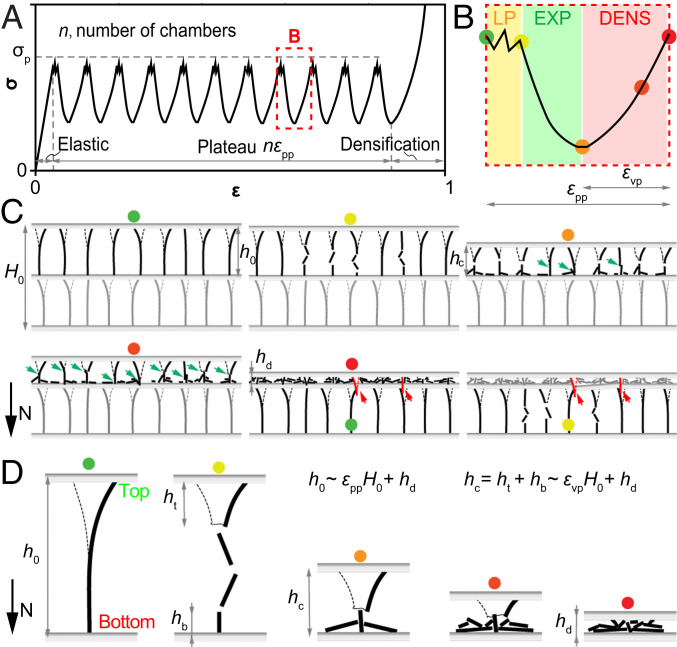
Compression tests performed on cubic samples (edge length, 5 to 10 mm, corresponding to 10 to 30 chambers) reveal the cuttlebone’s remarkable graceful failure behavior, despite its high porosity and mineral density (Fig. 2 A and B and SI Appendix, Fig. S7). More specifically, the stress–strain curves of cuttlebone, unlike engineering ceramic cellular solids, show three stages, including an elastic regime, a serrated stress plateau regime (ε up to 0.85), and a densification regime, which is a classic behavior observed in foams composed of ductile materials such as metals and polymers (Fig. 2A) (17). Within the plateau regime, the stress–strain curves exhibit periodic fluctuations (Fig. 2C), where the total number of periods corresponds to the number of chambers (n) in the tested sample. This results from the sequential failure of individual chambers (Fig. 2B and SI Appendix, Fig. S7). The peak stress of each period, ${\sigma }_p$, is relatively constant (1.58 ± 0.32 MPa; N = 212) despite the variations in chamber heights (Fig. 2D). The normalized peak-to-peak strain $\left(n{\epsilon }_{pp}=0.85\pm 0.13\right)$ and valley-to-peak strain $\left(n{\epsilon }_{vp}=0.42\pm 0.16\right)$ also show no significant dependence on chamber heights (Fig. 2E). Due to this graceful failure behavior, cuttlebone achieves an extremely high energy absorption capacity (W) of 0.6 to 1.5 MJ/m³ at a density $\left(\rho \right)$ of only 180 to 260 kg/m³. The resultant specific energy absorption $W/\rho$ is 4.4 ± 1.1 kJ/kg, which is superior or comparable to many advanced foams based on metals, polymers, and carbon (Fig. 2F) (35–46). Similar compression tests were also performed on wet samples, which exhibit a consistent mechanical response as dry samples (SI Appendix, Fig. S8).

Fig. 2.

Mechanical performance of the chambered cuttlebone structure under compression. (A) Stress–strain curves of 11 compression tests. (B) Snapshots of deformation stages corresponding to the black curve in A. (C) A typical period of the stress–strain curve exhibits three stages, namely, local penetration (LP), expansion (EXP), and densification (DENS). The red curve plots the relative density $\left({\rho }_d/{\rho }_s\right)$ of the damaged chamber during deformation. ${\epsilon }_{pp}$, ${\epsilon }_{vp}$: peak-to-peak strain and valley-to-peak strain in a stress–strain period. ${\rho }_s$ is the density of the constituent material. (D) Distributions of peak stress, ${\sigma }_p$, versus chamber height, $h_0$. (E) Distributions of normalized peak-to-peak strain, $n{\epsilon }_{pp}$, and normalized valley-to-peak strain, $n{\epsilon }_{vp}$, versus chamber height, $h_0$. (F) Energy absorption capacity (W) versus density $\left(\rho \right)$ for cuttlebone in comparison to representative synthetic foams reported in literature, including AlSi₁₀Mg open-cell foams (35, 36), titanium foams (37, 38), sintered fiber stainless-steel foams (39), carbon nanotube reinforced nanocomposites (40), stainless-steel foams (41, 42), carbon nanotube reinforced aluminum foams (43), nickel foams (44), Zn/Al/Cu alloy foams (45), and epoxy foams (46). The dashed lines represent different W/ρ values, and the shaded area highlights the standard deviation of W/ρ for cuttlebone. (G) Digital image correlation (DIC) results corresponding to the points marked in C. The deformation is mapped with Hencky strain.

Deformation Process: Asymmetric Fracture of the Wall, Septa Penetration, and Densification.

To gain a deeper understanding of the cuttlebone’s chamber-by-chamber damage process, we first utilized DIC to correlate the stress–strain response and the evolution of local strain fields during an individual stress period (Fig. 2 C and G). It is found that the failure of a single chamber does not occur at once instantaneously but progressively. In particular, we identify three important stages during each period: 1) local penetrations (LP) within the deforming chamber (stage iv, Fig. 2G), which manifest as some minor stress drops in the stress–strain curve (Fig. 2C); this process leads to the formation of multiple high strain regions (yellow arrows, stage iv, Fig. 2G); 2) expansions (EXP) of the failure within the damaging chamber (green arrows, stage v, Fig. 2G), where the stress decreases significantly; and 3) densification (DENS), where the fractured walls in the damaged chamber are gradually compacted, leading to stress increase (stage vi, Fig. 2G). Evaluating the area under 16 periods in one stress–strain curve further reveals that a significant amount of energy $\left(55\pm 19\%\right)$ in a stress period is dissipated by continuous fracture and contact of wall fragments during the densification process.

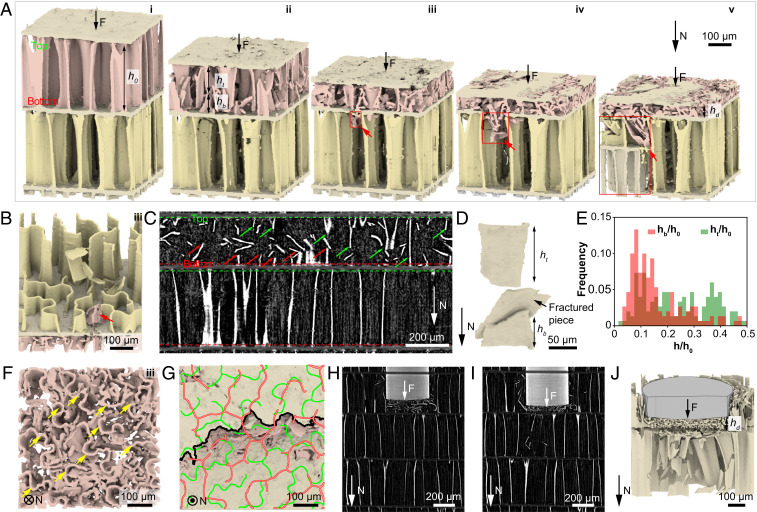
To further visualize and quantify the failure process in 3D, we conducted in situ mechanical tests coupled with synchrotron-based high-resolution µ-CT measurements (Methods). As shown in the serial X-ray projection images in SI Appendix, Fig. S9, the morphological evolution of the vertical walls and horizontal septa can be clearly observed during a compression test. Corresponding 3D reconstructions further illustrate the detailed structural evolution in 3D (Fig. 3). As one chamber is undergoing wall fracture and subsequent densification, the adjacent chamber remains intact until the local penetration of the septum by the fractured pieces (red arrows, Fig. 3 A and B). Continuing densification of the fractured chamber and local penetrations of the septum lead to the propagation of failure to the adjacent chamber (stage iii-v, Fig. 3A and SI Appendix, Fig. S10), consistent with the DIC results. More specifically, the failure of the adjacent chamber initiates when the damaged chamber has been compressed to a normalized height $h_d/h_0=0.23\pm 0.03$ (N = 8), corresponding to a relative density ${\rho }_d/{\rho }_s$ of $30.5\pm 4\%$ (Fig. 2C). Here, $h_d$ is the chamber height at maximum densification (stage v, Fig. 3A), and the relative density is the density of the damaged chamber $\left({\rho }_d\right)$ divided by the density of the constituent material $\left({\rho }_s\right)$.

Fig. 3.

Synchrotron µ-CT based in situ mechanical analysis. (A) 3D reconstruction of the progressive failure process of two adjacent chambers under compression. The red arrows and red boxes indicate the local penetration of a septum and expansion of wall fracture, respectively. $h_t$ and $h_b$ denote the heights of fractured wall attached to septum’s top and bottom sides, respectively. (B) A 3D rendering image highlighting a septum penetrated by fractured walls at stage iii in A. (C) A vertical reconstruction slice showing the fracture of vertical walls, where the green and red arrows indicate the top and bottom parts of the fractured walls, respectively. (D) A 3D rendering image of a representative fractured wall. (E) The distribution of normalized height $h_t/h_0$ and $h_b/h_0$ (N = 190). (F) Top view of the damaged chamber corresponding to stage iii in A. The yellow arrows indicate the intact top wall–septum connections. (G) A representative fracture path of a septum (black profile). The green and red profiles represent the adjacent wall patterns connected to the septum. (H and I) Two consecutive vertical reconstruction slices showing the deformation of the cuttlebone structure during a flat punch indentation test. (J) A 3D rendering image of the fractured chambers corresponding to I.

The in situ analysis also allows us to directly examine the fracture process and characteristics of individual walls. As shown in Fig. 3C, the walls fracture in a crack cascading manner under compression, similar to other brittle slender structures (47, 48). That is, walls typically fail by first forming cracks in the middle, which generates a burst of flexural waves that propagate from the newly formed crack surfaces, further breaking the wall into multiple pieces (Fig. 3D and SI Appendix, Fig. S11). Since the top portion of the wall is wavier than the bottom, it possesses more material to resist fracture, as evidenced by its larger remaining height $\left(h_t\right)$ in comparison to the pieces at the bottom $\left(h_b\right)$ shown in Fig. 3 A, C, and D (stage ii). Quantitative measurements of the tops and bottoms of the fractured walls yield $h_t/h_0=0.21\pm 0.15$ and $h_b/h_0=0.16\pm 0.11$ (N = 190; Fig. 3E). Such asymmetric fracture contributes to more intact wall–septa connections on the top than that at the bottom of the walls (Fig. 3F and SI Appendix, Fig. S12); therefore, the bottom septum is more prone to local penetration. Moreover, the septum breaks along a tortuous crack path guided by the top wall–septum connections (the green pattern in Fig. 3G), facilitating energy dissipation.

Similar localized and asymmetric fracture is also salient in the indentation tests, where damage is localized below the indenter and the septum remains intact until significant densification crushes the walls into pieces (Fig. 3 H–J and SI Appendix, Fig. S13). The observation that the septa remain undamaged until the chambers are compressed to ∼0.15 of the original height reveals the superior penetration resistance of the septa compared to the crushing resistance of the walls. This is related to the rotating plywood structure found in the septa (SI Appendix, Fig. S6), which has been demonstrated as a microstructure to enhance strength, damage tolerance, and toughness considerably (49–51). Moreover, the richer organic contents in the septa (8) may also improve the damage resistance (52). The tough septa are important to the observed layer-by-layer damage.

Optimum Wall Waviness: Balance of Stiffness and Energy Absorption.

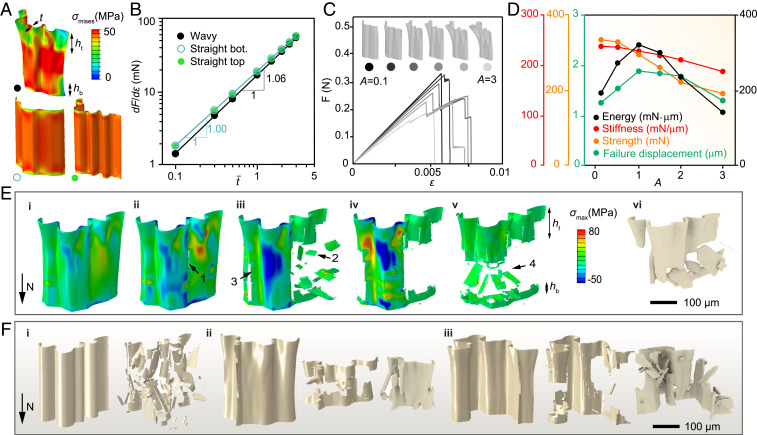
Both the in situ and conventional mechanical experiments have demonstrated the importance of the wall shape in maintaining structural integrity and achieving high energy absorption. Finite-element simulations were further conducted to gain deeper insights by providing a direct comparison of the mechanical performance between the wavy walls and straight walls (Methods and SI Appendix, Fig. S14; all models possess the same material content), where the straight walls were extruded based on the top and bottom wall profiles of the wavy wall. The resultant stress distributions are summarized in Fig. 4A, which reveal that, compared to the straight walls, the wavy wall exhibits significantly reduced stress (up to 50%) at the wavy end. Nonetheless, by plotting the scaling relation between stiffness and normalized thickness in Fig. 4B, we surprisingly found that the wavy wall exhibits a linear scaling relation and possesses over 95% stiffness of the straight walls. This linear scaling relation is direct evidence showing that the wavy walls utilize a compression-dominant deformation mechanism to maintain high stiffness (21, 22).

Fig. 4.

Balance of stiffness, strength, and progressive failure at the wall level. (A) A comparison of stress distribution between a wavy wall and straight walls at compressive strain $\epsilon =0.001$. The wavy wall (black point) is based on µ-CT reconstruction. The straight walls marked by the hollow circle and solid green circle are generated by extruding the bottom and the top profiles of the wavy wall, respectively. (B) The stiffness (defined as the slope of the force–strain curve) of wavy wall scales linearly (n = 1.06) with normalized thickness (normalized by the thickness of the µ-CT based model), demonstrating a compression-dominant deformation mechanism. (C) Force–strain curves of wavy walls with varying waviness amplitudes, A = 0.1, 0.5, 1, 1.5, 2, and 3. A = 1 corresponds to the µ-CT based model. (D) Stiffness, strength, failure displacement, and energy (work of fracture) plotted versus the waviness amplitude, A. (E) Simulation results of wall fracture (i–v) compared to µ-CT reconstructions (vi). The numbers mark the fracture sequence. (F) The straight wall fractures into small pieces catastrophically (i), while the wavy walls fracture more progressively into larger pieces (ii and iii). The second column in each case is from simulation, and the third column is from µ-CT reconstruction.

This linear scaling relation, however, will degrade if the wall waviness becomes too large, suggesting that cuttlebone may have evolved an optimal wall waviness. To confirm this, we conducted systematic simulations on walls with varying waviness. Note that, in the simulation, wall fracture is implemented by a brittle fracture model (SI Appendix, Fig. S15). All walls are set to have the same bottom profile ${\mathbf{P}}_{h=0}$ while their top profile $\left({\mathbf{P}}_{h=h_0}\right)$ varies to form different waviness. In particular, the top profile is modeled as the addition of an amplitude vector $\left(A\mathbf{V}\right)$ to the bottom profile (SI Appendix, Fig. S16):

$${\mathbf{P}}_{h=h_0}={\mathbf{P}}_{h=0}+A\cdot \mathbf{V},$$ [2]

where $\mathbf{V}$ is a set of vectors describing the normal directions of the bottom wall profile and A is the amplitude parameter, with A = 1 denoting the µ-CT based wall profile of cuttlebone. The stress–strain curves of walls with A = 0.1 to ∼3 are summarized in Fig. 4C, which show that less wavy walls (A = 0.1) have a higher stiffness but tend to break catastrophically, while excessively wavy walls (A = 3) have significantly degraded stiffness and strength due to prominent bending deformations. The calculated stiffness, strength, failure displacement, and energy absorption are plotted versus the waviness amplitude A in Fig. 4D. Optimal failure displacement and optimal energy absorption are found at A = 1, which is proved to avoid catastrophic damages as well as bending-induced premature failure. Specifically, as A increases from 0.1 to 1, the reductions in stiffness and strength are 4.0% and 11.6%, respectively, which are much less significant compared to the 49.4% increase of failure displacement and 60.0% increase of energy absorption. Moreover, the walls of the cuttlebone have a stochastic feature and A for some walls can be slightly off the optimum. Simulating different wall geometries reveals that the optimal A is in the range of 0.5 to ∼1.5 (SI Appendix, Fig. S17), indicating that the waviness of the cuttlebone is optimized statistically.

Our simulations also reveal that the stress of failure decreases at increasing wall waviness, revealing that the walls become weaker although their moment of inertia increases. This result opposes previous assumptions that the walls fail by buckling (5); instead, it suggests that the walls fail by strength-controlled fracture (the breaking strength of biogenic aragonite is reached before the walls buckle). In particular, the wavy geometry develops uneven stress distribution where regions with higher stress tend to fracture earlier, resulting in more progressive damages than the straight wall (Fig. 4 E and F, i, and SI Appendix, Fig. S18). The fractured patterns of the simulated walls are consistent with µ-CT reconstructions (Fig. 4 F, ii and iii, and SI Appendix, Fig. S19), confirming the validity of our simulation approach.

Beneficial Stress Shifts at the Chamber Level.

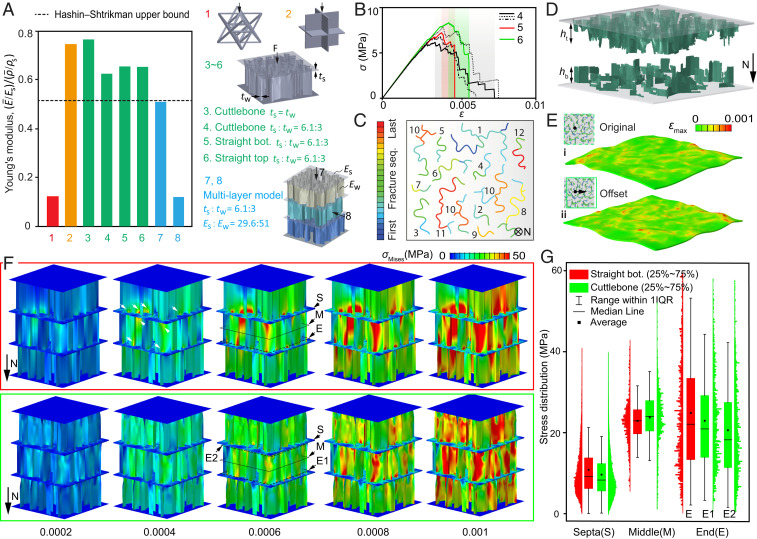
To further demonstrate the exceptional performance of cuttlebone at the chamber level, we compare the stiffness of cuttlebone chambers with two broadly acknowledged ultrastiff materials including an octet lattice (19) and a cubic metafoam (20) (structures 1 and 2, respectively), at a fixed volume fraction V_f = 0.07 (Methods and SI Appendix, Fig. S20). To fully reproduce the design of cuttlebone, septa are assumed to be softer and thicker than the vertical walls in structures 3 to 8, referring to the previous literature (8, 18). Simulations show that the cuttlebone chambers are over three times stiffer than the octet lattice (19) and are comparable to that of the cubic metafoam (20) (Fig. 5A and SI Appendix, Fig. S21). This ultrahigh stiffness at the chamber level is essential to the cuttlebone to withstand strong water pressures.

Fig. 5.

Mechanical behavior at the chamber level. (A) A comparison of stiffness between the octet truss, cubic foam, and the cuttlebone structures, all with a volume fraction V_f = 0.07 (the volume of septa is accounted). The chambers noted as straight bottom and straight top are generated by extruding the bottom and the top profiles of the wavy walls, respectively. t is the thickness and E is Young’s modulus; subscript s and w refer to septa and wall, respectively. The stiffness of the cuttlebone-based structure (no. 3) is five times greater than the octet truss and is comparable to the cubic foam. Structures 1 to 6 are constructed utilizing the same material $\left(E_s=E_w\right)$. The thickness and stiffness ratios adopted here are based on experimental data of cuttlebone. The Hashin–Shtrikman upper bound (62) presents the upper limit of the stiffness for isotropic composite materials, and it is plotted here as a reference for comparison. (B) Stress–strain curves of three cuttlebone chambers (no. 4) under compression compared to chambers with straight walls (nos. 5 and 6). (C) Fracture of the walls in a cuttlebone chamber; the color and number present the failure sequences of wall segments and wall clusters, respectively. (D) Postfracture morphology of a cuttlebone chamber. (E) Comparison of the septa deformation in the original wall overlapping pattern of cuttlebone (i) and the overlapping pattern with 50-µm offset (ii). The deformation is magnified by 50 times and the applied load is 1.5 N. (F) A comparison of stress distribution between straight-wall chambers (top row) and wavy-wall chambers (bottom row). The white arrows mark the high-stress regions. (G) Statistics of stress distribution at the septa (S), wall middle (M), and wall ends (E). IQR represents the interquartile range.

In Fig. 5B, the stress–strain responses of the cuttlebone chambers (three chambers marked by black lines are simulated to present the statistical behavior of damage) are further compared to straight wall-based chambers (red and green lines). Consistent with individual wall results, the wavy chambers yield slightly smaller stiffness and strength but more progressive failure (shade areas) and improved energy absorption. The complete failure sequence of the walls within one chamber is depicted in Fig. 5C, where fractures take place progressively and are distributed throughout the whole chamber. This observed progressive failure is contributed by the varying profiles and waviness gradient at the wall level; as we have demonstrated earlier, the statistic feature of single walls contributes to statistic mechanical response (SI Appendix, Figs. S17 and S18). Moreover, the postfracture morphology reproduces the asymmetric wall profile observed in experiments with $h_t/h_0=0.183$ and $h_b/h_0=0.126$, broadly consistent with the trend observed in experiments (Fig. 5D and SI Appendix, Fig. S22). It should be pointed out that the simulations (Fig. 5B) overestimate the stress compared to the experimental measurements (Fig. 2A), because the properties of pure aragonite instead of biogenic aragonite are assumed in the simulation. While the absolute value from the simulation may not be directly utilized as the strength of the cuttlebone, if we assume the strength of pure aragonite as the maximum strength possible for the vertical walls, the simulated strength (∼6.8 MPa) could be considered as an upper bound strength of the chambered cuttlebone structure.

By comparing the septa deformation of the original wall overlaying pattern (µ-CT based) with that of an offset wall overlaying pattern (SI Appendix, Fig. S23), we further explore how wall overlayer patterns affect the mechanical performance in cuttlebone. As shown in Fig. 5E, the offset model exhibits larger septum deformation than the original model, suggesting that an improper overlay pattern could lead to premature septum failure, unfavorable for postfracture performance. By contrast, the naturally formed overlapping, presumed as the optimal design, balances the deformation between septa and walls through a proper alignment (Fig. 1K). Here, quantitative descriptions of the optimal alignment have not yet been achieved; nevertheless, our results show that adding an arbitrary offset to the naturally formed pattern is generally unfavorable.

Finally, the stress distribution of a three-chamber structure reconstructed from µ-CT is compared to its straight-wall counterpart in Fig. 5F and SI Appendix, Figs. S24 and S25. The results reveal that the straight walls (Fig. 5F, top row) exhibit much more significant stress concentration at multiple locations near the septa (marked by white arrows) compared to the wavy-wall model. Statistical analysis of the stress magnitudes at wall middle, wall end, and septa are further conducted to gain a quantitative understanding of the stress distribution (Fig. 5G and SI Appendix, Fig. S26). Compared to the straight-wall structure, the wavy design, on the one hand, reduces stress on the septa and the wall ends, while, on the other hand, raises the stress at the middle portion of the walls. Remarkably, all these stress shifts are beneficial: 1) the reduced stress on the septa improves septa integrity, which leverages a higher plateau stress level and a more pronounced densification; 2) the higher stress level at the middle portion of the walls facilitates crack initiation therein, which controls the damage to a consistent location and thus improves mechanical robustness; and 3) the asymmetric stress distribution at the two wall ends facilitates asymmetric wall fracture, which is critical to directional damage propagation and enhanced postfracture contact performance (Fig. 6). These stress shifts explain the asymmetric fracture and significant densification observed experimentally, demonstrating nature’s ingenious design to achieve a stiff and damage-tolerant material by arranging a proper waviness gradient to the wall–septa structure.

Fig. 6.

Correlation between the macroscopic response and the microstructure of cuttlebone. (A) Cuttlebone exhibits the typical stress–strain response of cellular materials macroscopically. (B) Each period in the plateau regime is characterized by local penetration (LP), expansion (EXP), and densification (DENS). (C) The chamber level deformation exhibits local wall fracture, extensive wall contact (green arrows), and septum fracture induced by fractured wall segments (red arrows). (D) Asymmetric fracture at the wall level. $h_0$, $h_t$, $h_b$, and $h_d$ are wall heights illustrated in the plot, $H_0=n{h}_0$ is the sample height, and $h_c=h_t+h_b$ is the contact height. The geometric parameters are related to the peak-to-peak, and peak-to-valley strains by ${\epsilon }_{pp}=\left(h_0-h_d\right)/H_0$ and ${\epsilon }_{vp}=\left(h_c-h_d\right)/H_0$.

Structural Designs of Cuttlebone: Balance for Stiffness, Damage Tolerance, Low Density, and Openness.

Combining the experimental and computational results, a representative stress–strain response of the cuttlebone under compression is summarized schematically in Fig. 6A, which exhibits a two-scale characteristic behavior. Macroscopically, it presents an elastic response followed by a large serrated stress plateau and then densification. The plateau has a strain regime that consists of regularly shaped periods, $n{\epsilon }_{pp}$ (n and ${\epsilon }_{pp}$ are defined in Fig. 6), which is determined by the chambered microstructure. More specifically, each chamber contributes to a fluctuated period (Fig. 6B) characterized by three stages discussed earlier. As illustrated in Fig. 6C, the enhanced contact (green arrows) and directional septa penetration (red arrows) are characteristic at the chamber level. Ultimately, the balance between stiffness and damage tolerance in cuttlebone is contributed by microwalls, where the corrugated wavy shape leverages both effective stress transfer and extensive densification (Fig. 6D). Based on these schematics, the macroscopic response of the cuttlebone can be correlated to its microstructure by $n{\epsilon }_{pp}=\left(h_0-h_d\right)/h_0$ and $n{\epsilon }_{vp}=\left(h_c-h_d\right)/h_0$, where $n$, ${\epsilon }_{pp}$, ${\epsilon }_{vp}$, $h_t$, $h_b$, $h_d,$ and $h_0$ are parameters introduced earlier and illustrated in Fig. 6. These equations verified that enhanced contact (larger $h_c$) and improved septa integrity (smaller $h_d$) are critical for improved macroscopic response.

Finally, we highlight the outstanding performance of cuttlebone through a comparison with other porous cellular materials, aiming to provide insights for bio-inspired microstructural designs. Compared to the cancellous bones and echinoderms’ stereom that are based on open-cell designs consisting of branches and nodes (53, 54), the cuttlebone-like structure exhibits notably higher porosity. Higher specific stiffness could also be expected, as we have shown that the cuttlebone-like structure is three times stiffer than the octet truss with the same porosity. On the other hand, the wall-based yet open structure of cuttlebone offers notable fluid permeability, which is distinct to other wall-based cellular materials such as woods (55), honeycombs (17), and metafoams (21). This wall–septa design where each chamber is completely separated from others also ensures the skeleton’s buoyance regulation function even if some chambers are damaged (5, 16). Such a balance of low density, stiffness, damage tolerance, openness, and functional robustness in cuttlebone makes it a remarkable design motif for potential applications such as sandwich cores, heat exchangers, as well as spacecrafts and engine rotator blades.

Summary and Outlook.

Combining multiple experimental techniques, we reveal that cuttlebone derives high energy absorption and damage tolerance from its asymmetric wall fracture, extensive densification, and chamber-by-chamber failure. Our parametric simulations further provide quantitative knowledge of how wall waviness, wall overlaying, and their statistical variations enhance the mechanical performance synergistically. Together, our analysis establishes the relationship between the macroscopic response of cuttlebone and its microstructure and reveals that the cuttlebone is optimized for lightweight, high stiffness, and high energy absorption simultaneously. Here, we highlight several important strategies learned from this study on cuttlebone for the design of engineering cellular ceramics and lattice metamaterials. First, the corrugated wavy walls possess stiffness close to straight walls (>95%), yet they control maximum stress to well-defined locations, opening an avenue to “manipulate” the fracture path. This approach can be utilized to improve the reliability of ceramics lattice materials whose fractures often initiate at random unknown defects. Second, utilizing asymmetric structural characters like waviness gradient in cuttlebone, asymmetric fracture and directional damage propagation can be introduced. Here, we have shown that asymmetric fracture contributes to remarkably better postfracture performance in cuttlebone; similar designs could be useful in lightweight protective systems where high energy absorption is desired and the direction of protection is of more importance. Third, statistical variations of the microstructure play an important role in damage tolerance. In cuttlebone, both the wall shapes and wall alignment have statistical variations and are found to facilitate more progressive failure. Finally, we note that further research is required to elucidate the effects of the intrinsic mechanical properties of the biogenic aragonite in cuttlebone, particularly the contribution of the intracrystalline organics, which may also contribute to the observed mechanical performance of cuttlebone.

Methods

Electron Microscopy.

The cuttlebone samples were dissected from frozen adult cuttlefish S. officinalis. The samples were subsequently air dried at room temperature before analysis. Sections fractured from the dried cuttlebone were first mounted on SEM stubs and then coated with ∼8-nm Pt/Pd with a sputter coater (Leica Double Sputter Coater). Care was taken to induce fracture along specific orientations, including both transverse and horizontal directions. The samples were imaged with a field-emission scanning electron microscope (Zeiss; LEO 1550) with an accelerating voltage of 5 kV and at a working distance of ∼10 mm.

Compression Tests and DIC.

Cube-shaped samples (edge length, ∼10 mm) were cut from the frozen cuttlebone by using a low-speed diamond saw. The sample surfaces were further carefully trimmed parallel to septa using a razor blade. Wet samples were further infiltrated with deionized water in a vacuum chamber while the dry samples were obtained by drying them in an oven at 40 °C for 24 h. All samples (11 dry and 4 wet samples) were then tested in a quasistatic compression mode by applying load perpendicular to the septum plane at a rate of 0.5 mm/min with a universal testing machine (Instron; model 5948). The videos of the compression tests were recorded with an Amscope camera with a frame rate of 500 f/min, which was used for DIC analysis. The microstructure of the cuttlebone enabled direct image correlation without the introduction of extra speckle patterns. The strain fields were calculated using VIC-2D (Correlated Solution) with an incremental algorithm and a subset size of 35 pixels.

Synchrotron-Based In Situ Mechanical Tests.

Cube-shaped samples (edge length, ∼2 mm) consisting of three to four chambers were isolated from the middorsal region of cuttlebone and then carefully trimmed. The synchrotron-based in situ mechanical tests based on µ-CT were conducted at the beamline 2BM from the Advanced Photon Source, Argonne National Laboratory, utilizing a monochromatic X-ray beam with an energy of 27.4 keV. A customized in situ mechanical loading device was used for both synchrotron-based compression and indentation tests, through which the samples can be mechanically tested while allowing for X-ray imaging through its X-ray transparent window. For the in situ compression tests, load was applied by a stepper motor and the compressive force was measured by the load cell. For the in situ indentation tests, a tungsten rod with a flat punch end (diameter, 0.5 mm) was used to induce localized deformation. Tomography data were collected as the displacements were applied in steps of 0.1 mm monotonically. The beamline employs a single-crystal LuAG:Ce scintillator to convert X-ray into visible light, which was further magnified with a 5× or 10× long-working distance objective lens. Each scan was collected at 0.12° angular increment over a 180° rotation with an exposure time of 0.2 s (corresponding to the total scan time for a single tomography scan of 5 min). The projection images were collected by using a PCO-Edge high-speed CMOS detector (2,560 × 1,300 pixels), which resulted in voxel sizes of 0.65 or 1.3 µm depending on the objective lens. The reconstruction and segmentation of the obtained µ-CT data were conducted with the open source software Tomopy (56) and Ilastik (57), respectively. The reconstructed data were used for 3D volume rendering and quantitative analysis, such as cross-sectional length and surface curvature, via a combination of methods, including Avizo (Thermo Fisher Scientific), Fiji (58), Blender (www.blender.org) (59), and customized Matlab routines. In total, nine samples were tested, among which three were analyzed in detail.

Geometric Modeling.

The geometries of the vertical walls were built based on reconstructed tomography data. The collected data were first binarized, skeletonized, and filtered to remove the noise introduced during voxelization. Then, wall profiles at varying heights were extracted using a customized Matlab program, which were further imported into Solidworks (Dassault) to generate 3D models. Moreover, a general mathematical description of the wall was developed to investigate the wall shape parametrically. To do this, the top profile of a wall $\left({\mathbf{P}}_{h=h_0}\right)$ was modeled as the addition of a vector $\left(A\cdot \mathbf{V}\right)$ to the bottom profile $\left({\mathbf{P}}_{h=0}\right)$, i.e., ${\mathbf{P}}_{h=h_0}={\mathbf{P}}_{h=0}+A\cdot \mathbf{V}$, where $h_0$ is the height of the wall and $\mathbf{P}={\left[x,y\right]}^T$ represents points on the wall. Note that A controls the waviness amplitude, which is varied between 0.1 and 3 to generate walls with different waviness gradients. Since the wall profile evolves exponentially in the height direction (Eq. 1), the general description of the wavy wall is $\mathbf{P}\left(\overline{h}\right)=[1-\alpha \left(\overline{h}\right)]{\mathbf{P}}_{\overline{h}=0}+\alpha \left(\overline{h}\right){\mathbf{P}}_{\overline{h}=1}$, with $\alpha \left(\overline{h}\right)=\left(e^{\kappa \overline{h}}-1\right)/\left(e^{\kappa }-1\right)$ and $\overline{h}=h/h_0$, where $\kappa$ is a parameter fitted to the µ-CT data.

Finite-Element Simulation.

ABAQUS was utilized to simulate the mechanical response of cuttlebone under compression. The walls and septa were discretized with shell elements and tetrahedral elements, respectively. The walls and septa have Young’s moduli of 51 and 29.6 GPa, respectively, based on literature values (19). The elastic performance was calculated with general statics and the fracture process was simulated utilizing dynamic explicit. In the explicit simulations, the strain rate of loading was set as 0.05 s⁻¹. A smeared brittle cracking model and element deletion was implemented to capture the brittle fracture of the biogenic aragonite-based walls. Crack initiated when the maximum principal tensile stress exceeded the tensile strength of aragonite, σ_f, which was 102 MPa (60). The fracture energy of forming a unit area of crack surface in mode I, G_If, was used as the criteria of element deletion to avoid unreasonable mesh sensitivity (61). A material point failed when the critical fracture energy of this point was reached, and an element was deleted when all of the corresponding material points failed. A linear shear retention model was also included to consider the reduction of postcracked shear modulus once the crack was opened.

Data Availability.

All study data are included in the article and SI Appendix.