Integrating biological knowledge and gene expression data using pathway-guided random forests: a benchmarking study

Abstract

Motivation

High-throughput technologies allow comprehensive characterization of individuals on many molecular levels. However, training computational models to predict disease status based on omics data is challenging. A promising solution is the integration of external knowledge about structural and functional relationships into the modeling process. We compared four published random forest-based approaches using two simulation studies and nine experimental datasets.

Results

The self-sufficient prediction error approach should be applied when large numbers of relevant pathways are expected. The competing methods hunting and learner of functional enrichment should be used when low numbers of relevant pathways are expected or the most strongly associated pathways are of interest. The hybrid approach synthetic features is not recommended because of its high false discovery rate.

Availability and implementation

An R package providing functions for data analysis and simulation is available at GitHub (https://github.com/szymczak-lab/PathwayGuidedRF). An accompanying R data package (https://github.com/szymczak-lab/DataPathwayGuidedRF) stores the processed and quality controlled experimental datasets downloaded from Gene Expression Omnibus (GEO).

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Gene expression has been measured globally in patients and healthy controls with microarrays for many years and next-generation sequencing of RNA (RNA-Seq) nowadays enables even more insights into the molecular basis of diseases. This detailed information on the transcriptome, together with other omics layers, holds the promise to improve diagnosis, prognosis and therapy response prediction leading to personalized medicine.

Differential expression analysis is usually performed for each gene separately. Similarly, all genes are used as input for machine learning approaches to train mathematical models for stratification of individuals e.g. based on disease status or for predicting treatment response. However, interpretation of these gene level results is often challenging. Statistical testing might result in thousands of differentially expressed genes, sometimes with only moderate or small effects, and the selection of parsimonious prediction models usually leads to non-overlapping sets of genes with similar prediction performance (Drier and Domany, 2011; Ein-Dor et al., 2005).

A promising strategy to improve interpretability is to integrate external knowledge about the functional relationships of the genes. Detailed information about signaling and metabolic pathways has been collected in databases such as the Kyoto Encyclopedia of Genes and Genomes (KEGG) (Kanehisa and Goto, 2000) and Reactome (Croft et al., 2014), which are further integrated with other resources e.g. in the Molecular Signatures Database (MSigDB) (Subramanian et al., 2005) or the ConsensusPathDB (Kamburov et al., 2013). A detailed overview of available pathway databases can be found at Pathguide (Bader et al., 2006), which currently lists over 700 resources. Note that, in the following, we will utilize the term pathway as a synonym of ‘gene set’ i.e. we only use information about pathway membership and ignore any further topological or relationship information.

Many pathway analysis methods based on statistical tests have been proposed which can be classified according to different criteria (Ackermann and Strimmer, 2009; Khatri et al., 2012). One important aspect is the tested null hypothesis where competitive and self-contained tests can be distinguished (Tian et al., 2005). The latter uses only information within the given pathway and tests the null hypothesis that the gene expression levels of the pathway are not associated with the outcome. In contrast, in a competitive test the association between the pathway genes and the outcome is compared to the association between the genes outside the pathway and the outcome. Hence, a competitive method selects a pathway when the amount of differential expression of this pathway is significantly larger compared to other pathways.

Pathway analysis methods have also been developed in the context of machine learning approaches. In accordance with the categorization of statistical approaches based on the tested null hypothesis, we here define a similar grouping based on the dependency of a pathway specific result on the other pathways and genes. A so called self-sufficient method uses only information provided by the genes within a particular pathway. A straightforward strategy, herein referred to as prediction error (PE), is to evaluate the prediction performance of a model trained on a single pathway (Pang et al., 2006). Another approach similarly trains separate models for each pathway but uses the predictions as so called synthetic features (SF) in a global prediction model (Pan et al., 2014). Since the global model uses all SFs together, this is a hybrid approach. The two remaining methods use a competing strategy. The pathway hunting approach (Chen and Ishwaran, 2013), abbreviated as Hunting in the following, calculates a pathway importance score based on gene importance estimated by a global RF trained on all genes jointly. And the learner of functional enrichment (LeFE) method uses a similar approach as the competitive statistical tests by selecting pathways whose genes have significantly higher importance than genes outside the pathway (Eichler et al., 2007).

So far, these methods have mostly been compared to gene-based prediction models or statistical tests. To the best of our knowledge, no direct comparison of all the methods exists. Thus, our goal was an extensive and systematic benchmark study to analyze their strengths and weaknesses. As we were not involved in the original development of any of the approaches the neutrality of the study is ensured, which has been defined as one important characteristic of benchmarking (Boulesteix et al., 2017). For a comprehensive evaluation, it is necessary that the truth underlying the observed data is known so that the power as well as false-positive findings can be assessed. We generated synthetic gene expression data in two simulation studies, the first one covering a simplified setting with specific pathway characteristics and many causal pathways, and the second one modeling a more realistic scenario. As simulated data can never capture all of the characteristics of experimental data, we performed an additional evaluation on a range of publicly available gene expression datasets from studies on different diseases and tissues. Moreover, we also included two popular statistical approaches, the fast implementation of the gene set enrichment method (Subramanian et al., 2005), called FGSEA (Sergushichev, 2016), and sigPathway (Tian et al., 2005).

2 Materials and methods

2.1 Pathway-guided random forest approaches

The different pathway analysis approaches use the popular RF algorithm as base classifier. RF is a non-parametric ensemble method based on classification and regression trees (Breiman, 2001). Each tree is built on bootstrapped observations of the original sample and optimal splits are determined using a random subset of all predictor variables i.e. genes. Each tree predicts the class for a test observation and the final prediction of the forest is generated by majority voting. To interpret the prediction model, the importance of each gene can be estimated based on a variety of measurements. An intuitive choice is the reduction of impurity as induced by the splits in the forests, the so-called Gini importance. However, it has been shown that the Gini importance is biased if the predictor variables are of different scales or frequencies (Nicodemus, 2011; Strobl et al., 2007). In our comparison study we used a corrected Gini importance as implemented by Nembrini et al. (2018).

For a fair comparison, the different pathway-guided RF approaches (see Table 1 for an overview) were implemented in the R package PathwayGuidedRF which is available at GitHub (https://github.com/szymczak-lab/PathwayGuidedRF) and based on the RF implementation in the R package ranger (Wright and Ziegler, 2017).

Table 1.

Information about the different pathway guided RF approaches compared in the benchmarking study

Name	Approach	RF	Type	Selection criterion	P value	Ref.	Citationsa
Hunting	Pathway hunting	All genes	Competing	Pathway specific importance	Yes	Chen and Ishwaran (2013)	19
LeFE	LeFE	pathway	competing	Comparison of importance of genes within and outside of the pathway	Yes	Eichler et al. (2007)	11
PE	PE	Pathway	Self-sufficient	PE	Yes	Pang et al. (2006)	124
SF	SFs	Pathway	Hybrid	Importance of SFs	No	Pan et al. (2014)	10

^aBased on Web of Science (October 2019).

The parameters for RF and each method can be found in Table 2. Instead of the default value for mtry ($\sqrt{p}$ with p denoting the number of variables) we used a larger value, as recommended by Genuer et al. (2008), as our study is focused on pathway importance and not on prediction performance. The choice of $p^{3/4}$ is motivated by Ishwaran et al. (2011). As sensitivity analysis, we additionally report results using the mtry values of $\sqrt{p}$ and 0.5p for each pathway guided RF approach in the Supplementary File.

Table 2.

Parameters used for the pathway-guided RF approaches

Approach	Parameter	Description	Value
RF	ntree	Number of trees	1000
	mtry	Number of predictor variables selected at each split	Number of variables${}^{3/4}$
	nodesize	Minimal number of individuals in terminal node	1a
PE	no.perm	Number of permutations for empirical P value	50
LeFE	sample.factor	Multiple of number of genes to be selected from Outside of the pathway	6b
	sample.runs	Number of repetitions of comparisons with genes outside of the pathway	75b

^aDefault in ranger function.

^bDefaults in original publication.

PE, Hunting and LeFE provide a P value for each pathway and we selected pathways with a Benjamini–Hochberg adjusted P value < 0.05 (Benjamini and Hochberg, 1995). Selection of important pathways in the SF method is performed using the Boruta variable selection approach (Kursa et al., 2010) which instead of a P value returns one of the categories confirmed, tentative or unimportant for each variable i.e. pathways. In our study, only confirmed pathways were selected.

2.1.1. Prediction error

The pathway-guided RF based on PE evaluates each pathway separately and it does not consider any of the genes outside the pathway. A RF is trained for each pathway and the PE is estimated using the out-of-bag samples (Pang et al., 2006). In the analysis of several experimental datasets presented in the original publication, pathways with PEs smaller than an arbitrary threshold were selected. To provide a more objective criterion, we implemented a permutation test for estimating empirical P values which was used in the original publication only for the analysis of simulated data. Outcome values are repeatedly permuted and, thus, any association with the predictor variables is destroyed. In each step, a new RF is trained and its prediction performance is evaluated. To limit the number of permutations and thus the number of RFs that need to be trained, we use the permutation test approach proposed by Hediger et al. (2019). Mean and standard deviation of all OOB PEs across pathways and permutations are estimated. The P values are then derived using a normal distribution.

2.1.2. Synthetic features

The SF method (Pan et al., 2014) uses a two-stage approach. The first step is performed separately for each pathway. A pathway specific RF is trained and used to predict case probabilities for each individual using the out-of-bag sample which for each tree consists of those observations that were not in the bootstrap sample of that particular tree. The predictions of the pathway specific tree are a summary of the information within the pathway and stored as a single variable called SF. The SFs of all pathway-based RFs are then used as predictor variables in a new RF. In the original approach, this RF was evaluated regarding its prediction performance only. However, we are interested in using the approach to identify important pathways. We thus extended the method by pathway selection based on the Boruta approach (Kursa et al., 2010), one of the two best performing methods in our recent study comparing variable selection methods for high dimensional data (Degenhardt et al., 2019). In contrast to Vita (Janitza et al., 2018), the other well performing method, Boruta can be applied in low dimensional settings. This actually is necessary in the second stage RF that is based on the SFs of the respective pathways, resulting in relatively low numbers of variables.

2.1.3. Hunting

The Hunting approach (Chen and Ishwaran, 2013) starts with a standard RF using all genes as predictor variables and estimates variable importance for each gene. A pathway importance score is calculated as the average of the importance scores of all genes belonging to the pathway. A standardized version of this score (Z score) is calculated using the formulas provided in (Chen and Ishwaran, 2013) for the mean and standard deviation of random subsets of genes with the same size. A P value is then estimated assuming an asymptotic standard normal distribution of the Z score under the null hypothesis.

2.1.4. Learner of functional enrichment

The fourth approach under consideration is more similar to the statistical gene set enrichment methods because the importance of genes within the pathway is compared to the importance of genes outside the pathway (Eichler et al., 2007). For a pathway of size k, a set of $l·k$ of genes not part of the pathway is randomly selected. The factor l is set using the parameter sample.factor. A RF is then trained on the combined set of $(l+1)·k$ genes and the importance is determined for each gene. In the original manuscript, a permutation test based on the test statistic of the t-test is proposed to compare the difference between the mean importance of the two groups of genes. To reduce the computation time, we instead rely on standard statistical tests. We reported results using the nonparametric Wilcoxon rank sum test and included a comparison with the t-test and the Kolmogorov–Smirnov test in the Supplementary File. The random selection of genes outside the pathway as well as the subsequent P value calculation is repeated several times (parameter: sample.runs). Finally, the median P value is reported for each individual pathway.

2.2 Statistical pathway analysis methods

We included two commonly used statistical pathway analysis approaches in our comparison study. The first method is the popular gene set enrichment analysis (GSEA) (Subramanian et al., 2005) for which we used the efficient implementation provided in the R package fgsea (Sergushichev, 2016). All genes are ranked based on differential expression e.g. using the absolute value of the test statistic of the t-test in our study. The GSEA approach then tests if the genes in the particular pathway are primarily found at the top of the ranked list using a weighted Kolmogorov–Smirnov-like statistic. The second method is called sigPathway (Tian et al., 2005) and it is implemented in an R package with the same name. It calculates a pathway level test statistic as a weighted sum of the gene level statistics (t-statistic), which is then normalized for the size and correlation structure of the pathway. The P value is determined using the Wilcoxon rank sum test.

Both statistical procedures were run as competitive and self-contained tests by permutation on the gene or sample level, respectively (denoted with the suffixes _G and _S). As for the RF-based methods, P values were adjusted for multiple testing using the Benjamini–Hochberg approach (Benjamini and Hochberg, 1995).

2.3 Simulation studies

The pathway analysis approaches were compared in two different simulation studies based on case–control settings. In the first study, artificial models of correlation patterns and pathway structures are used to enable estimation of empirical power and detection of false-positive results depending on several pathway parameters, such as number of genes, correlation and amount of differential expression. In contrast, the second study is based on correlation patterns and effect sizes observed in experimental gene expression datasets.

The R code to generate the synthetic datasets is available in our R package PathwayGuidedRF (https://github.com/szymczak-lab/PathwayGuidedRF). Code for simulation study 1 is partly based on R code from Poisson et al. (2011) and for efficient generation of multivariate normally distributed synthetic expression values the R package Umpire (Zhang et al., 2012) was employed in simulation study 2.

2.3.1. Simulation study 1

In simulation study 1, pathways were simulated independently i.e. each gene belongs to only one pathway. Each pathway is defined by the following three characteristics: the number of genes, the pairwise correlation between genes within the pathway (correlation) and the proportion of differentially expressed genes (prop.de). We simulated one pathway for each combination of number of genes (20, 100, 200), correlation (0, 0.2, 0.6) and prop.de (0, 0.25, 0.5, 1) resulting in 36 pathways with the majority being causal. We included an additional null pathway (prop.de = 0, correlation = 0) with 1160 genes, so that the total number of genes is 5000. For each pathway, we simulated gene expression values for 100 samples using a multivariate normal distribution following the approach of Poisson et al. (2011). The gene specific means were randomly drawn from normal distributions with mean of 0 and variances $4s^2$ with s² following an inverse ${\chi }^2$ distribution (${\chi }_4^{-2}$). The covariance matrix was determined based on the variances $4s^2$ and the specified correlation. Depending on the number of genes and amount of signal (prop.de) of the pathway, the corresponding number of genes were randomly selected and the means in the first 50 samples were shifted according to an effect size randomly drawn from an uniform distribution between 0.2 and 0.3. We generated 100 replicates with independent sets of differentially expressed genes and different effect sizes. For each replicate, we simulated two datasets to evaluate prediction performance and stability of pathway identification. Furthermore, we simulated a complete null scenario where none of the pathways contains any differentially expressed genes. We used the same number and structure of pathways as in the scenario with true effects.

Each of the RF-based and statistical methods described in the previous subsection was applied to all of the 200 datasets and four evaluation criteria were calculated. The first one is the sensitivity assessing the proportion of the true pathways (with prop.de > 0) being identified. The second criterion is the false discovery rate (FDR) which denotes the frequency of falsely identified pathways among all pathways selected by a particular approach. Sensitivity and FDR were calculated for each of the 200 datasets independently. In contrast, the two remaining parameters use the two datasets of each replicate. Stability is calculated using Jaccard’s index (He and Yu, 2010), which is defined as the ratio of the length of the intersection and the length of the union of the two sets of pathways selected in the two datasets. Thereby, values of 1 and 0 indicate both sets being identical or disjunct, respectively. To evaluate prediction performance, a RF is trained on each dataset and classification error is evaluated on the other dataset and vice versa. Only genes within selected pathways are used for model building. Differences in the four evaluation criteria between the different pathway approaches across the simulation replicates were tested using the nonparametric Friedman test, followed by pairwise comparisons using the paired Wilcoxon test and Bonferroni adjustment of P values.

2.3.2. Simulation study 2

Simulation study 2 closely resembles correlation patterns and differential expression observed in experimental studies. The simulation is based on two of the publicly available gene expression datasets used in our evaluation on experimental data [whole blood: GSE50635 (Ko et al., 2013), kidney: GSE25902 (Naesens et al., 2011)]. Since analysis results are similar, we present results on the whole blood dataset in the main manuscript and provide information on the kidney dataset in the Supplementary File.

Pairwise correlations between genes were estimated in the control individuals using the Pearson correlation coefficient. To estimate differential expression a t-test assuming equal variances was applied for each gene separately followed by multiple testing adjustment using the Benjamini–Hochberg method (Benjamini and Hochberg, 1995). Test statistics of genes with adjusted P value < 0.05 were converted to differences in mean expression values based on the observed sample sizes of cases and controls and under the assumption of equal standard deviations of 1 in both groups. Synthetic gene expression values of all genes for 30 samples were simulated using a multivariate normal distribution with means of 0 and the estimated correlation matrix. Genes within a single pathway, the so-called target pathway, were simulated to be differentially expressed by shifting the mean values of the first 15 samples (=cases) by randomly drawn effect sizes from the estimated differences. We varied the proportion of differentially expressed genes (prop.de = 0.1, 0.25, 0.5, 0.75) and generated two datasets for each of the 100 replicates. A schematic overview of the simulation process is given in Supplementary Figure S1.

For our comparison, we calculated the empirical power to detect the target pathway, corresponding to the frequency of replicates in which the target pathway is selected. Furthermore, we reported the frequency of additionally selected pathways among all analyzed pathways for each replicate and method. Finally, we determined the number of selected pathways that do not share any gene with the target pathway for each replicate and method.

Similar as in simulation study 1, we simulated 100 replicates of a complete null scenario where none of the pathways contains any differentially expressed genes (prop.de = 0) utilizing the whole blood dataset. The methods were compared by the selection frequency of each individual pathway.

2.3.3. Experimental datasets

To evaluate the pathway-guided RF approaches under realistic analysis settings with true biological mechanisms, we performed a comparison based on several gene expression datasets publicly available in the NCBI GEO database (Barrett et al., 2012). The challenge in analyzing real data in contrast to simulated data is that the truth is unknown. To be able to use a particular pathway as a positive control, which should be detected by a well-performing method, we decided to focus on the hallmark gene sets (Liberzon et al., 2015) from the MSigDB (Subramanian et al., 2005). These pathways represent well-defined biological processes and were defined based, inter alia, on selected gene expression datasets. We chose 9 hallmark gene sets with overall 10 target pathways which were connected to a human case–control dataset containing at least 15 individuals per group. Table 3 shows that these datasets cover a range of different diseases, tissues and types of microarrays. Some studies were performed in a paired design. This property, however, was ignored in our study since we are only interested in the relative performance of the different methods. Clinical information and normalized expression measurements of each dataset were downloaded from GEO using the Bioconductor package GEOquery version 2.50.5 (Davis and Meltzer, 2007) and the following preprocessing and quality control steps were performed, if the relevant information was available. Affymetrix control probes were removed and only probes detected in more than 25% of the individuals (detection P value < 0.05) were kept. Probes were then log transformed (log2) if not already done and assigned to HGNC gene symbols using the annotation information provided in GEO. Probes assigned to multiple symbols were removed and symbols were corrected using the R package HGNChelper version 0.7.1. Finally, the probe with the largest median expression value for each symbol was selected. Individuals were removed if they had aberrant global distribution of expression values (determined based on boxplots and principal component analysis) or the reported sex was inconsistent with sex estimated based on expression values of sex specific genes such as EIF1AY, RPS4Y1, UTY or XIST (Jansen et al., 2014; Toker et al., 2016) (see Table 3 for datasets where individuals were excluded). The final datasets are provided as SummarizedExperiment objects in the R package DataPathwayGuidedRF available at GitHub (https://github.com/szymczak-lab/DataPathwayGuidedRF).

Table 3.

Information about the gene expression datasets used in the benchmarking on experimental data

GEO	Reference	Target pathway	Disease	Tissue	Design	Sample size (cases/controls)	Array (affymetrix)	Genes (total/ target) pathway
GSE27262	Wei et al. (2012)	GLYCOLYSIS	Non-small cell lung cancer	Lung	Paired	20a/22a	Genome U133Plus 2.0 Array	19 014/200
GSE33335	Cheng et al. (2012)	GLYCOLYSIS	Gastric cancer	Gastric	Paired	25/25	Exon 1.0 ST Array	17 025/200
GSE20257	Shaykhiev et al. (2011)	APICAL_SURFACE; APICAL_JUNCTION	Smoking (non-smoking versus smoking with COPD)	Small airway epithelium	Unpaired	23/42a,b	Genome U133Plus 2.0 Array	19 014/44; 200
GSE25902	Naesens et al. (2011)	ALLOGRAFT_ REJECTION	Post-transplant rejection versus baseline	Kidney	Unpaired	24/96b	Genome U133Plus 2.0 Array	19 014/200
GSE8671	Sabates-Bellver et al. (2007)	WNT_BETA_ CATENIN_SIGNALING	Coloncancer	Colon	Paired	32/32	Genome U133Plus 2.0 Array	12 483/42
GSE50635	Ko et al. (2013)	INTERFERON_ ALPHA_RESPONSE	Systemic lupuserythematosus	Blood	Unpaired	33/16b	Gene 1.0 ST Array	18 605/97
GSE40586	Lill et al. (2013)	COMPLEMENT	Bacterial meningitis	Blood	Unpaired	21/18	Gene 1.0 ST Array	18 593/200
GSE27034	Masud et al. (2012)	COAGULATION	Peripheral artery disease	Blood	Unpaired	19/17a	Genome U133Plus 2.0 Array	19 014/138
GSE30718	Famulski et al. (2012)	ALLOGRAFT_REJECTION	Acute kidney injury versus other	Kidney	Unpaired	28/19	Genome U133Plus 2.0 Array	19 014/200

^aSome individuals were removed due to quality control problems.

^bDownsampling was performed because of class imbalance.

In contrast to the simulation studies, three of the experimental datasets (GSE20257, GSE25902, GSE50635) exhibit a large class imbalance. It is well known that machine learning approaches and variable importance measures are prone to biased results because of the preference of the majority class (Blagus and Lusa, 2010). One possible solution is downsampling where the number of samples in each class is restricted by the size of the minority class. In the RF approach this procedure does not lead to data loss since a separate balanced bootstrap sample is drawn for each tree in the forest. The downsampling method is implemented in our R package.

Similar as in simulation study 2 we compared the methods based on the frequency the respective target pathway(s) is/are selected among all analyzed datasets and the frequency of additionally selected pathways among all analyzed pathways for each replicate and method.

For the run time investigation, a computer with 2 x Intel(R) Xeon(R) CPU E5-2620 v4 @ 2.10 GHz, 16 cores (32 threads) and 64 GB DDR4 RAM was used.

3 Results

3.1 Simulation study 1

The focus of the first simulation study is on pathways with specific characteristics. We simulated 36 pathways with different numbers of genes (20, 100, 200), proportions of differentially expressed genes (prop.de = 0, 0.25, 0.5, 1) and pairwise correlation between genes (correlation = 0, 0.2, 0.6) as well as an additional null pathway (prop.de = 0 and correlation = 0) to achieve the total number of 5000 genes. Each gene was assigned to a single pathway and mutually exclusive pathways were simulated. All pathway analysis methods under consideration were evaluated using several evaluation criteria including sensitivity, FDR, stability and classification error.

Figure 1A and B each shows two of the criteria with the median and interquartile ranges over 100 replicates given for each method and an optimal approach would be in the upper left corner of each of the plots (see also Supplementary Table S1 for results of statistical tests). Classification errors are similar for all methods and they are below 5% for each of the RF-based approaches. PE is one of the most sensitive methods i.e. it detected 89% of the true pathways (=pathways with prop.de > 0). In addition, this method usually identified none of the pathways with prop.de = 0 (FDR = 0) and the stability i.e. the consistency of selected pathways across datasets simulated under the same scenario, is high (88%). SF is the other approach with similar performance to PE. Hunting and LeFE have again a FDR of 0, but low power to detect true pathways with signal. Only LeFE has a relatively high stability of 73%, whereas Hunting usually selects many different pathways in the two datasets of each replicate (stability less than 40%).

Fig. 1.

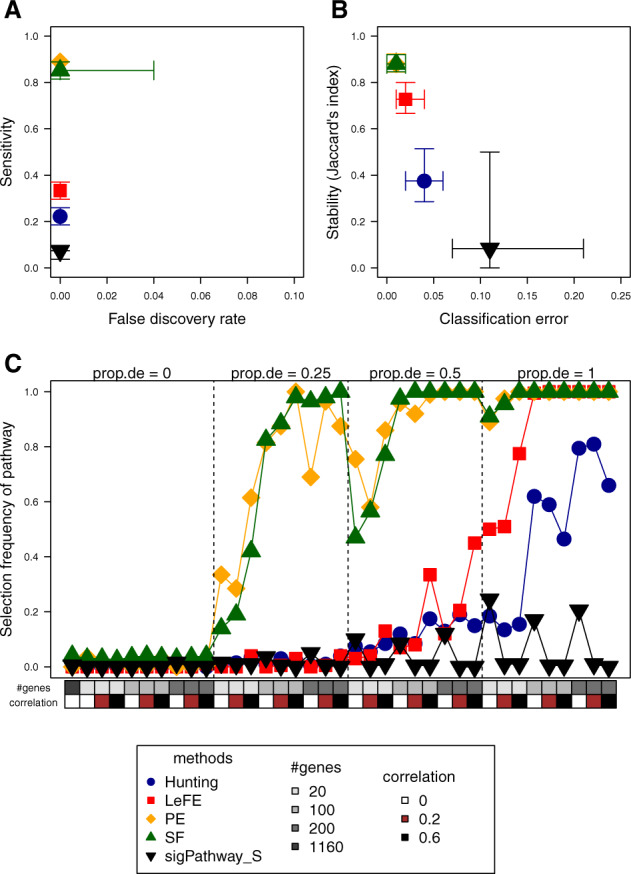
Performance of Hunting, LeFE, SF, PE and sigPathway with sample-level permutation in simulation study 1 with true effects. Shown are FDR versus sensitivity (A), classification error versus stability (B) and the selection frequency of each of the 37 pathways (C). Each subfigure displays the median (and interquartile range in A and B) over all 100 replicates of each method using different plotting symbols and colors. In (C), characteristics of each pathway [number of genes, pairwise correlation of genes, proportion of differentially expressed genes (prop.de)] are given at the bottom and top of the plot

The performance of Hunting is very similar if the number of trees is increased from 1000 to 10 000 (Supplementary Fig. S2). A comparison of different test statistics employed by the LeFE method shows that results for the Kolmogorov–Smirnov test are nearly identical to those of the Wilcoxon test, but sensitivity and stability drop substantially for the statistic of the t-test (Supplementary Fig. S2).

To analyze the impact of the mtry parameter in the RF algorithm, we performed sensitivity analyses using a smaller and a larger value of mtry (Supplementary Figs. S3–S6). Differences were negligible for LeFE and small for PE and SF. The largest differences were observed for Hunting where a smaller value of mtry was advantageous but even with this setting the other approaches perform better.

A comparative analysis of the selection frequency of each simulated pathway is presented in Figure 1C. The high sensitivity of PE and SF is demonstrated by their capability to detect pathways with strong signals in nearly all of the replicates as well as a power of at least 28.5 and 14%, respectively, for pathways with only very low numbers of differentially expressed genes (prop.de = 0.25 and number of genes = 20). Hunting and LeFE, however, are only able to identify large pathways with 100% of differentially expressed genes (prop.de = 1) in more than 50% of the replicates. While empirical power for pathways with at least 100 genes reaches 100% for LeFE, it is still considerably lower for Hunting.

Figure 2 shows results of a complete null scenario where all pathways were simulated with prop.de = 0, so that each identified pathway is a false positive finding. PE controls the number of false results well across all the investigated correlation patterns, while SF consistently shows selection frequencies of about 16% across all the pathways. In contrast, pathways detected by Hunting and LeFE have strong correlations. Notably, the number of false-positive findings is less pronounced for small pathways with only 20 genes.

Fig. 2.

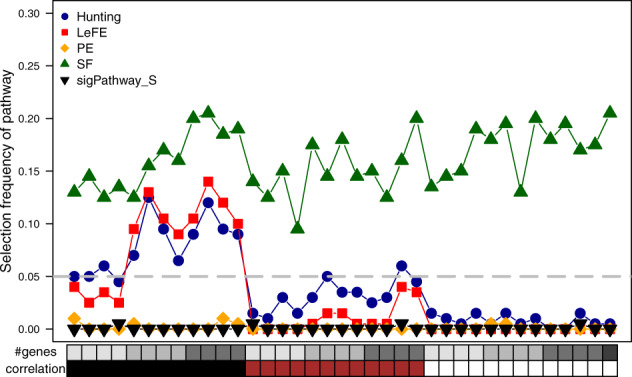
Performance of Hunting, LeFE, SF, PE and sigPathway with sample-level permutation in the null scenario of simulation study 1. The median selection frequency of each pathway across all 100 replicates is shown for each method using different plotting symbols and colors. Characteristics of each pathway (number of genes, pairwise correlation of genes, proportion of differentially expressed genes) are given at the bottom and top of the plot. The dashed line shows a selection frequency of 0.05

Compared to the RF-based approaches, the statistical method sigPathway_S (using permutations on the sample level) is the worst performing method (Fig. 1). Although FDR is also 0, the median sensitivity is only 1%, stability is 8% and the classification error is about 10%. Interestingly, the only pathways that are selected are those with uncorrelated genes. The other statistical methods (FGSEA with gene or sample level permutation) similarly show bad performance (Supplementary Fig. S7). In contrast, sensitivity and stability of sigPathway with gene level permutation are larger, however, FDR also increases to about 20%. The reason for this behavior is that correlated pathways are selected independently of the level of differential expression (Supplementary Fig. S7C).

3.2 Simulation study 2

The second simulation study is based on correlation patterns and effect sizes observed in two of the publicly available gene expression studies used in the comparison based on experimental data (see next subsection) which measured gene expression in two different tissues (kidney and whole blood). Expression values observed in the controls were used to estimate pairwise correlation and standardized effect sizes were determined based on differentially expression analysis. For each dataset, only genes in a single pathway, called target pathway, were simulated to be differentially expressed.

Pairwise correlations between genes within each pathway show values ranging from 0 to almost 1 (Supplementary Fig. S8) and low correlation coefficients are more frequent than medium and high coefficients (Supplementary Fig. S9). In each dataset, the corresponding target pathway exhibits a typical correlation pattern. However, the two datasets differ with respect to observed differential expression between cases and controls (Supplementary Fig. S10). In the whole blood dataset, only 0.26% of the genes were differentially expressed with small differences (maximum: 1.9). In contrast, the kidney dataset comprised substantially more differentially expressed genes and the observed effect sizes were more variable and thus included more extreme differences reaching absolute values of more than 10. In general, low numbers of overlapping genes between the pathways are common, while higher numbers of overlapping genes are very rare.

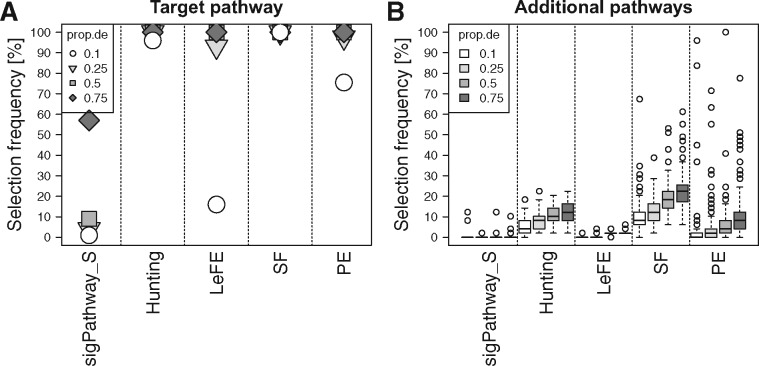
Figure 3 displays results of simulation study 2 utilizing the whole blood expression data, using different proportions of differentially expressed genes (prop.de). SF is the most powerful method by detecting the target pathway in 100% of the replicates for all values of prop.de. Furthermore, it also selects the largest number of additional pathways ranging from approximately 10% for a low proportion of differential expression (prop.de = 0.1) to over 20% for a large proportion (prop.de = 0.75). In contrast to the other methods, these additionally selected pathways frequently include those that do not share any gene with the target pathway (Supplementary Fig. S11A). This is in accordance with the results of the complete null scenario where SF shows selection frequencies of more than 10% in contrast to the other methods that almost never select any pathway (Supplementary Fig. S12). The Hunting approach has a high empirical power to select the target pathway for all values of prop.de and selects additional pathways with a frequency ranging from approximately 4% to around 12%. LeFE and PE show high empirical power for moderate to large amounts of differential expression (prop.de = 0.25, 0.5 and 0.75), while power for prop.de = 0.1 is reduced to 16 and 75.5%, respectively. However, LeFE rarely selects additional pathways, while PE does this with frequencies that are very low for prop.de = 0.1 and that exceed 8% for prop.de = 0.75. SigPathway with sample level permutation (SigPathway_S) performs comparatively weak in this simulation study, since it is considerably less powerful than the other methods. However, it also has a low selection frequency of additional pathways.

Fig. 3.

Performance of Hunting, LeFE, SF, PE and sigPathway with sample-level permutation in simulation study 2 (whole blood data). (A) The selection frequency to detect the target pathway (with simulated differential expression) over all 100 replicates. The proportions of additionally selected pathways for each replicate are summarized with boxplots in B. The amounts of differential expression in the target pathway are depicted with different shades of gray and different symbols (A)

The results for the simulation study utilizing the kidney expression data are similar (Supplementary Figs S11B and S13).

3.3 Experimental data

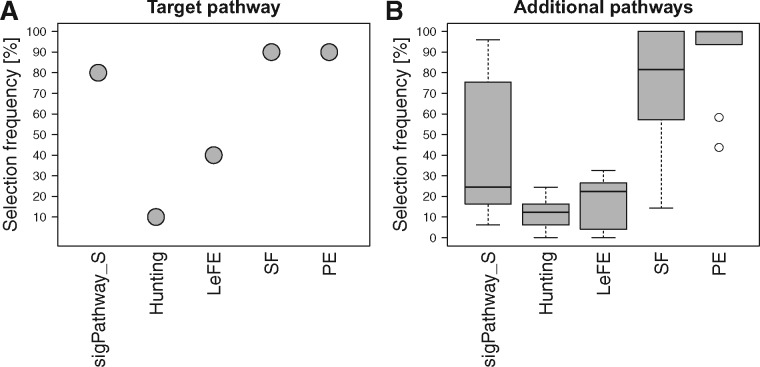
In addition to the simulation studies which could never include all of the subtleties of experimental data, we compared the different approaches on nine gene expression datasets. Each of them corresponds to one or two (for the smoking dataset) particular MSigDB hallmark gene set, denoted as target pathway in the following. PE and SF were the most powerful methods since they detected 90% of the target pathways (Fig. 4A). However, they also selected a very high percentage of the additional pathways that were analyzed (Fig. 4B). PE even identified all analyzed pathways in 50% of the datasets. In contrast, Hunting and LeFE selected the target pathway in only 10 and 40% of the datasets, respectively, but also identified <25% additional pathways. Compared to the RF based methods, sigPathway_S shows similar performance as SF and PE.

Fig. 4.

Performance of Hunting, LeFE, SF, PE and sigPathway with sample-level permutation on experimental datasets. For each method, (A) shows the proportion of datasets in which the target pathway was selected. The proportions of additionally selected pathways in each dataset are summarized by boxplots in B

The runtimes are in the minutes range for LeFE and PE and in the seconds range for Hunting and SF, as well as for sigPathway_S (Supplementary Fig. S14).

4 Discussion

In this study, we compared four RF-based methods which aim to select pathways important for a good prediction. Our results show that these methods can be separated into two groups with similar behavior and performance called self-sufficient (PE) and competing (Hunting and LeFE) approaches. Due to their stronger background dependency, competing methods feature a lower power, especially when large numbers of causal pathways (simulation study 1) and/or complex variable correlation patterns (experimental data) are present. They, however, rarely select additional pathways that do not or only marginally influence the outcome. This is especially obvious in the results of experimental data where the self-sufficient method selects almost all of the analyzed pathways while competitive methods select <25% of them.

The statistical approaches performed relatively weak in our simulation studies. The reason for this poor performance is that the simulated data have either small standardized effects (simulation study 1) or low samples sizes (simulation study 2). The low power of statistical pathway approaches under comparable scenarios has also been demonstrated in a semi-synthetic simulation study (Mathur et al., 2018) or with small microarray datasets where the GSEA approach resulted in nominal P values > 0.05 for almost all pathways (Tarca et al., 2013).

The runtime of the methods is acceptable, as it was in the seconds or minutes range for the experimental datasets (comprising 19–33 cases and 16–96 controls as well as 12 483–19 014 genes). Another time and also memory consuming part of our study was the data generation in simulation study 2 since multivariate normally distributed data were simulated based on large correlation matrices. A more efficient alternative could be the semi synthetic approach called Flexible Algorithm for Novel Gene set Simulation that was proposed by Mathur et al. (2018). They introduced the desired amount of differential expression into an experimental case–control dataset and then generated bootstrap samples for their evaluation.

In this study, we only investigated classification settings. However, for the analysis of quantitative and survival outcomes, similar results can be expected, as demonstrated by other comparison studies, such as Degenhardt et al. (2019). In fact, Hunting was proposed for the analysis of survival data (Chen and Ishwaran, 2013). We also restricted our analysis to microarray-based datasets. However, we expect similar performance of the approaches for different technologies such as RNA-Seq or other type of omics data (e.g. from genetics, epigenetics, proteomics or metabolomics). The RF approach is internally rank-based and thus nonparametric. Hence, it is applicable to predictor variables of different types (e.g. categorical in genetics or proportions in methylation data) or that are not normally distributed (e.g. counts in RNA-Seq or zero inflated in mass spectrometry based data). Integrating several types of omics data measured in the same individuals is also possible since the used corrected Gini importance does not prefer predictor variables of a specific type.

For the approaches that were evaluated in this study various variations are conceivable, e.g. alternative machine learning methods could be applied. This would be straightforward for PE because PEs are commonly reported for machine learning methods. Indeed, PE methods using regularized least squares classifiers (Maglietta et al., 2007) have been proposed for pathway analysis. The other approaches investigated in our study rely on importance scores, which need to be provided by alternative prediction modeling tools.

Possible objectives for further research include the following aspects. First, alternative importance measures might be of interest. In particular, our recently developed method called Surrogate Minimal Depth (Seifert et al., 2019) could be used to interrogate relationships between pathways or between the genes within important pathways. Second, additional analyses are needed to evaluate the effect of missing and misspecified pathway annotations on the performance of the different approaches. Third, a major limitation is the current focus on simple pathway membership, i.e. sets of genes. However, pathways are actually defined by their interconnections such as biochemical reactions or regulatory and signaling events. Several topology aware pathway analysis methods have been proposed which have proven to be superior to methods solely based on pathway membership (Ma et al., 2019; Nguyen et al., 2019). Both of these pathway-based approaches analyze each pathway separately ignoring the fact that genes might be members of several or many pathways. An alternative to detailed information on specific biological processes are networks which summarize genome-wide bimolecular interactions such as physical protein–protein interactions or regulatory relationships. Differentially expressed genes can be mapped onto those networks, followed by detection of disease relevant subnetworks or modules (Choobdar et al., 2019). Further research is needed to evaluate and compare machine-learning approaches that can incorporate pathway topology or network information such as Pan et al. (2013) and Anděl et al. (2015).

5 Conclusion

This study compared various methods for RF-guided pathway selection by analyzing different simulated and experimental datasets. We observed relevant differences between competing (Hunting and LeFE) and self-sufficient (PE) or hybrid methods (SF), leading to the following advice for their application: SF is not recommended due to its large number of false positive findings in scenarios of the complete null hypothesis. PE should be applied when large numbers of relevant pathways are expected. Hunting and LeFE, however, should be preferred if low numbers of relevant pathways are expected or the most strongly associated pathways are of interest.