Alphabet Projection of Spectra

Abstract

In the metabolomics, glycomics, and mass spectrometry of structured small molecules, the combinatoric nature of the problem renders a database impossibly large, and thus de novo analysis is necessary. De novo analysis requires an alphabet of mass difference values used to link peaks in fragmentation spectra when they are different by a mass in the alphabet divided by a charge. Often, this alphabet is not known, prohibiting de novo analysis. A method is proposed that, given fragmentation mass spectra, identifies an alphabet of m/z differences that can build large connected graphs from many intense peaks in each spectrum from a collection. We then introduce a novel approach to efficiently find recurring substructures in the de novo graph results.

INTRODUCTION

The mass spectrometric analysis of structured molecules is important for the analysis of glycoconjugates¹ and for drug discovery.² Often, these methods cannot rely on machine-generated databases (as can often be done for peptide search) because of the combinatoric nature of these small molecules, which would make a machine-generated database far too large to use. Fragmentation trees may be used for the analysis of small molecules where databases may not exist or are too large, but they rely on enumerating all molecular formulas that match the precursor mass.³ Enumerating over all molecular formulas for a precursor mass can become very costly, particularly for a larger precursor mass or with a fairly imprecise mass-to-charge measurement, and thus fragmentation trees may not be suitable in all cases. Spectral libraries generated by known small-molecule content can be used, but they need to be painstakingly curated; therefore, even if the resources are available to do so, they may not be suitable for applications that include unexpected compounds or reactions. Likewise, when an MS1 spectrum is generated by a few intact molecules, it may be possible to isolate the most abundant mass in the spectrum using only Fourier analysis.⁴

To date, de novo approaches, which link peaks in fragmentation spectra when they are different by a mass in the “alphabet”, are the best tools for these problems. For example, de novo peptide sequencing may be performed using an “alphabet” of 20 amino acid masses, whereas de novo glycan analysis may be performed using an alphabet of four common sugar residues. Once an alphabet is known, dynamic programming can be used to link peaks for linearly chained molecules (e.g., peptides)^5,6 or arbitrarily structured small molecules (e.g., sugars).^7,8 The ability to use certain “characters” in the alphabet can also be constrained to an arbitrary flowchart (for instance, it may state that a peptide with more than two of a given amino acid should not be considered) by performing dynamic programming on the Cartesian products between the graph of linked peaks and the flowchart from the constraints.⁹ Distinctions between fragmentation spectra can also be used to build graphs for a given alphabet by clustering spectra to find highly similar neighbor spectra and then attempting to match small changes between these neighboring spectra using the given alphabet.¹⁰ Approaches reminiscent of this can be used to better characterize biochemical pathways.¹¹

All of the above approaches need to know the alphabet, that is, the masses considered during the de novo; however, in a truly blind de novo application, this alphabet will not be known. This is important when identifying active compounds and therapeutic components in venoms¹² or plant products¹³ and can similarly be significant when finding drug metabolites produced. Even fundamental chemical components of the sugar alphabet (such as O-GlcNAc-P) were only discovered relatively recently;¹⁴ thus if there are more undiscovered components of the sugar alphabet, then any current sugar alphabet will be incomplete, and a blind approach may be the only way to use these undiscovered sugars in an alphabet.

Two approaches with partially blind aspects to them are the offset frequency function and the spectral networks. The offset frequency function, introduced by Dančík et al.,¹⁵ builds a de novo graph using the amino acid alphabet and then builds the empirical distribution of peak differences between peaks in the de novo peptide path and peaks not in the de novo peptide path; however, this approach needs to know the amino acid alphabet in advance. Spectral networks¹⁶ are likewise used for the analysis of peptides. For example, a pair of spectra-matching peptides with either overlapping sequences (e.g., EEAMPN and AMPNGGR) or a pair of modified and unmodified peptide spectra can be matched by sequence overlap after the database search; then, differing peaks in a spectral pair can elucidate sequence changes, modifications, and so on. Like the offset frequency function, this approach relies on knowledge of the amino acid alphabet and methods for sequencing peptide spectra (either de novo or database search) via that amino acid alphabet.

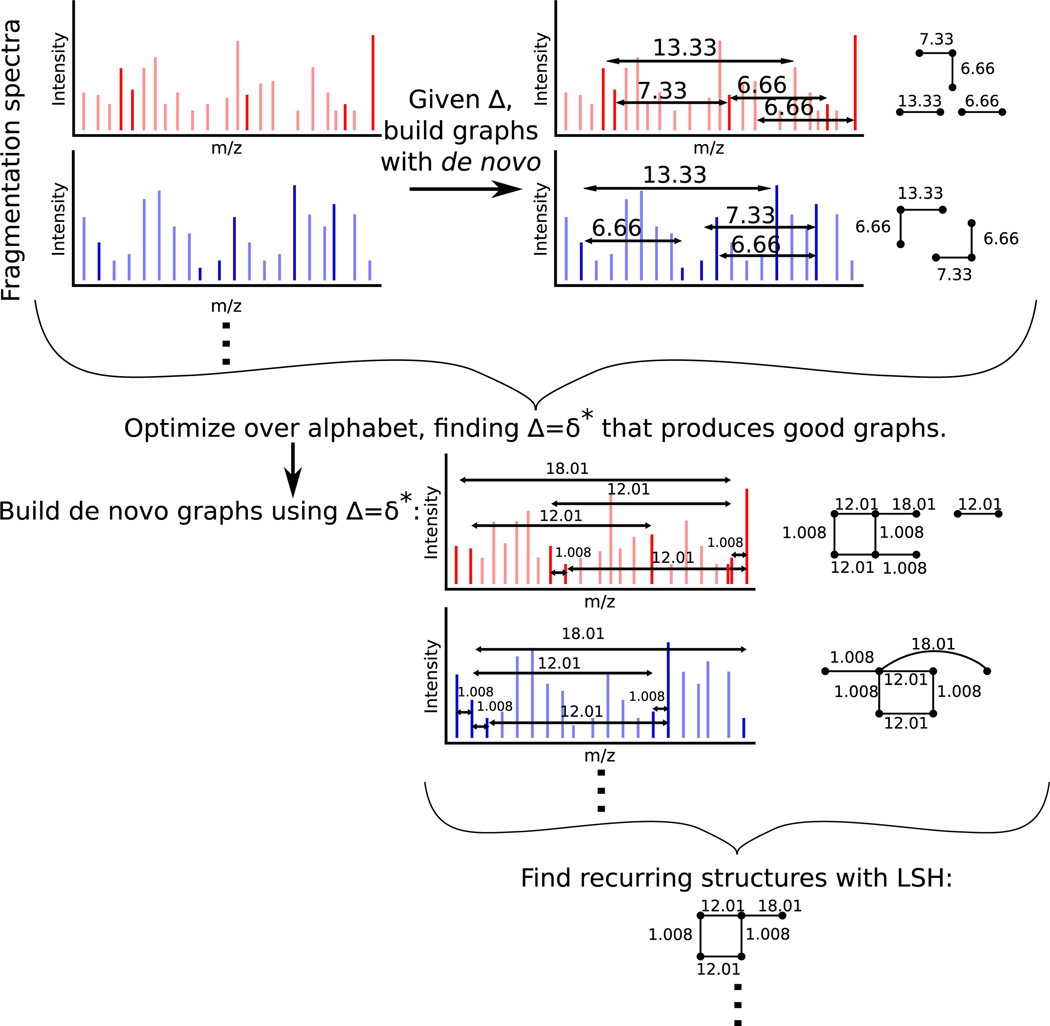
In this Article, we introduce an approach to perform blind de novo analysis of mass spectra and to estimate an alphabet from a collection of spectra (i.e., the “alphabet projection of the spectra”). Our approach seeks to find the alphabet that would best explain the most high-intensity peaks and simultaneously build the largest connected graphs. This approach is also informative as to which peaks can be linked by this alphabet; the graph produced by linking peaks in a de novo manner can be helpful to inferring the chemical structure of a compound. In this manner, the method proposed can also be seen as an unsupervised de novo approach (i.e., a de novo approach where the alphabet is not known in advance). We then introduce a hash-based method by which we can find the de novo graphs built with the inferred alphabet that recur in the fragmentation spectra (Figure 1).

Figure 1.

Zero-knowledge de novo analysis of fragmentation spectra. From a collection of fragmentation spectra, an alphabet δ* is inferred. This alphabet is used to perform de novo analysis and build graphs from the fragmentation spectra. Recurring structures in these de novo graphs are then efficiently found via locality-sensitive hashing (LSH).

METHODS

We use the notation from Table 1 to formalize the alphabet projection problem: We use variables i and j to index peaks in the spectra, whereas we use variable k to index the alphabet. For variables i and j, assume that the indices are ordered so that the masses are sorted in ascending order: $m_j^{(l)}>m_i^{(l)}\leftrightarrow j>i$.

Table 1.

Definitions of Notations Used Throughout the Paper^a

variable	meaning
$s^{(l)}$	indices of peaks in a fragmentation spectrum l
$m_i^{(l)}\text{for}i\in s^{(l)}$	m/z of peak i in spectrum $s^{(l)}$
$p_i^{(l)}\text{for}i\in s^{(l)}$	intensity of the peak at m/z in spectrum $s^{(l)}$
$D^{(l)}$	set of s(l), m(l), and $p_i^{(l)}$ for spectrum l
$m_j^{(l)}-m_i^{(l)}\text{for}i\in s^{(l)},j\in s^{(l)}$	m/z difference between two peaks in spectrum s(l)
Δ1, Δ2, Δ3, ..., Δd	alphabet of size d (units are mass, not m/z)
Є	maximum allowed error tolerance in m/z; if two m/z values are approximately equal, then the absolute value of their difference must be ≤Є.
$E_{z,i,j,k}^{(l)}\text{for}i\in s^{(l)},j\in s^{(l)},k\in \{1,2,\cdot \cdot \cdot ,d\}$	peaks i and j in spectrum s(l) can be connected by difference Δk using charge z; i.e., $\left|m_j^{(l)}-m_i^{(l)}-\frac{{\Delta }_k}{z}\right|\le \mathrm{Є}$ for some charge state
$E_z^{(l)}$	all edges for spectrum l that use charge state z
$g\left(E_z^{(l)}\right)=\left\{e_1,e_2,\dots \right\}$	collection of edges in the connected components of the graph defined by $E_z^{(l)}$
θ	hyperparameter that can be tuned to influence the acceptance rate; θ = 0 will accept all proposed changes; θ = ∞ will only accept changes that improve the likelihood

^aIn each spectrum $s^{(l)}$, a peak $i\in s^{(l)}$ has an m/z value $m_i^{(l)}$, with machine tolerance Є and intensity $p_i^{(l)}$. The set of $s^{(l)}$, $m_i^{(l)}$, and $p_i^{(l)}$ for all peaks in spectrum l forms $D^{(l)}$. The alphabet of size d, Δ₁, Δ₂, Δ₃, ..., Δ_d, is used to form a set of edges, $E_z^{(l)}$, for charge state z, and the set of edges forms connected components, $g(E_z^{(l)})=\{e_1,e_2,\dots \}$, of the graph defined by $E_z^{(l)}$.

Each neutral loss alphabet Δ = δ is the same constant, given size, d, and deterministically produces a graph consisting of the edges E; these edges connect every pair of peaks within one spectrum if the m/z difference between the peaks is within Є of the m/z difference created by dividing alphabet mass Δ_k by charge z

$$E_{z,i,j,k}^{(l)}=\{\begin{array}{l}1\left|m_j^{(l)}-m_i^{(l)}-\frac{{\mathrm{\Delta }}_k}{z}\right|\le \mathrm{Є}\hfill \\ 0\text{else}\hfill \end{array}$$

The edges E can be found deterministically once Δ and D are known; for this reason

$$\mathrm{Pr}(D|\mathrm{\Delta }=\delta )=\mathrm{Pr}(D|\mathrm{\Delta }=\delta ,E=e)=\mathrm{Pr}(D|E=e)$$

We assume that all spectra s⁽¹⁾, s⁽²⁾, ... (and their masses and intensities) are conditionally independent from one another given the graph induced by E

$$\begin{gathered} \mathrm{Pr}(D|\mathrm{\Delta }=\delta )=\mathrm{Pr}(D|E=e) \\ =\mathrm{Pr}\left(D^{(1)},D^{(2)},\dots |E=e\right) \\ =\prod _l\mathrm{Pr}\left(D^{(1)},D^{(2)},\dots |E=e\right) \\ =\prod _l\mathrm{Pr}\left(s^{(l)},m^{(l)},p^{(l)}|E=e\right) \end{gathered}$$

Conditional independence of the spectra given the edges is fairly reasonable because it resembles the fact that given the sample content (which is informed through the graph of connected peaks), the production of one fragmentation spectrum does not interfere with the process by which other fragmentation spectra are produced. Even the caveat, competition between abundant analytes in data-dependent acquisition (DDA), applies more to which precursors will be selected for fragmentation rather than how peaks in those fragmentation spectra can be connected.

We seek, δ*, a maximum a posteriori (MAP) estimate of Δ

$$\begin{gathered} {\delta }^{*}=\underset{\delta }{\mathrm{argmax}}\mathrm{Pr}(\mathrm{\Delta }=\delta |D) \\ =\underset{\delta }{\mathrm{argmax}}\prod _l\mathrm{Pr}(D^{(l)}|\mathrm{\Delta }=\delta )\cdot \mathrm{Pr}(\mathrm{\Delta }=\delta ) \\ =\underset{\delta }{\mathrm{argmax}}\prod _l\mathrm{Pr}(s^{(l)},m^{(l)},p^{(l)}|\mathrm{\Delta }=\delta )\cdot \mathrm{Pr}(\mathrm{\Delta }=\delta ) \end{gathered}$$

Noncombinatorial Approach

A naive approach to this problem is to empirically estimate the distribution of mass differences $m_j^{(l)}-m_i^{(l)}$ over all spectra l. This can be performed in an unweighted manner (all (i, j) pairs contribute equally to the distribution) or in a weighted manner (an (i, j) pair has contribution proportional to $p_j^{(l)}\cdot p_i^{(l)}$). Because exactly overlapping differences are improbable, the noncombinatorial approach treats two differences as equal if they are within Є of one another. The process of finding all differences $m_j^{(l)}-m_i^{(l)}$ can be done efficiently using the fast Fourier transform (FFT) by binning the spectrum by m/z then convolving the spectra with itself.

The alphabet Δ₁, Δ₂, ..., Δ_d is estimated as the top d peaks in the empirical distribution after being sorted by either the count in the unweighted case or the sum of the proportional $p_j^{(l)}\cdot p_i^{(l)}$ values in the weighted case. It is important to note that this noncombinatorial approach only cares about the abundance of the Δ values and does not take into account the connectivity of any graphs that are formed by the edges induced by Δ.

Combinatorial Approach

The noncombinatorial approach does not incentivize building of large connected graphs, such as long amino acid chains in a peptide or large forking substructures in glycoconjugate spectra.⁷ A combinatorial approach can be used to incentivize large connected graphs.

Efficient Graph Construction.

For each spectrum $D^{(l)}$, we efficiently build the graph of all possible connected peaks. In each spectrum $D^{(l)}$ and for each charge state z, we create an edge $E_{z,i,j,k}^{(l)}$ if and only if

$$\left|m_j^{(l)}-m_i^{(l)}-\frac{{\mathrm{\Delta }}_k}{z}\right|<\mathrm{Є}$$

This connects two peaks whose m/z difference is within Є of the predicted m/z difference from alphabet mass Δ_k using charge z.

Of course, for any charge state z and some fixed spectrum l consisting of n peaks, edges can be trivially formed in Θ(n·n·d); however, by sorting the $m^{(l)}$ values and the Δ values, this can be sped up: By proposing the peaks $m_i^{(l)}$ and $m_j^{(l)}$ first, we know that we are looking for an alphabet mass with $\frac{{\mathrm{\Delta }}_k}{z}$ within Є of $m_j^{(l)}-m_i^{(l)}$; because the search for Δ_k can be processed on the sorted array, this can be accomplished in Θ(n·n·log(d)) steps. Likewise, if we first propose starting peak $m_i^{(l)}$ and alphabet mass Δ_k, then we are searching for the ending peak $m_j^{(l)}$ with m/z value within Є of $m_i^{(l)}+\frac{{\mathrm{\Delta }}_k}{z}$; this can be accomplished in Θ(n·d·log(n)) steps. This problem is closely related to the famous 3SUM problem. (Here we have a generalization because it allows matches within Є instead of requiring exact matches as the classic 3SUM problem does.) Interestingly, there exists no known solution to the classic 3SUM problem in O(n^2−Ω(1)).¹⁷ Furthermore, the “within Є” criteria does not easily accommodate the use of hashing (used to achieve one O(n²) algorithm) or other advanced approaches.

In practice, we accelerate the log₂ search for each spectrum by computing a dense table of the cumulative counts of peaks with m/z at or below some target m/z value x. This table has bin widths of α

$$c_t^{(l)}=\left|\left\{i:m_i^{(l)}\le t\cdot \alpha \right\}\right|$$

If α ≥ Є, then we can then use this table to find bounds on indices with which we seed the log₂ search: The lower bound index for matches will be found by $c_{x\cdot \alpha -\alpha }^{(l)}$. The upper bound index for matches will be found by $c_{x\cdot \alpha +\alpha }^{(l)}$.

Using these bound values, we finish with two log₂ searches: One searches for the first peak with m/z crossing x − Є, and the other searches for the last peak with m/z not crossing x + Є. In practice, we observe a substantial speedup, even when the number of peaks in the spectrum is relatively low (Table 2). This $c^{(l)}$ table has the effect of uniformizing the m/z search space; for some distributions of m/z values, this can make the lookup run in constant time.

Table 2.

Runtimes to Find a Peak in a Spectrum within Є = 0.01 Da of the Target m/z Value, Repeated for 2²⁰ Such Searches on a Spectrum with 1000 Peaks^a

	alpha	naive search	log search	binned-log search
average runtime(s)	0.0001	0.45861	0.08461	0.01541
	0.005	0.45841	0.08472	0.00862
	0.01	0.45902	0.08344	0.00780
	0.02	0.45873	0.08342	0.00712
	0.05	0.45826	0.08483	0.00738
	0.1	0.45838	0.08464	0.00778
	0.5	0.45919	0.08490	0.01304
	1	0.45847	0.08479	0.01820

^aNote that for α < Є, the size of the window returned by the search must be widened to find the correct peak.

Furthermore, because the n peaks are stored in a contiguous, sorted order (in an array, not a balanced binary search tree), we can define all ending peaks j that would be within Є of starting peak i using alphabet mass Δ_k and record them with only two integers: the beginning of the matching window and the size of the matching window. This likewise introduces a considerable speed advantage over using a linked list of peak indices (which would not be cache localized). By choosing a large enough α, constructing a $c^{(l)}$ table for fragmentation spectrum l takes space roughly equivalent to the sorted m/z array, $m^{(l)}$, and the intensity array, $p^{(l)}$. An α that is sufficiently small will create a table that is too large to fit into a cache, causing cache misses and slowing the search. (This happens for α = 0.0001 in Table 2.) Too large of an α can create a large space for the two log searches, similarly slowing the search.

As a result of this, on a spectrum of the size of that in Table 2, we get an 11.7-fold speed-up over a standard log search.

MAP Estimation Using Sampling.

We use a Gibbs sampler¹⁸ to obtain a sequence of random samples of Δ, with one new Δ_k|Δ₁, Δ₂, ..., Δ_k−1, Δ_k+1, ..., Δ_d being proposed per iteration. For each univariate cross-section, the changes to Δ_k are proposed and accepted via Metropolis–Hastings.¹⁹

Each Δ_k is proposed from one of three proposal functions (with the choice of proposal function selected at uniform): The first proposal selects an m/z from the intensity-weighted distribution used for the noncombinatorial approach (selected from all possible m/z differences, not just the top d). The second proposal scales Δ_k to have an equivalent m/z value at some charge state. For example, if Δ_k = 3, then it may propose 1 (from z = 3 to z = 1), 2 (from z = 3 to z = 2), ... or 9 (from z = 1 to z = 3). The third proposal selects a random peak in some connected component for some charge state and then chooses a new value for Δ_k that would create a new edge incident to that peak, thereby adding a new edge to the connected component. The first and third proposal functions are topologically equivalent in that they have the same solution space from which to pull Δ_k; however, the third solution is greedy and guarantees that the value it selects will connect a peak to some already existing connected component. The first proposal function does not make this guarantee.

The updated joint probability Pr(D, Δ = δ′) is compared with the current joint probability Pr(D, Δ = δ). If Pr(D, Δ = δ′) > Pr(D, Δ = δ), then the new Δ_k = δ_k is accepted; otherwise, the probability of accepting the new Δ_k = δ_k is

$$\frac{\mathrm{Pr}\left(D,\mathrm{\Delta }={\delta }^{\prime }\right)}{\mathrm{Pr}(D,\mathrm{\Delta }=\delta )}$$

A value proportional to the joint probabilities can be computed as the product between a prior on Δ and a likelihood proportional to Pr(D|Δ).

Likelihood Model.

Here we model the process by which E creates the peaks in spectrum l. We partition $E^{(l)}$ into $E_1^{(l)},E_2^{(l)}$, ... connected components for each charge state z

$$\mathrm{Pr}\left(D^{(l)}|E^{(l)}\right)=\prod _z\mathrm{Pr}\left(D^{(l)}|E_z^{(l)}\right)$$

We compute $\mathrm{Pr}(D^{(l)}|E_z^{(l)})$ as the likelihood of the graph using a particular charge state z. Let $g(E_z^{(l)})$ be a collection of the edges in each connected component of the graph formed by $E_z^{(l)}$. We define the likelihood of the graph formed when using that particular charge state to be the sum of the likelihoods over these connected components

$$\mathrm{Pr}(D^{(l)}|E_z^{(l)})=\sum _{g\in g(E_z^{(l)})}\mathrm{Pr}(D^{(l)}|G=g)$$

Lastly, we define the likelihood of a single connected component g using a single charge state z on a single spectrum l using the intensities of the peaks joined by each edge

$$\mathrm{Pr}(D^{(l)}|G=g)=\prod _{(i,j)\in g}{p}_i\cdot p_j$$

The values p_i and p_j have been normalized by dividing by the minimal intensity value.

Prior Model.

The prior model has three requirements, which all produce a prior of either 0 or 1: The first requirement is that all alphabet masses be ≥1 − Є. This restricts alphabets to larger masses; being that smaller masses often have no chemical significance, if we do not enforce this, then small masses may be selected because they are actually differences between actual alphabet masses. The second requirement is that no two masses in the alphabet produce similar m/z values at any charge considered (e.g., Δ₁ = 1.00860, Δ₂ = 2.01720 would not be possible in the same alphabet). This prevents doubling (or tripling, etc.) up on a single alphabet mass strongly supported by the spectra. The third requirement is that no alphabet results be within 0.5 Da of one another (e.g., Δ₁ = 1, Δ₂ = 1.1 would not be possible in the same alphabet).

$$\begin{gathered} \mathrm{Pr}(\mathrm{\Delta })=\{\begin{array}{ll}1\hfill & \forall k,{\mathrm{\Delta }}_k\ge 1-\mathrm{Є}\hfill \\ 0\hfill & \text{else}\hfill \end{array}. \\ \prod _{k_1\ne k_2}\{\begin{array}{l}1\forall z_1,z_2,\frac{{\mathrm{\Delta }}_{k_1}\cdot z_1}{{\mathrm{\Delta }}_{k_2}\cdot z_2}\notin [1-\mathrm{Є},1+\mathrm{Є}]\hfill \\ 0\text{else}\hfill \end{array}. \\ \prod _{k_1\ne k_2}\{\begin{array}{ll}0\hfill & \left|{\mathrm{\Delta }}_{k_1}-{\mathrm{\Delta }}_{k_2}\right|<\frac{1}{2}\hfill \\ 1\hfill & \text{else}\hfill \end{array} \end{gathered}$$

For faster runtime, we encode the prior model using the random proposal distribution. Given the current alphabet Δ, we propose an alphabet Δ′ that is identical in all but one character Δ_k, which has been changed. We do this by first randomly choosing k, the index that will be changed, and then proposing ${\delta }_k^{\prime }$, a new value for Δ_k. The new value is proposed by one of the three proposal functions described above.

When exactly one value in the current alphabet (Δ_t) can produce an m/z too similar to the newly proposed mass (for some charge states z₁, z₂), we could simply reject the proposal as having a zero prior probability; however, that approach can lead to fixation in local optima of the likelihood surface because it can be difficult to exchange an alphabet mass with a multiple of itself that would produce an equivalent m/z at a different charge state. Instead, it is more efficient to simply assign k = t to overwrite Δ_t if the proposal is accepted. When two or more values in the current alphabet can produce an m/z too similar to the newly proposed mass (for some charge states z₁, z₂), then the modification to the alphabet would lower the prior probability to 0; therefore, the proposal is simply repeated without building the graphs or computing the likelihood.

The prior probability is completely accounted for in the proposal step, and thus we may substitute Pr(D|Δ) for Pr(D, Δ).

Adjusting Likelihood Steepness Using θ.

In traditional Metropolis–Hastings, a proposal from Δ to Δ′ will be accepted with the probability

$$\frac{\mathrm{Pr}\left(D,{\mathrm{\Delta }}^{\prime }\right)}{\mathrm{Pr}(D,\mathrm{\Delta })}$$

certainly accepting the proposal when Pr(D, Δ′) ≥ Pr(D, Δ). We allow for this to be distorted using hyperparameter θ, accepting the proposed change from Δ to Δ′ with probability

$${\left(\frac{\mathrm{Pr}\left(D,{\mathrm{\Delta }}^{\prime }\right)}{\mathrm{Pr}(D,\mathrm{\Delta })}\right)}^{\theta }$$

The motivation behind including θ is that the Markov chain Monte Carlo (MCMC) will not mix well if the surface is too steep and will not find the optimum efficiently if the surface is not steep enough. In this manner, θ = 0 results in always accepting proposed changes, and θ = ∞ results in only accepting changes that immediately improve the joint probability. In the experiments outlined here, we use θ = 1 but offer the ability to set θ to different values at the command line.

Additionally, our software implementation outputs the acceptance rate of proposals as well as the average deviation between log(Pr(D, Δ′)) and log(Pr(D, Δ)) to help adjust θ. For example, if you want to set θ to get roughly a 50% acceptance rate and you know that the previous run gave an average deviation between log(Pr(D, Δ′)) and log(Pr(D, Δ)) of x, then $e^x=\left(\frac{\mathrm{Pr}\left(D,{\mathrm{\Delta }}^{\prime }\right)}{\mathrm{Pr}(D,\mathrm{\Delta })}\right)$, and you can solve (e^x)^θ = 0.5 for θ.

The same objective could be accomplished using simulated annealing where a loose θ value turns hard according to some carefully selected cooling curve that allows for the most probable outcome to be expected with a probability of one if the simulation is ran long enough.²⁰

Ranking Masses in Δ.

If desired by the user, using a flag at runtime, the frequency in which masses are in the alphabet may be written to a file. This may be used to create a ranking of the Δ values based on how many iterations of the Gibbs sampler stayed in the alphabet. This is done for all masses, not just the masses in the final alphabet.

Mapping Δ to Canonical Masses.

Inferring masses from mass-to-charge gaps is difficult because two masses may look identical at different charge states. For this reason, the combinatorial approach sometimes finds integer multiples or fractions of a mass instead of the mass itself. For example, water has a mass of roughly 18.01057 Da; however, the combinatorial approach may find some Δ_k = 36.02114 = 2·18.01057. In general, if multiple charge states of neutral water losses are well represented, then we would expect that using Δ_k = 18.01057 will produce a superior likelihood compared with using Δ_k = 36.02114; therefore, the combinatorial approach would eventually choose the canonical mass. However, there are cases where using Δ_k = 36.02114 may produce a higher likelihood. For example, if three peaks indicate a double neutral loss of water peaks a, b, and c at xTh, (x + 18.01057)Th, and (x + 36.02114)Th, then Δ_k = 36.02114 can connect a → c using a charge state of z = 1 and also connect a → b and b → c using a charge state of z = 2. If the z = 3 charge state is not well represented (using Δ_k = 36.02114 will not find gaps of size 9.0075 Th produced by water at a charge state of z = 3), then the model will prefer Δ_k = 36.02114 to Δ_k = 18.01057.

For this reason, before we report the final mass alphabet Δ, for each ${\mathrm{\Delta }}_k\in \mathrm{\Delta }$, we compare the masses $\frac{{\mathrm{\Delta }}_k}{1},\frac{{\mathrm{\Delta }}_k}{2},\frac{{\mathrm{\Delta }}_k}{3},\dots ,\frac{{\mathrm{\Delta }}_k}{c}$, where c is the value of the max charge used in the Gibbs sampler. For each of the new candidate masses, ${\mathrm{\Delta }}_k^{\prime }$, the graphs produced over all spectra for its charge states $\frac{{\mathrm{\Delta }}_k^{\prime }}{z=1},\frac{{\mathrm{\Delta }}_k^{\prime }}{z=2},\frac{{\mathrm{\Delta }}_k^{\prime }}{z=3},\dots ,\frac{{\mathrm{\Delta }}_k^{\prime }}{z=c}$, are built. If $\frac{{\mathrm{\Delta }}_k}{1}$ and its charge states produce the most edges, then we report the mass as Δ_k (unchanged); if $\frac{{\mathrm{\Delta }}_k}{2}$ and its charge states produce the most edges, then we report the mass as $\frac{{\mathrm{\Delta }}_k}{2}$. In this manner, double neutral losses, double mass differences, and dimers do not force us to report multiples or fractions of the mass of interest.

Finding Recurring Structures via Similar Subgraphs

Given the Δ collection estimated by the Gibbs sampler, we are able to use the de novo approach to connect as many peaks as possible in each spectrum at every charge state of interest. On each spectrum and for each charge state, we record all connected components.

From this collection of graphs, we would like to find large connected components that are isomorphic to one another (i.e., one graph is the same as the other, but with renamed vertices); however, graph isomorphism is a difficult problem: although it is not known if it is NP-complete, it is thought to be recalcitrant enough to be employed in cryptography.²¹

For this reason, finding large, recurring structures in the de novo graphs appears difficult. This is made more difficult if we generalize to the optimization variant in which we find the largest isomorphic subgraphs of each graph rather than scoring each as “isomorphic” or “not isomorphic”.

Finding Graph Isomorphism with Cross-Correlation of Subspectra.

Fortunately, the graphs that we are using have a metric property in which distances are preserved. For instance, if a graph connects peaks at 2, 6, and 9 Th, then any isomorphic graph must connect peaks of the form xTh, (x + 4)Th, and (x + 7)Th (e.g., 90, 94, and 97 Th). For this reason, we can use the cross-correlation of the subspectra (i.e., the peaks that correspond to nodes in our graph) to discover the largest isomorphic subgraph. The cross-correlation shifts the two subspectra over one another and computes the dot product at each shift. The shift that produces the maximum dot product solves for x, and the peaks that align at that shift indicate corresponding nodes in the two subgraphs.

Using this approach, we can efficiently score pairs of connected components for similarity.

Locality-Sensitive Hashing Approach to Clustering Subgraphs.

We could use this cross-correlation approach to find the largest isomorphic subgraphs on all pairs of connected components found in all spectra; however, the runtime of this would be quadratic in the total number of connected components found (and this would be far more than quadratic in the number of spectra); this is not efficient enough to be applied to many spectra.

For this reason, we generalize locality-sensitive hashing (LSH) to find subspectra that have a high maximum value in the cross-correlation. (The maximum value of the cross-correlation is the measure of subgraph isomorphism described immediately above.)

LSH encodes objects (i.e., subspectra) as large vectors by binning them by m/z. The probability that a random plane cuts between two such vectors is $1-\frac{\psi }{\pi }$, where ψ is the angle between the two vectors;^22,23 therefore, by applying a random plane to an object, we get 1 bit of information for that object (e.g., a 0 is encoded by being on the negative side of the vector normal to the plane, and a 1 is encoded by being on the positive side of the vector normal to the plane). We can apply this procedure b times, thereby producing a b-length bitstring label for each object and thus binning each object into one of 2^b bins. If several planes are applied, then there is only a small probability that two dissimilar objects would reach the same bin. This has recently been applied to clustering mass spectra.²⁴

This standard LSH approach to clustering mass spectra cannot be applied in our case because we do not know the shift between a pair of subspectra that would allow them to align and produce a high dot product; LSH does not work in this case.

We introduce a means by which we can cluster spectra that allows spectra to be placed into a similar bin even when they are shifted. Given a vector a (from binning a spectrum) and a vector b (from binning a second spectrum) where both have length n, we note the value of index k for each discrete Fourier transform (DFT)

$$A_k=\sum _{i=0}^{n-1}{a}_i\cdot {\text{e}}^{-i\cdot k\cdot (2\pi /n)\sqrt{-1}}$$

$$B_k=\sum _{i=0}^{n-1}{b}_i\cdot {\text{e}}^{-i\cdot k\cdot (2\pi /n)\sqrt{-1}}$$

We note that a ≡ b; that is, a is equivalent to b up to rotation if $\exists u:a_{(i+u)\mathrm{mod}n}=b_i$. Thus we have

$$B_k=\sum _{i=0}^{n-1}{a}_{(i+u)\mathrm{mod}n}\cdot {\text{e}}^{-i\cdot k\cdot (2\pi /n)\sqrt{-1}}$$

$$=\sum _{i=0}^{n-1}{a}_i\cdot {\text{e}}^{-(i-u)\cdot k\cdot (2\pi /n)\sqrt{-1}}$$

because we can equivalently shift the a_i terms forward or the ${\text{e}}^{-i\cdot k\cdot (2\pi /n)\sqrt{-1}}$ terms backward by u. Thus

$$\begin{gathered} B_k=\sum _{i=0}^{n-1}{a}_{(i+u)\mathrm{mod}n}\cdot {\text{e}}^{-i\cdot k\cdot (2\pi /n)\sqrt{-1}}\cdot {\text{e}}^{u\cdot k\cdot (2\pi /n)\sqrt{-1}} \\ =A_k\cdot {\text{e}}^{u\cdot k\cdot (2\pi /n)\sqrt{-1}} \end{gathered}$$

That is, rotating a sequence will simply change the phases of each index of the DFT.

If we ignore the phase of each term in the DFT (using the magnitudes |A_k| and |B_k| at each index, known in signal processing as the “power spectra”), then two objects that are identical up to rotation must look identical.

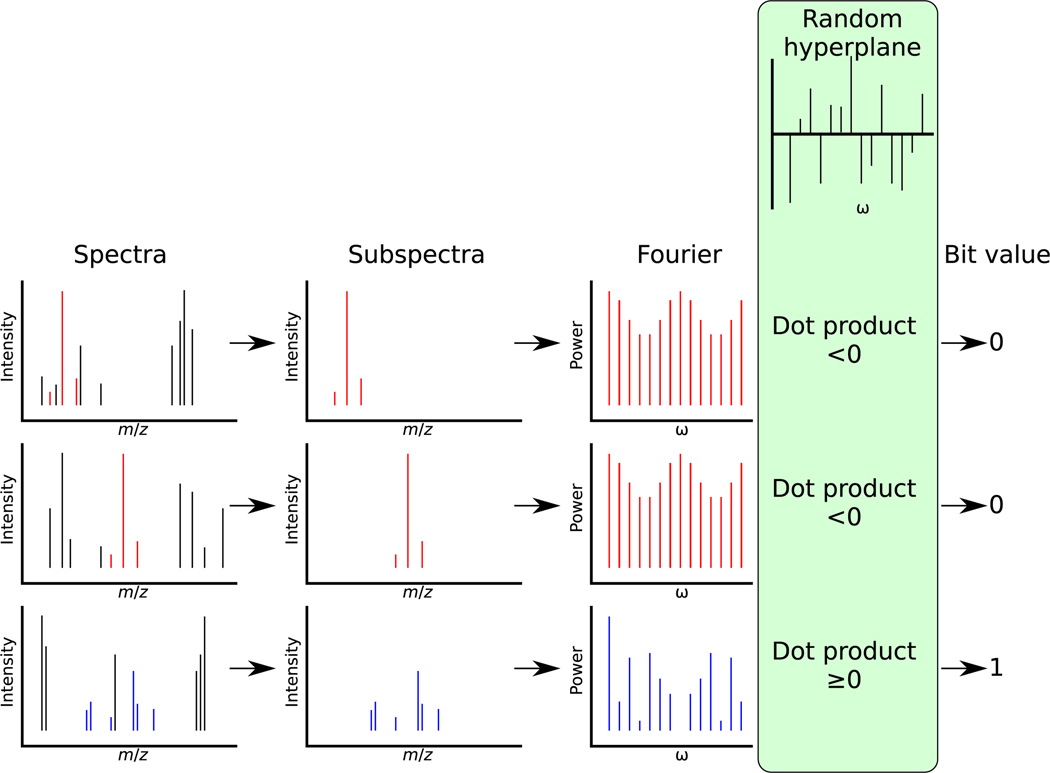
Thus, we use FFT²⁵ to create the power spectrum of each subspectrum derived from a connected component and then use LSH to bin similar power spectra. Bins that contain subspectra coming from many large connected graphs are indicative of de novo results that are likely reproduced in multiple spectra and multiple charge states. These recurring subgraphs give insight into common chemical structures found with the inferred alphabet Δ (Figure 2).

Figure 2.

LSH approach to finding similar subgraphs. In the left column, three spectra are shown with the subspectra (shown in color), which are peaks contained in a connected component produced by building the graph with the estimated mass alphabet Δ. The second column shows only those peaks in the subspectrum. The third column shows the absolute values of the DFTs of the subspectra. Each of these power spectra is dot-producted with a random hyperplane, and the sign of the resulting value is used to produce a single bit. When two connected components have large subgraphs isomorphic to one another, their subspectra must be shifted versions of each other, and thus their power spectra must be nearly identical. Two subspectra drawn (first and second rows) are similar in this manner, producing similar power spectra and thus a low probability of being separated by a random hyperplane. Repeating this process with several different random hyperplanes and concatenating the bits produces a hash, which has a high probability of binning together connected components that have substantial subgraph isomorphism.

Importantly, the cost of running the above procedure (ignoring the cost of performing the FFT for each subspectrum corresponding to a connected component) will be linear in the number of connected components investigated, an improvement from many quadratically computationally difficult graph isomorphism problems.

RESULTS

The values in the results are reported using five decimal places despite having machine tolerances of 0.02 and 0.05 Da. The reason for this is that we often find masses to a much higher precision. This is because if we have a set of masses that are within machine tolerance of the monoisotopic mass of water and connect at least one pair of peaks in a spectrum, then the distribution of the masses in the set should center around the true monoisotopic mass of water. For example, in the alphabet for the 62 expert-curated spectra which uses Є = 0.02 Da, we find water at a mass of 18.01068 Da, which is 0.000115 Da from the monoisotopic mass of water, and we find a mass of 30.01058 Da, which is accurate for the value of a serine/glycine substitution, 30.010565 Da, to four digits.²⁶

Ranking Masses in Δ

Tables 3 and 4 show the rankings of masses in alphabets for the 62 glycoconjugate spectra and 1891 glycoprotein spectra, respectively. In both instances, the Gibbs sampler was ran for 16 000 iterations. Taking into account the alphabet sizes for the two tables (8 and 16, respectively), you can see which masses were highly desirable. With some masses in almost every iteration, they must have been proposed early; this shows why having a great proposal function is crucial. These rankings are saved to file before the mapping to the canonical mass step.

Table 3.

Results from Ranking Masses in Δ for 62 Glycoconjugate Spectra^a

rank	Δ	frequency	label
1	42.01047	16000
2	84.02204	16000
3	188.01611	16000
4	130.00746	15997
5	0.98410	15953	neutron/deamidation
6	18.00746	15952	water
7	162.04746	15905	hexose
8	94.03555	15894

^aRankings of the masses by frequency of presence in Δ. The higher the frequency, the more times this mass (or a mass within Є of it) was included in the alphabet. This was run with Є = 0.02 Da and d = 8.

Table 4.

Results from Ranking Masses in Δ for 1891 Glycoprotein Spectra^a

rank	Δ	frequency	label
1	162.05000	16000	hexose
2	228.07500	15997	2× N
3	0.98210	15996	neutron/deamidation
4	18.01130	15986	water
5	42.00810	15909
6	30.02500	15899
7	180.06330	15756
8	57.00000	15721	G
9	23.00420	15692
10	144.06510	15650
11	790.37500	15648
12	202.10000	15590
13	17.01790	15569
14	720.25740	13857
15	2.07260	9725
16	839.37500	8935

^aRankings of the masses by frequency of presence in Δ. The higher the frequency, the more times this mass (or a mass within Є of it) was included in the alphabet. This was run with Є = 0.05 Da and d = 16.

Efficiency of LSH When Hashing Pairs of Similar and Dissimilar Graphs

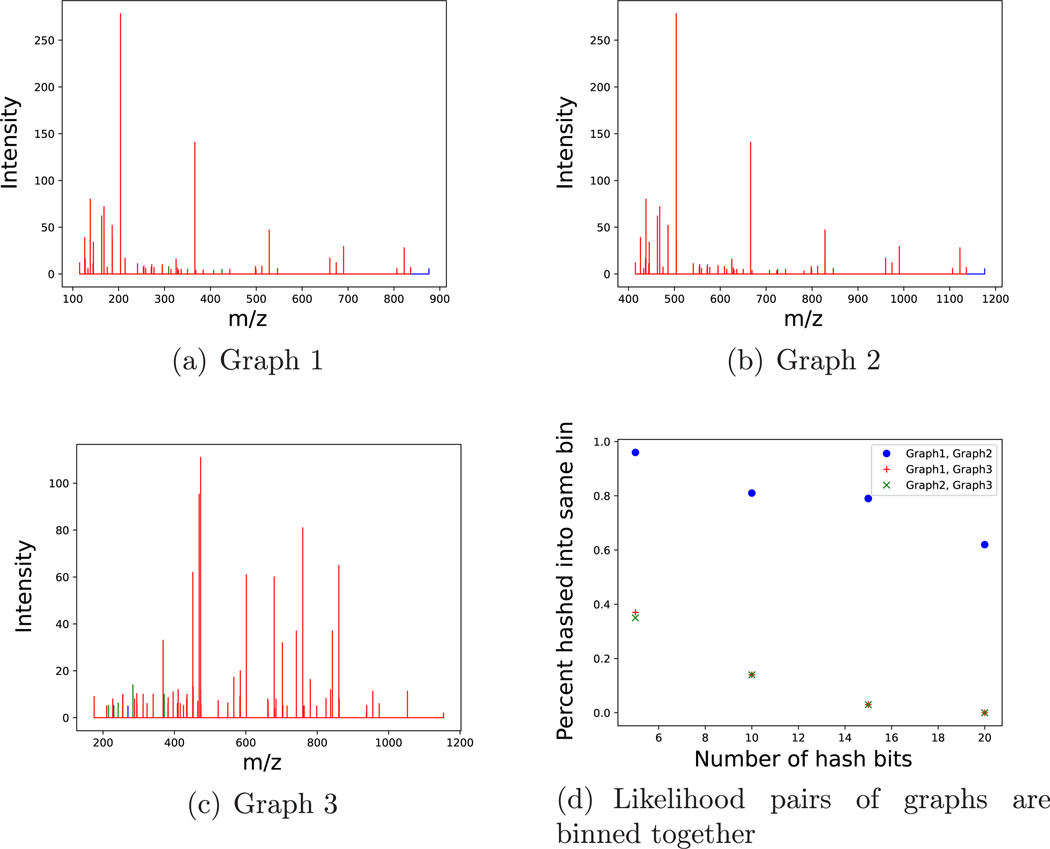
Now we look at how effective this LSH method is at putting a pair of similar but shifted graphs into the same bin versus a pair of very different graphs (Figure 3). De novo sequencing was performed on spectra taken from the 1891 glycoprotein data set with the alphabet from Table 8. The graphs are the bijective to the subspectra and are created by isolating the peaks connected by the alphabet. Graphs 1 and 2 are very similar but not exactly the same and are shifted by roughly 300 Da. Graph 3 is almost completely different from the first two. For hashes with different numbers of bits (i.e., different number of cutting planes), all pairs were binned together at different rates with the pair of similar graphs always being binned together at a significantly higher rate than any pair involving the dissimilar graph.

Figure 3.

Effectiveness of LSH on binning together pairs of similar but shifted graphs and pairs of dissimilar graphs. Three subspectra were created by applying de novo sequencing on the 1891 glycoprotein spectra with the alphabet from Table 8. (a,b) Graphs 1 and 2 are very similar subspectra (44 out of 55 similar peaks) but are shifted by roughly 300 Da. (c) Graph 3 is a very different subspectra from graphs 1 and 2. (d) Percentage of times each pair of graphs are binned together plotted versus the number of bits in each hash. In the subspectra, the different colored peaks represent being connected by Δ_k/c values of different charges.

Table 8.

Results When Running the Combinatorial Approach on 1891 Glycoconjugate Spectra with d = 16^a

mass value	manual interpretation	known a priori?	monoisotopic mass
1.02500	neutron/deamidation	yes	1.00860
1.94080
12.01713
18.00000	water	no	18.01056
30.02305
42.02500
57.00000	G	no	57.02146
96.05000
101.04583	T	no	101.04767
102.05000
113.06250	I/L	no	113.08406
114.05188	N	no	114.04292
128.06040	K/Q	no	128.09496/128.058578
162.06580	hexose	yes	162.04746
180.08750
240.10286

^aMasses are reported in ascending order and are rounded to five decimal points. Masses known a priori are labeled; these masses were not provided to the model but instead are known true-positives in advance.

Below, we look at the results from two data sets; both used 32 threads. The manually curated glycoconjugate data set has 62 spectra and was ran with Є = 0.02 Da. The horseradish peroxidase glycoprotein has 1891 spectra and was run with Є = 0.05 Da. Both data sets are available at the site listed in the “available” section. The Є values are machine-dependent and were recommended by the scientists who produced the data (Dr. Froehlich for the glycoconjugate data set and Dr. Shu and Dr. Yang for the glycoprotein data set). In each fragmentation spectrum, we remove peaks that are <1% of the maximum intensity in that spectrum.

Manually Curated Glycoconjugate Spectra from Human Urine.

Thousands of glycoconjugate spectra from human urine were manually curated by an expert to find 62 with strong evidence of glycoconjugates.⁷ A priori, four sugar residue masses (Hexose, HexNAc, dHex, and NeuAc) as well as the neutron mass (whose mass is roughly the shift to produce isotope peaks) are the only masses we expect. Note that these masses were not provided for analysis but are used only to validate the resulting masses found. A more detailed explanation of the sample preparation is available in ref 7.

Noncombinatorial results are shown with d = 8 for both the unweighted and weighted approaches (Table 5).

Table 5.

Most Frequent d = 8 Gap Pairs (i.e., m_j − m_i) on 62 Expert-Curated Glycoconjugate Spectra^a

rank	mass	molecule
1	0.99686	neutron/deamidation
2	18.00686	water
3	0.49686
4	60.01686
5	42.00686
6	162.04686	hexose
7	27.98686
8	36.01686
16	17.01686	ammonia
110	203.07686	HexNAc
923	146.06686	dHex
1765	291.09686	NeuAc
rank	mass	molecule
1	0.99686	neutron/deamidation
2	18.00686	water
3	0.49686
4	162.04686	hexose
5	60.01686
6	88.00686
7	36.01686
8	30.00686
17	17.01686	ammonia
136	203.08686	HexNAc
832	146.06686	dHex
1522	291.09686	NeuAc

^aTop table ranks using the unweighted frequency of gaps; bottom table weights each gap by the product of peak intensities p_i·p_j. Masses are rounded to five decimal points.

The combinatorial approach was run for 16 epochs per thread. Each epoch used 1000 iterations. The total real runtime of the analysis was 4 min. Combinatorial approach alphabet results are shown with d = 8 (Table 6).

Table 6.

Results When Running the Combinatorial Approach on 62 Expert-Curated Glycoconjugate Spectra with d = 8^a

mass value	manual interpretation	known a priori?	monoisotopic mass
1.00328	neutron	yes	1.00860
17.00746	ammonia	no	17.02655
18.01068	water	no	18.01057
30.01058
42.01071
88.01555
162.04746	hexose	yes	162.05282
203.06746	HexNAc	yes	203.07943

^aBecause the combinatorial approach assigns no ranks to the masses, they are reported in ascending order. Masses are rounded to five decimal points. Masses known a priori are labeled; these masses were not provided to the model but instead are known true-positives in advance.

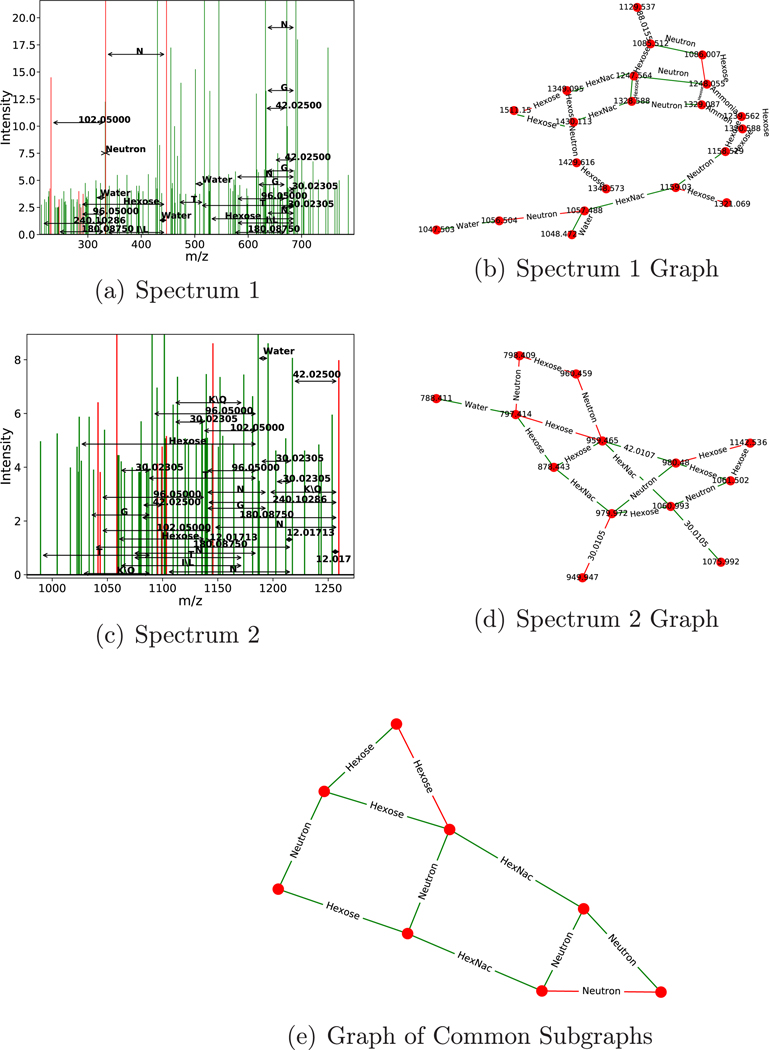
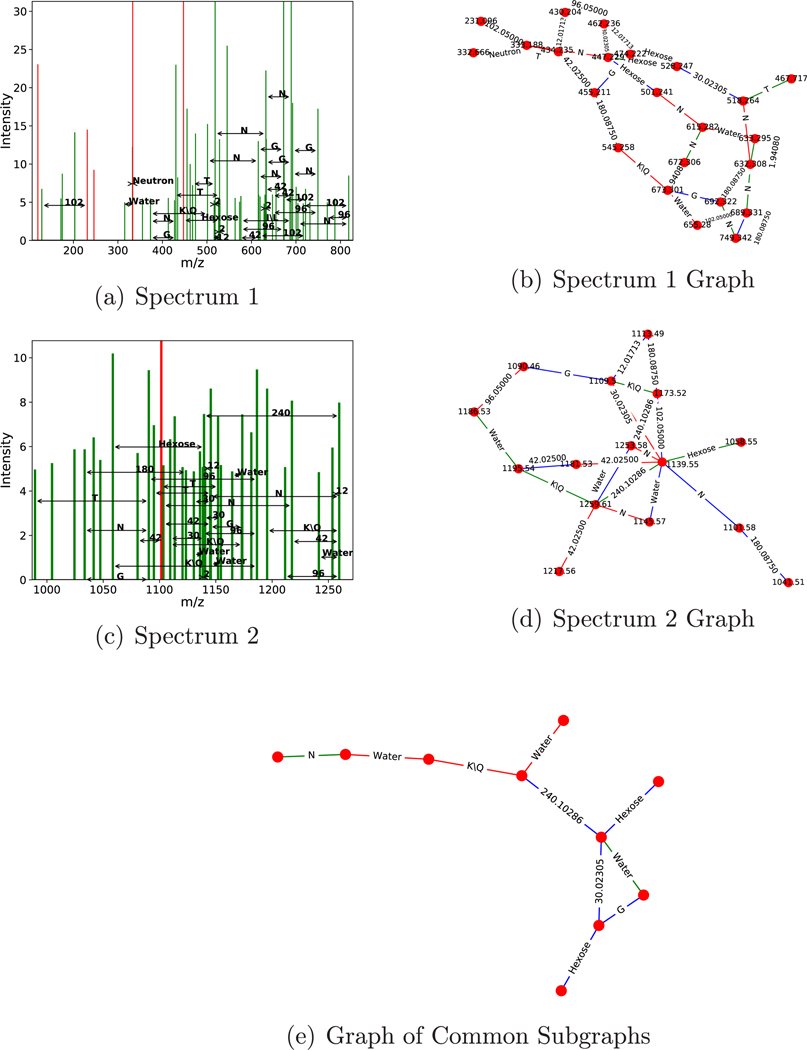
Examples of recurring structures found using LSH with the d = 8 alphabet projection (i.e., the alphabet reported in Table 6) are shown in Figure 4.

Figure 4.

Example similar subgraph pair found using LSH on results from 62 expert-curated glycoconjugate spectra. Two spectra (a,c) and their corresponding de novo graphs (b,d) found using the combinatorial approach. Spectra are drawn with peaks used in the graph colored red and unused peaks colored green. LSH is used to find this matching pair, and fast convolution finds the largest isomorphic subgraph in the pair (e). A minimal number of peaks were removed from panels b and d for legibility. The top subspectrum is from “120810_JF_HNU142_16.5710.5710.3”, and the bottom is from “120810_JF_HNU142_16.6444.6444.4”.

Horseradish Peroxidase Glycoprotein Standard Spectra.

Glycoprotein stain (Pierce Glycoprotein Staining Kit, catalog number 24562) containing horseradish peroxidase (UniProt accession P00433²⁷) was analyzed on an ABSciex Triple TOF 5600+ apparatus, producing 1891 fragmentation spectra (similar to ref 28).

The data were provided and processed blind without knowledge of their sample origins, only that sugars were present; like the 62 curated spectra, these sugars were not used in the analysis, only in the validation of the results. Thus like the first data set, the only a priori expected masses are of four common sugar residues (Hexose, HexNAc, dHex, and NeuAc) as well as the neutron mass. It is important to note that the presence of amino acids was not expected.

Noncombinatorial results are shown with d = 16 for both the unweighted and weighted (Table 7) approaches.

Table 7.

Most Frequent d = 16 Gap Pairs (i.e., m_j − m_i) on 1891 Glycoprotein Standard Spectra^a

rank	mass	molecule
1	18.00000	water
2	0.02500
3	0.97500	neutron/deamidation
4	113.07500	I/L
5	203.07500	HexNAc
6	17.02500	ammonia
7	17.00000	ammonia
8	1.00000	neutron/deamidation
9	0.05000
10	101.02500	T
11	0.00000
12	18.02500	water
13	17.97500	water
14	27.97499
15	113.05000	I/L
16	203.05000	HexNAc
18	162.05000	Hexose
54	146.05000	dHex
914	291.12500	NeuAc
rank	mass	molecule
1	18.00000	water
2	0.02500
3	203.07500	HexNac
4	113.07500	I/L
5	0.97500	neutron/deamidation
6	17.02500	ammonia
7	0.00000
8	17.00000	ammonia
9	0.05000
10	162.05000	hexose
11	101.02500	T
12	35.99999
13	1.00000	neutron/deamidation
14	203.05000	HexNac
15	41.02499
16	17.97500	water
53	146.05000	dHex
1112	291.10500	NeuAc

^aTop table ranks using the unweighted frequency of gaps; bottom table weights each gap by the product of peak intensities p_i·p_j. Masses are rounded to five decimal points.

The amino acids found with the d = 16 alphabet projection (i.e., the alphabet reported in Table 8) are G, T, I/L, N, and K/Q. (K and Q are listed together because the machine’s Є is too large to differentiate between the two for the mass found.) These amino acids can form a chain, LNGNL, which are the 241st through 245th amino acids in the peptide sequence. This includes the glycosylation site at the 244th amino acid (the second asparagine in LNGNL) in the sequence.²⁷ The amino acid chain TLNTT can also be produced from the alphabet. This chain covers the 226th through the 230th amino acids in the peptide sequence, which includes another glycosylation site that occurs at the 228th amino acid in the peptide sequence.

The weighted noncombinatorial approach, which found more amino acids than the unweighted noncombinatorial approach, was only able to find I/L, T, and A. Because of the lack of asparagine found by either noncombinatorial approach, neither one is able to build an amino acid chain that covers any of the glycosylation sites for this peptide.

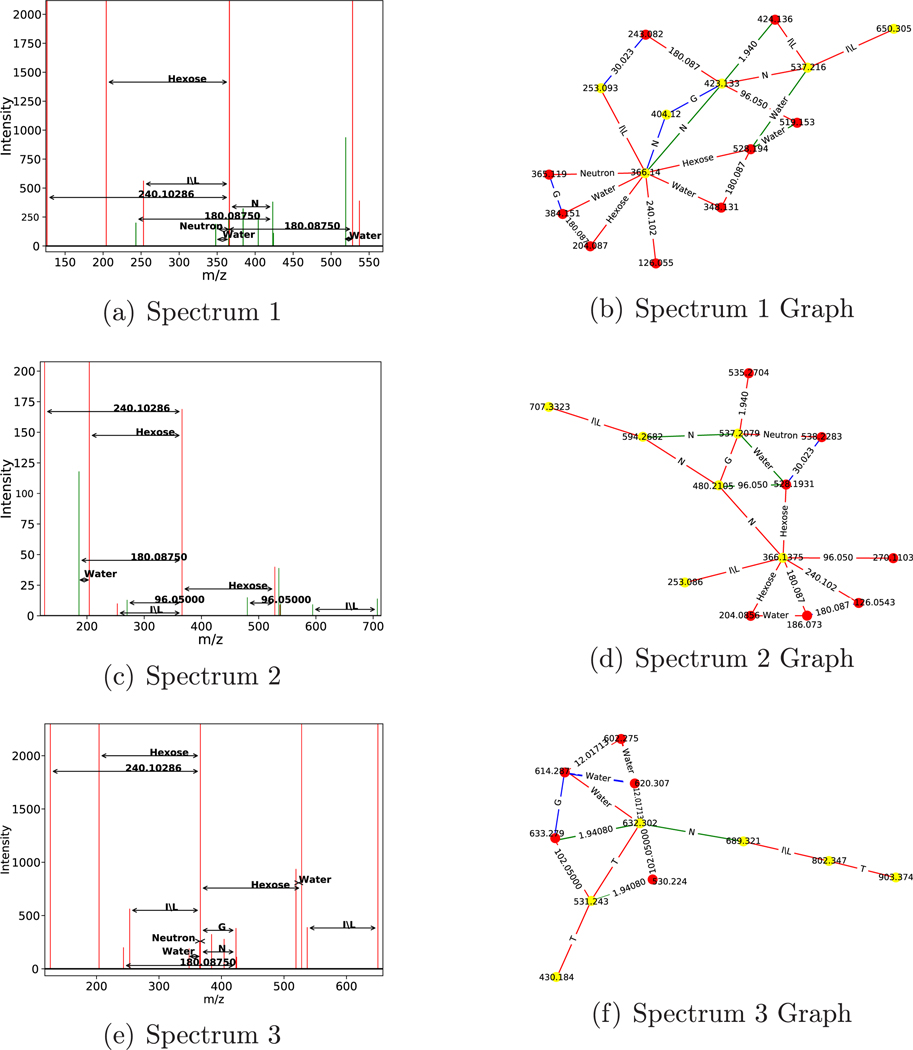
Examples of recurring structures found using LSH with the d = 16 are shown in Figure 5.

Figure 5.

Example similar subgraph pair found using LSH on results from 1891 glycoprotein standard spectra. Two spectra (a,c) and their corresponding de novo graphs (b,d) found using the combinatorial approach. Spectra are drawn with peaks used in the graph colored red and unused peaks colored green. LSH is used to find this matching pair, and fast convolution finds the largest isomorphic subgraph in the pair (e). Some peaks were removed from panels b and d for legibility. The top subspectrum is from “Locus:1.1.1.2518.2” and the bottom is from “Locus:1.1.1.8343.2”.

Examples of two subspectra, from two different spectra, and their connected de novo graphs, which include the amino acid chain LNGNL, are shown in Figure 6.

Figure 6.

Subgraphs with an amino acid chain matching glycosylation sites. Three spectra (a,c,e) and their corresponding de novo graphs (b,d,f) found using the combinatorial approach. The top two spectra contain the amino acid chain LNGNL, and the bottom contains the amino acid chain TLNTT. Graphs use red edges to mark charge z = 1, green edges to mark z = 2, and blue edges to mark z = 3. The nodes colored yellow represent nodes touched by the amino acid chain. Panels a and b came from spectrum titled “Locus:1.1.1.8405.3”. Panels c and d came from spectrum titled “Locus:1.1.1.8036.2”. Panels e and f came from “Locus:1.1.1.2523.2”.

The combinatorial approach was run for 16 epochs per thread. Each epoch used 1000 iterations. The total real runtime of the analysis was 4 h for d = 16 and 10.6 h for d = 64. The acceptance rate eventually decays, and similar results may be achievable with lower runtimes.

DISCUSSION

Alphabets Found with the Combinatorial Approach

Alphabet for 62 Expert-Curated Spectra Including Neutron, Water, Sugars, and More.

Even though no masses or chemical knowledge was provided to the combinatorial approach and we only expected four sugar resides and the neutron mass in advance, our approach finds masses close to water and ammonia in the 62 expert-curated spectra. The mass we do find that is within Є of the mass of a neutron is also within Є of the mass difference caused by deamidation. Deamidation is a modification to amino acids where a nitrogen and a hydrogen are replaced by an oxygen with a mass difference of 0.984 Da. These are both plausible, particularly because these data came from a urine sample. We also find masses close to hexose and to HexNAc in these data. Whereas the noncombinatorial approach does not assign a high rank to HexNAc, the combinatorial approach finds it with d = 8 because the connectivity improvement of HexNAc is superior enough to justify its low frequency and incidence to low-intensity peaks. Interestingly, we also find a mass at 88.01555 Da. This matches the difference between several pairs of saccharide oxonium ions:²⁹ Neu5Ac (292.103 Da) – HexNAc⁺ (204.087 Da) = 88.0162 Da; [Neu5Ac–H₂O]⁺ (274.092 Da) – [HexNAc–H₂O]⁺ (186.076 Da) = 88.0159 Da. Those are instances where the alphabet mass connects two whole glycan oxonium ions, but it also connects [HexNAc–2H₂O]⁺ (168.066 Da) to 256.082 Da and [HexNAc–C₂H₄O₂]⁺ to 232.081 Da. It appears that Neu5Ac generates a series of oxonium ions 292.103, 274.092, 256.082, and 232.081 Da. The second and third result from the loss of a water molecule, and the last results from the loss of two carbons. HexNAc generates series of oxonium ions 204.087, 186.076, 168.066, and 144.065 Da. Similar to Neu5Ac, the first two mass shifts are due to the loss of water molecules, and the final shift is due to the loss of two carbon atoms.

The other two unknown masses are 30.01058 and 42.01071 Da. 30.01058 Da is very close to the isotopic mass of H₂CO, 30.010565 Da. There are a few different things that can create a mass equal to H₂CO: the molecule hydroxymethyl, an alanine and glycine substitution, a glycine and serine substitution, or a formaldehyde-induced modification.²⁶

Similar to 30.010565 Da, there are a few known modifications that could create the 42.01071 Da mass: a glutamic acid and serine substitution or acetylation.²⁶ Similar to 88.01555 Da, there may be other analytes or differences between two other mass changes that form 30.010565 and 42.01071 Da.

Alphabet for 1891 Glycoprotein Standard Spectra Including Neutron, Amino Acids, Sugars, and More.

On the 1891 glycoprotein standard spectra, our approach discovers multiple amino acid masses without prior knowledge that are in the samples containing peptides. For d = 16, the combinatorial approach found glycine, arginine, and one or both of lysine/glutamine when neither noncombinatorial approach did. However, the weighted noncombinatorial approach found alanine, which the combinatorial approach did not find. Both the combinatorial and noncombinatorial approaches found isoleucine/leucine and threonine.

The fact that the combinatorial approach finds glycine and arginine is important because the amino acids in the alphabet can form the chains LNGNL and TLNTT. LNGNL covers the 241st through 245th amino acids in the peptide sequence, which includes the glycosylation site at the 244th amino acid (the second asparagine in LNGNL) in the sequence.²⁷ Similarly, TLNTT covers the 226th through the 230th amino acids in the peptide sequence, which includes another glycosylation site occurring at the 228th amino acid in the peptide sequence.

Both the 30.02305 and 42.02500 Da mass differences are within Є of the mass differences discussed in the previous section, so all possible explanations of those mass differences apply here as well. Similar to the alphabet for the 62 expert-curated spectra, the mass found that is within Є of a neutron mass is also within Є of deamidation.

Future Improvements.

Possible improvements to the model include parametrizing a penalty on masses too close to one another or even triplets of masses where Δ₁ ≈ Δ₂ + Δ₃. The user could supply a list of peaks in which the program should favor or be forced to connect, such as a precursor peak.

Because the method allows for us to seed the initial masses from the combinatorial approach, there will probably be a benefit to seeding them with the results of the noncombinatorial approach or to seeding them with available prior knowledge (i.e., the neutron mass and the four sugar residues) or with any masses known to be in the sample a priori.

Neither data set was charge deconvolved. However, charge deconvolution would allow the graph-building method to only connect peaks by $\frac{{\mathrm{\Delta }}_k}{z}$ when the two peaks have a charge equal to z.

An approach to making our method semisupervised could be as follows: First, run the program as it currently is to get an original alphabet. Second, try and find a known molecule in the alphabet (i.e., through mass decomposition) and populate a new alphabet with a family of molecules based on this known molecule. For example, if you blindly find an amino acid, then rerun the program with an alphabet larger than 21, seeding the first 21 with the amino acid masses. (Use the “-f” flag to protect the seeded alphabet masses.) Similarly, if you blindly find a sugar, then rerun the program while seeding the alphabet with sugar masses. This could be particularly useful for finding something like a post-translational modification on a peptide once an original alphabet containing amino acids is found.

Recurring Subgraphs

By finding an alphabet Δ and subgraphs that have a high degree of isomorphism to one another (Figures 4 and 6), we find results consistent with standard sugar trees.⁷ Because we expect a good alphabet Δ to produce connected components from different spectra with large isomorphic subgraphs, it may be possible to invert this notion: By first clustering spectra that have similar peaks (up to mass shifts), we could possibly use those clustered spectra to help estimate the alphabet Δ.

The convolutional/LSH approach proposed here may also be used to find spectra containing graphs with graph products.⁹ This may be useful for inferring chemical structure from the graphs built in this paper.