Abstract
Background
To establish a prediction model for cardiovascular diseases (CVD) in the general population based on random forests.
Methods
A retrospective study involving 498 subjects was conducted in Xi'an Medical University between 2011 and 2018. The random forest algorithm was used to screen out the variables that greatly affected the CVD prediction and to establish a prediction model. The important variables were included in the multifactorial logistic regression analysis. The area under the curve (AUC) was compared between logistic regression model and random forest model.
Results
The random forest model revealed the variables, including the age, body mass index (BMI), fasting blood glucose (FBG), diastolic blood pressure (DBP), triglyceride (TG), systolic blood pressure (SBP), total cholesterol (TC), waist circumference, and high‐density lipoprotein‐cholesterol (HDL‐C), were more significant for CVD prediction; the AUC was 0.802 in CVD prediction. Multifactorial logistic regression analysis indicated that the risk factors for CVD included the age [odds ratio (OR): 1.14, 95% confidence intervals (CI): 1.10‐1.17, P < .001], BMI (OR: 1.13, 95% CI: 1.06‐1.20, P < .001), TG (OR: 1.11, 95% CI: 1.02‐1.22, P = .023), and DBP (OR: 1.04, 95% CI: 1.02‐1.06, P = .001); the AUC was 0.843 in CVD prediction. The established logistic regression prediction model was Logit P = Log[P/(1 − P)] = −11.47 + 0.13 × age + 0.12 × BMI + 0.11 × TG + 0.04 × DBP; P = 1/[1 + exp(−Logit P)]. People were prone to develop CVD at the time of P > .51.
Conclusions
A prediction model for CVD is developed in the general population based on random forests, which provides a simple tool for the early prediction of CVD.
Keywords: cardiovascular disease, prediction model, random forest, risk factors
1. INTRODUCTION
Cardiovascular diseases (CVD) have been always the most common cause of morbidity and mortality worldwide. In 2013, 17.3 million people were estimated to die of CVD among 54 million total deaths, approximately accounting for 31.5% of all global deaths. 1 With economic growth, the prevalence of CVD is increasing obviously in developing countries. In 2016, there were about 4.34 million deaths from CVD in China, including 2.01 million deaths due to stroke and 1.74 million deaths due to coronary heart disease (CHD). 2 , 3 Early detection of CVD phenotypes and effective interventions is conductive to slowing the progression, during which CVD risk assessment and stratification play important roles. 4
Cardiovascular diseases risk assessment is not only an essential method of screening high‐risk CVD individuals, but also an important evidence of individualized therapeutic regimens formulated by clinicians. At present, several CVD risk prediction models have been developed, including Framingham risk model, 5 SCORE project, 6 QRISK model, 7 and pooled cohort equation, 8 which all belong to 10‐year risk assessment models of major CVDs in European and American countries. 3 According to the well‐established risk factors, the standard CVD risk prediction models can predict the future risk of CVD and make an unambiguous assumption that each risk factor is associated with CVD outcomes in a linear manner. 9 However, these models may oversimplify the complicated relationships involving a lot of risk factors without linear interactions. 10 Additionally, multiple versions of Framingham models are reported to overpredict the incidence of CHD, 11 , 12 , 13 and Framingham CVD model is poor in the calibration of the end point of major CVD. 14 There are also evidences suggesting that ORISK2 based on ORISK model is continuously undated to include additional risk factors like extension of age range, type 2 diabetes mellitus, and type 1 diabetes mellitus. 15 , 16 Therefore, it is necessary to investigate an approach that can integrate various risk factors better and confirm more accurate associations between outcomes and risk factors.
The random forest, a key data mining method in the field of machine‐learning that depends on a computer to learn all the complicated and non‐linear interactions among variables through minimization of errors between observed and predicted outcomes, 17 can achieve a higher accuracy in the disease prediction by using bootstrap aggregation and randomization of predictors. 18 , 19 , 20 , 21 Until now, there are few studies on the application of random forests to predict CVD risks in the general population. Therefore, this study was performed to establish a prediction model for CVD in the general population based on random forests.
2. METHODS
2.1. Study population
This study was conducted in Xi'an Medical University between 2011 and 2018, and a total of 498 subjects undergoing a physical examination were involved. All the subjects had complete physical examination data and could move by themselves; those staying in bed and those with CVD were excluded. The included subjects voluntarily participated in the study and were informed consent.
2.2. Data collection
A medical examination questionnaire was designed to obtain the basic information of subjects, including the age, gender, history of various diseases, and smoking. The body height, body weight, blood pressure, and waist circumference were achieved by the physical examination. The body mass index (BMI) was calculated based on the formula of the body weight in kilograms/body height in meters squared. Laboratory indicators included fasting blood glucose (FBG), total cholesterol (TC), triglycerides (TG), low‐density lipoprotein‐cholesterol (LDL‐C), and high‐density lipoprotein‐cholesterol (HDL‐C). The levels of FBG and blood lipids were detected in the next morning after an overnight of at least 8 hours though blood sampling.
2.3. Outcomes
The occurrence of a fatal or non‐fatal cardiovascular event was considered as the primary outcome. The outcome was based on the follow‐up results and was confirmed according to international classification of diseases‐10 (ICD‐10) diagnosis codes, especially I20‐I25 for coronary (ischemic) heart conditions and I60‐I69 for cerebrovascular conditions. 22
2.4. Statistical analysis
STATA 14.0 software (Stata Corporation) and R software (version 3.6.1) were used to analyze the data. The data with normal distribution were presented with the mean ± standard deviation ( ± s) by t test, whereas those with abnormal distribution were described with the median and quartile [M(Q1, Q3)] using Mann‐Whitney U rank‐sum test. The enumeration data were manifested as n (%) by chi‐square test or Fisher's exact test. P < .05 was considered statistically significant.
The random forest was a collection of various decision tree models. 23 Each tree was developed from bootstrap samples in the training dataset, and the randomly selected best subset of explanatory variables or features was used to split each node. In the forest, the class predictions produced by each tree were assembled and the model prediction was finally determined according to the majority vote. 24 Random allocation was used to assess the random forest prediction model; namely, the samples were randomly assigned into the nonoverlapping training samples for establishing the prediction model and testing samples for calculating the sensitivity, specificity, accuracy, positive predictive value, and negative predictive value of prediction models. The importance of variables could be reflected by the mean decreased Gini (MDG) index in random forest output results. The greater the MDG index, the more significant the variable. In this study, the random forest analysis was performed using R software, and the random forest algorithm was used to screen out the variables that greatly affected the CVD prediction and to establish a prediction model. Then, the screened important variables were included in the multifactorial logistic regression analysis. Stepwise method was used to screen the variables. The receiver operating characteristic (ROC) curve was drawn using CVD probability in the subjects of testing dataset and their physical examination results, and the area under the curve (AUC) of logistic regression model was compared with that of random forest model using Z test.
3. RESULTS
3.1. Selection and basic characteristics of study population
Totally, 1809 people underwent a physical examination, in which 307 cases of CVD were excluded. Among the rest 1502 people, 247 cases of CVD found by the physical examination were set as the case group, and then, 20% (n = 251) of 1255 people without CVD were randomly selected as the control group. A total of 498 subjects were finally included in this study. They were 22‐60 years old, with the mean age of (42.39 ± 9.33) years; their BMI was 16.50‐43.00 kg/m2, with the mean BMI of (24.12 ± 3.73) kg/m2. These subjects were randomly divided into the training set (n = 335) and testing set (n = 163). As shown in Table 1, no significant differences were shown between the training set and testing set regarding the basic characteristics of samples (P > .05). Additionally, the basic characteristics of subjects in case group and control group were compared in Table 2, and the results indicated that the differences were pronounced between two groups in the age, gender, BMI, waist circumference, FBG, SBP, DBP, TC, TG, smoking, activity level, chronic bronchitis, family history of stroke, and hypertension (P < .05).
Table 1.
The basic characteristics of samples in the training set and testing set ( ± s)/[M(Q1, Q3)]
| Variables | Training set (n = 335) | Testing set (n = 163) | χ2/t/Z | P |
|---|---|---|---|---|
| CVD (n, %) | ||||
| Yes | 169 (50.40) | 78 (47.90) | 0.29 | .587 |
| No | 166 (49.60) | 85 (52.10) | ||
| Age (y) | 42.44 ± 9.24 | 42.27 ± 9.54 | −1.89 | .850 |
| Gender (male/female) | 235 (70.10)/100 (29.90) | 121 (74.20)/42 (25.80) | 0.90 | .244 |
| BMI (kg/m2) | 23.97 ± 3.58 | 24.40 ± 4.01 | 1.15 | .248 |
| Waist circumference (cm) | 83.90 ± 14.82 | 85.25 ± 14.71 | 0.96 | .339 |
| FBG (mmol/L) | 5.02 (4.37, 5.67) | 5.00 (4.43, 5.65) | −0.02 | .986 |
| Diastolic blood pressure (DBP, mm Hg) | 80.84 ± 13.25 | 80.79 ± 11.76 | −0.04 | .967 |
| Systolic blood pressure (SBP, mm Hg) | 123.29 ± 17.69 | 123.70 ± 17.09 | 0.25 | .805 |
| TC (mmol/L) | 4.26 (3.70, 5.08) | 4.48 (3.80, 5.20) | −1.55 | .121 |
| TG (mmol/L) | 1.65 (1.10, 2.50) | 1.62 (1.10, 2.69) | −0.37 | .707 |
| HDL‐C (mmol/L) | 1.47 (1.17, 2.26) | 1.57 (1.18, 2.51) | −1.13 | .260 |
| LDL‐C (mmol/L) | 1.76 (1.23, 2.50) | 1.69 (1.20, 2.40) | 0.69 | .485 |
| Activity level | ||||
| Low | 93 (27.80) | 54 (33.10) | 2.78 | .249 |
| Middle | 193 (57.60) | 81 (49.70) | ||
| High | 49 (14.60) | 28 (17.20) | ||
| Smoking | ||||
| No | 188 (56.10) | 86 (52.80) | 0.69 | .707 |
| Smoking cessation | 27 (8.10) | 16 (9.80) | ||
| Yes | 120 (35.80) | 61 (37.40) | ||
| Stroke | ||||
| No | 332 (99.10) | 162 (98.80) | 0.12 | .728 |
| Yes | 3 (0.90) | 2 (1.20) | ||
| Pulmonary tuberculosis a | ||||
| No | 334 (99.70) | 162 (99.40) | – | .602 |
| Yes | 1 (0.30) | 1 (0.60) | ||
| Chronic bronchitis a | ||||
| No | 331 (98.80) | 162 (99.40) | – | .999 |
| Yes | 4 (1.20) | 1 (0.60) | ||
| Pneumonia a | ||||
| No | 161 (98.80) | 333 (99.40) | – | .600 |
| Yes | 2 (1.20) | 2 (0.60) | ||
| Lung cancer a | ||||
| No | 335 (100.00) | 163 (100.00) | – | .999 |
| Yes | 0 (0.00) | 0 (0.00) | ||
| Pulmonary emphysema a | ||||
| No | 334 (99.80) | 163 (100.00) | – | .999 |
| Yes | 1 (0.30) | 0 (0.00) | ||
| Family history of hypertension | ||||
| No | 222 (66.30) | 113 (69.30) | 0.46 | .495 |
| Yes | 113 (33.70) | 50 (30.70) | ||
| Family history of CHD | ||||
| No | 288 (86.00) | 137 (84.00) | 0.32 | .570 |
| Yes | 47 (14.00) | 26 (16.00) | ||
| Family history of diabetes mellitus | ||||
| No | 283 (84.50) | 140 (85.90) | 0.17 | .670 |
| Yes | 52 (15.50) | 23 (14.10) | ||
| Family history of stroke | ||||
| No | 305 (91.00) | 153 (93.90) | 1.18 | .277 |
| Yes | 30 (9.00) | 10 (6.10) | ||
| Family history of lung cancer a | ||||
| No | 159 (97.50) | 328 (97.90) | – | .755 |
| Yes | 4 (2.50) | 7 (2.10) | ||
Represented the data were analyzed by Fisher's exact test.
Table 2.
The basic characteristics of subjects in case group and control group ( ± s)/[M(Q1, Q3)]
| Variables | Case group (n = 247) | Control group (n = 251) | χ2/t/Z | P |
|---|---|---|---|---|
| Age (y) | 47.04 ± 7.87 | 37.82 ± 8.36 | 12.66 | <.001 |
| Gender (male/female) | 202 (81.78)/45 (18.20) | 154 (61.35)/97 (38.60) | 25.48 | <.001 |
| BMI (kg/m2) | 25.25 ± 3.55 | 23.01 ± 3.57 | 7.02 | <.001 |
| Waist circumference (cm) | 87.74 ± 14.19 | 81.00 ± 14.61 | 5.22 | <.001 |
| FBG (mmol/L) | 5.20 (4.64, 6.15) | 4.81 (4.26, 5.33) | 5.12 | <.001 |
| DBP (mm Hg) | 84.84 ± 13.87 | 76.87 ± 10.16 | 7.30 | <.001 |
| SBP (mm Hg) | 128.66 ± 19.36 | 118.28 ± 13.61 | 6.91 | <.001 |
| TC (mmol/L) | 4.41 (3.84, 5.25) | 4.20 (3.60, 4.93) | 2.59 | .010 |
| TG (mmol/L) | 1.93 (1.32, 3.00) | 1.40 (0.95, 2.13) | 5.48 | <.001 |
| HDL‐C (mmol/L) | 1.48 (1.15, 2.43) | 1.50 (1.19, 2.26) | −0.14 | .886 |
| LDL‐C (mmol/L) | 1.74 (1.18, 2.54) | 1.70 (1.25, 2.40) | −0.014 | .989 |
| Activity level | ||||
| Low | 74 (30.00) | 73 (29.10) | 9.55 | .008 |
| Middle | 147 (59.50) | 127 (50.60) | ||
| High | 26 (10.50) | 51 (20.30) | ||
| Smoking | ||||
| No | 110 (44.50) | 164 (65.30) | 22.11 | <.001 |
| Smoking cessation | 28 (11.30) | 15 (6.00) | ||
| Yes | 109 (44.10) | 72 (28.70) | ||
| Stroke a | ||||
| No | 243 (98.40) | 250 (99.60) | – | .213 |
| Yes | 4 (1.60) | 1 (0.40) | ||
| Pulmonary tuberculosis | ||||
| No | 246 (99.60) | 250 (99.60) | 0.00 | .991 |
| Yes | 1 (0.40) | 1 (0.40) | ||
| Chronic bronchitis | ||||
| No | 234 (94.70) | 248 (98.80) | 6.63 | .011 |
| Yes | 13 (5.30) | 3 (1.20) | ||
| Pneumonia a | ||||
| No | 246 (99.60) | 248 (98.80) | – | .624 |
| Yes | 1 (0.40) | 3 (1.20) | ||
| Lung cancer a | ||||
| No | 247 (100.00) | 251 (100.00) | – | .999 |
| Yes | 0 (0.00) | 0 (0.00) | ||
| Pulmonary emphysema a | ||||
| No | 247 (100.00) | 250 (99.60) | – | .330 |
| Yes | 0 (0.00) | 1 (0.40) | ||
| Family history of hypertension | ||||
| No | 150 (60.70) | 185 (73.70) | 9.52 | .002 |
| Yes | 97 (39.30) | 66 (26.30) | ||
| Family history of CHD | ||||
| No | 208 (84.20) | 217 (86.50) | 0.50 | .479 |
| Yes | 39 (15.80) | 34 (13.50) | ||
| Family history of diabetes mellitus | ||||
| No | 207 (83.80) | 216 (86.10) | 0.49 | .483 |
| Yes | 40 (16.20) | 35 (13.90) | ||
| Family history of stroke | ||||
| No | 220 (89.10) | 238 (94.80) | 5.58 | .018 |
| Yes | 27 (10.90) | 13 (5.20) | ||
| Family history of lung cancer a | ||||
| No | 244 (98.80) | 247 (98.40) | – | .999 |
| Yes | 3 (1.20) | 4 (1.60) | ||
Represented the data were analyzed by Fisher's exact test.
3.2. Random forest model
Totally 335 training samples were used to establish the random forest model. As indicated in Figure 1, 24 variables were ordered according to the MDG index. It was found that the variables, such as age, BMI, FBG, DBP, TG, SBP, TC, waist circumference, and HDL‐C, were more significant for CVD prediction. The random forest could better distinguish the people who would develop CVD from those who would not (Figure 2). The minimum error was 21.49% when the number of decision tree was 258 (Figure 3).
Figure 1.
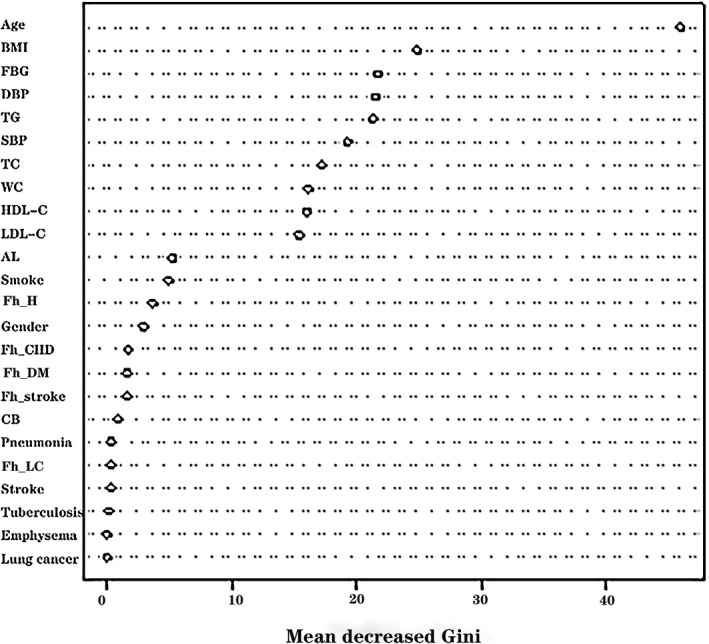
The influencing factors of cardiovascular diseases were ordered according to the mean decreased Gini index. AL, activity level; BMI, body mass index; CB, chronic bronchitis; DBP, diastolic blood pressure; FBG, fasting blood glucose; Fh_CHD, family history of coronary heart disease; Fh_DM, family history of diabetes mellitus; Fh_H, family history of hypertension; Fh_LC, family history of lung cancer; Fh_stroke, family history of stroke; HDL‐C, high‐density lipoprotein‐cholesterol; LDL‐C, low‐density lipoprotein‐cholesterol; SBP, systolic blood pressure; TC, total cholesterol; TG, triglycerides; WC, waist circumference
Figure 2.
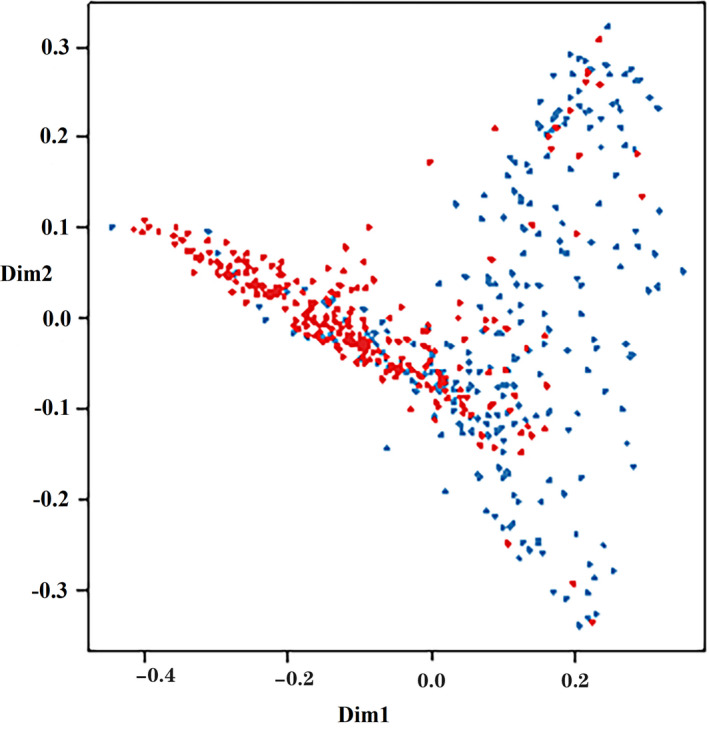
Multidimensional classification chart of the random forest. Red dot: training samples; blue dot: testing samples
Figure 3.
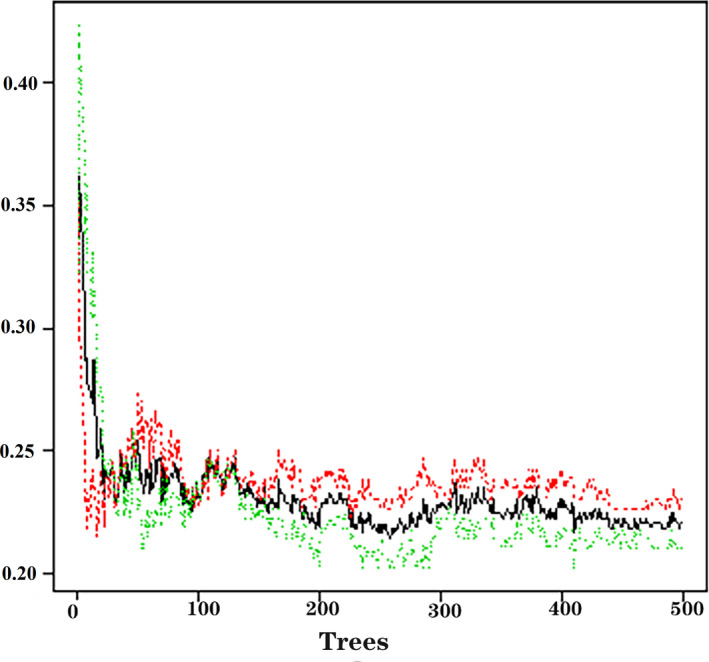
Relationship of dynamic changes between the prediction error and its 95% confidence interval of the random forest and the number of decision trees
A total of 163 testing samples were adopted to assess the efficacy of prediction model, and the results revealed that the accuracy, sensitivity, specificity, positive predictive value, and negative predictive value of prediction model were 72.89%, 78.82%, 79.23%, 73.62%, and 75.00%, respectively.
3.3. Logistic regression model
Nine variables more significant for CVD prediction in Figure 1 were involved in the multifactorial logistic regression analysis. As listed in Table 3, the risk factors for CVD included the age [odds ratio (OR): 1.14, 95% confidence intervals (CI): 1.10‐1.17, P < .001], BMI (OR: 1.13, 95% CI: 1.06‐1.20, P < .001), TG (OR: 1.11, 95% CI: 1.02‐1.22, P = .023), and DBP (OR: 1.04, 95% CI: 1.02‐1.06, P = .001).
Table 3.
Multifactorial logistic regression analysis
| Variables | OR (95% CI) | B | P |
|---|---|---|---|
| Age (y) | 1.14 (1.10‐1.17) | 0.13 | <.001 |
| BMI (kg/m2) | 1.13 (1.06‐1.20) | 0.12 | <.001 |
| TG (mmol/L) | 1.11 (1.02‐1.22) | 0.11 | .023 |
| DBP (mm Hg) | 1.04 (1.02‐1.06) | 0.04 | .001 |
The efficacy of prediction model was assessed using testing samples. It was found that the accuracy, sensitivity, specificity, positive predictive value, and negative predictive value of prediction model were 77.91%, 78.50%, 78.50%, 78.19%, and 77.65%, respectively.
3.4. Comparison of two prediction models
The AUCs of two prediction models were presented in Figure 4. In cardiovascular risk prediction, the ROC‐AUCs were 0.802 (95% CI: 0.735‐0.870, P < .001) for random forest model and 0.843 (95% CI: 0.808‐0.877, P < .001) for logistic regression model, and no statistical significance was shown (P > .05). In this study, however, the logistic regression model was chosen as a prediction model due to its supply of estimated relative risk (RR) for influencing factors. With Logit P as a dependent variable, logistic regression prediction model was established: Logit P = Log[P/(1 − P)] = −11.47 + 0.13 × age + 0.12 × BMI + 0.11 × TG + 0.04 × DBP; P = 1/[1 + exp(−Logit P)]. People were prone to develop CVD when the value of P was more than .51.
Figure 4.
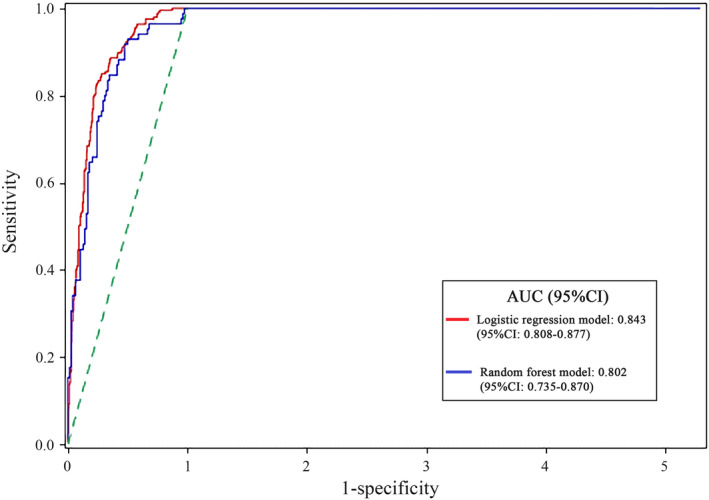
The receiver operating characteristic curves of testing samples in the two prediction models
4. DISCUSSION
In this study, we depended on random forests to establish a prediction model for CVD, and the results indicated that the random forest algorithm was effective in distinguishing the individuals who would develop CVD from those who would not. Unlike other established risk assessment methods, the random forest not confined to a small number of risk factors could incorporate all available risk factors. Additionally, the logistic regression prediction model based on the random forest was established; namely, the risk of developing CVD could be predicted according to the age, BMI, TG, and DBP, and the CVD might occur in people with the value of P > .51.
Age is perhaps the most important risk factor for the short‐term assessment of CVD. 25 With advancing age, the structure and function of vasculature change owing to increased oxidative stress, premature cellular senescence, and damage in synthesis and/or secretion of endothelium‐derived vasoactive molecules. These changes can result in the stiffening and thickening of vascular walls and other vascular complications. 26 , 27 , 28 It was estimated that 4.0% of people aged 18‐44 years had heart disease, and this prevalence increased to 11.9% in those aged 45‐64 years and 23.1% in those aged 65‐74 years, even up to 35.0% in those aged over 75 years. 29 In this study, it was found that the risk of developing CVD in the general population would increase 0.14‐folds at each addition of 1 year old.
BMI is used to classify the normal weight, overweight, and obesity, and is associated with the risk of developing CVD. 30 , 31 The age‐adjusted RR for CVD was higher in overweight people (males, RR: 1.21; females, RR: 1.20) and obese people (males, RR: 1.46; females, RR: 1.64). 32 When compared with normal‐weight adults, the overweight and obese adults had a higher level for each CVD biomarker, including C‐reactive protein, TC, TG, and LDL‐C. 33 Our results suggested that the cardiovascular risk would increase 0.13‐folds in the general population when 1 kg/m2 of BMI was added. It was reported that obesity was associated with a prothrombotic state, a proinflammatory state, atherogenic dyslipidemia, and insulin resistance, 34 , 35 which could increase the overall cardiac workload to satisfy the metabolic needs of the expanded adipose tissue by elevating the cardiac output. 36
Atherogenic dyslipidemia is associated with poor cardiovascular outcomes, which is characterized by a combination of increased TG and LDL‐C levels, lowered HDL‐C level and a dominance of small‐dense LDL‐C particles. 37 Dyslipidemia can increase the risk of developing CVD and determine the total risk of CVD in individuals through interaction with multiple risk factors. 25 At present, lowering LDL‐C level is considered as the primary therapeutic target in the management of dyslipidemia. 38 , 39 In this study, TG was presented to be an independent risk factor for CVD and played a crucial role in cardiovascular prediction, which were supported by several studies. 40 , 41 , 42 Additionally, in the population with LDL‐C level reaching the target value who received lipid‐lowering therapies, an association was present between TG and cardiovascular risk. 43 TG is transported in plasma by specific triglyceride‐rich lipoproteins (TRLs) which are thought to involve in the progression of atherosclerosis and CVD. Studies show that the variants in several key genes involved in the metabolism of TRLs have a strong correlation with CVD risk, and the strength of a variant's impact on TG level is closely associated with the degree of its effect on CVD. 44 , 45 And meanwhile, TRLs can promote the intimal cholesterol deposition and participate in activating and reinforcing some proapoptotic, proinflammatory, and procoagulant pathways. 46
A lower DBP (<70‐80 mm Hg) had a correlation with an increased risk of all‐cause death and myocardial infarction probably because of compromised coronary artery perfusion, consequently leading to cardiac ischemia. 47 In the first asymptomatic carotid surgery trial, DBP was confirmed to be the single independent risk factor related to peri‐procedural stroke or death. 48 The combined results of 9 major prospective studies demonstrated that there were continuous, positive, and independent associations of DBP with stroke and with coronary heart disease. 49 In this study, DBP was found to be a risk factor for CVD, and the risk of developing CVD would increase 0.04‐folds when 1 mm Hg of DBP was augmented.
The strengths of this study were the use of random forests to predict the risk of developing CVD in the general population. The explanatory power of predictive analytics was based on the factors included. 19 All the available risk factors were incorporated in this study via random forests, and then, important variables were screened out to establish the prediction model, which may make the predictive ability of the model more accurate. Moreover, the data required in the established prediction model could be easily obtained in clinic, which was conductive to the clinicians to promptly assess the individuals’ cardiovascular risk and implement personalized interventions for high‐risk individuals. However, the study population mainly came from the city. Inadequate population diversity may cause a poor efficacy of the established model when used in other populations.
5. CONCLUSIONS
A prediction model for CVD is developed in the general population based on random forests, which provides a simple tool for the early prediction of CVD. The risk of developing CVD can be predicted according to the individuals’ age, BMI, TG, and DBP.
AUTHOR CONTRIBUTIONS
XS and LS designed the study. XS, YYX, and ZJY drafted and wrote the manuscript. XW and PY contributed to data collection. YS and YYJ analyzed and interpreted the data. SJQ contributed to literature search. LS critically reviewed, edited, and approved the manuscript. All authors read and approved the final manuscript.
ETHICAL APPROVAL
The data in this article are from different provinces and different hospitals. It is finally compiled by a group company, so there is no ethics number when using it.
INFORMED CONSENT
Informed consent was obtained from all individual participants included in the study.
Su X, Xu Y, Tan Z, et al. Prediction for cardiovascular diseases based on laboratory data: An analysis of random forest model. J Clin Lab Anal. 2020;34:e23421 10.1002/jcla.23421
Funding information
This study was supported by Special Scientific Research Program of Department of Education of Shaanxi Province, China (Grant No. 19JK0770).
REFERENCES
- 1. Benjamin EJ, Blaha MJ, Chiuve SE, et al. Heart disease and stroke statistics‐2017 update: a report from the American heart association. Circulation. 2017;135(10):e146‐e603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Ben Abdelaziz A, Melki S, Ben Abdelaziz A, et al. Profile and evolution of the Global Burden of Morbidity in the Maghreb (Tunisia, Morocco, Algeria). The Triple burden of morbidity. Tunis Med. 2018;96(10–11):760‐773. [PubMed] [Google Scholar]
- 3. The Joint Task Force for Guideline on the assessment and management of cardiovascular risk in China. Guideline on the assessment and management of cardiovascular risk in China. Chin Circulat J. 2019;34(1):4‐28. [Google Scholar]
- 4. Cohn JN. Prevention of cardiovascular disease. Trends Cardiovasc Med. 2015;25(5):436‐442. [DOI] [PubMed] [Google Scholar]
- 5. D’Agostino RB, Vasan RS, Pencina MJ, et al. General cardiovascular risk profile for use in primary care: the Framingham Heart Study. Circulation. 2008;117(6):743‐753. [DOI] [PubMed] [Google Scholar]
- 6. Conroy RM, Pyörälä K, Fitzgerald AP, et al. Estimation of ten‐year risk of fatal cardiovascular disease in Europe: the SCORE project. Eur Heart J. 2003;24(11):987‐1003. [DOI] [PubMed] [Google Scholar]
- 7. Hippisley‐Cox J, Coupland C, Robson J, Brindle P. Derivation, validation, and evaluation of a new QRISK model to estimate lifetime risk of cardiovascular disease: cohort study using QResearch database. BMJ. 2010;341:c6624. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Goff DC, Lloyd‐Jones DM, Bennett G, et al. 2013 ACC/AHA guideline on the assessment of cardiovascular risk: a report of the American College of Cardiology/American Heart Association Task Force on Practice Guidelines. Circulation. 2014;129(25 Suppl 2):S49‐S73. [DOI] [PubMed] [Google Scholar]
- 9. Obermeyer Z, Emanuel EJ. Predicting the future – big data, machine learning, and clinical medicine. N Engl J Med. 2016;375(13):1216‐1219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Weng SF, Reps J, Kai J, Garibaldi JM, Qureshi N. Can machine‐learning improve cardiovascular risk prediction using routine clinical data? PLoS One. 2017;12(4):e0174944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Brindle P, Emberson J, Lampe F, et al. Predictive accuracy of the Framingham coronary risk score in British men: prospective cohort study. BMJ. 2003;327(7426):1267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Diverse Populations Collaborative Group . Prediction of mortality from coronary heart disease among diverse populations: is there a common predictive function? Heart. 2002;88(3):222‐228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Barroso LC, Muro EC, Herrera ND, Ochoa GF, Hueros JI, Buitrago F. Performance of the Framingham and SCORE cardiovascular risk prediction functions in a non‐diabetic population of a Spanish health care centre: a validation study. Scand J Prim Health Care. 2010;28(4):242‐248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Cook NR, Paynter NP, Eaton CB, et al. Comparison of the Framingham and Reynolds risk scores for global cardiovascular risk prediction in the multiethnic Women's Health Initiative. Circulation. 2012;125(14):1748‐1756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Collins GS, Altman DG. An independent and external validation of QRISK2 cardiovascular disease risk score: a prospective open cohort study. BMJ. 2010;340:c2442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Sharma H, Lencioni M, Narendran P. Cardiovascular disease in type 1 diabetes. Cardiovasc Endocrinol Metab. 2019;8(1):28‐34. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Dreiseitl S, Ohno‐Machado L. Logistic regression and artificial neural network classification models: a methodology review. J Biomed Inform. 2002;35(5–6):352‐359. [DOI] [PubMed] [Google Scholar]
- 18. Rigatti SJ. Random forest. J Insur Med. 2017;47(1):31‐39. [DOI] [PubMed] [Google Scholar]
- 19. Hillemacher T, Frieling H, Wilhelm J, et al. Indicators for elevated risk factors for alcohol‐withdrawal seizures: an analysis using a random forest algorithm. J Neural Transm. 2012;119(11):1449‐1453. [DOI] [PubMed] [Google Scholar]
- 20. Sarica A, Cerasa A, Quattrone A. Random forest algorithm for the classification of neuroimaging data in Alzheimer's disease: a systematic review. Front Aging Neurosci. 2017;9:329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Li Y, Ge D, Gu J, Xu F, Zhu Q, Lu C. A large cohort study identifying a novel prognosis prediction model for lung adenocarcinoma through machine learning strategies. BMC Cancer. 2019;19(1):886. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Roger VL, Go AS, Lloyd‐Jones DM, et al. Heart disease and stroke statistics–2011 update: a report from the American Heart Association. Circulation. 2011;123(4):e18‐e209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. Breiman L. Random forests. Mach Learn. 2001;45(1):5‐32. [Google Scholar]
- 24. Pavey TG, Gilson ND, Gomersall SR, Clark B, Trost SG. Field evaluation of a random forest activity classifier for wrist‐worn accelerometer data. J Sci Med Sport. 2017;20(1):75‐80. [DOI] [PubMed] [Google Scholar]
- 25. Yang X, Li J, Hu D, et al. Predicting the 10‐year risks of atherosclerotic cardiovascular disease in Chinese population: the China‐PAR project (prediction for ASCVD risk in China). Circulation. 2016;134(19):1430‐1440. [DOI] [PubMed] [Google Scholar]
- 26. Ghebre YT, Yakubov E, Wong WT, et al. Vascular aging: implications for cardiovascular disease and therapy. Transl Med. 2016;6(4). pii: 183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Minamino T, Komuro I. Vascular aging: insights from studies on cellular senescence, stem cell aging, and progeroid syndromes. Nat Clin Pract Cardiovasc Med. 2008;5(10):637‐648. [DOI] [PubMed] [Google Scholar]
- 28. Costantino S, Paneni F, Cosentino F. Ageing, metabolism and cardiovascular disease. J Physiol. 2016;594(8):2061‐2073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Centers for Disease Control and Prevention . Heart Disease. http://www.cdc.gov/nchs/fastats/heart‐disease.htm. Accessed September 15, 2019.
- 30. Zhu S, Heshka S, Wang ZM, et al. Combination of BMI and waist circumference for identifying cardiovascular risk factors in whites. Obes Res. 2004;12(4):633‐645. [DOI] [PubMed] [Google Scholar]
- 31. Zhao X, Gu J, Li M, et al. Pathway analysis of body mass index genome‐wide association study highlights risk pathways in cardiovascular disease. Sci Rep. 2015;5:13025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Wilson PW, D'Agostino RB, Sullivan L, Parise H, Kannel WB. Overweight and obesity as determinants of cardiovascular risk: the Framingham experience. Arch Intern Med. 2002;162(16):1867‐1872. [DOI] [PubMed] [Google Scholar]
- 33. Loprinzi PD, Crespo CJ, Andersen RE, Smit E. Association of body mass index with cardiovascular disease biomarkers. Am J Prev Med. 2015;48(3):338‐344. [DOI] [PubMed] [Google Scholar]
- 34. Luft VC, Schmidt MI, Pankow JS, et al. Chronic inflammation role in the obesity‐diabetes association: a case‐cohort study. Diabetol Metab Syndr. 2013;5(1):31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Emanuela F, Grazia M, de Marco R, Maria Paola L, Giorgio F, Marco B. Inflammation as a link between obesity and metabolic syndrome. J Nutr Metab. 2012;2012:476380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Blaes A, Prizment A, Koene RJ, Konety S. Cardio‐oncology related to heart failure: common risk factors between cancer and cardiovascular disease. Heart Fail Clin. 2017;13(2):367‐380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Halcox JP, Banegas JR, Roy C, et al. Prevalence and treatment of atherogenic dyslipidemia in the primary prevention of cardiovascular disease in Europe: EURIKA, a cross‐sectional observational study. BMC Cardiovasc Disord. 2017;17(1):160. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Jacobson TA, Ito MK, Maki KC, et al. National lipid association recommendations for patient‐centered management of dyslipidemia: part 1 ‐executive summary. J Clin Lipidol. 2014;8(5):473‐888. [DOI] [PubMed] [Google Scholar]
- 39. Grundy SM, Stone NJ, Bailey AL, et al. 2018 AHA/ACC/AACVPR/AAPA/ABC/ACPM/ADA/AGS/APhA/ASPC/NLA/PCNA Guideline on the Management of Blood Cholesterol: Executive Summary: A Report of the American College of Cardiology/American Heart Association Task Force on Clinical Practice Guidelines. J Am Coll Cardiol. 2019;73(24):3168‐3209. [DOI] [PubMed] [Google Scholar]
- 40. Borén J, Matikainen N, Adiels M, Taskinen MR. Postprandial hypertriglyceridemia as a coronary risk factor. Clin Chim Acta. 2014;431:131‐142. [DOI] [PubMed] [Google Scholar]
- 41. Patel A, Barzi F, Jamrozik K, et al. Serum triglycerides as a risk factor for cardiovascular diseases in the Asia‐Pacific region. Circulation. 2004;110(17):2678‐2686. [DOI] [PubMed] [Google Scholar]
- 42. Sarwar N, Danesh J, Eiriksdottir G, et al. Triglycerides and the risk of coronary heart disease: 10,158 incident cases among 262,525 participants in 29 Western prospective studies. Circulation. 2007;115(4):450‐458. [DOI] [PubMed] [Google Scholar]
- 43. Miller M, Cannon CP, Murphy SA, et al. Impact of triglyceride levels beyond low‐density lipoprotein cholesterol after acute coronary syndrome in the PROVE IT‐TIMI 22 trial. J Am Coll Cardiol. 2008;51(7):724‐730. [DOI] [PubMed] [Google Scholar]
- 44. Brahm A, Hegele RA. Hypertriglyceridemia. Nutrients. 2013;5(3):981‐1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Do R, Willer CJ, Schmidt EM, et al. Common variants associated with plasma triglycerides and risk for coronary artery disease. Nat Genet. 2013;45(11):1345‐1352. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Toth P. Triglyceride‐rich lipoproteins as a causal factor for cardiovascular disease. Vasc Health Risk Manage. 2016;12:171‐183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. Messerli FH, Mancia G, Conti CR, et al. Dogma disputed: can aggressively lowering blood pressure in hypertensive patients with coronary artery disease be dangerous? Ann Intern Med. 2006;144(12):884‐893. [DOI] [PubMed] [Google Scholar]
- 48. de Waard DD, de Borst GJ, Bulbulia R, Huibers A, Halliday A; Asymptomatic Carotid Surgery Trial‐1 Collaborative Group . Diastolic blood pressure is a risk factor for peri‐procedural stroke following carotid endarterectomy in asymptomatic patients. Eur J Vasc Endovasc Surg. 2017;53(5):626‐631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. MacMahon S, Peto R, Cutler J, et al. Blood pressure, stroke, and coronary heart disease. Part 1, prolonged differences in blood pressure: prospective observational studies corrected for the regression dilution bias. Lancet. 1990;335(8692):765‐774. [DOI] [PubMed] [Google Scholar]


