Graphical abstract
Keywords: COVID-19, Cointegration, Disease outbreaks, Market dynamics
Abstract
The COVID-19 brings back the debate about the impact of disease outbreaks in economies and financial markets. The error correction terms (ECT) and cointegration processing tools have been applied in studies for identifying possible transmission mechanisms between distinct time series. This paper adopts the vector error correction model (VECM) to investigate the dynamic coupling between the pandemics (e.g., the COVID-19, EBOLA, MERS and SARS) and the evolution of key stocks exchange indices (e.g., Dow-Jones, S&P 500, EuroStoxx, DAX, CAC, Nikkei, HSI, Kospi, S&P ASX, Nifty and Ibov). The results show that the shocks caused by the diseases significantly affected the markets. Nonetheless, except for the COVID-19, the stock exchange indices reveal a sustained and fast recovering when an identical length time window of 79 days is analyzed. In addition, our findings contribute to point a higher volatility for all financial indices during the COVID-19, a strong impact over the Ibov-Brazil and its poor recover when compared to the other indices.
1. Introduction
Pandemics such as the current COVID-19 are large-scale outbreaks of infectious diseases that can greatly increase the mortality over a wide geographic area and cause significant economic, social, and political disruption (Yamey et al., 2017, Madhav et al., 2017).
Based on evidences, experts suggest that the likelihood of pandemics occurrence has increased significantly (Jones et al., 2008, Morse et al., 2012). Issues such as global travel and integration, urbanization, land use, and intensive exploitation of the natural resources contribute significantly to stimulate this problem (Jones et al., 2008).
An epidemic can be defined as the occurrence, in a community or region, of cases of an illness. In turn, a pandemic emerges when the epidemic spreads over a very wide area, crossing international boundaries and usually affecting a large number of people (Porta, 2014).
Endemic diseases are far more common than pandemics. Nonetheless, both of them can have significant negative impact in public health and economy, with devastating effects in low- and middle-income countries (Olival et al., 2017). Mitigation measures cannot avoid significant social and economic perturbations (Fang et al., 2020, Katz et al., 2018). Further, the individual behavioral changes, such as fear-induced aversion to workplaces or other public gathering places are a primary cause of negative shocks to economic evolution during pandemics.
The main goal of this work is to investigate the bilateral relationship between the incidence of important recent disease outbreaks versus the evolution of worldwide stock exchanges indices. In what concerns pandemics we consider 4 cases, namely, the spread of the Coronavirus disease (COVID-19, 2019), Ebola virus disease (EVD, 2013), Middle East respiratory syndrome (MERS, 2012) and severe acute respiratory syndrome (SARS, 2003). With regard to financial indices we follow 11 indices namely the Dow Jones (USA), S&P 500 (USA), Euro Stoxx (Eurozone), DAX (Germany), CAC (France), Nikkei (Japan), HSI (Hong Kong), Kospi (South Korea), S&P (Australia), Nifty (India) and Ibov (Brazil). For this purpose, we adopt the Johansen cointegration test (Johansen, 2002, David et al., 2019b, Quintino et al., 2017) and the bivariate VECM (Colombage, 2009) exploited by the orthogonal impulse response (OIR) and the forecast error variance decomposition (FEVD). Additionally, in order to provide a better perspective and scope, we also evaluate the historical volatility and the recovering of the stock indices during those pandemics.
Steming this ideias the rest of the paper is organized as follows. In Section 2, a review of the literature is presented. In Section 3, the selected time series (TS) are described and the necessary mathematical and computational methods are introduced. In Section 4, the results obtained during 4 periods of outbreaks for the 11 TS are discussed. Finally, in Section 5, the main conclusions are outlined.
2. Literature review
Recently, several works focused on the relationship between the COVID-19 pandemic and its economic and financial aspects have been published in the literature (Ashraf, 2020, Conlon et al., 2020, Goodell, 2020, Goutte et al., 2020, Sharif et al., 2020, Yarovaya et al., 2020, Conlon and McGee, 2020, Shehzad et al., 2020, Goodell and Huynh, 2020). A simple statistical analysis of the impact of the COVID-19 pandemic on global financial market was explored in (Zhang et al., 2020). The findings of the (Baker et al., 2020) suggests that government restrictions on commercial activity and voluntary social distancing were the main reasons why the U.S. stock market reacted much more heavily to the COVID-19 than to the previous pandemics. An interesting global fear index was constructed and applied to stock return predictability revealing its importance for foreseeing the dynamics of stock returns during the COVID-19 pandemic (Salisu and Akanni, 2020). The global reaction of the financial markets, in terms of their poor results and volatility, as the Coronavirus epicentre moved from China to Europe and then to the US was analyzed by (Ali et al., 2020). Their findings revealed an increasing panic and quick deteriorating of the markets as the outbreak evolved from epidemic to pandemic. Lahmiri and Bekiros (2020) evaluated the impact of the COVID-19 pandemic on the randomness and volatility of the world major markets and examined the effect on their interconnections.
Studies with focus on these problems require analysing a plethora of variables (Machado and Lopes, 2020). For understanding the interconnection between such variables, we can employe multivariate analysis (Afifi et al., 2019). In this case, all variables are considered simultaneously and, consequently, their effects are not interpreted separately. Nonetheless, the multivariate analysis is a laborious task due the sheer bulk of data. One should note that is not sufficient to observe a set of variables and to apply multivariate techniques. In fact, if they are not correlated, then one has to consider the bivariate analysis to obtain more significative information. This strategy allows the association, correlation and assessement of two variables and, if properly applied, it provides solid and useful information in different applications (O’Flanagan et al., 2014, Aguiar-Conraria and Soares, 2014, David et al., 2019a, Volpi and Fiori, 2012).
Tools such as the Error Correction Models (ECM), Vector Error Correction Models (VECM) and cointegration were applied for studying pandemics and their economic impact (Cavicchioli and Pistoresi, 2019, Shi and Li, 2017, Sharifi et al., 2014, Hassouneh et al., 2012, Jiang and Liu, 2011). The Threshold Cointegration Error Correction Model (T-ECM) has been adopted mainly in term structure theory (Enders and Siklos, 2001, Gałecki and Osińska, 2019). A consistent T-ECM was also applied to investigate the non-linear adjusting process of the yield spread to its equilibrium value in response to changes in stock market volatility. The inter-relationships and the asymmetric co-movements between the yield spread, macroeconomic factors and the stock market volatility across five major world economies were studied (Evgenidis et al., 2017).
In the follow-up the data and methods adopted in this work, such as the cointegration analysis (Johansen, 2002, David et al., 2019b) and the VECM methodology (Colombage, 2009) are discussed.
3. Data and methodology
We consider the TS describing the 4 disease outbreaks and 11 key stock exchange indices. The data are available at the World Health Organization (WHO) website (https://www.who.int/) and at the Investing website (https://www.investing.com/).
We analyze the evolution of the number of cases of the 4 pandemics during first 79 days of available data versus the evolution of the financial indices during the same period. The work aims to measure the impact of the outbreaks against the indices. Fig. 1 shows the market data and the total number of cases for each of the disease outbreaks sets. In order to normalize the curves, the -score standardization is adopted (Glantz and Slinker, 2001).
Fig. 1.
The time evolution of 11 normalized financial indices and total number of cases of infection during the first 79 days of available data for the 4 outbreaks.
The stationarity of the TS are evaluated by means of the Augmented Dickey-Fuller (ADF) test (Dickey and Fuller, 1979). The presence of unit roots in a TS is detected by not rejecting the null hypothesis of the aforesaid test.
The trend, drift and constant are types of regression models that can properly identify the integration order () of a TS, that is, the number of times necessary to differentiate a TS that was originally non-stationary to become a stationary one. This is a necessary property to identify a cointegration relation between two TS (David et al., 2019b).
The cointegration process (Granger, 1981) is analyzed by means of the Johansen test (Johansen, 2002) and they are explained in the Sections 3.1 and 3.2, respectively. Whenever a cointegration relation is observed between the TS, the VECM equation (Davidson et al., 1978, Sargan, 1964) is estimated and the OIR and FEVD are analyzed.
We also calculate the historical market volatility for the 11 stock indices as the square root of the sum of squared returns over the past 79 trading days (Ederington and Guan, 2006).
3.1. Cointegration of time series
The cointegration relation between two TS was firstly introduced by Granger (Granger, 1981). Later, Engle and Granger (Engle and Granger, 1987) explored the cointegration and the error correction mainly for estimation and testing. A simple interpretation of a cointegration relation and the process of adjustment known as the error correction model was proposed by Murray (Murray, 1994). Smith et al. (Smith and Harrison, 1994) proposed an extension of the concepts by exploring the multiple cointegration with 3 or more cointegrated variables. Hereafter, in the scope of investigating the transmission process among the pandemics and stock exchanges, the cointegration hypothesis is considered.
Often, we observe some misinterpretation between the terms “cointegration” and “correlation”. Alexander (Alexander, 1999) pointed that a cointegration process takes into account both the concepts of integration and stationarity, while that is not considered in a correlation measure. Additionally, the correlation calculates a linear association between two TS. The cointegration of two or more TS can be studied, while a correlation is simply a coefficient in the range []. However, a cointegration process cannot be “quantified”, and, instead, it is “identified”.
The equilibrium error term for a TS was defined by Engle and Granger (Engle and Granger, 1987) as
| (1) |
where stands for the discrete-time sampling instants and is in the perfect equilibrium state that occurs when .
In addition, is said to be a stationary TS if its integration order is equal to 0. For each step represents the quantity needed to differentiate the TS in order to make it stationary (Murray, 1994). When a cointegration relation is revealed between two different TS such as, between and , both of them must be integrated at the same order. Thus, if , then is also true, where and are real constants and . Therefore, the error term can be rewritten as a linear combination as follows
| (2) |
This means that when , if both TS are integrated at , then the is said to be cointegrated of order zero , and the adjustment occurs for each step. However, it is possible the occurrence of some special cases, namely, , that would lead to a fractional differentiation process (David et al., 2018). In other words, this relation can also be expressed by defining the following error correction parameters and as
| (3) |
| (4) |
where and denote the cointegrated variables, and represent stationary white noise and and are the cointegration relations between the variables and , respectively.
In this work, we evaluate the cointegration process among the 4 pandemics, with respect to the 11 stock exchanges indices. The cointegration is calculated by means of the Johansen test, and the VECM is estimated when the cointegration between a particular disease with respect to the particular stock index is verified.
3.2. Vector error correction model (VECM)
The VECM is based on the generalized vector autoregression (VAR), that allows the adjustment of a regression model between multiple variables to evaluate their relationship (Davidson et al., 1978, Sargan, 1964).
Let us consider and as two non-cointegrated and non-stationary TS. The relation between these TS can be described using the VAR model of order for both variables as (Juselius, 2007)
| (5) |
| (6) |
where and are the equation autoregressive terms of and , respectively, and denote white-noise disturbances and the equation lag order . However, if the TS are not initialy stationary, then the log returns () in and can be applied in order to become stationary equations as (Cologni and Manera, 2008, Juselius, 2007):
| (7) |
Thus, the VAR() model is applied to the differences giving
| (8) |
| (9) |
If the two TS can exhibit a cointegrated relation between each other, then the Error Correction Term (ECT) represented by can be implemented and the VAR model becomes a VECM as follows (Mattos and Franco da Silveira, 2018, Baillie et al., 2002, Mahadevan and Asafu-Adjaye, 2007, Bekiros and Diks, 2008)
| (10) |
| (11) |
where and are matrices whose dimensions are , representing the TS and the cointegrated vectors, respectively. The parameters are related to the long-run equilibrium among the TS. The parameters reflect how fast the series tend to return the equilibrium after some perturbation by defining the steps to come back to equilibrium , such as . Moreover, from the ECT term one can extract the following relation that represents the equilibrium equation between and .
Statistical analysis, estimation, hypothesis testing and inference of cointegration vectors related to the and terms can be found in Johansen (1988), Johansen (1991), Breitung and Hassler (2002). The Johansen test verifies if the rank of the matrix is equal to zero (null hypothesis), that is, if . If , then this implicate the non-existence of the error correction term (ECT). Otherwise, if , then the null hypothesis is rejected and there is a cointegration relation between the TS. Johansen proposed two possibilities, namely, the Max-Eigen and the Trace tests, that are based in the assumption of pure unit root denoted by Lütkepohl (2005), Johansen (1991)
| (12) |
| (13) |
where denotes the likelihood ratio for testing the null hypothesis of , stands for the sample size, is the eigenvector associated with the matrix and is the maximum number of possible cointegrating vectors.
In contrast to the method for cointegration validation proposed by Engle-Granger (Engle and Granger, 1987), the Johansen test allows the study of more than one cointegration relation among the variables. For this reason, we adopt the Johansen approach for analysing possible cointegration processes between the disease incidence versus the stock index. Whenever a cointegration is detected, the VECM is applied for the stock indices.
4. Results and discussion
This section presents the obtained results for the stationarity of the TS, using the ADF method (Dickey and Fuller, 1979). The cointegration results achieved by means of the Johansen test based on the Max-Eigen and Trace criteria for 11 different financial indices against the 4 outbreaks are analyzed. Afterwards, the Hansen and Seo (2002) threshold existence significance test is explored. This test is important to decide if VECM is an appropriate model to carry out the work. The correlation, the VECM, the response from an orthogonal impulse (OIR) and the FEVD are depicted. The historical volatility during the 4 outbreaks for the 11 stock exchange indices is also obtained.
Table 1 and 2 summarize the obtained results for trend, drift and constant models.
Table 1.
The ADF stationarity test for the outbreaks TS. Confidence levels of 95% (*).
| Outbreaks | Trend | Drift | None |
|---|---|---|---|
| COVID-19 | 1.59 | 0.76 | 2.81 |
| COVID-19 | |||
| EBOLA | 2.50 | 3.80 | |
| EBOLA | |||
| MERS | 3.33 | 1.82 | 1.51 |
| MERS | |||
| SARS | 3.28 | 0.74 | |
| SARS | 3.42 | 1.27 | 1.10 |
| SARS | |||
Table 2.
The ADF stationarity test for the 11 financial indices TS during the outbreaks. Confidence levels of 95% (*).
| Index | COVID-19 |
EBOLA |
MERS |
SARS |
||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Trend | Drift | None | Trend | Drift | None | Trend | Drift | None | Trend | Drift | None | |
| Dow Jones | 1.06 | 1.07 | 0.75 | 0.32 | 2.13 | 1.62 | 2.36 | 3.12 | 1.63 | 2.11 | ||
| Dow Jones | ||||||||||||
| S&P 500 | 0.98 | 1.05 | 0.71 | 0.36 | 2.71 | 1.27 | 2.96 | 3.03 | 1.69 | 1.99 | ||
| S&P 500 | ||||||||||||
| Euro Stoxx | 1.00 | 0.92 | 1.00 | 2.09 | 2.19 | 0.04 | 2.14 | 1.05 | 1.32 | 1.52 | ||
| Euro Stoxx | ||||||||||||
| DAX | 0.78 | 0.97 | 0.86 | 2.41 | 2.60 | 0.48 | 2.24 | 0.75 | 1.77 | 3.24 | 2.47 | 2.16 |
| DAX | ||||||||||||
| CAC | 1.16 | 0.91 | 1.06 | 2.08 | 2.48 | 0.31 | 2.74 | 1.67 | 1.35 | 2.74 | 1.47 | |
| CAC | ||||||||||||
| Nikkei | 1.37 | 1.11 | 0.72 | 1.91 | 2.69 | 0.41 | 3.32 | 1.97 | 1.84 | 0.38 | 1.72 | |
| Nikkei | ||||||||||||
| HSI | 1.71 | 0.82 | 0.65 | 1.63 | 0.89 | 0.46 | 2.66 | 2.71 | 0.57 | 2.23 | 0.59 | 1.55 |
| HSI | ||||||||||||
| Kospi | 1.30 | 1.00 | 0.67 | 2.17 | 2.21 | 0.19 | 2.62 | 2.42 | 0.06 | 2.93 | 1.42 | 1.96 |
| Kospi | ||||||||||||
| S&P ASX | 1.09 | 0.79 | 1.37 | 2.67 | 1.63 | 0.05 | 3.21 | 1.08 | 2.31 | 2.31 | 1.20 | |
| S&P ASX | ||||||||||||
| Nifty | 2.04 | 0.81 | 1.01 | 2.20 | 0.11 | 2.23 | 2.06 | 0.66 | 1.11 | 0.99 | 1.80 | |
| Nifty | ||||||||||||
| Ibov | 1.44 | 0.91 | 1.24 | 2.70 | 2.54 | 0.34 | 2.13 | 2.41 | 0.91 | 2.81 | 1.21 | |
| Ibov | ||||||||||||
One can note that all financial indices are integrated at order with the COVID-19, EBOLA and MERS data and at order with the SARS data. Table 1 and Table 2 indicate also that the SARS data and the financial indices present cointegrations of orders and , respectively. This means that the significant results produced by the Johansen test can indicate a spurious result.
Table 3 shows the results of the Johansen cointegration test for the 11 financial indices against the 4 outbreaks. One can observe that the majority of the financial indices is strongly affected by the disease outbreaks. Moreover, we verify the cointegration of all stock exchange indices with the COVID-19, EBOLA and MERS. However, not all indices follow that trend in what concerns the SARS.
Table 3.
Johansen cointegration test for 11 different financial indices against 4 global outbreaks. Confidence levels of 90% (*), 95% (**) and 99% (***) for rejecting the null-hypothesis of no-cointegration.
| Index | Tests | Outbreaks |
|||
|---|---|---|---|---|---|
| COVID-19 | EBOLA | MERS | SARS | ||
| Dow Jones | Max-Eigen | 10.76 | |||
| USA | Trace | 16.74 | |||
| S&P 500 | Max-Eigen | 11.81 | |||
| USA | Trace | 11.81 | |||
| Euro Stoxx | Max-Eigen | ||||
| Eurozone | Trace | ||||
| DAX | Max-Eigen | ||||
| Germany | Trace | ||||
| CAC | Max-Eigen | 12.58 | |||
| France | Trace | ||||
| Nikkei | Max-Eigen | ||||
| Japan | Trace | ||||
| HSI | Max-Eigen | ||||
| Hong Kong | Trace | ||||
| Kospi | Max-Eigen | 10.21 | |||
| South Korea | Trace | 17.07 | |||
| S&P ASX | Max-Eigen | 13.57 | |||
| Australia | Trace | ||||
| Nifty | Max-Eigen | ||||
| India | Trace | ||||
| Ibov | Max-Eigen | ||||
| Brazil | Trace | ||||
Table 4, 6, 8 and 10 summarize the obtained results for the threshold effects by testing the significance of their existence through linear cointegration versus threshold cointegration. Indeed, the threshold cointegration test listed in Table 10 confirms that a linear cointegration would not be appropriate for a few TS involving the SARS, namely S&P 500, Nikkei, HSI and Nifty. Nevertheless, among the 44 possibilities (11 financial indices versus 4 outbreaks) listed in Table 4, Table 6, Table 8 and Table 10, it is observed that 39 of them did not reject the null-hypothesis for linear cointegration. Therefore, they should not be handled by using the threshold approach (Hansen and Seo, 2002).
Table 4.
Threshold existence significance test for the 11 financial indices against the COVID-19 data.
| Index | COVID-19 |
||||
|---|---|---|---|---|---|
| Confidence level | Critical value | Test statistics | -Value | Decision | |
| Dow Jones | 95% | 11.41 | 7.60 | 0.4 | Not Reject |
| Dow Jones | 99% | 13.66 | Not Reject | ||
| S&P 500 | 95% | 8.18 | 6.49 | 0.28 | Not Reject |
| S&P 500 | 99% | 9.97 | Not Reject | ||
| Euro Stoxx | 95% | 8.99 | 6.80 | 0.16 | Not Reject |
| Euro Stoxx | 99% | 10.49 | Not Reject | ||
| DAX | 95% | 9.59 | 7.56 | 0.2 | Not Reject |
| DAX | 99% | 12.02 | Not Reject | ||
| CAC | 95% | 8.92 | 6.53 | 0.35 | Not Reject |
| CAC | 99% | 10.50 | Not Reject | ||
| Nikkei | 95% | 9.72 | 6.13 | 0.47 | Not Reject |
| Nikkei | 99% | 13.35 | Not Reject | ||
| HSI | 95% | 8.95 | 6.19 | 0.41 | Not Reject |
| HSI | 99% | 10.50 | Not Reject | ||
| Kospi | 95% | 8.01 | 4.22 | 0.58 | Not Reject |
| Kospi | 99% | 8.73 | Not Reject | ||
| S&P ASX | 95% | 9.54 | 11.82 | 0.0 | Reject |
| S&P ASX | 99% | 10.80 | Reject | ||
| Nifty | 95% | 8.88 | 7.57 | 0.14 | Not Reject |
| Nifty | 99% | 9.57 | Not Reject | ||
| Ibov | 95% | 13.07 | 9.83 | 0.48 | Not Reject |
| Ibov | 99% | 14.76 | Not Reject | ||
Table 6.
Threshold existence significance test for the 11 financial indices against the EBOLA data.
| Index | EBOLA |
||||
|---|---|---|---|---|---|
| Confidence level | Critical value | Test statistics | -Value | Decision | |
| Dow Jones | 95% | 11.29 | 8.04 | 0.37 | Not Reject |
| Dow Jones | 99% | 14.04 | Not Reject | ||
| S&P 500 | 95% | 10.36 | 5.44 | 0.62 | Not Reject |
| S&P 500 | 99% | 11.97 | Not Reject | ||
| Euro Stoxx | 95% | 13.58 | 7.62 | 0.32 | Not Reject |
| Euro Stoxx | 99% | 15.67 | Not Reject | ||
| DAX | 95% | 13.10 | 8.66 | 0.34 | Not Reject |
| DAX | 99% | 15.28 | Not Reject | ||
| CAC | 95% | 12.28 | 7.56 | 0.48 | Not Reject |
| CAC | 99% | 14.74 | Not Reject | ||
| Nikkei | 95% | 12.64 | 5.79 | 0.75 | Not Reject |
| Nikkei | 99% | 16.69 | Not Reject | ||
| HSI | 95% | 12.37 | 6.25 | 0.66 | Not Reject |
| HSI | 99% | 16.94 | Not Reject | ||
| Kospi | 95% | 12.96 | 9.71 | 0.15 | Not Reject |
| Kospi | 99% | 15.98 | Not Reject | ||
| S&P ASX | 95% | 12.36 | 8.12 | 0.25 | Not Reject |
| S&P ASX | 99% | 13.81 | Not Reject | ||
| Nifty | 95% | 11.11 | 8.51 | 0.16 | Not Reject |
| Nifty | 99% | 14.88 | Not Reject | ||
| Ibov | 95% | 12.10 | 6.62 | 0.32 | Not Reject |
| Ibov | 99% | 15.32 | Not Reject | ||
Table 8.
Threshold existence significance test for the 11 financial indices against the MERS data.
| Index | MERS |
||||
|---|---|---|---|---|---|
| Confidence level | Critical value | Test statistics | -Value | Decision | |
| Dow Jones | 95% | 9.46 | 3.90 | 0.77 | Not Reject |
| Dow Jones | 99% | 13.26 | Not Reject | ||
| S&P 500 | 95% | 10.62 | 8.71 | 0.21 | Not Reject |
| S&P 500 | 99% | 12.52 | Not Reject | ||
| Euro Stoxx | 95% | 12.09 | 10.54 | 0.11 | Not Reject |
| Euro Stoxx | 99% | 13.52 | Not Reject | ||
| DAX | 95% | 10.04 | 9.22 | 0.1 | Not Reject |
| DAX | 99% | 11.22 | Not Reject | ||
| CAC | 95% | 13.83 | 17.04 | 0.0 | Reject |
| CAC | 99% | 14.30 | Reject | ||
| Nikkei | 95% | 8.69 | 6.91 | 0.18 | Not Reject |
| Nikkei | 99% | 9.85 | Not Reject | ||
| HSI | 95% | 8.86 | 5.54 | 0.4 | Not Reject |
| HSI | 99% | 9.58 | Not Reject | ||
| Kospi | 95% | 10.97 | 9.22 | 0.26 | Not Reject |
| Kospi | 99% | 14.39 | Not Reject | ||
| S&P ASX | 95% | 10.55 | 11.16 | 0.05 | Reject |
| S&P ASX | 99% | 12.89 | Not Reject | ||
| Nifty | 95% | 11.39 | 4.90 | 0.79 | Not Reject |
| Nifty | 99% | 11.98 | Not Reject | ||
| Ibov | 95% | 10.30 | 5.62 | 0.53 | Not Reject |
| Ibov | 99% | 11.79 | Not Reject | ||
Table 10.
Threshold existence significance test for the 11 financial indices against the SARS data.
| Index | SARS |
||||
|---|---|---|---|---|---|
| Confidence level | Critical value | Test statistics | -Value | Decision | |
| Dow Jones | 95% | 9.14 | 7.66 | 0.22 | Not Reject |
| Dow Jones | 99% | 11.51 | Not Reject | ||
| S&P 500 | 95% | 9.77 | 14.15 | 0.01 | Reject |
| S&P 500 | 99% | 11.12 | Reject | ||
| Euro Stoxx | 95% | 11.06 | 7.16 | 0.34 | Not Reject |
| Euro Stoxx | 99% | 11.95 | Not Reject | ||
| DAX | 95% | 9.86 | 11.04 | 0.03 | Reject |
| DAX | 99% | 12.28 | Not Reject | ||
| CAC | 95% | 8.67 | 6.05 | 0.44 | Not Reject |
| CAC | 99% | 11.99 | Not Reject | ||
| Nikkei | 95% | 10.70 | 14.29 | 0.0 | Reject |
| Nikkei | 99% | 13.44 | Reject | ||
| HSI | 95% | 8.20 | 13.61 | 0.0 | Reject |
| HSI | 99% | 11.11 | Reject | ||
| Kospi | 95% | 9.87 | 5.73 | 0.47 | Not Reject |
| Kospi | 99% | 11.59 | Not Reject | ||
| S&P ASX | 95% | 9.96 | 11.01 | 0.03 | Reject |
| S&P ASX | 99% | 14.46 | Not Reject | ||
| Nifty | 95% | 9.14 | 14.29 | 0.0 | Reject |
| Nifty | 99% | 10.50 | Reject | ||
| Ibov | 95% | 9.48 | 4.12 | 0.81 | Not Reject |
| Ibov | 99% | 11.49 | Not Reject | ||
Bearing this fact in mind and knowing that the OIR and the FEVD are VECM-based tools, we decided to maintain the cointegration relations between the financial indices and the outbreaks that showed a linear cointegration by means of the Johansen test.
In this context, we consider the VECM model as appropriate for describing the relationship between the outbreaks and the financial indices. Their results are analyzed for all pairs that presented a cointegration process by means of the Johansen criteria.
Table 5, 7, 9 and Table 11 11, list the correlation and the VECM parameters for the indices that revealed cointegration against the COVID-19, EBOLA, MERS and SARS data, respectively.
Table 5.
The Correlation and VECM equation parameters for the cointegrated indices against the COVID-19. Confidence levels: 90%(*), 95%(**) and 99% (***).
| TS | Correlation | Cointegration – parameters |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dow Jones | 0.595 | 0.0008 | 617,819.58 | 1.00 | 20.14 | 0.12 | 0.085 | 0.06 | 0.198 | 0.06 | 0.09 | 0.10 | 0.28* |
| COVID-19 | NA | NA | NA | NA | −0.036 | 0.024 | 0.0103 | 0.023 | 0.0001 | 0.018 | 0.01 | 0.008 | |
| S&P 500 | 0.589 | 0.00011 | 706,188.43 | 1.00 | 204.52 | 0.18 | 0.06 | 0.11 | 0.21 | 0.06 | 0.11 | 0.08 | |
| COVID-19 | NA | NA | NA | NA | 0.004 | 0.002 | 0.0011 | 0.003 | 0.0001 | 0.002 | 0.001 | 0.001 | |
| Euro Stoxx | 0.585 | 0.00002 | 224,483.82 | 1.00 | 52.02 | 0.04 | 0.05 | 0.20 | 0.03 | 0.07 | 0.09 | ||
| COVID-19 | NA | NA | NA | NA | 0.003 | 0.002 | 0.001 | 0.0001 | 0.0001 | 0.004 | 0.004 | 0.0001 | |
| DAX | 0.570 | 0.0002 | 246,991.05 | 1.00 | 16.13 | 0.048 | 0.042 | 0.17 | 0.052 | 0.05 | 0.11 | ||
| COVID-19 | NA | NA | NA | NA | 0.01 | 0.007 | 0.006 | 0.001 | 0.001 | 0.012 | 0.02 | 0.001 | |
| CAC | 0.606 | 0.0001 | 198,371.35 | 1.00 | 28.50 | 0.05 | 0.031 | 0.18 | 0.22 | 0.01 | 0.08 | 0.07 | 0.44 |
| COVID-19 | NA | NA | NA | NA | 0.004 | 0.004 | 0.001 | 0.001 | 0.001 | 0.01 | 0.005 | 0.001 | |
| Nikkei | −0.564 | 0.001 | 38,264.99 | 1.00 | 0.59 | 0.09 | 0.08 | 0.16 | 0.06 | 0.22 | 0.08 | 0.06 | 0.13 |
| COVID-19 | NA | NA | NA | NA | 0.002 | 0.02 | 0.01 | 0.01 | 0.02 | 0.004 | 0.01 | 0.003 | |
| HSI | 0.624 | 0.001 | 377,273.31 | 1.00 | 12.87 | 0.13 | 0.13 | 0.15 | 0.10 | 0.16 | 0.13 | 0.08 | |
| COVID-19 | NA | NA | NA | NA | 0.001 | 0.013 | 0.011 | 0.002 | 0.01 | 0.01 | 0.02 | 0.02 | |
| Kospi | 0.585 | 0.0001 | 423,829.28 | 1.00 | 180.14 | 0.02 | 0.04 | 0.03 | 0.04 | 0.08 | 0.012 | ||
| COVID-19 | NA | NA | NA | NA | 0.001 | 0.001 | 0.001 | 0.00002 | 0.0004 | 0.002 | 0.003 | ||
| S&P ASX | 0.662 | 0.00002 | 908,318.97 | 1.00 | 124.61 | 0.05 | 0.08 | 0.17 | 0.05 | 0.02 | |||
| COVID-19 | NA | NA | NA | NA | 0.004 | 0.003 | 0.002 | 0.004 | 0.004 | 0.001 | 0.004 | 0.011 | |
| Nifty | 0.750 | 0.0002 | 622,579.63 | 1.00 | 48.61 | 0.044 | 0.05 | 0.12 | 0.09 | 0.05 | 0.03 | ||
| COVID-19 | NA | NA | NA | NA | 0.01 | 0.005 | 0.003 | 0.01 | 0.00001 | 0.005 | 0.002 | 0.003 | |
| Ibov | 0.679 | 0.002 | 433,988.59 | 1.00 | 3.34 | 0.16 | 0.05 | 0.09 | 0.09 | 0.004 | 0.06 | 0.16 | 0.14 |
| COVID-19 | NA | NA | NA | NA | 0.13 | 0.12 | 0.03 | 0.08 | 0.06 | 0.14 | 0.09 | 0.04 | |
Table 7.
The Correlation and the VECM parameters for the cointegrated indices against the EBOLA. Confidence levels: 90%(*), 95%(**) and 99% (***).
| TS | Correlation | Cointegration – parameters |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dow Jones | 0.220 | 0.001 | 35,447.59 | 1.00 | 134.97 | 0.06 | 0.09 | 0.07 | 0.11 | 0.04 | 0.06 | ||
| EBOLA | NA | NA | NA | NA | 0.28 | 0.003 | 0.31 | 0.24 | 0.25 | 0.18 | 0.07 | ||
| S&P 500 | 0.077 | 0.00003 | 706,188.43 | 1.00 | 204.52 | 0.02 | 0.08 | 0.001 | 0.02 | 0.07 | |||
| EBOLA | NA | NA | NA | NA | 0.31 | 0.03 | 0.102 | 0.07 | 0.072 | 0.34 | |||
| Euro Stoxx | 0.013 | 0.0005 | 211,524.71 | 1.00 | 55.51 | 0.05 | 0.06 | 0.01 | NA | NA | NA | NA | NA |
| EBOLA | NA | NA | NA | NA | 0.32 | NA | NA | NA | NA | NA | |||
| DAX | 0.012 | 0.001 | 194,207.64 | 1.00 | 15.36 | 0.04 | 0.03 | 0.01 | NA | NA | NA | NA | NA |
| EBOLA | NA | NA | NA | NA | 1.19 | NA | NA | NA | NA | NA | |||
| CAC | 0.130 | 0.0005 | 673,102.67 | 1.00 | 131.93 | 0.02 | 0.04 | 0.0004 | NA | NA | NA | NA | NA |
| EBOLA | NA | NA | NA | NA | 1.17 | 0.95 | 0.21 | NA | NA | NA | NA | NA | |
| Nikkei | 0.110 | 0.004 | 38,264.99 | 1.00 | 0.59 | 0.03 | 0.03 | 0.03 | NA | NA | NA | NA | NA |
| EBOLA | NA | NA | NA | NA | 3.95 | 1.91 | 1.83 | NA | NA | NA | NA | NA | |
| HSI | 0.147 | 0.005 | 377,273.31 | 1.00 | 12.87 | 0.03 | 0.097 | 0.03 | NA | NA | NA | NA | NA |
| EBOLA | NA | NA | NA | NA | 1.08 | 1.74 | 5.22 | NA | NA | NA | NA | NA | |
| Kospi | 0.121 | 0.00003 | 423,829.28 | 1.00 | 180.14 | 0.08 | 0.06 | NA | NA | NA | NA | NA | |
| EBOLA | NA | NA | NA | NA | 0.06 | 0.02 | 0.05 | NA | NA | NA | NA | NA | |
| S&P ASX | 0.193 | 0.0005 | 148,745.06 | 1.00 | 25.05 | 0.10 | 0.001 | 0.001 | NA | NA | NA | NA | NA |
| EBOLA | NA | NA | NA | NA | 0.18 | 0.31 | 0.58 | NA | NA | NA | NA | NA | |
| Nifty | 0.248 | 0.0004 | 622,579.63 | 1.00 | 48.61 | 0.02 | 0.08 | 0.004 | NA | NA | NA | NA | NA |
| EBOLA | NA | NA | NA | NA | 1.63 | 0.03 | 1.27 | NA | NA | NA | NA | NA | |
| Ibov | 0.023 | 0.015 | 433,988.59 | 1.00 | 3.34 | 0.06 | 0.003 | NA | NA | NA | NA | NA | |
| EBOLA | NA | NA | NA | NA | 1.00 | NA | NA | NA | NA | NA | |||
Table 9.
The Correlation and the VECM parameters for the cointegrated indices against the MERS. Confidence levels: 90%(*), 95%(**) and 99% (***).
| TS | Correlation | Cointegration – parameters |
||||
|---|---|---|---|---|---|---|
| Dow Jones | 0.821 | 0.0003 | 40.02 | 1.00 | 3.04 | 0.13 |
| MERS | NA | NA | NA | NA | 0.46 | |
| S&P 500 | 0.907 | 0.03 | 866.26 | 1.00 | 0.59 | |
| MERS | NA | NA | NA | NA | 0.17 | |
| Euro Stoxx | 0.871 | 0.046 | 828.29 | 1.00 | 0.34 | 0.06 |
| MERS | NA | NA | NA | NA | 0.89 | |
| DAX | 0.896 | 698.51 | 1.00 | 0.10 | 0.06 | |
| MERS | NA | NA | NA | NA | 10.95 | |
| CAC | 0.885 | 0.005 | 875.93 | 1.00 | 0.25 | 0.09 |
| MERS | NA | NA | NA | NA | 4.95 | |
| Nikkei | 0.748 | 0.27 | 604.84 | 1.00 | 0.05 | 0.11 |
| MERS | NA | NA | NA | NA | 6.75 | |
| HSI | 0.554 | 0.06 | 4977.85 | 1.00 | 0.24 | 0.03 |
| MERS | NA | NA | NA | NA | 23.91 | |
| Kospi | 0.149 | 0.02 | 4256.99 | 1.00 | 2.23 | 0.15 |
| MERS | NA | NA | NA | NA | 2.81 | |
| S&P ASX | 0.737 | 0.002 | 2154.29 | 1.00 | 0.45 | 0.06 |
| MERS | NA | NA | NA | NA | 4.55 | |
| Nifty | 0.553 | 0.02 | 2344.75 | 1.00 | 0.42 | 0.03 |
| MERS | NA | NA | NA | NA | 4.59 | |
| Ibov | 0.603 | 0.10 | 0.0001 | 1.00 | 0.19 | |
| MERS | NA | NA | NA | NA | 10.60 | |
Table 11.
The Correlation and the VECM parameters for the cointegrated indices against the SARS. Confidence levels: 90%(*), 95%(**), 99% (***).
| TS | Correlation | Cointegration – parameters |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Euro Stoxx | 0.764 | 0.002 | 85,946.98 | 1.00 | 38.87 | 0.01 | 0.08 | 0.11 | 0.18 | 0.11 | |
| SARS | NA | NA | NA | NA | 0.03 | 0.02 | 0.06 | 0.03 | |||
| DAX | 0.842 | 0.004 | 42,377.28 | 1.00 | 15.74 | 0.07 | 0.13 | 0.18 | 0.09 | 0.14 | |
| SARS | NA | NA | NA | NA | 0.03 | 0.02 | 0.08 | 0.03 | 0.02 | ||
| CAC | 0.789 | 0.0004 | 102,221.10 | 1.00 | 35.71 | 0.06 | 0.04 | 0.03 | 0.05 | ||
| SARS | NA | NA | NA | NA | 0.008 | 0.04 | 0.08 | 0.05 | 0.02 | ||
| Nikkei | 0.557 | 216,169.39 | 1.00 | 22.86 | 0.12 | 0.04 | 0.08 | 0.07 | 0.01 | ||
| SARS | NA | NA | NA | NA | 0.16 | 0.08 | 0.01 | 0.12 | 0.01 | ||
| HSI | 0.689 | 0.0003 | 36,030.03 | 1.00 | 4.54 | 0.11 | 0.1 | 0.15 | NA | NA | NA |
| SARS | NA | NA | NA | NA | 0.04 | 0.011 | NA | NA | NA | ||
| S&P ASX | 0.827 | 99,120.12 | 1.00 | 35.22 | 0.10 | 0.02 | 0.07 | 0.03 | 0.18 | 0.003 | |
| SARS | NA | NA | NA | NA | 0.01 | 0.004 | 0.02 | 0.014 | 0.01 | ||
| Nifty | 0.343 | 458,310.35 | 1.00 | 351.78 | 0.06 | 0.02 | 0.10 | 0.14 | 0.11 | 0.06 | |
| SARS | NA | NA | NA | NA | 0.0002 | 0.01 | 0.001 | 0.004 | 0.01 | ||
| Ibov | 0.952 | 74,281.37 | 1.00 | 6.05 | 0.12 | 0.02 | 0.08 | 0.13 | 0.02 | 0.07 | |
| SARS | NA | NA | NA | NA | 0.05 | 0.32 | 0.05 | 0.07 | 0.15 | 0.07 | |
We now explore the OIR and apply the FEVD to measure the variance of the forecast error regarding the shocks of the outbreaks data. In order to normalize the OIR results, the -score standardization is also performed.
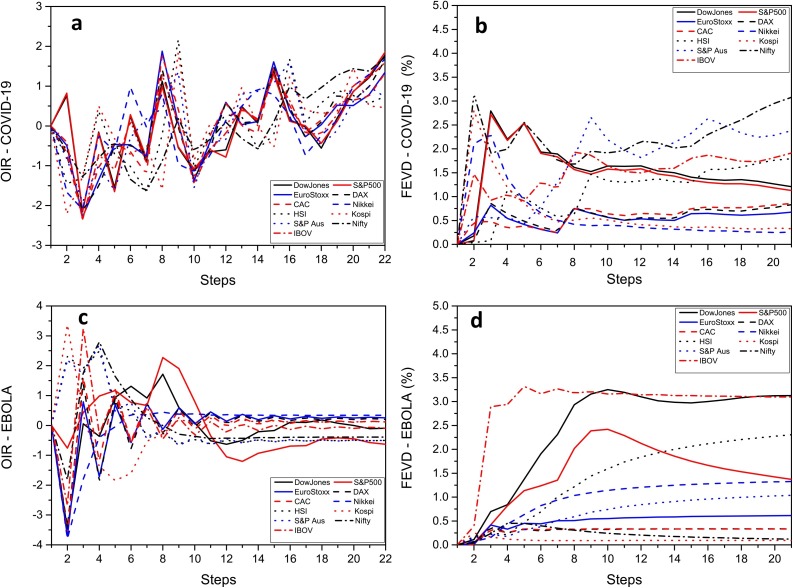
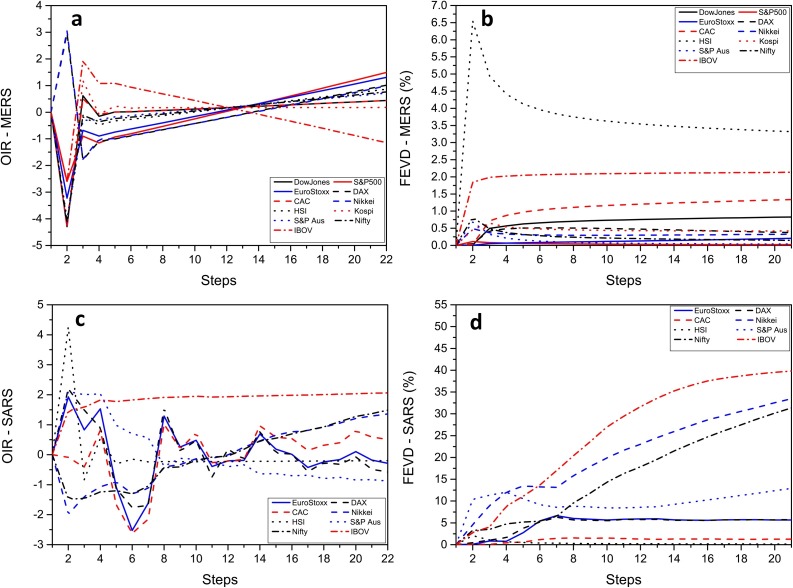
Fig. 2a,c, 3a and 3 c represent the OIR over time. On the other hand, Fig. 2b, 2 d, 3 b and 3 d depict the FEVD analysis for the 11 stock exchange indices also against the COVID-19, EBOLA, MERS and SARS data.
Fig. 2.
The OIR and the FEVD for the COVID-19 (a) and (b), and EBOLA (c) and (d).
Fig. 3.
The OIR and the FEVD for the MERS (a) and (b), and SARS (c) and (d).
Fig. 2a shows, for all indices, a transient response from an impulse in COVID-19 data. We note a strong negative shock at the first steps and afterward the tendence to maintain a significant volatility. Similarly, Fig. 2c shows identical initial negative shock patterns for most stock indices caused by the EBOLA outbreak. However, it tends to bounce back to equilibrium in the following steps. Fig. 2b confirms a significant influence of that initial negative shocks of COVID-19 by means of the FEVD analysis. Differently, from Fig. 2d one can note a high influence of the EBOLA in the Ibov, Dow Jones and S&P 500, but not so significant effect on the other indices.
Fig. 3a shows that, in general, all indices tended to be negatively influenced by the MERS outbreak. This effect is confirmed by the FEVD in Fig. 3b. Moreover, the HSI and Ibov are the most influenced in terms of the variance of their residuals. In turn, the shocks caused by the SARS provoked a strong initial negative response in the Nifty and Nikkei and a retarded negative shock in the CAC and EuroStoxx, as shown in Fig. 3c. However, when observing the FEVD in Fig. 3d one can note that the SARS affects mostly the Ibov, Nikkei, Nifty and HSI. This pattern would be expected in the Asian stocks, but the same would not be expected in the Ibov since the OIR showed a positive response. Probably, this result can be related to a false positive.
Table 5, 7, 9 and 11, show a significant number of lags for the VECM equations in all outbreaks, with exception for the MERS. We verify a 8-lags equation for all the stock exchange indices against the COVID-19 data which confirms a large influence of the outbreak with respect to the residuals of the steps. Also, when using the equilibrium relation it is shown that for all equations a huge number of steps is necessary to reach equilibrium back from the COVID-19. When looking to the indices relation with the EBOLA outbreak it is seen a high lagged VECM only for North American indices. However, all the indices shows high disequilibrium reflected by the parameter . The results for the indices against the MERS were expected since the disease lead a moderate number of cases if compared to the other outbreaks, which is also confirmed by the higher of values. Despite the SARS outbreak being mostly spread over Asian countries, the HSI presented a 3-lags equation rather than the 8-lags of the other indices.
In synthesis, with exception of the SARS, all stock indices are cointegrated with the COVID-19, EBOLA and MERS. This feature is not evinced by the SARS since some indices related mainly to the North America and Europe revealed a weak or even null cointegration.
Fig. 4 shows the historical market volatilities for the 11 stock indices during the period of the diseases episodes. In the map, we mark the historical volatility as the square root of the sum of squared returns over the past 79 trading days. With the exception of the Nikkey and HSI indices, all other indices experienced higher historical volatility during the analyzed period for the COVID-19, suggesting an unprecedented stock market impact caused for it and a greater difficulty to bounce back the financial indices. Moreover, one can note that among all indices explored in this work, the Ibov index was the most susceptible and strongly affected by the shocks due to the diseases.
Fig. 4.
Historical volatility observed during the 4 outbreaks for the 11 stock exchange indices.
We believe the results offer ground for some reflection about of heavy-handed restrictions on the economical activity in the scope of the efforts to contain pandemics. The healthcare rationale for travel restrictions, business closures, and social distancing mandates is clear, but it is also painfully evident that these policies bring great economic and financial negative consequences. Therefore, an important challenge is how to address health crisis created by pandemics (such as the COVID-19) and, simultaneously, to avoid strangle the economy.
A pandemic can be followed by sustained periods – over years or decades – with affected investment opportunities, possibly due to heightened desires to save, that is, due to an increase in precautionary saving or to a rebuilding of depleted wealth.
Several nations have adopted an aggressive counter-pandemic fiscal expansion that will boost the public debt further, reducing the national savings rate. In turn, this might put upward on the interest rate, even though that the expansion of public debt could be easier to sustain in the long-run. This movement can affect, among others, the subsequent low returns to assets, impacting (to some extent) the stock exchange indices worldwide.
Regarding the current COVID-19 pandemic, the global economic trajectory seems very different than was expected only some months ago.
5. Conclusions
This paper considered the Johansen cointegration test and the bivariate VECM analysis, exploited by the OIR and the FEVD, to investigate the bilateral relationship between the incidence of important 4 diseases outbreaks against 11 stock exchange indices. The historical volatilities of the same stock indices were also calculated. The results revealed that the shocks caused by the diseases has a significant effect upon the stock indices. Most of the indices suffered initial strong shocks due the impulse in each disease outbreak. However, differently from the others diseases, an impulse in the COVID-19 maintained a significant volatility after the initial period, showing recovering difficulties of the financial indices due the shock caused by COVID-19. Additionally, the higher historical volatility occurred mainly during the period of the COVID-19. The results point to a higher impact over the Ibov-Brazil and reveal its poor recovering dynamics when compared to the others indices. This phenomenon can be explained by the fact that, in general, there is a larger perception of risk by investors related to countries with larger economic and social fragility.
We highlight that our conclusions about the reasons for the remarkable stock market reaction to COVID-19 have a broad-brush character. There is much room for further research into the stock market reactions to particular fiscal and monetary policy actions during the pandemics and particularly during the ongoing COVID-19 spread.
Authors’ contributions
Sergio A. David: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Resources, Data Curation, Visualization, Writing – Original Draft, Writing – Review & Editing, Supervision, Project administration, Funding acquisition.
Claudio M. C. Inácio Jr.: Conceptualization, Data curation, Investigation, Methodology, Software, Formal analysis, Writing – Original draft preparation.
José A. Tenreiro Machado: Conceptualization, Visualization, Validation, Investigation, Writing – Reviewing and Editing, Supervision.
Conflict of interest
The authors declare no conflict of interest.
References
- Afifi A., May S., Donatello R., Clark V.A. CRC Press; 2019. Practical Multivariate Analysis. [Google Scholar]
- Aguiar-Conraria L., Soares M.J. The continuous wavelet transform: moving beyond uni-and bivariate analysis. J. Econ. Surv. 2014;28(2):344–375. [Google Scholar]
- Alexander C. vol. 2. Risk Books; 1999. Correlation and cointegration in energy markets; pp. 291–304. (Managing Energy Price Risk). [Google Scholar]
- Ali M., Alam N., Rizvi S.A.R. Coronavirus (COVID-19)-an epidemic or pandemic for financial markets. J. Behav. Exp. Finance. 2020:100341. doi: 10.1016/j.jbef.2020.100341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashraf B.N. Stock markets’ reaction to COVID-19: cases or fatalities? Res. Int. Bus. Finance. 2020:101249. doi: 10.1016/j.ribaf.2020.101249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baillie R.T., Booth G.G., Tse Y., Zabotina T. Price discovery and common factor models. J. Financ. Mark. 2002;5(3):309–321. [Google Scholar]
- Baker S.R., Bloom N., Davis S.J., Kost K., Sammon M., Viratyosin T. The unprecedented stock market reaction to COVID-19. Rev. Asset Pricing Stud. 2020 [Google Scholar]
- Bekiros S.D., Diks C.G. The relationship between crude oil spot and futures prices: cointegration, linear and nonlinear causality. Energy Econ. 2008;30(5):2673–2685. [Google Scholar]
- Breitung J., Hassler U. Inference on the cointegration rank in fractionally integrated processes. J. Econom. 2002;110(2):167–185. Long memory and nonlinear time series. [Google Scholar]
- Cavicchioli M., Pistoresi B. Unfolding the relationship between mortality, economic fluctuations, and health in Italy. Eur. J. Health Econ. 2019:1–12. doi: 10.1007/s10198-019-01135-1. [DOI] [PubMed] [Google Scholar]
- Cologni A., Manera M. Oil prices, inflation and interest rates in a structural cointegrated VAR model for the G-7 countries. Energy Econ. 2008;30(3):856–888. [Google Scholar]
- Colombage S.R. Financial markets and economic performances: empirical evidence from five industrialized economies. Res. Int. Bus. Finance. 2009;23(3):339–348. [Google Scholar]
- Conlon T., McGee R. Safe haven or risky hazard?. Bitcoin during the COVID-19 bear market. Finance Res. Lett. 2020:101607. doi: 10.1016/j.frl.2020.101607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conlon T., Corbet S., McGee R.J. Are cryptocurrencies a safe haven for equity markets?. An international perspective from the COVID-19 pandemic. Res. Int. Bus. Finance. 2020:101248. doi: 10.1016/j.ribaf.2020.101248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- David S.A., Quintino D.D., Inacio C.M.C., Jr., Machado J.A.T. Fractional dynamic behavior in ethanol prices series. J. Comput. Appl. Math. 2018;339:85–93. [Google Scholar]
- David S.A., Inácio C., Tenreiro Machado J.A. Ethanol prices and agricultural commodities: an investigation of their relationship. Mathematics. 2019;7(9):774. [Google Scholar]
- David S.A., Inácio C., Tenreiro Machado J.A. Quantifying the predictability and efficiency of the cointegrated ethanol and agricultural commodities price series. Appl. Sci. 2019;9(24):5303. [Google Scholar]
- Davidson J.E.H., Hendry D.F., Srba F., Yeo S. Econometric modelling of the aggregate time-series relationship between consumers’ expenditure and income in the United Kingdom. Econ. J. 1978;88:661–692. [Google Scholar]
- Dickey D.A., Fuller W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979;74(366a):427–431. [Google Scholar]
- Ederington L.H., Guan W. Measuring historical volatility. J. Appl. Finance. 2006;16(1) [Google Scholar]
- Enders W., Siklos P.L. Cointegration and threshold adjustment. J. Bus. Econ. Stat. 2001;19(2):166–176. [Google Scholar]
- Engle C.W.J., Granger R.F. Cointegration and error correction: representation, estimation and testing. Econometrica. 1987;55:251–276. [Google Scholar]
- Evgenidis A., Tsagkanos A., Siriopoulos C. Towards an asymmetric long run equilibrium between stock market uncertainty and the yield spread. A threshold vector error correction approach. Res. Int. Bus. Finance. 2017;39:267–279. [Google Scholar]
- Fang Y., Nie Y., Penny M. Transmission dynamics of the COVID-19 outbreak and effectiveness of government interventions: a data-driven analysis. J. Med. Virol. 2020;92(6):645–659. doi: 10.1002/jmv.25750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gałecki M., Osińska M. Economic Miracles in the European Economies. Springer; 2019. Threshold error correction model: a methodological overview; pp. 151–173. [Google Scholar]
- Glantz S., Slinker B. McGraw-Hill, Inc.; New York: 2001. Primer of Applied Regression & Analysis of Variance, ed. [Google Scholar]
- Goodell J.W. Covid-19 and finance: agendas for future research. Finance Res. Lett. 2020:101512. doi: 10.1016/j.frl.2020.101512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodell J.W., Huynh T.L.D. Did congress trade ahead?. Considering the reaction of us industries to COVID-19. Finance Res. Lett. 2020:101578. doi: 10.1016/j.frl.2020.101578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goutte S., Péran T., Porcher T. The role of economic structural factors in determining pandemic mortality rates: evidence from the COVID-19 outbreak in france. Res. Int. Bus. Finance. 2020:101281. doi: 10.1016/j.ribaf.2020.101281. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Granger C.W.J. Some properties of time series data and their use in econometric model specification. J. Econom. 1981;16:121–130. [Google Scholar]
- Hansen B.E., Seo B. Testing for two-regime threshold cointegration in vector error-correction models. J. Econom. 2002;110(2):293–318. Long memory and nonlinear time series. [Google Scholar]
- Hassouneh I., Radwan A., Serra T., Gil J.M. Food scare crises and developing countries: the impact of avian influenza on vertical price transmission in the Egyptian poultry sector. Food Policy. 2012;37(3):264–274. [Google Scholar]
- Jiang H., Liu C. Forecasting construction demand: a vector error correction model with dummy variables. Constr. Manag. Econ. 2011;29(9):969–979. [Google Scholar]
- Johansen S. Statistical analysis of cointegration vectors. J. Econ. Dyn. Control. 1988;12(2):231–254. [Google Scholar]
- Johansen S. Estimation and hypothesis testing of cointegration vectors in Gaussian vector autoregressive models. Econometrica. 1991;59(6):1551–1580. [Google Scholar]
- Johansen S. A small sample correction for the test of cointegrating rank in the vector autoregressive model. Econometrica. 2002;70(5):1929–1961. [Google Scholar]
- Jones K.E., Patel N.G., Levy M.A., Storeygard A., Balk D., Gittleman J.L., Daszak P. Global trends in emerging infectious diseases. Nature. 2008;451(7181):990–993. doi: 10.1038/nature06536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Juselius K. vol. 2. Oxford University Press; Oxford: 2007. (The Cointegrated VAR Model: Methodology and Applications (Advanced Texts in Econometrics)). [Google Scholar]
- Katz R., Wentworth M., Quick J., Arabasadi A., Harris E., Geddes K., Jha A. Enhancing public-private cooperation in epidemic preparedness and response. World Med. Health Policy. 2018;10(4):420–425. [Google Scholar]
- Lütkepohl H. Springer Science & Business Media; 2005. New Introduction to Multiple Time Series Analysis. [Google Scholar]
- Lahmiri S., Bekiros S. Randomness, informational entropy, and volatility interdependencies among the major world markets: the role of the COVID-19 pandemic. Entropy. 2020;22(8):833. doi: 10.3390/e22080833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Machado J.T., Lopes A.M. Rare and extreme events: the case of COVID-19 pandemic. Nonlinear Dyn. 2020:1. doi: 10.1007/s11071-020-05680-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madhav N., Oppenheim B., Gallivan M., Mulembakani P., Rubin E., Wolfe N. 2017. Pandemics: Risks, Impacts, and Mitigation. [PubMed] [Google Scholar]
- Mahadevan R., Asafu-Adjaye J. Energy consumption, economic growth and prices: a reassessment using panel VECM for developed and developing countries. Energy Policy. 2007;35(4):2481–2490. [Google Scholar]
- Mattos F.L., Franco da Silveira R.L. The expansion of the Brazilian winter corn crop and its impact on price transmission. Int. J. Financ. Stud. 2018;6 [Google Scholar]
- Morse S.S., Mazet J.A., Woolhouse M., Parrish C.R., Carroll D., Karesh W.B., Zambrana-Torrelio C., Lipkin W.I., Daszak P. Prediction and prevention of the next pandemic zoonosis. Lancet. 2012;380(9857):1956–1965. doi: 10.1016/S0140-6736(12)61684-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray M.P. A drunk and her dog: an illustration of cointegration and error correction. Am. Stat. 1994;48(1):37–39. [Google Scholar]
- O’Flanagan D., Barret A., Foley M., Cotter S., Bonner C., Crowe C., Lynch B., Sweeney B., Johnson H., McCoy B., et al. Investigation of an association between onset of narcolepsy and vaccination with pandemic influenza vaccine, Ireland April 2009-December 2010. Eurosurveillance. 2014;19(17):20789. [PubMed] [Google Scholar]
- Olival K.J., Hosseini P.R., Zambrana-Torrelio C., Ross N., Bogich T.L., Daszak P. Host and viral traits predict zoonotic spillover from mammals. Nature. 2017;546(7660):646–650. doi: 10.1038/nature22975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porta M. Oxford University Press; 2014. A Dictionary of Epidemiology. [Google Scholar]
- Quintino D.D., David S.A., Vian C.E.d.F. Analysis of the relationship between ethanol spot and futures prices in Brazil. Int. J. Financ. Stud. 2017;5(2):11. [Google Scholar]
- Salisu A.A., Akanni L.O. Constructing a global fear index for the COVID-19 pandemic. Emerg. Mark. Finance Trade. 2020;56(10):2310–2331. [Google Scholar]
- Sargan J.D. Wages and prices in the United Kingdom: a study in econometric methodology. Econom. Anal. Ntl. Econ. Plan. 1964;16:25–54. [Google Scholar]
- Sharif A., Aloui C., Yarovaya L. COVID-19 pandemic, oil prices, stock market, geopolitical risk and policy uncertainty nexus in the US economy: fresh evidence from the wavelet-based approach. Int. Rev. Financ. Anal. 2020:101496. doi: 10.1016/j.irfa.2020.101496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharifi R.H., Akhoondi N., Honarvar N., Mohammadi M. Effects of the human immunodeficiency virus (AIDS) epidemic on economic growth in Iran. J. Res. Health. 2014;4(3):770–777. [Google Scholar]
- Shehzad K., Xiaoxing L., Kazouz H. COVID-19’s disasters are perilous than global financial crisis: a rumor or fact? Finance Res. Lett. 2020:101669. doi: 10.1016/j.frl.2020.101669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shi W., Li K.X. Impact of unexpected events on inbound tourism demand modeling: evidence of middle east respiratory syndrome outbreak in South Korea. Asia Pac. J. Tour. Res. 2017;22(3):344–356. [Google Scholar]
- Smith R., Harrison A. A drunk, her dog, and a boyfriend: an illustration of multiple cointegration and error correction. Department Econ. Oper. Res. 1994 [Google Scholar]
- Volpi E., Fiori A. Design event selection in bivariate hydrological frequency analysis. Hydrol. Sci. J. 2012;57(8):1506–1515. [Google Scholar]
- Yamey G., Schäferhoff M., Aars O.K., Bloom B., Carroll D., Chawla M., Dzau V., Echalar R., Gill I.S., Godal T., et al. Financing of international collective action for epidemic and pandemic preparedness. Lancet Global Health. 2017;5(8):e742–e744. doi: 10.1016/S2214-109X(17)30203-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarovaya L., Brzeszczynski J., Goodell J.W., Lucey B.M., Lau C.K. 2020. Rethinking Financial Contagion: Information Transmission Mechanism During the COVID-19 Pandemic. Available at SSRN 3602973. [Google Scholar]
- Zhang D., Hu M., Ji Q. Financial markets under the global pandemic of COVID-19. Finance Res. Lett. 2020:101528. doi: 10.1016/j.frl.2020.101528. [DOI] [PMC free article] [PubMed] [Google Scholar]