Automated Segmentation of Thyroid Nodule, Gland, and Cystic Components From Ultrasound Images Using Deep Learning

Abstract

Sonographic features associated with margins, shape, size, and volume of thyroid nodules are used to assess their risk of malignancy. Automatically segmenting nodules from normal thyroid gland would enable an automated estimation of these features. A novel multi-output convolutional neural network algorithm with dilated convolutional layers is presented to segment thyroid nodules, cystic components inside the nodules, and normal thyroid gland from clinical ultrasound B-mode scans. A prospective study was conducted, collecting data from 234 patients undergoing a thyroid ultrasound exam before biopsy. The training and validation sets encompassed 188 patients total; the testing set consisted of 48 patients. The algorithm effectively segmented thyroid anatomy into nodules, normal gland, and cystic components. The algorithm achieved a mean Dice coefficient of 0.76, a mean true positive fraction of 0.90, and a mean false positive fraction of 1.61×10⁻⁶. The values are on par with a conventional seeded algorithm. The proposed algorithm eliminates the need for a seed in the segmentation process, thus automatically detecting and segmenting the thyroid nodules and cystic components. The detection rate for thyroid nodules and cystic components was 82% and 44%, respectively. The inference time per image, per fold was 107ms. The mean error in volume estimation of thyroid nodules for five select cases was 7.47%. The algorithm can be used for detection, segmentation, size estimation, volume estimation, and generating thyroid maps for thyroid nodules. The algorithm has applications in point of care, mobile health monitoring, improving workflow, reducing localization time, and assisting sonographers with limited expertise.

I. INTRODUCTION

The increase in incidence of thyroid cancer is faster than any other cancer at 4.5% per year over the last 10 years [1]. In 2018, an estimated 53,990 new thyroid cancer cases were diagnosed in the United States alone, and an estimated 2,060 people died due to thyroid cancer [2]. Thyroid nodules are mostly benign with a malignancy rate of 4.5–6% [3]. The United States Preventive Services Task Force recommends against screening, including neck palpation and ultrasound (US), for thyroid cancer in asymptomatic adults [1]. Due to the lack of a screening process, thyroid nodules are found incidentally by palpation or diagnostic imaging modalities like ultrasonography, computed tomography, magnetic resonance imaging, or positron emission tomography. Ultrasonography is the commonly used diagnostic tool for thyroid cancer as it is inexpensive and readily available. Besides differentiating between solid nodules and those consisting of cystic components, ultrasonography features are related to the pathology of the nodule. The sonographic features that indicate an increased risk of malignancy include hypoechoic solid nodules, taller-than-wide nodules, irregular margins, extra-thyroidal extension, and presence of micro-calcifications. Contrarily, presence of peripheral vascularity, round shape, hyper-or isoechogenicity, spongiform appearance, smooth margins, and cystic composition are associated with benign disease [4–6]. Sub-centimeter nodules identified by US are not recommended for fine needle aspiration (FNA) [7], as they lack the potential to be clinically significant thyroid cancers. Thus, estimating the size, volume, and shape of nodules plays a crucial role in the decision making process of FNA biopsy. Segmenting the thyroid nodules from normal thyroid gland using US images can help in estimating the above-mentioned parameters.

Segmenting US images is challenging due to the poor contrast between different anatomies and the presence of a granular speckle pattern. Different segmentation techniques for thyroid nodules have been proposed using US images, including radial basis function neural network [8], variable background active contour [9], genetically-optimized variable background active contour [10], localization-based active contour [11], local region-based active contour [12], geodesic active contour level set [13], active contour bilateral filtering ()[14], hybrid multi-scale model [15], identifying thin hyper-echoic lines associated with the lobes of thyroid glands [16], extreme learning machine [17], normalized cut [18], random forest and U-net convolutional neural network (CNN)[19], and manually segmenting the boundaries[20]. Most of the algorithms mentioned above use a manually drawn boundary, referred to as a seed, to initiate the segmentation algorithm. A seeded boundary is a rough estimate of the nodule boundary drawn by a user on the B-mode image. Drawing a seed impedes the algorithms from operating in real-time, limiting the use of seeded algorithms for retrospective analysis only. A seedless approach to segmenting thyroid nodules can enable real-time applications of segmentation algorithms in clinical workflow.

Thyroid nodules can be solid, cystic, predominantly solid, or predominantly cystic. Segmenting the cystic components inside a thyroid nodule can help to identify the nodule’s composition. Cystic components appear as hypoechoic regions under US imaging. However, hypoechoic regions inside the thyroid gland could be cystic components and should not be mistaken for arteries or veins present outside the thyroid gland, which are also hypoechoic structures. The segmentation algorithm needs to learn where the thyroid gland is on the ultrasound image and then look for cystic components inside the nodules.

Deep learning algorithms leverage the improvements in graphics processing units’ computing power to develop larger and more complex neural networks capable of segmenting ultrasound images for various anatomies [21–25]. Deep learning algorithms do not require a seed and are fully automated with an inference time in the range of milliseconds, enabling real-time implementation. In this paper, we propose a novel multi-prong CNN to semantically segment normal thyroid gland, thyroid nodules, and cystic components inside nodules from B-mode images. The algorithm can help the user detect and segment thyroid anatomy in real-time. The application of the algorithm includes detection, segmentation, size estimation, volume estimation, and generation of thyroid maps of thyroid nodules. The performance of the algorithm is validated against a manually segmented mask and compared against a conventional seeded algorithm.

II. MATERIALS AND METHODS

A. PATIENT POOL

A prospective study was conducted from April 2015 to September 2018. The study was approved by the Institutional Review Board and was Health Insurance Portability and Accountability Act compliant. Written consent was obtained from each patient. A total of 234 patients (177 female, 57 male; age 57±15 yrs.) underwent a clinical thyroid US exam using a GE LOGIQ E9 (GE Healthcare; Wauwatosa, Wisconsin USA) US scanner. The imaging protocol consisted of gathering B-mode images of all thyroid nodules for both longitudinal and transverse cross-sections by a board certified sonographer. Probe type, center frequency, time gain compensation, and imaging technique were optimized by the sonographer. A total of 914 thyroid US images were obtained from 234 patients. Images not showing the thyroid gland and images from patients that previously had a thyroidectomy were excluded. The dataset was divided into training, validation, and testing sets. The training and validation sets were comprised of 766 images corresponding to 186 patients. The testing set was comprised of 148 images corresponding to 48 patients. A 10-fold cross-validation technique was used for the training and validation set resulting in 10 unique models with different training and validation sets. The validation set was prepared by secluding 10% of data from the training set.

B. PRE-PROCESSING

The clinical US images were reshaped into a square sized 320 by 320 pixels with zero padding to preserve the image aspect ratio. Pixels in the images were normalized to a range between 0 and 1.

C. ARCHITECTURE

Fig. 1 illustrates the proposed architecture of a prong CNN algorithm. The prong refers to the shape of the network due to splitting of the architecture to create multiple outputs. The proposed architecture was inspired from multi-scale context aggregation by dilated convolutions technique [26]. A 10-fold cross-validation technique was adopted to improve the performance and reduce variance in prediction. Ten different prong CNN algorithms were trained by changing the training and validation sets using the 10-fold cross-validation technique. Throughout this manuscript the 10-fold cross-validated prong CNN algorithm is referred to as the multi-prong CNN (MPCNN). The output of the ten prong CNNs was postprocessed to obtain the segmentation mask as described later in the post-processing section. The MPCNN model was adapted from the Fully Convolutional Network[27], which in turn is based on the VGG-16 [28] classification network. The MPCNN consists of 6 convolutional blocks. The first four collect features at both the local and global levels. The last two blocks used dilated convolutions to expand the receptive field. The MPCNN was modified to have two separate outputs in order to simultaneously segment various thyroid anatomies. The first sigmoid output predicted the location of normal thyroid; the second softmax output predicted the position of the nodule, cystic component inside the nodule, and background. The two output approach allowed the network to predict overlaps in the normal thyroid gland, thyroid nodule, and cystic components. The parameters used in the MPCNN algorithm are summarized in Table I. The model weights and filters were initialized using random numbers from a random uniform distribution scaled by the number of inputs. The negative Sørensen-Dice coefficient has been commonly used as a loss function to assess the accuracy of segmentation [21]. A weighted negative Dice coefficient of different anatomies was used as a loss function. Due to the complexity associated with training VGG-16 networks, a three stage approach was adapted for training the model: the first stage comprised of the first four convolution blocks, the second added the fifth block, and the third stage added the sixth block. There are a total of 184,638,040 trainable parameters and a training time of ten hours per model. Attempts were made to utilize a VGG-16 model pretrained on the ImageNet [29] benchmark dataset. One channel ultrasound images was converted to a three channel image by copying the input. Attempts were made to retrain the model using the ultrasound dataset by retraining the whole model, retraining the last three blocks and retraining the last block. Retraining was attempted using learning rates between 1e-4 and 1e-6 without success. It is possible that the datasets are too different for the thyroid segmentation model to benefit from pretraining on the ImageNet dataset. Hyper-parameter optimization was performed by a combination of grid search and fine tuning using the python Spearmint library [21]. Training performance of the model is shown in Fig 2 showing training and validation loss and accuracy across all stages of training. There is a degree of overfit present in the model indicating greater performance is possible with more data or a different training scheme. The effect of introducing new layers can be seen as a periodic drop in performance until the new layers are trained. The algorithm was developed using Python (version 2.7.11, Python Software Foundation) and open-source deep learning libraries Tensorflow (version 0.9.0) [30] and Keras (version 1.1.0) [31].

Fig. 1.

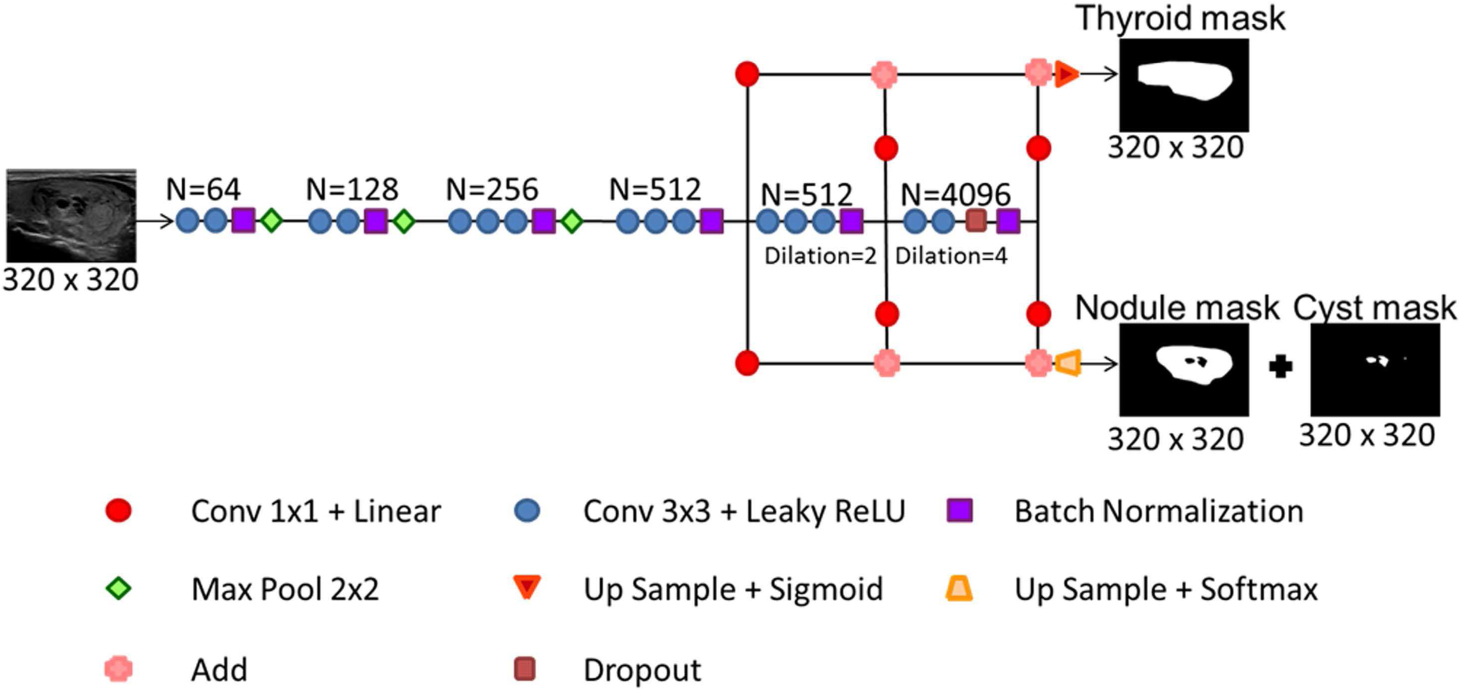
Architecture of a multi-prong convolutional neural network. N is the number of filters. Input is a B-mode image and output is the normal thyroid, thyroid nodule, and cyst mask.

TABLE I.

Parameters for Multi Prong Convolutional Neural Network Algorithm

Parameter	Prong CNN
Convolution layer: size, stride, padding	3×3, l×l, zero padding
Max pooling: size, stride, padding	2×2, 2×2, no zero padding
Dropout	0.5
Dilation rate	2(Dilation layer)
Optimizer, learning rate	Adam.0.5(stage×l0^−4)
Loss function	Negative mean Dice coefficient
Kernel initializer	LeCun uniform
Kernel regularizer	L2 (0.000075)
Activation function	Leaky rectified linear unit
Image size	320×320

Fig. 2.

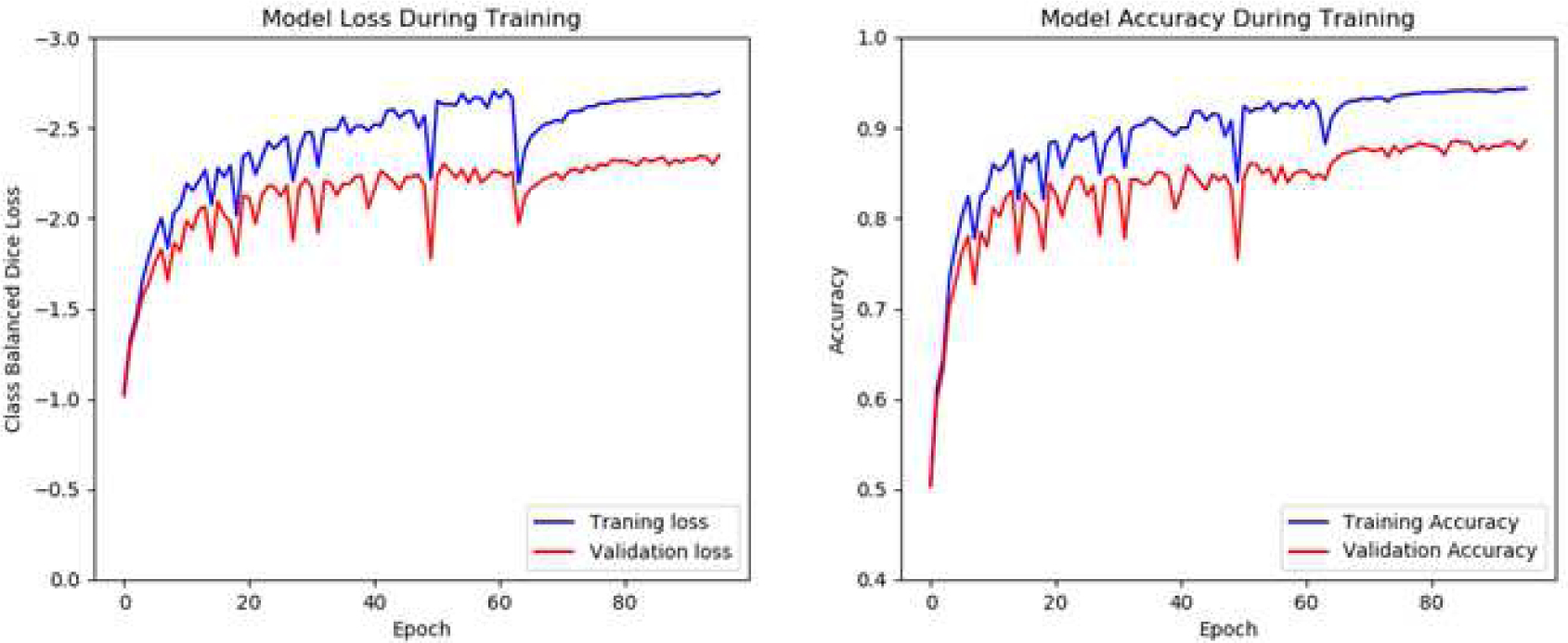
Training and validation characteristics of loss and accuracy for all stages of training. The blue line is the mean results on the training set during each epoch and the red line is the results on the validation at the end of each epoch.

D. DATA AUGMENTATION

Overfitting and small datasets are challenges often encountered in generalizing the results. The problem of overfitting is particularly apt for CNNs. Overfitting occurs due to the relatively high number of parameters in the algorithm compared to the number of features provided by US images. The most common approach used to avoid overfitting is to increase the amount of data using label-preserving transformations or simple image manipulations (e.g. rotating an image but not swapping color pallets). To ensure that data augmentation was done while observing the rules of US physics and preserving its associated sonographic features, only horizontal axis flipping was used. Conversely, vertical axis flipping was rejected due to the deep acoustic shadowing/enhancement feature.

E. POST-PROCESSING

A ten-fold prong net was developed resulting in ten different models. Post-processing was used to combine the results of the ten models into one. Equally weighted binary pixels from the ten-fold cross-validated MPCNN were averaged, and a threshold was used to implement majority voting. The majority voting threshold was set at 0.5. Using multiple models ensured that the algorithm did not converge to a local minimum and removed the uncertainty associated with randomly initialized seed.

F. LEVEL OF SUSPICION AND HISTOPATHOLOGICAL EXAMINATION

All thyroid nodules were categorized as low, intermediate, or high level of suspicion based on their sonographic pattern, as specified by American Thyroid Association guidelines[32]. Out of the 234 patients, 71 were evaluated as low suspicion, 82 as intermediate suspicion, and 81 as high suspicion. Patients with suspicious thyroid nodules underwent FNA biopsy or surgical excision biopsy after the US study as part of the clinical procedure. Using US guidance and standard sterile technique, a 25-gauge needle was used by one of our board-certified radiologists to obtain up to six fine needle aspirates for each nodule. Cytological diagnosis was made by a cytologist with more than 15 years of experience. Surgical histopathology results were considered conclusive over FNA biopsy results. Cytological and histopathological results were used to compare the performance of the segmentation algorithm in benign, malignant, and indeterminate thyroid nodules.

G. PARAMETERS FOR EVALUATION OF SEGMENTATION

The proposed MPCNN algorithm was evaluated using the Sørensen–Dice coefficient, true positive fraction (TPF), and false positive fraction (FPF). The Sørensen–Dice coefficient is a measure of similarity between the predicted area and the ground truth and will be referred to as Dice coefficient. Dice coefficient, TPF, and FPF range between 0 and 1. Dice coefficient and TPF values closer to 1 are indicative of a good prediction, whereas a FPF value closer to 1 indicates a bad prediction. Box plot distributions showing the performance of the above mentioned three parameters against different cross-sectional orientations, suspicion levels, and pathology were analyzed. These parameters will be collectively referred to as evaluation metrics.

H. COMPARISON WITH SEEDED ALGORITHM

To compare the performance of the MPCNN with a conventional seeded algorithm, a distance regularized level set segmentation (DRLS) algorithm [33] was implemented. Similar to MPCNN the clinical images were down-sampled to a size of 320 by 320 pixels. The seed for the algorithm was created by dilating the true mask with 20 pixels. An initial random search followed by a finer grid search was performed to find the seeded algorithm’s optimal parameters, which were lambda = 10, alpha = −0.9, and epsilon = 3; as defined by Chunming Li et al. [33]. A two-tailed unpaired t test was used to assess statistical significance between the various evaluation parameters for the two algorithms. P values less than 0.05 were considered significantly different.

I. DETECTION OF THYROID NODULES AND CYSTIC COMPONENTS

To quantify the detection rate, a hypothesis test was defined for thyroid nodules and cystic components as shown by equation 1.

$$H_{\mathit{\text{nodule}}/\mathit{\text{cystic}}\mathit{\text{component}}}=\{\begin{array}{ll}1:\hfill & \mathit{\text{Detect}}all\mathit{\text{nodules}}or\mathit{\text{cystic}}\mathit{\text{component}}inan\mathit{\text{image}}\hfill \\ 0:\hfill & \mathit{\text{Otherwise}}\hfill \end{array}$$ (1)

A high detection rate could enable the correct classification of thyroid nodules as either solid or cystic, potentially reducing their localization time.

J. VOLUME ESTIMATION

Volume for the largest thyroid nodule in the thyroid gland was measured in 5 patients. Two orthogonal images were used to estimate the three axes of the nodule. The length was measured from the longitudinal image as the maximal distance from the most cranial to the most caudal part of the nodule. The depth was also measured from the longitudinal image as the maximal distance from the most superficial to the deepest part of the nodule. The width of the nodule was measured from a transverse image as the maximal distance from the most medial to the most lateral part. The thyroid nodule was assumed to be an ellipsoid and the volume was estimated using the above three axes by the formula shown in equation 2.

$${\text{V}}_{\text{ellipsoid}}=\frac{\pi }{6}\ast {\text{D}}_{\text{length}}\ast {\text{D}}_{\text{width}}\ast {\text{D}}_{\text{depth}}$$ (2)

The selected five cases were used to demonstrate the ability of the algorithm to segment different nodules and estimate nodule volume. The estimated volume was compared against the volume calculated by the board certified radiologist.

III. RESULTS

The clinical suspicion level versus the mean and standard deviation values of evaluation metrics achieved during testing of the thyroid nodules and normal thyroid glands are summarized in Tables II and III, respectively. The mean and standard deviation values for all evaluation metrics for the cystic components inside the thyroid gland are summarized in Table IV. The box plots for Dice coefficient, TPF, and FPF versus suspicion level using the MPCNN and DRLS algorithms are shown in Fig. 3,4, and 5 respectively. The mean and standard deviation values of different metrics versus pathology achieved during testing for thyroid nodules and normal thyroid glands are summarized in Tables V and VI, respectively. The box plots for Dice coefficient, TPF, and FPF versus pathology using the MPCNN and DRLS algorithms are shown in Fig. 6, 7, and 8, respectively. The mean and standard deviation values of different metrics versus probe orientation achieved during testing for thyroid nodules, normal thyroid gland, and cystic components are summarized in Table VII. The box plots for Dice coefficient, TPF, and FPF versus probe orientation using the MPCNN and DRLS algorithms are shown in Fig. 9, 10, and 11, respectively. Fig. 12 depicts the variation in mean values of the Dice coefficient versus majority voting threshold values for thyroid nodules, normal gland, and cystic components. The MPCNN and DRLS algorithms both produced a mean Dice coefficient of 0.78 for the three thyroid anatomies, and a mean TPF of 0.77. The mean FPFs for the three thyroid anatomies using MPCNN and DRLS algorithms were 0.55×10⁻⁶ and 0.34×10⁻⁶, respectively. The inference time per image for a single model was 107 ms using the pascal architecture TITAN Xp GPU (Nvidia, Santa Clara, CA, USA). The MPCNN had an inference time of 1.07 seconds per image. Detection rates for thyroid nodules and cystic components were 82% and 44%, respectively. The mean size of thyroid nodules was 9.67±10.04 mm, and the mean size of cystic components was 2.22±2.99 mm. An overall pixel accuracy for the combined model output is 93.0% for thyroid, 84.3% for nodules and 67.4% for cysts.

TABLE II.

Mean and Standard Deviation Values of Evaluation Metrics From Testing Set Versus Suspicion Level for Thyroid Nodules Using the Multi-prong Convolutional Neural Network (MPCNN) Algorithm and the Distance Regularized Level Set (DRLS) Algorithm

Metrics	Algorithm	All cases (n=142)	Low suspicion (n=26)	Intermediate suspicion (n=47)	High suspicion (n=69)
Dice coefficient	MPCNN	0.75±0.24c	0.81±0.22	0.73±0.18	0.73±0.28
	DRLS	0.82±0.19c	0.86±0.20	0.81±0.17	0.81±0.20
TPF	MPCNN	0.74±0.27	0.82±0.22	0.73±0.22	0.71±0.31
	DRLS	0.79±0.21	0.86±0.21	0.79±0.19	0.76±0.22
FPF,×(1e-6)	MPCNN	0.35±0.48	0.40±0.41	0.43±0.59	0.28±0.39
	DRLS	0.30±0.60e	0.45±0.46	0.42±0.88	0.15±0.29

TPF = true positive fraction, FPF = false positive fraction, n = number of images, P = 0.0068

TABLE III.

Mean and Standard Deviation Values of Evaluation Metrics From Testing Set Versus Normal Thyroid Gland Containing Nodules Classified According to Suspicion Level Using the Multi-Prong Convolutional Neural Network (MPCNN) Algorithm and the Distance Regularized Level Set (DRLS) Algorithm

Metrics	Algorithm	All cases (n=148)	Low suspicion (n=26)	Intermediate suspicion (n=51)	High suspicion (n=71)
Dice coefficient	MPCNN	0.89±0.11c	0.91±0.07	0.85±0.15	0.91±0.07
	DRLS	0.94±0.03c	0.95±0.03	0.94±0.03	0.95±0.02
TPF	MPCNN	0.88±0.15d	0.90±0.12	0.82±0.19	0.91±0.10
	DRLS	0.94±0.05d	0.97±0.04	0.93±0.05	0.94±0.04
FPF, ×(1e-6)	MPCNN	0.73±1.14e	0.67±0.69	0.69±1.34	0.77±1.12
	DRLS	0.50±0.60e	0.82±0.59	0.43±0.64	0.44±0.54

TPF = true positive fraction, FPF = false positive fraction, n = number of images, P < 0.0001, P <0.0001, P =0.0307

TABLE IV.

Mean and Standard Deviation Values of Evaluation Metrics From Testing Set for All Cystic Regions Using the Multi-Prong Convolutional Neural Network (MPCNN) Algorithm and the Distance Regularize Level Set (DRLS) Algorithm

Metrics	Algorithm	All cases (n=68)
Dice coefficient	MPCNN	0.62±0.32
	DRLS	0.33±0.27
TPF	MPCNN	0.58±0.34
	DRLS	0.37±0.33
FPF ×(1e-6)	MPCNN	0.58±0.34
	DRLS	0.10±0.28

TPF = true positive fraction, FPF = false positive fraction, n = number of images, P0.0001, significant P = 0.0004, P < 0.0001

Fig. 3.

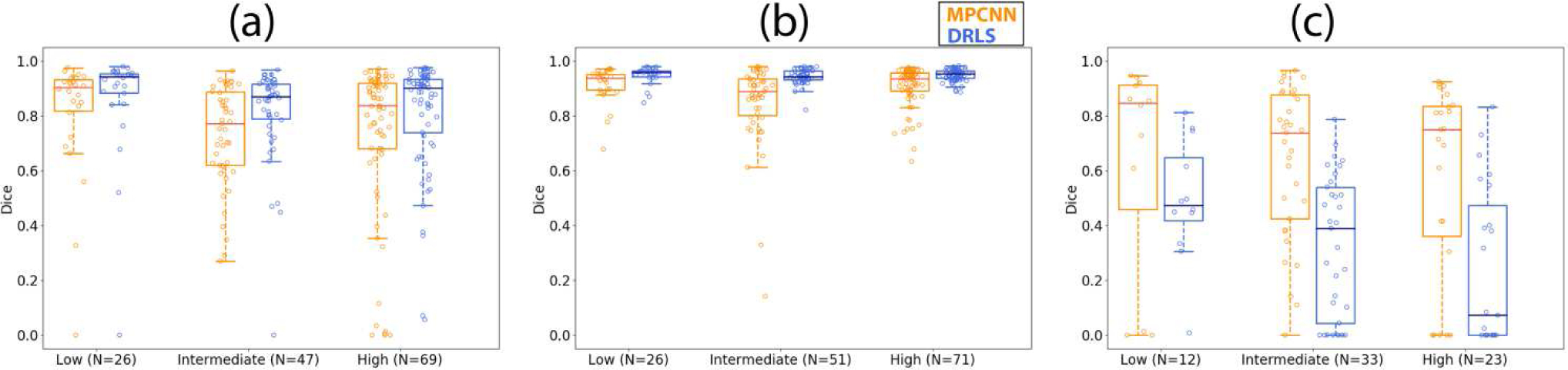
Boxplots showing the Dice coefficient versus different suspicion levels using the multi-prong convolutional neural network (MPCNN) and distance regularized level set (DRLS) algorithms for (a) thyroid nodules, (b) normal thyroid, and (c) cysts.

Fig. 4.

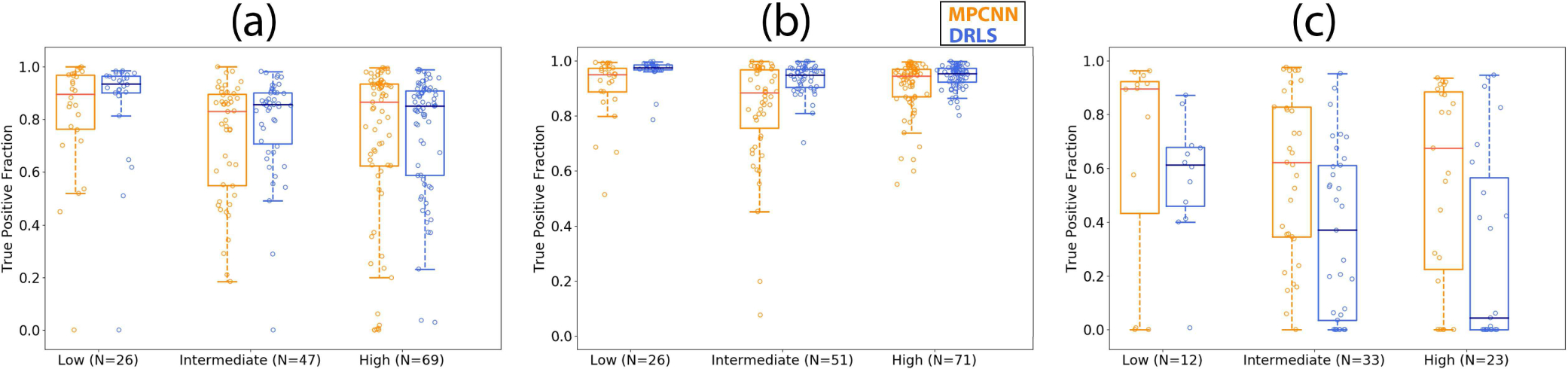
Boxplots showing the true positive fraction versus different suspicion levels using the multi-prong convolutional neural network (MPCNN) and distance regularized level set (DRLS) algorithms for (a) thyroid nodules, (b) normal thyroid, and (c) cysts.

Fig. 5.

Boxplots showing the false positive fraction versus different suspicion levels using the multi-prong convolutional neural network (MPCNN) and distance regularized level set (DRLS) algorithms for (a) thyroid nodules, (b) normal thyroid, and (c) cysts.

TABLE V.

Mean and Standard Deviation Values of Evaluation Metrics From Testing Set Versus Pathology for Thyroid Nodules Using the Multi-Prong Convolutional Neural Network (MPCNN) Algorithm and the Distance Regularized Level Set (DRLS) Algorithm

Metrics	Algorithm	Benign (11=94)	Malignant (n=31)	Indeterminate (n=17)
Dice coefficient	MPCNN	0.73±0.22	0.75±0.31	0.82±0.15
	DRLS	0.80±0.20	0.84±0.20	0.89±0.11
TPF	MPCNN	0.76±0.22	0.81±0.23	0.88±0.12
	DRLS	0.76±0.22	0.81±0.23	0.88±0.12
FPF, ×(1e-6)	MPCNN	0.33±0.70	0.20±0.33	0.29±0.34
	DRLS	0.33±0.70	0.20±0.33	0.29±0.34

TPF = true positive fraction, FPF = false positive fraction, n = number of images

TABLE VI.

Mean And Standard Deviation Values of Evaluation Metrics From Testing Set Versus Normal Thyroid Gland Containing Nodules Classified According to Pathology Using the Multi-Prong Convolutional Neural Network (MPCNN) Algorithm and the Distance Regularized Level Set (DRLS) Algorithm

Metrics	Algorithm	Benign (n=98)	Malignant (n=32)	Indeterminate (n=18)
Dice coefficient	MPCNN	0.90±0.08	0.88±0.14	0.85±0.16
	DRLS	0.95±0.03	0.95±0.02	0.94±0.03
TPF	MPCNN	0.89±0.12	0.87±0.17	0.85±0.21
	DRLS	0.94±0.05	0.96±0.04	0.94±0.05
FPF ×(1e-6)	MPCNN	0.78±1.29	0.56±0.64	0.72±0.96
	DRLS	0.48±0.64	0.59±0.57	0.46±0.42

TPF = true positive fraction, FPF = false positive fraction, n = number of images

Fig. 6.

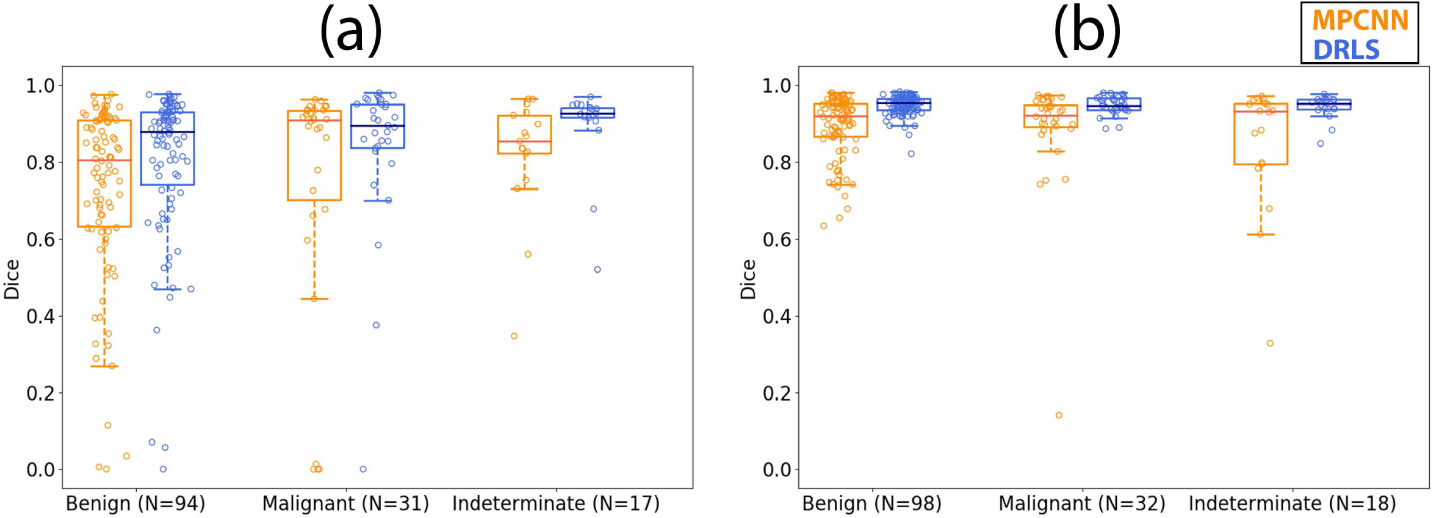
Boxplots showing the Dice coefficient versus pathology using the multi-prong convolutional neural network (MPCNN) and distance regularized level set (DRLS) algorithms for (a) thyroid nodules and (b) normal thyroid.

Fig. 7.

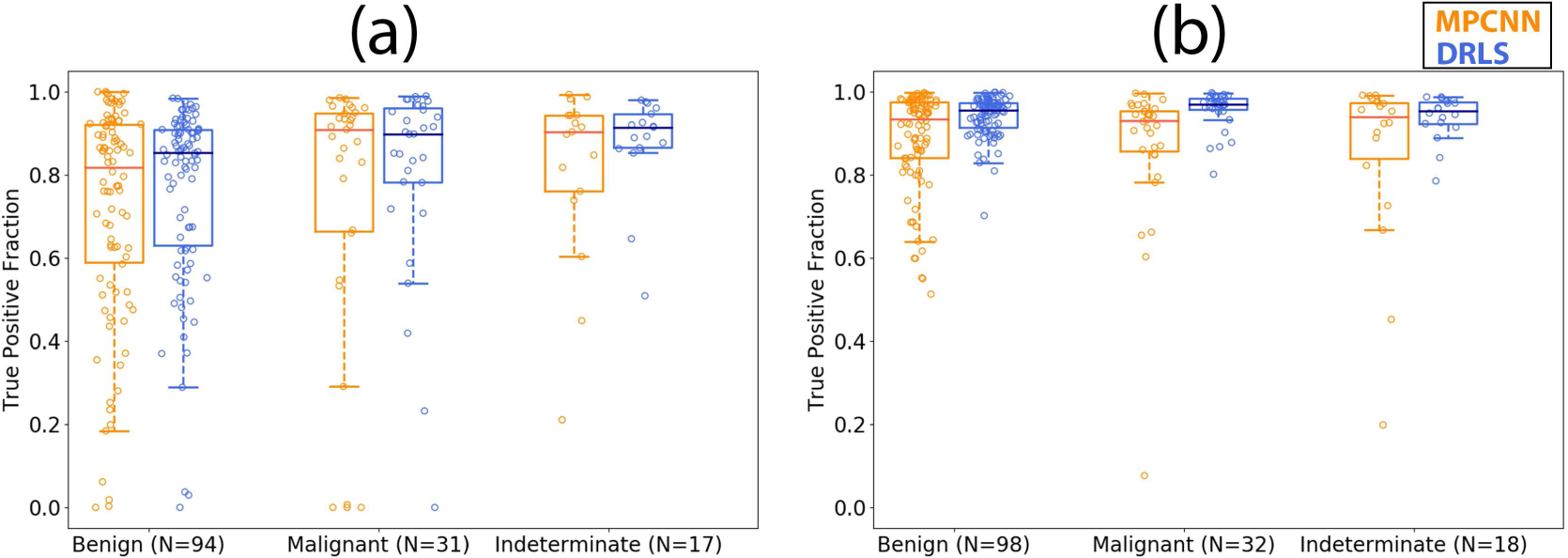
Boxplots showing the true positive fraction versus pathology using the multi-prong convolutional neural network (MPCNN) and distance regularized level set (DRLS) algorithms for (a) thyroid nodules and (b) normal thyroid.

Fig. 8.

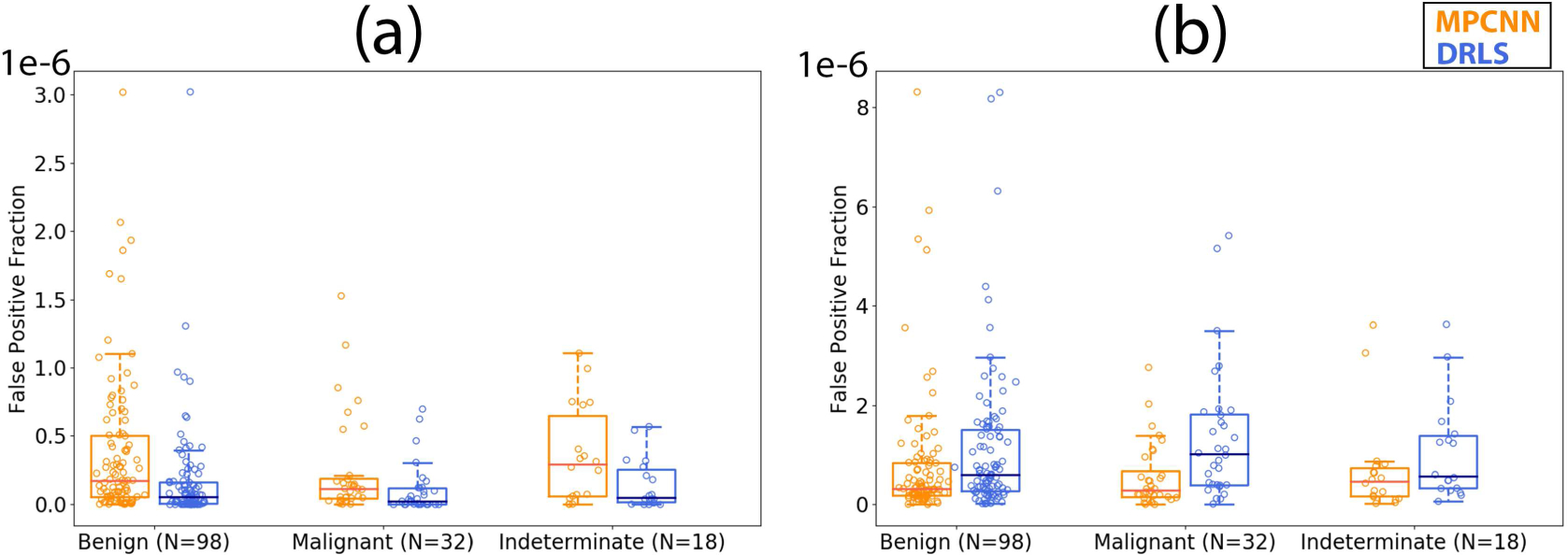
Boxplots showing the false positive fraction versus pathology using the multi-prong convolutional neural network (MPCNN) and distance regularized level set (DRLS) algorithms for (a) thyroid nodules and (b) normal thyroid.

TABLE VII.

Mean And Standard Deviation Values of Evaluation Metrics From Testing Set Versus Probe Orientation for Thyroid Nodules, Thyroid Gland and Cystic components Using the Multi-Prong Convolutional Neural Network (MPCNN) Algorithm and the Distance Regularized Level Set (DRLS) Algorithm

		Thyroid nodule		Thyroid gland		Cyst
Metrics	Algorithm	Transverse (n=64)	Longitudinal (n=78)	Transverse (n=68)	Longitudinal (n=80)	Transverse (n=30)	Longitudinal (n=38)
Dice coefficient	MPCNN	0.73±0.27	0.76±0.21	0.87±0.14	0.91±0.07	0.56±0.34	0.66±0.29
	DRLS	0.79±0.24	0.85±0.14	0.94±0.03	0.95±0.02	0.29±0.27	0.36±0.27
TPF	MPCNN	0.94±0.05	0.95±0.05	0.52±0.36	0.64±0.32	0.52±0.36	0.64±0.32
	DRLS	0.76±0.25	0.81±0.17	0.94±0.05	0.95±0.05	0.34±0.33	0.401=0.32
FPF,×(1e-6)	MPCNN	0.20±0.69	0.38±0.51	0.55±1.20	0.87±1.08	0.02±0.06	0.05±0.09
	DRLS	0.20±0.69	0.37±0.51	0.35±0.47	0.63±0.67	0.06±0.16	0.13±0.35

TPF = true positive fraction, FPF = false positive fraction, n = number of images

Fig. 9.

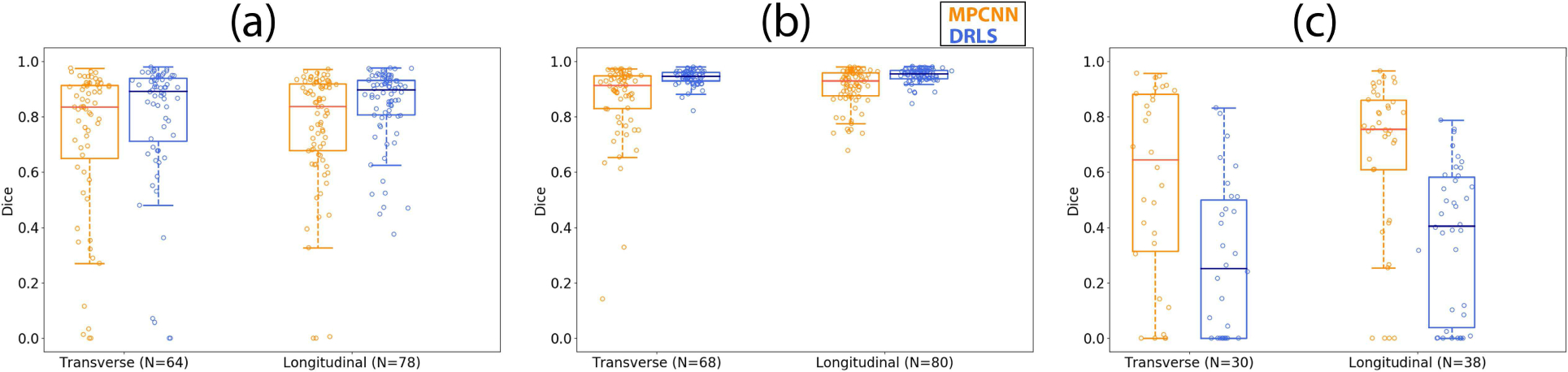
Boxplots showing the Dice coefficient versus orientation using the multi-prong convolutional neural network (MPCNN) and distance regularized level set (DRLS) algorithms for (a) thyroid nodules, (b) normal thyroid, and (c) cysts.

Fig. 10.

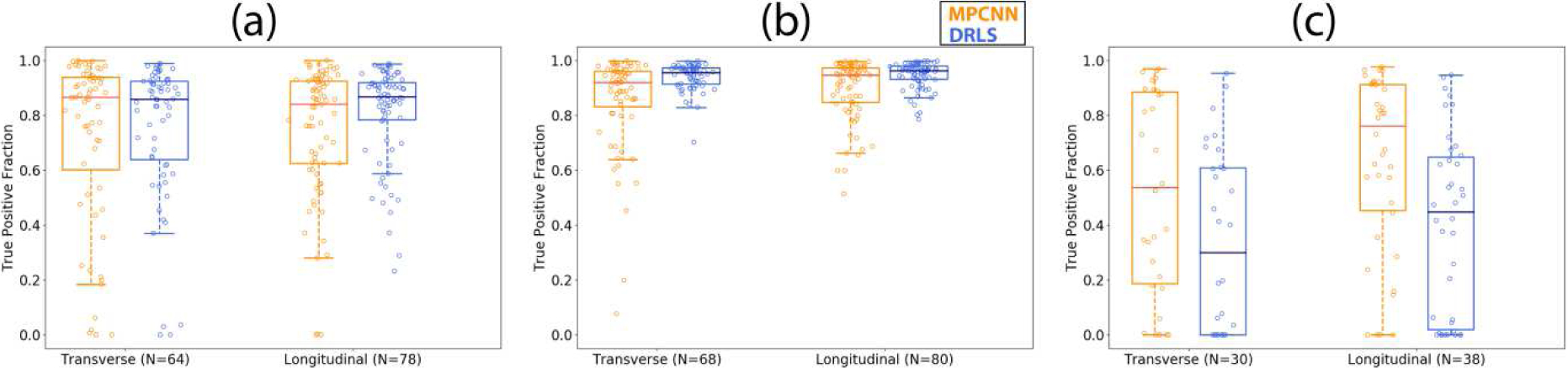
Boxplots showing the true positive fraction versus orientation using the multi-prong convolutional neural network (MPCNN) and distance regularized level set (DRLS) algorithms for (a) thyroid nodules, (b) normal thyroid, and (c) cysts.

Fig. 11.

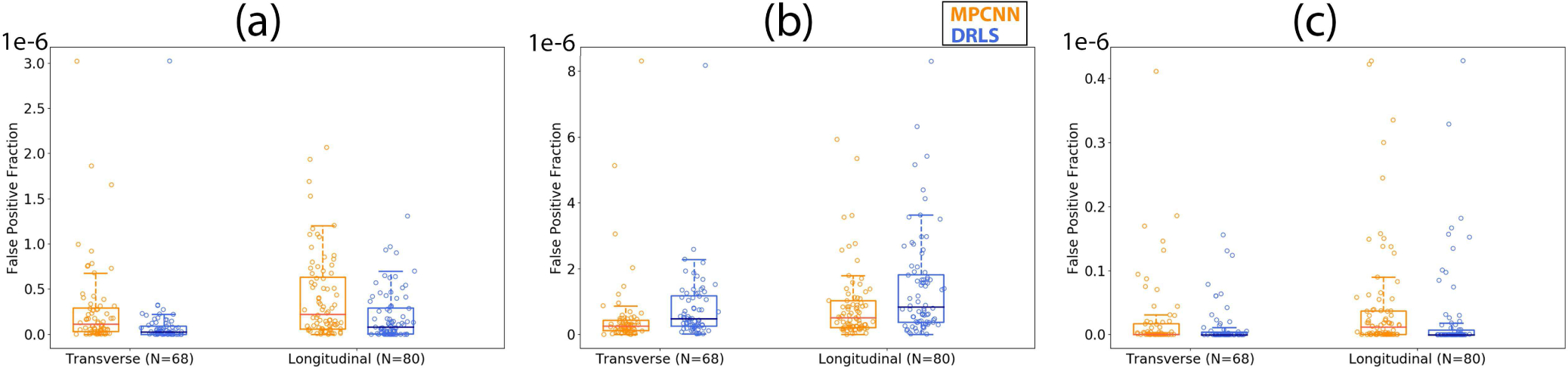
Boxplots showing the false positive fraction versus orientation using the multi-prong convolutional neural network (MPCNN) and distance regularized level set (DRLS) algorithms for (a) thyroid nodules, (b) normal thyroid, and (c) cysts.

Fig. 12.

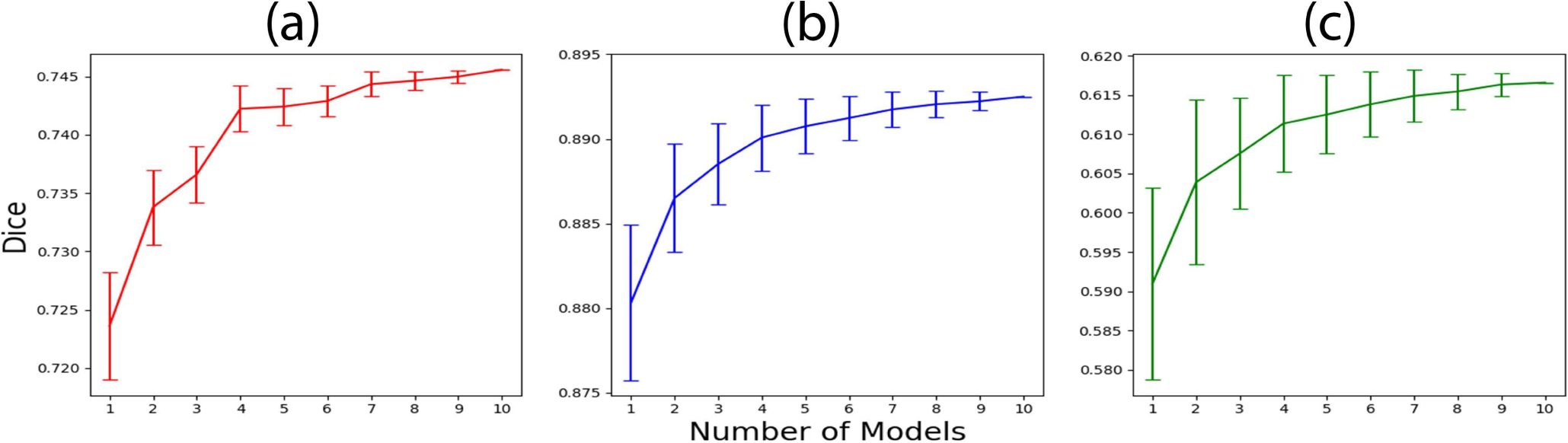
Dice coefficient values versus number of models along with error bars for (a) thyroid nodules, (b) normal thyroid, and (c) cysts.

REVIEW OF SELECTED CASES

The results of 5 different cases are reviewed to demonstrate the performance of the algorithm in the presence of different pathologies and sonographic features. Table VIII shows the estimated volume of the five review cases. The mean percentage error in volume estimation was 7.47%.

TABLE VIII.

Volume Estimation of the Five Review Cases Using the Multi-Prong Convolutional Neural Network (MPCNN) Algorithm, Compared Against Estimation by the Board Certified Radiologist

Case#		Radiologist				MPCNN			Error in volume estimation (%)
	Length (cm)	Width (cm)	Depth (cm)	Volume (cm3)	Length (cm)	Width (cm)	Depth (cm)	Volume (cm3)
1	3.80	2.65	2.05	10.81	3.70	3.25	2.06	12.95	16.52
2	3.49	2.75	2.06	10.33	3.55	2.53	2.04	9.60	7.07
3	3.98	2.66	2.33	12.90	3.86	2.44	2.43	11.99	7.05
4	5.94	3.59	4.48	50.08	5.47	3.97	4.69	53.28	6.39
5	1.99	1.60	1.88	3.14	1.95	1.63	1.88	3.13	0.32

A. CASE 1

Fig. 13(a) shows the B-mode image of a benign thyroid nodule with a characteristic smooth boundary typical for benign nodules. The manually segmented boundaries for the thyroid nodule and normal thyroid gland are shown in Fig. 13(b) using red and blue lines, respectively. The predicted boundaries are shown in Fig. 13(c). The mean Dice coefficient for the MPCNN was 0.95. The algorithm was able to capture both the normal thyroid gland and the thyroid nodules; it was not able to capture the low contrast edge of the thyroid gland on the top right side of the image. Moreover, the algorithm over-predicted the nodule region.

Fig. 13.

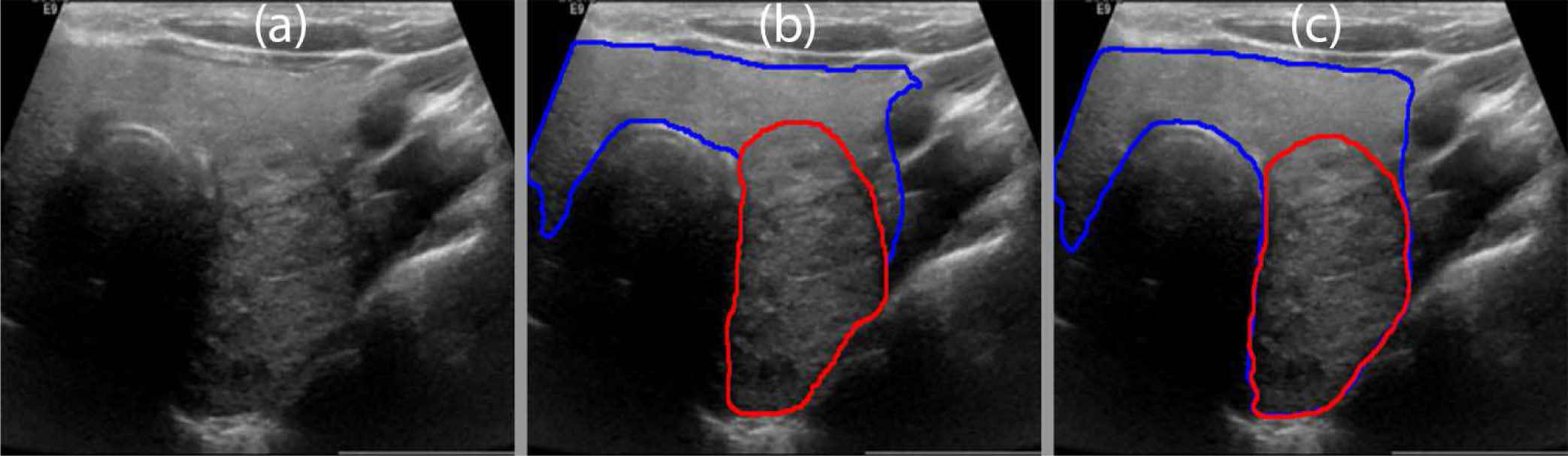
(a) B-mode image of a benign thyroid nodule. (b) Manual segmentation by a board-certified sonographer with thyroid nodule in red and normal thyroid in blue. (c) Predicted boundaries using the MPCNN algorithm.

B. CASE 2

The B-mode image of a benign thyroid nodule with degenerative changes is shown in Fig. 14(a). Almost the entire thyroid gland was covered by the nodule. The nodule had a cystic component. The manually segmented boundaries for the thyroid nodule, normal thyroid gland, and cystic component are shown in Fig. 14(b) using red, blue, and green lines, respectively. The predicted boundaries are shown in Fig. 14(c). The mean Dice coefficient for the MPCNN was 0.95. The algorithm correctly predicted both the thyroid gland and the cystic components inside the nodule while missing the top right corner of the nodule. Furthermore, the predicted thyroid nodule boundaries were not as smooth as the manually segmented boundaries.

Fig. 14.

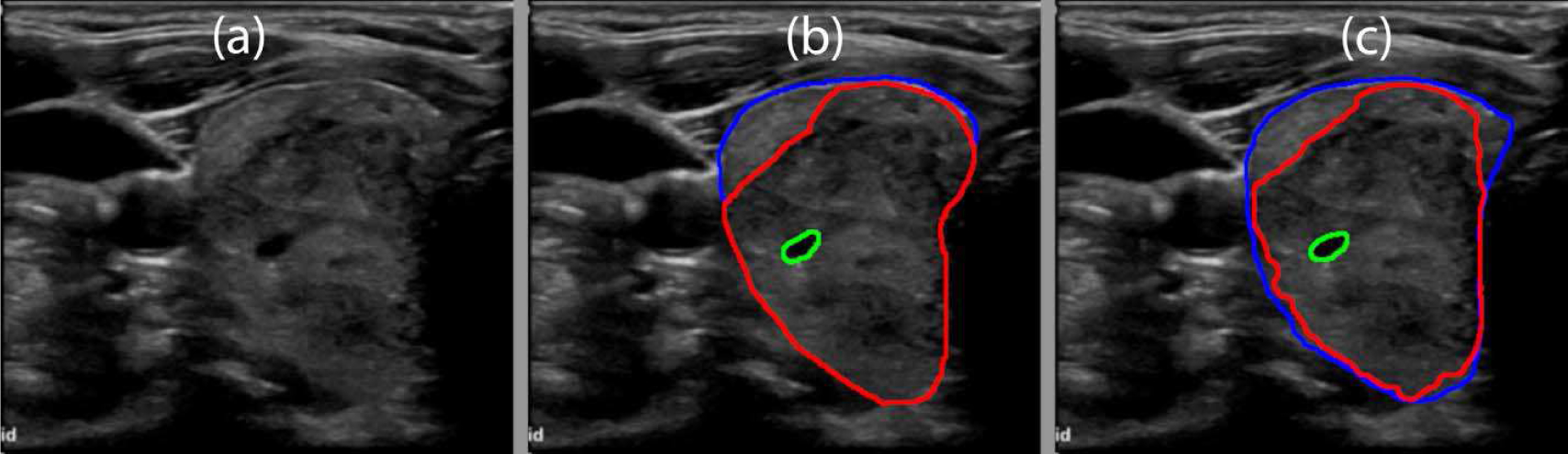
(a) B-mode image of a benign thyroid nodule with degenerative changes. (b) Manual segmentation by a board-certified sonographer with the thyroid nodule in red, normal thyroid in blue, and cyst in green. (c) Predicted boundaries using the multi-prong convolutional neural network with the thyroid nodule in red, normal thyroid in blue, and cyst in green. A mean Dice coefficient of 0.95 was achieved.

C. CASE 3

The B-mode image of a benign thyroid nodule with degenerative changes is shown in Fig. 15(a). The nodule had three cystic components. The manually segmented boundaries for the thyroid nodule, normal thyroid gland, and cystic components are shown in Fig. 15(b) using red, blue, and green lines, respectively. The predicted boundaries are shown in Fig. 15(c). The mean Dice coefficient for the MPCNN was 0.93. The algorithm was able to predict multiple cystic regions inside the thyroid nodule. The algorithm under-predicted the thyroid nodule and the nodule boundaries were not as smooth as the manual segmentation.

Fig. 15.

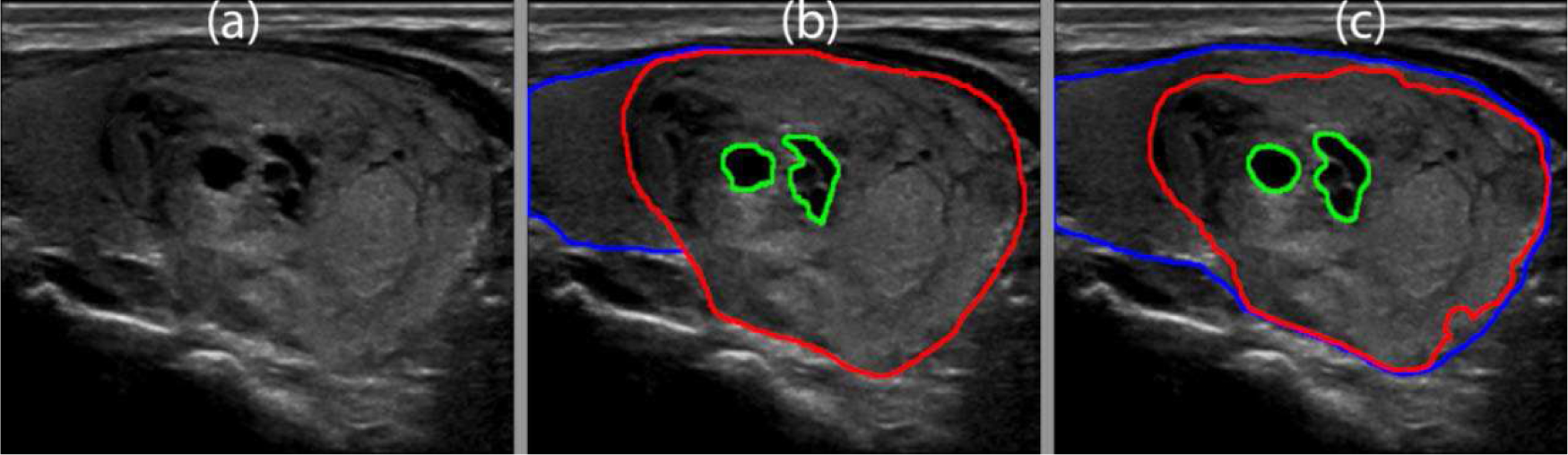
(a) B-mode image of a benign thyroid nodule with degenerative changes. (b) Manual segmentation by a board-certified sonographer with thyroid nodule in red, normal thyroid in blue, and cysts in green (c) Predicted boundaries using the multi-prong convolutional neural network with thyroid nodule in red, normal thyroid in blue, and cysts in green. A mean Dice coefficient of 0.93 was achieved.

D. CASE 4

The B-mode image of a suspicious thyroid nodule with cytological features suspicious for follicular neoplasm is shown in Fig. 16(a). Calcifications were seen inside the nodule, which covered almost the entire thyroid gland. The manually segmented boundaries for the thyroid nodule and normal thyroid gland are shown in Fig. 16(b) using red and blue lines, respectively. The predicted boundaries are shown in Fig. 16(c). The mean Dice coefficient for the MPCNN was 0.94. The algorithm predicted the thyroid gland and most of the thyroid nodule.

Fig. 16.

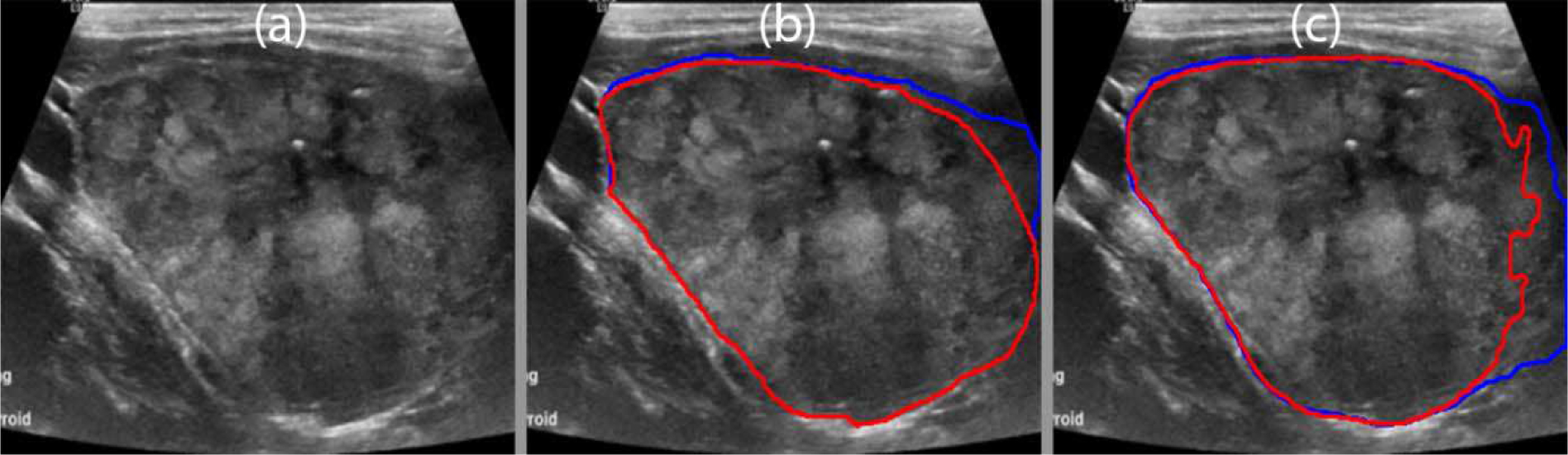
(a) B-mode image of a suspicious thyroid nodule with cytological features suspicious for a follicular neoplasm. (b) Manual segmentation by a board-certified sonographer with thyroid nodule in red and normal thyroid in blue. (c) Predicted boundaries using the multi-prong convolutional neural network with thyroid nodule in red and normal thyroid in blue. A mean Dice coefficient of 0.94 was achieved.

E. CASE 5

The B-mode image of a malignant thyroid nodule with cytological features consistent with papillary thyroid carcinoma is shown in Fig. 17(a). The nodule had multiple calcifications. The manually segmented boundaries for the thyroid nodule and normal thyroid gland are shown in Fig. 17(b) using red and blue lines, respectively. The predicted boundaries are shown in Fig. 17(c). The mean Dice coefficient for the MPCNN was 0.94. The algorithm under-predicted the thyroid nodule due to low contrast at the edges.

Fig. 17.

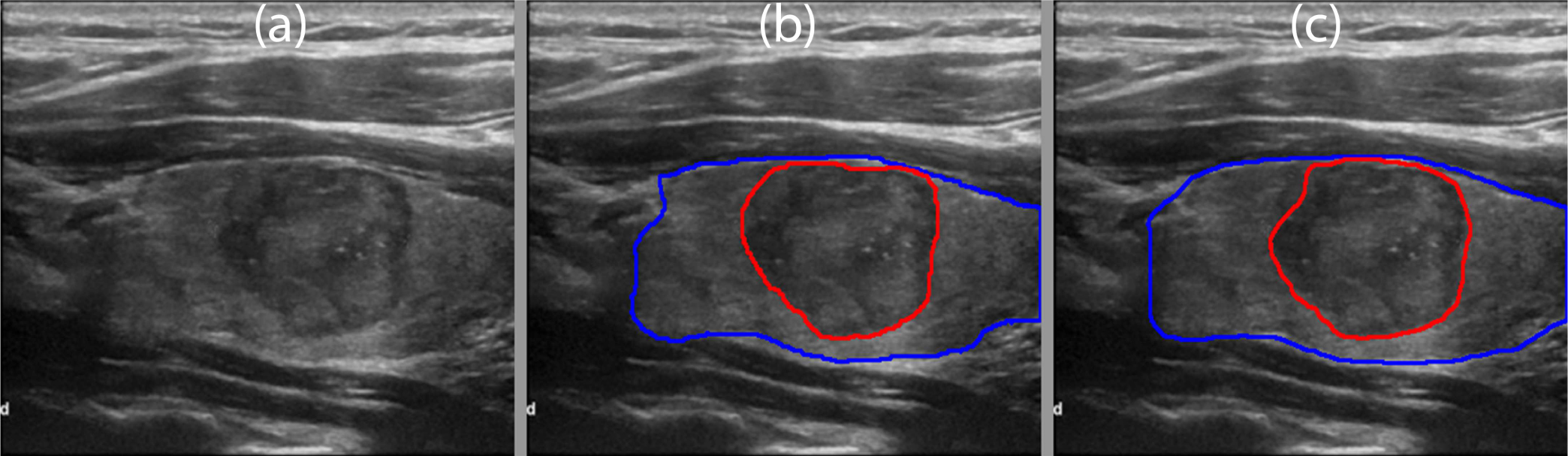
(a) B-mode image of a malignant thyroid nodule with cytological features consistent with papillary thyroid carcinoma. (b) Manual segmentation by a board-certified sonographer with thyroid nodule in red and normal thyroid in blue. (c) Predicted boundaries using the multi-prong convolutional neural network with thyroid nodule in red and normal thyroid in blue. A mean Dice coefficient of 0.94 was achieved.

IV. DISCUSSION

In this paper we presented a MPCNN algorithm which segmented the thyroid anatomy into thyroid nodule, normal thyroid gland, and cystic components. The proposed algorithm worked without user interference with a mean Dice coefficient on par with the conventional user-dependent, seed-based DRLS algorithm. The DRLS algorithm performed better in segmenting the thyroid nodule and normal thyroid gland; however, it performed poorly in segmenting cystic components. The better performance of the seeded algorithm in the thyroid nodule and normal thyroid gland was due to the choice of the seed. The seed was selected by dilating the manually segmented masks by 20 pixels. The seed selection was deliberate to highlight the capability of the MPCNN algorithm. The proposed algorithm did not require an initial seed and automatically identified the region of normal thyroid gland, thyroid nodule, and cystic components present inside the thyroid gland region. The proposed algorithm learned to differentiate between hypoechoic regions inside and outside the thyroid gland and only assigned the hypoechoic region inside the thyroid as cystic components. The complexity of the deep learning algorithm was dependent on the architecture and the data used to train the algorithm. A larger dataset with more unique and diverse cases could further improve algorithm performance. The poor performance of the DRLS algorithm for cystic components was due to the selection of DRLS parameters, which were fine-tuned for thyroid nodule and gland. The Dice coefficient of the MPCNN algorithm decreased with increasing suspicion level due to the irregular margins associated with higher suspicion cases. Similarly, the TPF decreased with increasing suspicion.

As shown in Table II, the majority of the images used for testing were in the intermediate and high suspicion categories. The MPCNN algorithm had a lower mean Dice coefficient, lower mean TPF, and higher mean FPF than the DRLS algorithm for thyroid nodule and normal thyroid gland, as shown in Tables II and III, respectively. The lower TPF and higher FPF values indicate that the MPCNN algorithm missed and overestimated the boundaries of the thyroid nodules and normal thyroid gland. Low suspicion cases showed the best Dice coefficients and TPF performance for the MPCNN algorithm. Intermediate and high suspicion cases were more challenging to segment compared to low suspicion cases due to the irregular boundaries associated with increased suspicion level. The MPCNN algorithm had a higher mean Dice coefficient and mean TPF than the DRLS algorithm for cystic components, as shown in Table IV. The performance of both algorithms in cystic components was low compared to thyroid nodule and thyroid gland. The MPCNN showed a higher FPF than DRLS, indicating over-prediction of the cystic components. The poor performance of the DRLS was due to the failure of the algorithm to stop converging at the edges.

The MPCNN algorithm had higher variance for both the Dice and TPF than the DRLS algorithm for all three thyroid regions. The difference in variance was small, indicating that the MPCNN and DRLS algorithms demonstrated equal reliability. The variance for high suspicion thyroid nodules was higher than that of low and intermediate suspicion, which could be attributed to the irregular margins associated with high suspicion cases. The variance for cystic components was high, reflecting the challenge in identifying cystic components. The DRLS performed statistically better than the MPCNN algorithm for the Dice coefficient in thyroid nodules, and for the Dice, TPF, and FPF in normal thyroid gland. However, the MPCNN algorithm performed statistically better than the DRLS for the Dice, TPF, and FPF in cystic components.

The performance of the MPCNN algorithm was slightly higher for malignant compared to benign thyroid nodules, as shown in Table V. However, higher variance was also shown in malignant nodules with irregular margins, indicating the lower reliability associated with that characteristic. Thyroid gland from benign nodules showed the highest Dice and TPF, as shown in Table VI. Large malignant thyroid nodules that covered most of the thyroid gland made it harder to distinguish normal gland from nodule. Cystic components were easier to identify in malignant nodules compared to benign, as shown in Table VII; however, the reliability was low, indicated by the high variance of the Dice and TPF values.

The mean Dice and TPF performances for the MPCNN algorithm were higher for all three structures in the longitudinal orientation compared to transverse, as shown in Table VIII. However, the FPF was also higher in the longitudinal orientation, indicating that the algorithm over-predicted in that direction. The variances of Dice and TPF were also low for the MPCNN algorithm for the three anatomies in the longitudinal orientation compared to the transverse. The better longitudinal orientation performance could be attributed to the higher contrast of the edges which arises from better contact with the neck, larger cross-sectional area of the thyroid gland, and less motion from the carotid artery compared to the transverse orientation.

The performance of the Dice coefficient for thyroid nodules, normal thyroid, and cystic components increased with an increasing number of models. Increasing the number of models removed the uncertainty associated with the algorithm converging in a local minimum by initializing the algorithm differently, but it did not improve the performance drastically. Although the improvement in mean value of the Dice was low, the decrease in variance suggests more reliable and reproducible results could be obtained with higher numbers of models. Furthermore, majority voting also contributed to the performance improvement by removing the regions which were predicted with low confidence. Increasing the number of models increased the inference time proportionally. Depending upon the application, the number of models could be traded off for faster performance. Real time applications require an inference time of a few tens of milliseconds. Using a single model, faster graphical processing unit and optimized code, the inference time of a few tens of milliseconds could be easily achieved.

The detection rate of thyroid nodules was higher than that of cystic components due to their larger size. Cystic components can be quite small, and the detection was a strict binary criterion; thus, all cystic components within the image had to be detected for a positive detection. Also, the detection criterion established for cystic components was very strict. Typically, very small cystic components would be ignored; thus, to set high standards for the algorithm, a strict criterion was used. The algorithm faces challenges in detecting small cystic components. This challenge is partly associated with the small input size, 320 by 320 pixels, of the thyroid image. If the size of the cystic component inside the nodule in pixels is comparable to the convolutional filter size, it is hard to extract that feature. Larger image input size may perform better in segmenting small cystic components. The ROC curve is displayed in Fig 18 was created by replacing the sigmoid and softmax output of the MPCNN with linear outputs. The output of each model was normalized between 0 and 1, the outputs of all models was summed and renormalized. Each pixel in the test set was treated as a binary classification problem; feature or not-feature for the thyroid, nodules and cysts. Fig 18 indicates high performance for the thyroid class and similar performance for both the nodule and cyst classes. This is likely reflects the bulk performance of the segmentation which correct segments the centers of features and struggles with the margins. This ROC curve ignores inter-class relationships in the normal MPCNN output that ultimately prioritizes one class over others; likely the model prioritizes nodule segmentation over cyst segmentation.

Fig. 18.

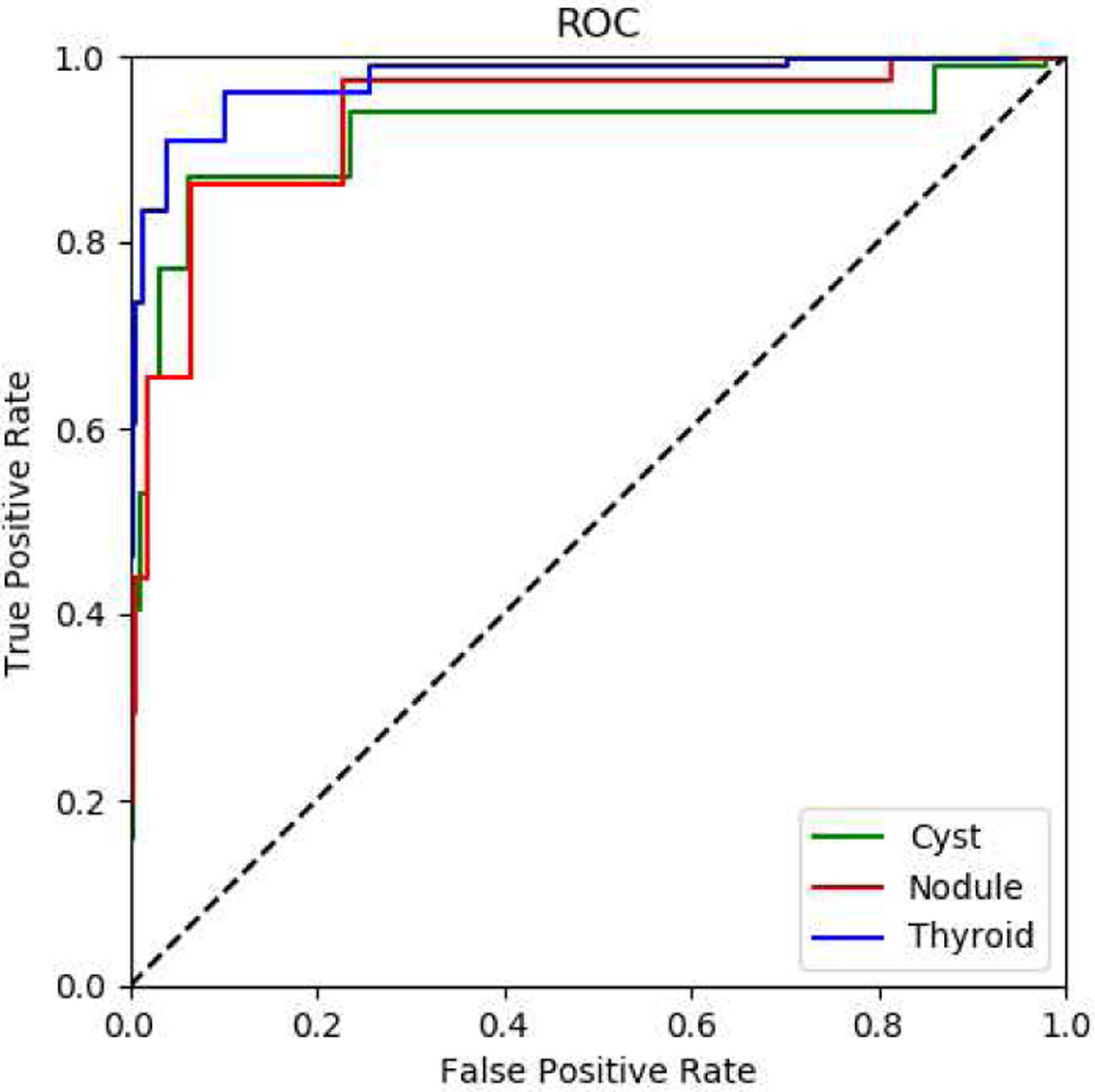
shows an ROC curve for the thyroid, nodules and cyst classes

Most of the previous work done on segmentation of the thyroid gland, nodules, and cystic components was done with semi-automated algorithms, limiting their use to post-sonographic exams. A recent paper segmented the thyroid gland using a U-net based convolutional neural network that had a Dice coefficient of 0.876 [19]. The performance of our algorithm was slightly better than their U-net based approach. Application of an original U-net based convolutional neural network [34] to our data set resulted in a low Dice value of 0.538 for the thyroid gland. We did not apply the U-net algorithm to the nodules and cysts, anticipating poor performance (results not reported). Chang et. al. used the radial basis function neural network, a patch based classification trained achieved an accuracy of 96.52, but on manually selected thyroid ROIs [8].

Freesmeyer et. al. have demonstrated that manual tracing is superior to ellipsoid model for healthy and deformed thyroid phantoms. An automatic segmentation model could provide similar improvements without additional the time commitments necessary for an expert to provide manual segmentations [35]. A recent study using three different computer segmentation approaches on 3D thyroid healthy ultrasound, selecting the features inside and outside of the thyroid and using Level Set, Graph Cut, and Pixel Classifier resulted in mean Dice Coefficients of 0.713, 0.748, and 0.601[36]. These results underperformed compared to our model and do not attempt to perform segmentations of nodules or of thyroids with nodules present which may have lowered performance.

Another study using variable Background Active Contour Model (VBAC) was able to achieve a mean IoU of 0.91 over the established ACWE which achieved an IoU of 0.848 [9]. IoU is a similar segmentation evaluation metric to Dice coefficient. Dice and IoU cannot be directly compared, however in my experience IoU is a ‘harsher’ metric and indicates that VBAC significantly outperforms our MPCNN model. They test using a smaller dataset and limit themselves only to hypoechoic cases.

The interobserver variability in estimating thyroid nodule volume is approximately 23.69% using the ellipsoid method [37]. The percentage error in volume estimation using the MPCNN algorithm was much lower than the value reported in the literature. The low percentage error in volume estimation showcases the feasibility of using the algorithm for estimating volume of thyroid nodules while decreasing the subjectivity associated with different observers.

Segmenting the thyroid anatomy into normal gland versus nodules and cystic components has various applications. In the clinic, estimating thyroid nodule size and volume is important as they are features that can be used for selecting the nodule for biopsy. After segmenting the thyroid nodule, its size and volume can be estimated. Lobulated or irregular margins, and taller-than-wider shape are also associated with increased risk in the stratification process. These features could be estimated after segmenting the thyroid nodule within the thyroid gland. Another possible application in the clinical setting could include the generation of thyroid maps, which are rough sketches showing the location of all thyroid nodules, their size and composition (i.e., solid or cystic). Furthermore, many clinics have an established protocol which includes collection of thyroid cine clips. These clips are gathered by traversing the probe from superior to inferior thyroid in transverse probe orientation. Each cine clip frame can be segmented to identify the location of thyroid nodules and cystic components; with this information, size and volume of each nodule can be estimated. Since the algorithm can predict cystic regions inside a nodule, it can also be used to classify the nodule as solid, cystic, predominantly solid, or predominantly cystic depending upon the percentage of cystic components inside the nodule. The algorithm can also be used in the continuing education of sonographers.

LIMITATIONS

During two-dimensional US scanning the sonographer had access to various planar views of the thyroid by varying the probe angle, orientation, and pre-compression. Probe angle can change the planar view, along with the deep acoustic shadowing or enhancement, allowing better visualization of anatomical parts. Pre-compression increases the contrast of nodule edges with respect to normal thyroid gland. Orientation can give a wider perspective of the nodule shape in three dimensions. During live scanning the sonographer was able to rock and angle the US probe to view the thyroid nodule from different directions, angles, orientations, and at different pre-compression levels. After the scanning the sonographer manually segmented the thyroid nodule. During manual segmentation the sonographer had access to prior information for the selection of boundaries gained from the experience of utilizing the previously mentioned probe motion techniques. On the other hand, the algorithm only had access to the single two-dimensional planar images when delineating the boundaries. Thus, the algorithm showed a fair performance compared to manual segmentation from the sonographer. For better segmentation, a three-dimensional view of the nodule from multiple angles, at different compression levels, and different orientations should be combined together. The algorithm was able to identify multiple cystic regions; however, it failed to identify very small ones. Even though the algorithm performed poorly on cystic components, it was significantly better than the conventional algorithm.

V. CONCLUSIONS

The MPCNN algorithm can segment the thyroid gland, nodules, and cystic components in real time without the need for an initial seed, and it performs on par with contemporary seeded algorithms (DRLS). The number of models in the algorithm can be traded for higher accuracy or faster performance. The algorithm can identify thyroid nodules and cystic components from normal thyroid gland; however, it fails to segment very small cystic components. The error in volume estimation for thyroid nodules was low, making the algorithm a feasible objective tool for volume estimation. The algorithm has applications in point of care, mobile health monitoring, improving workflow, reducing localization time and assisting sonographers with limited expertise.