Stock market returns, volatility, correlation and liquidity during the COVID-19 crisis: Evidence from the Markov switching approach

Highlights

• •It is the first work which focuses on three indicators of the financial market, namely volatility expectations, correlation expectations and illiquidity during the COVID-19 crisis.
• •We examine structural breaks in the stock market returns – implied volatility, stock market returns –implied correlation and stock market returns – market illiquidity relations.
• •We detect a structural break in the relationship between stock returns – correlation expectations preceding by one day the structural break in stock returns – volatility expectations.
• •Italy is recognized as the only one country transmitting fears from the data of COVID-19 cases to global fear gauges related to volatility and correlation.
• •Stock market illiquidity does not affect the stock market returns and does not depend on any COVID-19 official announcements of cases and deaths.

Abstract

This paper investigates the relationship between US stock market returns (S&P500) and three indicators of the market, namely implied volatility, implied correlation and liquidity. It also considers the short range dependence between both total confirmed cases and deaths in twelve countries and market movements. We use the two-regime Markov switching model to find the structural break between stock market returns and key stock market indicators. The findings show close dependence between returns and both implied volatility and implied correlation but not with liquidity. The findings indicate the unique role of Italy in crisis transmission.

1. Introduction

The new coronavirus appeared at the end of December 2019 in Wuhan, China and has quickly spread to all countries on the globe. On March 11, 2020 the World Health Organization (WHO) declared the coronavirus outbreak a pandemic and announced a name for the disease caused by the virus, namely COVID-19. Up to the middle of June 2020 the coronavirus infected more than 8.5 million people causing more than 450 thousand deaths. To prevent the transmission of COVID-19 in March most governments introduced a range of lockdown-type tools like restriction imposed on internal movement and international travel controls, school and university closures, non-essential shop, bar and restaurant closures, cancelling public events and the suspension of business activities of many companies. The preventive actions as well as consecutive announcements on new cases and deaths have generated huge risk on financial and commodity markets. Since the beginning of the year the S&P500 index dropped by 31.32% on March 23rd reaching its daily minimum equal to −12.77%. Other world stock indices behaved similarly. Especially stock markets in European countries absorbed the extremal risk at the same time. The coronavirus pandemic is bringing not only chaos on financial markets but also a crisis in real economies. According to April forecast of International Monetary Fund the Gross Domestic Product (GDP) for the US will shrink in 2020 by 8.2 percentage points (pp), for the European Union by 8.8 pp, China by 4.9 pp, Italy by 9.4 pp but Spain up to 10 pp.

The literature on the economic effects of COVID-19 has started to grow rapidly in the second quarter of 2020. A lot of papers in the finance area focus on the short-term impact of the coronavirus outbreak on stock market returns or volatility (Baker et al., 2020; Haroon and Rizvi, 2020; Liu et al., 2020; Morales and Andreosso-O´Callaghan, 2020; Okorie and Lin, 2020; Zaremba et al., 2020; Zhang et al., 2020). Other papers apply the new explanatory variable, e.g. the official announcements regarding new cases and deaths in order to explain the stock markets behavior. Empirical results of Akhtaruzzaman et al. (2020) show that dynamic conditional correlations (DCCs) between Chinese and G7 financial and nonfinancial stocks increased significantly during the COVID-19 period. China and Japan are recognized as transmitters of spillovers during the COVID-19 period suggesting that financial contagion follows a similar pattern to that of the virus contagion. Albulescu (2020) tests the impact of COVID-19 official announcements of cases and deaths on VIX index. His results show that new cases reported in China and outside China have a positive impact on VIX. Onali (2020) explores the impact of COVID-19 cases and related deaths on the US stock market (Dow Jones and S&P500 indices). Applying GARCH model he shows that changes in the number of cases and deaths in the US and six other countries in the first three months of 2020 did not have an impact on the US stock market returns, apart from the number of reported cases for China. However, VAR models suggest the number of reported deaths in Italy and France had a negative impact on stock market returns, and a positive impact on the VIX.

In this study we attempt to explain how the coronavirus pandemic has affected the US stock market. Unlike other studies we focus on three dimensions of a stock market, i.e. volatility, correlation and liquidity. According to modern portfolio theory the risk of a portfolio depends on two factors, i.e. volatility and correlation between portfolio constituents. The volatility is captured here by the Chicago Board Options Exchange (CBOE) volatility index (VIX) and correlation by the CBOE implied correlation index (JCJ and KCJ). The rationale for analysis of liquidity stems from the fact that investors are not concerned with liquidity itself when the financial market is stable but their perception is highly changeable when the financial market becomes more volatile and the problem of illiquidity arises (Będowska-Sójka and Echaust, 2020). As a liquidity proxy the Amihud measure is calculated (Amihud, 2002). To investigate the effect of COVID-19 on stock market returns, volatility, correlations and liquidity we use the Markov switching model that allows us to determine the structural break in the relationship between considered indicators and stock market returns. Additionally, the data on new cases and deaths reported in twelve countries (the United States, China and the European countries most affected by COVID-19 – reporting the most deaths) are included in our considerations. We concentrate mainly on the European countries, since the COVID-19 spread the fastest in Europe in the period of stock market turbulence.

This paper extends literature in threefold. Firstly, it is the first work which focuses on three indicators of the financial market, namely volatility expectations, correlation expectations and illiquidity. We found the structural break in the stock returns – implied volatility and stock returns – implied correlation relations during the COVID-19 crisis. Secondly, we study the impact of the official announcements on cases and deaths reported in different countries on market behavior. We discovered the significance of the cases variable provided from main epicenters of COVID-19 in Europe, mainly Italy. Thirdly, following Onali (2020) we use the two-regime Markov switching model to analyze the shifting trend of considered variables. The advantage of the model is that structural breaks are not explicitly imposed, but inferences are drawn on the basis of probabilistic estimates of the most likely state prevailing at each point in history (Simon, 1996). Such model allows us to specify the most important indicators in market spillover as well as the moment of distortion of financial market.

2. Data and methods

We use three indicators of the financial market in this study. The implied volatility index (VIX) is the real-time index that represents the market's expectation over the next 30-day horizon. The index is called a “fear gauge” or a “fear index” and reflects investors’ sentiment to trade. It is calculated on the basis of US S&P500 options prices. The predictive power of VIX for financial instability has been examined in many studies, e.g. (Banerjee et al., 2007; Bekaert and Hoerova, 2014; Kanas, 2013; Rubbaniy et al., 2014; Völkert, 2015). The implied correlation index (JCJ and KCJ, depending on maturity) is another important gauge for the financial market demonstrating the dependence between stocks. It is based on options written on the 50 largest companies in the S&P500 index. The index has been found to have predictive power for returns and volatility when it comes to the S&P500 index (Driessen et al., 2011; Fink and Geppert, 2017; Skintzi and Refenes, 2005). The Amihud liquidity measure (Amihud, 2002) is the most popular measure of liquidity. It belongs to cost-per-dollar-volume proxies (Fong et al., 2017) and measures stock illiquidity – the higher value of the measure, the less liquidity is delivered. In the daily version the Amihud measure is defined as:

$$A_t=\frac{\left|r_t\right|}{DVO{L}_t},$$ (1)

where r_t is a daily log-return, and DVOL_t is the daily dollar volume at time t.

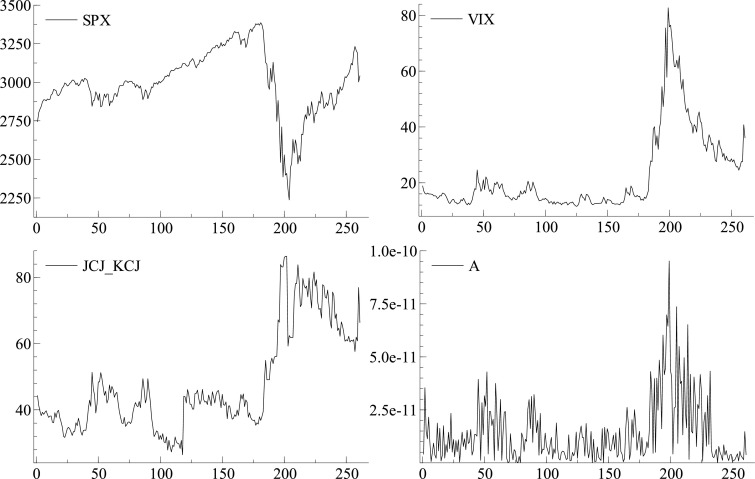
Financial data are available on the CBOE website except for the S&P500 volume, which is attainable on stooq.pl. These data cover the period from June 3, 2019 to June 12, 2020. We use the last year of data to ensure a sufficiently long-term time series to estimate models. The co-movement between the VIX, JCJ–KCJ and Amihud liquidity is clearly visible, especially in the second part of the period, when the S&P500 index dropped dramatically (Fig. 1 ). VIX and illiquidity measure behave in the same way, increasing their levels four times, but the average correlation among portfolio constituents driven by investors' rush to sell stocks all at once increased up to 80% in March 2020.

Fig. 1.

S&P500 index (SPX), implied volatility (VIX), implied correlation (JCJ_KCJ) and S&P500 illiquidity (A) in the period 03.06.2019–12.06.2020.

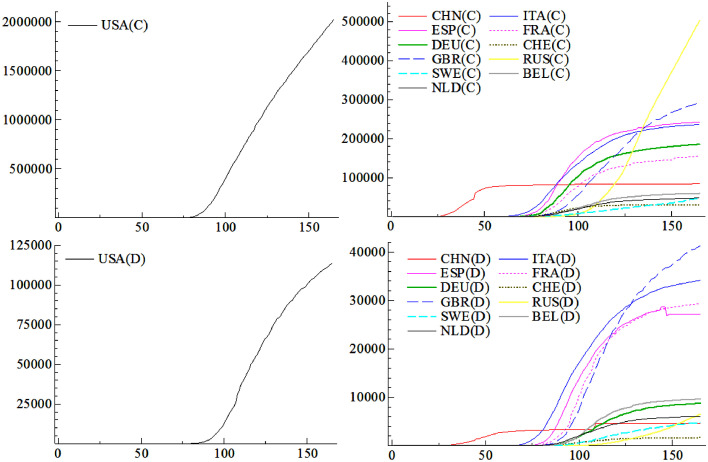
Data on COVID-19 are obtained from the World Health Organization for the period from December 31, 2019 to June 12, 2020. We can observe the dynamics of the total number of COVID-19 reported cases and deaths in selected countries and the scale of their growth in Fig. 2 .

Fig. 2.

Total number of COVID-19 confirmed cases (C) and deaths (D) in the United States, China and selected European countries in the period 31.12.2019–12.06.2020.

Since implied volatility, implied correlation and the Amihud liquidity demonstrate non-stationarity we used the first differences of log-values in the empirical study. Stationarity of the transformed data is verified with the Augmented Dickey-Fuller test (Dickey and Fuller, 1981). The Ljung-Box Q-test (Ljung and Box, 1978) indicates a significant 1-st order serial correlation in returns time-series, therefore the autoregression term is added to the basic Markov switching model (Hamilton, 1990). We consider two basic linear models:

$$r_t\left|s_t={\beta }_{0s_t}+{\beta }_{1s_t}\Delta \log \left(I_t\right)+{\epsilon }_t\right|s_t,$$ (2)

$$I_t\left|s_t={\beta }_{0s_t}+{\beta }_{1s_t}\Delta \log \left(1+C_t\right)+{\epsilon }_t\right|s_t,$$ (3)

where r_t is the log-return of the S&P500 index at time t, I_t is the market indicator (implied volatility, implied correlation or liquidity measure in Eq. (2) and all three and log-return in Eq. (3)), β_k (k = 0,  1) are model parameters, ε_t is stochastic error term ${\epsilon }_t|s_t\sim N\left(0,{\sigma }_{s_t}^2\right)$, s_t = 1 or 2 are regimes at time t, C_t represents the cumulative (since December 31, 2019) number of total cases or deaths at time t.

Our models assume that the explanatory variables switch between the two regimes depending on the Markov switching transition probabilities from state j to state i as denoted by

$$p_{ij}=P\left(s_{t+1}=i|s_t=j\right),i=1,2,j=1,2.$$ (4)

For any two-state Markov chain, the transition probabilities fulfill: p _1j + p _2j = 1 for j = 1,  2. The higher the value of p_ii is, the longer a given variable remains in regime i and the duration of a regime is equal to 1/(1 − p_ii). Parameters and residuals may be estimated using the Maximum Likelihood Estimation (MLE) method.

3. Results and discussion

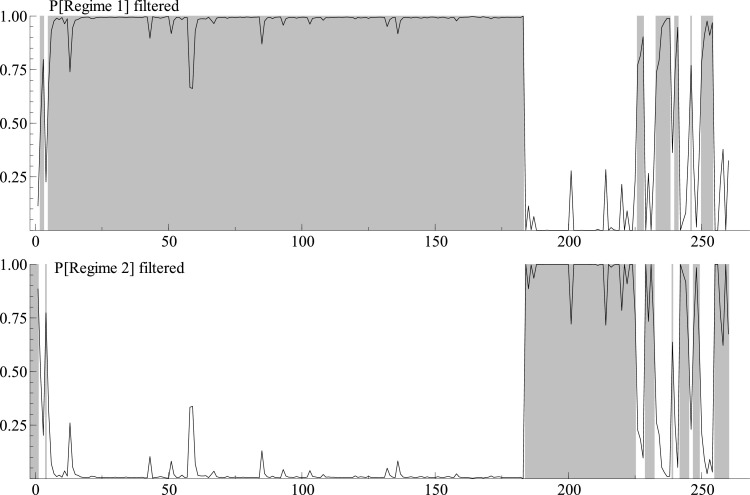
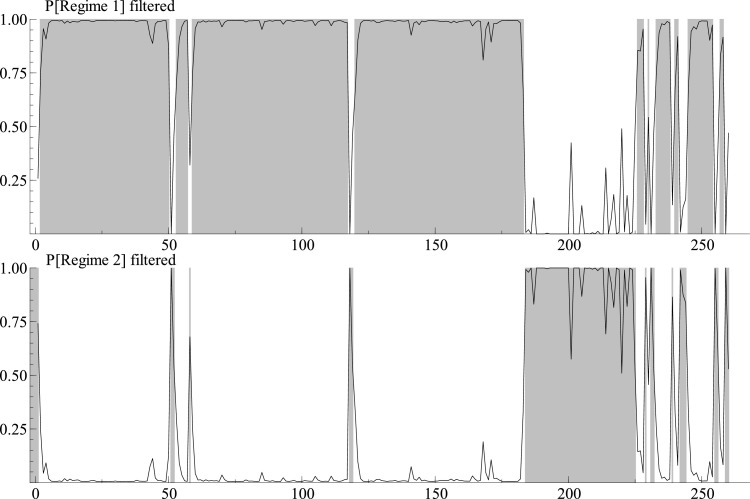
In the first part of the study we estimated the regime switching model (Eq. (2)) applying only financial data. We tried to explain the impact of implied volatility, implied correlation and illiquidity on S&P500 index returns. Before estimation of the regime switching model we regressed returns on three indicators separately. Table 1 shows the estimates of the univariate linear regression model (model 1) and the model with an additional first-order autoregressive term (model 2). The model coefficients are negative, suggesting a negative relationship between returns and all the three VIX, JCJ_KCJ and the Amihud measure. However, illiquidity is not significant at commonly accepted significance levels. We conclude then that there is no impact of illiquidity on stock market movements during the pandemic crisis. Additionally, all the estimated models exhibit autocorrelation, heteroscedasticity and non-normality in residuals. The Markov switching model overcomes these problems. Tables 2 and 3 present the regression results based on the two-regime Markov switching model. We used two different approaches here. In model 1 we allowed all parameters to switch between regimes, whereas in model 2 only the intercept and variance of residuals are switched. Table 2 gives the results for the S&P500 returns vs VIX relation, while Table 3 presents data for the S&P500 returns vs JCJ_KCJ relation. Since Amihud liquidity demonstrates no significant correlation with index returns we do not report the estimation results. The slope in both models describing the returns – VIX relationship is negative and significant for both regimes. In the high volatility regime (regime 2) the returns indicate a 3-fold higher sensitivity to changes in VIX than in the low volatility regime (regime 1). In the case of the S&P500 returns vs JCJ_KCJ relation the model without slope switching (model 2) performs better, since slope estimation indicates statistical significance in both regimes. When analyzing regime dating for VIX and JCJ_KCJ we come to the following conclusions. Omitting regime periods lasting only several days we obtain two main, high and low volatility periods (Figs. 3 ,4 ). The first switch from the low volatility state to the high volatility state took place on February 25, 2020 for VIX (indication from both models) and February 24, 2020 for JCJ_KCJ. Similar results (a switch on February 26, 2020) were obtained by Onali (2020) when analyzing a structural break in the relationship between the stock market returns and VIX. The latter date corresponds to the day when the White House sent the request to the US Congress asking for $1.25 billion in new funding to help the nation emerge from the COVID-19 crisis. Our findings suggest that the structural break in the relationship between stock returns and correlation expectations preceded by one day that in stock returns and volatility expectations. This conclusion is in line with a study of Echaust and Just (2020) and Skintzi and Refenes (2005), who concluded that while changes in the implied volatility do not affect future changes in the implied correlation, changes in the implied correlation appear to cause in the Granger sense future stock market volatility. The values for transition probabilities suggest that both states are highly persistent.

Table 1.

The linear regression model: the influence of VIX, JCJ_KCJ and the Amihud proxy on the S&P500 index returns. Model 1 shows a linear regression of S&P500 index returns (SPX) on three different independent variables, whereas Model 2 also adds the lagged returns r_ lag1 as an explanatory variable. The independent variables are: Δlog(VIX) – changes in the logarithm of daily VIX, Δlog(JCJ_KCJ) – changes in the logarithm of daily JCJ_KCJ, Δlog(A) – changes in the logarithm of the daily Amihud liquidity measure.

	Model 1			Model 2
Parameter	Estimate	Std. Error	p-value	Estimate	Std. Error	p-value
	SPX vs VIX			SPX vs VIX
Δlog(VIX)	−0.1579	0.0096	0.000	−0.1474	0.0095	0.000
r_ lag1				−0.1929	0.0431	0.000
	SPX vs JCJ_KCJ			SPX vs JCJ_KCJ
Δlog(JCJ_KCJ)	−0.0755	0.0164	0.000	−0.0722	0.0153	0.000
r_ lag1				−0.3461	0.0557	0.000
	SPX vs A			SPX vs A
Δlog(A)	0.0001	0.0008	0.921	−0.0004	0.0008	0.565
r_lag1				−0.3563	0.0583	0.000

Table 2.

The Markov switching model: the influence of VIX on the S&P500 index returns. In Model 1 all parameters switch, in Model 2 only the intercept and variance in residuals switch. The independent variable Δlog(VIX) denotes changes in the logarithm of daily VIX. Sigma is the residual standard deviation, p_ii (i = 1,  2) is the transition probability of staying in regime i.

Model 1.  SPX vs VIX
	Regime 1			Regime 2
Parameter	Estimate	Std. Error	p-value	Estimate	Std. Error	p-value
Constant	0.0010	0.0003	0.000	0.0010	0.0031	0.761
Δlog(VIX)	−0.0897	0.0036	0.000	−0.2405	0.0245	0.000
Sigma	0.0038	0.0002		0.0247	0.0024
p11	0.9717	0.0172
p22	0.9438	0.0410
Model 2. SPX vs VIX
	Regime 1			Regime 2
Parameter	Estimate	Std. Error	p-value	Estimate	Std. Error	p-value
Constant	0.0011	0.0003	0.000	−0.0009	0.0043	0.827
Δlog(VIX)	−0.0927	0.0036	0.000	−0.0927	0.0036	0.000
Sigma	0.0040	0.0002		0.0327	0.0033
p11	0.9810	0.0107
p22	0.9310	0.0455

Table 3.

The Markov switching model: the influence of JCJ_KCJ on the S&P500 index returns. In Model 1 all parameters switch, in Model 2 only the intercept and variance in residuals switch. The independent variable Δlog(JCJ_KCJ) denotes changes in the logarithm of daily JCJ_KCJ. Sigma is the residual standard deviation, p_ii (i = 1,  2) is the transition probability of staying in regime i.

Model 1. SPX vs JCJ_KCJ
	Regime 1			Regime 2
Parameter	Estimate	Std. Error	p-value	Estimate	Std. Error	p-value
Constant	0.0011	0.0004	0.006	−0.0020	0.0052	0.707
Δlog(JCJ_KCJ)	−0.0895	0.0072	0.000	−0.0603	0.0452	0.183
Sigma	0.0054	0.0003		0.0398	0.0038
p11	0.9654	0.0151
p22	0.8904	0.0517
Model 2. SPX vs JCJ_KCJ
	Regime 1			Regime 2
Parameter	Estimate	Std. Error	p-value	Estimate	Std. Error	p-value
Constant	0.0011	0.0004	0.006	−0.0013	0.0051	0.792
Δlog(JCJ_KCJ)	−0.0887	0.0071	0.000	−0.0887	0.0071	0.000
Sigma	0.0054	0.0003		0.0399	0.0039
p11	0.9654	0.0151
p22	0.8915	0.0512

Fig. 3.

Filtered regime probabilities estimated from the Markov switching Model 1: S&P500 index returns vs VIX in the period 04.06.2019–12.06.2020.

Fig. 4.

Filtered regime probabilities estimated from the Markov switching Model 1: S&P500 index returns vs JCJ_KCJ in the period 04.06.2019–12.06.2020.

The second part of the analysis is based on Eq. (3) and focuses on the impact of the total number of cases and deaths caused by COVID-19 in twelve countries on index returns, volatility, correlation and illiquidity. The model with parameters switching turned out to produce non-significant parameter estimations, then results based on the model with only variance switching are presented. Official announcements relating to new cases have no impact on index returns. However, the increase in the number of deaths in Italy, the Netherlands and Switzerland has a significant negative impact on S&P500 returns (Table 4 ). Note, that numbers of deaths in these countries are highly correlated indicating a simultaneous course of events. The results for VIX and JCJ_KCJ (Table 5, Table 6 ) highlight the impact of Italy in the systematic risk spillover to the US stock market. Only the number of new cases reported in Italy has a positive impact on both the implied volatility and implied correlation. There is also evidence that the implied correlation increases as an effect of COVID-19 deaths reported from Spain, Russia and Belgium. Finally, stock market illiquidity does not depend on any COVID-19 official announcements of cases and deaths. For the sake of brevity we do not report these results.

Table 4.

The Markov switching model: the influence of COVID-19 confirmed cases and deaths on the S&P500 index returns.

	SPX vs Cases			SPX vs Deaths
Parameter	Estimate	Std. Error	p-value	Estimate	Std. Error	p-value
Δlog(CHN)	−0.0029	0.0095	0.756	−0.0015	0.0082	0.851
Δlog(USA)	−0.0145	0.0103	0.163	0.0269	0.0292	0.359
Δlog(ITA)	−0.0166	0.0102	0.105	−0.0435	0.0202	0.034
Δlog(ESP)	−0.0108	0.0188	0.565	−0.0108	0.0192	0.576
Δlog(FRA)	−0.0312	0.0233	0.185	−0.0499	0.0281	0.079
Δlog(DEU)	0.0022	0.0093	0.815	0.0054	0.0237	0.818
Δlog(CHE)	−0.0324	0.0210	0.125	−0.0705	0.0332	0.036
Δlog(GBR)	−0.0115	0.0086	0.187	0.0147	0.0343	0.670
Δlog(RUS)	0.0033	0.0262	0.901	0.0222	0.0242	0.361
Δlog(SWE)	−0.0140	0.0280	0.616	−0.0263	0.0275	0.342
Δlog(BEL)	0.0130	0.0139	0.354	−0.0262	0.0222	0.240
Δlog(NLD)	−0.0184	0.0280	0.511	−0.0736	0.0298	0.015

Table 5.

The Markov switching model: the influence of COVID-19 confirmed cases and deaths on VIX.

	VIX vs Cases			VIX vs Deaths
Parameter	Estimate	Std. Error	p-value	Estimate	Std. Error	p-value
Δlog(CHN)	0.0980	0.0665	0.143	0.0435	0.0567	0.444
Δlog(USA)	−0.0227	0.0735	0.758	−0.1233	0.0648	0.060
Δlog(ITA)	0.1232	0.0466	0.009	−0.0571	0.1235	0.645
Δlog(ESP)	−0.0478	0.0810	0.556	−0.0667	0.0652	0.309
Δlog(FRA)	−0.0313	0.1075	0.772	−0.0857	0.0761	0.263
Δlog(DEU)	−0.1385	0.0901	0.127	−0.0965	0.0442	0.031
Δlog(CHE)	−0.0384	0.0924	0.679	−0.0223	0.0781	0.776
Δlog(GBR)	0.0726	0.0499	0.149	−0.1384	0.0626	0.029
Δlog(RUS)	−0.1378	0.0593	0.022	−0.0258	0.0468	0.582
Δlog(SWE)	−0.0911	0.1259	0.471	−0.0510	0.0630	0.420
Δlog(BEL)	−0.1441	0.0669	0.033	−0.0752	0.0494	0.131
Δlog(NLD)	−0.1296	0.1012	0.203	−0.0797	0.0706	0.262

Table 6.

The Markov switching model: the influence of COVID-19 confirmed cases and deaths on JCJ_KCJ.

	JCJ_KCJ vs Cases			JCJ_KCJ vs Deaths
Parameter	Estimate	Std. Error	p-value	Estimate	Std. Error	p-value
Δlog(CHN)	0.0681	0.0568	0.233	0.0239	0.0358	0.506
Δlog(USA)	0.0489	0.0342	0.155	0.0329	0.0360	0.362
Δlog(ITA)	0.0602	0.0289	0.039	0.0661	0.0336	0.052
Δlog(ESP)	0.0177	0.0395	0.655	0.0636	0.0264	0.017
Δlog(FRA)	0.0272	0.0369	0.463	0.0095	0.0379	0.803
Δlog(DEU)	0.0037	0.0283	0.897	0.0873	0.0457	0.059
Δlog(CHE)	−0.0004	0.0284	0.988	0.0036	0.0450	0.936
Δlog(GBR)	0.0385	0.0286	0.181	−0.0070	0.0381	0.854
Δlog(RUS)	0.0251	0.0479	0.601	0.0986	0.0409	0.018
Δlog(SWE)	0.0035	0.0323	0.914	0.0222	0.0391	0.572
Δlog(BEL)	0.0199	0.0301	0.509	0.1006	0.0417	0.018
Δlog(NLD)	0.0332	0.0350	0.345	0.0083	0.0376	0.825

4. Conclusions

This study attempts to examine firstly the influence of three key stock market indicators (implied volatility, implied correlation and liquidity) on the huge decline in the S&P500 index during the COVID-19 pandemic and secondly, the influence of COVID-19 cases and related deaths on the stock market returns and these three indicators. We found that the distortion of the expected correlation – returns relation appeared one day before the structural break in the expected volatility – returns relation. This finding may be useful for portfolio managers in predicting the market risk. However, illiquidity does not affect the stock market returns. Italy is recognized as the only one country transmitting fears from the COVID-19 cases to global fear gauges related to volatility and correlation. The reason is that Italy was the first and the hardest hit country in Europe. Moreover, the WHO has officially declared the outbreak of COVID-19 a pandemic after the spread of coronavirus disease in Italy. In contrary to previous studies we show no evidence that any COVID-19 variable reported from China could affect the US stock market. Probably too short time-series used in these studies could give misleading results. Moreover, the numbers of cases and deaths reported in China are negatively correlated with these reported in other countries. Future studies based on longer time-series will allow us to verify robustness of our findings.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.