A systematic review of the literature demonstrates some errors in the use of decision curve analysis but generally correct interpretation of findings

Abstract

Background:

Decision curve analysis is a widely used methodology in clinical research studies

Purpose:

We performed a literature review to identify common errors in the application of decision curve analysis (DCA) and provide practical suggestions for appropriate use of DCA.

Data Sources:

We first conducted an informal literature review and identified six errors found in some DCA. We then used Google Scholar to conduct a systematic review of studies applying DCA to evaluate a predictive model, marker or test.

Data Extraction:

We used a standard data collection form, to collect data for each reviewed article.

Data Synthesis:

Each article was assessed according to the 6 pre-defined criteria for a proper analysis, reporting and interpretation of DCA.

Data Synthesis:

Overall, 50 articles were included in the review: 54% did not select an appropriate range of probability thresholds for the x-axis of the DCA, with a similar proportion (50%) failing to present smoothed curves. Among studies with internal validation of a predictive model and correction for overfit, 61% did not clearly report whether the DCA had also been corrected. However, almost all papers correctly interpreted the DCA, used a correct outcome (92% for both) and clearly reported the clinical decision at issue (81%).

Limitations:

A comprehensive assessment of all DCAs was not performed. However, such a strategy would not influence the main findings.

Conclusions:

Despite some common errors in the application of DCA, our finding that almost all papers correctly interpreted the DCA results demonstrates that it is a clear and intuitive method to assess clinical utility.

Introduction

A common task in medical research is to assess the value of a diagnostic test, molecular marker or prediction model. The statistical methods typically used to do so include metrics such as sensitivity, specificity and area-under-the-curve (AUC)¹. However, it is difficult to translate these metrics into clinical practice: for instance, it is not at all clear how high AUC needs to be in order to justify use of a prediction model or whether, when comparing two diagnostic tests, a given increase in sensitivity is worth a given decrease in specificity^{2, 3}. It has been generally argued that because traditional statistical metrics do not incorporate clinical consequences – for instance, the AUC weights sensitivity and specificity as equally important – they cannot be used to guide clinical decisions.

Decision curve analysis (DCA) was developed to assess the clinical usefulness of a diagnostic test, marker or predictive model^4–6. In brief, DCA is a plot of net benefit against threshold probability. Net benefit is a weighted sum of true and false positives, the weighting accounting for differential consequences of each. For instance, it is much more valuable to find a cancer (true positive) than it is harmful conduct an unnecessary biopsy (false negative) and so it is appropriate to give a higher weight to true positives than false positives. Threshold probability is the minimum risk at which a patient or doctor would accept a treatment and is considered across a range to reflect variation in preferences. In the case of a cancer biopsy, for example, we might imagine that a patient would refuse a biopsy for a cancer risk of 1%, accept a biopsy for a risk of 99%, but somewhere in between, such as a 10% risk, be unsure one way or the other. The threshold probability is used both to determine positive (risk from the model under evaluation of 10% of more) versus negative (risk less than 10%) and as the weighting factor in net benefit. Net benefit for a model, test, or marker is compared to two default strategies of “treat all” (assuming all patients are positive) and “treat none” (assume all patients are negative).

Since being introduced to the methodologic literature more than a decade ago⁶, DCA has grown to become a widely used technique. As of April 2018, the original paper has been cited 833 times on Google Scholar (170 citations in 2017 alone), with empirical applications across medicine. DCA has been recommended by editorials in many top journals, including JAMA, BMJ, Annals of Internal Medicine, Journal of Clinical Oncology and PLoS Medicine ^7−117−11(7–11)[7–11]

Here, we report a literature review of empirical applications of DCA methodology in which we identify the nature and prevalence of common errors in application and interpretation. Our aim was to provide researchers with practical suggestions for a proper use of this methodology.

Methods

Informal review to identify common errors

We reviewed a selection of papers using DCA methodology that were published before January 2017. Our aim was to identify what we considered to be errors in the application or interpretation of DCA, the prevalence of which could then be evaluated in a systematic review. We first noted that investigators did not always clearly report the decision of interest: a model predicting disease recurrence after surgery, for instance, may be used to decide either for adjuvant treatments or intensive post-operative follow-up for those at higher risk. Second, although net benefit should be assessed over a reasonable range of threshold probabilities, several papers reported net benefit for all threshold probabilities from 0 to 1. This is problematic because no reasonable patient or doctor would demand say, a 90% risk of a cardiovascular event before they would accept prophylactic therapy or a 70% risk of cancer before proceeding to biopsy. That said, there are some cases where it is reasonable to give a very wide range of threshold probabilities. In the case of a model predicting survival for advanced cancer, for instance, patients may use the model for a wide range of personal decisions (such as travel plans, legal affairs, retirement) necessitating a wide range of threshold probabilities. However, models associated with a specific medical decision should use a restricted range of threshold probabilities related to that medical decision. A third, related problem is that some authors drew conclusions contradicted by the DCA results, typically, that their model was of value even though it had the highest net benefit over a small (and perhaps irrelevant) range of threshold probabilities. Fourth, DCA was often used when a model was built and validated on the same cohort, but it was sometimes unclear whether a method such as cross-validation had been used to correct for the consequent optimistic estimation of net benefit¹². The fifth problem we identified is largely semantic but can nonetheless make DCA interpretation difficult or confusing: the intervention resulting from a test positive must be coherent with the investigated outcome. To give a practical example, take the case of a model to predict postoperative mortality, used to determine whether patients should be treated surgically (those at low risk of death) or managed conservatively (those at high risk of death). By convention, in DCA, the model gives risk of the poor outcome, the intervention would be conservative management, and “treat all” would mean “conservative management irrespective of risk, no surgery”; simply labelling the figure as “treat all” may be confusing. Finally, although net benefit should, except in some unusual cases, monotonically decrease toward zero with increasing threshold, decision curves can show artifacts, especially where events are sparse at the tails of the probability distribution. Statistical smoothing techniques can be used to avoid such artifacts.

Literature search and study eligibility

Our aim was to identify and evaluate a representative selection of recent DCAs. We have no reason to believe that a comprehensive assessment of all DCAs would influence our main findings. For instance, if we identify that 10% of DCA papers have a particular limitation, it does not affect our conclusion that the problem is present but rare if the true rate is 5% or 20%; similarly, a prevalence of 40% vs. 60% would not affect a conclusion that a problem is common.

We searched Google Scholar in December 2017 to identify studies citing the initial methodological paper describing DCA⁶. To be eligible, cited papers had to be an English-language report including a DCA graph derived from an empirical data set. Papers were reviewed in reverse chronological order until 50 eligible studies were included. Studies not eligible for review were categorized as: non-English language; paper discussing statistical methodology (e.g. comparing different approaches to model evaluation); studies citing the DCA methodology in the text but not providing a DCA graph or analysis (e.g. stating that a future external validation should involve DCA); other reasons (conference abstract; letter to the editor). Note that this search will preferentially find DCAs based on expected utility theory, rather than regret theory, although the latter are rare in empirical practice.

Data extraction

We used a standard data collection form, to collect data for each reviewed article. Studies were categorized according to design (internal validation of a new model vs. external validation of a prespecified model), field of medicine (cancer, cardiovascular disease or other) and outcome (disease detection, disease recurrence, functional recovery after treatment, survival).

Each study was then assessed by each of the six criteria identified during the first literature review: the decision to be influenced by the model, test or marker should be explicitly described if not obvious from the context of the study; appropriate range of threshold probabilities investigated; correct interpretation of the decision curve; the intervention and outcome should be coherent; correction for overfit; curves should be smoothed if there are artifacts. We did not evaluate other aspects of good modeling practice, such as those described in the TRIPOD statement¹³ as our aim was related specifically to the DCA methodology. Full details of each criterion are given in the appendix.

Review methods

Eligibility, data extraction methods and the identification of the criteria for a proper application of DCA were formalized in a protocol that was piloted on 10 articles that were not included in the main analyses. In the pilot study each article was independently assessed by each researcher and the results were discussed to reach consistency in the methodology of the study assessment. Subsequently, all articles included in the main study were evaluated by 1 researcher (P.C.) with random check by a second (A.V.). None of these checks led to changes in the assessment of a paper.

Results

Overall, 92 articles were analyzed to reach the pre-defined number of 50 studies to be included (Fig. 1). The most common reasons for exclusion were that the article was either a review of statistical methodologies, or a narrative review on predictive tools concerning a specific disease (N=26).

Figure 1:

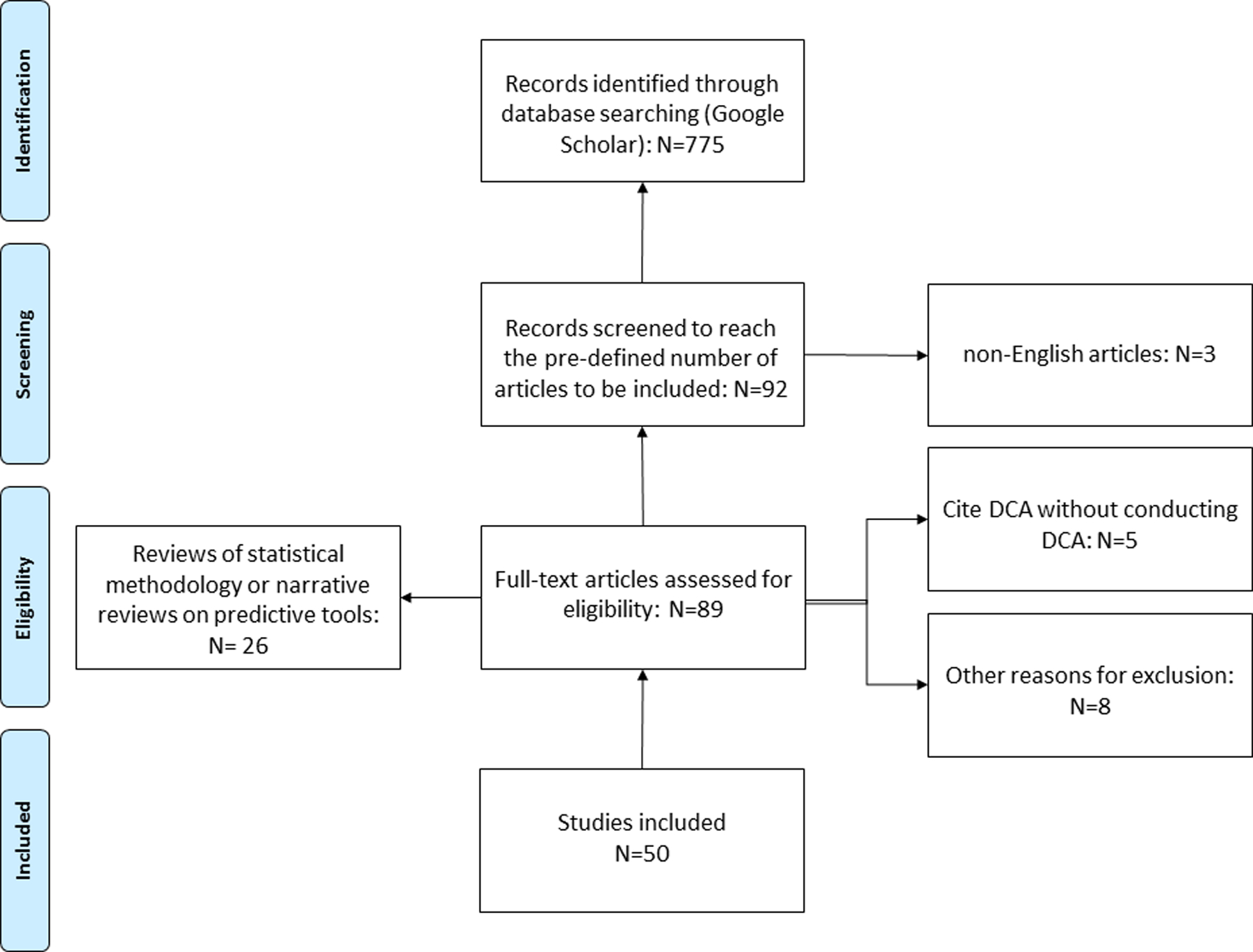
Flow charts showing inclusion and exclusion criteria of articles for the review. Articles were selected in reverse chronological order.

Table 1 reports the overall characteristics of the included articles. The majority of the studies were conducted in the field of cancer research (62%). The most common investigated outcome was disease detection (60%), followed by survival (30%). A new model, test or marker was tested with internal validation in 72% of cases. Reference details for each paper and scoring on each criterion are given in the supplementary appendix.

Table 1 –

Characteristics of the assessed studies (N=50)

Study design
External validation of a previously developed model	14 (28%)
New model with internal validation	36 (72%)
Study outcome
Disease detection	30 (60%)
Survival	15 (30%)
Functional recovery	1 (2.0%)
Disease recurrence	4 (8.0%)
Field of investigation
Cancer	31 (62%)
Cardiovascular diseases	6 (12%)
Other	13 (26%)

Table 2 reports the results for each methodologic criterion. A reasonable range of threshold probabilities was not used by about half of studies (54%); similarly, half of studies included unsmoothed curves with obvious artifacts (50%). On the other hand, almost all papers correctly interpreted the DCA and used a correct outcome (92% for both). Moreover, most papers (81%) clearly reported the decision that was to be informed by the marker, model or test. Among studies with internal validation of a new developed predictive tool, 78% corrected the results for overfit, mainly by bootstrapping (36%) or by splitting the dataset into a “training” vs. “validation” set (50%). However, only for 39% of these studies, was it clear whether the correction for overfit was applied for the calculation of net benefit in DCA.

Table 2 –

Assessment of the application and interpretation of decision curve analysis within the investigated studies (N=50)

Correction for overfit (N=36)*
No	8 (22%)
Yes	28 (78%)
Method of correction (N=28)
Bootstrap	10 (36%)
Cross-validation	4 (14%)
Training and validation sets	14 (50%)
DCA corrected for overfit (N=28)
No	17 (61%)
Yes	11 (39%)
Reporting smoothed curves
No	25 (50%)
Yes	25 (50%)
Appropriate range of threshold probabilities
No	27 (54%)
Yes	23 (46%)
Correct interpretation of the DCA
No	4 (8%)
Yes	46 (92%)
“Decision” clearly described (N=47)**
No	9 (19%)
Yes	38 (81%)
Outcome coherent with the intervention proposed (N=38)***
No	3 (8%)
Yes	35 (92%)

Keys: DCA= Decision Curve Analysis

^*Studies with internal validation

^**Excluding studies of models used for prognostic counseling

^***Studies clearly reporting the intervention associated with a positive test

Discussion

We systematically reviewed a sample of clinical research studies to evaluate the application and interpretation of DCA. Clinical studies are frequently designed for the development and validation of a predictive model using the same cohort of patients, indeed, this was the case for more than 70% of papers included in this review. This type of study is at risk for overfit¹², which can result in an optimistic evaluation of a model’s performance. In such cases, we suggest that investigators apply an appropriate method to correct their results for overfit, such as bootstrap resampling, cross-validation, or the use of training and validation sets^{14, 15}; furthermore, they should clearly report whether this method was also specifically applied to correct the net benefit provided by DCA⁴. Indeed, we have found that among studies correcting a model for overfit, more than 60% were unclear regarding the correction of net benefit DCA, thus raising the possibility that clinical utility was overestimated.

The DCA provides the estimate of the net benefit of a model, marker or test over a selected range of reasonable threshold probabilities. This range should consider how physicians or patients might reasonably vary in how they weight the harms and benefits associated with a treatment⁵. We observed that the interval of threshold probabilities was improperly selected (or not selected at all) in more than half of the cases, with authors frequently reporting net benefit across the whole range of probabilities from 0 to 1. This makes little sense for prediction models informing decisions such as whether to biopsy a patient for cancer: if a physician or patient demanded, say, a 70% risk of cancer before accepting biopsy, we would consider this irrational, and attempt to educate them on the relative risks and benefits of biopsy and cancer detection; we would take a similar approach if a patient or physician was considering biopsy for a 0.1% risk. DCA involves selection of a range of threshold probabilities that reflect reasonable variation in preferences or beliefs with respect to the medical decision at issue. Investigators should restrict the range of threshold probabilities shown on the x-axis so that this does not include threshold probabilities that are unreasonable or rarely found in practice.

More than half of the investigated studies presented a DCA graph in which at least one net benefit curve included an artifact. Except in the case where there are no false positives, net benefit monotonically decreases toward zero with increasing threshold probability. However, especially where events are sparse, empirical estimates of net benefit may be locally stable, or increase. We encourage the authors to create smoothed decision curves to avoid artifacts. This can be achieved either by using statistical smoothing algorithms, which is incorporated in most DCA software, or calculating net benefit at more widely spaced intervals of the x-axis.

Results of the DCA were correctly interpreted by investigators in more than 90% of cases. This finding confirms that DCA provides a clear and intuitive evidence of the clinical usefulness of a model, marker or test. This is not the case for other metrics. For instance, it is not clear what value of AUC is sufficient to justify use of a model, or what balance between sensitivity and specificity is acceptable or optimal for a diagnostic test^{2, 3}. Conversely, identifying the model with the highest clinical benefit for a selected range of threshold probabilities can be easily accomplished with DCA.

The interpretation of DCA can be confusing when the intervention informed by the model is not coherent with the investigated outcome. For example, take the case of a model to detect poor outcome of surgery, where patients at high risk would be managed conservatively. Incautious use of the phrase “treat all” may be misleading. The “treatment” for patients at high risk is no surgery. Hence authors should relabel the default strategies as “conservative management for all” and “surgery for all”. Inconsistency between the modelled outcome and the decision was rare – fewer than 10% of the reviewed studies – nonetheless, we recommend that investigators carefully think about the intervention resulting from the application of a model or test and how this is related to the predicted outcome.

By its very nature, DCA encourages investigators to consider the decisions that would be affected by the predictive model, marker or test. This is reflected by the high proportion of papers clearly reporting the decision of interest. However, the intervention to be pursued or avoided according to the predictive model or test was unclear in about 20% of cases. Unless it is obvious given the clinical context (e.g. risk of cancer in patients eligible for prostate biopsy), we encourage the authors to specify clearly in the methods section the clinical decision at issue, including a description of the clinical actions for patients at high vs. low risk. Note that some decision curves can include more than one decision (e.g. more intensive monitoring for patients at intermediate risk, drug therapy for patients at high risk), and in these cases, investigators would need to be explicit about the different interventions and threshold probabilities for multiple decisions.

Conclusions

Decision curve analysis is a commonly used methodology to evaluate prediction models, markers and diagnostic tests. We identified and reported the prevalence of six errors of analysis, reporting or interpretation. Clinical researchers should be aware of these pitfalls when using decision curve analysis. However, despite some common errors in application, our finding that almost all papers correctly interpreted the DCA results demonstrates that it is a clear and intuitive method to assess clinical utility.